19  统计计算

$$$$

每一个统计模型的背后都有一个优化问题，统计计算的任务就是求解优化问题。

19.1 回归问题与优化问题

1996 年出现 Lasso （Least Absolute Selection and Shrinkage Operator，简称 Lasso）(Tibshirani 1996)，由于缺少高效的求解算法，Lasso 在高维小样本特征选择研究中没有广泛流行，最小角回归（Least Angle Regression，简称 LAR）算法 (Efron 等 2004) 的出现有力促进了 Lasso 在高维小样本数据中的应用。为了解决 Lasso 的有偏估计问题，自适应 Lasso、松弛 Lasso， SCAD （Smoothly Clipped Absolute Deviation，简称 SCAD）(Kim, Choi, 和 Oh 2008)，MCP (Minimax Concave Penalty，简称 MCP)(Zhang 2010) 陆续出现。经典的普通最小二乘、广义最小二乘、岭回归、逐步回归、Lasso 回归、最优子集回归都可转化为优化问题。具体地，一个带 L1 正则项的线性回归模型，其对应的优化问题如下：

$$\arg \underset{\mathit{\beta },\lambda }{min}\frac{1}{2}||\mathit{y}-X\mathit{\beta }|{|}_2^2+\lambda ||\mathit{\beta }|{|}_1$$

其中，$X\in {\mathbb{R}}^{n\times k}$， $\mathit{y}\in {\mathbb{R}}^n$，$\mathit{\beta }\in {\mathbb{R}}^k$， $0<\lambda \in \mathbb{R}$ 。下面以逻辑回归模型为例，介绍 R 语言中求解此类优化问题的方法。

19.2 对数似然与损失函数

19.2.1 Logistic 分布

在介绍逻辑回归之前，先了解一下 Logistic 分布。一个均值为 $m$ ，方差为 $\frac{{\pi }^2}{3}{s}^2$ 的 Logistic 分布函数的形式为

$$F(x)=\frac{1}{1+\exp (-\frac{x-m}{s})}$$

密度函数的形式为

$$f(x)=\frac{\exp (-\frac{x-m}{s})}{s(1+\exp (-\frac{x-m}{s}){)}^2}=\frac{\exp (\frac{x-m}{s})}{s(1+\exp (\frac{x-m}{s}){)}^2}$$

密度函数与分布函数的关系如下：

$$\frac{dF(x)}{dx}=f(x)=sF(x)(1-F(x))$$

也就是说 Logistic 分布是上述微分方程的解。

(a) 概率密度函数

(b) 概率分布函数

图 19.1: 逻辑斯谛分布

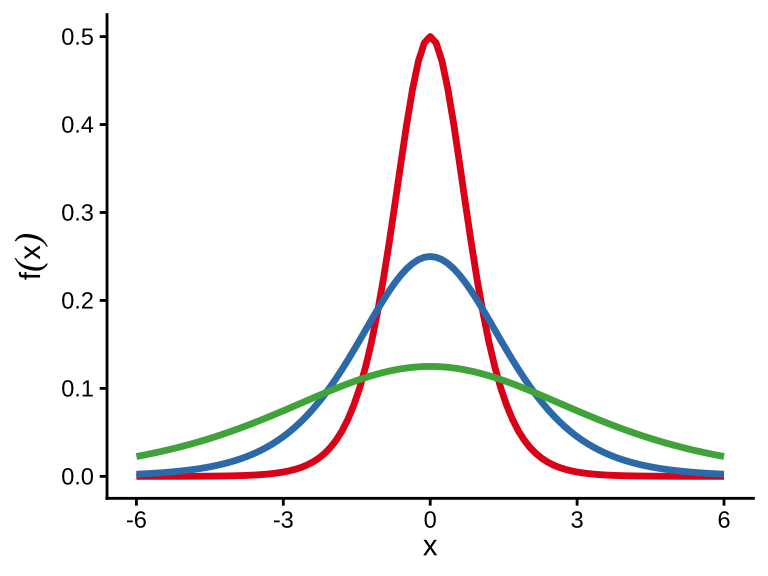
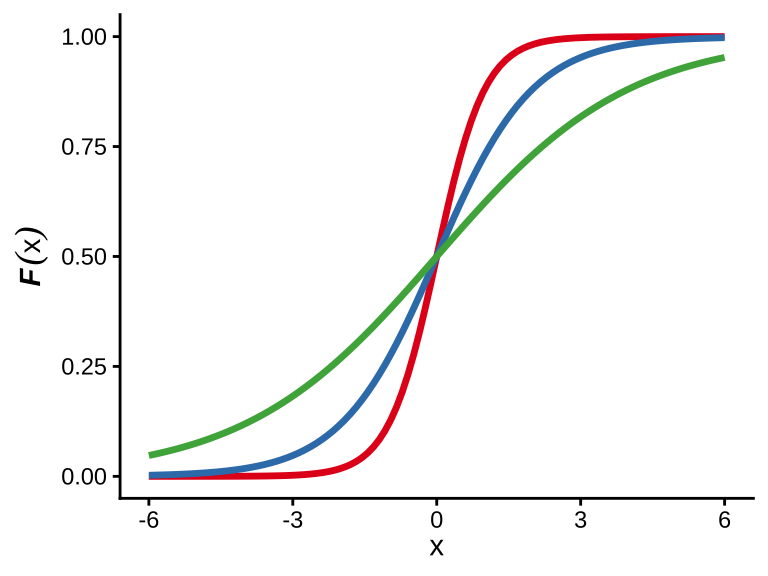
R 语言中分别表示逻辑斯谛分布的密度函数、分布函数、分位函数和随机数生成函数如下：

dlogis(x, location = 0, scale = 1, log = FALSE)
plogis(q, location = 0, scale = 1, lower.tail = TRUE, log.p = FALSE)
qlogis(p, location = 0, scale = 1, lower.tail = TRUE, log.p = FALSE)
rlogis(n, location = 0, scale = 1)

如果函数参数 location 或 scale 没有指定，则分别取默认值 0 和 1，就是标准的逻辑斯谛分布。位置参数（类似正态分布中的均值 $\mu$）为 location = m ，尺度参数（类似正态分布中的标准差 $\sigma$）为 scale = s，逻辑斯谛分布是一个长尾分布。

19.2.2 逻辑回归

响应变量 $Y$ 服从伯努利分布 $\mathrm{Bernoulli}(p)$，取值是 0 或 1，对线性预测 $X\mathit{\beta }$ 做 Logistic 变换

$$\mathit{p}=\mathsf{E}Y=\mathrm{Logistic}(X\mathit{\beta })=\frac{1}{1+e^{-(\alpha +X\mathit{\beta })}}=\frac{e^{\alpha +X\mathit{\beta }}}{1+e^{\alpha +X\mathit{\beta }}}$$

Logistic 的逆变换

$${\mathrm{Logistic}}^{-1}(\mathit{p})=\ln (\frac{\mathit{p}}{1-\mathit{p}})=\alpha +X\mathit{\beta }$$

记数据矩阵 $X$ 为

$$X=\left[\begin{array}{ccccc}{x}_{11}& x_{12}& x_{13}& \dots & x_{1k}\\ x_{21}& x_{22}& x_{23}& \dots & x_{2k}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ x_{n1}& x_{n2}& x_{n3}& \dots & x_{nk}\end{array}\right]=\left[\begin{array}{c}{\mathit{x}}_1^{\mathrm{\top }}\\ {\mathit{x}}_2^{\mathrm{\top }}\\ ⋮\\ {\mathit{x}}_n^{\mathrm{\top }}\end{array}\right]$$

每一行表示一次观测，每一列表示一个变量的 $n$ 次观测，记 $X=(X_1,X_2,\cdots ,X_k)$ 是一个 $n\times k$ 数据矩阵，其中 ${\mathit{x}}_i^{\mathrm{\top }}$ 表示矩阵 $X$ 的第 $i$ 行，一共有 $n$ 行，可以看作是 $1\times k$ 的矩阵，$X_j,j=1,2,\cdots ,k$ 表示矩阵 $X$ 的第 $j$ 列，一共有 $k$ 列。类似地， $\mathit{\beta }=({\beta }_1,{\beta }_2,\cdots ,{\beta }_k{)}^{\mathrm{\top }}$ 是一个列向量，可以看作是 $k\times 1$ 的矩阵，${\beta }_j$ 表示第 $j$ 个变量 $X_j$ 的系数。对第 $i$ 次观测

$${\mathrm{Logistic}}^{-1}(p_i)=\ln (\frac{p_i}{1-p_i})=\alpha +{\mathit{x}}_i^{\mathrm{\top }}\mathit{\beta }$$

关于参数 $\alpha ,\mathit{\beta }$ 的似然函数如下：

$$\begin{array}{}\text{(19.1)}& \begin{array}{rl}\mathcal{L}(\alpha ,\mathit{\beta })& =\prod _{i=1}^n{p}_i^{y_i}(1-p_i{)}^{1-y_i}\\ & =\prod _{i=1}^n(\frac{e^{\alpha +{\mathit{x}}_i^{\mathrm{\top }}\mathit{\beta }}}{1+e^{\alpha +{\mathit{x}}_i^{\mathrm{\top }}\mathit{\beta }}}{)}^{y_i}(\frac{1}{e^{\alpha +{\mathit{x}}_i^{\mathrm{\top }}\mathit{\beta }}}{)}^{1-y_i}\end{array}\end{array}$$

关于参数 $\alpha ,\mathit{\beta }$ 的对数似然函数如下：

$$\begin{array}{}\text{(19.2)}& \begin{array}{rl}\ell (\alpha ,\mathit{\beta })& =\log \mathcal{L}(\alpha ,\mathit{\beta })\\ & =\sum _{i=1}^n[y_i\log (p_i)+(1-y_i)\log (1-p_i)]\\ & =\sum _{i=1}^n[y_i\log (\frac{e^{\alpha +{\mathit{x}}_i\mathit{\beta }}}{1+e^{\alpha +{\mathit{x}}_i\mathit{\beta }}})+(1-y_i)\log (\frac{1}{e^{\alpha +{\mathit{x}}_i\mathit{\beta }}})]\end{array}\end{array}$$

对数似然函数 $\ell (\alpha ,\mathit{\beta })$ 关于参数 $\alpha ,\mathit{\beta }$ 的偏导数如下：

$$\begin{array}{}\text{(19.3)}& \begin{array}{rl}\frac{\partial \ell (\alpha ,\mathit{\beta })}{\partial \alpha }& =\sum _{i=1}^n[(\frac{y_i}{p_i}-\frac{1-y_i}{1-p_i})\frac{\partial p_i}{\partial \alpha }]\\ \frac{\partial \ell (\alpha ,\mathit{\beta })}{\partial \mathit{\beta }}& =\sum _{i=1}^n[(\frac{y_i}{p_i}-\frac{1-y_i}{1-p_i})\frac{\partial p_i}{\partial \beta }]\\ & =\sum _{i=1}^n[(\frac{y_i}{p_i}-\frac{1-y_i}{1-p_i})p_i(1-p_i){\mathit{x}}_i^{\mathrm{\top }}]\end{array}\end{array}$$

其中， $p_i=\frac{e^{\alpha +{\mathit{x}}_i\mathit{\beta }}}{1+e^{\alpha +{\mathit{x}}_i\mathit{\beta }}}$ ，要使 $\ell (\alpha ,\mathit{\beta })$ 取极大值，一般通过迭代加权最小二乘算法（Iteratively (Re-)Weighted Least Squares，简称 IWLS）求解此优化问题，它可以看作拟牛顿法的一种特殊情况，在 R 语言中，函数 glm() 是求解此类问题的办法。

19.3 数值优化问题求解器

19.3.1 optim()

从一个逻辑回归模型模拟一组样本，共 2500 条记录，即 $n=2500$，10 个观测变量，即 $k=10$，其中，只有变量 $X_1$ 和 $X_2$ 的系数非零，参数设定为 $\alpha =1,{\beta }_1=3,{\beta }_2=-2$，而 ${\beta }_i=0,i=3,\cdots ,10$ 模拟数据的代码如下：

set.seed(2023)
n <- 2500
k <- 10
X <- matrix(rnorm(n * k), ncol = k)
y <- rbinom(n, size = 1, prob = plogis(1 + 3 * X[, 1] - 2 * X[, 2]))

模拟数据矩阵 X 与上述记号 $X$ 是对应的，记号 ${{\mathit{x}}_i}^{\mathrm{\top }}$ 表示数据矩阵的第 $i$ 行。$\alpha$ 是逻辑回归方程的截距，$\mathit{\beta }$ 是 $k$ 维列向量，$X$ 是 $n\times k$ 维的矩阵且 $n>k$，$y$ 是 $n$ 维向量。极大化对数似然函数 式 19.2 ，就是求解一个多维非线性无约束优化问题。方便起见，将 $\alpha$ 合并进 $\mathit{\beta }$ 向量，另，函数 optim() 默认求极小，因此在对数似然函数前添加负号。

# 目标函数
log_logit_lik <- function(beta) {
  p <- plogis(cbind(1, X) %*% beta)
  -sum(y * log(p) + (1 - y) * log(1 - p))
}

高维情形下，没法绘制似然函数图形，退化到二维，如 图 19.2 所示，二维情形下的逻辑回归模型的负对数似然函数曲面。

图 19.2: 二维情形下的逻辑回归模型的负对数似然函数曲面

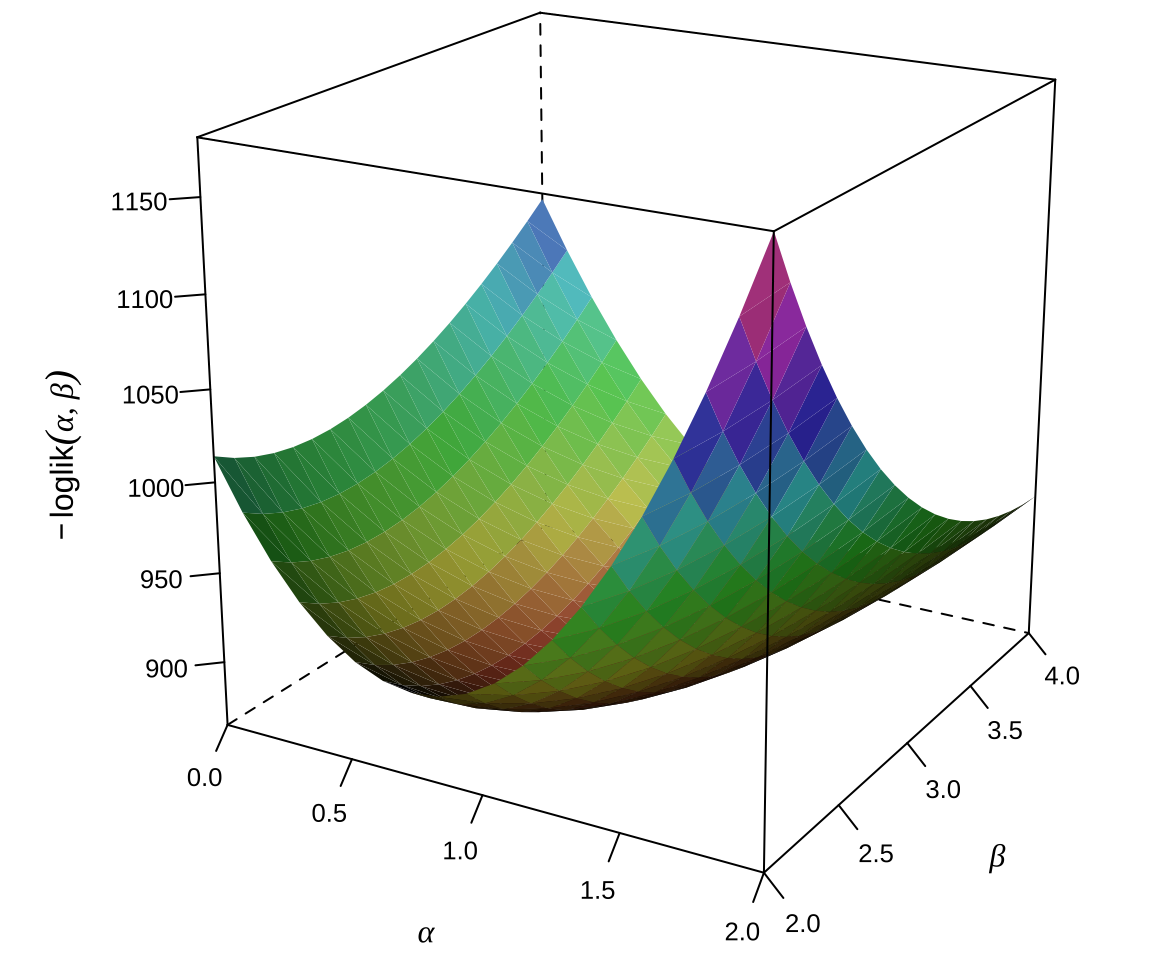
当用 Base R 函数 optim() 来求解时，发现 Nelder-Mead 算法收敛慢，易陷入局部最优解，即使迭代 10000 次，与真值仍然相去甚远。当用 SANN （模拟退火算法）求解此 11 维非线性无约束优化问题时，迭代 10000 次后，比较接近真值。

optim(
  par = rep(1, 11), # 初始值
  fn = log_logit_lik, # 目标函数
  method = "SANN",
  control = list(maxit = 10000)
)

#> $par
#>  [1]  1.0755086156  3.2857327374 -2.1172404451 -0.0268567120  0.0184306330
#>  [6]  0.0304496968  0.0045154725  0.1283816433 -0.0746276329 -0.0624193044
#> [11] -0.0001349772
#> 
#> $value
#> [1] 754.1838
#> 
#> $counts
#> function gradient 
#>    10000       NA 
#> 
#> $convergence
#> [1] 0
#> 
#> $message
#> NULL

根据目标函数计算其梯度，有了梯度信息，可以使用迭代效率更高的 L-BFGS-B 算法。

# 梯度函数
log_logit_lik_grad <- function(beta) {
  p <- plogis(cbind(1, X) %*% beta)
  -t((y / p - (1 - y) / (1 - p)) * p * (1 - p)) %*% cbind(1, X)
}

optim(
  par = rep(1, 11), # 初始值
  fn = log_logit_lik, # 目标函数
  gr = log_logit_lik_grad, # 目标函数的梯度
  method = "L-BFGS-B"
)

#> $par
#>  [1]  1.00802641  3.11296713 -2.00955313  0.05855394 -0.02650585  0.01330428
#>  [7]  0.02171815  0.10213455 -0.02949774 -0.08633384  0.08098888
#> 
#> $value
#> [1] 750.9724
#> 
#> $counts
#> function gradient 
#>       13       13 
#> 
#> $convergence
#> [1] 0
#> 
#> $message
#> [1] "CONVERGENCE: REL_REDUCTION_OF_F <= FACTR*EPSMCH"

相比于函数 optim()，R 包 nloptr 不但可以提供类似的数值优化功能，而且可以处理各类非线性约束，能力更强。仍然基于上面的优化问题， 调用 nloptr 包求解的代码如下：

library(nloptr)
nlp <- nloptr(
  x0 = rep(1, 11),
  eval_f = log_logit_lik,
  eval_grad_f = log_logit_lik_grad,
  opts = list(
    "algorithm" = "NLOPT_LD_LBFGS",
    "xtol_rel" = 1.0e-8
  )
)
nlp

#> 
#> Call:
#> 
#> nloptr(x0 = rep(1, 11), eval_f = log_logit_lik, eval_grad_f = log_logit_lik_grad, 
#>     opts = list(algorithm = "NLOPT_LD_LBFGS", xtol_rel = 1e-08))
#> 
#> 
#> Minimization using NLopt version 2.7.1 
#> 
#> NLopt solver status: 3 ( NLOPT_FTOL_REACHED: Optimization stopped because 
#> ftol_rel or ftol_abs (above) was reached. )
#> 
#> Number of Iterations....: 23 
#> Termination conditions:  xtol_rel: 1e-08 
#> Number of inequality constraints:  0 
#> Number of equality constraints:    0 
#> Optimal value of objective function:  750.97235708148 
#> Optimal value of controls: 1.008028 3.112977 -2.009557 0.05854534 -0.02650855 0.01330416 0.02171839 
#> 0.1021212 -0.02949994 -0.08632463 0.08098663

如果对数似然函数是多模态的，一般的求解器容易陷入局部最优解，推荐用 nloptr 包的全局优化求解器。

19.3.2 glm()

Base R 提供的函数 glm() 拟合模型，指定联系函数为 logit 变换。

fit_r <- glm(y ~ X, family = binomial(link = "logit"))
summary(fit_r)

#> 
#> Call:
#> glm(formula = y ~ X, family = binomial(link = "logit"))
#> 
#> Coefficients:
#>             Estimate Std. Error z value Pr(>|z|)    
#> (Intercept)  1.00803    0.07395  13.631   <2e-16 ***
#> X1           3.11298    0.13406  23.222   <2e-16 ***
#> X2          -2.00956    0.09952 -20.192   <2e-16 ***
#> X3           0.05855    0.06419   0.912    0.362    
#> X4          -0.02651    0.06588  -0.402    0.687    
#> X5           0.01330    0.06461   0.206    0.837    
#> X6           0.02172    0.06496   0.334    0.738    
#> X7           0.10212    0.06279   1.626    0.104    
#> X8          -0.02950    0.06474  -0.456    0.649    
#> X9          -0.08632    0.06482  -1.332    0.183    
#> X10          0.08099    0.06385   1.268    0.205    
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 3381.4  on 2499  degrees of freedom
#> Residual deviance: 1501.9  on 2489  degrees of freedom
#> AIC: 1523.9
#> 
#> Number of Fisher Scoring iterations: 6

或者也可以用函数 glm.fit()，效果类似，使用方式不同罢了。

fit_r2 <- glm.fit(x = cbind(1, X), y = y, family = binomial(link = "logit"))
coef(fit_r2)

#>  [1]  1.00802820  3.11297679 -2.00955727  0.05854534 -0.02650855  0.01330416
#>  [7]  0.02171839  0.10212118 -0.02949994 -0.08632463  0.08098663

函数 glm() 的参数是一个公式，函数 glm.fit() 的参数是矩阵、向量，用函数 glm() 拟合模型，其内部调用的就是函数 glm.fit()。

19.3.3 glmnet 包

调用 glmnet 包的函数 glmnet() 拟合模型，指定指数族的具体形式为二项分布，伯努利分布是二项分布的特殊形式，也叫两点分布或0-1分布。

library(Matrix)
library(glmnet)
fit_glm <- glmnet(x = X, y = y, family = "binomial")

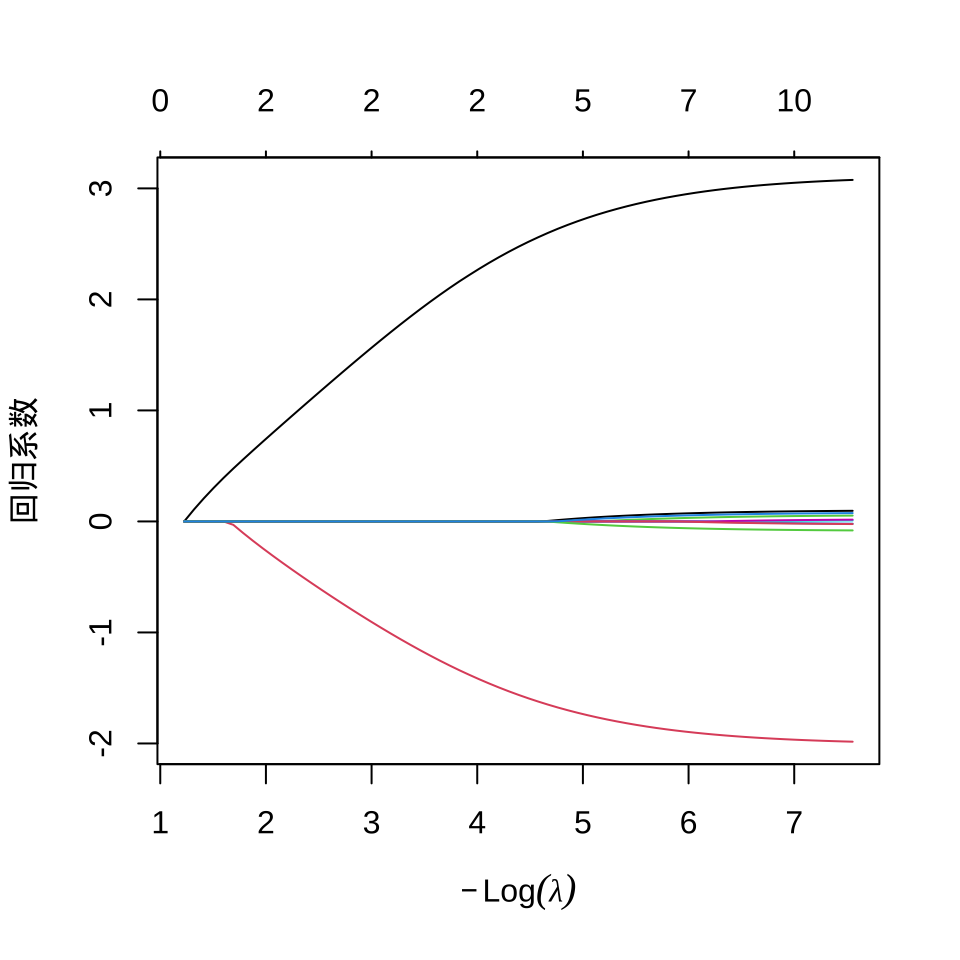
逻辑回归模型系数在 L1 正则下的迭代路径图

plot(fit_glm, ylab = "回归系数")

图 19.3: 回归系数的迭代路径

从图可见，剩余两个系数是非零的，一个是 3， 一个是 -2，其余都被压缩，而接近为 0 了。

plot(fit_glm$lambda,
  ylab = expression(lambda), xlab = "迭代次数",
  main = "惩罚系数的迭代路径"
)

图 19.4: 惩罚系数的迭代路径

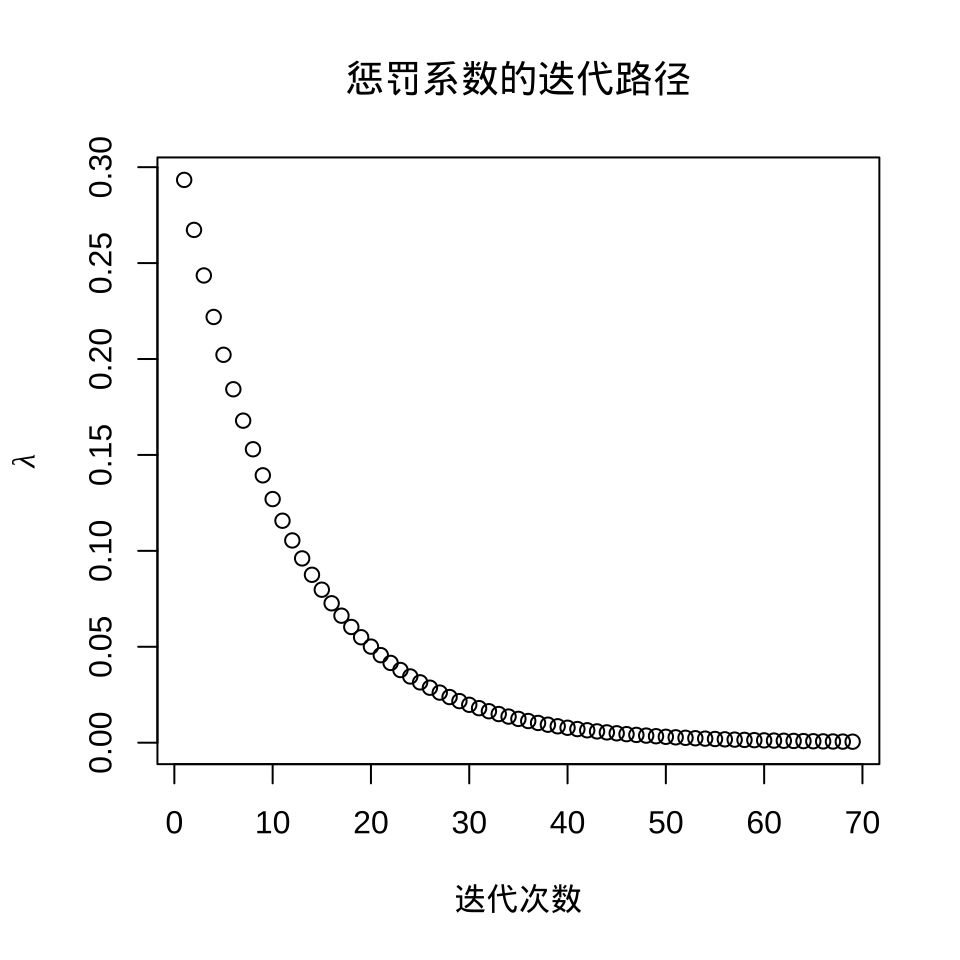
随着迭代的进行，惩罚系数 $\lambda$ 越来越小，接近于 0，这也是符合预期的，因为模型本来就是简单的逻辑回归，不带惩罚项。选择一个迭代趋于稳定时的 $\lambda$ 比如 0.0005247159，此时各个参数的取值如下：

coef(fit_glm, s = 0.0005247159)

#> 11 x 1 sparse Matrix of class "dgCMatrix"
#>                       s1
#> (Intercept)  0.997741857
#> V1           3.076358149
#> V2          -1.984018387
#> V3           0.052633923
#> V4          -0.020195037
#> V5           0.008065018
#> V6           0.015936357
#> V7           0.095722046
#> V8          -0.023589159
#> V9          -0.080864640
#> V10          0.075234011

截距 (Intercept) 对应 $\alpha =0.997741857$，而 ${\beta }_1=3.076358149$ 对应 V1，${\beta }_2=-1.984018387$ 对应 V2，以此类推。

19.4 评估模型的分类效果

逻辑回归模型是二分类模型，评估模型的分类效果，两个办法。

1. 可以用 AUC 指标或者 ROC 曲线，pROC 包和 ROCR 包都可以绘制 ROC 曲线。
2. 可以用 Wilcoxon 检验，越显著表示分类效果越好。

19.4.1 ROC 曲线和 AUC 值

ROC 是 Receiver Operating Characteristic 简写。随机抽取 2000 个样本作为训练集，余下的数据作为测试集。

dat <- cbind.data.frame(X, y)
set.seed(20232023)
idx <- sample(x = 1:nrow(dat), size = 2000, replace = F)
# 训练集
dat_train <- dat[idx, ]
# 测试集
dat_test <- dat[-idx, ]

函数 glm() 拟合训练集数据

fit_binom <- glm(y ~ ., data = dat_train, family = binomial(link = "logit"))

将训练好的模型用于测试集，调用函数 predict() 进行预测，type = "response" 获得预测概率值，它是对数几率，比值比的对数。

dat_test$pred <- predict(fit_binom, newdata = dat_test, type = "response")

返回值介于 0 - 1 之间，表示预测概率。在测试集上绘制 ROC 曲线。

pROC::plot.roc(
  y ~ pred, data = dat_test,
  col = "dodgerblue", print.auc = TRUE,
  auc.polygon = TRUE, auc.polygon.col = "#f6f6f6",
  xlab = "FPR", ylab = "TPR", main = "预测 ROC 曲线"
)

#> Setting levels: control = 0, case = 1

#> Setting direction: controls < cases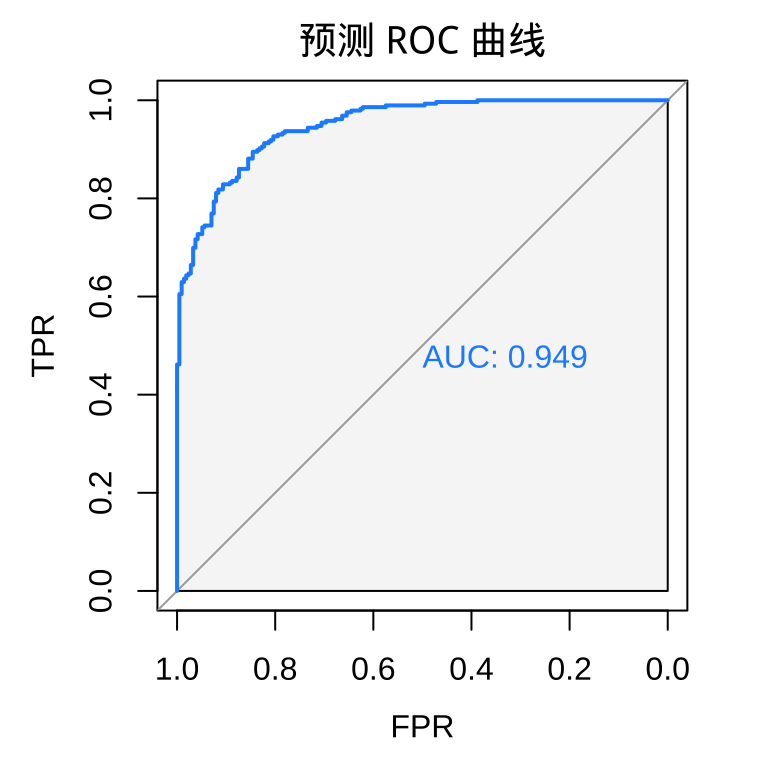

图 19.5: ROC 曲线

ROC 曲线越往左上角拱，表示预测效果越好。FPR 是 False Positive Rate 的缩写，TPR 是 True Positive Rate 的缩写。

# 计算 AUC 值
pROC::auc(y ~ pred, data = dat_test)

#> Setting levels: control = 0, case = 1

#> Setting direction: controls < cases

#> Area under the curve: 0.9487

AUC 是 area under curve 的缩写，表示 ROC 曲线下的面积，所以 AUC 指标越接近 1 越好。

19.4.2 Wilcoxon 检验

对每个标签的预测概率指定服从均匀分布，相当于随机猜测，所以最后 ROC 会接近对角线，而且样本量越大越接近，AUC 会越来越接近 0.5。如果预测结果比随机猜测要好，Wilcoxon 检验会显著，预测效果越好检验会越显著，表示预测 pred 和观测 y 越接近。

wilcox.test(pred ~ y, data = dat_test)

#> 
#>  Wilcoxon rank sum test with continuity correction
#> 
#> data:  pred by y
#> W = 3140, p-value < 2.2e-16
#> alternative hypothesis: true location shift is not equal to 0

Efron, Bradley, Trevor Hastie, Iain Johnstone, 和 Robert Tibshirani. 2004. 《Least angle regression》. The Annals of Statistics 32 (2): 407–99. https://doi.org/10.1214/009053604000000067.

Kim, Yongdai, Hosik Choi, 和 Hee-Seok Oh. 2008. 《Smoothly Clipped Absolute Deviation on High Dimensions》. Journal of the American Statistical Association 103 (484): 1665–73. https://doi.org/10.1198/016214508000001066.

Tibshirani, Robert. 1996. 《Regression Shrinkage and Selection via the Lasso》. Journal of the Royal Statistical Society. Series B (Methodological) 58 (1): 267–88. http://www.jstor.org/stable/2346178.

Zhang, Cun-Hui. 2010. 《Nearly unbiased variable selection under minimax concave penalty》. The Annals of Statistics 38 (2): 894–942. https://doi.org/10.1214/09-AOS729.