4 Exercise 2: Publishing history – fitting a quadratic

Source: Tweedie, F. J., Bank, D. A. and McIntyre, B. (1998) Modelling Publishing History, 1475–1640: Change points in the STC.

Context: The Short Title Catalogue (STC) is a list of all the books that were published in Scotland, England and Ireland between 1475 and 1640. We are interested in finding out if there are any changes in the number of books published between 1500 and 1640.

Data: books.csv

Columns:

              C1: Year (1500 – 1640)
              C2: Total number of books published

Read in the data using:

books <- read.csv("books.csv")

4.1 Exploratory analysis

  1. Produce a scatterplot of the data with Number of books on the y-axis and Year on the x-axis.

The R code plot() can be used to create scatter plots.

books <- read.csv("books.csv")
plot(Number.of.Books ~ Year, data = books, xlab = "Books", ylab = "Number of books")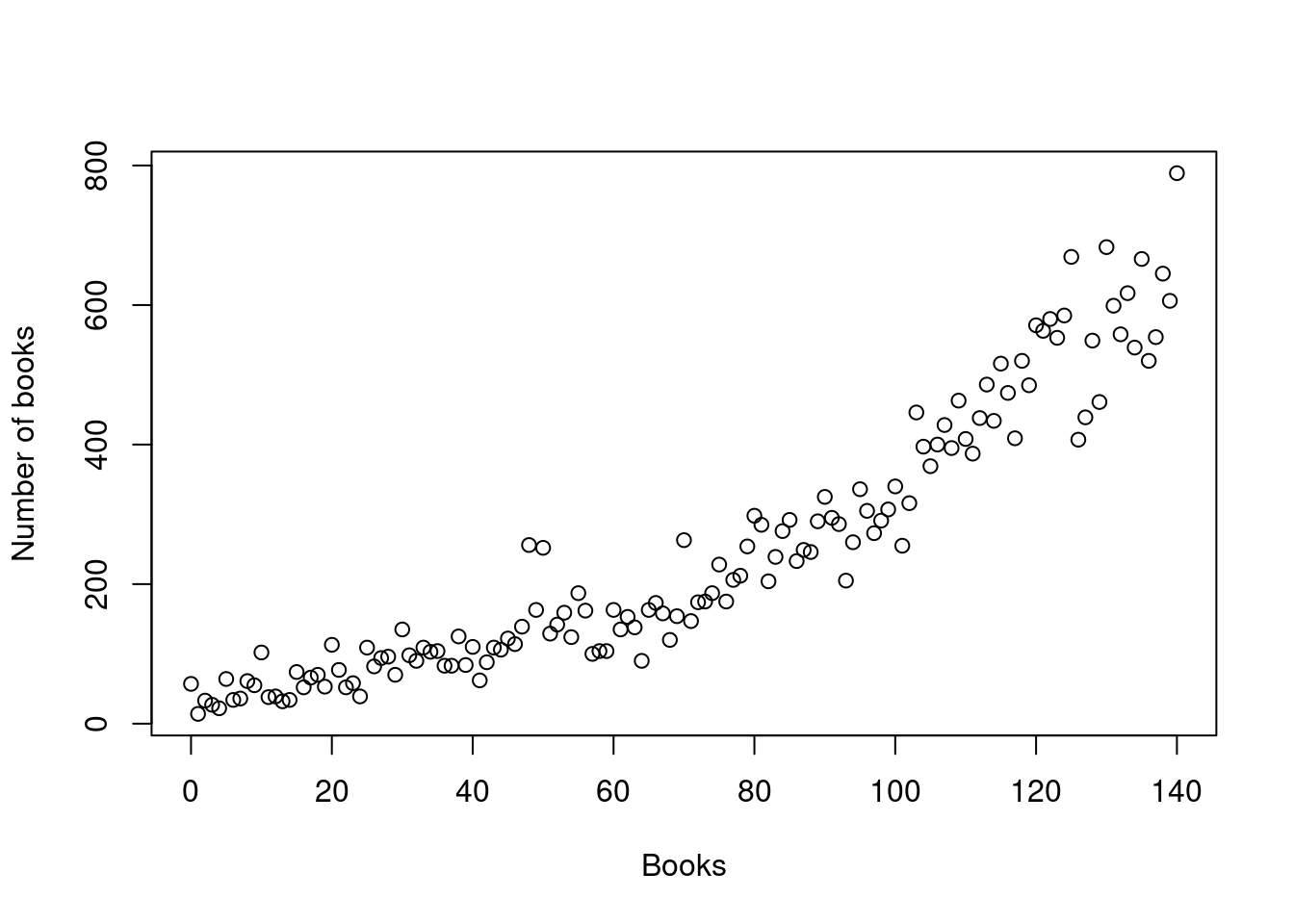

  1. Describe the shape of the relationship. Does it seem linear?

In this case, the relationship .

4.2 Fitting a linear model

  1. Attempt to fit a quadratic regression and output the model summary.

The following R code can be used to create a quadratic model:

bmodel <- lm(Number.of.Books ˜ Year + I(Yearˆ2), data = books) 
## 
## Call:
## lm(formula = Number.of.Books ~ Year + I(Year^2), data = books)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -129.856  -26.520   -3.263   22.053  141.426 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 59.977961  11.806071   5.080  1.2e-06 ***
## Year        -0.491710   0.389675  -1.262    0.209    
## I(Year^2)    0.033940   0.002694  12.599  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 47.39 on 138 degrees of freedom
## Multiple R-squared:  0.9368, Adjusted R-squared:  0.9359 
## F-statistic:  1023 on 2 and 138 DF,  p-value: < 2.2e-16

Note: year^2 needs to be 'protected' by I, the identity function.

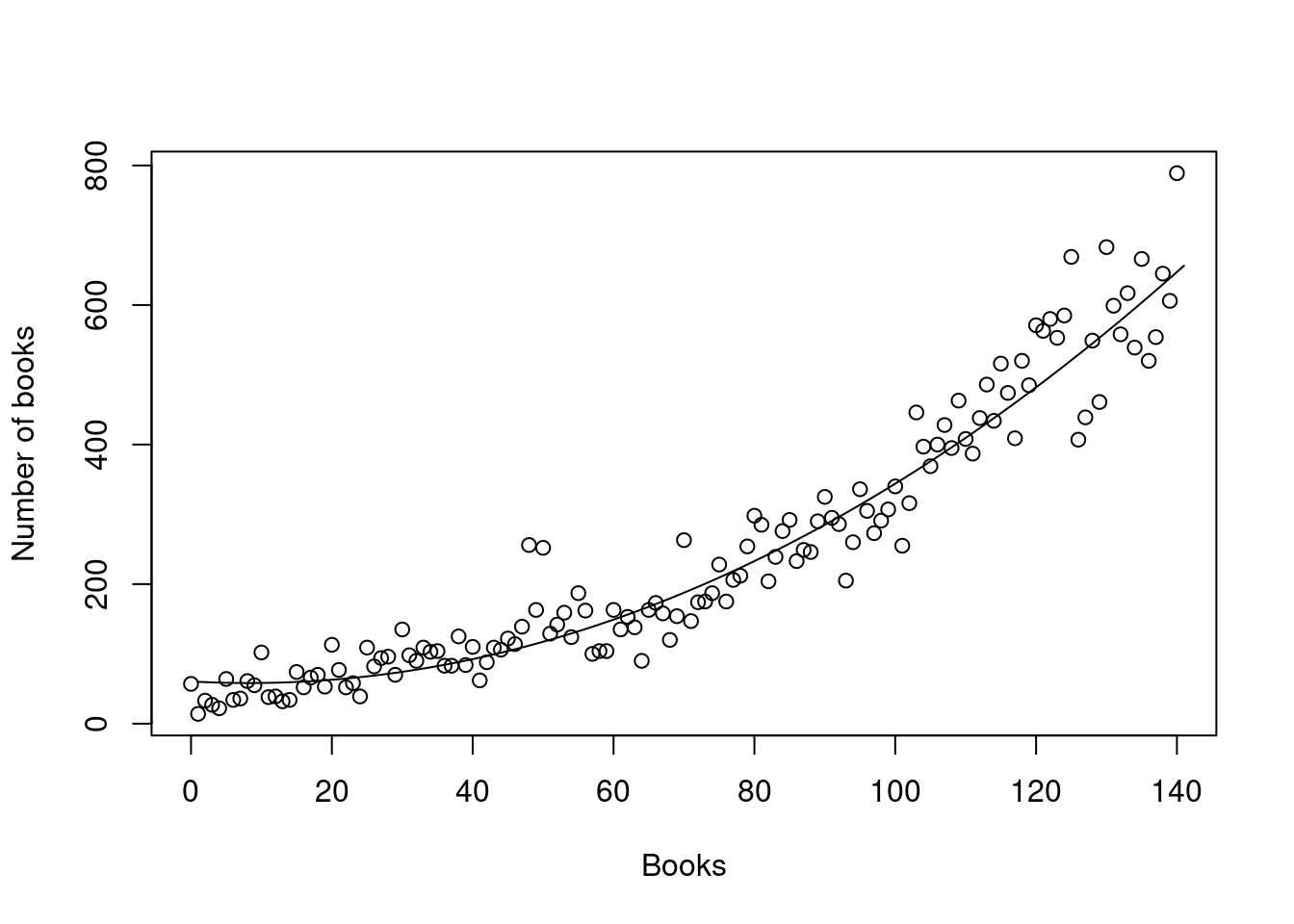
  1. Note down the equation of the quadratic line from (c) and plot the fitted line.
Total number of books = + Year + Year^2
  1. Plot the fitted line of the quadratic model.

The R command lines() can be used to plot the points obtained by using fitted() on the model.

plot(Number.of.Books ~ Year, data = books, xlab = "Books", ylab = "Number of books")
lines(fitted(bmodel))