3 Exercise 1: Hubble's Constant
Source: Hubble, E. (1929) A Relationship Between Distance and Radial Velocity among Extra-Galactic Nebulae, Proceedings of the National Academy of Science, 168.
Context: In 1929 Edwin Hubble investigated the relationship between distance and radial velocity of extragalactic nebulae (celestial objects). It was hoped that some knowledge of this relationship might give clues as to the way the universe was formed and what may happen later. His findings revolutionised astronomy and are the source of much research today on the ‘Big Bang’. Given here is the data that Hubble used for 24 nebulae. It is of interest to determine the effect of distance on velocity.
Columns:
Read in the data using:
hubble <- read.csv("hubble.csv")3.1 Exploratory analysis
- Produce a scatterplot of the data with Velocity on the y-axis.
plot(Velocity ~ Distance, data = hubble, xlab="Distance", ylab="Velocity")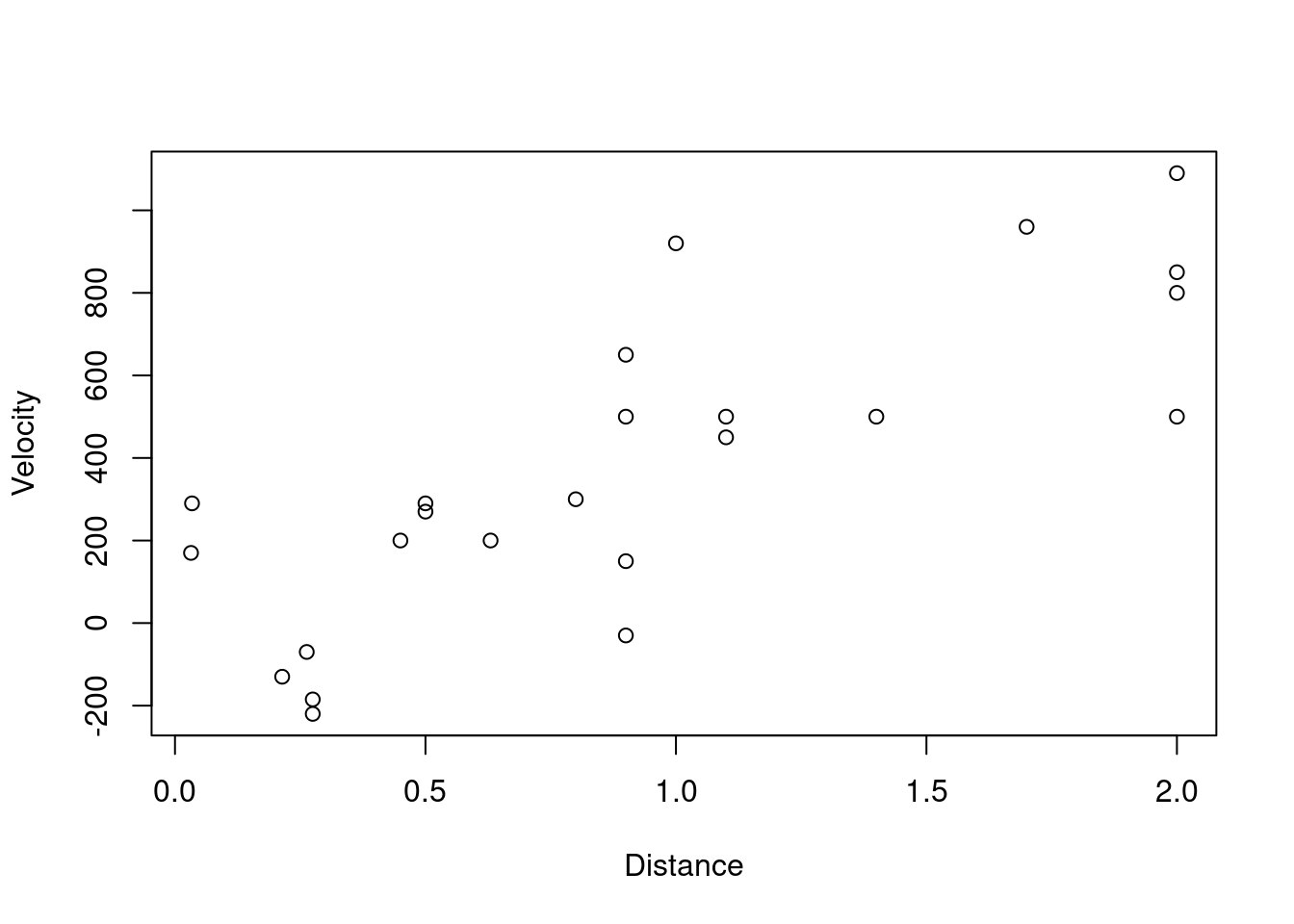
- Describe the shape of the relationship.
The relationship appears to be and it that the line passes through the origin.
3.2 Fitting a linear model
- Find the equation that best describes the relationship between Velocity and Distance.
lm(Velocity ~ Distance, data = hubble)
This fits a simple linear regression model with the response variable Velocity and the explanatory variable Distance.
- From the output in (c), note down the equation of the fitted line that is given:
This is the line of best fit, describing the effect of distance on velocity.
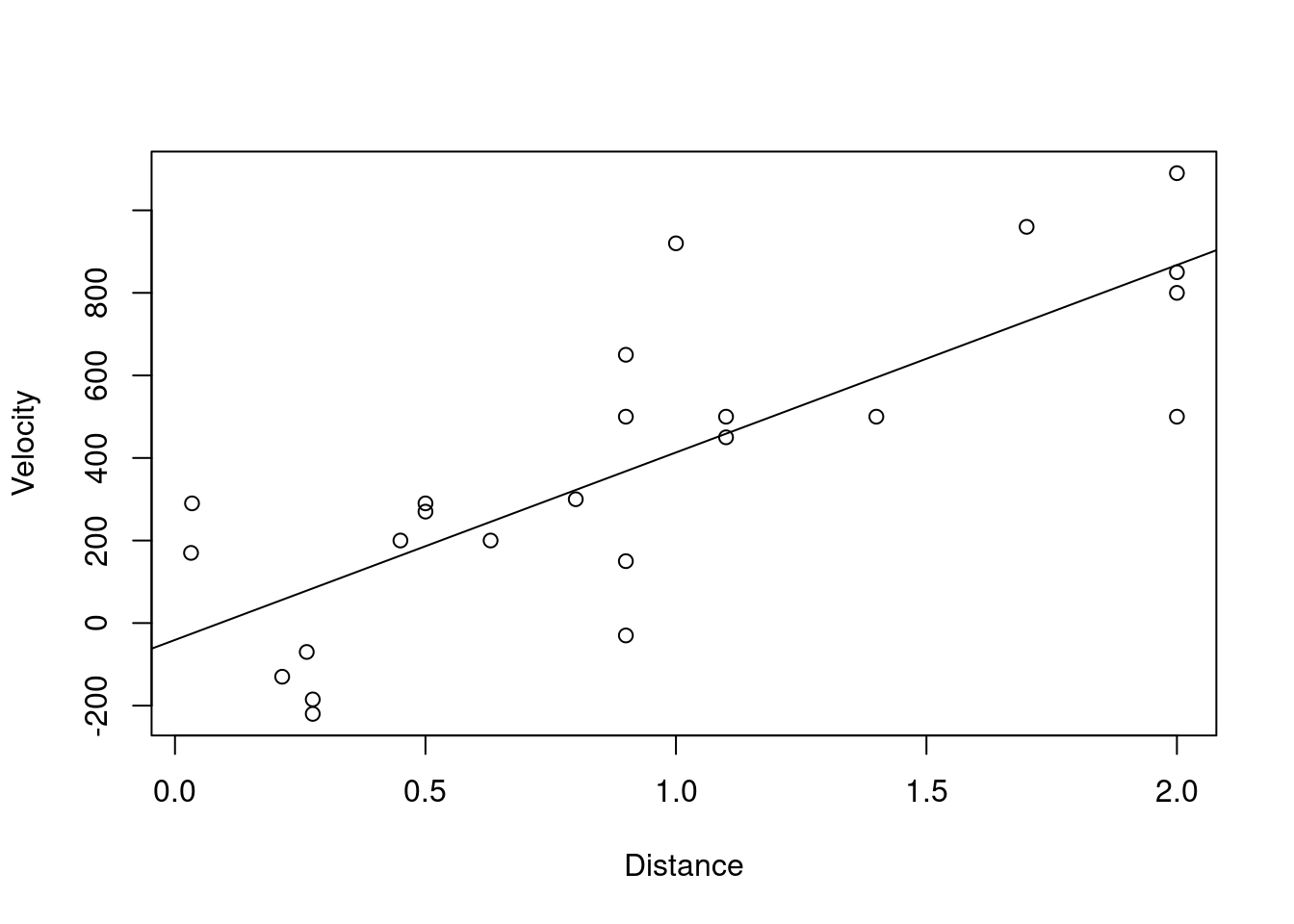
Plot of the data including the fitted line
- Obtain a plot of the fitted values.
A fitted line can be added to a plot using the command abline.
To obtain a plot of the fitted values, we need to store the regression in an object:
model <- lm(Velocity ˜ Distance, data = hubble)
A plot of the data can be re-produced as before with the fitted line added using the abline command. This
command uses the intercept and slope information from the fitted line in model. This is done using:
plot(Velocity ˜ Distance, data = hubble)
abline(model)
Fitting a linear model with no intercept
- Here, it is plausible from the data that the regression line should be forced to go through the origin. Attempt to create a model with no intercept.
The intercept can be removed from a linear model by adding -1 to the linear model.
The new equation of the line is given by Velocity = Distance
lm(Velocity ˜ -1 + Distance, data = hubble)
model.NoInt <- lm(Velocity ~ -1 + Distance, data = hubble)
coef(model.NoInt)## Distance
## 423.9373(Optional) Calculate the least squares estimate of the slope parameter for the model without an intercept.
- Add the best fitted lines for both models (with and without an intercept) onto the same plot of the data.
If we save the intercept only model fit using
model.NoInt <- lm(Velocity ˜ -1 + Distance, data = hubble)
a plot of the data can be re-produced as before with the fitted lines from both linear models added
using the abline command:
plot(Velocity ˜ Distance, data = hubble)
abline(model, col = "red")
abline(model.NoInt, col = "blue", lty = 2)
model.NoInt <- lm(Velocity ~ -1 + Distance, data = hubble)
plot(Velocity ~ Distance, data = hubble)
abline(model, col = "red")
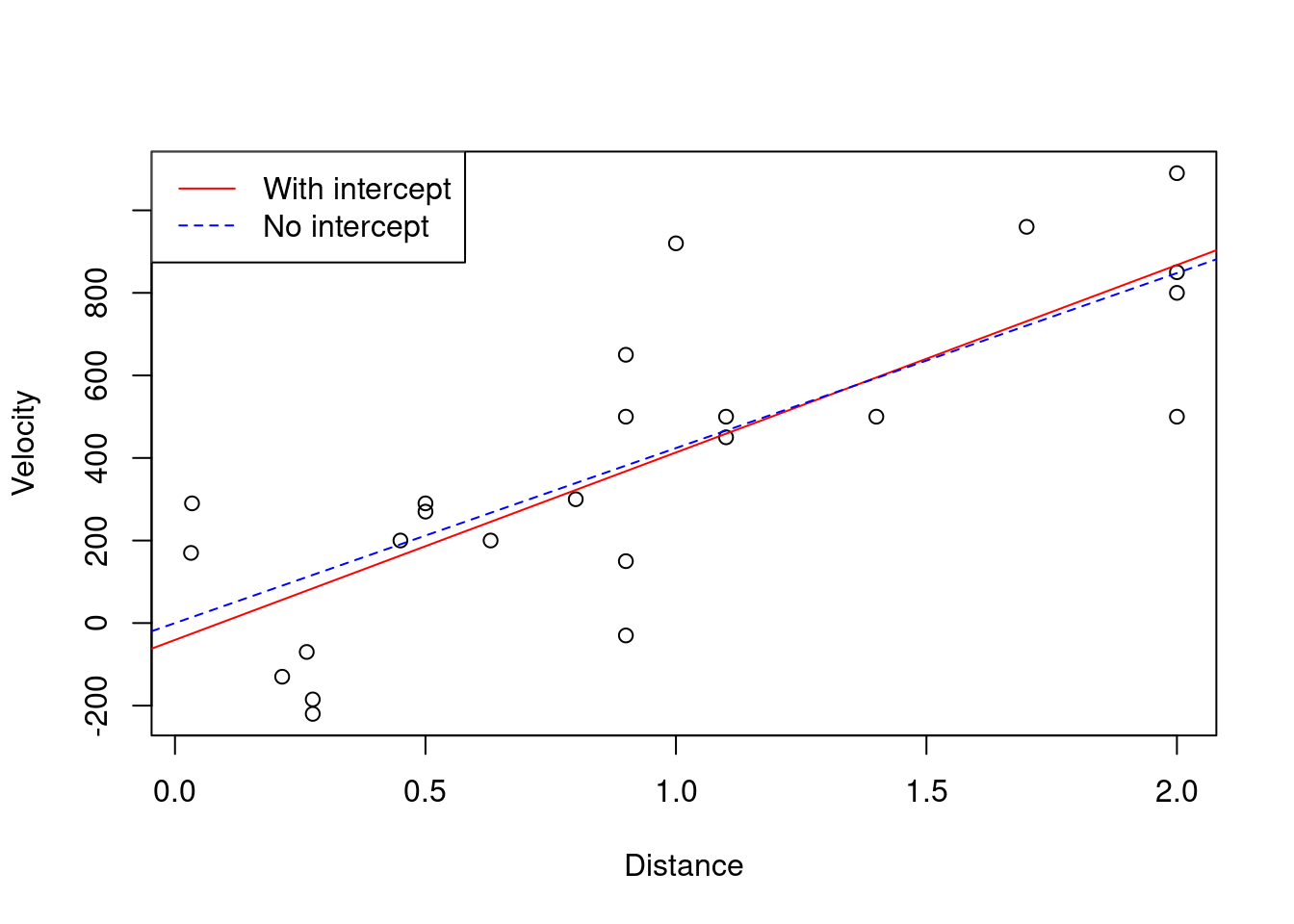
abline(model.NoInt, col = "blue", lty = 2)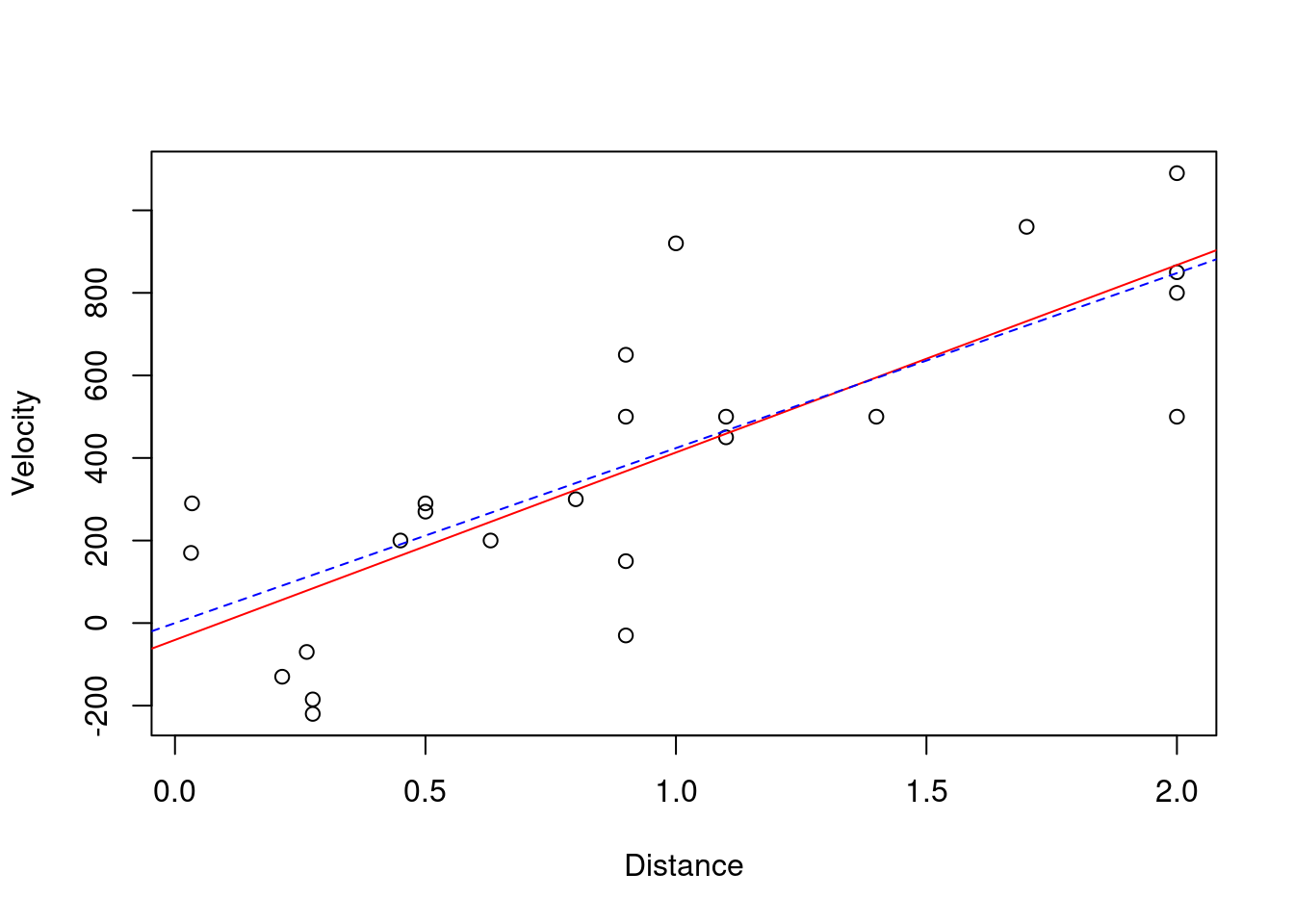
The lty argument changes the type/style of the line plotted, which is handy when printing in black
and white.
(Optional) Add a legend to distinguish between the lines plotted.
A legend can be added to a plot using the legend() command, then first specifying location ("topleft" fits well here and doesn't block any of the data points), a vector of the names of the lines, a vector of the respective colours, then finally the line types used.
model.NoInt <- lm(Velocity ~ -1 + Distance, data = hubble)
plot(Velocity ~ Distance, data = hubble)
abline(model, col = "red")
abline(model.NoInt, col = "blue", lty = 2)
legend("topleft", c("With intercept", "No intercept"), col = c("red", "blue"), lty = c(1, 2))