Capítulo 1 Primeiros passos
1.1 O que é R?
O R é uma linguagem e ambiente voltados para estatística computacional e gráficos. Aberto e gratuito, é compatível com Windows, UNIX e MacOS. Nos últimos anos o R tem crescido exponencialmente e possui aplicações nas mais variadas áreas de conhecimento, como: finanças, marketing, estatística, economia, farmacêutica, ciências sociais, biologia e etc. Tal fato posicionou o R como a sétima linguagem mais popular conforme o Ranking IEEE Spectrum de 2021.
O R pode se referir as duas coisas: ao software utilizado para executar o código escrito na linguagem R e à linguagem em si. Para mais informações, podemos visitar o site do Projeto R
1.2 Bibliografia indicada
Atualmente há centenas de bons livros sobre R, muitos deles disponibilizados de forma gratuita on-line. Há algumas obras em português ou traduzidas para o português mas a maioria da bibliografia mais famosa está em inglês. Segue uma lista da bibliografia indicada para iniciantes no R.
- R in a Nutshell: A Desktop Quick Reference (Adler 2012)
- Learning R: A Step-by-Step Function Guide to Data Analysis (Cotton 2013)
- R for Data Science: Import, Tidy, Transform, Visualize, and Model Data (H. Wickham e Grolemund 2017) (possui versão em português)
- 25 Recipes for Getting Started with R (Teetor 2011)
- R Cookbook: Proven Recipes for Data Analysis, Statistics, and Graphics (Teetor 2019)
- The Essential R Reference (Gardener 2012)
- R Graphics Cookbook - 2nd edition (Chang 2018)
1.3 Onde procurar ajuda?
Há uma infinidade de meios onde podemos encontrar tutoriais, dicas, vídeos e etc. No entanto, seguem alguns dos locais onde podemos solucionar problemas e esclarecer dúvidas.
- Documentação dos pacotes;
- Comunidade do RStudio;
- StackOverflow;
- GitHub.
1.4 Instalando o R
Para instalar o R, basta seguir os seguintes passos:
- Visite um dos CRAN Mirrors fazer o download do software. Sugerimos: (https://vps.fmvz.usp.br/CRAN/);
- Escolha a versão para o seu sistema operacional (Linux, Mac OS ou Windows);
- Na página seguinte, escolha a versão base;
- Baixe o arquivo disponível no link e instale!
1.5 Instalando o RStudio
O RStudio é um ambiente de interface gráfica para o R, ou melhor, um IDE (Integrated Development Environment). Atualmente o RStudio é considerado a melhor IDE para quem programa em R. Além de uma interface mais amigável, possui diversas funcionalidades que facilitam o aprendizado e a produtividade. O RStudio possui uma versão para desktop grátis e, para baixar e instalar, basta seguir os seguintes passos:
- Ir até a página de download do RStudio;
- Clicar em download para a versão grátis;
- Escolher o instalador de acordo com o seu sistema operacional (Windows, Mac OS, Linux);
- Após o download, realizar a instalação.
Há alguns anos o RStudio também passou a disponibilizar uma versão na nuvem através do RStudio Cloud, o que permite acessar o ambiente de qualquer navegador e compartilhar projetos de uma maneira muito simples com outras pessoas. Recentemente houve uma atualização dos planos disponíveis e dos respectivos recursos computacionais disponibilizados.
1.6 Preparando o ambiente de trabalho no RStudio
Uma vez instalado o RStudio, é hora de ajustarmos pequenos detalhes. Uma das primeiras coisas que sugerimos definir no RStudio é a posição de cada um dos principais painéis, quais sejam:
- Console: onde o código é executado. Nele é possível visualizar tudo que é executado e as saídas dos comandos executados no script ou no próprio console;
- Source: Onde ficará posicionado o script que está a desenvolver;
- Enviroment, history, connections e etc: Uma série de abas onde podemos visualizar os objetos do ambiente, histórico de execuções, conexões e etc.
- Plots, files, packages, help, viewer e etc. Visualização dos gráficos, arquivos e pastas, ajuda e etc.
A segunda coisa que sugerimos fazer é definir a aparência (Preferences > Apperance). Talvez não faça sentido para muitos, mas utilizar sempre a mesma aparência facilita o aprendizado e rapidamente identificar erros nos código. As cores ajudam muito a nos ambientarmos. Por questões de conforto visual, utilizar um tema com o fundo escuro ajuda bastante. Sugerimos o tema Idle Fingers. Tamanho da fonte, zoom e tema do RStudio também podem ser alterados na aba de aparência.
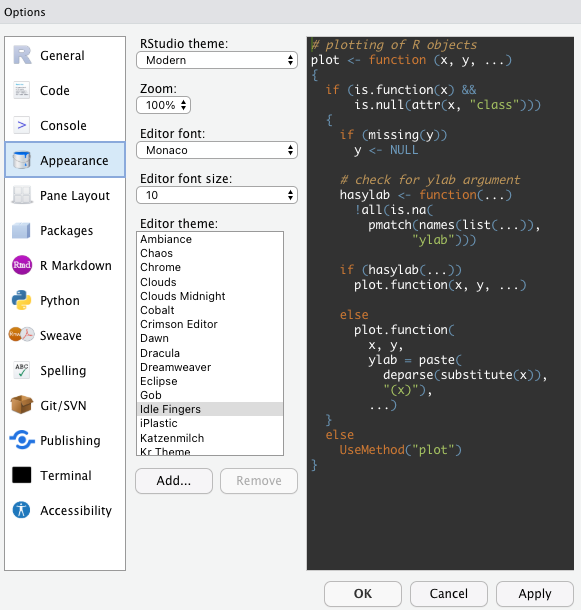
Figura 1.1: Definindo a aparência.
Sugerimos que o ambiente seja dividido nessas quatro partes, conforme apresentado na figura a seguir. Particularmente utilizamos nessa disposição, mas essa ordem pode ser alterada nas preferências do RStudio. O importante é que você utilize sempre a mesma disposição por questões de hábito. É algo muito pessoal.
1.7 Criando um projeto no RStudio
É recomendável que você crie um projeto referente a cada trabalho que você desenvolve no RStudio. Os projetos dividem o trabalho em seus próprios contextos, cada projeto possui seu diretório de trabalho, seu espaço, histórico e documentos.
Para criar um novo projeto basta ir em File > New Project… no menu superior do RStudio. A janela apresentada na Figura 1.2 irá aparecer.
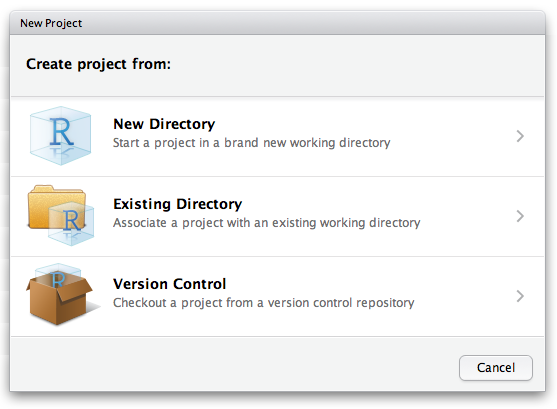
Figura 1.2: Criando projeto.
Uma outra facilidade de trabalhar com os projetos é que você pode facilmente mudar de um projeto para outro no menu do canto superior direito. Quando você muda de projeto, é possível retornar ao ponto que parou anteriormente, seus objetos carregados, scripts e janelas abertas estarão lá.
1.8 Operações básicas
1.9 Principais operações aritméticas e lógicas com R
Antes de iniciarmos as primeiras operações com o R, é necessário conhecer os principais operadores aritméticos e lógicos. Segue tabela com os principais operadores e uma breve descrição de cada um.
| Operador | Descrição |
|---|---|
+ |
Operador de adição |
- |
Operador de subtração |
* |
Operador de multiplicação |
/ |
Operador de divisão |
: |
Operador de sequência |
^ |
Operador exponencial |
%% |
Operador de módulo |
== |
Operador de igualdade |
> |
Operador “maior que” |
< |
Operador “menor que” |
<= |
Operador “menor ou igual” |
& |
Operador lógico “E” |
| |
Operador lógico “OU” |
Conhecido tais operadores, podemos realizar nossas primeiras operações no console do R. Segue alguns exemplos com os respectivos resultados
#Exemplo de soma
347 + 328## [1] 675#Exemplo de subtração
567 - 345## [1] 222#Exemplo de multiplicação
457 * 32## [1] 146241.10 Tipos numéricos
Recorrentemente lidamos com diferentes classes numéricas no R. Podemos nos deparar com números inteiros (integer), números decimais (numeric ou double) ou números complexos (complex). Para verificarmos a classe de um número, basta usarmos a função class()no número ou na variável que desejamos testar. Vejamos os exemplos a seguir:
class(3L) #Um número inteiro pode também ser representado acompanhado de um L## [1] "integer"class(3.435)## [1] "numeric"class(3 + 3i)## [1] "complex"Interessante observarmos que o R, por padrão, utiliza o . como separador decimal. Trabalharemos dessa forma dentro do R e faremos as adaptações necessárias na hora de exportar ou comunicar os resultados.
NOTA: Para representar o infinito, o R utiliza
Infe-Inf. Faça o teste realizando a seguinte operação no console:1 / 0
1.11 Caracteres
Além dos números, podemos criar, guardar e manipular dados do tipo carácter, ou seja, em texto. Os dados em texto são atribuídos entre aspas, vejamos:
t <- "Esse curso de R é razoável."
t## [1] "Esse curso de R é razoável."NOTA: Ao longo do conteúdo aprenderemos diversas funções para manipulação de texto!
1.12 Criando e removendo variáveis
Até então realizamos algumas operações sem a necessidade de armazenar dados. No entanto, em operações mais complexas é praticamente impossível não utilizarmos variáveis. Com a criação de uma variável, podemos facilmente reusá-la ao longo de nosso código. Vejamos um exemplo.
x <- 3
x + 10## [1] 13No exemplo anterior, criamos uma variável x para armazenar o valor numérico 3. Ao realizarmos a operação x + 10, automaticamente o valor atribuído a xé recuperado. Para criarmos uma variável, utilizamos o símbolo <-ou =. No entanto, a notação <- é a mais utilizada e será a adotada ao longo do nosso curso.
Os nomes das variáveis podem conter letras, números, pontos e sublinha (_), mas não podem iniciar com um número ou um ponto seguido de número. Também não podemos criar variáveis com palavras reservadas, como TRUE, FALSE e etc.
NOTA: Por questão de estética e praticidade, é recomendável que você mantenha os nomes das variáveis apenas com letras minúsculas. As variáveis devem ter nomes curtos e revelar um pouco da informação que guarda. Isso facilitará a leitura do código!
Aqui é importante destacar que o R é case sensitive (“sensível à capitalização”), ou seja, há uma distinção entre letras maiúsculas e minúsculas! Isso significa que uma variável chamada nome é diferente de uma denominada Nome, ou NOME.
Uma vez criada uma variável (ou qualquer outro objeto no R), podemos facilmente remove-la aplicando a função rm(). Vejamos o exemplo seguinte.
idade <- 25
rm(idade)1.13 Valores lógicos
No R, há três valores lógicos, são eles: TRUE, FALSE, e NA. Esses valores lógicos serão vistos durante todo o curso, uma vez que estão presentes em funções, operações lógicas, estruturas de dados e etc. Os valores TRUE e FALSE também podem ser substituídos por T e F respectivamente.
Em breve síntese, o valor lógico TRUE é normalmente retornado por uma operação lógica verdadeira e assume valor 1, enquanto o FALSE faz o papel inverso, assumindo valor 0.
Por sua vez o NA representa a ausência de valor e merece atenção máxima, principalmente quando está presente em estruturas de dados. O NA é altamente infeccioso e pode causar sérios problemas na filtragem e tratamento de dados. Veremos com mais detalhes nos capítulos seguintes como tratar e manipular valores ausentes. Para entendermos melhor o comportamento desses valores lógicos, vamos ao tópico seguinte.
1.14 NA e NULL
Apesar de serem bem parecidos em sua natureza o NA e o NULL possuem diferenças sutis mas de grande importância. De acordo com a própria documentação do R, o NULL representa o objeto nulo do R sendo o mesmo retornado por expressões e funções nas quais os valores são indefinidos. Por sua vez, o NA (Not Avaible) é uma constante lógica que possui um indicador de valor ausente. Podemos ver o comportamento dos dois ao aplicar a função class() em cada um deles.
class(NULL)## [1] "NULL"class(NA)## [1] "logical"1.15 Operações lógicas
Já vimos alguns operadores no item 1.9 e vamos aprender mais alguns nesse item.
O primeiro exemplo de operação lógica que vamos aprender é a igualdade. No R, o operador lógico de igualdade é o ==. Vejamos o exemplo que segue:
1 == 1## [1] TRUEComo, obviamente, 1 é igual a 1 o valor lógico retornado é o TRUE, o que confirma que a operação é verdadeira. Se quisermos testar se um valor é diferente de outro, usamos o operador != (não igual a). Exemplo a seguir.
3 != 4## [1] TRUEA mesma lógica segue com os demais operadores.
1 > 0## [1] TRUE100 < 1## [1] FALSE5 >= 6## [1] FALSEPara fazermos um teste conjunto, precisamos de outros operadores, como o & (E) e o | (OU). O primeiro é utilizado para quando queremos que os dois testes lógicos sejam atendidos simultaneamente.
x <- 10
y <- 11
x > 1 & y < 10## [1] FALSEVeja que primeiro foi testado se x é maior do que 1. Como a variável citada guardava o valor 10, o primeiro teste foi verdadeiro. No entanto, no segundo teste y não é menor do que 10, o que resulta em falha da segunda condição. Dessa forma, o valor final da operação é FALSE uma vez que ambas as condições não foram atendidas.
Por sua vez, se repetirmos o mesmo código com o operador | no lugar do &, teremos o valor TRUE como retorno, uma vez que pelo menos uma das condições foram atendidas.
x <- 10
y <- 11
x > 1 | y < 10## [1] TRUEPara finalizarmos esse item, vamos ver o operador !x (Não \(x\)) que serve para negar o resultado da operação. Segue exemplo.
w <- 10
!(w < 10)## [1] TRUEVeja que o resultado é o inverso da operação w < 10, uma vez que a mesma retornou TRUE.
NOTA: Entender as operações lógicas é de grande importância para a utilização de filtros, algo que veremos mais adiante.
1.16 Introdução às funções
O R já traz consigo, por padrão, diversas funções, sejam elas matemáticas, estatísticas, para leitura de arquivos, manipulação de texto e etc.
Vamos pensar inicialmente a função no R como uma função matemática. Vejamos a função seguinte.
\[f(x) = x + 2\] Fica fácil compreender que quando \(x\) for 0 o resultado da função será 2.
No R, as funções possuem comportamento semelhante. Em resumo, a função no R é como uma máquina que recebe a matéria prima de um lado e entrega o produto pronto do outro.
Segundo Grolemund (Grolemund 2014), todas as funções no R possuem as mesmas partes, quais sejam:
- nome: é como o usuário pode chamar a função, seguindo de
(); - os argumentos: as partes onde o usuário pode apontar valores e configurar para alcançar o resultado desejado;
- o corpo: A parte do código que o R executa sempre que a função é chamada;
- os valores padrão: argumentos opcionais que podem ser configurados pelo usuário;
- o resultado: o resultado gerado pela função.
Vejamos algumas funções básicas no quadro a seguir.
| Função | Descrição |
|---|---|
sum() |
Retorna a soma |
mean() |
Retorna a média |
sd() |
Retorna o desvio padrão |
median() |
Retorna a mediana |
var() |
Retorna a variância |
cor() |
Retorna a correlação entre dois vetores |
min() |
Retorna o mínimo |
max() |
Retorna o máximo |
range() |
Retorna o mínimo e o máximo |
summary() |
Retorna um sumário dos dados |
quantile() |
Retorna os quantis do conjunto numérico |
round() |
Retorna o valor arredondado |
NOTA: Lembre-se que para ler sobre qualquer função no R basta digitarmos
?seguidos do nome da função no console. Lá é possível ver exemplos de utilização, seus argumentos, sua descrição e etc.
Veremos com mais detalhes argumentos importantes de cada uma dessas funções nos tópicos seguintes e também como criarmos nossas próprias funções.
1.17 Exercícios
Resolva os exercícios sem a utilização do R.
Exercício 1.1 Qual o valor de T após a operação que segue?
T <- 100Exercício 1.2 Qual o valor final de y no código abaixo?
y <- 10
y <- 10 + yExercício 1.3 Qual o valor da soma de k + w no código a seguir?
k <- "10"
w <- "32"
k + wExercício 1.4 Você saberia explicar o motivo da operação abaixo retornar o valor lógico F?
x <- 3
x & 0## [1] FALSEExercício 1.5 Qual o resultado da operação lógica abaixo?
1 > 0 & 1 == 0 & 1 <=0Exercício 1.6 Qual o resultado da operação lógica abaixo?
!NA