2 Repaso de Estadística
La base necesaria para la econometría consiste en tener un entendimiento importante de algunos fundamentos de probabilidad e inferencia estadística. Esta sección hace un repaso no exhaustivo de algunos conceptos fundamentales que emplearemos. Se recomienda, sin embargo, que aquellos que no se sientan cómodos con alguos fundamentos básicos hagan una revisión de dichos conceptos para fortalecer su entendimmento de los temas vistos posteriormente. Crash course statistics es una referencia útil y fácilmente accesible para aquellos que quieran hacer un repaso de conceptos básicos de estadística.
2.1 Probabilidad
Esta sección consiste es un repaso muy breve y general de conceptos de probabilidad que se utilizarán a lo largo del curso1. En general, cuando hablamos de probabilidad es usual distinguir entre variables discretas y continuas. En términos prácticos, las variables discretas son aquellas que toman un pequeño número de valores posibles. Por su parte, las variables continuas son aquellas que pueden tener un número infinito de valores posibles. Usualmente, se les identifica como variables que toman un valor dentro de cierto rango de valores posibles.
Las variables suelen ser descritas por una función de densidad (pdf), la cual describe la probabilidad de que una variable tome cierto valor: \(f(x_j) = P(X=x_j) = p_j\) . Dicha función de densidad suele estar ligada a la función de densidad acumulada (cdf), que describe la probabilidad de que una variable tenga un valor menor o igual a cierto número: \(F(x_j) = P(X\leq x_j)\).
Cuando involucramos en nuestro análisis más de una variable, es común hacer referencia a la función de densidad conjunta: \(f_{X,Y}(x_j,y_k)= P(X = x_j,Y = y_k)\) y a la función de densidad marginal: \(f_X(x_j) = P(X = x_j )\). En el caso en que las variables \(X\) y \(Y\) sean independientes: \(f_{X,Y}=(x_j, y_k) = f_X(x_j)f_Y(y_k)\). Asimismo, con más de una variable, será común referirnos a la densidad condicional: \(f_{Y|X}(y_k|x_j) = \frac{f_{X,Y}(x_j,y_k)}{f_X(x_j)}\) . [En adelante, para simplificar únicamente utilizaremos \(x\) en vez de \(x_j\) y \(y\) en vez de \(y_k\). El único propósito de untilizar \(x_j\) y \(y_k\) era para indicar que son valores específicos, i.e. algún número. En adelante, cuando utilicemos minúsculas estaremos haciendo referencia a valores específicos.]
Valor esperado. El valor esperado es una medida de tendencia central. Si \(X\) es una variable discreta que toma \(k\) distintos posibles valores, tendremos que: \[E[X]=\sum_{j=1}^kx_jf(x_j)\] Asimismo, en el caso continuo: \[E[X]=\int_{-\infty}^{\infty}xf(x)\] Propiedades del valor esperado:
\(E(a) = a\), donde \(a\) es una constante
\(E(aX + bY + c) = aE(X) + bE(Y ) + c\), donde \(a,b,c\) son constantes
Varianza. La varianza describe, en promedio, que tan lejos suele estar una variable del valor esperado (\(\mu_X = E(X)\)). \[\sigma^2_X= Var(X) = E[(X-\mu_X)^2] = E(X^2)-\mu_X^2\] La desviación estándar es simplemente: \[\sigma_X=\sqrt{Var(X)}\]
Propiedades de la varianza:
\(Var(a) = 0\)
\(Var(aX+b)=a^2Var(X)\)
\(Var(aX\pm bY)=a^2Var(X)+b^2Var(Y)\pm ab Cov(X,Y)\)
Covarianza. La covarianza mide la relación entre dos variables. Una covarianza positiva indica que ambas variables suelen moverse en la misma dirección. Una covarianza negativa indica lo contrario \((\mu_Y = E(Y ))\) \[\sigma_{X,Y} = Cov(X, Y ) = E[(X-\mu_X)(Y-\mu_Y)]\] Propiedades de la covarianza:
\(Cov(X, Y ) = 0\) si \(X\) y \(Y\) son independientes
\(Cov(aX + b, cY + d) = acCov(X, Y )\), donde \(a, b, c, d\) son constantes
El coeficiente de correlación es simplemente: \(\rho_{X,Y} = corr(X,Y) = \frac{Cov(X,Y )}{\sigma_X\sigma_Y}\)
2.2 Notación
El análisis econométrico empírico generalmente involucra llevar a cabo una inferencia a partir de los datos a los cuales se tiene acceso (la muestra) acerca del comportamiento de cierta población. Obtener muestras representativas de la población acerca de la cual se busca aprender algo es fundamental y suele ser en un tema a desarrollar por si solo. A lo largo del curso daremos esta pregunta por resuelta y supondremos que tenemos acceso a datos de muestras representativas de cierta población.
La población es un grupo definido de unidades de observación que pueden estar o no restringidas de distintas formas (por ejemplo: geográfica, económica o demográficamente). Una unidad de observación puede ser desde una acción, como por ejemplo, un mensaje de texto enviado vía celular o una ruta específica de un punto a otro que una persona se traslada, hasta un ente con una identidad específica que puede ser desde individuos, empresas, ciudades o países. En resumen, la población es el grupo objetivo que se pretende estudiar. En gran parte de los estudios suele establecerse que nos interesa conocer algún aspecto específico de la población, típicamente un estadístico. Por ejemplo, es común indicar que nos interesa conocer la media de una variable o la correlación entre dos variables de dicha población. Siempre que nos interese un estadístico en específico, nos referiremos a éste como el parámetro poblacional de interés.
Por su parte, la muestra es un subconjunto de la población el cual será utilizado en el análisis empírico para poder decir algo acerca de la población. La muestra será aquella de la cual recopilaremos información que tendremos concentrada en una base de datos que utilizaremos con programas estadísticos para llevar a cabo el análisis. La inferencia generalmente conlleva hacer una estimación utilizando datos de la muestra con el objetivo de obtener conclusiones acerca de la población. Por ejemplo, utilizando diversas estrategias se plantean estimadores del parámetro poblacional, mismos que emplean datos de una muestra para dar evidencia e información específica de dicho parámetro.
Es importante conocer los detalles de la estrategia utilizada para recabar la muestra, ya que esto es indicativo de si dicha muestra es representativa de la población que se pretende2. Algunas causas de sesgos muestrales comunes incluyen sesgo de respuesta (i.e. el hecho de que las personas que no contestan no son personas al azar), problemas comprendiendo las preguntas y problemas encontrando ciertos tipos de individuos en la población. Estos problemas suelen llevar a sesgos muestrales, lo cual significa que la muestra puede no ser representativa de la población objetivo. Para evaluar esto, es útil tener una base de datos de comparación (i.e. un benchmark) que te permita determinar si las características de tu muestra son similares a aquellas características de la población objetivo. Los censos nacionales son un buen ejemplo de este tipo de benchmarks.
En estadística, generalmente nos referiremos al uso de muestras aleatorias debido a que eso nos asegura representatividad. En las muestras aleatorias cada uno de sus componentes se selecciona de forma independiente y proviene de una distribución común \(\{Y_1,\dots,Y_n\}\). En este caso se dice que \(Y_i\) es una variable aleatoria independiente e idénticamente distribuida (i.i.d.). Las variables aleatorias \(\{Y_1,\dots,Y_n\}\) son variables desconocidas. Una vez que la muestra es recabada tendremos un conjunto de números \(\{y_1,\dots, y_n\}\), los cuales utilizaremos para llevar a cabo inferencia.
Ejemplo: Supón que nuestra variable de interés es la media de la edad de los alumnos cursando educación superior en México.
¿Cuál es la población?
¿Cómo recabarías una muestra para poder obtener/hacer una estimación válida?
¿Qué sucedería si yo recabo una muestra basada en los alumnos del ITAM o de la clase?
A continuación buscamos utilizar nuestra muestra para conocer algo acerca del parámetro. Para ello plantearemos un estimador. El estimador en si es una fórmula que utiliza como insumo los elementos de la muestra y entrega como resultado un valor que pretende aproximar al parámetro poblacional objetivo. Es incorrecto pensar en que el estimador tiene valores específicos (a pesar de que el parámetro poblacional si lo tenga) dado que el estimador en si es una estrategia que se plantea para aproximar lo mejor posible al parámetro poblacional. Al utilizar los valores específicos de la base de datos a la cual tenemos acceso y aplicar la fórmula del estimador para obtener un valor específico, estaremos hablando de un valor estimado. Para calificar si un estimador es apropiado y si es mejor o peor que otro, solemos hablar de propiedades que nos ayudan a calificarlo, como insesgadez y eficiencia.
Ejemplo: Continuando con el ejemplo de la media de edad de alumnos en educación superior en México: supongamos a partir de aquí que se recaba una muestra aleatoria \(\{Y_1,\dots,Y_n\}\)
Parámetro: \(\mu\). Es un número específico que típicamente no es conocido. En este caso, es la media de la edad de todos los alumnos cursando educación media superior en México.
Estimador: \(W=h(Y_1,\dots,Y_n)\). Es una fórmula que genera un estimador del parametro.
Valor estimado: \(w=h(y_1,\dots,y_n)\). Es un número específico que resulta de aplicar la fórmula del estimador a la muestra recabada.
Definimos a continuación las propiedades deseables de los estimadores:
El estimador (\(W\)) de un parámetro (\(\mu\)) es insesgado si su valor esperado es igual al parámetro: \(E(W)=\mu\). Si un estimador es insesgado, esto no quiere decir que el valor estimado será igual al parámetro (o incluso cercano a éste), ya que esto dependerá de la muestra que sea recabada.
Un estimador (\(W_1\)) es más eficiente relativamente a otro (\(W_2\)) si \(Var(W_1)\leq Var(W_2)\).
Ejemplo: Consideremos dos estimadores para el parámetro \(\mu\):
El valor promedio: \(W_1=\frac{1}{n}\sum_{i=1}^n Y_i=\bar{Y}\)
El promedio de edad de dos personas de mi muestra elegidas al azar: \(W_2=\frac{Y_a+Y_b}{2}\)
¿Son estos estimadores insesgados?, ¿cuál es más eficiente?, ¿qué valor estimado estará más cerca de la media poblacional?
2.3 Propiedades asintóticas de los estimadores
En el ejemplo anterior podemos deducir que el estimador \(W_1\) se vuelve más eficiente conforme el tamaño de muestra aumenta. Las propiedades asintóticas de los estimadores son aquellas que aplican cuando se tienen muestras grandes. Sin embargo, no es claro de qué tamaño necesita ser el número de observaciones (\(n\)) para que la muestra sea considerada como grande y sea correcto aplicar las propiedades asintóticas a los estimadores. Generalmente, esto depende de la distribución poblacional de la variable de interés, pero en la mayoría de los casos en los que utilizamos encuestas, aplicar propiedades asintóticas será razonable.
Ejemplo: Dar un ejemplo mostrando dos distribuciones normales, una más dispersa que la otra.
Consistencia. La consistencia se refiere al comportamiento de la distribución muestral del estimador conforme el tamaño de la muestra se incrementa. Conforme aumentamos el tamaño de la muestra, la distribución de \(W_1\) se volverá más concentrada alrededor de \(\mu\). Por lo tanto, menos probable será que un valor estimado se ubique lejos de \(\mu\).
Ejemplo: ¿Es el estimador \(W_2\) consistente?
Ley de Grandes Números (LGN). La ley de grandes números nos dice que si queremos aproximarnos a la media poblacional, podemos hacerlo en gran medida si elegimos muestras lo suficientemente grandes y utilizamos el estimador del promedio. Sin embargo, utilizando la LGN únicamente obtenemos estimadores puntuales y no tenemos información acerca de su distribución.
Teorema Central del Límite (TCL). Sea \(\{Y_1,\dots,Y_n\}\) una muestra aleatoria con media \(\mu\) y varianza \(\sigma^2\). Entonces, \[\begin{equation} Z_n=\frac{\sqrt{n}(\overline{Y}_n-\mu)}{\sigma}\xrightarrow{d}N(0,1) \text{ conforme $n\xrightarrow{}\infty$} \end{equation}\]
Intuitivamente, este resultado indica que, sin importar la distribución poblacional de Y, la distribución de la variable \(Z_n\) (que es la versión estandarizada de \(\overline{Y}_n\)) se aproxima en gran medida a una distribución normal estándar (\(N(0,1)\)) conforme el tamaño de la muestra (\(n\)) aumenta3.
2.4 Pruebas de hipótesis
En la gran mayoría de las aplicaciones empíricas de econometría tendremos que llevar a cabo pruebas de hipótesis. En dichas pruebas de hipótesis es importante notar que evaluamos si el parámetro es igual a cierto valor en el caso de la hipótesis nula. Esto es particularmente adecuado debido a que el parámetro es un número específico que es (usualmente) desconocido para el econometrista. Generalmente, durante el curso asumiremos que las muestras son grandes y por tanto podemos aplicar propiedades asintóticas, Esto quiere decir que en la mayoría de los casos podremos utilizar la distribución normal y ji-cuadrada para llevar a cabo las pruebas de hipótesis.
Para repasar cómo llevar a cabo pruebas de hipótesis supongamos que estamos interesados en evaluar si la media de edad de los alumnos en educación media superior en México es igual a \(20\). Cabe señalar que nuestra hipótesis es acerca del valor de un parámetro poblacional y utilizaremos una muestra para evaluar dicha hipótesis. La hipótesis nula debe establecerse como igualdad debido a que en la evaluación de la hipótesis se asume que es cierta y eso genera una distribución para el estadístico que se utilizará. En nuestro ejemplo, establecemos la siguiente hipótesis nula:
\[\begin{equation*} H_0: \mu=20 \end{equation*}\]
La hipótesis alternativa se establece para especificar la zona de rechazo de la hipótesis nula. Generalmente, en una prueba se busca rechazar la hipótesis nula en favor de la alternativa. En nuestro caso, la hipótesis alternativa será: \[\begin{equation*} H_1: \mu\neq 20 \end{equation*}\]
La hipótesis alternativa puede también ser establecida como \(\mu>20\) (o \(\mu<20\)). Este sería el caso si lo que nos interesa es evaluar si la media poblacional es mayor (menor) a \(20\). Es importante recordar que como resultado de la prueba de hipótesis, la hipótesis nula puede ser rechazada o no rechazada. Sin embargo, es incorrecto decir que es aceptada. Formalmente, en el ejemplo anterior podríamos concluir ya sea que: (i) hay evidencia suficiente para rechazar que la media poblacional es igual a \(20\) con \(x\%\) de significancia, o que (ii) no hay evidencia suficiente para rechazar que la media poblacional es igual a 20 con \(x\%\) de significancia.
Para establecer el nivel de significancia \(x\%\) (o alternativamente el nivel de confianza \([1-x]\%\)), hay que tomar en cuenta los dos tipos de errores que podemos cometer al evaluar pruebas de hipótesis:
Error tipo I: Podemos rechazar la hipótesis nula siendo que esta es verdadera
Error tipo II: Podemos no rechazar la hipótesis nula siendo esta falsa
Típicamente, el nivel de significancia se establece basado en el error tipo I, que generalmente busca reducirse en las pruebas de hipótesis. Dada nuestra notación, el nivel de significancia se define como:
\[x\%=Pr(\text{Rechazar}\phantom{t}H_0|H_0)=Pr(\text{Error tipo I})\]
El valor de \(x\%\) será una valor que tendremos que asumir para llevar a cabo la prueba de hipótesis. El valor más común es de 0.05 (o \(5\%\)) de significancia, seguido de 0.01 y 0.1 (lo cual es equivalente a \(95\%\), \(99\%\) y \(90\%\) de nivel de confianza, respectivamente).
El error tipo II suele estar ligado al poder estadístico. Más adelante en el curso discutiremos cómo utilizar el poder estadístico para determinar el número de observaciones que se requieren para llevar a cabo un análisis estadístico experimental.
Supongamos por el momento que elegimos un nivel de significancia de \(5\%\) y que nuestra muestra de estudiantes mexicanos es aleatoria y consta de \(1000\) individuos. Supongamos que el promedio muestral de edad es de \(21.5\) y la varianza de las edades de \(500\).
Tenemos 3 alternativas para llevar a cabo la prueba de hipótesis:
2.4.1 Estadístico \(t\)
Para utilizar este método utilizamos la media y la desviación estándar estimada. La idea es asumir que la hipótesis nula es verdadera. Dado que asumimos esto, querremos determinar qué tan probable es que obtengamos un valor estimado \(\overline{y}=21.5\), dado que proviene de una distribución de la variable aleatoria \(\overline{Y}\) que es normal (por propiedades asintóticas) con media \(20\) y desviación estándar \(\sqrt{500/1000}\).
Tomando dichos supuestos y aplicando el TCL estandarizamos \(\overline{Y}\), con lo cual derivamos nuestro estadístico \(t\), mismo que tendrá una distribución \(N(0,1)\):
\[\begin{equation} t=\frac{(\overline{Y}-\mu_0)}{\sqrt{S^2/n}} \longrightarrow~N(0,1) \end{equation}\]
Y finalmente, de dicha distribución obtenemos un valor: \[\begin{equation*} \widehat{t}=\frac{(21.5-20)}{\sqrt{500/1000}}=2.1213 \end{equation*}\]
Una vez que tenemos dicho valor utilizamos la distribución de la normal estándar para comparamos este valor con un referente que esté en el límite de ser razonable (el valor crítico). Para ello empleamos el nivel de significancia. Utilizando un \(5\%\) de significancia determinamos que valor crítico (en términos absolutos) representa el \(95\%\) del cdf de la distribución normal estándar. Dicho valor (1.96) se compara con el valor estimado para determinar qué tan probable es observarlo dada la distribución de la cual asumimos que proviene (debido a que supusimos que la hipótesis nula es cierta). Dado que el estadístico-\(t\) es mayor que el valor crítico rechazamos la hipótesis nula con un \(5\%\) de significancia a favor de la hipótesis alternativa.
2.4.2 Valor-p
El valor-p nos dice hasta qué nivel de significancia la hipótesis nula sería rechazada. Siempre que el nivel de significancia sea mayor al valor-p, la hipótesis nula sería rechazada. Para determinar significancia a los niveles usuales, este valor usualmente se compara con \(0.01\), \(0.05\) y \(0.1\). Sin embargo, el valor-p tiene el significado en si mismo de informar que probabilidad existe de observar un valor igual o más extremo que el obtenido de la muestra. En nuestro ejemplo:
\[\begin{equation} \textit{valor-p}=2\cdot(1-F(|t|))=0.034 \end{equation}\]
Es importante, tener en consideración que en el caso en que la hipótesis alternativa sea unilateral (one-sided), \(\textit{valor-p}=(1-F(|t|))\).
2.4.3 Intervalo de confianza
Si nuevamente utilizamos un nivel de significancia de \(5\%\), necesitaremos determinar un intervalo de confianza del \(95\%\). Dicho intervalo de confianza se genera de la siguiente forma:
\[\begin{equation} \begin{split} Pr\biggl(-1.96<\frac{\sqrt{n}(\overline{Y}-\mu)}{S}<1.96\biggl)&=0.95\\ Pr\biggl(\overline{Y}-1.96\cdot\frac{S}{\sqrt{n}}<\mu<\overline{Y}+1.96\cdot\frac{S}{\sqrt{n}}\biggl)&=0.95\\ \end{split} \end{equation}\]
En el caso del intervalo de confianza es importante recordar que la incertidumbre radica en el intervalo dado que \(\overline{Y}\) es una variable aleatoria. El intervalo lo podemos interpretar como: de cada \(100\) muestras aleatorias que obtengamos, \(95\%\) de ellas tendrán al valor real del parámetro poblacional \(\mu\). No podemos decir que una vez que calculemos el intervalo, con \(95\%\) de probabilidad éste contendrá el valor real del parámetro. Recordemos que el parámetro es un valor específico (no aleatorio), por lo tanto, se encuentra o no en el intervalo.
En nuestro caso, el intervalo de \(95\%\) será: \([20.114,22.88]\). Dado que \(20\) no se encuentra dentro del intervalo, rechazamos la hipótesis nula con un \(5\%\) de significancia.
Para las pruebas unilaterales la alternativa al intervalo de confianza es el límite (o cota) inferior o superior. Imaginemos que en el caso de nuestro ejemplo nuestra hipótesis alternativa es:
\[\begin{equation*} H_1: \mu > 20 \end{equation*}\]
En este caso nos interesaría comparar a el valor propuesto (\(20\)) con la cota inferior (\(C_I\)), dado que nuestro “intervalo” consistiría en: \([C_I,\infty)\). Para calcular la cota:
\[\begin{equation} \begin{split} Pr\biggl(\mu > \overline{Y}-1.64\cdot\frac{S}{\sqrt{n}} \biggl)&=0.95\\ Pr\biggl(\frac{\sqrt{n}(\overline{Y}-\mu)}{S} < 1.64 \biggl)&=0.95\\ \end{split} \end{equation}\]
En el caso de nuestro ejemplo la cota inferior sería \(20.34\), y como dicho valor es mayor a \(20\), concluiríamos que la hipóitesis nula se rechazaría a favor de nuestra nueva hipótesis alternativa unilateral.Ejemplo
Imaginen que queremos estimar el número promedio de contactos de Facebook que tienen los alumnos en el ITAM. Dicho número existe y es desconocido. Le llamaremos parámetro poblacional y lo denotaremos como \(\mu_x\). Para poder obtener dicho número tendríaamos que entrevistar a TODOS los alumnos del ITAM y preguntarles estos datos para finalmente poder calcular un promedio. Sin embargo, llevar a cabo ese ejercicio puede ser costoso (en términos de tiempo) y tedioso. Afortunadamente, la estadística nos ofrece una alternativa.
Imaginen que en lugar de entrevistar a todos los alumnos del ITAM (a los cuales nos referiremos para propósitos de este ejercicio como la población decidimos entrevistar a algunos. Con esto conformamos una muestra que denotaremos como \(\{X_1,\dots,X_n\}\) y utilizamos esos datos para calcular un promedio. A dicho promedio le llamaremos un estimador y lo denotaremos como \(\bar{X}_n\).
Antes de seguir adelante detengámonos a pensar:
¿Qué estrategia seguirían para elegir a esa muestra?
¿Qué sucedería si, dada la situación de Covid, decido solo recopilar información de aquellos estudiantes que son amigos míos en FB?
¿Cuántas personas necesito entrevistar para tener una muestra decente?
Ahora pensemos que les deje este ejercicio de tarea y cada uno de ustedes elije una muestra y calcula el promedio. Tomémos el caso de uno de ustedes. El alumno elegido por mi (lo llamaremos alumno A) resulta que obtuvo una muestra que denotaremos como \(\{x^A_1,\dots,x^A_n\}\) y a partir de dicha muestra obtuvo un promedio que denotaremos como \(\bar{x}_A\), al cual llamaremos valor estimado (en clase tendremos un número específico). Sin embargo, pudiera haber ocurrido que en vez de elegir al alumno A hubiera elegido al otro alumno (lo llamaremos alumno B). En este caso, la muestra y, por lo tanto, el valor estimado hubieran sido distintos. Es por ello, que al estimador, es decir, al promedio de los valores de la muestra lo llamaremos variable aleatoria. Con estimador, solo me refiero a la estrategia que seguimos, es decir, a aplicar la formula de la media utilizando los datos obtenidos por el alumno \(i\).
Imaginemos ahora que no imponemos que tienen que elegir la media como estimador. Cada persona elige libremente su estrategia (i.e. estimador). Una vez que todos ustedes recabaron muestras aleatorias, es decir, independientes e idénticamente distribuidas, i.i.d. ¿Qué podría hacer para comparar los estimadores de dos alumnos y decidir con cuál quedarme? Para esto necesitaremos los conceptos de insesgadez y eficiencia.
Ahora, supongamos que ya elegí al mejor estimador de entre todos los que tenía disponibles en el salón. Utilizando este estimador tengo valores específicos para los estimadores de la media y de la varianza:
\[\begin{equation} \begin{split} \bar{x}_n=&\sum_{i=1}^n x_i=215 \\ \sigma^2_{\bar{x}}=&\frac{\sigma^2_x}{n}=2500 \end{split} \end{equation}\]
¿Con estos datos puedo asegurar que \(\bar{x}_n\) es el valor mas cercano a \(\mu_x\) de entre todos los posbiles valores estimados que me propusieron? En caso de que no, ¿por qué no simplemente elijo el valor estimado mas cercano a \(\mu_x\) de entre todos los que me hayan propuesto?
Imaginemos ahora que un estudiante sabe que estamos haciendo estos cálculos y asegura ser muy popular dado que tiene \(100\) contactos de Facebook. Cuando les mencionamos que nuestro mejor estimador es \(250\) se burla de nosotros y asegura que la media realmente es \(150\). ¿Podríamos asegurar con certeza que se equivoca?
R: No. Pero el uso de la estadística se enfoca más en cuestionarse qué tan probable es que yo haya obtenido un valor estimado de \(250\) dado que el valor verdadero de \(\mu_x\) es \(150\). Para esto utilizaremos pruebas de hipótesis. Pero antes de poder llevar a cabo pruebas de hipótesis necesitamos saber algo acerca de la distribución de \(\bar{X}_n\). Para esto utilizaremos la ley de grandes números y el teorema central del límite.
Utilizando el teorema central del límite llego a la conclusión de que puedo utilizar una distribución \(N(250,50)\) para evaluar mis pruebas de hipótesis. Ahora puedo llevar a cabo el siguiente ejercicio. Imaginémos que le decimos al estudiante popular: “supongamos que estas en lo correcto y \(\mu_x=150\). Dado que eso es cierto veamos la probabilidad de observar una media mayor o igual a \(250\) en una muestra aleatoria.”
\[\begin{equation} \begin{split} Pr(\bar{X} \geq 250) &= Pr\biggl(\frac{\bar{X}-150}{\sqrt{2500}} \geq \frac{250-150}{\sqrt{2500}} \biggl) \\ &= Pr(Z \geq 2) = 0.02275 \end{split} \end{equation}\]
Por lo tanto, no podemos asegurar que este estudiante se equivoque, si estuviera en la correcto es muy poco probable que con una muestra aleatoria de las características que tenemos, sería muy poco probable observar la media que observamos. Este cálculo que acabamos de realizar es cercano a lo que conocemos como el valor-p. El valor-p nos dice cuál es la probabildad de obtener un estadístico (en este caso la media) que sea más inusual que el observado, dado que la hipótesis planteada es cierta.
El ejercicio que llevamos a cabo anteriormente en realidad es literalmente lo que hacemos al llevar a cabo una prueba de hipótesis. En clase veremos más formalmente todos los elementos de una prueba de hipótesis y enq eu consisten las alternativas para evaluarla.2.5 Bootstrap
En el caso de las pruebas de hipótesis anteriores estamos basando los resultados en el teorema central del límite. Para aplicar el TCL calculamos analíticamente la varianza de la media como:
\[\begin{equation} Var(\overline{Y})=\frac{\sigma^2}{n} \end{equation}\] donde \(\sigma^2\) es la varianza de \(Y_i\).
En el caso de TCL asumimos que una versión estandarizada de \(\overline{Y}\) (\(Z_n\)) converge en distribución a una normal estándar. Una alternativa a este procedimiento consiste en generar una distribución empírica de \(\overline{Y}\) y utilizar dicha distribución para calcular la varianza. Un problema con esta idea radica en que para generar una distribución empírica de \(\overline{Y}\) necesitamos varias observaciones de \(\overline{Y}\).
El método de bootstrap genera diversas observaciones partiendo de una muestra aleatoria \(\{Y_1,\dots,Y_n\}\) siguiendo los siguientes pasos:
Utilizando las observaciones de la muestra, elige una submuestra aleatoria de tamaño \(n\) (mismo tamaño que la muestra) con reemplazo. Esto quiere decir que habrá observaciones que se repitan más de una vez
Usando la submuestra calcula el estimador (\(\overline{Y}\) en nuestro ejemplo)
Repite los pasos anteriores \(M\) veces. Con esto tendrás \(M\) observaciones para \(\overline{Y}\): \(\{\overline{Y}_1,\dots,\overline{Y}_M\}\) y habrás generado una distribución empírica
Genera los estimadores: \[\begin{equation} \begin{split} E(\overline{Y})=&\frac{1}{M}\sum\limits_{k=1}^M \overline{Y}_k\\ Var(\overline{Y})=&\frac{1}{M}\sum\limits_{k=1}^M (\overline{Y}_k-E(\overline{Y}))^2 \end{split} \end{equation}\]
Utiliza dichos estimadores para llevar a cabo pruebas de hipótesis
Este método puede ser aplicado con la mayoría de los estimadores que veremos durante el curso. Es un método de gran utilidad siempre que sea dificil calcular una varianza para llevar a cabo pruebas de hipótesis. En particular podría utilizarse para calcular errores estándar de los coeficientes en una regresión. En dicho caso los pasos a seguir son los mismos que los descritos anteriormente. Lo que sucedería en el caso de una regresión de mínimos cuadrados ordinarios es que se llevaría a cabo una regresión con cada una de las submuestras elegidas en el primer paso. Con ello se obtendrían \(M\) posibles coeficientes para cada variable. El error estándar podría calcularse como la desviación estándar para cada uno de los coeficientes.
Existe también la posibilidad de utilizar una submuestra de tamaño menor al tamaño de la muestra original (\(n\)). En dicho caso, tendría que llevarse a cabo un ajuste al cálculo de la varianza. Supongamos que se eligen submuestras de tamaño \(L\). Todos los pasos serían los mismos que los descritos anteriormente, con la diferencia que el estimador de la varianza se calcularía como:
\[\begin{equation} Var(\overline{Y})=\frac{L}{n}\frac{1}{M}\sum\limits_{k=1}^M (\overline{Y}_k-E(\overline{Y}))^2 \end{equation}\]
Ejemplo
Bootstrap e intervalos de confianza para la media muestral
A continuación se presenta un ejemplo de Bootstrap realizado en R. En el ejemplo utilizaremos datos sobre la pandemia de COVID-19 provenientes del sitio Our World in Data. La base contiene información sobre la pandemia hasta el día 27 de agosto de 2020 para 188 países. En este ejemplo nos interesará estimar la media de la tasa de contagios \(\left(TC=\frac{\text{Casos Confirmados}}{\text{Población}}\right)\).
options(scipen=999)
## Iniciaremos trabajando con toda la población ##
Pop<-as.data.frame(read.csv('COVID.csv'))#Cargamos la base poblacional
#Antes de comenzar el ejemplo
#revisemos de forma rápida las variables con las que contamos:
library(tidyverse)
as_tibble(Pop)## # A tibble: 188 x 25
## ISO_code continent country confirmed deaths confirmed_per_m… deaths_per_mill…
## <fct> <fct> <fct> <int> <int> <dbl> <dbl>
## 1 ABW North Am… Aruba 1760 8 16485. 74.9
## 2 AFG Asia Afghan… 38126 1401 979. 36.0
## 3 AGO Africa Angola 2332 103 71.0 3.13
## 4 ALB Europe Albania 8927 263 3102. 91.4
## 5 AND Europe Andorra 1098 53 14211. 686.
## 6 ARE Asia United… 68020 378 6877. 38.2
## 7 ARG South Am… Argent… 370175 7839 8190. 173.
## 8 ARM Asia Armenia 43067 861 14534. 291.
## 9 ATG North Am… Antigu… 94 3 960. 30.6
## 10 AUS Oceania Austra… 25205 549 988. 21.5
## # … with 178 more rows, and 18 more variables: stringency_index <dbl>,
## # population <int>, population_density <dbl>, median_age <dbl>,
## # aged_65_older <dbl>, aged_70_older <dbl>, gdp_pc <dbl>,
## # extreme_poverty <dbl>, cardiovasc_death_rate <dbl>,
## # diabetes_prevalence <dbl>, female_smokers <dbl>, male_smokers <dbl>,
## # handwashing_facilities <dbl>, hospital_beds_per_thousand <dbl>,
## # life_expectancy <dbl>, people_tested <int>, tests_performed <int>,
## # tests_uu <lgl>Pop<-Pop%>%mutate(
TC=confirmed/population
) #Creamos la variable de Tasa de Contagios (TC)
library(ggplot2)
library(scales)
ggplot(Pop,aes(TC))+geom_histogram(aes(y=..count../sum(..count..)),
fill='palegreen4',bins = 25)+
xlab('Tasa de Contagio')+ylab('Proporción')+
ggtitle('Histograma para TC (Utilizando la población)')+
theme_minimal()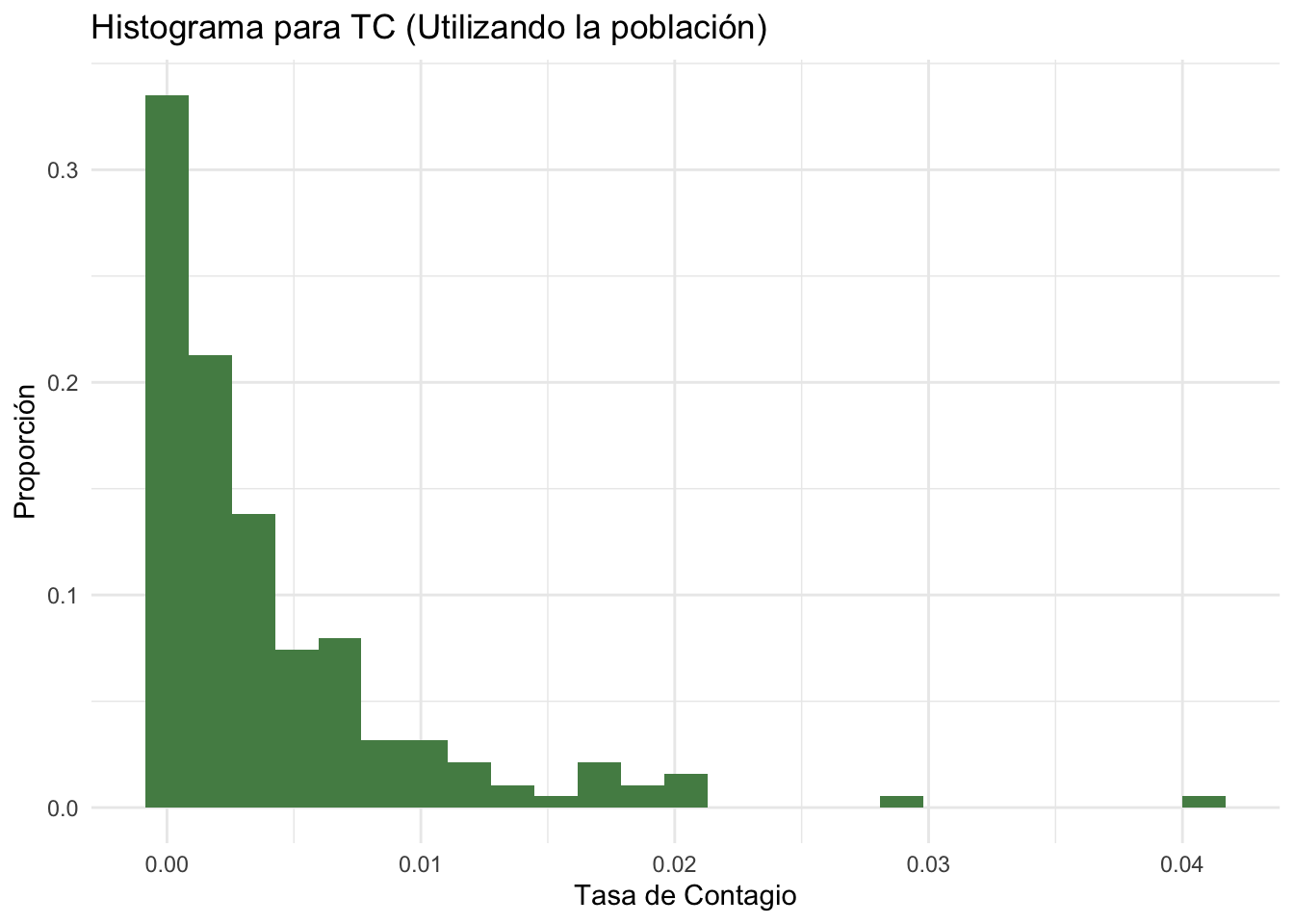
## [1] 0.004158544## Trabajemos ahora con una muestra de la población ##
#Ahora crearemos una muestra aleatoria de tamaño 100 a partir
#de la base poblacional
Samp<-sample_n(Pop,100,replace = FALSE)
Samp<-Samp%>%mutate(
TC=confirmed/population
)
#Realizamos nuevamente un histograma
ggplot(Samp,aes(TC))+geom_histogram(aes(y=..count../sum(..count..)),
fill='slategray3',bins = 25)+
xlab('Tasa de Contagio Muestral')+ylab('Proporción')+
ggtitle('Histograma para TC (Utilizando la muestra)')+
theme_minimal()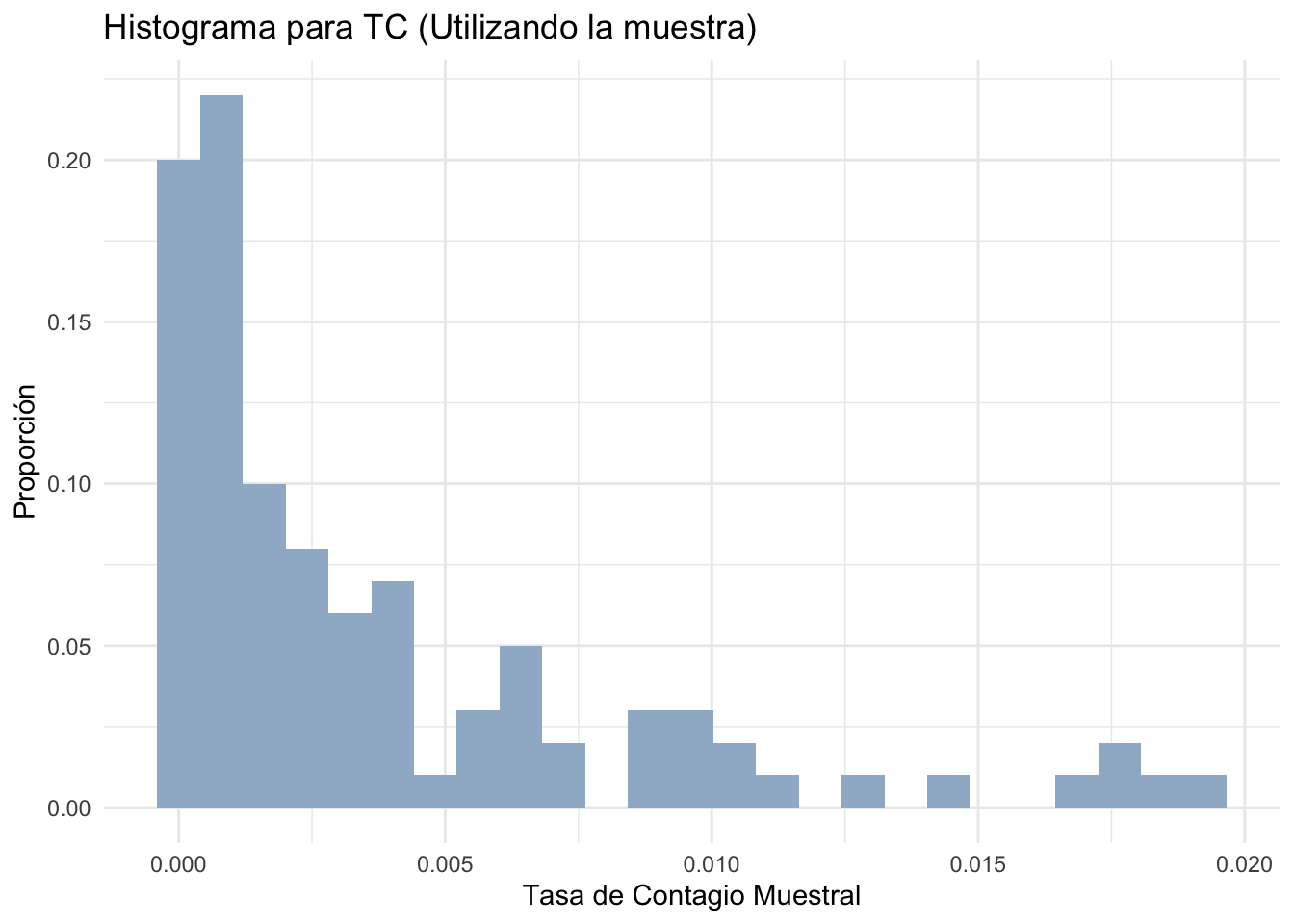
#Esta gráfica nos muestra el histograma de la variable TC
#a partir de la muestra
(meanTC<-mean(Samp$TC,na.rm = TRUE)) #Calculamos la media muestral## [1] 0.004156287## [1] 0.00004069051## [1] 0.0000004069051#Realizamos un Bootstrap de 1,000 submuestras del tamaño
#de la muestra original (n=100)
meanBoot<-c() #Creamos un vector vacío
for (n in 1:1000){
meanBoot<-c(meanBoot,mean(sample(Samp$TC,100,replace = TRUE)))
}
meanBoot<-as.data.frame(meanBoot)
#Ahora crearemos un histograma para la
#media muestral de TC (calculadas a partir de bootstrap)
ggplot(meanBoot,aes(meanBoot))+
geom_histogram(aes(y=..count../sum(..count..)),fill='lightblue',
bins = 20)+
xlab('Medias muestrales (Bootstrap)')+ylab('Proporción')+
geom_vline(xintercept=meanTCpop,colour='red4')+
geom_label(mapping = aes(x = meanTCpop, y =.05,
label = round(meanTCpop,6),
hjust = -.5, vjust =-.5),colour='red4')+
ggtitle('Histograma de la media muestral')+
theme_minimal()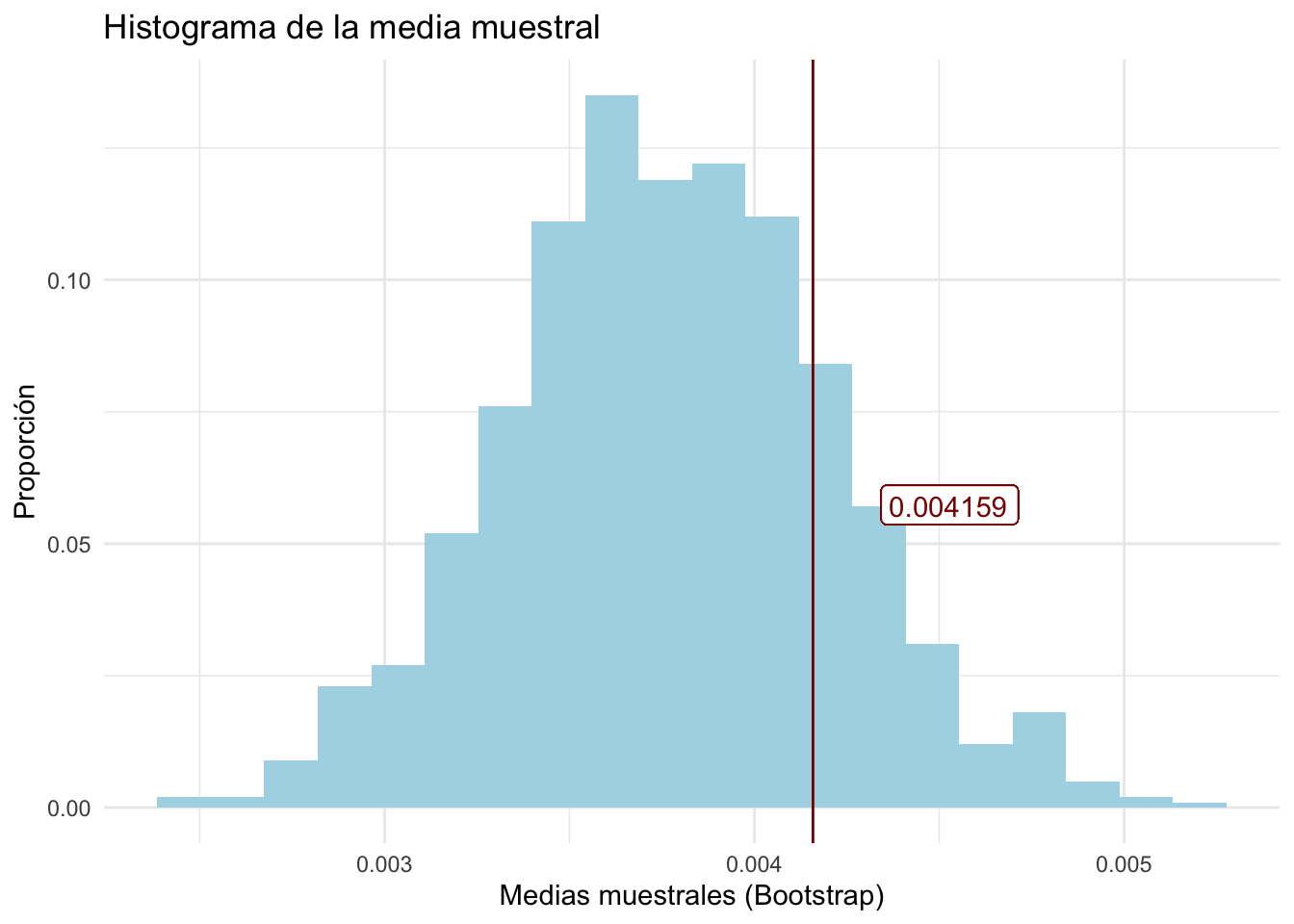
#La línea vertical muestra la media poblacional de TC
#dicho numero es nuestro objetivo
#Utilizando los resultados del Bootstrap, podemos estimar
#la varianza de la media muestral de TC:
(varTCbar_boot<-var(meanBoot$meanBoot))## [1] 0.0000004170734#Comparemos los valores de la varianza de la media muestral
#de TC que hemos obtenido:
paste('De forma analítica obtuvimos: ', varTCbar)## [1] "De forma analítica obtuvimos: 0.000000406905087870913"## [1] "A través del Bootstrap se obtuvo: 0.000000417073432474772"##Ahora calcularemos intervalos de confianza al 95% para
#la media de TC considerando dos estrategias##
#1) Usemos el estimador de la media muestral
#y el de la varianza de la media muestral
llimitm_1<-meanTC-1.96*sqrt(varTCbar)
ulimitm_1<-meanTC+1.96*sqrt(varTCbar)
paste('El IC al 95% (', llimitm_1,',',ulimitm_1,')')## [1] "El IC al 95% ( 0.0029060203781041 , 0.0054065535896931 )"#2) Usemos los resultados que obtuvimos en Bootstrap
llimitm_2<-mean(meanBoot$meanBoot)-1.96*sqrt(varTCbar_boot)
ulimitm_2<-mean(meanBoot$meanBoot)+1.96*sqrt(varTCbar_boot)
paste('El IC al 95% (', llimitm_2,',',ulimitm_2,') (Bootstrap)')## [1] "El IC al 95% ( 0.00288013315951664 , 0.00541171708915049 ) (Bootstrap)"#Grafiquemos los intervalos de confianza anteriores
lowerm<-c(llimitm_1,llimitm_2)
upperm<-c(ulimitm_1,ulimitm_2)
meansm<-c(meanTC,mean(meanBoot$meanBoot))
estm<-c('Tradicional','Bootstrap')
intervalsm<-data_frame(estm,lowerm,meansm,upperm)
ggplot(intervalsm,aes(x=meansm,y=estm))+
geom_point()+
geom_errorbarh(aes(xmin=lowerm,xmax=upperm),
size=1,height=0.1)+
xlab('Tasa de Contagios')+ylab('Método')+
geom_vline(xintercept = meanTCpop,colour='red4')+
ggtitle('Intervalos de Confianza al 95% para la media de TC')+
theme_minimal()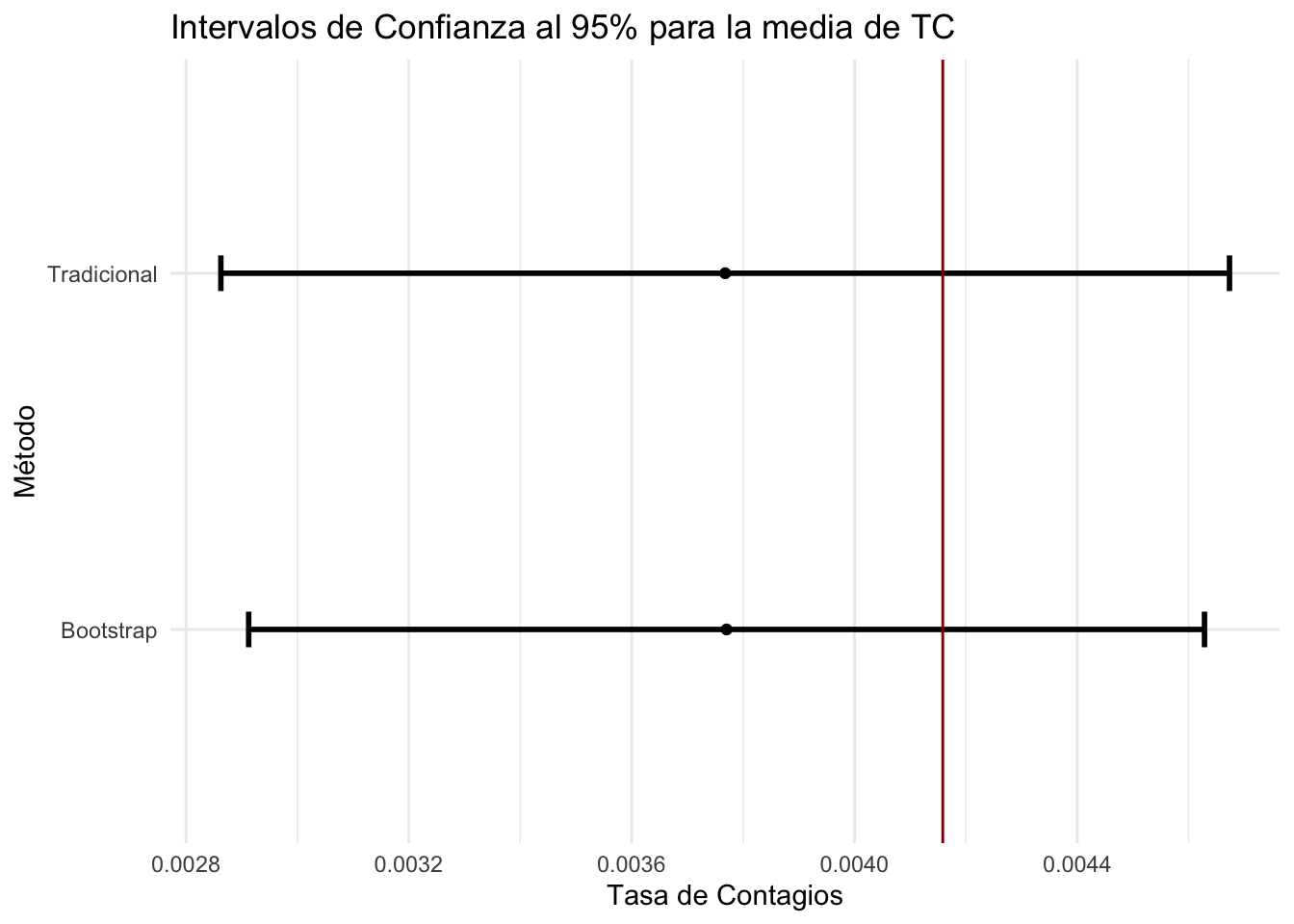
Ejemplo
Bootstrap e intervalos de confianza para otros estadísticos
Consideremos nuevamente la base de datos que utilizamos en el ejemplo anterior. Ahora estaremos interesados en calcular el ratio del percentil 90 entre el percentil 10 \(\left(\varphi=\frac{P_{90}}{P_{10}}\right)\) para la tasa de mortalidad \(\left(TM=\frac{\text{Muertes}}{\text{Casos Confirmados}}\right)\). Este ratio nos indica cuántas veces mayor es la tasa de mortalidad del pais en el percentil 90 contra aquel del percentil 10.
## Iniciaremos trabajando con toda la población ##
Pop<-Pop%>%mutate(
TM=deaths/confirmed
) #Creamos la variable de Tasa de Mortalidad (TM)
#Graficamos el histograma poblacional de TM
ggplot(Pop,aes(TM))+
geom_histogram(aes(y=..count../sum(..count..)),fill='palegreen4',
bins = 25)+
xlab('Tasa de Mortalidad')+ylab('Proporción')+
ggtitle('Histograma para TM (Utilizando la población)')+
theme_minimal()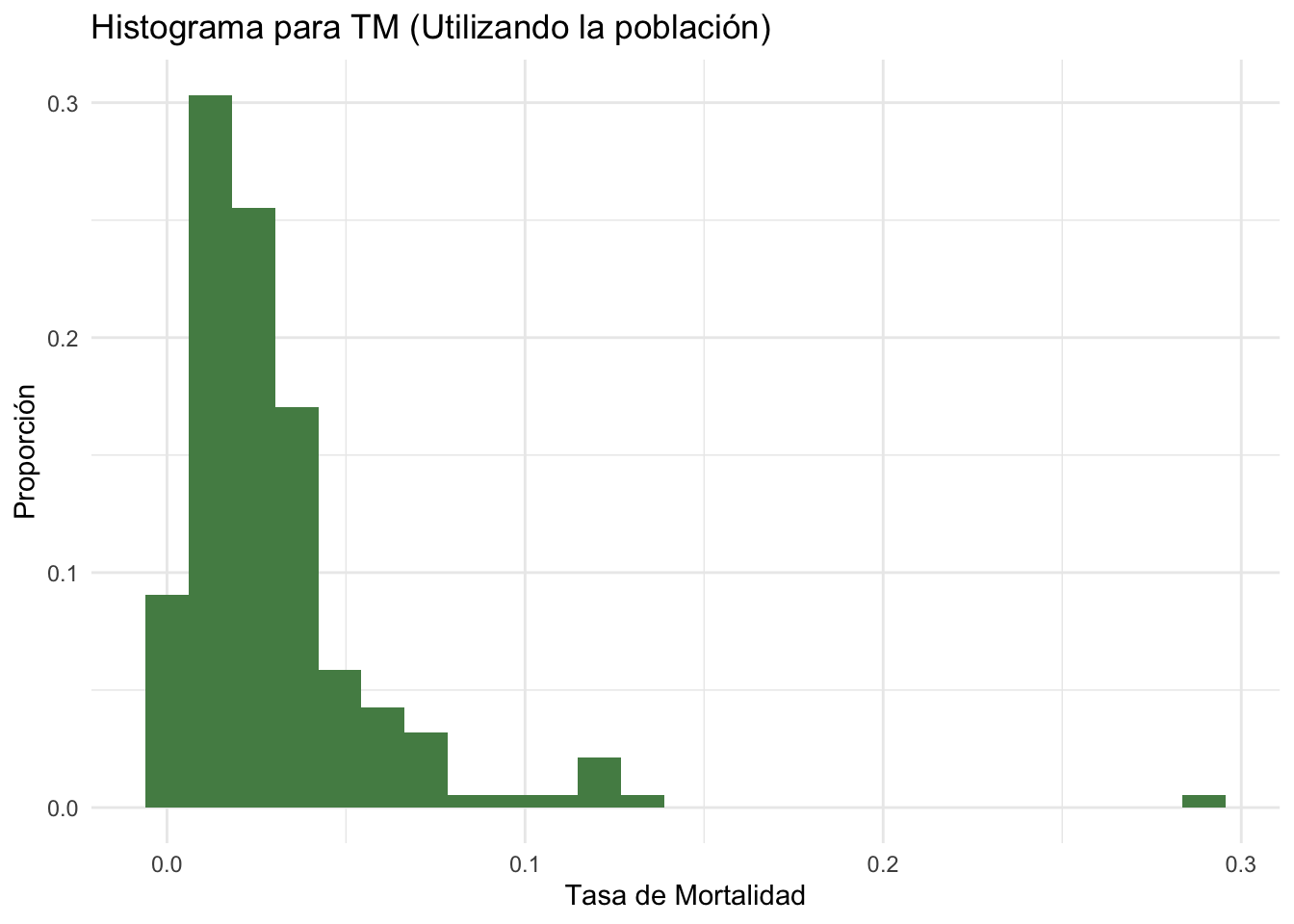
#Calculamos ahora el ratio de P_90 entre P_10:
p90pop<-quantile(Pop$TM,0.9,type = 2)
p10pop<-quantile(Pop$TM,0.1,type = 2)
rat90_10pop<-p90pop/p10pop
paste('El ratio es igual a ',rat90_10pop)## [1] "El ratio es igual a 9.51356560415122"## Trabajemos ahora con una muestra de la población ##
#Utilizaremos la muestra con la que trabajamos en
#el ejemplo anterior
Samp<-Samp%>%mutate(
TM=deaths/confirmed
)
#Graficamos el histograma de TM para la muestra
ggplot(Samp,aes(TM))+
geom_histogram(aes(y=..count../sum(..count..)),fill='slategray3',bins = 25)+
xlab('Tasa de Mortalidad')+ylab('Proporción')+
ggtitle('Histograma para TM (Utilizando la muestra)')+
theme_minimal()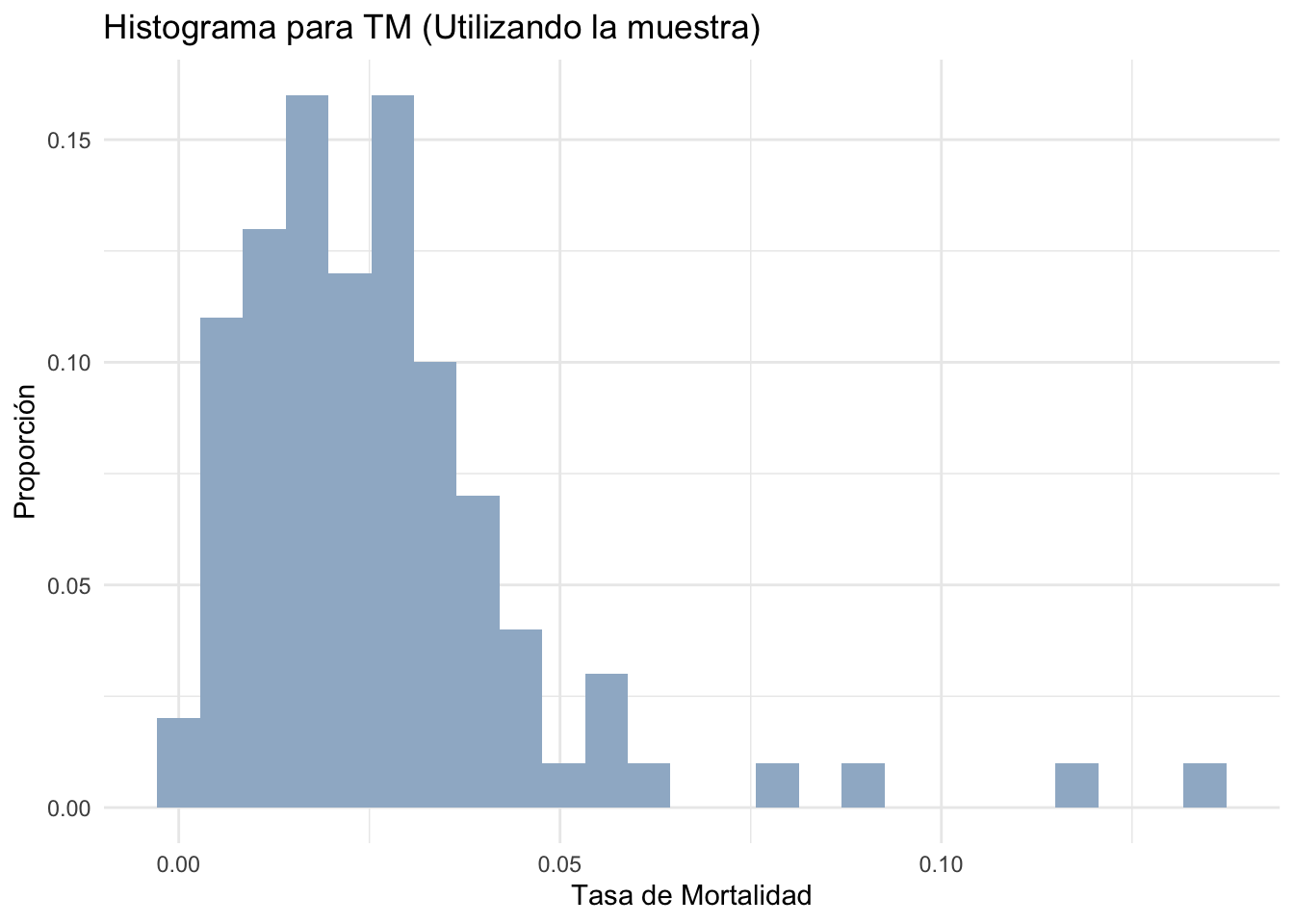
#A partir de la muestra estimaremos el ratio P_90 entre P_10:
p90samp<-quantile(Samp$TM,0.9,type = 2)
p10samp<-quantile(Samp$TM,0.1,type = 2)
rat90_10samp<-p90samp/p10samp
paste('El valor estimado del ratio es igual a ',rat90_10samp)## [1] "El valor estimado del ratio es igual a 9.89484687905606"#A diferencia del ejemplo anterior, para el caso de este ratio
#es complicado obtener una expresión analítica para su varianza.
#Por tanto, para estimar dicha varianza utilizaremos Bootstrap:
rat90_10Boot<-c()
for (n in 1:1000){
sampleboot<-c()
sampleboot<-sample(Samp$TM,100,replace = TRUE)
rat90_10Boot<-c(
rat90_10Boot,
quantile(sampleboot,0.9,type = 2)/quantile(sampleboot,0.1,type = 2))
}
rat90_10Boot<-as.data.frame(rat90_10Boot)
#Ahora crearemos un histograma para el ratio
#(calculadas a partir de bootstrap)
ggplot(rat90_10Boot,aes(rat90_10Boot))+
geom_histogram(aes(y=..count../sum(..count..)),fill='lightblue',
bins = 20)+
xlab('Ratio P_90/P_10 (Bootstrap)')+ylab('Proporción')+
geom_vline(xintercept=rat90_10pop,color='red4')+
geom_label(mapping = aes(x = rat90_10pop, y =.125,
label = paste(round(rat90_10pop,6)),
hjust=-.5,vjust=-.5),colour='red4')+
ggtitle('Histograma del ratio P_90/P_10')+
theme_minimal()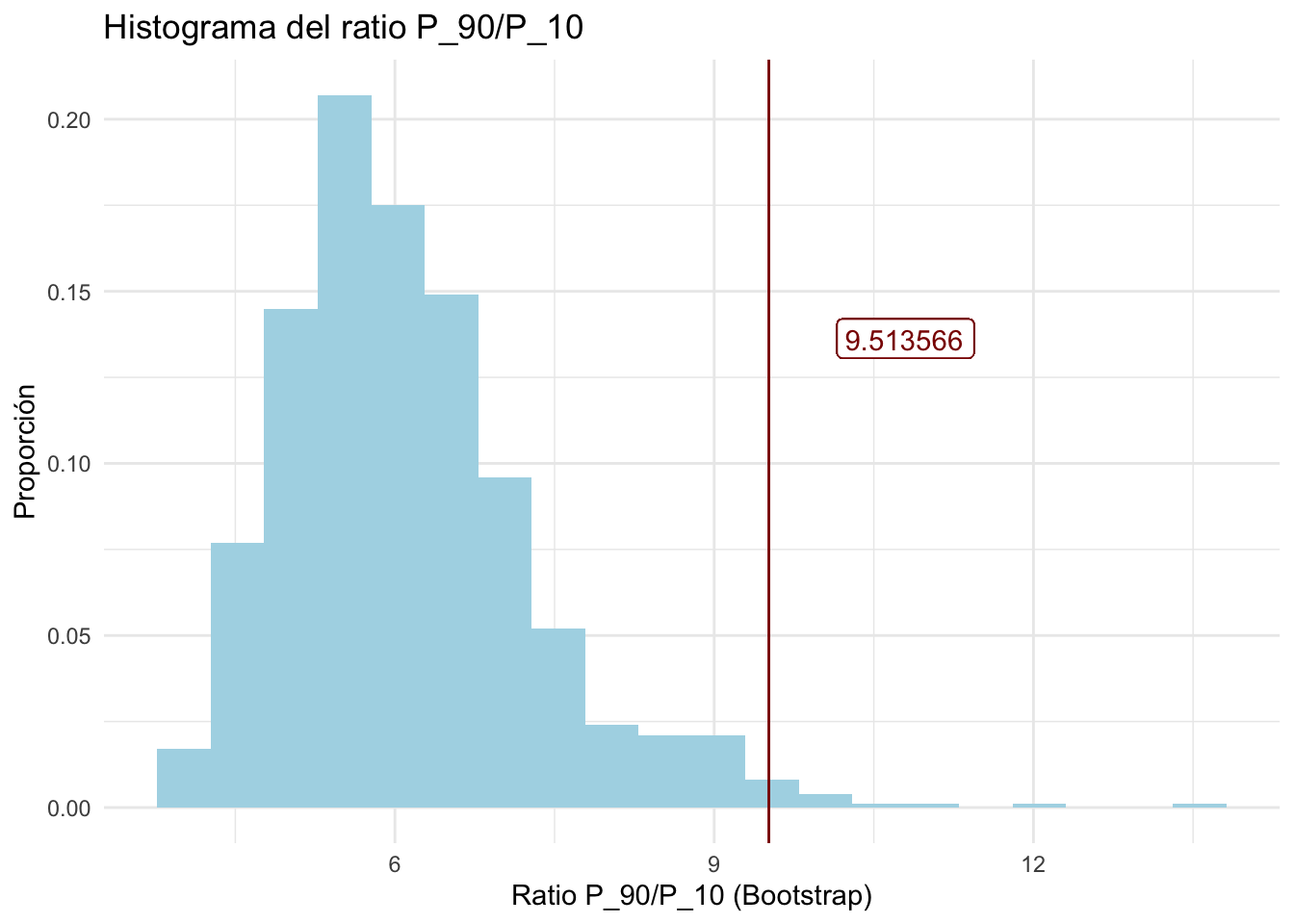
#La línea vertical muestra el valor del ratio P_90/P_10 poblacional
#el cual es el número que tenemos como objetivo
#Al observar el histograma, podemos notar que la distribución
#del ratio P_90/P_10 muestral no corresponde a la de una Normal
#Considerando esto último, calculemos intervalos de confianza
#al 95% utilizando las submuestras del Bootstrap a través de dos estrategias:
#1) Asumamos que el ratio P_90/P_10 muestral se distribuye Normal:
llimitr_1<-mean(rat90_10Boot$rat90_10Boot)-1.96*sd(rat90_10Boot$rat90_10Boot)
ulimitr_1<-mean(rat90_10Boot$rat90_10Boot)+1.96*sd(rat90_10Boot$rat90_10Boot)
paste('El IC al 95% es (', llimitr_1,',',ulimitr_1,') asumiendo normalidad')## [1] "El IC al 95% es ( 5.58510673347569 , 16.2811134671227 ) asumiendo normalidad"#Asumiendo normalidad
#1) Utilicemos la distribución empírica que obtuvimos a través del
#Bootstrap para el ratio P_90/P_10 muestral
#Para esto calculamos el valor del percentil 2.5 y el del percentil 97.5.
#De esta forma obtenemos el intervalo de valores en los cuales se acumula el 95%:
llimitr_2<-quantile(rat90_10Boot$rat90_10Boot,.025,type = 2)
ulimitr_2<-quantile(rat90_10Boot$rat90_10Boot,.975,type = 2)
paste('El IC al 95% es (', llimitr_2,',',ulimitr_2,') utilizando la distribución empírica')## [1] "El IC al 95% es ( 6.8022426153951 , 17.1003416545612 ) utilizando la distribución empírica"#Utilizando la distribución empírica
#Grafiquemos los intervalos de confianza anteriores
lowerr<-c(llimitr_1,llimitr_2)
upperr<-c(ulimitr_1,ulimitr_2)
meansr<-c(mean(rat90_10Boot$rat90_10Boot),mean(rat90_10Boot$rat90_10Boot))
estr<-c('Normal','Dist. Empírica')
intervalsr<-data_frame(estr,lowerr,meansr,upperr)
ggplot(intervalsr,aes(x=meansr,y=estr))+
geom_point()+
geom_errorbarh(aes(xmin=lowerr,xmax=upperr),size=1,height=0.1)+
xlab('Tasa de Letalidad')+ylab('Método')+
geom_vline(xintercept = rat90_10pop,colour='red4')+
ggtitle('Intervalos de Confianza al 95% para el ratio P_90/P_10')+
theme_minimal()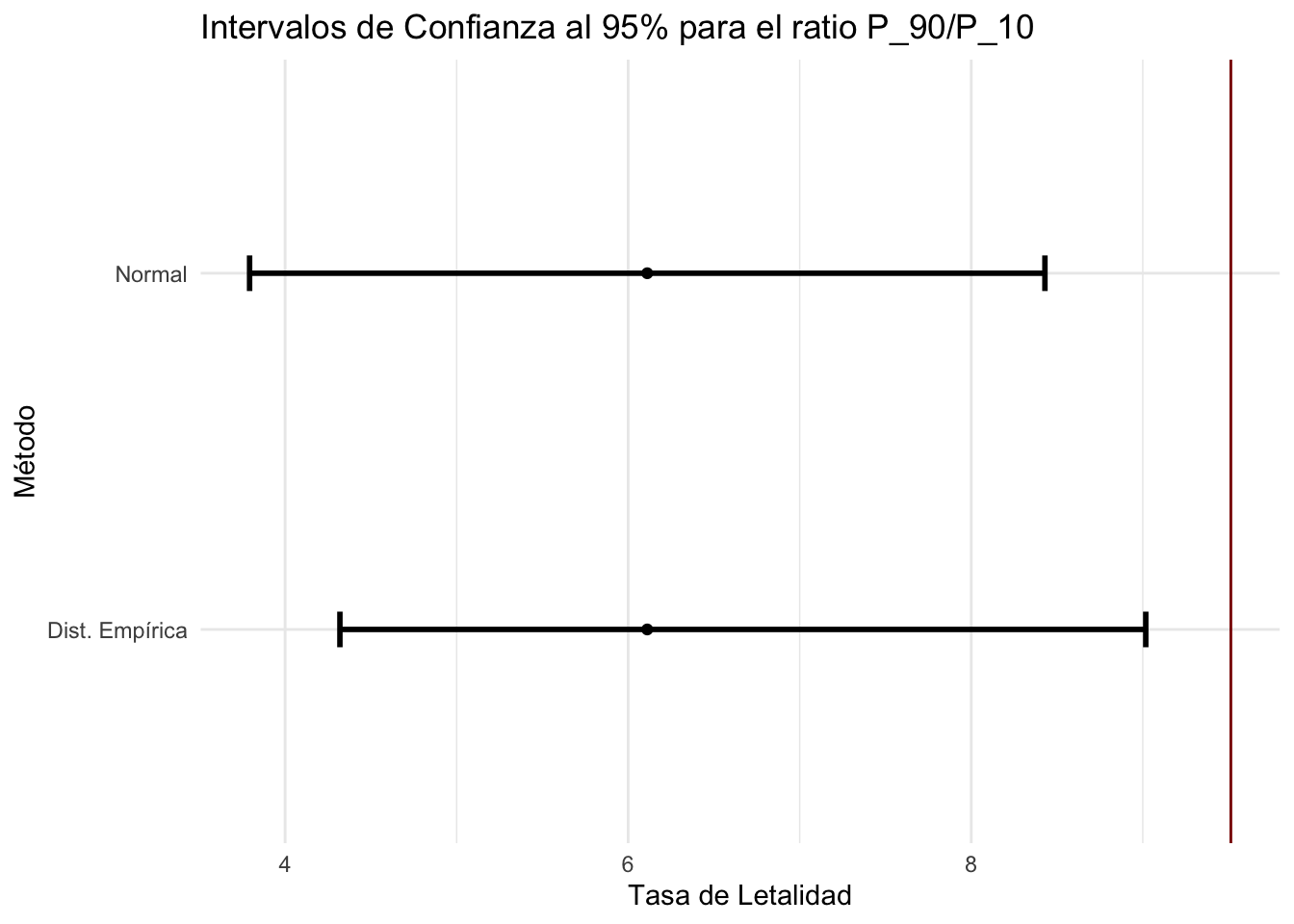
Aquellos alumnos que sientan que necesitan un repaso más a detalle, se recomienda que revisen el capítulo 2 del Stock y Watson o el apéndice B del Wooldridge.↩︎
Para conocer mas acerca de muestreo se recomienda ver el video https://youtu.be/Rf-fIpB4D50↩︎
En clase haremos simulaciones utilizando la página http://faculty.carrollu.edu/ckuster/CT/Central\%20Limit\%20Theorem\%20Simulation.html para dar una mayor intuición acerca del tema.↩︎