4 Efectos Fijos y Aleatorios

En la nota anterior concluimos que el modelo MCO es extremadamente útil, ya que con muestras grandes y pocos supuestos podemos estimar relaciones funcionales entre dos variables que son sencillas de interpretar. Sin embargo, subrayamos que una limitación importante del modelo cuando queremos establecer relaciones causales es el sesgo por variables omitidas. En esta nota se explicará un modelo que para resolver el problema de sesgo por variables omitidas impone supuestos en dichas variables omitidas y hace uso de una estructura de datos de panel.

4.1 Datos de Panel

Tradicionalmente nos referimos a datos de panel (o datos longitudinales) cuando nuestra unidad de observación (ya sea un individuo, una familia, una empresa, un país, etc.) es captada en dos o más ocasiones a través del tiempo. Es importante que la misma unidad (i.e. el mismo individuo, la misma empresa, etc.) sea captada en cada momento a través del tiempo⁶. En este caso, la notación que utilizaremos para las variables es \(Y_{it}\), donde \(i\) es el subíndice que indica al individuo y \(t\) el que indica tiempo. Por ejemplo, si tenemos una muestra de ingreso y educación para 100 individuos en 3 años, nuestra muestra será \((Ing_{it},Educ_{it})_{(i=1,\dots,100),(t=1, 2, 3)}\). En particular, \((Ing_{54,2},Educ_{54,2})\) representará el ingreso y la educación para el individuo 54 en el año 2.

Sin embargo, cabe resaltar que en la especificación del modelo no es estrictamente necesario que \(t\) represente tiempo. Por ejemplo, \(i\) podría representar familias y \(t\) podría representar hermanos; \(i\) podría representar municipios y \(t\) ciudades; \(i\) podría representar partidos políticos y \(t\) candidatos.

La clave de la estructura de la base de datos de panel es que exista un factor en común -\(i\)- que permita agrupar a más de una observación. En el ejemplo clásico de distintas observaciones a través del tiempo, el factor común es el individuo, quien es observado en distintos momentos. En los otros ejemplos planteados, las familias, los municipios y los partidos políticos son factores que comparten distintas observaciones.

Se dice que una base de datos de panel es balanceada cuando cada individuo es observado en todos los momentos del tiempo. En el contexto de los otros ejemplos que planteamos, esto quiere decir que cada agrupación \(i\) tiene la misma cantidad de componentes (i.e. cada familia de la muestra tiene la misma cantidad de hermanos, etc.). Muchos de los modelos presentados a continuación no requieren de un panel balanceado forzosamente, pero es importante tomar en cuenta (especialmente en el ejemplo clásico de unidades observadas a lo largo del tiempo) que un panel no balanceado puede resultar de pérdida de observaciones a lo largo del tiempo. Esto se conoce como abandono de la muestra (sample attrition) y puede ser un factor relevante, ya que podría estar relacionado con tener una muestra sesgada.

Introducción a Datos Panel

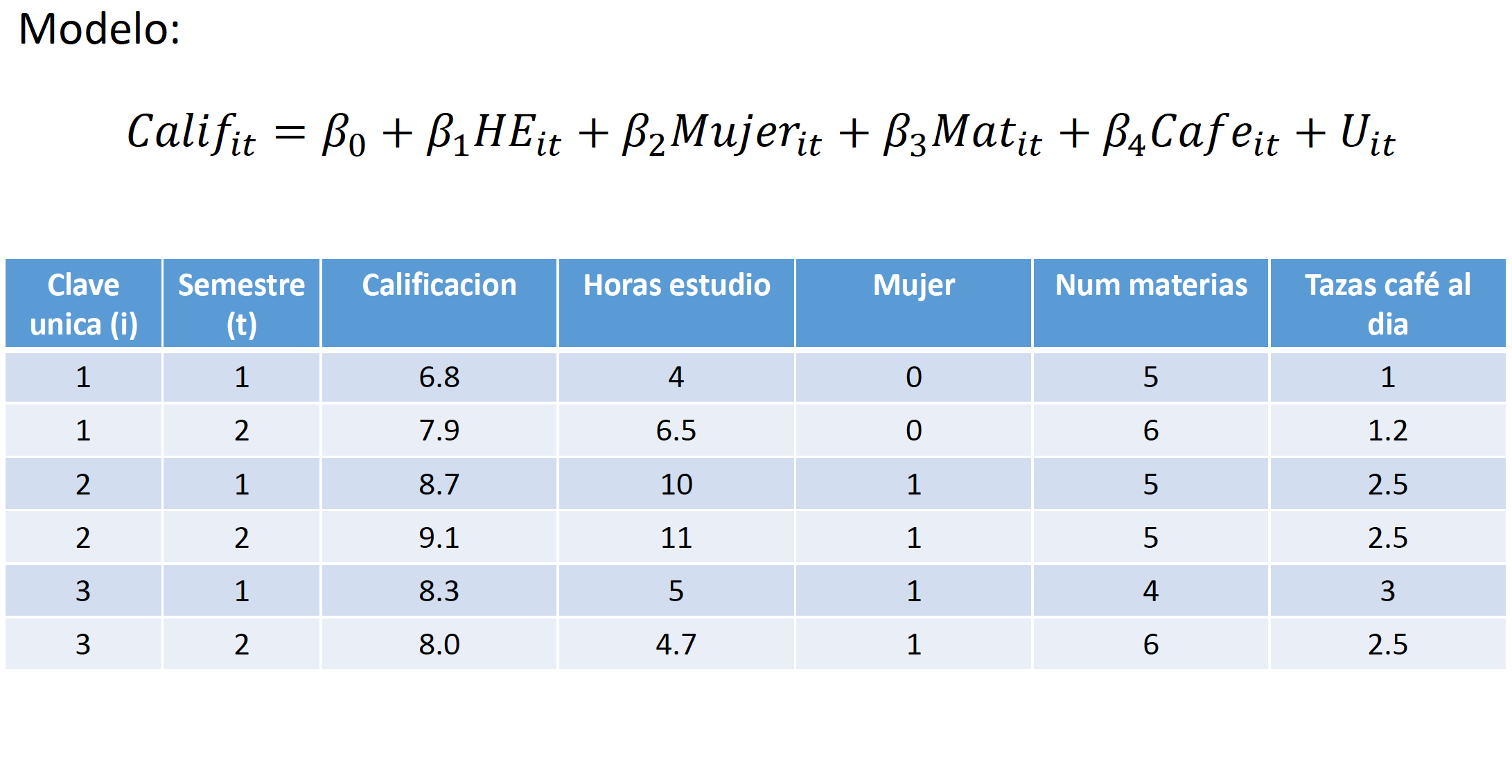
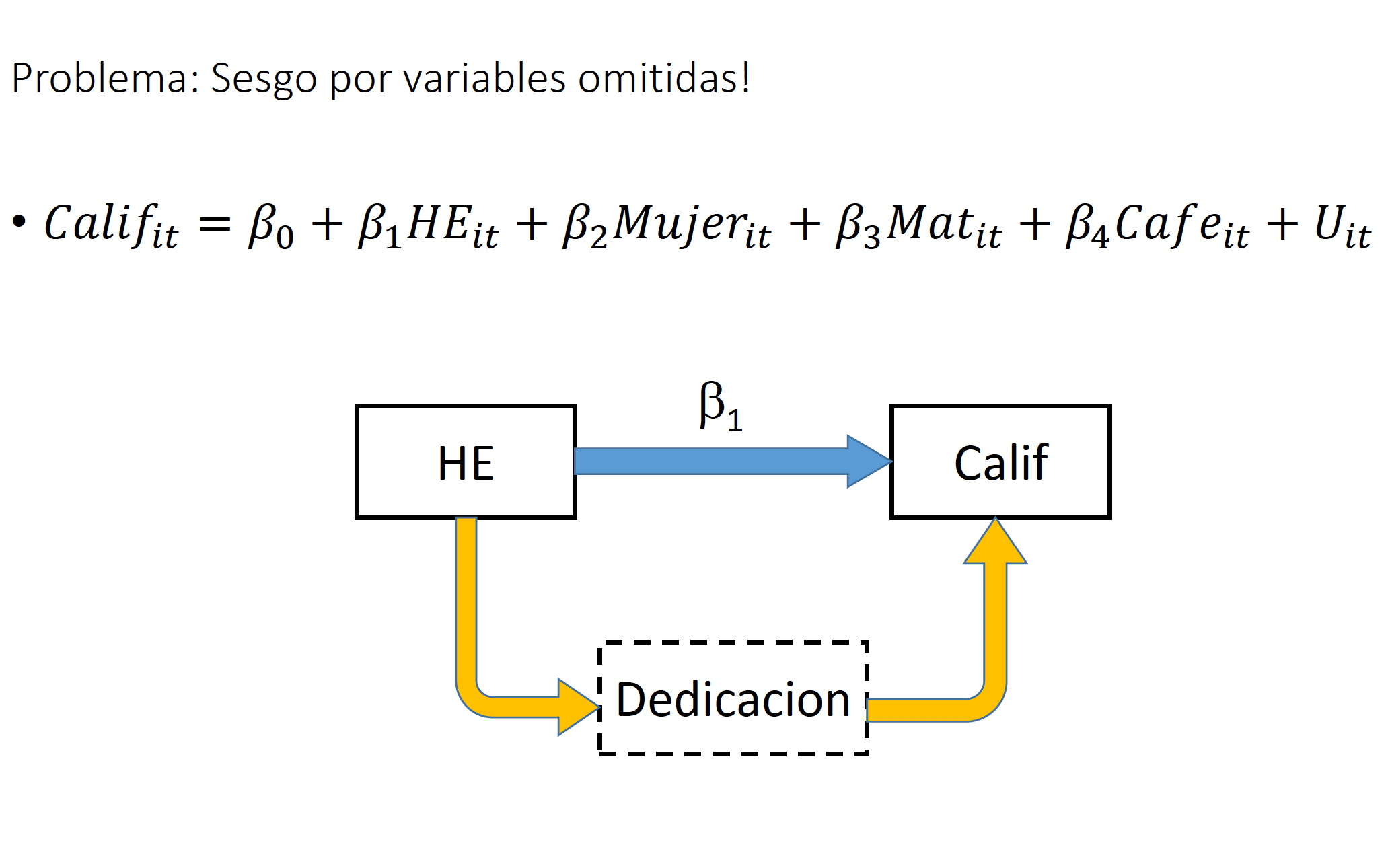
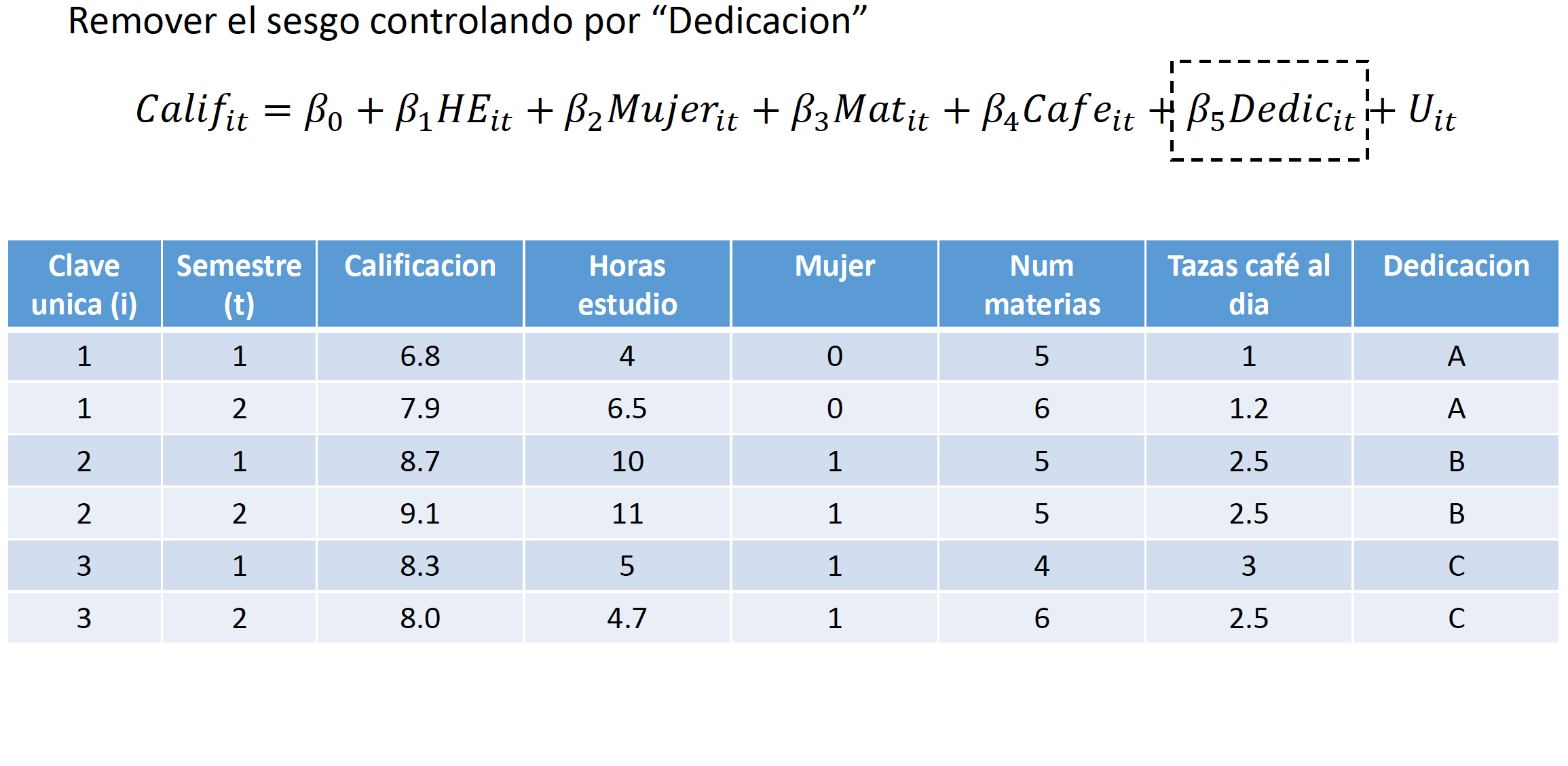
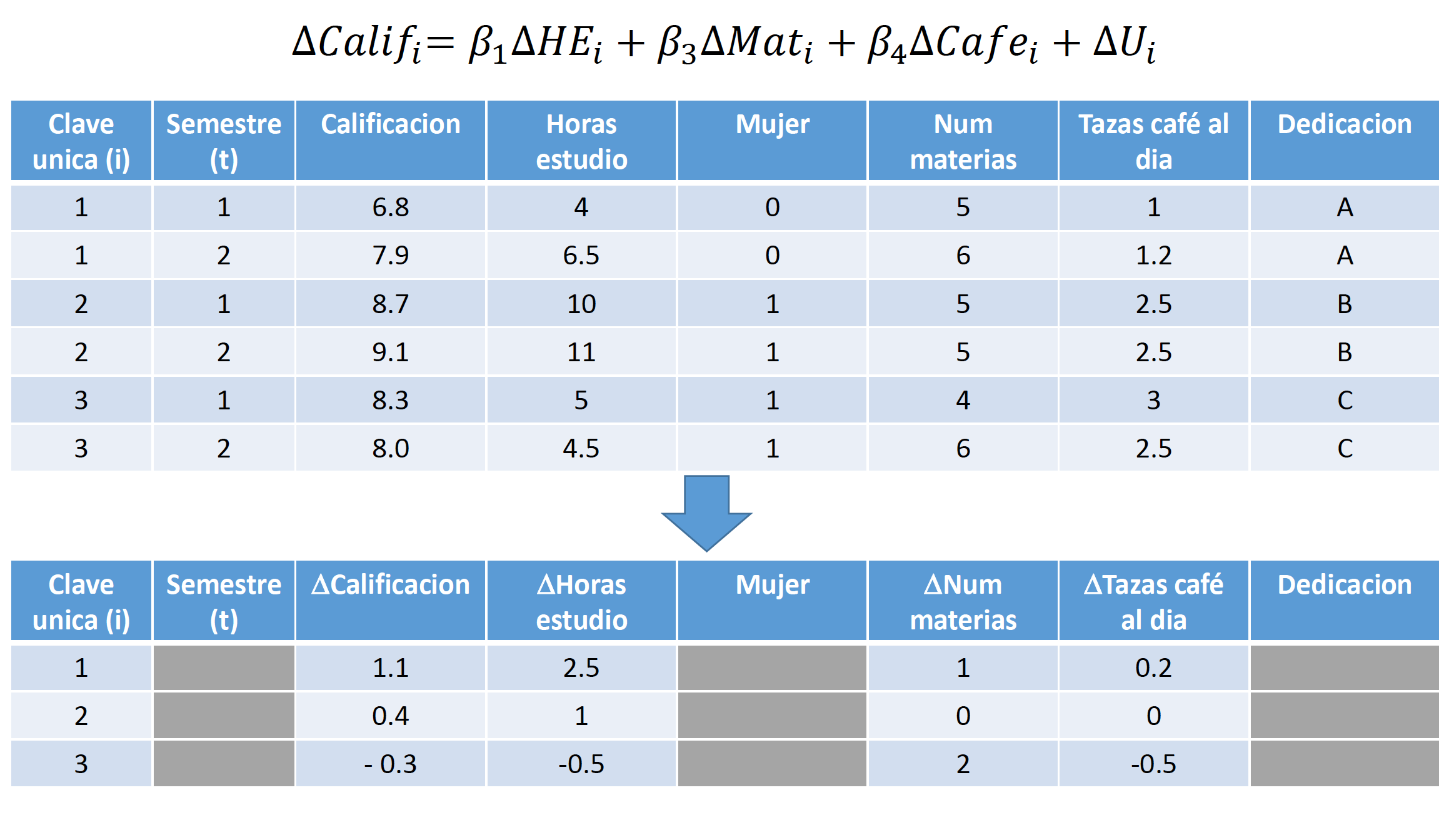
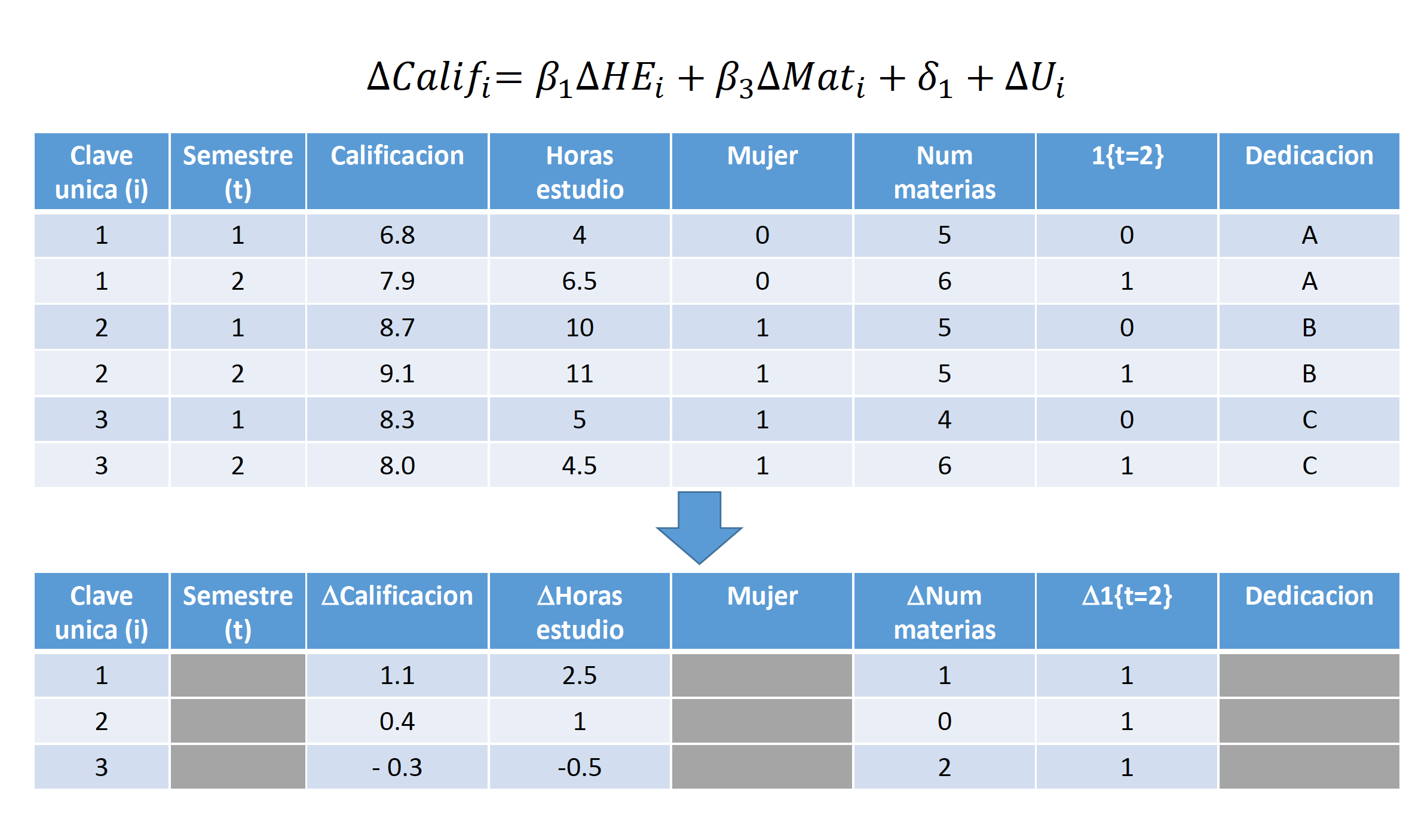
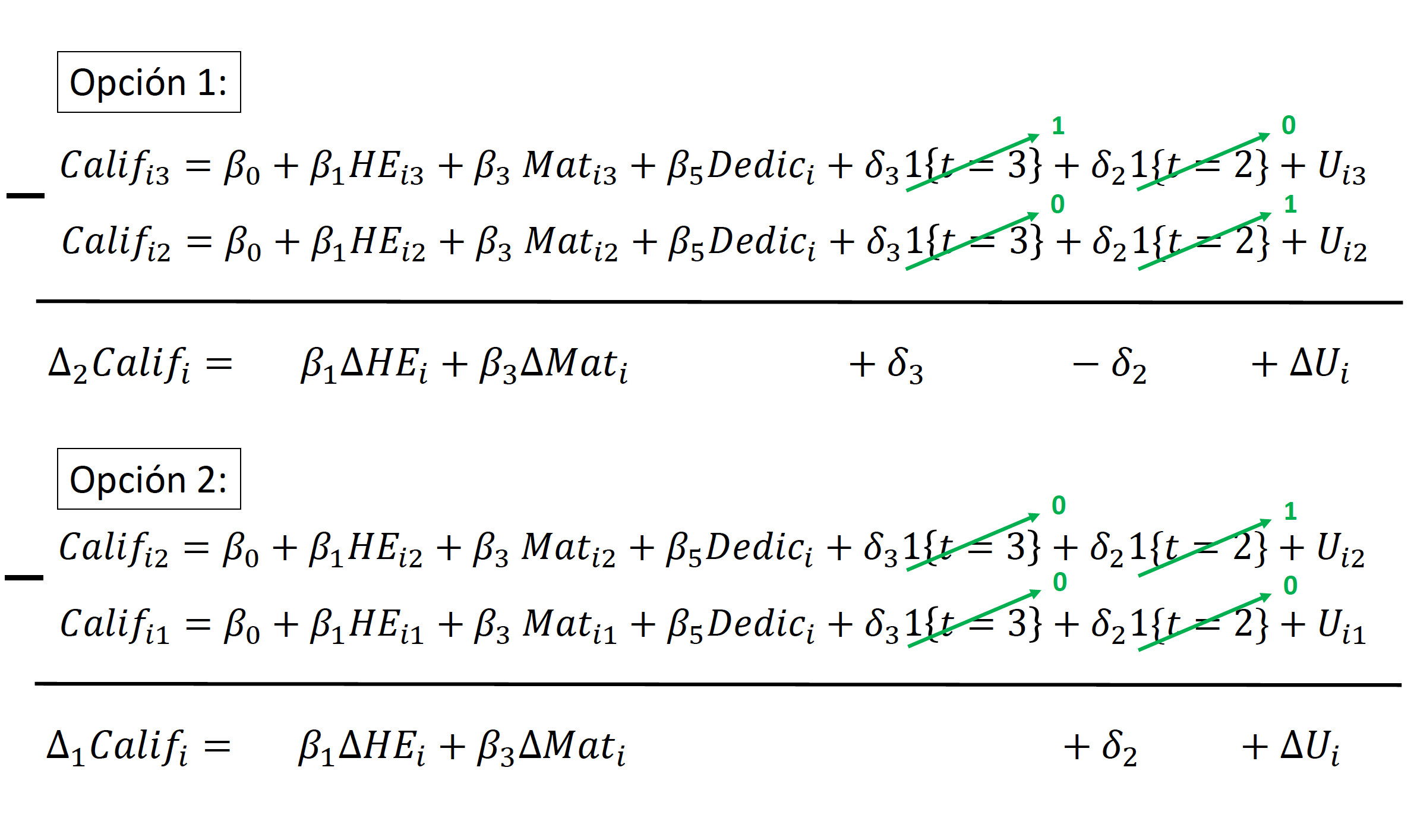
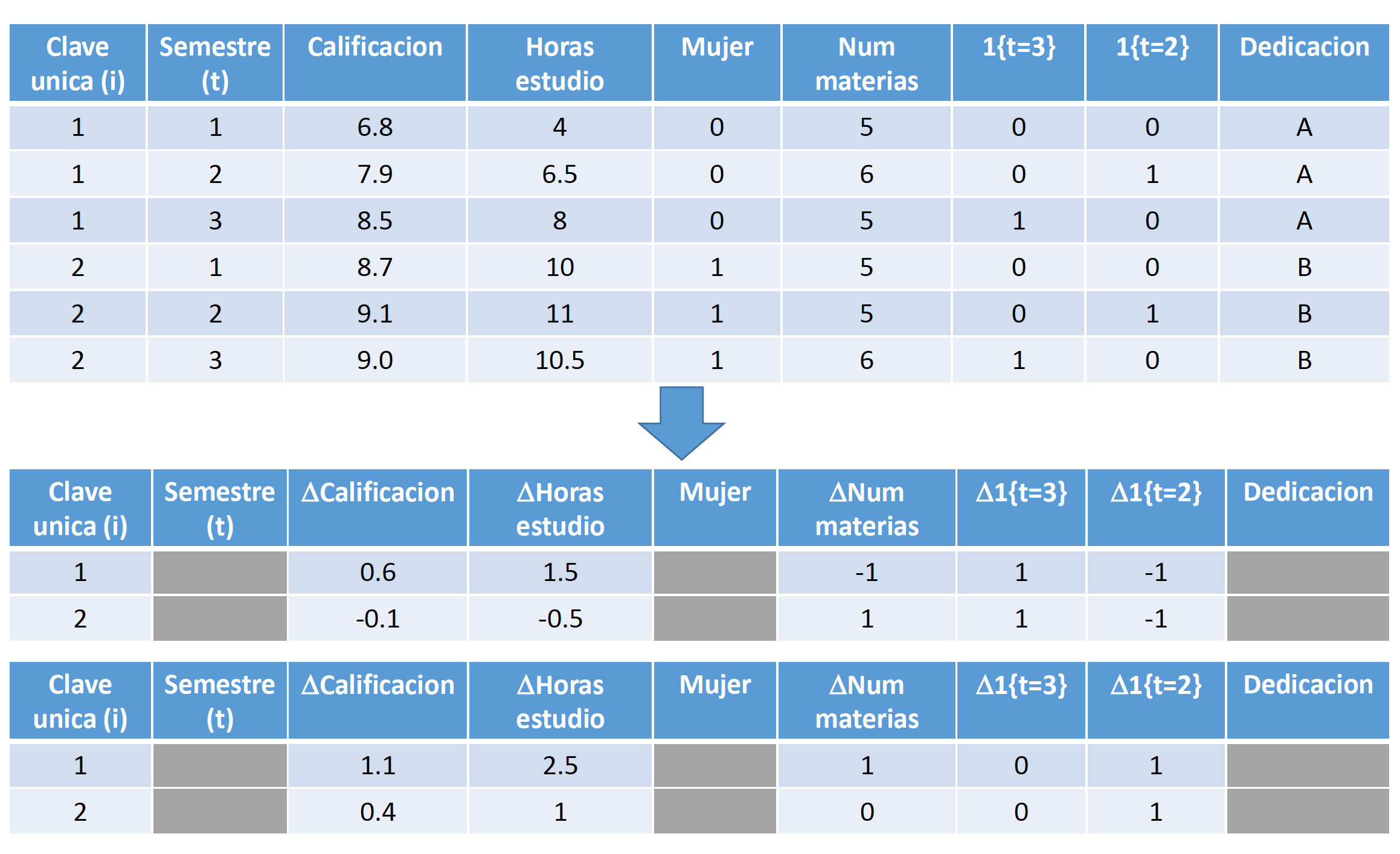
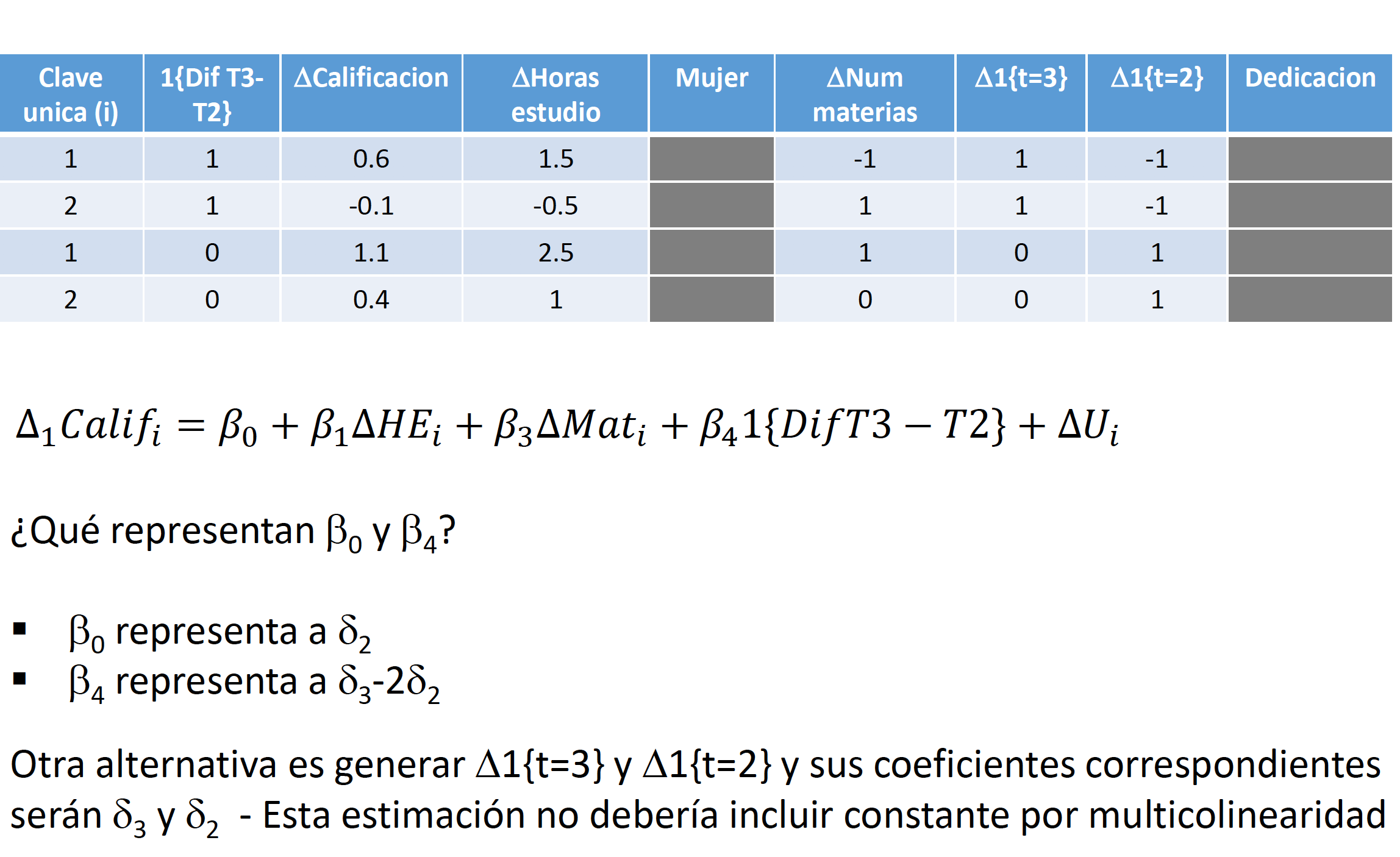
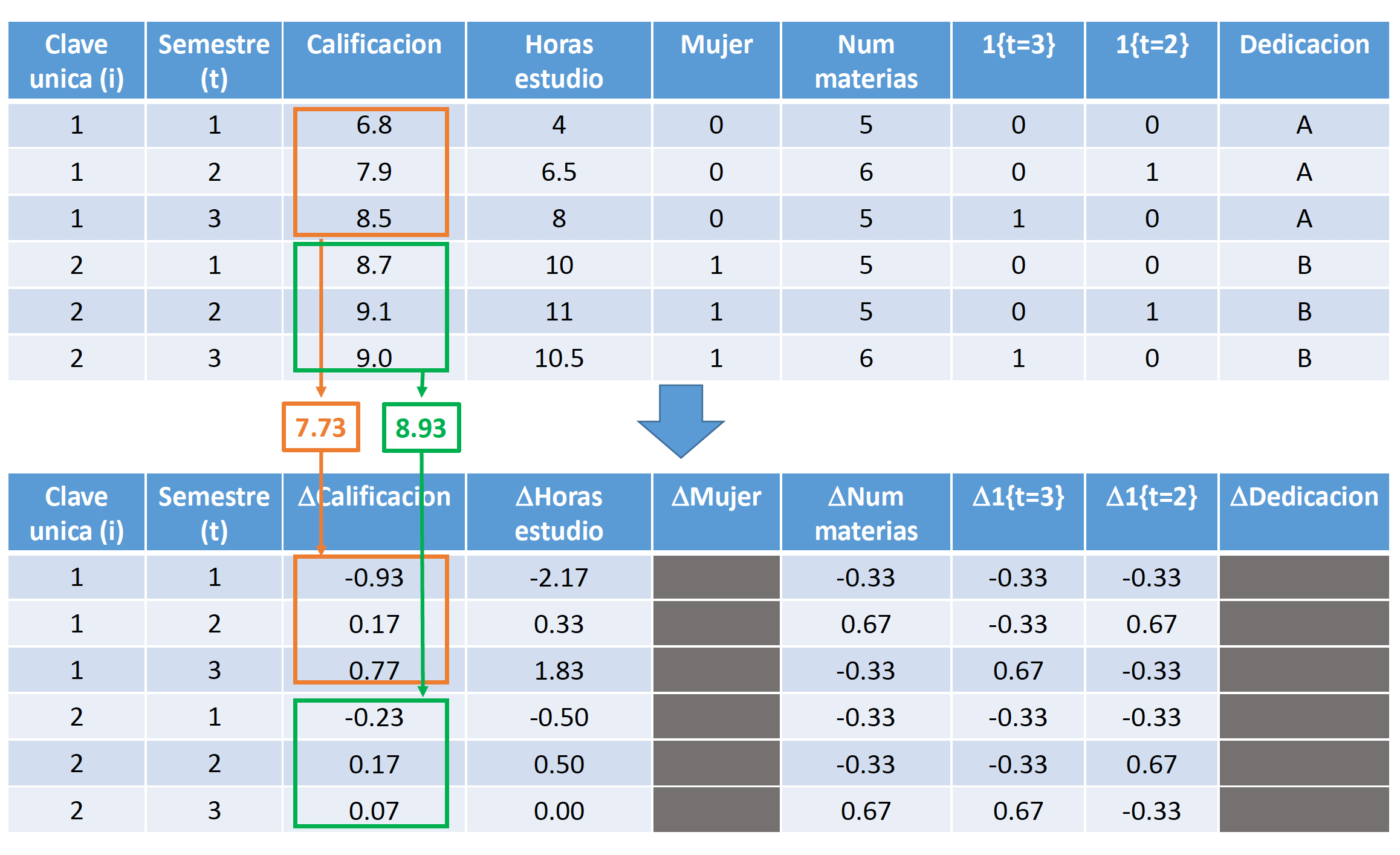
4.2 Estimador de Primeras Diferencias (First Differences)

Empecemos por discutir un caso sencillo donde tenemos varias observaciones \(i\) en dos periodos de tiempo. Supongamos que queremos estimar los rendimientos educativos utilizando el siguiente modelo⁷: \[\log{(w_{it})}=\beta_0+\beta_1Educ_{it}+\beta_2Exper_{it}+\delta_2D2_t+\dots+U_{it}\]

En la nota anterior señalamos que un posible problema de utilizar MCO para estimar esta especificación es que existe un problema de sesgo por variables omitidas. En particular, la variable de educación podría estar capturando el efecto de la habilidad intrínseca de cada individuo. Supongamos que dicha habilidad natural no varia a través del tiempo y no es observada (i.e. no esta disponible en nuestra base de datos). Esto quiere deicr que para eliminar el sesgo, nos interesaría estimar el siguiente modelo:

\[\begin{equation} \log{(w_{it})}=\beta_0+\beta_1Educ_{it}+\beta_2Exper_{it}+\delta_2D2_t+\gamma A_i+\dots+U_{it} \tag{4.1} \end{equation}\]

donde \(A_i\) representa la habilidad del individuo \(i\). Nótese que esta variable no tiene un subíndice \(t\), ya que la habilidad de cada individuo no varía a través del tiempo, pero si varía de un individuo a otro. En nuestro caso, solo tenemos dos momentos en el tiempo (\(t=1,2\)), por lo tanto, si tomamos la diferencia de \(t=2\) menos \(t=1\) para cada individuo:

\[\log{(w_{i2})}-\log{(w_{i1})}=\delta_2+\beta_1(Educ_{i2}-Educ_{i1})+\beta_2(Exper_{i2}-Exper_{i1})+\dots+(U_{i2}-U_{i1})\]

Este modelo se conoce como el modelo de primeras diferencias. Para estimarlo, utilizamos la metodología de MCO. Nótese que esta metodología nos permite remover cualquier sesgo por variables omitidas, siempre y cuando dichas variables omitidas no cambien a lo largo de \(t\) para cada individuo.

Para poder estimar este modelo, se deben cumplir los siguientes supuestos:

1. Se deben cumplir los supuestos de MCO que establecimos en la nota anterior: (i) muestra i.i.d.; (ii) relación lineal en el modelo; (iii) no multicolinearidad

2. Los coeficientes deben ser constantes a lo largo del tiempo (eso se refleja en que los coeficientes no tienen un subíndice \(t\) en el modelo⁸.

Cabe recordar que una condición de primer órden que surge al derivar el modelo MCO establece que no hay covarianza entre los errores y las variables independientes (\(E(X_iU_i)=0\)). En el modelo de primeras diferencias, esto se traduce como \(E((X_{it}-X_{it-1})(U_{it}-U_{it-1}))=0\). Es decir, no debe existir covarianza entre la diferencia de los errores y la diferencia de las variables independientes.

Es importante señalar que cualquier variable omitida que no sea constante a través del tiempo para cada individuo, puede causar sesgo en este modelo. En nuestro ejemplo, una mejora alimenticia es un ejemplo de variable que podría seguir causando sesgo. Asimismo, es importante que exista variación en la variable independiente. En nuestro ejemplo, esto podría causar conflicto, ya que es de esperarse que la muestra este compuesta por individuos adultos perceptores de ingresos. En este grupo, sería de esperarse que la variable educación no cambie mucho.

Por último, cabe señalar que estos modelos no permitirán estimar el efecto de variables que no cambian a lo largo del tiempo, como género, raza, etc. Esto sucede ya que estas variables serán eliminadas también siguiendo el procedimiento que utilizamos para eliminar a \(A_i\). Por lo tanto, la diferencia de estas variables será multicolinear con la diferencia de la variable \(A_i\) y la constante.

• Dar ejemplo de los estudios con gemelos en E.U. para eliminar el sesgo por habilidad.

• Otro ejemplo: ¿cómo el desempleo afecta las tasas de crimen?

El modelo de primeras diferencias tambien puede estimarse si se tiene más de dos observaciones para cada \(i\) a través del tiempo. Generalmente, si se tienen \(T\) periodos, el modelo sería: \[\begin{equation*} \begin{split} Y_{it}-Y_{it-1}= \delta_t-\delta_{t-1}+\beta_1(X_{1it}-X_{1it-1})+\dots+\beta_K(X_{Kit}-X_{Kit-1})+(U_{it}-U_{it-1}) \end{split} \end{equation*}\]

En este caso, cada unidad \(i\) tendría \(T-1\) observaciones. El procedimiento consistiría en estimar la regresión utilizando MCO. Si la base de datos de panel es balanceada, se tendrían \(N*(T-1)\) observaciones.

4.3 Modelo de Efectos Fijos

4.3.1 Derivación

En esta sección revisaremos lo que tradicionalmente se conoce como el modelo de efectos fijos. La motivación de este modelo es la misma que la del modelo de primeras diferencias: eliminar el sesgo que puede causar una variable que sea constante dentro de un mismo grupo: \(A_i\).

Siguiendo con nuestro ejemplo anterior (y asumiendo una base de datos de panel balanceada) tomemos la ecuación [(4.1)] y calculemos el promedio para cada individuo asumiendo en este caso que existen \(T\) periodos de tiempo:

\[\begin{equation} \overline{\log{(w_i)}}=\beta_0+\beta_1\overline{Educ}_i+\beta_2\overline{Exper}_i+ \delta_2\frac{1}{T}+\dots+\delta_T\frac{1}{T}+A_i+\overline{U}_i \tag{4.2} \end{equation}\]

Siguiendo el mismo procedimiento que en primeras diferencias, tomamos la diferencia entre las ecuaciones (4.1) y (4.2) y esto resulta en (para \(t=1,\dots,T\))⁹:

\[\begin{equation} \begin{split} \log{(w_{it})}-\overline{\log{(w_i)}}= & \beta_1(Educ_{it}-\overline{Educ}_i)+\beta_2(Exper_{it}-\overline{Exper}_i)+\dots+\\ & +\dots+\delta_t-\overline{\delta}+(U_{it}-\overline{U}_i) \end{split} \tag{4.3} \end{equation}\]

Igual que en el caso del modelo de primeras diferencias, este modelo ya no incluye la variable \(A_i\) que no es observada y que potencialmente generaba sesgo. Asimismo, los supuestos establecidos en la sección de primeras diferencias deben cumplirse para poder estimar este modelo con el método de MCO. La principal diferencia entre este modelo y el de primeras diferencias radica en la condición de primer órden de la derivción de MCO, que en este caso se vuelve: \[E((X_{it}-\overline{X}_i)(U_{it}-\overline{U}_i))=0\] Esta condición es más restrictiva que la condición de primeras diferencias ya que requiere que la variable de error de cada \(t\) no este correlacionada con la variable independiente \(X\) en cada \(t\).

4.3.1.1 Utilizando Variables Dummy para la estimación

Una metodología mas sencilla para estimar el modelo (4.3) partiendo del modelo (4.1) consiste en generar variables dummy para los factores \(i\) que agrupan a distintas observaciones. En la explicación del modelo (4.1) señalamos que el propósito es eliminar la variable no observada \(A_i\) que tiene la característica de variar entre distintos individuos -\(i\)- pero es constante a través del tiempo para un mismo individuo o agrupación -\(i\)-. Si modificamos el modelo agregando dummies para cada individuo o grupo -\(i\)-, el efecto de la variable no observada \(A_i\) será absorbido por estas variables dado que será colinear con dichas variables. Por lo tanto, nuestra especificación será:

\[\begin{equation} \log{(w_{it})}=\beta_0+\beta_1Educ_{it}+\beta_2Exper_{it}+\eta_2A2_i+\dots+\eta_NAN_i+\delta_2D2_t+\dots+\delta_TDT_t+U_{it} \tag{4.4} \end{equation}\]

donde \(Aj_i\) es una dummy igual a uno si \(i=j\) y cero eoc¹⁰.

Es importante recordar la interpretación de las variables dummy: te dicen la diferencia de una media ponderada de los individuos que pertenecen al grupo identificado con la variable dummy respecto al grupo de referencia (i.e. la variable dummy omitida). En el caso de la ecuación (4.2), se calcula directamente la media para cada \(i\) usando las diferentes observaciones de \(i\) en \(t\). Y en el modelo de efectos fijos (ecuación (4.3)), se quita dicho efecto al tomar la diferencia de la variable dependiente respecto a este promedio. Por lo tanto, la especificación del modelo utilizando variables dummy (ecuación (4.4)) será equivalente al modelo de efectos fijos (ecuación (4.3)) y estimará los mismos valores para los coeficientes y sus respectivos errores estandar.

4.3.2 Base de datos de panel no balanceados

Las derivaciones en los modelos anteriores asumen una base de datos de panel balanceada. Esto quiere decir que para todo \(i\), existen \(T\) observaciones. Sin embargo, es posible que este supuesto no se cumpla por diversas razones dependiendo de la estructura de la base de datos. Por ejemplo, si \(i\) representa individuos y \(t\) tiempo, es posible que algunos individuos no sea posible encontrarlos para volver a entrevistarlos, ya sea por defunción, migración, que no quieran volver a contestar la encuesta, etc. En el caso de \(i\) siendo familias y \(t\) hermanos, es posible que distintas familias tengan distinto número de hermanos.

El hecho de que cada grupo tenga diferente número de observaciones \(t\) no impide aplicar el modelo de efectos fijos o la especificación utilizando variables dummies para estimar los coeficientes de interés. Lo único que es importante señalar es que aquellos \(i\) que únicamente cuenten con una observación serán eliminados del modelo ya que la variable dummy predeciría perfectamente su variable dependiente.

La preocupación más importante surge desde el punto de vista del sesgo que esta selección pueda generar. Dicha selección sólamente será razón de preocupación cuando exista correlación entre algún factor no observado que cambie a lo largo del tiempo y este relacionado con la variable dependiente. Si las observaciones que causan que el panel no sea balanceado tienen valores no aleatorios de estos factores no observados, entonces podría existir una preocupación de sesgo. Por ejemplo, supongamos que queremos estimar la influencia de la altura de una persona sobre sus ingresos. La salud es una variable que cambia a los largo del tiempo en los distintos individuos y que puede estar corrleacionada con la altura y ser un factor determinante de los ingresos. En este caso es posible que las personas que causen que la base no sea balanceada tengan peor salud. Por lo tanto, esto sería una indicación de un posible sesgo en la variable de altura. Además de la salud, otra variable no observada puede ser el componente genético. El componente genético también es una variable no observada que está relacionada con la altura y puede ser un determinante de ingreso. Sin embargo, el componente genético es específico de cada individuo y no cambia a lo largo del tiempo. A pesar que el componente genético de las personas que causan que la base no sea balanceada no sea aleatorio, esto no será preocupación de sesgo, ya que el modelo de efectos fijos absorbe todos los factores no observados que no cambian para cada \(i\).

4.4 Errores Estándar

Para tener una estimación válida de los modelos anteriores utilizando MCO es importante que se cumplan los supuestos que establecimos en el modelo MCO. Un supuesto de particular importancia es el de i.i.d. Dicho supuesto nos permitía asumir que las matriz de varianza-covarianza de los errores únicamente tenía valores sobre la diagonal (ya que no existía covarianza entre dos errores distintos por ser independientes las observaciones).

En el caso del uso de datos de panel este supuesto es muy restrictivo. En particular, dos observaciones utilizadas en el modelo (4.3) pueden compartir una misma \(i\). Por ejemplo, en las observaciones (\(i=1\), \(t=1\)) e (\(i=1\), \(t=2\)), asumir que los errores \(U_{1,1}\) y \(U_{1,2}\) sean independientes es un supuesto muy restrictivo y probablemente no válido.

En los casos de homocedasticidad y heterocedasticidad asumíamos que nuestra matriz de varianza-covarianza de los errores era una diagonal dado que los errores eran independientes entre si. Sin embargo, ahora asumiremos que los errores pueden estar correlacionados dentro de un cluster o grupo, que estará definido por \(i\). Esto quiere decir que nuestra matriz de varianza-covarianza de los errores tendrá algunos elementos fuera de la diagonal distintos a cero.

Existen distintas maneras de corregir este problema de los errores estándar. Uno consiste en calcular los errores estandar clustered. Este método es sencillo de llevar a cabo en Stata. Unicamente se tiene que especificar al final de la regresión “, cl(var_cl)” donde var_cl es la variable que indica los clusters (o grupos).

Esta opción calcula la varianza de la siguiente forma: \[\widehat{Var(\beta)}=\hat{\alpha}\hat{\Lambda}\hat{\alpha}\] donde: \[\begin{equation*} \begin{split} \hat{\alpha}=&(\frac{1}{NT}\sum_{i=1}^n\sum_{t=1}^TX_{it}X_{it}')^{-1}\\ \hat{\Lambda}=&\frac{1}{NT}\sum_{i=1}^{N}w_{it}w_{it}'\\ w_{it}=&\sum_{t=1}^TX_{it}\hat{U}_{it} \end{split} \end{equation*}\] En estas especificaciones, \(i\) indica los grupos o clusters, \(N\) es el número total de clusters, \(T\) es el número de observaciones por cluster y \(X_{it}\) es un vector \(Kx1\) que incluye las \(K\) variables de control para cada par \((i,t)\).

Ver la Nota “Ecuaciones clase 27-SEPT” (disponible en Comunidad ITAM) para detalles de la derivación de este tipo de errores y su comparación con los errores homocedásticos y heterocedásticos.

4.5 Modelo de Efectos Aleatorios

En la sección 3.11.2, discutimos que existe una especificación de errores estándar más eficiente que la especificación de errores heterocedasticos: mínimos cuadrados ponderados. Dicha especificación consistía en ponderar las variables dependiente y regresores y estimar una regresión utilizando las variables ponderadas bajo el supuesto de homocedasticidad. El modelo de efectos aleatorios se basa en la misma lógica.

Este modelo parte de la misma base que el modelo de efectos fijos (ecuación (4.1)): \[\begin{equation} \log{(w_{it})}=\beta_0+\beta_1Educ_{it}+\beta_2Exper_{it}+\delta_2D2_t+\gamma A_i+\dots+U_{it} \end{equation}\] Sin embargo, difiere del modelo de efectos fijos en el sentido de que el factor \(A_i\) no causa sesgo por variables omitidas ya que se basa en el supuesto de que: \[Cov(X_{it},A_i)=0\text{ para } t=1,\dots,T\] En este caso, estimar la ecuación (4.1) utilizando MCO no generaría un estimador insesgado. El único requisito en términos de errores estándar es incluir errores tipo cluster, como discutimos en la sección anterior. La ventaja del modelo de efectos aleatorios consiste en que generará un estimador insesgado más eficiente que MCO donde además se corrige la estimación de los errores estandar por la posible covarianza dentro de un cluster.

El modelo de efectos aleatorios parte de la base de conjuntar el factor \(A_i\) con \(U_{it}\) en el término de error de la regresión:

\[\begin{equation} \log{(w_{it})}=\beta_0+\beta_1Educ_{it}+\beta_2Exper_{it}+\delta_2D2_t+\dots+V_{it} \tag{4.5} \end{equation}\] donde \(V_{it}=\gamma A_i+U_{it}\).

Este modelo no podrá ser estimado mediante MCO ya que no cumple con la condición de i.i.d. En particular, la estructura de la matriz de varianza-covarianza de los errores no será una matriz con elementos distintos a cero únicamente en la diagonal (como se asume en homocedasticidad y heterocedasticidad). En lugar de esto, el modelo de efectos aleatorios consiste en asumir la siguiente estructura para la matriz de varianza-covarianza de los errores:

\[\begin{equation*} E(V_{it}V_{js})= \begin{cases} \sigma_a^2+\sigma_u^2 & \text{ si } i=j \text{ y } t=s\\ \sigma_a^2 & \text{ si } i=j \text{ y } t\neq s\\ 0 & \text{ si } i\neq j \end{cases} \end{equation*}\]

donde \(\sigma_a^2=Var(A_i)\) y \(\sigma_u^2=Var(U_{it})\). Implicitamente se está asumiendo que \(Cov(A_i,U_{it})=0\). (Ilustrar la matriz de varianza-covarianza y compararla con el caso de errores homocedasticos y heterocedasticos).

Utilizando estos parametros (\(\sigma_a^2\) y \(\sigma_u^2\)) se lleva a cabo la siguiente transformación al modelo base (ecuación (4.5)):

\[\begin{equation} \begin{split} \log{(w_{it})}-\lambda\overline{\log{(w_i)}}=&\beta_0(1-\lambda)+\beta_1(Educ_{it}-\lambda\overline{Educ}_{i})+\\ &\beta_2(Exper_{it}-\lambda\overline{Exper}_{i})+\delta_t-\lambda\hat{\delta}+(V_{it}-\lambda\overline{V}_i) \end{split} \tag{4.6} \end{equation}\]

donde: \(\lambda=1-\left(\frac{\sigma_u^2}{\sigma_u^2+T\sigma_a^2}\right)^{\frac{1}{2}}\). Esto corresponde a restar una proporción de la media. Cabe notar que el modelo de efectos fijos resulta si \(\lambda=1\), mientras que un simple MCO con una base de datos transversal agrupada (pooled OLS) resulta si \(\lambda=0\).

Para estimar \(\lambda\) necesitamos estimadores para \(\sigma_a^2\) y \(\sigma_u^2\). Para llevar a cabo esto y estimar el modelo de efectos fijos podemos seguir el siguiente procedimiento:

1. Estimar el modelo base (ecuación (4.5)), utilizando MCO con la base de datos transversal agrupada (pooled OLS)

2. Utilizar los coeficientes para calcular los residuales (\(\hat{V_{it}}\))

3. Estimar \(\sigma_a^2\) como: \(\hat{\sigma}_a^2=\frac{\sum_{i=1}^N \sum_{t=1}^{T-1} \sum_{s=t+1}^T \hat{V}_{it} \hat{V}_{is}}{\frac{NT(T-1)}{2}}\)

4. Estimar \(\sigma_u^2\) como: \(\hat{\sigma}_u^2=\hat{\sigma}_v^2-\hat{\sigma}_a^2\) donde \(\hat{\sigma}_v^2=\frac{\sum_{i=1}^N \sum_{t=1}^T \hat{V}_{it}^2}{NT}\)

5. Utilizar \(\hat{\sigma}_u^2\) y \(\hat{\sigma}_a^2\) para estimar \(\hat{\lambda}\)

6. Utilizar MCO para estimar la ecuación (4.6) utilizando el valor estimado \(\hat{\lambda}\)

Esto puede llevarse a cabo utilizando Stata y el comando xtreg. Antes de utilizar el comando xtreg es necesario indicarle a Stata que variables dan la estructura de base de datos de panel a la base que se utiliza (es decir, que es \(i\) y que es \(t\)). Para ello es necesario utilizar el comando xtset variable_i variable_t. Una vez que se llevo a cabo esto se puede indicar xtreg y x1 x2 ... xK, re y Stata estimará el modelo de efectos aleatorios. La mayor parte de los paquetes estadísticos (incluyendo Stata) generará como resultado además de los coeficientes de la regresión estimadores de los parametros \(\hat{\lambda}\), \(\hat{\sigma}_u^2\) y \(\hat{\sigma}_a^2\).