3 Mínimos Cuadrados Ordinarios

La teoría microeconómica suele establecer, a través de modelos, relaciones funcionales entre dos variables para explicar cómo toman decisiones los agentes. Por ejemplo, supongamos que estamos interesados en analizar la relación que existe entre educación e ingreso en la sociedad mexicana. Dicha relación puede ser representada utilizando algún modelo teórico como un problema de maximización, donde cada individuo elige un nivel de escolaridad para maximizar sus ingresos. La solución a dicho problema puede establecer una relación: \[\begin{equation} Y=f(edu) \end{equation}\]

donde \(Y\) representa ingreso, \(edu\) representa educación y \(f(\cdot)\) describe la relación funcional entre ambas variables (cabe señalar que no estamos restringiendo la función \(f(\cdot)\) de ninguna forma). Una característica de esta relación será que a cada nivel educativo le corresponde únicamente un nivel de ingreso. Sin embargo, ¿qué sucedería si utilizamos datos empíricos para analizar esta relación?

Utilizando datos de la ENIGH⁴ 2010, la siguiente tabla (Tabla 1) muestra la proporción de individuos entre \(21\) y \(65\) años que se encuentran laborando y que reportan distintos niveles de ingreso y educación al momento de la encuesta.

Ingreso Mensual	Sin esc	Prim	Sec	M.S	N/CT	Prof	Posgdo	Total
1000	2.07	7.56	3.95	1.46	0.56	1.06	0.03	16.67
2000	0.94	5.24	3.15	1.38	0.49	0.87	0.03	12.11
3000	0.75	5.18	4.24	1.91	0.65	1.00	0.05	13.78
4000	0.41	4.28	4.26	2.29	0.77	1.20	0.06	13.28
5000	0.28	2.74	3.50	2.12	0.86	1.24	0.05	10.80
6000	0.10	1.44	2.13	1.45	0.73	1.26	0.06	7.15
7000	0.04	0.88	1.54	1.23	0.67	1.35	0.09	5.80
8000	0.02	0.46	0.88	0.76	0.41	1.22	0.09	3.84
9000	0.03	0.34	0.64	0.67	0.44	1.20	0.12	3.45
10000	0.08	0.76	1.34	1.60	1.42	6.50	1.43	13.12
Total	4.72	28.89	25.64	14.86	7.00	16.90	1.99	100.00

La Tabla 1 muestra la densidad conjunta de educación e ingreso. Es decir, cada celda da el valor de \(p(edu_j,y_i)\) que representa la proporción de individuos que reportan recibir un ingreso igual a \(y_i\) y tienen una educación igual a \(edu_j\). Por ejemplo, dado que la muestra elegida incluye a un total de \(44,270\) individuos, la celda que corresponde a secundaria y \(\$5,000\) pesos mensuales indica que \(1,549\) individuos reportan estos niveles de escolaridad e ingreso en la encuesta.

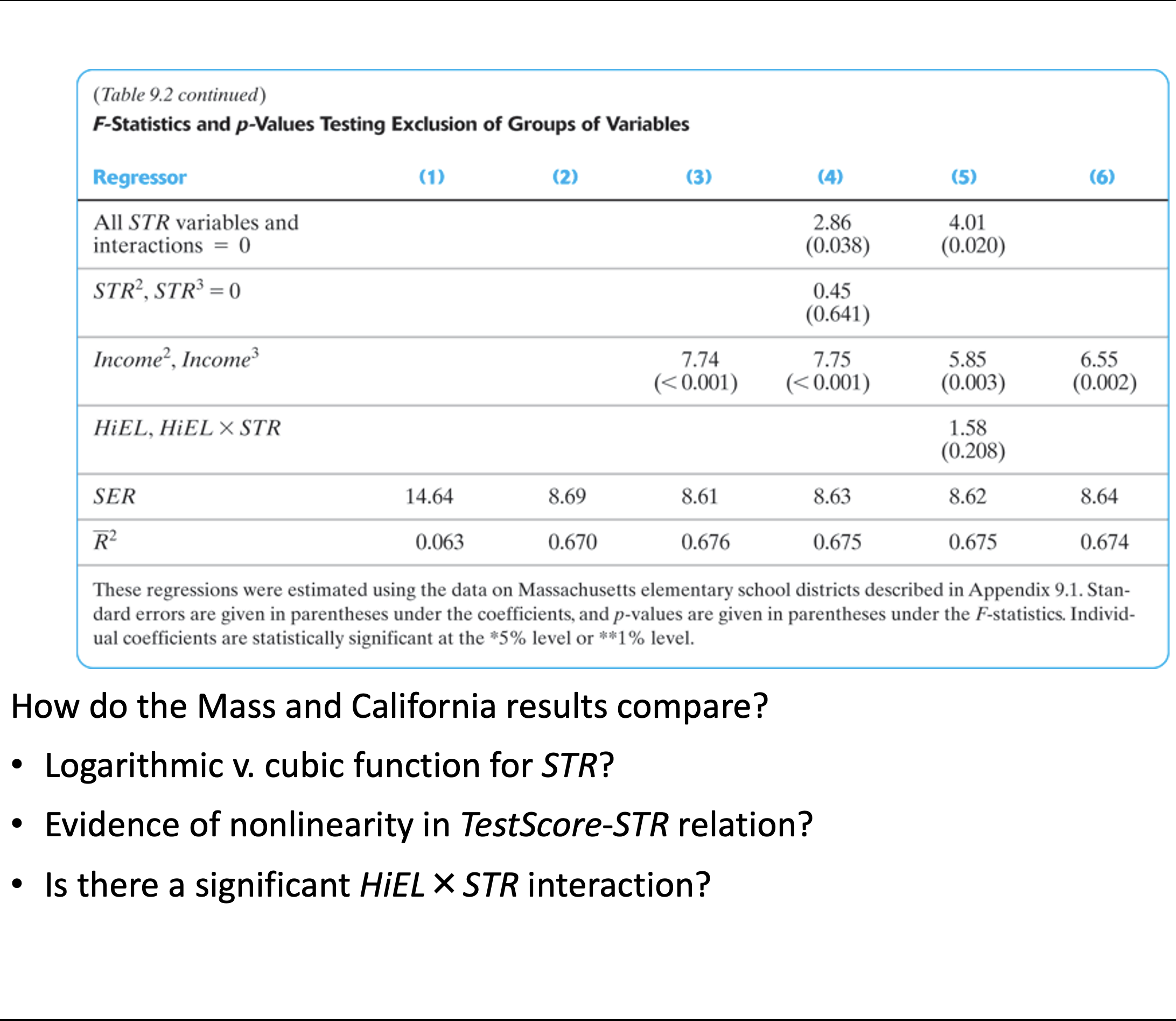
A partir de la Tabla 1 puede notarse que, contrario a la teoría donde existe una relación funcional, la relación empírica entre educación e ingreso no es deterministica. Es decir, a cada nivel de educación no le corresponde solamente un nivel de ingreso. De lo contrario, se vería en la Tabla 1 que, en cada columna, todos los renglones excepto uno tendrían un valor igual a cero. No obstante, lo que sí puede observarse en la Tabla 1 es una tendencia que muestra que los individuos con mayor nivel educativo tienden a percibir mayores ingresos. Esto se ilustra más claramente con la siguiente tabla (Tabla 2) que muestra las frecuencias condicionales.

Cada celda de la Tabla 2 representa \(p(y|edu)\), la frecuencia de ingreso condicional a los distintos niveles educativos. Por ejemplo, de acuerdo a esta tabla el \(38.39\%\) de los individuos que tienen educación media superior perciben un ingreso mayor a \(\$5,000\) pesos mientras que solamente el \(68.23\%\) de los individuos con educación superior reciben dicho nivel de ingreso.

Una forma de utilizar los datos empíricos para generar una relación uno a uno es utilizar la tabla de densidades condicionales para calcular la media condicional de ingresos. Dicha media es definida para cada nivel de educación \(j\) (\(edu_j\)) como: \[\begin{equation} m_{y|edu_j}=\sum_i y_i\cdot p(y_i|edu_j) \end{equation}\]

Ingreso Mensual	Sin esc	Prim	Sec	M.S	N/CT	Prof	Posgdo	Total
1000	43.81	26.18	15.40	9.79	7.97	6.25	1.34	16.67
2000	19.24	18.13	12.31	9.30	6.93	5.15	1.61	12.11
3000	15.97	17.94	16.53	12.84	9.27	5.93	2.42	13.78
4000	8.69	14.82	16.63	15.42	11.03	7.09	2.96	13.28
5000	5.85	9.50	13.66	14.26	12.34	7.36	2.42	10.80
6000	2.05	4.98	8.29	9.74	10.42	7.44	2.82	7.15
7000	0.91	3.06	6.00	8.28	9.58	7.98	4.44	5.80
8000	0.51	1.59	3.43	5.10	5.82	7.23	4.30	3.84
9000	0.68	1.18	2.51	4.49	6.36	7.12	6.05	3.45
10000	1.59	2.62	5.24	10.78	20.27	38.46	71.64	13.12
Total	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00

Utilizando estos valores se genera una relación uno a uno entre nivel educativo y de ingreso que se ilustra en las gráficas a continuación. En la Figure 3.1 se ilustra utilizando los niveles de escolaridad y en la Figure 3.2, se transforma el nivel a años de escolaridad. En la segunda gráfica puede observarse que no resultaría sencillo especificar una forma funcional para representar la relación entre ingreso y años de escolaridad.

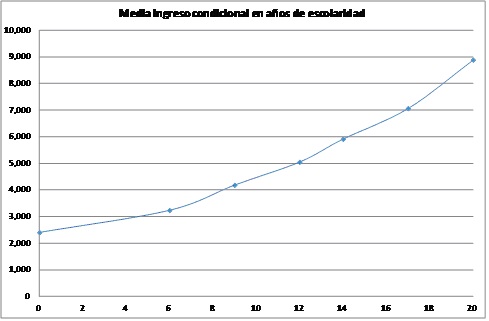
Figure 3.1: Medias condicionales por nivel educativo

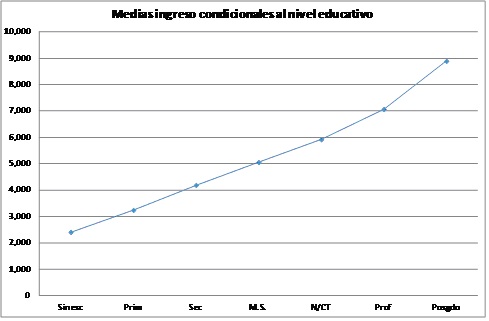
Figure 3.2: Medias condicionales por nivel educativo

En la primera parte de este curso aprenderemos cómo utilizar la metodología de Mínimos Cuadrados Ordinarios para poder utilizar datos empíricos para estimar una forma funcional determinada.

3.1 Derivación de Mínimos Cuadrados Ordinarios

3.1.1 Regresión simple

Partiendo con una muestra aleatoria \(\{Y_i,X_i\}\) i.i.d., una manera de representar con una forma funcional la relación entre dos variables consiste en asumir que la relación entre dichas variables es lineal: \[\begin{equation} Y_i=\beta_0+\beta_1X_i+U_i \tag{3.1} \end{equation}\]

Asumir que la relación es lineal implica que el cambio de la variable dependiente (\(Y_i\)) por un cambio marginal en la variable independiente (\(X_i\)) es constante. La variable \(U_i\) corresponde al error de la estimación o la parte no explicada del modelo. Nos referimos a ésta como la parte no explicada ya que el resto de la ecuación (\(\beta_0+\beta_1X_i\)) representa una relación en la que la variable \(X_i\) pretende aproximar o explicar de la mejor manera posible a la variable dependiente, \(Y_i\).

Ejemplo: Aumentar de \(4\) a \(5\) años el nivel de escolaridad daría el mismo rendimiento que aumentar de \(16\) a \(17\).

Una vez que asumimos esa relación lineal tenemos que determinar una manera óptima de elegir los estimadores \(\beta_0\) y \(\beta_1\). El método de mínimos cuadrados ordinarios consiste en minimizar el cuadrado de los errores de la estimación (\(U_i\)): \[\begin{equation} \min_{\beta_0,\beta_1}\phantom{tt}E(U_i^2) \end{equation}\]

Esta minimización da como resultado: \[\begin{equation} \begin{split} \beta_0=&E(Y_i)-\beta_1E(X_i)\\ \beta_1=&\frac{E(Y_iX_i)-E(Y_i)E(X_i)}{E(X_i^2)-E(X_i)^2}=\frac{Cov(X_i,Y_i)}{Var(X_i)} \end{split} \tag{3.2} \end{equation}\]

Por lo tanto, partiendo de (3.2) obtenemos los estimadores de MCO: \[\begin{equation} \begin{split} \hat{\beta}_0=&\frac{1}{n} \sum_{i=1}^n Y_i-\hat{\beta}_1 \sum_{i=1}^n X_i\\ \hat{\beta}_1=&\frac{\sum_{i=1}^n Y_iX_i- \sum_{i=1}^n Y_i \sum_{i=1}^n X_i}{\sum_{i=1}^n X_i^2- (\sum_{i=1}^n X_i)^2} \end{split} \tag{3.3} \end{equation}\]

Los valores estimados correspondientes se obtienen a partir del análogo muestral.

Las dos condiciones de primer orden que resultan de la derivación anterior son clave para obtener los estimadores \(\hat{\beta}_0\) y \(\hat{\beta}_1\). Más adelante regresaremos a estos supuestos:

\[\begin{equation} \begin{split} E(Y_i-\beta_0-\beta_1X_i)=E(U_i)=&0\\ E((Y_i-\beta_0-\beta_1X_i)U_i)=E(X_iU_i)=&0 \end{split} \end{equation}\]

La primera condición de primer orden (\(E(U_i)=0\)) simplemente indica que por el hecho de incluir una constante en la estimación (\(\beta_0\)), el valor esperado de los errores debería estar centrados en cero.

La segunda condición de primer orden (\(E(X_iU_i)=0\)) indica que la variable explicativa (\(X_i\)) no está correlacionada con los errores o la parte no explicada del modelo.

Es importante señalar que los errores \(U_i\) representan todo aquello que no es incluido dentro del modelo.

3.1.2 Regresión multiple

El caso anterior ilustra la derivación del modelo MCO en el caso de una regresión simple (i.e. con una sola variable explicativa). Para aumentar la cantidad de variables explicativas será útil la representación vectorial. Para esto, empecemos por notar que al incluir más variables explicativas, nuestro planteamiento para la estimación será:

\[\begin{equation} Y_i=\beta_0+\beta_1X_{1i}+\beta_2X_{2i}+\dots+\beta_KX_{Ki}+U_i \tag{3.4} \end{equation}\]

Sea \(X_i\) un vector de dimensión \(K+1\), donde el primer componente es la constante (\(1\)) y los demás corresponden a las variables \(X_{li}\) que son incluidas como controles en la estimación (3.4). Similarmente, \(\beta\) será un vector de dimensión \(K+1\) que incluye todos los coeficientes [\(\beta_0~~\beta_1~~\dots~~\beta_K\)] de la estimación. Utilizando esta notación, la ecuación (3.4) puede ser reescrita como:

\[\begin{equation} Y_i=X_i'\beta+U_i \quad\text{para $i=1,\dots,n$} \end{equation}\]

Siguiendo la misma metodología minimizo el valor esperado de los errores al cuadrado: \[\begin{equation} \min_\beta E(Y_i-X_i' \bf{\beta})^2 \end{equation}\]

Esto da como resultado la siguiente expresión para el parámetro: \[\begin{equation} \beta={E(\textbf{X}_i\textbf{X}_i')^{-1}E(\textbf{X}_i\textbf{Y}_i)} \end{equation}\]

Partiendo de esto, el estimador seria : \[\begin{equation} \hat{\beta}=\biggl(\sum\limits_{i=1}^n X_iX_i' \biggl)^{-1}\biggl(\sum\limits_{i=1}^n X_iY_i \biggl) \tag{3.5} \end{equation}\]

Y finalmente, el valor estimado se calcula con el análogo muestral de (3.5).

Utilizando las propiedades asintóticas, es posible demostrar que: \[\begin{equation} \begin{split} \hat{\beta}& \overset{p}\to \beta\\ \sqrt{n}(\hat{\beta}-\beta) &\overset{d}\to N(0,\alpha \Sigma \alpha') \end{split} \end{equation}\]

donde, \[\begin{equation*} \begin{split} \bf{\alpha}=&E(X_iX_i')^{-1}\\ \bf{\Sigma}=&E(U_i^2X_iX_i') \end{split} \end{equation*}\]

Demostración \(\hat{\beta} \overset{p}\to \beta\):

\[\begin{equation*} \begin{split} \hat{\beta}-\beta&=\biggl(\sum\limits_{i=1}^n X_i X_i'\biggl)^{-1}\biggl(\sum\limits_{i=1}^n X_i Y_i\biggl) - \beta\\ &=\biggl(\sum\limits_{i=1}^n X_i X_i'\biggl)^{-1}\biggl(\sum\limits_{i=1}^n X_iX_i'\beta\biggl)+ \biggl(\sum\limits_{i=1}^n X_i X_i'\biggl)^{-1}\biggl(\sum\limits_{i=1}^n X_iU_i\biggl) -\beta\\ &= \biggl(\frac{1}{n}\sum\limits_{i=1}^n X_i X_i'\biggl)^{-1}\biggl(\frac{1}{n}\sum\limits_{i=1}^n X_iU_i\biggl) \end{split} \end{equation*}\] pero, \[\begin{equation*} \begin{split} \biggl(\frac{1}{n} \sum\limits_{i=1}^n X_iX_i'\biggl)^{-1} & \overset{p}\to E(X_iX_i')^{-1}\\ \biggl(\frac{1}{n} \sum\limits_{i=1}^n X_iU_i\biggl) & \overset{p}\to E(X_iU_i)=0\\ \end{split} \end{equation*}\]

Por lo tanto, \[\begin{equation*} \hat{\beta} \overset{p}\to \beta \end{equation*}\]

Demostracion \(\sqrt{n}(\hat{\beta}-\beta)\overset{d}\to N(0,\alpha\mathbf{\Sigma}\alpha'):\)

\[\begin{equation*} \begin{split} \sqrt{n}(\hat{\beta}-\beta)&=\biggl(\frac{1}{n}\sum\limits_{i=1}^n X_i X_i'\biggl)^{-1}\biggl(\frac{1}{\sqrt{n}}\sum\limits_{i=1}^n X_iU_i\biggl) \end{split} \end{equation*}\]

pero, \[\begin{equation*} \biggl(\frac{1}{n} \sum\limits_{i=1}^n X_iX_i'\biggl)^{-1} \overset{p}\to E(X_iX_i')^{-1}=\alpha\\ \end{equation*}\]

Además, sea \(W_i=X_iU_i\). Por lo tanto tendremos que: \[\begin{equation*} \begin{split} E(W_i)&=E(X_iU_i)=0\\ Var(W_i)&=E(X_iU_iU_i'X_i')\\ &=E(U_i^2X_iX_i')=\Sigma \end{split} \end{equation*}\]

El segundo término se puede transformar en: \[\begin{equation*} \frac{1}{\sqrt{n}} \sum\limits_{i=1}^nX_iU_i=\sqrt{n} \frac{1}{n}\sum\limits_{i=1}^nW_i \overset{d}\to N(0,\Sigma) \end{equation*}\]

Por lo tanto, \[\begin{equation*} \sqrt{n}(\hat{\beta}-\beta) \overset{d}\to N(0,\alpha \Sigma \alpha') \end{equation*}\]

3.2 Homocedasticidad y heterocedasticidad

Hasta ahora nuestros únicos supuestos en el modelo MCO han sido: (i) que nuestra muestra es aleatoria (i.i.d), y (ii) la relación lineal entre \(Y_i\) y \(X_i\).

El supuesto de homocedasticidad indica que la varianza condicional de los errores es constante (i.e. no cambia con el nivel de \(X\)). Dicho supuesto es restrictivo, sin embargo, no es necesario para poder realizar inferencia. Si en cambio asumimos heterocedasticidad, no es necesario asumir que la varianza de los errores es constante y, por lo tanto, podemos estimar la varianza de los coeficientes con el análogo muestral de \(\alpha \Sigma \alpha'\).

Empecemos con el caso de heterocedasticidad. Para obtener un estimador consistente de \(\alpha \Sigma \alpha'\) basta utilizar: \[\begin{equation} \begin{split} \hat{\alpha}&=\biggl( \frac{1}{n} \sum\limits_{i=1}^n X_iX_i'\biggl)^{-1} \overset{p}\to E(X_iX_i')^{-1}=\alpha\\ \hat{\Sigma}&=\biggl( \frac{1}{n} \sum\limits_{i=1}^n \hat{U}_i^2X_iX_i'\biggl)^{-1} \overset{p}\to E(U_i^2X_iX_i')^{-1}=\Sigma\\ \hat{U}_i&=Y_i-X_i'\hat{\beta} \end{split} \end{equation}\]

Utilizando propiedades de LGN (propiedades de Slutsky), tendremos que \(\hat{\alpha} \hat{\Sigma} \hat{\alpha}' \overset{p}\to \alpha \Sigma \alpha'\)

En el caso de homocedasticdad, estamos asumiendo que la varianza de los errores dado \(X_i\) es constante: \[\begin{equation} Var(U_i|X_i)=E(U_i^2|X_i)=\sigma^2 \tag{3.6} \end{equation}\]

Si aplicamos este supuesto (3.6) al segundo factor de la varianza (\(\Sigma\)), tenemos: \[\begin{equation} E(U_i^2X_iX_i')=E(E(U_i^2|X_i)X_iX_i')=\sigma^2E(X_iX_i') \end{equation}\]

Por lo tanto, la varianza \(\alpha \Sigma \alpha'\) se reduce a: \[\begin{equation} \alpha \Sigma \alpha'=E(X_iX_i')^{-1} \sigma^2E(X_iX_i') E(X_iX_i')^{-1}=\sigma^2E(X_iX_i')^{-1} \end{equation}\]

Dado que \(E(U_i^2)\) es un estimador consistente de \(\sigma^2\), para obtener un estimador consistente de la varianza únicamente necesitamos: \[\begin{equation*} \begin{split} \hat{\sigma}^2&=\frac{1}{n} \sum\limits_{i=1}^n \hat{U}_i^2\\ \hat{\sigma}^2 \hat{\alpha} & \overset{p}\to \sigma^2E(X_iX_i')^{-1} \end{split} \end{equation*}\]

En clase ilustraremos la diferencia entre el supuesto de homocedasticidad y heterocedasticidad con un gráfico. A lo largo del curso asumiremos heterocedasticidad, que es el supuesto menos restrictivo.

3.3 Pruebas de hipótesis en el Modelo de Regresión Lineal

3.3.1 Unidimensionales. Un coeficiente o una combinación lineal de coeficientes

Si partimos del resultado que demostramos previamente: \[\begin{equation} \sqrt{n}(\hat{\bf{\beta}}-\bf{\beta}) \overset{d}\to N(0,\bf{\alpha \Sigma \alpha'}) \end{equation}\]

Necesitamos seguir los siguientes pasos para establecer la distribución necesaria para llevar a cabo las pruebas de hipótesis. Dado que \(\beta\) es un vector de dimensión \(K\), para llevar a cabo pruebas de hipótesis podemos tomar el producto \(l'\beta\) donde \(l\) es un vector de dimensión \(K\) también⁵: \[\begin{equation} l'\beta=\sum\limits_{j=1}^K l_j\beta_j \end{equation}\]

Con esta definición podríamos establecer la prueba de hipótesis de la siguiente forma:

\[\begin{equation*} \begin{split} H_0: & \quad l'\beta=0 \\ H_1: & \quad l'\beta \neq 0 \end{split} \end{equation*}\] Nótese que en vez del valor “\(0\)” se puede usar cualquier constante. Este planteamiento permite hacer pruebas de hipótesis para coeficientes de forma individual. Esto es lo más común en la práctica, donde evaluamos la representatividad de un coeficiente individual. También pueden evaluarse combinaciones lineales de coefientes, como por ejemplo \(\beta_1+\beta_2\), además de combinaciones lineales más complejas. La motivación para hacer pruebas de hipótesis con combinaciones lineales la analizaremos más a profundidad en la siguiente sección ya que la combinación adecuada a evaluar generalmente viene motivada por la interpretación de los coeficientes. En ese momento discutiremos algunos ejemplos. Por lo pronto basta entender que el planteamiento de \(l'\beta\) permite hacer estimaciones de combinaciones tan complejas como: \(\beta_1+\frac{1}{2}~\beta_2-4~\beta_4\). En este caso, si estamos estimando una especificación con \(4\) variables (más la constante), \(l'=[0~~1~~\frac{1}{2}~~0~~4]\).

Para poder evaluar pruebas de hipótesis como lo hicimos en el repaso de estadística necesitaremos asociar a \(l'\beta\) con una distribución. Dado que \(\hat{\alpha} \hat{\Sigma} \hat{\alpha}' \overset{p}\to \alpha \Sigma \alpha'\), por propiedades de LGN (Slutsky): \[\begin{equation*} (l'\hat{\alpha} \hat{\Sigma} \hat{\alpha}' l)^{1/2} \overset{p}\to (l'\alpha \Sigma \alpha' l)^{1/2} \end{equation*}\]

Entonces, por propiedades de CLT (Slutsky): \[\begin{equation*} \frac{l'[\sqrt{n}(\hat{\beta}-\beta)]}{(l'\hat{\alpha} \hat{\Sigma} \hat{\alpha}' l)^{1/2}} \overset{d}\to \frac{1}{(l'\alpha \Sigma \alpha' l)^{1/2}}N(0,l'\alpha \Sigma \alpha' l)=N(0,1) \end{equation*}\]

De manera que si definimos el error estándar como: \[\begin{equation*} SE=\biggl( \frac{l'\hat{\alpha} \hat{\Sigma} \hat{\alpha}' l}{n}\biggl)^{1/2} \end{equation*}\]

Tenemos que: \[\begin{equation} \frac{l'(\hat{\beta}-\beta)}{SE} \overset{d}\to N(0,1) \end{equation}\]

Y a partir de esto podemos generar intervalos de confianza y llevar a cabo pruebas de hipótesis.

3.3.2 Multidimensionales. Varios coeficientes o combinaciones lineales de coeficientes.

Si quisiéramos llevar a cabo pruebas de hipotesis multi-dimensionales, en vez de un intervalo de confianza necesitaríamos generar una elipse de confianza (o una región de confianza). Llevar a cabo pruebas de hipótesis de forma independiente (como lo veremos en clase) implica dejar de considerar la covarianza que puede existir entre los coeficientes.

Supongamos que queremos evaluar la siguiente prueba hipótesis: \[\begin{equation} \begin{split} H_0: & \quad \beta_2=0 \\ & \quad \beta_3=0 \\ H_1: & \quad e.o.c. \end{split} \end{equation}\] Para hacer una representación matricial de esta prueba de hipótesis podemos generar una matriz \(L\) de dimensión \((h \times K)\) donde \(h\) es el número de condiciones (o ecuaciones) que estamos considerando en la prueba de hipótesis. En el caso de nuestro ejemplo \(h=2\) porque son dos condiciones las que se quieren verificar (\(\beta_2=0\) y \(\beta_3=0\)). Por lo tanto, nuestra prueba de hipótesis sería: \[\begin{equation*} \begin{split} H_0: & \quad L~\beta=0 \\ H_1: & \quad e.o.c. \end{split} \end{equation*}\]

En este caso, si nuevamente tuviesemos una especificación con 4 variables (más la constante), \(L\) sería una matriz de tamaño \(2 \times 5\): \[\begin{equation} L=\begin{bmatrix} 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{bmatrix} \end{equation}\]

Al igual que en el caso anterior, la motivación a la prueba de hipótesis que se quiere evaluar debe venir de la interpretación de los coeficientes y veremos ejemplos relacionados. La igualdad del lado derecho nuevamente no necesariamente debe ser un vector \(h\) de ceros. Asimismo, la matriz \(L\) puede ser mas complicado, lo único necesario es que cada renglón (o condición) a evaluar debe ser una combinación lineal de coeficientes, de la misma forma que \(l'\beta\). Por ejemplo, si se quisieran evaluar las siguientes condiciones: \[\begin{equation*} \begin{split} H_0: & \quad 2~\beta_1+\beta_2=0 \\ & \quad \frac{1}{3}~\beta_1-3~\beta_3=0 \\ & \quad \beta_1+\beta_2+\beta_3+\beta_4=0 \\ H_1: & \quad e.o.c. \end{split} \end{equation*}\]

La matriz \(L\) correspondiente sería: \[\begin{equation*} L=\begin{bmatrix} 0 & 2 & 1 & 0 & 0 \\ 0 & \frac{1}{3} & 0 & -3 & 0 \\ 0 & 1 & 1 & 1 & 1 \end{bmatrix} \end{equation*}\]

Siguiendo el mismo procedimiento que en el caso unidimensional: \[\begin{equation} L \sqrt{n} (\hat{\beta}-\beta) \overset{d}\to N(0,L \alpha \Sigma \alpha' L') \end{equation}\]

Además en este caso: \[\begin{equation*} \widehat{Var(L\hat{\beta})}=\frac{L \hat{\alpha} \hat{\Sigma} \hat{\alpha}' L'}{n} \end{equation*}\]

Y por teoría de probabilidad (producto de normales estandár es una ji-cuadrada con grados de libertad igual a la dimensión de la varianza): \[\begin{equation} (L\hat{\beta}-L\beta)' \biggl[ \frac{L \hat{\alpha} \hat{\Sigma} \hat{\alpha}' L'}{n}\biggl]^{-1} (L\hat{\beta}-L\beta) \overset{d}\to \chi_h^2 \end{equation}\]

En clase explicaremos e ilustraremos por qué no es correcto utilizar dos intervalos de confianza generados a partir del caso de pruebas de hipótesis unidimensionales para el caso \(h=2\).

---

Pruebas de Hipótesis Multidimensionales

---

---

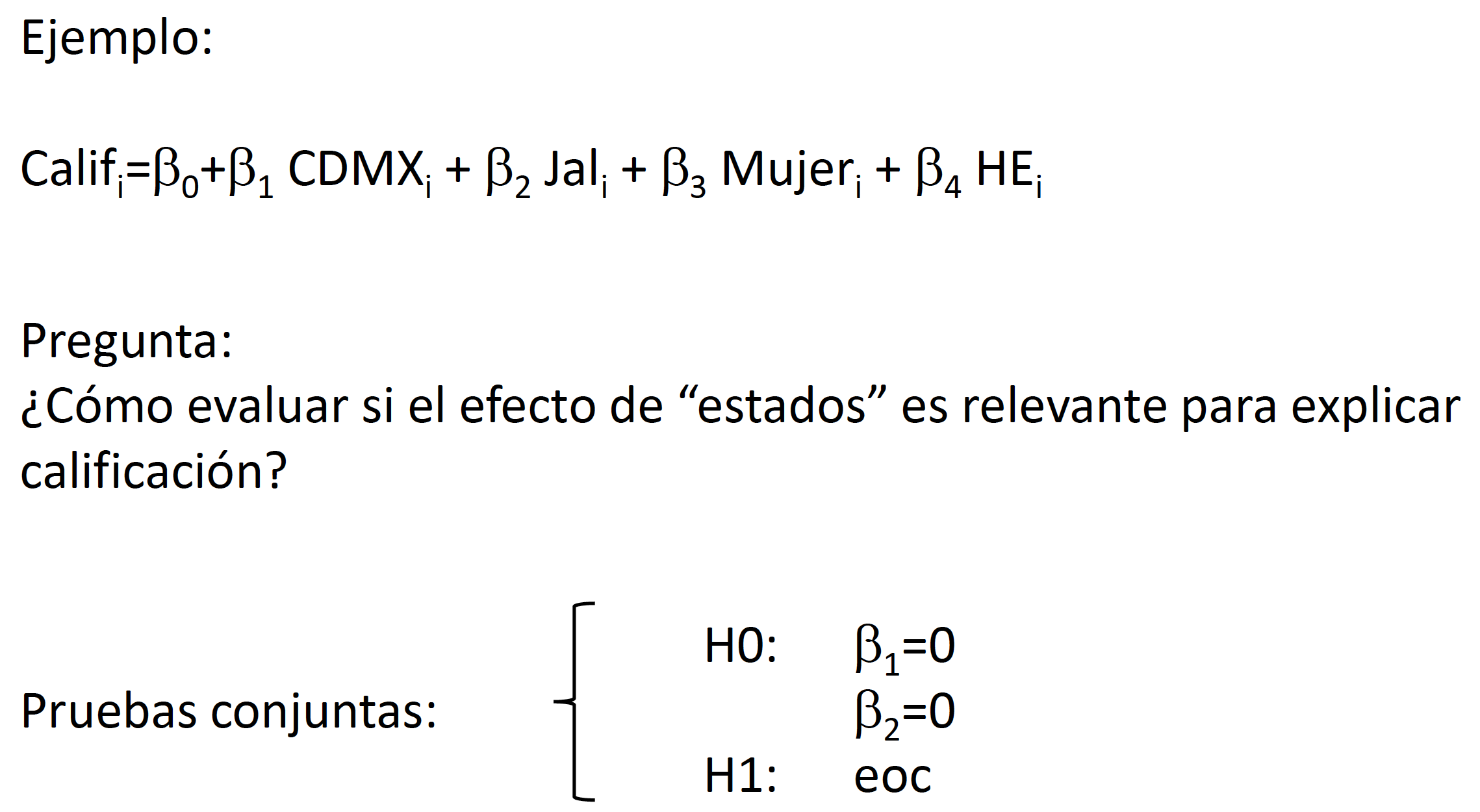
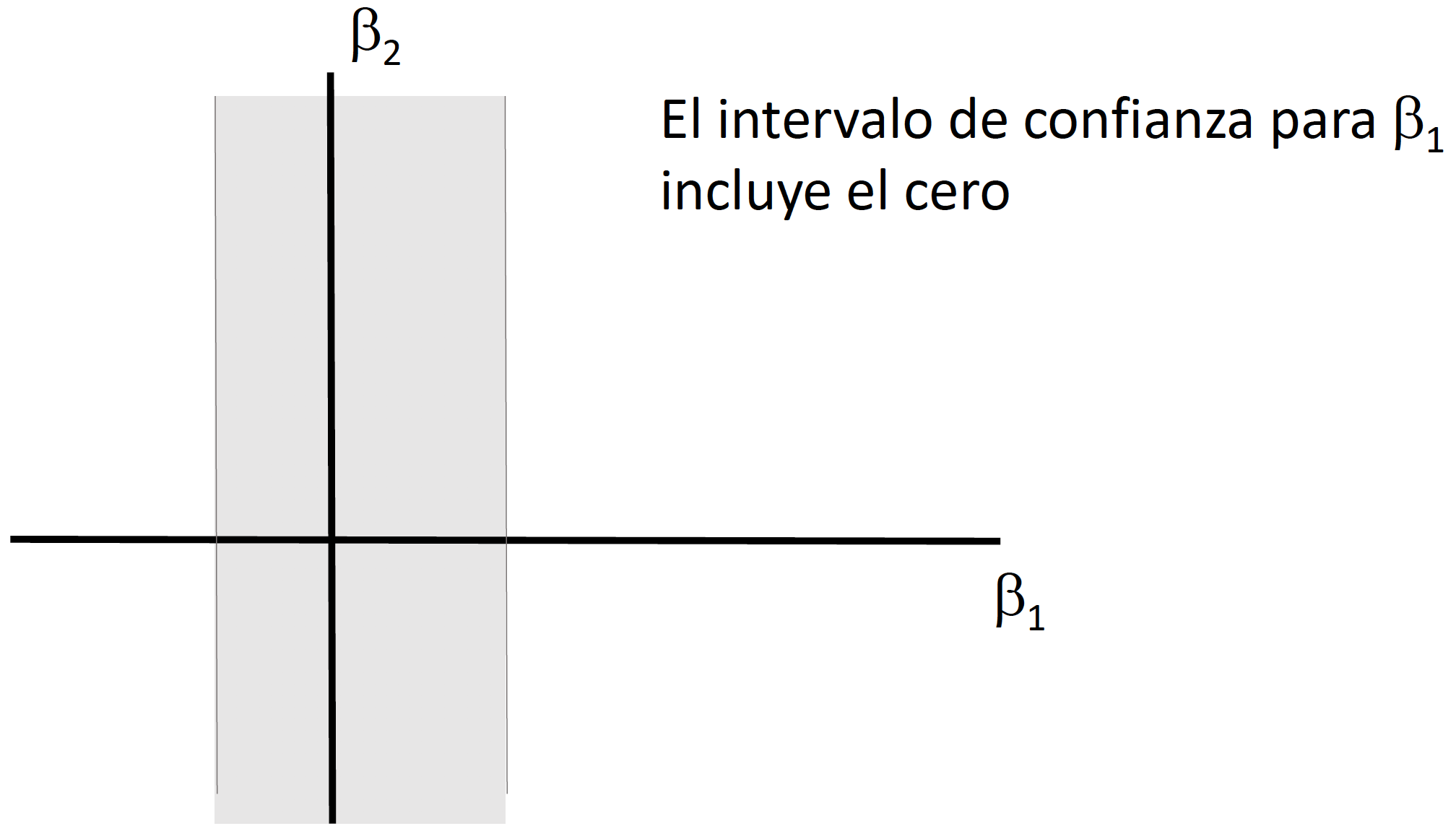
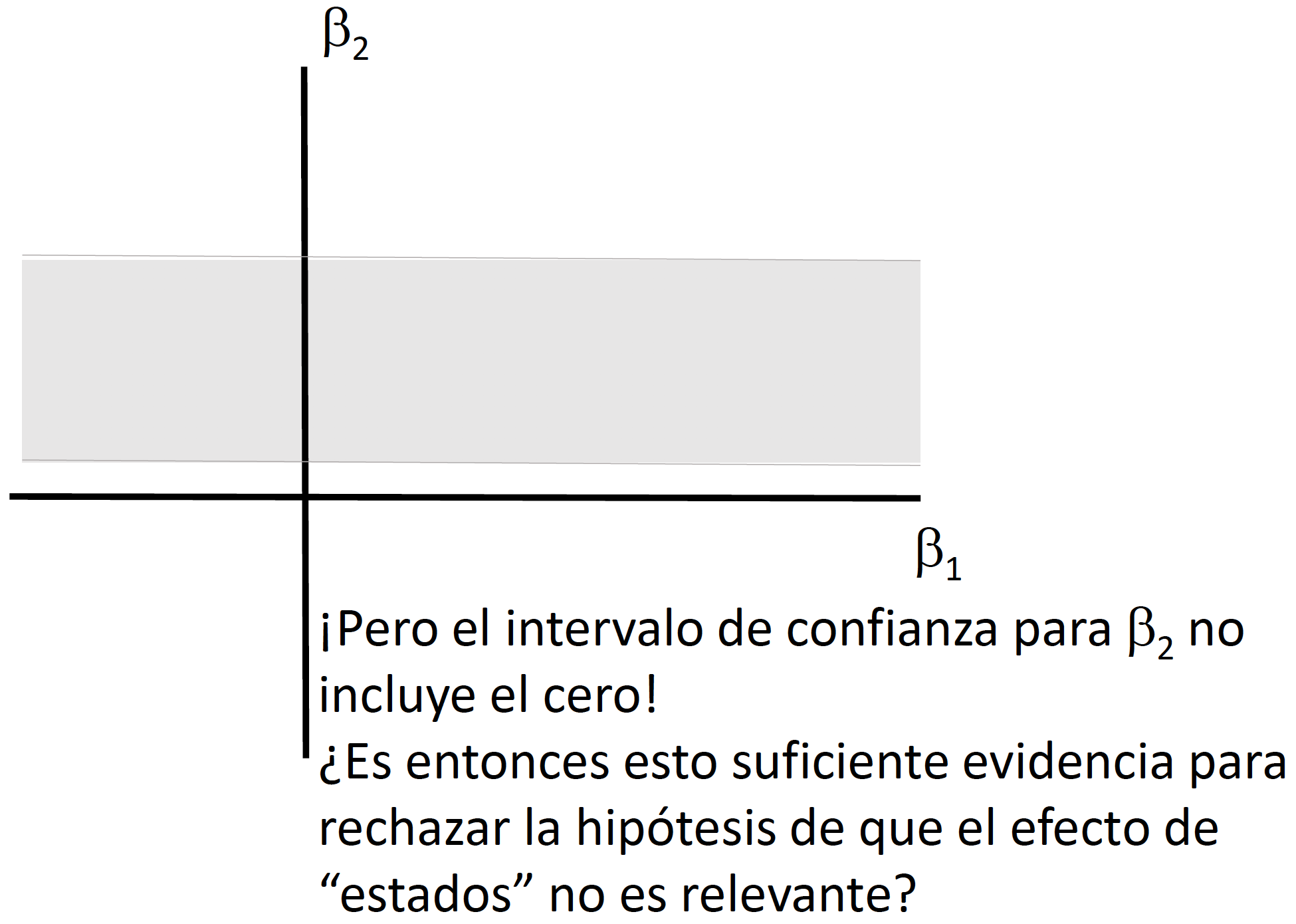
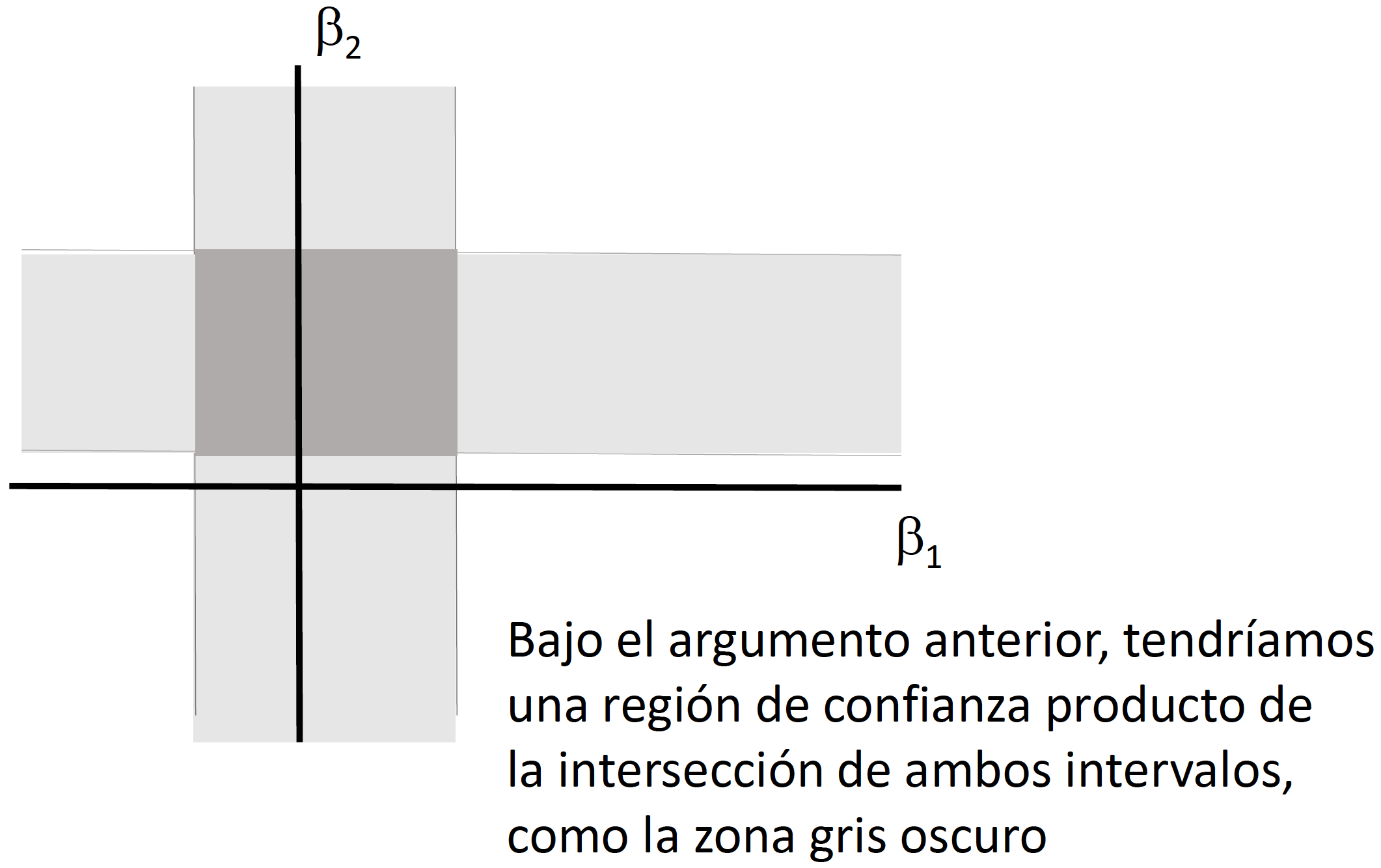
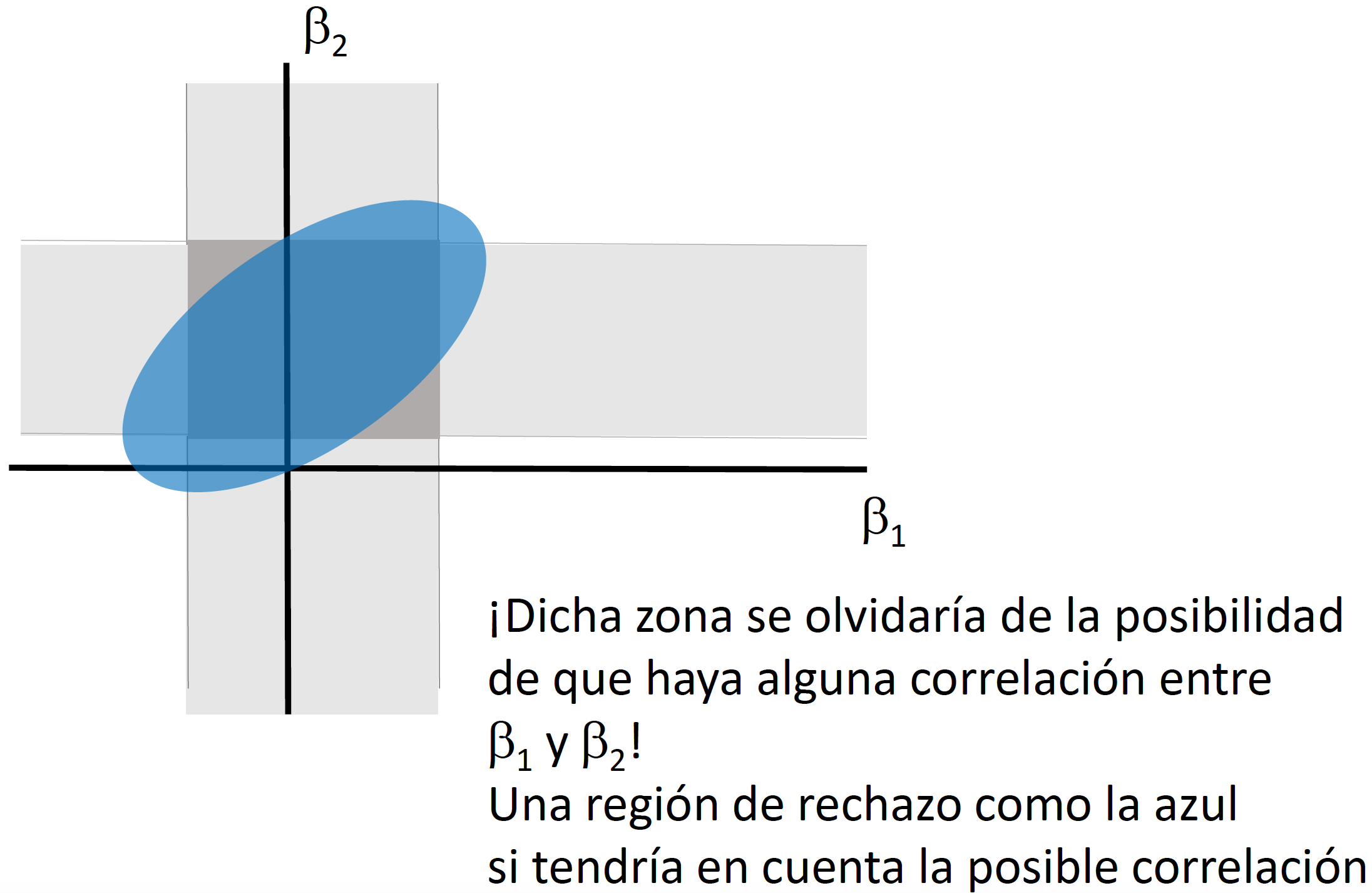
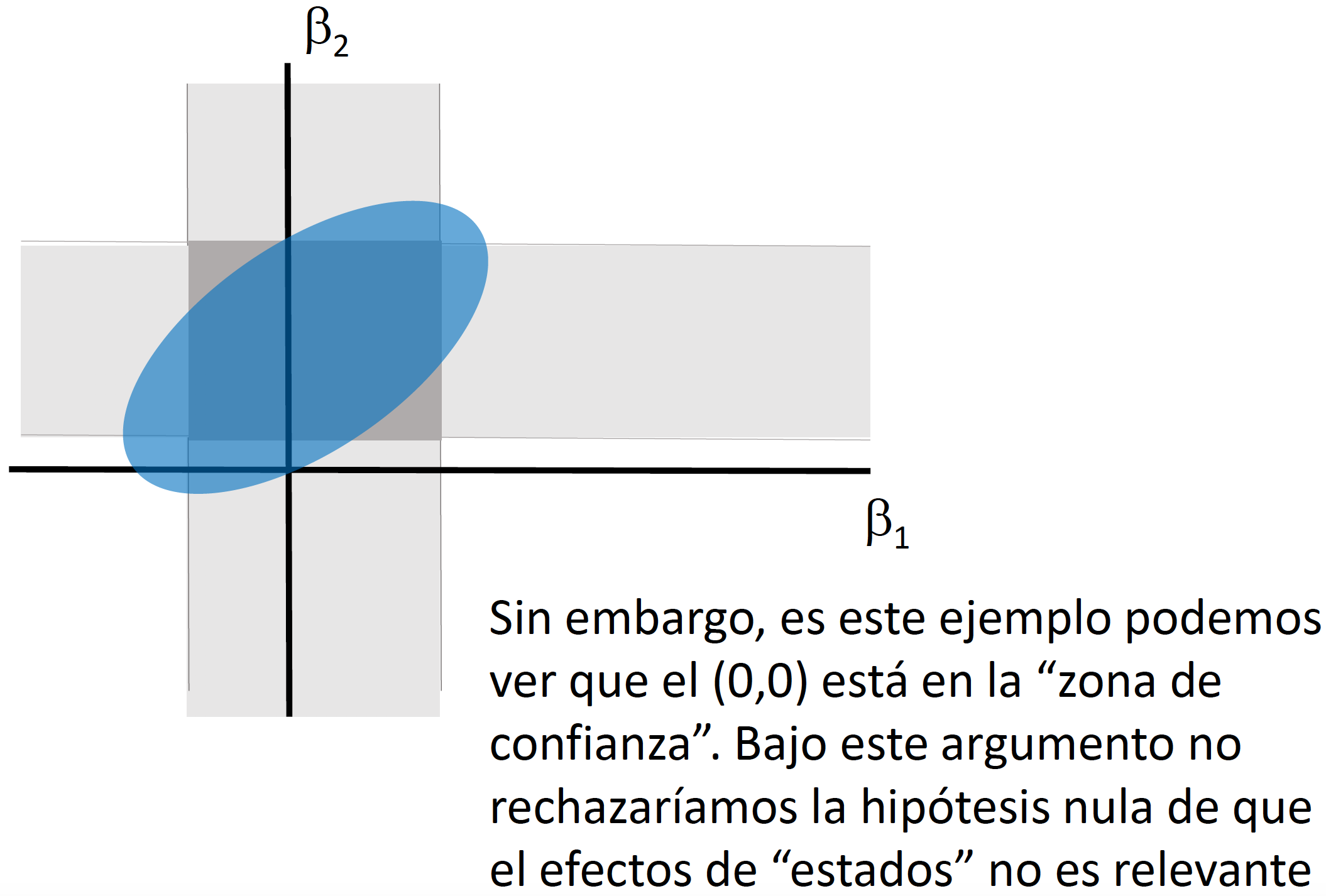
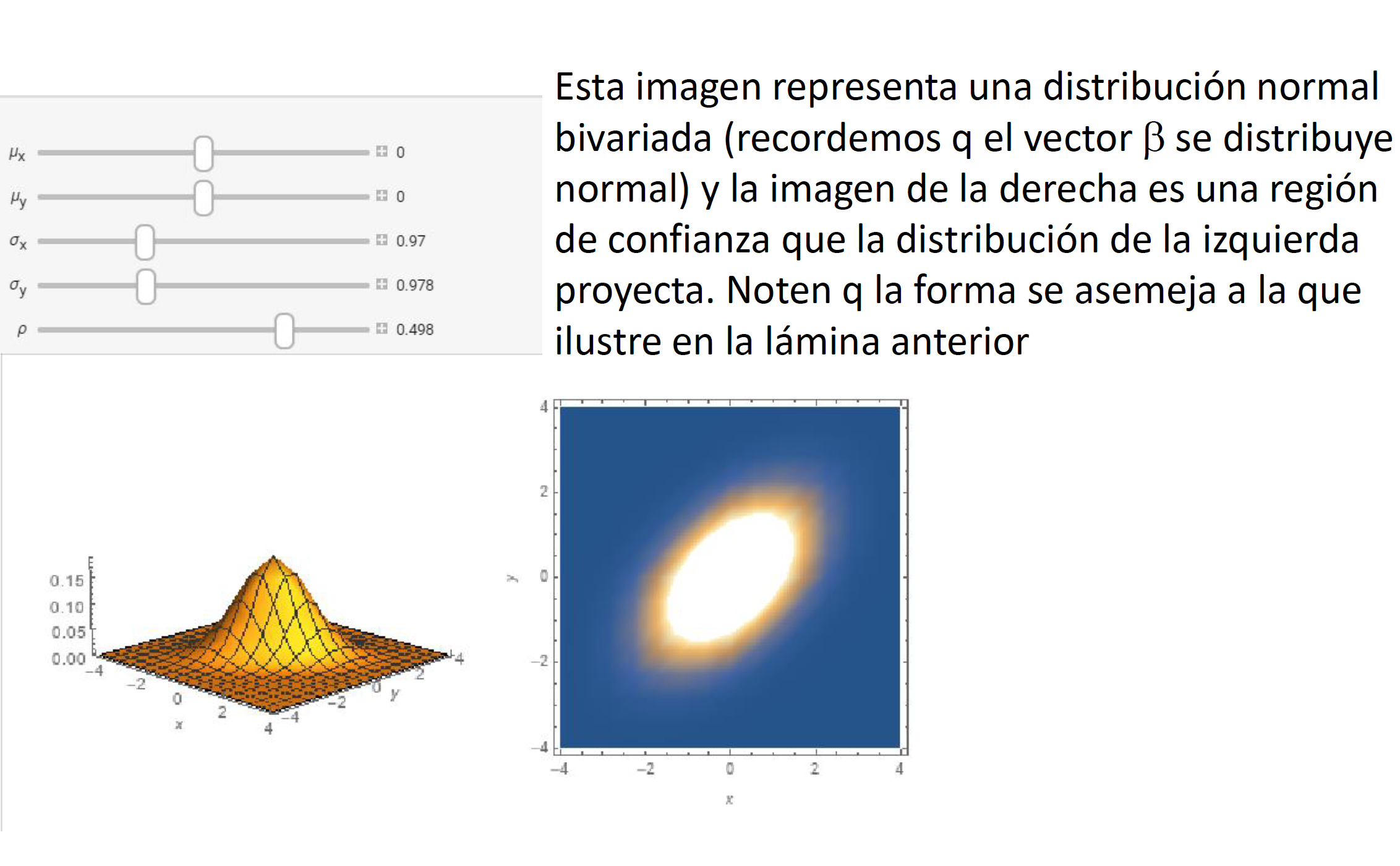
Ejemplo

Tablas de Resultados de Regresión

---

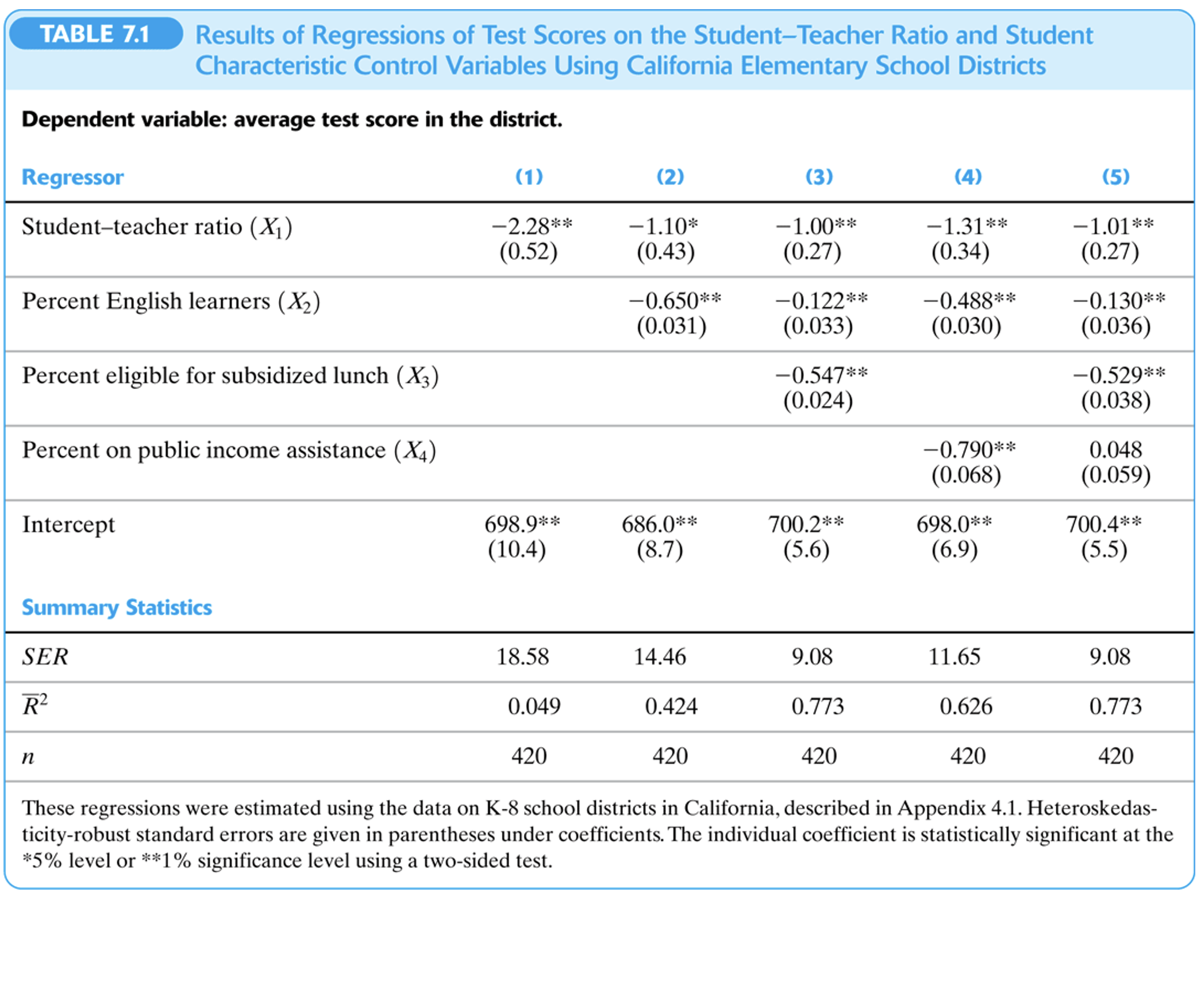
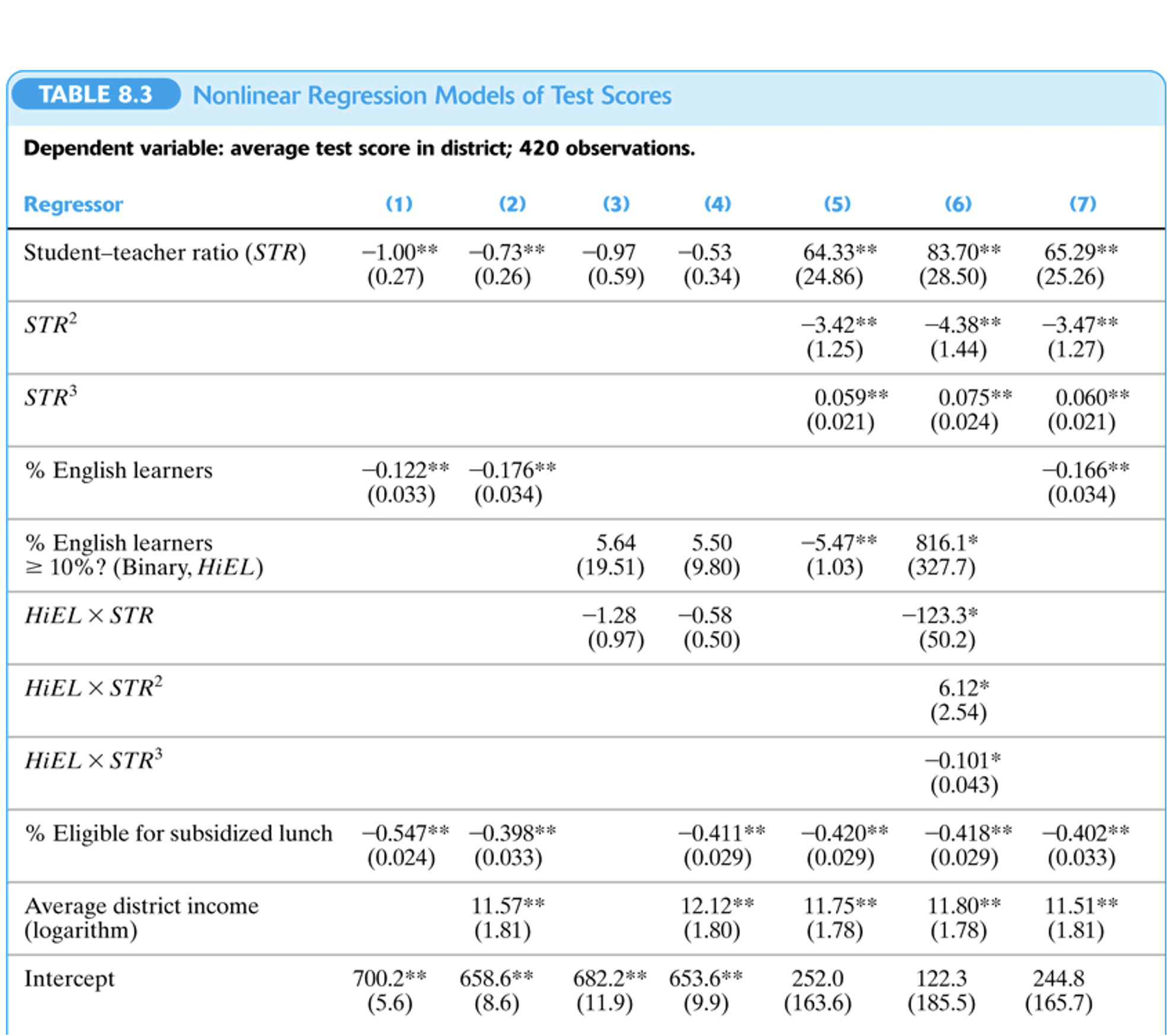
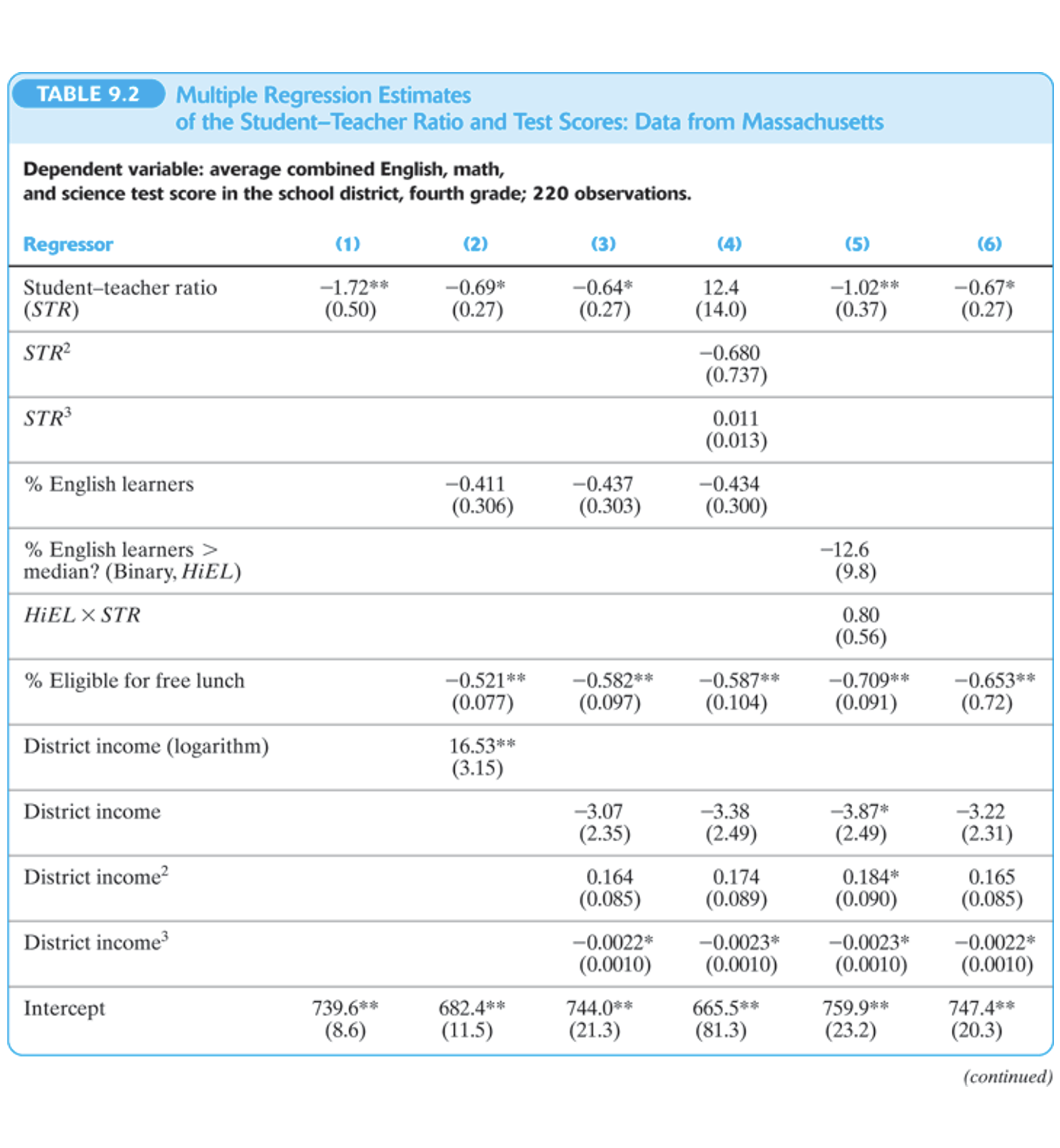
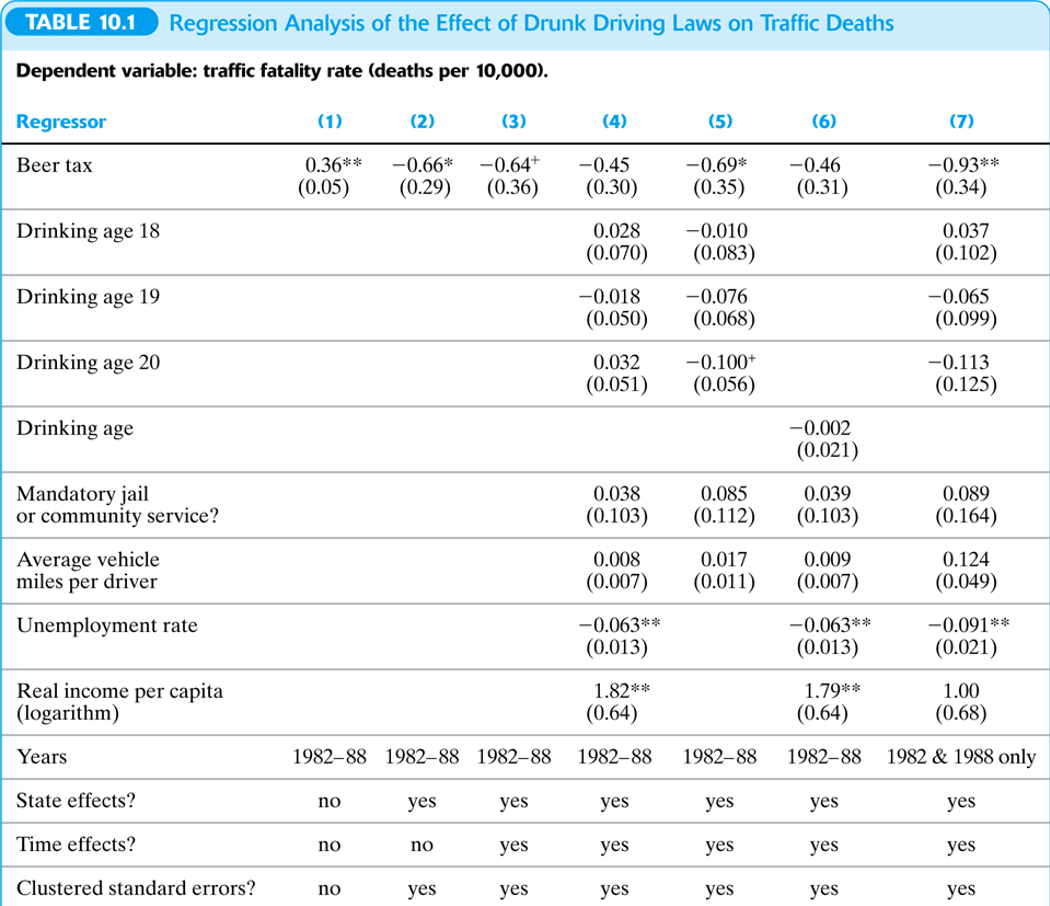
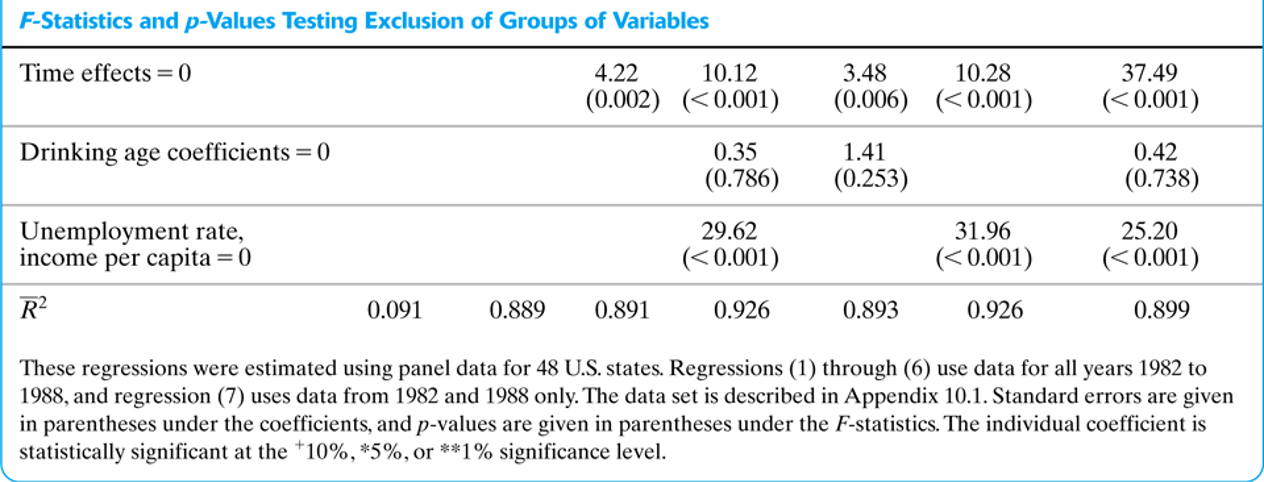
3.4 Interpretación de coeficientes

Generalmente estamos interesados en uno de los parámetros que estamos estimando (sea \(\beta_1\)). La interpretación del coeficiente estimado en el caso de una regresión multivariada es que indica el cambio en la variable dependiente (\(Y\)) por un cambio marginal en la variable \(X_1\) (\(\Delta X_1=1\)), tomando todas las demás variables de control (\(X_2,\dots,X_K\)) constantes (caeteris paribus).

3.4.1 Caso simple

En la interpretación de coeficientes es importante tomar en cuenta en qué unidades se miden las variables dependiente (\(Y\)) y la variable de control que cambia marginalmente (\(X_1\)).

Supongamos que estimamos la siguiente especificación con MCO: \[\begin{equation} Y_i=\beta_0+\beta_1X_{1i}+\beta_2X_{2i}+\dots+\beta_KX_{Ki}+U_i \tag{3.7} \end{equation}\]

Veamos el resultado de aumentar en una unidad la variable \(X_1\) (\(\Delta X_1=1\)) dejando todas las demás variables constantes: \[\begin{equation} Y_i'=\beta_0+\beta_1(X_{1i}+1)+\beta_2X_{2i}+\dots+\beta_KX_{Ki}+U_i \end{equation}\]

En este caso, el cambio de la variable dependiente será: \[\begin{equation} \Delta Y_i=Y_i'-Y_i=\beta_1 \end{equation}\]

Por lo tanto, \(\beta_1\) representará el cambio en \(Y_i\) que resulta de incrementar \(X_1\) en una unidad manteniendo todas las demás variables constantes. Durante la clase veremos ejemplos prácticos.

3.4.2 Formas funcionales

A pesar de que la forma lineal de la especificación del modelo MCO parece ser muy restrictiva en principio, es posible hacer transformaciones de las variables independientes y con ello lograr una mejor aproximación de la relación entre dos variables.

Llevar a cabo transformaciones permite hacer una estimación más exacta en términos estadísticos y más correcta en términos teóricos.

Para decidir qué tipo de transformación es más pertinente utilizar en cada caso debe considerarse:

• De acuerdo a la teoría, qué función representa de manera mas fidedigna la relación entre dos variables

• De acuerdo a los datos empíricos, qué función describe de manera más exacta la relación entre los datos observados

3.4.3 Transformación polinomial

En el caso de transformaciones para generar distintas formas funcionales (como se discute en la sección anterior) es importante considerar que las interpretaciones de los coeficientes cambian de forma importante.

Para empezar, tomemos el caso de una transformación polinomial de alguna variable de interés. Supongamos que estimamos la siguiente regresión:

\[\begin{equation} Y_i=\beta_0+\beta_1X_{1i}+\beta_2X_{1i}^2+\dots+\beta_KX_{Ki}+U_i \tag{3.8} \end{equation}\]

Si en este caso queremos ver el cambio en la variable dependiente \(Y\) por un cambio marginal en \(X_1\), es importante notar que la variable \(X_1\) aparece en más de un término en la estimación (3.8). Por lo tanto, si queremos aproximar el efecto de un aumento marginal de \(X_1\) (i.e. \(\partial X_1=1\)), calculamos la derivada respecto de \(X_1\): \[\begin{equation*} \frac{\partial Y_i}{\partial X_{1i}}=\beta_1+2\beta_2X_{1i} \end{equation*}\] Lo que la ecuación anterior indica es que ahora, por la forma cuadrática, el efecto de un aumento marginal de \(X_1\) sobre \(Y\) depende del nivel de \(X_1\) del cual partimos. Por lo tanto, el efecto será distinto dependiendo del individuo. En particular, el coeficiente \(\beta_1\) corresponde al cambio en \(Y\) asociado a un aumento de una unidad de \(X_1\) condicional en que el valor inicial de \(X_1=0\). Por otra parte \(\beta_2\) tiene una interpretación relacionada a cómo este efecto marginal va cambiando conforme se incrementa \(X_1\): \[\begin{equation*} \frac{\partial^2 Y_i}{\partial X_{1i}^2}=2\beta_2 \end{equation*}\] En la ecuación anterior podemos ver que el signo de \(\beta_2\) determina el signo de \(\frac{\partial^2 Y_i}{\partial X_{1i}^2}\). Es decir, \(\beta_2\) nos dice si la relación entre \(Y_i\) y \(X_{1i}\) es cóncava o convexa. En otras palabras, nos dice si el cambio de \(Y\) por un cambio marginal de \(X_1\) es creciente o decreciente.

En (3.8) empleamos un polinomio de grado \(2\). Sin embargo, podemos utilizar un polinomio de mayor grado en la especificación. Cabe notar, sin embargo, que dicho cambio debe estar sustentado teóricamente o con evidencia empírica (mostrada en los datos), ya que conforme aumenta el polinomio la interpretación de algún efecto partiendo de los coeficientes se vuelve más complicado.

3.4.4 Transformación logarítmica

En el caso de una transformación logarítmica, los coeficientes cambian en su interpretación. Una característica particular de los logaritmos es que provocan que la variable sobre la cual está aplicado el logaritmo ya no utilizará sus unidades en la interpretación. Esto es de gran ayuda en casos en los cuales las unidades que se están utilizando no son fáciles de interpretar o de conocimiento universal (e.g. calificaciones en un país en específico). En vez de utilizar sus unidades, los cambios en esta variable estarán expresados en términos porcentuales. Esto es útil en casos en los cuales suelen ser comunes los cambios porcentuales (e.g. variables monetarias).

La transformación logarítmica puede aplicarse tanto a la variable dependiente como a controles de la estimación. Empecemos por ver cómo interpretar el coeficiente de algún control cuando la variable dependiente es un logaritmo: \[\begin{equation} \ln{(Y_i)}=\beta_0+\beta_1X_{1i}+\dots+\beta_KX_{Ki}+U_i \tag{3.9} \end{equation}\]

Para ver cómo interpretaríamos ahora un coficiente veamos el caso de \(\beta_1\). Primero calculamos la derivada respecto de \(X_1\): \[\begin{equation*} \beta_1=\frac{\partial \ln{(Y_i)}}{\partial X_{1i}}=\frac{\partial Y_i/\partial X_{1i}}{Y_i} \end{equation*}\]

En este caso, para un cambio de \(X_{1i}\) en una unidad (i.e. \(\partial X_{1i}=1\)), tenemos que \(\beta_1\) representa un cambio de \(Y_i\) igual a \(\frac{\partial Y_i}{Y_i}\). Para expresar esto en tasa (en términos porcentuales) tenemos que multiplicar por \(100\) ambos lados para obtener que: \(100\cdot\beta_1=100\cdot\biggl(\frac{\partial Y_i}{Y_i}\biggl)\%\). Nótese que las unidades de \(Y_i\) en este caso ya no influyen en la interpretación del coeficiente, pero las de \(X_{1i}\) sí. En resumen, en este caso tendremos que un aumento de una unidad de \(X_{1i}\) conlleva un aumento de \(100\cdot\beta_1\%\) en \(Y_i\).

Imaginemos ahora que en vez de (3.9), hacemos una transformación logarítmica para uno de los controles:

\[\begin{equation} Y_i=\beta_0+\beta_1\ln{(X_{1i})}+\dots+\beta_KX_{Ki}+U_i \tag{3.10} \end{equation}\]

En el caso de (3.10), la interpretación de \(\beta_1\) surgiría de: \[\begin{equation*} \beta_1=\frac{\partial Y_i}{\partial \ln{(X_{1i})}}=\frac{\partial Y_i}{\partial X_{1i}/X_{1i}} \end{equation*}\]

Sin embargo, esto llevaría a una interpretación poco intuitiva ya que si asumimos que el denominador cambia en una unidad (i.e. \(\frac{\partial X_{1i}}{X_{1i}}=1\)) implicaría que \(X_{1i}\) aumenta en \(100\%\). Para hacer más intuitiva la interpretación multiplicamos y dividimos entre \(100\) de manera tal que obtenemos:

\[\begin{equation*} \beta_1=\frac{\partial Y_i}{\partial \ln{(X_{1i})}}=\frac{\partial Y_i}{\partial X_{1i}/X_{1i}}\cdot\frac{100}{100} \end{equation*}\]

Ahora es más intuitivo asumir que el denominador cambia en una unidad (i.e. \(\partial X_{1i}/X_{1i}\cdot100=1\)) ya que esto implicaría que \(X_{1i}\) aumenta en \(1\%\) (i.e. \(\partial X_{1i}/X_{1i}=1/100\)). Sin embargo, el cambio realizado afecta también al numerador. Si asumimos que el denominador es igual a \(1\), la ecuación anterior resulta en: \[\begin{equation*} \beta_1=\partial Y_i\cdot 100 \end{equation*}\]

Esto quiere decir que el cambio en \(Y_i\) es de \(\beta_1/100\). Por lo tanto, la interpretación correcta del coeficiente \(\beta_1\) en (3.10) es que, caeteris paribus, un cambio de \(X_{1i}\) en \(1\%\) conlleva un cambio de \(\beta_1/100\) unidades de \(Y_i\). Cabe señalar que ahora las unidades de \(X_{1i}\) no influyen en la interpretación, pero las de \(Y_i\) sí.

Por último, vemos qué sucede si empleamos logaritmos de ambos lados, tanto en la variable dependiente como en el control: \[\begin{equation} \ln{(Y_i)}=\beta_0+\beta_1\ln{(X_{1i})}+\dots+\beta_KX_{Ki}+U_i \tag{3.11} \end{equation}\]

En el caso de (3.11), la interpretación de \(\beta_1\) surgiría de: \[\begin{equation*} \beta_1=\frac{\partial \ln{(Y_i)}}{\partial \ln{(X_{1i})}}=\frac{\partial Y_i/Y_i}{\partial X_{1i}/X_{1i}} \end{equation*}\]

Nuevamente, dado que tenemos logaritmo del lado derecho, como en (3.10), siguiendo la misma estrategia multiplicamos y dividimos entre \(100\) para interpretar el cambio en \(X_{1i}\) como un cambio de \(1\%\), por lo tanto tendremos: \[\begin{equation*} \beta_1=\frac{\partial Y_i/Y_i}{\partial X_{1i}/X_{1i}}\cdot\frac{100}{100} \end{equation*}\]

Para interpretar \(\beta_1\) vemos que un cambio de una unidad en el denominador (i.e. \(\partial X_{1i}/X_{1i}\cdot100=1\)) equivale a un aumento de \(1\%\) en \(X_{1i}\) (i.e. \(\partial X_{1i}/X_{1i}=1/100\)). Entonces, si el denominador es igual a \(1\) nos queda que \(\beta_1=100*\partial Y_i/Y_i\). En este caso, ya no hay necesidad de multiplicar por \(100\), ya que el cambio porcentual de \(Y_i\) (i.e. \(\partial Y_i/Y_i\)) ya está expresado en tasa debido a que esta multiplicado por \(100\). En resumen, para interpretar \(\beta_1\) no hace falta multiplicar o dividir entre \(100\) como en los casos anteriores. Simplemente tendremos que, caeteris paribus, un aumento de \(1\%\) en \(X_{1i}\) conlleva un cambio de \(\beta_1\%\) en \(Y_i\). En este caso, las unidades de \(Y_i\) y \(X_{1i}\) no importan.

La siguiente tabla resume todas las posibles interpretaciones de la transformación logarítmica dependiendo de la posición del logaritmo en la especificación lineal:

Var. Dep (\(Y\))	Var. Indep (\(X_1\))	Interpretación del coef. de \(X_1\) (\(\beta_1\))
\(\ln{(Y)}\)	\(X_1\)	\(\Delta X_1=1 \Rightarrow \Delta Y=(100\beta_1)\%\)
\(Y\)	\(\ln{(X_1)}\)	\(\Delta X_1=1\% \Rightarrow \Delta Y=(\beta_1/100)\)
\(\ln{(Y)}\)	\(\ln{(X_1)}\)	\(\Delta X_1=1\% \Rightarrow \Delta Y=(\beta_1)\%\)

3.4.5 Variables Dummy

Otra interpretación interesante surge cuando la variable dependiente es una variable dummy (i.e. una variable dicotómica \(X_1=\{0,1\}\)). En estos casos no tiene sentido interpretar a \(\beta_1\) como el cambio en \(Y\) tras un cambio marginal en la variable independiente (\(\Delta X_1=1\)).

Para entender la interpretación del coeficiente de una variable dummy es conveniente repasar que representa la variable en el caso de una regresión lineal simple. Supongamos que la variable dummy representa ser mujer (i.e. \(X_{1i}=1\) si el individuo \(i\) es mujer y \(X_{1i}=0\) si es hombre). Supongamos que estimamos la siguiente regresión: \[\begin{equation} Calif_i=\beta_0+\beta_1X_{1i}+U_i \end{equation}\]

donde \(Calif_i\) representa el promedio escolar de la persona \(i\).

En este caso la media condicional de ser mujer y hombre, respectivamente son: \[\begin{equation*} \begin{split} E(Calif_i|X_{1i}=1) &= \beta_0+\beta_1\\ E(Calif_i|X_{1i}=0) &= \beta_0 \end{split} \end{equation*}\]

Por lo tanto, \(\beta_1\) representa la diferencia en calificación de ser mujer respecto de ser hombre: \[\begin{equation} \beta_1= E(Calif_i|X_{1i}=1) - E(Calif_i|X_{1i}=0) \end{equation}\]

Similarmente, supongamos que una persona se caracteriza por la región en la que vive y existen cuatro distintas posibilidades de regiones: {NE, NW, SE, SW}. Para expresar esto en una regresión podemos crear variables dummy para cada región (i.e. \(NE_i=1\) si \(i\) vive en el NE, \(NE_i=0\) eoc) y estimar la siguiente regresión: \[\begin{equation*} Calif_i=\beta_0 + \beta_1 NE_i + \beta_2 NW_i + \beta_3 SE_i +U_i \end{equation*}\]

Aquí es importante dejar una de las cuatro regiones como región omitida (o de referencia). Esto es necesario, ya que de lo contrario la variable constante será multicolinear con las cuatro variables regionales. Matemáticamente, si hacemos esto, la matriz \(\biggl(\frac{1}{n}\sum\limits_{i=1}^n X_iX_i'\biggl)\) no sería invertible, por lo tanto, no podríamos estimar los coeficientes.

En el ejemplo anterior, \(\beta_3\) será interpretada como la calificación de un individuo promedio que habita en la región SE respecto a la de un individuo promedio que habita en la región SW. La selección de la región de referencia fue subjetiva en este caso. Cualquier región podría haber sido elegida como la de referencia.

Ejemplo: ¿Cómo cambiarían los coeficientes si la región de referencia elegida hubiera sido NW?

3.4.6 Interacciones

Las interacciones resultan de utilizar el producto de dos variables como una variable independiente adicional. Generalmente, dicho producto ocurre entre dos variables dummy o una variable dummy y una continua.

3.4.6.1 Interacción de dos variables tipo dummy

Consideremos un modelo donde queremos explicar el total de horas laboradas basado en el sexo y estado civil del individuo. Sea \(X_{1i}\) una variable indicador para mujer (\(X_{1i}=1\) si \(i\) es mujer y \(X_{1i}=0\) si es hombre) y \(X_{2i}\) una variable indicador para estado civil (\(X_{2i}=1\) si \(i\) es casado y \(X_{2i}=0\) si es soltero). Tomemos el siguiente modelo:

\[\begin{equation} Y_i= \beta_0 + \beta_1 X_{1i} + \beta_2X_{2i} + \beta_3X_{1i}X_{2i} + U_i \end{equation}\]

Para entender la interpretación del coeficiente de la interacción (\(\beta_3\)) consideremos nuevamente medias condicionales: \[\begin{equation*} \begin{split} [A]&= E[Y_i|X_{1i}=0,X_{2i}=0] = \beta_0\\ [B]&= E[Y_i|X_{1i}=0,X_{2i}=1] = \beta_0+\beta_2\\ [C]&= E[Y_i|X_{1i}=1,X_{2i}=0] = \beta_0+\beta_1\\ [D]&= E[Y_i|X_{1i}=1,X_{2i}=1] = \beta_0+\beta_1+\beta_2+\beta_3 \end{split} \end{equation*}\]

Por lo tanto tenemos que: \[\begin{equation*} \begin{split} \beta_2&=[B]-[A] \\ \beta_2+\beta_3&=[D]-[C]\\ \beta_3&=([D]-[C])-([B]-[A]) \end{split} \end{equation*}\]

\(\beta_2\) representa horas extra que trabaja un hombre casado respecto a un soltero. \(\beta_2+\beta_3\) representa horas extra que trabaja una mujer casada respecto a una soltera. \(\beta_3\) representa si estar casado respecto a estar soltero representa una diferencia mayor para una mujer que para un hombre. Dicho de otra manera, indica si el plus de horas de trabajo por estar casado es diferente para una mujer que para un hombre.

3.4.6.2 Interacción de una variable tipo dummy y una variable continua

Supongamos ahora que una de nuestras variables es continua. En vez de la variable dummy casado/soltero supongamos que tenemos una variable que indica el nivel de educación de la persona. Podría interresarnos analizar si los retornos a un año adicional de educación son similares entre hombres y mujeres. Para ello establecemos el siguiente modelo: \[\begin{equation} Ing_i=\beta_0+\beta_1Educ_i+\beta_2Mujer_i+\beta_3Educ_i\cdot Mujer_i \end{equation}\]

En este modelo \(Ing_i\) representa el ingreso mensual de una persona medida en pesos; \(Educ_i\), el nivel educativo medido en años completados; y \(Mujer_i\) es una variable dummy igual a \(1\) si la persona es mujer.

Utilizando este modelo, los retornos a un año adicional de educación para los hombres son: \[\begin{equation*} \begin{split} E(Ing_i|Mujer_i=0)&=\beta_0+\beta_1Educ_i\\ \frac{\partial E(Ing_i|Mujer_i=0)}{\partial Educ_i}&=\beta_1 \end{split} \end{equation*}\]

Similarmente, los retornos a un año adicional de educación para las mujeres son: \[\begin{equation*} \begin{split} E(Ing_i|Mujer_i=1)&=(\beta_0+\beta_2)+(\beta_1+\beta_3)Educ_i\\ \frac{\partial E(Ing_i|Mujer_i=1)}{\partial Educ_i}&=\beta_1+\beta_3 \end{split} \end{equation*}\]

Por lo tanto, \(\beta_3\) representa la diferencia en los retornos entre hombres y mujeres. Dicho de otra manera, \(\beta_3\) indica qué tan mayores son los retornos a un año adicional de educación para las mujeres que para los hombres. \[\begin{equation*} \beta_3=\frac{\partial E(Ing_i|Mujer_i=1)}{\partial Educ_i}-\frac{\partial E(Ing_i|Mujer_i=0)}{\partial Educ_i} \end{equation*}\]

3.4.6.3 Interacción de dos variables continuas

Por último, podemos utilizar un modelo con interacciones donde las dos variables involucradas en la interacción son variables continuas. En este caso, el modelo nos puede indicar si los rendimientos marginales respecto a una variable dependen de la otra variable incluida en la interacción.

Por ejemplo, supongamos que especificamos el siguiente modelo: \[\begin{equation} Ing_i=\beta_0+\beta_1Educ_i+\beta_2Calidad_i+\beta_3Educ_i*Calidad_i \end{equation}\] donde \(Calidad_i\) es un índice que mide la calidad de la educación recibida. En este caso los retornos por un año adicional de educación serán: \[\begin{equation*} \frac{\partial E(Ing_i)}{\partial Educ_i}=\beta_1+\beta_3Calidad_i \end{equation*}\] Lo que nos indica el resultado anterior es que dichos retornos a la educación pueden depender del nivel de calidad.

%Discutir en este caso como se obtienen los coeficientes (\(\beta\)’s). Dar un ejemplo con retornos a horas de práctica en un video juego.

3.5 El estadístico \(R^2\)

Una medida comúnmente utilizada para describir qué función describe de mejor manera los datos empíricamente es el estadístico \(R^2\). Cabe señalar que no es recomendable elegir el modelo a utilizar basándose únicamente en el estadístico \(R^2\). Este estadístico aumenta si incrementamos la cantidad de variables a incluir en la regresión. Sin embargo, no en todos los casos es conveniente añadir controles en una regresión, especialmente si nos interesa llevar a cabo inferencia causal. Antes de recurrir a esta alternativa se recomienda utilizar la teoría para justificar el modelo a emplear.

El estadístico \(R^2\) se calcula como: \[\begin{equation} \begin{split} R^2&=\frac{\sum\limits_{i=1}^n (\widehat{Y}_i-\overline{Y})^2}{\sum\limits_{i=1}^n (Y_i-\overline{Y})^2}\\ &=1-\frac{\sum\limits_{i=1}^n \widehat{U}_i^2}{\sum\limits_{i=1}^n (Y_i-\overline{Y})^2}\\ &=1-\frac{SSR}{SST} \end{split} \end{equation}\]

El estadístico \(R^2\) representa la parte de la varianza de \(Y_i\) que es explicada por el modelo MCO.

3.6 Modelo de Probabilidad Lineal

Ahora veremos qué sucede en casos en los cuales la variable dependiente es una decisión binaria. En este caso, nuestra variable dependiente será una variable tipo dummy (\(Y_i=\{0,1\}\)). En este caso, nos referiremos a la estimación como un modelo de probabilidad lineal, el cual consiste en simplemente estimar un modelo de MCO con errores heterocedásticos:

\[Y_i=X_i'\beta+U_i\]

En este caso, aplican los supuestos del modelo de MCO, tal como lo revisamos anterioremente. Sin embargo, una particularidad es la interpretación de los coeficientes. Dado que nuestra variable dependiente es una variable binaria, el modelo se puede especificar de la siguiente forma:

\[E(Y_i|X_i)=1\cdot Pr(Y_i=1|X_i)+0\cdot Pr(Y_i=0|X_i)=Pr(Y_i=1|X_i)=X_i'\beta\]

En clase mostramos cómo se ve este modelo gráficamente.

Por lo tanto, cada coeficiente (\(\beta_j\)) representará (caeteris paribus) el cambio en la probabilidad (medida en puntos porcentuales) de que \(Y_i=1\) por un cambio marginal en \(X_j\). Ejemplo, si nuestra variable dependiente es inscribirse o no a la universidad y una de las variables independientes es la educación de la madre, el coeficiente de esta variable representará el cambio de la probabilidad (medido en puntos porcentuales) de que el individuo se inscriba a la universidad por un aumento de un año en la educación de la madre.

En el caso del modelo de probabilidad lineal, los errores siempre deberán asumirse como heterocedásticos, ya que:

\[Var(Y_i|X_i)=Pr(Y_i=1|X_i)\cdot(1-Pr(Y_i=1|X_i))=X_i'\beta(1-X_i'\beta)\]

Sin embargo, un problema de este modelo, por su diseño lineal, es que es posible que nos lleve a predecir valores imposibles (es decir, fuera del rango 0-1) para la variable dependiente. Existen modelos que corrigen este problema y estiman valores de la probabilidad estrictamente entre 0 y 1, siendo probit y logit los casos más conocidos. Estos modelos forman parte de la categoría de modelos de estimadores de máxima verosimilitud (MLE).

3.7 Sesgo por variables omitidas

En esta sección, el propósito es estimar cuál es la diferencia en los coeficientes entre estimar una regresión con \(K\) variables (que llamaremos regresión larga por simplicidad) utilizando MCO y estimar otra regresión que omita una de esas variables (por simplicidad omitiremos la variable \(X_K\)).

Sea la regresión larga: \[\begin{equation} Y= \beta_0 + \beta_1X_1+\dots+\beta_{K-1}X_{K-1} + \beta_KX_K + U \tag{3.12} \end{equation}\]

Sea la regresión omitiendo la variable \(X_K\) (regresión corta): \[\begin{equation} Y=\alpha_0+\alpha_1X_1+\dots+\alpha_{K-1}X_{K-1}+V \tag{3.13} \end{equation}\]

Queremos establecer cuál es la relación entre \(\beta_j\) y \(\alpha_j\) para \(j=\{0,1,\dots,K-1\}\).

Definamos a la regresión residual como: \[\begin{equation} X_K=\gamma_0+\gamma_1X_1+\dots+\gamma_{K-1}X_{K-1}+W \tag{3.14} \end{equation}\]

Sustituyendo (3.14) en (3.12) obtenemos: \[\begin{equation*} Y=\beta_0+\beta_1X_1+\dots+\beta_{K-1}X_{K-1}+\beta_K(\gamma_0+\gamma_1X_1+\dots+ \gamma_{K-1}X_{K-1}+W)+U \end{equation*}\]

Reordenando los términos obtenemos: \[\begin{equation} Y=\tilde{\beta}_0+\tilde{\beta}_1X_1+\dots+\tilde{\beta}_{K-1}X_{K-1}+\beta_KW+U \end{equation}\] donde \(\tilde{\beta}_j=\beta_j+\beta_K\gamma_j\) para \(j=\{0,1,\dots,K-1\}\).

Nótese que ésta última regresión es lo mismo que (3.13) si definimos al error como \(V=\beta_KW+U\). Por lo tanto, las condiciones de primer órden que nos llevarían a resolver ésta ultima regresión y (3.13) son las mismas. Esto implica que \(\tilde{\beta}_j=\alpha_j\). Por lo tanto, el sesgo se define como: \[\begin{equation*} \alpha_j-\beta_j=\beta_K\gamma_j \end{equation*}\]

El signo del sesgo estará entonces definido por los signos de los coeficientes \(\beta_K\) y \(\gamma_j\).

---

Ejemplo

Sesgo por variables omitidas

Figure 3.3: Ejemplo de sesgo por variables omitidas. Fuente: Pace~svwiki / CC BY-SA

---

3.8 Validez externa e interna

En esta nota hemos revisado la manera en la que se deriva el modelo MCO. En la sección anterior mencionamos el problema más común para hacer inferencia causal utilizando los resultados del modelo MCO (sesgo por variables omitidas). Sin embargo, existen otras consideraciones importantes cuando queremos llevar a cabo inferencia utilizando nuestros resultados.

3.9 Validez externa

Hay validez externa cuando los resultados de un análisis llevado a cabo con una muestra de una población específica son válidos y generalizables para otras poblaciones.

Ejemplo: Llevar a cabo análisis del impacto de una política social para hogares pobres en México (e.g. Progresa/Oportunidades) puede tratar de generalizarse para otros países en desarrollo de características similares a las de México.

Los problemas más comunes relacionados con validez externa son:

• Diferencias en las poblaciones. Por ejemplo, en medicina se hacen muchos estudios con ratones y siempre existe la controversia si el efecto será similar en seres humanos.

• Diferencias en contexto. Los resultados pueden no ser generalizables a poblaciones similares si características del contexto pueden causar diferencias importantes. Algunos ejemplos incluyen diferencias geográficas, diferencias en leyes, diferencias ambientales, etc.

3.10 Validez interna

Hay validez interna cuando los resultados de un análisis llevado a cabo con una muestra son válidos y generalizables para la población de la cual se extrajo dicha muestra.

Los problemas más comunes relacionados con validez interna son:

• Sesgo por variables omitidas. Discutido la sección anterior.

• Especificación incorrecta de la forma funcional. Discutido en la sección 3.4.2.

• Error de medición. En algunos casos, es posible que una o más variables disponibles en la base de datos a utilizar en el análisis tengan errores. Dichos errores pueden surgir por errores en la medición, en la captura de datos, que los encuestados no recuerden precisamente algún dato, preguntas mal estructuradas o poco claras, respuestas falsas intencionales, etc.

Para determinar cuál puede ser el efecto de llevar a cabo una regresión con errores en las variables consideremos lo siguiente:

Sea \(\tilde{X}\) la variable \(X\) medida con error, donde el error se define como: \(w_i=\tilde{X}_i-X_i\).

Por simplicidad tomemos el caso de una regresión simple, donde queremos estimar el coeficiente \(\beta_1\): \[\begin{equation} Y_i=\beta_0+\beta_1X_i+U_i \end{equation}\]

Sin embargo, dado que en nuestra base de datos únicamente tendremos disponible a \(\tilde{X}_i\), realmente estaremos estimando la siguiente regresión: \[\begin{equation} Y_i=\tilde{\beta}_0+\tilde{\beta}_1\tilde{X}_i+V_i \tag{3.15} \end{equation}\]

Nótese que el error cambió en este caso, ya que: \(V_i=\beta_1X_i-\tilde{\beta}_1\tilde{X}_i+U_i\).

En el caso de la regresión (3.15), el coeficiente estimado será: \[\begin{equation*} \tilde{\beta}_1=\frac{Cov(\tilde{X},Y)}{Var(\tilde{X})} \end{equation*}\]

En este caso nos interesará determinar la relación entre \(\tilde{\beta}_1\) y \(\beta_1\), donde: \[\begin{equation*} \beta_1=\frac{Cov(X,Y)}{Var(X)} \end{equation*}\]

Para establecer la relación: \[\begin{equation*} \begin{split} \tilde{\beta}_1&=\frac{Cov(\tilde{X},Y)}{Var(\tilde{X})}=\frac{Cov(X+w,Y)}{Var(X+w)}\\ &=\frac{Cov(X,Y)}{Var(X)}\frac{Var(X)}{Var(X+w)}+\frac{Cov(w,Y)}{Var(X+w)}\\ &=\beta_1\biggl(\frac{\sigma_X^2}{Var(X+w)}\biggl)+\frac{Cov(w,\beta_0+\beta_1X+U)}{Var(X+w)} \end{split} \end{equation*}\]

Si suponemos que los errores no están correlacionados \(Cov(w,U)=0\): \[\begin{equation*} \tilde{\beta}_1=\beta_1\biggl(\frac{\sigma_X^2+Cov(w,X)}{Var(X+w)} \biggl) \end{equation*}\]

Un caso particular se conoce como el error de medición clásico. Este tipo de error asume que los errores de medición (\(w\)) no están correlacionados con el valor real de \(X\). Este tipo de errores pueden surgir, por ejemplo, si hay errores aleatorios de captura.

En este caso, tendremos que \(Cov(w,X)=0\), por lo tanto: \[\begin{equation} \tilde{\beta}_1=\beta_1\biggl(\frac{\sigma_X^2}{\sigma_X^2+\sigma_w^2}\biggl) \end{equation}\]

Esto quiere decir que hay un sesgo de atenuación. Es decir, el coeficiente estimado en la regresión que utiliza las variables con errores de medición (3.15) será menor en valor absoluto que el coeficiente que resultaría si se utilizarán los valores sin error.

Debe tenerse en cuenta que en algunos casos los errores de medición pueden ser sistemáticos, por lo tanto, asumir que los errores de medición son clásicos puede ser incorrecto. Por ejemplo, en preguntas tales como ingresos mensuales, número de bebidas alcohólicas consumidas regularmente por semana, horas de ejercicio o estudio a la semana, etc. Es común pensar que hay errores sistemáticos reportando los datos por parte de los que contestan las encuestas. En este caso, la dirección del sesgo estará influido también por el factor \(Cov(w,X)\).

• Datos faltantes y sesgo muestral. El problema de datos faltantes se refiere a que algunas observaciones en la base de datos reportaron de manera incompleta la información requerida o dicha información no estaba disponible. El sesgo muestral surge si los entes de la población seleccionados para formar la muestra no son representativos de la población en general. Estos problemas son relevantes porque amenazan el supuesto de i.i.d. Existen métodos estadísticos diseñados para tratar con estos problemas, pero dichos métodos no están incluidos en el temario del curso.

• Causalidad simultánea. Este problema surge cuando además de haber una relación causal de la variable \(X\) a \(Y\), también existe una relación causal de \(Y\) a \(X\). Dado que la estimación de los coeficientes implica calcular la correlación condicional entre las variables, la estimación estará sesgada. Ejemplo: Supongan que les interesa ver la relación entre tamaño del salón de clase y calificaciones. Supongan que el gobierno establece una iniciativa que dice que las escuelas con mejores resultados recibirán mas recursos. Esto puede llevar a la contratación de maestros y por lo tanto, a la disminución del tamaño del salón de clases. En este caso, establecer la relación causal de tamaño de clases a calificaciones requerirá que se recurran a otros métodos, como variables instrumentales y métodos experimentales que cubriremos más adelante en el curso.

3.11 Variaciones al modelo de Mínimos Cuadrados Ordinarios

3.11.1 Regresiones cuantílicas

El problema de mínimos cuadrados ordinarios consiste en minimizar: \[\begin{equation} E(Y_i-X_i'\beta)^2 \end{equation}\]

Esta estimación nos da como resultado una estimación de la media de \(Y_i\) condicional en las variables que se eligen como controles en el modelo, \(X_i\). Sin embargo, en algunos casos nos puede interesar hacer inferencia para distintos partes de la distribución de \(Y_i\). Por ejemplo, supongamos que nos interesa medir los retornos educativos para distintas partes de la distribución del ingreso (para los individuos de mayores y menores ingresos). En este caso modificamos el problema de minimización planteado hacia el siguiente: \[\begin{equation} \min_{\beta_\tau}\phantom{tt}\rho_\tau |Y_i-X_i'\beta_\tau| \end{equation}\] donde \(\rho_\tau\) es un ponderador de los errores absolutos y \(\tau\) es un indicador del cuantil \(100\tau\) (Figure: 3.4):

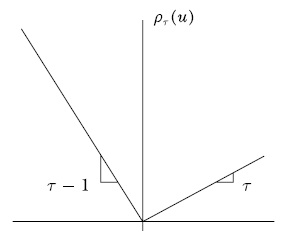
Figure 3.4: Ponderador de errores

Por ejemplo, \(\rho_{0.5}\) es el ponderador para el cuantil \(50\). Utilizando este ponderador generaremos un estimador de la mediana de \(Y_i\) utilizando las variables explicativas \(X_i\). Similarmente, \(\rho_{0.9}\) es el ponderador para el cuantil \(90\) y generará un estimador del cuantil \(90\) de \(Y_i\) utilizando las variables explicativas \(X_i\).

Ejemplo con retornos educativos.

3.11.2 Mínimos cuadrados ponderados

Como vimos en la sección 3.2, el supuesto de homocedasticidad asume que la varianza de los errores no depende del nivel de \(X_i\). Como describimos, el incentivo a utilizar homocedasticidad es que conlleva mayor eficiencia en la estimación de los coeficientes de MCO. El modelo de mínimos cuadrados ponderados (Weighted Least Squares, WLS) consiste en llevar a cabo una transformación de las variables para poder estimar el modelo asumiendo homocedasticidad y obtener estimadores más eficientes.

Este modelo se basa en la idea que la varianza del error depende de una función de \(X_i\): \[\begin{equation} Var(Ui|Xi)=\sigma^2h(X_i) \end{equation}\]

Sin embargo, este modelo asume que la función \(h(\cdot)\) es conocida y se puede estimar. Generalmente este es un supuesto restrictivo.

Suponiendo, que la función \(h(\cdot)\) se puede estimar, los pasos para llevar a cabo la estimación de este modelo son los siguientes:

Cada una de las variables se divide entre la raíz de \(h(X_i)\): \[\begin{align*} Y_i^* &=\frac{Y_i}{\sqrt{h(X_i)}} &\qquad X_{1i}^*&=\frac{X_{1i}}{\sqrt{h(X_i)}} \\ X_{Ki}^* &=\frac{X_{Ki}}{\sqrt{h(X_i)}} &\qquad U_i^*&=\frac{U_i}{\sqrt{h(X_i)}} \end{align*}\]

Y se puede estimar el siguiente modelo: \[\begin{equation} Y_i^* =\widetilde{\beta}_0+\beta_1X_{1i}^* +\dots+\beta_KX_{Ki}^* +U_i^* \end{equation}\]

En este caso puede verse que el error tendrá una varianza homocedástica (constante) y por lo tanto podemos estimar los parámetros (\(\beta\)’s) utilizando el modelo MCO. Es importante tomar en cuenta que:

• El valor estimado de los parámetros cambiará, pero el estimador sigue siendo consistente

• Este nuevo valor estimado tendrá errores estándar menores (típicamente). Por lo tanto, la estimación será más eficiente.

Sin embargo, el supuesto importante es que la forma de la función \(h(\cdot)\) es conocida. Además, otro inconveniente es que la función \(h(\cdot)\) no puede ser negativa para ningún valor de \(X_i\) (de otra manera estaríamos diciendo que la varianza pudiera ser negativa para algunos valores de \(X_i\)). Una manera de evitar esto es con el modelo de FGLS (Feasible Generalized Least Squares - Mínimos Cuadrados Generalizados Factibles). Dicho modelo asume la siguiente especificación para la función \(h(\cdot)\): \[\begin{equation} h(X_i)=\exp{(\delta_0+\delta_1X_{1i}+\dots+\delta_KX_{Ki})} \end{equation}\]

En este caso, la función \(h(\cdot)\) cumplirá la condición de ser positiva en todo el dominio de \(X_i\).

Los pasos a seguir para llevar a cabo la estimación FGLS son:

1. Estima la regresión \(Y_i=\beta_0+\beta_1X{1i}+\dots+\beta_KX{Ki}\)

2. Obtén los residuales: \(\hat{U}_i=Y_i-\hat{\beta}_0-\hat{\beta}_1X{1i}-\dots-\hat{\beta}_KX{Ki}\)

3. Estima la regresión \(\log{(\hat{U}_i^2)}=\delta_0+\delta_1X_{1i}+\dots+\delta_KX_{Ki}\)

4. Obtén los valores estimados de \(h(X_i)\): \(\widehat{h(X_i)}\)

5. Sigue los pasos del modelo WLS utilizando los \(\widehat{h(X_i)}\) estimados para modificar la variable dependiente y las independientes

Este procedimiento resulta en un estimador consistente y asintóticamente más eficiente que MCO.

---

4. Encuesta Nacional de Ingreso y Gasto de los Hogares, INEGI↩︎

5. Previamente habíamos indicado que \(\beta\) tiene dimensión \(K+1\). En adelante solo usamos dimensión \(K\) para simplificar la notación. En términos esctrictos podríamos decir que previamente la dimensión era \(K'+1\) y definir a \(K=K'+1\).↩︎