ՄԱՍ 4 Դիֆերենցիալ ուժեղարարար։

Դիֆերենցիալ ուժեղարաը առաջին անգամ հանդես է եկել վակումաին լամպերովիրականացված։ Միկրոէլեկտրոնիկաի զարգացման արագությունը հաշվի առնելովկարելի է ասել որ դա շատ վաղ անցիալում էր։ Սակայն Դիֆերենցիալ տոպոլոգիան միշտ կարևորագույն դեր է ունեցել և անբաժանելի մաս է հանդիսանում ժամանակակից էլեկտրոնիկայում։ Նախքան ուժեղարարների հատկությունների ուսումնասիրումը անհրաժեշտ է իմանալ թե ինչ է դիֆերենցիալ ազդանշանը ուստի այդտեղից էլ կսկսենք։

4.1 դիֆերենցիալ ազդանշան։

Ընդհանրապես ազդանշան ասելով մենք հասկանում ենք լարման կամ հոսանքիփոփոխություն որոնք ստացվում են տարբեր աղբյուրներից։ իտարբերություն «մեկ հաղորդալարով» փոխանցվող ազդանշանի որի արժեքը չափում ենք ֆիքսված մակարդակի նկատմամբ «ազդանշանի և մակարդակի տարբերությունը» դիֆերենցիալ ազդանշանը հաղորդվում է երկու հաղորդալարով և չափվում է դրանց տարբերությամբ։ Ըստ էության դրանք նույն ամպլիտուդով սակայն հակառակ փուլերով մեծություններ են առանձին վերցրած որոնք տատանվում են ընդհանուր մակարդակի շուրջ «common-mode»։ ազդանշանի այսպիսի ձևափոխման հիմնական նպատակը այն է որ ավելի աղմուկակայուն է։

Figure 4.1: …

Եթե ստեղծում ենք այն պայմանը որ երկու հաղորդալալերի վրա պառազիտիկ էֆեքտները հավասար չափով են գումարվում «թողնում են նույն ազդեցությունը» ինչպես պատկերված է նկ (3.1)-ոմ ընդունման կետում երբ չափում ենք ազդանշանը երկու հաղորդալալերի պոտենցիալների տարբերությունը ստացվում է ճանապարին ավելացած աղմուքները առանց ջանքերի դուրս են գալիս։

4.2 դիֆերենցիալ զույգ։

Դիֆերենցիալ ազդանշանի ուժեղացման համար այն ինչ կարող ենք առաջարկել ընկած է նախորդ բաժնում կատարած դիտարկումների հիման վրա։ Ըստ էության անհրաժեշտ է երկու միանման ուժեղարարներ զույգ ազդանշանները առանձին ուժեղացնելու համար։

Նկարում պատկերված է դիֆերենցիալ զույգ։ Երկու դիֆերենցիալ մուտքերը՝ $V_{in1}$ և $V_{in2}$ , որոնք ունեն որոշակի ընդանուր մակարդակ՝ միացված են ՄՕԿ֊երի փականներին։ երկու ելքերը տատանվում են ելքային ընդհանուր պոտենցիալի շուրջ և միասին կազմում են դիֆերենցիալ ազդանշան։

Figure 4.2: …

Սխեման հանդիսանում է դիֆերենցիալ ուժեղարար սակայն ունի մի շատ կարևոր թերություն։ Ինչ տեղի կունենա երբ մութքային ընդհանուր մակարդակը տատանվի։ Կախված փոփոխության չափից հնարաոր է ՄՕԿ֊երը դուրս գան հագեցման ռեժիմից, կամ փականի պոսենցիալը չգերազանցի շեմաին լարումը։ Նշված երկու սահմանաին դեպքերի միջև ընկած հատվածում ելքային ընդհանու մակարդակը կարծես հետևում է մութքային մակարդակի փոփոխությանը։ Կարող ենք արդյոք ձևափոխել այնպես որ ստանանք կայուն ուժեղացում և ֆիքսված ելքային ընդհանուր մակարդակ։ Պարզվում է այո։

Նկարում պատկերված է առաջին լավարկումը ըստ որի երկու ճուղերով անցնող հոսանքի գումարը միշտ մնում է նույնը $I_{D1} + I_{D2} = I_{SS}$, իսկ երբ $V_{in1} = V_{in2}$ Նշված սահմանաին միջակայքում անկախ մութքային ընդհանուր պոտենցիալի արժեքից ելքի ընդանուր պոտենցիալը կլինի $V_{DD} - R_{D} I_{SS}/2$

Figure 4.3: …

Նախքան արդեն մեզ հայտնի հետազոտությունների շարքը սկսելը օգտակար է իմանալ թե ինչ է տեղի ունենում շղթայում։ Դիցուկ $V_{in1} − V_{in2}$֊ը փոփոխվում է $−∞$-ից մինչև $+∞$: Եթե $V_{in1}$-ը շատ ավելի բացասական է, քան $V_{in2}$-ը, $M1$-ը փակ կլինի, $M2$-ը բացված, հետևաբար $I_{D2} = ISS$։ Այսպիսով, $V_{out1} = V_{DD}$, $V_{out2} = V_{DD} - R_{D} I_{SS}$: Ենթադրենք $V_{in1}$֊ը մոտենում է $V_{in2}$֊ին $M1$-ը աստիճանաբար բացվում է որշակի հոսանք սկսում է անցնել առաջին ճուղով հետևաբար $V_{out1}$֊ը սկսում է փոքրանալ քանի որ $I_{D1} + I_{D2} = I_{SS}$ երկրորդ ճուղով անցնող հոսանքը սկսում է փոքրանալ իսկ $V_{out2}$֊ը մեծանալ։ երբ $V_{in1} = V_{in2}$֊ին երկու ճուղերով անցնում է նույն $I_{SS}/2$ հոսանքը հետևաբար ելքերը հավասարվում են իրար $V_{out1} = V_{out2}=V_{DD} - R_{D} I_{SS}/2$ որը ելքային ընդանուր մակարդակն «CM» է։ այս կետը հանդիսանում է համաչապության կետ $V_{in1} − V_{in2}$ հետագա մեծացումը բերում է նրան որ իվերջո ամբողջ $I_{SS}$ հոսանքը անցնում է առաջին ճուղով։

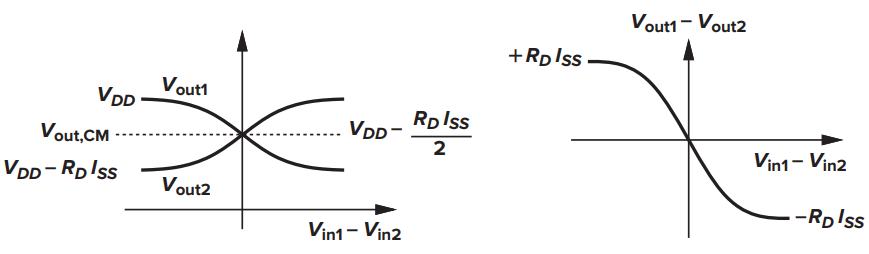
Figure 4.4: …

Վերլուծությունը բացահայտում է դիֆերենցիալ զույգի երկու կարևոր հատկանիշ:

Մեծագույն և փոքրագույն ելքի արժեքները համապատասխանաբար $V_{DD}$ և ${V_{DD} - R_{D} I_{SS}}$ է ընդ որում այն կախված չէ մութքային ընդհանուր մակարդակից։
փոքր ազդանշանի ամենամեծ ուժեղացումը $V_{in1} = V_{in2}$ կետում է տեղի ունենում։ «Հետագայում խիստ կապացուցենք» այժմ կարող ենք ասել որ $V_{in1} - V_{in2}$֊ի որոշակի միջակայքից դուրս ուժեզացման գործակիցը հավասարվում է $0$֊ի։

Որպիսի պարզենք արդյոք հոսանքի աղբյուր ավելացնելով ճնշում ենք մութքի ընդհանուր մակարդակի տատանումների դերը ելքի ընդանուր մակարդակի վրա կազմենք «Spice» նկարագրություն որտեղ $V_{in1} = V_{in2}$ միացված են իրար, որպես հոսանքի աղբյուր միացնենք ՄՕԿ տրանզիստոր։ Հետազոտենք արդյոք մութքային ընդհանու մակարդակի կամայական արժեքի դեպքում ելքի ընդհանու մակարդակը նույնն է։ Հետազոտության համար բավական է մութքի լարումը փոփոխել և գրանցել արձյունքները։

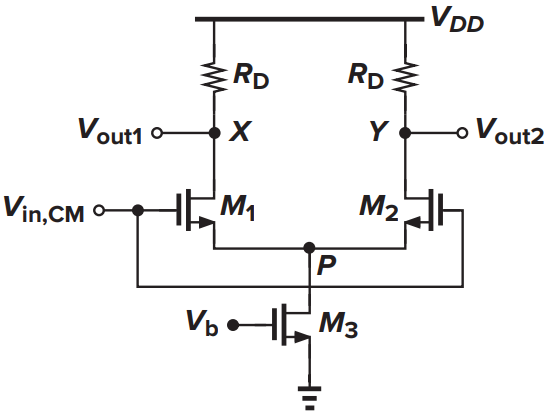
Figure 4.5: …

Figure 4.6: …

Figure 4.7: …

Գրաֆիկները ստացվել են «Spice» հետազոտության արդյունքում տարբեր $V_b$֊ի համար։ Ինչպես ցույց է տրված գրաֆիկներում քանի դեռ մութքի լարումը փոքր է $M_{1}$ և $M_{2}$֊ի շեմային լարումից շղթայով հոսանք չի անցնի հետևաբար ելքերը հավասար են սնման լարմանը, $P$ կետում լարումը 0 է ուստի $M_{3}$֊ը գտնվում է խորը գծաին ռեժիմում։ Երբ մուտքի ընդանուր մակարդակը աստիճանաբար բարձրանում է սկսում է գերազանցել $M_{1}$ և $M_{2}$֊ի շեմային լարումը շղթայով սկսում է հոսանք անցնել որը բերում է նրան որ $P$ հանգույցի պոտենցիալը աստիճանաբար բարձրանում է։ $P$֊ի այն փոքրագույն արժեքը որից հետո $M_{3}$֊ը դուրս է գալիս գծային ռեժիմից $V_{b}- V_{TH3}$ է։ Դիցուկ դա տեղի է ունենում $V_{GS} = V_{in}- V_{P}$ արժեքի դեպքում։ Հետևաբար շղթաի կոռեկտ աշխատանքի համար անհրաժեշտ է որ մուտքի ընդհանու մակարդակը $V_{in , CM} ≥ V_{GS} + V_{b} - V_{TH3}$:

Ի՞նչ կլինի, եթե $V_{in} շարունակենք մեծացնել։ Որպիսի $M_{1}$֊ը և $M_{2}$֊ը մնան հագեցման ռեժիմում անհրաժեշտ է $V_{out1,out2} > V_{in} - V_{TH}$: Ընդունենք որ երբ $M_{3}$-ը հագեցման ռեժիմում է $I_{SS} ≈ Const$ նշանակում է $V_{out} = V_{DD} - R_{D} I_{SS}/2$: Հետևաբար մութքային ընդհանու մակարդակը ունի սահմանափակում նաև վերևից $V_{in , CM} ≤ V_{DD} - R_{D} I_{SS}/2 + V_{TH}$:

Ուսուցողական է նաև ժամանակաին հետազոտությունը։ Որպես այդպիսին նույն դիֆերենցիալ ազդանշանին գումարենք աղմուքներ ստացված ազդանշանը կիրառենք երկու նույն դիֆերենցիալ զույգին միայն այն տարբերությամբ որ առաջին դեպքում բացակայում է հոսանքի աղբյուրը իսկ երկրորդ դեպքում որպոս հոսանքի աղբյուր միացված է ՆՄՕԿ տրանզիստոր։ Ինչպես պատկերված է նկարում։

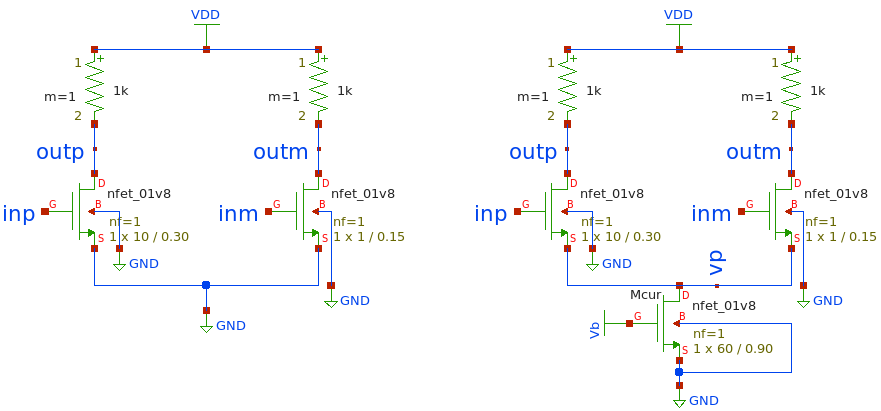
Figure 4.8: …

Դիֆերենցիալ ազդանշանները առանձին վերցրած ունեն գրաֆիկում պատկերված տեսքը՝

Figure 4.9: …

Որքան էլ ազդանշանները առանձին վերցրած բարդ տեսք ունեն բավական է չափել դրանց մեջ պոտենցիալների տարբերությունը և կտեսնենք ներդաշնակ տատանում։

Figure 4.10: …

Այժմ պատկերենք ելքերի տարբերությունը առաջին սխեմաի համար։

Figure 4.11: …

Ինչպես նշված էր վերևում դիֆերենցիալ մուտքը և ելքը այդքան էլ իրար նման չէն։ ՈՒժեղարարին այդքան էլ չի հաջողվել մուտքի ընդհանուր մակարդակի փոփոխությանը չարձագանքել։

Figure 4.12: …

Ինչպես տեսնում ենք երբ միացված է հոսանքի աղբյուր էական տարբերվում է ելքը։ Այո շղթայով անցնող հոսանքը այդքան էլ հաստատուն չէ և արձագանքում է արագ փոփոխություններին սակայն պետք է ուշադրություն դարձնել

Նշնեք որ եթե աղմուքները գումարվել են նախքան ազդանշանը դիֆերենցիալ դարձնելը ապա ուժեղացումից հետո պետք չէ ակնկալել որ աղմուքի մակարդակը կճնշվի։

4.3 Մեծ ազդանշանային վարքագիծ

Դիտարկենք նկ․ 3.3-ում ներկայացված դիֆերենցիալ զույգը: Մեր նպատակն է որոշել $V_{out1} - V_{out2}$ և $V_{in1} - V_{in2}$֊ի միջև կապը: Հայտնի է որ՝ $V_{out1} = V_{DD} − R_{D1} I_{D1}$ և $V_{out2} = V_{DD} − R_{D2} I_{D2}$ հետևաբար $V_{out1} - V_{out2} = R_{D1} I_{D1} - R_{D2} I_{D2}$ եթե $R_{D1} = R_{D2} = R_{D}$՝ $V_{out1} - V_{out2} = R_{D}(I_{D1} - I_{D2})$։ Այսպիսով խնդիրը կարող ենք համարել լուծված եթե գտնենք $I_{D1} - I_{D2}$֊ի և $V_{in1} - V_{in2}$֊ի միջև կապը։ ենթադրենք $M_{1}$-ը և $M_{2}$-ը հագեցած են, և $λ = 0$: Քանի որ $P$ հանգույցում լարումը մի կողմից հավասար է $V_{in1} - V_{GS1}$ միուս կողմից $V_{in2} - V_{GS2}$ կարող ենք գրել՝

\[\begin{equation} V_{in1} - V_{in2} = V_{GS1} - V_{GS2}։ \tag{1.1} \end{equation}\]

ՄՕԿ֊ի ՎԱԲ֊ից հայտնի է որ՝

\[\begin{equation} V_{GS} = \sqrt{\frac{2 I_{D}}{ μ_n C_{ox} \frac{W}{L}}} - V_{TH}։ \tag{1.2} \end{equation}\]

(3.1) և (3.2)֊ից կունենանք՝

\[\begin{equation} V_{in1} - V_{in2} = \sqrt{\frac{2 I_{D1}}{ μ_n C_{ox} \frac{W}{L}}} - \sqrt{\frac{2 I_{D2}}{ μ_n C_{ox} \frac{W}{L}}} ։ \tag{1.3} \end{equation}\]

(3.3) արտահայտության երկու կողմը բարձրացնենք քառակուսի հաշվի առնելով որ $I_{D1} + I_{D2} = I_{SS}$ կունենանք՝

\[\begin{equation} (V_{in1} - V_{in2})^2 = \frac{2}{ μ_n C_{ox} \frac{W}{L}} (I_{SS} - 2 \sqrt{I_{D1} I_{D2}}) \\ 2 \sqrt{I_{D1} I_{D2}} = I_{SS} - \frac{1}{2} μ_n C_{ox} \frac{W}{L} (V_{in1} - V_{in2})^2 \tag{1.4} \end{equation}\]

(3.4)֊ը երկու մասը կրկին բարցրացնենք քառակուսի հաշվի առնելով որ՝ $4I_{D1} I_{D2} = (I_{D1}+I_{D2})^2 - (I_{D1} - I_{D2})^2 = I_{SS}^2 - (I_{D1} - I_{D2})^2$ կունենանք՝

\[\begin{equation} (I_{D1} - I_{D2})^2 = - \frac{1}{4} (μ_n C_{ox} \frac{W}{L})^2 (V_{in1} - V_{in2})^4 + I_{SS} μ_n C_{ox} \frac{W}{L}(V_{in1} - V_{in2})^2 \tag{1.5} \end{equation}\] \[\begin{equation} I_{D1} - I_{D2}= \frac{1}{2} μ_n C_{ox} \frac{W}{L} (V_{in1} - V_{in2}) \sqrt{\frac{4 I_{SS}} { μ_n C_{ox} \frac{W}{L} } - (V_{in1} - V_{in2})^2 } \\ = \sqrt{μ_n C_{ox} \frac{W}{L} I_{SS}} (V_{in1} - V_{in2}) \sqrt{1- \frac{μ_n C_{ox} W/L}{4 I_{SS}} (V_{in1} - V_{in2})^2} \tag{1.6} \end{equation}\]

$M_{1}$ , $M_{2}$ , $M_{3}$֊ը միասին գործում են որպես $V_{in1} - V_{in2}$ լարումով ղեկավարվող $I_{D1} - I_{D2}$ հոսանքի աղբյուր ընդ որում երբ $V_{in1} - V_{in2} =0$֊ի $I_{D1} - I_{D2} = 0$: $|V_{in1} - V_{in2}|$ աճին զուգահեռ աճում է նաև $|I_{D1} - I_{D2}|$֊ը։ Նախքան ստացված արտահայտության հետագա ուսումնասիրությունը, հաշվենք $M_{1}$-ի և $M_{2}$-ի համարժեք $G_m$: Նշ․ $\Delta V_{in} = V_{in1} - V_{in2}$ և $\Delta I_{D} = I_{D1} - I_{D2}$

\[\begin{equation} \frac{\partial \Delta I_{D}}{\partial \Delta V_{in}} = \frac{1}{2} μ_n C_{ox} \frac{W}{L} \frac{ \frac{4 I_{SS}}{μ_n C_{ox} W/L} - 2 \Delta V_{in}^2} {\sqrt{\frac{4 I_{SS}}{μ_n C_{ox} W/L} - \Delta V_{in}^2}} \tag{1.7} \end{equation}\]

Հեշտ է համոզվել որ $G_{m}$֊ը ընդունում է իր առավելագույն արժեքը երբ $\Delta V_{in} = 0$: Փոքր ազդանշանի ուժեղացման գործակցի համար «ընդհանուր մակարդակի շուրջ փոքր ամպլիտուդով փոփոխվող ազդանշան» կարող ենք գրել՝

\[\begin{equation} |A_{v}| = \sqrt{μ_n C_{ox} \frac{W}{L} I_{SS}} R_{D} \tag{1.8} \end{equation}\]

(3.8)֊ը կարելի է գրել նաև $|A_{v}| = g_{m}R_D$: Այս ձևափոխությունը ստացվում է այն դեպքում երբ $\Delta V_{in} \to 0$ որի արդյունքում երկու ճուղերով անցնում է $I_{SS}/2$ հոսանքը։

(3.7)֊ում $G_{m}$֊ը հավասարվում է 0֊ի երբ $\Delta V_{in} = \sqrt{2 \frac {2 I_{SS}}{μ_n C_{ox} W/L}}$:

Այժմ ավելի մանրամասն քննենք (3.6) հավասարումը: Եթե ${(V_{in1} - V_{in2})^2 \ll \frac {4I_{SS}}{μ_n C_{ox} W/L}}$ այն կարող ենք գրել՝

\[\begin{equation} I_{D1} - I_{D2} = \sqrt{μ_n C_{ox} \frac{W}{L} I_{SS}} (V_{in1} - V_{in2}) \tag{1.9} \end{equation}\]

(3.9)֊ը նույնությամբ կրկնում է (3.6)֊ի դիֆերենցումից ստացված հավասարությունը։ $|V_{in1} - V_{in2}|$֊ի մեծացումը բերում է $|I_{D1} - I_{D2}|$֊ի մեծացմանը։ Սակայն $\Delta V_{in} = \sqrt{\frac{4 I_{SS}}{μ_n C_{ox} W/L}}$ արժեքում $\Delta I_{D}$֊ը պետք է հավասարվի 0֊ի որը իրականում տեղի չի ունենում։ Պետճառն այն է որ բոլոր հավասարությունները ստացվել են ենթադրելով որ $M_{1}$֊ը և $M_{2}$֊ը ոչ միայն բաց են այլ նաև երկուսն էլ հագեցման ռեժիմում են։ իրականում $| \Delta V_{in} |$ մեծացումը կբերի նրան որ ամբողջ $I_{SS}$ հոսանքը կանցնի մի ճուղով։

4.4 Փոքր֊ազդանշանի վերլուծություն։

$\Delta V_{out}$֊ի և $\Delta V_{in}$֊ի միջև կապը ստացվեց ենթադրելով որ ՄՕԿ֊երը գտնվոմ են հագեցման ռեժիմում, իսկ $\Delta V_{in}$֊ը ընդանուր մակարդակի շուրջ տատանվող երկու փոքր ամպլիտուդով մեծություններ են արցյունքում ստացվեց $\Delta V_{out} = g_{m} R_{D} \Delta V_{in}$: նույն արձյունքը կարաղ ենք ստանալ նաև կազմելով փոքր ազդանշան մոդել։ Դա կանենք երկու տարբեր եղանակներով։

Եղանակ 1

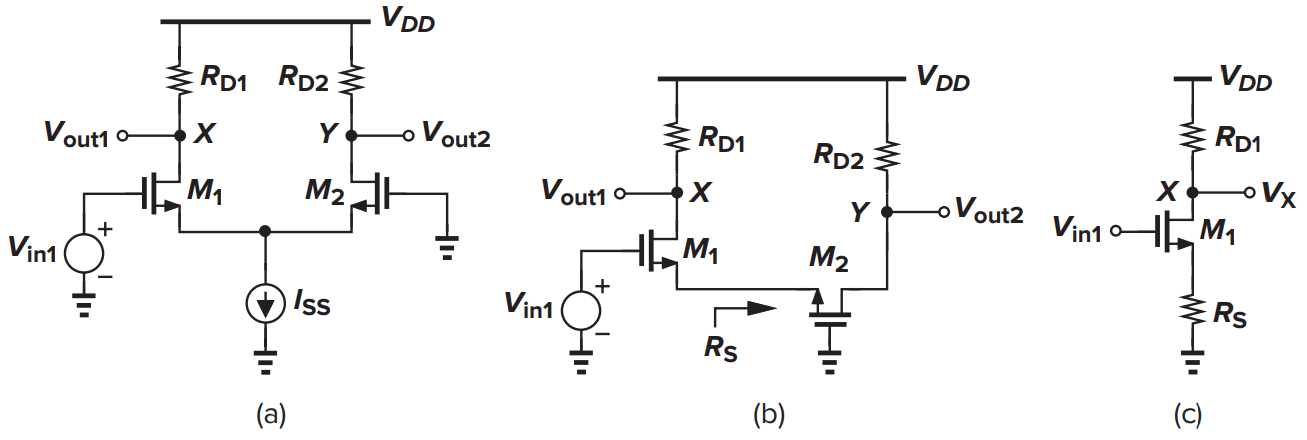
Figure 4.13: …

այս եղանակով երկու մուտքերը դիտարկում ենք որպես առանձին ազդանշաններ և օգտվում ենք վերադրման սկզբունքից։ Ըստ վերադրման սկզբունքի շղթաի արձագանքը հավասար առանձին ազդեցությունների արձագանքների գումարին։ Այսպիսով $V_{in2}$֊ը կարող ենք ներկայացնել որպես հաստատուն ընդհանուր մակարդակի և փոփոխական մասերի գումար։ գտնենք $V_{in1}$֊ի արձագանքը $X$ և $Y$ կետերում երբ $V_{in2}$֊ը միայն հաստատուն մասն է։ Փոքր֊ազդանշանի մոդելը ներկայացված է նկ․ (3.13) ում։ այսպիսի միացումը մեզ արդեն հայտնի ընդհանուր ակունքով ուժեղարարին, որի ակունքը միացված է դիմադրությամբ «$M_{2}$֊ն համարժոք դիմադրությունը»։ Եթե անտեսում ենք հոսքուղու մոդուլացիան և հարթակ էֆեկտը $M_{2}$֊ին համարժեք դիմադրությանը կլինի $R_{S} = \frac{1}{g_{m2}}$:

\[\begin{equation} \frac{V_{X}}{V_{in}} = \frac{- R_{D}}{\frac{1}{g_{m1}} + \frac{1}{g_{m2}}} \tag{1.10} \end{equation}\]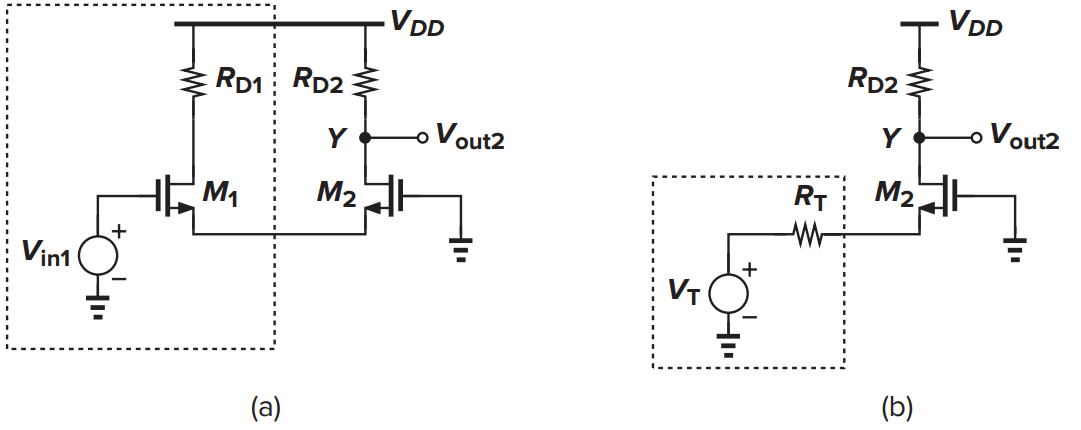

Figure 4.14: …

$V_{Y}$֊ը հաշվելու համար ինչպես ցույց է տրված նկարում $M_{2}$֊ը համարվում է ակունքի հետևորդ, ակոիմքին միացված է $M_{1}$֊ը որը պետք է փոխարինենք Տվինենի համարժեքին։

VY-ը հաշվարկելու համար մենք նշում ենք, որ M1-ը մղում է M2-ին որպես աղբյուրի հետևորդ և փոխարինում Vin1-ը և M1-ը Thevenin-ով: համարժեք (նկ.4.18). Թեվենինի լարումը VT = Vin1 և դիմադրությունը RT = 1/gm1: Այստեղ գործում է M2-ը որպես ընդհանուր դարպասի փուլ, ցուցադրելով շահույթ, որը հավասար է