Chapitre2 Validation du modèle

Objectif du chapitre: La validation du modèle régressif linéaire est une étape très importante, même cruciale, dont dépendent la justesse des enseignements que l’on peut déduire du modèle et les pronostiques réalisés à l’aide de celui-ci. Dans ce chapitre, on présente quelques outils permettant de vérifier si le modèle est adapté aux données disponibles, s’il est pertinent et s’il est digne de confiance pour une utilisation ultérieure. Ainsi, la vérification de l’hypothèse de linéarité, l’étude des propriétés statistiques des résidus et l’identification des points influents sur la droite de régression seront les aspects abordés dans les paragraphes suivants.

2.1 Introduction

Le jeu de données anscombe a été proposé à titre pédagogique et montre bien que, pour la validation d’un modèle de régression linéaire, on ne peut pas se fier uniquement aux résultats des différentes inférences statistiques réalisées sur les coefficients du modèle tel que présenté dans le paragraphe 1.2.2 du chapitre 1. D’autres vérifications supplémentaires sont nécessaires et feront l’objet de ce chapitre. Pour une description détaillée de ce jeu de données, tapez help(anscombe) dans la console R.

# Lecture de données
# ==================
data(anscombe)   
attach(anscombe)

x1	x2	x3	x4	y1	y2	y3	y4
10	10	10	8	8.04	9.14	7.46	6.58
8	8	8	8	6.95	8.14	6.77	5.76
13	13	13	8	7.58	8.74	12.74	7.71
9	9	9	8	8.81	8.77	7.11	8.84
11	11	11	8	8.33	9.26	7.81	8.47
14	14	14	8	9.96	8.10	8.84	7.04
6	6	6	8	7.24	6.13	6.08	5.25
4	4	4	19	4.26	3.10	5.39	12.50
12	12	12	8	10.84	9.13	8.15	5.56
7	7	7	8	4.82	7.26	6.42	7.91
5	5	5	8	5.68	4.74	5.73	6.89

Comme on peut le constater, le fichier contient 11 lignes et 8 colonnes. On remarque que les colonnes \(x_1, x_2, x_3\) sont identiques.

Pour chaque paire \((x_i,y_i), i \in \{1,...,4\}\) on construit un modèle régressif linéaire ayant pour variable explicative \(x_i\) et pour variable expliquée \(y_i\). Les lignes de code R ci-dessous, permettent d’afficher les coefficients des ces modèles:

# Construction des modèles régressifs
# ===================================
mdlLR1<-lm(y1~x1, data = anscombe)
mdlLR2<-lm(y2~x2, data = anscombe)
mdlLR3<-lm(y3~x3, data = anscombe)
mdlLR4<-lm(y4~x4, data = anscombe)

# Affichage des tests pour les coefficients des modèles
# =====================================================
summary(mdlLR1)$coefficients
summary(mdlLR2)$coefficients
summary(mdlLR3)$coefficients
summary(mdlLR4)$coefficients

Résultats pour le modèle mdlLR1 (y1~x1)
             Estimate Std. Error  t value    Pr(>|t|)
(Intercept) 3.0000909  1.1247468 2.667348 0.025734051
x1          0.5000909  0.1179055 4.241455 0.002169629

Résultats pour le modèle mdlLR2 (y2~x2)
            Estimate Std. Error  t value    Pr(>|t|)
(Intercept) 3.000909  1.1253024 2.666758 0.025758941
x2          0.500000  0.1179637 4.238590 0.002178816

Résultats pour le modèle mdlLR3 (y3~x3)
             Estimate Std. Error  t value    Pr(>|t|)
(Intercept) 3.0024545  1.1244812 2.670080 0.025619109
x3          0.4997273  0.1178777 4.239372 0.002176305

Résultats pour le modèle mdlLR4 (y4~x4)
             Estimate Std. Error  t value    Pr(>|t|)
(Intercept) 3.0017273  1.1239211 2.670763 0.025590425
x4          0.4999091  0.1178189 4.243028 0.002164602

Comme on peut le constater, les coefficients de chaque modèle sont à une décimale près les mêmes et significatifs statistiquement. Si l’on se référait seulement à ces résultats, on pourrait conclure que le modèle de régression linéaire est approprié dans les 4 cas de figure. Toutefois, l’affichage graphique sous forme de nuage de points de 4 paires de variables \((x_i,y_i), i \in \{1,...,4\}\) nous permettra de mieux discerner sur la validité des modèles (voir figure 2.1):

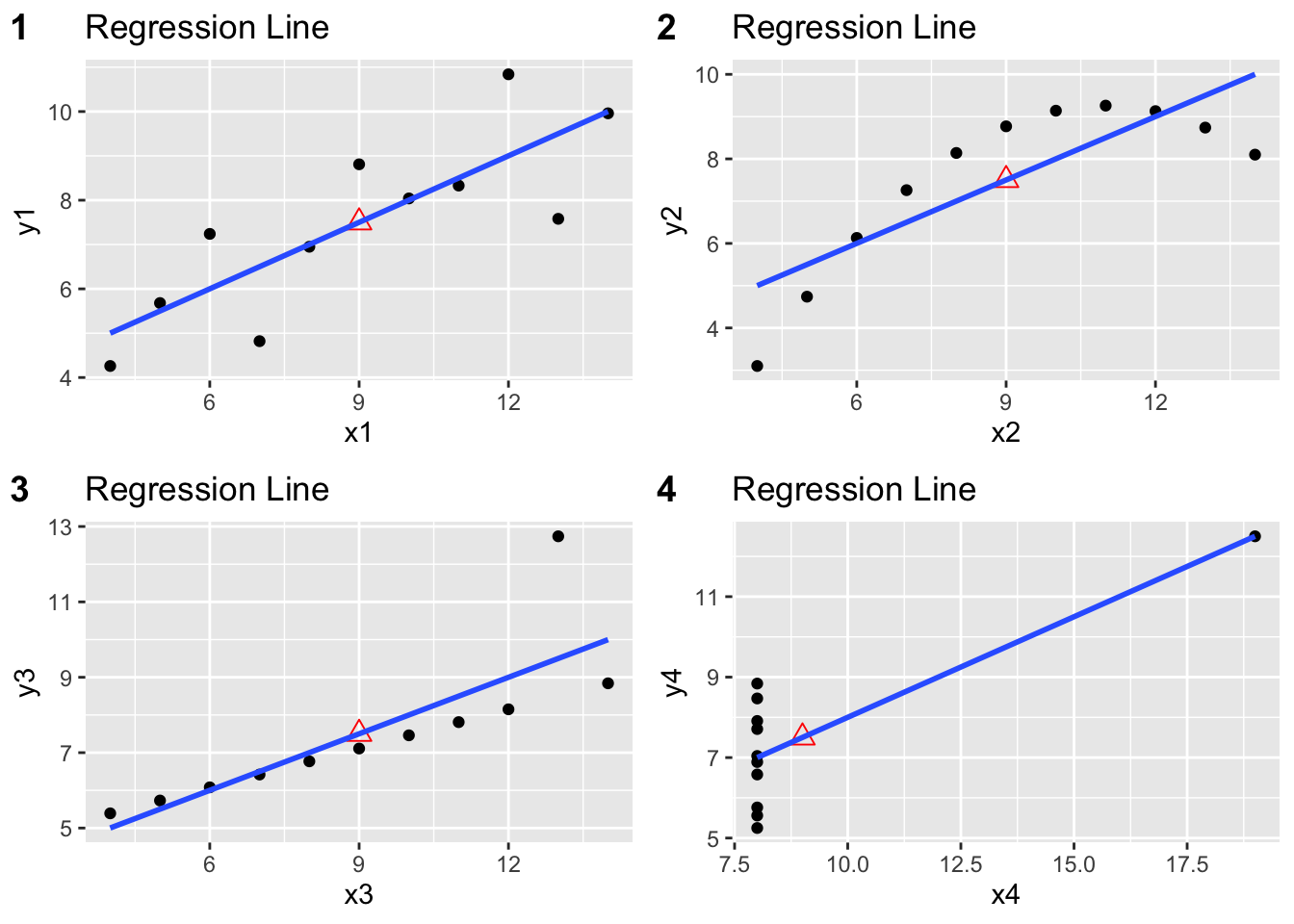
Figure 2.1: Nuages de points pour les 4 modèles du fichier anscombe

Remarque:On peut visuellement constater que le modèle régressif linéaire est approprié seulement dans le cas du couple \((x_1,y_1)\). En effet, dans le cas du couple \((x_2,y_2)\) on remarque une relation non-linéaire (forme parabolique de la disposition des points). Dans le cas du couple \((x_3,y_3)\) on observe qu’il y a un point qui s’écarte de manière significative de la droite de régression. Enfin, dans le cas du couple \((x_4,y_4)\), la pente de la droite de régression est donnée uniquement par la présence d’un point qui à une autre valeur pour la varible \(x_4\) que les autres points.

2.2 Vérifier l’hypothèse de linéarité du modèle

Pour vérifier cette hypothèse le test statistique RESET de Ramsey² est utilisé. Le code R ci-dessous permet de réaliser ce test sur les résidus du modèle mdlLR2 (\(y_2\sim x_2\)):

library(lmtest)
# Tester une dépendance quadratique 
# (H0: y = beta0 + beta1 x + e; H1: y = beta0 + beta1 x + beta2 x^2 + e )
resettest(mdlLR2, power = 2)

    RESET test

data:  mdlLR2
RESET = 4925016, df1 = 1, df2 = 8, p-value < 2.2e-16

Remarque: Comme on peut le constater, la p-value du test RESET de Ramsey pour le modèle mdlLR2 (\(y_2\sim x_2\)) est inférieure à 2.2e-16, ce qui veut dire qu’au seuil de signification de 1%, on peut rejeter l’hypothèse nulle, donc vraisemblablement il y a une dépendance quadratique entre les deux variables. Ceci est en accord avec l’observation faite sur la base du graphique 2.1.

L’analyse visuelle des résidus d’un modèle de régression linéaire permet également d’estimer le bien fondé d’une relation linéaire entre deux variables aléatoires \((X,Y)\) et donc implicitement de la validité du modèle de régression linéaire. En effet, si le modèle est linéaire, alors:

\[\begin{align} \hat{e}=y-\hat{y}&=Y|X-E\left[Y|X\right]=\beta_0+\beta_1x+e-\hat{\beta}_0-\hat{\beta}_1x=\\ &=\left(\beta_0-\hat{\beta}_0\right)+\left(\beta_1-\hat{\beta}_1\right)x+e \approx e \tag{2.1} \end{align}\]

car \(\hat{\beta}_0\) et \(\hat{\beta}_1\) sont proches de \(\beta_0\) et respectivement \(\beta_1\), étant les estimateurs ponctuels obtenus par la méthode des moindres carrés expliquée dans le paragraphe 1.2.1.

Proposition 2.1 Si le modèle reliant deux variables aléatoires (\(X\), \(Y\)) est linéaire, alors les résidus estimés du modèle doivent ressembler à une erreur aléatoire.

La ligne de code R suivante permet d’afficher les résidus du modèle de régression linéaire mdlLR2 créé précédemment:

# Afficher les résidus du modèle mdlLR2(y2~x2) 
# =============================================
mdlLR2$residuals

         1          2          3          4          5 
 1.1390909  1.1390909 -0.7609091  1.2690909  0.7590909 
         6          7          8          9         10 
-1.9009091  0.1290909 -1.9009091  0.1290909  0.7590909 
        11 
-0.7609091 

En effet, si en représentant graphiquement les résidus en fonction de \(x\), on décèle une certaine forme particulière, alors on peut remettre en cause la validité du modèle linéaire. Par exemple, considérons que le vrai modèle reliant les variables aléatoires \((X,Y)\) est quadratique:

\[\begin{equation} y=Y|X=\beta_0+\beta_1x+\beta_2x^2+e \end{equation}\]

et que l’on estime à tort que ce modèle est linéaire, alors:

\[\begin{align} \hat{e}=y-\hat{y}&=Y|X-E\left[Y|X\right]=\beta_0+\beta_1x+\beta_2x^2+e-\hat{\beta}_0-\hat{\beta}_1x=\\ &=\left(\beta_0-\hat{\beta}_0\right)+\left(\beta_1-\hat{\beta}_1\right)x+beta_2x^2+e \approx beta_2x^2+e \end{align}\]

ce qui conduit à un graphique des résidus estimés en fonction de \(x\) sur lequel on remarquera une certaine allure quadratique dans la disposition des points.

Le graphique des résidus selon les valeurs approchées (Residuals vs. Fitted) peut être utilisé conjointement avec le test RESET de Ramsey lors d’une analyse visant à établir si le modèle linéaire décrit bien les données dont on dispose. Le code R ci-dessous permet d’afficher ce graphique dans le cas du modèle mdlLR2:

library(olsrr)
ols_plot_resid_fit(mdlLR2)   # Pour mdlLR2 - le graphique des résidus vs. valeurs approximées 

Si les résidus sont disposés de manière aléatoire autour de la droite horizontale centrée sur zéro (en rouge), alors on peut considérer que le modèle est linéaire (voir la figure 2.2).

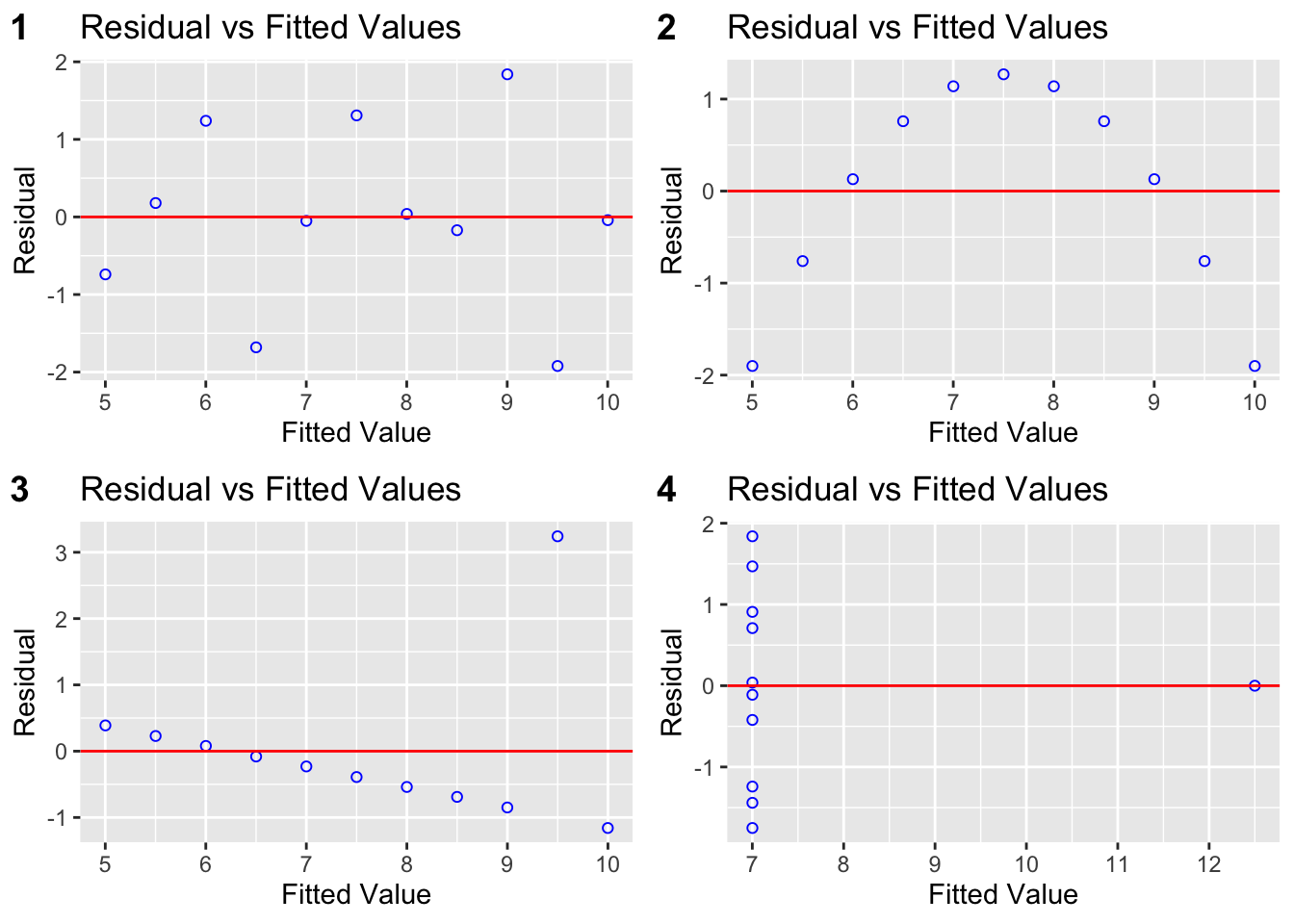
Figure 2.2: Résidus selon les valeurs attendues pour les 4 modèles régressifs linéaires du fichier anscombe

Remarque: On voit facilement que le modèle linéaire n’est pas addapté dans le cas du modèle mdlLR2 (disposition de points selon une parabole, ce qui indique un modèle non-linéaire).

2.3 Analyse des résidus du modèle de régression linéaire

On rappelle que les résidus d’un modèle linéaire doivent satisfaire les contraintes mentionnées dans l’équation (1.2).

2.3.1 Vérifier l’hypothèse de normalité de la distribution des résidus

Des outils graphiques et des tests statistiques permettent de vérifier cette hypothèse de normalité de la distribution des résidus du modèle de régression linéaire.

Parmi les tests statistiques, on mentionne à titre d’exemple: le test Shapiro-Wilk³, le test Anderson-Darling⁴, le test Kolmogorof-Smirnof⁵, Cramér–von Mises⁶, etc. Le code R ci-dessous permet de réaliser ces différents tests statistiques sur les résidus du modèle mdlLR1 (\(y_1\sim x_1\)):

# Différents tests de normalité pour les résidus
# ==============================================
library(nortest)
shapiro.test(mdlLR1$residuals)     # Test de Shapiro-Wilk
cat(" \n")
ad.test(mdlLR1$residuals)          # Test d'Anderson-Darling
cat(" \n")
lillie.test(mdlLR1$residuals)      # Test de Lilliefors (où Kolmogorof-Smirnof)
cat(" \n")
cvm.test(mdlLR1$residuals)         # Test de Cramér–von Mises

    Shapiro-Wilk normality test

data:  mdlLR1$residuals
W = 0.94211, p-value = 0.5456

    Anderson-Darling normality test

data:  mdlLR1$residuals
A = 0.34493, p-value = 0.4147

    Lilliefors (Kolmogorov-Smirnov) normality test

data:  mdlLR1$residuals
D = 0.1693, p-value = 0.5084

    Cramer-von Mises normality test

data:  mdlLR1$residuals
W = 0.061124, p-value = 0.3362

Remarque: Les p-values des différents tests illustrés ci-dessus étant supérieures à 5%, on peut conclure qu’au seuil de significativité de 5% l’hypothèse de normalité de la distribution des résidus du modèle mdlLR1 (\(y_1\sim x_1\)) ne peut pas être rejetée.

Parmi les outils graphiques les plus utilisés, on peut citer: le graphique quantile-quantile, l’histogramme, la boîte à moustache - voir la figure 2.3.

library(olsrr)
ols_plot_resid_qq(mdlLR1)       # Graphique quantile-quantile des résidus
ols_plot_resid_hist(mdlLR1)     # Histogramme des résidus
ols_plot_resid_box(mdlLR1)      # Boite à moustache des résidus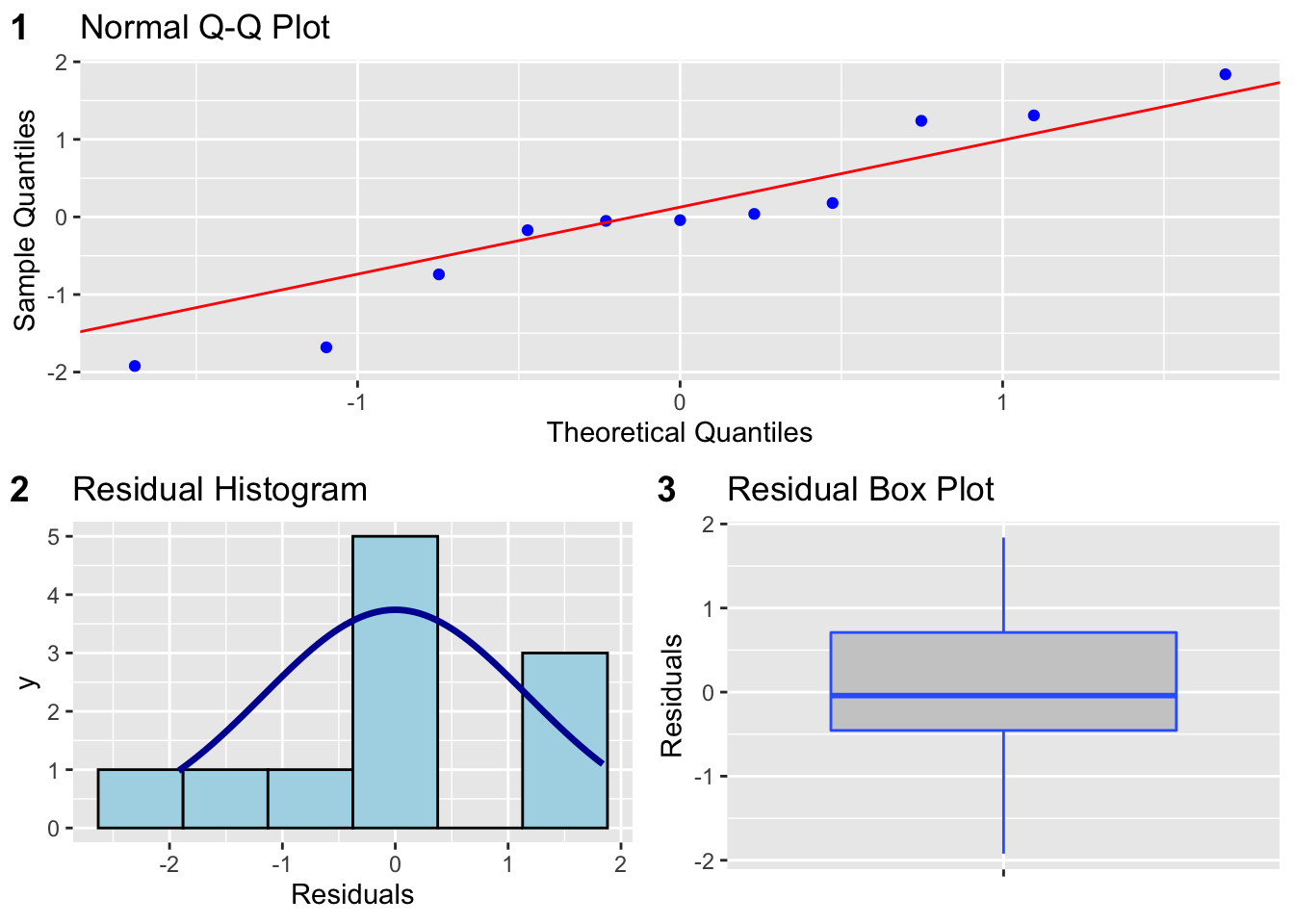

Figure 2.3: Outils graphiques pour évaluer la normalité des résidus du modèle mdlLR1(y1~x1)

2.3.2 Vérifier l’hypothèse de moyenne nulle des résidus

Pour vérifier cette hypothèse le test de Student⁷ est utilisé. Le code R ci-dessous permet de réaliser ce test statistique sur les résidus du modèle mdlLR1 (\(y_1\sim x_1\)):

# Test (H0: moyenne résidus = 0; H1: moyenne résidus <> 0)
t.test(mdlLR1$residuals)

    One Sample t-test

data:  mdlLR1$residuals
t = 2.6771e-17, df = 10, p-value = 1
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 -0.7881295  0.7881295
sample estimates:
  mean of x 
9.46952e-18 

Remarques: 1) La moyenne éstimée des résidus du modèle mdlLR1 (\(y_1\sim x_1\)) est de 9.47x10^-18; 2) L’intervalle de confiance à 95% pour la moyenne des résidus contient la valeur nulle, donc au seuil de significativité de 5% on ne peut pas rejeter l’hypothèse que la moyenne des résidus soit nulle; 3) La p-value du test est égale à 1 (>0.05), donc au seuil de significativité de 5% on ne peut pas rejeter l’hypothèse que la moyenne des résidus soit nulle.

2.3.3 Vérifier l’hypothèse d’homogénéité de la dispersion des résidus

Pour vérifier cette hypothèse le test de Breusch-Pagan⁸ est utilisé. Le code R ci-dessous permet de réaliser ce test statistique sur les résidus du modèle mdlLR1 (\(y_1\sim x_1\)):

# Test (H0: Var(e) = const; H1: Var(e) <> const)
library(lmtest)
bptest(mdlLR1)

    studentized Breusch-Pagan test

data:  mdlLR1
BP = 0.65531, df = 1, p-value = 0.4182

Remarque: La p-value du test étant supérieure à 5%, on ne peut pas rejeter l’hypothèse selon laquelle les résidus ont une variance homogéne au seuil de signification de 5%.

Le graphique de la racine carée des valeurs absolues des résidus standardisés selon les valeurs approximées (“Scale-Location”) peut être utilisé également pour vérifier visuellement l’hypothèse d’égale variance (également appelée homoscédasticité) des résidus. Ci-dessous, on explique ce que l’on entend par résidus standardisés d’un modèle de régression linéaire.

A partir de l’équation (2.8), on déduit que:

\[\begin{equation} \tag{2.2} \hat{e}_i=y_i-\hat{y_i}=\left[1-h_{ii}\right]y_i-\sum_{j\neq i} h_{ij}y_j \end{equation}\]

et, par conséquent:

\[\begin{align} Var\left[\hat{e}_i\right]&=Var\left[(1-h_{ii})y_i-\sum_{j\neq i} h_{ij}y_j\right]=\\ &=(1-h_{ii})^2\sigma^2+\sum_{j\neq i} h_{ij}^2\sigma^2=\\ &=\sigma^2\left[ 1-2h_{ii}+h_{ii}^2+\sum_{j\neq i} h_{ij}^2\right]=\\ &=\sigma^2\left[ 1-2h_{ii}+\sum_{j=1}^n h_{ij}^2\right] \end{align}\]

On remarque que:

\[\begin{align} \sum_{j}^n h_{ij}^2&=\sum_{j=1}^n \left[\frac{1}{n}+\frac{(x_i-\bar{x})(x_j-\bar{x})}{s_{xx}}\right]^2=\\ &=\frac{1}{n}+2\sum_{j=1}^n \frac{1}{n} \cdot \frac{(x_i-\bar{x})(x_j-\bar{x})}{s_{xx}} + \sum_{j=1}^n \frac{(x_i-\bar{x})^2(x_j-\bar{x})^2}{s_{xx}^2}=\\ &=\frac{1}{n}+0+\frac{(x_i-\bar{x})^2}{s_{xx}}=h_{ii} \end{align}\]

et, donc:

\[\begin{equation} \tag{2.3} Var\left[\hat{e}_i\right]=\sigma^2(1-h_{ii}) \end{equation}\]

où: \(h_{ii}=\frac{1}{n}+\frac{(x_i-\bar{x})^2}{\sum_{j=1}^n (x_j-\bar{x})^2}\).

Résidu standardisé (définition): Le résidu standardisé d’un modèle régressif linéaire est donné par l’équation suivante:

\[\begin{equation} \tag{2.4} r_i=\frac{\hat{e}_i}{s \sqrt{1-h_{ii}}} \end{equation}\]

où: \(s=\sqrt{\frac{1}{n-2}\sum_{j=1}^n \hat{e}_j^2}\) est un estimateur ponctuel de \(\sigma\) obtenu à partir des résidus du modèle régressif linéaire.

Remarque: Dans le cas où le résidu \(i\) est suspecté comme étant anormalement élevé (correspondant à un point qui s’éloigne significativement de la droite de régression), il est préférable d’exclure ce point du calcul afin de ne pas biaiser l’estimateur de \(\sigma\). Dans ce cas, on utilise la formule suivante pour le calcul de \(s\): \(s=\sqrt{\frac{1}{n-3}\sum_{j=1\ j\neq i}^n \hat{e}_j^2}\) et on parle des résidus studentisés à la place des résidus standardisés.

A titre d’exemple, on illustre ci-dessous les graphiques Scale-Location des 4 modèles régressifs sur le jeu de données anscombe:

par(mfrow=c(2,2))
plot(mdlLR1, which = 3)
plot(mdlLR2, which = 3)
plot(mdlLR3, which = 3)
plot(mdlLR4, which = 3)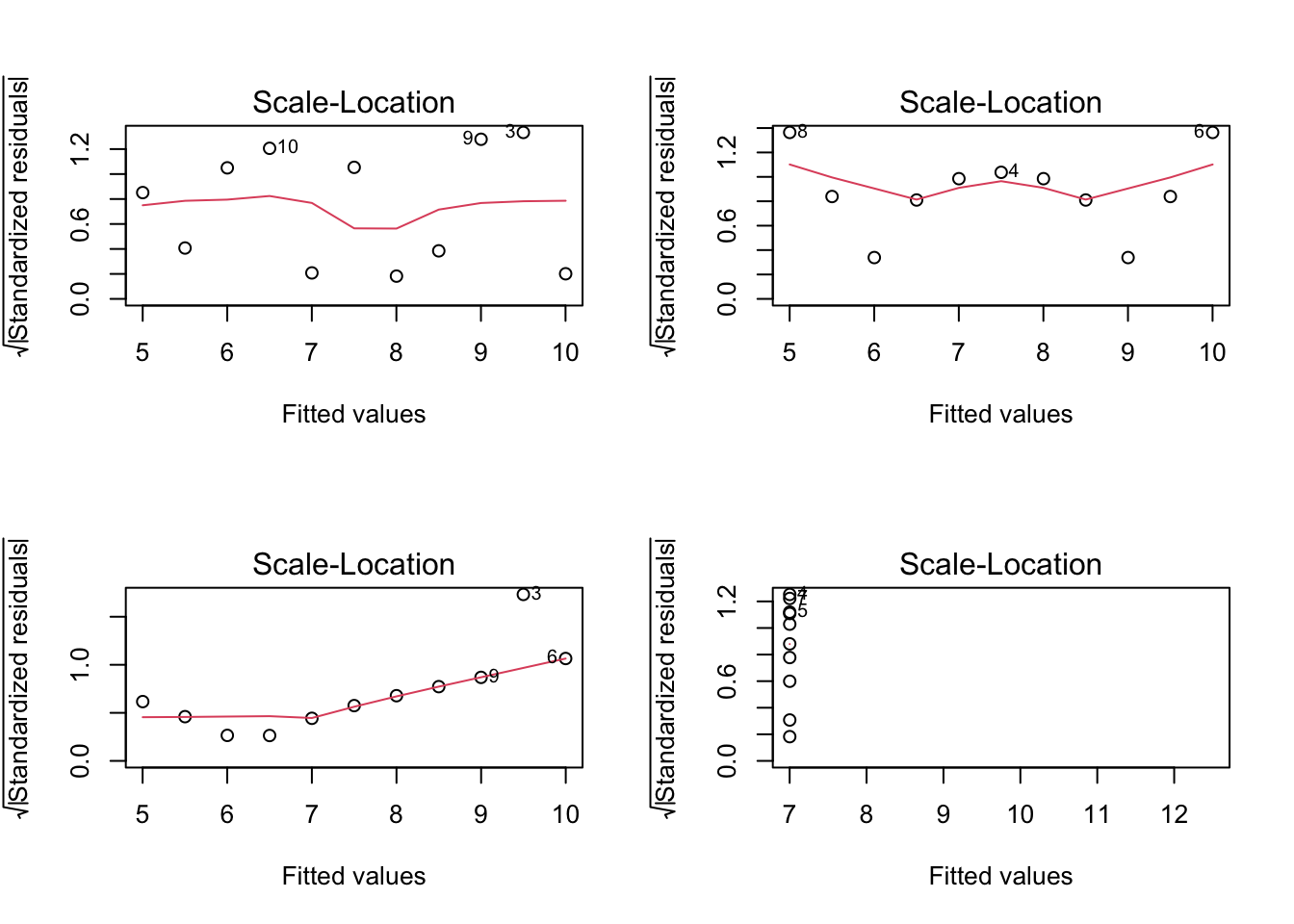

Figure 2.4: Scale-Location pour le jeu de données anscombe

Si la ligne rouge est à peu près horizontale sur le tracé, l’hypothèse d’homoscédasticité est vraisemblablement satisfaite. Une ligne de pente positive indique une augmentation de la variance avec les valeurs de \(x\) et une ligne de pente négative indique une diminution de la variance avec les valeurs de \(x\).

Remarques: On voit particulièrement bien que dans le cas du modèle mdlLR3(\(y_3\sim x_3\)) la variance des résidus a la tendance d’augmenter (ce qui peut être dû à la présence d’un point qui s’écarte de façon importante de la droite de régression). Dans le cas du modèle mdlLR2(\(y_2\sim x_2\)), on remarque que la variance des résidus est fluctuante (diminution-augmentation-diminution-augmentation), ce qui peut être causé par la présence d’une non-liniarité. Enfin, on voit que dans le cas du modèle mdlLR4(\(y_4\sim x_4\)) la droite rouge n’apparait pas sur le graphique, ce qui peut expliquer qu’il y a un seul point qui à lui tout seul détermine la direction de cette droite.

Lorsque la variance des résidus n’est pas homogène, deux approches peuvent être utilisées pour remédier au problème: opérer certaines transformations sur les variables du modèle (voir le chapitre 3), utiliser l’approche des moindres carrées pondérées. Ignorer la non homogénéité de la variance des résidus lorsqu’elle existe conduit à l’invalidation des tous les outils d’inférence statistique (p-values, intervalles de confiance, intervalles des prédictions, etc.).

2.3.4 Vérifier l’hypothèse d’indépendance des résidus

Pour vérifier cette hypothèse le test de Durbin-Watson⁹ est utilisé. Le code R ci-dessous permet de réaliser ce test statistique sur les résidus du modèle mdlLR1 (\(y_1\sim x_1\)):

# Test (H0: ei sont indépendants; H1: ei sont dépendants)
library(lmtest)
dwtest(mdlLR1, alternative = "two.sided")

    Durbin-Watson test

data:  mdlLR1
DW = 3.2123, p-value = 0.0241
alternative hypothesis: true autocorrelation is not 0

Remarque: Au seuil de significativité de 1%, on ne peut pas rejeter l’hypothèse selon laquelle les résidus du modèle mdlLR1 (\(y_1\sim x_1\)) sont indépendants (autocorrélation nulle).

2.4 Identification des points influents

Il s’agit ici d’identifier les points qui exercent une influence significative sur l’équation de la droite de régression. On entend par cela que l’équation de la droite de régression change de façon importante lorsque l’on supprime ces points. La figure 2.5 en donne une illustration:

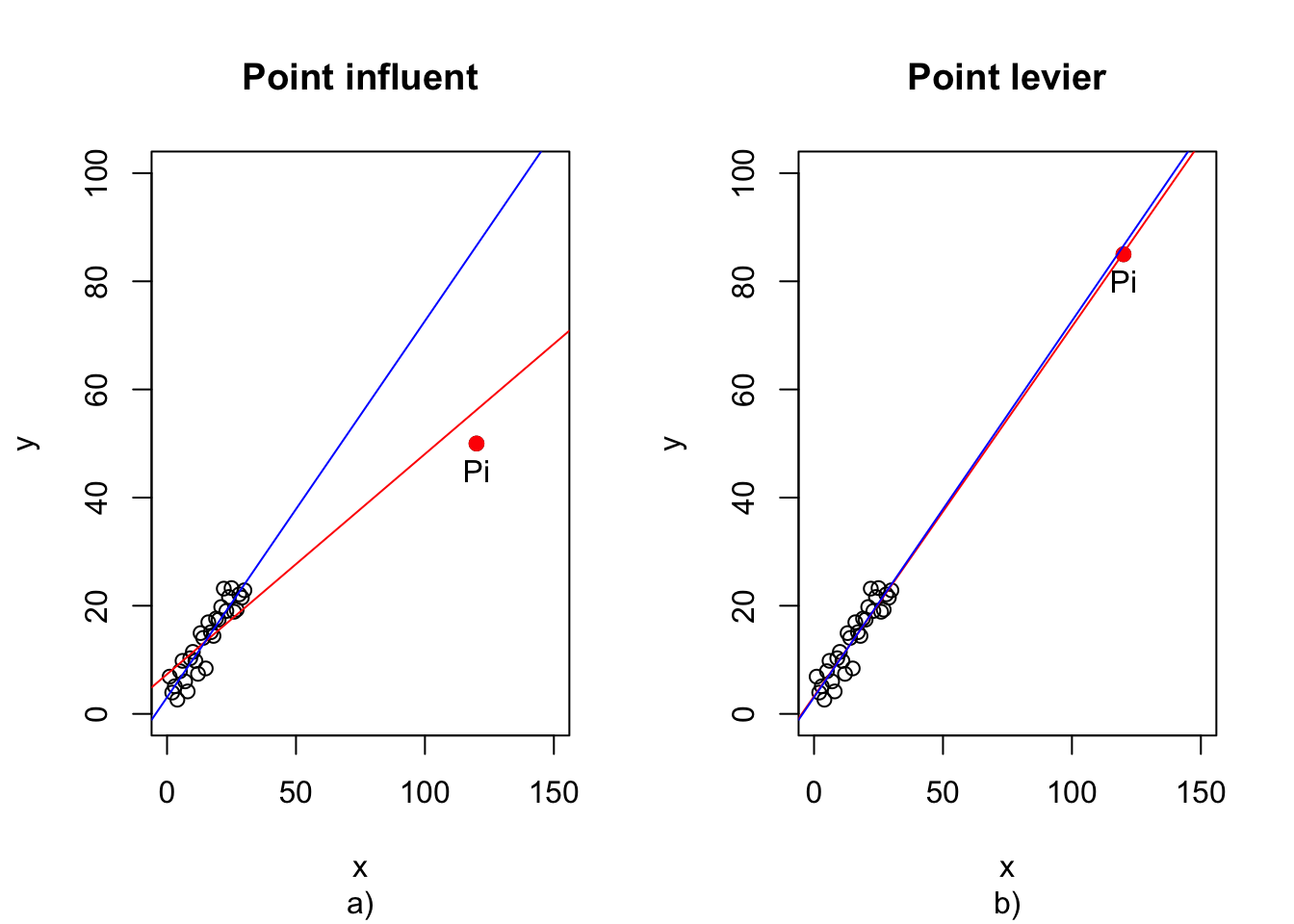
Figure 2.5: Illustration d’un point influent et d’un point levier

Pour caractériser de manière plus formelle les points influents, on introduit tout d’abord quelques concepts supplémentaires:

Point levier: On appelle point levier un point dont la coordonnée sur l’axe \(X\) est significativement différente de celles des autres points. Ainsi, dans la figure 2.5 b) le point Pi dont la coordonnée sur l’axe \(X\) est de 120, se détache clairement des autres points dont les coordonnées sur l’axe \(X\) sont comprises entre 0 et 35. On peut donc considérer le point Pi comme étant un point levier pour la droite de régression.

Dans la figure 2.5 a), le point Pi à la même coordonnée sur l’axe \(X\) que dans la figure 2.5 b), donc c’est également un point levier selon la définition. Toutefois, la différence avec la figure 2.5 b) est que dans le cas de la figure 2.5 a) le point Pi a une coordonnée sur l’axe \(Y\) qui est significativement différente de celle que l’on aurait attendu selon le modèle de régression linéaire définit par les autres points (voir la droite bleue). De ce fait, le point Pi “attire” la droite de régression vers lui (droite rouge) et change considérablement l’équation de celle-ci. On dit dans ce cas que le point Pi est un point influent.

Remarque: La différence majeure entre un point influent et un point levier réside dans le fait que dans le cas du point influent le résidu de celui-ci est atypique (significativement plus grand en valeur absolue) que celui des autres points, alors que dans le cas d’un point levier, son résidu n’est pas atypique par rapport aux résidus des autres points.

Dans la suite, on se propose d’identifier une règle permettant de statuer sans ambiguïté si un point peut être considéré comme étant un point levier.

2.4.1 Règle pour identifier les points leviers

Tout d’abord, pour un échantillon donné, la valeur ajustée s’écrit:

\[\begin{equation} \hat{y}_i=b_0+b_1x_i \end{equation}\]

où: \(b_0=\bar{y}-b_1\bar{x}\) (voir l’équation (1.8)) et \(b_1=\sum_{j=1}^n c_jy_j\) (voir l’équation (1.15)) avec \(c_j=\frac{x_j-\bar{x}}{s_{xx}}\).

Par conséquent,

\[\begin{align} \hat{y}_i&=\bar{y}-b_1\bar{x}+b_1x_i=\bar{y}+b_1(x_i-\bar{x})=\\ &=\frac{1}{n}\sum_{j=1}^n y_j+\sum_{j=1}^n \frac{x_j-\bar{x}}{s_{xx}} y_j (x_i-\bar{x})=\\ &=\sum_{j=1}^n \left[ \frac{1}{n}+\frac{(x_i-\bar{x})(x_j-\bar{x})}{s_{xx}}+ \right]y_j=\\ &=\sum_{j=1}^n h_{ij}y_j \tag{2.5} \end{align}\]

où:

\[\begin{equation} \tag{2.6} h_{ij}=\frac{1}{n}+\frac{(x_i-\bar{x})(x_j-\bar{x})}{s_{xx}} \end{equation}\]

On remarque que:

\[\begin{align} \sum_{j=1}^n h_{ij}&=\sum_{j=1}^n\left[\frac{1}{n}+\frac{(x_i-\bar{x})(x_j-\bar{x})}{s_{xx}}\right]=\\ &=\frac{n}{n}+\frac{(x_i-\bar{x})}{s_{xx}}\sum_{j=1}^n (x_j-\bar{x})=1 \tag{2.7} \end{align}\]

car \(\sum_{j=1}^n (x_j-\bar{x})=0\).

On en déduit que :

\[\begin{equation} \tag{2.8} \hat{y}_i=h_{ii}y_i+\sum_{j\neq i} h_{ij}y_j \end{equation}\]

où:

\[\begin{equation} \tag{2.9} h_{ii}=\frac{1}{n}+\frac{(x_i-\bar{x})^2}{\sum_{j=1}^n (x_j-\bar{x})^2} \end{equation}\]

Le terme \(h_{ii}\) dans l’équation (2.9) porte le nom de levier du point \(i\).

Remarques: 1) Le numérateur du deuxième terme dans l’expression du levier du point \(i\) (voir l’équation (2.9)) est proportionnel à la distance qui sépare le point \(i\) du centré de gravité (moyenne) de l’ensemble de points sur l’axe \(X\); 2) \(h_{ii}\) donne une indication de la manière dont le point \(i\) impacte sur la prédiction de la valeur \(\hat{y}_i\): en effet, si \(h_{ii} \approx 1\) alors les autres termes \(h_{ij}\) sont proches de zéro (voir l’équation (2.7)) et donc selon l’équation (2.8) on obtient que: \(\hat{y}_i \approx y_i\), ce qui veut dire que la valeur prédite sera proche de la valeur rééle quelques soient les autres valeurs.

En remplaçant les valeurs concrètes \(x_i\) et \(\bar{x}\) dans l’équation (2.9) par les valeurs aléatoires \(X_i\) et respectivement \(\bar{X}\), on déduit que :

\[\begin{align} E\left[h_{ii}\right]&=\frac{1}{n}+E\left[\frac{(X_i-\bar{X})^2}{\sum_{j=1}^n (X_j-\bar{X})^2}\right]=\\ &=\frac{1}{n}+E\left[\frac{nVar\left[X_i\right]}{\sum_{j=1}^n nVar\left[X_j\right]}\right]=\\ &=\frac{1}{n}+E\left[\frac{n\sigma^2}{n\sum_{j=1}^n \sigma^2}\right]=\frac{1}{n}+E\left[\frac{1}{n}\right]=\frac{2}{n} \tag{2.10} \end{align}\]

On considère qu’un point \(i\) est un point levier si:

\[\begin{equation} \tag{2.11} h_{ii}>2\times\frac{2}{n}=\frac{4}{n} \end{equation}\]

A titre d’exemple, le code R ci-dessous illustre comment afficher les leviers des différents points qui ont servi à la construction du modèle mdlLR4 \((y_4 \sim x_4)\) du jeu de données anscombe:

library(olsrr)
# Affichage des leviers pour le jeu de données (y4~x4) du fichier anscombe
leviers_mdlLR4<-cbind(x4,y4,ols_leverage(mdlLR4))
colnames(leviers_mdlLR4)[3]<-"Leverage"
leviers_mdlLR4
plot(leviers_mdlLR4[,3], ylab = "Leviers", main="Leviers pour le jeu de données (y4~x4)")
abline(h=4/length(leviers_mdlLR4[,3]), col="red")

      x4    y4 Leverage
 [1,]  8  6.58      0.1
 [2,]  8  5.76      0.1
 [3,]  8  7.71      0.1
 [4,]  8  8.84      0.1
 [5,]  8  8.47      0.1
 [6,]  8  7.04      0.1
 [7,]  8  5.25      0.1
 [8,] 19 12.50      1.0
 [9,]  8  5.56      0.1
[10,]  8  7.91      0.1
[11,]  8  6.89      0.1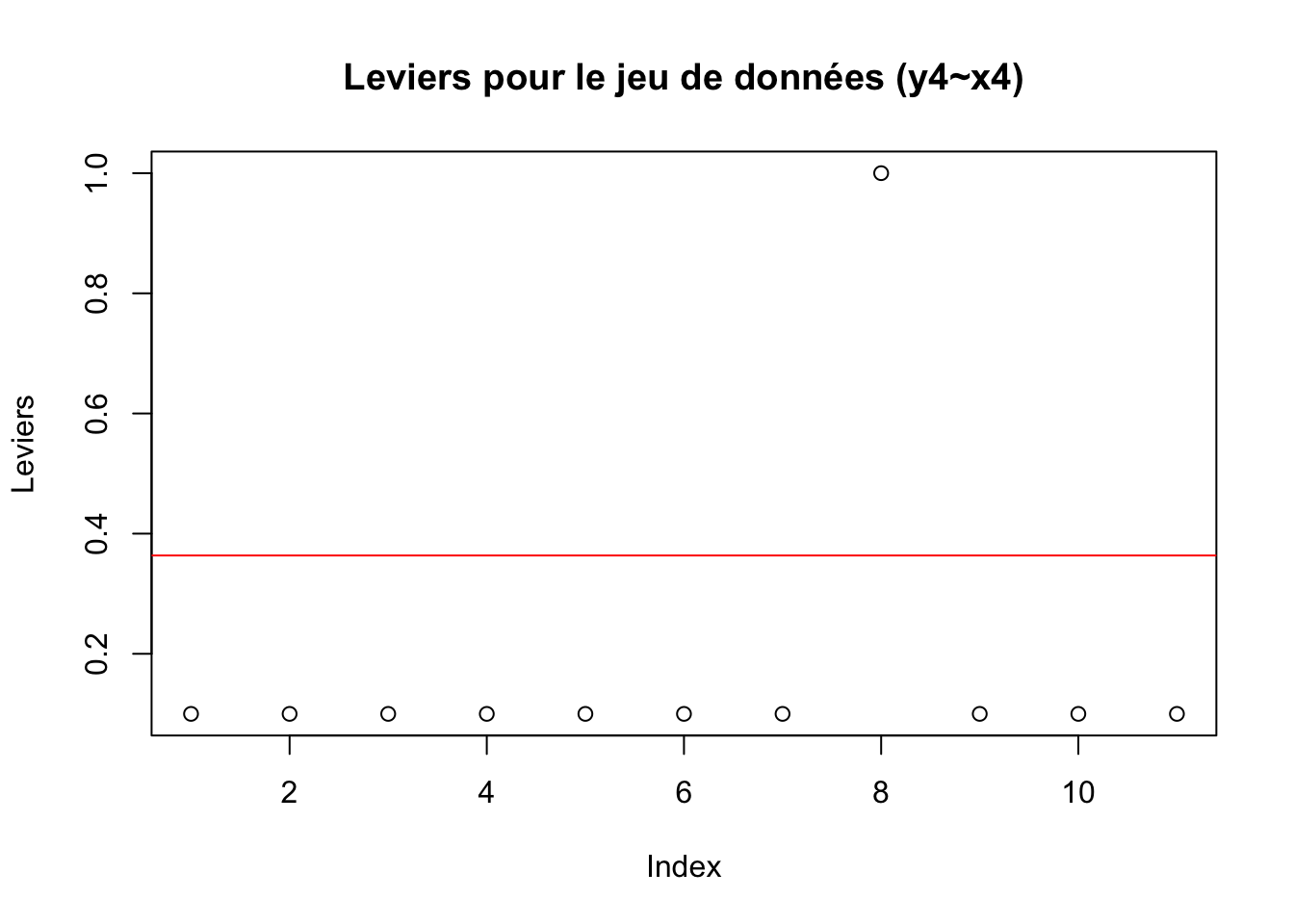

Remarques: 1) Pour le calcul des leviers on utilise la fonction R ols_leverage() en précisant comme paramètre de cette fonction le nom du modèle de régression linéaire; 2) On constate que le point n°8 de coordonnées (19, 12.5) présente un levier de 1 > 4/11 = 0.3636364, donc ce point est un point levier (voir aussi la figure 2.1).

Les points leviers, même s’ils n’ont pas d’influence indésirable sur l’estimation des coefficients, conduisent à la réduction de l’erreur standard estimée et à l’augmentation de la valeur du coefficient de détermination \(R^2\) (voir le chapitre @ref()). Par conséquent, leurs présence doit être attentivement analysée et une décision judicieuse doit être prise concernant leurs intégration dans le modèle.

2.5 Identification des points atypiques

Il s’agit des points qui s’écartent significativement par rapport à la droite de régression. Pour identifier ces points, on peut utiliser les résidus standardisés et/ou studentisés. Les lignes de code R suivantes, permettent de calculer et d’afficher les résidus standardisés et les résidus studentisés du modèle mdlLR1 \((y_1 \sim x_1)\) du jeu de données anscombe:

# Calcul des résidus standardisés et studentisés pour le jeu de données (y1~x1) du fichier anscombe
stdRes_mdlLR1<-cbind(x1,y1,rstandard(mdlLR1), rstudent(mdlLR1))
colnames(stdRes_mdlLR1)[3:4]<-c("Std.Res", "Stud.Res")
stdRes_mdlLR1

# Afichage des résidus standardisés et studentisés pour le jeu de données (y1~x1) du fichier anscombe
library(olsrr)
ols_plot_resid_stand(mdlLR1) # graphique des résidus standardisés
ols_plot_resid_stud(mdlLR1)  # graphique des résidus studentisés

   x1    y1     Std.Res    Stud.Res
1  10  8.04  0.03324397  0.03134464
2   8  6.95 -0.04331791 -0.04084477
3  13  7.58 -1.77793266 -2.08109891
4   9  8.81  1.11028824  1.12679993
5  11  8.33 -0.14810075 -0.13980118
6  14  9.96 -0.04050923 -0.03819595
7   6  7.24  1.10190458  1.11695887
8   4  4.26 -0.72515977 -0.70458079
9  12 10.84  1.63487302  1.83833042
10  7  4.82 -1.45488131 -1.56846043
11  5  5.68  0.16606601  0.15680897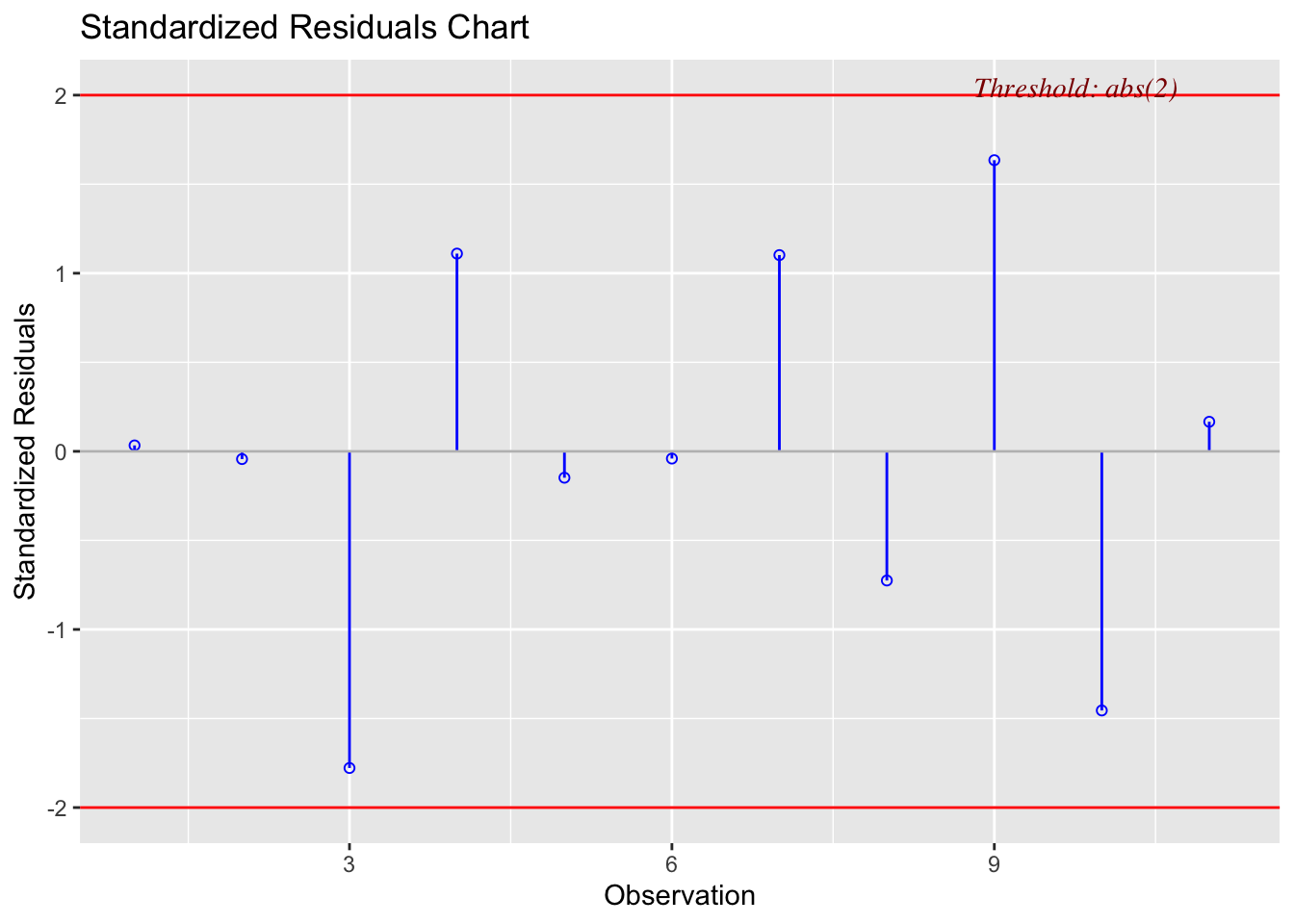

Figure 2.6: Résidus standardisés du modèle mdlLR1(y1~x1)

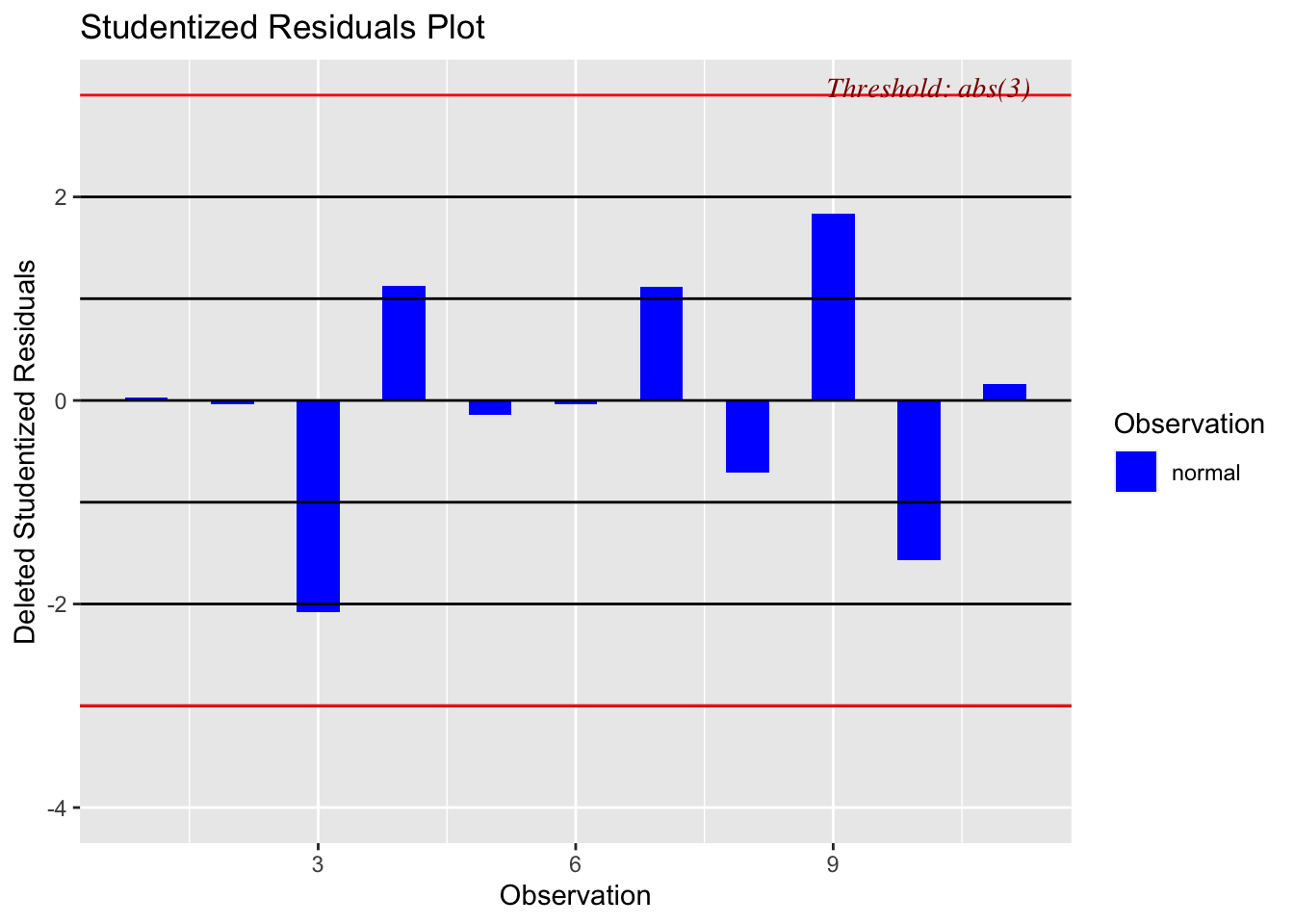
Figure 2.7: Résidus studentisés du modèle mdlLR1(y1~x1)

Remarques: 1) Les fonctions R rstandard() et rstudent() sont utilisées pour le calcul des résidus standardisés et repsectivement studentisés; 2) On peut constater que les résidus standardisés du modèle mdlLR1 \((y_1 \sim x_1)\) sont tous situés dans l’intervalle [-2,2], ce qui indique qu’il n’y a pas de résidu atypique pour ce jeu de données; 3) Le résidus studentisés sont tous dans l’intervalle [-3,3], ce qui indique qu’il n’y a pas de résidu atypique pour ce jeu de données).

Les points atypiques ne doivent pas être automatiquement supprimés de l’analyse seulement parce qu’ils ne sont pas en accord avec le modèle. Une analyse attentive doit être réalisée à leur sujet car ils peuvent révéler des problèmes concernant le modèle utilisé. Ainsi, ils peuvent conduire à la considération d’un modèle alternatif dans lequel ces points ne sont plus atypiques. Parfois, la prise en considération de certaines nouvelles variables explicatives peut résoudre le problème.

2.6 Identification des points influents

On a vu dans le paragraphe précédent qu’un point levier n’est pas forcement un point influent. Pour qu’il le soit, il doit avoir en plus un résidu atypique (c.à.d. qu’il s’écarte de manière significative de la droite de régression). Une règle générique pour détecter si un point levier peut être considéré comme influent sur la droite de régression est d’analyser le résidu standardisé (équation (2.4)) de ce point. En effet, si le résidu standardisé d’un point levier n’est pas dans l’intervalle [-2, 2], alors on peut considérer que ce point est un point influent. Pour des jeux de données volumineux, l’intervalle peut être plus large ([-4,4]). Si la présence d’un point influent est suspectée, alors il peut s’avérer plus judicieux d’utiliser les résidus studentisés à la place des résidus standardisés (on évite ainsi d’avoir un biais dans l’estimation de l’écart-type des résidus). Si le résidu studentisé d’un point levier n’est pas dans l’intervalle [-3, 3], alors on peut considérer que ce point est un point influent.

Puisqu’un point influent se caractérise par un levier important et un résidu en valeur absolue significativement plus grand que celui des autres points, un graphique très utile est celui des résidus studentisés selon les leviers:

# Affichage des résidus standardisés en fonction des leviers pour le jeu de données (y1~x1) du fichier anscombe
ols_plot_resid_lev(mdlLR1)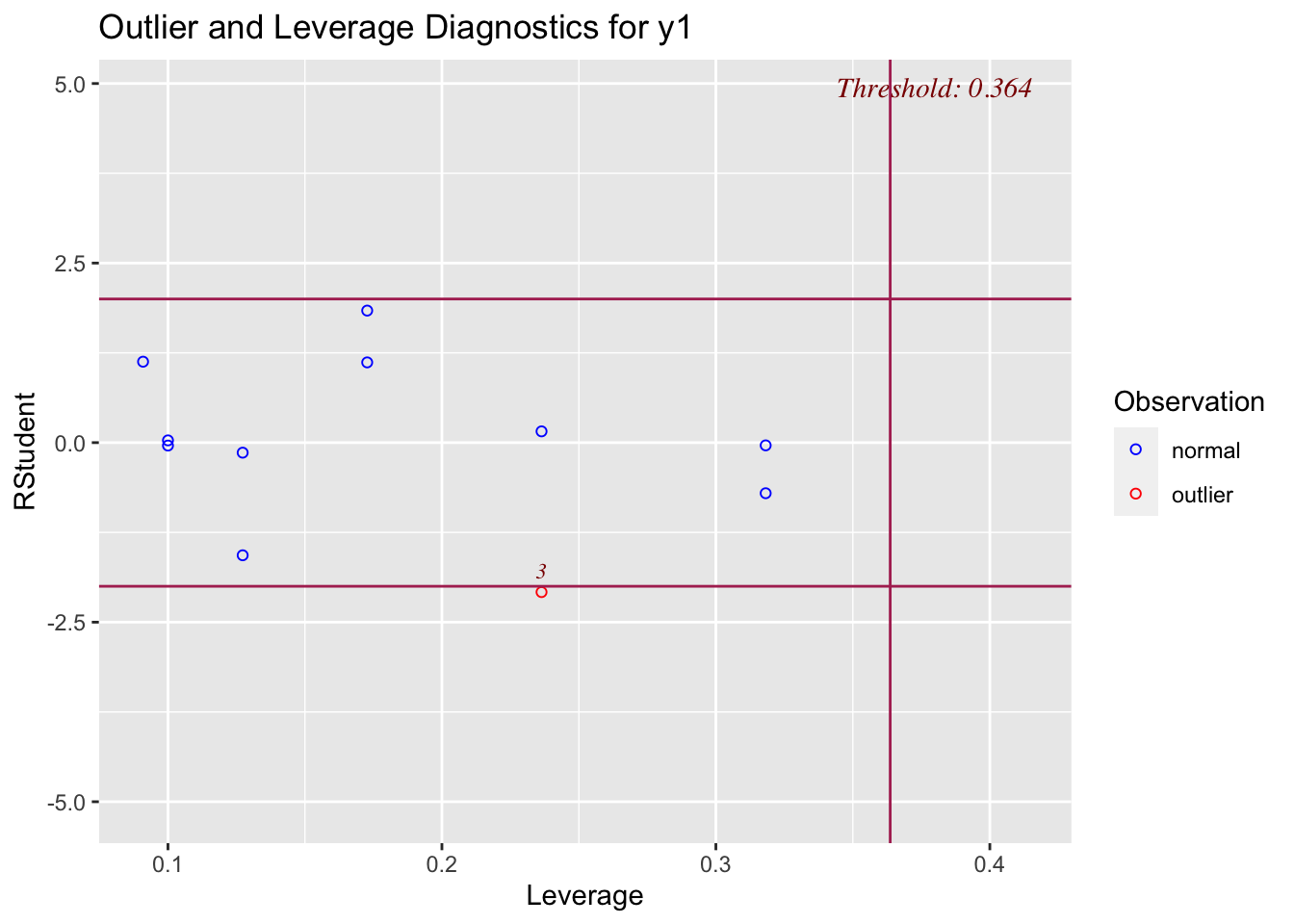

Figure 2.8: Graphique de l’influence de points dans le cadre du modèle mdlLR1(y1~x1) fichier anscombe

Remarque: Le point n°3 présente un résidu studentisé qui n’est pas dans l’intervalle [-2,2] mais son levier ne dépasse pas le seuil de 4/11 = 0.364 (voir le paragraphe 2.4.1), donc c’est le point qui s’écarte le plus par rapport à la droite de régression sans être toutefois un point influent.

Le test de Bonferroni est souvent associé à ce graphique et permet de statuer si le résidu studentisé le plus extrême est une valeur atypique. La ligne de code R suivante, permet de réaliser le test de Bonferroni dans le cas du modèle mdlLR1 \((y_1 \sim x_1)\) du jeu de données anscombe:

# Test de Bonferroni pour le jeu de données (y1~x1) du fichier anscombe
library(RcmdrMisc)
outlierTest(mdlLR1)

No Studentized residuals with Bonferroni p < 0.05
Largest |rstudent|:
   rstudent unadjusted p-value Bonferroni p
3 -2.081099           0.070994      0.78093

Remarque: Comme on peut le constater, on teste l’observation n°3 dont le résidu studentisé est le plus êxtreme (-2.081099). Selon le test t de Student, la p-value est de 0.070994 (donc au seuil de significativité de 5%, on ne peut pas rejeter l’hypothèse nulle, donc cette observation ne présente pas un résidu atypique). Selon l’approche de Bonferroni, au seuil de significativité de 5%, la conclusion est d’avantage renforcée (résidu non-atypique) car la p-value de ce test est de 0.78093.

La distance de Cook est également une statistique utilisée pour évaluer l’influence d’un point sur la droite de régression. Cette distance est donnée par la formule suivante:

\[\begin{equation} \tag{2.12} D_i=\frac{\sum_{j=1}^{n} \left(\hat{y}_{j(i)}-\hat{y}_j \right)^2}{2S^2} \end{equation}\]

où: \(\hat{y}_j\) représente la j-ième valeur attendue selon le modèle; \(\hat{y}_{j(i)}\) représente la j-ième valeur attendue selon le modèle de régression linéaire construit sans l’observation i; S représente l’écart-type des résidus.

On peut démontrer que:

\[\begin{equation} \tag{2.13} D_i=\frac{r_i^2}{2}\times \frac{h_{ii}}{1-h_{ii}} \end{equation}\]

où: \(r_i\) est le i-ième résidu standardisé (voir l’équation (2.4)) et \(h_{ii}\) est le levier du point i (voir l’équation (2.9)).

Remarque: Une distance de Cook importante peut être le résultat soit d’un résidu standardisé grand, soit d’un levier important, soit des deux.

D’un point de vue empirique, il est considéré que si la distance de Cook d’un point dépasse la limite de 4/(n-2), alors le point respectif peut être considéré comme atypique pour le modèle linéaire (soit le point s’écarte beaucoup par rapport à la droite de régression, soit il a un levier important, soit il est influent).

La ligne de code R suivante, permet de calculer les distances de Cook pour le modèle mdlLR3 \((y_3 \sim x_3)\) du jeu de données anscombe:

## Calcul des distances de Cook pour le jeu de données (y3~x3) du fichier anscombe
distCook_mdlLR3<-cbind(x3,y3,cooks.distance(mdlLR3))
colnames(distCook_mdlLR3)[3]<-"dist.Cook"
distCook_mdlLR3

## Affichage des distances de Cook pour le jeu de données (y3~x3) du fichier anscombe
distCook_mdlLR3<-cbind(x3,y3,cooks.distance(mdlLR3))
plot(distCook_mdlLR3[,3], ylab="Distances de Cook")
abline(h=4/(length(distCook_mdlLR3[,3])-2), col="red")

   x3    y3    dist.Cook
1  10  7.46 0.0117646226
2   8  6.77 0.0021414813
3  13 12.74 1.3928494503
4   9  7.11 0.0054731354
5  11  7.81 0.0259838693
6  14  8.84 0.3005708107
7   6  6.08 0.0005176411
8   4  5.39 0.0338173336
9  12  8.15 0.0595359333
10  7  6.42 0.0003546293
11  5  5.73 0.0069478084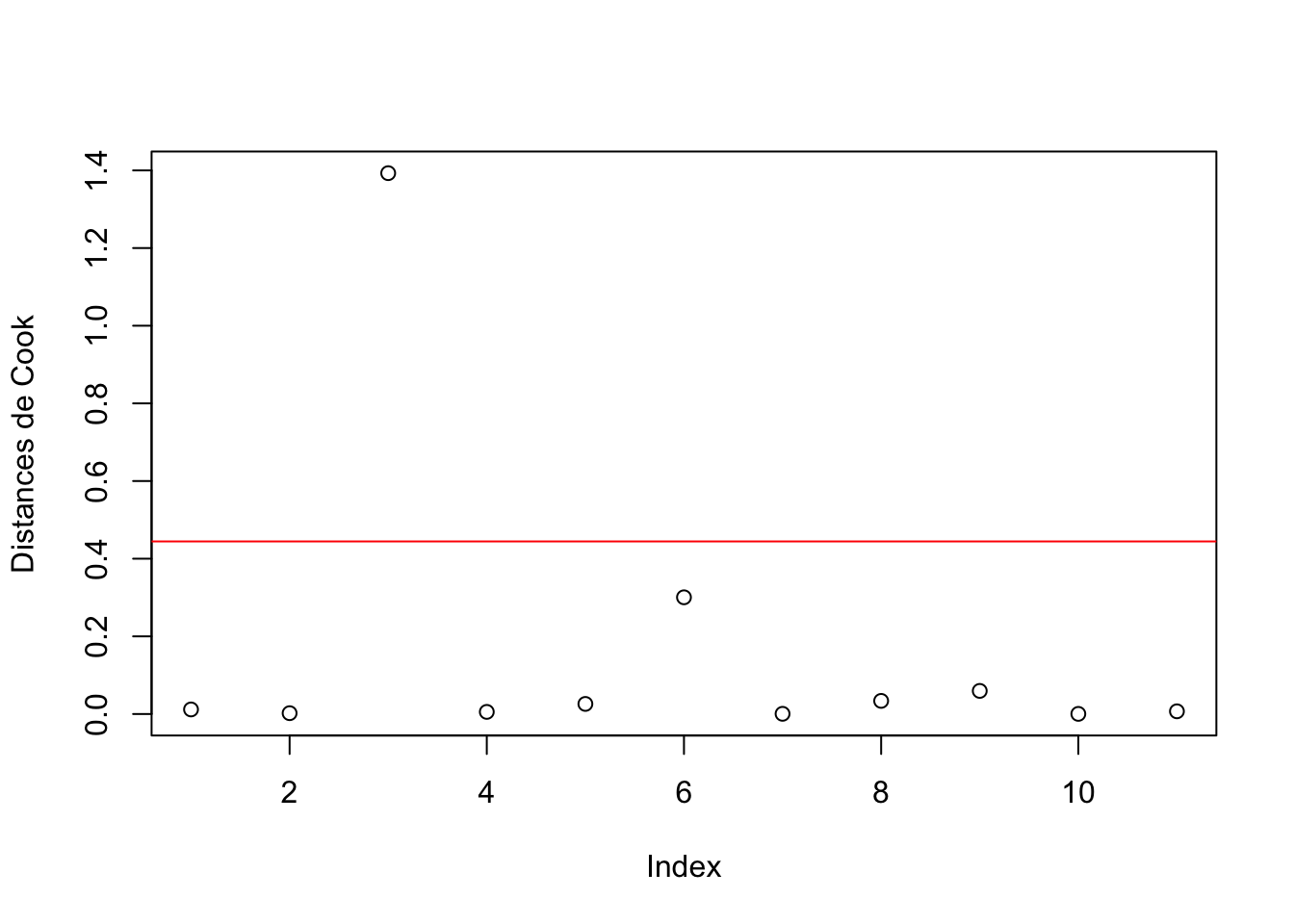

Figure 2.9: Distances de Cook dans le cadre du modèle mdlLR3(y3~x3)

Remarques: 1) Pour le calcul des distances de Cook on utilise la fonction R cooks.distance() en précisant comme paramètre de cette fonction le nom du modèle de régression linéaire; 2) On peut constater que la distance de Cook du point n°3 de coordonnées (13, 12.74) est de 1.3928494503 > 4/(11-2) = 0.44444, donc ce point peut être considéré comme atypique dans le cadre de ce modèle régressif.

Un graphique très utile pour le diagnostic d’un éventuel point influent sur la droite de régression est le graphique des résidus standardisés selon leur levier (“Residual vs Leverage”) sur lequel on superpose les limites pour la distance de Cook. Si un point sur ce graphique se situe en dehors de l’intervalle définit par les lignes en pointillées, il s’agit d’une observation influente. A titre d’exemple, on illustre les graphiques Residuals vs Leverage des 4 modèles régressifs sur le jeu de données anscombe:

par(mfrow=c(2,2))
plot(mdlLR1, which = 5)
plot(mdlLR2, which = 5)
plot(mdlLR3, which = 5)
plot(mdlLR4, which = 5)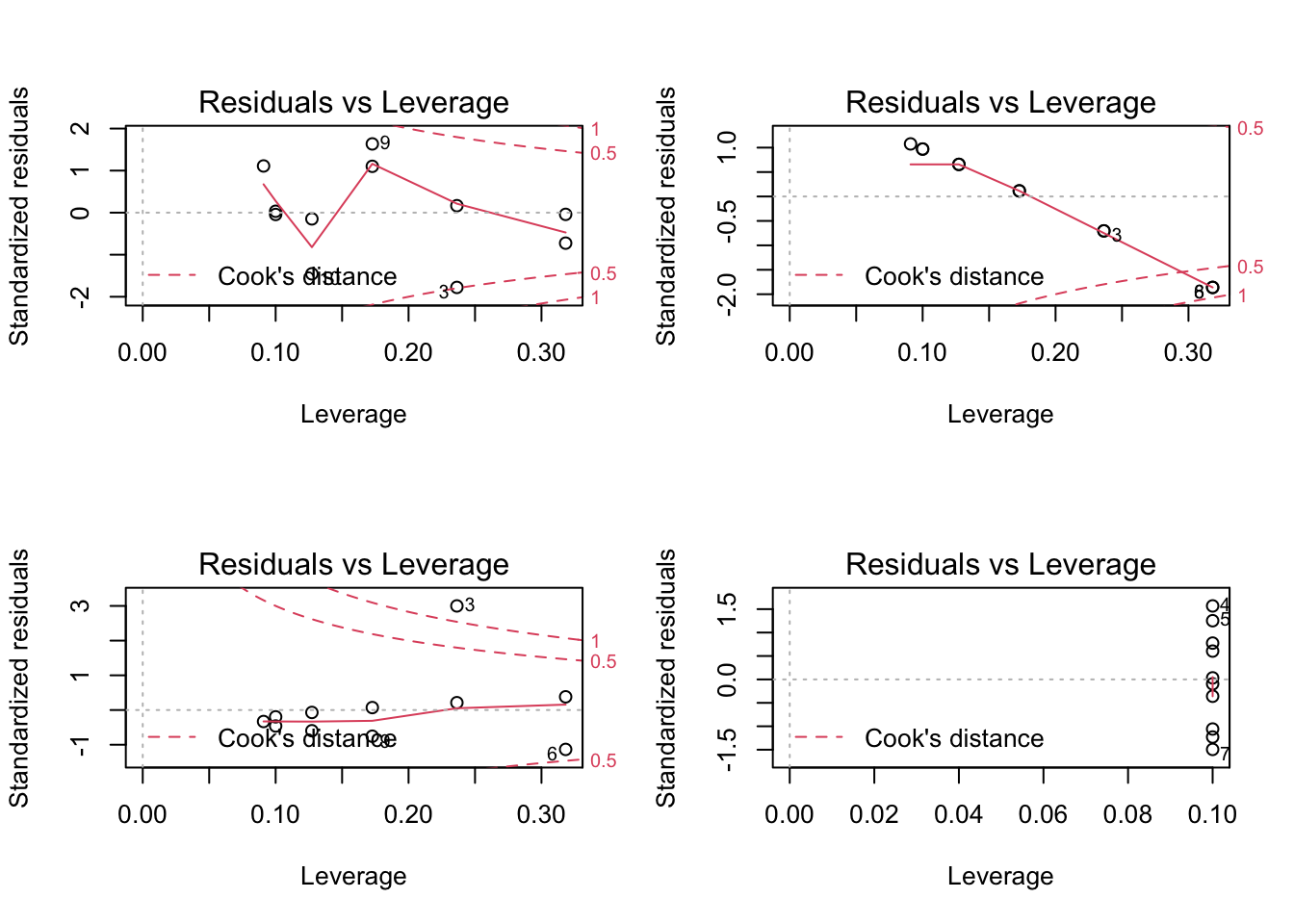

Figure 2.10: Residual vs Leverage pour le jeu de données anscombe

Remarques: On voit dans le cas du modèle mdlLR3(\(y_3\sim x_3\)) que le point n°3 se situe au délà de la deuxième limite pour la distance de Cook (1), toutefois sont levier n’est pas anormalement élevé, donc ce point a une influence assez réduite sur la droite de régression. Dans une moindre mesure, on peut dire la même chose au sujet du point n°6 du modèle mdlLR2(\(y_2\sim x_2\)) et du point n°3 du modèle mdlLR1(\(y_1\sim x_1\)) qui se situe juste sur la première limite de la distance de Cook (0.5). Quant au modèle mdlLR4(\(y_4\sim x_4\)), le levier du point qui détermine à lui seul l’orientation de la droite de régression (voir la figure 2.1) étant de 1, ce point n’est pas affiché sur le graphique.

Un tableau de bord très utile pour l’analyse, qui regroupe les différents indicateurs statistiques est donné par la ligne de code R suivante:

# Tableau de bord pour le diagnostic
influenceIndexPlot(mdlLR1)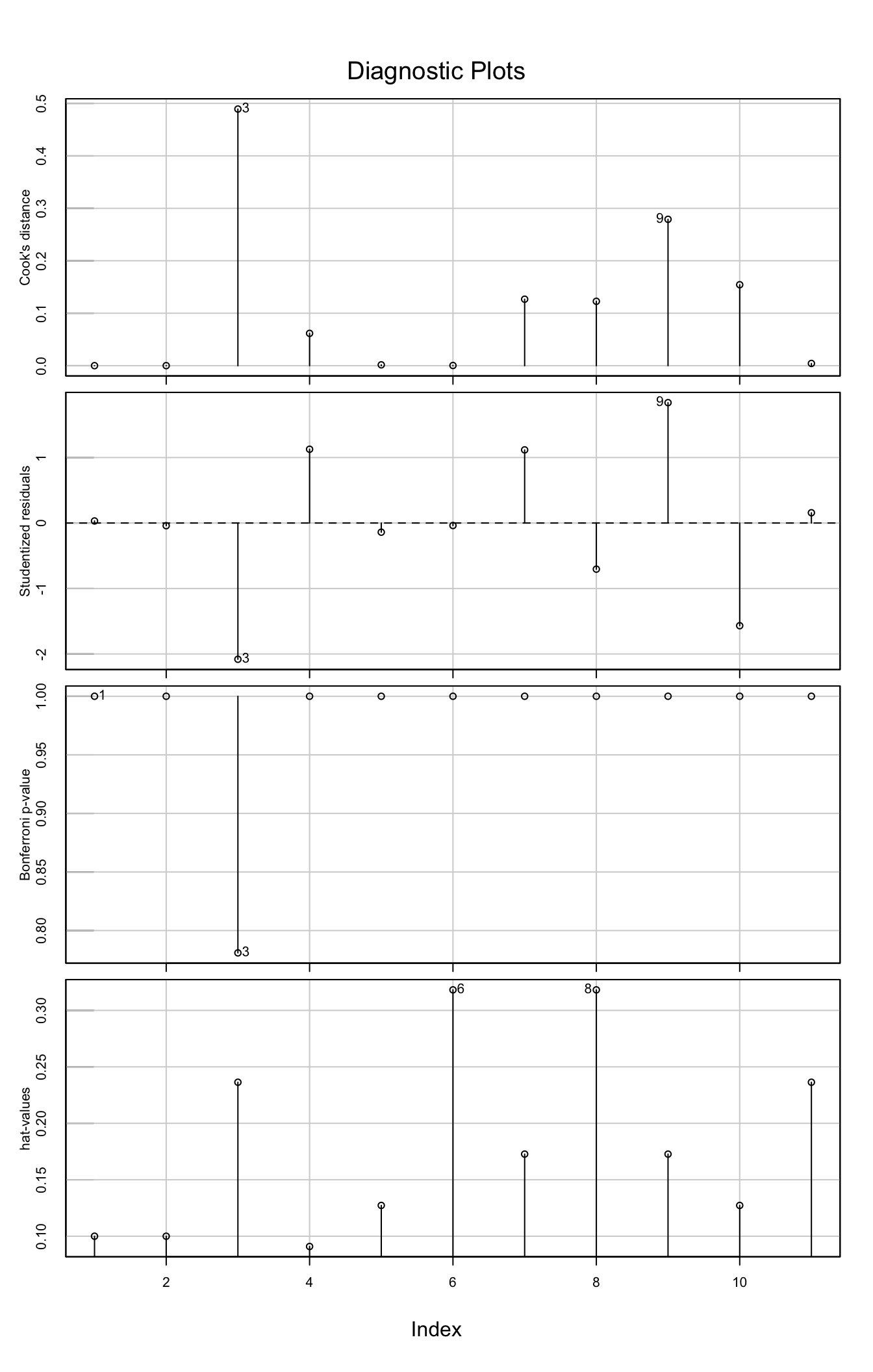

Figure 2.11: Graphique de diagnostic pour l’influence des points dans le cadre du modèle mdlLM1(y1~x1) du fichier anscombe

Comme on peut le constater, ce graphique réunit visuellement sur la même feuille les indicateurs statistiques suivants: les distances de Cook, les résidus studentisés, les p-values du test de Bonferroni, les leviers. Il est donc très aisé de cibler les points qui sont susceptibles d’être des points influents sur la droite de régression. Malheureusement, les limites permettant de savoir à partir de quelle valeur on doit réagir pour ces indicateurs n’apparaissent pas sur le graphique.

Remarque: On voit aisement sur ce graphique que le point sur lequel il faudrait se pencher tout d’abord est le point n°3 (car il a le plus grand résidu studentisé, un levier assez grand et par conséquent une distance de Cook la plus grande; toutefois, selon le test de Bonferroni, ce point ne peut pas être considéré comme atypique car la p-value > 5%). En conclusion, on ne peut pas considérer que ce point soit un point influent sur la droite de régression.

2.6.1 Que faire en présence des points influents ?

Il faut faire une analyse attentive dans chaque cas pour essayer de déterminer si ces points sont inhabituels ou s’ils se différencient d’une certaine manière des autres points. Si la réponse à cette question est affirmative, alors il faut supprimer ces points et ajuster de nouveau le modèle linéaire sur les points restants. Parfois, l’ajout d’une variable explicative supplémentaire ou certaines transformations des variables \((X,Y)\) - voir le chapitre suivant - peuvent résoudre le problème.

2.7 Fiche de synthèse du code R

On réunit ici les différents morceaux de code R présentés dans ce chapitre pour donner un aperçu global de la manière dont on peut valider un modèle de régression linéaire. A titre d’exemple, on aborde le modèle de régression linéaire utilisé dans la fiche de synthèse du chapitre 1 - voir l’exemple 1.2 du paragraphe 1.5. Le code présenté ci-dessous se trouve dans le fichier codeRLS_l2.r dans le répertoire codeR dans Moodle.

library(olsrr)
library(lmtest)
library(nortest)
library(RcmdrMisc)

# Vérifier l'hypothèse de linéarité du modèle
# ===========================================

# Visuellement (graphique)
#-------------------------
ols_plot_reg_line(Rendement, Temperature)     # affichage de la droite de régression
ols_plot_resid_fit(mdlLR)                     # graphique des résidus selon les valeurs approchées

# Numériquement (test)
#---------------------
resettest(mdlLR, power = 2)                   # tester une dépendance quadratique 
resettest(mdlLR, power = 3)                   # tester une dépendance cubique 

# Analyse des résidus du modèle
# =============================

# Normalité de la distribution
#-----------------------------
# Visuellement (graphiques)
ols_plot_resid_qq(mdlLR)                      # autres graphiques possibles :
                                              # - histogramme : ols_plot_resid_hist()
                                              # - boite à moustaches : ols_plot_resid_box()

# Numériquement (tests)
shapiro.test(mdlLR$residuals)                 # autres tests possibles:   
                                              # - ad.test() 
                                              # - lillie.test()
                                              # - cvm.test()
# Moyenne nulle
#--------------
t.test(mdlLR$residuals)                       # (H0: moyenne résidus = 0; H1: moyenne résidus <> 0)

# Homogénéité de la dispersion des résidus
#-----------------------------------------
# Visuellement (graphique)
plot(mdlLR, which = 3)

# Numériquement (test)
bptest(mdlLR)                                 # (H0: Var(e) = const; H1: Var(e) <> const)

# Indépendance des résidus
#--------------------------
dwtest(mdlLR, alternative = "two.sided")      # (H0: ei sont indépendants; H1: ei sont dépendants)

# Identification des points influents
# ===================================

# Points leviers
#---------------
# Numériquement
leviers_mdlLR<-cbind(Temperature,Rendement,ols_leverage(mdlLR))
colnames(leviers_mdlLR)[3]<-"Leverage"
leviers_mdlLR

# Graphiquement
plot(leviers_mdlLR[,3], ylab = "Leviers", main="Leviers pour le jeu de données (Rendement~Température)")
abline(h=4/length(leviers_mdlLR[,3]), col="red")

# Points atypiques
#-----------------
# Calcul des résidus standardisés et studentisés 
stdRes_mdlLR<-cbind(Temperature,Rendement,rstandard(mdlLR), rstudent(mdlLR))
colnames(stdRes_mdlLR)[3:4]<-c("Std.Res", "Stud.Res")
stdRes_mdlLR

# Affichage graphique des résidus standardisés et studentisés 
ols_plot_resid_stand(mdlLR) # graphique des résidus standardisés
ols_plot_resid_stud(mdlLR)  # graphique des résidus studentisés

# Test de Bonferroni
outlierTest(mdlLR)

# Points influents
#-----------------
ols_plot_resid_lev(mdlLR) # résidus selon les leviers

# Distances de Cook
distCook_mdlLR<-cbind(Temperature,Rendement,cooks.distance(mdlLR))
colnames(distCook_mdlLR)[3]<-"dist.Cook"
distCook_mdlLR

plot(distCook_mdlLR[,3], ylab="Distances de Cook")
abline(h=4/(length(distCook_mdlLR[,3])-2), col="red")
atyp<-which(distCook_mdlLR[,3]>(4/(length(distCook_mdlLR[,3])-2)))
points(x=atyp,y=distCook_mdlLR[,3][atyp],pch=19, col="red")
text.default(x=atyp,y=distCook_mdlLR[,3][atyp], 
             labels = c(toString(atyp[1]), toString(atyp[2])),
             pos = c(1, 1), col="red")

# Graphique des résidus standardisés selon leur levier
plot(mdlLR, which = 5)

# Tableau de bord
influenceIndexPlot(mdlLR)

Ci-dessous, on interprète les résultats obtenus:

Vérifier si le modèle linéaire est approprié pour décrire les données: on constate dans la figure 2.12 que le modèle linéaire est tout à fait adapté au jeu de données. En effet, le points sur le graphique sont disposés de manière aléatoire autour de la droite de régression.

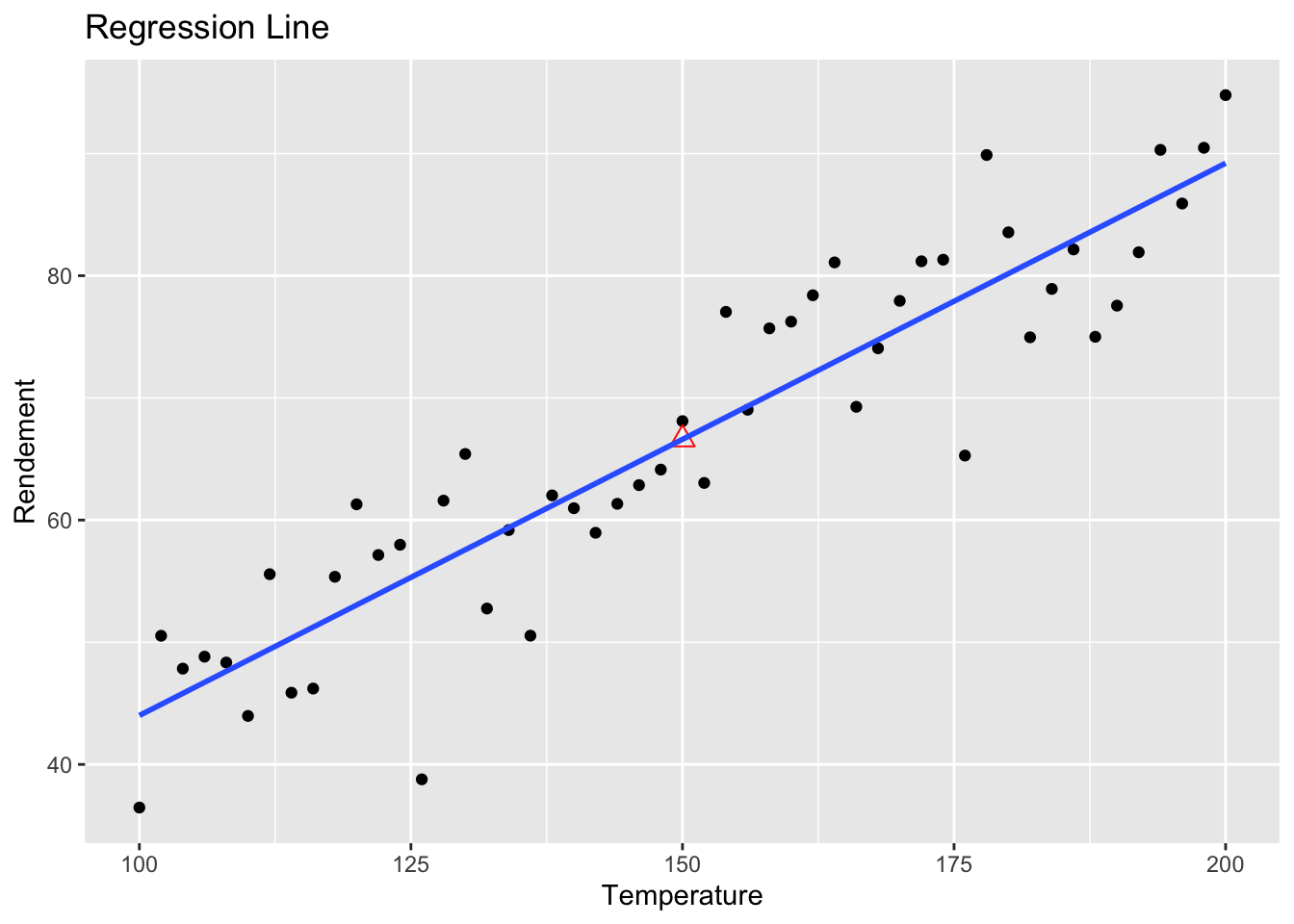
Figure 2.12: Affichage de la droite de régression linéaire sur le graphique Rendement-Température

Ce constat est validé aussi par le graphique des résidus selon les valeurs attendues (figure 2.13) où l’on peut voir que les résidus sont disposés de manière aléatoire d’un côté et de l’autre de la droite horizontale centrée sur zéro. Aucune tendance non-linéaire n’est visible sur ce graphique.

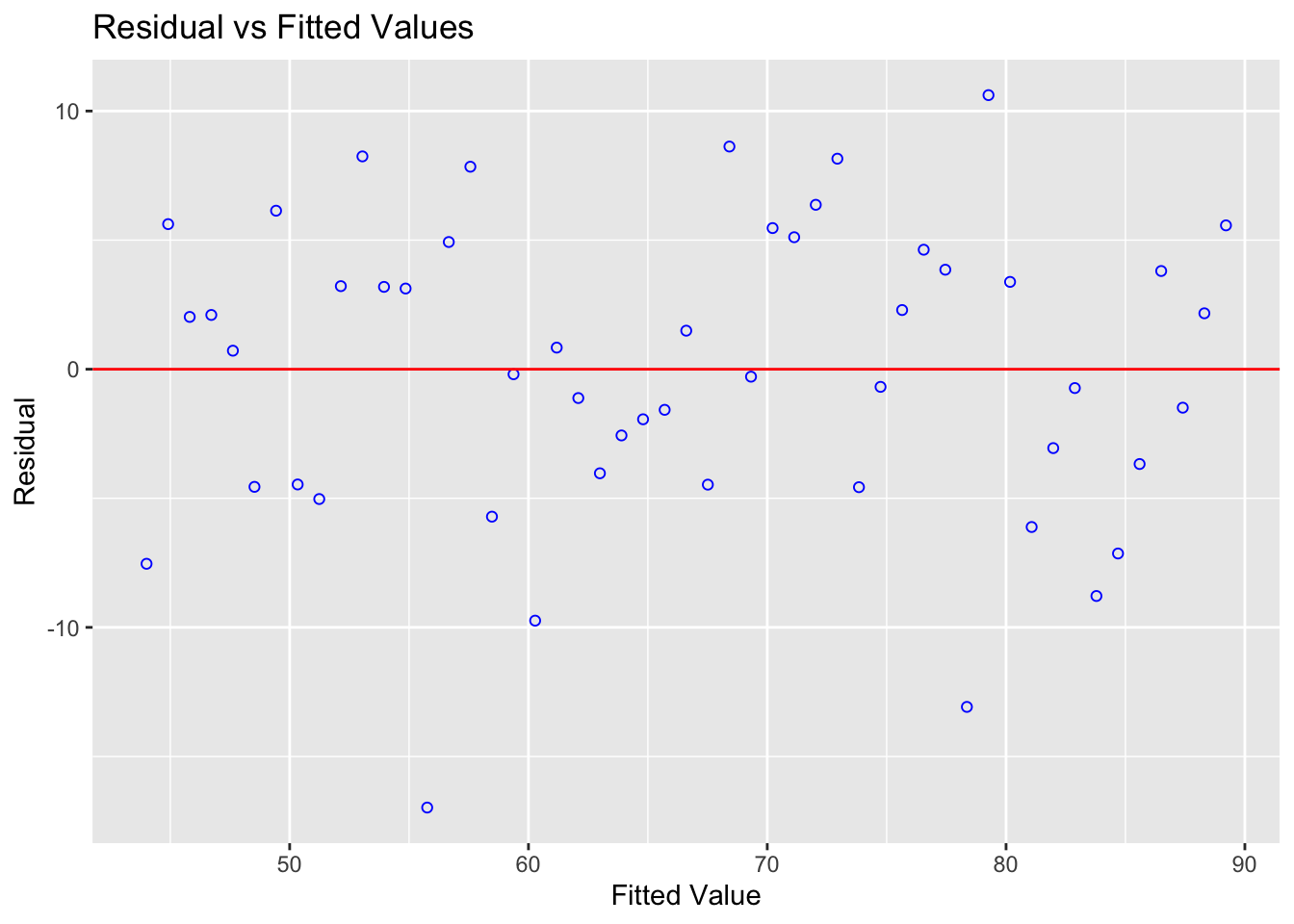
Figure 2.13: Residuals vs. Fitted

Le test RESET renforce ce constat (p-values > 0.7 pour les dépendances quadratique et cubique), donc on peut considérer au seuil de significativité de 5% que le modèle linéaire est approprié pour décrire la dépendance entre la température et le rendement.

    RESET test

data:  mdlLR
RESET = 0.053848, df1 = 1, df2 = 48, p-value = 0.8175

    RESET test

data:  mdlLR
RESET = 0.076484, df1 = 1, df2 = 48, p-value = 0.7833

Conclusion: sur la base des vérifications visuelles (graphiques) et numériques (tests), on peut considérer que le modèle linéaire est tout à fait approprié pour décrire la relation établie entre la température et le rendement.

Vérifier que les résidus sont i.i.d. \(N(0,\sigma^2)\): on commence, tout d’abord par vérifier que les résidus suivent une loi normale. Visuellement, on constate que les résidus semblent distribués selon une loi normale: points alignés approximativement selon une droite sur le graphique Q-Q (voir la figure 2.14); histogramme en accord avec la courbe en cloche de Gauss (voir la figure 2.15); boîte à moustache des résidus qui n’est pas en désacord avec l’hypothèse de loi normale pour les résidus (voir la figure @ref(fig: grBOXres)).

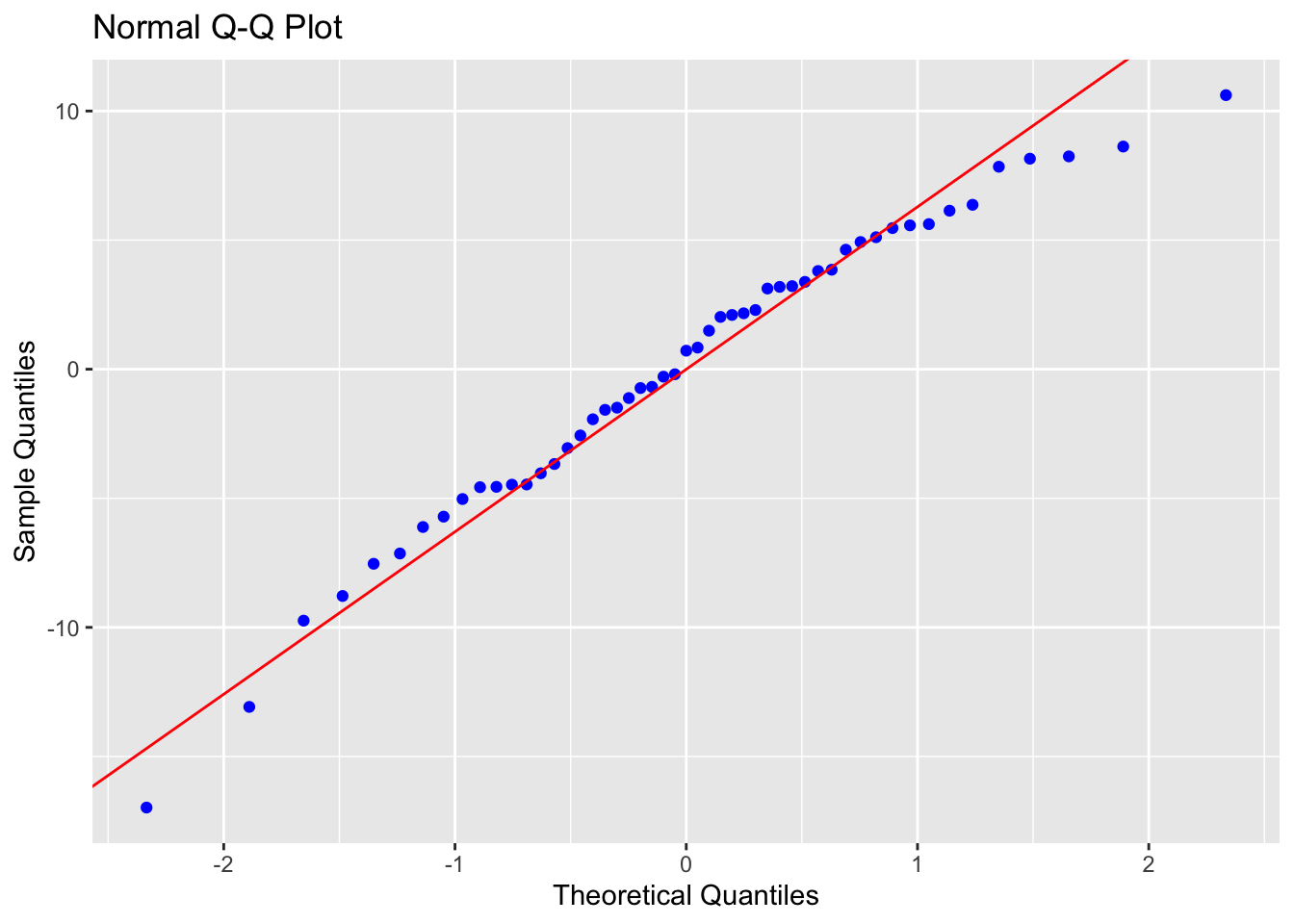
Figure 2.14: Graphique de normalité Q-Q pour la distribution des résidus

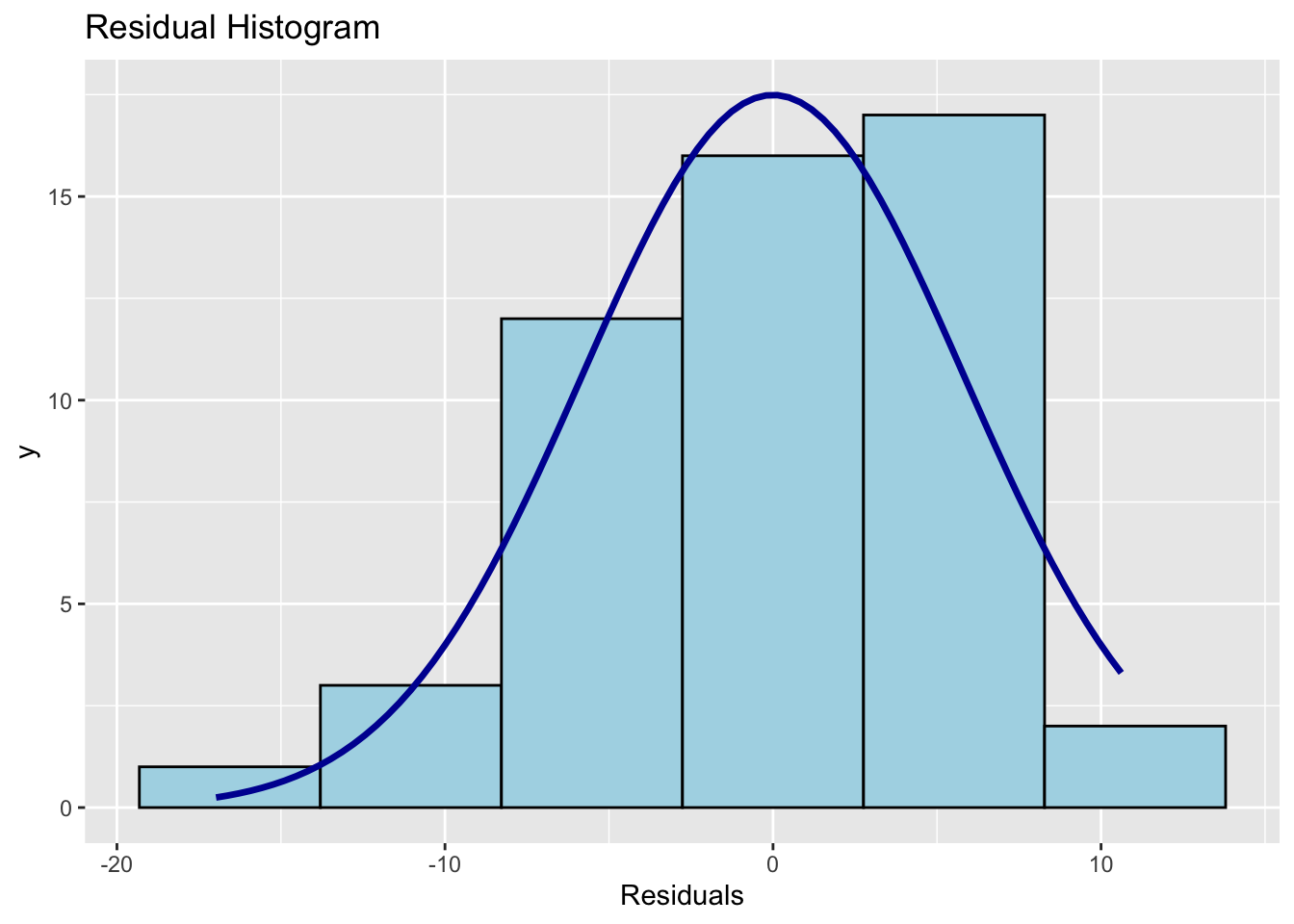
Figure 2.15: Histogramme des résidus

Figure 2.16: Histogramme des résidus

Toutefois, un test numérique permet de trancher à ce sujet sans aucune subjectivité. On constate que la p-value du test de Shapiro-Wilk est de 0.3197 > 0.05, donc au seuil de significativité de 5% on peut considérer que les résidus du modèle de régression linéaire sont distribués selon la loi normale.

    Shapiro-Wilk normality test

data:  mdlLR$residuals
W = 0.97393, p-value = 0.3197

On continue par tester l’hypothèse selon laquelle la moyenne des résidus est nulle. La p-value du test de Student étant de 1 > 0.05, on peut considérer au seuil de significativité de 5% que la moyenne des résidus est nulle.

    One Sample t-test

data:  mdlLR$residuals
t = 2.1469e-17, df = 50, p-value = 1
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 -1.635647  1.635647
sample estimates:
   mean of x 
1.748329e-17 

Remarque: On arrive à la même conclusion sur la base de l’intervalle de confiance à 95% pour la moyenne des résidus. Comme on peut le constater, zéro est dans l’intervalle, donc on ne peut pas rejeter l’hypothèse selon laquelle la moyenne des résidus soit nulle et ceci au seuil de signification de 5%.

On teste que la variance des résidus soit homogène: visuellement (voir la figure ??) on constate sur le graphique des résidus standardisés en fonction des valeurs attendues que l’on obtient un arrangement des résidus autour d’une droite à peu près horizontale, ce qui indique que l’hypothèse d’homogéneité de la variance des résidus est vraisemeblablement vraie.

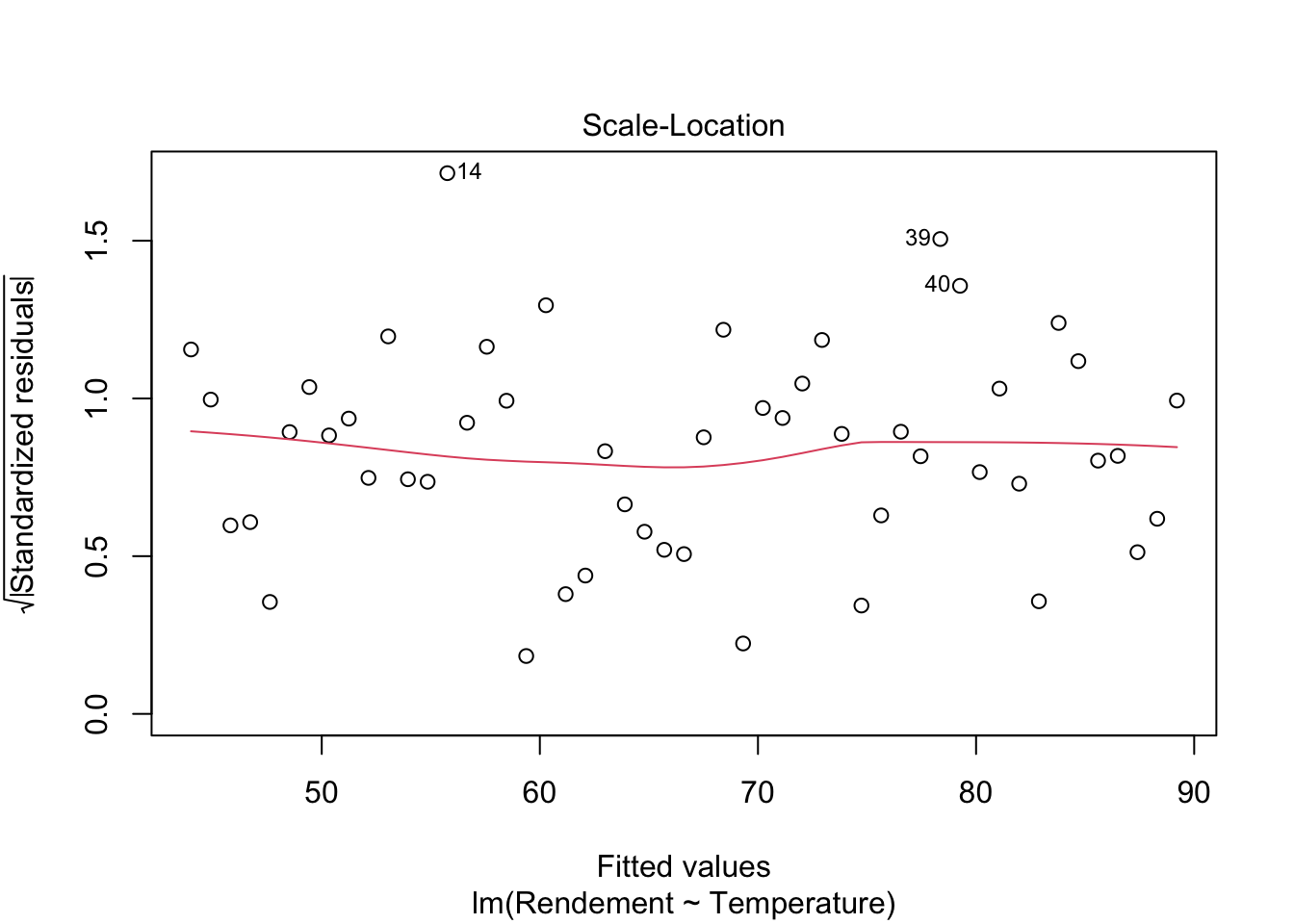
Figure 2.17: Graphique des résidus standardisés selon les valeurs attendues

On complète cette inspection visuelle par le test de Breush-Pagan:

    studentized Breusch-Pagan test

data:  mdlLR
BP = 0.01488, df = 1, p-value = 0.9029

Selon ce test, on constate qu’au seuil de significativité de 5%, l’hypothèse d’homogéneité de la variance des résidus ne peut pas être rejetée (p-value = 0.9029).

Enfin, on teste l’indépendance des résidus selon le test de Durbin-Watson:

    Durbin-Watson test

data:  mdlLR
DW = 2.1325, p-value = 0.7425
alternative hypothesis: true autocorrelation is not 0

On constate qu’au seuil de significativité de 5%, l’hypothèse d’indépendance des résidus ne peut pas être rejetée (p-value = 0.7425).

Conclusion: sur la base des vérifications visuelles (graphiques) et numériques (tests), on peut considérer que les résidus du modèle de régression linéaire reliant le rendement à la température sont indépendants et identiquement distribués selon une loi normale de moyenne nulle et de variance constante. Ceci constitue un argument important pour valider ce modèle.

Toutefois, avant de conclure à une validation de ce modèle, il est judicieux de vérifier qu’il n’y a pas des points influents sur la droite de régression. Pour cela, on identifie les éventuels points leviers:

      Temperature Rendement   Leverage
 [1,]         100     36.47 0.07616893
 [2,]         102     50.53 0.07173454
 [3,]         104     47.84 0.06748115
 [4,]         106     48.82 0.06340875
 [5,]         108     48.34 0.05951735
 [6,]         110     43.97 0.05580694
 [7,]         112     55.57 0.05227753
 [8,]         114     45.87 0.04892911
 [9,]         116     46.21 0.04576169
[10,]         118     55.36 0.04277526
[11,]         120     61.29 0.03996983
[12,]         122     57.14 0.03734540
[13,]         124     57.98 0.03490196
[14,]         126     38.78 0.03263952
[15,]         128     61.59 0.03055807
[16,]         130     65.41 0.02865762
[17,]         132     52.76 0.02693816
[18,]         134     59.18 0.02539970
[19,]         136     50.54 0.02404223
[20,]         138     62.02 0.02286576
[21,]         140     60.97 0.02187029
[22,]         142     58.96 0.02105581
[23,]         144     61.33 0.02042232
[24,]         146     62.86 0.01996983
[25,]         148     64.13 0.01969834
[26,]         150     68.10 0.01960784
[27,]         152     63.04 0.01969834
[28,]         154     77.04 0.01996983
[29,]         156     69.03 0.02042232
[30,]         158     75.69 0.02105581
[31,]         160     76.24 0.02187029
[32,]         162     78.40 0.02286576
[33,]         164     81.09 0.02404223
[34,]         166     69.27 0.02539970
[35,]         168     74.06 0.02693816
[36,]         170     77.94 0.02865762
[37,]         172     81.18 0.03055807
[38,]         174     81.31 0.03263952
[39,]         176     65.28 0.03490196
[40,]         178     89.88 0.03734540
[41,]         180     83.55 0.03996983
[42,]         182     74.96 0.04277526
[43,]         184     78.92 0.04576169
[44,]         186     82.15 0.04892911
[45,]         188     75.00 0.05227753
[46,]         190     77.55 0.05580694
[47,]         192     81.92 0.05951735
[48,]         194     90.30 0.06340875
[49,]         196     85.91 0.06748115
[50,]         198     90.47 0.07173454
[51,]         200     94.78 0.07616893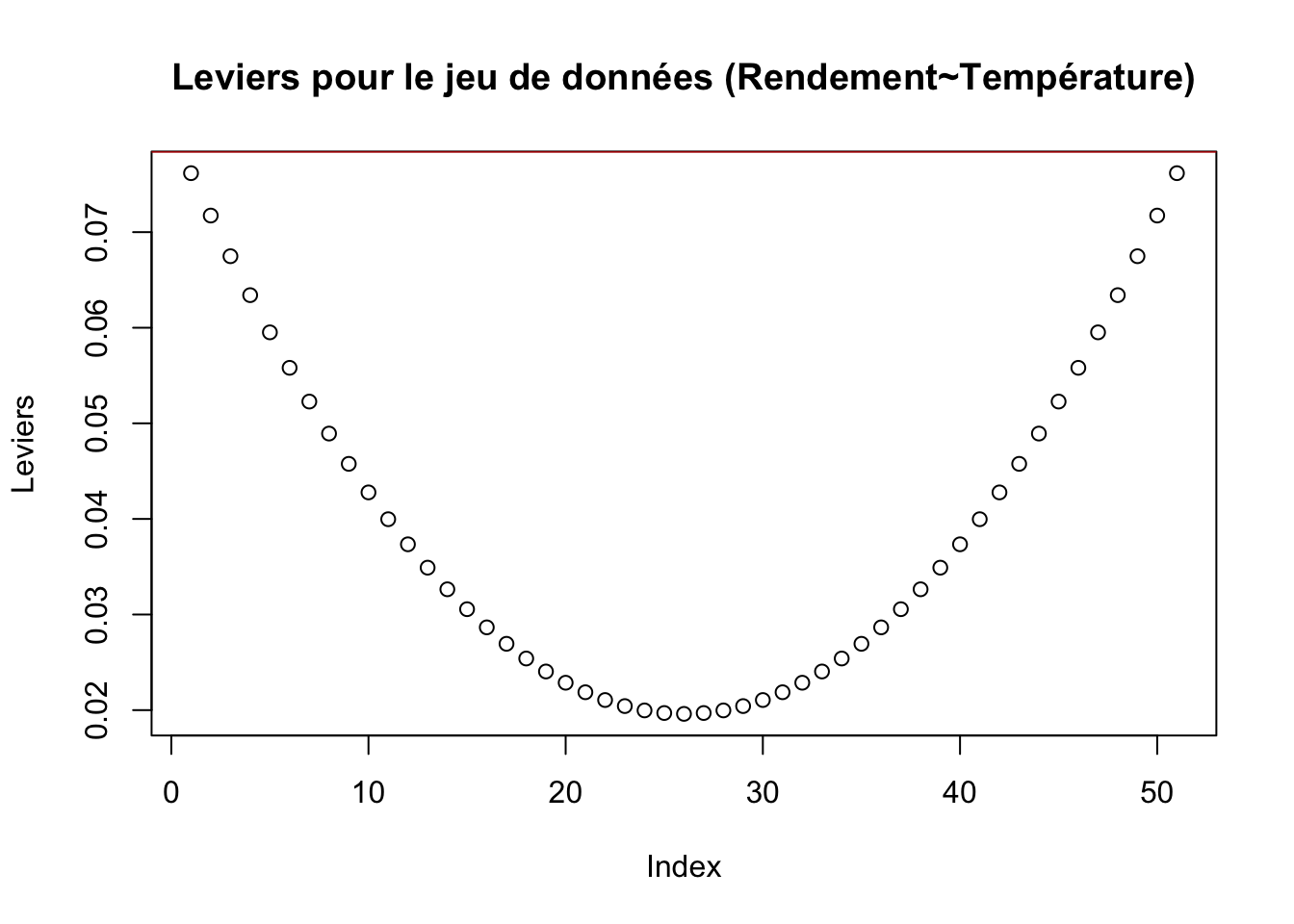

Figure 2.18: Graphique des leviers du modèle (Rendement~Température)

Comme aucun levier n’est significatif (ne dépasse pas la limite en rouge sur la figure 2.18), il n’y a visiblement pas de points leviers dans ce jeu de données.

On continue par l’identification des éventuels points atypiques:

   Temperature Rendement     Std.Res    Stud.Res
1          100     36.47 -1.33473109 -1.34573124
2          102     50.53  0.99285279  0.99270552
3          104     47.84  0.35704160  0.35384011
4          106     48.82  0.36962537  0.36634532
5          108     48.34  0.12592152  0.12465015
6          110     43.97 -0.79824945 -0.79524974
7          112     55.57  1.07349884  1.07520709
8          114     45.87 -0.77931330 -0.77614508
9          116     46.21 -0.87630768 -0.87419681
10         118     55.36  0.55974748  0.55578609
11         120     61.29  1.43210047  1.44803989
12         122     57.14  0.55329494  0.54933869
13         124     57.98  0.54149754  0.53755437
14         126     38.78 -2.93859794 -3.20449970
15         128     61.59  0.85181138  0.84938686
16         130     65.41  1.35461550  1.36655358
17         132     52.76 -0.98553466 -0.98523994
18         134     59.18 -0.03364644 -0.03330172
19         136     50.54 -1.67814488 -1.71082308
20         138     62.02  0.14409908  0.14265133
21         140     60.97 -0.19229845 -0.19039797
22         142     58.96 -0.69356661 -0.68984740
23         144     61.33 -0.44121166 -0.43755632
24         146     62.86 -0.33347568 -0.33043050
25         148     64.13 -0.27051122 -0.26793681
26         150     68.10  0.25659702  0.25413599
27         152     63.04 -0.76876817 -0.76551371
28         154     77.04  1.48298098  1.50186091
29         156     69.03 -0.04980325 -0.04929368
30         158     75.69  0.94046913  0.93933949
31         160     76.24  0.87992421  0.87786243
32         162     78.40  1.09665496  1.09897731
33         164     81.09  1.40505236  1.41953107
34         166     69.27 -0.78795959 -0.78486612
35         168     74.06 -0.11800156 -0.11680785
36         170     77.94  0.39589493  0.39246254
37         172     81.18  0.80013964  0.79715773
38         174     81.31  0.66703478  0.66321117
39         176     65.28 -2.26643832 -2.37090462
40         178     89.88  1.84182447  1.88951287
41         180     83.55  0.58755413  0.58358718
42         182     74.96 -1.06342182 -1.06487443
43         184     78.92 -0.53255691 -0.52862673
44         186     82.15 -0.12744978 -0.12616349
45         188     75.00 -1.53597773 -1.55819810
46         190     77.55 -1.25050119 -1.25791000
47         192     81.92 -0.64459089 -0.64070173
48         194     90.30  0.66903840  0.66522164
49         196     85.91 -0.26271646 -0.26020518
50         198     90.47  0.38261654  0.37925913
51         200     94.78  0.98674048  0.98646982

Selon le graphique des résidus standardisés (voir la figure 2.19), les points n°14 er n°39 semblent être les plus éloignés de la droite de régression (en déhors de l’intervalle [-2,2] qui définit un point non-atypique).

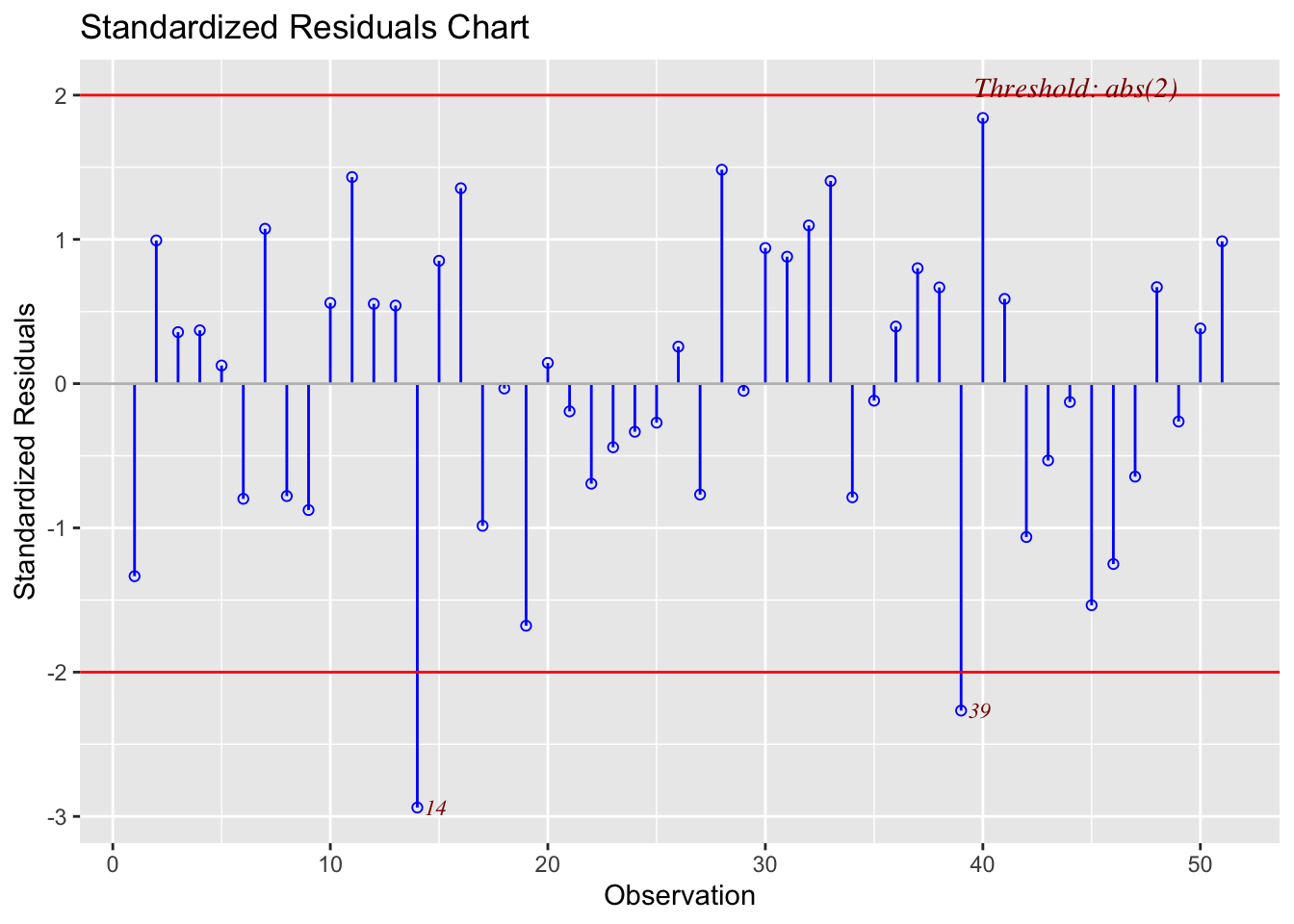
Figure 2.19: Graphique des résidus standardisés

Le point n°14 présente également un résidu studentisé significatif (en déhors de l’intervalle [-3,3]) - voir la figure 2.20. Par conséquent, on peut suspecter le point n°14 comme étant atypique pour le modèle de régression reliant le rendement à la température.

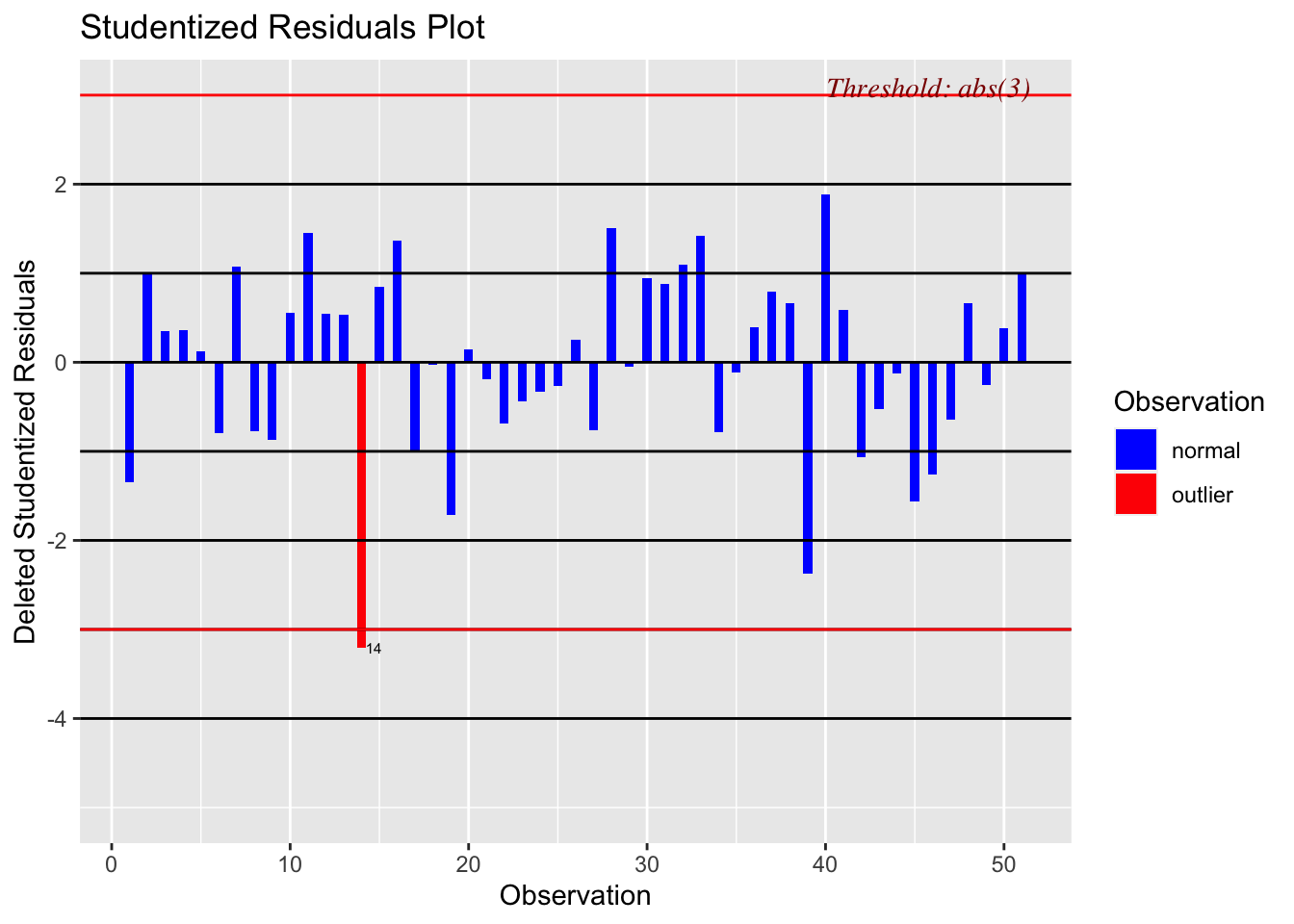
Figure 2.20: Graphique des résidus studentisés

Toutefois, selon le test de Bonferroni, le point n°14 n’est pas atypique (p-value = 0.12271), donc, au final, on peut conclure qu’il n’y a pas de point atypique dans ce jeu de données.

No Studentized residuals with Bonferroni p < 0.05
Largest |rstudent|:
   rstudent unadjusted p-value Bonferroni p
14  -3.2045           0.002406      0.12271

L’absence des points leviers et de points atypiques nous permettrait de conclure qu’il n’y a pas de points influents non plus dans ce jeu de données. Toutefois, ci-dessous on fait les vérifications de rigueur afin de nous imprégner du formalisme.

Le graphique des résidus selon les leviers (voir la figure 2.21) confirme les constats réalisés précédement: il n’y a pas de points leviers; les points n°14 et n°39 s’éloignent le plus par rapport à la droite de régression (sans toutefois qu’ils soient des points atypiques selon le test de Bonferroni).

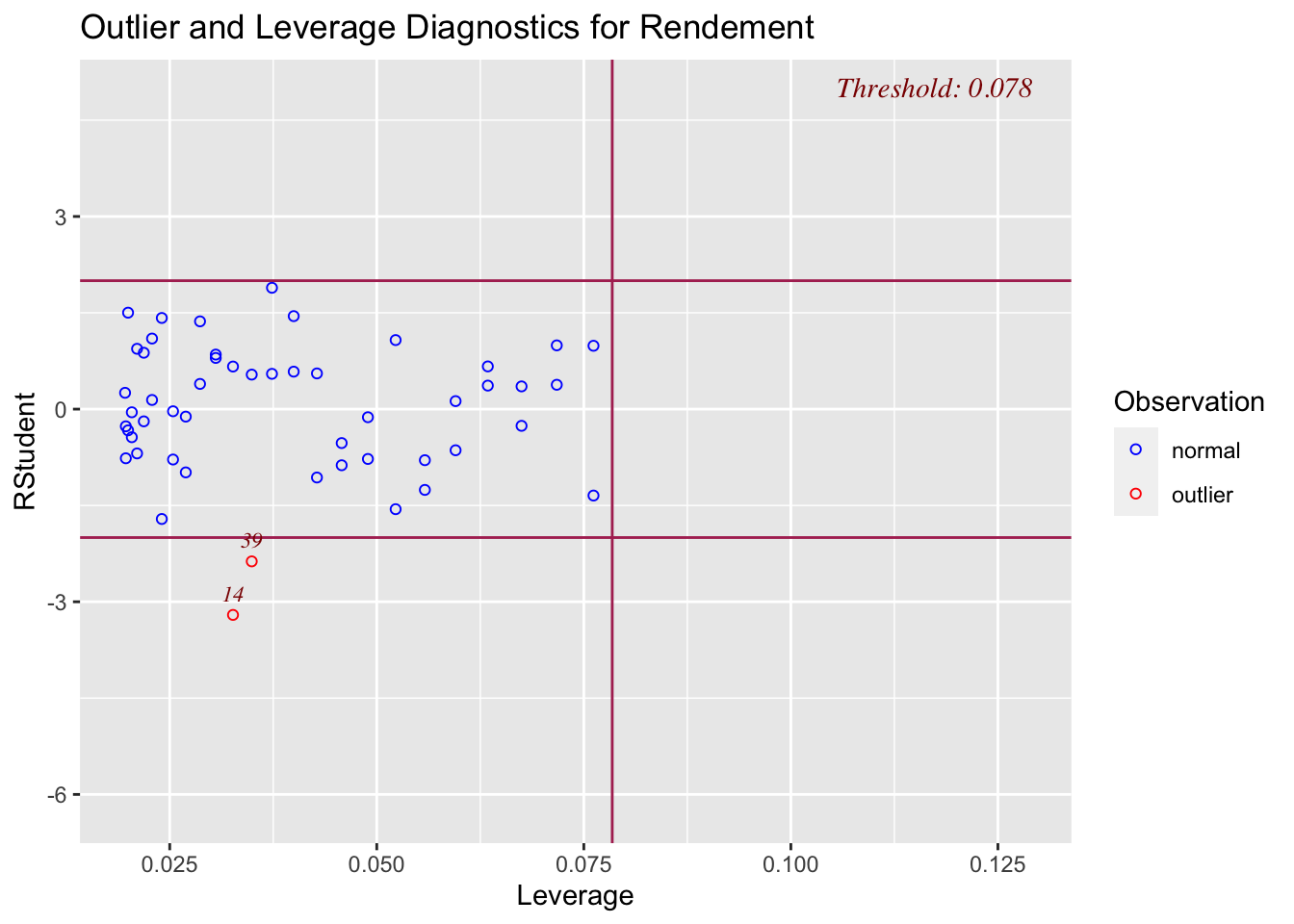
Figure 2.21: Graphique des résidus selon les leviers

Même conclusion sur le graphique des distances de Cook (voir la figure 2.22), ou les points n°14 et n°39 apparaissent comme ayant des distances de Cook significatives (car ils ont des résidus plus grands que les autres points).

   Temperature Rendement    dist.Cook
1          100     36.47 7.344172e-02
2          102     50.53 3.808867e-02
3          104     47.84 4.612459e-03
4          106     48.82 4.624797e-03
5          108     48.34 5.017214e-04
6          110     43.97 1.883105e-02
7          112     55.57 3.178389e-02
8          114     45.87 1.562243e-02
9          116     46.21 1.841316e-02
10         118     55.36 7.000565e-03
11         120     61.29 4.269376e-02
12         122     57.14 5.938134e-03
13         124     57.98 5.302020e-03
14         126     38.78 1.456819e-01
15         128     61.59 1.143565e-02
16         130     65.41 2.706885e-02
17         132     52.76 1.344440e-02
18         134     59.18 1.475198e-05
19         136     50.54 3.468747e-02
20         138     62.02 2.429539e-04
21         140     60.97 4.134087e-04
22         142     58.96 5.173212e-03
23         144     61.33 2.029225e-03
24         146     62.86 1.133009e-03
25         148     64.13 7.352084e-04
26         150     68.10 6.584203e-04
27         152     63.04 5.937870e-03
28         154     77.04 2.240661e-02
29         156     69.03 2.585542e-05
30         158     75.69 9.512026e-03
31         160     76.24 8.656026e-03
32         162     78.40 1.407153e-02
33         164     81.09 2.431637e-02
34         166     69.27 8.090585e-03
35         168     74.06 1.927405e-04
36         170     77.94 2.312052e-03
37         172     81.18 1.009034e-02
38         174     81.31 7.506238e-03
39         176     65.28 9.288299e-02
40         178     89.88 6.580109e-02
41         180     83.55 7.186431e-03
42         182     74.96 2.526736e-02
43         184     78.92 6.800600e-03
44         186     82.15 4.178329e-04
45         188     75.00 6.506893e-02
46         190     77.55 4.621315e-02
47         192     81.92 1.314713e-02
48         194     90.30 1.515204e-02
49         196     85.91 2.497292e-03
50         198     90.47 5.656576e-03
51         200     94.78 4.013850e-02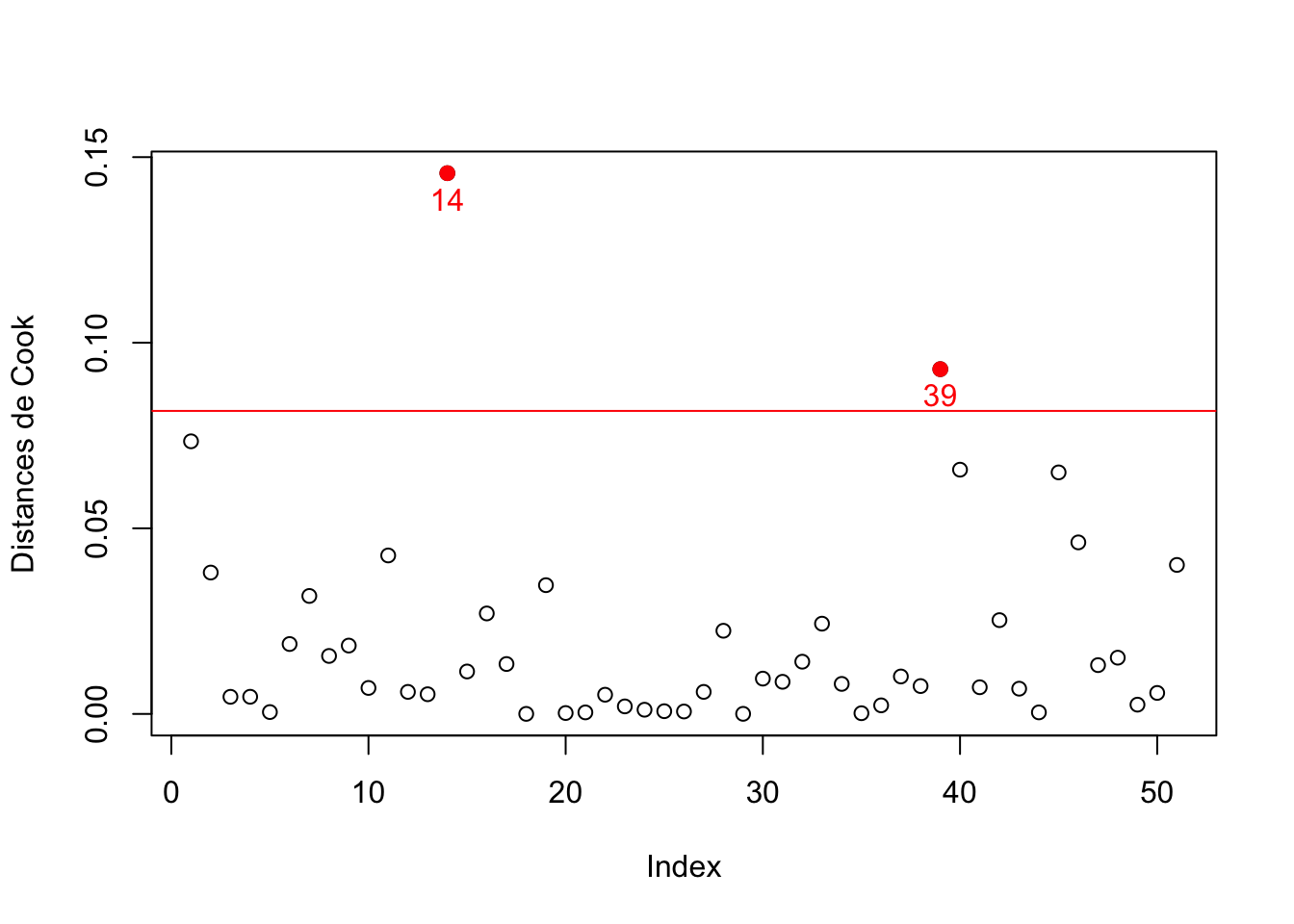

Figure 2.22: Graphique des distances de Cook

Enfin, la représentation des résidus standardisés selon les leviers (avec les limites pour les distances de Cook superposées), enlève tout supçon concernant une éventuelle influence des points n°14 et n°39 sur la droite de régression. En effet, on constate (voir la figure 2.23) que ces points n’influent pas de manière significative sur la droite de régression (pas de dépassement des limites en rouge pour les distances de Cook selon les leviers).

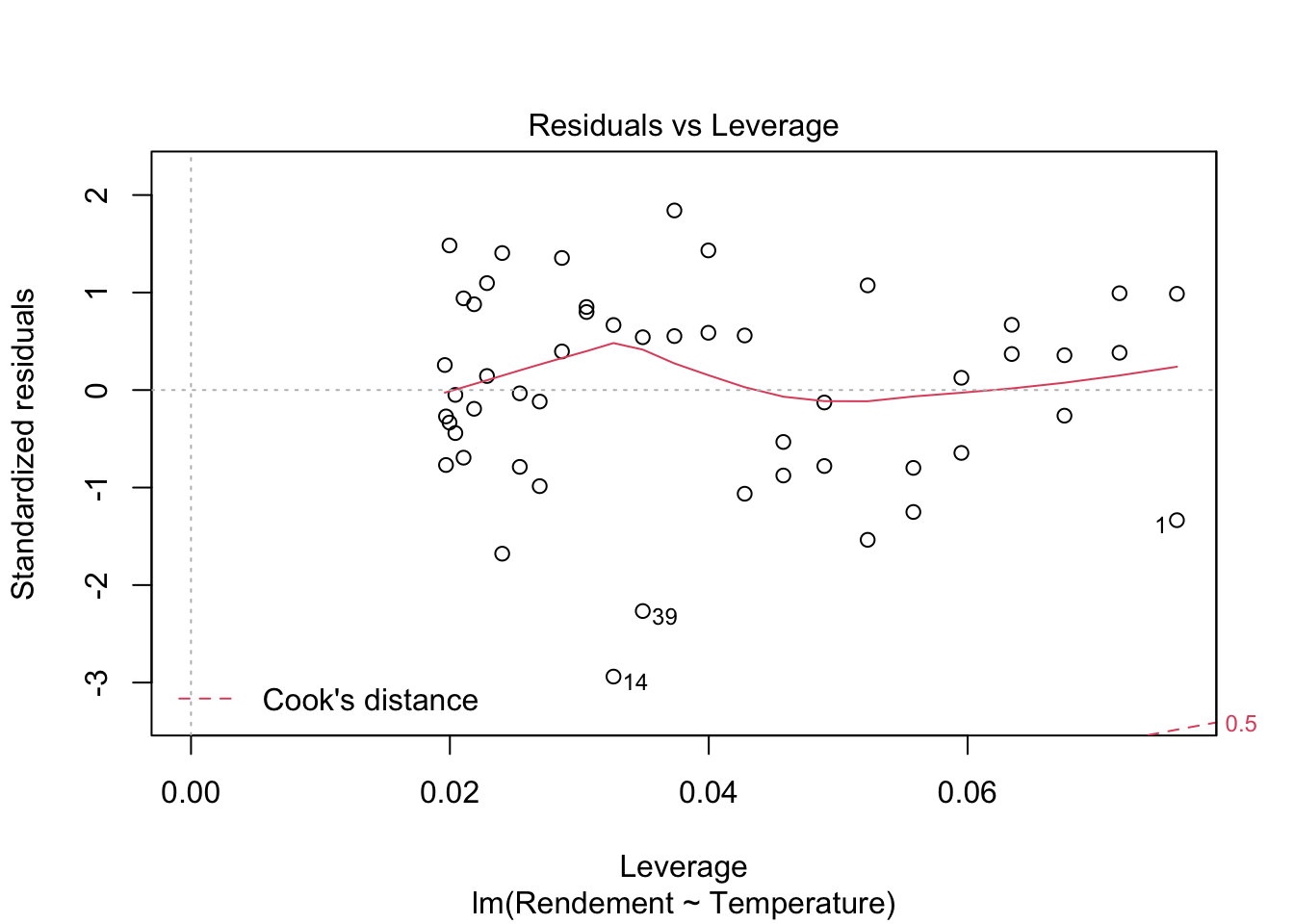
Figure 2.23: Graphique des résidus standardisés selon les leviers (avec les limites pour les distances de Cook superposées)

En réunissant les différents indicateurs précédemment abordés, le tableau de bord pour le diagnostic des éventuels points influents (voir la figure 2.24) confirme que le point n°14 ne peut pas être considéré comme un point influent (il n’est pas atypique selon le test de Bonferroni, il n’a pas un levier trop important ni une dsitance de Cook significative).

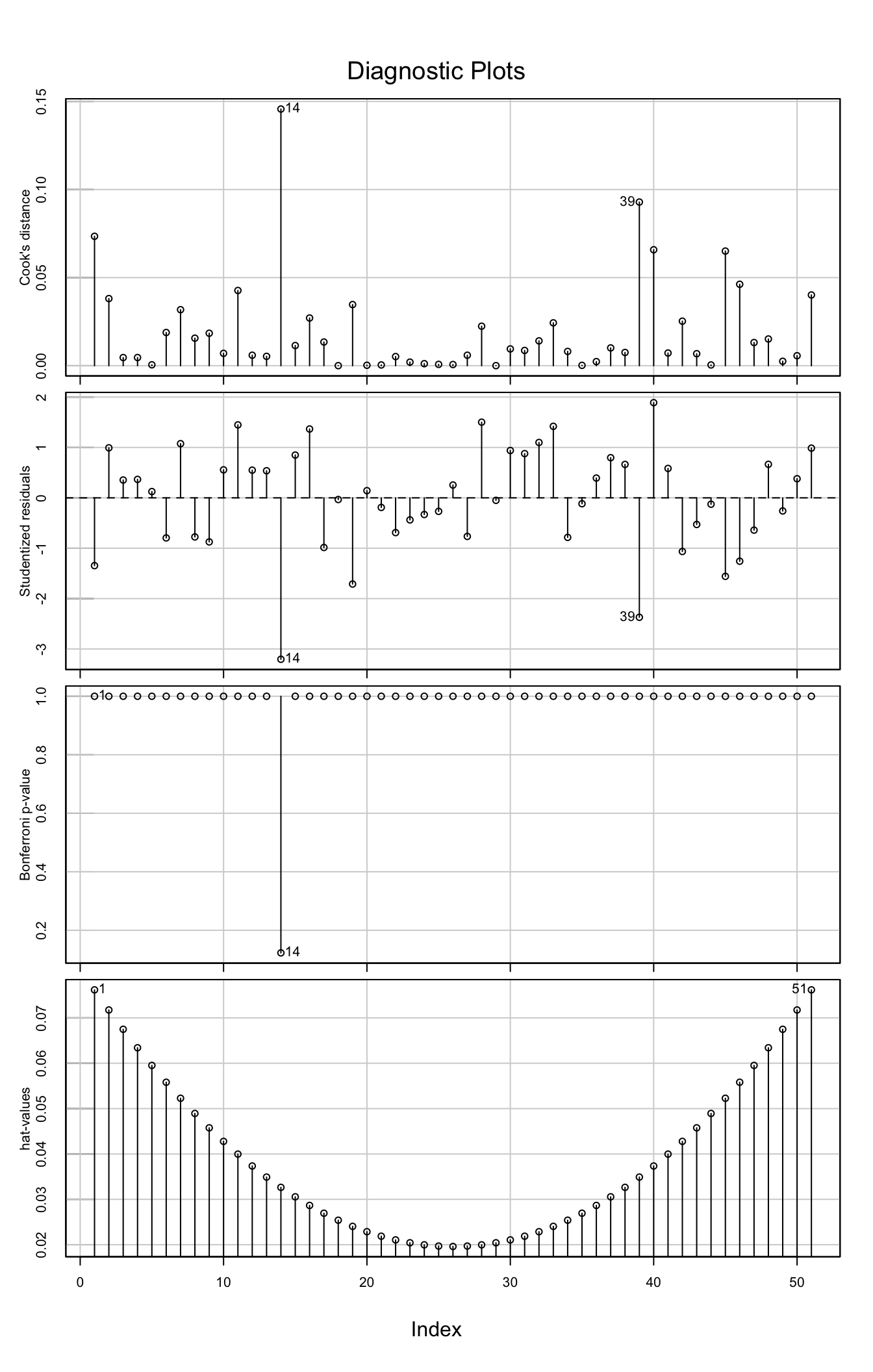
Figure 2.24: Tableau de bord pour le diagnostic

Conclusion: il n’y a pas de points atypiques, leviers ou influents dans le jeu de données.

Conclusion générale: Au vu des différentes vérifications réalisés ci-dessus, on peut valider le modèle de régression linéaire caractérisant la relation entre le rendement et la température identifié au chapitre précédent.