Chapitre3 Transformations

Objectif du chapitre: Dans ce chapitre on présente des approches qui peuvent être utilisées lorsque la variance des résidus n’est pas homogène. On montre également comment résoudre des problèmes dues à la non-linéarité de la rélation entre les deux variables du modèle.

3.1 Transformations pour stabiliser la variance des résidus

Dans ce paragraphe on se place dans le contexte où la variance des résidus n’est pas homogène. On a vu dans le chapitre 2 que l’homogénéité des résidus peut être testée à l’aide du test de Breush-Pagan et visualisée à l’aide du graphique des résidus standardisés selon les valeurs approchées (voir le paragraphe 2.3.3).

L’exemple ci-dessous, basé sur le jeu de données trees, illustre cette situation où l’homoscédasticité des résidus n’est pas respectée:

# Ouverture du fichier de données
#================================
data("trees")
attach(trees)
head(trees)  
  Girth Height Volume
1   8.3     70   10.3
2   8.6     65   10.3
3   8.8     63   10.2
4  10.5     72   16.4
5  10.7     81   18.8
6  10.8     83   19.7

Il s’agit d’un fichier de données dans lequel on trouve trois colonnes de type numérique: Girth (circonférence), Height (hauteur), Volume (volume) caractérisant des arbres dans une forêt. On se propose, dans cet exemple, de déduire le volume de bois à partir de la hauteur de l’arbre. Pour cela, on construit un modèle de régression linéaire reliant ces deux variables:

# Construction du modèle de régression linéaire
#==============================================
mdlLR<-lm(Volume~Height, data = trees)

# Affichage graphique
#====================
par(mfrow=c(1,2))
plot(Height, Volume)         #graphique Volume~Height
abline(mdlLR, col="red")     #droite de régression
plot(mdlLR, which = 3)       #graphique "Scale-Location"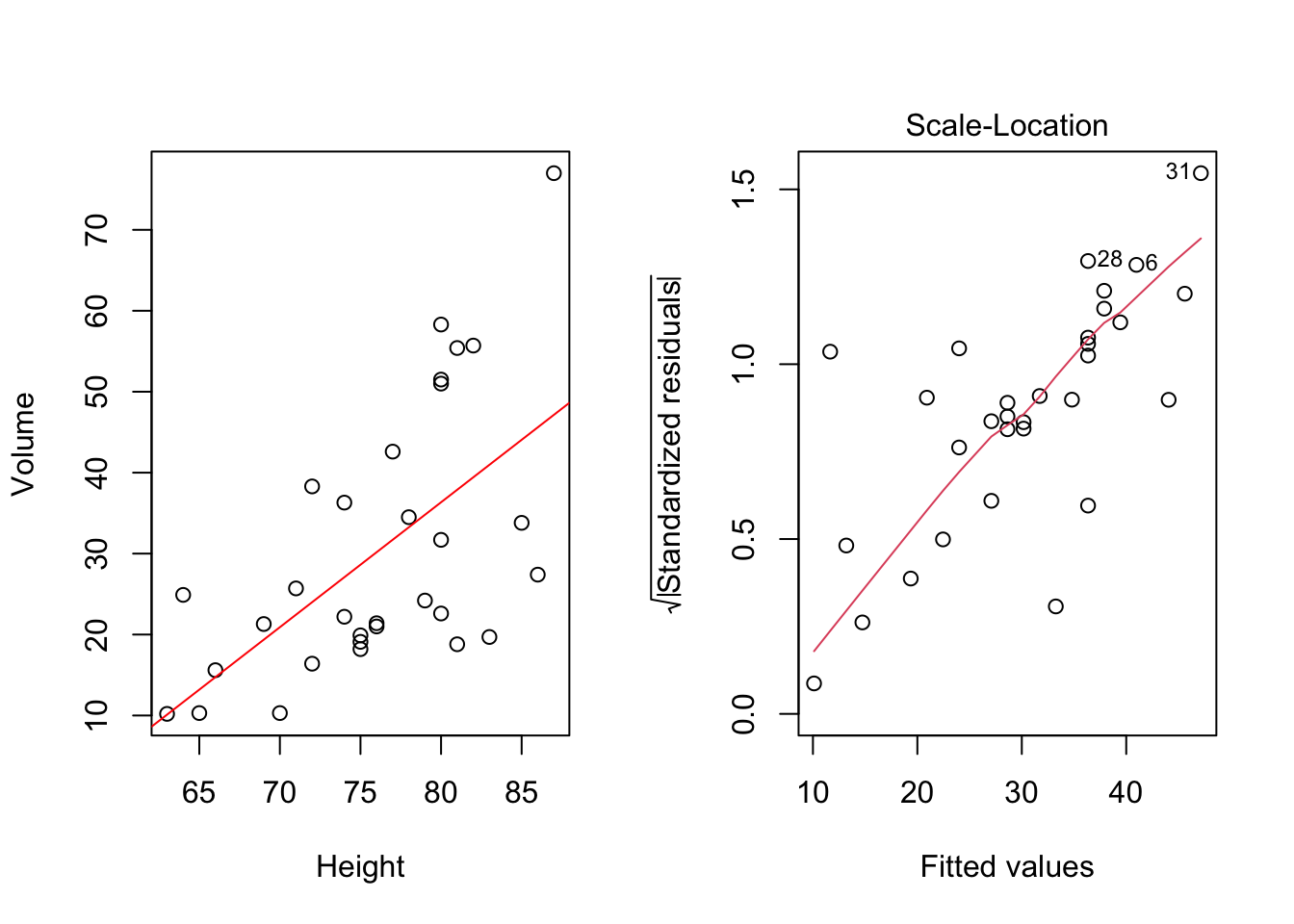

Figure 3.1: Modèle régressif linéaire Volume~Height

On voit assez bien dans la figure 3.1 que la dispersion des points autour de la droite de régression tend à augmenter au fur et à mesure que la hauteur des arbres augmente. Lorsque l’on s’attache à valider ce modèle, on constate sur le graphique des résidus standardisés selon les valeurs approchées (“Scale-Location”) que la variance des résidus n’est pas homogène car on a une claire tendance croissante dans la moyenne des résidus standardisés (ligne rouge), ce qui traduit une dispersion plus importante du volume de bois lorsque la hauteur des arbres augmente. En effet, au seuil de signification de 5%, le test de Breush-Pagan rejette l’hypothèse d’homogéneité de la dispersion des résidus:

# Test de Breush-Pagan
#=====================
bptest(mdlLR)

    studentized Breusch-Pagan test

data:  mdlLR
BP = 12.207, df = 1, p-value = 0.0004762

Par conséquent, on ne peut pas accepter ce modèle de régression linéaire et il faut trouver une manière de stabiliser la variance des résidus. Diverses transformations des variables existent et on s’attache dans ce chapitre à les passer en revue. Pour cet exemple, une transformation logarithmique des deux variables, permet de résoudre le problème (voir la figure 3.2).

# Construction du modèle de régression linéaire
#==============================================
mdlLR1<-lm(log(Volume)~log(Height), data = trees)

# Affichage graphique
#====================
par(mfrow=c(1,2))
plot(log(Height), log(Volume))   #graphique log(Volume)~log(Height)
abline(mdlLR1, col="red")         #droite de régression
plot(mdlLR1, which = 3)           #graphique "Scale-Location"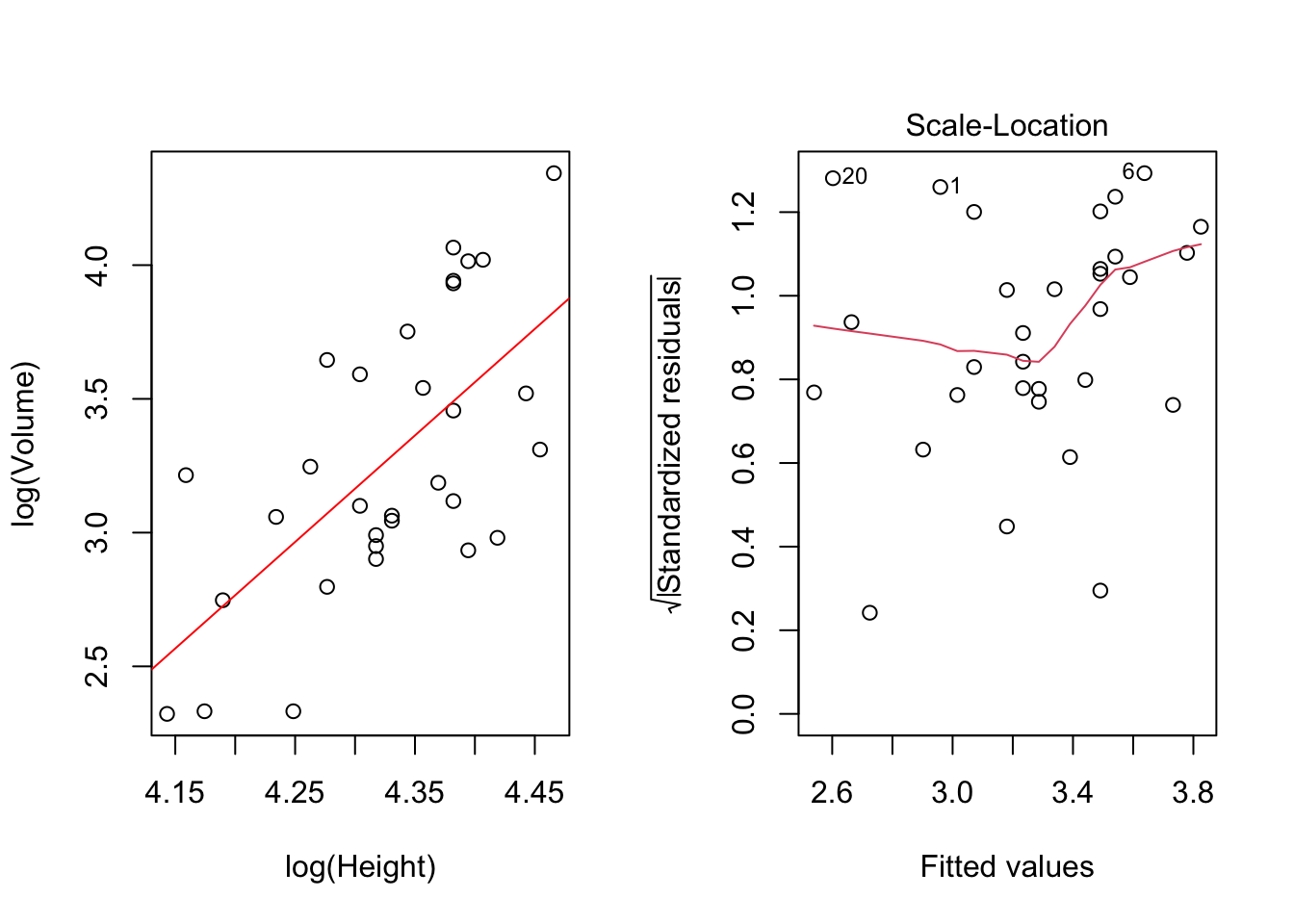

Figure 3.2: Modèle régressif linéaire log(Volume)~log(Height)

# Test de Breush-Pagan
#=====================
bptest(mdlLR1)

    studentized Breusch-Pagan test

data:  mdlLR1
BP = 1.2172, df = 1, p-value = 0.2699

On remarque, autant dans la figure 3.2 que dans le résultat du test de Breush-Pagan qu’après avoir utilisé le logarithme, le problème de dispersion non-homogène des résidus a été résolu.

Pour mieux se rendre compte de l’importance de stabiliser la variance des résidus avant d’utiliser un modèle régressif pour faire des prédictions, ci-dessous on montre les résultats des prédictions avec les deux modèles (sans logarithme et avec logarithme pour les variables):

# Prédictions avec le modèle Volume~Hauteur
#==========================================
# valeur prédite et intervalle de confiance à 95% pour deux valeurs de Hauteur: 65 et 85
predict(mdlLR, newdata = list(Height=c(65, 85)), interval = "prediction")
       fit       lwr      upr
1 13.19412 -15.95301 42.34125
2 44.06112  15.34005 72.78218

# Prédictions avec le modèle log(Volume)~log(Hauteur)
#====================================================
# valeur prédite et intervalle de confiance à 95% pour deux valeurs de Hauteur: 65 et 85
exp(predict(mdlLR1, newdata = list(Height=c(65, 85)), interval = "prediction"))   
       fit       lwr      upr
1 14.35489  5.901271 34.91841
2 41.77677 17.485680 99.81300

Remarques: On constate que le volume de bois prédit par le modèle lorsque les variables ne sont pas transformées est inférieur à la valeur prédite par le modèle avec les variables transformées par une transformation logarithmique (13.19412 vs. 14.35489) dans le cas d’un arbre de petite hauteur (65) et que l’intervalle de confiance à 95% est plus large. Au contraire, pour un arbre de grande hauteur (85), le modèle sans variables transformées prédit un volume plus grand que celui prédit par le modèle avec les variables transformées par une transformation logarithmique (44.06112 vs. 41.77677) et l’intervalle de confiance à 95% est plus étroit.

On peut affirmer donc que lorsque l’on ignore la variance non-homogène des résidus, on commet des erreur de prédiction qui peuvent s’avérer très significatives selon le cas.

Dans d’autres situations, au lieu de transformer les variables par une transformation logarithmique, il convient mieux d’utiliser la racine carrée. C’est par exemple le cas des données issues des processus de comptage comme illustré dans l’exemple suivant proposé par Foster, Stine et Waterman¹⁰:

Exemple 3.1 (Élaboration d'une offre de nettoyage contractuel) Une entreprise d’entretien d’immeubles envisage de soumettre une offre pour un contrat de nettoyage de bureaux d’entreprise dispersés dans un complexe de bureaux. Les coûts supportés par l’entreprise de maintenance sont proportionnels au nombre d’équipes de nettoyage nécessaires à cette tâche. Des données récentes sont disponibles sur le nombre de pièces qui ont été nettoyées par un nombre variable d’équipes. Pour un échantillon de 53 jours, des registres ont été conservés sur le nombre d’équipes utilisées et le nombre de pièces nettoyées par ces équipes - voir le fichier Nettoyage.xlsx dans le répertoire Base de données dans Moodle. On veut développer un modèle de régression linéaire pour prédire le nombre de chambres pouvant être nettoyées par 4 équipes et par 16 équipes.

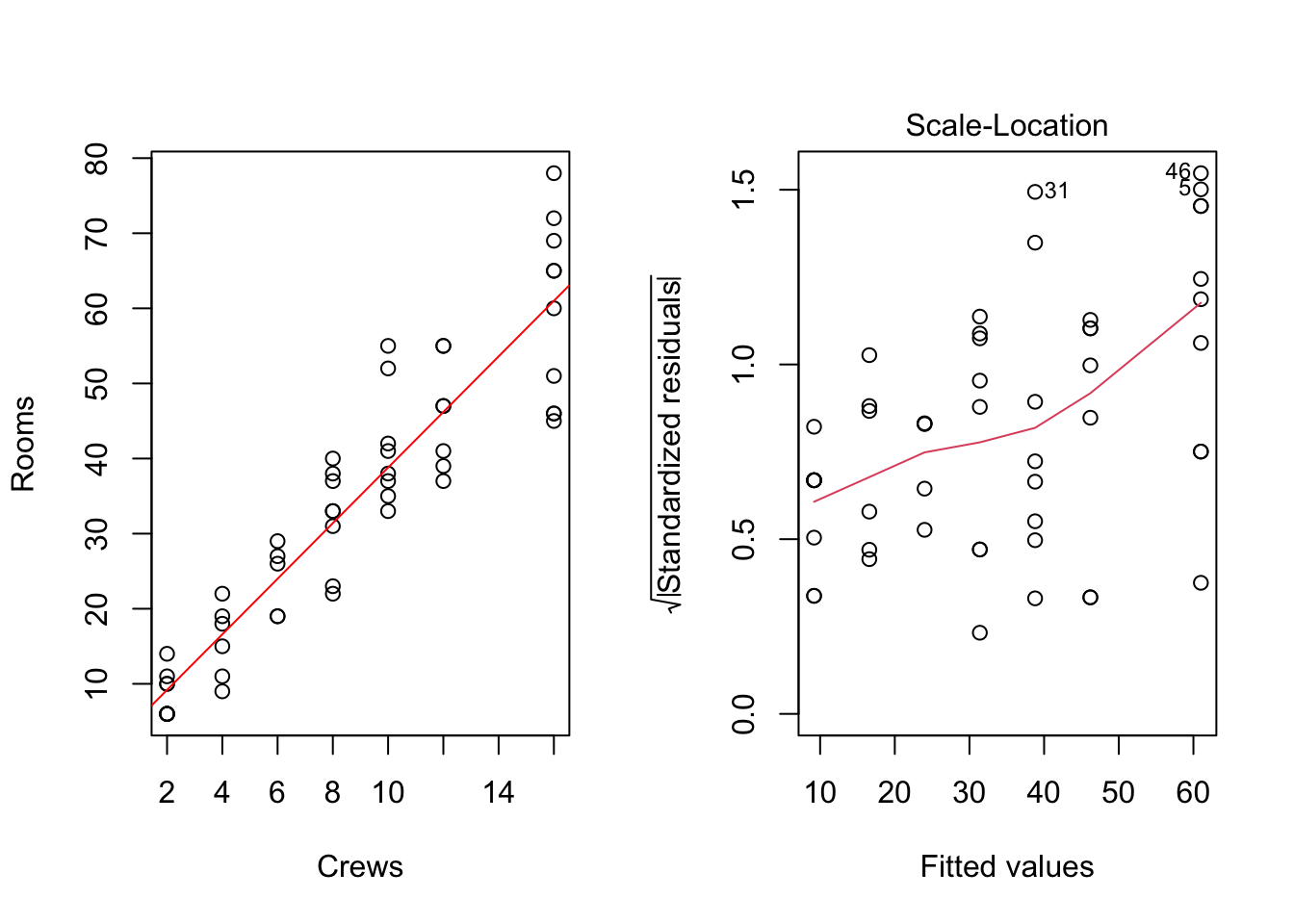
Figure 3.3: Modèle régressif linéaire Rooms~Crews

    studentized Breusch-Pagan test

data:  mdlLR
BP = 14.518, df = 1, p-value = 0.0001389

Remarque: Comme dans l’exemple précédent, on constate ici aussi une augmentation de la variabilité pour le nombre de bureaux nettoyés au fur et à mesure que le nombre d’équipes de nettoyage augmente. Le test de Breusch-Pagan confirme le fait que la variance des résidus ne peut pas être considérée comme homogene au seuil de signification de 5% (p-value = 0.0001389).

Après avoir utilisé la transformation par la racine carrée des deux variables (Crews et Rooms), on constate que le problème de non-homogénéité des résidus est résolu (voir la figure 3.4 et le résultat du test de Breusch-Pagan).

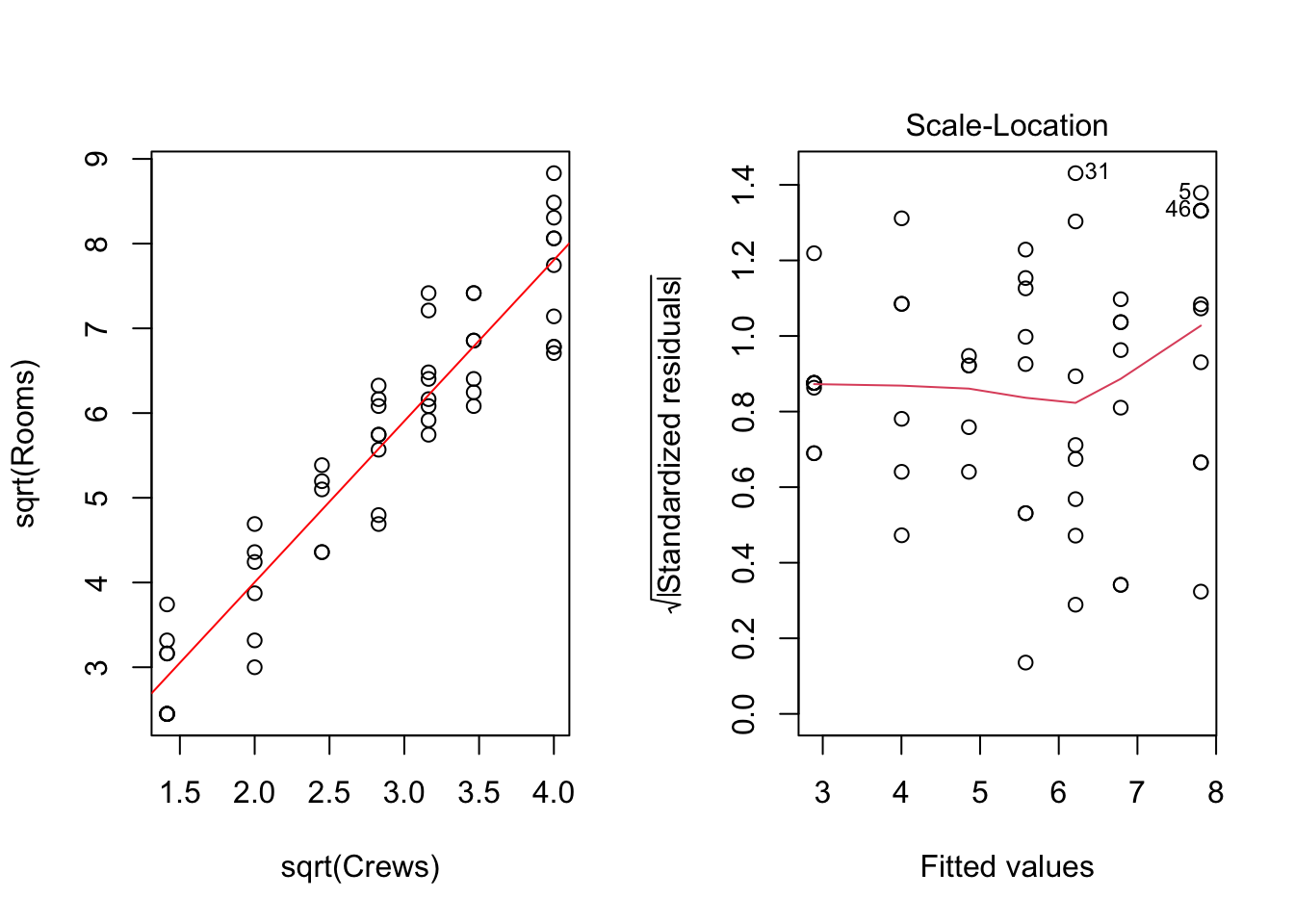
Figure 3.4: Modèle régressif linéaire sqrt(Rooms)~sqrt(Crews)

    studentized Breusch-Pagan test

data:  mdlLR
BP = 2.947, df = 1, p-value = 0.08604

Remarque: Les données de type comptage sont souvent bien modélisées par la distribution de Poisson. Dans ces cas, il convient généralement d’utiliser une transformation de type racine carrée des deux variables dans le modèle afin de rendre la variance des résidus homogène.

En utilisant le modèle avec les variables transformées par la racine carrée, on obtient les prédictions suivantes:

# Valeurs prédites de Rooms et intervalles de confiance à 95% lorsque Crews = 4 et 16
ceiling((predict(mdlLR, newdata = list(Crews=c(4, 16)), interval = "prediction"))^2)
  fit lwr upr
1  17   8  28
2  61  44  82

Remarque: Comme il s’agit dans cet exemple des données de type comptage (valeurs entieres), on a utilisé la fonction ceiling qui permet d’arrondir le résultat de la prédiction à l’entier supérieur.

3.2 Transformations de puissance

Il arrive souvent lorsque l’on veut construire un modèle linéaire pour modéliser la relation entre deux variables \((X,Y)\) de constater sur le graphique cartésien que la dépendance entre les deux variables n’est pas linéaire. Par exemple, supposons que la relation reliant les variables \((X,Y)\) est donnée par l’équation suivante:

\[\begin{equation} Y=g(\beta_0+\beta_1X+e) \end{equation}\]

où: \(g\) est une fonction inconnue.

Ce modèle peut être ramené à un simple modèle linéaire en utilisant l’inverse de la fonction \(g\):

\[\begin{equation} g^{-1}(Y)=\beta_0+\beta_1X+e \end{equation}\]

Dans ce qui suit, on passera en revue les approches pour estimer \(g^{-1}\).

Si l’on connaissait \(\beta_0\) et \(\beta_1\) on pourrait trouver le profile de la fonction \(g^{-1}\) en affichant \(Y\) sur l’axe horizontal et \(\beta_0+\beta_1X\) sur l’axe vertical. Malheureusement, \(\beta_0\) et \(\beta_1\) ne sont pas connus. Toutefois, si \(X\) a une distribution elliptique symétrique, alors \(g^{-1}\) peut être estimé à partir du graphique cartésien \(Y\) (sur l’axe horizontal) et les valeurs approximées à partir du modèle \(\hat{Y}=\hat{\beta}_0+\hat{\beta}_1X\) (sur l’axe vertical). On appelle ce graphique le graphique de la réponse inverse.

Exemple 3.2 (Exemple d'illustration du graphique de la réponse inverse) Prenons à titre d’exemple, deux variables \((X,Y)\) tel que représenté dans la figure 3.5. On voit bien sur le graphique que la relation entre les deux variables n’est pas linéaire. Ce constat est confirmé par le graphique des résidus par rapport aux valeurs approchées (Residuals vs Fitted). D’autre part, le test de Breusch-Pagan rejette l’hypothèse de homoscedasticité des résidus au seuil de signification de 5% (p-value = 0.0001829) - voir aussi le graphique des résidus standardisés par rapport aux valeurs approchées (Scale-Location) où l’on peut voir d’abord une diminution et ensuite une augmentation de la variance des résidus avec les valeurs approchées. Toutes ces remarques, nous conduisent à reconsidérer l’application directe d’un modèle linéaire sur ces données et nous amènent à explorer l’utilisation d’une transformation afin de linéairiser la relation entre les deux variables et résoudre le problème de non-homogéneité de la variance des résidus.

    studentized Breusch-Pagan test

data:  mdlLR
BP = 13.999, df = 1, p-value = 0.0001829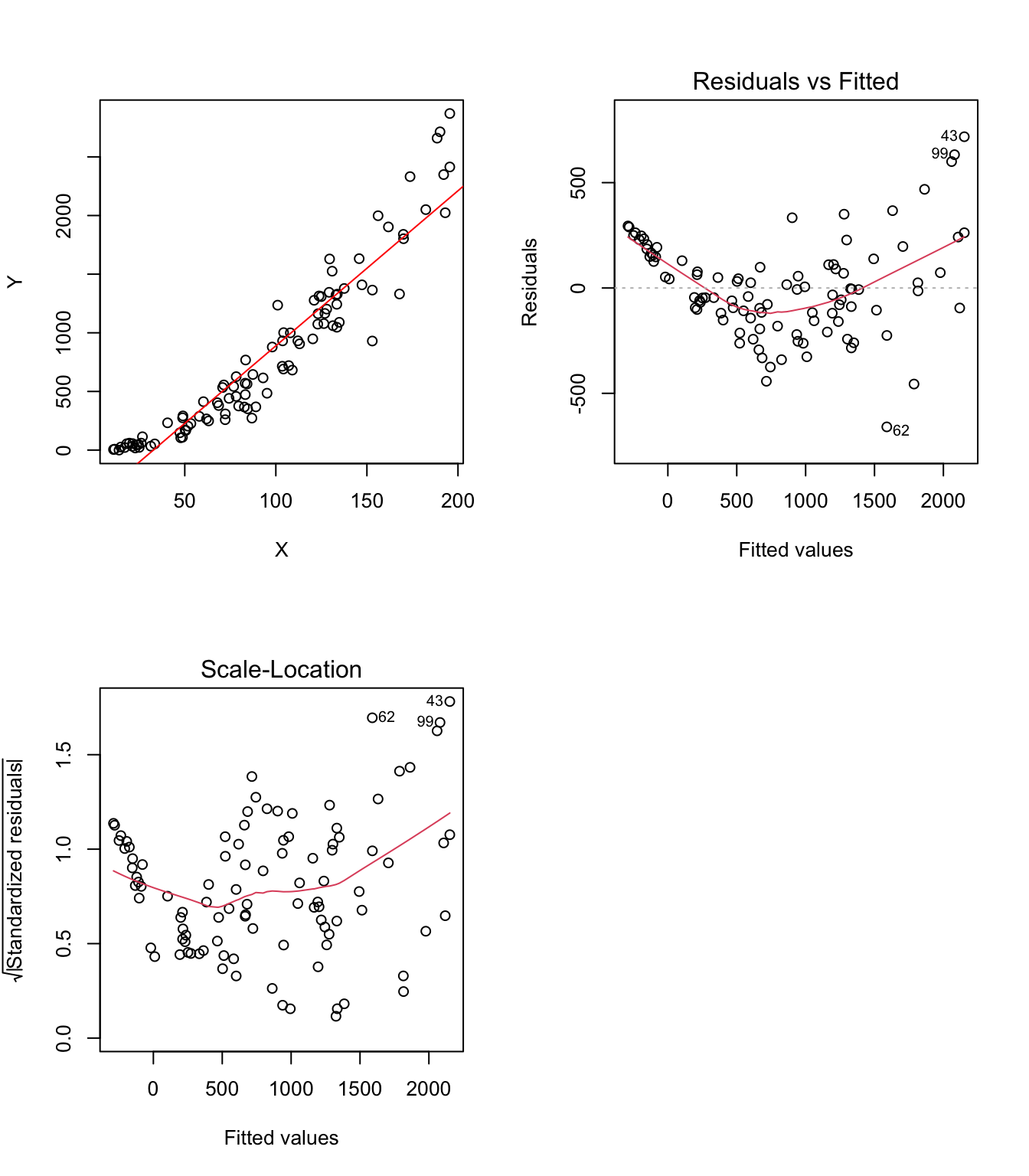

Figure 3.5: Exemple de relation non-linéaire entre X et Y

On fait donc appel au graphique de la réponse inverse qui s’affiche en executant la ligne de code R suivante:

mdlLR<-lm(Y~X)
inverseResponsePlot(mdlLR)

Figure 3.6: Graphique de la réponse inverse

      lambda      RSS
1  0.5399845  2205697
2 -1.0000000 43664003
3  0.0000000 16452860
4  1.0000000  4723475

Remarque: On constate que la courbe qui s’adapte au mieux aux données correspond à la puissance de 0.53998455 (pour laquelle le RSS - Residual Sum of Squares - est le plus réduit 2205697) - ligne continue de couleur noire sur le graphique. Ceci, nous amène à conclure que :

\[\begin{equation} \hat{y}=\hat{\beta}_0+\hat{\beta}_1x=Y^{0.54} \end{equation}\]

donc, si l’on veut linéariser la relation entre les deux variables aléatoires, il suffit de faire appel à la transformation ci-dessus mentionnée pour Y.

Une autre solution pour trouver l’estimation de la fonction inverse (\(g^{-1}\)), est de faire appel à une transformation de puissance. En statistique, une transformation de puissance est une famille de fonctions appliquées pour créer une transformation monotone de données. Il s’agit d’une technique de transformation de données utilisée pour:

• stabiliser la variance
• rendre les données plus semblables à une distribution normale
• améliorer la validité des mesures d’association (telles que la corrélation de Pearson entre les variables)
• etc.

On a déjà montré dans le paragraphe précédent comment une transformation peut résoudre le problème de non-homogéneité de la variance des résidus, donc on détaillera d’avantage ci-après pourquoi il est important de rendre les distributions des deux variables \((X,Y)\) aussi proches que possible de la loi normale en utilisant une certaine transformation.

Théorème 3.1 (Régression dans le cas des variables normalement distribuées) Si deux variables aléatoires \((X,Y)\) ont des distributions gaussiennes, alors la régression de l’une dans l’autre est linéaire.

Démonstration. Supposons que \(X\sim N(\mu_X,\sigma_X)\) et \(Y\sim N(\mu_Y,\sigma_Y)\) et que le coefficient de corrélation entre les deux variables est \(Cor\left[X,Y\right]=\rho_{XY}\). Alors, on peut montrer que la distribution conditionnelle:

\[\begin{equation} y_i|x_i \sim N\left(\mu_Y-\rho_{XY}\frac{\sigma_Y}{\sigma_X}\mu_X+\rho_{XY}\frac{\sigma_Y}{\sigma_X}x_i; \sigma^2_Y\left(1-\rho^2_{XY}\right)\right) \end{equation}\]

Ceci peut être interprété comme suit:

\[\begin{equation} \tag{3.1} y_i|x_i \sim N\left(\beta_0+\beta_1x_i;\sigma^2\right) \end{equation}\]

où: \(\beta_0=\mu_Y-\rho_{XY}\frac{\sigma_Y}{\sigma_X}\mu_X\), \(\beta_1=\rho_{XY}\frac{\sigma_Y}{\sigma_X}\) et \(\sigma^2=Var\left[Y|X\right]=\sigma^2_Y\left(1-\rho^2_{XY}\right)\).

Autrement dit, pour deux variables aléatoires \((X,Y)\) normalement distribuées, la régression de \(Y\) en \(X\) est linéaire :

\[\begin{equation} E\left[Y|(X=x_i)\right]=\beta_0+\beta_1x_i \end{equation}\]

D’après l’équation (3.1) on déduit que la densité de probabilité conditionnelle de \(Y\) sachant \(X\) est:

\[\begin{equation} f(y_i|x_i)=\frac{1}{\sigma \sqrt{2\pi}}\exp\left[-\frac{(y_i-\beta_0-\beta_1x_i)^2}{2\sigma^2}\right] \end{equation}\]

En assumant que les \(n\) observations \((x_i,y_i)\) qui constituent l’échantillon aléatoire sont indépendantes, alors l’expression de la fonction de vraisemblance sachant \(Y\) est donnée par l’expression suivante:

\[\begin{align} L(\beta_0,\beta_1,\sigma^2|Y)=\prod^n_{i=1} f(y_i|x_i)&=\prod^n_{i=1} \frac{1}{\sigma \sqrt{2\pi}}\exp\left[-\frac{(y_i-\beta_0-\beta_1x_i)^2}{2\sigma^2}\right]=\\ &= \left(\frac{1}{\sigma \sqrt{2\pi}}\right)^n \exp\left[-\frac{1}{2\sigma^2}\sum^n_{i=1}(y_i-\beta_0-\beta_1x_i)^2\right] \end{align}\]

Par conséquent, le logarithme de la fonction de vraisemblance est donné par:

\[\begin{equation} \tag{3.2} \log \left[L(\beta_0,\beta_1,\sigma^2|Y)\right]=-\frac{n}{2}\log(2\pi)-\frac{n}{2}\log(\sigma^2)-\frac{1}{2\sigma^2}\sum^n_{i=1}(y_i-\beta_0-\beta_1x_i)^2 \end{equation}\]

Les estimateurs de \(\beta_0\) et \(\beta_1\) par la méthode de maximum de vraisemblance s’obtiennent en minimisant le dernier terme dans l’équation (3.2):

\[\begin{equation} \log\left[L(\hat{\beta}_0,\hat{\beta}_1,\sigma^2|Y)\right] =-\frac{n}{2}\log(2\pi)-\frac{n}{2}\log(\sigma^2)-\frac{1}{2\sigma^2}RSS \end{equation}\]

où: \(RSS=\sum^n_{i=1}(y_i-\hat{\beta}_0-\hat{\beta}_1x_i)^2\) représente la somme carrée résiduelle.

L’estimateur de \(\sigma^2\) s’obtient comme suit:

\[\begin{equation} \hat{\sigma}^2_{MLE}=\frac{1}{n}RSS \end{equation}\]

Parmi les fonctions de transformation de puissance, les transformations de Box-Cox et Yeo-Johnson sont les plus connues.

3.2.1 Transformation de Box-Cox

La transformation de Box-Cox est donnée par: \[\begin{equation} \tag{3.3} BC(x,\lambda) = \begin{cases} \frac{x^\lambda-1}{\lambda} & \quad \text{si } \lambda \neq 0\\ ln(x) & \quad \text{si } \lambda = 0 \end{cases} \end{equation}\]

Etant donné un échantillon de valeurs \(x=\{x_1, x_2,...,x_n\}\), une possibilité pour trouver la valeur du paramètre de puissance (\(\lambda\)) dans l’équation (3.3) est de maximiser le logarithme de la fonction de maximum de vraisemblance:

\[\begin{equation} \tag{3.4} f(x,\lambda)=-\frac{n}{2}ln\left[\sum^n_{i=1}\frac{[x_i(\lambda)-\bar{x}(\lambda)]^2}{n} \right]+(\lambda-1)\sum^n_{i=1}ln(x_i) \end{equation}\]

où: \(x_i(\lambda)=BC(x_i,\lambda)\) et \(\bar{x}(\lambda)=\frac{1}{n}\sum^n_{i=1}x_i(\lambda)\) est la moyenne arithmétique des données transformées.

Remarque: La transformation Box-Cox donnée dans l’équation (3.3) est valide selulement si les valeurs de \(x\) sont positives. Toutefois, une transformation de Box-Cox qui peut être utilisée aussi pour des données négatives est:

\[\begin{equation} \tag{3.5} BC(x,\lambda_1, \lambda_2) = \begin{cases} \frac{(x+\lambda_2)^{\lambda_1}-1}{\lambda_1} & \quad \text{si } \lambda_1 \neq 0\\ ln(x+\lambda_2) & \quad \text{si } \lambda_1 = 0 \end{cases} \end{equation}\]

Il est important de préciser qu’il y a aussi une approche multivariée de Box-Cox pour transformer plusieurs variables simultanément. La méthode Box-Cox multivariée utilise un paramètre de transformation distinct pour chaque variable. Il n’y a pas non plus de classification indépendante/dépendante des variables. Depuis sa création, la transformation multivariée de Box-Cox a été utilisée dans de nombreux contextes, notamment la régression linéaire. Comme précisé précédemment, lorsque les variables sont transformées en normalité conjointe, elles deviennent approximativement linéairement liées, constantes en variance conditionnelle et marginalement normales en distribution. Ce sont des propriétés très utiles pour l’analyse statistique.

Exemple 3.3 (Exemple de transformation Box-Cox de la variable Y) Pour illustrer la transformation Box-Cox, reprenons l’exemple 3.2 et estimons à l’aide de celle-ci le paramètre \(\lambda\) pour la transformation de \(Y\). Le code R suivant permet de faire ce calcul:

library(RcmdrMisc)
summary(powerTransform(mdlLR, family="bcPower"))
boxCox(mdlLR)

bcPower Transformation to Normality 
   Est Power Rounded Pwr Wald Lwr Bnd Wald Upr Bnd
Y1     0.507         0.5       0.4464       0.5676

Likelihood ratio test that transformation parameter is equal to 0
 (log transformation)
                           LRT df       pval
LR test, lambda = (0) 258.2728  1 < 2.22e-16

Likelihood ratio test that no transformation is needed
                         LRT df       pval
LR test, lambda = (1) 133.93  1 < 2.22e-16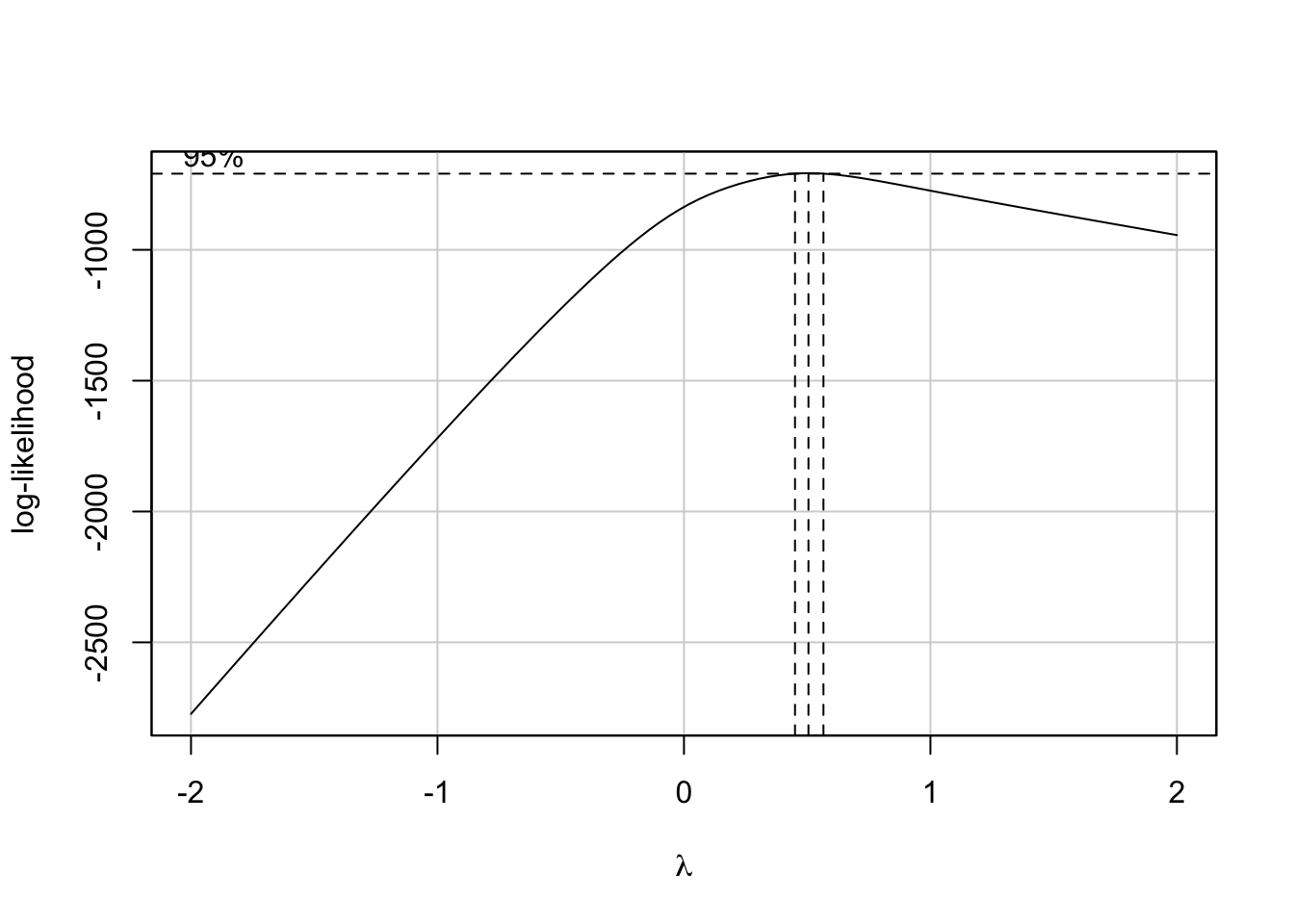

Figure 3.7: Le graphique de la fonction de vraisemblance

Remarques: 1) La fonction R powerTransform dont le paramètre family prend la valeur "bcPower" permet de réaliser la transformation de Box-Cox de la variable dépendante \(Y\); 2) La valeur \(\lambda\) estimée est de 0.507 et l’intervalle de confiance à 95% pour ce paramètre est [0.4464-0.5676]; 3) Un test pour évaluer si le paramètre \(\lambda\) peut être considéré null (transformation logarithmique) et un test pour évaluer si une transformation n’est pas nécessaire sont également réalisés. Dans notre cas, une transformation est nécessaire (p-value < 2.22e-16) mais il ne s’agit pas d’une tranformation logarithmique (p-value < 2.22e-16); 4) La fonction R boxCox permet de tracer le graphique de la fonction de vraisemblance; les lignes verticales en pointillé représentent: la valeur estimée du paramètre \(\lambda\) (au milieu) et les limites de l’intervalle de confiance à 95% pour ce paramètre.

Exemple 3.4 (Exemple de transformation Box-Cox des variables X et Y) Reprenons l’exemple traité précédemment (fichier trees) en nous proposant de prédire le volume en fonction de la circonférence de l’arbre (Volume~Girth).

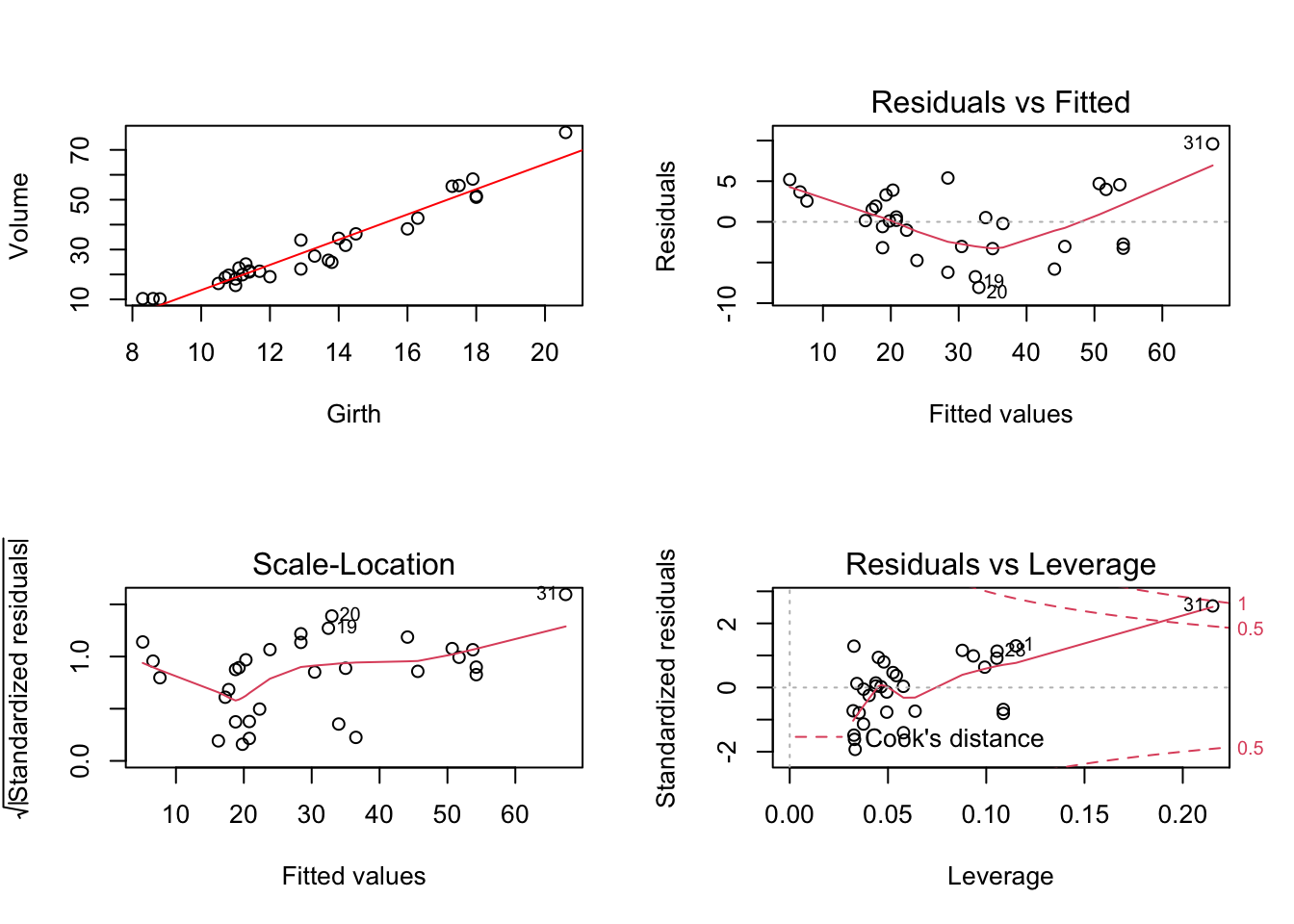
Figure 3.8: Modèle régressif linéaire Volume~Girth

    studentized Breusch-Pagan test

data:  mdlLR
BP = 5.6197, df = 1, p-value = 0.01776

On voit dans la figure 3.8 qu’il y a plusieurs soucis lorsque l’on veut utiliser un modèle linéaire. Ainsi, le graphique cartésien (Volume, Girth) montre que la relation entre les deux caractéristiques n’est pas tout à fait linéaire. Cette conclusion est renforcée en regardant le graphique Residuals vs Fitted où l’on peut voir très bien que la relation entre les deux caractéristiques est non-linéaire. Le graphique Scale-Location montre que la variance des résidus est non-homogène. Le test de Breusch-Pagan confirme ce constat au seuil de signification de 5% (p-value = 0.01776). Enfin, le graphique Residual vs Leverage montre que le point n°31 doit être analysé de plus près étant suspecté comme ayant une influence importante au niveau de la droite de régression.

D’autre part, dans la figure 3.9 on voit que les distributions de Volume et Girth ne semblent pas normales, et le test de Shapiro-Wilk confirme ceci au seuil de signification de 5%.

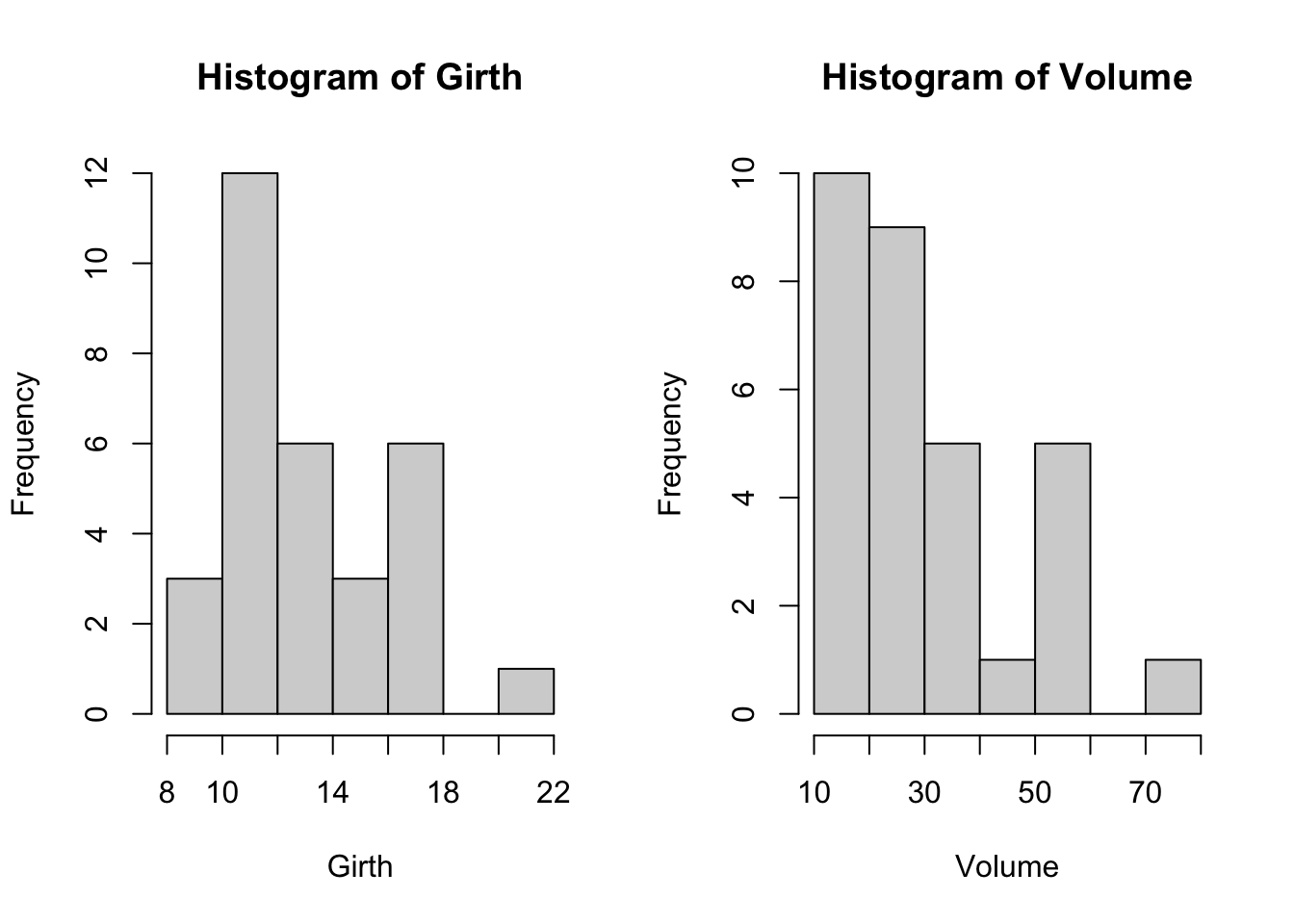
Figure 3.9: Histogrammes de Volume et Girth

    Shapiro-Wilk normality test

data:  Girth
W = 0.94117, p-value = 0.08893

    Shapiro-Wilk normality test

data:  Volume
W = 0.88757, p-value = 0.003579

Tous ces constats, nous amènent à prendre en considération une approche de transformation qui concernera les deux variables. Deux solutions s’offrent à nous:

Solution n°1: Transformer la variable explicative (\(X\)) par une transformation Box-Cox et ensuite prendre en considération un modèle régressif de la forme:

\[\begin{equation} Y=g(\beta_0+\beta_1BC(X,\lambda)+e) \end{equation}\]

où: \(Y\) est la variable expliquée; \(BC(X,\lambda)\) est la transformée Box-Cox de \(X\) et \(g\) est une fonction inconnue.

Ensuite, comme expliqué plus haut, utiliser le graphique de la réponse inverse afin de décider quelle est la méilleure transformation \(g^{-1}\) pour \(Y\).

Le code R ci-dessous illustre l’implémentation de cette solution pour le fichier trees (prédiction du volume en fonction de la circonférence de l’arbre Volume~Girth):

# Transformation Box-Cox pour la variable Girth
library(RcmdrMisc)
summary(powerTransform(Girth, family="bcPower"))

bcPower Transformation to Normality 
      Est Power Rounded Pwr Wald Lwr Bnd Wald Upr Bnd
Girth   -0.2126           1      -1.6738       1.2486

Likelihood ratio test that transformation parameter is equal to 0
 (log transformation)
                             LRT df   pval
LR test, lambda = (0) 0.08103377  1 0.7759

Likelihood ratio test that no transformation is needed
                           LRT df    pval
LR test, lambda = (1) 2.579602  1 0.10825

Remarques: On constate que la valeur estimée du paramètre \(\lambda\) est de -0.2126. Toutefois, l’intervalle de confiance à 95% pour ce paramètre [-1.6738 1.2486] contient la valeur de zéro, ce qui nous informe sur le fait qu’au seuil de signification de 5% on peut considérer que le paramètre \(\lambda\) n’est pas significativement différent de zéro. Par conséquent, une transformation logarithmique pour la variable Girth semblerait la plus appropriée. Cette conclusion est renforcée par le test du rapport de vraisemblance dont la p-value est de 0.7759. On pourrait aussi ne pas transformer la variable Girth car au seuil de signification de 5% le test de Shapiro-Wilk ne rejete pas la normalité de la distribution (p-value=0.08893) et le test du rapport de vraisemblance pour \(\lambda = 1\) présente une p-value de 0.10825. On décide toutefois d’utiliser une transformation logarithmique pour la variable Girth car elle permet d’avoir une distribution avec une allure plus proche de celle de la loi normale (voir l’histograme de la figure 3.10) et le test de Shapiro-Wilk (p-value = 0.3207 pour la variable transformée vs. p-value = 0.08893 pour la variable non-transformée). Par ailleurs, cette transformation nous permet également d’illustrer cette approche, donc elle convient aussi pour les besoins pédagogiques.

# Transformation logarithmique pour la variable Girth
logGirth<-log(Girth)

# Visualisation de l'effet de la transformation
hist(logGirth)

# Test de normalité sur la variable transformée
shapiro.test(logGirth)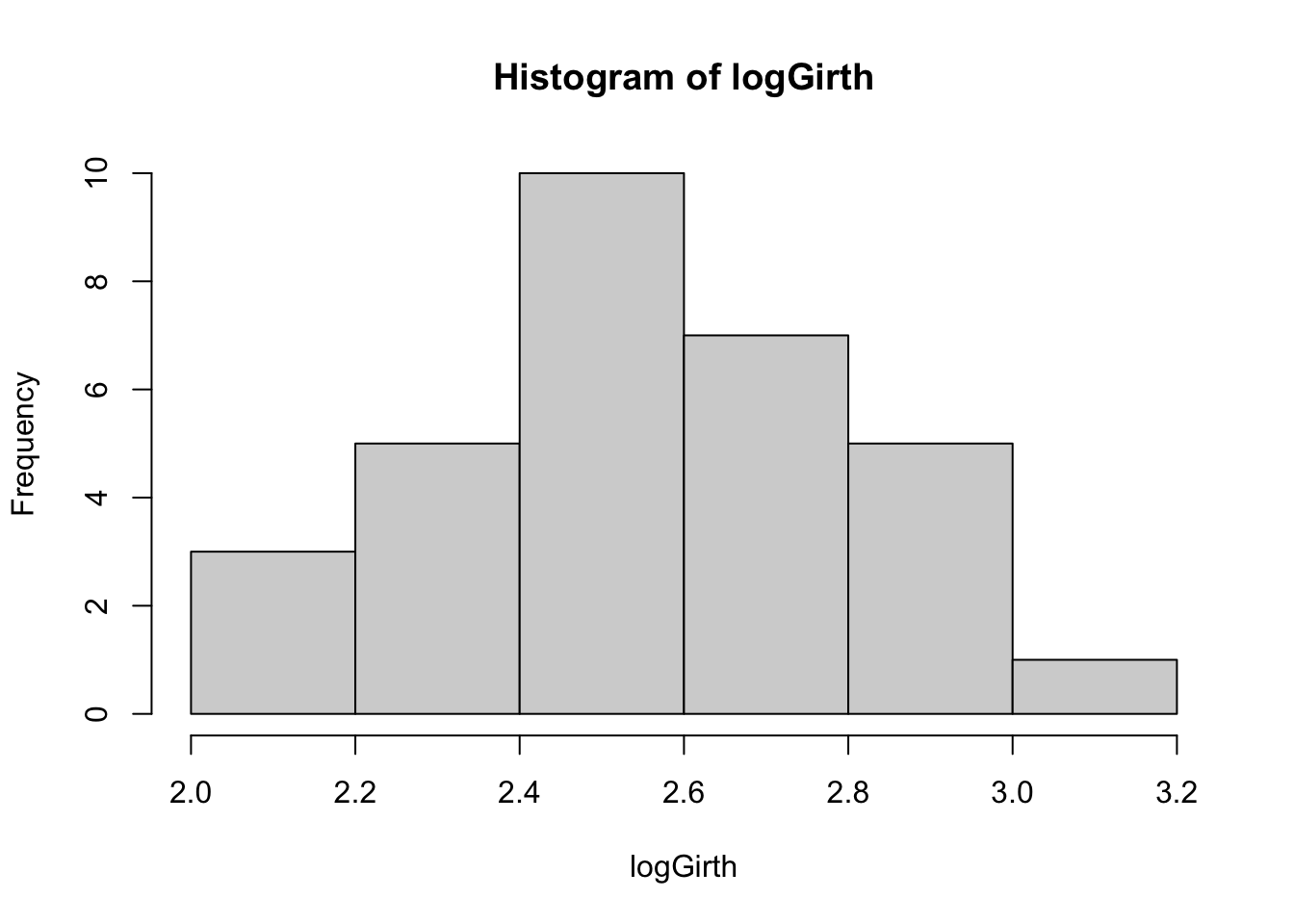

Figure 3.10: Histogramme de la variable Girth après la transformation logarithmique

    Shapiro-Wilk normality test

data:  logGirth
W = 0.96156, p-value = 0.3207

On continue par la construction du modèle régressif Volume~log(Girth) et l’utilisation du graphique de la réponse inverse pour déterminer la meilleure transformation de la variable Volume. Le code R ci-dessous illustre cette démarche:

# Construction du modèle régressif
mdlLR<-lm(Volume~log(Girth), data = trees)

#Graphique de la réponse inverse
inverseResponsePlot(mdlLR)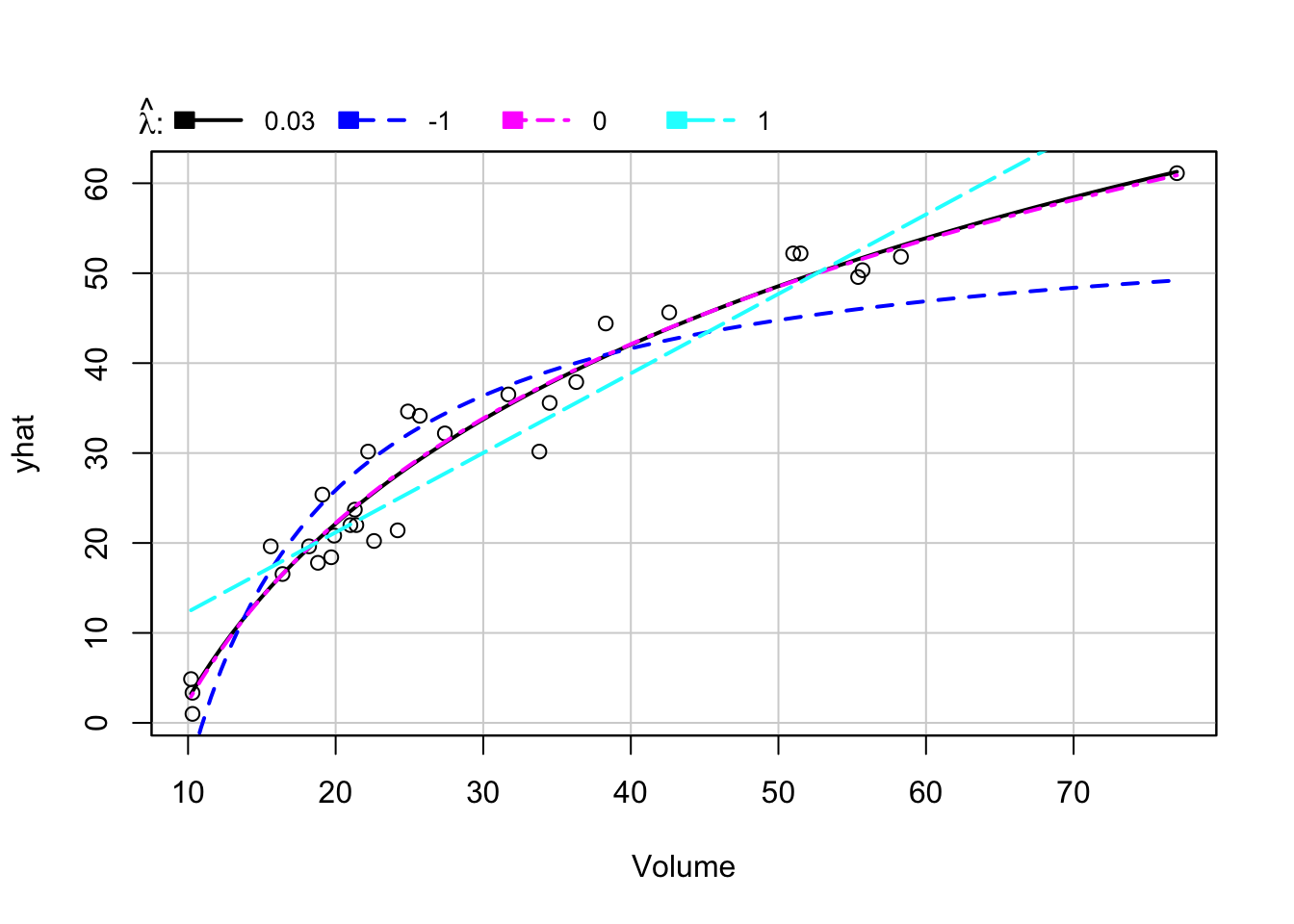

(#fig:grRIvolLogirth )Graphique de la réponse inverse pour Volume~log(Girth)

       lambda      RSS
1  0.03225169 329.7540
2 -1.00000000 988.0891
3  0.00000000 330.4236
4  1.00000000 832.9369

Remarque: On constate que le paramètre optimal \(\lambda\) estimé pour la transformation de la variable Volume est de 0.03225169. Toutefois, on n’est pas très loin de \(\lambda = 0\) (RSS = 329.7540 vs. RSS = 330.4236). Qui dit \(\lambda = 0\) dit transformation logarithmique pour la variable Volume. Par conséquent, on transformera aussi la variable Volume par une transformation logarithmique (voir la figure 3.11) ce qui permet par ailleurs de rendre la distribution de celle-ci plus proche de la loi normale selon le test de Shapiro-Wilk (p-value = 0.3766).

# Transformation logarithmique pour la variable Volume
logVolume<-log(Volume)

# Visualisation de l'effet de la transformation
hist(logVolume)

# Test de normalité sur la variable transformée
shapiro.test(logVolume)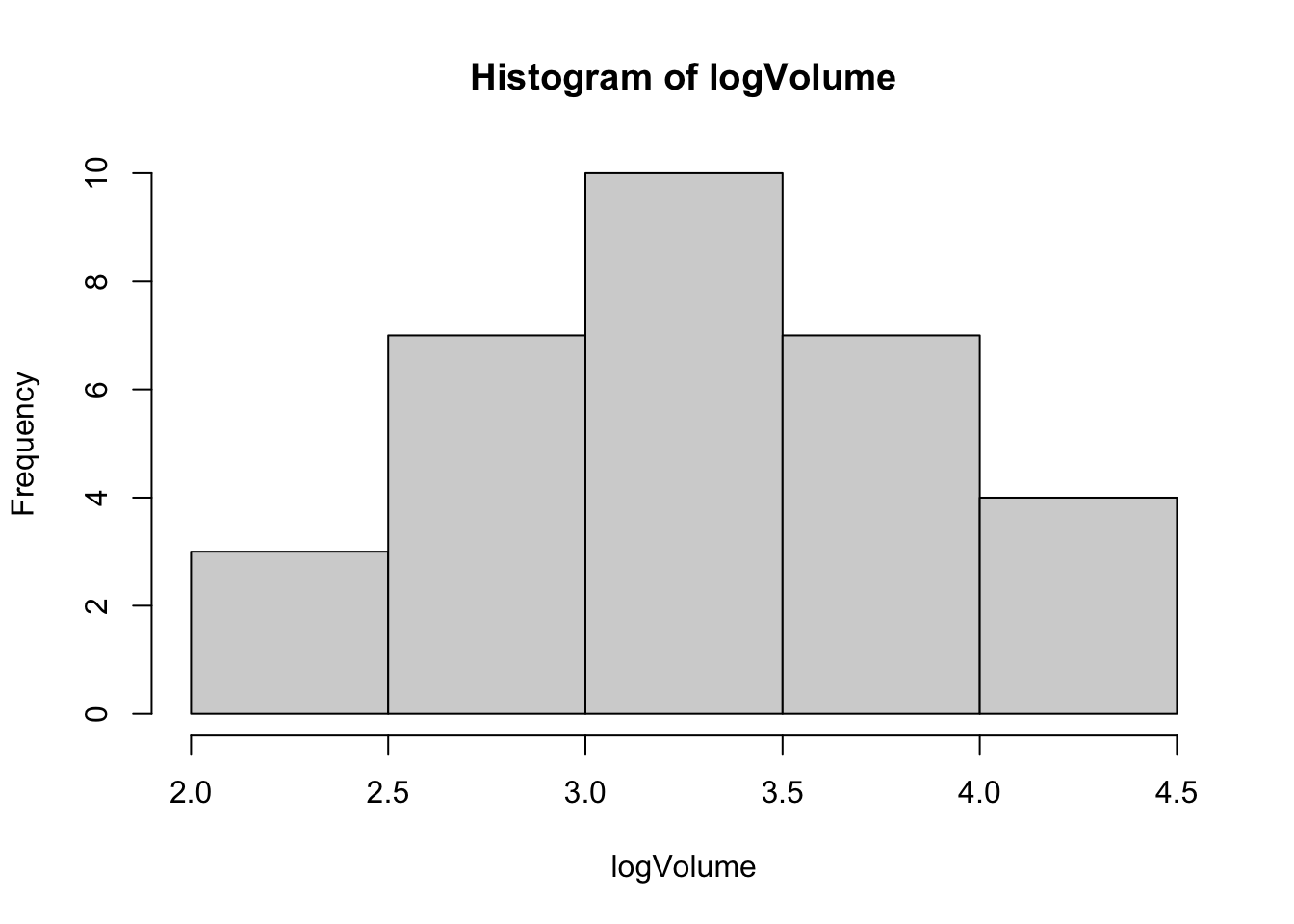

Figure 3.11: Histogramme de la variable Volume après la transformation logarithmique

    Shapiro-Wilk normality test

data:  logVolume
W = 0.96427, p-value = 0.3766

Après avoir utilisé la transformation logarithmique sur les deux variables Girth et Volume, on peut constater que les problèmes illustrés dans la figure 3.8 sont résolus. En effet, on n’a plus de non-linéarité sur le graphique Residual vs Fitted, on n’a plus de problème de non-homogéneité de la dispersion des résidus (voir le graphique Scale-Location et test de Breusch-Pagan) et on a également résolu le problème relevé précédemment sur le graphique Residuals vs Leverage ou le point n°31 apparaissait comme atypique.

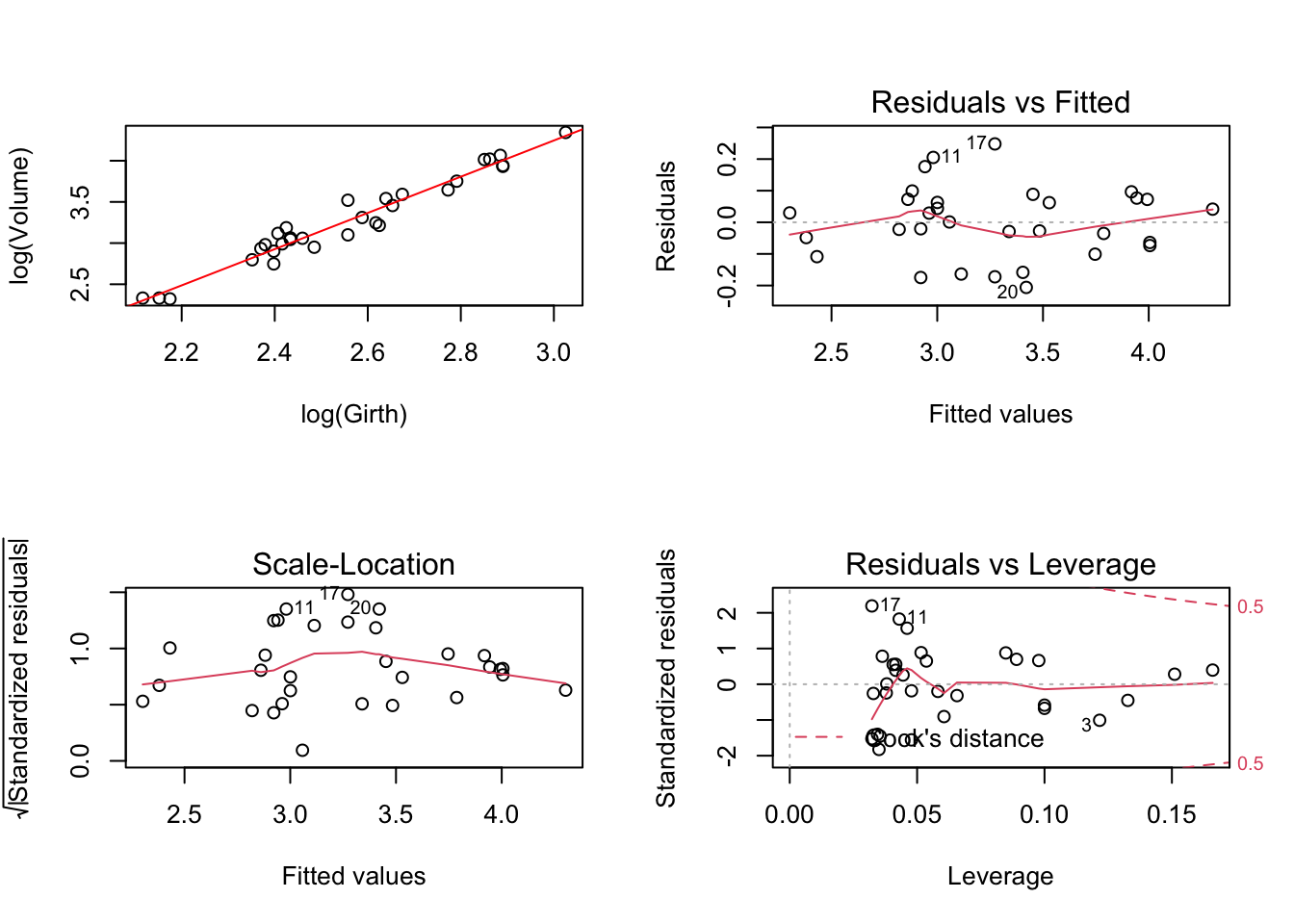
Figure 3.12: Modèle régressif linéaire log(Volume)~log(Girth)

    studentized Breusch-Pagan test

data:  mdlLR
BP = 0.18165, df = 1, p-value = 0.67

Ceci confirme le fait que nous avons opté pour la bonne transformation qui était nécessaire avant de modéliser la relation entre les deux variables par un modèle linéaire.

Solution n°2: Transformer les variables \(X\) et \(Y\) simultanément en utilisant la transformation multivariée de Box-Cox.

Le code R suivant permet d’implémenter cette solution:

# Retenir seulement les colonnes Girth et Volume du fichier trees dans une matrice
DataSet<-as.matrix(trees[,-2])

# Appliquer la transformation Box-Cox multivariée
summary(powerTransform(DataSet,family="bcPower"))

bcPower Transformations to Multinormality 
       Est Power Rounded Pwr Wald Lwr Bnd Wald Upr Bnd
Girth     0.0491           1      -1.1319       1.2302
Volume    0.0355           0      -0.4552       0.5261

Likelihood ratio test that transformation parameters are equal to 0
 (all log transformations)
                               LRT df    pval
LR test, lambda = (0 0) 0.02822754  2 0.98599

Likelihood ratio test that no transformations are needed
                             LRT df       pval
LR test, lambda = (1 1) 23.47317  2 7.9959e-06

Remarques: 1) On voit que la valeur de zéro est dans les deux intervales de confiance à 95%, donc on en déduit qu’au seuil de signification de 5% les paramètres de puissance pour les transformations de Girth et Volume ne sont pas significativement différents de zéro (donc des transformations logarithmiques seront nécessaires pour ces variables) - ce constat est renforcé par le test du rapport de vraisemblance dont la p-value est de 0.98599; 2) Le test du rapport de vraisemblance confirme aussi qu’une transformation est nécessaire (p-value = 7.9959e-06).

On arrive donc à la même conclusion que celle obtenue par l’approche précédente (solution n°1) qui consiste à transformer par une transformation logarithmique les deux variables avant d’implémenter le modèle de régression linéaire.

3.2.2 Transformation de Yeo-Johnson

Si l’on regarde la transformation de Box-Cox qui admet des valeurs \(x\) négatives (voir l’équation (3.5)), on constate que cette transformation est applicable seulement si les valeurs de \(x\) sont bornées inférieurement (\(x+\lambda_2>0\)). Pour remédier à cet inconvénient, Yeo et Jonshon ont proposé la transformation suivante:

\[\begin{equation} \tag{3.6} YJ(x,\lambda) = \begin{cases} \frac{(x+1)^\lambda-1}{\lambda} & \quad \text{si } x \geq 0 \text{ et } \lambda \neq 0\\ ln(x+1) & \quad \text{si } x \geq 0 \text{ et } \lambda = 0 \\ -\frac{(-x+1)^{2-\lambda}-1}{2-\lambda} & \quad \text{si } x < 0 \text{ et } \lambda \neq 2\\ -ln(-x+1) & \quad \text{si } x < 0 \text{ et } \lambda = 2\\ \end{cases} \end{equation}\]

ce qui fait de cette transformation une généralisation de la transformation de Box-Cox.

Comme dans le cas de la transformation de Box-Cox, la valeur du paramètre \(\lambda\) est trouvée par la méthode du maximum de vraisemblance.

Pour illustrer cette transformation de Yeo-Johnson, le code R ci-dessous montre sur l’exemple de la prédiction du volume selon la circonférence (voir le fichier trees) comment réaliser les calculs:

# Retenir seulement les colonnes Girth et Volume du fichier trees dans une matrice
DataSet<-as.matrix(trees[,-2])

# Appliquer la transformation Yeo-Johnson
summary(powerTransform(DataSet,family="yjPower"))

yjPower Transformations to Multinormality 
       Est Power Rounded Pwr Wald Lwr Bnd Wald Upr Bnd
Girth    -0.0049           1      -1.2794       1.2696
Volume    0.0038           0      -0.5090       0.5165

 Likelihood ratio test that all transformation parameters are equal to 0
                                LRT df    pval
LR test, lambda = (0 0) 0.001978603  2 0.99901

Remarques: 1) La transformation de Yeo-Johnson s’obtient en fixant le paramètre family de la fonction powerTransform égale à "yjPower". 2) On peut constater que les résultats obtenus par l’approche de transformation de Yeo-Johnson sont très similaires avec ceux obtenus par la méthode de Box-Cox illustrée précédemment. Ainsi, selon le test du rapport de maximum de vraisemblance, on peut constater, qu’au seuil de signification de 5%, les paramètres de transformation pour les deux variables peuvent être considérés comme nulls, ce qui conduit à une transformation logarithmique pour chaque cas.

3.3 Fiche de synthèse du code R

On réunit ici les différents morceaux de code R présentés dans ce chapitre pour donner un aperçu global de la manière dont on peut exploiter les fonctions de transformation de puissance lorsque leur utilisation est nécessaire dans le cadre de la construction ou de la validation d’un modèle de régression linéaire.

A titre d’exemple, dans le fichier de données airfares.xlsx (voir le répertoire Base de Données dans Moodle) on trouve le tarif aérien aller simple (en dollars américains) et la distance (en miles) de la ville A à 17 autres villes des États-Unis. L’intérêt porte sur la modélisation des tarifs aériens en fonction de la distance. Le code présenté ci-dessous se trouve dans le fichier codeRLS_l3.r dans le répertoire codeR dans Moodle.

# Lecture de données du fichier
# =============================
library(readxl)
DataSet <- read_excel("airfares.xlsx")
attach(DataSet)

# Construction du modèle de régression linéaire
# =============================================
mdlLR<-lm(Fare~Distance)

# Diagnostic graphique pour la validation du modèle
# =================================================
par(mfrow=c(2,2))
plot(Distance, Fare)
abline(mdlLR, col="red")
plot(mdlLR, which = 1) 
plot(mdlLR, which = 3) 
plot(mdlLR, which = 5)

# Test de Breusch-Pagan pour l'homogéneité de la variance des résidus
#====================================================================
bptest(mdlLR)

# Tests de normalité pour les deux variables
# ==========================================
library(car)
par(mfrow=c(2,2))
hist(Distance)
qqPlot(Distance)
hist(Fare)
qqPlot(Fare)

shapiro.test(Distance)
shapiro.test(Fare)

# SOLUTION N°1: 
#=============

# Transformation de Box-Cox de la variable Distance
#--------------------------------------------------
summary(powerTransform(Distance,family="bcPower"))

# Construction du modèle régressif Fare~log(Distance)
#----------------------------------------------------
mdlLR1<-lm(Fare~log(Distance))

# Utilisation du graphique de la réponse inverse
#-----------------------------------------------
inverseResponsePlot(mdlLR1)

# SOLUTION N°2: Utilisation de la transformation Box-Cox multivariée
#===================================================================
summary(powerTransform(DataSet[,-1],family="bcPower"))

# SOLUTION N°3: Utilisation de la transformation Yeo-Johnson
#============================================================
summary(powerTransform(DataSet[,-1],family="yjPower"))

detach(DataSet)

Interprétation des résultats

On remarque tout d’abord sur le graphique Residuals vs Fitted (voir la figure 3.13) que la relation entre les deux variables (Fare et Distance) n’est pas linéaire (forme parabolique de la disposition des points). Deuxièmement, sur le graphique Scale-Location on constate que la variance des résidus tend à augmenter lorsque Distance augmente (tendance monotone croissante sur la dernière portion du graphique).

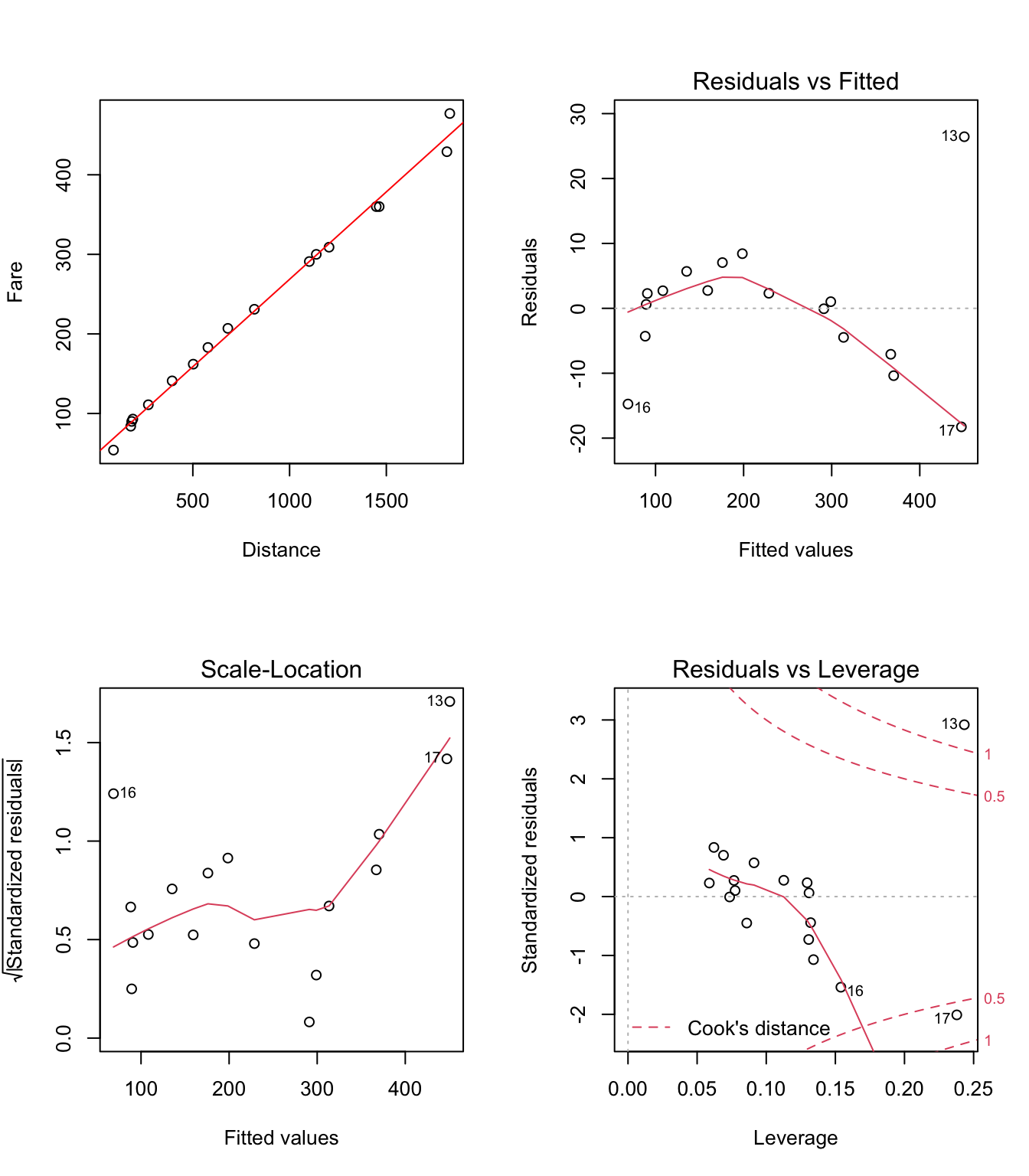
Figure 3.13: Graphiques pour la validation du modèle linéaire Fare~Distance

Ce constat est confirmé par le test de Breusch-Pagan :

    studentized Breusch-Pagan test

data:  mdlLR
BP = 5.1899, df = 1, p-value = 0.02272

Enfin, sur le graphique Residuals vs Leverage il semblerait qu’il y a deux points (n°13 et n°17) qui sont atypiques.

Tous ces constats, nous amènent à prendre en considération la nécessité de transformer une ou les deux variables. Pour savoir sur laquelle des deux variables on portera tout d’abord notre attention, on étudie les distributions de Fare et Distance (voir la figure 3.14).

[1] 13 17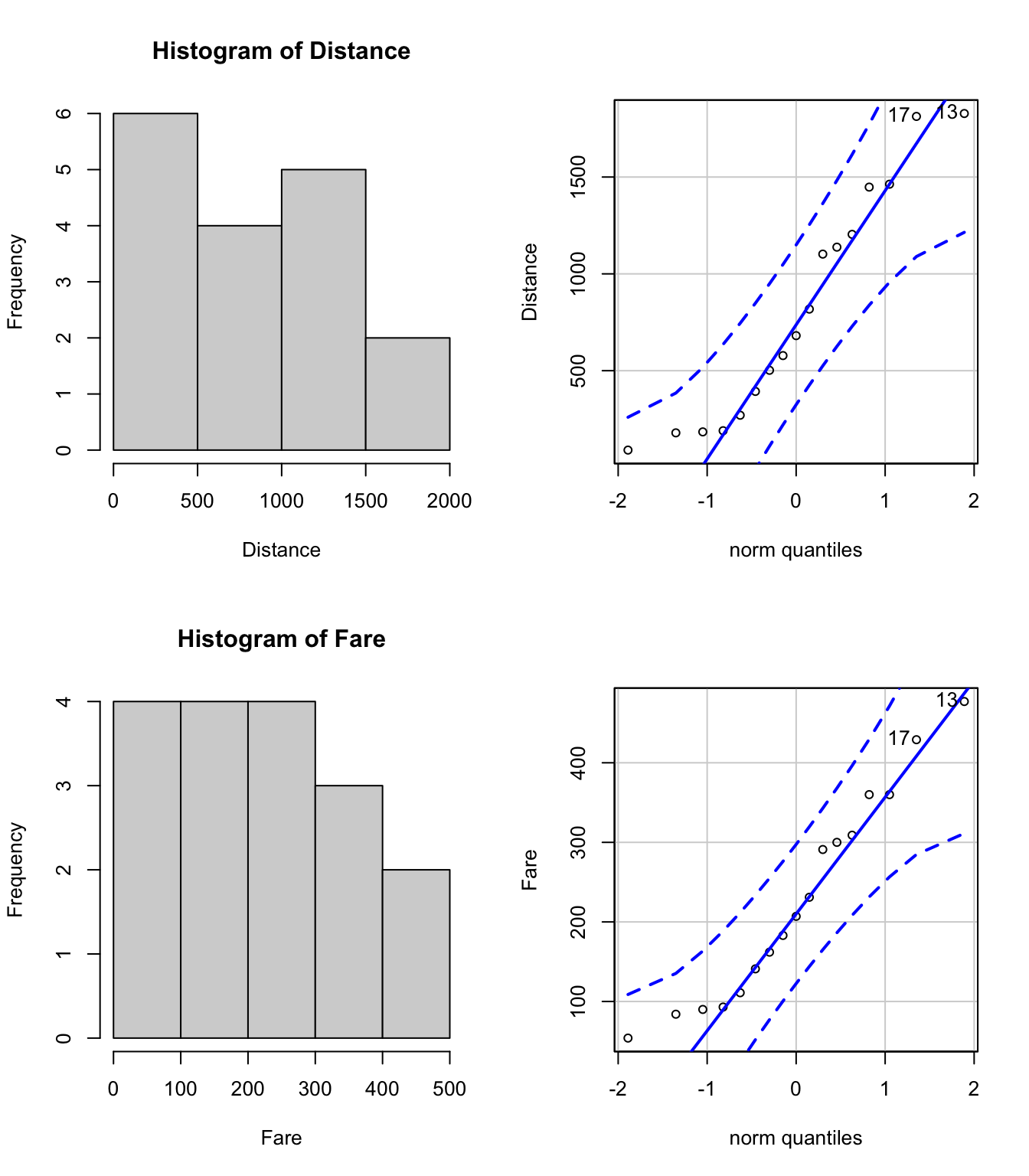

Figure 3.14: Graphiques de normalité

[1] 13 17

Malgré les allures qui sont assez différentes de celle de la courbe en cloche de Gauss sur les histogrammes et des écarts assez prononcés par rapport à la droite sur les graphique quantile-quantile (voir les points 13 et 17), le test de Shapiro-Wilk ne rejete pas l’hypothèse de distribution normale pour ces deux variables :

    Shapiro-Wilk normality test

data:  Distance
W = 0.91288, p-value = 0.1119

    Shapiro-Wilk normality test

data:  Fare
W = 0.94165, p-value = 0.3382

Cela est dû au fait que le volume de données est faible (17 points en tout) et, dans ce cas, les tests statistiques sont très conservateurs (il est difficile de rejeter l’hypothèse nulle qui est privilégié par le test en étant considérée vraie au départ). Par conséquent, on ne peut pas cibler une variable en particulier pour la transformer. Trois solutions peuvent être envisagées dans ce cas. Elles seront détaillées ci-dessous:

• Solution n°1: Transformer Distance par une transformation Box-Cox et utiliser la réponse inverse ensuite

La transformation Box-Cox de Distance donne le résultat suivant:

bcPower Transformation to Normality 
         Est Power Rounded Pwr Wald Lwr Bnd Wald Upr Bnd
Distance    0.3465           0      -0.2718       0.9649

Likelihood ratio test that transformation parameter is equal to 0
 (log transformation)
                           LRT df    pval
LR test, lambda = (0) 1.262247  1 0.26123

Likelihood ratio test that no transformation is needed
                           LRT df     pval
LR test, lambda = (1) 3.863185  1 0.049357

Remarques: 1) Une transformation de Distance est nécessaire selon le test du rapport de vraisemblance (p-value = 0.049357); 2) L’estimation du paramètre de puissance \(\lambda\) est de 0.3465, mais cette valeur n’est pas significativement différente de zéro au seuil de signification de 5% (voir l’intervalle de confiance à 95% [-0.2718 0.9649] qui contient la valeur zéro). 3) En conclusion, une transformation logarithmique s’impose pour Distance, ce qui est par ailleurs confirmé par le test du rapport de vraisemblance (p-value = 0.26123).

Le graphique de la réponse inverse (voir la figure 3.15) permet de constater que la transformation de puissance optimale pour la variable Fare est -0.1632631 (RSS = 562.818).

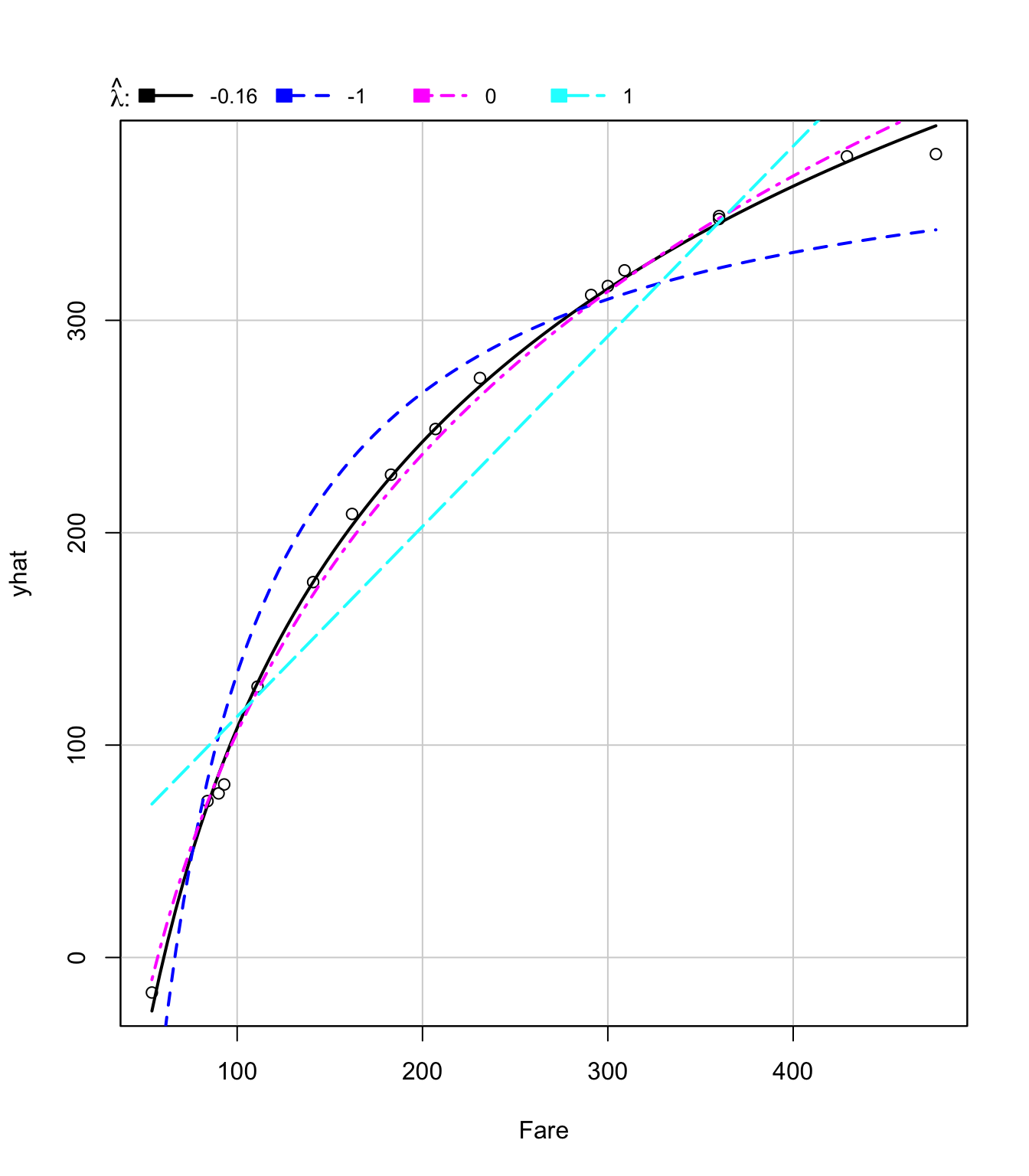
Figure 3.15: Graphiques de la réponse inverse pour Fare~log(Distance)

      lambda       RSS
1 -0.1632631   562.818
2 -1.0000000 15882.800
3  0.0000000  1145.946
4  1.0000000 25241.899

Donc selon cette approche, le modèle de régression linéaire devrait avoir l’équation suivante:

\[\begin{equation} Fare^{-0.16}=\beta_0+\beta_1*log(Distance)+e \end{equation}\]

Remarque: On constate sur la figure 3.15 que la courbe pour le paramètre de puissance optimal (\(\lambda = -0.16\)) n’est pas très différente de celle qui correspond à \(\lambda = 0\) (transformation logarithmique sur la variable Fare).

• Solution n°2: Transformer Distance et Fare par une transformation Box-Cox multivariée

Le résultat obtenu par cette approche est présenté ci-dessous:

bcPower Transformations to Multinormality 
         Est Power Rounded Pwr Wald Lwr Bnd Wald Upr Bnd
Fare       -0.0207           0      -0.4549       0.4135
Distance    0.1098           0      -0.2315       0.4512

Likelihood ratio test that transformation parameters are equal to 0
 (all log transformations)
                             LRT df      pval
LR test, lambda = (0 0) 11.73688  2 0.0028273

Likelihood ratio test that no transformations are needed
                             LRT df       pval
LR test, lambda = (1 1) 19.99211  2 4.5579e-05

Remarques: 1) Au moins une transformation est nécessaire selon le test du rapport de vraisemblance (p-value = 4.5579e-05); 2) La transformation logarithmique des deux variables n’est pas nécessaire selon le test du rapport de vraisemblance (p-value = 0.0028273); 3) Les estimateurs des transformations de puissance pour Fare et Distance sont -0.0207 et respectivement 0.1098 (pas significativement différents de zéro au seuil de signification de 5% - voir les intervalles de confiances à 95%).

Donc selon cette approche, le modèle de régression linéaire devrait avoir l’équation suivante:

\[\begin{equation} Fare^{-0.0207}=\beta_0+\beta_1*Distance^{0.1098}+e \end{equation}\]

• Solution n°3: Transformer Distance et Fare par une transformation Yeo-Johnson

Le résultat obtenu par cette approche est présenté ci-dessous:

yjPower Transformations to Multinormality 
         Est Power Rounded Pwr Wald Lwr Bnd Wald Upr Bnd
Fare       -0.0290           0      -0.4658       0.4079
Distance    0.1066           0      -0.2353       0.4484

 Likelihood ratio test that all transformation parameters are equal to 0
                             LRT df      pval
LR test, lambda = (0 0) 12.09769  2 0.0023606

Remarques: 1) La transformation logarithmique des deux variables n’est pas nécessaire selon le test du rapport de vraisemblance (p-value = 0.0023606); 2) Les estimateurs des transformations de puissance pour Fare et Distance sont -0.0290 et respectivement 0.1066 (pas significativement différents de zéro au seuil de signification de 5% - voir les intervalles de confiances à 95%).

Donc selon cette approche, le modèle de régression linéaire devrait avoir l’équation suivante:

\[\begin{equation} Fare^{-0.029}=\beta_0+\beta_1*Distance^{0.1066}+e \end{equation}\]

Remarque: On constate que ce modèle est très similaire à celui obtenu par la transformation Box-Cox multivarié.

A titre illustratif, on présente ci-dessous les graphiques de diagnostic pour ces modèles (avec des variables transformées):

• Pour la solution n°1: \(Fare^{-0.16}=\beta_0+\beta_1*log(Distance)+e\)

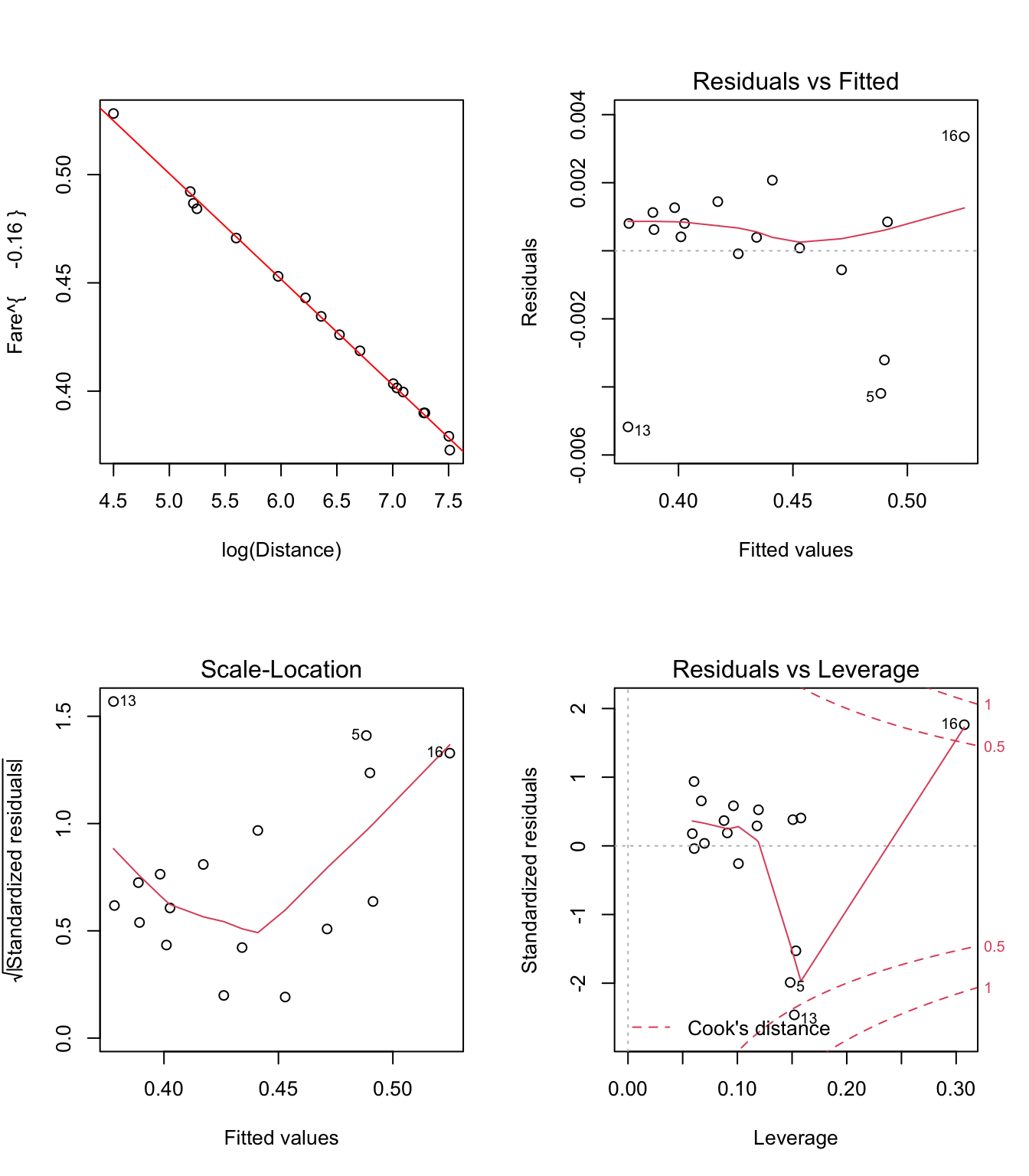
Figure 3.16: Graphiques pour la validation du modèle linéaire Fare^(-0.16)~log(Distance)

• Pour la solution n°2: \(Fare^{−0.0207}=\beta_0+\beta_1*Distance^{0.1098}+e\)

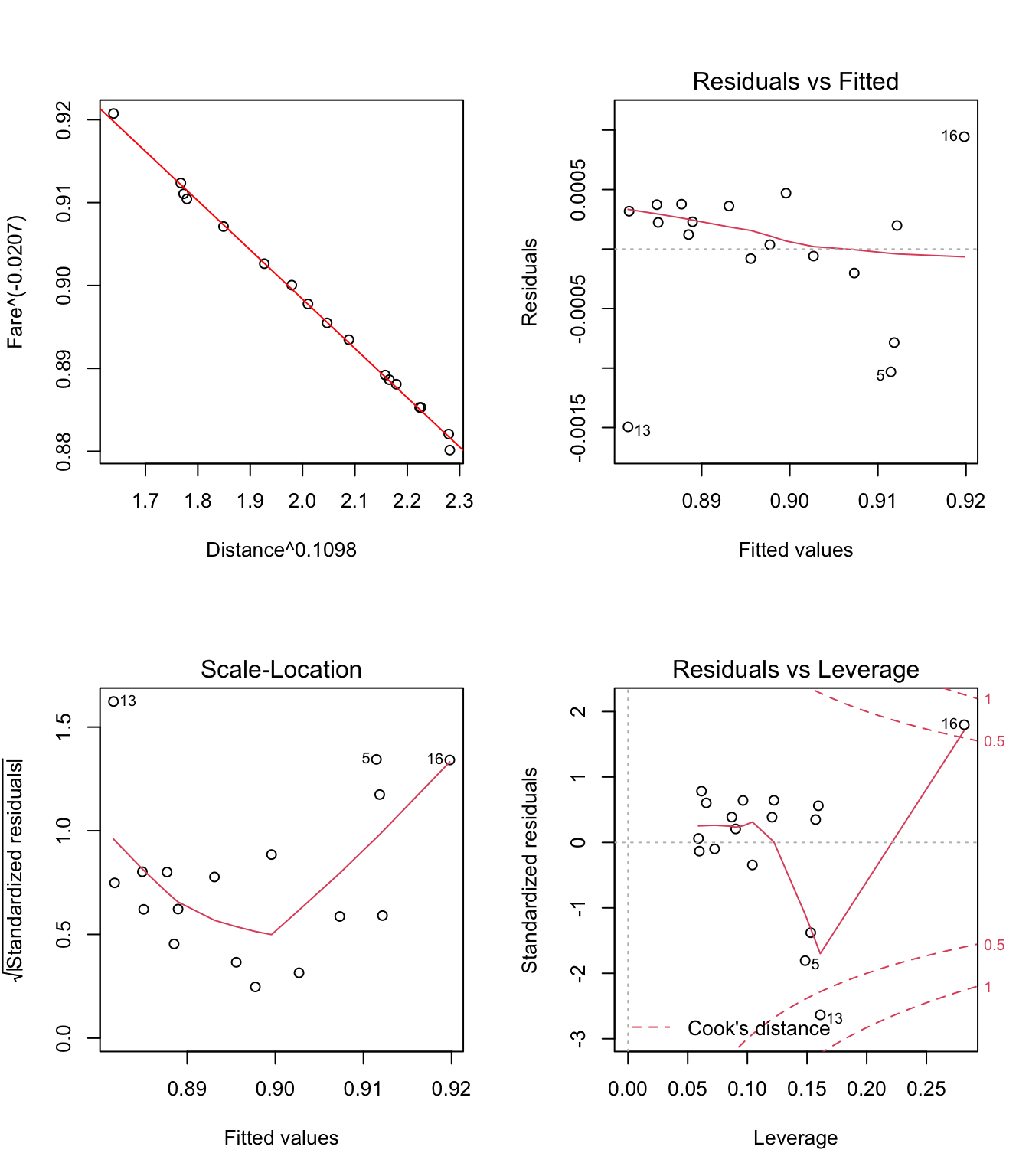
Figure 3.17: Graphiques pour la validation du modèle linéaire Fare^{{−0.0207}~Distance}{0.1098}

• Pour la solution n°3: \(Fare^{−0.029}=\beta_0+\beta_1*Distance^{0.1066}+e\)

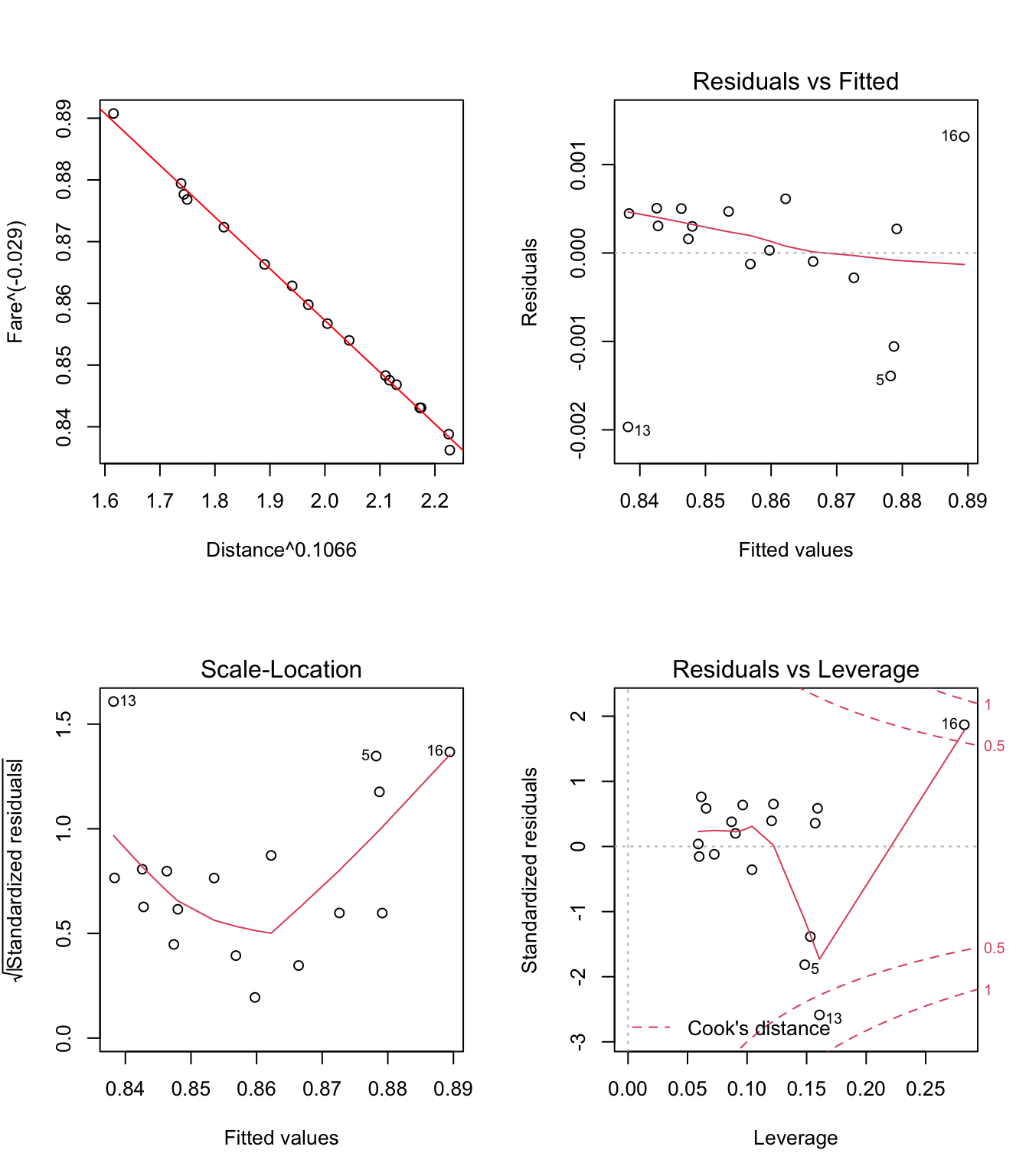
Figure 3.18: Graphiques pour la validation du modèle linéaire Fare^{{−0.029}~Distance}{0.1066}

Remarques: 1) On peut constater sur les figures 3.16, 3.17 et 3.18 que les effets des trois transformations présentées dans les solutions n°1, n°2 et respectivement n°3 sont très similaires: a) elles ont pour conséquence d’elliminer le problème de non-linéarité (voir les graphiques Residuals vs Fitted); b) la variance des résidus semble toujours augmenter lorsque la variable Distance augmente (voir graphiques Scale-Location), mais cette fois-ci, le test de Breusch-Pagan rejette cette hypothèse au seuil de signification de 5%:

    studentized Breusch-Pagan test

data:  mdlLR1
BP = 0.47177, df = 1, p-value = 0.4922

    studentized Breusch-Pagan test

data:  mdlLR2
BP = 0.043658, df = 1, p-value = 0.8345

    studentized Breusch-Pagan test

data:  mdlLR3
BP = 0.10685, df = 1, p-value = 0.7438

2. Il reste encore à étudier de plus près le cas des points n°13 et n°16 pour voir s’il ne sont pas éventuellement des points influents.

En conclusion, quelque soit la transformation retenue parmi les trois présentées précédemment, on obtient un modèle de régression qui est linéaire et dont le problème d’héteroscédasticité n’apparaît plus.