Chapitre1 Concepts de base

Objectif du chapitre: Apprendre à construire un modèle de régression linéaire simple à partir d’un jeu de données. Savoir interpréter les paramètres du modèle et faire de l’inférence statistique à leur sujet. Utiliser le modèle de régression linéaire pour faire des pronostics. Comprendre comment les calculs peuvent être implémentés dans le logiciel R.

1.1 Le modèle linéaire

On dit que deux variables aléatoires \((X,Y)\) sont reliées linéairement si:

\[\begin{equation} \tag{1.1} Y=\beta_0+\beta_1X+e \end{equation}\]

où: \(\beta_0\) et \(\beta_1\) sont les paramètres du modèle linéaire reliant Y à X; \(e\) est l’erreur aléatoire (appelée aussi résidu).

L’erreur aléatoire \(e\) est causée par des phénomènes aléatoires qui ne peuvent être ni prédits ni expliqués (variation non-expliquée dans le modèle, appelée aussi variation résiduelle).

Hypothèse 1.1 (Caractérisation statistique de l'erreur aléatoire) Pour toute valeur donnée \(x\) de \(X\), les erreurs aléatoires sont indépendantes et identiquement distribuées selon une loi normale de moyenne nulle et de même variance \((\sigma^2)\):

\[\begin{equation} \tag{1.2} e|(X=x) \sim i.i.d. N(0,\sigma^2) \; \forall x \end{equation}\]

où: l’acronyme i.i.d. signifie indépendantes et identiquement distribuées; \(\sigma^2\) est la variance des résidus:

\[\begin{equation} \tag{1.3} \sigma^2=Var[Y|(X=x)] \; \forall x \end{equation}\]

On verra dans le chapitre 2 comment vérifier ces hypothèses.

Lorsque l’on veut modéliser statistiquement la relation entre deux variables aléatoires reliées linéairement, on se propose de trouver une équation analytique permettant de prédire la valeur que prendra \(Y\) pour une valeur donnée de \(X\). Cela, revient à trouver ce que l’on appelle l’équation de la droite de régression de \(Y\) en \(X\):

\[\begin{equation} \tag{1.4} \hat{y}=E[Y|(X=x)]=E[\beta_0+\beta_1x]+E[e|(X=x)]=\beta_0+\beta_1x \end{equation}\]

où: \(\hat{y}\) est appelée valeur prédite par le modèle linéaire lorsque \(X=x\) (ou valeur ajustée de \(Y\) sachant que \(X=x\)).

1.2 Estimation des paramètres du modèle linéaire

Dans ce paragraphe on présente l’approche utilisée pour estimer les paramètres (\(\beta_0\) et \(\beta_1\)) du modèle de régression linéaire lorsque l’on dispose d’un échantillon de données. Les expressions des intervalles de confiance pour ces paramètres sont déduites. La construction des tests d’hypothèse pour vérifier si \(\beta_0\) et \(\beta_1\) sont significativement différents de zéro d’un point de vue statistique est également présentée.

1.2.1 Approche d’estimation des moindres carrés

En pratique, pour la construction du modèle linéaire, on dispose seulement d’un échantillon de valeurs du couple de variables aléatoires \((X,Y)\): \(ech=\{(x_1,y_1), (x_2,y_2),...,(x_n,y_n)\} = \{(x_i,y_i)|i \in \{1,...,n\}\). Ceci est illustré dans l’exemple ci-dessous qui servira de référence pour les calculs effectués avec le logiciel R dans ce chapitre:

Exemple 1.1 (Teneur en protéines brutes dans les farines de blé) On cherche à appliquer la spectrométrie proche infrarouge pour analyser la teneur en protéines brutes dans des lots de farines de blé. Une étude préliminaire a montré que l’absorption lumineuse à la longueur d’onde de 2200 nm (1 nm = 10^–9 m) pouvait être représentative de la teneur en protéines. Dix lots de farines de blé ont été collectés et analysés par la méthode de référence, qui est ici le dosage des protéines brutes par la méthode normalisée de Kjeldahl. On dispose, pour ces dix lots, de la mesure spectrométrique à 2200 nm (variable prédictive \(X\)) et de la teneur en protéines, exprimée en pourcentage de la matière sèche des farines (variable à prédire \(Y\)) - voir le fichier TeneurProteinesFarine.xlsx dans le répertoire Base de données dans Moodle.

Absorption_Lumin	Teneur_Prot
0.9006	9.1
0.9468	13.0
0.9416	13.1
0.9373	11.6
0.9118	9.8
0.9082	9.8
0.9440	12.5
0.9599	13.8
0.9749	15.5
0.9663	14.1

Remarque: Dans cet exemple: \(n=10\), \(x_i,\:i \in \{1,...,10\}\) sont les 10 valeurs d’absorption lumineuse observées, \(y_i,\:i \in \{1,...,10\}\) sont les 10 valeurs de teneur en protéines correspondantes. Si l’on répétait l’expérience un grand nombre de fois, on obtiendrait à chaque fois d’autres valeurs \(x_i\) et \(y_i\). Donc, on peut considérer que \(x_i\) est une réalisation concrète d’une variable aléatoire \(X_i\) (la \(i^{ème}\) position dans l’échantillon de taille \(n\) de \(X\)) et \(y_i\) est une réalisation concrète d’une variable aléatoire \(Y_i\) (la \(i^{ème}\) position dans l’échantillon de taille \(n\) de \(Y\)).

Disposant seulement d’un échantillon (\(ech\)) et non de toute la population, les paramètres \(\beta_0\) et \(\beta_1\) du modèle linéaire ne seront jamais connus. Leurs estimateurs ponctuels (\(b_0\) et \(b_1\)) se déduisent de manière à ce que la droite de régression de \(Y\) en \(X\) passe de manière optimale entre les points de coordonnées \(\{(x_1,y_1), (x_2,y_2),...,(x_n,y_n)\}\) dans le plan cartésien XY.

L’équation de la droite de régression est:

\[\begin{equation} \tag{1.5} \hat{y}_i=E[Y|X=x_i]=b_0+b_1x_i, \: \forall x_i \in \{x_1,...,x_n\} \end{equation}\]

où: \(\hat{y}_i\) est appelée valeur prédite par le modèle linéaire lorsque \(X=x_i\) ou valeur ajustée de \(Y\) sachant que \(X=x_i\).

Mais, qu’est-ce que l’on entend par optimale lorsque l’on affirme que “la droite de régression passe de manière optimale entre les points de coordonnées \(\{(x_1,y_1), (x_2,y_2),...,(x_n,y_n)\}\) dans le plan cartésien XY” ? Dans la figure 1.1, on illustre quatre modèles régressifs linéaires utilisées pour ajuster les données de l’exemple 1.1.

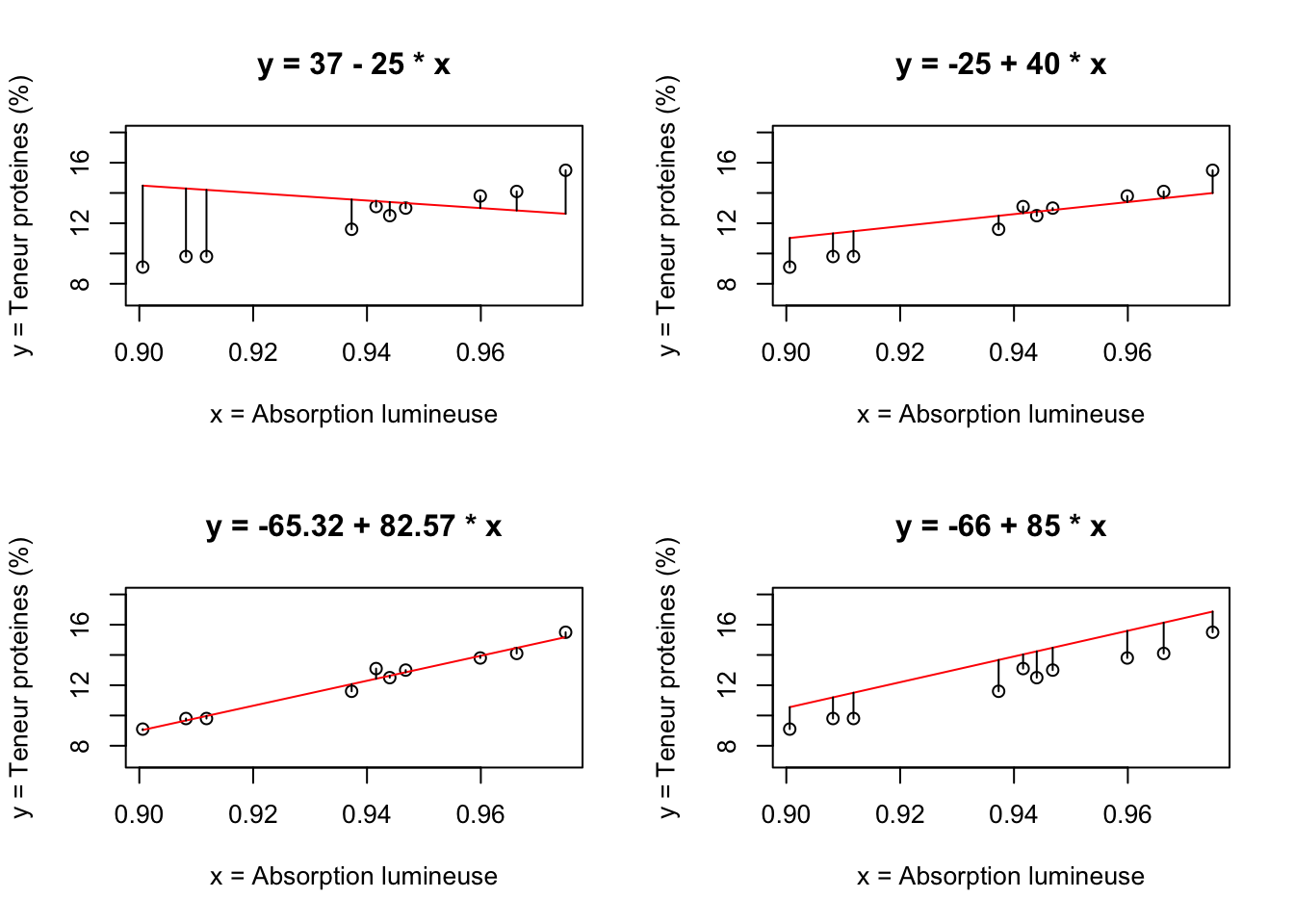
Figure 1.1: Droites de régression et résidus

Comme on peut le voir, la droite de régression dont l’équation est \(\hat{y}=-65.32+82.57x\) semble être celle qui s’ajuste le mieux aux données, car la distance qui sépare la valeur \(y_i\) de son correspondant sur la droite de régression (\(\hat{y}_i\)) est la plus petite sur l’ensemble de données. On en déduit que, par le mot optimal dans l’affirmation précédente, on entend minimiser les écarts suivants:

\[\begin{equation} \tag{1.6} \hat{e}_i = y_i - \hat{y}_i=Y|(X=x_i)-E[Y|(X=x_i)] \end{equation}\]

où: \(\hat{e}_i\) représente l’estimation ponctuelle du résidu du modèle linéaire dans \(X=x_i\).

Mathématiquement, cet objectif se décline en considérant que les estimateurs ponctuels des paramètres inconnus du modèle (\(\beta_0\) et \(\beta_1\)) se trouvent comme étant les valeurs \(b_0\) et \(b_1\) qui minimisent la somme des écarts au carré entre \(\hat{y}_i\) et \(y_i\) (méthode d’estimation dite des moindres carrées):

\[\begin{equation} \tag{1.7} min(RSS) = min\sum_{i=1}^n (y_i - \hat{y}_i)^2 \Leftrightarrow min\sum_{i=1}^n (y_i - b_0 - b_1x_i)^2 \end{equation}\]

où: \(RSS\) est la somme carrée résiduelle (Residual Sum of Squares).

Pour trouver le minimum de \(RSS\) on résout le système d’équations:

\[\begin{equation*} \left\{ \begin{aligned} & \frac{dRSS}{db_0}=0\\ & \frac{dRSS}{db_1}=0 \end{aligned} \right. \end{equation*}\]

Après le développement des équations, les solutions obtenues pour \(b_0\) et \(b_1\) sont:

\[\begin{equation} \tag{1.8} b_0=\bar{y}-b_1\bar{x} \end{equation}\]

\[\begin{equation} \tag{1.9} b_1=\frac{\sum_{i=1}^n x_iy_i-n\bar{x}\bar{y}}{\sum_{i=1}^n x_i^2 -n\bar{x}^2}=\frac{\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^n (x_i-\bar{x})^2}=\frac{s_{xy}}{s_{xx}} \end{equation}\]

où: \(\bar{x}=\frac{1}{n}\sum_{i=1}^n x_i\), \(\bar{y}=\frac{1}{n}\sum_{i=1}^n y_i\) et \(s_{xy}=\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})\); \(s_{xx}=\sum_{i=1}^n (x_i-\bar{x})^2\)

En utilisant le logiciel R pour faire ces calculs, on trouve pour l’exemple 1.1, le résultat suivant:

# Lecture de données
library(readxl)
DataSet <- read_excel("TeneurProteinesFarine.xlsx")
attach(DataSet)

# Construction du modèle de régression linéaire
mdlLR<-lm(Teneur_Prot~Absorption_Lumin)

# Affichage des coefficients du modèle
mdlLR$coefficients
#>      (Intercept) Absorption_Lumin 
#>        -65.31714         82.57250

Remarques: 1) La fonction read_excel est utilisée pour la lecture du fichier de données .xlsxl (dans notre cas: TeneurProteinesFarine.xlsx); 2) Si le fichier de données ne se trouve pas dans le même répertoire que le fichier du code R, alors il faut indiquer le chemin complet vers le fichier .xlsx; 3) La fonction attach() permet de pouvoir utiliser directement les noms des variables (entêtes de colonnes dans le fichier .xlsx) dans le code R; 4) La fonction lm() permet de créer le modèle linéaire (dans notre cas mdlLR): on indique d’abord la variable dépendante Y (dans notre cas Teneur_Prot); le symbole ~ indique la dépendance; ensuite on indique la variable explicative X (dans notre cas Absorption_Lumin); 5) Pour afficher les coefficients du modèle de régression linéaire on utilise la commande mdlLR$coefficients, ce qui conduit aux résultats suivants: (Intercept) qui est l’estimation de l’ordonnée à l’origine (c.à.d. \(b_0\)) et Absorption_Lumin qui est le coefficient directeur de la droite de régression (c.à.d. \(b_1\)).

On en déduit que l’équation du modèle linéaire régressif qui s’ajuste le mieux sur les données de l’échantillon est: \(\hat{y}=-65.32+82.57x\). La ligne rouge dans le graphique situé en bas à gauche dans la figure 1.1 correspond à cette équation. L’interprétation des deux coefficients du modèle est la suivante:

• \(b_1=82.57\): si l’on augmente l’absorption lumineuse de 0.01 unités, alors la teneur en protéines augmente de 0.8257% (car \(b_1>0\), donc la pente de la droite est positive).
• \(b_0=-65.32\): si l’absorption lumineuse serait égale à 0, alors la teneur en protéines serait de -65.32%; bien entendu, d’un point de vue physique cela n’a pas de sens (il faut prendre des précautions lorsque l’on sort du domaine expérimental, c.à.d. celui qui a servi à la construction du modèle!)

Il est important de noter que lorsque l’on dispose d’un échantillon concret de valeurs \(\{(x_1,y_1), (x_2,y_2),...,(x_n,y_n)\}\), les coefficients estimés (\(b_0\) et \(b_1\)) n’ont rien d’aléatoire [voir les équations (1.8) et (1.9) et l’exemple ci-dessus]. Toutefois, \(x_i\) et \(y_i\) sont les valeurs que prennent \(X_i\) (variable aléatoire qui représente la \(i^{ème}\) position dans l’échantillon de valeurs de \(X\)) et \(Y_i\) (variable aléatoire qui représente la \(i^{ème}\) position dans l’échantillon de valeurs de \(Y\)) lors du tirage aléatoire. En remplaçant dans les équations (1.8) et (1.9) les valeurs concrètes \(x_i\) et \(y_i\) par les variables aléatoires \(X_i\) et \(Y_i\), on obtient les formules caractérisant les variables aléatoires appelées estimateurs ponctuels de \(\beta_0\) et de \(\beta_1\):

\[\begin{equation} \tag{1.10} \hat{\beta}_0=\bar{Y}-\hat{\beta}_1\bar{X} \end{equation}\]

\[\begin{equation} \tag{1.11} \hat{\beta}_1=\frac{\sum_{i=1}^n X_iY_i-n\bar{X}\bar{Y}}{\sum_{i=1}^n X_i^2 -n\bar{X}^2}=\frac{\sum_{i=1}^n (X_i-\bar{X})(Y_i-\bar{Y})}{\sum_{i=1}^n (X_i-\bar{X})^2}=\frac{S_{XY}}{S_{XX}} \end{equation}\]

où: \(\bar{X}=\frac{1}{n}\sum_{i=1}^n X_i\); \(\bar{Y}=\frac{1}{n}\sum_{i=1}^n Y_i\); \(S_{XY}=\sum_{i=1}^n (X_i-\bar{X})(Y_i-\bar{Y})\); \(S_{XX}=\sum_{i=1}^n (X_i-\bar{X})^2\).

Remarques: 1) \(\hat{\beta}_0\) et \(\hat{\beta}_1\) sont des variables aléatoires; 2) \(b_0\) et \(b_1\) sont des réalisations concrètes de \(\hat{\beta}_0\) et \(\hat{\beta}_1\) sur un échantillon concret \(\{(x_1,y_1), (x_2,y_2),...,(x_n,y_n)\}\). La figure 1.2 illustre cet aspect:

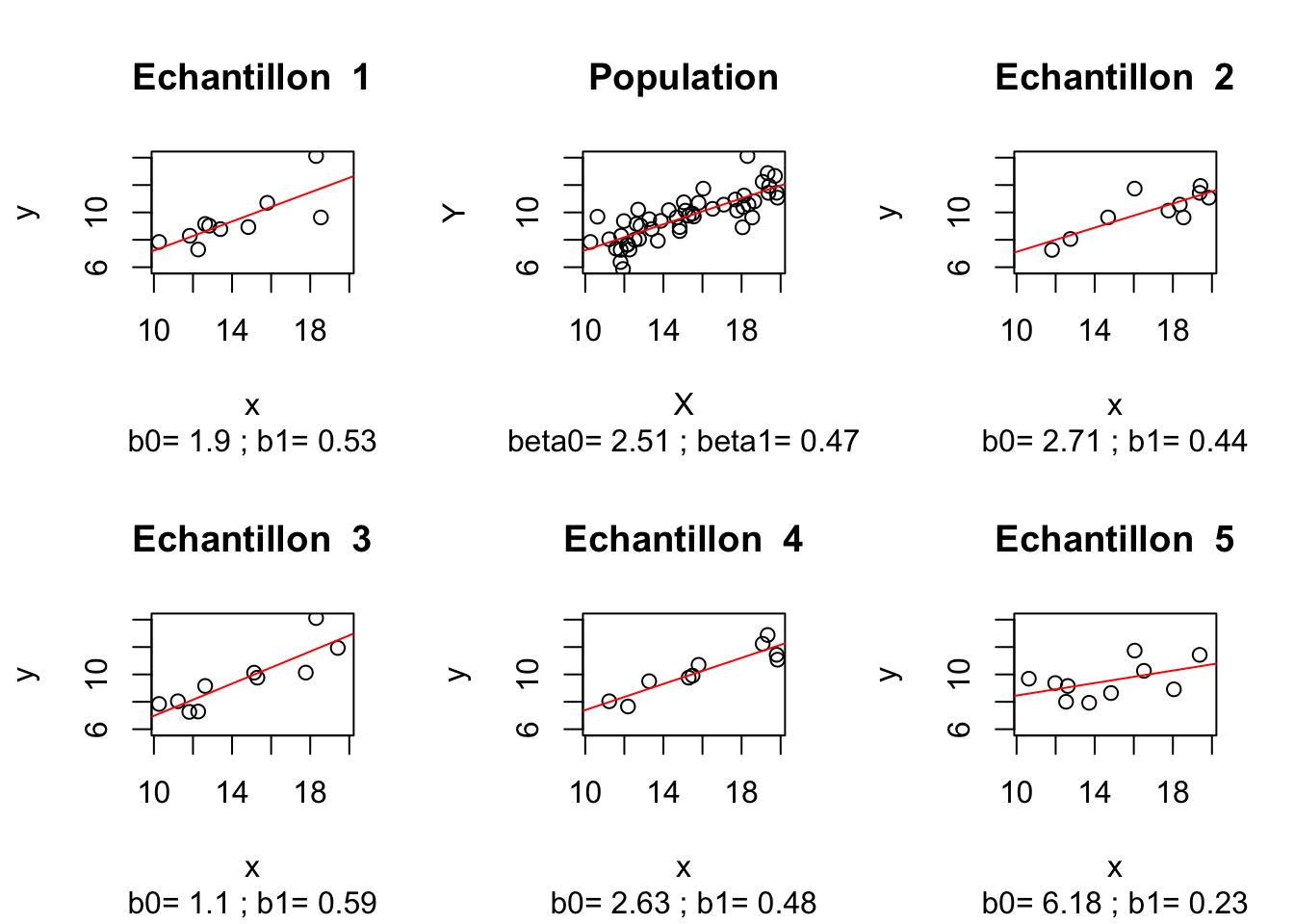
Figure 1.2: Valeurs concrètes des estimateurs ponctuels sur 5 échantillons aléatoires

En effet, on constate que si l’on disposait de toute la population, alors on connaîtrait les valeurs de \(\beta_0\) et \(\beta_1\) (on remarque que ces valeurs sont fixes et n’ont rien d’aléatoire). Par la méthode de moindres carrés exposée précédement, sur un échantillon aléatoire prélevé de la population, on peut calculer une estimation (\(b_0\), \(b_1\)) des valeurs inconnues (\(\beta_0\), \(\beta_1\)). Cette estimation est une approximation des valeurs inconnues (\(\beta_0\), \(\beta_1\)) et représente une réalisation particulière des variables aléatoires (\(\hat{\beta}_0\), \(\hat{\beta}_1\)) - voir les équations (1.10) et (1.11).

1.2.2 Inférences concernant les coefficients du modèle linéaire

Dans ce paragraphe on va caractériser statistiquement les variables aléatoires \(\hat{\beta}_0\) et \(\hat{\beta}_1\), c’est-à-dire que l’on déterminera pour chacune la loi de distribution la caractérisant ainsi que ses paramètres.

1.2.2.1 Distribution de \(\hat{\beta}_1\)

Théorème 1.1 (Propriétés statistiques de l'estimateur du coefficient directeur de la droite de régression) Si l’hypothèse 1.1 est vérifiée, l’estimateur ponctuel du coefficient directeur de la droite de régression est une variable aléatoire ayant les propriétés suivantes:

\[\begin{equation} \tag{1.12} \hat{\beta}_1|X \sim N\left(\beta_1,\frac{\sigma^2}{s_{xx}}\right) \end{equation}\]

Démonstration. Pour démontrer ce théorème, on démontre tout d’abord les trois propositions suivantes:

Proposition 1.1 Pour un échantillon aléatoire donné, \(\hat{\beta}_1\) est un estimateur ponctuel sans biais de \(\beta_1\):

\[\begin{equation} \tag{1.13} E[\hat{\beta}_1|X]=\beta_1 \end{equation}\]

Démonstration. \[\begin{align} E[\hat{\beta}_1|X]&=E[\hat{\beta}_1|(X_1=x_1,...,X_n=x_n)]=\\ &=E\left[\sum_{i=1}^n C_iY_i|(X_1=x_1,...,X_n=x_n)\right]=\\ &=E\left[\sum_{i=1}^n\left(\frac{x_i-\bar{x}}{s_{xx}}\right)Y_i|(X_i=x_i)\right]=\\ &=E\left[\sum_{i=1}^nc_iY_i|(X_i=x_i)\right]=\\ &=\sum_{i=1}^nc_iE[Y_i|(X_i=x_i)]=\sum_{i=1}^nc_i(\beta_0+\beta_1x_i)=\\ &=\beta_0\sum_{i=1}^n c_i+\beta_1\sum_{i=1}^n c_ix_i=\beta_1 \end{align}\]

car

\[\begin{align} \sum_{i=1}^n c_i&=\frac{1}{s_{xx}}\sum_{i=1}^n(x_i-\bar{x})=\frac{1}{s_{xx}}\left(\sum_{i=1}^n x_i-n\bar{x}\right)\\ &=\frac{1}{s_{xx}}\left(n\bar{x}-n\bar{x}\right)=0 \end{align}\]

et

\[\begin{align} \sum_{i=1}^n c_ix_i&=\sum_{i=1}^n\left(\frac{x_i-\bar{x}}{s_{xx}}\right)x_i=\frac{1}{s_{xx}}\sum_{i=1}^n(x_i^2-\bar{x}x_i)=\\ &=\frac{1}{s_{xx}}\left(\sum_{i=1}^nx_i^2-n\bar{x}^2\right)=\frac{1}{s_{xx}}\sum_{i=1}^n\left(x_i-\bar{x}\right)^2=\frac{1}{s_{xx}}s_{xx}=1. \end{align}\]

Proposition 1.2 L’efficacité de \(\hat{\beta}_1\) est d’autant meilleure que la variance de l’échantillon aléatoire \(x_i,\:i \in \{1,...,n\}\) est grande:

\[\begin{equation} \tag{1.14} Var[\hat{\beta}_1|X]=\frac{\sigma^2}{s_{xx}} \end{equation}\]

Démonstration. \[\begin{align} Var[\hat{\beta}_1|X]&=Var[\hat{\beta}_1|(X_1=x_1,...,X_n=x_n)]=\\ &=Var\left[\sum_{i=1}^n C_iY_i|(X_1=x_1,...,X_n=x_n)\right]=\\ &=Var\left[\sum_{i=1}^n\left(\frac{x_i-\bar{x}}{s_{xx}}\right)Y_i|(X_i=x_i)\right]=\\ &=Var\left[\sum_{i=1}^nc_iY_i|(X_i=x_i)\right]=\sum_{i=1}^n{c_i}^2Var[Y_i|(X_i=x_i)]=\\ &=\sigma^2\sum_{i=1}^n{c_i}^2=\sigma^2\sum_{i=1}^n \left(\frac{x_i-\bar{x}}{s_{xx}}\right)^2=\\ &=\frac{\sigma^2}{s_{xx}^2}\sum_{i=1}^n(x_i-\bar{x})^2=\frac{\sigma^2}{s_{xx}^2}s_{xx}=\frac{\sigma^2}{s_{xx}} \end{align}\]

Remarque: \(s_{xx}\) est à un coefficient près la variance des valeurs \(\{x_1,..., x_n\}\).

Il est important à retenir cet aspect car l’expérimentateur à souvent le choix des valeurs pour la variable explicative (X).

Proposition 1.3 L’estimateur du coefficient directeur de la droite de régression est une combinaison linéaire de Y_i:

\[\begin{equation} \tag{1.15} \hat{\beta}_1=\sum_{i=1}^n C_iY_i \end{equation}\]

Démonstration. En effet, le terme \(S_{XY}\) dans l’équation (1.11) se développe de la manière suivante:

\[\begin{align} S_{XY}=\sum_{i=1}^n (X_i-\bar{X})(Y_i-\bar{Y})&=\sum_{i=1}^n (X_i-\bar{X})Y_i-\bar{Y}\sum_{i=1}^n (X_i-\bar{X})\\ &=\sum_{i=1}^n (X_i-\bar{X})Y_i \end{align}\]

car, \(\sum_{i=1}^n (X_i-\bar{X})=0\).

Donc, en notant par \(C_i=\frac{X_i-\bar{X}}{S_{XX}}\), on obtient l’expression donnée dans l’équation (1.15)

Si l’hypothèse 1.1 est vérifiée, on en déduit que \(Y_i|X\) est distribué selon la loi normale. Par conséquent, \(\hat{\beta}_1|X\) est normalement distribué car addition des lois normales [voir l’équation (1.15)].

Donc, en prenant en compte les propositions 1.3, 1.1 et 1.2, le théorème 1.1 est démontré.

1.2.2.2 Distribution de \(\hat{\beta}_0\)

Théorème 1.2 (Propriétés statistiques de l'estimateur de l'ordonnée à l'origine de la droite de régression) Si l’hypothèse 1.1 est vérifiée, l’estimateur ponctuel de l’ordonnée à l’origine de la droite de régression est une variable aléatoire ayant les propriétés suivantes:

\[\begin{equation} \tag{1.16} \hat{\beta}_0|X \sim N\left(\beta_0,\sigma^2\left(\frac{1}{n}+\frac{\bar{x}^2}{s_{xx}}\right)\right) \end{equation}\]

Démonstration. Pour démontrer ce théorème, on démontre tout d’abord les deux propositions suivantes:

Proposition 1.4 Pour un échantillon aléatoire donné, \(\hat{\beta}_0\) est un estimateur ponctuel sans biais de \(\beta_0\):

\[\begin{equation} \tag{1.17} E[\hat{\beta}_0|X]=\beta_0 \end{equation}\]

Démonstration. Dans l’équation (1.10) on a donné l’expression mathématique de l’estimateur ponctuel du coefficient directeur de la droite de régression. On en déduit que:

\[\begin{equation} E[\hat{\beta}_0|X]=E[\bar{Y}|X]-E[\hat{\beta}_1|X]E[\bar{X}|X] \end{equation}\]

En développant les deux termes de cette équation, on obtient:

\[\begin{align} E[\bar{Y}|X]&=E\left[\frac{1}{n}\sum_{i=1}^{n}\left[Y_i|(X_i=x_i)\right]\right]=\\ &=\frac{1}{n}\sum_{i=1}^{n}E[Y_i|(X_i=x_i)]=\\ &=\frac{1}{n}\sum_{i=1}^{n}E[\beta_0+\beta_1x_i+e_i]=\\ &=\beta_0+\frac{\beta_1}{n}\sum_{i=1}^{n}x_i=\beta_0+\beta_1\bar{x} \end{align}\]

\[\begin{equation} E[\hat{\beta}_1|X]E[\bar{X}|X]=\beta_1\bar{x} \end{equation}\]

Par conséquent:

\[\begin{equation} E[\hat{\beta}_0|X]=\beta_0+\beta_1\bar{x}-\beta_1\bar{x}=\beta_0 \end{equation}\]

Proposition 1.5 L’efficacité de \(\hat{\beta}_0\) est d’autant meilleure que la variance de l’échantillon aléatoire \(x_i,\:i \in \{1,...,n\}\) est grande:

\[\begin{equation} \tag{1.18} Var[\hat{\beta}_0|X]=\sigma^2\left(\frac{1}{n}+\frac{\bar{x}^2}{s_{xx}}\right) \end{equation}\]

Démonstration. \[\begin{align} Var[\hat{\beta}_0|X]&=Var[\bar{Y}-\hat{\beta}_1\bar{X}|X]=\\ &=Var[\bar{Y}|X]+Var[\hat{\beta}_1\bar{X}|X]-2Cov[\bar{Y},\hat{\beta}_1\bar{X}|X]=\\ &=Var[\bar{Y}|X]+\bar{x}^2Var[\hat{\beta}_1|X]-2Cov[\bar{Y},\hat{\beta}_1\bar{X}|X] \end{align}\]

En développant les termes de cette équation, on obtient:

\[\begin{align} Var[\bar{Y}|X]&=Var\left[\frac{1}{n}\sum_{i=1}^{n}[Y_i|(X_i=x_i)]\right]=\\ &=\frac{1}{n^2}\sum_{i=1}^{n}Var[Y_i|(X_i=x_i)]=\\ &=\frac{1}{n^2}\sum_{i=1}^{n}\sigma^2=\frac{n\sigma^2}{n^2}=\frac{\sigma^2}{n} \end{align}\]

Selon l’équation (1.14) on a \(Var[\hat{\beta}_1|X]=\frac{\sigma^2}{s_{xx}}\). Enfin, en utilisant l’équation (1.15) on en déduit que:

\[\begin{align} Cov[\bar{Y},\hat{\beta}_1\bar{X}|X]&=Cov\left[\frac{1}{n}\sum_{i=1}^{n}Y_i,\bar{x}\sum_{i=1}^{n}c_iY_i]\right]=\\ &=\frac{\bar{x}}{n}\sum_{i=1}^{n}Cov[Y_i,c_iY_i]=\frac{\bar{x}}{n}\sum_{i=1}^{n}c_iCov[Y_i,Y_i]=\\ &=\frac{\bar{x}\sigma^2}{n}\sum_{i=1}^{n}c_i=0 \end{align}\]

Par conséquent, \(Var[\hat{\beta}_0|X]=\sigma^2\left(\frac{1}{n}+\frac{\bar{x}^2}{s_{xx}}\right)\)

Si l’hypothèse 1.1 est vérifiée, on en déduit que \(Y_i|X\) est distribué selon la loi normale. Par conséquent, \(\bar{Y}|X\) est normalement distribué car addition des lois normales et implicitement \(\hat{\beta}_0|X\) est normalement distribué [voir l’équation (1.10)]. Donc, en prenant additionnellement en compte les propositions 1.4 et 1.5, le théorème 1.2 est démontré.

1.2.2.3 Intervalles de confiance pour \(\beta_0\) et \(\beta_1\)

A partir de l’équation (1.12), on peut écrire que:

\[\begin{equation} Z=\frac{\hat{\beta}_1-\beta_1}{\frac{\sigma}{\sqrt{s_{xx}}}} \sim N(0,1) \end{equation}\]

Toutefois, en pratique \(\sigma\) est inconnu et on le remplace par l’écart-type des résidus estimés du modèle linéaire (\(S\)):

\[\begin{equation} \tag{1.19} T=\frac{\hat{\beta}_1-\beta_1}{\frac{S}{\sqrt{s_{xx}}}}=\frac{\hat{\beta}_1-\beta_1}{se(\hat{\beta}_1)} \sim t_{n-2} \end{equation}\]

où: \(S=\sqrt{\frac{1}{n-1}\sum_{i=1}^n(Y_i-\hat{Y}_i)^2}\), \(se(\hat{\beta}_1)=\frac{S}{\sqrt{s_{xx}}}\) est appelée l’erreur standard estimée de \(\hat{\beta}_1\); \(t_{n-2}\) est la loi de Student ayant \(n-2\) dégrées de liberté.

Dans ce cas, l’intervalle de confiance à \(100(1-\alpha)\%\) pour \(\beta_1\) est donné par:

\[\begin{equation} \tag{1.20} \hat{\beta}_1-t_{\frac{\alpha}{2},n-2}se(\hat{\beta}_1) \le \beta_1 \le \hat{\beta}_1+t_{\frac{\alpha}{2},n-2}se(\hat{\beta}_1) \end{equation}\]

où: \(t_{\frac{\alpha}{2},n-2}\) est le seuil de probabilité d’ordre \(\frac{\alpha}{2}\) pour la loi de Student ayant \(n-2\) degrés de liberté.

Remarque: Lorsque l’on dispose d’un échantillon \(\left\{(x_i,y_i)|i \in \left\{1,2,...,n\right\}\right\}\), l’expression de l’intervalle de confiance à \(100(1-\alpha)\%\) pour \(\beta_1\) devient:

\[\begin{equation} \tag{1.21} b_1-t_{\frac{\alpha}{2},n-2}\frac{s}{\sqrt{s_{xx}}} \le \beta_1 \le b_1+t_{\frac{\alpha}{2},n-2}\frac{s}{\sqrt{s_{xx}}} \end{equation}\]

où: \(s=\sqrt{\frac{1}{n-1}\sum_{i=1}^n(y_i-\hat{y}_i)^2}\).

De la même manière, en partant de l’équation (1.12), on peut écrire que:

\[\begin{equation} Z=\frac{\hat{\beta}_0-\beta_0}{\sigma\sqrt{\frac{1}{n}+\frac{\bar{x}^2}{s_{xx}}}} \sim N(0,1) \end{equation}\]

Toutefois, en pratique \(\sigma\) est inconnu et on le remplace par l’écart-type des résidus estimés du modèle linéaire (\(S\)):

\[\begin{equation} \tag{1.22} T=\frac{\hat{\beta}_0-\beta_0}{S\sqrt{\frac{1}{n}+\frac{\bar{x}^2}{s_{xx}}}}=\frac{\hat{\beta}_0-\beta_0}{se(\hat{\beta}_0)} \sim t_{n-2} \end{equation}\]

où: \(se(\hat{\beta}_0)={S\sqrt{\frac{1}{n}+\frac{\bar{x}^2}{s_{xx}}}}\) est appelée l’erreur standard estimée de \(\hat{\beta}_0\); \(t_{n-2}\) est la loi de Student ayant \(n-2\) dégrées de liberté.

Dans ce cas, l’intervalle de confiance à \(100(1-\alpha)\%\) pour \(\beta_0\) est donné par:

\[\begin{equation} \tag{1.23} \hat{\beta}_0-t_{\frac{\alpha}{2},n-2}se(\hat{\beta}_0) \le \beta_0 \le \hat{\beta}_0+t_{\frac{\alpha}{2},n-2}se(\hat{\beta}_0) \end{equation}\]

où: \(t_{\frac{\alpha}{2},n-2}\) est le seuil de probabilité d’ordre \(\frac{\alpha}{2}\) pour la loi de Student ayant \(n-2\) degrés de liberté.

Remarque: Lorsque l’on dispose d’un échantillon \(\left\{(x_i,y_i)|i \in \left\{1,2,...,n\right\}\right\}\), l’expression de l’intervalle de confiance à \(100(1-\alpha)\%\) pour \(\beta_0\) devient:

\[\begin{equation} \tag{1.24} b_0-t_{\frac{\alpha}{2},n-2}{s\sqrt{\frac{1}{n}+\frac{\bar{x}^2}{s_{xx}}}} \le \beta_0 \le b_0+t_{\frac{\alpha}{2},n-2}{s\sqrt{\frac{1}{n}+\frac{\bar{x}^2}{s_{xx}}}} \end{equation}\]

Le code ci-dessous illustre, dans le cas de l’exemple 1.1, la manière dont on peut déduire les intervalles de confiance à 95% pour \(\beta_0\) et \(\beta_1\) à l’aide du logiciel R:

confint(object = mdlLR,level = 0.95)
#>                      2.5 %    97.5 %
#> (Intercept)      -75.52564 -55.10864
#> Absorption_Lumin  71.70598  93.43902

Remarque: La fonction confint permet d’afficher les limites des intervalles de confiance pour les coefficients du modèle; les paramètres de cette fonction sont: object - un objet de type “linear model” (dans notre cas mdlLR); level - le niveau de confiance souhaité pour l’intervalle.

1.2.2.4 Tests d’hypthèses pour \(\beta_0\) et \(\beta_1\)

Il est d’usage de tester si le coefficient \(\beta_1\) est différent de zéro:

\[\begin{equation*} \left\{ \begin{aligned} & H_0: \beta_1=0\\ \\ & H_1: \beta_1 \ne 0 \end{aligned} \right. \end{equation*}\]

La variable de test est donnée dans l’équation (1.19), donc, pour réaliser le test, on calcule la valeur concrète \(t\) de \(T\) sur l’échantillon de données et si \(t_{\frac{\alpha}{2},n-2}<t\) ou si \(t<-t_{\frac{\alpha}{2},n-2}\) alors on rejette l’hypothèse nulle et on considère qu’au seuil de signification \(\alpha\) le coefficient directeur de la droite de régression (\(\beta_1\)) est significativement différent de zéro.

Pour ce qui concerne le test d’hypothèse du coefficient \(\beta_0\) :

\[\begin{equation*} \left\{ \begin{aligned} & H_0: \beta_0=0\\ & H_1: \beta_0 \ne 0 \end{aligned} \right. \end{equation*}\]

la seule différence par rapport à \(\beta_1\) est que la variable de test est donnée par l’expression mentionnée dans l’équation (1.22).

Remarque: On rappelle que les logiciels de calcul statistique utilisent la p.value pour la prise de décision. La p.value est la probabilité que la statistique de test (\(T\)) soit encore plus extrême que \(t\): \(p.value=P(|T|>t)\). Si la p.value < \(\alpha\) alors on rejette l’hypothèse nulle.

Le code ci-dessous illustre, dans le cas de l’exemple 1.1, la manière dont on peut réaliser les tests d’hypothèses pour les coefficients du modèle de régression linéaire (\(\beta_0\) et \(\beta_1\)) à l’aide du logiciel R:

summary(mdlLR)$coefficients
#>                   Estimate Std. Error   t value
#> (Intercept)      -65.31714   4.426922 -14.75453
#> Absorption_Lumin  82.57250   4.712274  17.52286
#>                      Pr(>|t|)
#> (Intercept)      4.378994e-07
#> Absorption_Lumin 1.148568e-07

où: la colonne Estimate contient les estimateurs ponctuels de \(\beta_0\) et respectivement de \(\beta_1\) [voir les équations (1.8) et (1.9)]; la colonne Std. Error contient les erreurs standard estimées (estimateurs ponctuels de \(se(\hat{\beta}_0)\) et respectivement \(se(\hat{\beta}_1)\)); la colonne t value est la valeur concrete \(t\) de la statistique du test (\(T\)) sur l’échantillon de données [voir les équations (1.22) et (1.19)]; enfin, la colonne Pr(>|t|) est la p.value du test.

Interprétation des résultats: On peut constater que, dans le cas des données de l’exemple 1.1, la p.value du test d’hypothèse pour les deux coefficients du modèle est très petite (< 0.05), donc on peut considérer que les deux coefficients de la droite de régression sont significativement différents de zéro. La même conclusion peut être tirée en regardant les intervalles de confiances à 95% pour les deux coefficients du modèle [voir le paragraphe 1.2.2.3]: puisque la valeur de zéro n’est ni dans l’intervalle de confiance de \(\beta_0\) ni dans celui de \(\beta_1\), on peut affirmer qu’au seuil de signification de 5%, les deux coefficients du modèle ne peuvent pas être considérés nulls.

1.3 Intervalle de confiance pour la droite de régression

Dans ce paragraphe on déduit l’expression de l’intervalle de confiance pour la droite de régression caractérisant la population toute entière. On rappelle que cette droite de régression est inconnue dans la pratique parce que l’on dispose seulement d’un échantillon de données \(\left\{(X_i,Y_i)|i \in \left\{1,2,...,n\right\}\right\}\) prélevé de la population.

Théorème 1.3 (Propriétés statistiques de l'éstimateur de la droite de régression) Si l’hypothèse 1.1 est vérifiée, on démontre que: \[\begin{equation} \tag{1.25} \hat{y}|(X=x) \sim N\left(\beta_0+\beta_1x, \sigma^2\left[\frac{1}{n}+\frac{(x-\bar{x})^2}{s_{xx}}\right]\right) \end{equation}\]

Démonstration. On rappelle que la droite de régression caractérisant la population est donnée par l’équation (1.4). Une estimation de celle-ci sur la base de données de l’échantillon est:

\[\begin{equation} \tag{1.26} \hat{y}|(X=x)=\hat{\beta}_0+\hat{\beta}_1x \end{equation}\]

Par conséquent, à partir des équations (1.13) et (1.17) on peut en déduire que:

\[\begin{align} E[\hat{y}|X=x]&=E[\hat{\beta}_0+\hat{\beta}_1x]=E[\hat{\beta}_0|X=x]+E[\hat{\beta}_1|X=x]x\\ &=\beta_0+\beta_1x \tag{1.27} \end{align}\]

\[\begin{align} Var[\hat{y}|X=x]&=Var[\hat{\beta}_0+\hat{\beta}_1x|X=x]=\\ &=Var[\hat{\beta}_0|X=x]+Var[\hat{\beta}_1|X=x]x^2+2xCov(\hat{\beta}_0,\hat{\beta}_1|X=x) \end{align}\]

où: \(Var[\hat{\beta}_0]\) et \(Var[\hat{\beta}_1]\) sont données par les équations (1.18) et respectivement (1.14) et:

\[\begin{align} Cov(\hat{\beta}_0,\hat{\beta}_1|X=x)&=Cov(\bar{y}-\hat{\beta}_1\bar{x},\hat{\beta}_1|X=x)=\\ &=Cov(\bar{y},\hat{\beta}_1|X=x)-\bar{x}Cov(\hat{\beta}_1,\hat{\beta}_1)=0-\bar{x}Var[\hat{\beta}_1]=\\ &=-\frac{\sigma^2\bar{x}}{s_{xx}} \end{align}\]

Par conséquent, on obtient:

\[\begin{align} Var[\hat{y}|X=x]&=\sigma^2\left(\frac{1}{n}+\frac{\bar{x}^2}{s_{xx}}\right)+\frac{\sigma^2}{s_{xx}}x^2-2x\frac{\sigma^2\bar{x}}{s_{xx}}=\\ &=\sigma^2\left[\frac{1}{n}+\frac{(x-\bar{x})^2}{s_{xx}}\right] \tag{1.28} \end{align}\]

En corroborant ces résultats avec le fait que \(\hat{\beta}_0\) et \(\hat{\beta}_1\) ont des distributions normales [voir les équations (1.16) et (1.12)], le théorème est démontré.

Par conséquent:

\[\begin{equation} Z=\frac{\hat{y}|(X=x)-(\beta_0+\beta_1x)}{\sigma\sqrt{\frac{1}{n}+\frac{(x-\bar{x})^2}{s_{xx}}}} \sim N(0,1) \end{equation}\]

En pratique, souvent la valeur de \(\sigma\) est inconnue et on la remplace par son meilleur estimateur (\(S\)) qui est la variance estimée des résidus. Dans ce cas:

\[\begin{equation} \tag{1.29} T=\frac{\hat{y}|(X=x)-(\beta_0+\beta_1x)}{S\sqrt{\frac{1}{n}+\frac{(x-\bar{x})^2}{s_{xx}}}} \sim t_{n-2} \end{equation}\]

où: \(t_{n-2}\) est la loi de Student ayant (n-2) degrés de liberté.

Donc, l’intervalle de confiance \(100(1-\alpha)\%\) pour la droite de régression de la population est:

\[\begin{equation} \tag{1.30} \hat{\beta}_0+\hat{\beta}_1x-t_{\frac{\alpha}{2},n-2}se(\hat{y})\leq \hat{y} \leq \hat{\beta}_0+\hat{\beta}_1x+t_{\frac{\alpha}{2},n-2}se(\hat{y}) \end{equation}\]

où: \(se(\hat{y})=S\sqrt{\frac{1}{n}+\frac{(x-\bar{x})^2}{s_{xx}}}\); \(t_{\frac{\alpha}{2},n-2}\) est le seuil de probabilité d’ordre \(\frac{\alpha}{2}\) pour la loi de Student ayant \(n-2\) degrés de liberté.

Remarque: Dans l’équation (1.30) on remarque que la largeur de l’intervalle de confiance est minimale pour \(x=\bar{x}\) et augmente au fur et à mesure que \(x\) s’écarte par rapport à \(\bar{x}\).

Remarque: Lorsque l’on dispose d’un échantillon \(\left\{(x_i,y_i)|i \in \left\{1,2,...,n\right\}\right\}\), l’expression de l’intervalle de confiance à \(100(1-\alpha)\%\) pour \(\hat{y}\) devient:

\[\begin{equation} \tag{1.31} b_0+b_1x-t_{\frac{\alpha}{2},n-2}se(\hat{y})\leq \hat{y} \leq b_0+b_1x+t_{\frac{\alpha}{2},n-2}se(\hat{y}) \end{equation}\]

où: \(se(\hat{y})=s\sqrt{\frac{1}{n}+\frac{(x-\bar{x})^2}{s_{xx}}}\); \(t_{\frac{\alpha}{2},n-2}\) est le seuil de probabilité d’ordre \(\frac{\alpha}{2}\) pour la loi de Student ayant \(n-2\) degrés de liberté.

Le code R ci-dessous illustre, dans le cas de l’exemple 1.1, la manière dont on peut déduire l’intervalle de confiance à 95% pour la droite de régression lorsque l’absorption lumineuse est de 0.90:

(predRL<-predict(object = mdlLR, newdata = data.frame("Absorption_Lumin" = 0.90), 
              interval = "confidence", level = 0.95))
#>        fit      lwr      upr
#> 1 8.998112 8.499569 9.496655

La fonction predict est utilisée ici pour prédire avec le modèle régressif les valeurs de la teneur en protéines selon des valeurs choisies d’absorption lumineuse. Les paramètres de cette fonction sont: object - le modèle linéaire utilisé lors de la réalisation des prédictions (dans notre cas mdlLR); newdata - les valeurs pour la variable explicative (données sous forme de data.frame) pour lesquelles on souhaite faire une prédiction à l’aide du modèle (dans notre cas "Absorption_Lumin" = 0.93); interval - le type d’intervalle de confiance pour accompagner la prédiction (ici en choisissant "confidence" on a l’intervalle de confiance pour la droite de régression); level - le niveau de confiance pour l’intervalle. La variable predRL contient la valeur prédite de la teneur en protéines (fit) et les limites de l’intervalle de confiance à 95% pour la droite de régression (lwr et upr) - voir la figure 1.3.

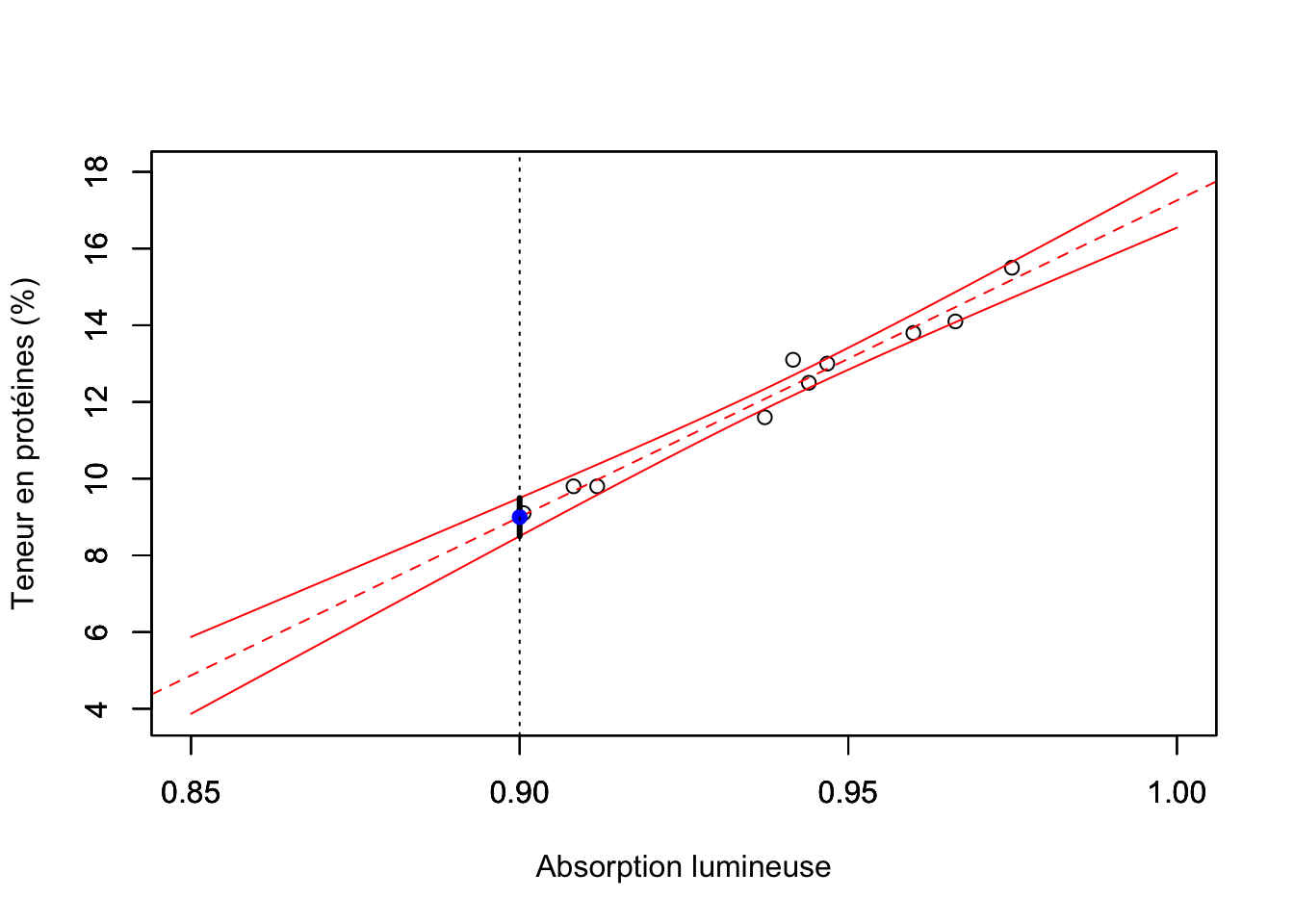
Figure 1.3: Intervalle de confiance à 95% pour la droite de régression

Remarque: on voit bien dans la figure 1.3 que plus on s’éloigne de la moyenne de l’absorption lumineuse (\(\bar{x}\)) et plus l’amplitude de l’intervalle de confiance pour la droite de régression augmente.

1.4 Intervalle de confiance pour la valeur prédite

Dans ce paragraphe on déduit l’expression de l’intervalle de confiance pour la valeur prédite de \(Y\) lorsque \(X=x\).

Théorème 1.4 (Propriétés statistiques de l'estimateur de la valeur prédite) Si l’hypothèse 1.1 est vérifiée, on démontre que:

\[\begin{equation} \tag{1.32} Y-\hat{y}|(X=x) \sim N\left(0, \sigma^2\left[1+\frac{1}{n}+\frac{(x-\bar{x})^2}{s_{xx}}\right]\right) \end{equation}\]

Démonstration. On rappelle qu’une estimation (\(\hat{y}\)) de la valeur prédite (\(Y\)) à l’aide du modèle est donnée dans l’équation (1.26).

Si les hypothèses mentionnées dans l’équation (1.2) sont vérifiées, alors:

\[\begin{equation} \tag{1.33} E[Y-\hat{y}|(X=x)]=E[Y|(X=x)]-E[\hat{\beta}_0+\hat{\beta}_1x|(X=x)]=0 \end{equation}\]

Sachant que \(\hat{y}\) est indépendant de \(Y\), on déduit que:

\[\begin{align} \tag{1.34} Var[Y-\hat{y}|(X=x)]&=Var[Y|X=x]+Var[\hat{y}|X=x]-\\ &-2Cov[Y,\hat{y}|X=x]=\\ &=\sigma^2+\sigma^2\left[\frac{1}{n}+\frac{(x-\bar{x})^2}{s_{xx}}\right]-0\\ &=\sigma^2\left[1+\frac{1}{n}+\frac{(x-\bar{x})^2}{s_{xx}}\right] \end{align}\]

Et comme \(Y\), \(\hat{\beta}_0\) et \(\hat{\beta}_1\) sont distribués selon des lois normales, il en résulte que \(Y-\hat{y}|(X=x)\) suit aussi une loi normale, donc le théorème est démontré.

Il en résulte que:

\[\begin{equation} Z=\frac{Y-\hat{y}|(X=x)}{\sigma\sqrt{1+\frac{1}{n}+\frac{(x-\bar{x})^2}{s_{xx}}}}\sim N(0,1) \end{equation}\]

En pratique, la valeur de \(\sigma\) est inconnue, donc on la remplace par son meilleur estimateur ponctuel \(S\) (l’écart-type des résidus estimés du modèle). Dans ce cas:

\[\begin{equation} \tag{1.35} T=\frac{Y-\hat{y}}{S\sqrt{1+\frac{1}{n}+\frac{(x-\bar{x})^2}{s_{xx}}}}\sim t_{n-2} \end{equation}\]

où: \(t_{n-2}\) est la loi de Student ayant (n-2) degrés de liberté.

Donc, l’intervalle de confiance \(100(1-\alpha)\%\) pour la valeur prédite de \(Y\) est:

\[\begin{equation} \tag{1.36} \hat{\beta}_0+\hat{\beta}_1x-t_{\frac{\alpha}{2},n-2}se(Y)\leq Y \leq \hat{\beta}_0+\hat{\beta}_1x+t_{\frac{\alpha}{2},n-2}se(Y) \end{equation}\]

où: \(se(Y)=S\sqrt{1+\frac{1}{n}+\frac{(x-\bar{x})^2}{s_{xx}}}\); \(t_{\frac{\alpha}{2},n-2}\) est le seuil de probabilité d’ordre \(\frac{\alpha}{2}\) pour la loi de Student ayant \(n-2\) degrés de liberté.

Remarque: Dans l’équation (1.36) on remarque que la largeur de l’intervalle de confiance est minimale pour \(x=\bar{x}\) et augmente au fur et à mesure que \(x\) s’écarte par rapport à \(\bar{x}\).

Remarque: Lorsque l’on dispose d’un échantillon \(\left\{(x_i,y_i)|i \in \left\{1,2,...,n\right\}\right\}\), l’expression de l’intervalle de confiance à \(100(1-\alpha)\%\) pour \(Y\) devient:

\[\begin{equation} \tag{1.37} b_0+b_1x-t_{\frac{\alpha}{2},n-2}se(Y)\leq Y \leq b_0+b_1x+t_{\frac{\alpha}{2},n-2}se(Y) \end{equation}\]

où: \(se(Y)=s\sqrt{1+\frac{1}{n}+\frac{(x-\bar{x})^2}{s_{xx}}}\); \(t_{\frac{\alpha}{2},n-2}\) est le seuil de probabilité d’ordre \(\frac{\alpha}{2}\) pour la loi de Student ayant \(n-2\) degrés de liberté.

Le code R ci-dessous illustre, dans le cas de l’exemple 1.1, la manière dont on peut déduire l’intervalle de confiance à 95% pour la valeur prédite de la teneur en protéines lorsque l’absorption lumineuse est de 0.90:

# on prédit à l'aide du modèle les valeurs correspondantes de y accompagnées par l'intervalle de confiance (IC) pour la la valeur prédite
(predY<-predict(object = mdlLR, newdata = data.frame("Absorption_Lumin" = 0.9),
              interval = "prediction", level = 0.95))
#>        fit      lwr      upr
#> 1 8.998112 8.036311 9.959914

On remarque que le paramètre interval de la fonction predict prend la valeur "prediction" lorsque l’on veut calculer l’intervalle de confiance pour la valeur prédite. La variable predY contient la valeur prédite (fit) et les limites de l’intervalle de confiance à 95% (lwr et upr) - voir aussi la figure 1.4.

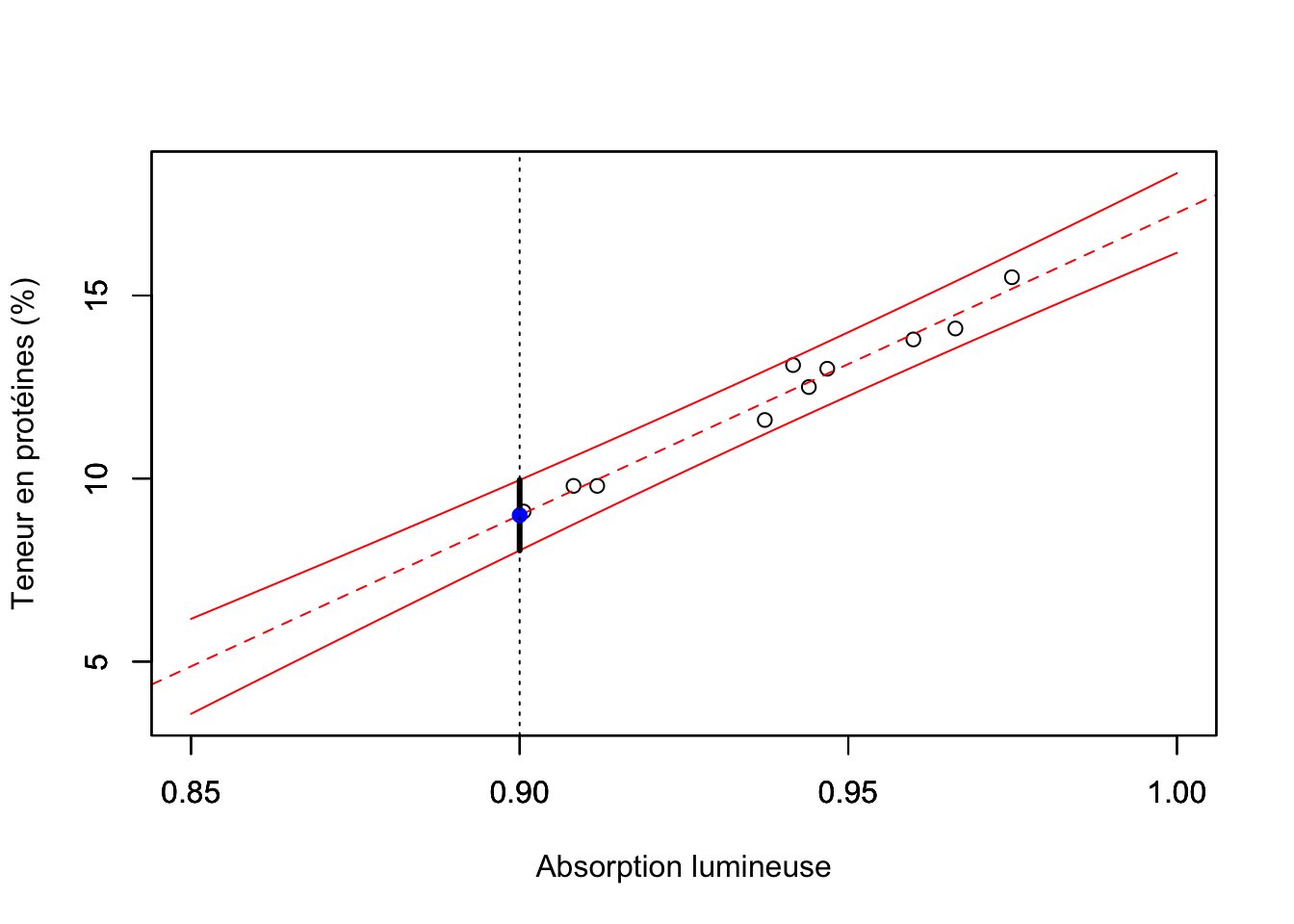
Figure 1.4: Intervalle de confiance à 95% pour la valeur prédite

Remarques: 1) On voit dans la figure 1.4 que l’amplitude de l’intervalle de confiance de la valeur prédite augmente lorsque l’on s’éloigne de la valeur d’absorption lumineuse moyenne (\(\bar{x}\)); 2) En comparant les figures 1.3 et 1.4, on voit que l’amplitude de l’intervalle de confiance pour la valeur prédite est plus large que celle de l’intervalle de confiance pour la droite de régression.

1.5 Fiche de synthèse du code R

Dans ce paragraphe, on réunit les différents morceaux de code R présentés dans les paragraphes précédents pour donner un aperçu global de la manière dont on peut élaborer un modèle de régression linéaire sur un nouvel exemple d’étude de cas:

Exemple 1.2 (Rendement procédé chimique) L’analyse de la température (en °C) de fonctionnement d’un procédé chimique par rapport au rendement (en %) d’une réaction qui a lieu lors de la fabrication d’un certain produit, a donné les résultats disponibles dans le fichier Rendement.xlsx dans la Base de données dans Moodle.

Le code présenté ci-dessous se trouve dans le fichier codeRLS_l1.r dans le répertoire codeR dans Moodle.

Remarque: on place le fichier de données Rendement.xlsx et le code ci-dessous dans le même répértoire pour éviter d’écrire tout le chemin vers le fichier de données lors de l’ouverture.

# Lecture de données du fichier
# =============================
library(readxl)
DataSet <- read_excel("Rendement.xlsx")
attach(DataSet)

# Construction du modèle de régression linéaire
# =============================================
mdlLR<-lm(Rendement~Temperature)

# Affichage des tests pour les coefficients du modèle
# ===================================================
summary(mdlLR)$coefficients

# Affichage des intervalles de confiance pour les coefficients du modèle
# ======================================================================
confint(object = mdlLR, level = 0.95)

# Affichage du graphique avec la droite de régression superposée
# ==============================================================
plot(x = Temperature, y = Rendement)
abline(mdlLR, col="red", lty=1)  # affichage de la droite de régression

# Intervalle de confiance à 95% du rendement prédit lorsque la température est de 159 °C
# ======================================================================================
(predY<-predict(object = mdlLR, newdata = data.frame("Temperature" = 159), 
        interval = "prediction", level = 0.95))

# Intervalle de confiance à 95% du rendement moyen prédit lorsque la température est de 129 °C
# ==========================================================================================
(predRL<-predict(object = mdlLR, newdata = data.frame("Temperature" = 129), 
        interval = "confidence", level = 0.95))

detach(DataSet)

L’execution de ce code, conduit aux résultats suivants:

#> [1] "Affichage des tests pour les coefficients du modèle"
#>               Estimate Std. Error    t value     Pr(>|t|)
#> (Intercept) -1.1955354 4.27134182 -0.2798969 7.807348e-01
#> Temperature  0.4520199 0.02794254 16.1767628 2.742724e-21
#> [1] "Affichage des intervalles de confiance pour les coefficients du modèle"
#>                  2.5 %    97.5 %
#> (Intercept) -9.7791182 7.3880473
#> Temperature  0.3958673 0.5081726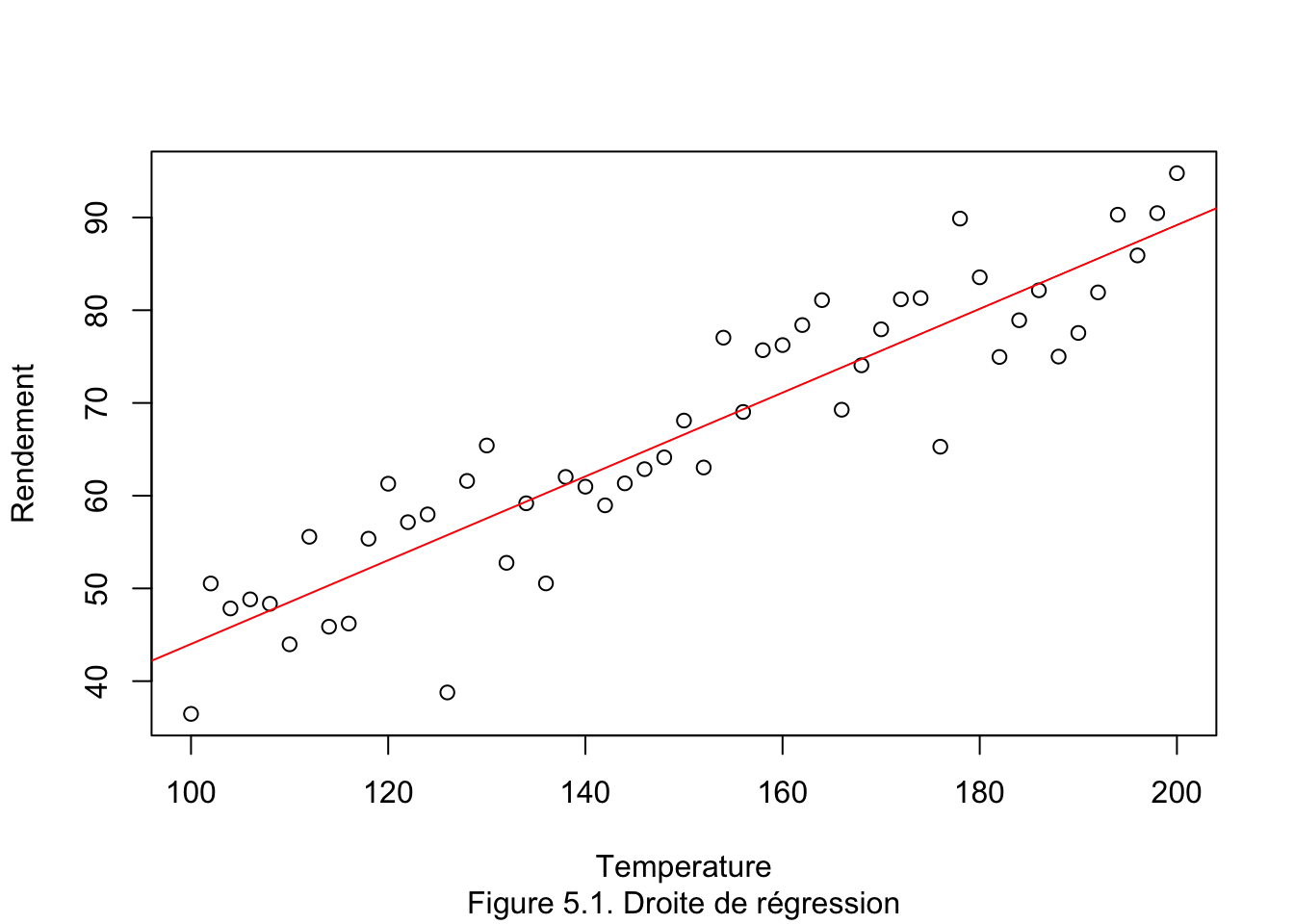

#> [1] "Intervalle de confiance à 95% du rendement prédit lorsque la température est de 159 °C"
#>        fit      lwr      upr
#> 1 70.67563 58.74433 82.60693
#> [1] "Intervalle de confiance à 95% du rendement moyen prédit lorsque la température est de 129 °C"
#>        fit      lwr      upr
#> 1 57.11503 55.08446 59.14561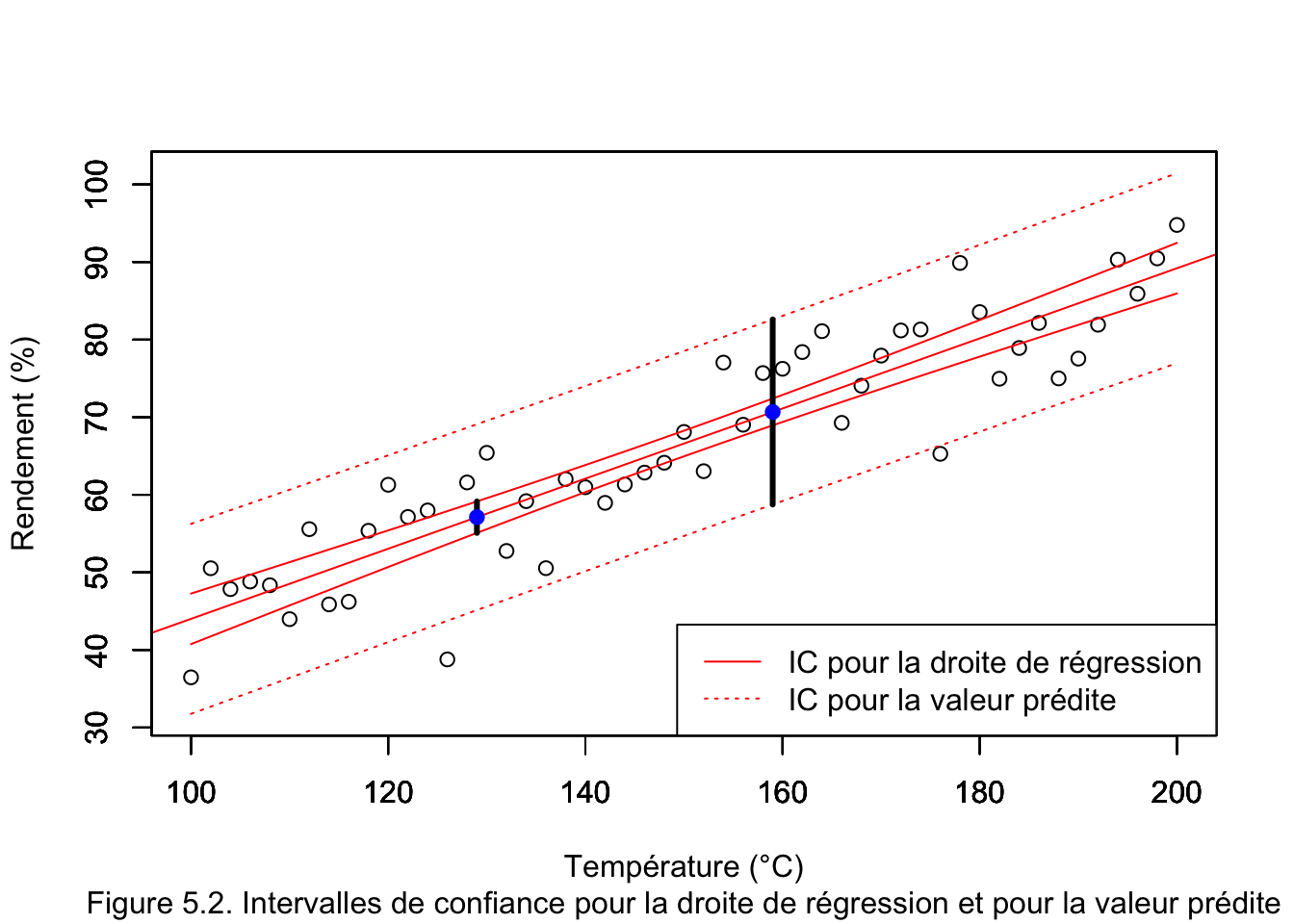

Interprétation des résultats:

• Le modèle régressif linéaire est approprié pour expliciter le rendement par la température [voir figure (5.1)].
• Interprétation des coefficients du modèle:
  • ordonnée à l’origine ((Intercept) = -1.196): n’est pas significativement différente de zéro (p.value = 7.81e-01); par conséquent, on peut considérer que si la température est de 0°C le rendement sera nul.
  • coefficient directeur de la droite (Temperature = 0.452): significativement différent de zéro (p.value = 2.74e-21); par conséquent, une augmentation de la température de 10°C conduit à une augmentation du rendement de 4.52 %.
• Interprétation des intervalles de confiance à 95 % pour les coefficients du modèle:
  • ordonnée à l’origine (\(-9.78\leq\beta_0\leq7.39\)): comme la valeur de zéro est dans l’intervalle, on conclue qu’au seuil de signification de 5 %, \(\beta_0\) ne peut pas être considéré considéré comme étant différent de zéro.
  • coefficient directeur de la droite (\(0.396\leq\beta_1\leq0.508\)): comme la valeur de zéro n’est pas dans l’intervalle, on conclue qu’au seuil de signification de 5 %, \(\beta_1\) peut être considéré considéré comme étant différent de zéro.
• Prédictions à l’aide du modèle:
  • Si la température est de 159°C le rendement estimé par le modèle sera de 70.68 % (voir aussi sur la figure (5.2) l’intersection de la droite verticale à T = 159 avec la droite de régression).
  • L’intervalle de confiance à 95 % pour le rendement lorsque la température est de 159°C est: \(58.74\% \leq\) rendement \(\leq 82.61\%\) (voir aussi sur la figure (5.2) l’intersection de la droite verticale à T = 159 avec l’IC pour la valeur prédite).
  • Si la température est de 129°C le rendement estimé par le modèle sera de 57.12 % (voir aussi sur la figure (5.2) l’intersection de la droite verticale à T = 129 avec la droite de régression).
  • L’intervalle de confiance à 95 % pour le rendement espéré (moyen) lorsque la température est de 129°C est: \(55.08\% \leq\) rendement moyen \(\leq 59.15\%\) (voir aussi sur la figure (5.2) l’intersection de la droite verticale à T = 129 avec l’IC pour la droite de régression).