3  ตัวดำเนินการ

วัตถุประสงค์

1. เพื่อให้เข้าใจเกี่ยวกับนิพจน์ ตัวดำเนินการ และตัวถูกดำเนินการ

2. เพื่อให้เข้าใจลำดับความสำคัญของตัวดำเนินการ

3. เพื่อให้สามารถสร้างนิพจน์และใช้ตัวดำเนินการที่เหมาะสมในการเขียนโปรแกรมได้

โปรแกรมคอมพิวเตอร์ส่วนใหญ่มีการดำเนินการกับข้อมูลเพื่อให้ได้ผลลัพธ์ตามที่ต้องการโดยการสร้างนิพจน์ที่ประกอบไปด้วยตัวดำเนินการและตัวถูกดำเนินการ ผลลัพธ์ที่ได้มีหลายรูปแบบ เช่น ตัวเลข ข้อความ ค่าทางตรรกศาสตร์ เป็นต้น

3.1 นิพจน์ ตัวดำเนินการ และตัวถูกดำเนินการ

นิพจน์ (expression) คือ สิ่งที่สร้างผลลัพธ์และให้ค่าคืนกลับมา ซึ่งหมายถึงการนำตัวแปรหรือค่ามาสัมพันธ์กันด้วยเครื่องหมายการคำนวณ (เช่น + - * / ) หรือเครื่องหมายเปรียบเทียบ (เช่น > < = ) หรือเครื่องหมายทางตรรกะ (เช่น และ (&&), หรือ (||), นิเสธ (!) เป็นต้น ตัวอย่างเช่น

int x = 10, y = 20; 
int result1 =  x + y;

จากตัวอย่างข้างต้น x + y คือ นิพจน์

int a = 3, b = 4, c = 5, m =  2, n = 1; 
int result2 = a + b % 5 – 1 * c;
int result3 = (a>b) || (m>n);

a+b%5-1*c เป็นตัวอย่างของนิพจน์การคำนวณให้ค่าเป็นตัวเลข และ (a>b) || (m>n) เป็นตัวอย่างของนิพจน์ตรรกะให้ค่าเป็นค่าความจริงทางตรรกศาสตร์ คือ true เมื่อค่าความจริงเป็นจริง หรือ false เมื่อค่าความจริงเป็นเท็จ

ตัวถูกดำเนินการ (operand) คือค่าที่ใช้ในการสร้างผลลัพธ์ ซึ่งหมายถึงค่าหรือตัวแปรในนิพจน์ที่ถูกดำเนินการด้วยตัวดำเนินการ เช่น นิพจน์ x + y ตัวแปร x และ y คือตัวถูกดำเนินการเพราะนิพจน์นำค่า x และ y มาดำเนินการบวกกันเพื่อให้ได้ผลลัพธ์คือผลบวกของค่าในตัวแปรทั้งสอง

ตัวดำเนินการ (operator) คือ สัญลักษณ์ซึ่งกระทำกับค่าตั้งแต่ 1 ค่าขึ้นไปเพื่อสร้างผลลัพธ์ออกมา ตัวดำเนินการแบ่งเป็น 4 ประเภทหลัก คือ

1. ตัวดำเนินการคำนวณ (arithmetic operators)

2. ตัวดำเนินการกำหนดค่า (assignment operators)

3. ตัวดำเนินการตรรกะ (logical operators)

4. ตัวดำเนินการสัมพันธ์ (relational operators)

3.2 ตัวดำเนินการคำนวณ

ตัวดำเนินการคำนวณเป็นตัวดำเนินการในการคำนวณทางคณิตศาสตร์ ซึ่งมีสัญลักษณ์ดังตารางที่ 3.1

ตารางที่ 3.1 ตัวดำเนินการคำนวณ

เครื่องหมาย	การดำเนินการ	ตัวอย่างการใช้งาน
+	บวก	z = x + y
-	ลบ	z = x – y
*	คูณ	z = x * y
/	หาร	z = x / y
%	หารเอาเศษ (modulus)	z = x % y

ตัวอย่างที่ 3.1 โปรแก รม OperatorEx1.java

    public class OperatorEx1 {
        public static void main (String args[])  {
                int x = 1, y = 3, z = 6, a;
            a = x + y; 
            System.out.println(“a = ” + a);
            a = z - x;
            System.out.println(“a = ” + a);
            a = z / y;
            System.out.println(“a = ” + a);
            a = z % (x + y);
            System.out.println(“a = ” + a);
        }       
    }       

ผลลัพธ์ของโปรแกรม คือ

a = 4

a = 5

a = 2

a = 2

จากตัวอย่างที่ 3.1 บรรทัดที่ 11 ตัวแปร a มีค่าเท่ากับ 6% (1+3) เท่ากับ 6%4 ผลลัพธ์ที่ได้คือ 2 เนื่องจาก 6 หาร 4 เท่ากับ 1 เศษ 2 เครื่องหมาย % เป็นการหารเอาเศษทำให้ได้ผลลัพธ์เท่ากับ 2

ตัวอย่างที่ 3.2 โปรแกรม OperatorEx2.java

    //Arithmetic operator example.
    public class OperatorEx2 {
        public static void main (String args[])   {
            int x = 1;
            int y = 3;
            int z = 5;
            int result = x/y/z;         
            System.out.println(“result = ” + result);
        }       
    }       

ผลลัพธ์ของโปรแกรม คือ

result = 0

จากตัวอย่างที่ 3.2 ตัวแปร x, y และ z เป็นตัวเลขจำนวนเต็มทำให้เมื่อนำมาดำเนินการหารกันผลลัพธ์ ที่ได้คือ 0 ซึ่งเป็นตัวเลขจำนวนเต็ม ดังนั้นข้อสังเกตสำคัญคือข้อมูลหรือตัวแปรชนิดเดียวเมื่อนำมาดำเนินการกันย่อมทำให้ได้ผลลัพธ์ที่เป็นชนิดเดียวกันด้วย

ตัวอย่างที่ 3.3 โปรแกรม OperatorEx3.java

    //Arithmetic operator example.
    public class OperatorEx3 {
        public static void main (String args[])   {
                int x = 4;
            int y = 3;
            int result = 2*x/y*2 ;          
            System.out.println(“result = ” + result);
        }       
    }       

ผลลัพธ์ของโปรแกรม คือ

result = 4

จากตัวอย่างที่ 3.3 ผลลัพธ์ที่เก็บในตัวแปร result จะมีค่าเท่ากับ 4 อธิบายได้ดังนี้

\[ \begin{aligned} \text { result } & =((2 * 4) / 3) * 2 \\ & =(8 / 3) * 2 \\ & =2 * 2 \\ & =4 \end{aligned} \]

ตัวอย่างที่ 3.4 โปรแกรม OperatorEx4.java

    //Arithmetic operator example.
    public class OperatorEx4 {
        public static void main (String args[])   {
                int x = 11;
            int y = 3;
            int result = x % y;     
            System.out.println(“result = ” + result);
        }       
    }      

ผลลัพธ์ของโปรแกรม คือ

result = 2

จากตัวอย่างที่ 3.4 ผลลัพธ์ของโปรแกรมอธิบายได้ดังนี้ 11%3 ได้ผลลัพธ์เท่ากับ 2 เนื่องจาก 11 หาร 3 ได้ผลหารเป็น 3 เศษ 2

นอกจากนี้ตัวดำเนินการคำนวณที่กล่าวไปแล้วในภาษาจาวายังมีตัวดำเนินการแบบเพิ่มหรือลดทีละหนึ่ง ดังตารางที่ 3.2

ตารางที่ 3.2 ตัวดำเนินการแบบเพิ่มหรือลดทีละหนึ่ง

เครื่องหมาย	การดำเนินการ	ตัวอย่างการใช้งาน	การทำงาน
++	เพิ่มค่าทีละหนึ่ง	y = ++x	เพิ่มค่าก่อน
		y = x++	เพิ่มค่าทีหลัง
–	ลดค่าทีละหนึ่ง	y = –x	ลดค่าก่อน
		y = x–	ลดค่าหลัง

ตารางที่ 3.3 ตัวอย่างการใช้งานตัวดำเนินการแบบเพิ่มหรือลดทีละหนึ่ง

ตัวอย่างการใช้งาน	ความหมาย
y = ++x	บวกค่าในตัวแปร x เพิ่มขึ้นอีกหนึ่งก่อนที่จะกำหนดค่า x ให้กับตัวแปร y
y = x++	กำหนดค่า x ให้กับตัวแปร y ก่อนที่จะบวกค่าในตัวแปร x เพิ่มขึ้น 1 (บวกค่าให้กับตัวแปร x เพิ่มขึ้นอีกหนึ่งทีหลัง)
y = –x	ลบค่าในตัวแปรx ลงหนึ่งก่อนที่จะกำหนดค่า x ให้กับตัวแปร y
y = x–	กำหนดค่า x ให้กับตัวแปร y ก่อนที่จะลบค่าในตัวแปร x ลดลงหนึ่ง (ลบค่าให้กับตัวแปร x ลดลงหนึ่งทีหลัง)

ตัวอย่างที่ 3.5 โปรแกรม OperatorEx5.java

    //Arithmetic operator example.
    public class OperatorEx5 {
        public static void main (String args[])   {
                int x = 1, y;
            y = ++x;
            System.out.println(“y = ” + y + “, x = ” + x);
            y = x++;
            System.out.println(“y = ” + y + “, x = ” + x);
            y = --x;
            System.out.println(“y = ” + y + “, x = ” + x);
            y = x--;
            System.out.println(“y = ” + y + “, x = ” + x);
        }       
    }      

ผลลัพธ์ของโปรแกรม คือ

y = 2, x = 2

y = 2, x = 3

y = 2, x = 2

y = 2, x = 1

จากตัวอย่างที่ 3.5 กำหนดให้เริ่มต้นตัวแปร x มีค่าเท่ากับ 1 ผลการดำเนินงานจากคำสั่งบรรทัดที่ 5 มีการเพิ่มค่าให้ตัวแปร x อีก 1 ก่อนแล้วจึงกำหนดค่าให้ตัวแปร y ทำให้ทั้งตัวแปร x และ y มีค่าเท่ากับ 2 แต่คำสั่งในบรรทัดที่ 7 นำค่าในตัวแปร x คือ 2 ไปกำหนดค่าให้ตัวแปร y ก่อนจึงค่อยเพิ่มค่า x อีก 1 ทีหลังทำให้ y มีค่าเท่ากับ 2 และเมื่อทำการเพิ่มค่า x ทำให้ตัวแปร x มีค่าเพิ่มขึ้นเป็น 2 การดำเนินการ – ในบรรทัดที่ 9 จะทำการลดค่า x ลง 1 ก่อนแล้วจึงกำหนดค่าให้ตัวแปร y แต่ในบรรทัดที่ 11 จะนำค่า x ไปกำหนดค่าให้ y ก่อนแล้วค่อยลดค่า x อีก 1 ทีหลัง

ตัวอย่างที่ 3.6 โปรแกรม OperatorEx6.java

    //Arithmetic operator example.
    public class OperatorEx6 {
        public static void main (String args[])   {
            int x = 1;
            System.out.println(“x = ” + ++x);
            System.out.println(“x = ” + x);
            System.out.println(“x = ” + x--);
            System.out.println(“x = ” + x);
        }       
    }      

ผลลัพธ์ของโปรแกรม คือ

x = 2

x = 2

x = 2

x = 1

จากตัวอย่างที่ 3.6 เริ่มต้นกำหนดให้ x = 1 โปรแกรมในบรรทัดที่ 5 ก่อนการพิมพ์ค่า x ออกทางจอภาพจะดำเนินการเพิ่มค่า x ก่อนดังนั้นผลลัพธ์ที่แสดงออกมาคือ x = 2 และในบรรทัดที่ 6 เมื่อพิมพ์ค่า x จะเห็นได้ว่าค่า x เปลี่ยนไปเป็น 2 แล้ว แต่สำหรับบรรทัดที่ 7 ผลการพิมพ์จะพิมพ์ค่า x = 2 เนื่องจากการดำเนินการลดค่า x จะทำทีหลังการพิมพ์ค่า x หลังจากทำคำสั่งบรรทัดที่ 7 แล้ว บรรทัดที่ 8 ผลการพิมพ์ค่า x ออกทางจอภาพคือ x = 1 จะเห็นได้ว่าค่าตัวแปร x มีการลดค่าลงแล้ว

3.3 ตัวดำเนินการกำหนดค่า

ตัวดำเนินการกำหนดค่าเป็นสัญลักษณ์ในการกำหนดค่าให้กับตัวแปรและอ็อบเจกต์ ดังตารางที่ 3.4

ตารางที่ 3.4 ตัวดำเนินการกำหนดค่า

เครื่องหมาย	ตัวอย่างการใช้งาน	ความหมาย
=	y = x	เป็นการนำค่าในตัวแปร x ไปกำหนดค่าให้กับตัวแปร y
+=	y += x	มีความหมายเหมือนกับ y = y + x
		มีการดำเนินการ คือ นำค่าในตัวแปร y บวกกับค่าในตัวแปร x แล้วนำผลลัพธ์ที่ได้ไปกำหนดค่าให้ y เป็นค่าใหม่
-=	y -= x	มีความหมายเหมือนกับ y = y - x
*=	y *= x	มีความหมายเหมือนกับ y = y * x
/=	y /= x	มีความหมายเหมือนกับ y = y / x
%=	y %= x	มีความหมายเหมือนกับ y = y % x

ตัวอย่างที่ 3.7 โปรแกรม OperatorEx7.java

    // Assignment operator example.
    public class OperatorEx7 {
        public static void main (String args[])  {
            int x = 3, y = 6;
            y += x;
            System.out.println(“y = ”  +  y +  “, x = ”  +  x);
            y /= x;
            System.out.println(“y = ”  +  y +  “, x = ”  +  x);
            y %= x;
            System.out.println(“y = ”  +  y +  “, x = ”  +  x);
        }       
    }      

ผลลัพธ์ของโปรแกรม คือ

y = 9, x = 3

y = 3, x = 3

y = 0, x = 3

จากตัวอย่างที่ 3.7 โปรแกรมบรรทัดที่ 4 เป็นการประกาศและกำหนดค่าให้ x = 3 และ y = 6 บรรทัดที่ 5 เป็นการนำค่า y + x ซึ่งมีค่าเท่ากับ 6 + 3 ได้ผลลัพธ์คือ 9 นำค่า 9 ไปกำหนดค่าให้ตัวแปร y ดังนั้นเมื่อสิ้นสุดคำสั่งบรรทัดที่ 5 ตัวแปร y จะเปลี่ยนค่าไปเป็น 9 คำสั่งบรรทัดที่ 7 เป็นการนำค่า y / x ซึ่งมีค่าเท่ากับ 9 / 3 ได้ผลลัพธ์คือ 3 นำค่า 3 ไปกำหนดค่าให้ตัวแปร y ดังนั้นเมื่อสิ้นสุดคำสั่งบรรทัดที่ 7 ตัวแปร y จะเปลี่ยนค่าไปเป็น 3 และคำสั่งบรรทัดที่ 9 เป็นการนำค่า y % x ซึ่งมีค่าเท่ากับ 3 / 3 ได้ผลลัพธ์คือ 0 นำค่า 0 ไปกำหนดค่าให้ตัวแปร y ดังนั้นเมื่อสิ้นสุดคำสั่งบรรทัดที่ 9 ตัวแปร y จะเปลี่ยนค่าไปเป็น 0

3.4 ตัวดำเนินการสัมพันธ์

ตัวดำเนินการเปรียบเทียบเป็นสัญลักษณ์แทนการดำเนินการที่นำข้อมูล 2 ค่ามาเปรียบเทียบกัน ผลการเปรียบเทียบจะให้ค่าความจริงเป็นจริง (true) หรือเท็จ (false) เท่านั้น ตัวดำเนินการเปรียบเทียบเป็นดังตารางที่ 3.5

ตารางที่ 3.5 ตัวดำเนินการเปรียบเทียบ

เครื่องหมาย	การเปรียบเทียบ	ตัวอย่างการใช้งาน
==	เท่ากับ	x == y
!=	ไม่เท่ากับ	x != y
<	น้อยกว่า	x < y
<=	น้อยกว่าหรือเท่ากับ	x<= y
>	มากกว่า	x > y
>=	มากกว่าหรือเท่ากับ	x >= y

ตัวอย่างที่ 3.8 โปรแกรม OperatorEx8.java

    //Relational operator example.
    public class OperatorEx8 {
        public static void main (String args[])  {
                int x = 4, y = 6;
            boolean result;
            result = x == y;
            System.out.println(x + “ == ” + y + “ is ” + result);
            result = x != y;
            System.out.println(x + “ != ” + y + “ is ” + result);
            result = x > y;
            System.out.println(x + “ > ” + y + “ is ” + result);
            result = x < y;
            System.out.println(x + “ < ” + y + “ is ” + result);
            result = x >= y;
            System.out.println(x + “ >= ” + y + “ is ” + result);
            result = x <= y;
            System.out.println(x + “ <= ” + y + “ is ” + result);
        }       
    }   
            System.out.println(x + “ != ” + y + “ is ” + result);
            result = x > y;
            System.out.println(x + “ > ” + y + “ is ” + result);
            result = x < y;
            System.out.println(x + “ < ” + y + “ is ” + result);
            result = x >= y;
            System.out.println(x + “ >= ” + y + “ is ” + result);
            result = x <= y;
            System.out.println(x + “ <= ” + y + “ is ” + result);
        }       
    }   

ผลลัพธ์ของโปรแกรม คือ

4 == 6 is false

4 =! 6 is true

4 > 6 is false

4 < 6 is true

4 >= 6 is true

4 <= 6 is false

การดำเนินการเปรียบเทียบข้อความหรือ String สามารถใช้เมท็อด equals ซึ่งจะให้ค่าเป็น true ถ้าข้อความเหมือนกัน และให้ค่าเป็น false ถ้าข้อความต่างกัน ดังตัวอย่างที่ 3.9

ตัวอย่างที่ 3.9 โปรแกรม OperatorEx9.java

    //String comparison example 
    public class OperatorEx9 {
        public static void main (String args[])  {
                String str = "Test";
            boolean result1  = str.equals("Test");
            boolean result2  = str.equals("Testing");       
            System.out.println(“result1 = ” + result1);
            System.out.println(“result2 = ” + result2);
        }       
    }   

ผลลัพธ์ของโปรแกรม คือ

result1 = true

result2 = false

3.5 ตัวดำเนินการตรรกะ

ตัวดำเนินการตรรกะใช้เพื่อเชื่อมนิพจน์ตรรกะเข้าด้วยกันแล้วทำให้ได้ผลเป็นนิพจน์ตรรกะใหม่ ซึ่งผลลัพธ์ที่ได้จะให้ค่าความจริงเป็นจริง (true) หรือเท็จ (false) เท่านั้น ตัวดำเนินการตรรกะเป็นดังตารางที่ 3.6 และตารางค่าความจริงเป็นดังตารางที่ 3.7

ตารางที่ 3.6 ตัวดำเนินการตรรกะ

เครื่องหมาย	ความหมาย
&&	และ
||	หรือ
!	นิเสธ

ตารางที่ 3.7 ตารางค่าความจริงทางตรรกศาสตร์

TRUE	FALSE	true && false	true || false	!true	!false
FALSE	FALSE	FALSE	FALSE	TRUE	TRUE
FALSE	TRUE	FALSE	TRUE	TRUE	FALSE
TRUE	FALSE	FALSE	TRUE	FALSE	TRUE
TRUE	TRUE	TRUE	TRUE	FALSE	FALSE

จากตารางที่ 3.7 กรณีดำเนินการและ (&&) ค่าความจริงจะเป็นจริงกรณีเดียว คือ true && true ส่วนการดำเนินการหรือ (||) จะให้ค่าเป็นเท็จในกรณีเดียว คือ false || false

ตัวอย่างที่ 3.10 โปรแกรม OperatorEx10.java

    //Logical operator example.
    public class OperatorEx10 {
        public static void main (String args[])  {
                boolean result1 = t && f;
            boolean result2 = t || f;
            boolean result3 = !f;
            boolean result4 = !(t && f);
            boolean result5 = !t && f;
            boolean result6 = t && !f;
            boolean result7 = f || !t;
            System.out.println(“result1 = ” + result1);
            System.out.println(“result2 = ” + result2);
            System.out.println(“result3 = ” + result3);
            System.out.println(“result4 = ” + result4);
            System.out.println(“result5 = ” + result5);
            System.out.println(“result6 = ” + result6);
            System.out.println(“result7 = ” + result7);     
        }       
    }

ผลลัพธ์ของโปรแกรม คือ

result1 = false

result2 = true

result3 = true

result4 = true

result5 = false

result6 = true

result7 = false

ตัวอย่างที่ 3.11 โปรแกรม OperatorEx11.java

    // Logical operator example.
    public class OperatorEx11 {
        public static void main (String args[])  {
                int x = 3, y = 6;
            System.out.println (x > y);
            System.out.println (x >= y);    
            System.out.println (x < y); 
            System.out.println (x <= y);    
            System.out.println (x == y);    
            System.out.println (x != y);
            System.out.println ((x = = 3)&&(y !=6));    
            System.out.println ((x = = 3) || (y !=6)); 
            System.out.println (!(x != y)); 
        }       
    }   

ผลลัพธ์ของโปรแกรม คือ

false

false

true

true

false

true

false

true

false

จากตัวอย่างที่ 3.11 อธิบายการทำงานของโปรแกรมได้ดังนี้

3 > 6 ผลลัพธ์คือ false

3>=6 ผลลัพธ์คือ false

3 < 6 ผลลัพธ์คือ true

3<=6 ผลลัพธ์คือ true

3==6 ผลลัพธ์คือ false

3 !=6 ผลลัพธ์คือ true

(3==3) && (6!=6) ได้ค่าความจริงคือ

true && false ผลลัพธ์คือ false

(3==3) || (6!=6) ได้ค่าความจริงคือ true || false ผลลัพธ์คือ true

!(3!=6) ได้ค่าความจริงคือ !true ผลลัพธ์คือ false

3.6 ลำดับความสำคัญของตัวดำเนินการ

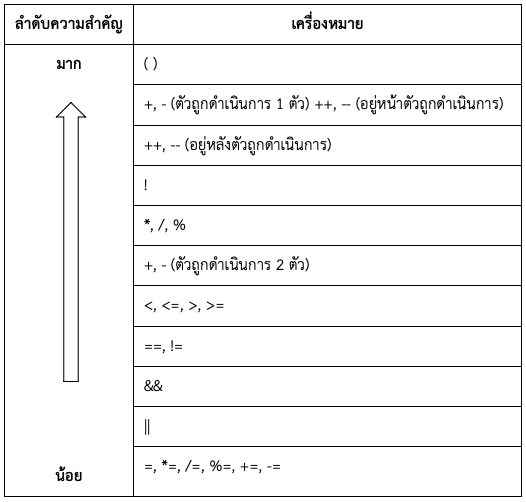
ภาษาจาวากำหนดความสำคัญหรือการทำก่อน (precedence) เพื่อกำหนดว่าตัวดำเนินการได้ควรทำก่อนหรือหลัง โดยมีข้อกำหนดดังนี้คือ ตัวดำเนินการที่มีความสำคัญมากกว่าจะดำเนินการก่อน ในกรณีที่มีตัวดำเนินการที่มีความสำคัญเท่ากันจะทำจากตัวดำเนินการทางซ้ายก่อนแล้วไปยังตัวดำเนินการทางขวา ลำดับความสำคัญของตัวดำเนินการเป็นดังตารางที่ 3.8

ตารางที่ 3.8 ลำดับความสำคัญของตัวดำเนินการ

ตัวอย่างที่ 3.12 โปรแกรม OperatorEx12.java

    //Precedence example.
    public class OperatorEx12 {
        public static void main (String args[])  {
                int x = 6;
            int y = 4;
            int z = 2;
            int result1 = x + y / z;
            System.out.println(“result = ” + result);
        }       
    }

ผลลัพธ์ของโปรแกรม คือ

result = 8

จากตัวอย่างที่ 3.12 ผลลัพธ์ของโปรแกรมตัวแปร result จะมีค่าเท่ากับ 8 เนื่องจากเครื่องหมาย / มีความสำคัญมากกว่าเครื่องหมาย + จึงอธิบายลำดับการทำงานได้ดังนี้ result = 6 + (4 / 2) = 6 + 2 = 8

ตัวอย่างที่ 3.13 โปรแกรม OperatorEx13.java

    //Precedence example.
    public class OperatorEx13 {
        public static void main (String args[])  {
                int x = -1;
            int y= 10;
            int z = 2;
            int result1 = -x+y*z ; 
            int result2 = -x+y/z ;
            System.out.println(“result1 = ” + result1);
            System.out.println(“result2 = ” + result2);
        }       
    }

ผลลัพธ์ของโปรแกรม คือ

result1 = 21

result2 = 6

จากตัวอย่างที่ 3.13 อธิบายลำดับการคำนวณได้ดังนี้

\[ \begin{aligned} & \text { result1 }=-(-1)+(10 * 2)=1+20=21 \\ & \text { result2 }=-(-1)+(10 / 2)=1+5=6 \end{aligned} \]

ตัวอย่างที่ 3.14 โปรแกรม OperatorEx14.java

    //Precedence example.
    public class OperatorEx14 {
        public static void main (String args[])  {
                int x = 4;
            int y= 3;
            int result = x * y++;           
            System.out.println(“result = ” + result);
            System.out.println(“y = ” + y);
        }       
    }

ผลลัพธ์ของโปรแกรม คือ

result = 12

y = 4

จากตัวอย่างที่ 3.14 อธิบายลำดับการคำนวณจากคำสั่ง result1 = x * y++ ได้ดังนี้

ขั้นตอนที่ 1 result1 = x * y = 4 * 3 = 12

ขั้นตอนที่ 2 y = y + 1 = 3 + 1 = 4 (ตัวดำเนินการลดค่าทีละหนึ่งทำทีหลัง)

วงเล็บเป็นเครื่องหมายที่ช่วยในการกำหนดหรือควบคุมลำดับการทำงานของตัวดำเนินการ โดยต้องทำงานในวงเล็บก่อนเสมอ ดังตัวอย่างที่ 3.15

ตัวอย่างที่ 3.15 โปรแกรม OperatorEx15.java

    //Precedence example.
    public class OperatorEx15 {
        public static void main (String args[])  {
                int x = 6;
            int y = 4;
            int z = 2;
            int result1 = x + y / z; 
            int result2 = (x + y) / z;          
            System.out.println(“result1 = ” + result1);
            System.out.println(“result2 = ” + result2);
        }       
    }

ผลลัพธ์ของโปรแกรม คือ

result1 = 8

result2 = 5

จากตัวอย่างที่ 3.15 อธิบายลำดับการคำนวณได้ดังนี้

\[ \begin{aligned} & \text { result1 }=6+(4 / 2)=8 \\ & \text { result2 }=(6+4) / 2=5 \end{aligned} \]

สำหรับการคำนวณทางคณิตศาสตร์ในภาษาจาวากำหนดลำดับความสำคัญจากมากไปน้อยหรือลำดับการทำงานก่อนหลัง ดังนี้

1. คำนวณในวงเล็บเป็นลำดับแรกสุด

2. เรียกใช้เมท็อดแล้วนำค่าผลลัพธ์ที่ได้มาใช้ในการคำนวณในขั้นต่อไป

3. ติดลบ

4. ทำการคูณหรือหาร (เรียงจากซ้ายไปขวา)

5. ทำการบวกหรือลบ (เรียงจากซ้ายไปขวา)

6. ทำการให้ค่าหรือกำหนดค่าด้วยเครื่องหมาย =

แบบฝึกหัด

1. ให้หาคำตอบจากคำสั่งต่อไปนี้ พร้อมทั้งแสดงวิธีทำ โดยกำหนดค่าตัวแปร ดังนี้ int A = 5, B =1 0 , C = 15;

   1.1 int result1 = (A*B)+(C+B)/B;

   1.2 int result2 = C+B/A*B;

   1.3 int result3 = B-A+C/(A*C);

   1.4 int result4 = ((A/2*C)+10)*(B/2);

   1.5 int result5 = (C*10/A)+(A*C)%C;

2. ให้หาคำตอบจากคำสั่งต่อไปนี้ พร้อมทั้งแสดงวิธีทำ โดยกำหนดค่าตัวแปร ดังนี้ int a = 7, b = 3, int c = 2;

   2.1 int result6 = -c % b + a / b;

   2.2 int result7 = (++a * b) + c–;

   2.3 boolean result8 = (c < 5) || (b < c+a) && (a == b);

   2.4 boolean result9 = (a > b) || !(a <= c) && b > c / 2;

   2.5 boolean result10 = a < b && !(a <= c) && b > c / 2;

   2.6 boolean result11 = (a > b) && !(a <= c) || b > c / 2

3. ให้แสดงผลลัพธ์ที่พิมพ์ออกทางจอภาพจากส่วนของโปรแกรมต่อไปนี้ พร้อมทั้งอธิบายผลลัพธ์ที่ได้

3.1

System.out.println("x++ = " + x++);
System.out.println("x = " + x);
System.out.println("++y = " + ++y);
System.out.println("y = " + y);

3.2

int result1 = (x+2)%3 *++x ;
System.out.println("result = " + result1);
int result2 = (y+2)%3 *y++ ;
System.out.println("result2 = " + result2);

4. ให้เขียนโปรแกรมเพื่อรับค่าตัวเลขจำนวนเต็ม 2 จำนวน แล้วนำผลบวก ผลลบ ผลคูณ ผลหาร และการเปรียบเทียบว่าจำนวนที่ 1 มากกว่าจำนวนที่ 2 หรือไม่ แล้วแสดงผลทางจอภาพ โดยจัดรูปแบบหน้าจอดังนี้

ตัวอย่าง การทำงานของโปรแกรมเมื่อป้อนเลข 9 และ 2

Enter number 1: 9

Enter number 2: 2

9 + 2 = 11

9 - 2 = 7

9 * 2 = 18

9 / 2 = 4.5

9 > 2 = true

5. ให้เขียนโปรแกรมผ่อนชำระหนี้ (loan amortization) โดยรับข้อมูลจำนวนเงินกู้ (loan amount) จำนวนปี (number of years) และอัตราดอกเบี้ยต่อปี (annual interest rate) จากผู้ใช้มาคำนวณหาจำนวนเงินที่ต้องจ่ายต่อเดือน (monthly payment) และจำนวนเงินที่ต้องจ่ายทั้งหมด (total payment) แล้วแสดงผลลัพธ์ออกทางจอภาพ

จำนวนเงินที่จ่ายต่อเดือน (monthly payment) คำนวณได้จากสูตรต่อไปนี้

\[ \mathrm{x}=\mathrm{y} \div\left[\frac{1-\left(1+\frac{\mathrm{i}}{12}\right)^{-12^* \mathrm{n}}}{\left(\frac{\mathrm{i}}{12}\right)}\right] \]

โดยที่

    x   คือ จำนวนเงินที่จ่ายต่อเดือน (monthly payment)

    y   คือ จำนวนเงินกู้ (loan amount)

    n   คือ จำนวนปี (number of years)

    i   คือ อัตราดอกเบี้ยต่อปี (annual interest rate) 

    i/12    คือ อัตราดอกเบี้ยต่อเดือน (monthly interest rate)

ตัวอย่าง เช่น
กู้เงิน 10000 บาท อัตราดอกเบี้ยต่อปี 7% (0.07) จำนวนปี 1 ปี (ผ่อนชำระให้หมดภายใน 1 ปี)

\[ \begin{aligned} x & =10000 /[(1-(1+(0.07 / 12))-12 * 1) /(0.07 / 12)] \\ & =865.26 \end{aligned} \]

จำนวนเงินที่จ่ายต่อเดือน (monthly payment) หรือต้องผ่อนชำระต่อเดือนเป็นเงิน 865.26 บาท จำนวนเงินที่ต้องจ่ายทั้งหมด (total payment) = x * (n * 12) = 865.26 * (1 * 12) = 10383.21 ดังนั้นต้องจ่ายเงินทั้งหมดเป็นเงิน 10383.21 บาท

ตัวอย่าง ผลลัพธ์ของโปรแกรมเมื่อป้อนจำนวนเงินกู้ 10000 บาท จำนวนปี 1 ปี และอัตราดอกเบี้ยต่อปี 0.07 (7%)

Loan Amount: 10000

Number of Years: 1

Annual Interest Rate: 0.07

Monthly Payment = 865.26

Total Payment = 10383.21

คำแนะนำ การหาค่ายกกำลังในภาษาสามารถเรียกใช้เมท็อด pow ของคลาส Math ได้ เช่น การหาค่า 23 เขียนดังนี้ Math.pow(2, 3) จะให้ค่าคือ 8.0, การหาค่า 3.52.5 เขียนดังนี้ Math.pow(3.5, 2.5) จะให้ค่าคือ 22.91765 เป็นต้น