第1章 なぜ統計を学ぶのか
汝,アンケートに答えるなかれ
世界情勢に関する質問に答えるなかれ
言われるがままにテストを受けるなかれ
汝,統計家と同席するなかれ
社会科学に手を染めるなかれ— W・H・オーデン1
1.1 統計の心理学
多くの学生が驚くように,心理学教育においては統計が重要な部分を占めています。しかし大方の予想通り,心理学教育の中で統計が好かれることはありません。だいたい,統計が好きなら心理学ではなく統計のクラスにいることでしょう。当然ながら,心理学にやたらと統計が出てくるという事実を学生の多くは好ましく思っていません。こうしたことを踏まえると,まずは統計に対して人々が感じている一般的な疑問に答えるところから始めた方がよさそうです。
この問題の大部分は,統計そのものの考え方と密接に関連しています。統計とは何なのでしょうか。統計は何のためにあるのでしょうか。なぜ科学者はそこまで統計に固執するのでしょうか。これらはどれも,統計に関するもっともな疑問です。まず最後の疑問から見てみましょう。科学者という集団は,ありとあらゆるものに対して統計的検定をするということに奇妙なほどこだわっているように見えます。実際,私たちは統計をよく使うのですが,それが当たり前のようになっていて,なぜそうするのかについて説明することを忘れがちです。これは,科学者,とりわけ社会科学者は,統計を使わない限りその結果は信頼できないという,ある種の信条のようなものを持っているからです。学生たちは,私たちがみな完全に狂っていると思っているもしれません。なぜなら,この非常に単純な質問に誰も答えてくれないからです。
なぜ統計を使うのだろうか。なぜ科学者は常識を使わないのだろうか。
これはある意味素朴な疑問ですが,非常に的を射た質問でもあるのです。これに対する答えには優れたものがたくさんありますが2,私の考えでは,もっとも素晴らしい回答は「自分自身をあまり信用していないから」という非常に単純なものです。私たちはみな人間ですから,人間が持つさまざまな先入観の影響を受けやしないか,誘惑や意志の弱さによる影響を受けやしないかと不安なのです。統計の多くは,基本的に安全装置だといえます。データの評価に「常識」を用いるということは,自分の直感を信頼するということです。言葉による議論や人間の合理性に基づいて正しい答えが導けるということを意味するのです。科学者の多くはこうしたアプローチが有効だとは考えていません。
こう考えてみると,これはとても心理学的な問題のように思えます。私は心理学科の人間ですから,この点から話を掘り下げていきましょう。この「常識」によるアプローチは本当に信頼できるものだといえるでしょうか。言葉による議論のためには言語が必要ですが,言語は万能ではなく,他に比べて言語化が難しい対象があるものです。ただ,言語化できないものがだめだというわけではありません(たとえば量子電磁力学は素晴らしい理論ですが,言語的に説明するのは困難です)。それに,私たちの「直感」は科学的な問題を解決するようにはできていません。これは日々の推論をうまくやりくりするためのものなのです。生物学的進化は文化的変化より進行が遅いということもあって,直感は現在私たちが生きている世界とは別世界の日常的問題を解決するためのものだといえるのです。もっとも基本的なこととして,常識的かつ論理的な判断を行うためには,「帰納」を用いる必要があります。賢明な推論を行い,眼前にあるデータにとどまらない,世界一般についての知識を得られなくてはならないのです。もしさまざまな阻害要因の影響を受けずにこれをできるというなら,私が所有しているスカイツリーの権利を売って差し上げましょう。ともあれ,次のセクションで見るように,私たちは(推測の必要がない)「演繹問題を解くときですら,先入観の影響を受けずにはいられないのです。
1.1.1 信念バイアスの呪縛
人間は,たいていの場合とても賢い生き物です。(同意しない人も多いかもしれませんが)地球上の生物の中では確実に一番でしょう。私たちの心はじつに驚くべきもので,思考や理性によって信じられないような偉業を成し遂げることができるのです。だからといって人間が完璧であるというわけではありません。心理学者が長年にわたり示してきたことの1つに,人間は中立を保つのがとても下手だということがあります。つまり,偏見に左右されず公平にデータを評価するということが苦手なのです。その好例が,論理的思考における信念バイアスです。ある三段論法が論理的に妥当(つまり前提が正しいなら結論が正しい)かどうかを判断する際,私たちの判断は,その三段論法の結論がもっともらしいどうかによって影響されてしまう傾向があるのです。たとえば,以下はもっともらしい結論を伴う論理的に正しい三段論法です。
タバコはすべて高価である(前提1)
ある依存性物質には安価なものもある(前提2)
したがって,ある依存性物質はタバコではない(結論)
以下は,結論は信じがたいけれども論理的には正しい三段論法です。
すべての依存性物質は高価である(前提1)
一部のタバコは安価である(前提2)
それゆえ,一部のタバコには依存性がない(結論)
2つめの三段論法の論理構造は1つめの三段論法の構造とまったく同一で,これらはどちらも論理的に筋が通ったものなのです。しかし,2つめの三段論法では,前提1が誤りである可能性が高いため,その結果として結論も間違いである可能性があります。ただ,そこはここでの話とはまったく別の問題です。三段論法は前提の論理的帰結として結論を導き出すものであって,そうであれば演繹的には問題ありません。つまり,三段論法が正しくあるために,必ずしも真の命題を含んでいなければならないわけではないのです。
一方で,以下はもっともらしい結論を伴う誤った三段論法です。
依存性物質はすべて高価である(前提1)
タバコの一部は安価である(前提2)
したがって,依存性物質の一部はタバコではない(結論)
最後に,信じがたい結論の伴う誤った三段論法も示しておきます。
すべてのタバコは高価である(前提1)
依存性物質の一部は安価である(前提2)
それゆえ,タバコの一部には依存性がない(結論)
さて,何が真実で何がそうでないかを判断する際,私たちが先入観に影響されることなく,純粋にその三段論法の論理的価値のみに基づいて判断できるとしましょう。その場合,正しい三段論法では100%の人が正しいと答え,誤った三段論法を正しいと答える人は0%になるはずです。つまり,もしこれを調べる実験をしたら,そのデータは次のようになるでしょう。
| もっともらしい結論 | 信じがたい結論 | |
|---|---|---|
| 正しい三段論法 | 100%が「正しい」と回答 | 100%が「正しい」と回答 |
| 誤った三段論法 | 0%が「正しい」と回答 | 0%が「正しい」と回答 |
もし心理学的なデータがこのようなものであれば(あるいはこれに近似したものであれば),人間の直感を信用してよいといえるかもしれません。そうすれば,科学者が自分の常識を基準にデータを評価しても問題ないということになり,統計のような得体の知れないものに悩まされる必要もないわけです。しかし,すでに心理学の授業をいくつか受けた後なら,結果がどうだったかの想像はつくと思います。
古典的な研究の1つに,まさにこれを確かめようとしたEvans, Barston, and Pollard (1983) の実験があります。彼らの研究では,先入観(すなわち信念)がデータ構造に一致している場合には,期待通りの結果になりました。
| もっともらしい結論 | 信じがたい結論 | |
|---|---|---|
| 正しい三段論法 | 92%が「正しい」と回答 | |
| 誤った三段論法 | 8%が「正しい」と回答 |
完璧とはいえませんが,かなりいい線をいっています。しかし,結論の正しさに対する私たちの直感が三段論法の論理構造と一致していない場合はどうだったでしょうか。
| もっともらしい結論 | 信じがたい結論 | |
|---|---|---|
| 正しい三段論法 | 92%が「正しい」と回答 | 46%が「正しい」と回答 |
| 誤った三段論法 | 92%が「正しい」と回答 | 8%が「正しい」と回答 |
なんとまあ,これではだめですよね。どうやら人は,自分の持つ信念に反した妥当な三段論法を提示された場合,その三段論法が正しいものだと認識するのがとても困難なようなのです(正しく認識できたのは46%のみでした)。さらにひどいことには,自分が持っている先入観と一致した結論を持つ誤った三段論法を提示された場合,それが誤りであるということを見抜ける人はほとんどいないのです(92%の人が間違えています)3。
ただ,よく見てみれば,このデータはそれほどひどいものではありません。全体としては,60%の人の判断が正解で,これは当てずっぽうよりは高い正答率ですから,先入観は補正されているのです(まったくの当てずっぽうなら正答率は50%になるはずです)。とはいえ,あなたが「データ評価」の専門家だったとして,判断の正解率を60%から(たとえば)95%にしてくれるような魔法のツールを誰かが提供してくれるとしたら,きっとそれに飛びつきますよね? きっとそのはずです。ありがたいことに,実際にそうしたツールがあるのです。ただし,魔法ではありません。それが統計なのです。科学者が統計を好む1番の理由がこれです。つまり,私たちはあまりに簡単に「信じたいものを信じる」傾向を持っているからです。そうではなくて「データを信じる」のなら,自分の先入観を抑制するためのちょっとした助けが必要になります。それが統計の役目です。つまり,統計は私たちが公正さを保つ手助けをしてくれるのです。
1.2 シンプソンのパラドックス
以下は実際にあった物語(のはず)です。1973年,カリフォルニア大学バークレー校では,学部卒業後に大学院に進学する学生についてある心配事を抱えていました。とくに問題とされていたのは,男女で合格率が大きく異なっていることでした。表にまとめると次のようになります。
| 志願者数 | 合格率 | |
|---|---|---|
| 男性 | 8442 | 44% |
| 女性 | 4321 | 35% |
このようなことから,訴訟沙汰になるのではと心配されていたのです4 。13,000人近い志願者で,男女の合格率が9%も違うというのは,偶然にしては大きすぎます。かなり説得力のあるデータですよね。しかしもし,私が「このデータには実際には女性に有利な(ある種の)弱いバイアスが反映されている」と言ったとしたら,きっと私のことを頭がおかしいか性差別主義者だと思ったことでしょう。
奇妙なことに,ある意味実際にそのとおりなのです。この入試データをもっと詳しく見てみると,違ったストーリーが見えてきます(Bickel, Hammel, and O’Connell 1975)。学科別で見てみると,多くの学科では女性志願者の方が男性志願者よりも合格率がわずかに高いのです。次の表は,規模の大きな6つの学科での入試に関する数字をまとめたものです(プライバシー上の理由から学科名は伏せてあります)。
| 学科 | 志願者数 | 合格率 | 志願者数 | 合格率 |
|---|---|---|---|---|
| A | 825 | 62% | 108 | 82% |
| B | 560 | 63% | 25 | 68% |
| C | 325 | 37% | 593 | 34% |
| D | 417 | 33% | 375 | 35% |
| E | 191 | 28% | 393 | 24% |
| F | 272 | 6% | 341 | 7% |
驚くべきことに,ほとんどの学部で女性の方が男性よりも合格率が高いのです。にもかかわらず,大学全体では女性の合格率は男性より低いのです。なぜこのようなことが起きるのでしょうか。このどちらも正しいなどということがあり得るのでしょうか。
その種明かしはこうです。まず,学科ごとの合格率が均等ではない点に注意してください。ある学科(AやBなど)は合格率が高くなっていますが,その他の学科(Fなど)では,たとえ成績の良い学生だったとしても,志願者の大半が不合格になっています。つまり,ここに示した6つの学科では,A学科がもっとも進学しやすく,次いでB,C,D,E,Fという順になっています。次に,男性と女性では志願する学科に違いがある点に注意してください。男性志願者の多い順に学科を並べると,A>B>D>C>F>Eとなります(「簡単」な学科は太字にしてあります)。全体的に,男性は合格率の高い学科に志願する傾向があるのです。さて,これと女性志願者の分布を比べてみましょう。女性の志願者数順に学科を並べるとC>E>D>F>A>Bとなり,かなり順序が違います。つまり,これらのデータから示唆されることは,女性はより「難しい」学科に志願者しているということです。実際,図1.1を見てみると,この傾向が体系的で非常にはっきりしたものであることがわかります。こうした効果はシンプソンのパラドックスと呼ばれています。よくあることではないものの実際に起こりうることなのです。しかし,この現象に初めて出くわしたとき,多くの人はとても驚き,それが現実であるということを受け入れようとすらしません。でもこれは現実なのです。ここには統計における非常に重要な教訓が数多く含まれているのですが,ここではとくに重要なポイントを強調しておきたいと思います。それは,研究とは難しいものであり,気を抜いていると直感に反したたくさんの巧妙な罠にはまってしまうということです。科学者が統計を好み,そして研究法を教える2つ目の理由がこれです。科学は難しいものであり,ときに真実は複雑なデータの隅々に巧妙に隠されているものだからです。
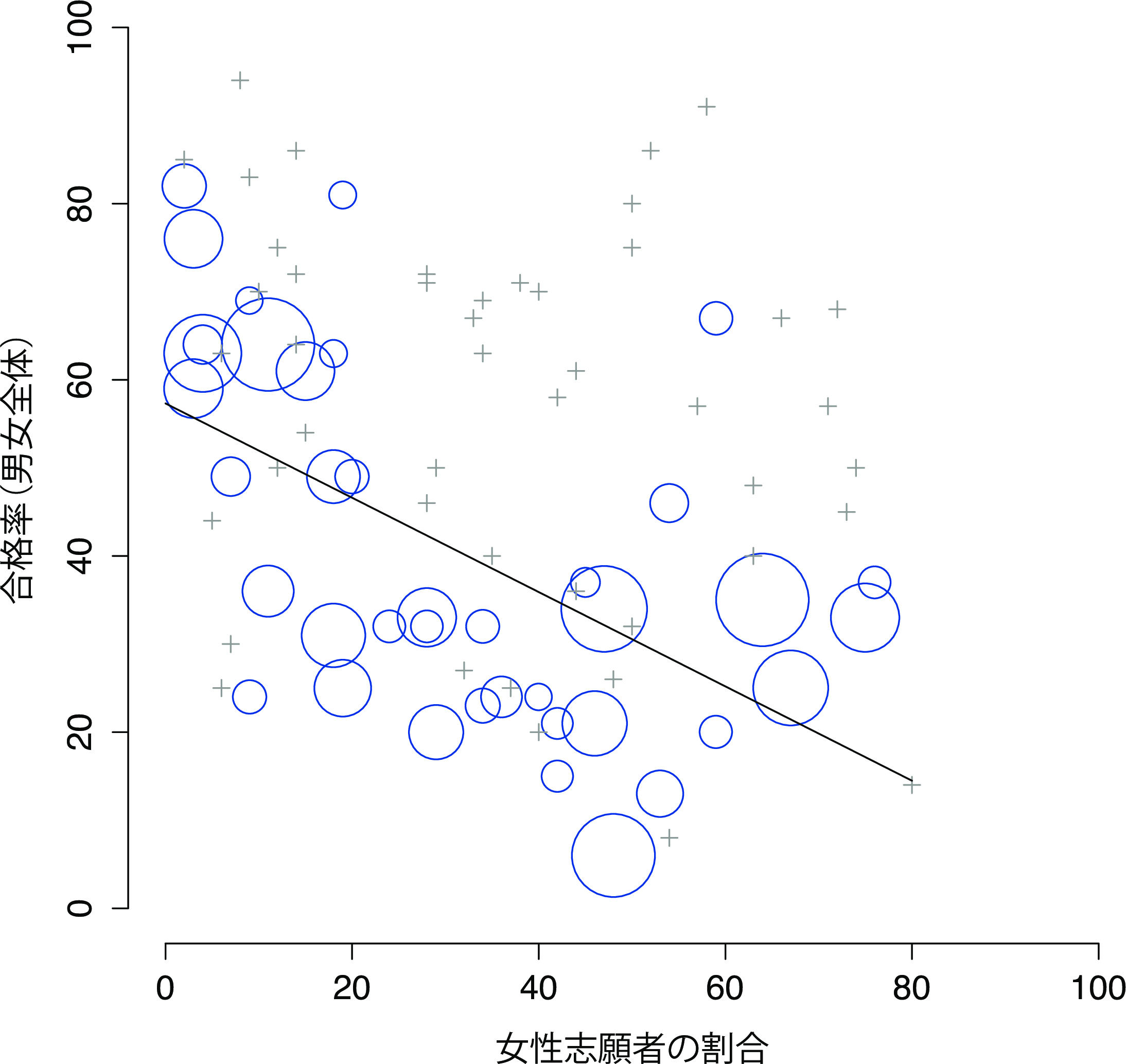
図1.1: バークレー校1973年入試データ。この図には少なくとも1人以上の女性志願者があった85の学科の合格率と女性志願者率が示されている。この図はBickel, Hammel, & O’Connell (1975)の図1を再構成したもの。図中の円は志願者40人以上の学科で,円が大きいほど志願者が多いことを示す。+の企業は志願者40人未満の学科。
この話を終える前に,非常に重要なことをもう1つだけ指摘しておきたいと思います。これは,研究法の授業ではしばしば見過ごされがちな点です。それは,統計で解決できるのは問題の一部だけだということです。先ほどの話は,バークレー校の入試が女性志願者に対して不公平になっているのではないかという懸念から始まったものでした。「集計」データでは確かに大学が女性を差別しているかのように見えますが,「個別」データで各学科を個別に見てみると,実際にはそれぞれの学科には女性優遇といえなくもないようなわずかな偏りがありました。大学全体での合格率における性別の偏りは,女性がより難易度の高い学科を選ぶ傾向にあったことが原因だったのです。法的見地からすれば,これで大学への疑義は晴れたといえるでしょう。大学院入試の判定は学科ごとに行われるものですし,学科単位で判定することには正当な理由もあります。個別の学科レベルでは,判定に大きな偏りはなく(女性の方がやや有利であるという偏りは非常に弱いもので,学科間で一貫しているわけではありません)。学生がどの学科に志願するかを大学が指定することはできませんし,入試判定は学科単位で行われるので,その結果に何らかの偏りが生じたとしても大学が責任を問われることはまずないでしょう。
先ほどのいささか軽薄な発言の根拠はここにあったわけですが,でもこれで終わりではないはずです。この問題に社会学的・心理学的観点から興味を持ったのだとすれば,志願者の分布が男女ではっきり異なっているのがなぜなのかに疑問を持つのではないでしょうか。男性には工学系への入学を希望する傾向があり,文学系に女性が多いのはなぜでしょうか。また,女性の志願率が高い学科では男性の志願率が高い学科に比べて全体の合格率が低いのはなぜでしょうか。各学科の入試判定が公平だったとしても,こうした形で性差別が反映されているということはあり得ないでしょうか。その可能性はあります。仮に,男性は「ハードサイエンス」を好む傾向にあり,女性は「人文科学」を好む傾向にあるとしましょう。そして,人文学科の合格率が低い理由が,人文学に対する政府の予算が少ないためだったとしましょう(たとえば,博士課程の学生数は,政府が資金提供する研究プロジェクトの有無と結びついていることがよくあります)。これは性差別なのでしょうか。それとも単に人文科学の価値がわかっていないだけなのでしょうか。もし政府上層にいる人物が人文科学系の研究資金を削減した理由が,人文学は「役に立たない女の遊び」だからという考えに基づくものだったとしたらどうでしょうか。これはきわめて露骨な性差別といえるでしょう。これらはどれも統計で扱えるようなものではありませんが,研究プロジェクトにとっては重要な問題です。もしこうしたわかりにくい性差別の全体的な構造効果に関心があるなら,おそらく集計データと個別データの両方を見たいと思うことでしょう。しかし,あなたがバークレー校で意思決定を行う立場にいるなら,個別データにしか関心がないかもしれません。
要するに,統計では答えを出せないような重要な問題というのは数多くあるわけですが,そうした問題の答えがデータの分析方法や解釈方法に多大な影響を与えることになるのです。このような理由から,統計はデータについて知ることを助けてくれるツールであるということをつねに忘れないようにしなくてはなりません。それ以上でもそれ以下でもないのです。強力なツールではありますが,注意深い思考に変わるものではありません。
1.3 心理学における統計
ここまでのところで,科学全般でなぜそれほどまでに統計を重視するのかが少しはわかってもらえたのではないかと思います。ただ,心理学における統計の役割については,とくに心理学の授業でなぜこんなに統計の講義があるのかなど,まだいろいろと疑問があることでしょう。そこでここではそれらの疑問のいくつかに答えてみようと思います。
心理学はなぜこんなに統計ばかりなのですか
それにはいくつかの理由があり,率直に言ってその理由は重要なものからそうでないものまでさまざまです。一番重要な理由としてあげられるのは,心理学は統計科学であるということです。どういうことかというと,私たちが研究の「対象」にしているのは人間です。実際の,複雑で,見事なまでに乱雑で,腹立たしいほど思い通りにならない人間が相手なのです。物理学の場合,その「対象」は電子のようなものです。物理学にもさまざまに複雑な側面を持っていますが,電子には個人の意思というものはありません。電子には意見はありませんし,それぞれに奇妙で気まぐれな個体差があるわけでもなく,実験途中で飽きてしまったりもしないし,実験者に文句を言ったり,データをぐちゃぐちゃにしてやろうしたりはしないのです(私はそんなことしていませんよ)。基本的なレベルにおいて,心理学は物理学より難易度が高いのです5。
基本的に,私たちが皆さんに統計を教えるのは,心理学者は物理学者と違って統計が得意でなければならないからなのです。実際,物理学の世界では,「実験で統計が必要になるようなら,実験方法を改善すべきだ」と言われることもあります。物理学者がそのようなことを言えるのは,社会科学者が相手にしている広大な混沌に比べて,彼らの扱う対象が哀れなほどに単純だからなのです。これは心理学に限った話ではありません。社会科学の大半は統計に強く依存しています。それは私たちが実験が下手だからというわけではなく,私たちの扱う問題が解決困難なものだからです。私たちが統計を教えるのは,本当にそれが必要だからなのです。
誰か他の人に統計をやってもらってはだめなのですか
ある程度は可能ですが,完全に任せることはできません。心理学を研究するうえで完璧な統計学者である必要などないというのは正しいですが,統計に関する能力はある程度身につけておかなければなりません。私の考えでは,すべての心理学研究者が統計の基本を身につけるべき理由は3つあります。
まず根本的な理由として,統計は研究デザインと複雑に絡み合っています。心理学で研究をうまく計画できるようになりたいなら,少なくとも統計の基礎を理解しておく必要があります。
2つめに,心理学の研究についてよりよく知りたければ,心理学の文献を読んで理解することが必要になるはずです。そして心理学ではほぼすべての論文で統計分析の結果が報告されています。つまり,本当に心理学を理解したいのなら,他の人がデータをどう処理したのかについて理解する必要があるのです。そしてそのためには統計がある程度理解できなくてはなりません。
3つめに,誰か他の人に統計をすべてお願いするには現実的に考えて大きな問題があるのです。それは,統計分析はお金がかかるということです。退屈しのぎにオーストラリア政府が大学の学費をいくらに設定しているかを調べてみれば,興味深いことに気づくはずです。なんと統計は「国家的優先事項」に分類されていて,他の分野とくらべて学費はダントツに安いのです。これは統計専門家の数が大いに不足しているからです。これを心理学研究者の視点から見た場合,需要と供給のバランスから考えて心理学者には大きな不利となります。その結果として,現実世界で心理学の研究をしようとすれば,ほぼすべての状況において統計専門家を雇う金銭的余裕などないという残酷な事実に直面することになるのです。こうした経済学的な理由により,結局は自給自足するしかありません。
こうした理由の大部分は,研究者以外にもあてはまるものであるという点に注意してください。心理臨床の専門家を目指していて,その分野のトップにいたいなら,科学論文を読む力が役立ちます。そしてそれらの論文は統計に強く依存していのです。
仕事とか研究とか臨床活動とかどうでもいいんですけど,それでも統計は必要ですか
なんともまあ,困ったものですね。ただ,それでも統計は重要だと思います。統計はある意味すべての人にとって重要なものだからです。私たちは21世紀にいて,データはいたるところにあります。率直にいって,今日私たちが暮らしている世界では,統計の基礎知識は生存競争を勝ち抜くためのツールとでもいえるものなのです。この点については次のセクションで取り上げることにします。
1.4 日常場面における統計
「私たちは情報に溺れている
しかし,私たちは知識に飢えている」
— 複数著者の言葉だが,オリジナルはおそらくJ・ネイスビッツによる
講義ノートを作り始めたとき,私はABCニュースのウェブサイトに掲載されていた最新20件のニュース記事を見てみました。その20件の記事のうち8件には,私が統計的トピックと呼んでいるものが含まれていて,そのうち6件に間違いがありました。参考までに,もっとも多かった誤りはベースライン・データが報告されていないというものでした。たとえば,Xという状況で5%の人がYという特徴を持つとする記事で,その特徴が通常ではどの程度一般的なのかが書かれていなかったりするのです。ここで指摘したいのは,ジャーナリストが統計を知らないということではなく(たいていその通りなのですが),誰かが間違いを犯したときやあなたをだまそうとしているとき,それに気づくのに統計の基礎知識がとても役立つということなのです。実際,統計知識を持っていることによる一番の影響は,新聞記事に腹が立つということ,そしてそれ以上の比率でインターネット記事に対して腹が立つということです。その典型的な例はセクション4.1.5で取り上げています。本書の将来的な版では,この線に沿ってそうした逸話をできるだけたくさん取り上げるつもりです。
1.5 統計より大事なのは研究法である
ここまでは,主に統計について話をしてきました。そのせいで,私はいつも統計のことばかり考えているのではないかと思った人もいるかもしれません。それはあながち間違いではありませんが,ただ,統計より広い概念として研究法があります。研究法の授業ではたいてい,研究デザインの用い方に関するさまざまなトピックについて,とくに人間を相手とした研究で遭遇する問題について学ぶことになるでしょう。しかし,学生の99%はその授業に統計が含まれていることに対して恐怖を感じています。だからここでは統計中心に話を進めてきたのです。ここまでで,統計は重要であるということ,そして何より統計を恐れる必要などないということがわかってもらえたのではないでしょうか。そう言うわけで,研究法入門の授業ではかなりの部分で統計を扱うのが一般的です。これは(普通は)講師が意地悪だからというわけではありません。実際はまったくその逆です。入門クラスで統計中心になることが多いのは,研究法について深く学ぶ前に必ずと言っていいほど統計が必要になるからです。それはなぜでしょうか。他の授業課題でも統計の訓練を受けてきていることが前提となっているものが多く,その他の方法論的なツールよりも統計への依存度の方がはるかに高いからです。学部の授業課題で自分自身の研究をゼロからデザインするということはそうそうありませんが(これをしようと思えば,研究法に関するたくさんの知識が必要です),他の誰かがデザインした研究で集められたデータを分析したり解釈したりする課題は普通にあります(これをしようと思えば,統計が必要になります)。その意味で,他の授業でよい成績をとれるようになるためにも統計はより緊急性のあるものなのです。
ただし,「緊急」であることと「重要」であることは別であるということに注意してください。これらはどちらも大事なことです。ここではっきり強調しておきますが,研究法はデータ分析と同じくらい重要です。ですから本書ではそこにかなりの時間を割いています。ただ,統計にはある種の普遍性があり,そしてほとんどの心理学研究において統計は中心的なツールセットになっていますが,研究法はそこまで普遍的ではありません。どの場面にもあてはまる一般原則もいくつかありますが,研究法の多くは領域ごとにかなり異なったものになっており,それぞれの研究領域に特定的なものです。重要なのはより細かな部分であり,そうした詳細部分が統計法入門や研究法入門の授業で取り上げられることはあまりありません。
これはオーデンの1946年の詩『Under Which Lyre: A Reactionary Tract for the Times』からの引用で,この詩はハーバード大学卒様式の式辞の一部として述べられたものです。この詩にはなかなか興味深い背景があります。http://harvardmagazine.com/2007/11/a-poets-warning.html↩
科学者には一般常識が欠けているというのも1つの理由といえるかもしれません。↩
かなり皮肉を込めた言い方をすれば,この事実だけで私がインターネットで見たものの95%は説明できます。↩
以前の版では実際に訴えられたかのような記載をしていました。しかしそれは誤りでした。この問題については素晴らしい解説がありますのでそちらをご覧ください。https://www.refsmmat.com/posts/2016-05-08-simpsons-paradox-berkeley.html この件を指摘してくれたウィルフレッド・ヴァン・ハータム氏に大いに感謝いたします。↩
物理学が科学として私たちよりごくほんのちょっぴり進歩しているのはそのせいかもしれません。↩