Chapter 3 Set Theory
3.1 Sets in Mathematics
Intuitively, we understand the concept of sets. In dictionaries, you will find definitions like a group or collection of things that belong together or resemble one another.
In mathematics, sets have a pretty precise definition:
- A set is a well-defined collection of objects.
- Each object in a set is called an element of the set.
- Two sets are equal if they have exactly the same elements in them.
- A set that contains no elements is called a null set or an empty set.
- If every element in Set A is also in Set B, then Set A is a subset of Set B.
Example: if A is the set of first five charachters of the alphabet, then: A = {a,b,c,d,e}
In R we can create this set as follows.
We can decide on the name of the set. Here, we use SetA.
The two characters “<” and “-” form an arrow pointing to the left. Remember that this arrow consists of two characters!
We combine the characters on the right of the arrow, using the c() function
We then assign this combination to SetA, on the lefthand side.
Once we have defined SetA, we can check if certain elements, like “a” and “f” are elements of the set.
## [1] TRUE## [1] FALSELikewise, we can create a set of numbers, from 1 to 100.
You can use arrows pointing to the right, as you see below! But it’s very uncommon to do so. Normally, we use the logic Object <- Created from, rather than Created from -> Object. So, we will do it once and never again, for illustration.
## [1] 100## [1] TRUE## [1] FALSE3.2 Relations between Sets
3.2.1 Empty Set
An empty set is a set without elements.
## [1] 0## [1] FALSE3.2.2 Identical Sets
Apart from the sequence of elements, the two sets below are identical.
All elements of A occur in B, and all elements of B are part of A.
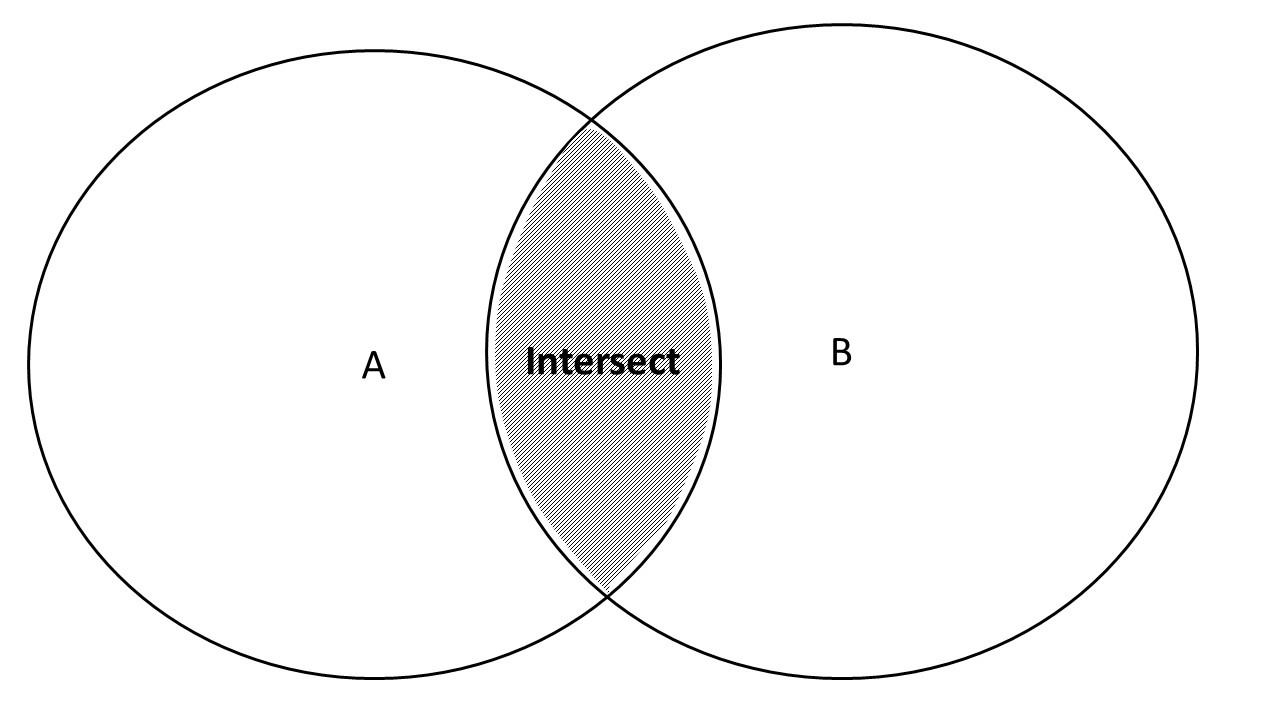
## [1] TRUE TRUE TRUE TRUE## [1] TRUE TRUE TRUE TRUEThe overlap between two sets, is called the intersection.
The intersection is graphically displayed below.
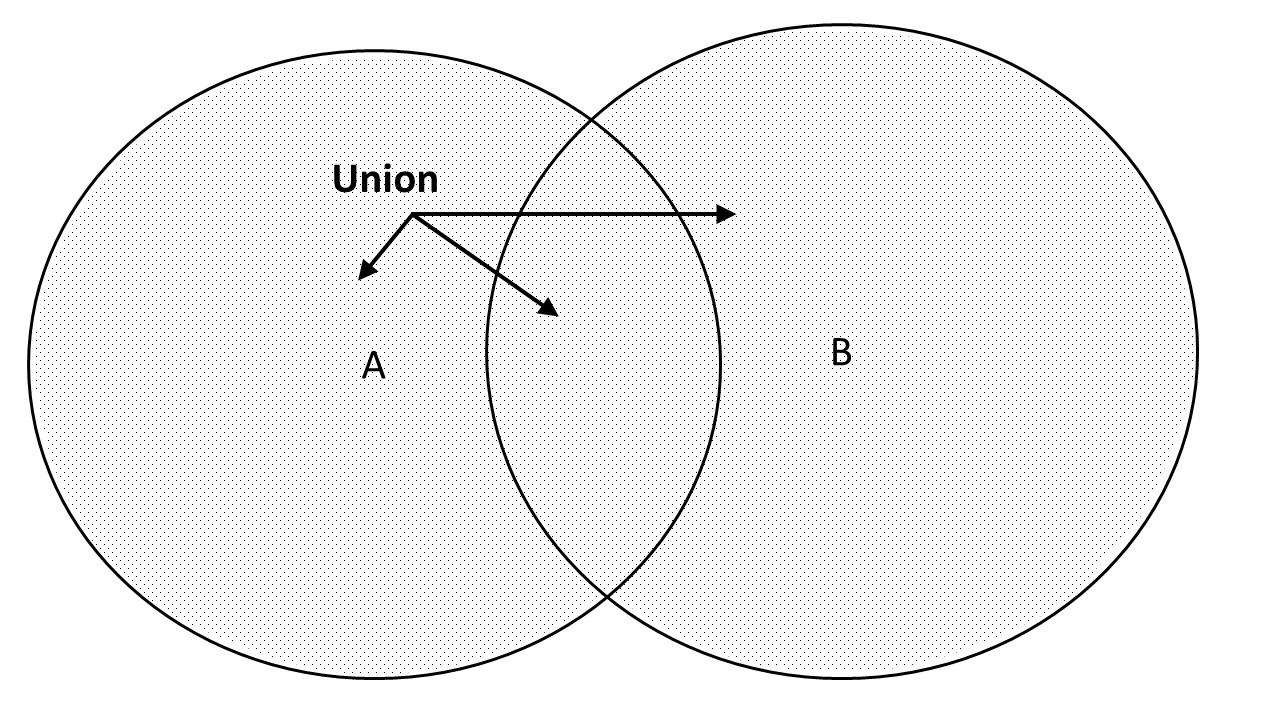
All elements that are part of two sets combined (either A, B or both) form the union of the two sets.
In a graph:
The intersect of two sets is written as \(A \cap B\).
The union of two sets is written as \(A \cup B\). A little trick to help you remember is that the \(\cup\) symbol resembles the first character (“u”) of the word “union”.
We can test the differences and similarities using the commands below.
## character(0)## [1] TRUE## [1] "1" "3" "4" "6"Let’s look at some other examples.
The two sets below are not identical, and contain duplicates.
From the result we see that duplicates are removed! The element “a” appears twice in SetA, but only once in the union of both sets.
## [1] "a" "b" "c" "d" "e"There are various functions in R that help you detect unique and duplicate cases.
Two of these functions are unique() and duplicated().
Applying unique() to a set, filters out any duplicates.
The function duplicated() indicates, for each element, starting from the first element in the set, if it is the same as any of the preceding elements. Since the first element, by definition, has no predecessor, the indication has to be FALSE.
If, like in SetA, the second element is identical to the first element, it will be TRUE.
Going through the entire set, we generate a list of duplicates: elements with indicator TRUE.
Note that duplication means that the same elements occurs twice or more. That is, triplication, quadruplication, and so on, are just subsets of duplication: elements appearing three times or more, are a subset of elements apperaring twice or more.
We can use the result of duplicated() to index SetA. SetA has five elements (including duplicates). We can index these elements using square brackets [ ].
- For example, SetA[1] returns the first element of SetA.
- And SetA[3:5] returns the third to fifth elements of SetA.
- An alternative way for the latter, would be to use a list of TRUE and FALSE indicators, here c(F,F,T,T,T).
Note that TRUE and FALSE, in this and many other cases, can be abbreviated as T and F. It is considered bad practice in programming. But you will encounter it time and again.
## [1] "a"## [1] "b" "c" "d"## [1] "b" "c" "d"Since the duplicated() function produces a list of TRUE and FALSE values, we can use it to index SetA.
However, duplicated() returns TRUE for duplicated elements. If we want to detect unique elements, we use the NOT operator (the exclamation mark, !) to change the TRUE indicators to FALSE, and vice versa.
## [1] "a" "a" "b" "c" "d"## [1] "a" "b" "c" "d"## [1] FALSE TRUE FALSE FALSE FALSE## [1] "a" "b" "c" "d"Differences between sets can be checked using the setdiff() function. The function only compares two sets at the time, and the order is important, as you see below!
## [1] "a" "b"## [1] "e"3.2.3 Advanced
To challenge your skills, we can define the union of sets A and B as follows:
- Elements unique to A, plus:
- Elements unique to B, plus:
- Elements in the interesection of A and B.
We can sort the combination of these three parts alphabetically, and check if indeed the result is equal to what we have defined as the union.
The all() function can be used to see if all elements of one set, are contained by the other.
## [1] "a" "b" "c" "d" "e"## [1] TRUEAn alternative to the above code, is to first create an object (say, combi) as the sorted elements of the combined parts. Then, we compare combi to the result of the union() function. It makes our code slightly more readable.
Adding some comments (text after “#”), always helps making your code more readable.
# union, as combination of unique and intersecting elements
combi <- sort(c(setdiff(SetA, SetB), setdiff(SetB, SetA), intersect(SetB, SetA)))
all(combi == union(SetA, SetB)) # check if combi equals the result of union()## [1] TRUELet’s see what happens if duplicated elements of one set, are checked against another set.
All elements of set C (duplicated elements “a”) are part of D.
One element of D, is not contained in A.
## [1] TRUE TRUE## [1] TRUE## [1] TRUE FALSE## [1] FALSEThis is what we would expect: “a”, though a duplicated element in setC, occurs in SetD (where “a” only occurs once).
3.3 Sets of Numbers
Sets can contain any type of element: characters, binary indicators (like TRUE or FALSE), numbers, and more.
It can be tedious to create sets of characters or words, as you have to do a lot of typing.
Sets of numbers are often easier, especially if it’s a line of numbers, say from 1, 2 .. to 99.
You can use the length() function to return the number of elements (here: numbers).
You can access specific elements using square brackets (indexing). Note that curved brackets () do not work, for indexing. Computers can be very picky.
## [1] -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
## [20] 9 10## [1] 21## [1] -8## [1] TRUE3.4 Application of Set Theory, and Sets
You may wonder why all of the above would be of interest to a data scientist like yourself.
There are a least three reasons.
- Logical thinking
First of all, dealing with data and data analysis will force you to think logically.
Even when working with just one data set, say, a (partial) list of employees in your organization who have filled out survey questionnaire, requires you to first assess the quality of the list.
How many employees have filled out the survey twice or more (and what do we do with duplicates, especially if responses by duplicate respondents are inconsistent)? Is the list of (unique) respondents a subset of employees? Is the response rate the same for all departments of the organization? And so on and so forth.
Answers to such questions can be obtained using the tools discussed above, or any out of many alternative tools. But it is the thinking that counts!
- Comparing data sets
One of the starting points in the data mining process, is data understanding.
Often, your analysis is based on data from various sources. Before you start your analysis, you have to understand all sources in depth.
Combining, or merging, data sets from various sources almost without exception reveals errors, inconsistencies and gaps. Applying the basics of set theory will help you in preparing high-quality, analyzable data sets. Or to put it negatively: data science follows the garbage-in-garbage-out principle!
- Probability theory
In some of the modules, we will use probability theory. Concepts like conditional probablitity have close links to set theory. It helps if you’re familiar with the terminologies, and with notations like \(\cup\) and \(\cap\).
3.5 Exercises
3.5.1 Exercise 1
Given are the following sets:
A = {2,4,6,8,10,12,14,16}
B = {1,2,3,4,5,6,7}
C = {3,6,9,12,15,18}
- A \(\cap\) B = (Intersection of A and B)
- A \(\cap\) C =
- B \(\cap\) C =
- A \(\cap\) B \(\cap\) C =
- A \(\cup\) B = (Union of A and B)
- A \(\cup\) B \(\cup\) C =
3.5.1.1 Solutions
Let’s first create the sets A, B and C.
We use the seq() function in R. You can find documentation on this function here.
For a sequence of numbers that runs from 2 to 16, in steps of 2, like A, we type seq(2,16,2).
B can be defined as seq(1,7,1), but c(1:7) is shorter. B <- 1:7 would work as well.
## [1] 2 4 6 8 10 12 14 16## [1] 1 2 3 4 5 6 7## [1] 3 6 9 12 15 18- A \(\cap\) B
## [1] 2 4 6- A \(\cap\) C
## [1] 6 12- B \(\cap\) C
## [1] 3 6- A \(\cap\) B \(\cap\) C
intersect(A, B, C) will give an error message, as intersect() only works on two sets!
We can do it in 2 steps; first, we determine the intersection of A and B; followed by the intersection of that result with C!
You can imagine that this is doable for three sets.
But if we were to find the intersection between many sets, then the expression would get very lengthy!
A better alternative is to use the Reduce() function.
Often, you can find solutions to this kind of challenges by just googling.
The Reduce() function, for example, we found on link
## [1] 6## [1] 6- A \(\cup\) B
## [1] 1 2 3 4 5 6 7 8 10 12 14 16- A \(\cup\) B \(\cup\) C
## [1] 1 2 3 4 5 6 7 8 9 10 12 14 15 16 183.5.1.2 Are you in for a challenge?
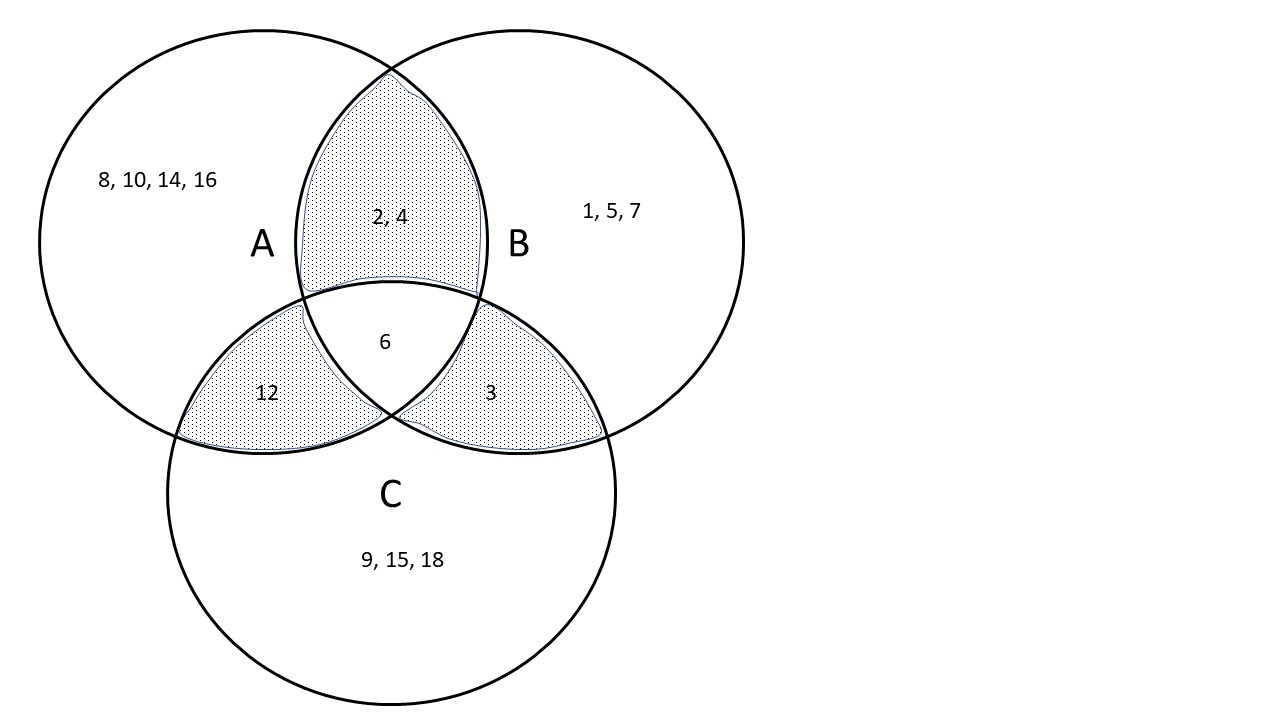
Which elements are in intersections of sets, but not in all sets?
## [1] 2 4 6## [1] 6 12## [1] 3 6## [1] 2 3 4 6 12## [1] 6## [1] 2 3 4 12You see that elements 2, 3, 4 and 12 are in pairwise intersections, but not in the three-way intersection!
Graphically, just to convince you:
3.5.2 Exercise 2
Are the following statements true or false?
- {2,4} \(\subset\) (A \(\cap\) B)
- 6 \(\in\) (A \(\cap\) B \(\cap\) C)
- {6} \(\subset\) (A \(\cap\) B)
- (A \(\cap\) B) \(\subset\) (A \(\cup\) B)
3.5.2.1 Solutions
- {2,4} \(\subset\) (A \(\cap\) B)
## [1] TRUE- 6 \(\in\) (A \(\cap\) B \(\cap\) C)
See below, under c.
- {6} \(\subset\) (A \(\cap\) B)
## [1] 6## [1] TRUE# Alternatively (as in b.), define 6 as a single element rather than a set of one element
6 %in% trios## [1] TRUE- (A \(\cap\) B) \(\subset\) (A \(\cup\) B)
This is true in general. Elements in the intersection of A and B, are by definition part of both A and B. The intersection is therefore a subset of all elements in A or B!
Just to train the formulation of this exercise in R:
## [1] TRUE3.5.3 Exercise 3
A = {1,2,3,4,5,6}
B = {5,6}
C = {1,2,5,6}
D = {2,3,4}
E = {2,3,4,5}
Complete the statement with one of the symbols:
- \(\in\) (element of)
- \(\notin\) (not an element of)
- \(\subset\) (subset of)
- \(\supset\) (superset; if A is subset of B, then B is superset of A)
- \(\cap\) (intersection)
- \(\cup\)
- B….C
- B….C = B
- B….C = C
- B….D = 0 (empty set)
- C….D = A
- D….E = D
- 4….C \(\cap\) B
- D….E….A
3.5.3.1 Solutions
Use reason to answer each of the questions!
As an additional challenge, formulate the sets in R, and use any of the commands introduced in this chapter to check your answer!
- \(\subset\) (B is obviously a subset of C, as all elements of B are also in C)
- \(\cap\) (the intersect of B and C, is equal to B, as B is a subset of B)
- \(\cup\) (the combined elements of B and C, are equal to C, as C is a superset of B)
- \(\cap\) (as B and D have no elements in common, the interesect is the empty set)
- \(\cup\) (all elements of C and D combined, match A)
- \(\cap\) or \(\subset\)
- \(\notin\) (4 is not part of the intersection of B and C; it is not even part of the union of B and C)
- \(\subset\) (D is a subset of E, which in turn is a subset of A; you can conclude that therefore D is a subset of A)
Working with data files (in data science) requires logical thinking. Set theory is a good exercise in logical thinking!
3.5.4 Exercise 4
Consider the following sets.
- A = {x | x is an even number and x<20; x is a positive natural number}
- B = {x | x is a multiple of 3 and x<20; x is a positive natural number}
- C = {x | x is an odd numbber and x<20; x is a positive natural number}
This looks cryptic.
Set A, for example, reads like the set of numbers x conditioned by the following rules. x is:
- a positive natural number (1, 2, 3 to infinity)
- smaller than 20, and
- divisible by 2.
We can enumerate these numbers easily: 2, 4, 6 .. up to 18.
Set B then is 3, 6, 9 .. up to 18.
And Set C is 1, 3, 5 .. up to 19.
Determine:
- A \(\cap\) B
- A \(\cap\) B \(\cap\) C
- A \(\cup\) B \(\cup\) C
Again, create the sets in R and use the proper functions to get the solutions!
3.5.4.1 Solutions
- {6, 12, 18}
- 0 (empty set)
- {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19}
## [1] 2 4 6 8 10 12 14 16 18## [1] 3 6 9 12 15 18## [1] 1 3 5 7 9 11 13 15 17 19## [1] 6 12 18## numeric(0)## [1] 2 4 6 8 10 12 14 16 18 3 9 15 1 5 7 11 13 17 19