Chapter 2 The value of money
2.1 The centipede game
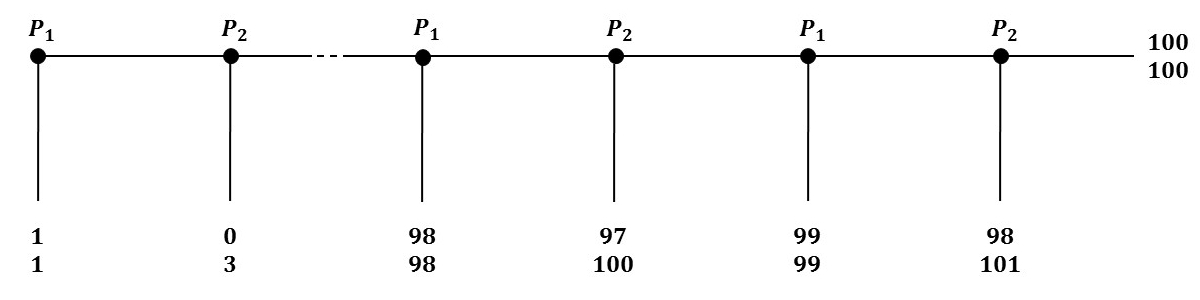
Figure 2.1: The centipede game
The centipede game starts with player \(P_1\) deciding if the game should continue or not. If this player stops the game, then both players receive a payoff of \(1\). If the game continues, player \(P_2\) must in turn decide if the game should stop or continue. If the game stops, player \(P_1\) receives a \(0\) payoff, while player \(P_2\) receives a payoff of \(3\). If the game goes one, player \(P_1\) must play, and so on.
The game is limited in nuber of turns: if both players always choose to continue the game, each one of them will receive \(100\) as payoff.
If two people who do not know each other were to play this game once in their life, how would they play? Game theory tells us that, if they are rational (and if they know they both are), the game will stop at the very first turn.
While it might seem surprising, it is a strongly established fact. If we consider the last turn, it is clear that \(P_2\) will selfishly end the game to get \(101\) rather than continue it to get only \(100\) (as the two players do not know each other, \(P_2\) has no reason to do a suboptimal choice for the sake of \(P_1\)).
But as \(P_1\) knows that, just before \(P_2\) can selfishly end the game, \(P_1\) will do it, so that they both receive \(99\). But \(P_2\) is smart, he has very well understood what was at stake! And so he will end the game the turn before. And so on, until we conclude that \(P_1\) has no better choice than choosing to end the game at the very first step even though they could have won a lot more, had they been more cooperative (or less rational).
2.2 The money temporal paradox
The case of money is somewhat similar to the centipede game. We often accept to give someone tangible goods in exchange os some piece of paper called “money”. By doing so, we are putting ourselves in the shoes of \(P_1\), renouncing to a payoff of \(1\) (the goods we own) to get some money with no direct utility instead. Our only hope is that another person in the economy will some day be willing to give us something in return for the money.
The trouble is that we know for sure that, one day, the money we use will cease to have value: economic crises, wars, natural hazards or the end of the world itslef will dramatically affect its value in the long run. So one day the money we use will not have any value anymore, implying that the day before everyone should refuse any payment with this money. So the day before the money has no value anymore, it has already no value. And so on, to the point where money should never have any value.
Then, is money valued only by irrational people? Actually, even if we knew for sure that one day the money we use would be worthless, the uncertainty on the fatidic date would be enough to convince us to use it. While in the centipede game each player can predict with absolute certainty what will happen, our situation does not allow that: in order to take decisions, we have to balance the risk with the potential positive outcomes. The uncertainty is here what allows us to rationally create value.
2.3 The infinite centipede game
To illustrate this fact, we have to modify the centipede game a bit. Let us consider an infinite centipede game, where at the beginning of the game the players have to choose the probabilities \(p_1\) (for player \(P_1\)) and \(p_2\) (for player \(P_2\)) with which they will continue the game when it is their turn to play.
For the sake of simplicity, let us assume that there is no time preference, and that the game will continue forever unless one of the players ends it (it is possible to establish similar results if we do not make such simplifications, but with a lot more computations).
If \(p_1 = p_2 = 1\), then the payoff for both players is \(\infty\).
If the payoffs at each step of the game are computed as in figure 2.1, then there are exactly two pure Nash equilibria:
- the first one is characterised by \(p_1 = p_2 = 0\): if one player does not want to cooperate at all, the other for sure has no interest in any kind of cooperation either
- the second one is characterised by \(p_1 = p_2 = 1\): if one player is willing to cooperate no matter what, the other has every reason to do the same to get the infinite payoff.
These two Nash equilibria are not equivalent: one is worth \(0\) for both players, while the other is worth an infinite payoff. The uncertainty about the outcome of this game is finally not so big: we can reasonably expect both players to choose \(p_1 = p_2 = 1\).
2.4 Solving the paradox
The money temporal paradox seems to be solved. But does the infinite centipede game imply that we should always accept any fiat money as payment?
Actually, everything depends on the coefficients of the game: if the payoffs are not increasing but decreasing with time, it is clear that rational players would choose not to play the game, or more exactly to play \(p_1 = p_2 = 0\).
Thus it appears that the value of money resides in the fact that, by helping people to exchange goods and services, it helps in creating a thriving market where opportunities get better over time: in other words, the intrinsic value of money resides in its characteristics facilitating trade.