3.1 Ringkasan Data

R Commander dapat menghasilkan sejumlah ringkasan statistik seperti tabel frekuensi, jumlah observasi yang kosong (missing value), mean, median, simpangan baku, dll. Beberapa menu ringkasan data yang dapat digunakan pada menu Statistics/Summaries, antara lain:

Active data set : membuat ringkasan data berupa nilai min, max, kuartil 1, median, mean, dan kuartil 3 untuk jenis data numeric. Sedangkan untuk jenis data factor atau character/string akan dihasilkan tabel frekuensi.
Numerical summaries... : membuat ringkasan data spesifik untuk variabel numerik, seperti: mean, median, kuartil, simpangan baku, kurtosis, dll. baik untuk variabel tunggal maupun agregat variabel numeric berdasarkan variabel factor.
Frequency distributions... : membuat tabel distribusi frekuensi variabel factor atau character/string. Selain itu, menu ini menyajikan opsi untuk menampilkan uji goodness-of-fit untuk melakukan uji apakah proporsi frekuensi pada tiap kelompok kategori sesuai dengan ekspektasi yang kita harapkan. Dalam hal ini kita dapat pula menguji apakah proporsi observasi pada tiap kelompok sama (tiap kelompok homogen).
Count missing observations : menampilkan data terkait jumlah observasi kosong pada tiap variabel dataset.
Table of statistics : menampilkan ringkasan data variabel numeric tunggal atau agregat berdasarkan satu fungsi statistik tertentu.
Correlation matrix : menampilkan matrix korelasi dua atau lebih variabel numerik. Menu ini juga menampilkan opsi apakah nilai p-value dan adjusted p-value metode Holm setiap pasang korelasi variabel perlu ditampilkan.

3.1.1 `Active Data Set`

Pada Chapter 3.1.1, penulis akan memberikan contoh penerapan menu Statistics/Summaries/Active data set pada dataset iris dan mtcars. Berikut adalah ringkasan data untuk kedua dataset tersebut:

summary(iris)

##   Sepal.Length   Sepal.Width    Petal.Length 
##  Min.   :4.30   Min.   :2.00   Min.   :1.00  
##  1st Qu.:5.10   1st Qu.:2.80   1st Qu.:1.60  
##  Median :5.80   Median :3.00   Median :4.35  
##  Mean   :5.84   Mean   :3.06   Mean   :3.76  
##  3rd Qu.:6.40   3rd Qu.:3.30   3rd Qu.:5.10  
##  Max.   :7.90   Max.   :4.40   Max.   :6.90  
##   Petal.Width        Species  
##  Min.   :0.1   setosa    :50  
##  1st Qu.:0.3   versicolor:50  
##  Median :1.3   virginica :50  
##  Mean   :1.2                  
##  3rd Qu.:1.8                  
##  Max.   :2.5

summary(mtcars)

##       mpg            cyl            disp      
##  Min.   :10.4   Min.   :4.00   Min.   : 71.1  
##  1st Qu.:15.4   1st Qu.:4.00   1st Qu.:120.8  
##  Median :19.2   Median :6.00   Median :196.3  
##  Mean   :20.1   Mean   :6.19   Mean   :230.7  
##  3rd Qu.:22.8   3rd Qu.:8.00   3rd Qu.:326.0  
##  Max.   :33.9   Max.   :8.00   Max.   :472.0  
##        hp             drat            wt      
##  Min.   : 52.0   Min.   :2.76   Min.   :1.51  
##  1st Qu.: 96.5   1st Qu.:3.08   1st Qu.:2.58  
##  Median :123.0   Median :3.69   Median :3.33  
##  Mean   :146.7   Mean   :3.60   Mean   :3.22  
##  3rd Qu.:180.0   3rd Qu.:3.92   3rd Qu.:3.61  
##  Max.   :335.0   Max.   :4.93   Max.   :5.42  
##       qsec            vs              am       
##  Min.   :14.5   Min.   :0.000   Min.   :0.000  
##  1st Qu.:16.9   1st Qu.:0.000   1st Qu.:0.000  
##  Median :17.7   Median :0.000   Median :0.000  
##  Mean   :17.8   Mean   :0.438   Mean   :0.406  
##  3rd Qu.:18.9   3rd Qu.:1.000   3rd Qu.:1.000  
##  Max.   :22.9   Max.   :1.000   Max.   :1.000  
##       gear           carb     
##  Min.   :3.00   Min.   :1.00  
##  1st Qu.:3.00   1st Qu.:2.00  
##  Median :4.00   Median :2.00  
##  Mean   :3.69   Mean   :2.81  
##  3rd Qu.:4.00   3rd Qu.:4.00  
##  Max.   :5.00   Max.   :8.00

Secara umum format sintaks pada menu tersebut adalah sebagai berikut:

summary(dataset)

3.1.2 `Numerical Summaries`

Pada Chapter 3.1.2 akan ditampilkan cara membuat ringkasan data numerik variabel Sepal.Length dan Sepal.Width pada dataset iris dengan agregasi menggunakan variabel Species. Untuk melakukannya jalankan tahapan berikut:

Pilih menu Statistics/Summaries/Numerical summaries.../.
Pada tab Data di jendela Numerical Summaries, pilih variabel numeric (jika ingin memilih lebih dari satu tekan tombol shift+ klik). Dalam hal ini penulis akan memilih variabel Sepal.Length dan Sepal.Width.
Untuk membuat ringkasan variabel numerik berdasarkan grup data atau factor, klik tombol Summarize by: pada tab Data dan pilih variabel factor yang digunakan. Dalam hal ini penulis memilih variabel Species. Klik OK.
Pada tab Statistics, centang statistika deskriptif yang akan ditampilkan. Klik OK.

Ringkasan tahapan tersebut divisualisasikan pada Gambar 3.1.

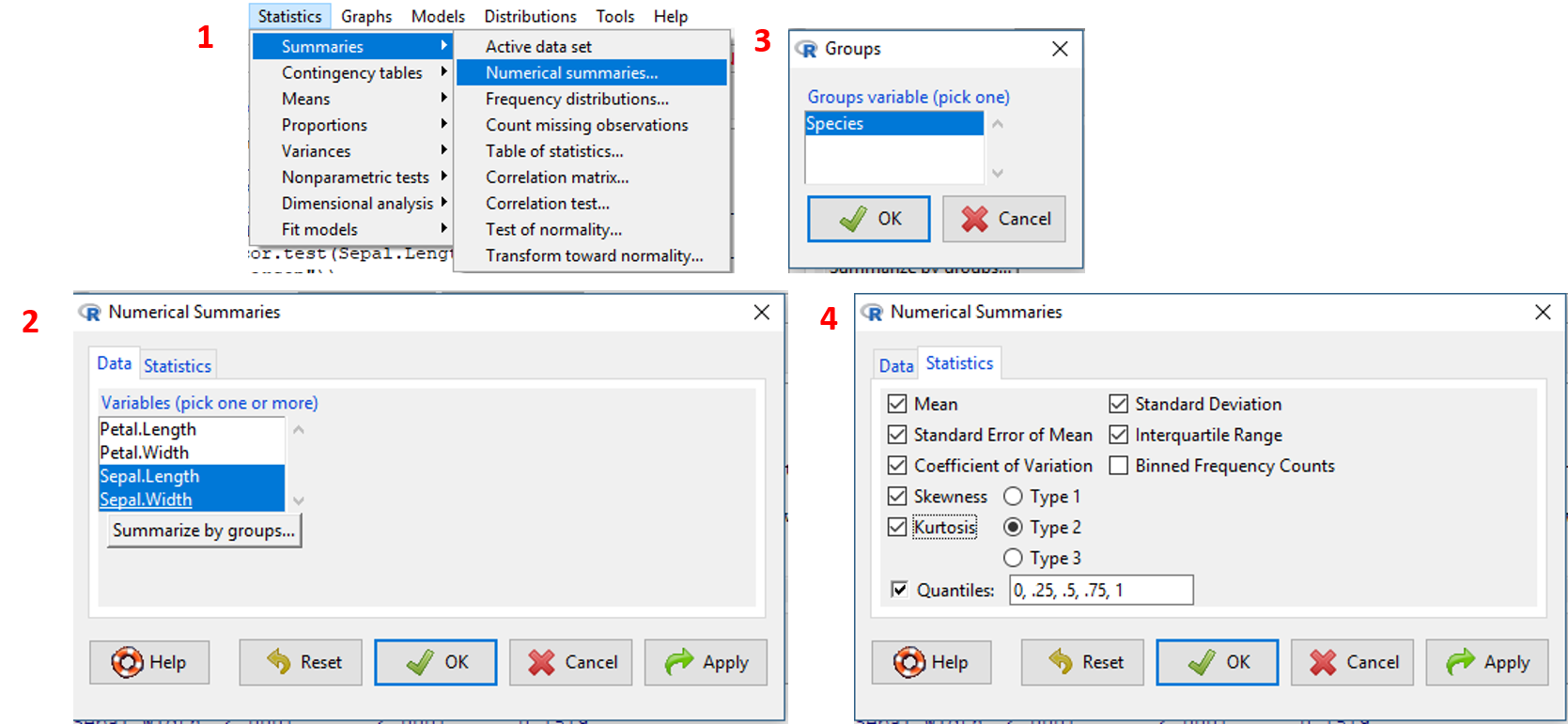
Gambar 3.1: Tampilan langkah membuat ringkasan data variabel numeric dataset iris.

Tampilan ringkasan data variabel Sepal.Length dan Sepal.Width berdasarkan variabel factor Species adalah sebagai berikut:

## Warning: package 'RcmdrMisc' was built under R version
## 3.6.2

## Loading required package: car

## Warning: package 'car' was built under R version 3.6.2

## Loading required package: carData

## Loading required package: sandwich

## Warning: package 'sandwich' was built under R version
## 3.6.2

numSummary(iris[,c("Sepal.Length", "Sepal.Width"), 
                drop=FALSE], 
  groups=iris$Species, statistics=c("mean", "sd", 
  "se(mean)", "IQR", "quantiles", "cv", "skewness", 
  "kurtosis"), quantiles=c(0,.25,.5,.75,1), type="2")

## 
## Variable: Sepal.Length 
##             mean     sd se(mean)   IQR      cv
## setosa     5.006 0.3525  0.04985 0.400 0.07041
## versicolor 5.936 0.5162  0.07300 0.700 0.08696
## virginica  6.588 0.6359  0.08993 0.675 0.09652
##            skewness kurtosis  0%   25% 50% 75% 100%  n
## setosa       0.1201  -0.2527 4.3 4.800 5.0 5.2  5.8 50
## versicolor   0.1054  -0.5330 4.9 5.600 5.9 6.3  7.0 50
## virginica    0.1180   0.0329 4.9 6.225 6.5 6.9  7.9 50
## 
## Variable: Sepal.Width 
##             mean     sd se(mean)   IQR     cv skewness
## setosa     3.428 0.3791  0.05361 0.475 0.1106  0.04117
## versicolor 2.770 0.3138  0.04438 0.475 0.1133 -0.36284
## virginica  2.974 0.3225  0.04561 0.375 0.1084  0.36595
##            kurtosis  0%   25% 50%   75% 100%  n
## setosa       0.9547 2.3 3.200 3.4 3.675  4.4 50
## versicolor  -0.3662 2.0 2.525 2.8 3.000  3.4 50
## virginica    0.7061 2.2 2.800 3.0 3.175  3.8 50

Format umum sintaks tersebut adalah sebagai berikut:

numSummary(dataset[,c("NamaVariabel",....), 
                drop=FALSE], 
  groups=dataset$NamaVariabel, statistics=c("mean", ...), 
  type="...")

Pada fungsi tersebut terdapat 3 buah tipe yang digunakan untuk menghitung nilai skewness dan kurtosis. Ketiga tipe tersebut memiliki bentuk persamaan yang berbeda-beda, dimana tipe 1 merupakan persamaan yang sering digunakan pada textbook lama, tipe 2 merupakan persamaan yang digunakan pada aplikasi SAS dan SPSS, sedangkan tipe 3 merupakan persaman yang digunakan pada aplikasi MINITAB dan BMDP. Untuk memperoleh informasi terkait ketiga tipe tersebut, jalankan sintaks berikut;

?e1071::skewness
?e1071::kurtosis

3.1.3 `Frequency Distributions`

Untuk data dengan jenis kategorikal, ringkasan data yang dapat dilakukan adalah dengan membuat tabel frekuensi untuk mengetahui jumlah observasi pada tiap kategorinya. Sebagai contoh, kita ingin mengetahui proporsi observasi pada tiap Species pada dataset iris. untuk melakukannya jalankan langkah-langkah berikut:

Pilih menu Statistics/Summaries/Frequency distributions.../.
Pada jendela yang muncul, pilih satu atau beberapa (tekan shift + klik) variabel factor.
Centang pada check box Chi-square goodness-of-fit test jika ingin menampilkan hasil uji goodness-of-fit distribusi data (uji ini hanya dapat dilakukan pada satu variabel). Klik OK
Jika check box dicentang, akan muncul jendela dialog yang meminta pembaca untuk mengisi hipotesis propabilitas dari distribusi observasi pada masing-masing kategori. Secara default, probabilitas akan diatur seragam untuk setiap kategori. Klik OK.

Visualisasi tahapan tersebut ditampilkan pada Gambar 3.2.

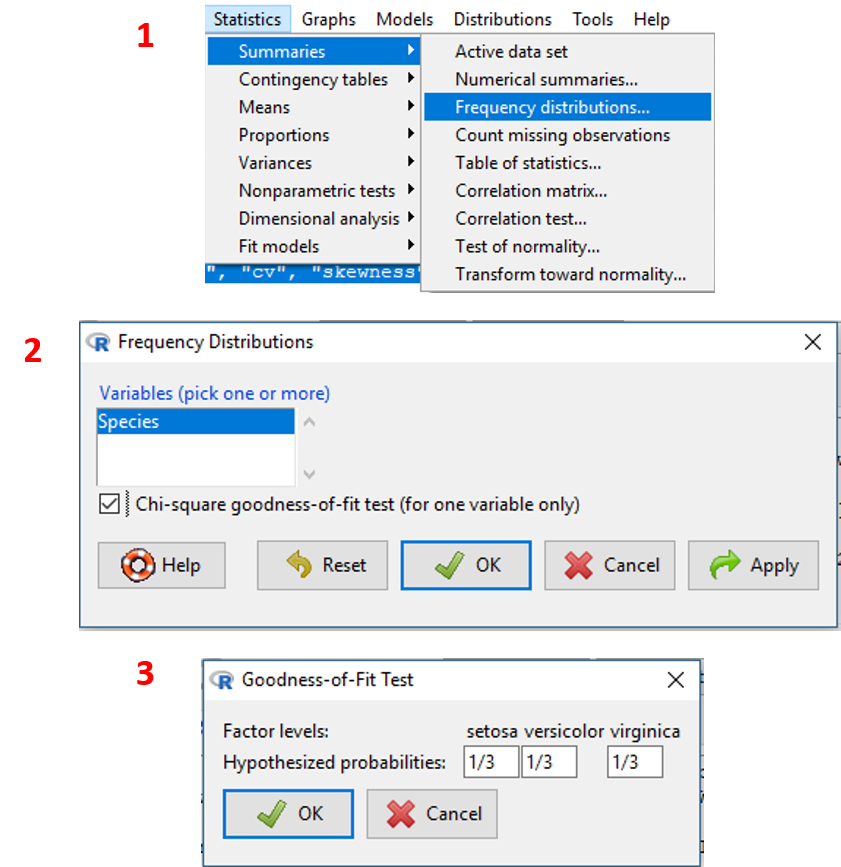
Gambar 3.2: Tampilan langkah membuat tabel frekuensi pada dataset iris.

Sintaks dan output yang muncul pada proses tersebut adalah sebagai berikut:

local({
  .Table <- with(iris, table(Species))
  cat("\ncounts:\n")
  print(.Table)
  cat("\npercentages:\n")
  print(round(100*.Table/sum(.Table), 2))
  .Probs <- c(0.333333333333333,0.333333333333333,
              0.333333333333333) 
  chisq.test(.Table, p=.Probs)
})

## 
## counts:
## Species
##     setosa versicolor  virginica 
##         50         50         50 
## 
## percentages:
## Species
##     setosa versicolor  virginica 
##      33.33      33.33      33.33

## 
##  Chi-squared test for given probabilities
## 
## data:  .Table
## X-squared = 1.5e-28, df = 2, p-value = 1

Berdasarkan output yang dihasilkan, dapat diperhatikan bahwa 150 observasi yang ada pada dataset iris tersebar secara merata pada tiap kelas factor. Pada output yang dihasilkan dapat diperhatikan pula bahwa terdapat tiga bagian output. Bagian pertama adalah vektor frekuensi observasi pada tiap kelas factor, bagian kedua output berupa vektor persentase observasi tiap kelas dari total observasi yang ada, dan bagian ketiga adalah statistika uji dalam hal ini adalah uji Chi-square.

Secara umum sintaks tersebut dapat dituliskan seperti berikut:

local({
  .Table <- with(dataset, table(NamaVariabel))
  cat("\ncounts:\n")
  print(.Table)
  cat("\npercentages:\n")
  print(round(100*.Table/sum(.Table), 2))
  .Probs <- c(0.333333333333333,0.333333333333333,
              0.333333333333333) 
  chisq.test(.Table, p=.Probs)
})

3.1.4 `Count Missing Observations`

Menu Statistics/Summaries/Count missing observations dapat digunakan untuk mengecek apakah pada setiap variabel dataset terdapat missing value. Output yang dihasilkan berupa sebuah vektor dengan nama vektor dan nilai vektor berupa jumlah observasi dengan missing value yang ada pada tiap variabel. Berikut adalah contoh sintaks dan output yang dihasilkan untuk mengecek missing value pada dataset iris, mtcars, dan VADeaths:

# iris
sapply(iris, function(x)(sum(is.na(x)))) # NA counts

## Sepal.Length  Sepal.Width Petal.Length  Petal.Width 
##            0            0            0            0 
##      Species 
##            0

# mtcars
sapply(mtcars, function(x)(sum(is.na(x)))) # NA counts

##  mpg  cyl disp   hp drat   wt qsec   vs   am gear carb 
##    0    0    0    0    0    0    0    0    0    0    0

# VADeaths
sapply(VADeaths, function(x)(sum(is.na(x)))) # NA counts

##  [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

Berdasarkan output yang dihasilkan, dapat disimpulkan bahwa ketiga dataset tersebut tidak memiliki observasi dengan nilai kosong (missing value).

Format umum sintaks tersebut adalah sebagai berikut:

sapply(dataset, function(x)(sum(is.na(x))))

3.1.5 `Table of Statistics`

Pada Chapter 2.9.2 kita telah belajar cara untuk membuat ringkasan nilai satu atau beberapa variabel berdasarkan level variabel factor. Output yang dihasilkan berdasarkan menu tersebut adalah dataframe hasil agregasi. Pada Chapter 3.1.5 kita akan belajar kembali proses tersebut. Hal yang membedakan dari proses sebelumnya adalah menu Statistics/Summaries/Table of statistics menghasilkan output berupa vektor.

Pada Chapter 3.1.5 kita akan mencoba untuk mencari rata-rata seluruh variabel numerik berdasarkan variabel Species. Untuk melakukannya jalankan langkah-langkah berikut:

Pilih menu Statistics/Summaries/Table of statistics.
Pada kotak Factors, pilih satu atau beberapa variabel factor sebagai variabel pengelompok. Dalam hal ini variabel Species dipilih.
Pada kotak Response variables, satu atau beberapa variabel numeric yang hendak dihitung tabel statistiknya. Pada contoh kali ini penulis memilih seluruh variabel numeric.
Pada bagian Statistics, pilih statistik yang akan dihasilkan. Dalam hal ini penulis ingin menghitung nilai mean pada setiap kelompok spesies pada setiap variabel. Klik OK.

Visualisasi tahpan tersebut ditampilkan pada Gambar 3.3.

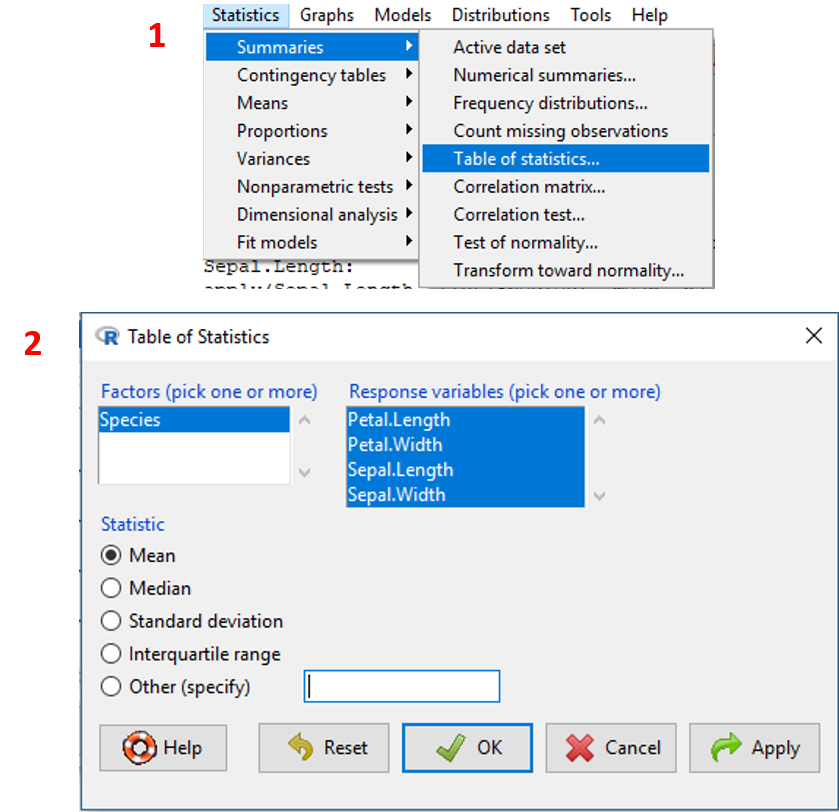
Gambar 3.3: Tampilan langkah membuat tabel statistik pada dataset iris.

Sintaks dan output yang dihasilkan pada tahapan tersebut adalah sebagai berikut:

# Table for Petal.Length:
with(iris, tapply(Petal.Length, 
                  list(Species), mean, na.rm=TRUE))

##     setosa versicolor  virginica 
##      1.462      4.260      5.552

# Table for Petal.Width:
with(iris, tapply(Petal.Width, 
                  list(Species), mean, na.rm=TRUE))

##     setosa versicolor  virginica 
##      0.246      1.326      2.026

# Table for Sepal.Length:
with(iris, tapply(Sepal.Length, 
                  list(Species), mean, na.rm=TRUE))

##     setosa versicolor  virginica 
##      5.006      5.936      6.588

# Table for Sepal.Width:
with(iris, tapply(Sepal.Width, 
                  list(Species), mean, na.rm=TRUE))

##     setosa versicolor  virginica 
##      3.428      2.770      2.974

Secara umum berdasarkan output yang dihasilkan, spesies anggrek virginica memiliki nilai rata-rata panjang petal, lebar petal dan dan panjang sepal yang lebih besar dibanding yang lainnya, sedangkan spesies setosa memiliki ukuran petal dan panjang sepal yang lebih kecil serta lebar sepal yang lebih besar dibandingkan spesies anggrek lainnya. Selain itu, diketahui bahwa spesies anggrek versicolor memiliki ukuran sepal dan petal yang berada diantara dua spesies anggrek lainnya.

Format umum sintaks tersebut adalah sebagai berikut:

with(dataset, tapply(NamaVariabel, 
                     list(VariabelFactor), 
                     mean, na.rm=TRUE))

3.1.6 `Correlation Matrix`

MenuStatistics/Summaries/Correlation matrix akan menghasilkan matriks korelasi antar variabel numeric. Metode yang tersedia untuk menghitung nilai korelasi antara dua buah variabel numeric adalah metode Pearson product-moment (metode parametrik) dan Spearman rank-order (metode nonparametrik). Pada menu tersebut juga tersedia pilihan apakah akan menampilkan nilai p-value dan adjusted p-value (metode Holm) pada masing-masing nilai korelasi.

Pada Chapter 3.1.6 kita akan membuat matriks korelasi pada seluruh variabel numeric dataset iris. Untuk melakukannya jalankan langkah-langkah berikut:

Pilih menu Statistics/Summaries/Correlation matrix.
Pada kotak Variables, pili seluruh variabel numeric dengan cara tekan Shift+klik atau Shift + arrow up/down.
Pada bagian Type of Correlation, pilih Pearson product-moment (pembaca dapat memilih jenis korelasi lainnya).
Pada bagian Observations to Use, pilih Complete observation (observasi tanpa missing value pada seluruh variabelnya) atau Pairwise-complete observation (observasi tanpa missing value hanya pada variabel yang akan dipasangkan satu sama lain).
Centang pada check box Pairwise p-value jika ingin menampilkan p-value dan adjusted p-value nilai korelasi. Klik OK.

Visualisasi tahapan tersebut ditampilkan pada Gambar 3.4.

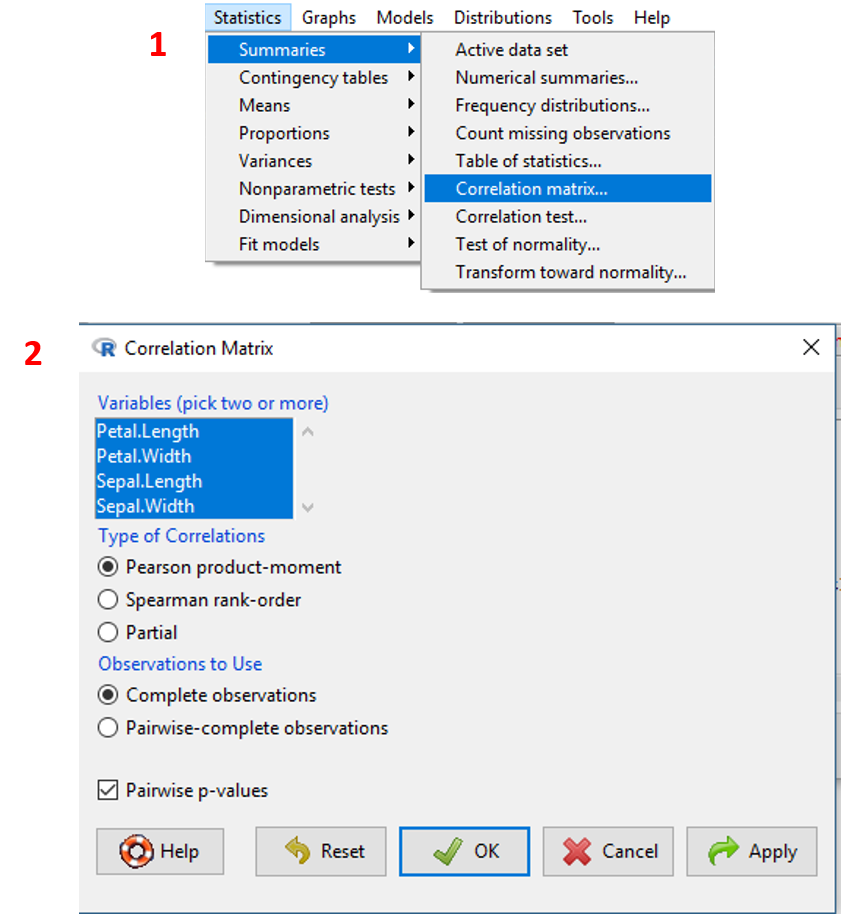
Gambar 3.4: Tampilan langkah membuat matriks korelasi pada dataset iris.

Sintaks dan output yang dihasilkan pada tahapan tersebut adalah sebagai berikut:

library(lattice, pos=18)
library(survival, pos=18)
library(Formula, pos=18)
library(ggplot2, pos=18)
library(Hmisc, pos=18)

## Warning: package 'Hmisc' was built under R version
## 3.6.2

## 
## Attaching package: 'Hmisc'

## The following object is masked _by_ 'package:RcmdrMisc':
## 
##     Dotplot

## The following objects are masked from 'package:base':
## 
##     format.pval, units

rcorr.adjust(iris[,c("Petal.Length","Petal.Width","Sepal.Length",
  "Sepal.Width")], type="pearson", use="complete")

## 
##  Pearson correlations:
##              Petal.Length Petal.Width Sepal.Length
## Petal.Length       1.0000      0.9629       0.8718
## Petal.Width        0.9629      1.0000       0.8179
## Sepal.Length       0.8718      0.8179       1.0000
## Sepal.Width       -0.4284     -0.3661      -0.1176
##              Sepal.Width
## Petal.Length     -0.4284
## Petal.Width      -0.3661
## Sepal.Length     -0.1176
## Sepal.Width       1.0000
## 
##  Number of observations: 150 
## 
##  Pairwise two-sided p-values:
##              Petal.Length Petal.Width Sepal.Length
## Petal.Length              <.0001      <.0001      
## Petal.Width  <.0001                   <.0001      
## Sepal.Length <.0001       <.0001                  
## Sepal.Width  <.0001       <.0001      0.1519      
##              Sepal.Width
## Petal.Length <.0001     
## Petal.Width  <.0001     
## Sepal.Length 0.1519     
## Sepal.Width             
## 
##  Adjusted p-values (Holm's method)
##              Petal.Length Petal.Width Sepal.Length
## Petal.Length              <.0001      <.0001      
## Petal.Width  <.0001                   <.0001      
## Sepal.Length <.0001       <.0001                  
## Sepal.Width  <.0001       <.0001      0.1519      
##              Sepal.Width
## Petal.Length <.0001     
## Petal.Width  <.0001     
## Sepal.Length 0.1519     
## Sepal.Width

Berdasarkan nilai korelasi Pearson yang dihasilkan dapat kita peroleh sejumlah informasi penting, antara lain:

variabel Petal.Length dan variabel Petal.Width memiliki korelasi positif dan kuat yang menunjukkan bahwa panjang petal pada tanaman anggrek yang besar akan diikuti oleh lebar petal tanaman anggrek yang besar dan sebaliknya.
variabel Sepal. Lenght berkorelasi kuat dan positif dengan variabel Petal.Length dan variabel Petal.Width yang menunjukkan bahwa ukuran petal tanaman anggrek yang besar akan diikuti oleh panjang sepal tanaman anggrek yang besar dan sebaliknya.
variabel Sepal.Width berkorelasi negatif dan lemah terhadap variabel lainnya yang menunjukkan bahwa besar kecil ukuran petal dan panjang sepal tidak serta-merta dikuti oleh besar kecilnya lebar sepal pada tanaman anggrek.

Format umum dari fungsi rcorr.adjust() adalah sebagai berikut:

rcorr.adjust(dataset[,c("NamaVariabel")], 
             type=c("pearson","spearman"), 
             use=c("complete","pairwise.complete"))