Chapter 2 Week 2 - Chi-Squared Tests
Outline:
- Statistical Inference
Introductory Examples: Goodness of Fit
Test Statistics & the Null Hypothesis
The Null Hypothesis: \(H_0\)
The Test Statistic, \(T\)
Distribution of the Test Statistic
The Null Distribution
Degrees of Freedom
The Statistical Table
Using the \(\chi^2\) Table
Examples of Using the Table
The Significance Level \(\alpha\), and the Type I Error
The Goodness of Fit Examples Revisted
The Formal Chi Squared, \(\chi^2\), Goodness of Fit Test
The Chi Squared, \(\chi^2\), Test of Independence – The two-way contingency table
- Using R
Using the rep and factor functions to enter repeating categorical data into R.
Using R for Goodness of Fit Tests
Using R for Tests of Independence – Two Way Contingency Table
Workshop for Week 2
Work relating to Week 1 – R – importing data, exploring data using graphs and numerical summaries. Project selection and planning.
Things YOU must do in Week 2
• Revise and summarise the lecture notes for week 1;
• Read your week 2 lecture notes before the lecture;
• Attend your first workshop/computer lab;
• Read the workshop on learning@griffith before your workshop;
• Download and install R and RStudio on your personal computer(s) [links are on L@G in Other Resources];
• Get to know your tutor and some of your fellow students in the workshop;
• Start working with R;
2.1 STATISTICAL INFERENCE – AN INTRODUCTION
From last weeks notes:
Statistical Inference: a set of procedures used in making appropriate conclusions and generalisations about a whole (the population), based on a limited number of observations (the sample).
and
There are two basic branches of statistical inference: estimation and hypothesis testing.
During the rest of this course you will learn a number of different statistics tests used for hypothesis testing and estimation (refer to the end of this week’s notes).
2.1.1 Some Goodness of Fit Examples
2.1.1.1 Example 1 – Gold Lotto: Is it fair or are players being ripped off?
In Queensland, Saturday night Gold Lotto involves the selection of eight numbers from a pool of 45. Numbers are not replaced so each can only be selected once on any draw. The following table is based on an extract from the Sunday Mail (July 2017), and gives a summary (in the first two columns) of the number of times each of the numbers, 1 to 45, has been drawn over a large subset of games.
The total of all the numbers of times drawn is 7120 (166 + 162+ … + 155 + 152) and, since eight numbers are drawn each time, this means that the data relate to 890 games. The organisers guarantee that the mechanism used to select the numbers is unbiased: therefore all numbers are equally likely to be selected.
Is this true?
There are 45 numbers and if each number is equally likely to be selected on each of the 7120 draws, each number should have been selected 158.2222 times (7120/45). [This is an approximation, which is OK given the large number of draws we have. Why is this an approximation?]
How different from this expected number of 158.2222, can an observed number of times be before we begin to claim ‘foul play’?
The table below also shows the differences between 158.2222 and the observed frequency of occurrence for each number. Intuitively it would make sense to add up all these differences and see how big the sum is. But, this doesn’t work. Why? Also in the table are the squares for each of the differences – maybe the sum of these values would mean something? But, if these squared differences are used it means that all differences of say two are treated equally. Is it fair for the difference between the numbers 10 and 12 to be treated the same as the difference between 1000 and 1002? A way to take this into account is to scale the squared difference by dividing by the expected value – in this example this scaling will be the same as all expected values are 158.2222.
The final column in the table gives the scaled squared differences:
\[\begin{equation} \frac{(\text{observed number - expected number})^2}{(\text{expected number})^2} = \frac{(O - E)^2}{E} \end{equation}\]
The sum of the final column can be expressed as:
\[\begin{equation} T = \sum_{i=1}^{k} \frac{(O - E)^2}{E} \end{equation}\]
where the summation takes place over all the bits to be added – that is, the total number of categories for which there are observations. Here \(k = 45\), the 45 Gold Lotto numbers.
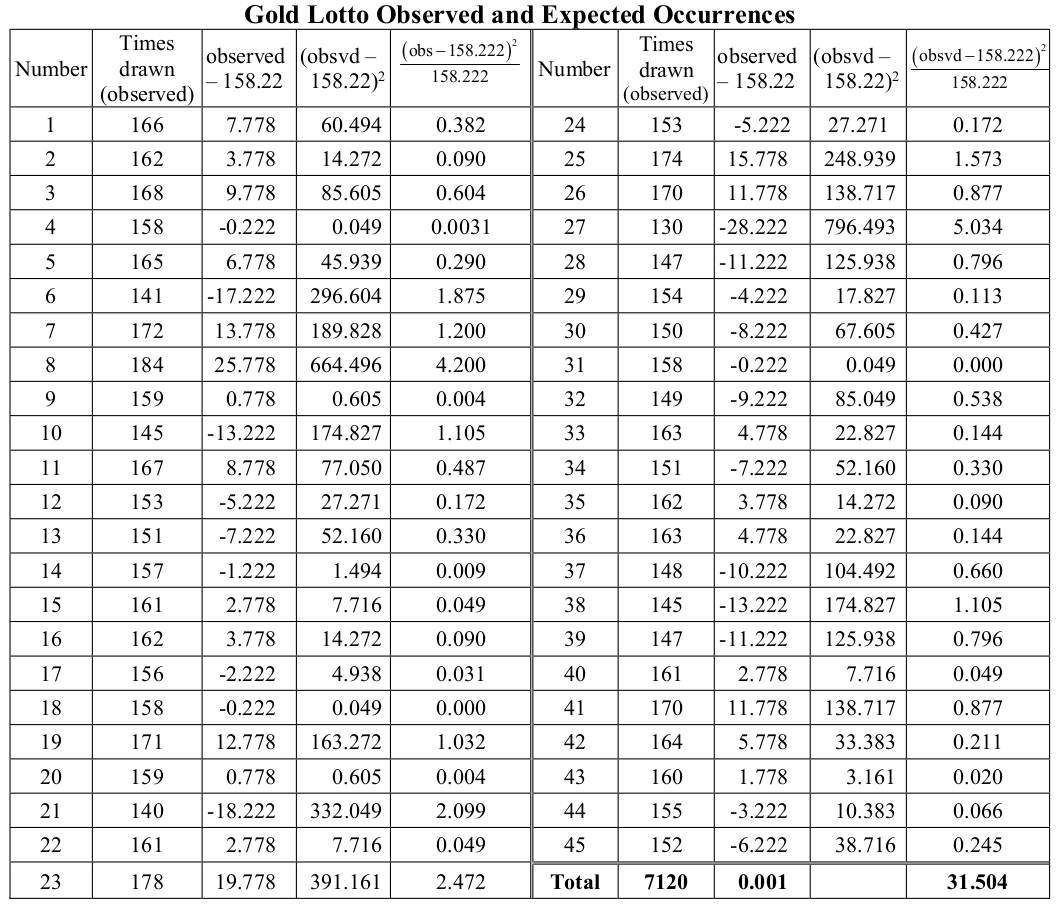
How bad is the lack of fit? Is a sum of 31.504 (31.386 in 2015) a lot more than we would expect if the numbers are drawn randomly? Are any of the values in the last column ‘very’ big? How big is ‘very’ big for any single number?
2.1.1.2 Example 2 – Occupational Health and Safety: How do gloves wear out?
Plastic gloves are commonly used in a variety of factories. The following data were collected in a study to test the belief that all parts of such gloves wear out equally. Skilled workers who all carried out the same job in the same factory used gloves from the same batch over a specified time period. Four parts on the gloves were identified: the palm, fingertips, knuckle and the join between the fingers and the palm. A ‘failure’ is detected by measuring the rate of permeation through the material; failure occurs when the rate exceeds a given value. A total of 200 gloves were assessed.
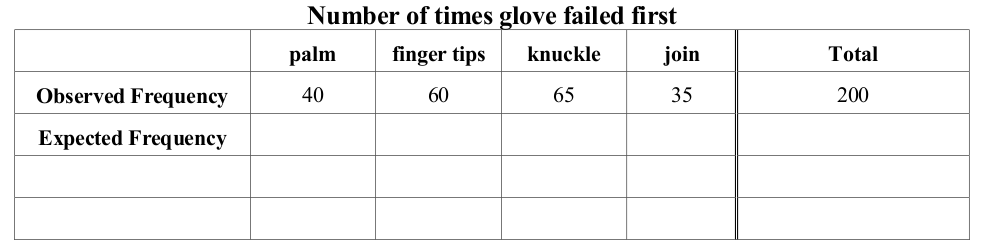
If the gloves wear evenly we would expect each of the four positions to have the same number of first failures. That is, the 200 gloves would be distributed equally (uniformly) across the four places and each place would have 200/4 = 50 first failures. How do the numbers shape up to this belief of a uniform distribution? Are the observed numbers much different from 50?
2.1.1.3 Example 3 - Credit Card Debt
A large banking corporation claims that there is no problem with credit card debt as 50% of people pay the full debt owing, 20% pay half of the debt, 25% pay the minimum repayment, and only 5% fail to pay at least the minimum. They have been requested to prove that their claim is correct and have collected the following information for the previous month on 160 of their credit card customers selected at random.

Do the data support the bank’s statements?
If the distribution of credit card payments is as stipulated by the bank we would expect to see 80 paying all of the debt, 32 paying half, 40 paying the minimum and only 8 failing to pay. How do the observed data compare with these expected numbers? Is the bank correct in its claims?
2.1.1.4 Example 4 – Mendel’s Peas
(Mendel, G. 1986 Verusuche über Pflanzen-Hybriden. Verhandlungen des naturforschenden Vereines in Brünn 4, 3-47. English translation by Royal Horticultural Society of London, reprinted in Peters, J. A. 1959. Classic Papers in Genetics. Prentice-Hall, Englewood Cliffs, NJ)
Perhaps the best-known historical goodness of fit story belongs to Mendel and his peas. In his work (published in 1866), Mendel sought to prove what we now accept as the basic laws of Mendelian genetics in which an offspring receives discrete genes from each of its parents. Mendel carried out numerous breeding experiments with garden peas which were bred in a way that ensured they were heterozygote, that is, they had one of each of two possible alleles, at a number of single loci each of which controlled clearly observed phenotypic characteristics. One of the alleles was a recessive and the other dominant so that for the recessive phenotype to be present, the offspring had to receive one of the recessive alleles from both parents. Individuals who had one or two of the dominant alleles would all appear the same phenotypically.
Mendel hypothesised two things. Firstly he believed that the transmission of a particular parental allele (of the two possible) was a random event, thus the probabilities that an offspring would have the recessive or the dominant allele from one of the parents were 50:50. Secondly, he believed that the inheritance of the alleles from each parent were independent events; the probability that a particular allele would come from one parent was not in any way affected by which allele came from the other parent. If his beliefs were true, the offspring from the heterozygote parents would appear phenotypically to have a ratio between the dominant and recessive forms of 3:1.
This phenomenon is illustrated in the table below for the particular pea characteristic of round or wrinkled seed form. The wrinkled form is recessive, thus for a seed to appear wrinkled it must have a wrinkled allele from both of its parents; all other combinations will result in a seed form that appears round. The two possible alleles are indicated as r and w.
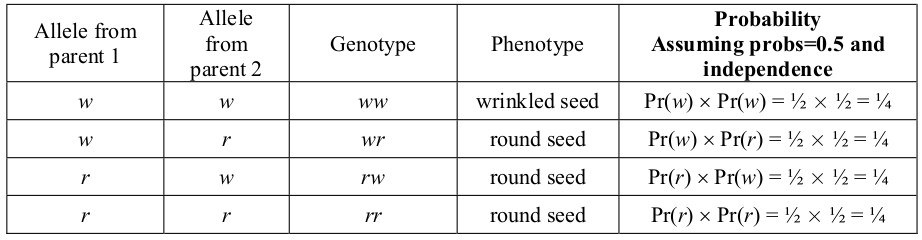
From the table it can be seen that the probabilities associated with the wrinkled and round phenotypic seed forms are 1⁄4 and 3⁄4, respectively. The following table gives the actual results from one of Mendel’s experiments.

2.1.2 Test Statistics & the Null Hypothesis
2.1.2.1 The Null Hypothesis
The belief or proposal that allows us to calculate the expected values is known as the null hypothesis. It represents a known situation that we take as being true; it is the base line. The observed values from the sample of data are used to test the null hypothesis. If the null hypothesis is true, how likely is it that we would observed the results we saw in the sample of data? What is \(Pr(\text{data} | \text{null hypothesis})\)? If the results from the sample are unlikely under the null hypothesis, we reject it in favour of something else, the alternative hypothesis.
In the Gold Lotto, we are told by the organisers that there is no bias in the selection process and that each number is equally likely to be drawn. Assuming this belief (hypothesis) to be true, we determined that each of the 45 numbers should have been selected equally often, namely 158.22 times.
In the gloves example it was suggested that each part would wear evenly thus the number of first failures would be the same for all four parts – 50 each in the 200 gloves.
For the credit card example, a specific distribution was proposed by the banking organisation, namely the probabilities of 0.50, 0.20, 0.25 and 0.05 for each of the outcomes of full debt payment, half debt payment, payment of minimum amount and no payment. It was this distribution that was to be tested with the observed sample of 160 customers – under the null hypothesis, 80 customers should have paid out in full, 32 should have paid half their debt, 40 should have paid just the minimum payment and 8 should have made no payment at all.
In Mendel’s peas examples, the hypotheses that would be used are:
\[\begin{align*} H_0: & \text{ the alleles making up an individual’s genotype associate independently and each has a probability of 0.5.} \\ H_1: & \text{ the alleles making up an individual’s genotype do not associate independently.} \end{align*}\]
\(H_0\): null hypothesis.
\(H_1\) or \(H_A\) : alternative hypothesis.
The basis of all statistical hypothesis testing is to assume that the null hypothesis is true and then see what the chances are that this situation could produce the data that are obtained in the sample. If the sample data are unlikely to be obtained from the situation described by the null hypothesis, then probably the situation is different; that is, the null hypothesis is not true.
2.1.2.2 The Test Statistic
The issue in each of the above examples is to find an objective way of deciding whether the difference between the observed and expected frequencies is ‘excessive’. Clearly we would not expect the observed to be exactly equal to the expected in every sample we take. A certain amount of ‘leeway’ must be acceptable. But, when does the difference become so great that we say we no longer believe the given hypothesis?
The first step is to determine some measure which expresses the ‘difference’ in a meaningful way. In the above examples the measure used is the sum of the scaled squares of the differences. We call this measure the test statistic.
In the Gold Lotto example the test statistic was 31.504 across the entire 45 numbers. How ‘significant’ is this value of 31.504? What sorts of values would we get for this value if the observed frequencies had been slightly different – suppose the number of times a 19 was chosen was 160 instead of 171; or that 27 had been observed 138 times instead of 130. If the expected value for each number is 158.22, how much total difference from this across the 45 numbers can be tolerated before a warning bell sounds to the authorities? What distribution of values is ‘possible’ for this test statistic from different samples if the expected frequency truly is 158.22? If all observed frequencies were very close to 158 and 159, the test statistic would be about zero. But, we would not really be surprised (would not doubt that the numbers occur equally often) if all numbers were 158 or 159 except two, one having an observed value of 156 say, and the other 160, say. In this case the test statistic would be < 0.2 – this would not be a result that would alarm us. Clearly there are many, many possible ways that the 7120 draws could be distributed between the 45 numbers without us crying ‘foul’ and demanding that action be taken because the selection process is biased.
It would be impossible to list out all the possible sets of outcomes for the Gold Lotto case in a reasonable amount of time. Instead, consider the simple supposedly unbiased coin which is tossed 20 times. If the coin truly is unbiased we expect to see 10 heads and 10 tails. Would we worry if the result was 11 heads and 9 tails? or 12 heads and 8 tails?
Using the same test statistic as in the Lotto example, these two situations would give:
\(T = \frac{(9 – 10)^2}{10} + \frac{(11 – 10)^2}{10} = 0.2\)
and
\(T = \frac{(8 – 10)^2}{10} + \frac{(12 – 10)^2}{10} = 0.8\).
What about a result of 14 heads and 6 tails? (T = 3.2)
And 15 heads and 5 tails? (T = 5.0)
With the extreme situation of 15 heads and 5 tails, the test statistic is starting to get much bigger.
2.1.3 Distribution of the Test Statistic
2.1.3.1 The Null Distribution
Each of the possible outcomes for any test statistic has an associated probability based on the hypothesised situation. It is the accumulation of these probabilities that gives us the probability distribution of the test statistic under the null distribution.
If the proposed (hypothesised) situation is true, some of the outcomes will be highly likely (eg if a coin really is unbiased, 10 heads and 10 tails or 11 heads, and 9 tails will be highly likely). Other outcomes will be most unlikely (eg 19 heads and 1 tail, or 20 heads and no tails, if the coin is unbiased). Suppose we toss the coin 20 times and get 16 heads and 6 tails. How likely is this to occur if the coin is unbiased? You will see in a later lecture how the probability associated with each of these outcomes can be calculated exactly for the coin example. However, for the moment we will use ‘mathemagic’ to find all the required probabilities.
In general, the test statistic, which has been calculated using the sample of data, must be referred to the appropriate probability distribution. Depending on where the particular value of the test statistic sits in the relative scale of probabilities of the null distribution (on how likely the particular value is), a decision can then be made about the validity of the proposed belief (hypothesis).
In the Gold Lotto example, we have a test statistic of 31.504 but, as yet, we have no way of knowing whether or not this value is likely if the selection is unbiased. We need some sort of probability distribution which will tell us which values of the test statistic are likely if the ball selection is random. If we had this distribution we could see how the value of 31.504 fits into the belief of random ball selection. If it is not likely that a value as extreme as this would occur, then we will tend to reject the belief that selection of the numbers is fair.
The test statistic used in the above examples was first proposed by Karl Pearson in the late 1800’s. Following his publication in the 1900s it became known as The Pearson (Chi-Squared) Test Statistic
In his 1900 work, Pearson showed that his test statistic has a probability distribution which is approximately described by the Chi-Squared distribution. This is a theoretical mathematical function which has been studied and whose probability distribution has a shape like this:
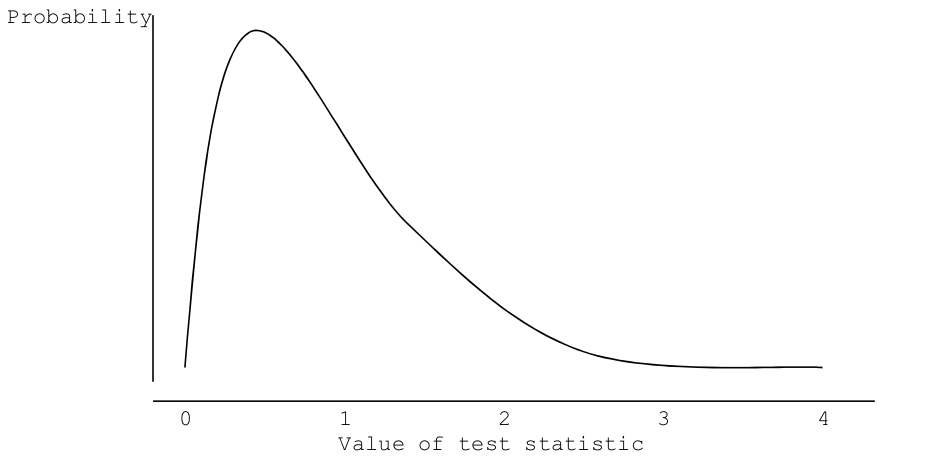
The exact shape of the chi-squared distribution changes depending on the degrees of freedom involved in the calculation process. Degrees of Freedom (DF) will be discussed below.
The distribution shows what values of the test statistic are likely (those that have a high probability of occurring). Values in the tail have a small probability of occurring and so are unlikely. If our calculated test statistic lies in the outer extremes of the distribution we will doubt the validity of the null distribution as a description of the population from which our sample has been taken. Since we are interested in knowing whether or not our calculated test statistic is ‘extreme’ within the probability distribution, we will look at the values in the ‘tail’ of the distribution – this is discussed further in section 1.3.3.
2.1.3.2 Degrees of Freedom
The concept of degrees of freedom arises often in statistical inference. It is best understood by the following example. Suppose you are asked to select 10 numbers at random. Your answer will include any 10 numbers you like; there are no constraints and you can freely select any ten numbers. But, now suppose that you are asked to select 10 numbers whose total must be 70. How many numbers can you now select freely? The first nine numbers can be anything at all. But, the tenth number must be something that makes the sum of all 10 numbers equal to 70. The single constraint concerning the total has limited your freedom of choice by one. Only nine numbers could be chosen freely, the final number was determined by the total having to be 70.
In all the chi-squared situations above, the expected frequencies are determined by applying the stated hypothesised probability distribution and using the total number of observations in the sample. Thus, a constraint is in place: the sum of the expected frequencies must equal the total number of observations. This represents a single constraint so the degrees of freedom will be one less than the number of categories for which expected values are given.
For the Gold Lotto there are 45 categories (the numbers) for which expected values are needed. The sum across these 45 expected values must be 7120, thus only 44 frequencies could be selected freely, the final or 45th frequency being completely determined by the 44 previous values and the total of 7120.
In the occupational health and safety example there are four categories (the four parts of the glove) across which the sum of the expected frequencies must be 200. The degrees of freedom must be three (4 – 1 = 3).
The banking institution example - four categories giving three degrees of freedom.
For Mendel’s peas - 2 categories giving 1 degree of freedom.
A number of the mathematical probability distributions, including the chi-squared, which are used in statistical inference vary a little depending on the degrees of freedom associated with them. The effects of different degrees of freedom vary for different types of distributions. For chi-squared, the effects are discussed below.
2.1.3.3 The Statistical Table
One of the most common ways of presenting the null distribution of a test statistic is with the statistical table. A statistical table consists of selected probabilities from the cumulative probability distribution of the test statistic if the null hypothesis is true. The selected probabilities will represent different areas of the ‘tail’ of the distribution, and the actual probabilities chosen for inclusion in a table depend on a number of things. To some extent they are subjective and vary depending on the person who creates the table. Conventionally probabilities of 0.05 (5%) and 0.01 (1%) (for significance levels of 0.05 and 0.01) are used most frequently.
The type of distribution used depends on the type of data involved, on the type of hypothesis (or belief) proposed, and the test statistic used. For example, a researcher might be interested in testing a belief about the difference in mean pH level between two different types of soil. Thus, a frequency distribution which is appropriate for a test statistic describing ‘the difference between two means’ will be needed.
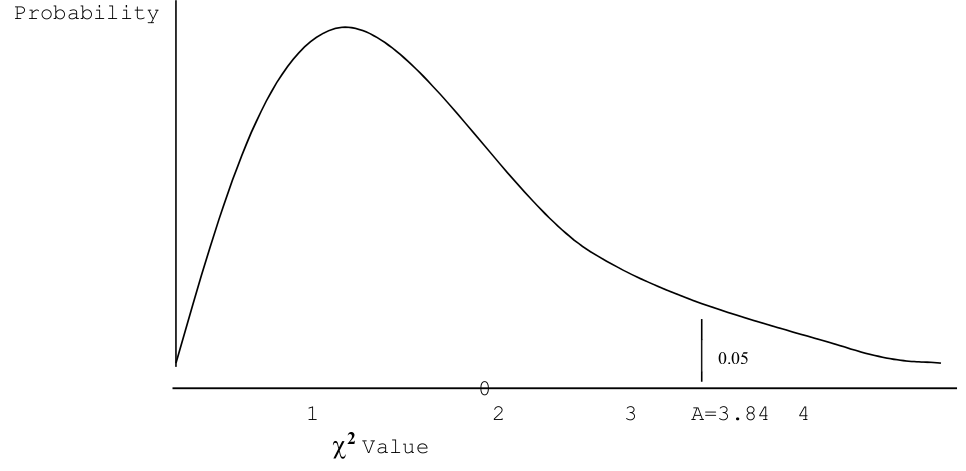
The statistical table needed in the examples of goodness of fit presented above is the chi- squared (\(\chi^2\)) table. It is based on the \(\chi^2\) distribution, whose general shape is given in the picture above (also see lectures). The associated table is known as a chi-squared, \(\chi^2\), table and a copy is given in the statistical tables section of the L@G site.
2.1.3.4 Using the \(\chi^2\) Table
In order to read the \(\chi^2\) table we need to know the degrees of freedom of the test statistic relevant for the given situation. Degrees of freedom are denoted by the Greek letter \(\nu\), which is pronounced ‘new’ (this is the most common symbol used for degrees of freedom). Values for \(\nu\) are given in the first column of the table. The remaining columns in the table refer to quantiles, \(\chi^2(p)\) , which are the chi-squared values required to achieve the specific cumulative probabilities \(p\) (ie probability of being less than or equal to the quantile).
We are interested in extreme values; that is, exceptionally large values of the test statistic. Thus, the interesting part of the distribution is the right hand tail. To obtain the proportion of chi-squared values lying in the extreme right hand tail of the distribution, that is, the proportion of chi-squared values greater than the particular quantile, the nominated \(p\) is subtracted from 1. The actual numbers in the bulk of the table are the \(\chi^2\) values that give the stated cumulative probability, the quantile, for the nominated degrees of freedom. For this particular table the probabilities relate to the left hand tail of the distribution and are the probability of getting a value less than or equal to some specified \(\chi^2\) value. For example, the column headed \(0.950\) contains values, say A, along the x-axis such that: \(Pr(\chi^2_\nu \leq A) = 0.95\).
Conversely, there will be 5% of values greater than A, \(Pr (\chi^2_\nu > A) = 1 - 0.95 = 0.05\). This can be seen graphically in the following figure, where the chi-squared distribution for one degree of freedom is illustrated.
As you look down the column for \(\chi^2(0.95)\) you will notice that the values of A vary. The rows are determined by the degrees of freedom, and thus the A value also depends on the degrees of freedom. What is actually happening is that the \(\chi^2\) distribution changes its shape depending on the degrees of freedom, \(\nu\). The value of the degrees of freedom is incorporated into the expression as follows:
\[ \chi^2_\nu(0.95) \]
This means the point in a \(\chi^2\) with \(\nu\) degrees of freedom that has 95% of values below it (or, equally, 5% of values above it).
2.1.3.5 Examples Using the \(\chi^2\) Table
- If df = 2 what is the \(\chi^2\) value which leads to a right hand tail of 0.05? That is, find A such that: \(Pr(\chi^2_2 > A) = 0.05\).
Solution: Degrees of freedom of 2 means use the 2nd row; tail probability of 0.05 implies the 0.95 quantile, thus the 4th column giving: A = 5.99.
- If df = 3 what is the \(\chi^2\) value which leads to a right hand tail of 0.05? That is, find A such that: \(Pr(\chi^2_3 > A) = 0.05\)
Solution: Degrees of freedom of 3 means use the 3rd row; tail probability of 0.05 implies the 0.95 quantile and thus the 4th column giving: A = 7.82.
- If df = 1 what is the \(\chi^2\) value which leads to a right hand tail of 0.01? That is, find A such that: \(Pr(\chi^2_1 > A) = 0.01\)
Solution: Find the value in the 1st row (degrees of freedom one) and 0.99 quantile, 2nd column (quantile for 0.99 has an extreme right tail probability of 0.01): A = 6.64.
2.1.3.6 The Significance Level, \(\alpha\), and The Type I Error
The tail probability that we select as being ‘extreme’ is the probability that the null hypothesis will be rejected when it is really true. It is the error we could be making when we conclude that the data are such that we cannot accept the proposed distribution. This error is known as the Type I Error. More will be said about errors in a later section. For the moment you need to understand that the level of significance is a measure of the probability that a Type I Error may occur.
The value chosen for the level of significance (and thus the probability of a Type I Error) is purely arbitrary. It has been traditionally set at 0.05 (one chance in 20) and 0.01 (one chance in 100), partly because these are the values chosen by Sir Ronald A. Fisher when he first tabulated some of the more important statistical tables. Error rates of 1 in 20 and 1 in 100 were acceptable to Fisher for his work. More will be said about this in later sections. Unless otherwise stated, in this course we will use a level of significance of \(\alpha = 0.05\).
The value, A, discussed in section 1.3.4 is known as the critical value for the specified significance level. It is the value against which we compare the calculated test statistic to decide whether or not to reject the null hypothesis.
2.1.3.7 The Goodness of Fit Examples Revisited
- Gold Lotto
Degrees of freedom \(\nu\)= 44.
Using significance level of \(\alpha = 0.05\) means the 0.95 quantile is needed. With df = 50, from the 4 th column we get 67.5.
(Note that the table does not have a row for df = 44 so we use the next highest df, 50)
Critical region is a calculated value > 67.5
The calculated test statistic for the gold lotto sample data is: T = 31 which does not lie in the critical region.
Do not reject \(H_0\) and conclude that the sample does not provide evidence to reject the proposal that the 45 numbers are selected at random (\(\alpha = 0.05\)).
- Occupational Health and Safety – Glove Wearing
Degrees of freedom = 3.
Critical value from \(\chi^2\) table with df = 3 using significance level of 0.05 requires quantile of 0.95 = 7.82.
Critical region is a calculated value > 7.82.
Calculated test statistic: T =
Write your conclusion:
- Bank Customers and Credit Cards
Degrees of freedom = 3.
Critical value from \(\chi^2\) table with df = 3 using significance level of 0.05 requires 0.95 quantile = 7.82
Critical region is a calculated value > 7.82
Calculated test statistic: T =
Write your conclusion:
- Mendel’s Peas
Degrees of freedom = 1. Critical value from \(\chi^2\) table with df = 1 using significance level of 0.05 (0.95 quantile) = 3.84.
Critical region is a calculated value > 3.84.
Calculated test statistic: T = 0.5751 which does not lie in the critical region.
Do not reject \(H_0\) and conclude that the sample does not provide sufficient evidence to reject the proposal that the alleles, each with probability of 0.5, are inherited independently from each parent ( \(\alpha = 0.05\)).
2.1.4 The Formal Chi-Squared, \(\chi^2\) , Goodness of Fit Test
Research Question:
The values are not as specified (eg uniformly; in some specified ratios such as 20%, 50%, 10%, 15%, 5%).
Null Hypothesis \(H_0\):
Within the population of interest, the distribution of the possible outcomes is as specified. [Nullifies the Research Question]
Alternative Hypothesis \(H_1\):
The distribution within the population is not as specified. [Matches the Research Question]
Sample:
Selected at random from the population of interest.
Test Statistic:
\[T = \sum_{i=1}^{k} \frac{(O - E)^2}{E}\] calculated using the sample data.
Null Distribution:
The Chi-Squared, \(\chi^2\), distribution and table.
Significance Level, \(\alpha\):
Assume 0.05 (5%).
Critical Value, A:
Will depend on the degrees of freedom \(\nu\), which in turn depends on the number of possible outcomes (categories, \(k\)).
Critical Region:
That part of the distribution more extreme than the critical value – part of the distribution where the \(\chi^2\) value exceeds A.
Conclusion:
If \(T > A\) (i.e. \(T\) lies in the critical region) reject \(H_0\) in favour of the alternative hypothesis \(H_1\).
Interpretation:
If \(T > A\) the null hypothesis is rejected. Conclude that the alternative hypothesis is true with significance level of 0.05. The null hypothesis has been falsified.
If \(T \leq A\) the null hypothesis is not rejected. Conclude that there is insufficient evidence in the data to reject the null hypothesis – note that this does not prove the null.
2.1.5 The \(\chi^2\) Test of Independence – The Two-Way Contingency Table
A second form of the goodness of fit test occurs when the question raised concerns whether or not two categorical variables are independent of each other. For example, are hair colour and eye colour independent of each other? Are sex and dexterity (right or left handedness) independent of each other? Is the incidence of asthma in children related to the use of mosquito coils? Does the type of credit card preferred depend on the sex of the customer? Do males prefer Android phones and females prefer iPhones?
Recall the use of the definition of independent events in the basic rules of probability: this is the way in which the expected values are found.
The main difference between this form of the chi-squared test and the goodness of fit test lies in the calculation of the degrees of freedom. If the concept does not change, what would you expect the degrees of freedom to be for the example given below? This will be discussed in lectures.
Example
One hundred students were selected at random from the ESC School and their hair and eye colours recorded. These values have then been summarised into a two-way table as follows.
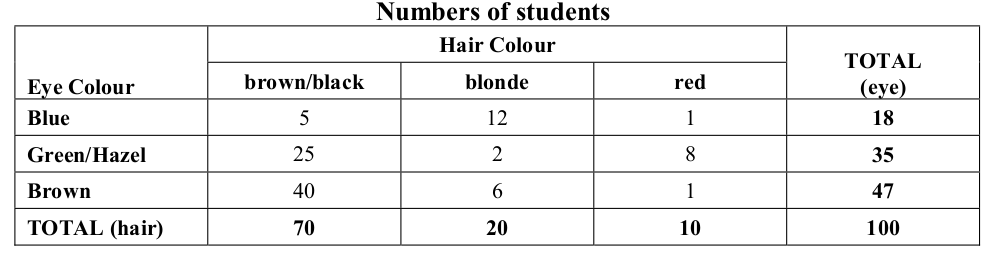
Do these data support or refute the belief that a person’s hair and eye colours are independent?
If the two characteristics are independent then the probability of a particular hair colour and a particular eye colour will be the probability associated with the particular hair colour multiplied by the probability associated with the relevant eye colour.
From the table, the probabilities for each eye colour are found by taking the row sum and dividing by the total number of people, 100.
\[\begin{align*} Pr(\text{blue eyes}) &= \frac{18}{100} = 0.18 \\ Pr(\text{green/hazel eyes}) &= \frac{35}{100} = 0.35 \\ Pr(\text{brown eyes}) &= \frac{47}{100} = 0.47 \end{align*}\]
Similarly, the probabilities for the hair colours are found using the column totals.
\[\begin{align*} Pr(\text{brown/black hair}) &= \frac{70}{100} = 0.70 \\ Pr(\text{blonde hair}) &= \frac{20}{100} = 0.20 \\ Pr(\text{red hair}) &= \frac{10}{100} = 0.10 \end{align*}\]
The combined probabilities for each combination of hair and eye colour, under the hypothesis that these characteristics are independent, are found by simply multiplying the probabilities together. For example, under the assumption that hair and eye colour are independent, the probability of having blue eyes and red hair is:
\[\begin{align*} Pr(\text{Blue Eyes and Red Hair}) &= Pr(\text{blue eyes}) \times Pr(\text{red hair}) \\ &= \frac{18}{100} \times \frac{10}{100} \\ &= \frac{18 \times 10}{100 \times 100} \\ &= 0.018 \end{align*}\]
We would therefore expect 0.018 of the 100 people (ie 1.8 people) to have both blue eyes and red hair, if the assumption that hair and eye colour are independent is true. We can calculate the expected values of all combinations of hair and eye colour in this way. In fact by following the example we can formulate an equation for the expected value of a cell defined by the \(\text{r}^{\text{th}}\) row and \(\text{c}^{\text{th}}\) column as:
\[ E(\text{r, c}) = \frac{(\text{Row r Total}) \times (\text{Column c Total})}{\text{Overall Total}}. \]
Using this formula, we can calculate the expected values of each cell as shown in the following table. Note that the expected values are displayed in italics:
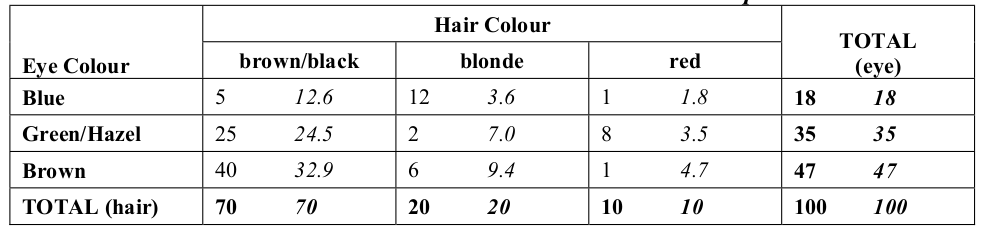
Once the observed and expected frequencies are available, Pearson’s Chi Squared Test Statistic is found in the same way as before
\[\begin{align*} T &= \frac{(5 - 12.6)^2}{12.6} + \frac{(25 - 24.5)^2}{24.5} + \frac{(40 - 32.9)^2}{32.9} + \ldots + \frac{(1 - 4.7)^2}{4.7} \\ &= 39.582 \end{align*}\]
The degrees of freedom are \(2 \times 2 = 4\) (check you understand this).
The critical value from a \(\chi^2\) table with df = 4 using significance level of 0.05 is \(\chi^2_4(0.95) = 9.49\).
The test statistic of 39.582 is much larger than this critical value of 9.49. We say that the test is significant - the null hypothesis that hair and eye colours are independent is rejected. We conclude that hair and eye colour are not independent (\(\alpha = 0.05\)).
2.2 Using R (Week 2)
2.2.1 Using rep and factor to Enter Data Manually in R
Sometimes, when the amount of data is reasonably small, it can be convenient to enter data into R manually (as opposed to importing it into R from Excel, say).
Recall the rainfall example from week 1 lecture notes. This data was presented in a table in the notes, and we then expanded it out (by expanding District and Season in repeating patterns) into Excel so we could import it. We need not have done that: instead, we could have typed the rainfall measurements into R by hand and then used some functions in R to create the repeating patterns for District and Season.
Note that this approach is an alternative to the import data approach. You do one or the other, not both. If the data you wish to use is already in “Excel” form, import it using the methods we saw in the week 1 lectures. If the data are small and appear in a table like the rainfall data, then this new approach can be useful.
Here’s the rainfall data as it appears in the table from week 1:
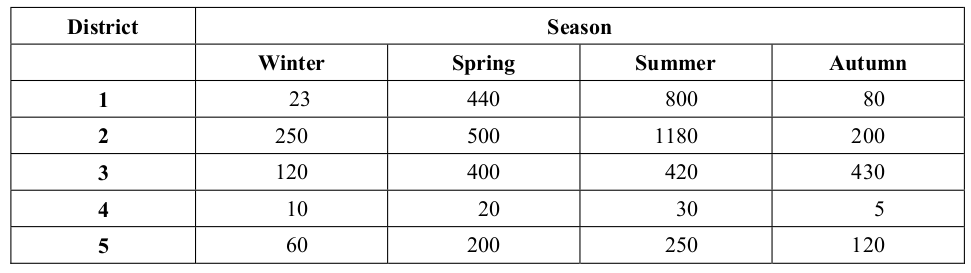
We can type the rainfall measurements into R as follows (note that we are typing it in by row, not by column – this makes a difference as to how we do the next bit):
rain <- c(23, 440, 800, 80,
250, 500, 1180, 200,
120, 400, 420, 430,
10, 20, 30, 5,
60, 200, 250, 120)
rain## [1] 23 440 800 80 250 500 1180 200 120 400 420 430 10 20 30
## [16] 5 60 200 250 120Next we can create the variable district using the rep() function. This function repeats
the values you give it a specified number of times:
## [1] 1 1 1 1 2 2 2 2 3 3 3 3 4 4 4 4 5 5 5 5rep() takes two arguments, separated by a comma. The first argument are the things
you want to replicate (in this case the numbers from 1 to 5 inclusive). The second
argument is the number of times you want these things to be replicated. Note that the
second argument must match the dimension of the first argument – since there are 5
numbers in the first argument, there must be 5 numbers in the second (each number in the
second argument matches how many times its counterpart in the first argument gets
replicated). In this example we want the numbers 1 to 5 to each be replicated 4 times
(once for each season).
Note that we can use R functions inside R functions (even the same function). If we look carefully at the second argument above, we can see that c(4,4,4,4,4) is just the number 4 replicated 5 times. This could be written rep(4,5). This kind of thing happens a lot (where you want to replicate each thing a set the same number of times each) and so rep also has an argument called each that allows you to specify how many times each element in the first argument should be replicated. Therefore, alternatives
to the above code is:
## [1] 1 1 1 1 2 2 2 2 3 3 3 3 4 4 4 4 5 5 5 5## [1] 1 1 1 1 2 2 2 2 3 3 3 3 4 4 4 4 5 5 5 5Now let’s look at the Season variable. The season variable is slightly different to the
district variable in that Season has character values (words/letters, not numbers). This is
not a major problem in R. However, to handle this type of variable we need to introduce
another function called factor(). The factor() function is the way we tell R
that a variable is categorical. Categorical variables do not necessarily have to have
character values (District is also a categorical variable, for example), but any variable that
has character values is categorical.
Entering character data into R is simple: we treat it like normal data but we put each value in quotes:
## [1] "Winter" "Spring" "Summer" "Autumn"Note the way the Season data appears in the table – the above character sequence appears once for each of the 5 rows (remember, we entered the rain data on a row by row basis). Therefore, we need to replicate this entire sequence 5 times.
## [1] Winter Spring Summer Autumn Winter Spring Summer Autumn Winter Spring
## [11] Summer Autumn Winter Spring Summer Autumn Winter Spring Summer Autumn
## Levels: Autumn Spring Summer WinterThis new variable season is a factor, and it replicates the character variable seasons 5 times. Factors have levels. Levels are just the names of the categories that make up the factor. R list levels in alpha-numeric order.
Note we could have done all this at once using:
## [1] Winter Spring Summer Autumn Winter Spring Summer Autumn Winter Spring
## [11] Summer Autumn Winter Spring Summer Autumn Winter Spring Summer Autumn
## Levels: Autumn Spring Summer WinterFinally, remember we said District is also categorical (make sure you understand why). If
you create a variable but forget to make it categorical at the time by using factor(), you
can always come back and fix it:
## [1] 1 1 1 1 2 2 2 2 3 3 3 3 4 4 4 4 5 5 5 5
## Levels: 1 2 3 4 5Now we have entered each variable into R manually, we can place them into their own
data set. R calls data sets “data frames”. The function data.frame() lets you put your
variables into a data set that you can call whatever you want:
## district season rain
## 1 1 Winter 23
## 2 1 Spring 440
## 3 1 Summer 800
## 4 1 Autumn 80
## 5 2 Winter 250
## 6 2 Spring 500
## 7 2 Summer 1180
## 8 2 Autumn 200
## 9 3 Winter 120
## 10 3 Spring 400
## 11 3 Summer 420
## 12 3 Autumn 430
## 13 4 Winter 10
## 14 4 Spring 20
## 15 4 Summer 30
## 16 4 Autumn 5
## 17 5 Winter 60
## 18 5 Spring 200
## 19 5 Summer 250
## 20 5 Autumn 120Once your variables are in a data frame (in this case in a data frame called rainfall.dat), R
will keep them in that data frame. However, the variables are also individually just
hanging around in the workspace, so we should clean up our mess (we can safely delete
variables once we put them into a data frame). To see what is in our workspace we can use the function ls(), which lists the contents of the R workspace. The rm() function removes variables
from the R workspace – use it cautiously!
## [1] "district" "district.a" "district.b" "hangover.model"
## [5] "hangovers" "hangovers.lsd" "harv.model" "harvester"
## [9] "harvester.lsd" "rain" "rainfall" "rainfall.dat"
## [13] "season" "seasons"## [1] "hangover.model" "hangovers" "hangovers.lsd" "harv.model"
## [5] "harvester" "harvester.lsd" "rainfall" "rainfall.dat"2.2.2 Using R for Goodness of Fit Tests
The R function chisq.test() does goodness of fit tests. It requires you to enter the
data (ie the observed data in each category) and in general it also requires you to enter the
probabilities associated with each category under the null hypothesis assumptions. When
the null hypothesis assumption is “equally likely” or “uniformity” (as in the gold lotto
and gloves examples) you may omit entering the probabilities for each category.
However, if the probabilities under the null hypothesis are different for the categories
(like the credit cards example, or Mendel’s peas) you must enter these probabilities in the
same order that you enter the observed data.
For the lotto example:
lotto <- c(166,159,156,174,163,170,162,145,158,170,151,164,168,167,171,130,162,160,158,153,159,147,163,
155,165,151,140,154,148,152,141,157,161,150,145,172,161,178,158,147,184,162,153,149,161)
lotto.test <- chisq.test(lotto)
lotto.test##
## Chi-squared test for given probabilities
##
## data: lotto
## X-squared = 30.841, df = 44, p-value = 0.9333We will talk more about p-values in later lectures. For now, if the p-value is bigger than or equal to 0.05 it means we cannot reject the null hypothesis. If the p-value is smaller than 0.05, we reject the null in favour of the alternative hypothesis.
In this example we see that we cannot reject the null hypothesis, and conclude that there is insufficient evidence to suggest the game is “unfair” at the 0.05 level of significance.
For the credit card debt example:
credit.cards <- c(70, 20, 50, 20) # Enter the data
creditcard.test <- chisq.test(credit.cards, p = c(0.5, 0.2, 0.25, 0.05))
# Note we have to give it the probabilities in the null hypothesis using the p = ... argument.
creditcard.test##
## Chi-squared test for given probabilities
##
## data: credit.cards
## X-squared = 26.25, df = 3, p-value = 8.454e-06Note that here we needed to specify the probabilities for each category (50%, 20% etc).
Also note here that R outputs scientific notation for small p-values – 8.454e-06 means
0.000008454, which is very much smaller than 0.05. We therefore reject the null in
favour of the alternative hypothesis and conclude that the Bank’s claims about credit card
repayments are false at the 0.05 level of significance.
2.2.3 Using R for Tests of Independence – Two Way Contingency Table
The chisq.test() function can also be used to do the Chi-Squared test of
Independence. The test needs your data to be in table form, like in the hair eye colour
example above. If you do not have it in that form because your data are raw and not
tabulated, the table() function in R can be used to create the table. We will show an
example of this form in the lectures.
Below is the code required to do the test of independence between hair and eye colour given in the example above:
hair.eyes <- as.table(rbind(c(5, 12, 1), c(25, 2, 8), c(40, 6, 1))) # Make the table with the data
hair.eyes## A B C
## A 5 12 1
## B 25 2 8
## C 40 6 1dimnames(hair.eyes) <- list(Eye = c("Blue", "Green", "Brown"),
Hair = c("Brown", "Blonde", "Red")) # We don't need to, but we can give the rows and columns names.
hair.eyes## Hair
## Eye Brown Blonde Red
## Blue 5 12 1
## Green 25 2 8
## Brown 40 6 1## Warning in chisq.test(hair.eyes): Chi-squared approximation may be incorrect##
## Pearson's Chi-squared test
##
## data: hair.eyes
## X-squared = 39.582, df = 4, p-value = 5.282e-08Note the warning message: one of the assumptions of the Chi-Squared test of independence is that no more than 20% of all expected cell frequencies are less than 5. We can see the expected cell frequencies by using:
## Hair
## Eye Brown Blonde Red
## Blue 12.6 3.6 1.8
## Green 24.5 7.0 3.5
## Brown 32.9 9.4 4.7We can see that 4 of the 9 cells have expected frequencies less than 5. This can be an issue for the test of independence but ways to fix it are beyond the scope of this course.
From the output we see the p-value is less than 0.05, so we therefore reject the null in favour of the alternative hypothesis and conclude that hair and eye colour are dependent on each other at the 0.05 level of significance.