Chapter 3 Mechanics
3.1 Introduction
Combat mechanics are at the core of the warrior class, and deeply impact our talent and gearing choices and combat rotation. Therefore, it is important to build a solid foundational understanding of these mechanics in order to make the correct decisions and understand the theory behind our choices moving forward.
There are two types of melee attacks: white (auto attacks) and yellow (special attacks). Yellow attacks function exactly like white attacks, except they cannot glance. Each white attack made by players against enemy mobs will result in one of the following:
- Miss
- Dodge
- Parry
- Glancing blow
- Block
- Critical Strike
- Hit
A mob being attacked from behind cannot block or parry, and thus these two outcomes are removed from the roll table. This means our white attacks can only either miss, be dodged, glance, hit, or critically hit. Therefore, in order to maximize our damage we need to minimize \(P(Miss)\) and \(P(Dodge)\), maximize \(P(Crit)\), and increase the damage done by glancing blows, seeing as how \(P(Glance)\) is fixed at \(.4\). In the subsequent sections, we will take a deeper look into how we can achieve that.
3.2 Miss Chance, Glancing Blows, and Weapon Skill
3.2.1 Miss Chance
Blizzard has confirmed that players have an 8% chance ^[Note that, due to the inherent hit suppression against level 63 mobs, the hit cap and the \(P(Miss)\) are different until 305 weapon skill. This behavior is further explained in @ref(weapon_skill) to miss a creature that is 3 levels above them (Blizzard 2019b). Empirical work from magey and others (magey et al. 2019) further corroborates a formula originally proposed by Beaza during vanilla (Beaza 2006), which can be summarized as:
If the target is a mob and the difference between its defense rating and the attacker’s weapon skill is 11 or more:
\[\begin{equation} P\left(Miss\right)\ =\ 5\ +\ \left(\left(T_{lvl}\times 5\right)-Atk_{skill}\right)\times 0.2 \tag{3.1} \end{equation}\]If the target is a mob and the difference between its defense rating and the attacker’s weapon skill is 10 or less:
\[\begin{equation} P\left(Miss\right)\ =\ 5\ +\ \left(\left(T_{lvl}\times 5\right)-Atk_{skill}\right)\times 0.1 \tag{3.2} \end{equation}\]Where \(T_{lvl}\) is the target’s level, and \(Atk_{skill}\) is the attacker’s weapon skill rating. While simple, this formula carries immense significance - it means that that by having 305 weapon skill, a player only has a 6% chance to miss an enemy mob 3 levels higher, which includes raid bosses. Conversely, a player with only 300 weapon skill will have an 8% chance to miss. This is a huge difference, especially in conjunction with the other benefits that weapon skill brings. It is important to note, however, that this is the behavior exhibited by wielding one weapon. If dual wielding, the probability of missing an attack is calculated as:
\[\begin{equation} P\left(DW_{miss}\right)\ =\ \left(P\left(Miss\right)\ \times\ 0.8\right)\ +\ 0.2 \tag{3.3} \end{equation}\]As a disclaimer, magey notes that further testing is still required to assert the correctness of this formula.
3.2.2 Glancing Blows
Glancing blows are a type of attack that can only occur when fighting an enemy of equal or higher level, and are restricted to white attacks. In accordance with Beaza, magey et al. have determined the glancing blow probability to be as follows:
\[\begin{equation} P\left(Glancing\right)\ =\ 0.1\ +\ \left(T_{lvl}\times5\ -\ \min\left(Atk_{lvl}\times 5,\ Atk_{skill}\right)\right)\times 0.02 \tag{3.4} \end{equation}\]Where \(Atk_{lvl}\) is the player’s level, and \(Atk_{skill}\) is the player’s weapon skill value. Knowing that, we can compute the probability that our white attacks will glance, and the damage penalty that that glancing blow carries against enemies of different levels:
| Level Difference | Probability | Damage Penalty |
|---|---|---|
| 0 | 0.1 | 0.05 |
| 1 | 0.2 | 0.05 |
| 2 | 0.3 | 0.15 |
| 3 | 0.4 | 0.35 |
This means that against a level 63 enemy mob (all raid bosses) and with 300 weapon skill our white attacks have a 40% chance of being glancing blows, therefore only being capable of dealing 65% of their maximum damage. Needless to say this is an immense DPS loss and should be mitigated as much as possible, and the only way that can be done is through increasing the player’s weapon skill.
3.2.3 Weapon Skill
magey’s work again corroborates the impact of weapon skill on glancing blow probability, damage, and miss probability according to Beaza’s formulas ((3.4), (3.1) and (3.2)). The table below summarizes that impact, but it is important to note that not all values have been experimentally confirmed due to the difficulty in acquiring specific weapon skill values that inherently comes from WoW itemization.
| Weapon Skill | % damage dealt by glancing blow | Glancing Blow Damage Increase | Miss Probability | Hit Cap |
|---|---|---|---|---|
| 300 | 0.65 | 0.000 | 0.080 | 0.090 |
| 301 | 0.69 | 0.062 | 0.078 | 0.088 |
| 302 | 0.73 | 0.120 | 0.076 | 0.086 |
| 303 | 0.77 | 0.180 | 0.074 | 0.084 |
| 304 | 0.81 | 0.250 | 0.072 | 0.082 |
| 305 | 0.85 | 0.310 | 0.060 | 0.060 |
| 306 | 0.89 | 0.370 | 0.059 | 0.059 |
| 307 | 0.93 | 0.430 | 0.058 | 0.058 |
| 308 | 0.95 | 0.460 | 0.057 | 0.057 |
| 309 | 0.95 | 0.460 | 0.056 | 0.056 |
| 310 | 0.95 | 0.460 | 0.055 | 0.055 |
| 311 | 0.95 | 0.460 | 0.054 | 0.054 |
| 312 | 0.95 | 0.460 | 0.053 | 0.053 |
| 313 | 0.95 | 0.460 | 0.052 | 0.052 |
| 314 | 0.95 | 0.460 | 0.051 | 0.051 |
| 315 | 0.95 | 0.460 | 0.050 | 0.050 |
As we can see, weapon skill not only reduces the glancing blow damage penalty, it also reduces the hit cap and the \(P(Miss)\).
The glancing blow damage penalty reduction is more easily shown graphically:
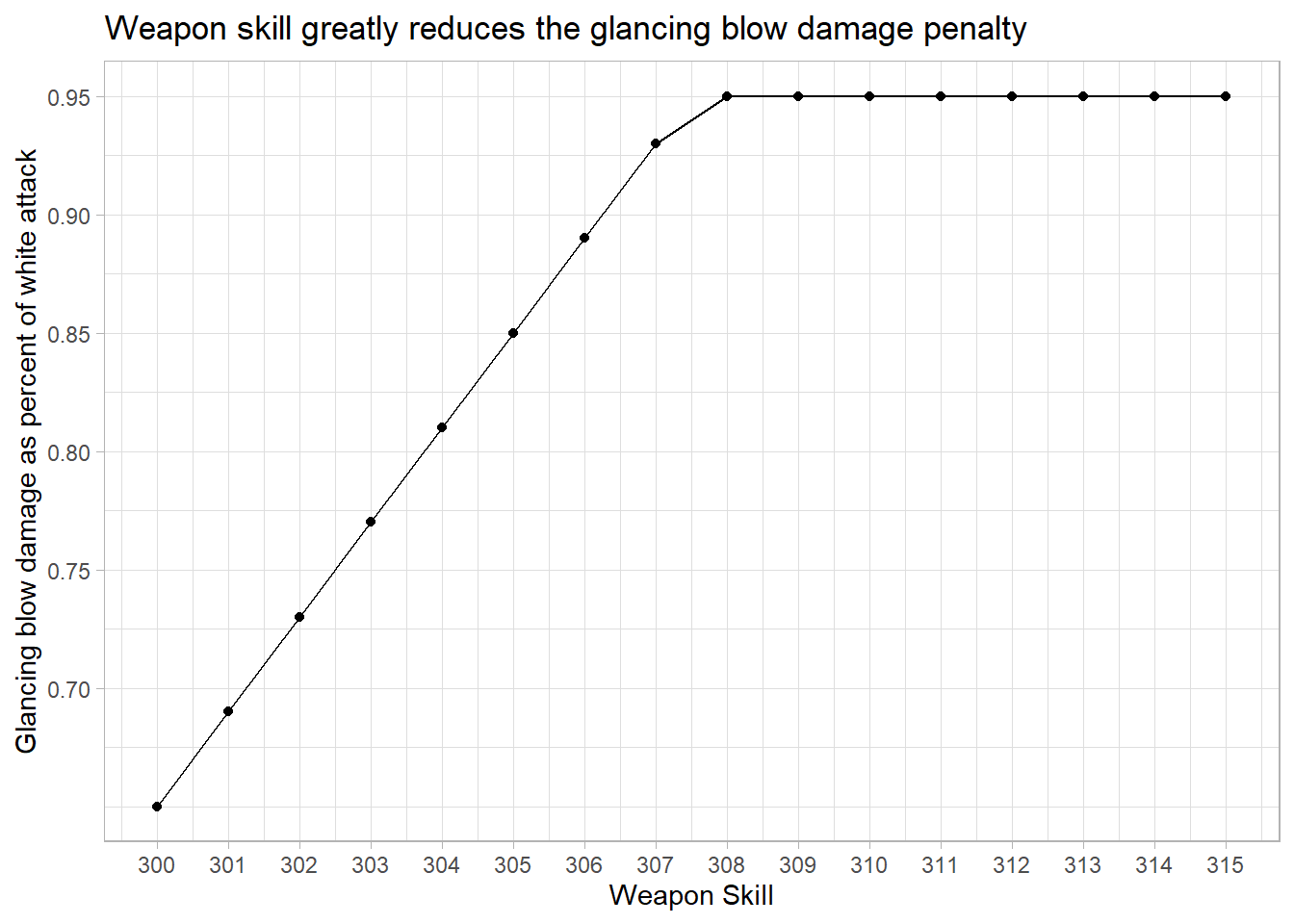
Figure 3.1: Weapon skill greatly reduces the glancing blow damage penalty
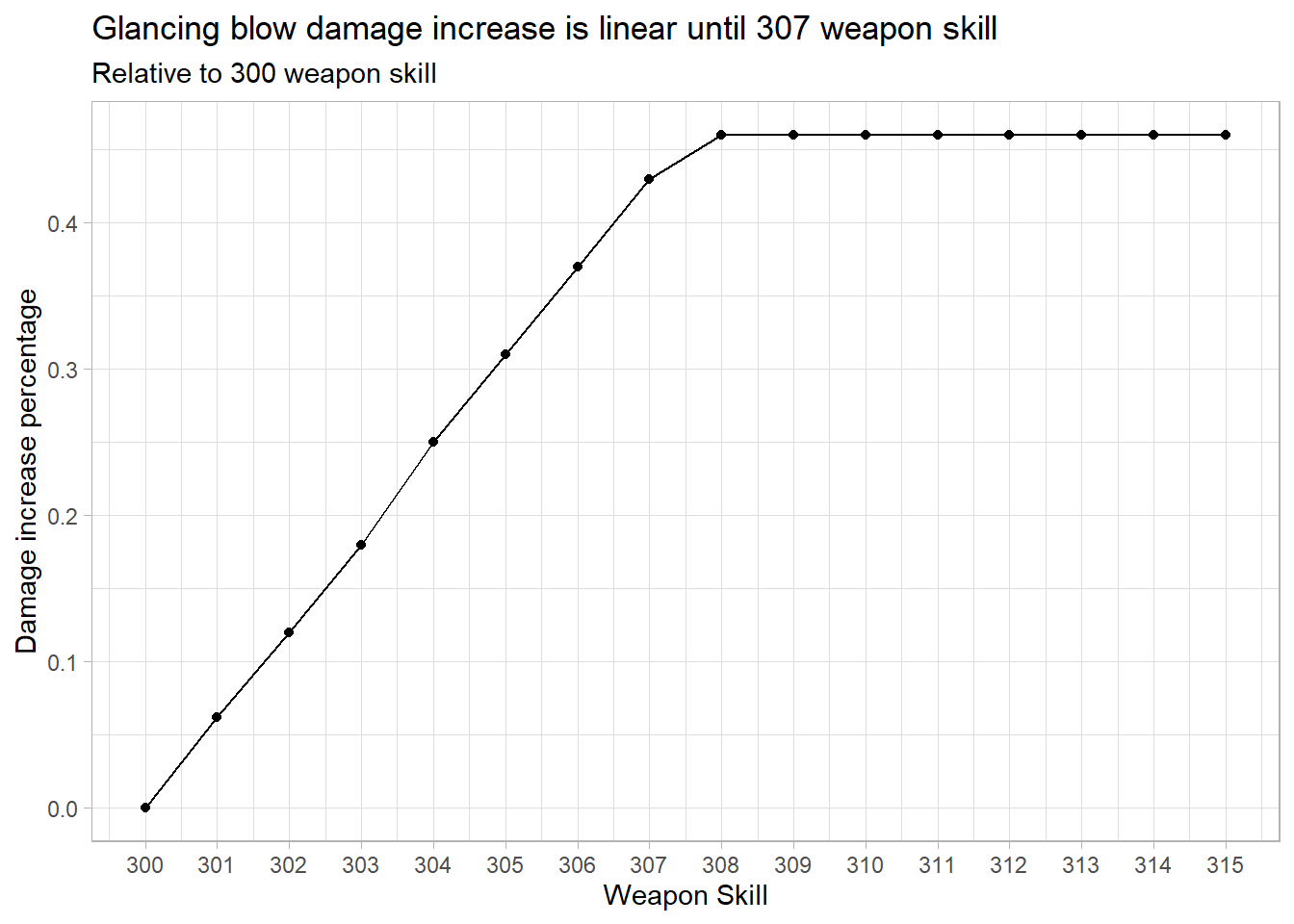
Figure 3.2: Weapon skill increases damage on glancing, relative to 300 weapon skill.
As we can see, our glancing blows increase in damage linearly with weapon skill until 307 weapon skill. This is incredibly important, as it indicates 308 weapon skill to being the soft cap for glancing blow damage penalty reduction - meaning the player gains no benefits in this aspect if their weapon skill is higher than 308 when facing a raid boss.
Similarly, the impact of weapon skill on the \(P(Miss)\) and hit cap is clearer when shown graphically:
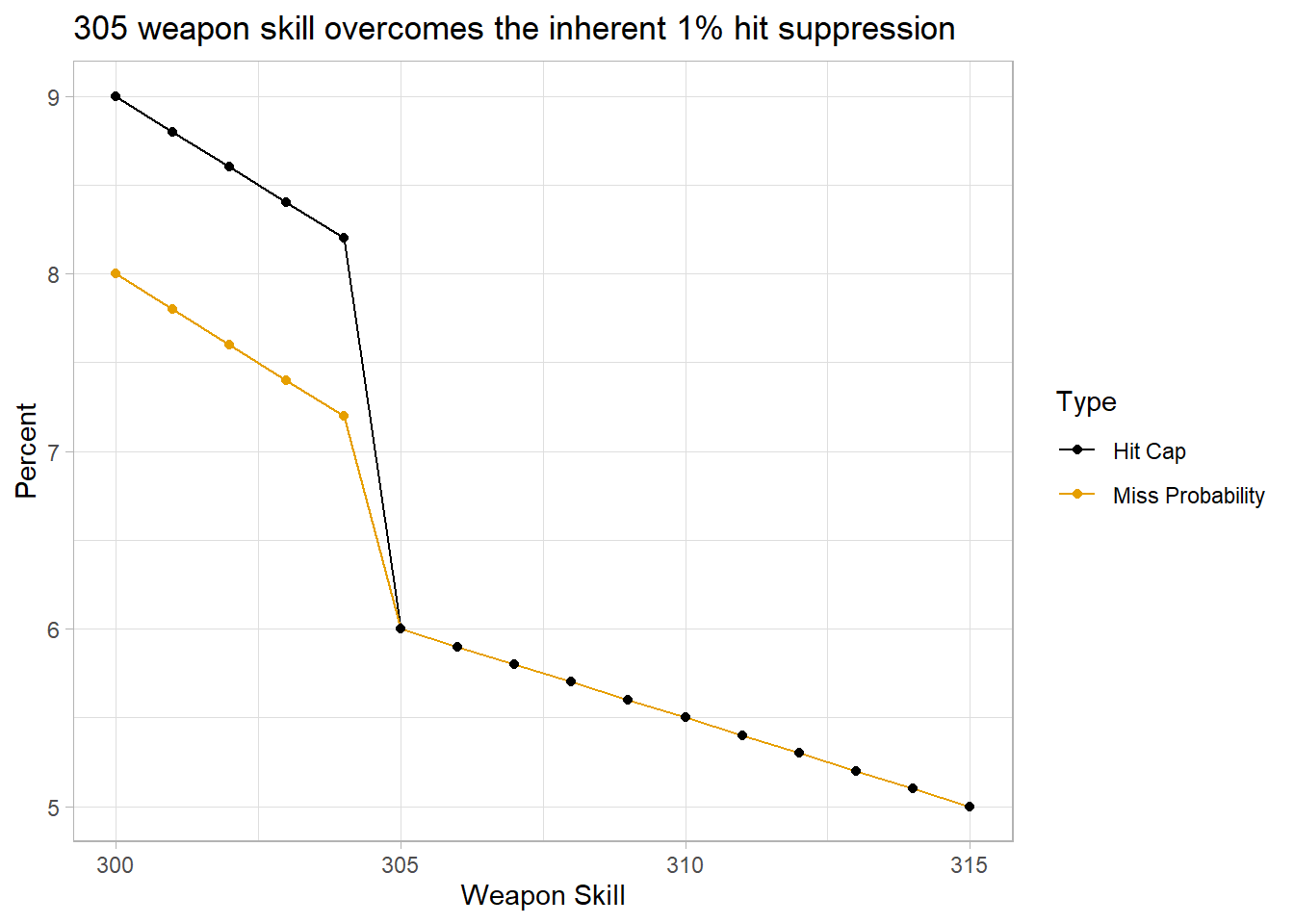
Figure 3.3: Weapon skill contributes to overcome the 1% hit suppression and the miss probability, but suffers steep diminishing returns after 305.
As we can see, the player’s hit cap starts 1% higher than \(P(Miss)\) at 300 weapon skill. This is because vanilla WoW code explicitly suppresses the first 1% of +hit gained from talents or gear against enemy mobs with more than 10 defense skill above the player’s weapon skill (Blizzard 2019a), in accordance with (3.1). This hit suppression is not applied, however, if the difference between the attacker’s weapon skill and the enemy mob’s defense skill is less than 10 (3.2). Note that values past 305 weapon skill suffer from steep diminishing returns, where an increase of 10 points past that only translates to a hit cap decrease of 1%.
This is why weapon skill is so important: not only does it reduce the glancing blow damage penalty, it removes the inherit 1% hit suppresion, and significantly reduces \(P(Miss)\) until 305. This is also why a weapon skill of at least 305 and at most 308 is highly recommended. The first 5 points are crucial to overcome the 1% hit deficit, and the 8 points enables us to reach the maximum glancing blow damage. This is a complicated threshold to reach, however, as there are very few items in World of Warcraft that add small amounts of Weapon Skill that would enable you to get to 308. Furthermore, the fact that weapon skill’s value in respect to hit chance is vastly diminished after 305 clearly indicates that 305 weapon skill is the most optimal weapon skill value for Fury Warriors in Classic WoW.
This is why any weapon skill bonus of over 5, whether given by a racial (orcs with axes, humans with maces and swords) or an item is so good - it means that single piece of gear is enough to overcome the hit suppresion versus raid bosses, as well as reducing your \(P(Miss)\) by 2%, and glancing blow damage penalty reduction. This is a massive advantage, especially compared to the alternative which is gearing for weapon skill through items such as Edgemaster’s Handguards, since the player with the built in weapon skill essentially has one extra item slot over a non-human, non-orc player. This is also why items that give good stats in addition to weapon skill, such as Aged Core Leather Gloves (ACLG), are incredibly good.
3.3 The Crit Cap
Due to the nature of the two-roll system in World of Warcraft combat, attacks past a certain \(P(Crit)\) dictate every non-glancing auto attack will result in a critical strike. This threshold is also known as the crit cap, and decreasing \(P(Miss)\) and \(P(Dodge)\) through an increase in Weapon Skill or increasing \(P(Hit)\) will increase it. Since we cannot decrease \(P(Glance)\), we can calculate the crit cap as:
\[\begin{equation} \small Crit_{cap}\ =\ 100-P\left(Miss\right)-P\left(Dodge\right)-P\left(Block\right)-P\left(Parry\right)-P\left(Glance\right)+Crit_{\sup} \tag{3.5} \end{equation}\]Where \(Crit_{sup}\) is the innate crit suppresion against a level 63 mob (magey et al. 2019). As the player’s gear level increases through phases, so does their \(P(Crit)\) - which when taken into account with world buffs makes reaching the crit cap a real possibility, regardless of the interaction it may have with HS queueing (hsq). This is because even when simulating fights with perfect HS queueing/unqueueing a very large proportion of main hand swings are still white, and as such result the relative value of hit increases throughout phases.
3.4 Flurry
Flurry is a 5 point talent that, when maxed, increases the warrior’s attack speed by 30% for the next 3 swings after dealing a critical strike. This represents a very significant damage increase, and as such warrior itemization values crit very highly in order to obtain higher and higher flurry uptimes, which can be calculated as follows:
\[\begin{equation} F_{up}\ =\ 1\ -\ \left(\left(1-P\left(Crit\right)\right)^A\right) \tag{3.6} \end{equation}\]Where \(F_{up}\) is the uptime, \(P(Crit)\) is the player’s crit chance, and \(A\) is the number of attacks made in one cycle of Flurry (3 from auto attack swings, and generally one additional from an instant attack; 4 is a reasonable number for a dual wielding player). Flurry is often misunderstood - the main misconception being that 33% crit will translate to 100% flurry uptime. This is incorrect, as shown by the following graph:
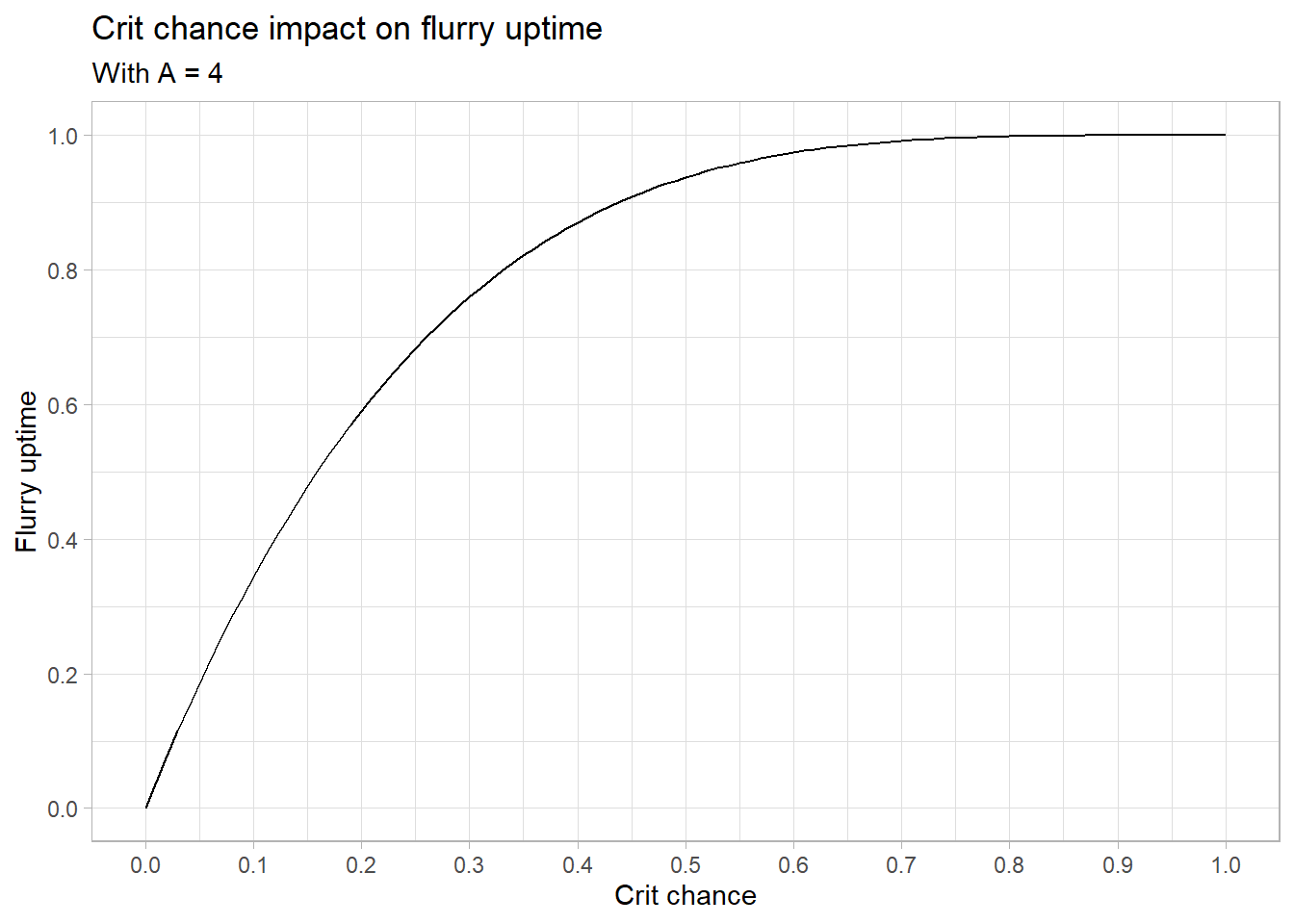
Figure 3.4: Increase in critical strike chance increases flurry uptime.
We can we now see that a \(P(Crit) = .33\) only actually results in roughly 80% Flurry uptime. In fact, any amount of crit under 100% (or the crit cap) will result in less than 100% Flurry uptime, with increasing amounts of crit becoming less valuable the higher your \(P(Crit)\) is. This is to say that the amount of Flurry uptime gained going for 1% crit to 11% crit is much greater than going from 40% to 50%, despite both cases representing a 10% overall \(P(Crit)\) increase.
References
Beaza. 2006. “Miss Chance in World of Warcraft,” November. https://wowwiki.fandom.com/wiki/Miss?oldid=347982.
Blizzard. 2019a. “Hit Cap Clarification.” https://us.forums.blizzard.com/en/wow/t/bug-hit-tables/185675/32.
Blizzard. 2019b. “Attack Table Clarifications.” https://classic.wowhead.com/news=292085/hit-cap-in-classic-wow-clarifications?webhook.
magey, Vilius, dmzor, Pufffymuffins, Towneh, Scylla, and Pyte. 2019. “Attack Table in Classic Wow.” https://github.com/magey/classic-warrior/wiki/Attack-table.