5  Matrizen (II)

5.1 Matrix als lineare Transformation

Eine Matrix kann als kompakte Schreibweise für eine lineare Transformation aufgefasst werden. Die Spalten der Matrix geben an, wohin die natürlichen Basisvektoren transformiert werden. Und $\mathbf{Ax}$ ist die lineare Transformation des Vektors $\mathbf{x}$.

Wenn zwei lineare Transformationen nacheinander ausgeführt werden, entspricht das dem Matrixprodukt. Wenn ein Vektor $\mathbf{x}$ zuerst durch eine Matrix $\mathbf{A}$ transformiert wird und anschließend noch eine lineare Transformation $\mathbf{B}$ durchgeführt wird, dann erhält man $$\mathbf{y}=\mathbf{BAx}.$$ Das gleiche Resultat erhält man durch eine einzelne lineare Transformation mit der Matrix $\mathbf{C}=\mathbf{BA}$. Die Matrixmultiplikation fasst also zwei Schritte zu einem zusammen. Damit wird auch klar, warum das Matrixprodukt nicht kommutativ ist.

5.2 Einheitsmatrix

Eine besondere Matrix ist die Einheitsmatrix (engl. identity matrix). Sie transformiert einen Vektor auf sich selber. Sie hat auf der Diagonalen Einsen und überall sonst Nullen. Die Einheitsmatrix der Dimension $(n\times n)$ wird als ${\mathbf{I}}_n$ oder (wenn die Dimension klar ist) einfach als $\mathbf{I}$ notiert. Einheitsmatrizen sind quadratisch und sehen so aus: $${\mathbf{I}}_n=\left[\begin{array}{cccc}1& 0& \dots & 0\\ 0& 1& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & 1\end{array}\right].$$ Für jede beliebige Matrix $\mathbf{A}$ (also auch für Spalten- oder Zeilenvektoren) gilt $$\mathbf{AI}=\mathbf{IA}=\mathbf{A},$$ sofern die Dimensionen passen.

In R generiert man eine Einheitsmatrix der Dimension $(n\times n)$ mit der Funktion diag (leider ist dieser Name nicht sehr intuitiv):

diag(3)

     [,1] [,2] [,3]
[1,]    1    0    0
[2,]    0    1    0
[3,]    0    0    1

5.3 Rang einer Matrix

Unter dem Rang einer Matrix versteht man die Anzahl der linear unabhängigen Spalten (oder Zeilen) einer Matrix. Der Rang kann niemals größer sein als das Minimum von Spaltenzahl und Zeilenzahl der Matrix. Für eine Matrix $\mathbf{A}$ mit Dimensionen $(m\times n)$ gilt also immer, dass $rg(\mathbf{A})\le min(m,n)$. Da die Zahl der linear unabhängigen Zeilen immer gleich der Zahl der linear unabhängigen Spalten ist, braucht man nicht zu sagen, ob man den “Zeilenrang” oder den “Spaltenrang” angibt - die beiden sind gleich: $$rg(A)=rg(A^{\prime }).$$ Wenn $rg(\mathbf{A})=min(m,n)$ ist, sagt man auch, dass die Matrix vollen Rang hat. Eine quadratische Matrix der Dimension $(n\times n)$ mit vollem Rang nennt man auch regulär. Wenn sie keinen vollen Rang hat, heißt sie singulär.

Für den Rang gibt es eine Reihe von Rechenregeln. So gilt $$rg(\mathbf{A})=rg({\mathbf{A}}^{\prime })=rg({\mathbf{A}}^{\prime }\mathbf{A})=rg(\mathbf{A}{\mathbf{A}}^{\prime }).$$ Der Rang eines Matrixprodukt kann nicht größer sein als die Ränge der beiden Faktormatrizen, d.h. $$rg(\mathbf{AB})\le min(rg(\mathbf{A}),rg(\mathbf{B})).$$ Multipliziert man eine Matrix $\mathbf{A}$ mit einer quadratischen Matrix $\mathbf{B}$ vollen Rangs, so hat das Produkt den Rang von $\mathbf{A}$, $$rg(\mathbf{AB})=rg(\mathbf{A}).$$ Auch für die Summe zweier Matrizen lässt sich eine Aussage über den Rang treffen. Es gilt $$rg(\mathbf{A}+\mathbf{B})\le rg(\mathbf{A})+rg(\mathbf{B}).$$

Leider gibt es in R standardmäßig keine Funktion, die den Rang einer Matrix berechnet. Das Paket pracma stellt jedoch die Funktion Rank zur Verfügung, mit der man den Rang leicht ausrechnen kann. Beispielsweise hat die Matrix

library(pracma)
A <- matrix(1:9, 3, 3)
A

     [,1] [,2] [,3]
[1,]    1    4    7
[2,]    2    5    8
[3,]    3    6    9

den Rang

Rank(A)

[1] 2

Diese Matrix hat also keinen vollen Rang, sie ist singulär. Jede der drei Spalten lässt sich als Linearkombination der beiden anderen Spalten ausdrücken. Mit Hilfe der Funktion nullspace, die ebenfalls von dem Paket pracma bereit gestellt wird, kann man die Skalare finden, für die gilt $${\lambda }_1{\mathbf{x}}_1+\dots +{\lambda }_n{\mathbf{x}}_n=\mathbf{0}.$$ Für die Beispielmatrix ergibt sich

lambda <- nullspace(A)
lambda

           [,1]
[1,]  0.4082483
[2,] -0.8164966
[3,]  0.4082483

Wir überprüfen, ob die Linearkombination der drei Spalten von A mit diesen drei Skalaren tatsächlich den Nullvektor ergibt.

lambda[1]*A[,1] + lambda[2]*A[,2] + lambda[3]*A[,3]

[1] -4.440892e-16 -4.440892e-16  8.881784e-16

Zur Notation: Mit e-16 ist die wissenschaftliche Schreibweise $\times {10}^{-16}$ gemeint. Der Nullvektor wird zwar nicht exakt getroffen, aber die Abweichung ist erst in der 16. Nachkommastelle zu sehen. Diese kleinen Abweichungen werden durch Rundungsfehler verursacht. Wenn das Ergebnis auf viele Stellen (z.B. 12) nach dem Komma gerundet wird, ergibt sich tatsächlich der Nullvektor,

round(lambda[1]*A[,1] + lambda[2]*A[,2] + lambda[3]*A[,3], 12)

[1] 0 0 0

Die exakte Lösung ist ${\lambda }_1={\lambda }_3=20/49$ und ${\lambda }_2=-40/49$.

Die drei Skalare, die in dem Vektor lambda zusammengefasst sind, stellen nicht die einzige Lösung dar. Multipliziert man sie mit einer beliebigen Konstante (außer Null), so erhält man drei andere Skalare, die ebenfalls auf den Nullvektor führen.

Der Rang einer Matrix lässt sich auch mit dem Gauß-Jordan-Verfahren bestimmen, das wir ja bereits in Kapitel Abschnitt 2.7.3 kennen gelernt haben. Wie sieht das an der Beispielmatrix $\mathbf{A}$ aus? $$\begin{array}{cccl}1& 4& 7& (I)\\ 2& 5& 8& (II)\\ 3& 6& 9& (III)\end{array}$$ Zuerst subtrahieren wir $2(I)$ von $(II)$ und im gleichen Schritt $3(I)$ von $(III)$. $$\begin{array}{cccl}1& 4& 7& (I)\\ 0& -3& -6& (II)\\ 0& -6& -12& (III)\end{array}$$ In nächsten Schritt subtrahieren wir $2(II)$ von $(III)$. $$\begin{array}{cccl}1& 4& 7& (I)\\ 0& -3& -6& (II)\\ 0& 0& 0& (III)\end{array}$$ Da die letzte Zeile nur aus Nullen besteht, hat die Matrix keinen vollen Rang. Dass der Rang der Matrix 2 (und nicht nur 1) beträgt, erkennt man daran, dass die ersten beiden Zeilen linear unabhängig voneinander sind. Wenn als Ergebnis der Gauß-Jordan-Methode an Ende zwei Zeilen ausschließlich Nullen enthalten, dann hat die Matrix den Rang 1.

5.4 Determinante

Die Determinante einer $(2\times 2)$-Matrix gibt an, auf das Wie-viel-Fache eine Fläche sich durch eine lineare Transformation verändert. Wenn die Determinante 2 beträgt, dann verdoppelt sich eine Fläche durch die lineare Transformation. Ist die Determinante 0.5, dann halbiert sich die Fläche.

Als Beispiel betrachten wir die lineare Transformation $$\mathbf{A}=\left[\begin{array}{cc}2& -1\\ 1& 1\end{array}\right]$$ Die folgende Abbildung zeigt, wie sich das Einheitsquadrat (das durch die beiden natürlichen Basisvektoren gebildet wird) vergrößert.

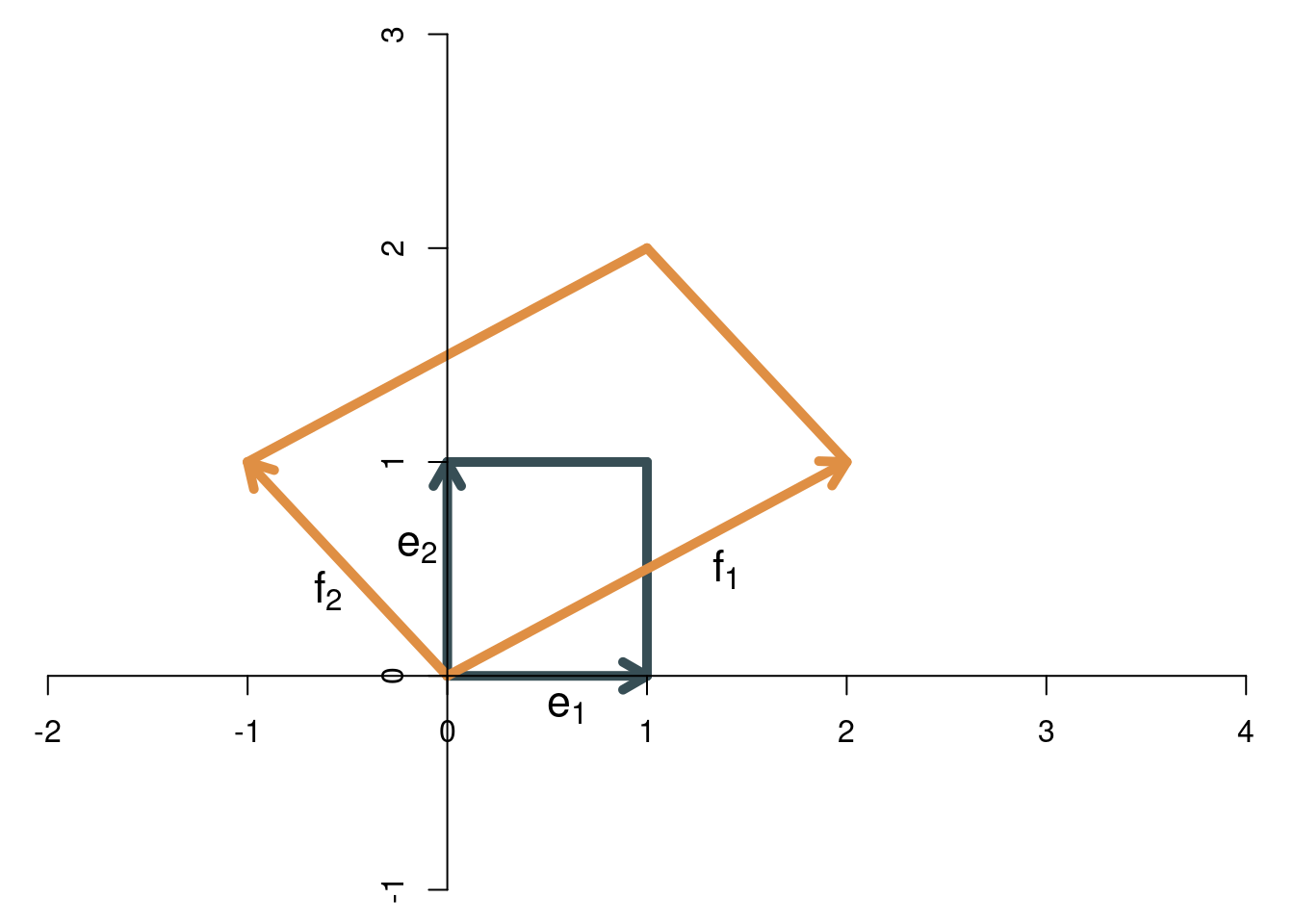
Die Fläche des Einheitsquadrats ist 1, die Fläche der Transformation (also des Parallelogramms) beträgt 3. Die Determinante der Matrix ist also $$det(\mathbf{A})=3.$$ Ein Hinweis zur Notation: In der ökonometrischen Literatur wird die Determinante sehr häufig auch als $|\mathbf{A}|$ geschrieben.

Die Determinante einer $(2\times 2)$-Matrix kann allgemein wie folgt berechnet werden: $$det(\mathbf{A})=a_{11}{a}_{22}-a_{12}{a}_{22}.$$ Für die Beispielmatrix erhält man $$det\left(\left[\begin{array}{cc}2& -1\\ 1& 1\end{array}\right]\right)=2\cdot 1-(-1)\cdot 1=3.$$ Wenn die Basisvektoren ihre relative Ausrichtung ändern - wenn also der erste Basisvektor nach der Transformation nicht mehr rechts, sondern links vom zweiten Basisvektor liegt, dann “klappt die Abbildung um” und die Determinante ist negativ. Als Beispiel sehen wir uns die folgende lineare Transformation an: $$\mathbf{B}=\left[\begin{array}{cc}-2& -1\\ -1& 1\end{array}\right]$$ Die beiden Basisvektoren vor und nach der Transformation zeigt die Abbildung:

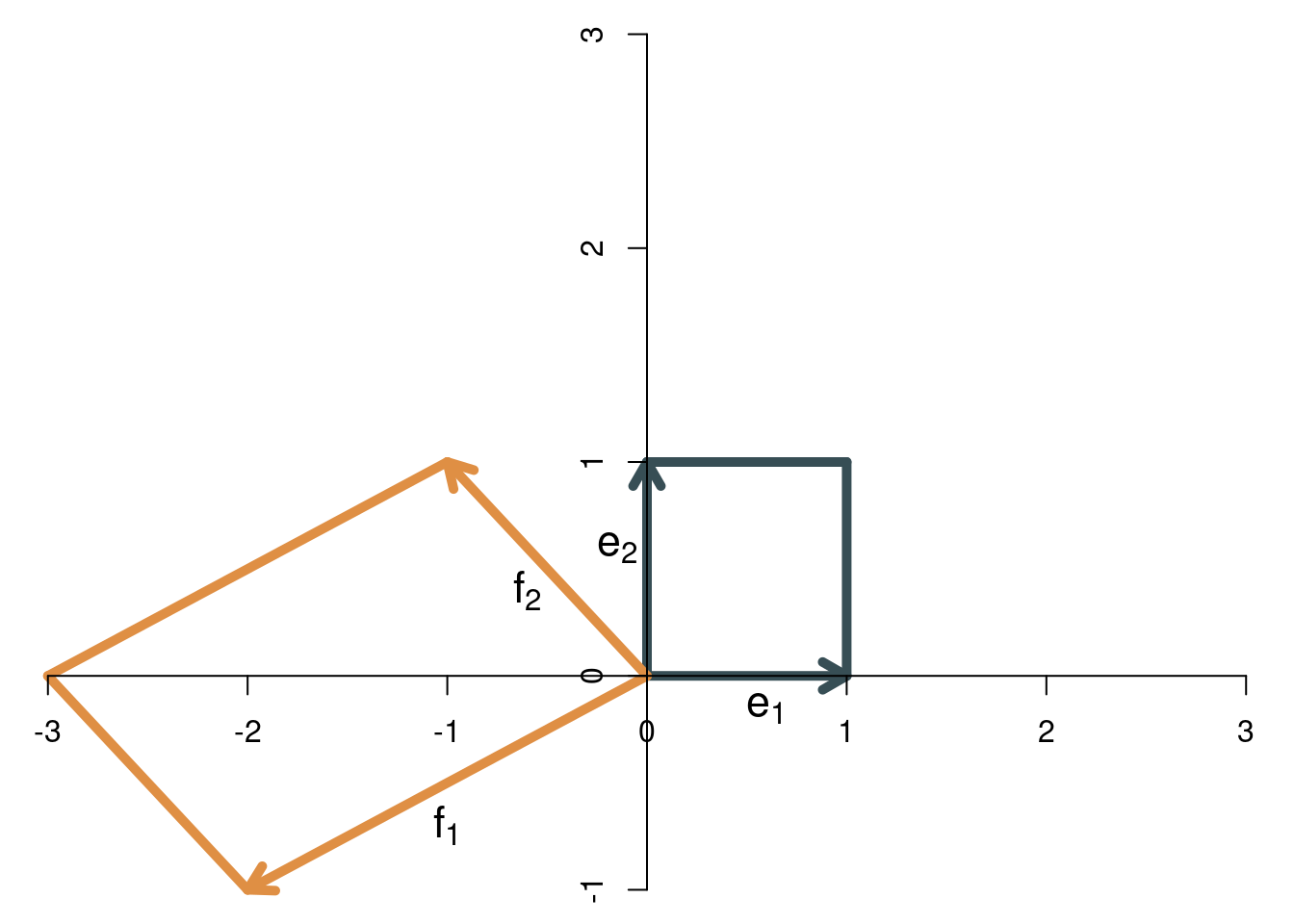
Die Determinante ist betragsmäßig genauso groß wie in dem vorherigen Beispiel. Da die Abbildung aber “umgeklappt” ist, ist jetzt negativ, nämlich $det(\mathbf{B})=-3$. Das ergibt sich auch durch die Formel $$det\left(\left[\begin{array}{cc}-2& -1\\ -1& 1\end{array}\right]\right)=-2\cdot 1-(-1)\cdot (-1)=-3.$$ Kann es auch passieren, dass die Determinante den Wert Null annimmt? Ja, und zwar dann, wenn die Fläche der Abbildung auf Null schrumpft, weil die beiden Basisvektoren nach der Transformation linear abhängig sind. Sie zeigen dann in die gleiche (oder genau entgegengesetzte) Richtung, so dass die Abbildung kein Parallelogramm ergibt, sondern nur eine Gerade. Die Fläche einer Gerade ist 0, so dass die Determinante in diesem Fall 0 ist. Mit anderen Worten: An der Determinante kann man erkennen, ob die Matrix vollen Rang hat. Der Rang ist nicht voll, wenn die Determinante Null ist. Da der Rang einer Matrix mit der linearen Unabhängigkeit der Spaltenvektoren zusammenhängt, kann die Determinante auch zur Feststellung der linearen Unabhängigkeit von Vektoren dienen: Wenn die Determinante ungleich Null ist, dann sind die Vektoren linear unabhängig.

Im dreidimensionalen Raum hat die Determinante eine ähnliche geometrische Interpretation. Sie gibt für eine $(3\times 3)$-Matrix an, auf das Wie-viel-Fache sich das Volumen eines Einheitswürfels durch die lineare Transformation vergrößert (oder verkleinert). Wenn die transformierten Basisvektoren alle in einer Ebene liegen (also einer durch eine Linearkombination der beiden anderen darstellbar ist), dann ist das Volumen Null. In diesem Fall nimmt auch die Determinante den Wert 0 an. Das gleiche gilt, wenn die transformierten Basisvektoren alle auf einer Geraden liegen. Die Determinante gibt also auch für $(3\times 3)$-Matrizen an, ob sie vollen Rang haben oder nicht. Wenn die Determinante 0 ist, hat die Matrix keinen vollen Rang. Ob der Rang 2 oder 1 (oder 0) ist, kann man an der Determinante jedoch nicht erkennen.

Die analytische Formel für die Berechnung der Determinante ist bei ($3\times 3)$-Matrizen schon recht komplex, nämlich $$\begin{array}{rl}det(\mathbf{A})& =a_{11}{a}_{22}{a}_{33}+a_{12}{a}_{23}{a}_{31}+a_{13}{a}_{21}{a}_{32}\\ & -a_{31}{a}_{22}{a}_{13}-a_{32}{a}_{23}{a}_{11}-a_{33}{a}_{21}{a}_{12}.\end{array}$$ Determinanten sind auch für noch höherdimensionale Räume definiert. Für eine quadratische $(n\times n)$-Matrix ($n>1$) ist die Determinante rekursiv definiert. $$det(\mathbf{A})=\sum _{j=1}^n(-1{)}^{j+1}{a}_{1j}det({\mathbf{A}}_{\mathbf{1}\mathbf{j}}),$$ wobei ${\mathbf{A}}_{1j}$ die Matrix ist, die sich aus $\mathbf{A}$ ergibt, wenn man die erste Zeile und die $j$-te Spalte herausstreicht. Ab Dimension $(4\times 4)$ ist es sehr aufwendig, Determinanten “per Hand” zu berechnen, nur für den zweidimensionalen (und teilweise den dreidimensionalen) Fall sind die Formeln noch einigermaßen übersichtlich.

Determinanten berechnet man natürlich normalerweise nicht “per Hand”. In R gibt es die Funktion det für die Berechnung von Determinanten. Für die $(2\times 2)$-Matrix [ =] ergibt sich zum Beispiel

A <- matrix(1:4, 2, 2)
det(A)

[1] -2

Die Determinante der $(3\times 3)$-Matrix [ =] ist

A <- matrix(1:9, 3, 3)
det(A)

[1] 0

Die drei Vektoren $(1,2,3)$, $(4,5,6)$ und $(7,8,9)$ sind folglich linear abhängig (wie wir ja weiter oben bereits gesehen haben) .

Allgemein gilt für $(n\times n)$-Matrizen $$det(\mathbf{A})\ne 0⟺rg(\mathbf{A})=n.$$ Reguläre Matrizen haben vollen Rang und eine Determinante ungleich 0, singuläre Matrizen haben keinen vollen Rang und eine Determinante von 0.

Es gibt noch weitere Rechenregeln für Determinanten, die manchmal hilfreich sind. Die Determinante der Transponierten entspricht der Determinante der Ausgangsmatrix, $$det({\mathbf{A}}^{\prime })=det(\mathbf{A}).$$

Für die Determinante des Produkts zweier Matrizen gilt $$det(\mathbf{AB})=det(\mathbf{A})\cdot det(\mathbf{B}).$$ Mit der geometrischen Interpretation ist dieser Zusammenhang klar: Wenn wir eine Fläche zuerst mit $\mathbf{B}$ transformieren und anschließend mit $\mathbf{A}$, so vervielfacht sich die Fläche im ersten Schritt um $det(\mathbf{B})$ und die so vergrößerte (oder verkleinerte) Fläche vervielfacht sich im zweiten Schritt um $det(\mathbf{A})$.

Ferner gilt für eine $(n\times n)$-Matrix $$det(\lambda \mathbf{A})={\lambda }^{n}det(\mathbf{A}).$$ Auch dieser Zusammenhang erschließt sich intuitiv mit der geometrischen Sichtweise. Wenn jede Spalte in $\mathbf{A}$ mit $\lambda$ multipliziert wird, bedeutet das, dass alle Basisvektoren um das $\lambda$-fache weiter gestreckt (oder gestaucht werden) als ohne die Skalarmultiplikation. Im zweidimensionalen Fall werden also beide Vektoren um das $\lambda$-fache verlängert (oder verkürzt), so dass die Fläche sich um ${\lambda }^2$ verändert. Für jede weitere Dimension muss der Faktor mit einem weiteren $\lambda$ multipliziert werden.

5.5 Inverse Matrix

Matrizen können als Repräsentation von linearen Transformationen aufgefasst werden. Wie in Kapitel Kapitel 3 für den zweidimensionalen Fall gezeigt wurde, gibt eine Matrix $$\mathbf{A}=\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]$$ an, dass der erste natürliche Basisvektor nach $(a_{11},a_{21}{)}^{\prime }$ transformiert wird, der zweite nach $(a_{12},a_{22}{)}^{\prime }$. Entsprechend wird jeder andere Punkt $(x_1,x_2{)}^{\prime }$ nach $$\mathbf{y}=\mathbf{Ax}=\left[\begin{array}{c}{a}_{11}{x}_1+a_{12}{x}_2\\ a_{21}{x}_1+a_{22}{x}_2\end{array}\right]$$ bewegt. Kann man die lineare Transformation wieder rückgängig machen? Gibt es eine andere lineare Transformation, die dazu führt, dass der transformierte Punkt $\mathbf{y}$ wieder an seinen Ursprungsort $\mathbf{x}$ zurückkehrt? Die Antwort auf diese Frage lautet: Ja, aber nicht immer.

Eine Rücktransformation ist unter der Bedingung möglich, dass die Basisvektoren durch die lineare Transformation nicht linear abhängig werden. Mit anderen Worten, wenn die lineare Transformation dazu führt, dass die Basisvektoren linear abhängig sind, dann kann die Transformation nicht mehr rückgängig gemacht werden. Die Matrix $\mathbf{A}$ muss also vollen Rang haben bzw. es muss sich um eine reguläre Matrix handeln.

Die Matrix, die die lineare Transformation $\mathbf{A}$ rückgängig macht, nennt man inverse Matrix oder kurz Inverse (engl. inverse - mit der Betonung auf der zweiten Silbe) von $\mathbf{A}$ und schreibt ${\mathbf{A}}^{-1}$. Wenn also $$\mathbf{y}=\mathbf{Ax},$$ dann gilt $$\mathbf{x}={\mathbf{A}}^{-1}\mathbf{y}.$$ Da ${\mathbf{A}}^{-1}$ den Effekt von $\mathbf{A}$ aufhebt, gilt $${\mathbf{A}}^{-1}\mathbf{A}=\mathbf{I},$$ es ergibt sich also die Einheitsmatrix. Das gleiche gilt auch in die andere Richtung, d.h. $$\mathbf{A}{\mathbf{A}}^{-1}=\mathbf{I}.$$

Beispiel:

Die Inverse der Matrix $$\mathbf{A}=\left[\begin{array}{cc}2& -1\\ 1& 1\end{array}\right]$$ ist $${\mathbf{A}}^{-1}=\left[\begin{array}{cc}\frac{1}{3}& \frac{1}{3}\\ -\frac{1}{3}& \frac{2}{3}\end{array}\right].$$ Wie man leicht nachprüfen kann, ergibt sowohl ${\mathbf{AA}}^{-1}$ als auch ${\mathbf{A}}^{-1}\mathbf{A}$ die Einheitsmatrix.

Die Inverse der Transponierten ist $$({\mathbf{A}}^{\prime }{)}^{-1}=({\mathbf{A}}^{-1}{)}^{\prime }.$$

Beim Invertieren einer Matrixmultiplikation muss man aufpassen, weil das Matrixprodukt nicht kommutativ ist. Es gilt $$(\mathbf{A}\mathbf{B}{)}^{-1}={\mathbf{B}}^{-1}{\mathbf{A}}^{-1}.$$ Dass die Reihenfolge sich ändert, wird in der geometrischen Sichtweise klar: Die Transformation $\mathbf{AB}$ bedeutet, dass zuerst $\mathbf{B}$ angewendet wird und anschließend $\mathbf{A}.$ Um die beiden Transformationen wieder rückgängig zu machen, muss nun zuerst $\mathbf{A}$ durch ${\mathbf{A}}^{-1}$ zurücktransformiert werden. Und anschließend wird der Effekt von $\mathbf{B}$ durch ${\mathbf{B}}^{-1}$ aufgehoben.

Die Determinante der Inversen ist $$det({\mathbf{A}}^{-1})=det(\mathbf{A}{)}^{-1}=\frac{1}{det(\mathbf{A})}.$$ Dieser Zusammenhang ist leicht geoemtrisch interpretierbar. Die Determinante der Inversen gibt an, auf das Wie-viel-Fache sich eine Fläche durch die Transformation ${\mathbf{A}}^{-1}$ verändert. Da ${\mathbf{A}}^{-1}$ die Transformation $\mathbf{A}$ gerade zurückgängig macht, muss die Fläche wieder auf ihre ursprüngliche Größe zurückgesetzt werden. Wenn sie also bei der Transformation mit $\mathbf{A}$ auf das $det(\mathbf{A})$-Fache angewachsen ist, dann muss sie bei der inversen Transformation um den Faktor $1/det(\mathbf{A})$ wachsen.

Die Inverse hat nicht nur die geometrische Interpretation, dass sie eine lineare Transformation rückgängig macht. Das wichtigste Einsatzfeld der Inversen besteht in den Wirtschaftswissenschaften und speziell in der Ökonometrie darin, bei der Lösung linearer Gleichungssysteme zu helfen. Darauf gehen wir in Kapitel 7 näher ein.

Wie findet man konkret die Inverse einer gegebenen Matrix? Man kann die Inverse entweder per Hand oder mit R (bzw. anderen Computerprogrammen) finden. Der Weg per Hand ist natürlich mühsamer, aber dennoch sollte man ihn kennen, weil in einigen Situationen R als Werkzeug nicht zur Verfügung steht, z.B. weil einige (oder alle) Matrixelemente nicht mit ihren konkreten numerischen Werten gegeben sind, sondern nur als Symbole. Wir sehen uns zuerst an, wie man die Inverse in R berechnet.

Leider hat die R-Funktion für die Berechnung der Inversen einen nicht gerade intuitiven Namen. Sie lautet solve.

Beispiel:

Die Inverse von

A <- matrix(c(2,1,-1,1), 2, 2)
A

     [,1] [,2]
[1,]    2   -1
[2,]    1    1

ist die Matrix

invA <- solve(A)
invA

           [,1]      [,2]
[1,]  0.3333333 0.3333333
[2,] -0.3333333 0.6666667

Zur Kontrolle berechnen wir die beiden Matrixprodukte

A %*% invA

             [,1] [,2]
[1,] 1.000000e+00    0
[2,] 5.551115e-17    1

und

invA %*% A

     [,1]          [,2]
[1,]    1 -5.551115e-17
[2,]    0  1.000000e+00

Als Ergebnis erhält man in beiden Fällen die Einheitsmatrix. Die kleinen Abweichungen sind wieder darauf zurückzuführen, dass reelle Zahlen in R (oder anderen Computerprogrammen) nicht immer exakt repräsentiert werden können. Es kommt dann zu Rundungsfehlern, die jedoch meist nicht ins Gewicht fallen. Die Möglichkeit von Rundungsfehlern sollte man bei der Arbeit mit numerischen Verfahren immer im Hinterkopf behalten. Eine naive Kontrolle, ob invA wirklich die Inverse von A ist, führt nämlich zum falschen Ergebnis:

all(A %*% invA == diag(2))

[1] FALSE

Runden auf 12 Stellen hilft.

all(round(A %*% invA, 12) == diag(2))

[1] TRUE

Achtung: Die Schreibweise A^(-1) ist in R möglich, es gibt keine Fehlermeldung. Das Ergebnis von A^(-1) ist aber nicht die inverse Matrix von A. Stattdessen werden von allen Elementen der Matrix die Kehrwerte berechnet. In R ergibt also

A^(-1) %*% A

     [,1] [,2]
[1,]    0 -1.5
[2,]    3  0.0

nicht die Einheitsmatrix! Das ist ein gefährlicher Fehler, weil er nicht zu einer Fehlermeldung führt.

Für die Berechnung per Hand ist eine Variante des Gauß-Jordan-Verfahrens gut geeignet (vgl. Abschnitt 2.7.3). An einem Beispiel lässt sich das am besten veranschaulichen. Wir suchen die Inverse der $(3\times 3)$-Matrix $$\mathbf{A}=\left[\begin{array}{ccc}2& -1& 3\\ 4& 3& 0\\ 1& -2& 3\end{array}\right].$$ Zunächst ergänzt man die Matrixelemente auf der rechten Seite um die Einheitsmatrix (abgetrennt mit einem senkrechten Strich). Die Zeilen numerieren wir mit römischen Ziffern. $$\begin{array}{ccccccl}2& -1& 3& 1& 0& 0& (I)\\ 4& 3& 0& 0& 1& 0& (II)\\ 1& -2& 3& 0& 0& 1& (III)\end{array}$$ Nun werden die drei Zeilen mit den üblichen erlaubten Umformungen Schritt für Schritt so verändert, dass auf der linken Seite die Einheitsmatrix entsteht. Die Elemente rechts vom Strich werden dabei mit verändert. Zuerst wird das Element unten links auf 0 gesetzt, dazu rechnen wir $(II)-4(III)$ und erhalten: $$\begin{array}{ccccccl}2& -1& 3& 1& 0& 0& (I)\\ 4& 3& 0& 0& 1& 0& (II)\\ 0& 11& -12& 0& 1& -4& (III)\end{array}$$ Als nächstes eleminieren wir die 4 in der ersten Spalte, indem wir $(II)$ durch $2(I)-(II)$ ersetzen: $$\begin{array}{ccccccl}2& -1& 3& 1& 0& 0& (I)\\ 0& -5& 6& 2& -1& 0& (II)\\ 0& 11& -12& 0& 1& -4& (III)\end{array}$$ Nun ersetzt man die 11 in der unteren Zeile, anschließend die 3 in der ersten Zeile usw., bis die Seite links vom senkrechten Strich eine Diagonalmatrix ist. Dann wird die Diagonalmatrix durch geeignete Multiplikationen der drei Zeilen zur Einheitsmatrix umgeformt. Wenn links vom Strich die Einheitsmatrix steht, dann hat man rechts vom Strich die Inverse. Wir lassen die einzelnen weiteren Schritte hier aus Platzgründen aus. Am Ende erhält man $$\begin{array}{ccccccl}1& 0& 0& -3& 1& 3& (I)\\ 0& 1& 0& 4& -1& -4& (II)\\ 0& 0& 1& \frac{11}{3}& -1& -\frac{10}{3}& (III)\end{array}$$ Die Inverse von $$\mathbf{A}=\left[\begin{array}{ccc}2& -1& 3\\ 4& 3& 0\\ 1& -2& 3\end{array}\right]$$ ist also $${\mathbf{A}}^{-1}=\left[\begin{array}{ccc}-3& 1& 3\\ 4& -1& -4\\ \frac{11}{3}& -1& -\frac{10}{3}\end{array}\right].$$ Was geschieht, wenn die Matrix $\mathbf{A}$ singulär ist und es keine Inverse gibt? Das Gauß-Jordan-Verfahren kann bei singulären Matrizen eingesetzt werden, man muss also nicht wissen, ob die Matrix, deren Inverse man sucht, überhaupt invertierbar ist. Bei den Umformungen einer singulären Matrix tritt an irgendeiner Stelle die Situation auf, dass alle Elemente einer Zeile gleich Null sind. Damit lässt sich die Matrix links vom Strich nicht in die Einheitsmatrix überführen.

Beispiel:

Wir versuchen, die singuläre Matrix $$\left[\begin{array}{ccc}2& -1& 3\\ 4& 3& 0\\ 6& 2& 3\end{array}\right]$$ mit dem Gauß-Jordan-Verfahren zu invertieren. $$\begin{array}{ccccccl}2& -1& 3& 1& 0& 0& (I)\\ 4& 3& 0& 0& 1& 0& (II)\\ 6& 2& 3& 0& 0& 1& (III)\end{array}$$ Der erste Schritt soll auf eine 0 in der unteren linken Ecke führen. Dazu rechnen wir (z.B.) 3(I)-(III) und erhalten $$\begin{array}{ccccccl}2& -1& 3& 1& 0& 0& (I)\\ 4& 3& 0& 0& 1& 0& (II)\\ 0& -5& 6& 3& 0& -1& (III)\end{array}$$ Der nächste Schritt ersetzt die 4 in der zweiten Zeile durch eine 0, dazu rechnen wir 2(I)-(II): $$\begin{array}{ccccccl}2& -1& 3& 1& 0& 0& (I)\\ 0& -5& 6& 2& -1& 0& (II)\\ 0& -5& 6& 3& 0& -1& (III)\end{array}$$ Subtrahiert man nun die dritte von der zweiten Zeile und schreibt die Differenz in die letzte Zeile, dann bestehen alle Elemente der letzten Zeile (links vom Strich) aus Nullen. Das zeigt, dass die Matrix singulär ist. Man kann also das Verfahren abbrechen, denn es gibt keine Inverse.