3  Lineare Transformationen

Wir bezeichnen eine Funktion $f:{\mathbb{R}}^n\to {\mathbb{R}}^m$ als lineare Transformation, wenn sie additiv $$\begin{array}{r}f(\mathbf{x}+\mathbf{z})=f(\mathbf{x})+f(\mathbf{z})\end{array}$$ und homogen $$\begin{array}{r}f(\lambda \mathbf{x})=\lambda f(\mathbf{x}),\lambda \in \mathbb{R}\end{array}$$ ist. Für $n=m=1$, haben lineare Transformationen die Gestalt $$y=f(x)=ax,$$ wobei $a\in \mathbb{R}$ ein Skalar ist. In diesem Fall ist $f$ also eine Gerade mit Steigung $a$, die durch den Ursprung verläuft. Der Fall für den wir uns zunächst interessieren, ist jedoch durch $n=m=2$ geben. Das heißt, wir betrachen lineare Transformationen deren Input- als auch Outputvektor zweidimensional sind, also $$\mathbf{y}=f(\mathbf{x})$$ mit $\mathbf{x},\mathbf{y}\in {\mathbb{R}}^2$ (diese Annahme geben wir später wieder auf). Für das intuitive Verständnis ist es am einfachsten, wenn man sich eine lineare Transformation als Bewegung oder Verschiebung von Punkten vorstellt. Der Punkt $\mathbf{x}$ bewegt sich zum neuen Punkt $\mathbf{y}$. Das gilt natürlich nicht für einen Punkt, sondern für alle Punkte $\mathbf{x}\in {\mathbb{R}}^2.$

3.1 Zwei Dimensionen

Im Abschnitt 2.7.2 haben wir gesehen, dass sich jeder Vektor als Linearkombination der natürlichen Basisvektoren schreiben lässt, $$\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=x_1\left[\begin{array}{c}1\\ 0\end{array}\right]+x_2\left[\begin{array}{c}0\\ 1\end{array}\right].$$ Aus den zwei Bedingungen für lineare Transformationen folgt, dass $$f\left(\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\right)=x_{1}f\left(\left[\begin{array}{c}1\\ 0\end{array}\right]\right)+x_{2}f\left(\left[\begin{array}{c}0\\ 1\end{array}\right]\right).$$ Mit anderen Worten: Um den neuen Punkt zu finden, an dem $\mathbf{x}$ nach der linearen Transformation landet, brauchen wir nur die beiden Punkte, an denen die natürlichen Basisvektoren landen. Die lineare Transformation ergibt sich dann als Linearkombination der transformierten Basisvektoren, wobei die beiden Skalare für die Linearkombination die gleichen sind wie vorher!

Das hat weitreichende Konsequenzen! Es bedeutet insbesondere, dass die lineare Transformation eindeutig beschrieben werden kann, indem wir festlegen, wohin sich die beiden Basisvektoren bewegen.

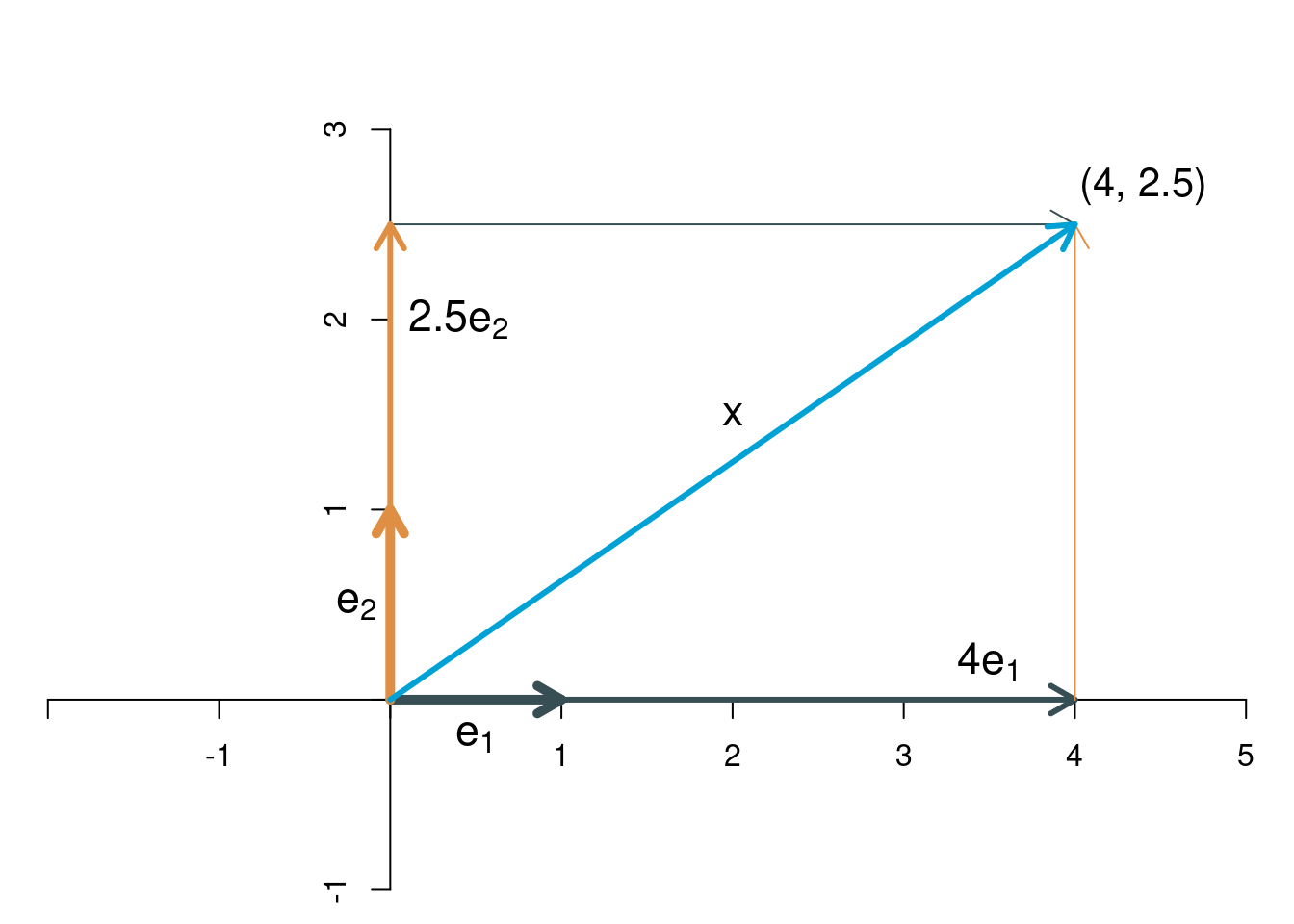
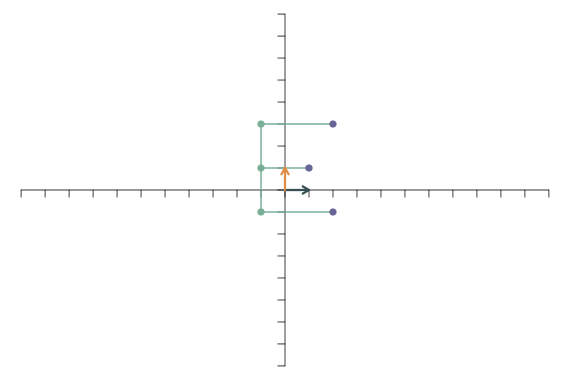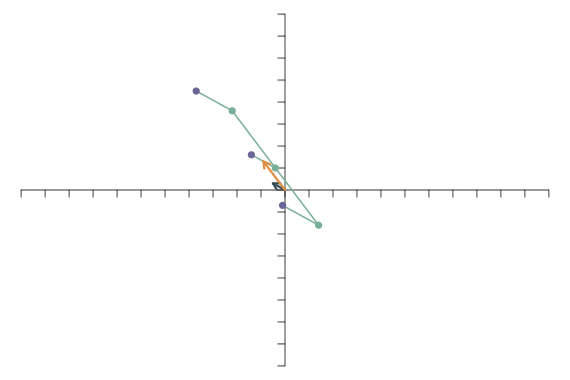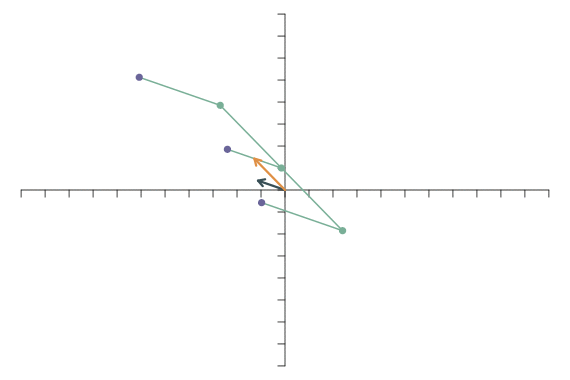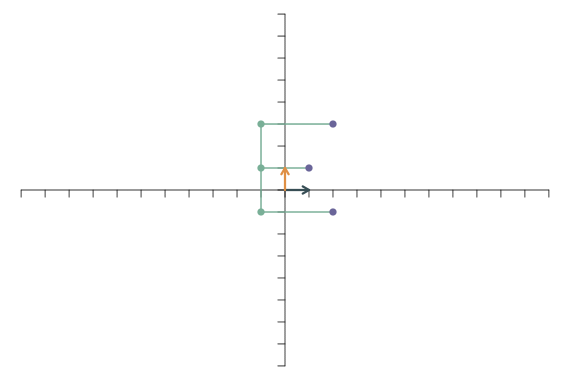
Diese Mechanik sehen wir uns an einem Beispiel genauer an. Der Vektor $$\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\left[\begin{array}{c}4\\ 2.5\end{array}\right]$$ kann geschrieben werden als $$4\left[\begin{array}{c}1\\ 0\end{array}\right]+2.5\left[\begin{array}{c}0\\ 1\end{array}\right].$$ Grafisch lässt sich das so darstellen:

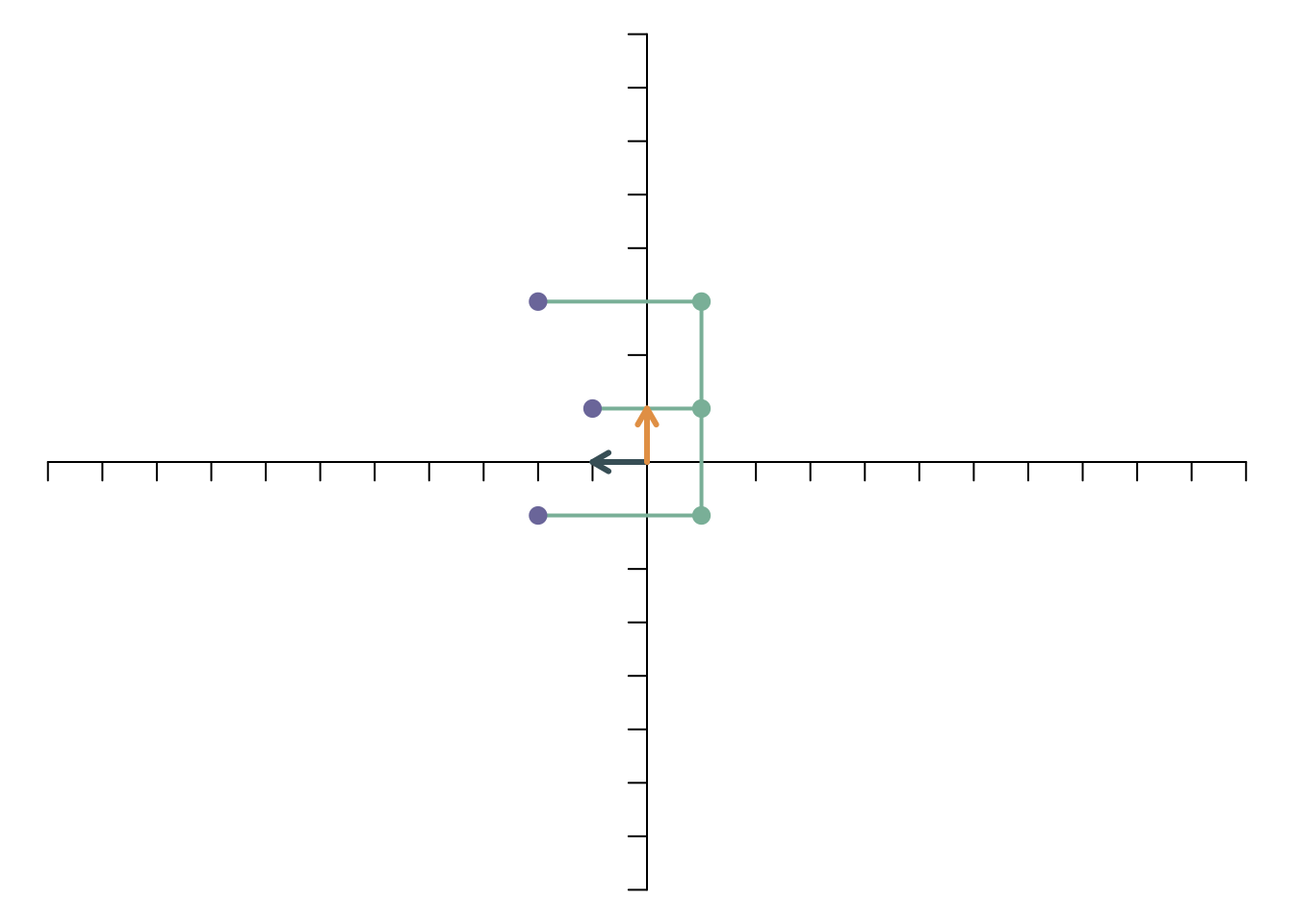
Nun wenden wir eine lineare Transformation auf die beiden Basisvektoren an. Das lässt sich gut vorstellen als eine Bewegung der beiden Basisvektoren auf neue Positionen. Der erste Basisvektor soll auf dem Punkt $(2,1)$ landen, der zweite Basisvektor auf $(-1,1)$. Die transformierten Basisvektoren werden in dem folgenden Bild mit ${\mathbf{f}}_1$ und ${\mathbf{f}}_2$ bezeichnet.

Nun wenden wir eine lineare Transformation auf die beiden Basisvektoren an. Das lässt sich gut vorstellen als eine Bewegung der beiden Basisvektoren auf neue Positionen. Der erste Basisvektor soll auf dem Punkt $(2,1)$ landen, der zweite Basisvektor auf $(-1,1)$. Die transformierten Basisvektoren werden in dem folgenden Bild mit ${\mathbf{f}}_1$ und ${\mathbf{f}}_2$ bezeichnet.

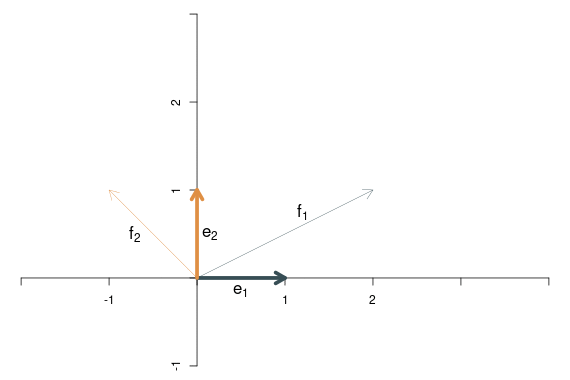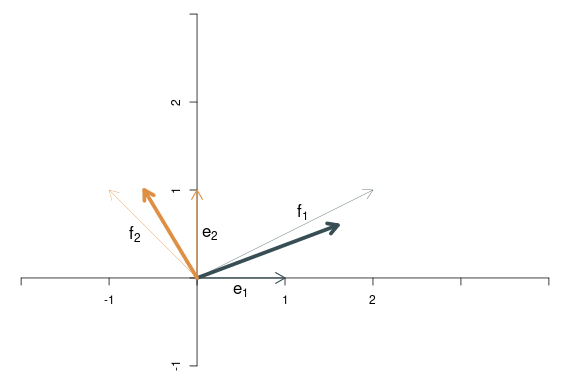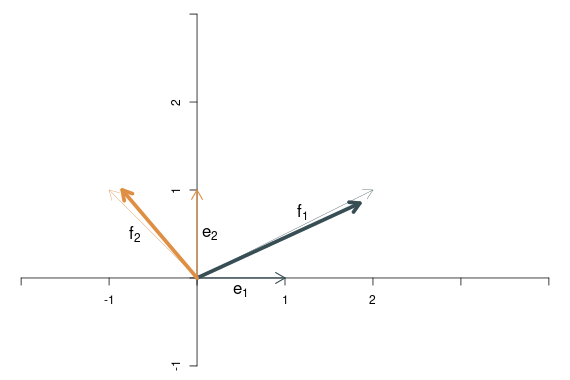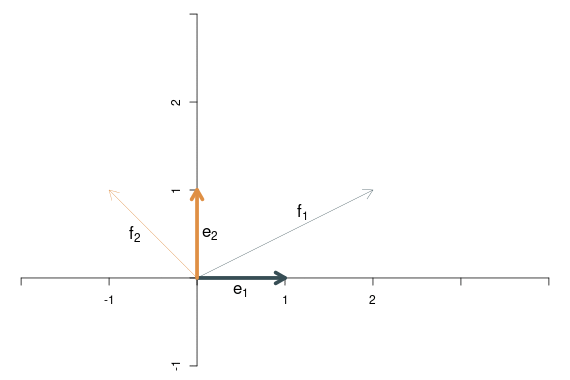
Der linear transformierte Punkt $\mathbf{y}=f(\mathbf{x})$ ergibt sich nun als Linearkombination der linear transformierten Basisvektoren, $x_1{\mathbf{f}}_1+x_2{\mathbf{f}}_2$, d.h. $$\left[\begin{array}{c}{y}_1\\ y_2\end{array}\right]=4\left[\begin{array}{c}2\\ 1\end{array}\right]+2.5\left[\begin{array}{c}-1\\ 1\end{array}\right]=\left[\begin{array}{c}5.5\\ 6.5\end{array}\right]$$

Stellt man sich die lineare Transformation wiederum als Bewegung vor, dann sieht es so aus:

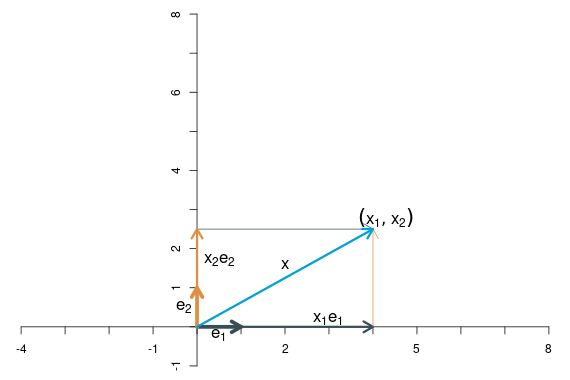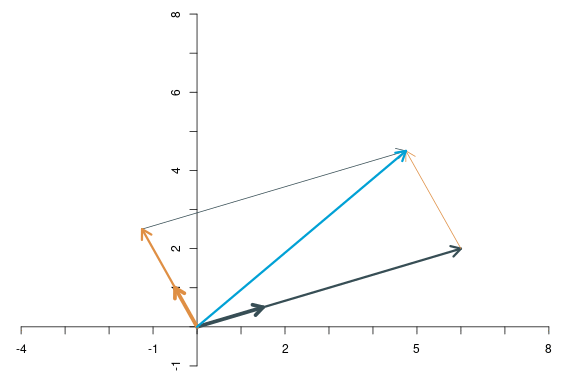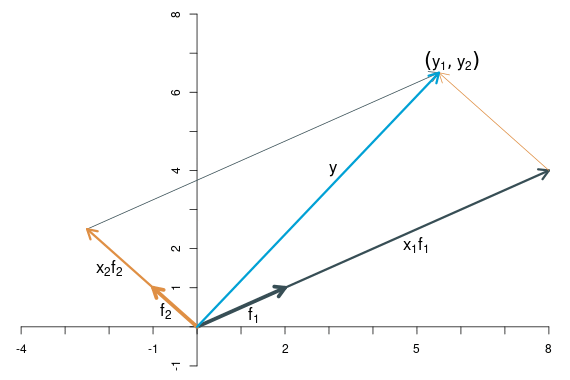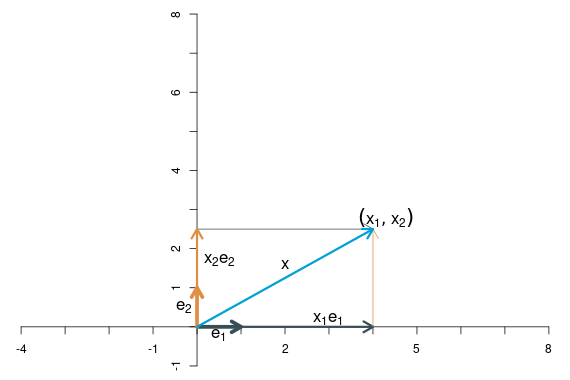
Bei der linearen Transformation bewegen sich jedoch nicht nur einzelne Punkte, sondern alle Punkte der Ebene werden auf diese Weise verschoben. Aus den beiden Eigenschaften $$\begin{array}{rl}f(\mathbf{x}+\mathbf{y})& =f(\mathbf{x})+f(\mathbf{y})\\ f(\lambda \mathbf{x})& =\lambda f(\mathbf{x})\end{array}$$ ergibt sich,

• dass der Nullpunkt unverändert bleibt,
• dass alle Geraden nach der Transformation weiterhin Geraden sind,
• dass Parallelen nach der Transformation immer noch parallel sind.

Winkel zwischen zwei Geraden ändern sich durch eine lineare Transformation hingegen im Allgemeinen (natürlich gibt es auch Transformationen, bei denen auch die Winkel gleich bleiben).

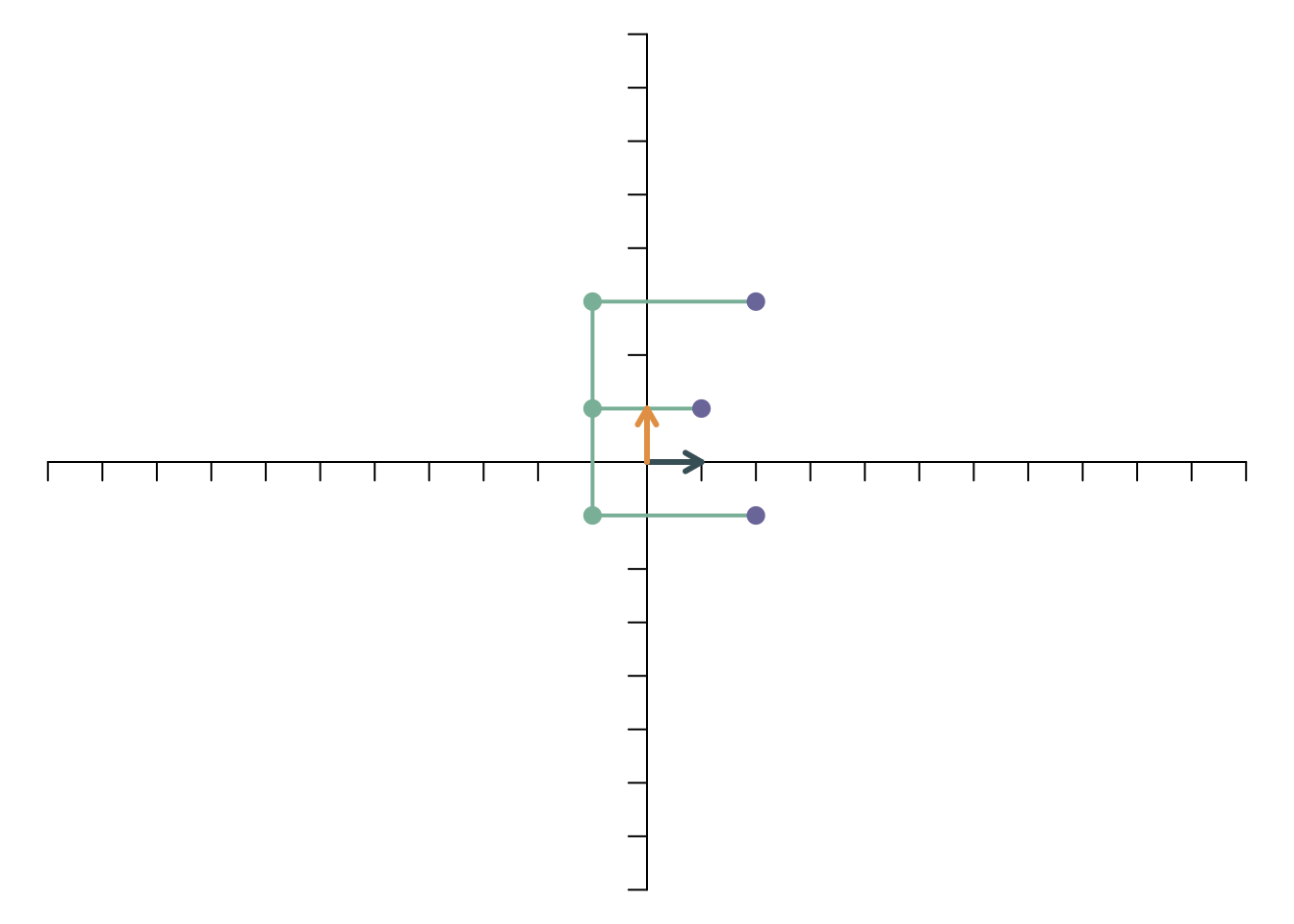
Die folgenden Abbildungen zeigen mehrere lineare Transformationen. Wir betrachten konkret sechs Punkte, die durch einige Verbindungslinien zu einem “E” werden, und untersuchen, wo diese Punkte nach der jeweiligen Transformation liegen. Außerdem sind zur Verdeutlichung die beiden Basisvektoren in die Abbildung eingefügt worden. Vor der Transformation sind die Punkte wie folgt positioniert (die unterschiedlichen Farben erleichtern es zu erkennen, ob die Transformation zu einer Spiegelung geführt hat).

Als erstes betrachten wir die lineare Transformation, bei der nur einer der beiden Basisvektoren gestreckt wird (in diesem Fall der für die y-Richtung), $${\mathbf{f}}_1=\left[\begin{array}{c}1\\ 0\end{array}\right],{\mathbf{f}}_2=\left[\begin{array}{c}0\\ 2\end{array}\right].$$ Das führt dazu, dass die Abbildung entlang der y-Richtung verlängert wird, Punkte auf der x-Achse bleiben unverändert.

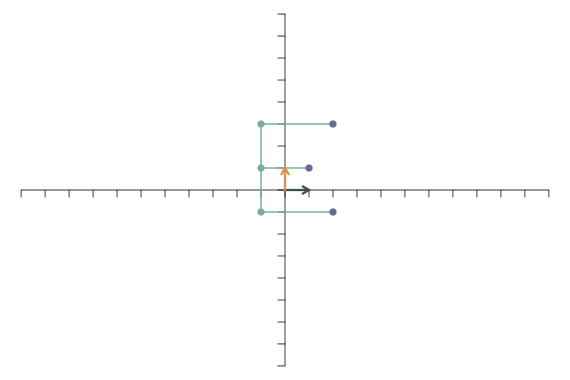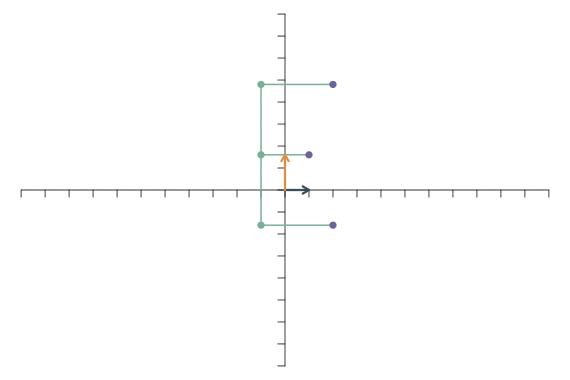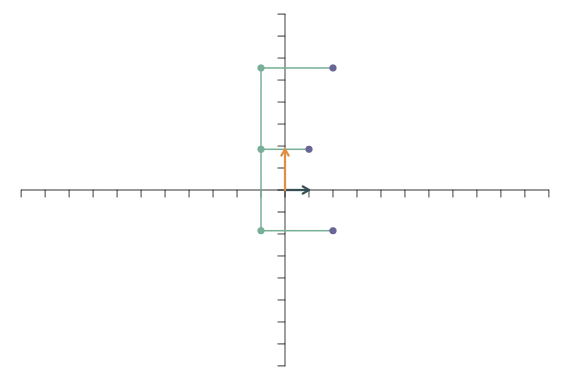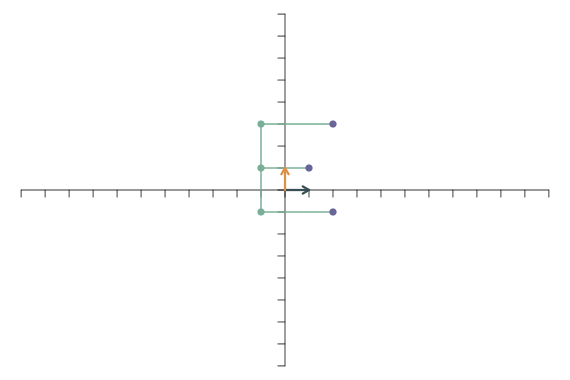
Analog dazu führt die lineare Transformation $${\mathbf{f}}_1=\left[\begin{array}{c}4\\ 0\end{array}\right],{\mathbf{f}}_2=\left[\begin{array}{c}0\\ 1\end{array}\right].$$ zu einer Streckung in x-Richtung:

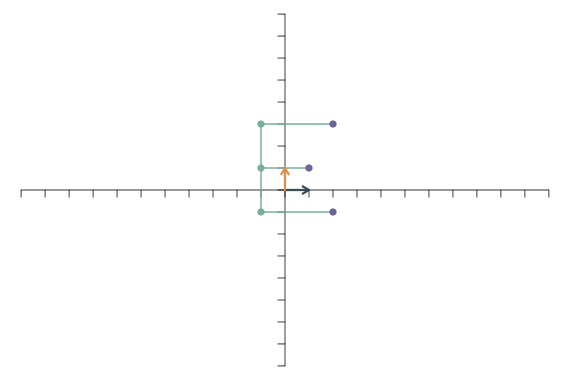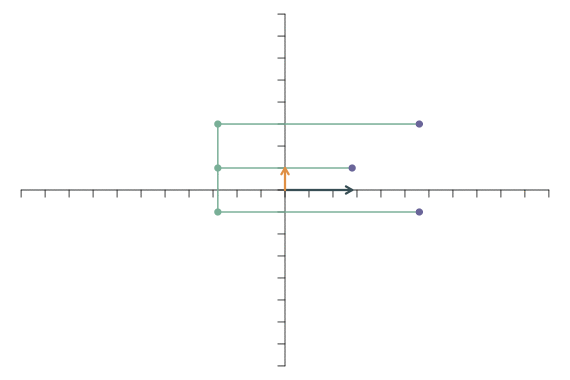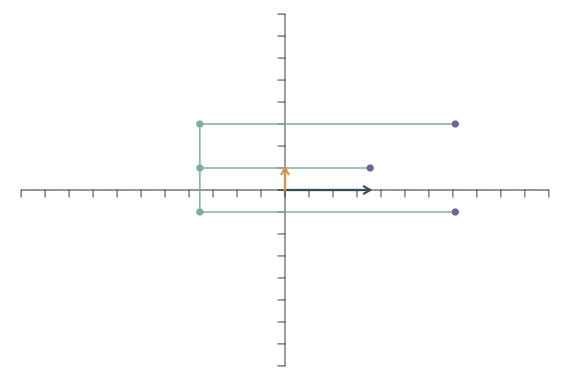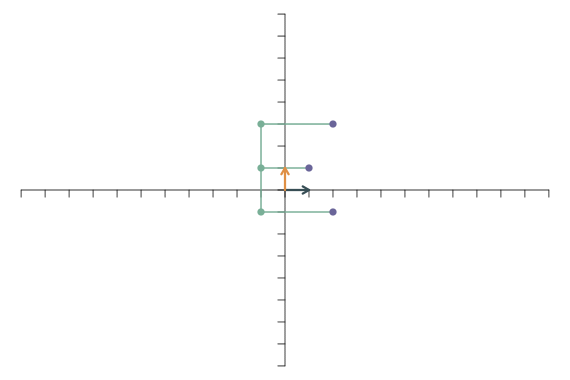
Die lineare Transformation $${\mathbf{f}}_1=\left[\begin{array}{c}5\\ 0\end{array}\right],{\mathbf{f}}_2=\left[\begin{array}{c}0\\ 0.5\end{array}\right].$$ kombiniert beides: In y-Richtung wird gestaucht (weil der Faktor 0.5 kleiner als 1 ist), in x-Richtung wird gestreckt.

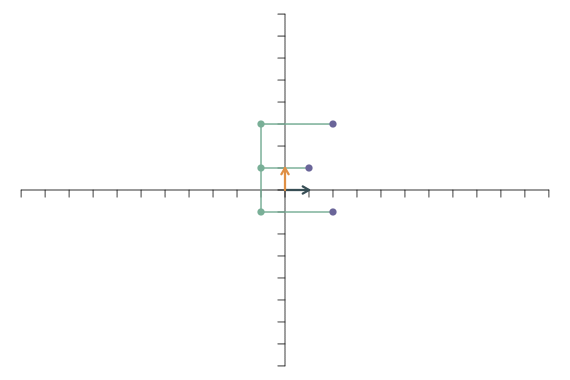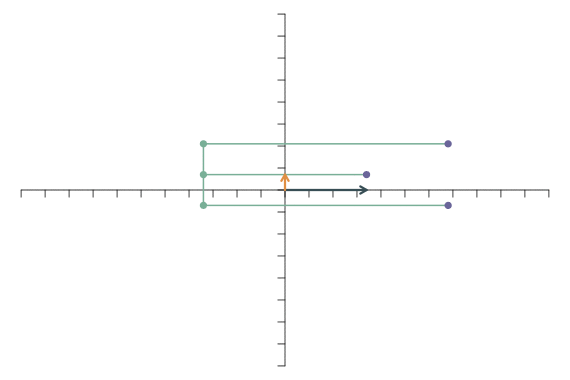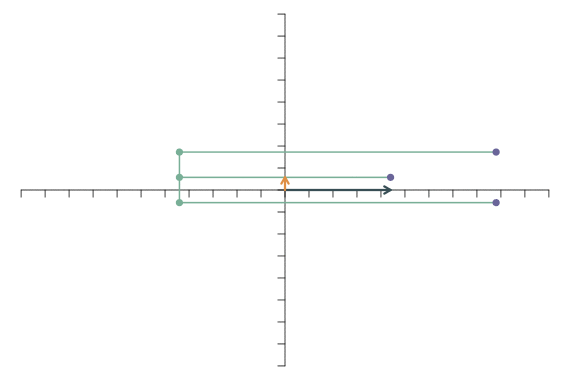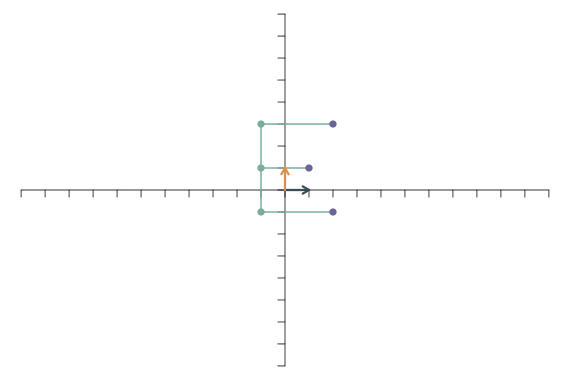
Eine interessante Klasse von linearen Transformationen sind Rotationen. Bei einer Rotation werden die beiden Basisvektoren um einen Winkel $\theta$ um den Nullpunkt herum gedreht. Sie werden weder verlängert noch verkürzt und der Winkel zwischen den beiden Basisvektoren bleibt ein rechter Winkel. Die transformierten Basisvektoren sind dann $${\mathbf{f}}_1=\left[\begin{array}{c}\cos (\theta )\\ \sin (\theta )\end{array}\right],{\mathbf{f}}_2=\left[\begin{array}{c}-\sin (\theta )\\ \cos (\theta )\end{array}\right].$$ Bei einer Drehung um $\theta =\pi /4$ (bzw. 45 Grad) ergibt sich folgende transformierte Abbildung:

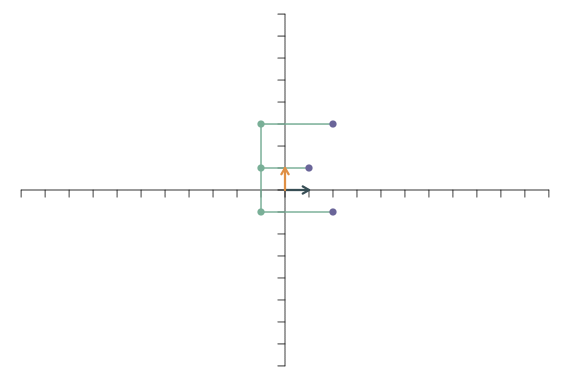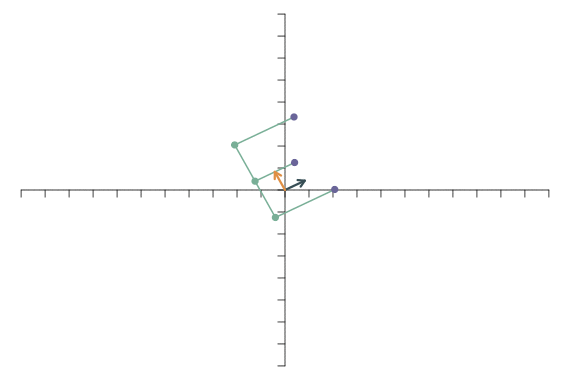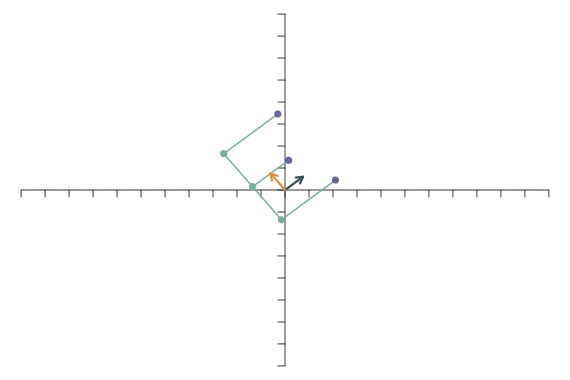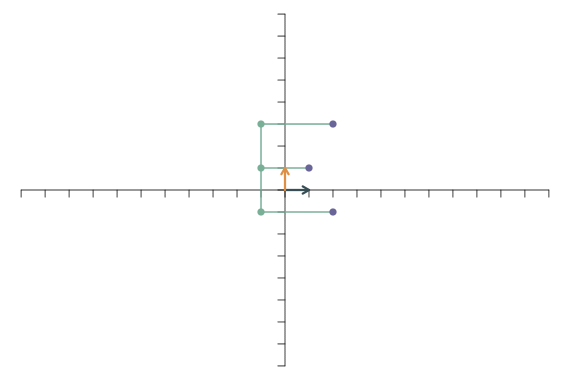
Die Multiplikation eines Basisvektors mit $-1$ führt zu einer Spiegelung. Wenn der erste Basisvektor nicht mehr nach rechts, sondern nach links zeigt, werden die Punkte an der y-Achse gespiegelt: $${\mathbf{f}}_1=\left[\begin{array}{c}-1\\ 0\end{array}\right],{\mathbf{f}}_2=\left[\begin{array}{c}0\\ 1\end{array}\right].$$

Das zugehörige Bild sieht so aus:

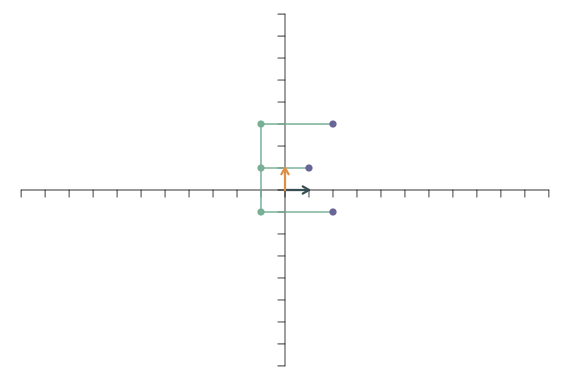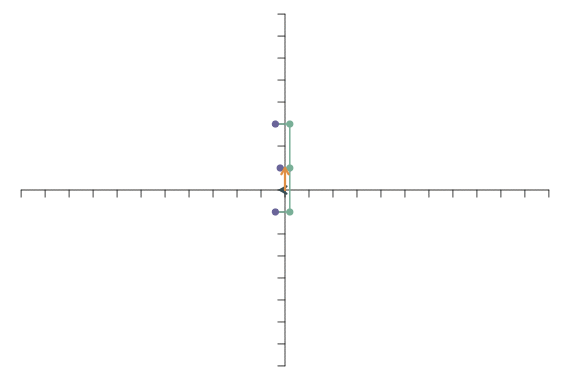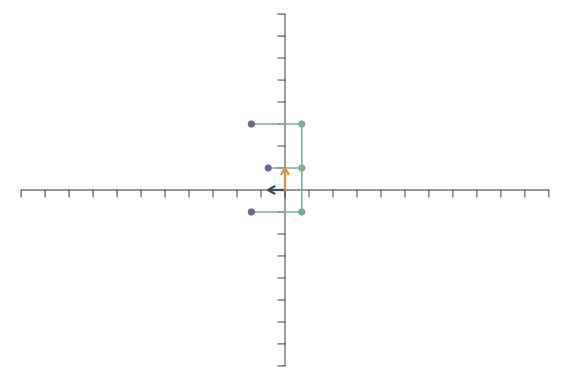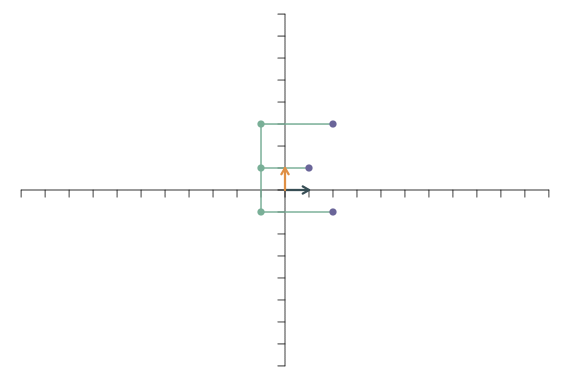
Als letztes Beispiel betrachten wir die lineare Transformation $${\mathbf{f}}_1=\left[\begin{array}{c}-1.5\\ 0.5\end{array}\right],{\mathbf{f}}_2=\left[\begin{array}{c}-1.5\\ 1.5\end{array}\right].$$ Die Transformation des ersten Basisvektors zeigt also nicht mehr nach rechts, sondern nach links und ein wenig nach oben. Der zweite Basisvektor zeigt nicht mehr direkt nach oben, sondern nach oben links. Beide Vektoren sind etwas länger als vor der Transformation. Die resultierende Abbildung sieht so aus:

An allen Abbildungen erkennt man, dass Geraden nach einer linearen Transformation immer noch Geraden sind, denn die drei grünlichen Punkte auf der Längsseite des “E”s liegen in allen Beispielen weiterhin auf einer Geraden. Man erkennt ebenfalls, dass transformierte Paralellen parallel bleiben, denn die drei “Arme” des “E”s sind auf allen Abbildungen parallel zueinander. Schließlich wird deutlich, dass Winkel sich im Allgemeinen ändern. Die drei “Arme” sind nicht auf allen Abbildungen rechtwinklig zu der Linie, auf der die drei grünlichen Punkte liegen.

Wie sehen die neuen Koordinaten eines Punktes nach der linearen Transformation aus? Als Beispiel betrachten wir den Punkt $(x_1,x_2)$. Wie wir bereits gesehen haben, ergibt er sich als Linearkombination der natürlichen Basisvektoren, $$\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=x_1\left[\begin{array}{c}1\\ 0\end{array}\right]+x_2\left[\begin{array}{c}0\\ 1\end{array}\right].$$

Die neuen Koordinaten ergeben sich, indem man die natürlichen Basisvektoren durch die transformierten Basisvektoren ersetzt. Als Beispiel nehmen wie die letzte Transformation von oben, bei der die neuen Basisvektoren $${\mathbf{f}}_1=\left[\begin{array}{c}-1.5\\ 0.5\end{array}\right],{\mathbf{f}}_2=\left[\begin{array}{c}-1.5\\ 1.5\end{array}\right].$$ sind. Der linear transformierte Punkt $(x_1,x_2)$ wird also zu $$\begin{array}{rl}\left[\begin{array}{c}{y}_1\\ y_2\end{array}\right]& =x_1\left[\begin{array}{c}-1.5\\ 0.5\end{array}\right]+x_2\left[\begin{array}{c}-1.5\\ 1.5\end{array}\right]\\ & =\left[\begin{array}{c}-1.5x_1-1.5x_2\\ 0.5x_1+1.5x_2\end{array}\right].\end{array}$$ Das ganze lässt sich übersichtlicher darstellen, wenn man die neuen Basisvektoren in quadratischer Form, also als Matrix, anordnet. Matrizen werden wir im folgenden Kapitel ausführlich behandeln. $$\left[\begin{array}{c}{y}_1\\ y_2\end{array}\right]=\left[\begin{array}{cc}-1.5& -1.5\\ 0.5& 1.5\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right].$$ Um sich zu merken, wie man bei dieser Darstellungsweise die neuen Koordinaten bestimmt, ist folgendes allgemeines Schema hilfreich: $$\begin{array}{lc}& \left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\\ & \downarrow \\ \left[\begin{array}{cc}a& c\\ b& d\end{array}\right]\begin{array}{c}⟶\\ ⟶\end{array}& \begin{array}{c}a{x}_1+c{x}_2\\ b{x}_1+d{x}_2\end{array}\end{array}$$

3.2 Verkettung

Nach der linearen Transformation des Vektors bzw. Punkts $(x_1,x_2)$ erhält man als Resultat den neuen Punkt $(y_1,y_2)$. Führt man nun eine zweite lineare Transformation durch, dann wird der Punkt $(y_1,y_2)$ transformiert und ergibt den neuen Punkt $(z_1,z_2)$.

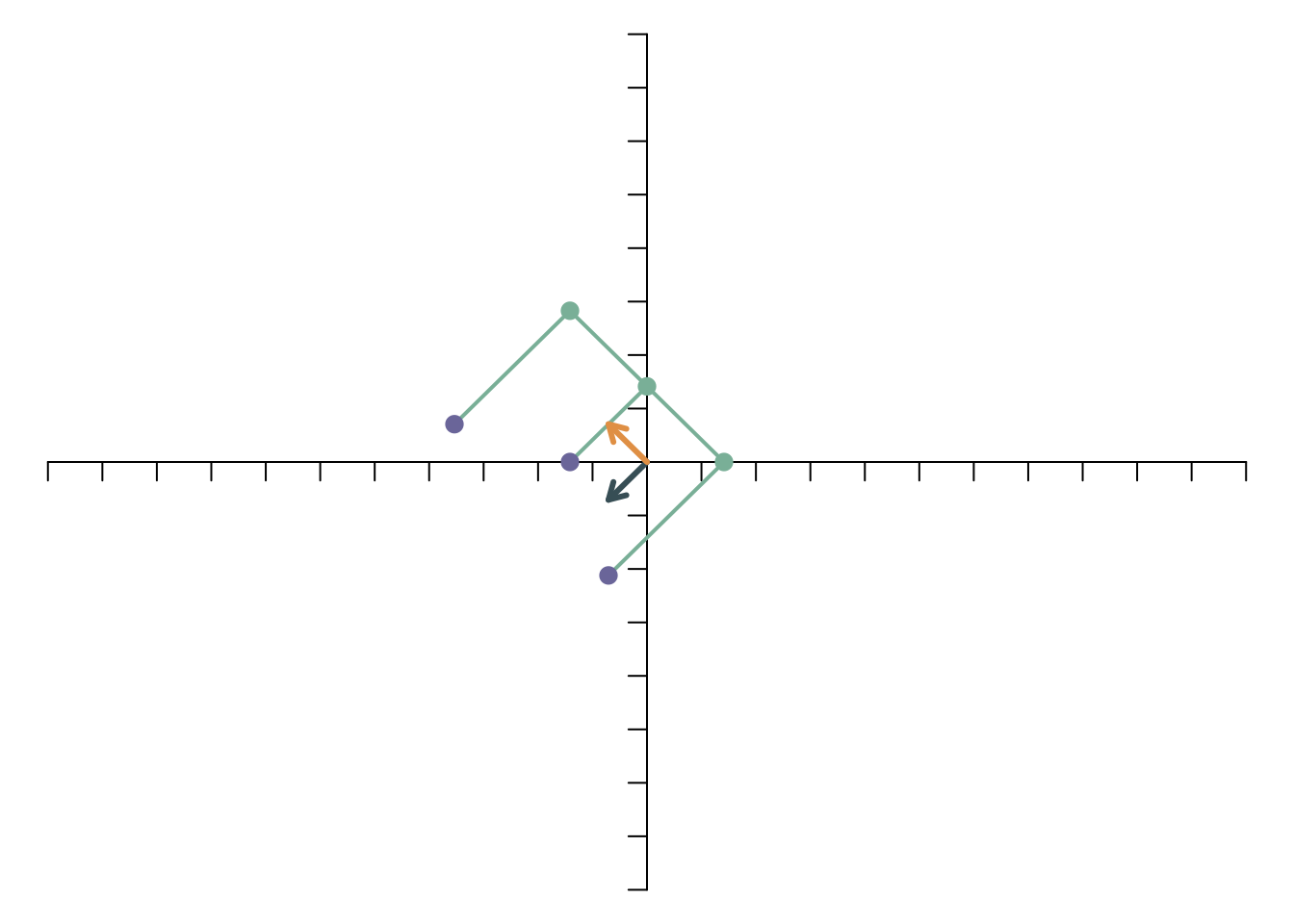
Um das an einem einfachen Beispiel zu veranschaulichen, betrachten wir noch einmal die Spiegelung an der y-Achse (in Matrixnotation) $$\left[\begin{array}{c}{y}_1\\ y_2\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right].$$ Angewendet auf die Punkte des “E”s erhält man dieses Ergebnis der linearen Transformation (wie wir weiter oben schon gesehen haben):

Nun wenden wir auf die transformierten Punkte eine zweite lineare Transformation an, und zwar als Beispiel die Rotation um 45 Grad gegen den Uhrzeigersinn.

Wenn man das “E” zuerst rotiert und anschließend spiegelt, erhält man als Abbildung

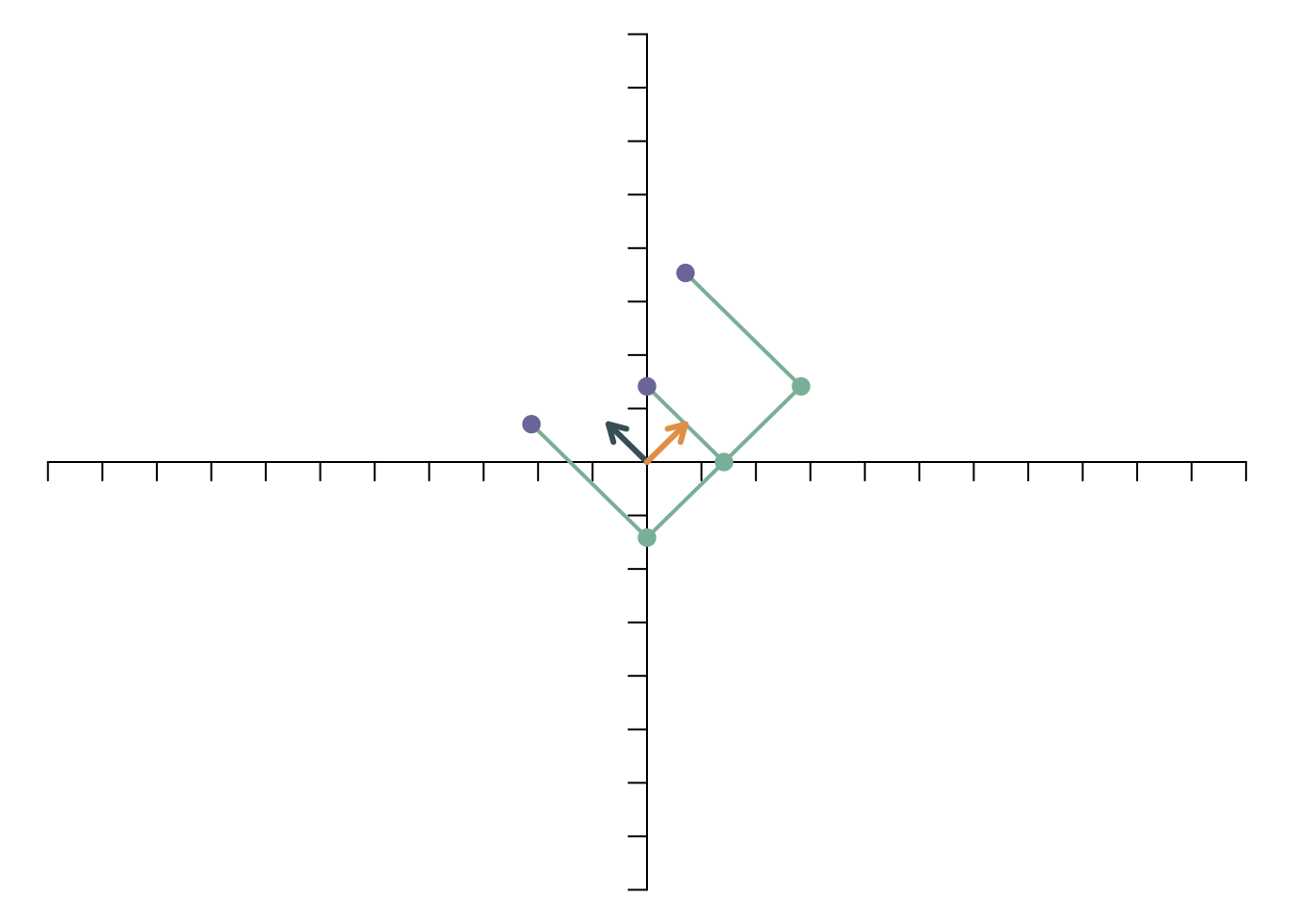
Die beiden Abbildung sind offensichtlich nicht gleich. Die Reihenfolge der linearen Transformationen spielt also eine wichtige Rolle. Sie sind nicht kommutativ.

Außerdem wird deutlich, dass man mit einer zweiten linearen Transformation den Effekt der ersten Transformation rückgängig machen könnte. Wie man diese “inverse” Transformation findet, werden wir später in Abschnitt 5.5 sehen.

3.3 Lineare Abhängigkeit

Bisher sind wir stillschweigend davon ausgegangen, dass die beiden transformierten Basisvektoren ${\mathbf{f}}_1$ und ${\mathbf{f}}_2$ linear unabhängig sind, also nicht genau in die gleiche Richtung zeigen. Was passiert, wenn ${\mathbf{f}}_1$ und ${\mathbf{f}}_2$ linear abhängig sind?

Zunächst schauen wir uns an, was mit dem “E” (aus den Bespielen von oben) passiert, wenn die beiden Basisvektoren nach der linearen Transformation in die gleich Richtung zeigen. Als ${\mathbf{f}}_1$ und ${\mathbf{f}}_2$ setzen wir $${\mathbf{f}}_1=\left[\begin{array}{c}1\\ 0.5\end{array}\right]{\mathbf{f}}_2=\left[\begin{array}{c}2\\ 1\end{array}\right].$$ Die lineare Transformation läuft wie folgt ab:

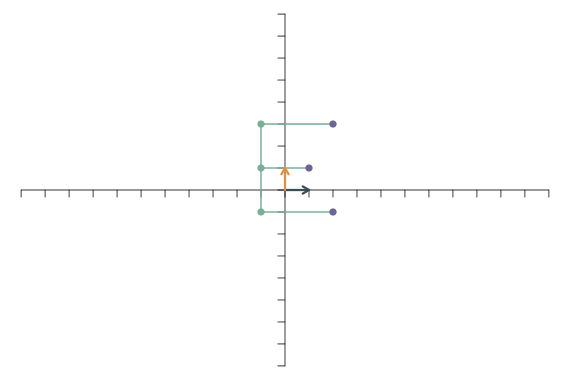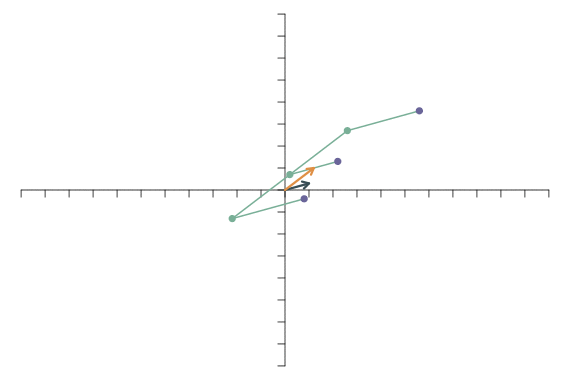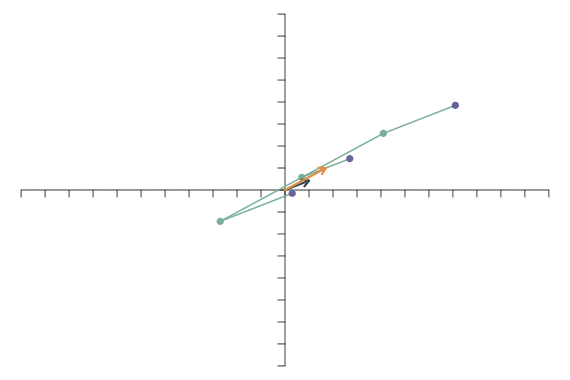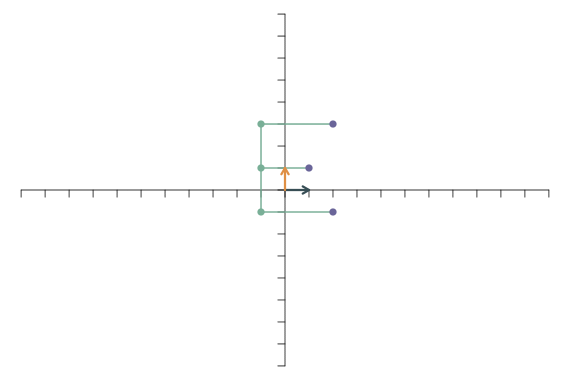
Alle Punkte liegen auf einer Geraden! Die Abbildung liegt also nicht mehr im zweidimensionalen Raum, sondern hat nur noch eine Dimension. Ein solcher Dimensionsverlust tritt auf, wenn die transformierten Basisvektoren nicht mehr linear unabhängig sind. Nach einem Dimensionsverlust kann man die lineare Transformation nicht mehr durch eine andere (inverse) lineare Transformation rückgängig machen.

3.4 Drei Dimensionen

Im dreidimensionalen Raum werden lineare Transformationen auf die gleiche Weise durchgeführt. Man untersucht, wo die drei natürlichen Basisvektoren nach der linearen Transformation liegen. Anschließend kann jeder Punkt $(x_1,x_2,x_3)$ als Linearkombination der drei transformierten Basisvektoren dargestellt werden. Auch die kompakte Darstellung durch eine Matrix ist möglich. Dazu schreibt man die drei transformierten Basisvektoren als Spalten nebeneinander.

Auch im dreidimensionalen Raum (und in noch höherdimensionalen Räumen) gilt, dass der Nullpunkt sich nicht verändert, dass Geraden nach der linearen Transformation immer noch Geraden sind, dass Parallelen weiterhin parallel zueinander liegen und dass Winkel sich im Allgemeinen verändern.

Was passiert im dreidimensionalen Fall, wenn die transformierten Basisvektoren linear abhängig sind? Hier gibt es mehr Möglichkeiten als bei nur zwei Dimensionen. Wir untersuchen zuerst den Fall, dass zwei transformierte Basisvektoren unabhängig sind, der dritte aber eine Linearkombination dieser beiden ist. Die folgende Abbildung ist eine Reproduktion aus Abschnitt 2.7.4.

Man erkennt, dass die lineare Transformation zu einer Verringerung der Dimension führt. Der ursprünglich dreidimensionale Raum wird auf zwei Dimensionen (nämlich die eingezeichnete Ebene) reduziert. Die Abbildung eines dreidimensionalen Objekts wäre also ein zweidimensionales Objekt.

Wenn die transformierten Basisvektoren alle drei in die gleiche Richtung zeigen (wenn sie also alle paarweise linear abhängig sind), dann wird der dreidimensionale Raum auf einen eindimensionalen Raum (nämlich die hellblaue Gerade) reduziert. Die transformierten Punkte eines dreidimensionalen Objekts würden alle auf dieser Geraden liegen.

Es gibt auch eine lineare Transformation, die in einen nulldimensionalen Raum abbildet (nämlich die Matrix, die nur aus Nullen besteht, so dass alle Punkte auf dem Koordinatenursprung landen), aber diesen Fall ignorieren wir, denn er ist nicht besonders interessant und spielt im Weiteren keine Rolle.

Matrizen können nicht nur als Repräsentation einer linearen Transformation aufgefasst werden. Sie dienen auch als Werkzeug, das große Datenmengen mit wenig Notationsaufwand erfasst. Auch zum Lösen von linearen Gleichungssystemen sind Matrizen hilfreich. Darauf gehen wir in den folgenden Abschnitten näher ein.