Chapter 4 Exercicio
- Considere os conjuntos de dados house price cenário 1 e cenário 2.
- Faça uma análise descritiva para ambos os conjuntos. O que se pode notar de diferente?
- Ajuste um modelo de regressão linear simples para ambos conjuntos no qual o valor seja explicado pela a área. Discuta.
- Se uma casa possuir 1300 ft², qual seria o preço esperado de acordo com o modelo do cenário 1? E de acordo com o modelo do cenário 2?
4.1 Análise descritiva - Cenário 1
Coletando os dados
library(readxl)
cenario1 = read_excel("dados/Data_HousePrice_Area.xlsx", sheet = "Cenario 1")
print(cenario1)## # A tibble: 10 × 2
## `Square Feet` `House Price`
## <dbl> <dbl>
## 1 1400 245
## 2 1600 312
## 3 1700 279
## 4 1875 308
## 5 1100 199
## 6 1550 219
## 7 2350 405
## 8 2450 324
## 9 1425 319
## 10 1700 255price=cenario1$`House Price`
square=cenario1$`Square Feet`
print(price)## [1] 245 312 279 308 199 219 405 324 319 255print(square)## [1] 1400 1600 1700 1875 1100 1550 2350 2450 1425 1700plot(price,square,main="Dispersão do Preço de Casa por Área")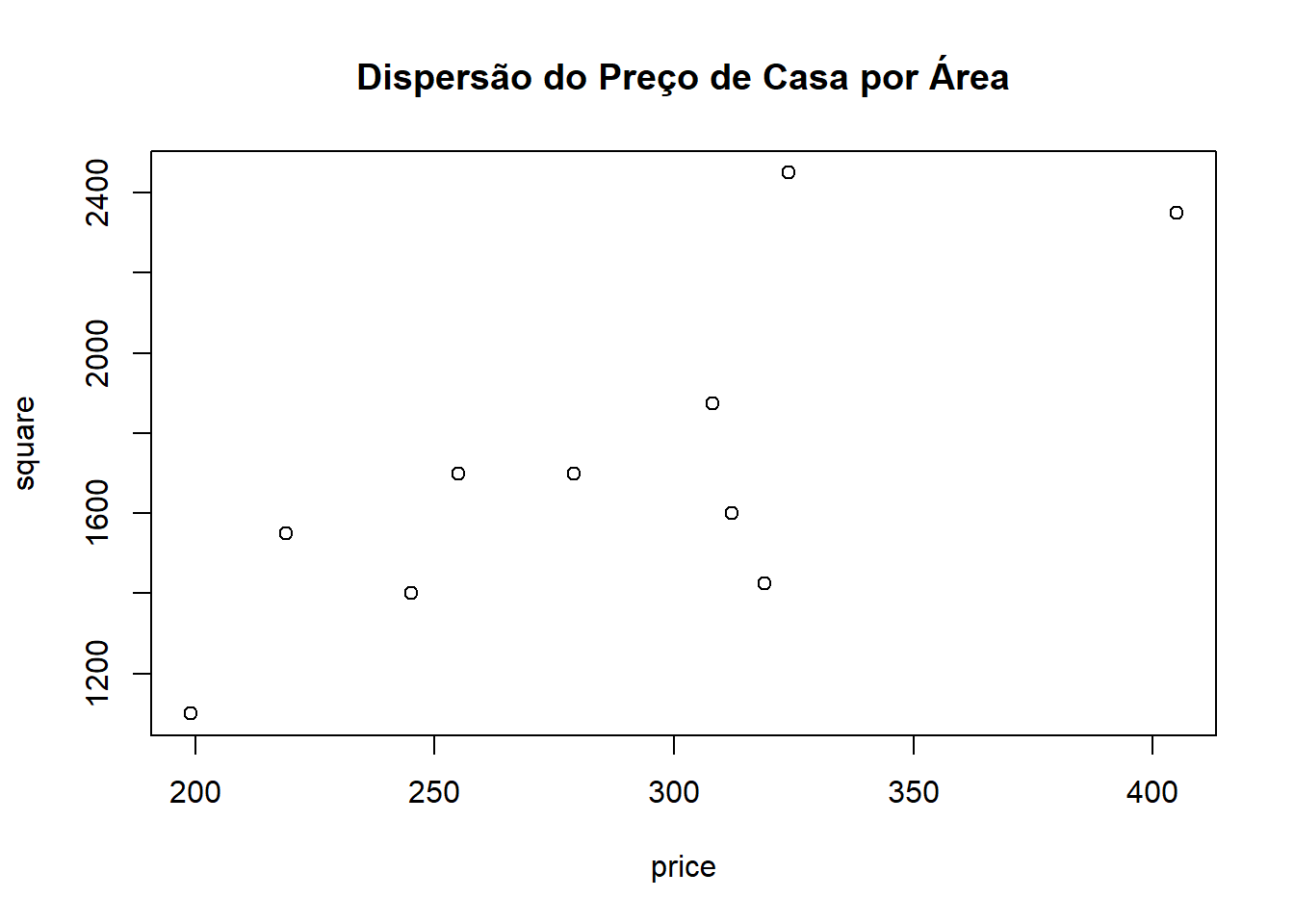
4.2 Análise descritiva - Cenario 2
Leitura da base de Dados
cenario2 = read_excel("dados/Data_HousePrice_Area.xlsx", sheet = "Cenario 2")
print(cenario2)## # A tibble: 10 × 2
## `Square Feet` `House Price`
## <dbl> <dbl>
## 1 1400 245
## 2 1800 312
## 3 1700 279
## 4 1875 308
## 5 1200 199
## 6 1480 219
## 7 2350 405
## 8 2100 324
## 9 2000 319
## 10 1700 255plot(cenario2,main="Dispersão do Preço de Casas por Area - Cenario 2")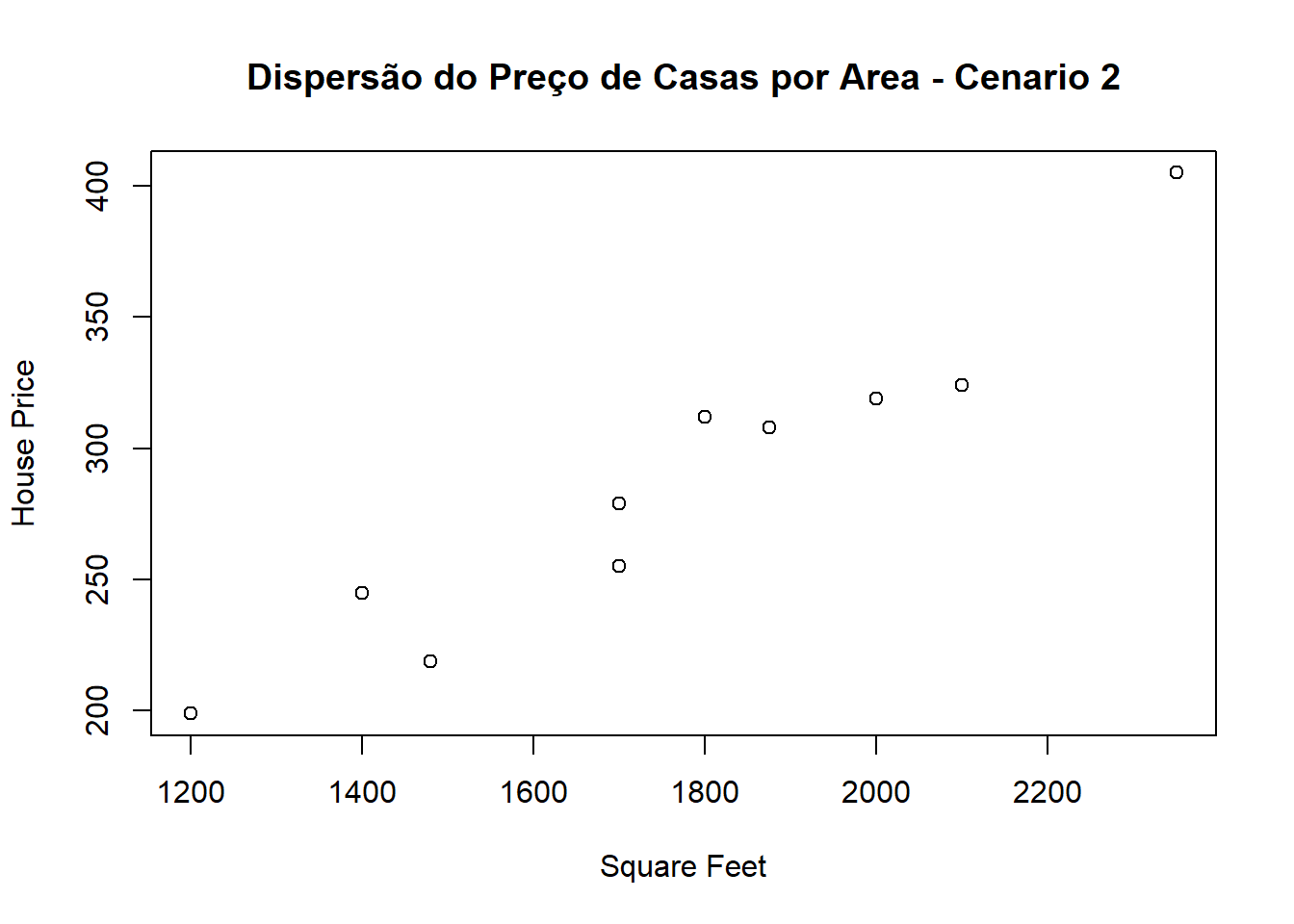
4.3 Gráfico de dispersão
Montagem do gráfico de dispersão para os dois cenários, comparando o preço da casa e sua área
par(mfrow = c(1,2))
plot(cenario1, col = 2, pch = 16, xlab = "Area", ylab = "Preco", main = "Cenário 1")
plot(cenario2, col = 3, pch = 17, xlab = "Area", ylab = "Preco", main = "Cenário 2")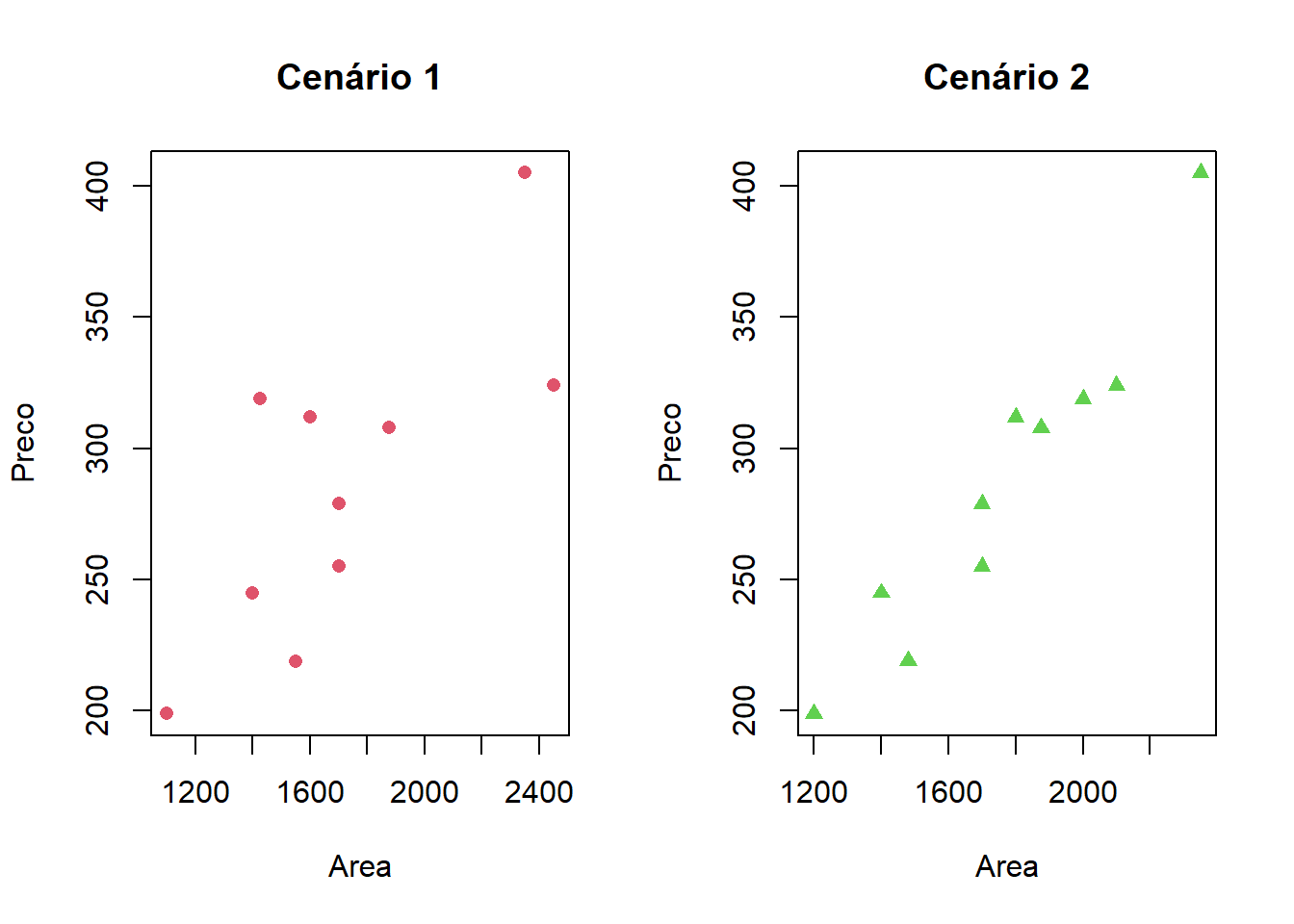
4.4 Modelo de Regresão Linear
md_Cenario1 = lm(`House Price` ~ `Square Feet`, data = cenario1)
summary(md_Cenario1)##
## Call:
## lm(formula = `House Price` ~ `Square Feet`, data = cenario1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -49.388 -27.388 -6.388 29.577 64.333
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 98.24833 58.03348 1.693 0.1289
## `Square Feet` 0.10977 0.03297 3.329 0.0104 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 41.33 on 8 degrees of freedom
## Multiple R-squared: 0.5808, Adjusted R-squared: 0.5284
## F-statistic: 11.08 on 1 and 8 DF, p-value: 0.01039md_Cenario2 = lm(`House Price` ~ `Square Feet`, data = cenario2)
summary(md_Cenario2)##
## Call:
## lm(formula = `House Price` ~ `Square Feet`, data = cenario2)
##
## Residuals:
## Min 1Q Median 3Q Max
## -21.323 -16.654 2.458 15.838 19.336
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -9.64509 30.46626 -0.317 0.76
## `Square Feet` 0.16822 0.01702 9.886 9.25e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 17.56 on 8 degrees of freedom
## Multiple R-squared: 0.9243, Adjusted R-squared: 0.9149
## F-statistic: 97.73 on 1 and 8 DF, p-value: 9.246e-064.4.1 Aplicando a reta de regresão no Grafico
par(mfrow = c(1,2))
plot(cenario1$`House Price` ~ cenario1$`Square Feet`, col = 2, pch = 16, xlab = "Area", ylab = "Preço", main = "Cenário 1")
abline(md_Cenario1, col = 1, lwd = 2)
plot(cenario2$`House Price` ~ cenario2$`Square Feet`, col = 3, pch = 17, xlab = "Area", ylab = "Preço", main = "Cenário 2")
abline(md_Cenario2, col = 1, lwd = 2)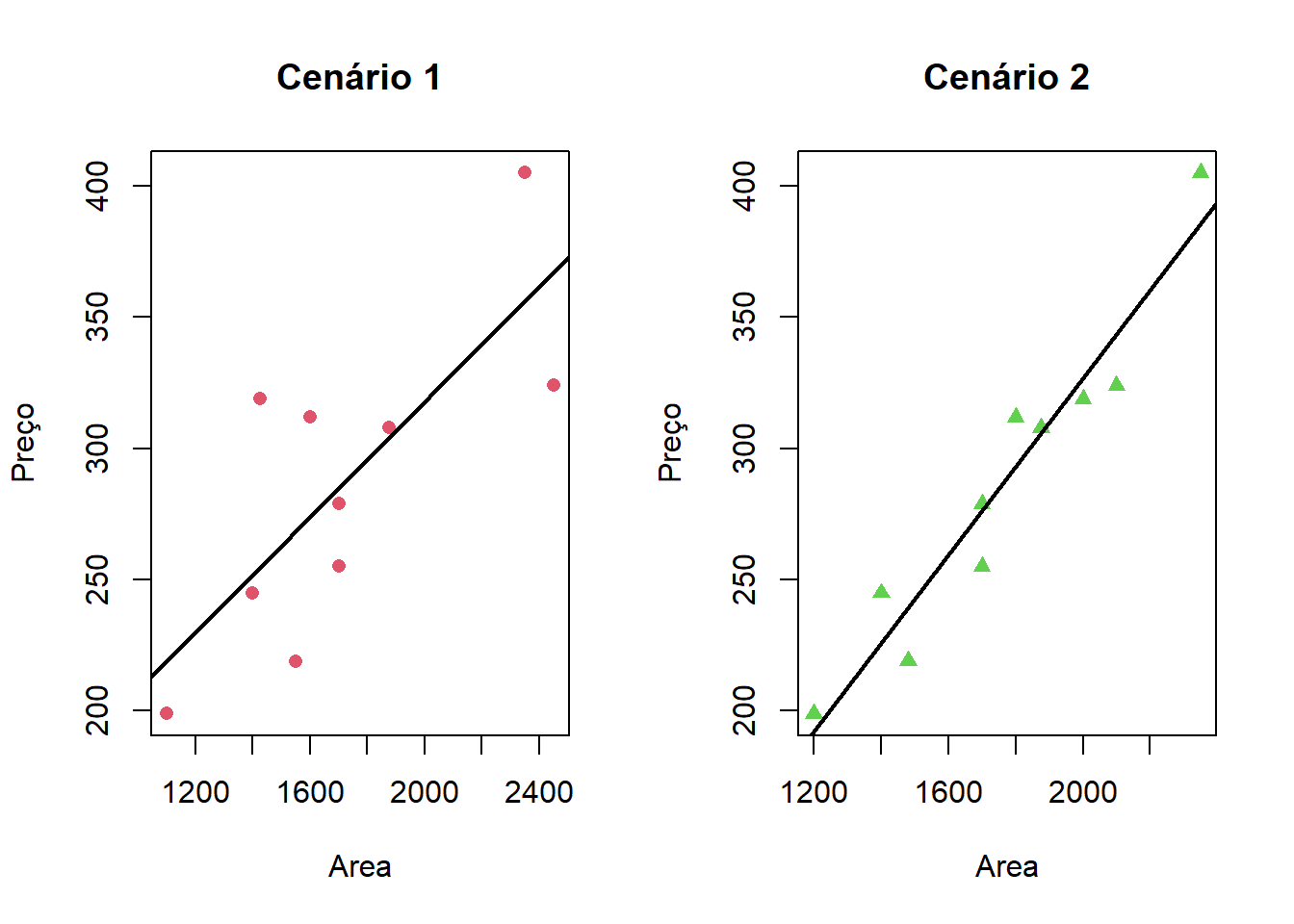
Se uma casa possuir 1300 ft², qual seria o preço esperado de acordo com o modelo do cenário 1?
Area = 1300
resA = round(md_Cenario1$coefficients[1] + Area * md_Cenario1$coefficients[2])
print( resA )## (Intercept)
## 241