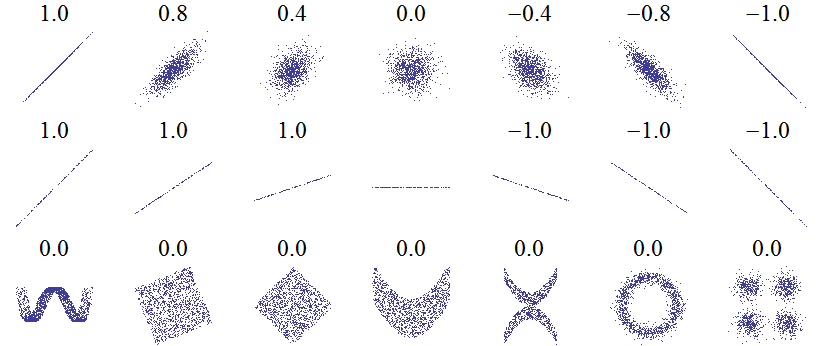
1 线性关系
在检验两个变量是否线性相关时先要检验P值1,P值小于0.05说明有95%的信心认为两个变量线性相关。如果P值大就算皮尔逊相关系数的绝对值再大也没有信心,很可能是误差2。但P值只是告诉我们存在线性相关关系,到底有多相关,数据点呈现一条清晰的直线还是一堆散乱的点是还是要靠皮尔逊相关系数。
确认完P值后即可看皮尔逊相关系数。该系数在-1到1之间。1表示图像是一条清晰的斜率为正的直线。系数大不大反映相关性是不是明显,跟斜率无关。
皮尔逊积矩相关系数 - 维基百科,自由的百科全书 (wikipedia.org)
1.1 求两个变量的相关系数cor()
创建一个名为dummy.df的Data,看一下它的图像
x <- c(-1.9006597, 0.8135983, -1.2121355, -2.0939632, 0.1068298, -0.4694056,
0.6290269, -1.7365614, -0.2018499, -0.6426151)
y <- c(-4.797071, 21.682396, 43.127952, 8.875319, 21.572073, 19.036167,
33.407646, 39.961134, 45.670589, -10.051775, -16.920633, 20.400339,
-12.357543, -43.7676, 32.171503, -6.046173, 27.774508, -28.002436,
18.830691, 8.72121)
dummy.df <- data.frame(x, y)
plot(dummy.df)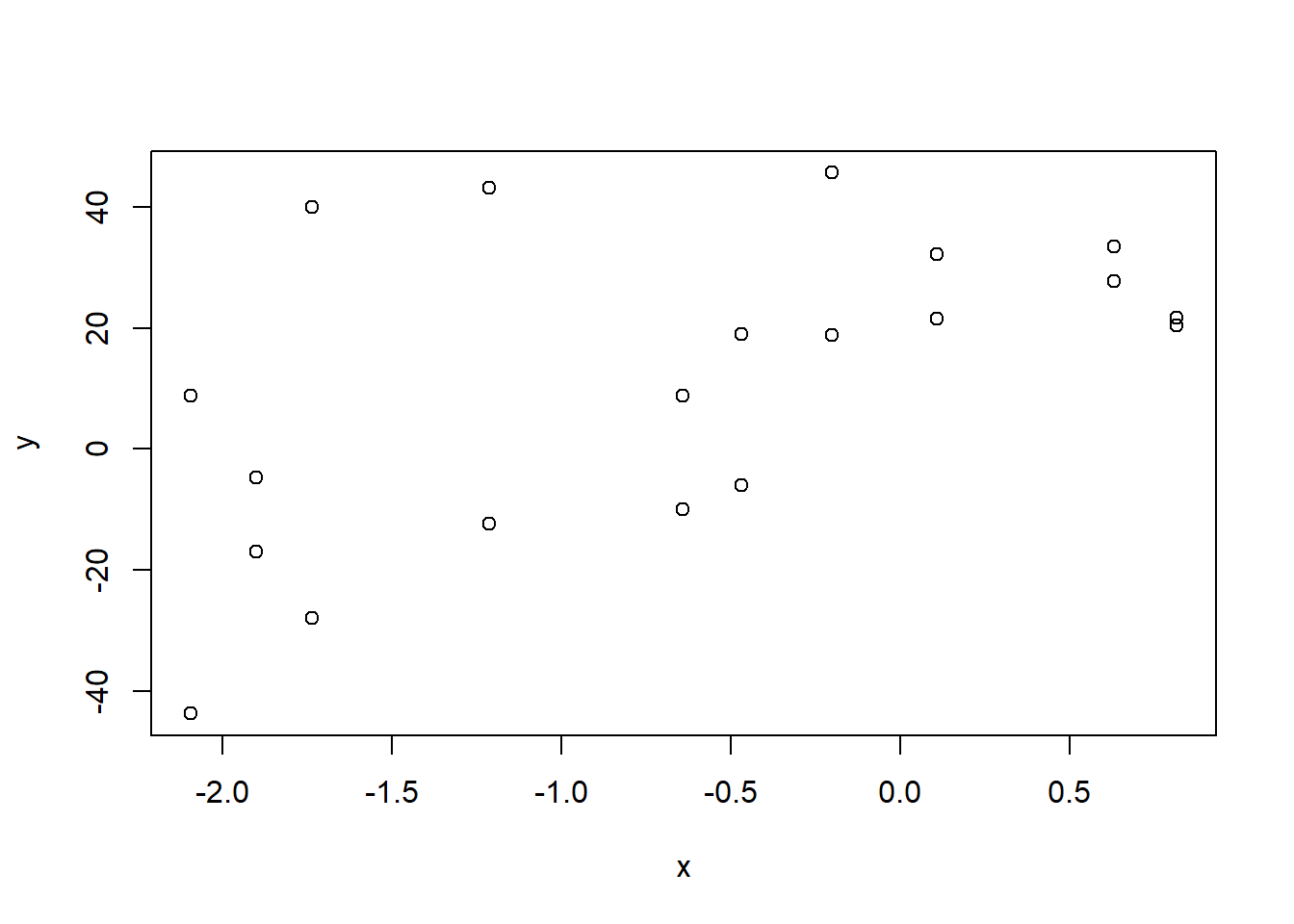
用cor()函数可以得到皮尔逊相关系数,即知道两个变量是否线性相关,这里x和y的相关系数0.5552626,即正线性相关。cor()默认:method = “pearson”
cor(dummy.df)## x y
## x 1.0000000 0.5552626
## y 0.5552626 1.00000001.2 做一条拟合数据的直线
lm()拟合直线,因为x 和 y 是data dummy.df里的变量,所以要写data=。如果是value则不需要。
dummy.lm <- lm(y ~ x, data = dummy.df)下面的20.05为截距和13.55为斜率,都是拟合直线的参数。表示 \(\widehat y=20.05+13.55x\)。
dummy.lm##
## Call:
## lm(formula = y ~ x, data = dummy.df)
##
## Coefficients:
## (Intercept) x
## 20.05 13.55用summary()同样可以看到Coefficients下的参数20.053和13,550。同时还可以看到P值为0.011048(第二行,第一行是截距的p值,不用关心),说明我们可以很自信地说x和y有线性关系。下面的Multiple R-squared:0.3083表示y有30.83%是可以用x解释的。
summary(dummy.lm)##
## Call:
## lm(formula = y ~ x, data = dummy.df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -35.448 -12.412 -0.366 6.675 43.438
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 20.053 5.705 3.515 0.00247 **
## x 13.550 4.784 2.833 0.01104 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 21.1 on 18 degrees of freedom
## Multiple R-squared: 0.3083, Adjusted R-squared: 0.2699
## F-statistic: 8.023 on 1 and 18 DF, p-value: 0.01104画拟合dummy.df图像的直线。abline只能画直线,不像line能画折线
plot(dummy.df)
abline(dummy.lm)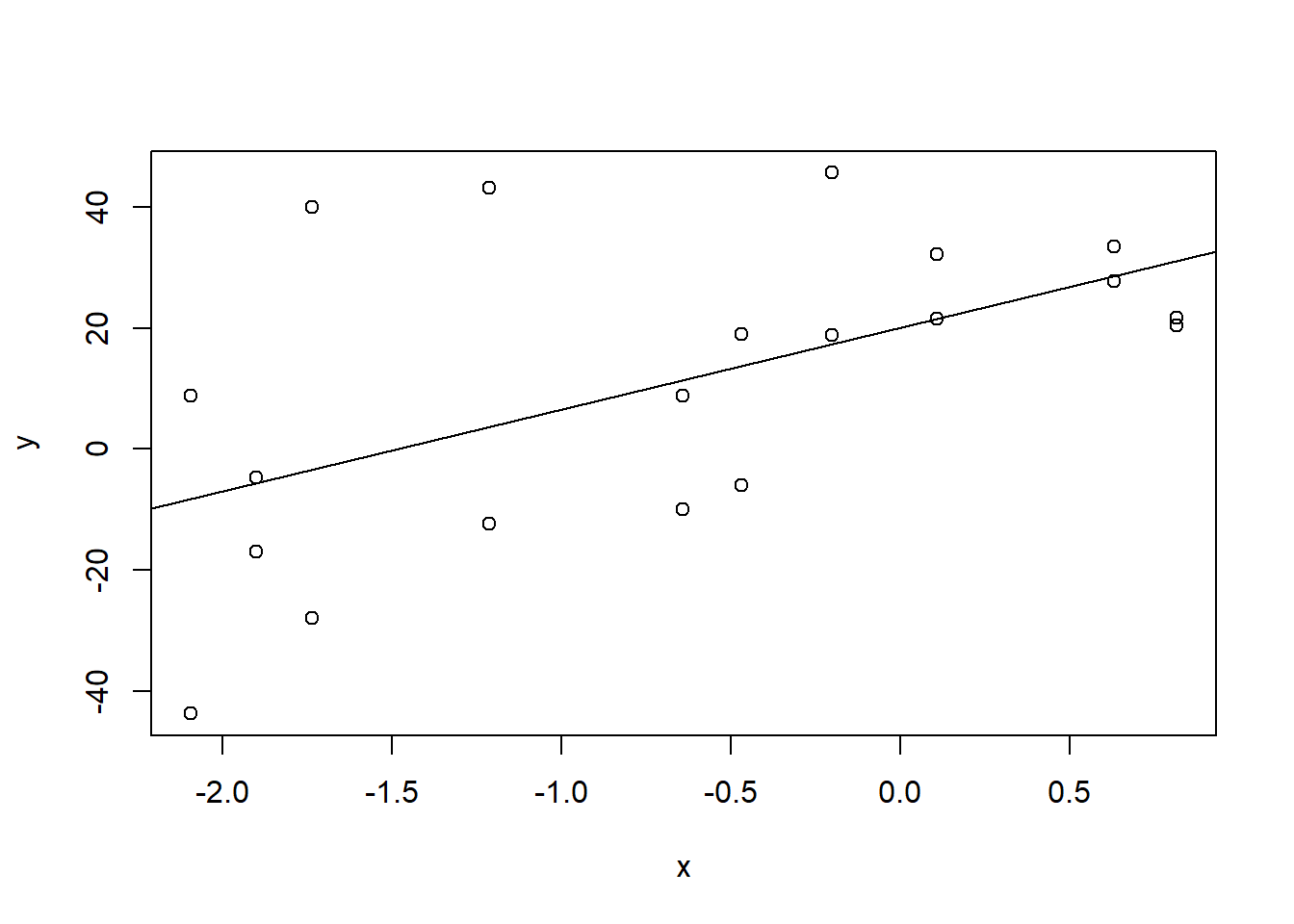
1.3 多因素线性回归
这里用到了LungCapData数据,下载地址
读取数据
library(readxl)
LungCapData <- read_excel("LungCapData.xls")看一眼数据,第一列是肺活量,后面分别是年龄,体重,是否吸烟,性别和是否剖腹产
head(LungCapData)## # A tibble: 6 x 6
## LungCap Age Height Smoke Gender Caesarean
## <dbl> <dbl> <dbl> <chr> <chr> <chr>
## 1 6.48 6 62.1 no male no
## 2 10.1 18 74.7 yes female no
## 3 9.55 16 69.7 no female yes
## 4 11.1 14 71 no male no
## 5 4.8 5 56.9 no male no
## 6 6.22 11 58.7 no female no建一个回归方程。LungCap~.表示把肺活量作为因变量,其他所有变量都作为自变量。用它们预测肺活量。
lm.mlt <- lm(LungCap ~ ., data = LungCapData)看一下这个回归方程。所有的p值都有星,表示那些年龄、体重之类都和肺活量有线性关系。Coefficients 最左边的 Estimate 为正是正相关,为负是负相关。在这里年龄增加,体重增加,或性别为男肺活量都会高,而抽烟和剖腹产的人肺活量小。
summary(lm.mlt)##
## Call:
## lm(formula = LungCap ~ ., data = LungCapData)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.3388 -0.7200 0.0444 0.7093 3.0172
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -11.32249 0.47097 -24.041 < 2e-16 ***
## Age 0.16053 0.01801 8.915 < 2e-16 ***
## Height 0.26411 0.01006 26.248 < 2e-16 ***
## Smokeyes -0.60956 0.12598 -4.839 1.60e-06 ***
## Gendermale 0.38701 0.07966 4.858 1.45e-06 ***
## Caesareanyes -0.21422 0.09074 -2.361 0.0185 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.02 on 719 degrees of freedom
## Multiple R-squared: 0.8542, Adjusted R-squared: 0.8532
## F-statistic: 842.8 on 5 and 719 DF, p-value: < 2.2e-16在lm.mlt这个模型中所有的变量都被用上了,但也有可能少用几个变量预测会更准。比如只用性别和体重去掉其他的因素。用模型的 AIC 值可以比较模型的好坏。这里的五个变量已经可以有很多种组合了。用 step() 函数可以自动比较所有的组合,选出最好的模型。结果告诉我现在的这个五自变量模型就是最好的。trace=F可以不显示中间的计算步骤。
step(lm.mlt, trace = F)##
## Call:
## lm(formula = LungCap ~ Age + Height + Smoke + Gender + Caesarean,
## data = LungCapData)
##
## Coefficients:
## (Intercept) Age Height Smokeyes Gendermale
## -11.3225 0.1605 0.2641 -0.6096 0.3870
## Caesareanyes
## -0.2142生成的这个模型可以直接赋给一个变量
lm.final <- step(lm.mlt, trace = F)