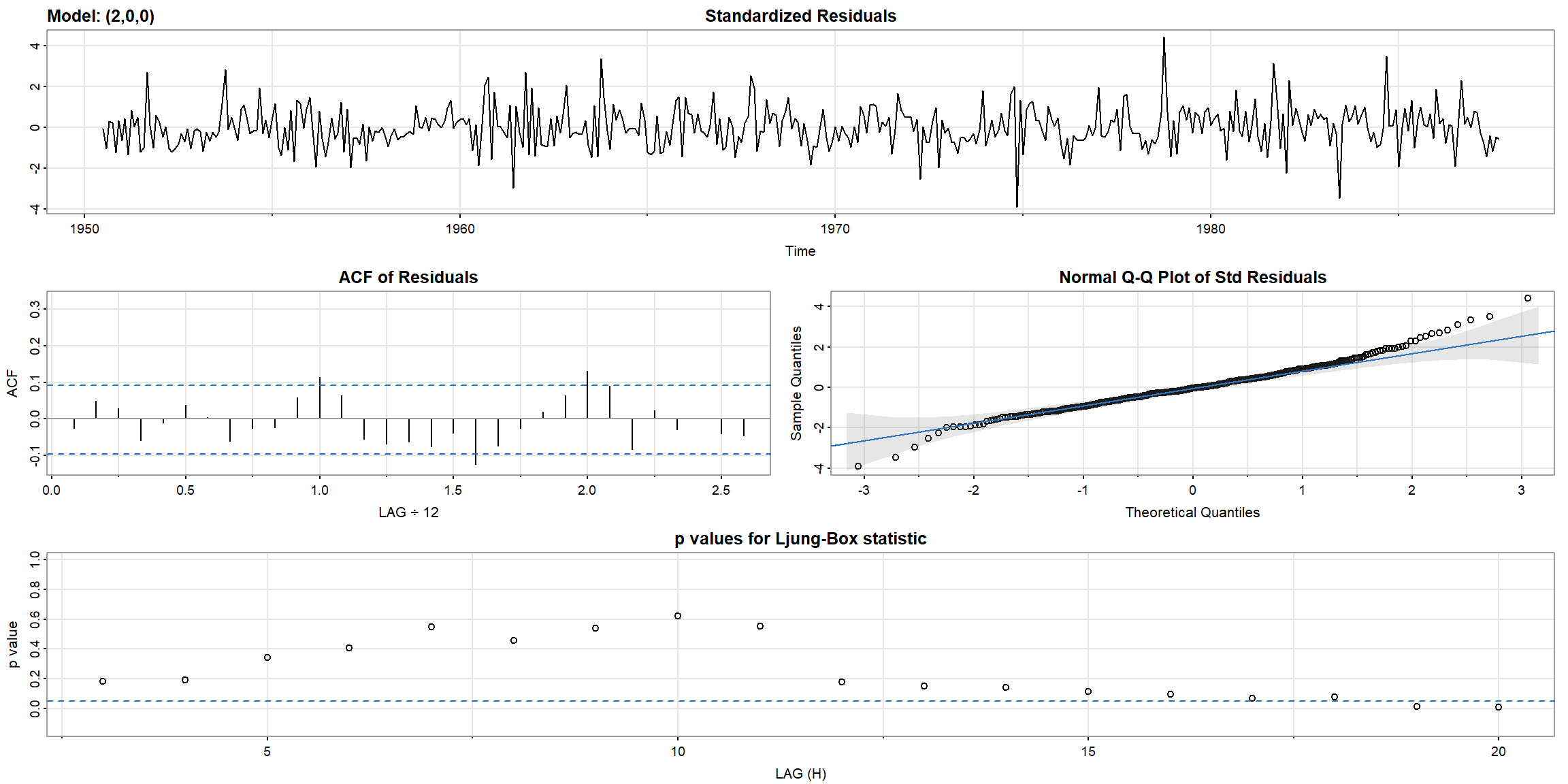
Sec 1 Example of Time Series Data

library(astsa)

1.1 Characteristics of Time Series

1.1.1 Practical data

判斷以下範例為何不是 (weakly) stationary

Example 1.1 (p.2)

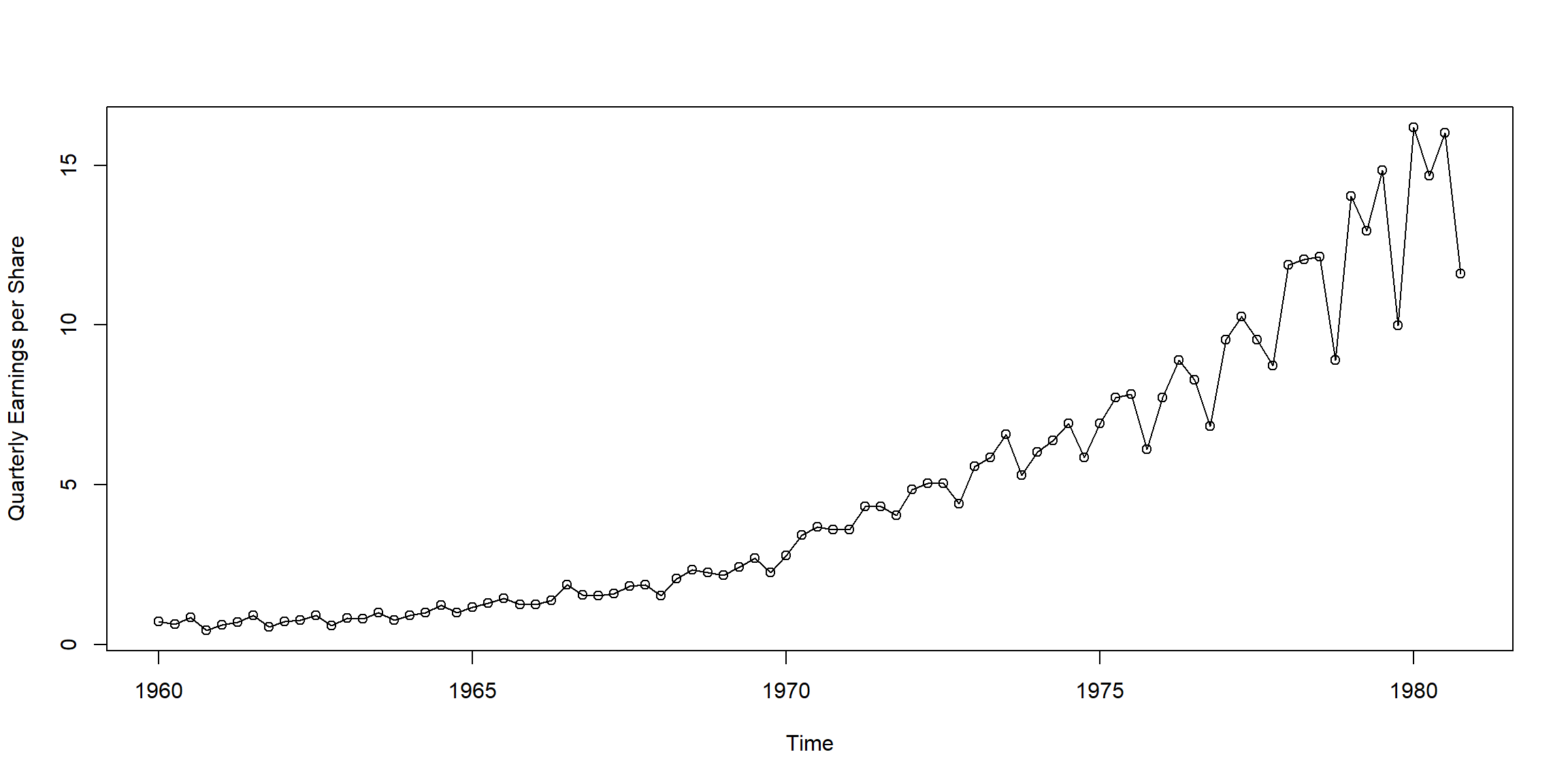
plot(jj, type="o", ylab="Quarterly Earnings per Share")




Example 1.2 (p.3)

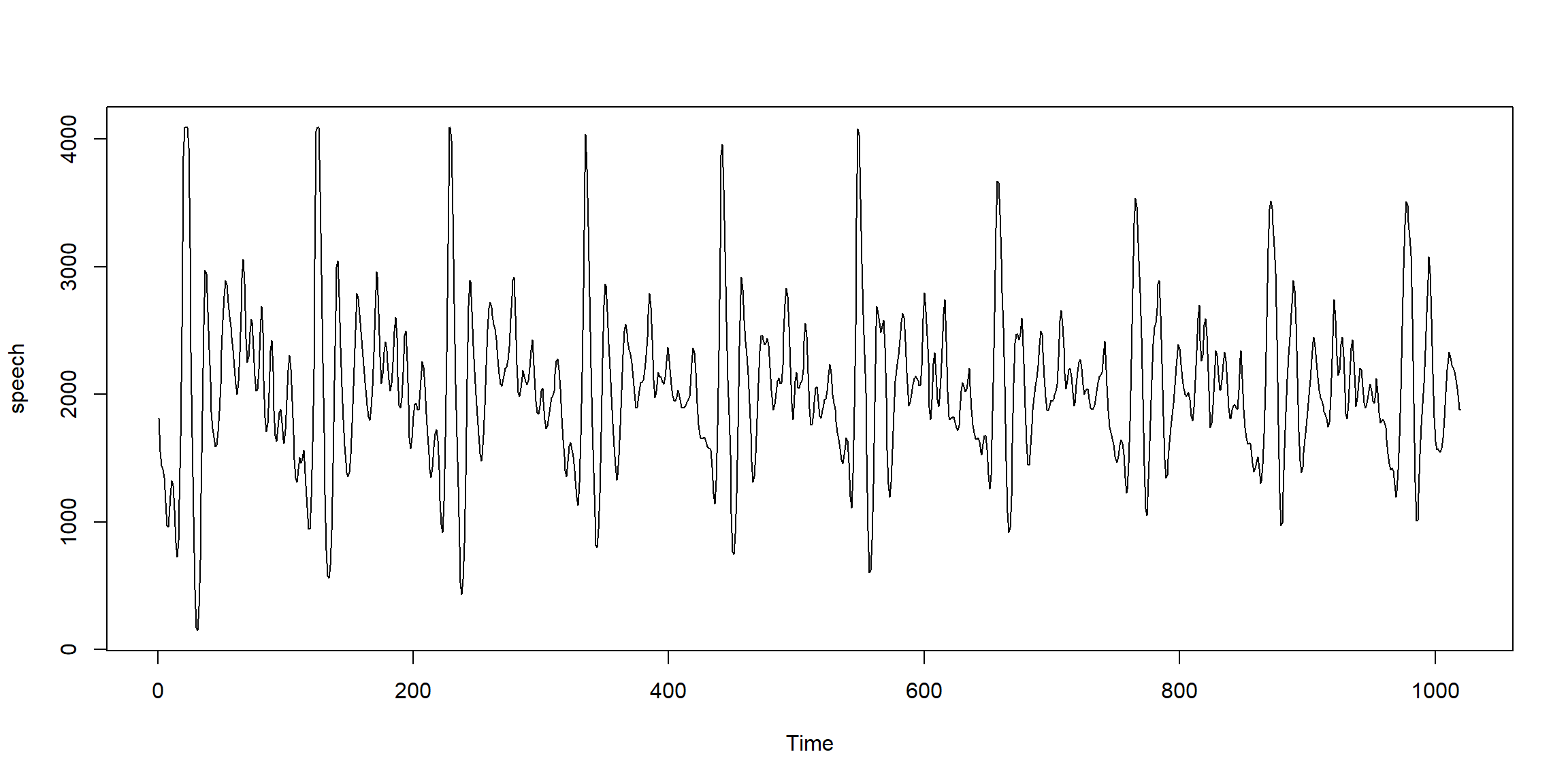
plot(globtemp, type="o", ylab="Global Temperature Deviations")




Example 1.3 (p.3) Voice record

plot(speech)




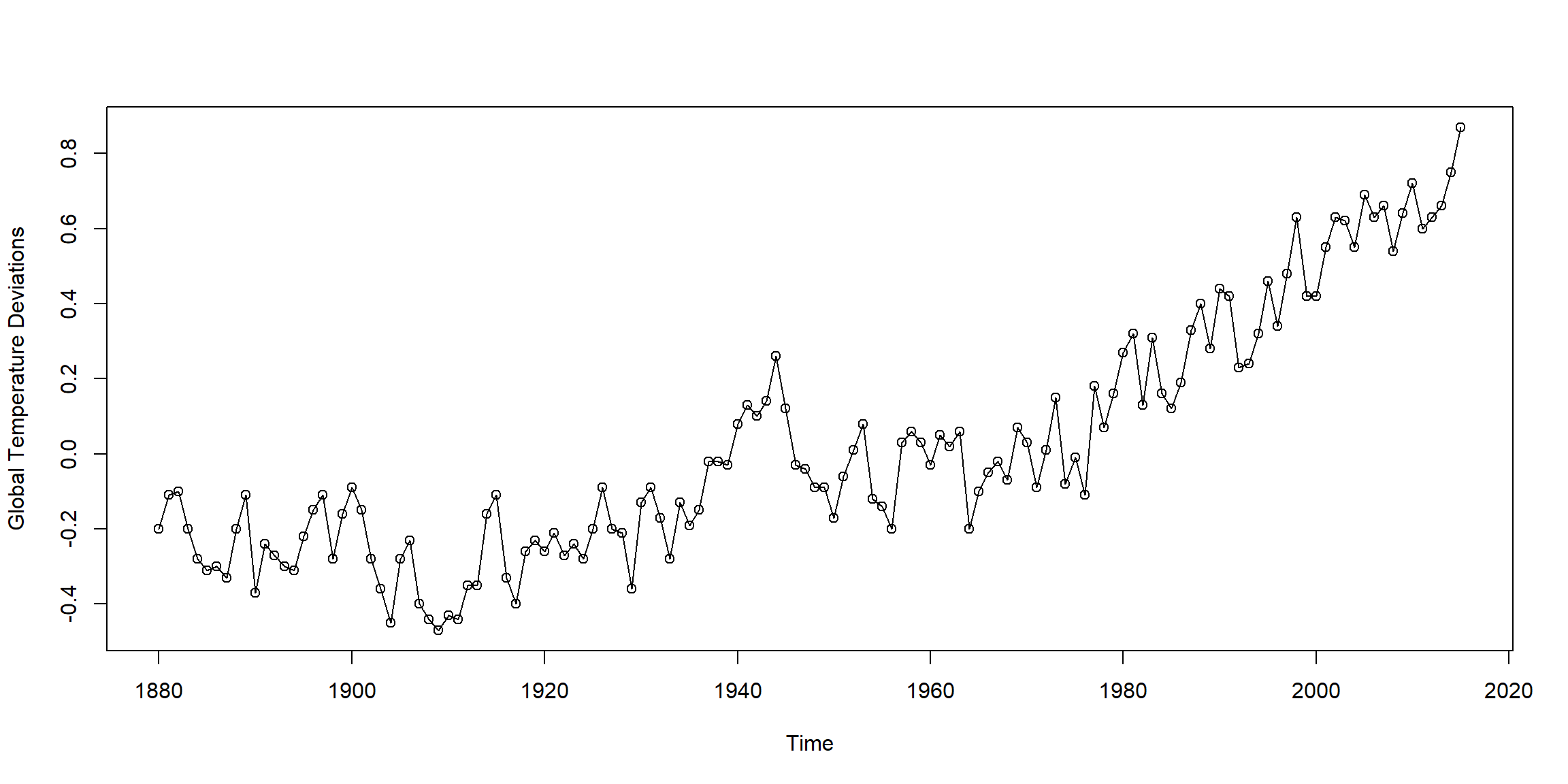
Example 1.5 (p.5)

par(mfrow = c(2,1)) # set up the graphics
plot(soi, ylab="", xlab="", main="Southern Oscillation Index\nindex of ocean ccurrent 洋流")
plot(rec, ylab="", xlab="", main="Recruitment\nindex of fish amount")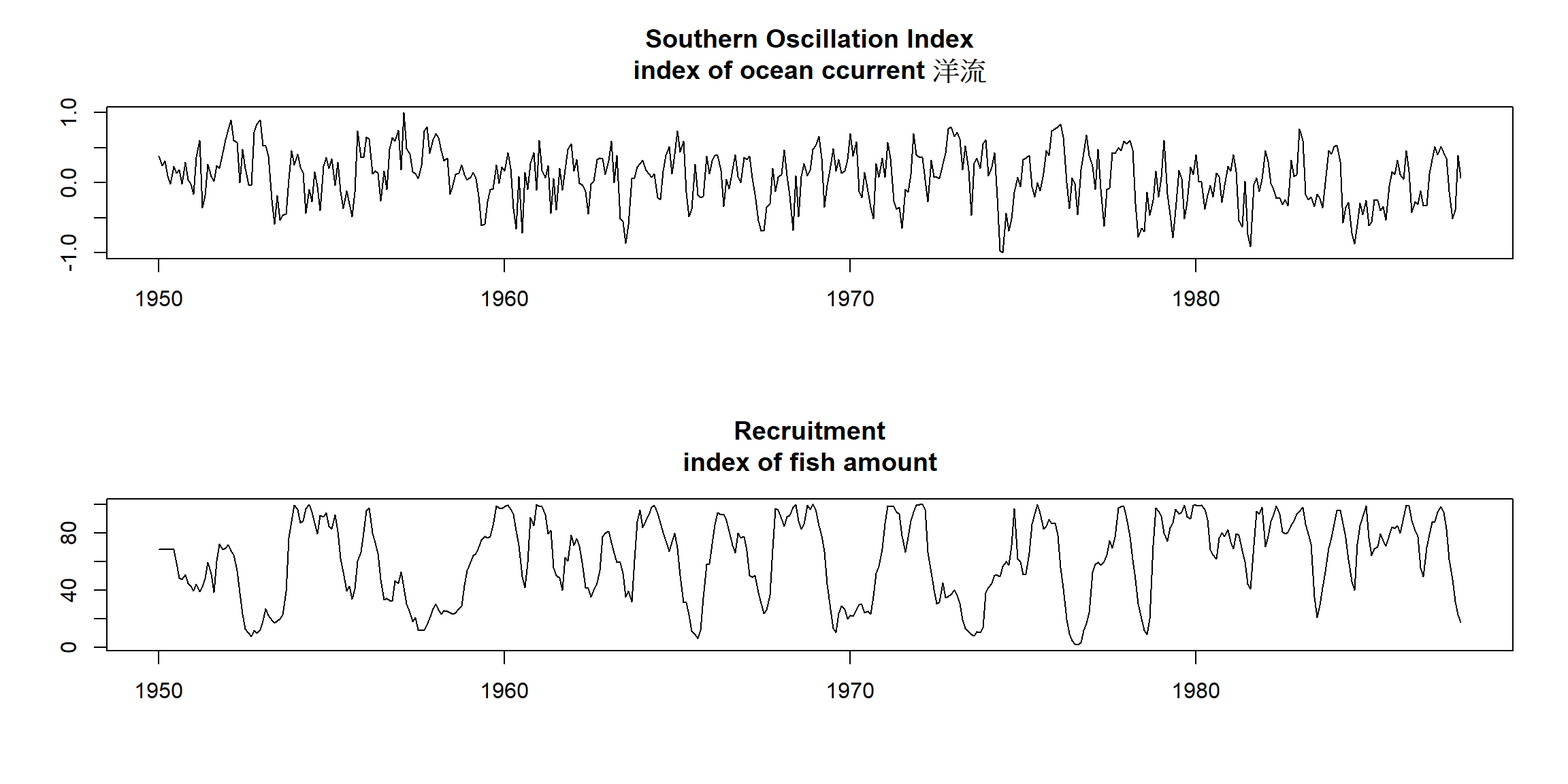




Example 1.6 (p.5) MRI data

par(mfrow=c(2,1))
ts.plot(fmri1[,2:5], col=1:4, ylab="BOLD", main="Cortex")
ts.plot(fmri1[,6:9], col=1:4, ylab="BOLD", main="Thalamus & Cerebellum")
mtext("Time (1 pt = 2 sec)",side = 1,line = 2)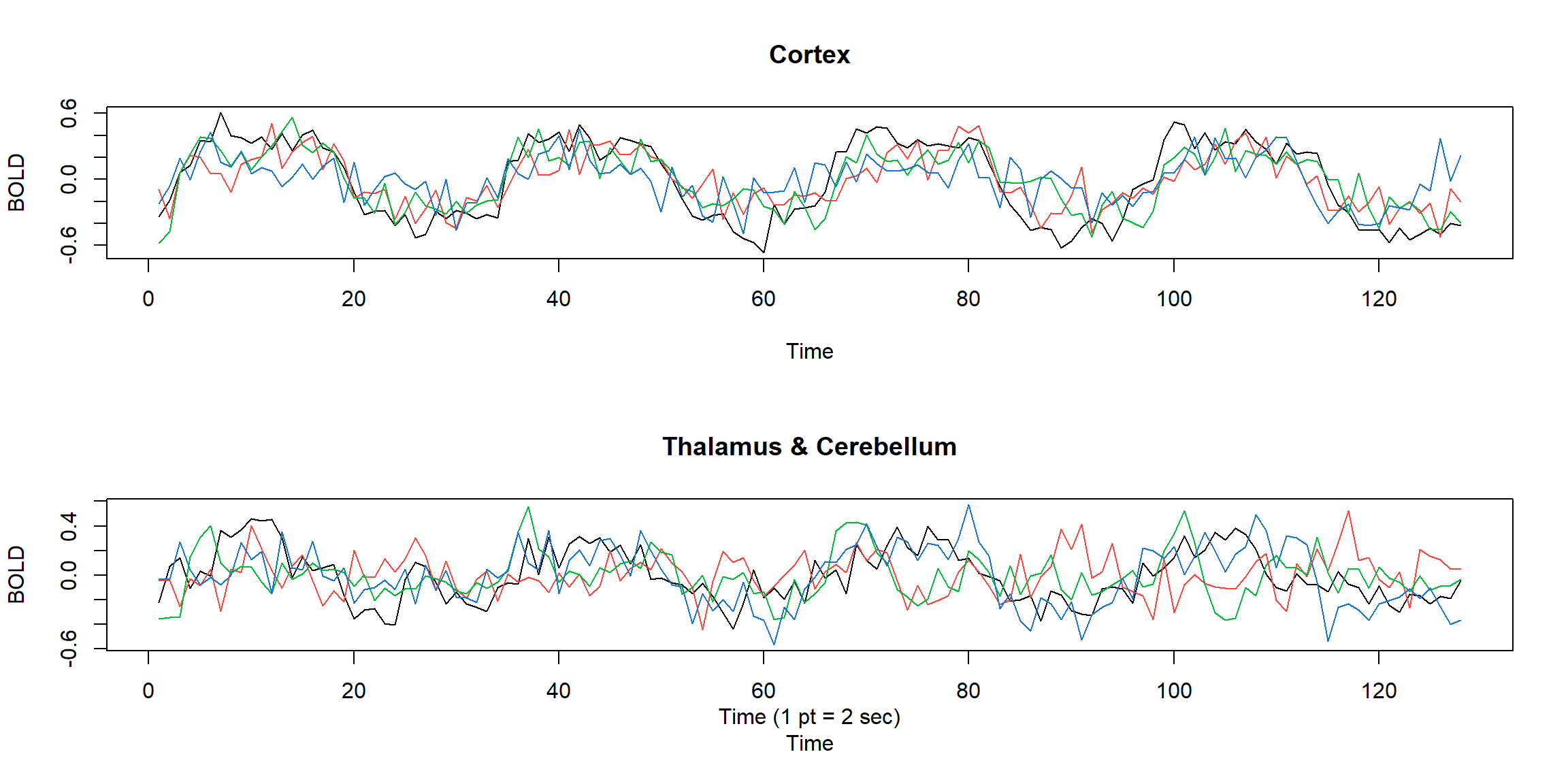




Example 1.7 (p.6)

par(mfrow=c(2,1))
plot(EQ5, main="Earthquake")
plot(EXP6, main="Explosion")




1.1.2 White Noise (WN)

Example 1.9 (p.10)

set.seed(0921)
w = rnorm(500,0,1) # 500 N(0,1) variates
v = filter(w, sides=2, filter=rep(1/3,3)) # moving average
par(mfrow=c(2,1))
plot.ts(w, main="white noise")
plot.ts(v, ylim=c(-3,3), main="moving average")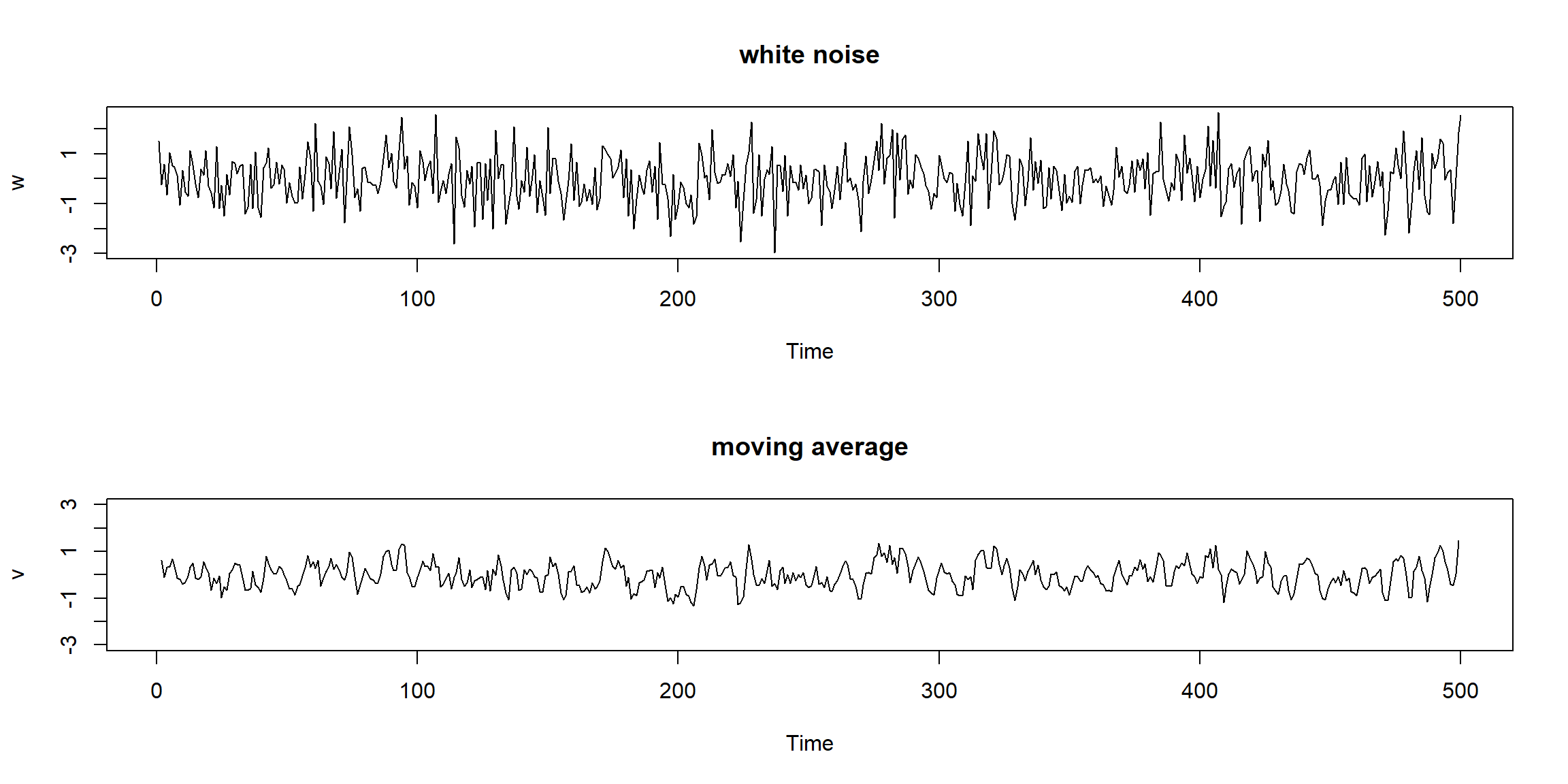

\[W_t\sim N(0,1)\]

  • sides=2, center at lag 0

\[V_t=\frac1 3(W_{t-1}+W_t+W_{t+1})\]

  • sides=1, for past value only
\[V_t=\frac1 3(W_t+W_{t-1}+W_{t-2})\]

Example 1.10 (p.11)

set.seed(0921)
w = rnorm(550,0,1) # 50 extra to avoid startup problems
x = filter(w, filter=c(1,-.9), method="recursive")[-(1:50)] # remove first 50
plot.ts(x, main="autoregression")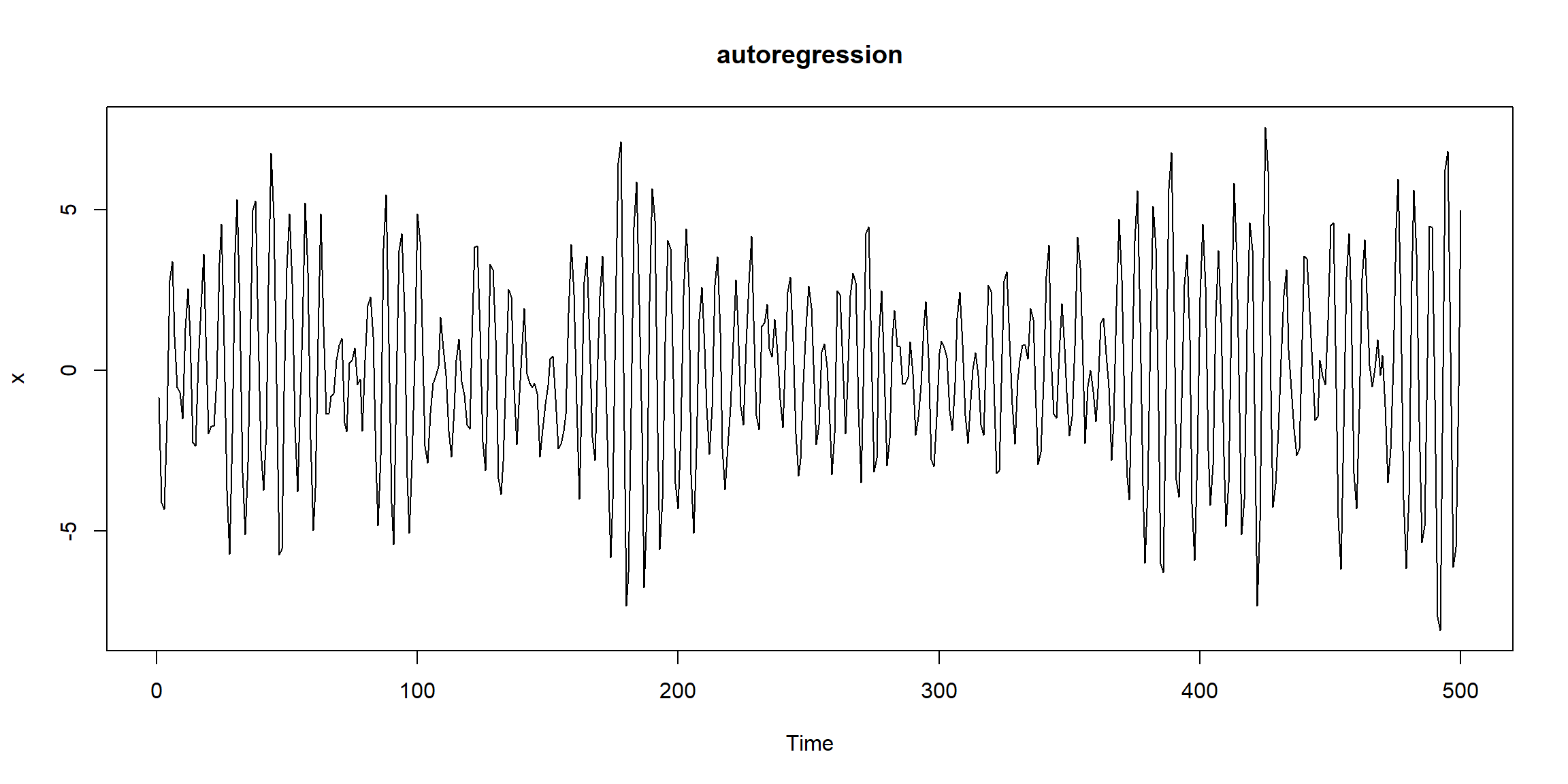

\[W_t\sim N(0,1)\] \(X_t=W_t-0.9W_{t-1}\) (default sides=1)

\(X_t\) and \(X_{t+1}\) are negatively correlated, means when
  • \(X_t\uparrow\:\Rightarrow X_{t+1}\downarrow\)
  • \(X_t\downarrow\:\Rightarrow X_{t+1}\uparrow\)

1.1.3 Random Walk

Example 1.11 (p.11)

set.seed(154) # so you can reproduce the results
w = rnorm(200,0,1); x = cumsum(w) # two commands in one line
wd = w +.2; xd = cumsum(wd)
plot.ts(xd, ylim=c(-5,55), main="random walk")
lines(x, col=2)
lines(.2*1:200,lty="dashed")
legend('topleft', col=c(1,2,1), lty=c(1,1,2), 
       legend = c(expression(X[d]),expression(X[t]),expression(E(X[t]))))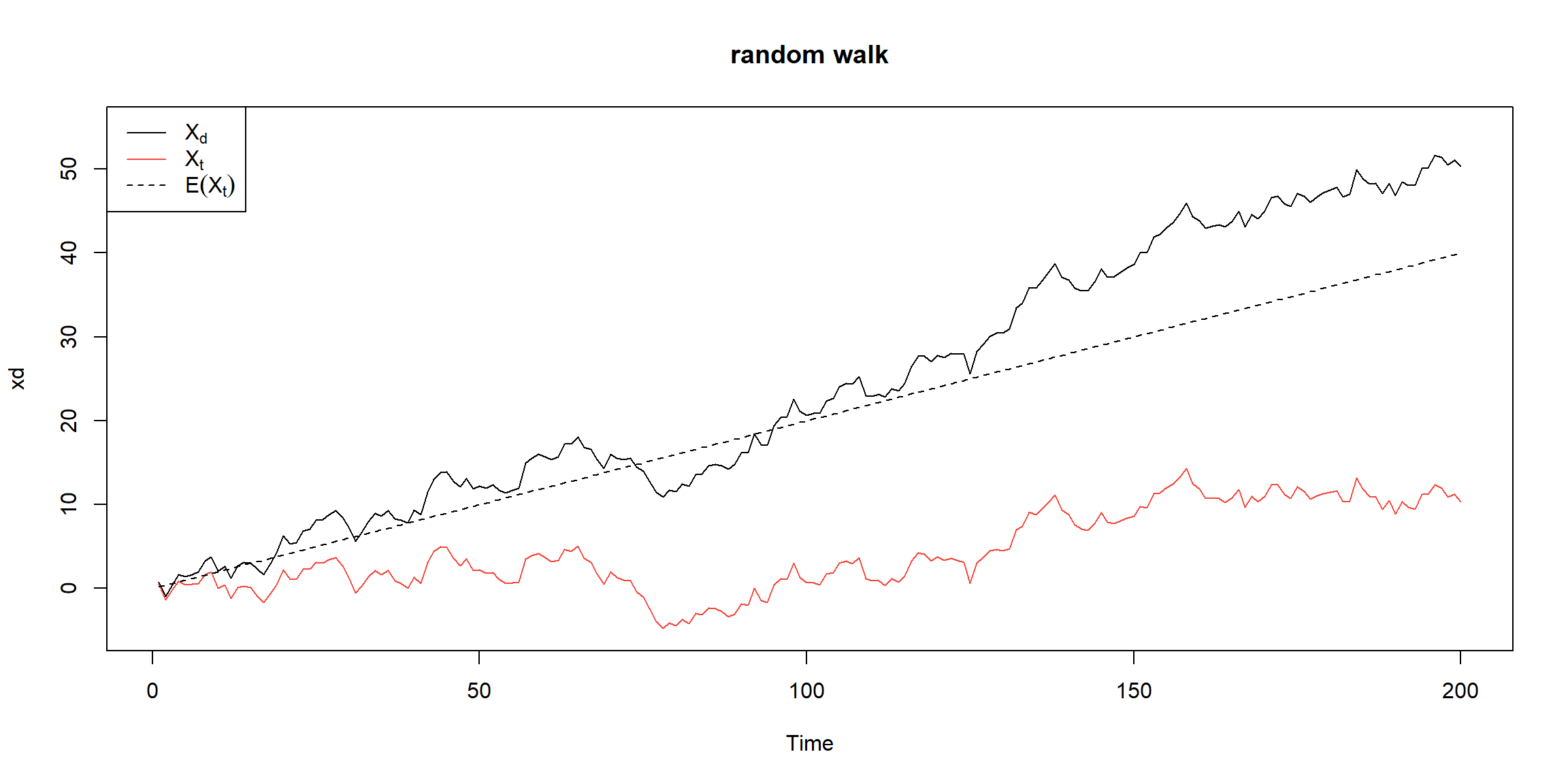

\(X_t\) is not stationary, \(\because Var(X_t)\) depends on t.

\(X_d\) is not stationary, \(\because E(X_d)\) depends on t.

  • \(W_t\sim N(0,1)\)
  • \(X_t=W_1+W_2+...+W_t\)
    • \(Var(X_t)=Var(W_1)+Var(W_2)+...+Var(W_t)=1\cdot t=t\)
  • \(W_d=W_t+0.2\)
  • \(X_d=\sum W_d=\sum W_t+0.2\cdot t\)
    • \(E(X_d)=0.2\cdot t\)
\(E(aX+b)=aE(X)+b\)
\(Var(aX+b)=a^2Var(X)\)

1.1.4 Noise influence periodic

Example 1.12 (p.12)

cs = 2*cos(2*pi*1:500/50 + .6*pi); w = rnorm(500,0,1)
par(mfrow=c(3,1), mar=c(3,2,2,1), cex.main=1.5)         # help(par) for info
plot.ts(cs, main=expression(x[t]==2*cos(2*pi*t/50+.6*pi)))
plot.ts(cs+w, main=expression(x[t]==2*cos(2*pi*t/50+.6*pi) + N(0,1)))
plot.ts(cs+5*w, main=expression(x[t]==2*cos(2*pi*t/50+.6*pi) + N(0,25)))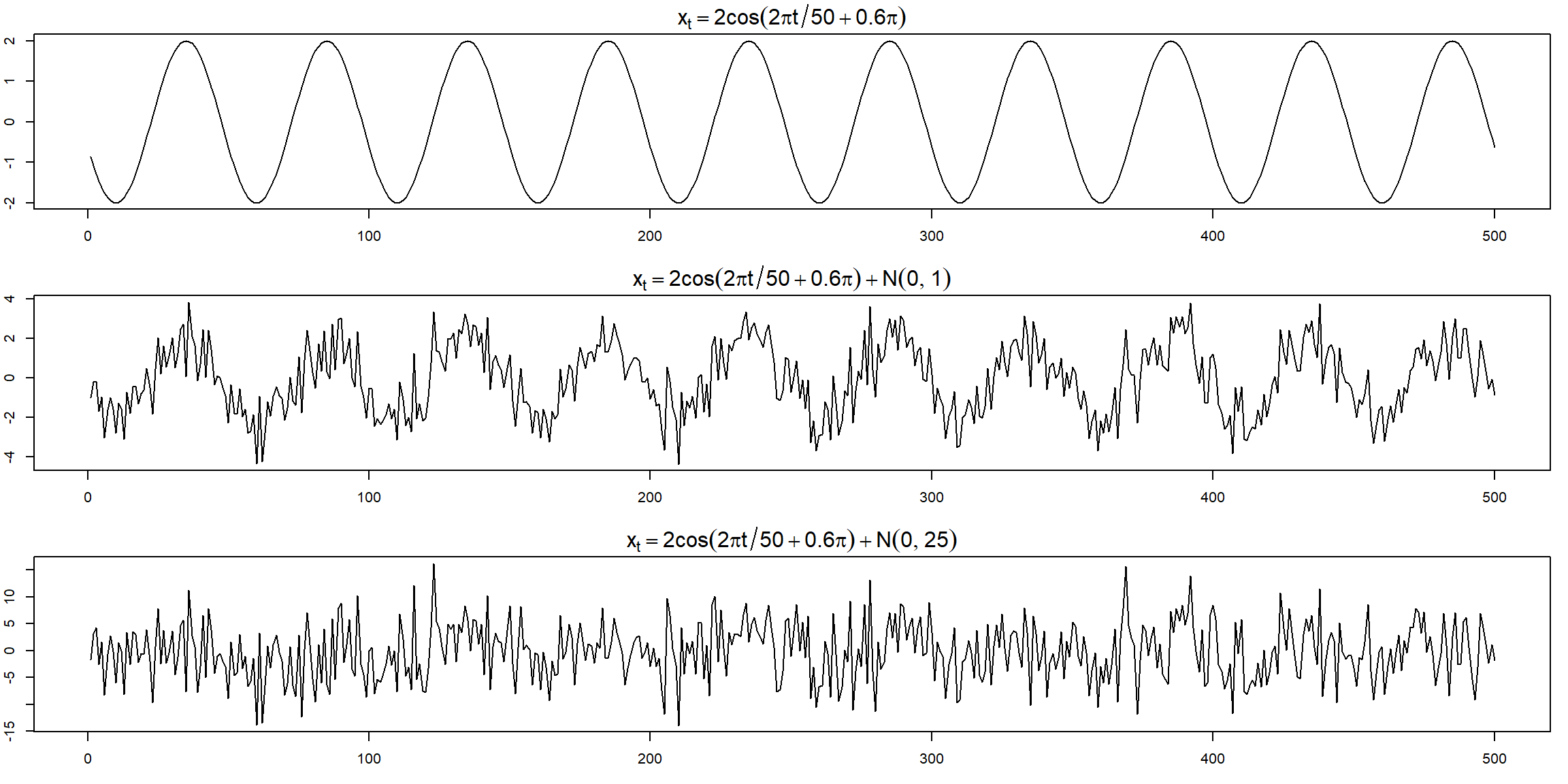

The periodic behavior became less obvious when the noise is large.

1.1.5 How lag influence plot

Example 1.24 (p.24) \[y_t=Ax_{t-l}+w_t\]

  • \(l>0\), \(x_t\) lead \(y_t\)
    • \(y_t=x_{t-1}+w_t\)
    • \(x\) lead \(y\)
  • \(l<0\), \(x_t\) lag \(y_t\)
    • \(y_t=x_{t+1}+w_t\)
    • \(x\) lag \(y\)

Assume \(w_t\) is uncorrelated with \(x_t\), the cross-covariance function is \[\gamma_{yx}(h)=cov(y_{t+h},x_t)=cov(Ax_{t+h-l}+w_{t+h},x_t)\\=cov(Ax_{t+h-l},x_t)=A\gamma_x(h-l)\]

When \(h=l\), \(\gamma_{yx}(h)=\gamma_x(0)\)

x = rnorm(100)
y = lag(x, -5) + rnorm(100)
par(mfrow=c(1,1))
ccf <- ccf(y, x, type='covariance', 
           ylab='CCovF', xlab='lag h', main=expression(paste('l=5 with', hat(gamma)[yx](h))))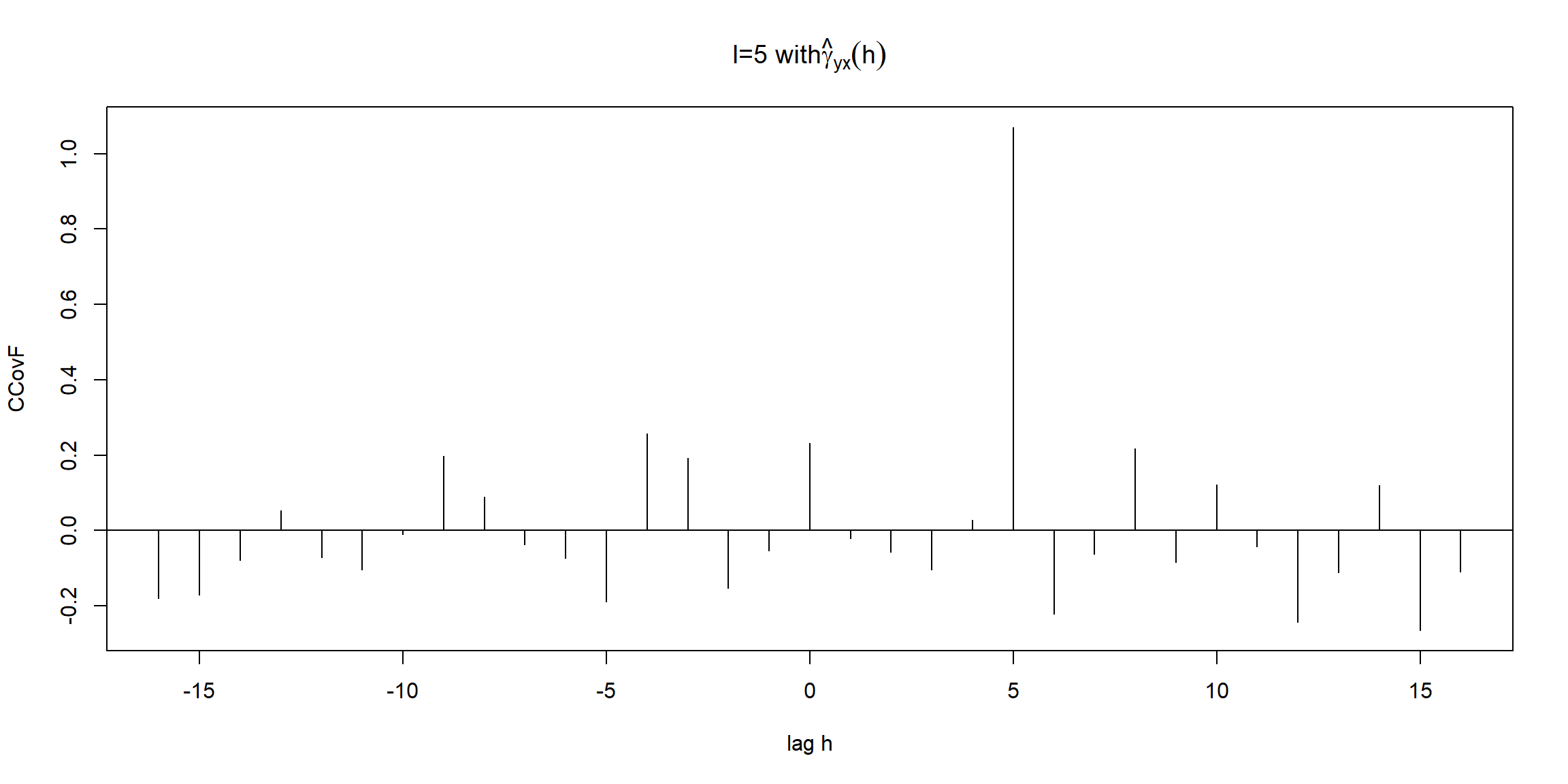

  • \(X\sim N(0,1)\)
  • \(y_t=X_{t-5}+W_t, W_t\sim N(0,1)\)
  • \(\require{enclose} \enclose{horizontalstrike}{Corr(y_t, X_{t+h})=\big\{\substack{1,\:h=5\\0,\:o.w.}}\)
  • \(l=5\to\gamma_{yx}(h)=\gamma_x(h-5)\)
    • \(lag\:h=5 \to\gamma_{yx}(5)=\gamma_x(0)=variance(X)=1\)
    • \(y_{t+h}=Ax_{t+h-5}+w_{t+h}\)
      • \(i=|h-l|=|h-5|\)
      • \(h>5\to\gamma_{yx}(h)=cov(Ax_{t+i},x_t)\to x\:leads\)
      • \(h<5\to\gamma_{yx}(h)=cov(Ax_{t-i},x_t)\to y\:leads\)

Example 1.25 (p.28)

par(mfrow=c(1,2))
r = round(acf(soi, 6, plot=FALSE)$acf[-1], 3)
plot(lag(soi,-1), soi, ylab=expression(X[t]), xlab=expression(X[t-1]))
arrows(-1,-1,1,1, col=2, angle = 15, lwd=5)
legend('topleft', legend=r[1])
plot(lag(soi,-6), soi, ylab=expression(X[t]), xlab=expression(X[t-6]))
arrows(-1,1,1,-1, col=2, angle = 15, lwd=5)
legend('topleft', legend=r[6])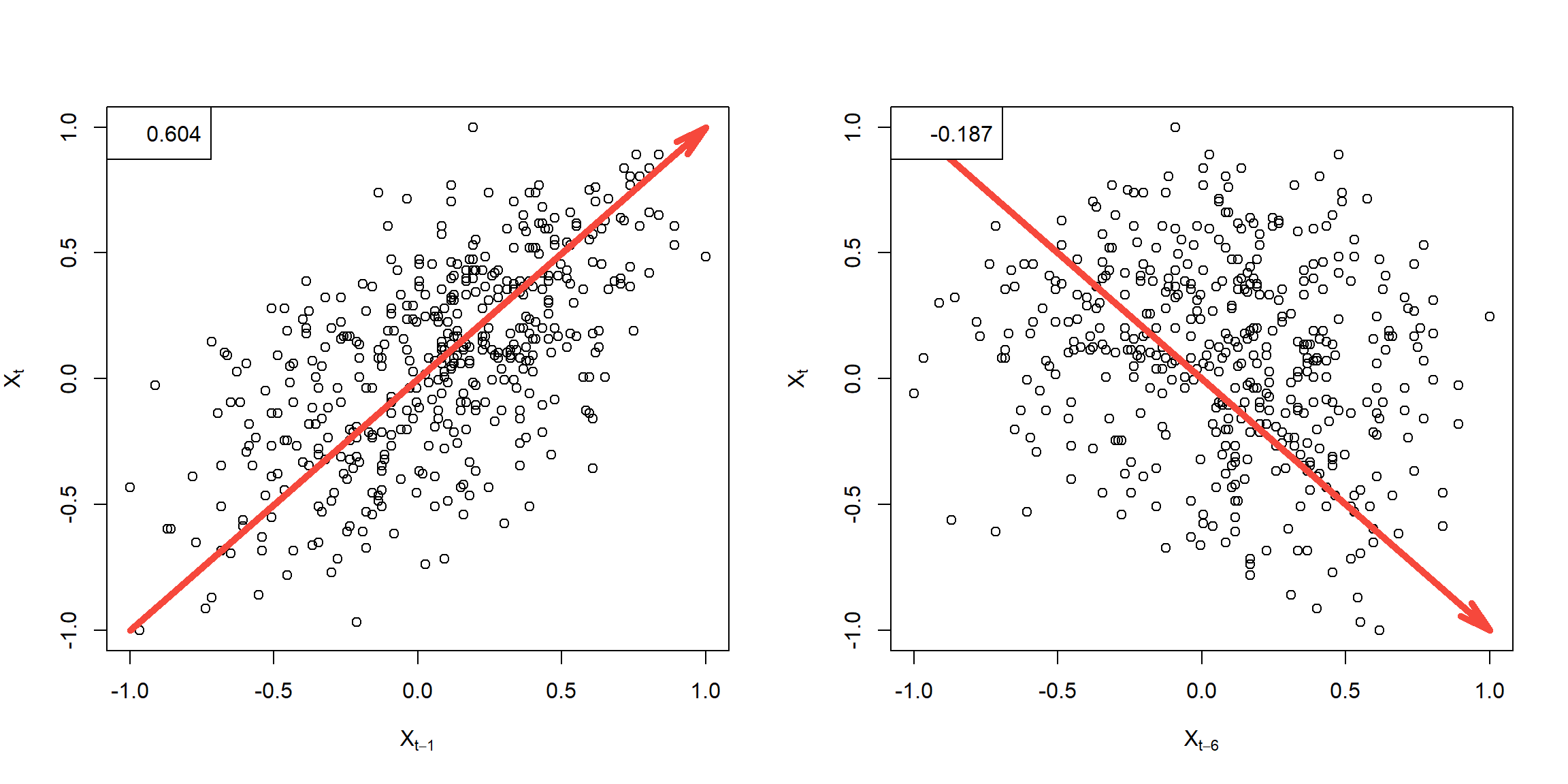

1.2 Explore Data

1.2.1 Estimate a linear trend

Example 2.1 (p.45) \[x_t=a+b\cdot t+W_t\]

summary(fit <- lm(chicken~time(chicken)))
## 
## Call:
## lm(formula = chicken ~ time(chicken))
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -8.7411 -3.4730  0.8251  2.7738 11.5804 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   -7.131e+03  1.624e+02  -43.91   <2e-16 ***
## time(chicken)  3.592e+00  8.084e-02   44.43   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.696 on 178 degrees of freedom
## Multiple R-squared:  0.9173, Adjusted R-squared:  0.9168 
## F-statistic:  1974 on 1 and 178 DF,  p-value: < 2.2e-16
plot(chicken, type="o",ylab="cents per pound")
abline(fit, lwd=2, col=2) # add regression line to the plot
legend('topleft', expression(a+bt), lwd=2, col=2)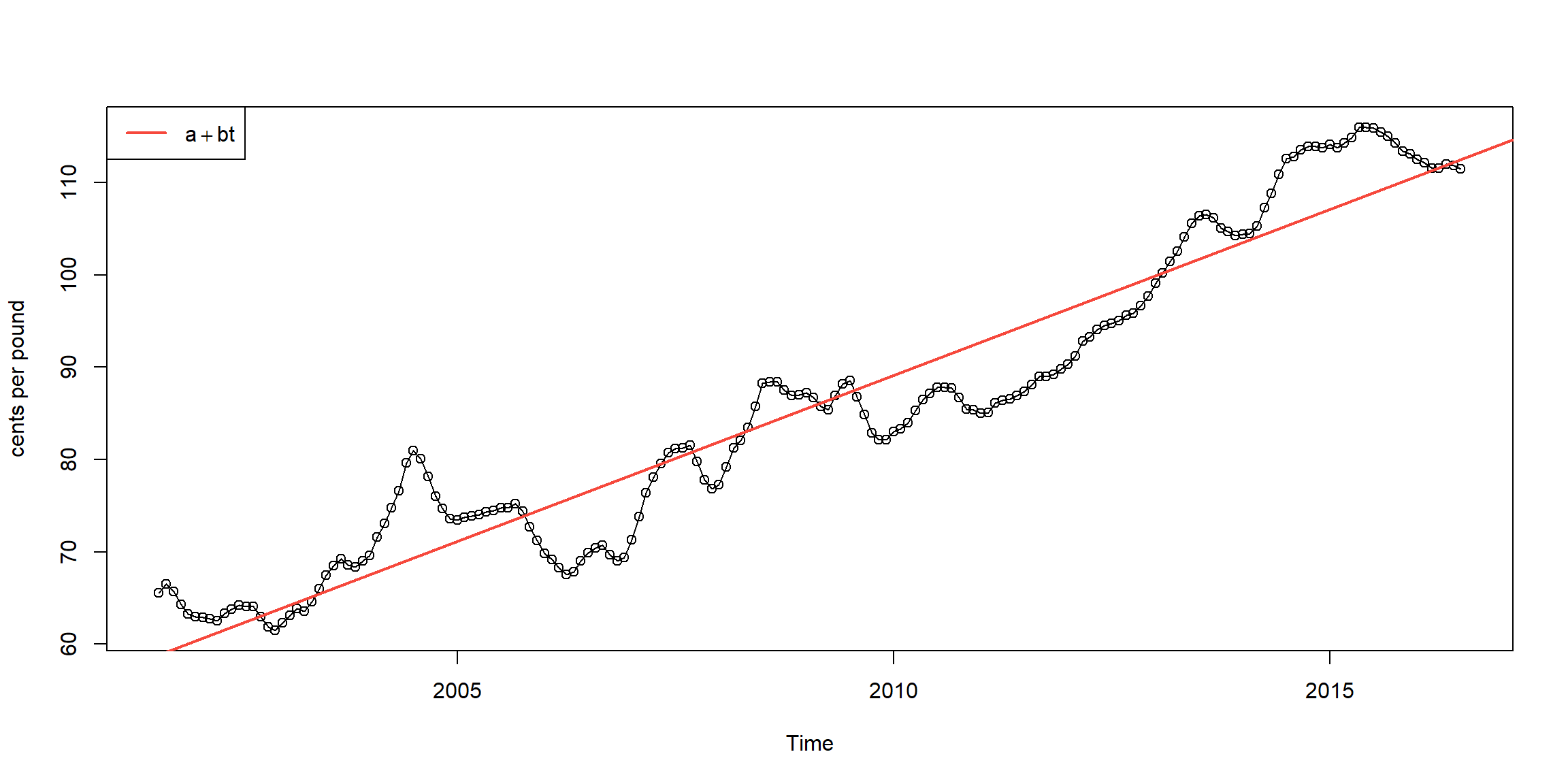

1.2.2 Detrend and Differencing

Example 2.4 and 2.5 (p.54, 58) \[x_t=a+b\cdot t+W_t\]

  • detrended: \(X_t-a-b\cdot t\)
  • first difference: \(\nabla X_t=X_t-X_{t-1}\)
fit = lm(chicken~time(chicken), na.action=NULL) # regress chicken on time
par(mfrow=c(2,1), mar=c(3,4,2,1))
plot(resid(fit), type="o", main="detrended")
plot(diff(chicken), type="o", main="first difference")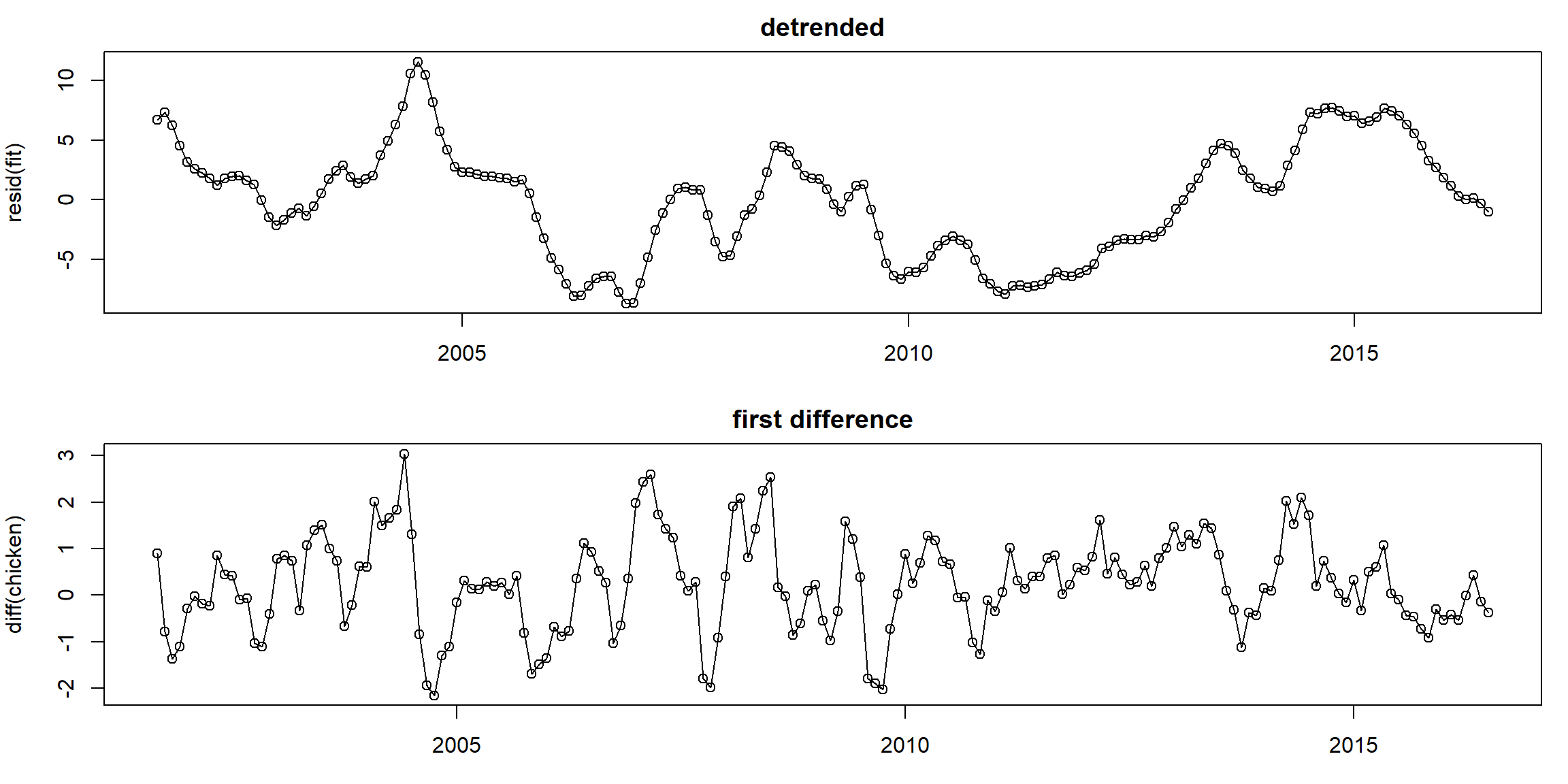

par(mfrow=c(3,1), mar=c(4,3,3,1)) # plot ACFs
acf(chicken, 48, main="chicken")
acf(resid(fit), 48, main="detrended")
acf(diff(chicken), 48, main="first difference")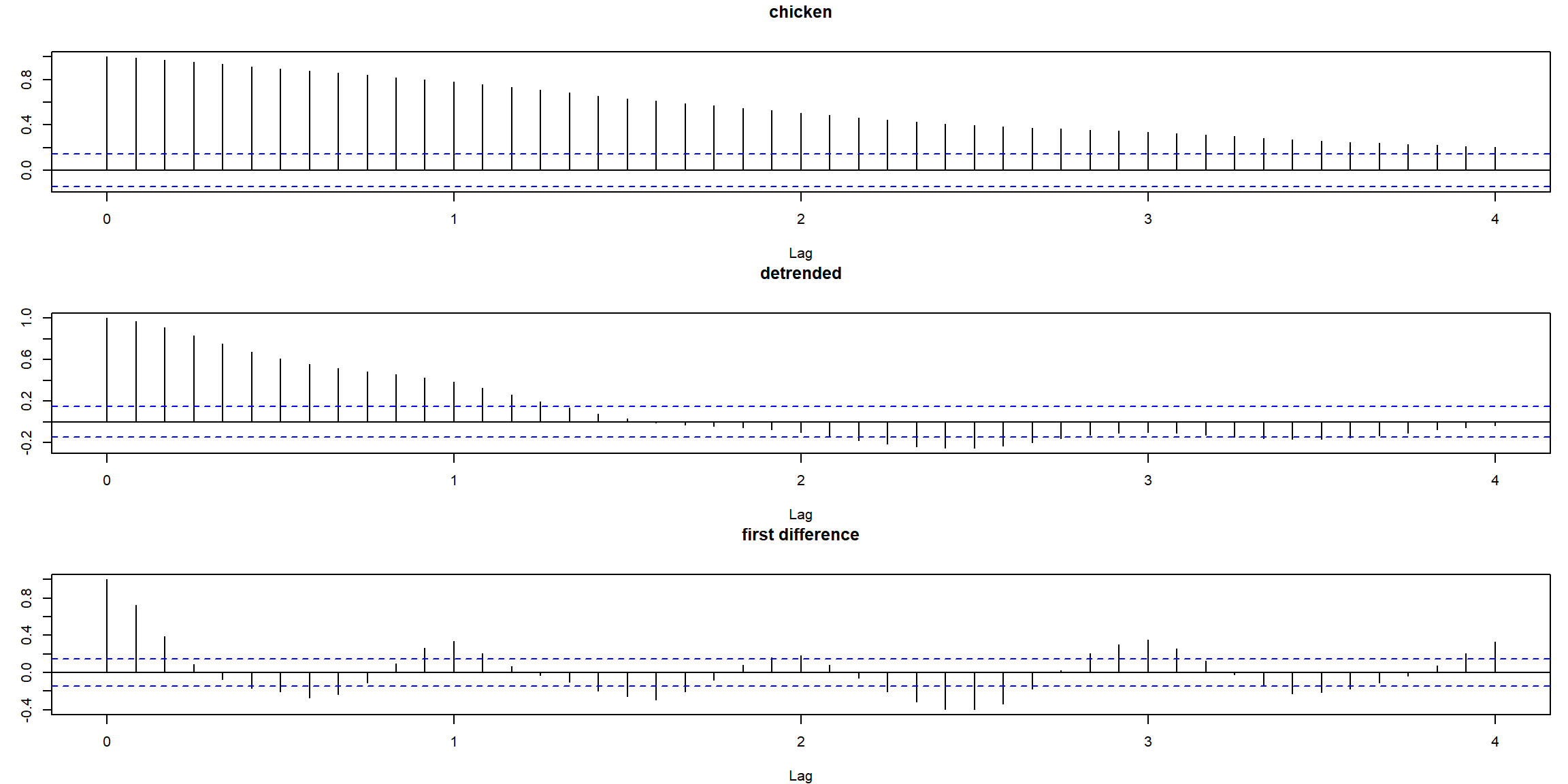

  • first difference does better than regression
  • ACF of stationary process decays fast to zero

Example 2.6 (p.58)

par(mfrow=c(2,1), mar=c(4,4,3,1))
plot(diff(globtemp), type="o")
mean(diff(globtemp)) # drift estimate = .008
## [1] 0.007925926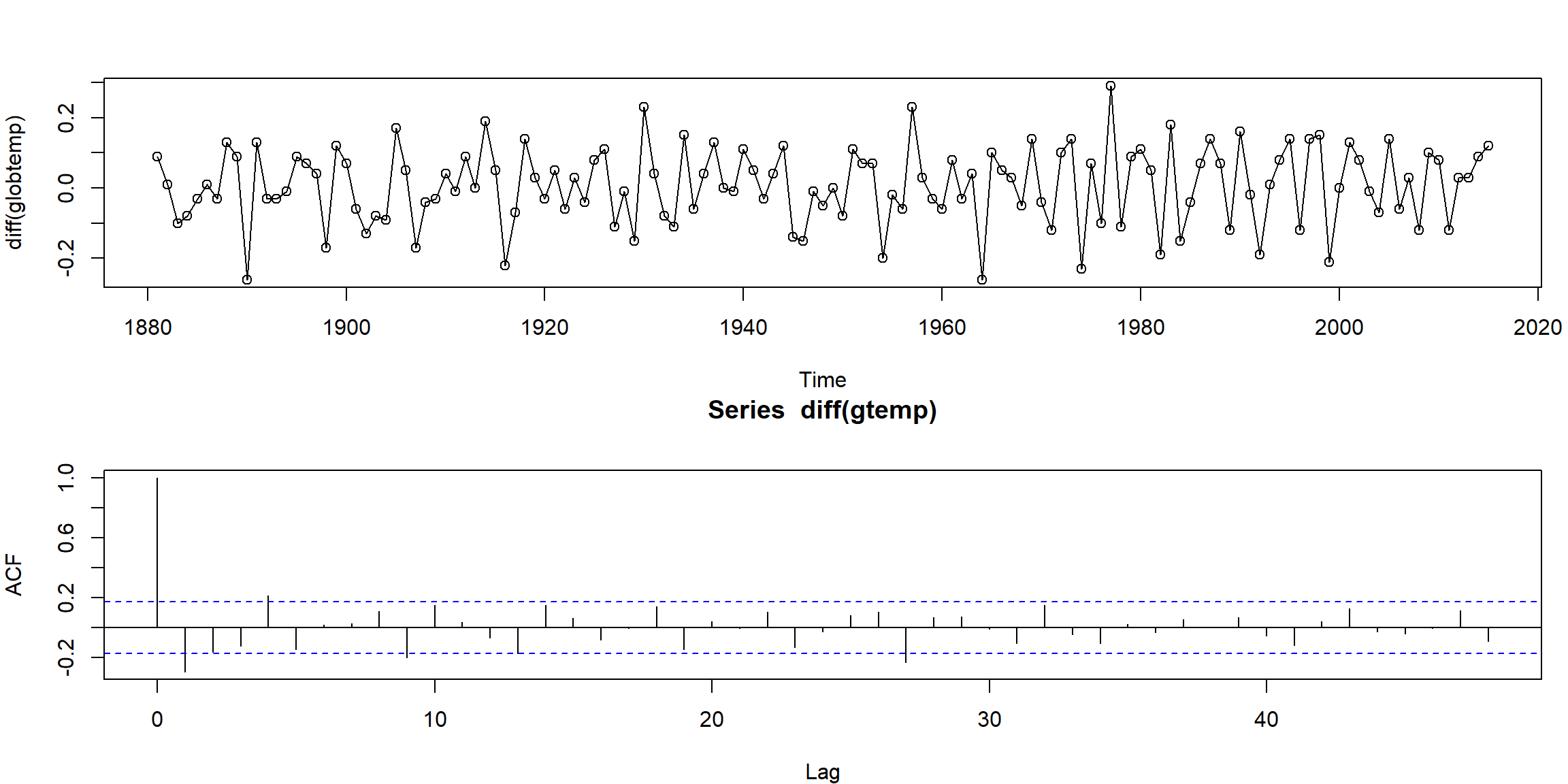
acf(diff(gtemp), 48)

  • look stationary after first-order differencing

1.2.3 Smoothing

Example 2.13 (p.67) lowess

  • lowess(x, y = NULL, f = 2/3)
    • f: the smoother span (band width)
plot(soi)
lines(lowess(soi, f=.05), lwd=2, col=4) # El Nino cycle
lines(lowess(soi), lty=2, lwd=2, col=2) # trend (with default span)
legend('topright', c('seasonality','trend'), col=c(4,2), lty=c(1,2), lwd=2)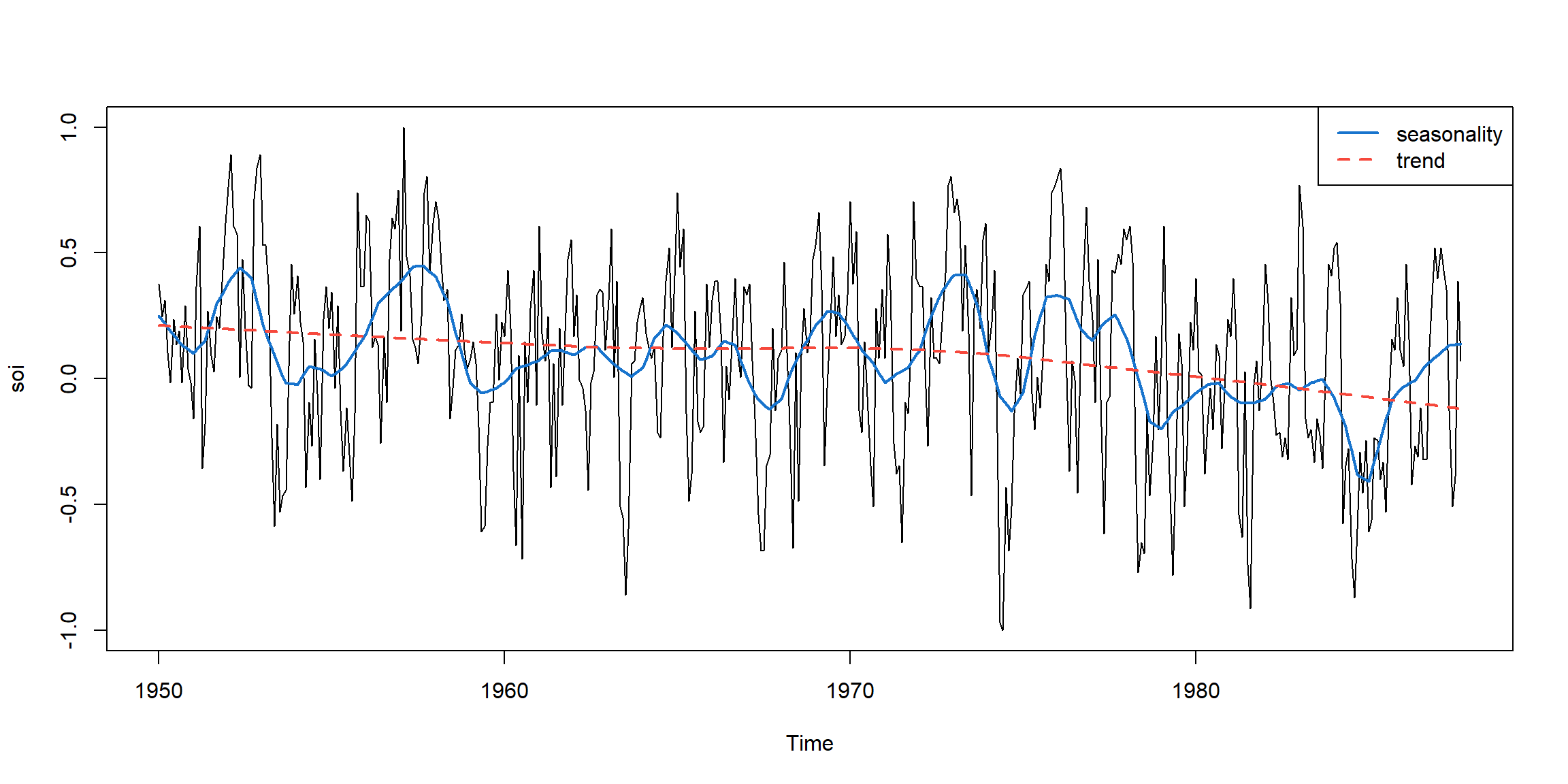

  • seasonality: small band width
  • trend: large band width

Example 2.14 (p.68) smooth.spline

  • smooth.spline(x, y, spar = NULL)
    • x: predictor
    • y: response
    • spar: smoothing parameter, typically (but not necessarily) in (0,1]
plot(soi)
lines(smooth.spline(time(soi), soi, spar=.5), lwd=2, col=4)
lines(smooth.spline(time(soi), soi, spar= 1), lty=2, lwd=2, col=2)
legend('topright', c('seasonality','trend'), col=c(4,2), lty=c(1,2), lwd=2)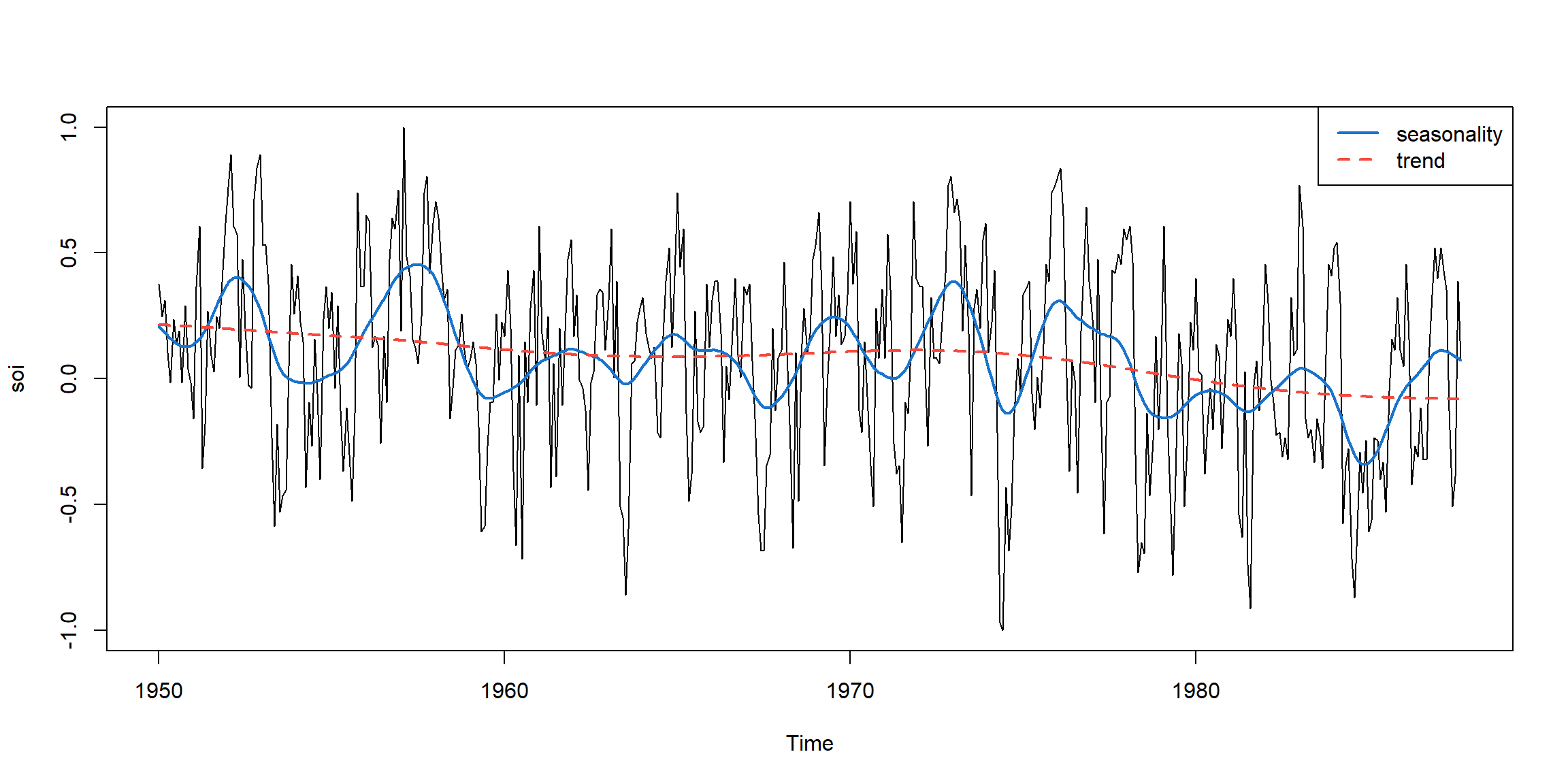

1.3 Time Series model

Example 3.2 (p.78) AR(1)

  • arima.sim: Simulate from an ARIMA model.
    • order: c(p, d, q) \(\to\) AR order, degree of differencing, MA order.
    • ARIMA(0,0,0) is white noise.
  • If AR(2) \(\to\) order=c(2,0,0), ar=c(.5, .1)
par(mfrow=c(2,1), mar=c(3,4,2,1))
plot(arima.sim(list(order=c(1,0,0), ar=.9), n=100), ylab="x",
     main=(expression(AR(1)~~~phi==+.9)))
plot(arima.sim(list(order=c(1,0,0), ar=-.9), n=100), ylab="x",
     main=(expression(AR(1)~~~phi==-.9)))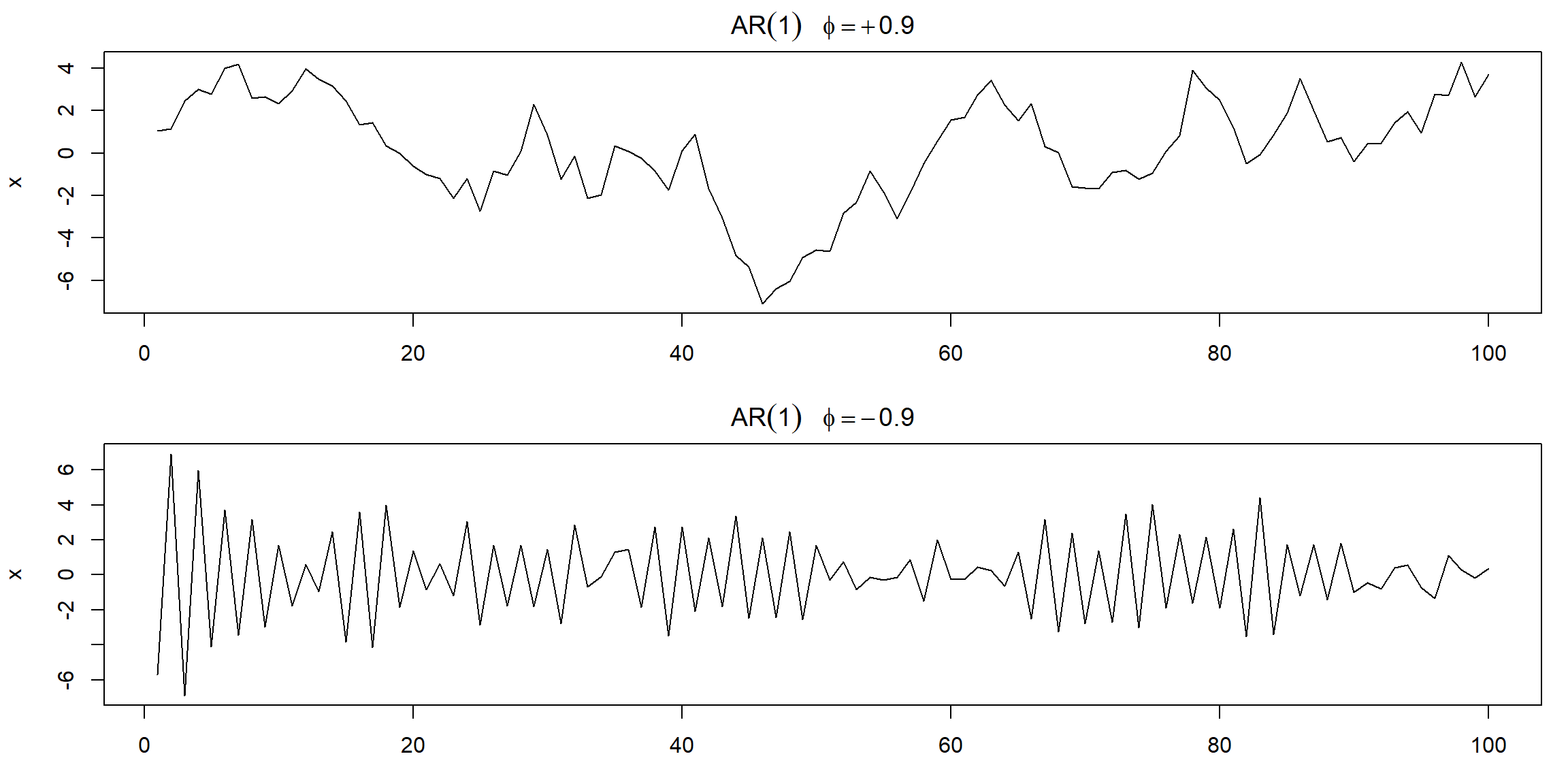

top bottom
\(\rho(h)=\color{red}{(0.9)}^h, h\geq0\) \(\rho(h)=\color{red}{(-0.9)}^h, h\geq0\)
positively correlated negatively correlated
look like trend fluctuate rapidly

Example 3.5 (p.82) MA MA(1) model \(x_t=w_t+\theta w_{t-1}\) \[ E(x_t)=0\\ \gamma(h)=\Bigg\{\begin{array}{ll} (1+\theta^2)\sigma^2_w,&h=0\\ \theta\sigma^2_w,&h=1\\ 0,&h>1 \end{array}\\ \rho(h)=\Big\{\begin{array}{ll} \frac{\theta}{1+\theta^2},&h=1\\ 0,&h>1 \end{array} \]

par(mfrow = c(2,1), mar=c(3,4,2,1))
plot(arima.sim(list(order=c(0,0,1), ma=.9), n=100), ylab="x",
     main=(expression(MA(1)~~~theta==+.5)))
plot(arima.sim(list(order=c(0,0,1), ma=-.9), n=100), ylab="x",
     main=(expression(MA(1)~~~theta==-.5)))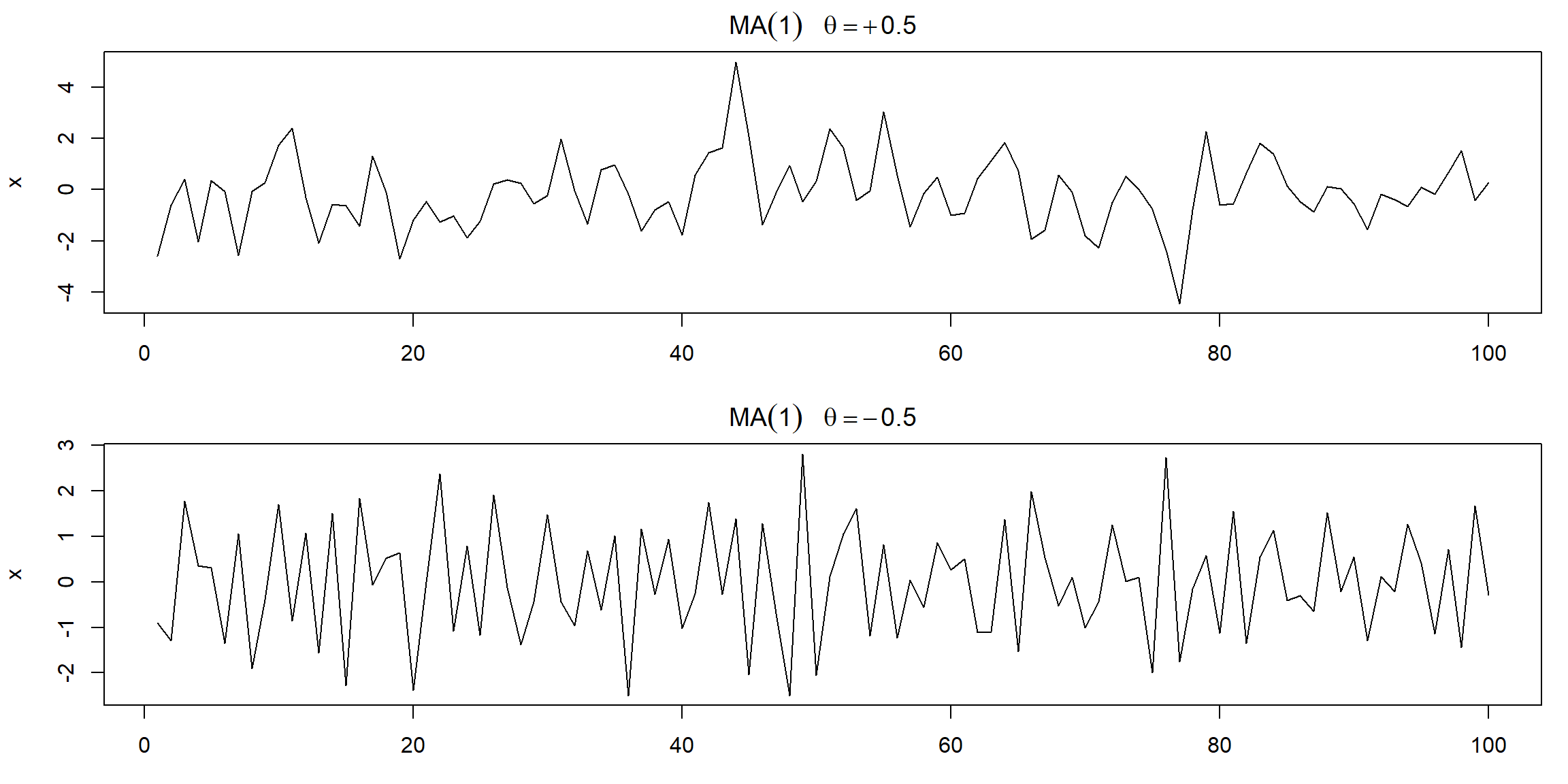

top bottom
\(\theta=0.5\Rightarrow x_t, x_{t-1}\) are positively correlated \(\theta=-0.5\Rightarrow x_t, x_{t-1}\) are negatively correlated
\(\rho(1)=\frac{0.5}{1+0.5^2}=0.4\Rightarrow\) weak dependence
  • The series for which \(\theta=0.5\) is smoother than the series for \(\theta=-0.5\).

Example 3.7 (p.84) parameter redundency If we were unaware of parameter redundancy, we might claim the data are correlated when in fact they are not

\[ X_t\sim N(5,1),\text{ fit ARIMA(1,1) to X}\\ X_t=\phi X_{t-1}+W_t+\theta W_{t-1} \]

set.seed(8675309)
x = rnorm(150, mean=5) # generate iid N(5,1)s
out <- arima(x, order=c(1,0,1)); out # estimation
## 
## Call:
## arima(x = x, order = c(1, 0, 1))
## 
## Coefficients:
##           ar1     ma1  intercept
##       -0.9595  0.9527     5.0462
## s.e.   0.1688  0.1750     0.0727
## 
## sigma^2 estimated as 0.7986:  log likelihood = -195.98,  aic = 399.96
  • \(\phi=\) -0.96, \(\theta=\) 0.95
  • \((1+0.96B)X_t=(1+0.95B)W_t\)

Example 3.8 (p.86) ARMA to MA

ARMAtoMA(ar = .9, ma = .5, 10) # for a list
##  [1] 1.4000000 1.2600000 1.1340000 1.0206000 0.9185400 0.8266860 0.7440174
##  [8] 0.6696157 0.6026541 0.5423887
plot(ARMAtoMA(ar = .9, ma = .5, 10), 
     ylab = expression(psi [j]))

ARMAtoMA(ar = -.5, ma = -.9, 10) # first 10 pi-weights
##  [1] -1.400000000  0.700000000 -0.350000000  0.175000000 -0.087500000
##  [6]  0.043750000 -0.021875000  0.010937500 -0.005468750  0.002734375

Example 3.11 (p.92) AR(2)

z = c(1,-1.5,.75) # coefficients of the polynomial
(a = polyroot(z)[1]) # = 1+0.57735i,print one root = 1 + i/sqrt(3)
## [1] 1+0.57735i
  • polyroot: 解根

\[f(x)=1-1.5x+0.75x^2\]

arg = Arg(a)/(2*pi) # arg in cycles/pt
1/arg # =12,the period
## [1] 12

\[ z=x+iy\\ r=\sqrt{x^2+y^2}\\ \phi=Arg(z)\\ x=r\cdot cos(\phi),\;y=r\cdot sin(\phi) \]

set.seed(90210)
ar2 = arima.sim(list(order=c(2,0,0), ar=c(1.5,-.75)), n = 144)  # simulated data
plot(1:144/12,ar2,type="l",xlab="Time (one unit = 12 obs)")
abline(v=0:12, lty="dotted",lwd=2)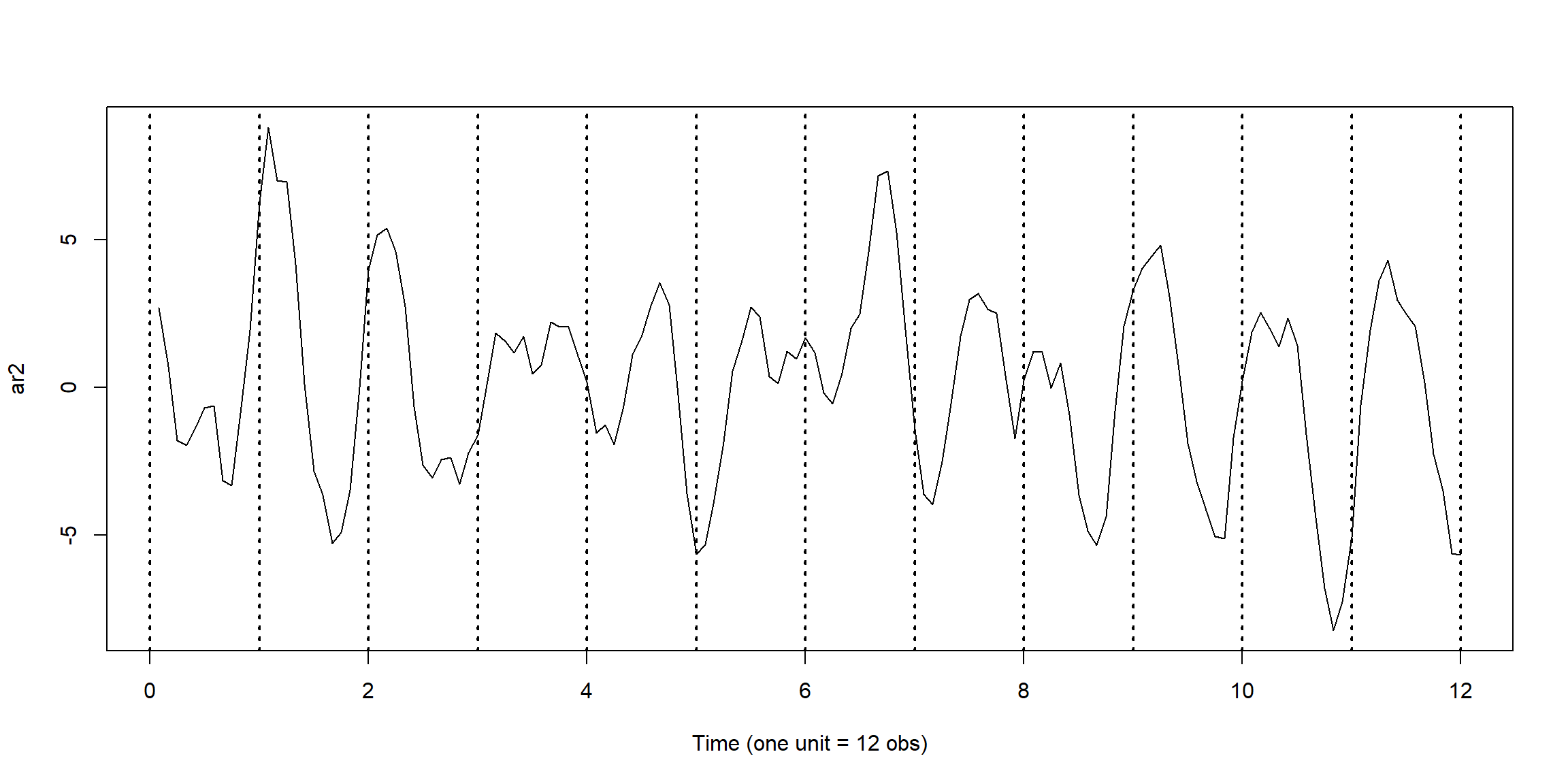

\[X_t=1.5X_{t-1}-0.75X_{t-2}+W_t\]

  • has seasonality with period \(d=12\)
  • AR(2) process is not stationary
  • MA(q) process is always stationary
ACF = ARMAacf(ar=c(1.5,-.75), ma=0, 50) # theoretical
par(mfrow = c(2,1), mar=c(3,4,3,1))
plot(ACF, type="h", xlab="lag", main="theoretical ACF")
abline(h=0)
acf(ar2, lag.max = 50, main="sample ACF")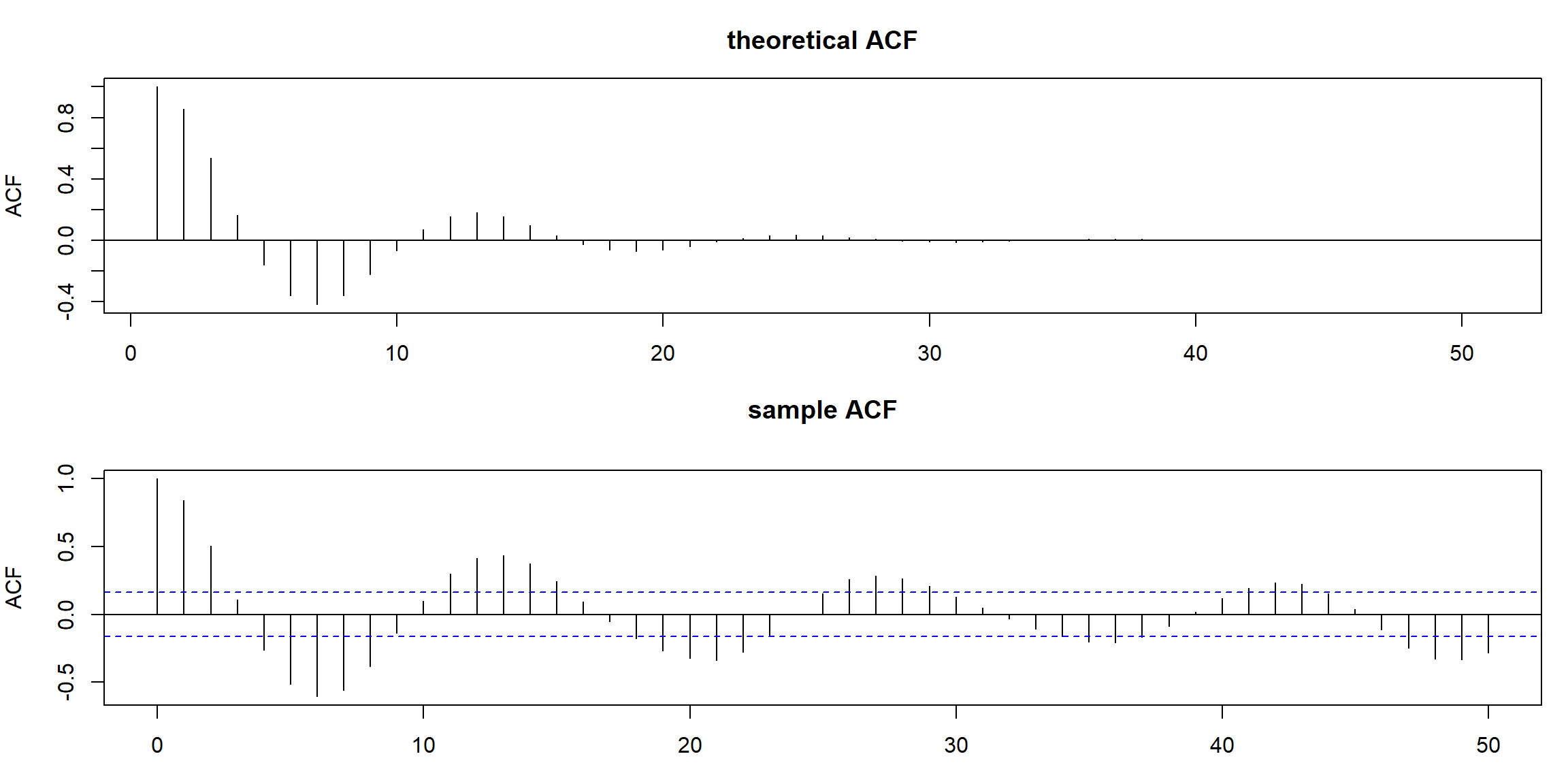

  • ARMAacf: theoretical ACF (when model is given)
  • acf: sample ACF (when data is given)
  • ACF has periodic pattern

Example 3.16 (p.98) PACF of AR(p)

ar2.acf = ARMAacf(ar=c(1.5,-.75), ma=0, 24)[-1]
ar2.pacf = ARMAacf(ar=c(1.5,-.75), ma=0, 24, pacf=TRUE)
par(mfrow=c(1,2), mar=c(4,4,1,1))
plot(ar2.acf, type="h", xlab="lag"); abline(h=0)
plot(ar2.pacf, type="h", xlab="lag")
abline(h=0); axis(1, at=c(1:5))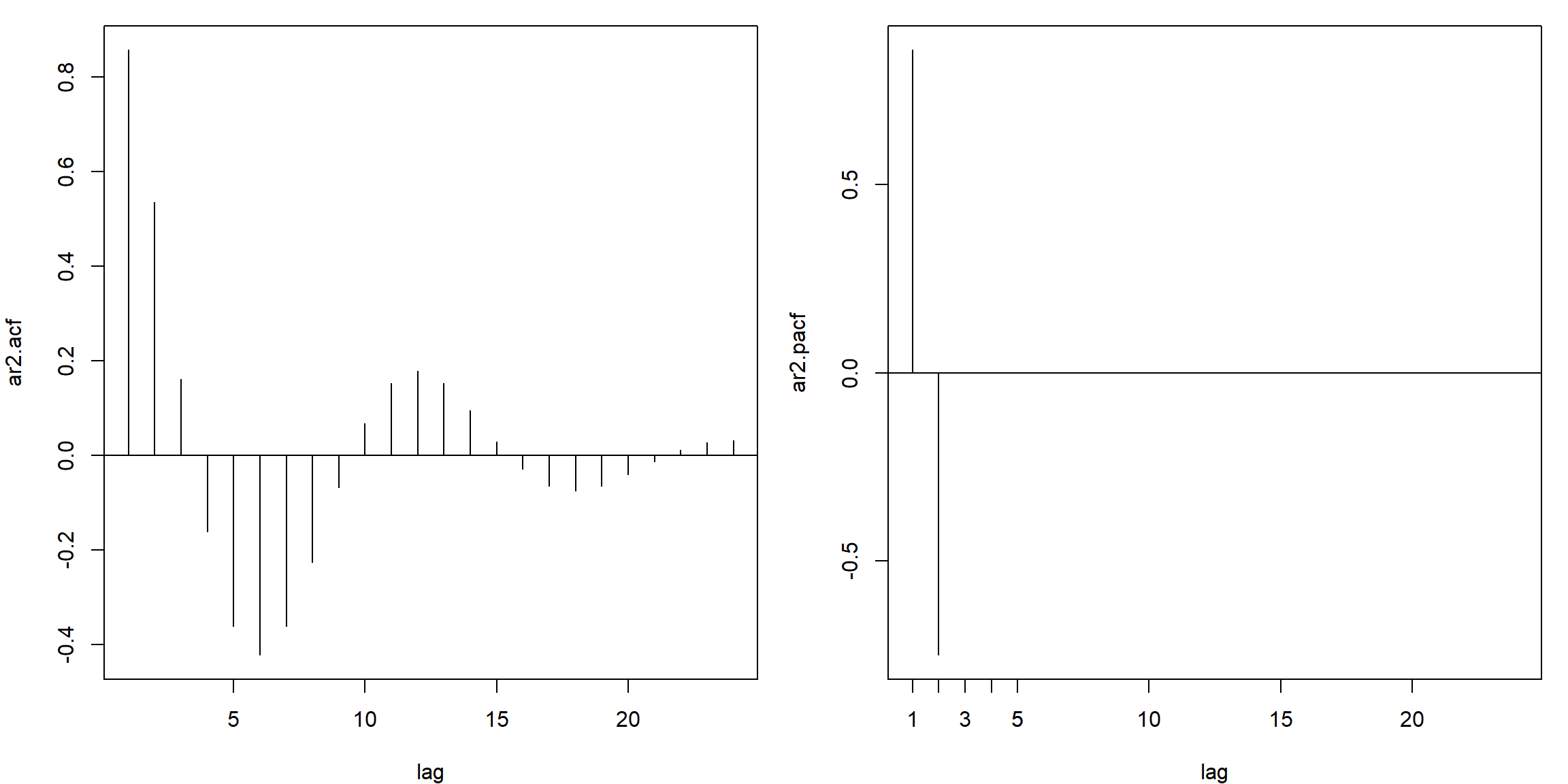

  • PACF: cut off after lag 2

Example 3.29 (p.115) Simulate 50 obs. from MA(1) with \(\theta_1=0.9\)

set.seed(2)
ma1 = arima.sim(list(order = c(0,0,1), ma = 0.9), n = 50)
acf(ma1, plot=FALSE)[1] # = .507 (lag 1 sample ACF)
## 
## Autocorrelations of series 'ma1', by lag
## 
##     1 
## 0.507
  • True ACF: \(\rho(1)=\frac{\theta_1}{1+\theta_1^2}=\) 0.4972376

1.3.1 Behavior of the ACF and PACF for ARMA models

AR(p) MA(q) ARMA(p, q)
ACF Tails off Cuts off after lag q Tails off
PACF Cuts off after lag p Tails off Tails off

1.4 Fit model with different method

在對資料進行建模前，可以用ACF, PACF初步分析，判斷p, q需要選多少

1.4.1 Preliminary Analysis

Example 3.18 (p.99) Preliminary Analysis of the Recruitment Series

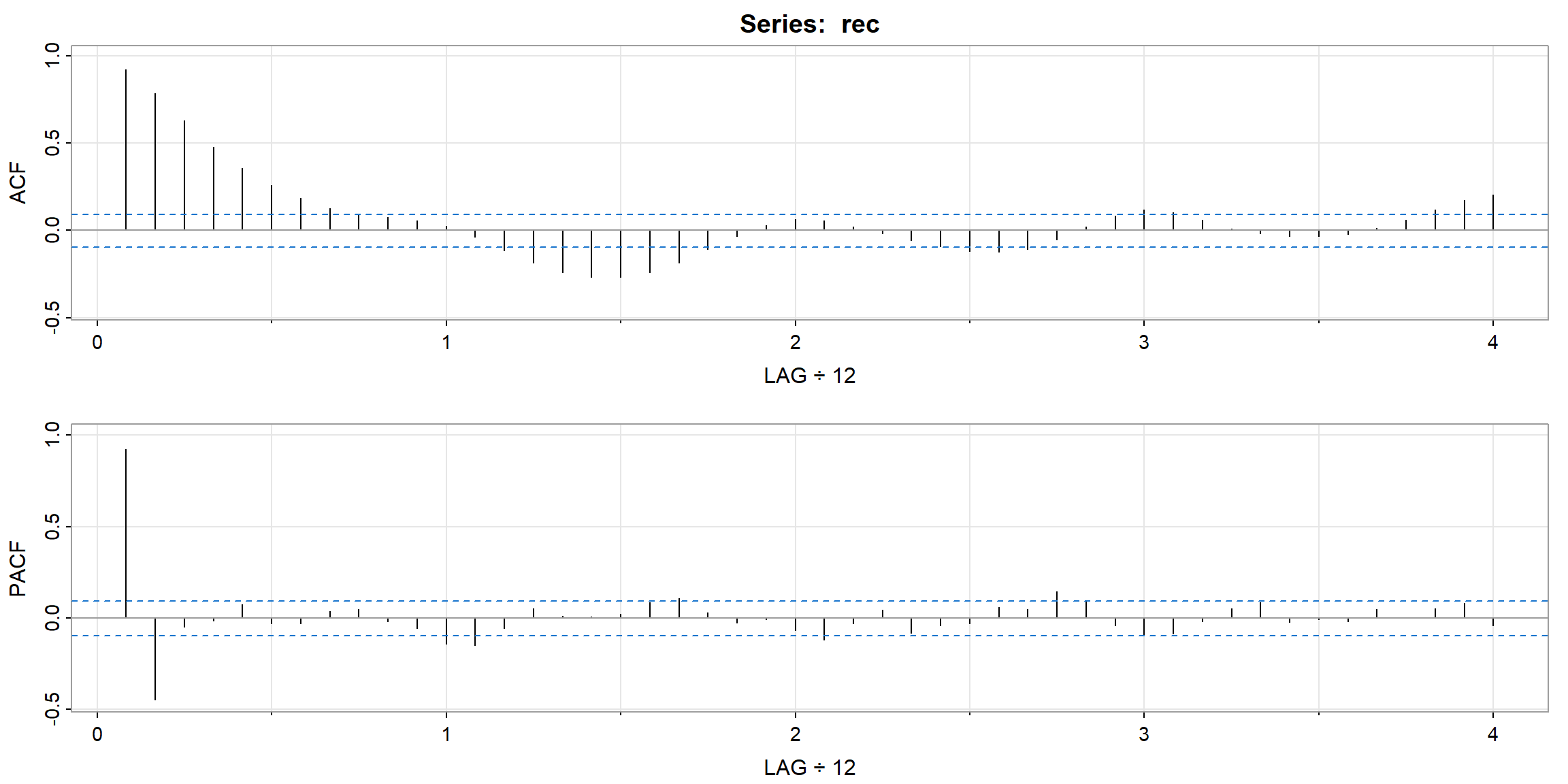
value <- acf2(rec, 48) # will produce values and a graphic

  • ACF decay very fast \(\to\) stationary
  • PACF cut-off after lag 2 (its PACF \(\approx\) 0 after lag 2) \(\to\) AR(2) is suitable for the data
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
ACF 0.92 0.78 0.63 0.48 0.36 0.26 0.18 0.13 0.09 0.07 0.06 0.02 -0.04 -0.12 -0.19 -0.24
PACF 0.92 -0.44 -0.05 -0.02 0.07 -0.03 -0.03 0.04 0.05 -0.02 -0.05 -0.14 -0.15 -0.05 0.05 0.01
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
ACF -0.27 -0.27 -0.24 -0.19 -0.11 -0.03 0.03 0.06 0.06 0.02 -0.02 -0.06 -0.09 -0.12 -0.13 -0.11
PACF 0.01 0.02 0.09 0.11 0.03 -0.03 -0.01 -0.07 -0.12 -0.03 0.05 -0.08 -0.04 -0.03 0.06 0.05
33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48
ACF -0.05 0.02 0.08 0.12 0.10 0.06 0.01 -0.02 -0.03 -0.03 -0.02 0.01 0.06 0.12 0.17 0.20
PACF 0.15 0.09 -0.04 -0.10 -0.09 -0.02 0.05 0.08 -0.02 -0.01 -0.02 0.05 0.01 0.05 0.08 -0.04

1.4.2 Fit AR(2) model to Recruitment Series

Example 3.25 (p.110) Fit AR(2) to rec data by OLS

regr = ar.ols(rec, order=2, demean=FALSE, intercept=TRUE)
fore = predict(regr, n.ahead=24)
ts.plot(rec, fore$pred, col=1:2, xlim=c(1980,1990), ylab="Recruitment")

# 95% CI
U = fore$pred+1.96*fore$se; L = fore$pred-1.96*fore$se
xx = c(time(U), rev(time(U))); yy = c(L, rev(U))
polygon(xx, yy, border = 8, col = gray(.6, alpha = .2))
lines(fore$pred, type="p", col=2)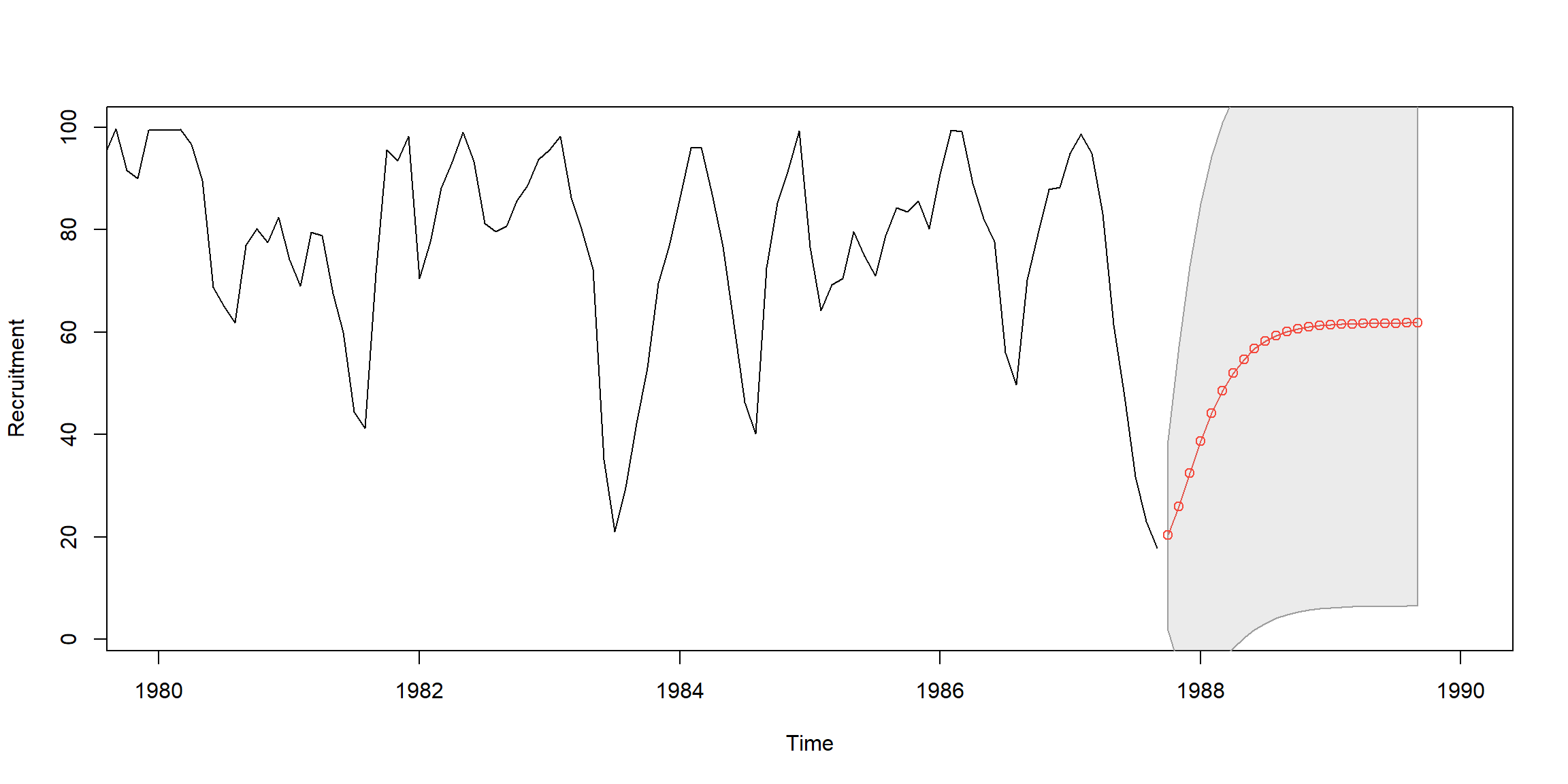

Example 3.28 (p.115) Fit AR(2) to rec data by Yule-Walker

rec.yw = ar.yw(rec, order=2)
rec.yw$x.mean # = 62.26278 (mean estimate)
rec.yw$ar # = 1.3315874, -.4445447 (coefficient estimates)
sqrt(diag(rec.yw$asy.var.coef)) # = .04222637, .04222637 (standard errors)
rec.yw$var.pred # = 94.79912 (error variance estimate)
rec.pr = predict(rec.yw, n.ahead=24)
# 95% CI
U=rec.pr$pred+1.96*rec.pr$se
L=rec.pr$pred-1.96*rec.pr$se
minx=min(rec,L);maxx=max(rec,U)
ts.plot(rec, rec.pr$pred, xlim=c(1980,1990),ylim=c(minx,maxx))
lines(rec.pr$pred,col="red",type="o")
lines(U, col="blue", lty="dashed")
lines(L, col="blue", lty="dashed")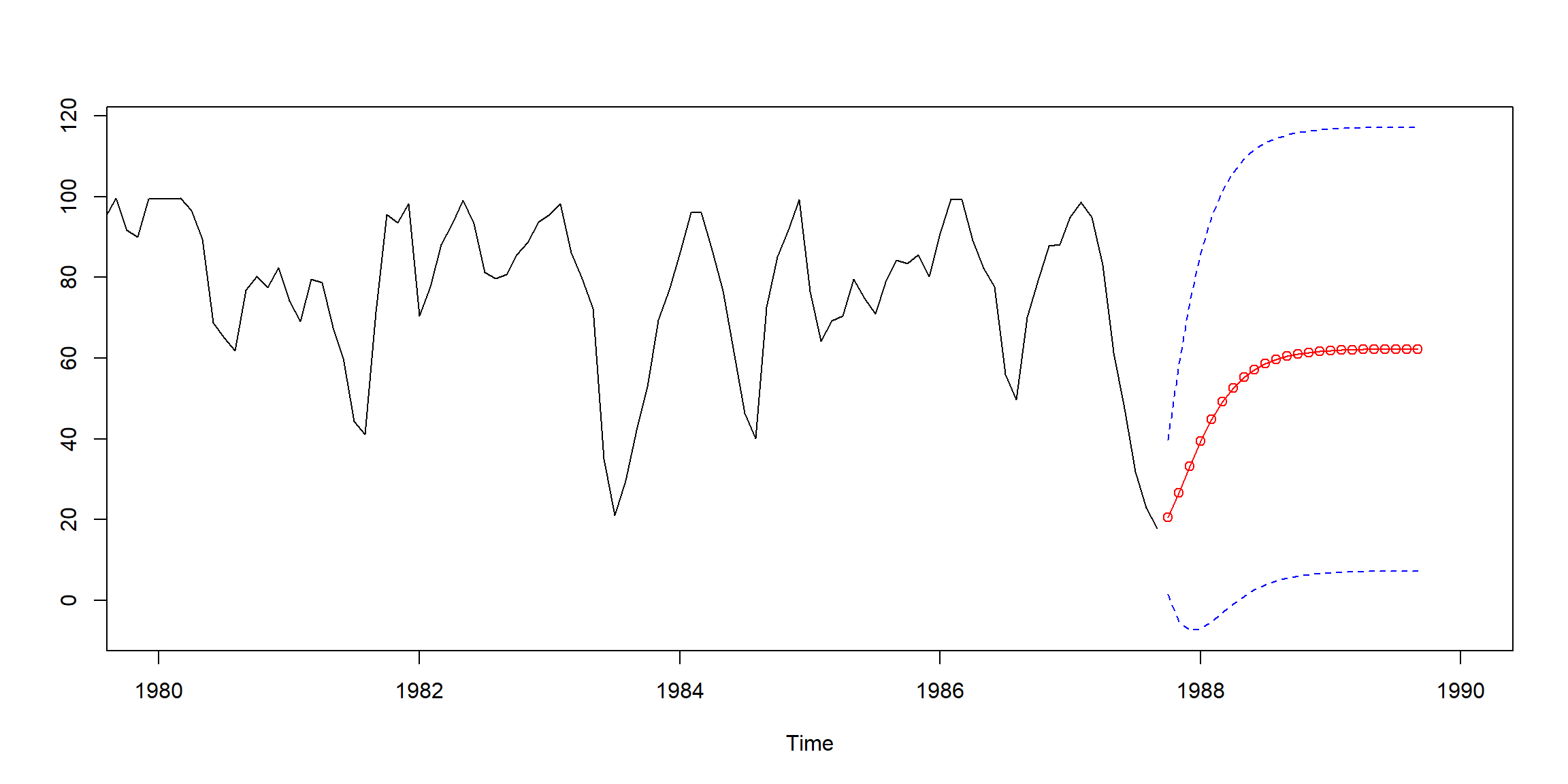

Example 3.31 (p.120) Fit AR(2) to rec data by MLE

rec.mle = ar.mle(rec, order=2)
rec.mle$x.mean # 62.26
rec.mle$ar # 1.35, -.46
sqrt(diag(rec.mle$asy.var.coef)) # .04, .04
rec.mle$var.pred # 89.34

1.4.3 compare AR(2) model’s coef. estimated by OLS, YW, and MLE

OLS YW MLE
1.354, -0.463 1.332, -0.445 1.351, -0.461
  • Its coefficient estimator is similar

1.5 Analysis of GNP Data

Example 3.39, 3.40 (p.136, 139)

plot(gnp)

val <- acf2(gnp, 50)

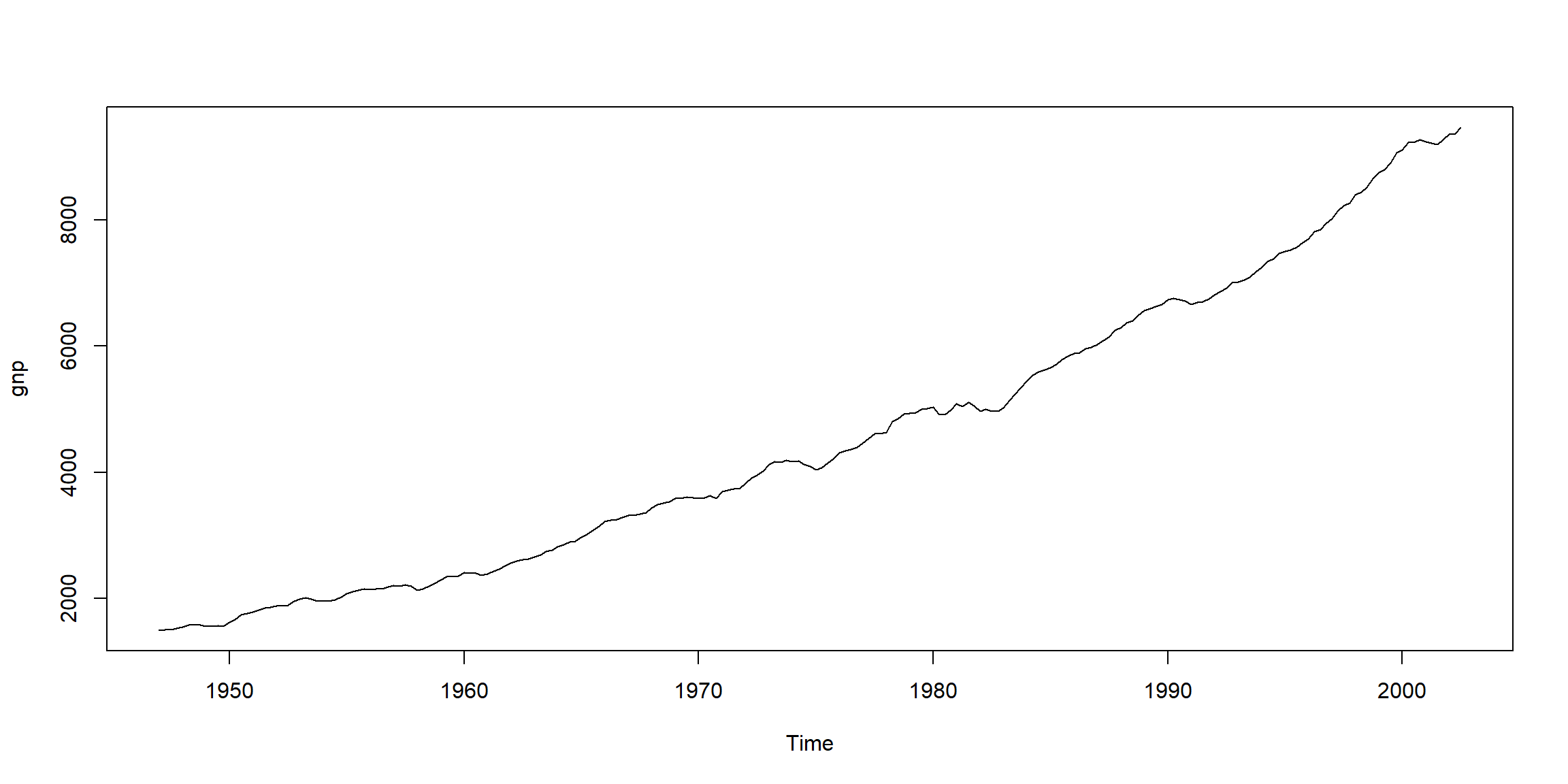
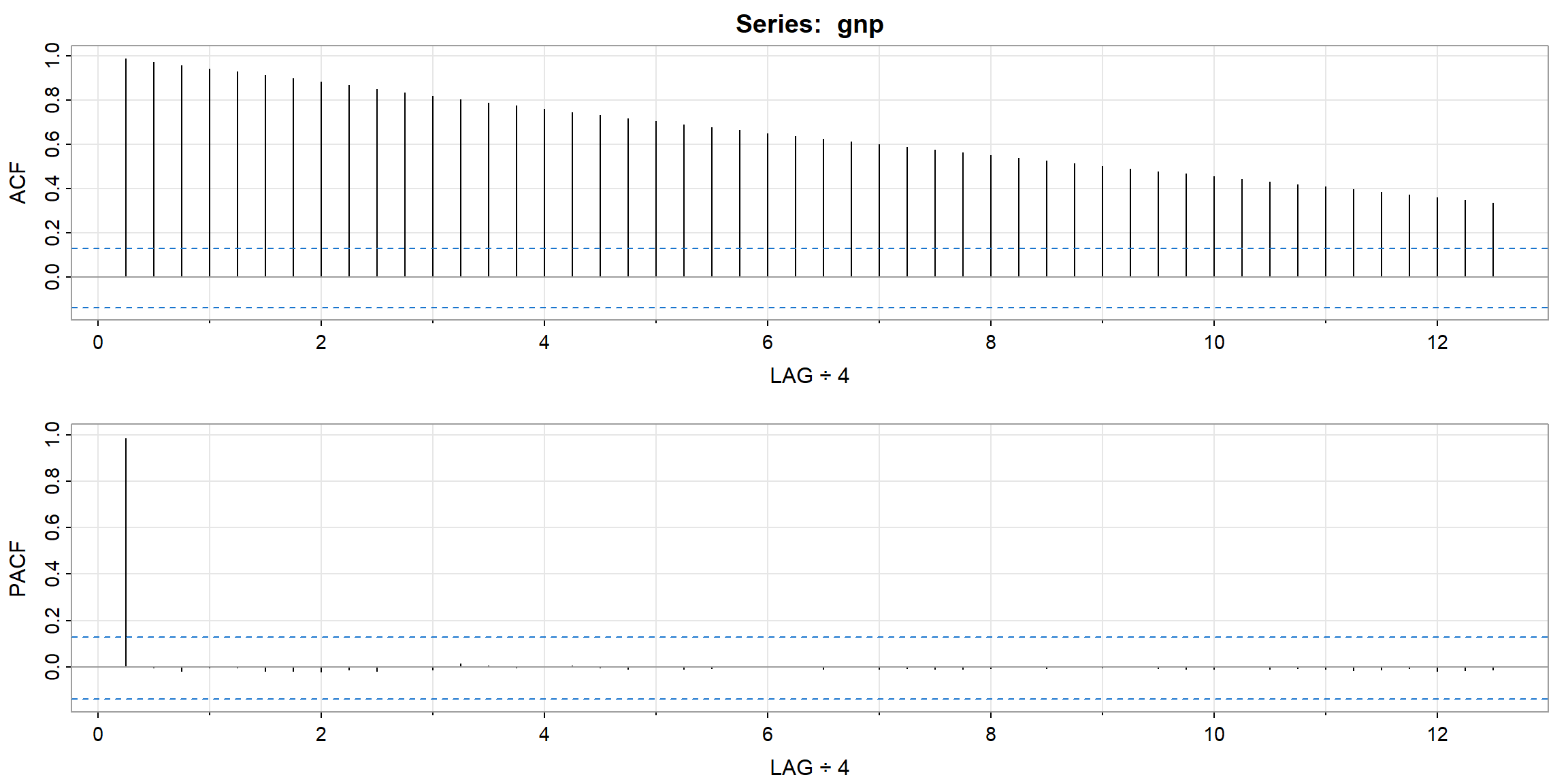
  • ACF looks not stationary
gnpgr = diff(log(gnp)) # growth rate
  • \(diff(log(X_t))=logX_t-logX_{t-1}=log\frac{X_t}{X_{t-1}}, \;growth\)
    • \(diff(log(X_t))>0, \uparrow\)
    • \(diff(log(X_t))<0, \downarrow\)
plot(gnpgr, ylab="GNP growth rate", lwd=2)
abline(h=mean(gnpgr), lty=2, col=2, lwd=2)
legend("topright", legend = "average growth rate", lty=2, lwd=2, col=2)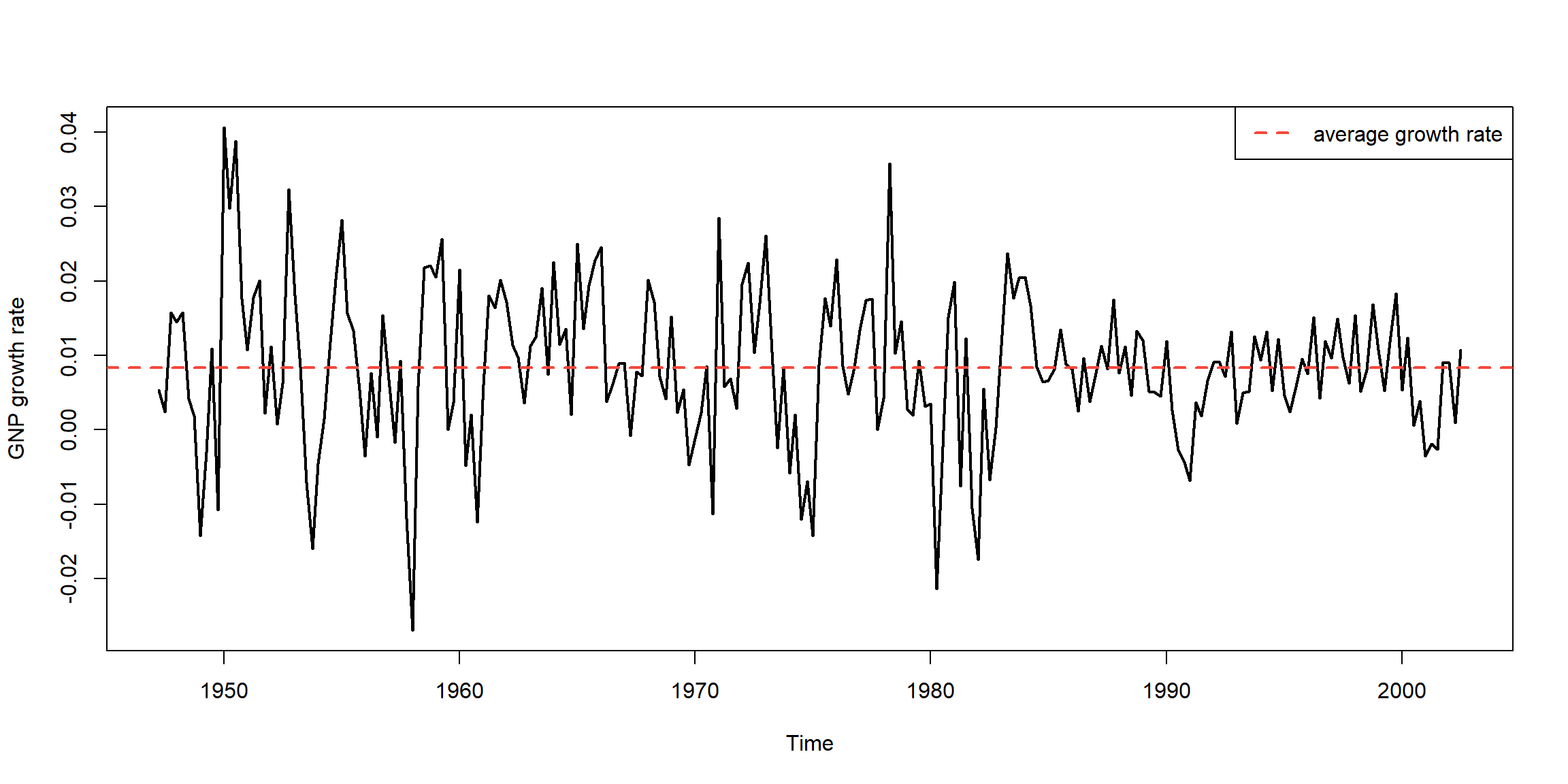

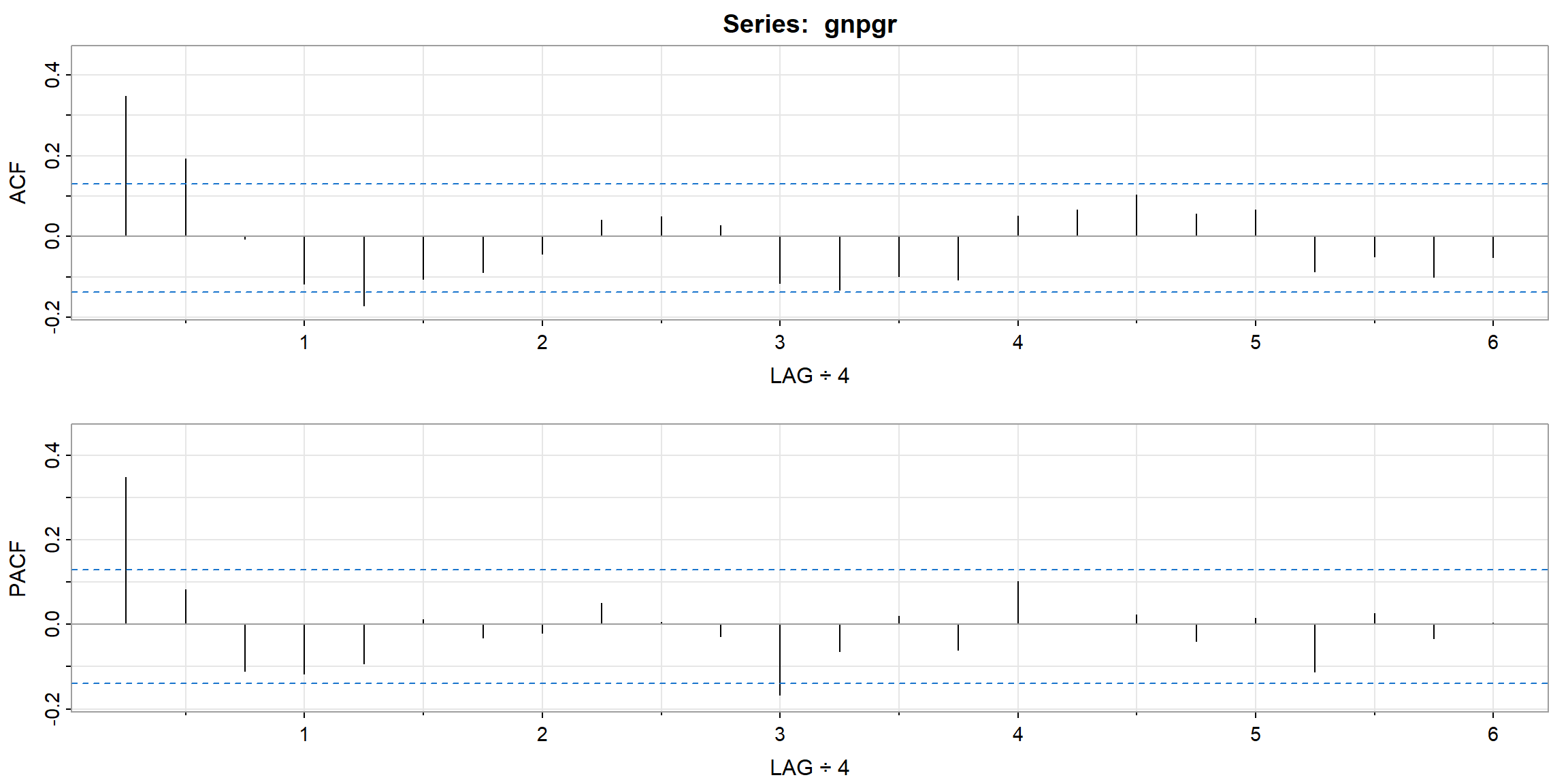
val <- acf2(gnpgr, 24)

  • ACF cut-off after lag 2 \(\Rightarrow\) MA(2)
  • PACF cut-off after lag 1 \(\Rightarrow\) AR(1)
1 2 3 4 5 6 7 8 9 10 11 12
ACF 0.35 0.19 -0.01 -0.12 -0.17 -0.11 -0.09 -0.04 0.04 0.05 0.03 -0.12
PACF 0.35 0.08 -0.11 -0.12 -0.09 0.01 -0.03 -0.02 0.05 0.01 -0.03 -0.17
13 14 15 16 17 18 19 20 21 22 23 24
ACF -0.13 -0.10 -0.11 0.05 0.07 0.10 0.06 0.07 -0.09 -0.05 -0.10 -0.05
PACF -0.06 0.02 -0.06 0.10 0.00 0.02 -0.04 0.01 -0.11 0.03 -0.03 0.00

1.5.1 Diagnostics

out1 <- sarima(gnpgr, 1, 0, 0) # AR(1)

out2 <- sarima(gnpgr, 0, 0, 2) # MA(2)

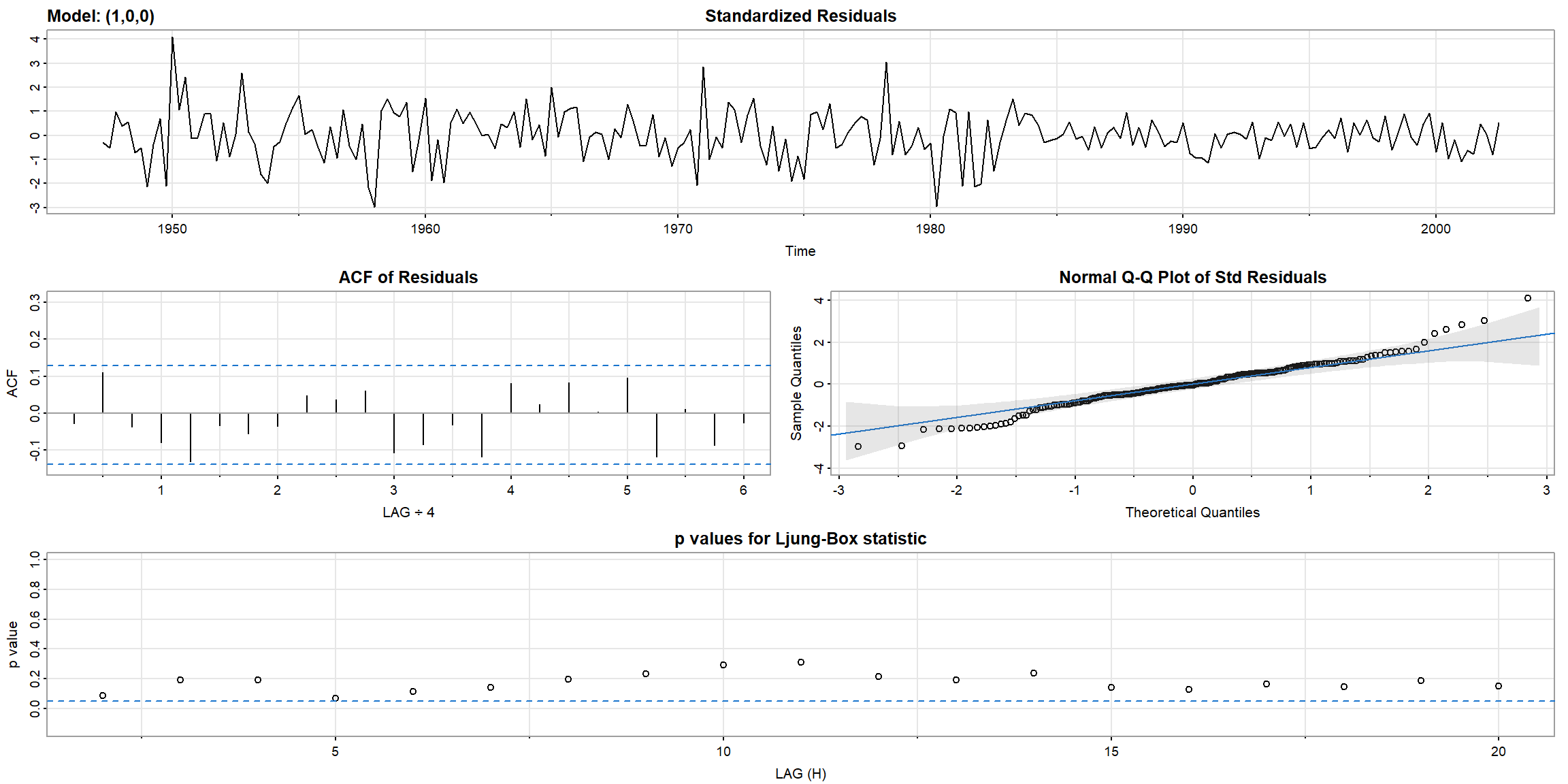
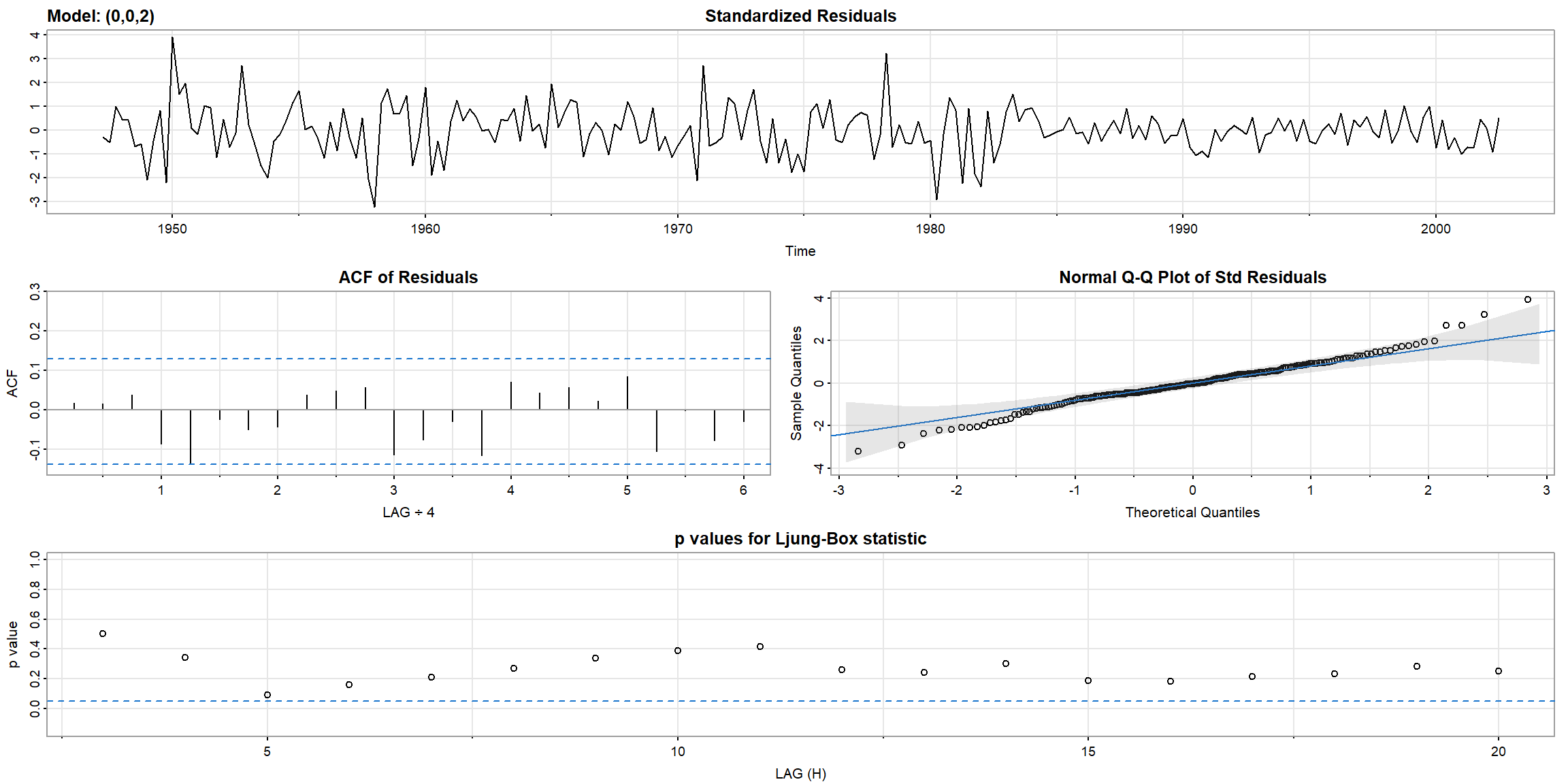
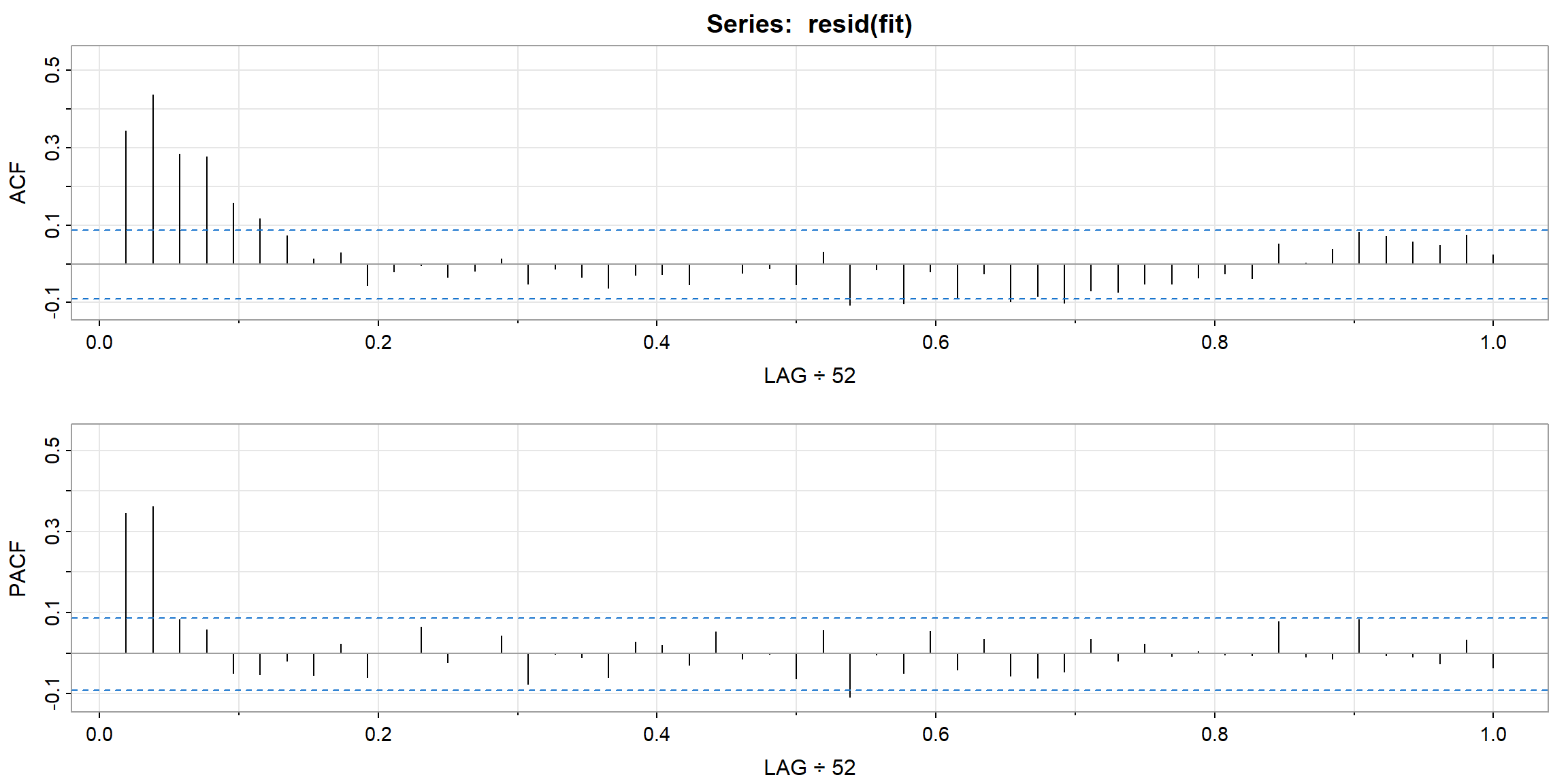
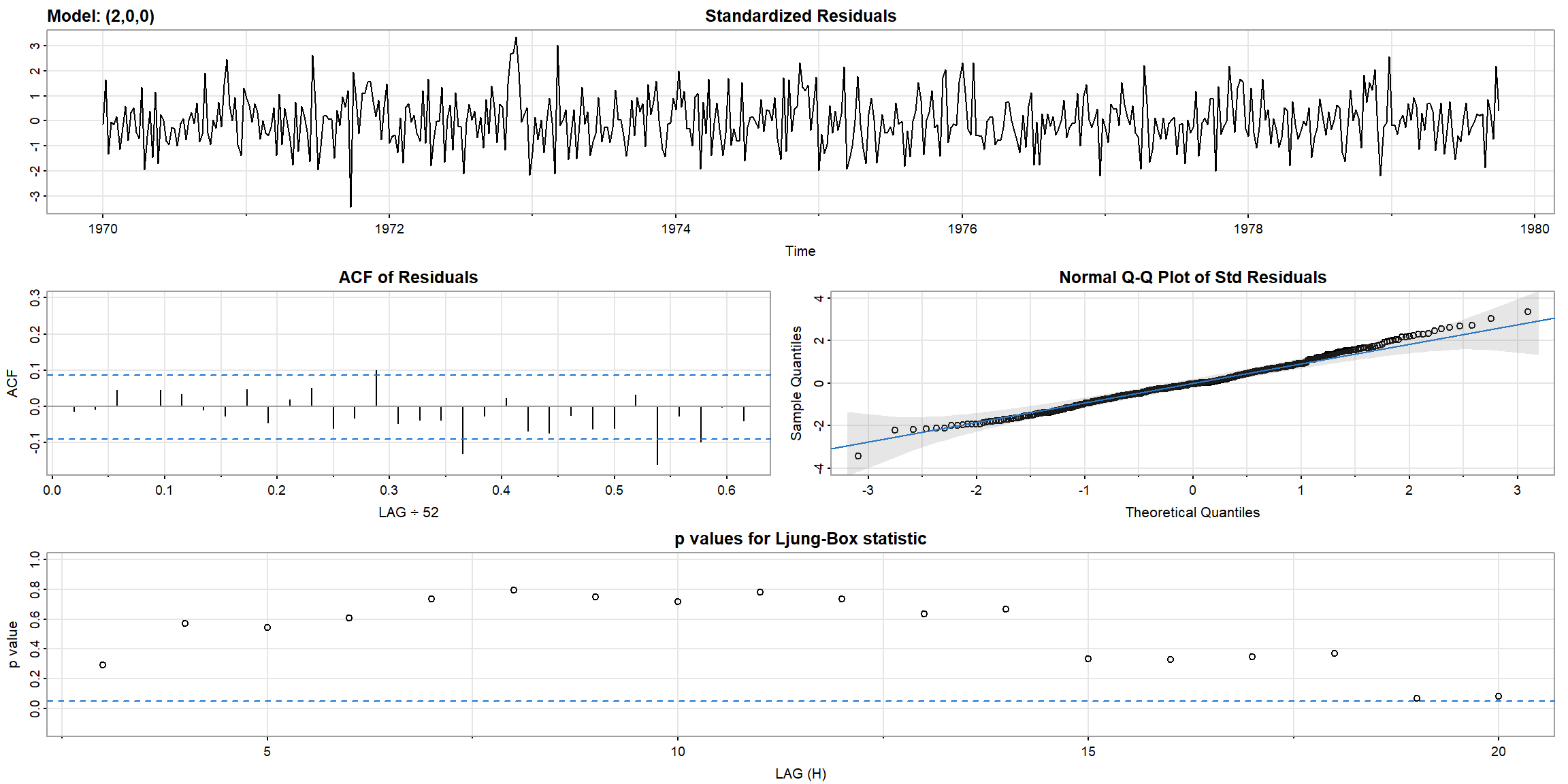
  • In Ljung-Box statistic, both model’s p-value>0.05, \(\therefore\) AR(1) is suitable for gnpgr
ARMAtoMA(ar=.35, ma=0, 10) # prints psi-weights
##  [1] 3.500000e-01 1.225000e-01 4.287500e-02 1.500625e-02 5.252187e-03
##  [6] 1.838266e-03 6.433930e-04 2.251875e-04 7.881564e-05 2.758547e-05

1.5.2 model selection

Both AR(1) and MA(2) are suitable. Then, which one is better?

  • Use AIC, AICC or BIC, the smaller the better.
model AIC AICc BIC
AR(1) -6.44694 -6.4466932 -6.4009579
MA(2) -6.4501328 -6.4496369 -6.3888233
  • Since MA(2) model’s AIC, AICC and BIC are smaller than AR(1) model’s, MA(2) is better.

1.6 Model Diagnostics

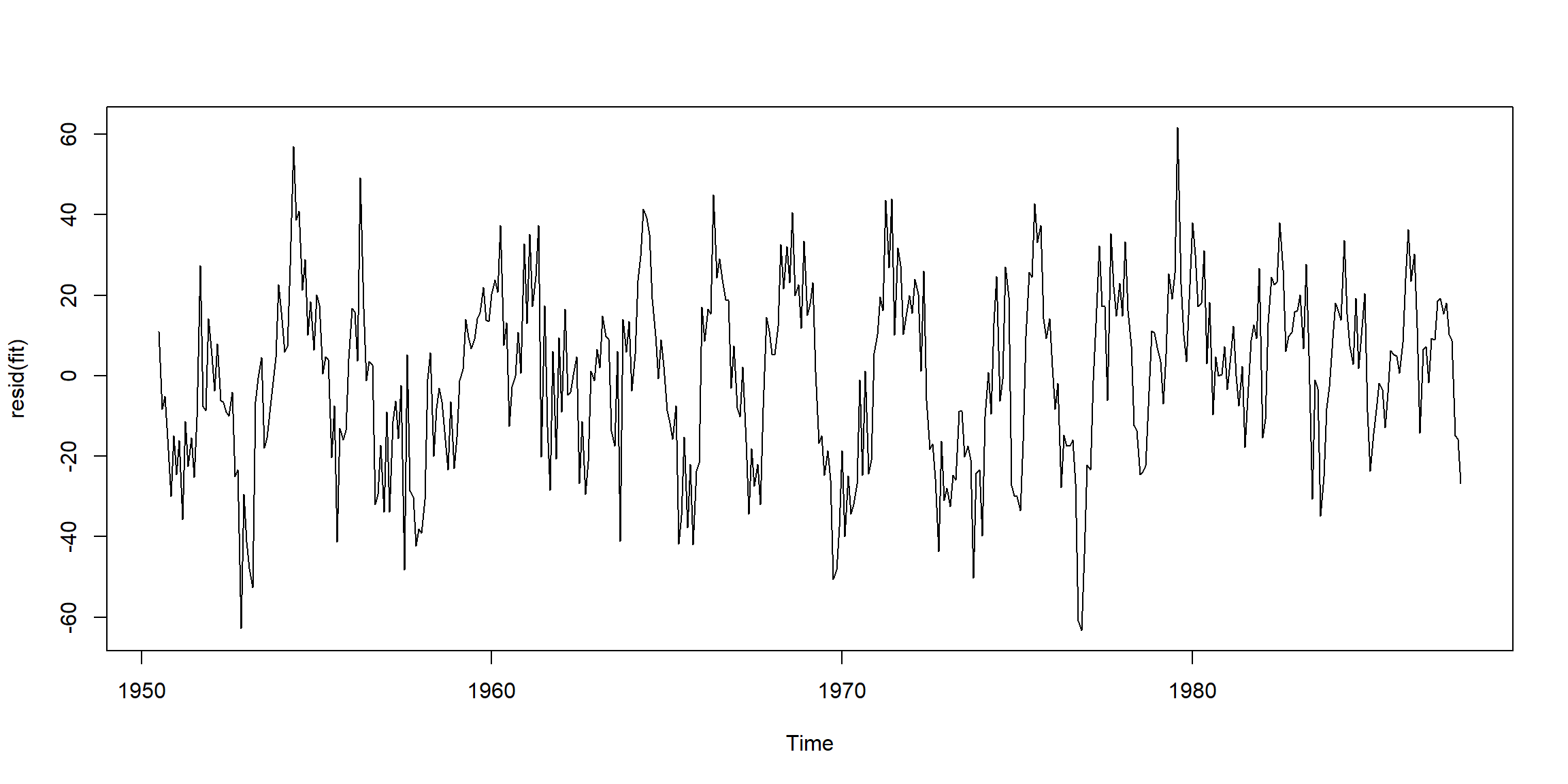
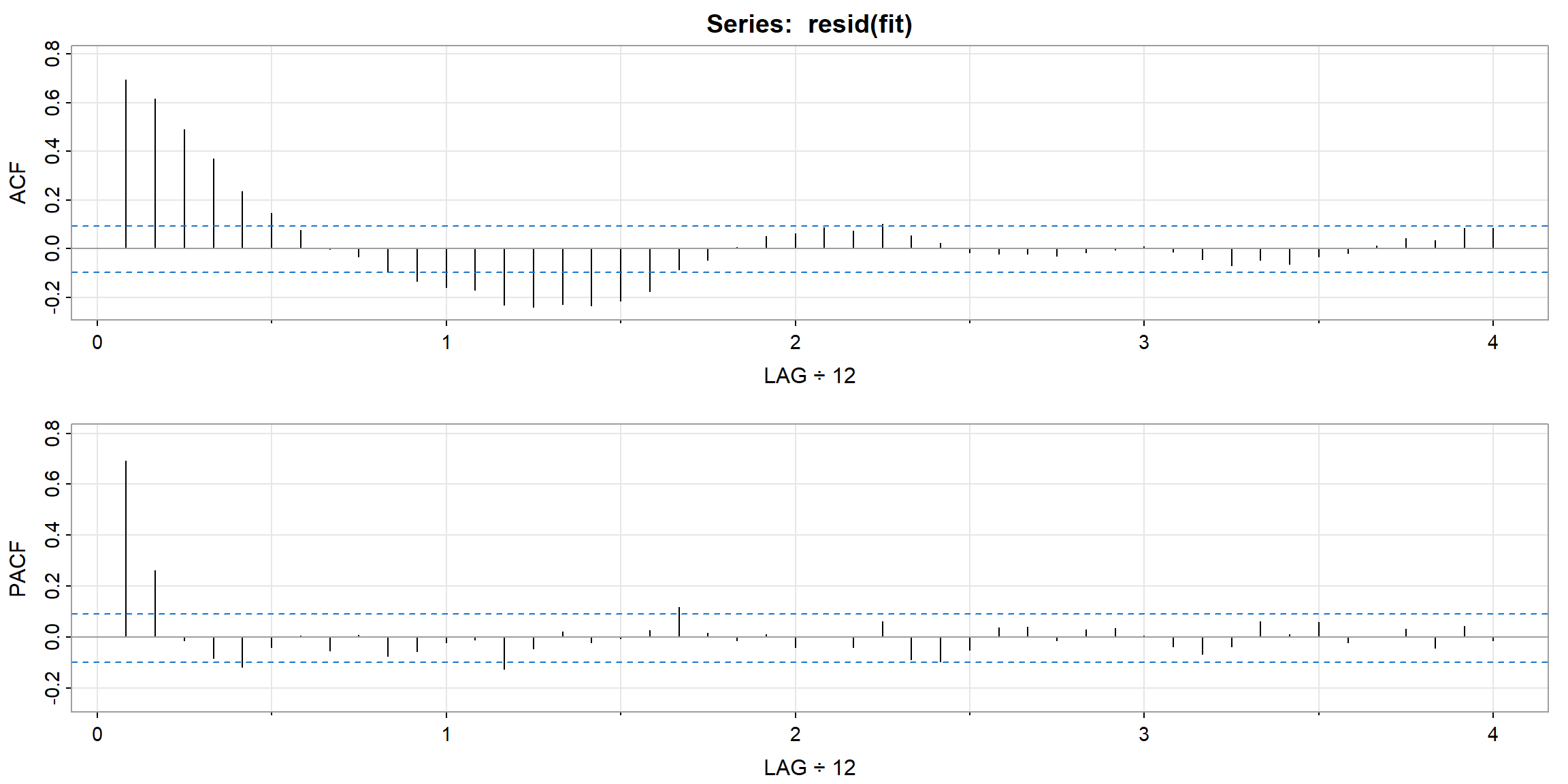
Example 3.41 (p.140) Diagnostics for the Glacial Varve Series

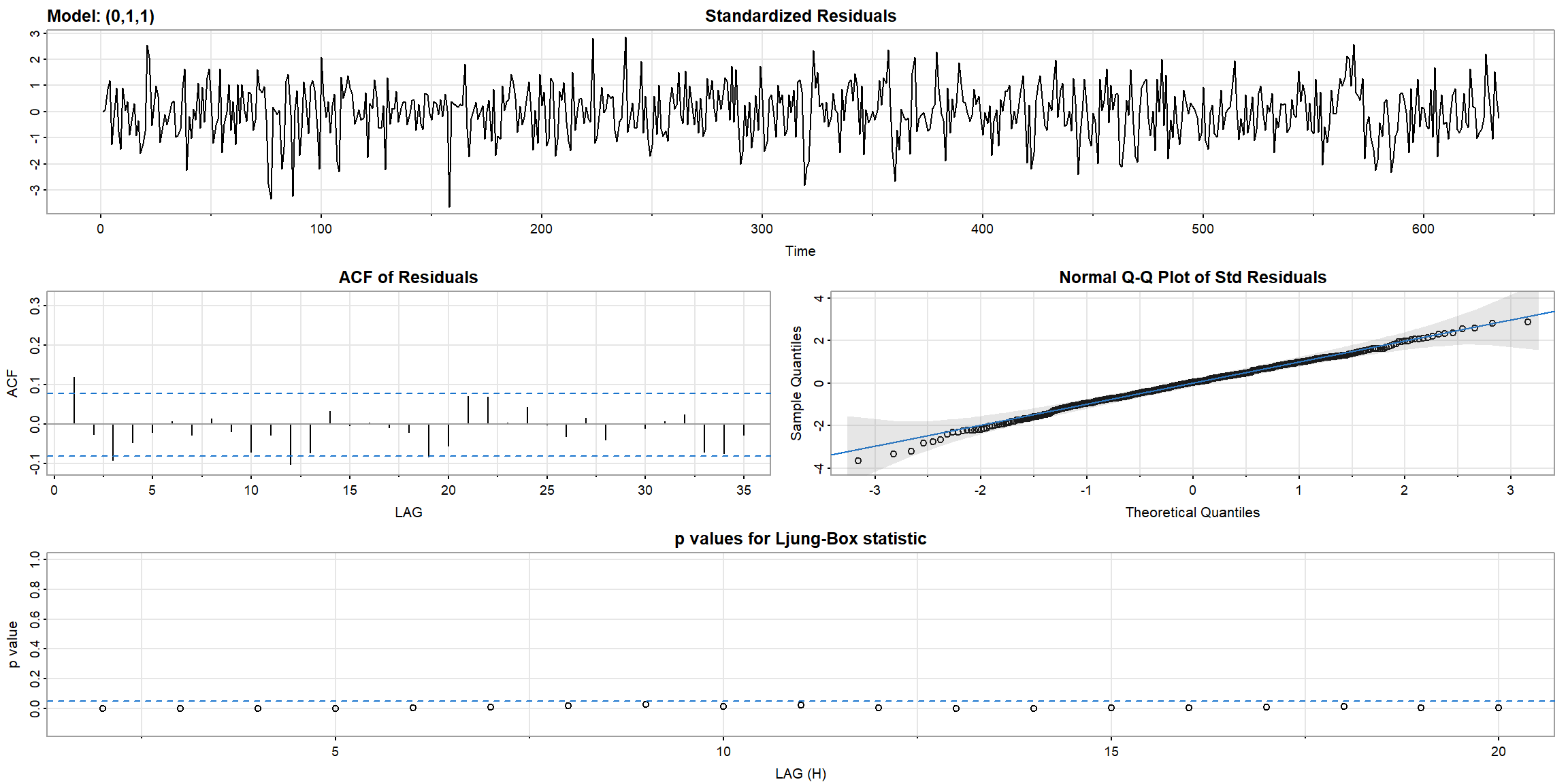
sarima(log(varve), 0, 1, 1, no.constant=TRUE) # ARIMA(0,1,1)

  • ACF outside the CI, and p-value$$0.05, \(\therefore\) ARIMA(0,1,1) is not suitable for log(varve)
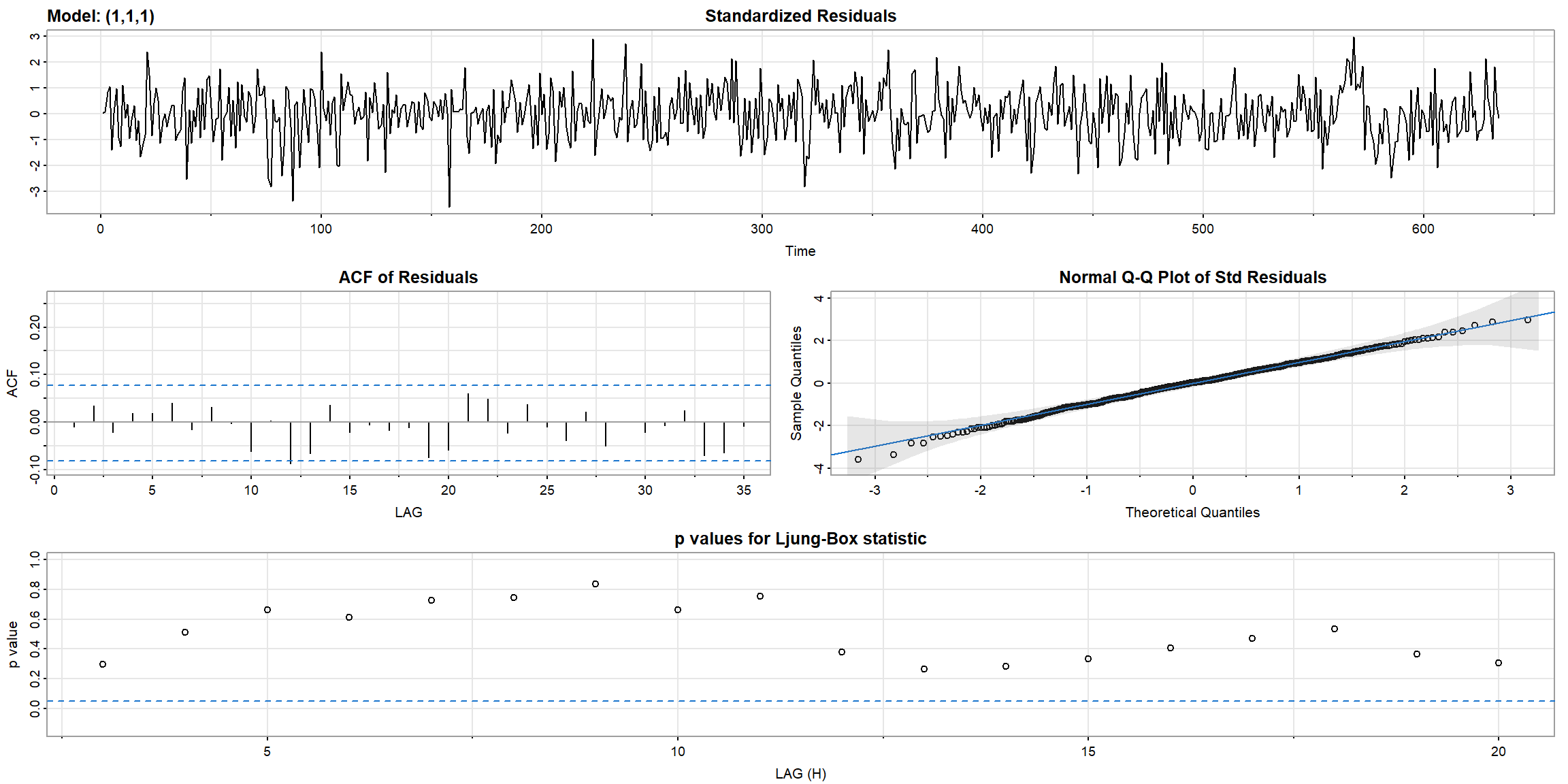
sarima(log(varve), 1, 1, 1, no.constant=TRUE) # ARIMA(1,1,1)

  • all ACF inside the CI, and all p-value above 0.05, \(\therefore\) ARIMA(1,1,1) is suitable for log(varve).

1.7 Regression with Autocorrelated Errors

Example 3.44 (p.144) Mortality, Temperature and Pollution

  • 配適模型查看溫度(temperature)、顆粒物水平(particulate levels)與心血管死亡率(cardiovascular mortality)的關係

\[M_t=\beta_1+\beta_2t+\beta_3T_t+\beta_4T^2_t+\beta_5P_t+x_t\]

trend = time(cmort); temp = tempr - mean(tempr); temp2 = temp^2
fit <- lm(cmort~trend + temp + temp2 + part, na.action=NULL)
round(summary(fit)$coef, 3) |> knitr::kable()
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2831.490 199.557 14.189 0
trend -1.396 0.101 -13.820 0
temp -0.472 0.032 -14.941 0
temp2 0.023 0.003 7.990 0
part 0.255 0.019 13.541 0 
acf2(resid(fit), 52) # implies AR2

sarima(cmort, 2,0,0, xreg=cbind(trend,temp,temp2,part))

  • ACF outside the CI, but the p-value are above 0.05, \(\therefore\) AR(2) is not good enough for cmort.

Example 3.45 (p.145) Regression with Lagged Variables

\[R_t=\beta_0+\beta_1S_{t−6}+\beta_2D_{t−6}+\beta_3D_{t−6}S_{t−6}+wt\]

dummy = ifelse(soi<0, 0, 1)
fish = ts.intersect(rec, soiL6=lag(soi,-6), dL6=lag(dummy,-6), dframe=TRUE)
fit <- lm(rec ~ soiL6*dL6, data=fish, na.action=NULL)
round(summary(fit)$coef, 3) |> knitr::kable()
Estimate Std. Error t value Pr(>|t|)
(Intercept) 74.479 2.865 25.998 0.000
soiL6 -15.358 7.401 -2.075 0.039
dL6 -1.139 3.711 -0.307 0.759
soiL6:dL6 -51.244 9.523 -5.381 0.000 
attach(fish)
## The following object is masked from package:astsa:
## 
##     rec
plot(resid(fit))

acf2(resid(fit)) # indicates AR(2)

intract = soiL6*dL6 # interaction term
sarima(rec,2,0,0, xreg = cbind(soiL6, dL6, intract))

  • ACF outside the CI, and the p-value are below 0.05, \(\therefore\) AR(2) is not suitable.

1.8 Multiplicative Seasonal ARIMA Models

  • 先一階差分再看季節性 * 季節性資料優先處理季節性，再看需不需要差分

Example 3.46 (p.146) A Seasonal AR Series

\[(1 − 0.9\cdot B^{12})x_t = w_t\]

set.seed(666)
phi = c(rep(0,11),.9)
sAR = arima.sim(list(order=c(12,0,0), ar=phi), n=37)
sAR = ts(sAR, freq=12)
layout(matrix(c(1,1,2, 1,1,3), nc=2))
par(mar=c(3,3,2,1), mgp=c(1.6,.6,0))
plot(sAR, axes=FALSE, main='seasonal AR(1)', xlab="year", type='c')
Months = c("J","F","M","A","M","J","J","A","S","O","N","D")
points(sAR, pch=Months, cex=1.25, font=4, col=1:4)
axis(1, 1:4); abline(v=1:4, lty=2, col=gray(.7))
axis(2); box()
ACF = ARMAacf(ar=phi, ma=0, 100)
PACF = ARMAacf(ar=phi, ma=0, 100, pacf=TRUE)
plot(ACF,type="h", xlab="LAG", ylim=c(-.1,1)); abline(h=0)
plot(PACF, type="h", xlab="LAG", ylim=c(-.1,1)); abline(h=0)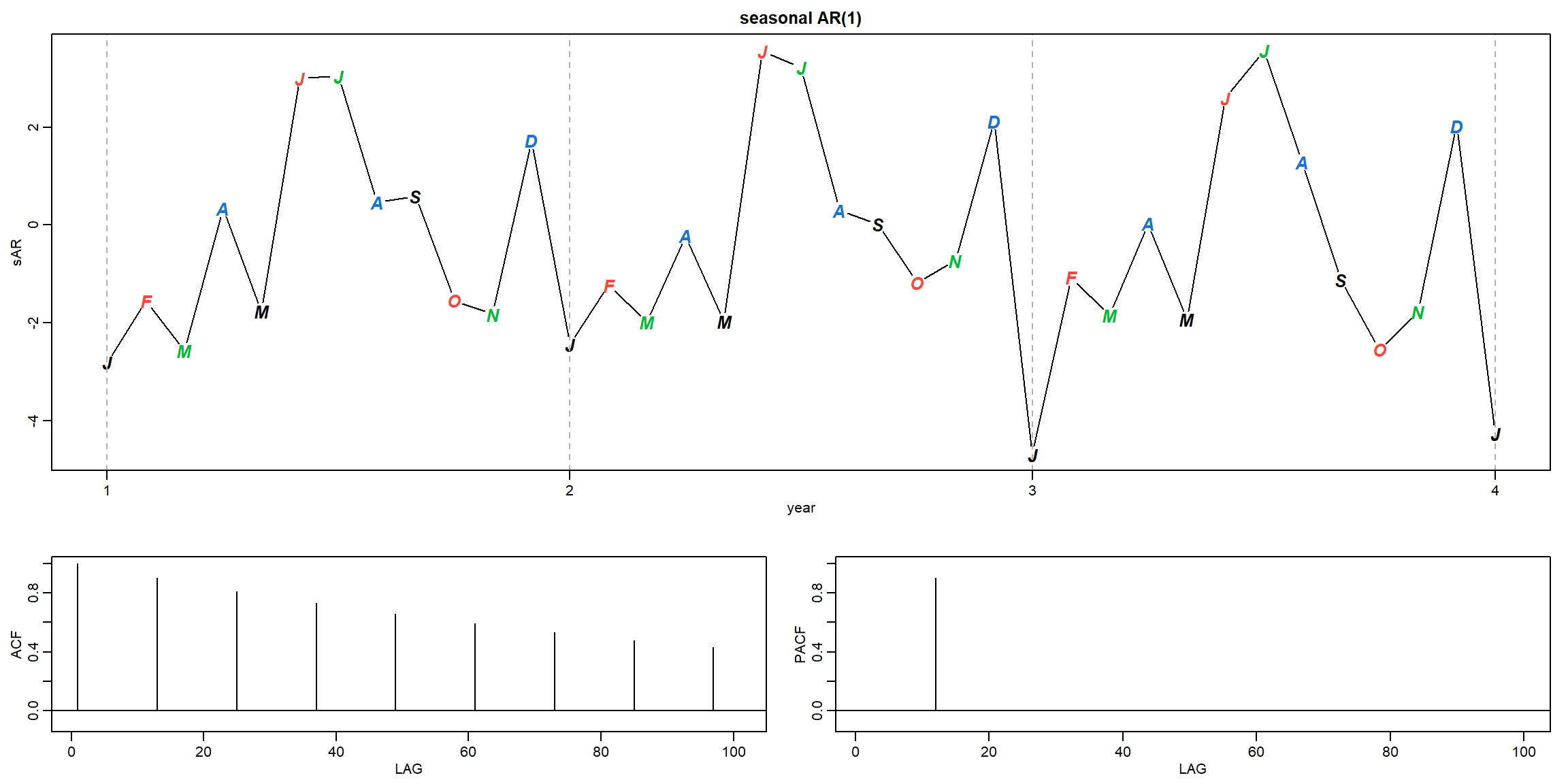

  • Theoretical ACF tails off at lag 12, 24, 36, …
  • Theoretical PACF cut-off at lag 12
acf2(sAR, max.lag = 35)

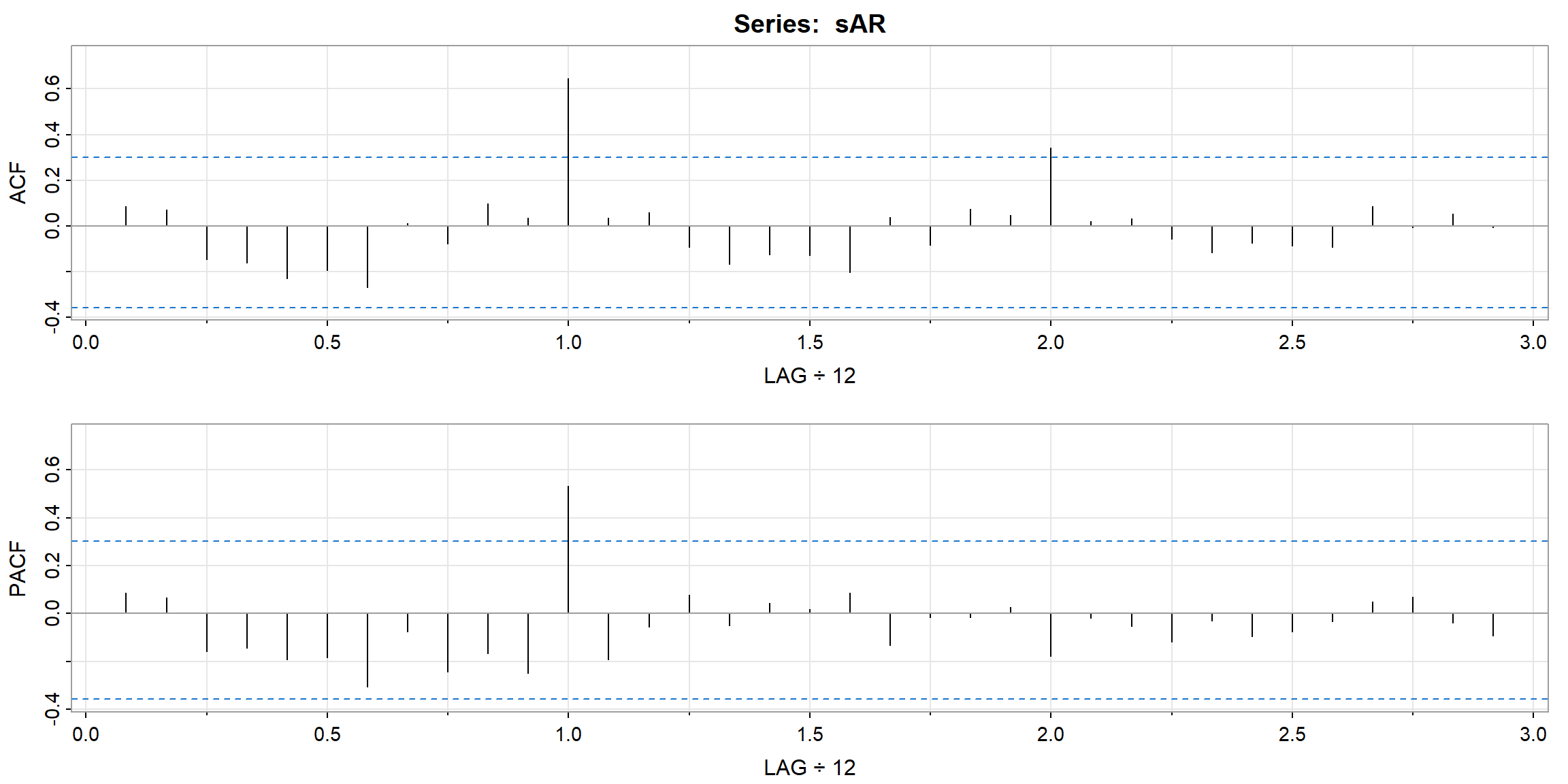
  • Those patterns are also observed in the sample ACF and PACF.

Example 3.47 (p.145) seasonal ARMA

\[X_t-.8X_{t-12}=W_t-.5W_{t-1}\]

phi = c(rep(0,11),.8)
ACF = ARMAacf(ar=phi, ma=-.5, 50)[-1] # [-1] removes 0 lag
PACF = ARMAacf(ar=phi, ma=-.5, 50, pacf=TRUE)
par(mfrow=c(1,2))
plot(ACF, type="h", xlab="LAG", ylim=c(-.4,.8)); abline(h=0)
axis(1, at=0:50, label=F); axis(1, at=seq(0,50,by=10), lwd=2)
plot(PACF, type="h", xlab="LAG", ylim=c(-.4,.8)); abline(h=0)
axis(1, at=0:50, label=F); axis(1, at=seq(0,50,by=10), lwd=2)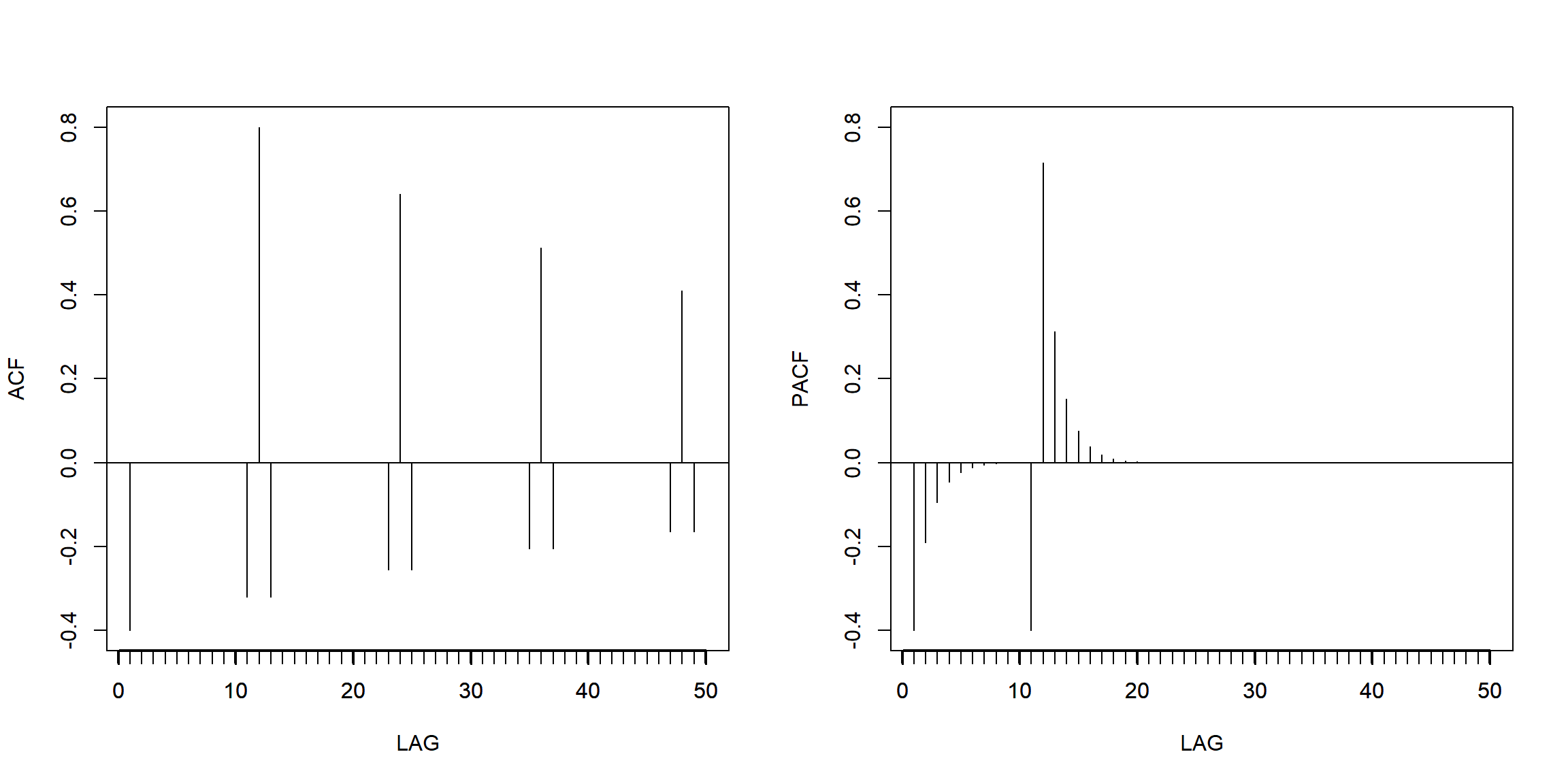

  • PACF cut-off at lag 12, so \(AR(1)_{12}\) is suitable.
  • ACF cut-off at lag 1, so \(MA(1)\) is suitable.

1.9 Periodogram

Example 4.1 (p.167) A Periodic Series

x1 = 2*cos(2*pi*1:100*6/100) + 3*sin(2*pi*1:100*6/100)
x2 = 4*cos(2*pi*1:100*10/100) + 5*sin(2*pi*1:100*10/100)
x3 = 6*cos(2*pi*1:100*40/100) + 7*sin(2*pi*1:100*40/100)
x = x1 + x2 + x3

par(mfrow=c(2,2), mar=c(4,4,2,1))
plot.ts(x1, ylim=c(-10,10), main=expression(omega==6/100~~~A^2==13))
plot.ts(x2, ylim=c(-10,10), main=expression(omega==10/100~~~A^2==41))
plot.ts(x3, ylim=c(-10,10), main=expression(omega==40/100~~~A^2==85))
plot.ts(x, ylim=c(-16,16), main="sum")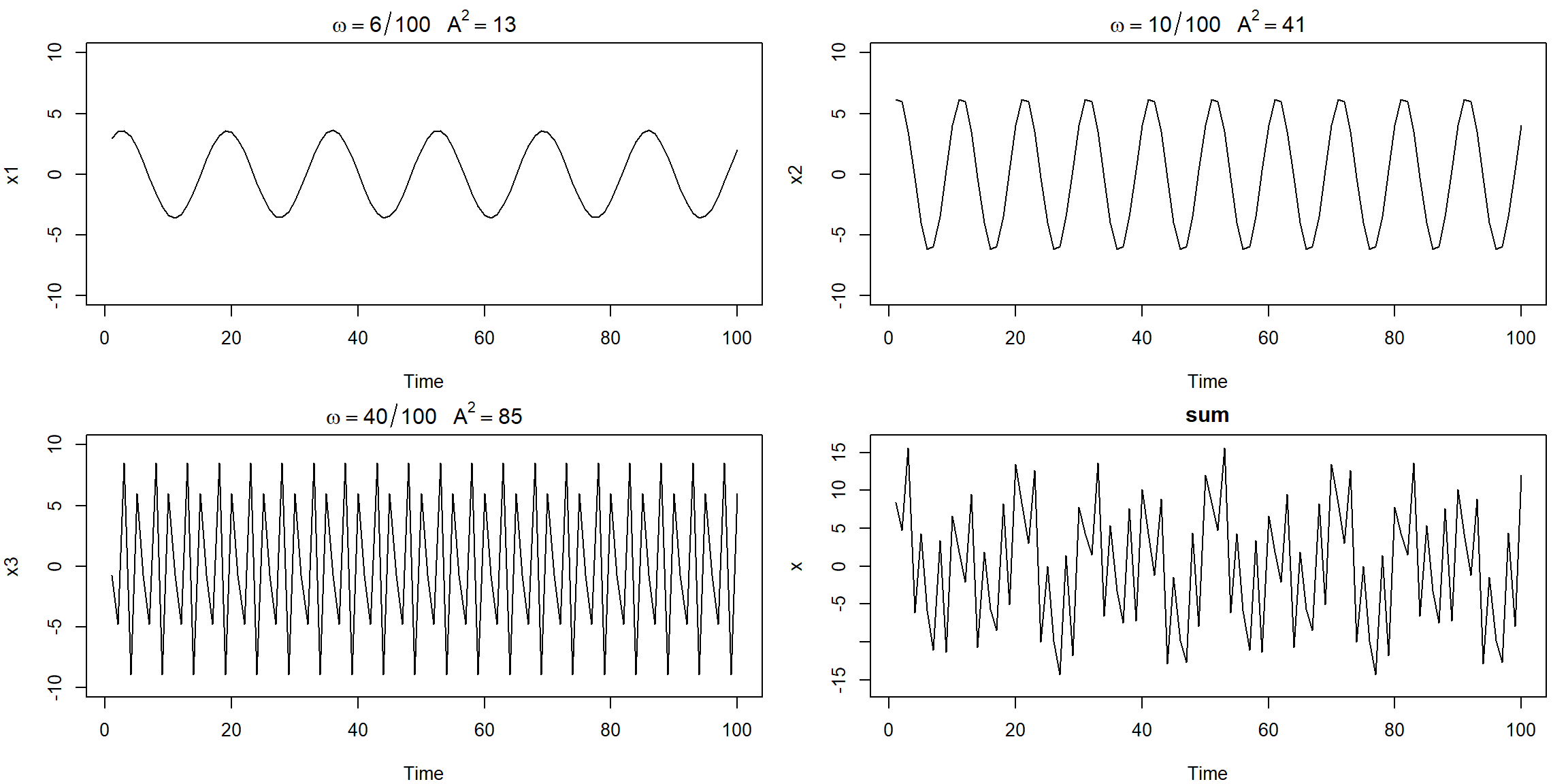

when there is many periodic, it is hard to see

  • A: height of the peak
    • for \(x_1\), \(A^2=2^2+3^2=13\), the maximum and minimum values that \(x_1\) will attain are \(\pm\sqrt{13}=\pm3.61\)
  • \(\omega=\frac jn\): j = repeated times

Example 4.2 (p.169) Estimation and the Periodogram

P = Mod(2*fft(x)/100)^2; Fr = 0:99/100
plot(Fr, P, type="o", xlab="frequency", ylab="scaled periodogram")
abline(v=0.5, col="red", lty=2)
points(x=Fr[7], y=P[7], col="red", pch=1, cex=3);text(x=Fr[7], y=P[7], labels = "6/100", pos=3, col="red")
points(x=Fr[11], y=P[11], col="red", pch=1, cex=3);text(x=Fr[11], y=P[11], labels = "10/100", pos=3, col="red")
points(x=Fr[41], y=P[41], col="red", pch=1, cex=3);text(x=Fr[41], y=P[41], labels = "40/100", pos=1, col="red")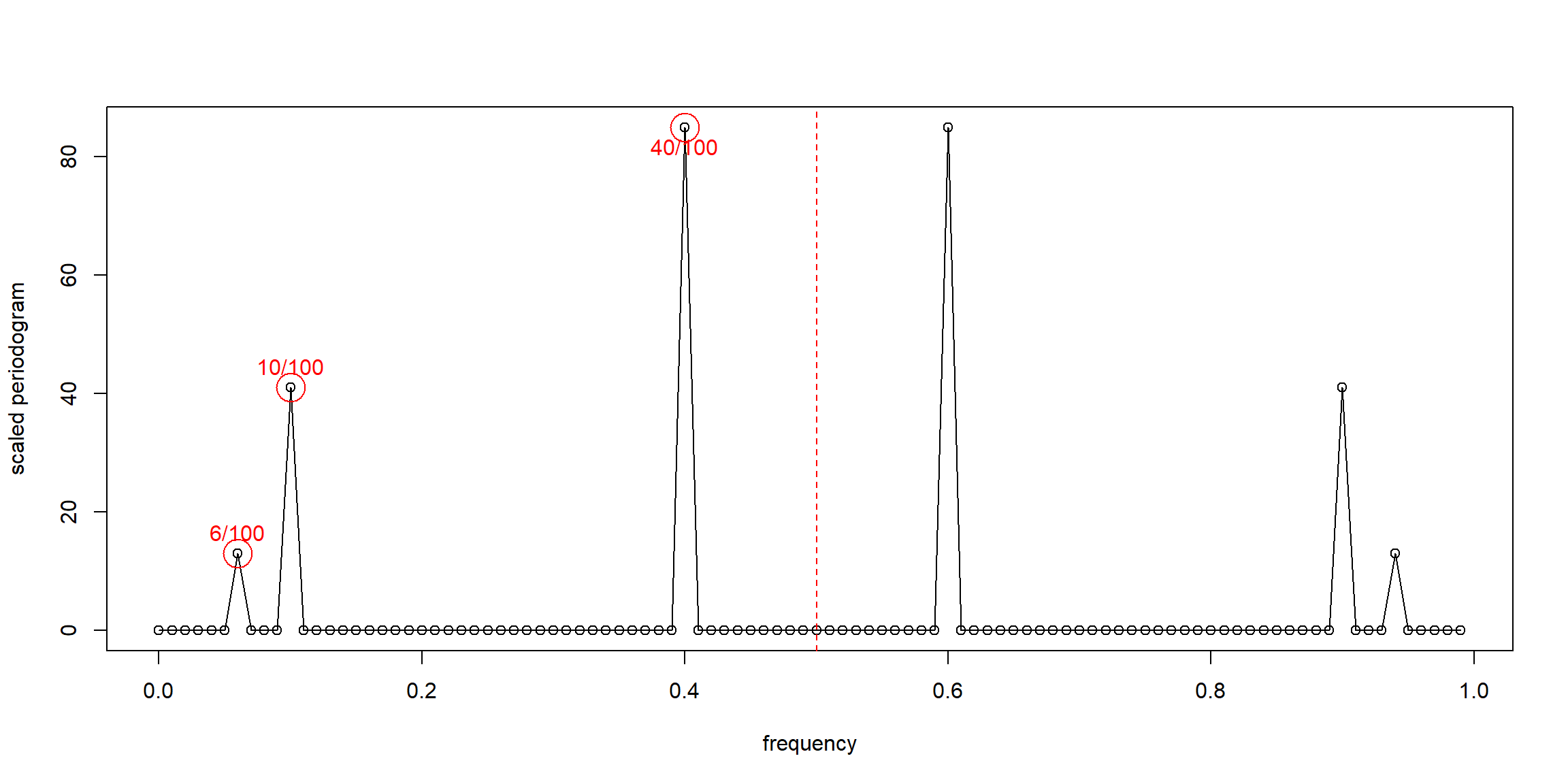

  • the plot is symmetric: \(I(\omega_j)=I(\omega_{n-j})\)
  • period: \(T=\frac nj\)
    • \(T_1=\frac {100}6\), \(T_2=\frac{100}{10}\), \(T_3=\frac{100}{40}\)
  • \(\omega_j=\frac jn\)
    • \(\omega_1=\frac 6{100}\), \(\omega_2=\frac {10}{100}\), \(\omega_3=\frac {40}{100}\)

Example 4.7 (p.176) spectral density 

par(mfrow=c(3,1), mar=c(4,4,1,1))
arma.spec(main="White Noise")
arma.spec(ma=.5, main="Moving Average")
arma.spec(ar=c(1,-.9), main="Autoregression")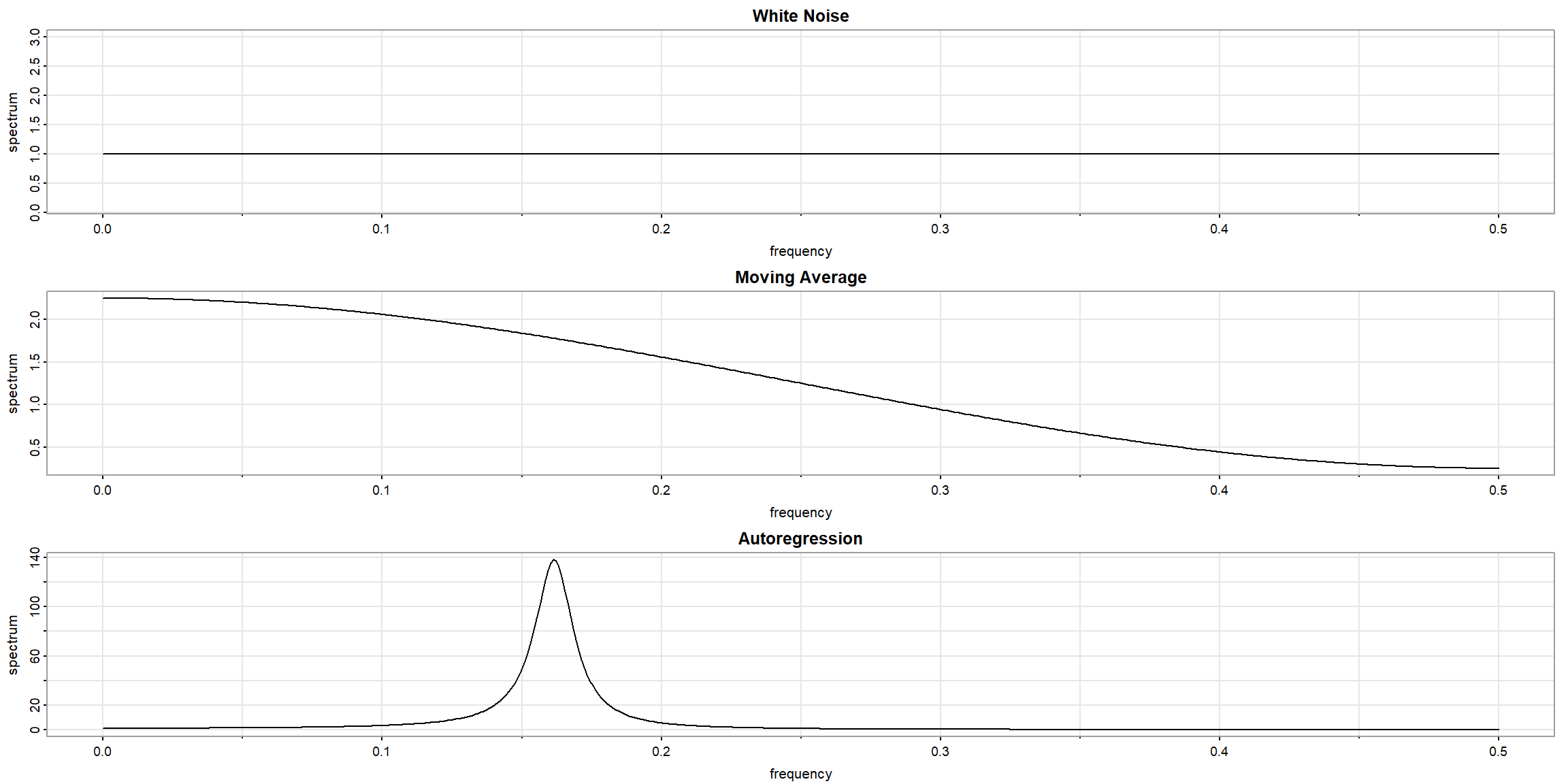

  • Top: White Noise
  • Middle: MA(1), \(\theta_1=0.5\)
  • Bottom: AR(2), \(\phi_1=1, \phi_2=-0.9\)

Example 4.10 (p.182) Spectral ANOVA

periodogram is symmetric

\[\omega_1=\frac15,\omega_2=\frac25\]

\[SS=2\cdot I(\omega_j)\]

x = c(1, 2, 3, 2, 1)
c1 = cos(2*pi*1:5*1/5); s1 = sin(2*pi*1:5*1/5)
c2 = cos(2*pi*1:5*2/5); s2 = sin(2*pi*1:5*2/5)
omega1 = cbind(c1, s1); omega2 = cbind(c2, s2)
anova(lm(x~omega1+omega2)) # ANOVA Table
## Analysis of Variance Table
## 
## Response: x
##           Df  Sum Sq Mean Sq F value Pr(>F)
## omega1     2 2.74164 1.37082     NaN    NaN
## omega2     2 0.05836 0.02918     NaN    NaN
## Residuals  0 0.00000     NaN
  • \(2.74=2\cdot I(\frac15)=2\cdot1.37\)

\(\downarrow\) \(I(0)\) \(I(\frac15)\) \(I(\frac25)\) \(I(\frac35)\) \(I(\frac45)\)

Mod(fft(x))^2/5 # the periodogram (as a check)
## [1] 16.20000000  1.37082039  0.02917961  0.02917961  1.37082039

Example 4.13 (p.187) CI

  • n=480, \(\because\) periodogram is symmatric, only need to print half of them
  • 1 unit = 40
par(mfrow=c(2,1), mar=c(4,4,1,1))
soi.per = mvspec(soi, log="no")
abline(v=1/4, lty=2)
rec.per = mvspec(rec, log="no")
abline(v=1/4, lty=2)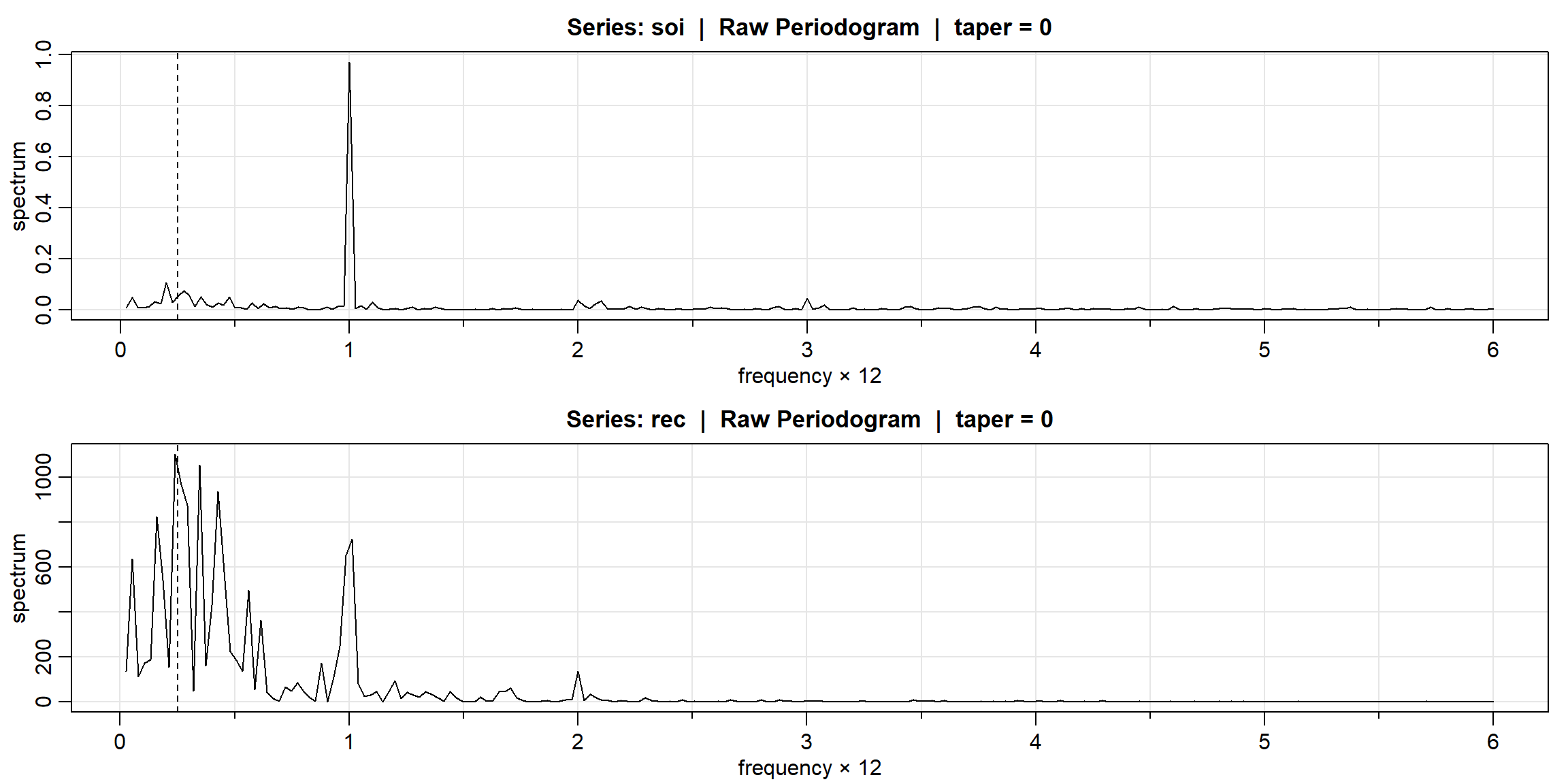

  • the peak appear at j=10, 40

\[\frac{2I(\omega_j)}{f(\omega_j)}\sim\chi^2(2)\]

\[\text{95% CI for }f(\omega_j)=[\frac{2I(\omega_j)}{\chi^2_.975}, \frac{2I(\omega_j)}{\chi^2_.025}]\]

  • \(\downarrow I(\omega_j)\)
soi.per$spec[40] # 0.97223; soi pgram at freq 1/12 = 40/480
soi.per$spec[10] # 0.05372; soi pgram at freq 1/48 = 10/480
## [1] 0.9722312
## [1] 0.05372962
  • \(\downarrow CI\): huge interval is a useless interval
U = qchisq(.025,2) # 0.05063
L = qchisq(.975,2) # 7.37775

2*soi.per$spec[10]/L # 0.01456
2*soi.per$spec[10]/U # 2.12220

2*soi.per$spec[40]/L # 0.26355
2*soi.per$spec[40]/U # 38.40108
## [1] 0.0145653
## [1] 2.122207
## [1] 0.2635573
## [1] 38.40108