Sec 2 About Time Series

2.1 What is time series?

  1. Observations (obs.) could be
  • univariate or multiivariate
  • discrete (count) or continuous (measurement)
  1. Set of obs. recorded sequentially (has a natural order)
  • time
  • spatial ordering, eg. \(1^{st}\) plaint in a row, \(2^{nd}\) plaint in a row
  • depth, eg. soil (土壤) PH: 1m down, 2m down
  1. Recording interval could be
  • regular, eg. hourly, daily, monthly
  • irregular, eg. earthquake, observe stock price at transaction times
    • take average or median to change it into regular

2.2 Plot of time series data

plot data vs time to look:

  • trend: upward or downward (整體趨勢)
  • repetitive pattern is unknown or unknown:
    • periodicity: in regular pattern, eg. 1.3 years
    • seasonality: known period, eg. 1 year, 12 month for mothly data
  • heteroskadesticity \(\sigma^2_t\): changing variance
  • dependence: positive or negative
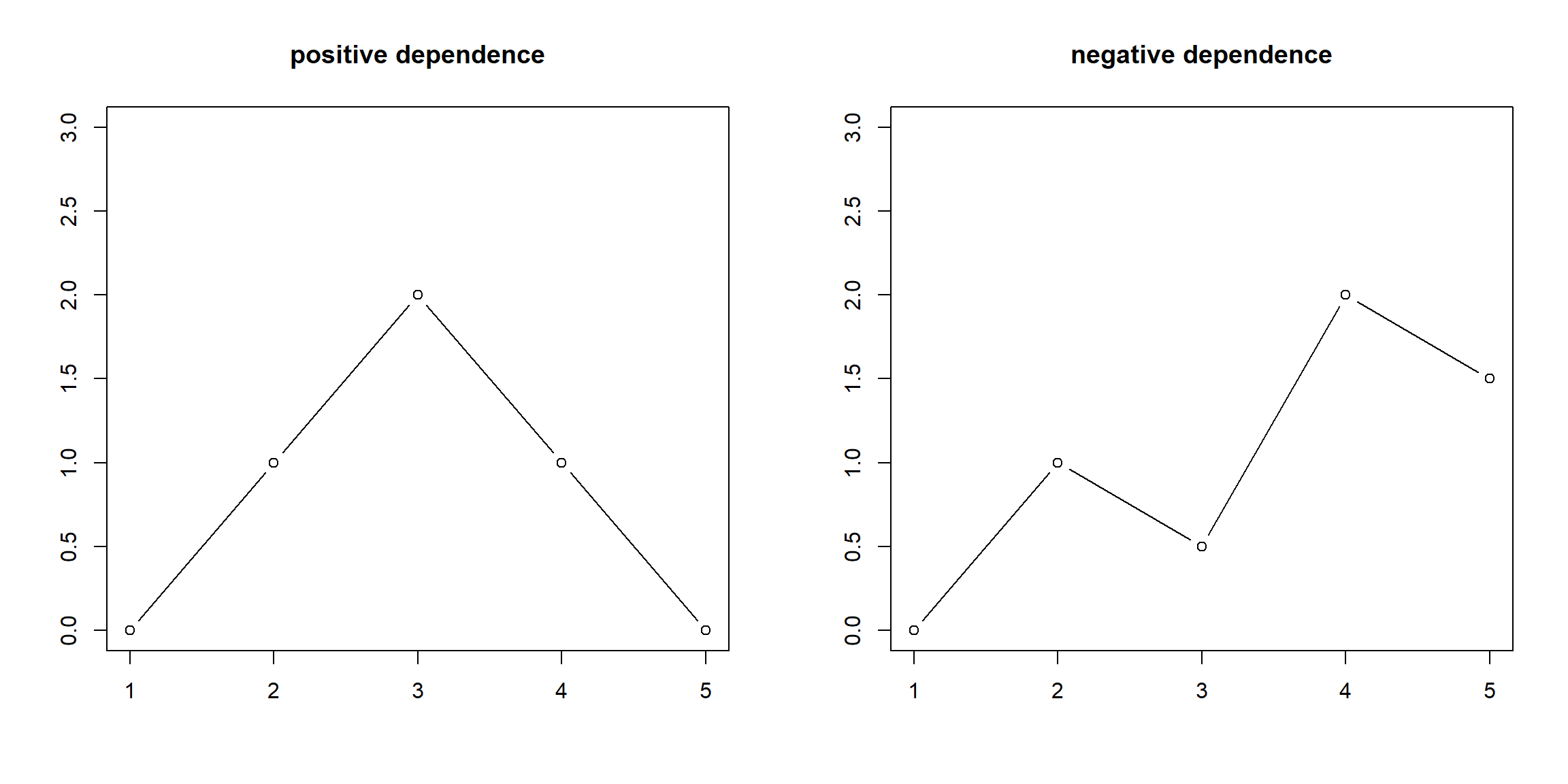
    • successive obs. (\(x_t, x_{t+1}\)) are similar or dissimilar
  • missing, outliers

2.3 Why use time series

  • difference between Regression (reg.) and Time Series (TS)
    • Reg.: need (X, Y)
      X之間獨立 (independent, indep.), X和Y之間不獨立 (dependent, dep.)
    • TS: only need X (times)
      X之間 dep.
  1. Often in time series data:
  • trend 不好使用 global regression function 來 fitted
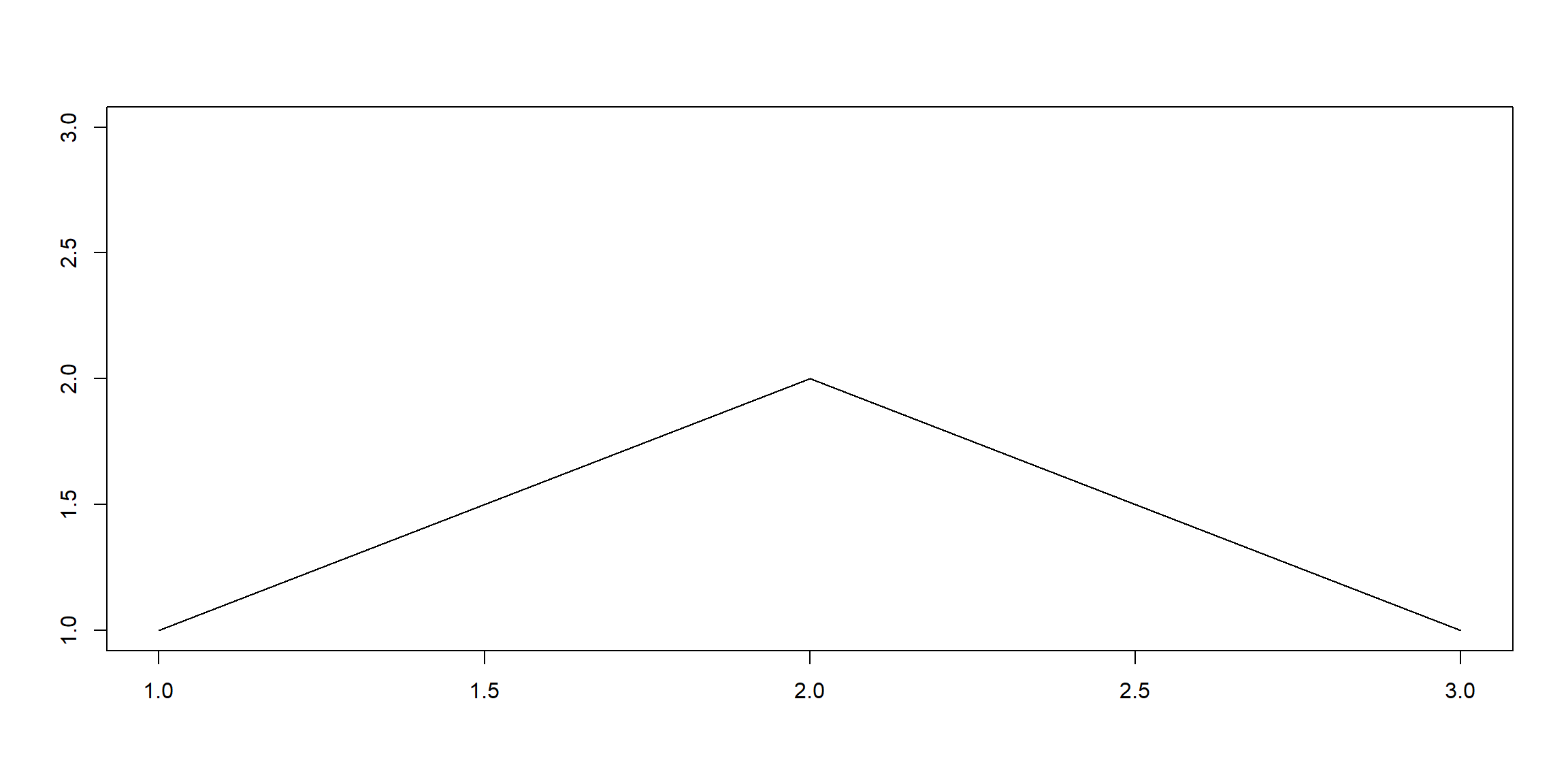
    • 如下圖，就需要2個 reg.
  • display time-varying local behavior
  • often have seasonality
  1. Ignore dependence often lead to:
  • inefficient estimates of reg. parameters
  • poor prediction
  • standard errors (std.): unrealistically small
    • confidence interval (CI.): unrealistically narrow
    • hypothesis testing: improper inferences

2.4 Objective of time series analysis

  1. provide an interpretable model of data
  • often involve multivariate series
  • test if the variable is significance (sig.) influence
  1. predict future values of series
  • predictive model often do not try to explain

2.5 Modeling strategy

\[\hat{y}_{t+1}=trend+dependence\] \[trend \leftarrow reg., \:dependence \leftarrow TS\]

  1. difficulties
  • random variables (r.v.) not identically distributed
  • r.v. not independent
  • different means due to trend or seasonality
  • different variance
  1. try to make it easier
  • to focus on modeling dependence
    • eliminate trend and seasonality
    • eliminate changing variance
  • model remainder as dependent but identically distributed