Sec 3 Base Definition

3.1 Variance, Covariance, Correlation

<Def> Covariance

$$Cov(X_s, X_t)=E[(X_s-\mu_s)(X_t-\mu_t)]$$ <Def> Correlation

$$Corr=\frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}}$$

• Variance of linear combination

$$Var\left(a_0+\sum_{j=1}^pa_jX_j\right)=\sum_{j=1}^p\sum_{k=1}^pa_ja_k\cdot Cov(X_j,X_k)$$

• Covariance of linear combination

$$Cov\left(a_0+\sum_{j=1}^pa_jX_j, b_0+\sum_{k=1}^qb_kY_k\right)=\sum_{j=1}^p\sum_{k=1}^qa_jb_k\cdot Cov(X_j,Y_k)$$

3.2 Uncorrelated, Independent

• r.v. with zero correlation $\Rightarrow$ uncorrelated
• independent + finite variance $\Rightarrow$ uncorrelated
• uncorrelated $\nRightarrow$ independent

<Def> uncorrelated

$$Corr(X,Y)=0$$

<Def> independent

$$P(X\cap Y)=P(X)P(Y)$$

3.3 Autocovariance, Autocorrelation, Cross-covariance, Cross-correlation

3.3.1 Population

<Def> autocovariance function

$$Cov(X_s, X_t)= \gamma_X(s,t)=E[(X_s-\mu_s)(X_t-\mu_t)]$$ $$measuring\:time: s,t=t_1,t_2,...$$

<Def> autocorrelation function (ACF)

$$\rho(s,t)=\frac{\gamma(s,t)}{\sqrt{\gamma(s,s)\gamma(t,t)}}=\frac{Cov(X_s,X_t)}{\sqrt{Var(X_s)Var(X_t)}}$$ <Def> cross-covariance function

$$\gamma_{XY}(s,t)=E[(X_s-\mu_{X_s})(Y_t-\mu_{Y_t})]$$

<Def> cross-correlation function (CCF)

$$\rho_{XY}(s,t)=\frac{\gamma_{XY}(s,t)}{\sqrt{\gamma_X(s,s)\gamma_Y(t,t)}}=\frac{Cov(X_s,Y_t)}{\sqrt{Var(X_s)Var(Y_t)}}$$

Covariance: different covatiate Autocovariance: same variable but at different time

3.3.2 Stationary Case

times series $\{X_t\}$ is stationary

<Def> autocovariance function $$\gamma(h)=Cov(X_t, X_{t+h})\\ \color{red}{\gamma(0)=Var(X_t)}$$

<Def> autocorrelation function (ACF) $$\rho(h)=Corr(X_t, X_{t+h})=\frac{Cov(X_t, X_{t+h})}{\sqrt{Var(X_t)Var(X_{t+h})}}=\frac{\gamma(h)}{\gamma(0)}$$

two times series $\{X_t\},\{Y_t\}$ are jointly stationary

<Def> cross-covariance function $$\gamma_{XY}(h)=Cov(X_t, Y_{t+h})=E[(X_t-\mu_{X})(Y_{t+h}-\mu_{Y})]\\ \text{ is a function only of lag h}$$

<Def> cross-correlation function (CCF) $$\rho_{XY}(h)=Corr(X_t, Y_{t+h})=\frac{\gamma_{XY}(h)}{\sqrt{\gamma_X(0)\gamma_Y(0)}}$$

3.3.3 Sample

<Def> sample autocovariance function $$\hat\gamma(h)=n^{-1}\sum_{t=1}^{n-h}(X_t-\bar X)(X_{t+h}-\bar X)$$

<Def> sample autocorrelation function (ACF) $$\hat\rho(h)=\frac{\hat\gamma(h)}{\hat\gamma(0)}$$

<Prop> large sample distribution of ACF $$\hat\rho_X(h)\sim N(0,\frac{1}{\sqrt{n}})\\ \text{ if }X_t\text{ is }WN\text{ and n large}$$ $H_0: \text{follow WN assumption}$

• accept WN assumption, if all ACF are within $\pm1.96\times\frac{1}{\sqrt n}$
• see the follow example 3.1

acf(diff(gtemp), 48)

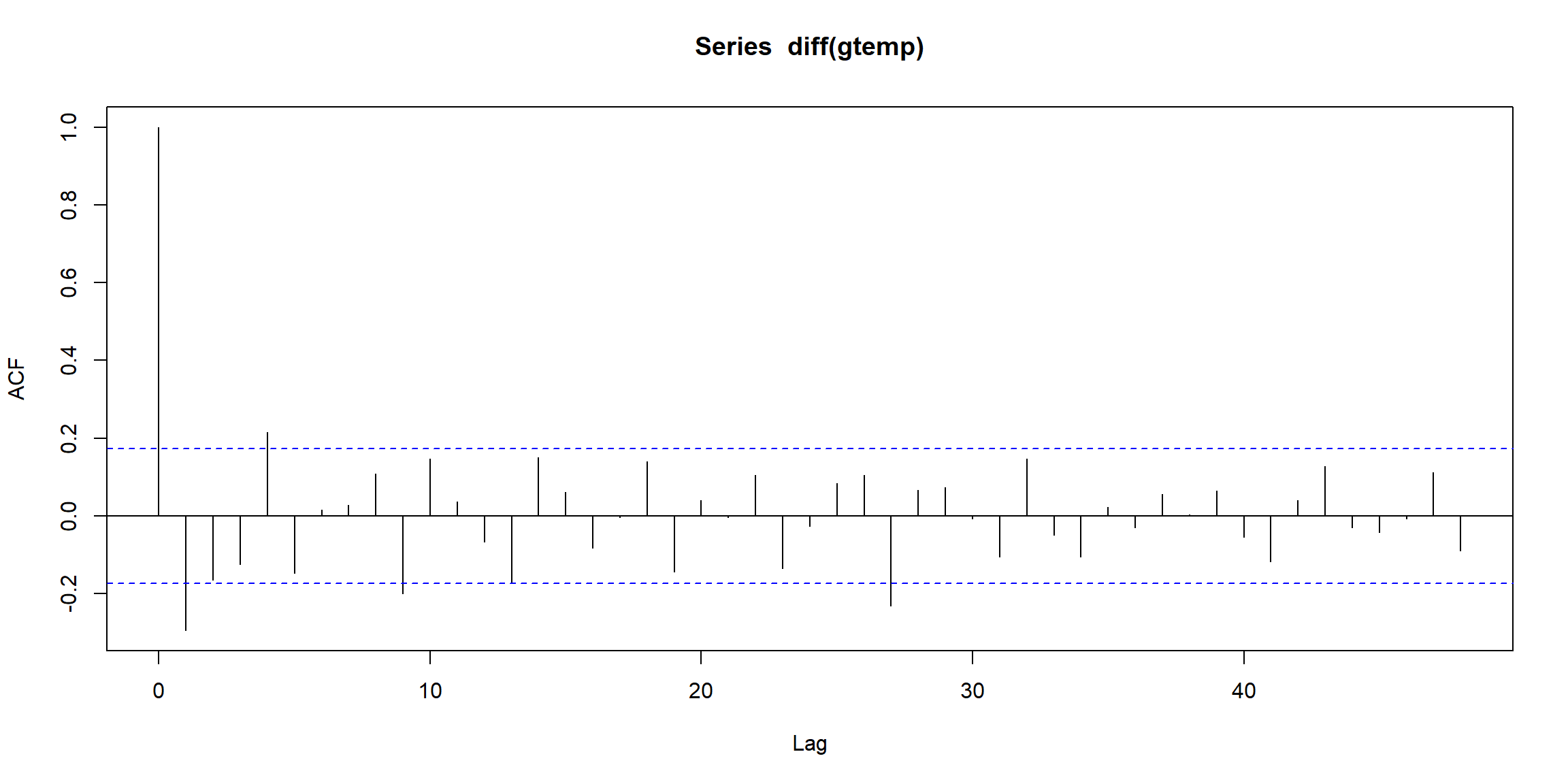
Figure 3.1: The ACF plot

<Def> sample cross-covariance function $$\hat\gamma_{XY}(h)=n^{-1}\sum_{t=1}^{n-h}(X_t-\bar X)(Y_{t+h}-\bar Y)$$

<Def> sample cross-correlation function (CCF) $$\hat\rho_{XY}(h)=\frac{\hat\gamma_{XY}(h)}{\sqrt{\hat\gamma_X(0)\hat\gamma_Y(0)}}$$

<Prop> large sample distribution of CCF $$\hat\rho_{XY}(h)\sim N(0,\frac1n)\\ \text{ if at least one process is white independent noise}$$