3 Superfícies Quádricas

3.1 Superfícies de Revolução

Superfície de revolução é a superfície gerada por uma curva plana (chamada geratriz) que gira \(360^\circ\) em torno de uma reta (chamada eixo) situada no plano da curva. Neste caso, o traço da superfície em um plano perpendicular ao eixo é uma circunferência e a equação da superfície de revolução é obtida pela equação da geratriz.

3.2 Superfícies Quádricas Centradas

Chama-se quádrica qualquer subconjunto \(\Omega\) de \(\mathbb{E}^3\) que possa ser descrito, em relação a um sistema ortogonal de coordenadas, por uma equação de segundo grau \[ ax^2+by^2+cz^2+dxy+exz+fyz+gx+hy+iz+j=0 \]

A equação geral do 2º grau, com coeficientes diferentes de 0 e através de mudanças de coordenadas pode ser transformada na forma:

\[\begin{equation} Ax^2+By^2+Cz^2=D \; \; \text{(quádricas cêntricas)} \tag{3.1} \end{equation}\]

e

\[\begin{equation} \left\{ \begin{aligned} Ax^2+By^2=Cz\\ Ax^2+By^2=Cy\\ Ax^2+By^2=Cx\\ \end{aligned} \right. \; \; \text{(quádricas não cêntricas)} \tag{3.2} \end{equation}\]

Se nenhum dos coeficientes da equação (3.1) for nulo, ela pode ser escrita sob uma das formas: \[ \pm \frac{x^2}{a^2}\pm \frac{y^2}{b^2} \pm \frac{z^2}{c^2}= 1 \]

As possíveis combinações de sinais nesta equação permitem concluir a existência de apenas três tipos de superfícies, conforme sejam três, dois ou um o número de coeficientes positivos dos termos do 1º membro da equação.

Observação. Se os coeficientes forem todos negativos, não existe lugar geométrico.

3.3 Elipsóide

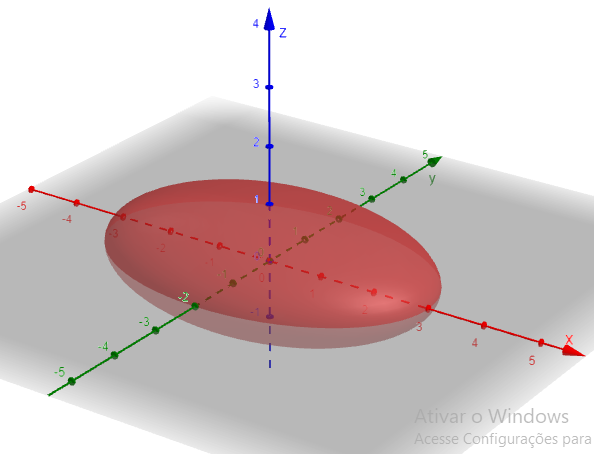
Figura 3.1: Elipsóide..

O elipsoide é uma superfície quádrica que pode ser descrita como uma forma tridimensional que se assemelha a uma esfera alongada ou achatada. Um elipsóide é uma superfície quadriculada tridimensional que pode ser descrita como o conjunto de todos os pontos no espaço que satisfazem uma equação do tipo: \[ \frac{{(x - h)^2}}{{a^2}} + \frac{{(y - k)^2}}{{b^2}} + \frac{{(z - l)^2}}{{c^2}} = 1 \]

Onde \((h,k,l)\) é o centro do elipsóide e \(a\), \(b\) e \(c\) são os comprimentos dos semi-eixos nas direções \(x\), \(y\) e \(z\) respectivamente. Os semi-eixos representam as distâncias do centro do elipsóide até os pontos onde a superfície intersecta os eixos coordenados.

Caso o elipsoide esteja centrado na origem, ela terá a equação: \[ \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1 \] onde \(a\), \(b\) e \(c\) \(\in \mathbb{R}\), que determinam o tamanho e a forma do elipsoide.

O elipsoide possui várias propriedades notáveis. Em primeiro lugar, é uma superfície de revolução, o que significa que pode ser gerado pela rotação de uma elipse em torno de um eixo. Isso resulta em uma forma simétrica em relação aos eixos coordenados.

A superfície do elipsoide é suave e contínua, sem bordas ou singularidades. Ela exibe simetria esférica, o que significa que qualquer plano que passe pelo centro do elipsoide o divide em duas metades iguais.

3.4 Cone

Um cone é uma superfície quádrica tridimensional. Especificamente, um cone é gerado ao traçar uma linha reta infinita, chamada geratriz, a partir do vértice e rotacioná-la em torno do vértice mantendo a direção constante. Essa rotação resulta em uma superfície em forma de cone que se estende indefinidamente. Conforme a imagem:

Figura 3.2: Processo de formação do Cone.

Um cone é uma superfície tridimensional que pode ser descrita como o conjunto de todos os pontos no espaço que satisfazem uma equação do tipo: \[ \frac{{(x - h)^2}}{{a^2}} + \frac{{(y - k)^2}}{{b^2}} = \frac{{(z - l)^2}}{{c^2}} \] Onde \((h,k,l)\) é o vértice do cone e \(a\) e \(b\) são os comprimentos dos semi-eixos nas direções \(x\) e \(y\), respectivamente. O parâmetro \(c\) representa a altura do cone. A superfície do cone se estende infinitamente em direção ao infinito em sua “ponta” no eixo \(z\), enquanto a base do cone é definida pelo círculo formado pelo valor constante de \[\frac{{(x - h)^2}}{{a^2}} + \frac{{(y - k)^2}}{{b^2}}\] à medida que \(z\) varia.

Se o cone estiver centrado na origem, sua equação será: \[ \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=0 \] onde \(a\), \(b\) e \(c\) \(\in \mathbb{R}\), que determinam a forma e a orientação do cone.

O cone possui várias propriedades matemáticas notáveis. Por exemplo, ele exibe uma simetria rotacional em torno de seu eixo, o que implica que as propriedades de uma seção cônica são invariantes sob rotações em torno desse eixo. Além disso, o vértice do cone é um ponto especial que possui propriedades distintas das demais partes da superfície.

3.5 Hiperbolóide de uma folha

O hiperboloide de uma folha é uma superfície quádrica tridimensional que pode ser obtida através da rotação de uma hipérbole em torno de seu eixo transversal. A superfície da hiperbolóide de uma folha pode ser descrita como o conjunto de todos os pontos no espaço que satisfazem uma equação do tipo: \[ \frac{{(x - h)^2}}{{a^2}} + \frac{{(y - k)^2}}{{b^2}} - \frac{{(z - l)^2}}{{c^2}} = 1 \] Onde \((h, k, l)\) é o centro do hiperbolóide e \(a\), \(b\) e \(c\) são os comprimentos dos semi-eixos nas direções \(x\), \(y\) e \(z\), respectivamente. O hiperbolóide de uma folha tem a forma de duas folhas hiperbólicas que se estendem infinitamente em direções opostas em relação ao eixo \(z\). A superfície do hiperbolóide de uma folha é aberta e não possui uma superfície de base.

Caso a hiperbolóide de uma folha esteja centrada na origem, sua equação será:

\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2}= 1 \] onde \(a\), \(b\) e \(c\) \(\in \mathbb{R}\) que determinam a forma e a orientação do hiperboloide.

O hiperboloide de uma folha apresenta várias propriedades geométricas notáveis. Sua forma consiste em uma única folha hiperbólica que se estende infinitamente. A superfície possui duas partes distintas, uma em cada lado da folha hiperbólica.

Uma característica interessante do hiperboloide de uma folha é que ele não possui bordas ou singularidades. No entanto, possui uma linha chamada de eixo central, que é a interseção da superfície com o plano \(xy\). O eixo central pode ser tanto retilíneo como curvo, dependendo dos parâmetros do hiperboloide.

3.6 Hiperbolóide de duas folhas

o hiperboloide de duas folhas é uma superfície quádrica que pode ser obtida pelo deslocamento de uma hipérbole no espaço tridimensional. A superfície hiperbolóide de duas folhas pode ser descrita como o conjunto de todos os pontos no espaço que satisfazem uma equação do tipo: \[ \frac{{(x - h)^2}}{{a^2}} + \frac{{(y - k)^2}}{{b^2}} - \frac{{(z - l)^2}}{{c^2}} = -1 \] Onde \((h, k, l)\) é o centro do hiperbolóide e \(a\), \(b\) e \(c\) são os comprimentos dos semi-eixos nas direções \(x\), \(y\) e \(z\), respectivamente. Ao contrário do hiperbolóide de uma folha, o hiperbolóide de duas folhas possui duas folhas hiperbólicas que se estendem infinitamente em direções opostas em relação ao eixo \(z\). A superfície do hiperbolóide de duas folhas também é aberta e não possui uma superfície de base. A principal diferença em relação ao hiperbolóide de uma folha é o na equação, o que resulta em uma diferença de curvatura nas folhas do hiperbolóide.

Caso a hiperbolóide de duas folhas esteja centrada na origem, sua equação será:

\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2}= -1 \] onde \(a\), \(b\) e \(c\) \(\in \mathbb{R}\) que determinam a forma e a orientação do hiperboloide.

O hiperboloide de duas folhas apresenta várias propriedades notáveis. Por exemplo, é uma superfície de revolução, o que significa que pode ser gerado pela rotação de uma curva planar em torno de um eixo. Nesse caso, uma hipérbole é rotacionada em torno do eixo z ou em um eixo paralelo ao eixo z.

A superfície do hiperboloide de duas folhas consiste em duas “folhas” hiperbólicas simétricas em relação ao plano xy. Cada folha se estende indefinidamente, com uma abertura hiperbólica que se afasta dos eixos coordenados. O hiperboloide de duas folhas não possui bordas ou arestas.

3.7 Parabolóide Elíptico

O parabolóide elíptico é uma superfície tridimensional que pode ser obtida pela rotação de uma parábola em torno de seu eixo.

A superfície do parabolóide elíptico consiste no conjunto de todos os pontos no espaço que satisfazem uma equação do tipo:

\[ \frac{{(x - h)^2}}{{a^2}} + \frac{{(y - k)^2}}{{b^2}} = \frac{{z - l}}{{c}} \]

Onde \((h, k, l)\) é o vértice do parabolóide e \(a\) e \(b\) são os comprimentos dos semi-eixos nas direções \(x\) e \(y\), respectivamente. O parâmetro \(c\) controla a abertura do parabolóide. A superfície do parabolóide elíptico tem a forma de uma tigela alongada e é aberta para cima. O eixo \(z\) é a direção de simetria do parabolóide, enquanto as direções \(x\) e \(y\) determinam a curvatura da superfície nas respectivas direções.

Caso o parabolóide elíptico esteja centrado na origem, sua equação será: \[ z=\frac{x^2}{a^2}+\frac{y^2}{b^2} \] onde \(a\), \(b\) e \(c\) \(\in \mathbb{R}\) que determinam a forma e a orientação do parabolóide elíptico.

O parabolóide elíptico possui várias propriedades geométricas interessantes. Sua forma consiste em uma abertura parabólica voltada para cima ou para baixo, dependendo dos valores dos parâmetros \(a\) e \(b\). Ele pode ser simétrico em relação ao plano \(xy\) ou possuir assimetria.

Uma característica notável é que o parabolóide elíptico é um objeto unidirecional, ou seja, sua curvatura é constante apenas em uma direção, ao longo do eixo \(z\). Isso o diferencia de superfícies como a esfera, que possui curvatura constante em todas as direções.

3.8 Parabolóide Hiperbólico

O parabolóide hiperbólico é uma superfície tridimensional que pode ser obtida pela rotação de uma parábola em torno de seu eixo.

A superfície do parabolóide hiperbólico consiste no conjunto de todos os pontos no espaço que satisfazem uma equação do tipo: \[ \frac{{(x - h)^2}}{{a^2}} - \frac{{(y - k)^2}}{{b^2}} = \frac{{z - l}}{{c}} \] Onde \((h,k,l)\) é o vértice do parabolóide e \(a\) e \(b\) são os comprimentos dos semi-eixos nas direções \(x\) e \(y\), respectivamente. O parâmetro \(c\) controla a abertura do parabolóide. Ao contrário do parabolóide elíptico, o parabolóide hiperbólico tem uma curvatura oposta nas direções \(x\) e \(y\). A superfície do parabolóide hiperbólico se estende infinitamente e possui duas folhas que se afastam uma da outra à medida que se afastam do vértice. O eixo \(z\) é a direção de simetria do parabolóide.

Caso o parabolóide hiperbólico esteja centrado na origem, sua equação será:

\[ z=\frac{x^2}{a^2}-\frac{y^2}{b^2} \]

onde \(a\), \(b\) e \(c\) \(\in \mathbb{R}\) que determinam a forma e a orientação do parabolóide hiperbólico.

O parabolóide hiperbólico possui várias propriedades geométricas interessantes. Sua forma consiste em duas folhas hiperbólicas simétricas, voltadas para cima e para baixo. É importante ressaltar que essas folhas são infinitas, estendendo-se ao infinito em todas as direções.

Uma característica notável é que o parabolóide hiperbólico é um objeto unidirecional, ou seja, sua curvatura é constante apenas em uma direção, ao longo do eixo z. Isso o diferencia de superfícies como a esfera, que possui curvatura constante em todas as direções.

3.9 Exemplos

Exemplo 3.1 Obtenha uma equação e faça o esboço do gráfico da superfície gerada pela rotação da cônica \(x^2 - 4z^2 = 16\) e indentifique a superfície em cada caso.

1. em torno do eixo \(x\);
2. em torno do eixo \(y\).

Solução. \[ x^2 - 4z^2 = 16 \Longleftarrow \frac{x^2}{16}-\frac{z^2}{4}=1 \] é uma hipérbole, onde \(a^2=16\) e \(b^2=4\) \(\Rightarrow\) \(a=4\) e \(b=2\) Portando, a equação é uma hipérbole de eixo real sobre o eixo das abscissas (eixo \(x\)) e eixo imaginário sobre o eixo das cotas (eixo \(z\))

Solução (a). Seja \(Q=(x,0,z_1)\) um ponto pertecente a hipérbole \(x^2-4x^2=16\).\ Logo, \[\begin{align*} x^2-4x^2=16 &\rightarrow& x^2-16=4{z_1}^2\\ &\rightarrow& {z_1}^2= \frac{x^2-16}{4} \end{align*}\]

Ao girar a curva (hipérbole) em torno do eixo dos \(x\), o ponto \(Q=(x,0,z_1)\) descreverá uma circunferência cujo centro é o ponto \(R(x, 0, 0)\). Sendo \(P(x, y, z)\) um ponto genérico dessa circunferência, tem-se que \(\overline{PR}=\overline{QR}=\) o raio da circunferência. Assim,

\[\begin{align} \overline{PR}&=\sqrt{(x-x)^2 + (y-0)^2 + (z-0)^2} \\ &=\sqrt{(x-x)^2 + (0-0)^2 + (z_1-0)^2} \\ &=\overline{QR} \end{align}\]

\[ \therefore y^2+z^2 = {z_1}^2 (II) \] Com isso, I e II vem:

\[ y^2+z^2 = \frac{x^2-16}{4} \Longrightarrow 4y^2 + 4z^2 = x^2 - 16 \Longrightarrow x^2-4y^2-4z^2=16 \] A superfície é uma hiperboloide de revolução de duas folhas.

3.10 Anotações

3.10.1 Por que quádricas?

O termo quádrica foi adotado para evocar o fato de que as equações que as descrevem são equações de segundo grau, ou equações quádricas (definição 25-1). Sob o mesmo critério, adotar-se cúbica para designar lugares geométricos descritos por equações de terceito grau, quâantica, se o grau for 4, etc.

3.10.2 Por que elipsoide, hiperboloide, paraboloide?

O critério para a escolha desses números basea-se nas interseções das quádricas com planos paralelos aos planos coordenados. Quando se obtem exclusivamente elipes, não há melhor nome do que elpsoide. Como, porém, não há exclusividade de hipérboles em nenhum caso, o nome hiperboloide é usado quando as hipérboles prevalecem. Da mesma forma, na prevalença de parábolas o nome mais adequado é parabolóide.

3.10.3 O que dizer dos sobrenomes uma folha e duas folhas dado aos hiperboloides?

Pelo critério utilizado para dar sobrenome aos paraboloides, todos os hiperboloides (exceto os de rotação) são elipticos, pois as fatias, quando não são hiperboles, são elipes (no caso do de rotação, circunferencias). Por isso, para distinguir os hiperboloides, utilizam-se de sobrenomes sugestivos uma folha e duas folhas.