2 Cônicas

2.0.1 Contexto Histórico

Antes mesmo de introduzirmos o conteúdo de superfícies quadricas é necessário compreender as cônicas que servem de base para esse estudo. Sendo assim, daremos início a parábola e uma breve contextualização histórica. Apolônio de Pergamo foi um matemático e astrônomo grego que viveu por volta de (262 a.c - 190 a.c), ele também era conhecido como o grande Geometra. Além disso, produziu muitas obras, porém muitas delas foram perdidas.

Segundo Bezerra (2010, p. 40), “foi Apolônio quem mostrou que bastaria um cone circular reto de duas folhas qualquer para se obter as três (seções) cônicas; o que deveria variar era o ângulo de interseção do plano com uma das duas geratrizes”.

As cônicas se origina após a intersecção de um plano sobre um cone duplo. Ou seja, dependendo da forma que o plano corte o cone obtemos uma parábola, elipse ou hipérbole.

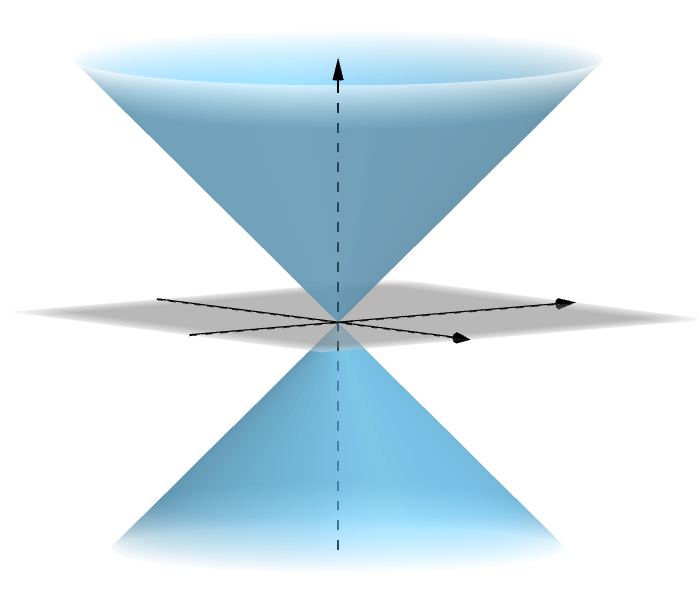
Figura 2.1: Cone de duas folhas.

2.1 Parabola

Definição 2.1 (Parábola) Dado um plano \(\alpha\), uma reta \(d\) e um ponto \(F\), tal que \(F \notin d\). Parábola é o conjunto de todos os pontos pertencentes ao plano \(\alpha\) que são equidistantes a \(F\) e \(d\).

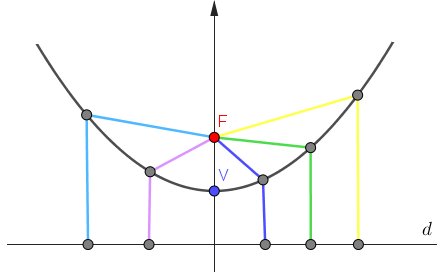
Figura 2.2: Gráfico dos pontos equidistantes.

Note que no gráfico existe vários segmentos de reta a qual as cores iguais representam os segmentos de retas que possuem o mesmo comprimento. Além disso, podemos destacar que os segmentos de reta que tocam a reta diretiz são perpendiculares a ela. O objetivo desse gráfico é mostrar graficamente a definição da parábola a qual \[d(F,P) = d(P,D)\text{,}\] em que \(P\) é um ponto pertencente a parábola e \(D \in d\). Podemos deixar isso mais claro com um simples exemplo. Considere a parábola \(x^2 = 2y - 1\) que pode ser vista como \(y = \dfrac{1}{2}x^2 + \dfrac{1}{2}\).

Através de nossa lei de formação da parábola é possível encontrar todos os seus elementos. Deste modo, ao atribuir \(x=0\) determinamos o valor do vértice da parábola \(V\left(0,\dfrac{1}{2}\right)\) sendo um ponto muito importante, já que ele se encontra no eixo de simetria da parábola e é ponto médio entre o Foco e o ponto \(D\), onde \(D \in d\) e ao eixo de simetria simultaneamente. Ou seja, com essa informação é possível determinar o Foco \(F\) e a reta diretriz \(d\). Então

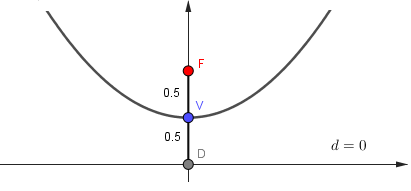
Figura 2.3: Gráfico da distância entre o Foco e o Vértice.

É fácil ver o Foco \(F(0,1)\) e a reta diretiz \(d = 0\). A partir disso vamos atribuir valores a \(x\) e verificar a definição da parábola. Portanto, vamos tomar o ponto \(D_1 (2,0)\), quando \(x=2\), temos que \(y=\dfrac{5}{2}\), logo \(P_1 \left(2,\dfrac{5}{2}\right)\). Agora vamos verificar a definição da parábola a qual \(d(F, P_1) = d(P_1 , D_1)\). Portanto, \[\begin{eqnarray*} d(F, P_1) &=& \sqrt{(0 - 2)^2 + \left(1 - \frac{5}{2} \right)^2} = \sqrt{4 + \frac{9}{4}} = \sqrt{\frac{25}{4}} = \frac{5}{2} \\ d(P_1, D_1) &=& \sqrt{(2 - 2)^2 + \left( \frac{5}{2} - 0 \right)^2} = \sqrt{\frac{25}{4}} = \frac{5}{2}. \end{eqnarray*}\]

De fato, isso é válido para toda a parábola, veja o gráfico abaixo.

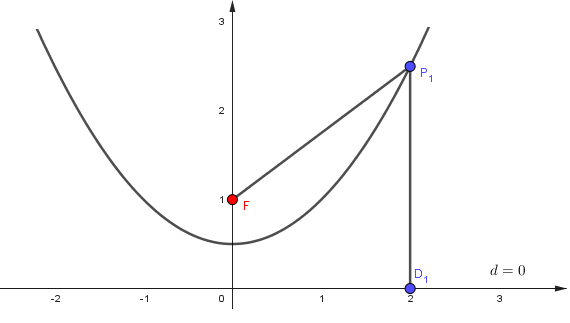
Figura 2.4: Parábola centrada na origem.

2.1.1 Elementos da parábola

Para compreender a parábola é fundamental conhecer os nomes de seus elementos. Desse modo, temos a tabela a seguir:

Tabela 2.1. Elementos da parábola

Focos	É o ponto \(F\)
Diretriz	É a reta \(d\)
Eixo de simetria	é a reta que passa por \(F\) e é perpendicular a \(d\)
Vértice	é o ponto \(V\) de intersecção da parábola com o seu eixo

Podemos destacar algumas informações importantes sobre os os elementos da parábola. Com relação ao Foco… Quanto maior o valor do parámetro \(p\) na parábola, maior será a extensão de sua concavidade.

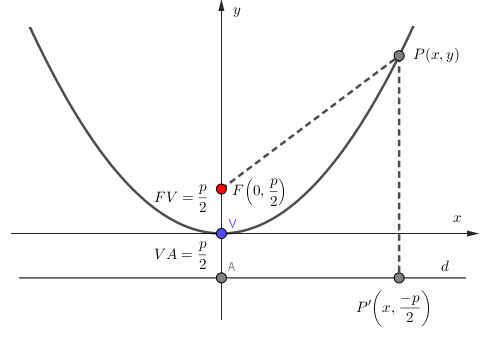
Figura 2.5: Parábola centrada na origem

Além disso, tem-se uma relação importante, a partir do parámetro \(p\). \[VF = \dfrac{p}{2}.\] Pela definição de parábola temos que \(d(P,F) = d(PP')\) ou \(\lvert PF\rvert=\lvert PP'\rvert\), com \(F \notin d\). Utilizaremos \(P(x,y), F\left(0,\dfrac{p}{2}\right) \ \text{e} \ P'\left(x, -\dfrac{p}{2}\right)\).

\[\begin{eqnarray*} d(P,F) &=& d(PP') \\ \left| \left(x-0, y-\frac{p}{2} \right) \right| &=& \left| \left(x-x, y-\left(-\frac{p}{2} \right) \right) \right| \\ % \left| \left(x, y-\frac{p}{2} \right) \right| &=& \left| \left(0 , y + \frac{p}{2} \right) \right| \sqrt{(x-0)^{2} + \left(y-\frac{p}{2} \right)^{2}} &=& \sqrt{(x-x)^{2} + \left(y + \frac{p}{2} \right)^{2}} \\ \sqrt{x^{2} + \left(y-\frac{p}{2} \right)^{2}} &=& \sqrt{\left(y + \frac{p}{2} \right)^{2}} \\ x^{2} + \left(y - \frac{p}{2} \right)^{2} &=& \left(y + \frac{p}{2} \right)^{2} \\ x^{2} + y^{2} -yp + \frac{p^{2}}{4} &=& y^{2} + yp + \frac{p^{2}}{4} \\ x^{2} - yp &=& yp \\ x^{2} &=& 2yp. \end{eqnarray*}\]

Portanto, \(x^{2} = 2py\) é a equação reduzida da parábola de vértice na origem.

Figura 2.6: Parábola com concavidade para cima.

Observação. O número real \(p \neq 0\) é chamado de parâmetro da parábola.

Figura 2.7: Parábola com concavidade para baixo.

Exercicio 2.1 Encontre o foco e a diretiz da parábola \(x^2 = 16y\). Construa o gráfico.

Solução. Primeiramente, precisamos determinar o parámetro \(P\) da parábola, pois ele será necessário para encontrar o foco \(F\). Como conhecemos a equação dessa parábola podemos igualar à equação reduzida e determinar \(p\). Deste modo, \(x^2 = 2py\) e \(x^2 = 16y\), então: \[\begin{eqnarray*} 2py &=& 16y \\ 2p &=& 16 \\ p &=& 8. \end{eqnarray*}\] Agora que temos o valor de \(p\), podemos encontrar \(F\) através da relação \(VF = \dfrac{p}{2}\). Portanto, \[\begin{eqnarray*} VF = \frac{8}{2} \Rightarrow VF = 4. \end{eqnarray*}\] Ou seja, \(F(0,4)\) e a reta diretriz: \(y = -4\).

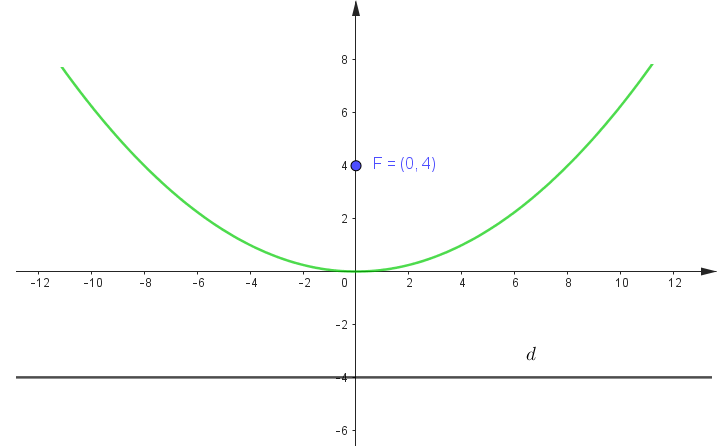
Figura 2.8: Gráfico do Exercício 1.

2.1.2 Equação da parábola de vértice fora da origem

Agora vamos estudar o caso em que o eixo de simetria da parábola é paralelo ao eixo \(y\). Então, considere um parábola de vértice \(V(h,k)\) e eixo paralelo ao eixo \(y\), de modo que \(h\) e \(k\) são coordenadas de \(v\) em relação ao sistema \(xOy\). Neste sentido, temos um novo sistema \(aOb\) onde a origem \(O'\) é igual a \(V\).

Vimos anteriormente a equação reduzida da parábola e através dela podemos uma nova equação com o sistema \(aOb\). Então, temos: \[\begin{eqnarray*} a^2 = 2pb. \end{eqnarray*}\]

Agora vamos analisar o seu gráfico a seguir: \[\begin{eqnarray*} (x-h)^2 = 2p(y - k). \end{eqnarray*}\]

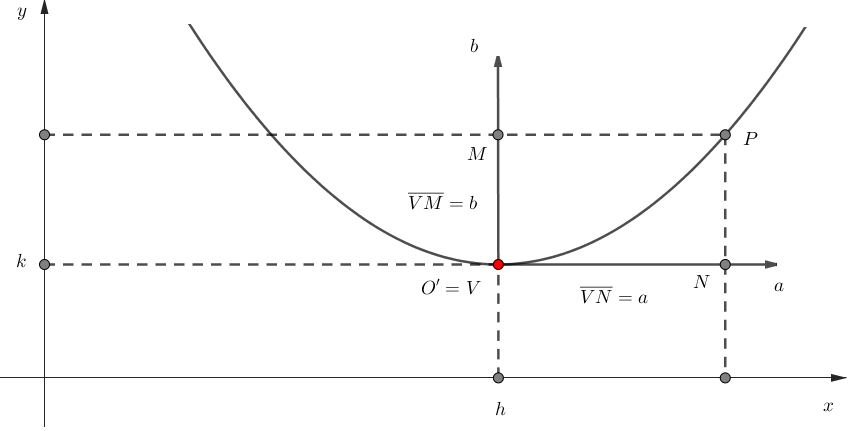
Figura 2.9: Parábola fora da origem.

Através do gráfico podemos tomar algumas conclusões, então: \[a = x -h \ \text{e} \ b = y - k.\] Podemos substituir esses valores na equação reduzida da parábola: \[\begin{eqnarray*} a^2 &=& 2pb \\ (x-h)^2 &=& 2p(y-k). \end{eqnarray*}\] Essa é a forma padrão de uma equação da parábola com vértices \(V(h,k)\) e eixo de simetria paralelo ao eixo \(y\). Analogamente, temos o segundo caso que se trata da parábola com eixo de simetria paralelo ao eixo \(x\). Portanto, ser expressado como: \[\begin{eqnarray*} (y - k)^2 = 2p(x - h). \end{eqnarray*}\]

Observação. Perceba que tanto para o primeiro caso (parábola de eixo de simetria paralelo ao eixo \(y\)) quanto para o segundo caso se \((h,k) = (0,0)\), teremos exatemente a equação geral da parábola centrada na origem.

Assim seria o gráfico de uma parábola fora da origem com eixo de simetria paralelo ao eixo \(x\).

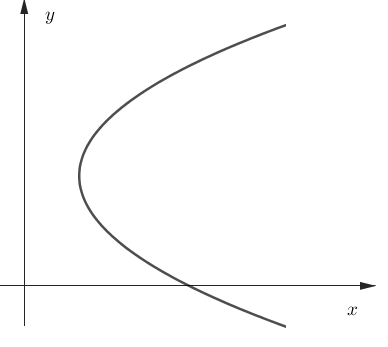
Figura 2.10: Parábola fora da origem com eixo paralelo a x.

2.1.3 Equação da parábola na forma explícita

É forma de equação da parábola que encontramos com maior frequência, pois é bem destacada no estudo de funções e equações quadráticas. Anteriormente foi visto que uma parábola pode ser expressa por: \[\begin{eqnarray*} (x - h)^2 = 2p(y - k) \end{eqnarray*}\] e através dela tendo o parâmetro e o vértice é possível determinar qualquer equação da parábola. Deste modo, por exemplo podemos tomar \(V(3 , -2)\) e \(p = 1\). Então: \[\begin{eqnarray*} (x-3)^2 = 2(y + 2) \end{eqnarray*}\] Agora vamos desenvolver o produto notável para que seja possível isolar \(y\): \[\begin{eqnarray*} x^2 -6x + 9 &=& 2y + 4 \\ x^2 -6x + 5 &=& 2y \\ \frac{1}{2}x^2 - 3x + \frac{5}{2} &=& y \end{eqnarray*}\] Portanto, tem-se: \[\begin{eqnarray*} y = \frac{1}{2}x^2 -3x + \frac{5}{2}. \end{eqnarray*}\] Sendo assim, sua forma padrão que é dada por: \[\begin{eqnarray*} y = ax^2 + bx + c. \end{eqnarray*}\] Essa é a forma de representação mais comum das parábolas, chamada de forma explícita.

Observação. Perceba que em \(y = ax^2 + bx + c\), onde \(a \neq 0\), é garantido que seu gráfico da parábola terá o eixo de simetria paralelo ao eixo \(y\).

Vale ressaltar alguns detalhes algumas informações que facilitam a construção do gráfico de uma parábola na forma explícita. Primeiramente, observe que caso queira encontrar o ponto de interseção da parábola no eixo \(y\), podemos tomar \(x = 0\), isso resulta em: \[\begin{eqnarray*} y = ax^2 + bx + c \Rightarrow y = c. \end{eqnarray*}\] Ou seja, o ponto que toca o eixo \(y\) é exatemente \((0,c)\). De fato, quanto a parábola em questão tiver o eixo de simetria paralelo a \(y\). Caso queira descobrir o ponto ou os pontos que tocam o eixo \(x\) de forma análoga tomamos \(y = 0\). Então: \[\begin{eqnarray*} y = ax^2 + bx + c \Rightarrow ax^2 + bx + c = 0. \end{eqnarray*}\] Isso é exatemente uma equação do \(2^{\circ}\) grau a qual já conhecemos vários possíveis métodos para resolvê-la. Nesse sentido, como resultado podemos ter uma, duas ou nenhuma raiz pertencentes ao conjunto dos números reias.

Agora iremos resolver um exemplo a partir de forma explícita, com o objetivo de ensinar passo a passo na construção de seu gráfico.

Exercicio 2.2 Seja \(y = x^2 -5x + 6\) uma parábola, determine o seu gráfico e vértice.

Solução. Antes da contrução de seu gráfico vamos determinar os seus elementos começando pelo vértice. Portanto, para encontrar o vértice é necessário lembrar de algumas fórmulas vistas em funções quadráticas, sendo elas comumente chamadas de \(y\) do vértice e \(x\) do vértice dadas por: \[\begin{eqnarray*} V \left(-\frac{b}{2a} , -\frac{\Delta}{4a} \right). \end{eqnarray*}\] Por outro lado, também podemos ao conhecimento de cálculo diferencial e determinar o ponto crítico, essa seria uma outra alternativa possível para determinar \(x_v\) e \(y_v\). Uma terceira opção seria lembra da definição da parábola e utilizar a sua propriedade do eixo de simetria que divide a parábola em dois lados simétrico exatamente no seu vértice. Isso nos ajuda da seguinte maneira, primeiro encontre as raízes da equação. Por soma e produto podemos determinar facilmente que as raízes são: \[x_1 = 2 \ \text{e} \ x_2 = 3.\] Como sabemos as raízes podemos determinar \(x_v\), pois como se trata de uma parábola temos raízes simétricas, ou seja, \(x_v\) é o ponto médio entre as raízes da parábola. Também sabemos que dado \(x_v\) é possível determinar o \(y_v\), pois \(y_v = f(x_v)\). Veja o gráfico abaixo:

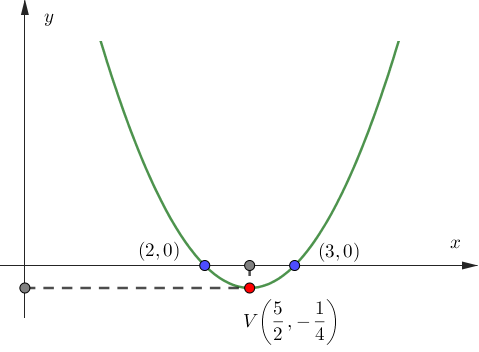
Figura 2.11: Gráfico da parábola \(y = x^2 -5x +6\).

2.2 Elipse

Definição 2.2 (Elipse) Uma elipse com focos \(F_1\) e \(F_2\), com eixo maior medindo \(2a > d(F_1,F_2)\), é o lugar geométrico formado pelos pontos pertencentes ao plano \(\alpha\), cuja soma das distâncias a dois pontos fixos \(F_1\) e \(F_2\) é igual a \(2a\). Ou seja, se tivermos \(F_1\) e \(F_2\), com \(d(F_1,F_2) = 2c\), e um número \(a>c\), podemos dizer que \(P\) é um ponto dessa elipe se

\[\begin{equation} d(P, F_1)+d(P,F_2)=2a, \tag{2.1} \end{equation}\]

e definimos a elipse como \[Elipse= \{ P \in \alpha \, \lvert \, \, d(P,F_1)+d(P,F_2)=2a\}.\]

Geometricamente, temos que a soma das distâncias \(d_1\) e \(d_2\) é igual a \(2a\), ver Figura 2.12.

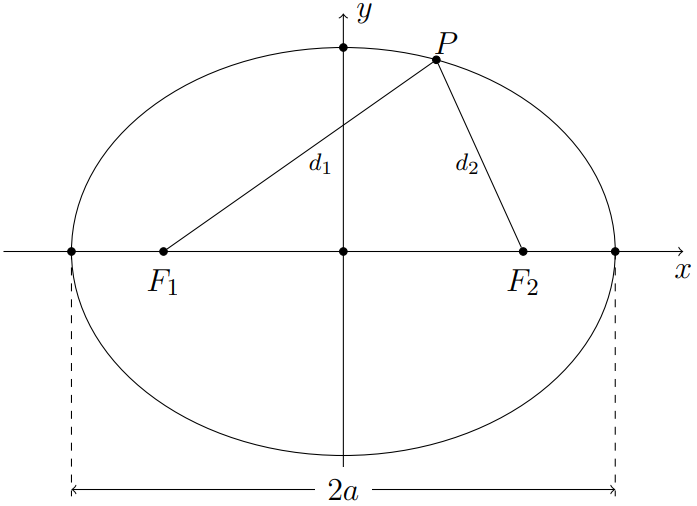
Figura 2.12: A soma das distâncias \(d_1\) e \(d_2\) equivale a constante \(2a\).

2.2.1 Elementos da Elipse

Na Figura 2.13 temos os principais elementos da elipse, e logo abaixo temos suas respectivas definições.

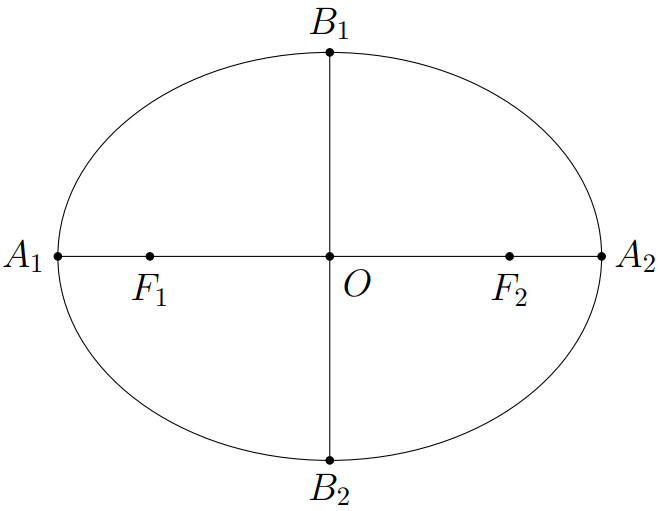
Figura 2.13: Elementos da Elipse.

Algumas denominações:

• Chamamos \(F_1\) e \(F_2\) de focos da elipse;
• \(d(F_1,F_2) =\) distância focal da elipse;
• \(O\) é o centro;
• A reta que contém os focos \(F_1\) e \(F_2\) é chamada de reta focal da elipse;
• O segmento \(\overline{A_1A_2}\) é chamado de eixo focal da elipse, conhecido também como eixo maior da elipse;
• O segmento \(\overline{B_1B_2}\) é conhecido como eixo menor da elipse;
• A amplitude focal é o comprimento de uma corda que contenha um dos focos da elipse e é perpendicular ao eixo focal desta;
• A menor região retangular que contém a elipse é chamada de retângulo fundamental da elipse.

2.2.2 Equação da Elipse

Para encontrarmos a equação da elipse, vamos primeiro definir um sistema de coordenadas. Vamos considerar o eixo \(x\) como a reta que passa pelos focos \(F_1\) e \(F_2\), com origem em \(O\) situada no ponto médio do segmento \(\overline{F_1F_2}\), e \(y\) sendo a reta perpendicular a esse segmento, que passa por \(O\). A Figura 2.14 ilustra esse sistema de coordenadas.

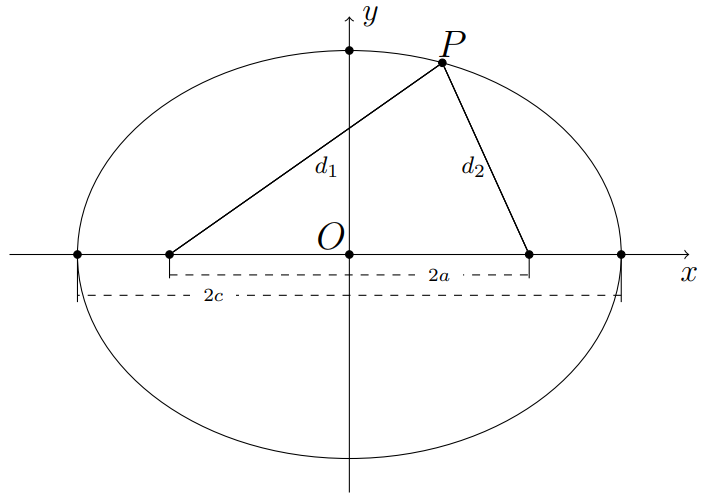
Figura 2.14: Construção do sistema de coordenadas.

Nesse sistema de coordenadas, vamos assumir que os focos \(F_1\) e \(F_2\) possuem coordenadas \((-c,0)\) e \((c,0)\), respectivamente, em que \(c\) é um número real positivo. Se tomarmos um ponto genérico \(P=(x,y)\), teremos que a equação (2.1) ficará da seguinte forma:

\[\begin{align} d\left(P,F_1\right)+d\left(P,F_2\right)&=2a \\ d\left((x,y),(-c,0)\right)+d\left((x,y),(c,0)\right)&=2a \\ \sqrt{(x-(-c))^2+(y-0)^2}+\sqrt{(x-c)^2+(y-0)^2}&=2a \\ \sqrt{(x+c)^2+(y)^2}+\sqrt{(x-c)^2+(y)^2}&=2a \\ \sqrt{(x+c)^2+y^2}&=2a-\sqrt{(x-c)^2+y^2} \tag{2.2} \end{align}\]

Ao elevar ambos os membros de (2.2) ao quadrado, teremos:

\[\begin{align} \left(\sqrt{(x+c)^2+y^2}\right)^2&=\left(2a-\sqrt{(x-c)^2+y^2}\right)^2 \\ (x+c)^2+y^2&=4a^2-4a\sqrt{(x-c)^2+y^2}+(x-c)^2+y^2 \tag{2.3} \end{align}\]

Desenvolvendo os quadrados de (2.3), teremos:

\[\begin{align} x^2+2cx+c^2+y^2&=4a^2-4a\sqrt{x^2-2cx+c^2+y^2}+x^2-2cx+c^2+y^2 \end{align}\]

Simplificando as parcelas iguais:

\[\begin{align} 2cx&=4a^2-4a\sqrt{x^2-2cx+c^2+y^2}-2cx \\ 2cx+2cx-4a^2&=-4a\sqrt{x^2-2cx+c^2+y^2} \\ 4cx-4a^2&=-4a\sqrt{x^2-2cx+c^2+y^2} \\ 4(cx-a^2)&=-4a\sqrt{x^2-2cx+c^2+y^2} \\ cx-a^2&=-a\sqrt{x^2-2cx+c^2+y^2} \tag{2.4} \end{align}\]

Eleva ambos os membros de (2.4) ao quadrado:

\[\begin{align} (cx-a^2)^2&=\left(-a\sqrt{x^2-2cx+c^2+y^2}\right)^2 \\ c^2x^2-2cxa^2+a^4&=a^2(x^2-2cx+c^2+y^2) \\ c^2x^2-2a^2cx+a^4&=a^2x^2-2a^2cx+a^2c^2+a^2y^2 \\ c^2x^2+a^4&=a^2x^2+a^2c^2+a^2y^2 \tag{2.5} \end{align}\]

Soma \(-c^2x^2-a^2c^2\) a ambos os membros de (2.5):

\[\begin{align} c^2x^2+a^4-c^2x^2-a^2c^2&=a^2x^2+a^2c^2+a^2y^2-c^2x^2-a^2c^2 \\ a^4-a^2c^2&=a^2x^2+a^2y^2-c^2x^2 \\ a^2(a^2-c^2)&=x^2(a^2-c^2)+a^2y^2 \end{align}\]

Substituindo \(b^2=a^2-c^2\), temos:

\[\begin{align} a^2b^2=x^2b^2+a^2y^2. \tag{2.6} \end{align}\]

Ao dividir (2.6) por \(a^2b^2\), sendo \(a^2b^2\neq 0\), chegaremos a seguinte expressão:

\[\begin{align} \dfrac{1}{a^2b^2}(x^2b^2+a^2y^2)&=\dfrac{1}{a^2b^2}(a^2b^2) \\ \dfrac{x^2b^2}{a^2b^2}+\dfrac{a^2y^2}{a^2b^2}&=1 \\ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}&=1. \end{align}\]

A partir disso, temos a seguinte proposição:

Proposição 2.1 Dado uma elipse \(\mathcal{E}\) com focos \(F_1=(-c,0)\) e \(F_2=(c,0)\) e eixo maior medindo \(2a\), sua equação é dada por

\[\begin{align} \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1, \tag{2.7} \end{align}\]

conhecida como equação reduzida da elipse ou forma canônica da elipse, em que \(b\) é tal que \[a^2=b^2+c^2.\]

A interpretação geométrica de \(a\) e \(b\) pode ser observada a partir da equação reduzida. Se fizermos \(y=0\) em (2.7), iremos obter a seguinte expressão: \[\begin{align*} \dfrac{x^2}{a^2}+\dfrac{0^2}{b^2}&=1 \\ \dfrac{x^2}{a^2}&=1\\ x^2&=a^2 \\ x&=\pm a. \end{align*}\]

Ou seja, \(x\) está variando de \(-a\) a \(+a\), e como \(A_1\) e \(A_2\) é a delimitação do eixo maior da elipse, temos que \(A_1=(-a,0)\) e \(A_2=(a,0)\) são pontos da elipse, sendo eles conhecidos como vértices.

No outro caso, se fizermos \(x=0\) na equação (2.7), iremos obter a seguinte expressão:

\[\begin{align*} \dfrac{0^2}{a^2}+\dfrac{y^2}{b^2}&=1 \\ \dfrac{y^2}{b^2}&=1 \\ y^2&=b^2 \\ y&=\pm b \end{align*}\]

Como em nosso sistema de coordenadas o eixo \(y\) está relacionado com o eixo menor da elipse, \(y\) estará variando de \(-b\) a \(+b\) e, assim, temos os pontos \(B_1=(0,-b)\) e \(B_2=(0,b)\) sendo extremidades desse eixo. Podemos visualizar, na Figura 2.15, como esses parâmetros se comportam.

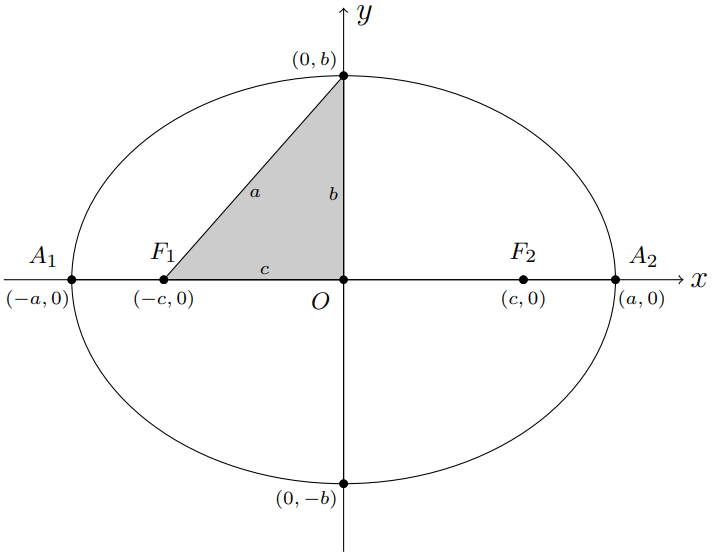
Figura 2.15: Relação dos parâmetros \(a^2=b^2+c^2\) .

2.2.3 Gráfico da Elipse

O gráfico da elipse é dado por \[\text{Graf}=\begin{Bmatrix}(x,y)\,\bigg|\, \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 \end{Bmatrix}.\]

Podemos observar, na Figura 2.16 e 2.17, dois exemplos do gráfico da elipse.

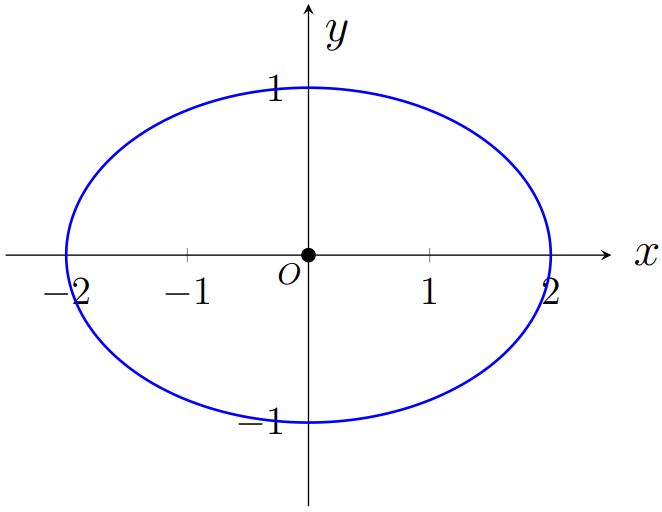
Figura 2.16: Elipse \(\dfrac{x^2}{4}+y^2=1\)

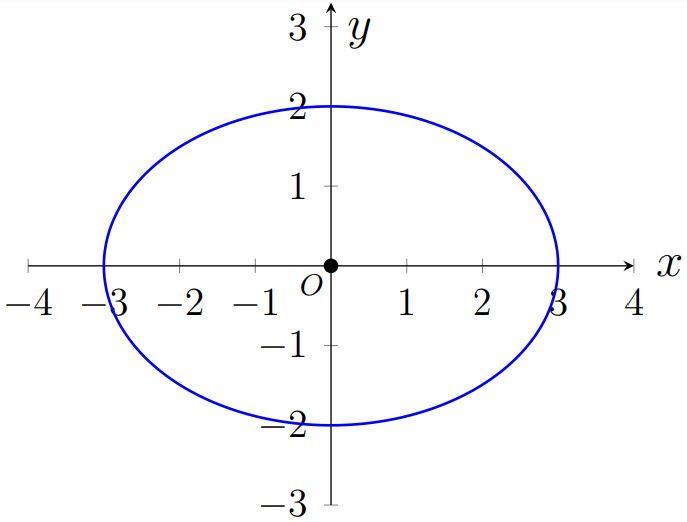
Figura 2.17: Elipse \(\dfrac{x^2}{9}+\dfrac{y^2}{4}=1\)

2.2.4 Elipse com centro na origem e reta focal coincidente com o eixo \(OX\)

Esse caso coincide com o que fizemos no tópico 2.2.2. Desse modo, a forma canônica da elipse com centro na origem e reta focal coincidente com o eixo \(OX\) é dada por \[\begin{align} \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1. \end{align}\]

2.2.5 Esboço da Elipse

Inicialmente vamos considerar uma elipse \(\mathcal{E}\) de equação \[\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1,\] em que \(a,b>0\). Isolando o \(y\), teremos: \[\begin{align} \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}&=1 \\ \dfrac{y^2}{b^2}&=1-\dfrac{x^2}{a^2} \\ \dfrac{y^2}{b^2}&=\dfrac{a^2-x^2}{a^2} \\ y^2&=\dfrac{b^2}{a^2}(a^2-x^2) \\ y&=\pm \dfrac{b}{a}\sqrt{a^2-x^2}. \end{align}\]

Se quisermos esboçar o gráfico de \(\mathcal{E}\) no primeiro quadrante, basta estudarmos o gráfico da seguinte função: \[\begin{align*} f: [0, a] &\longrightarrow \mathbb{R} \\ x&\longmapsto \dfrac{b}{a}\sqrt{a^2-x^2} \end{align*}\]

Observação. Note que se tivermos \(x>a\), implica que \((a^2-x^2)<0\), tendo a consequência de \(f\) não ficar bem definida, pois teremos a raiz quadrada de um número negativo. Assim, consideraremos a função \[\begin{align*} y=\dfrac{b}{a}\sqrt{a^2-x^2}, \quad x \in [0, a]. \end{align*}\]

Dessa forma, teríamos o seguinte gráfico no primeiro quadrante:

Figura 2.18: Gráfico da função \(y=\dfrac{b}{a}\sqrt{a^2-x^2},\quad x\in [0,a].\)

2.2.6 Elipse com centro na origem e reta focal coincidente com o eixo \(OY\)

Nesse caso, agora teremos que os focos serão dados por \(F_1=(0, -c)\) e \(F_2=(0, c)\), os vértices da elipse sobre a reta focal serão iguais a \(A_1=(0, -a)\) e \(A_2=(0,a)\), e os vértices da elipse sobre a reta não focal serão \(B_1=(-b,0)\) e \(B_2=(b,0)\). Desse modo, teremos que a equação da elipse de centro na origem e reta focal sendo o eixo \(y\) é igual a \[\begin{align*} \dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1, \end{align*}\] e o gráfico dessa equação é igual ao representado na Figura 2.19.

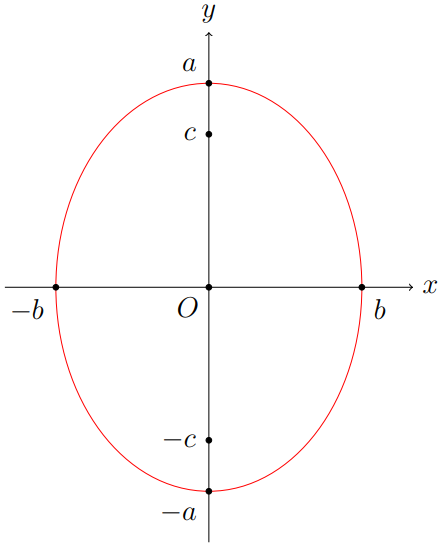
Figura 2.19: Elipse \(\mathcal{E}=\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\) .

2.2.7 A excentricidade da elipse

A excentricidade da elipse é dada por \[e=\dfrac{c}{a}, \quad 0<e<1,\] e é responsável pela forma da elipse.

2.2.8 Elipse com centro no ponto \(\mathcal{P}=(h,k)\)

Geralmente, a elipse de equação \[\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\] tem centro em \((0,0)\) e eixos de simetria equivalendo a \(x=0\) e \(y=0\). Entretanto, quando essa elispe é transladada \(h\) unidades horizontalmente e \(k\) unidades verticalmente, uma nova elipse é formada.

2.2.8.1 Caso em que a reta focal é paralela ao eixo \(OX\)

A nova elipse formada quando transladada \(h\) unidades horizontalmente e \(k\) unidades verticalmente, nesse caso, terá a seguinte equação \[\begin{align*} \dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1. \end{align*}\]

O centro é transladado para o ponto \(\mathcal{P}=(h,k)\), e os focos, os vértices, as extremidades do eixo menor e eixos de simetria são modificados de acordo com a seguinte regra:

Tabela 2.2. Transformação dos elementos.

	\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)		\(\dfrac{(x-x_0)^2}{a^2}+\dfrac{(y-y_0)^2}{b^2}=1\)
Centro	\((0,0)\)	\(\longrightarrow\)	\((h,k)\)
Focos	\((c,0)\) e \((-c,0)\)	\(\longrightarrow\)	\((c+h, k)\) e \((-c+h, k)\)
Vértices	\((a,0)\) e \((-a,0)\)	\(\longrightarrow\)	\((a + h, k)\) e \((-a + h, k)\)
Extremidades do eixo menor	\((0, b)\) e \((0, -b)\)	\(\longrightarrow\)	\((h, b + k)\) e \((h, -b + k)\)
Eixos de simetria	\(x = 0\) e \(y = 0\)	\(\longrightarrow\)	\(x = h\) e \(y = k\)

2.2.8.2 Caso em que a reta focal é paralela ao eixo \(OY\)

De forma análoga, é possível verificar que a forma canônica da equação da elipse, sendo ela centrada no ponto \((h,k)\), com o eixo focal paralelo ao eixo \(OY\) é dada por:

\[\begin{align*} \dfrac{(x-h)^2}{b^2}+\dfrac{(y-k)^2}{a^2}=1. \end{align*}\]

2.3 Hipérbole

A Hipérbole é o lugar geométrico dos pontos de um plano cuja diferença das distâncias, em valor absoluto, a dois pontos fixos desse plano, também denominados de focos, é constante. Tendo a seguinte definição:

Definição 2.3 (Hipérbole) Dados dois pontos fixos \(F_1\) e \(F_2\) e um número real positivo \(a\), definimos uma hipérbole com focos \(F_1\) e \(F_2\), como o conjunto de todos os pontos \(P\) do plano, tais que o módulo da diferença de suas distâncias a esses dois pontos é constante e igual a \(2a\).

Sendo assim, se considerarmos dois pontos distintos \(F_1\) e \(F_2\), em um plano \(\alpha\), tal que a distância entre esses dois pontos \(d(F_1, F_2) = 2c\), seja um número real \(a\) onde o dobro de \(a\) é menor que a distância entre \(F_1\) e \(F_2\). Ou seja, \(2a < 2c\).

Ao conjunto de todos os pontos \(P\) de um plano, tal que: \[\begin{equation} \lvert d(P,F1) - d(P,F2)\rvert = 2a. \tag{2.8} \end{equation}\]

Por exemplo, sejam os pontos \(P, Q, R, S, F_1\) e \(F_2\), pontos pertencentes a um mesmo plano e \(F_1F_2 = 2c\), temos:

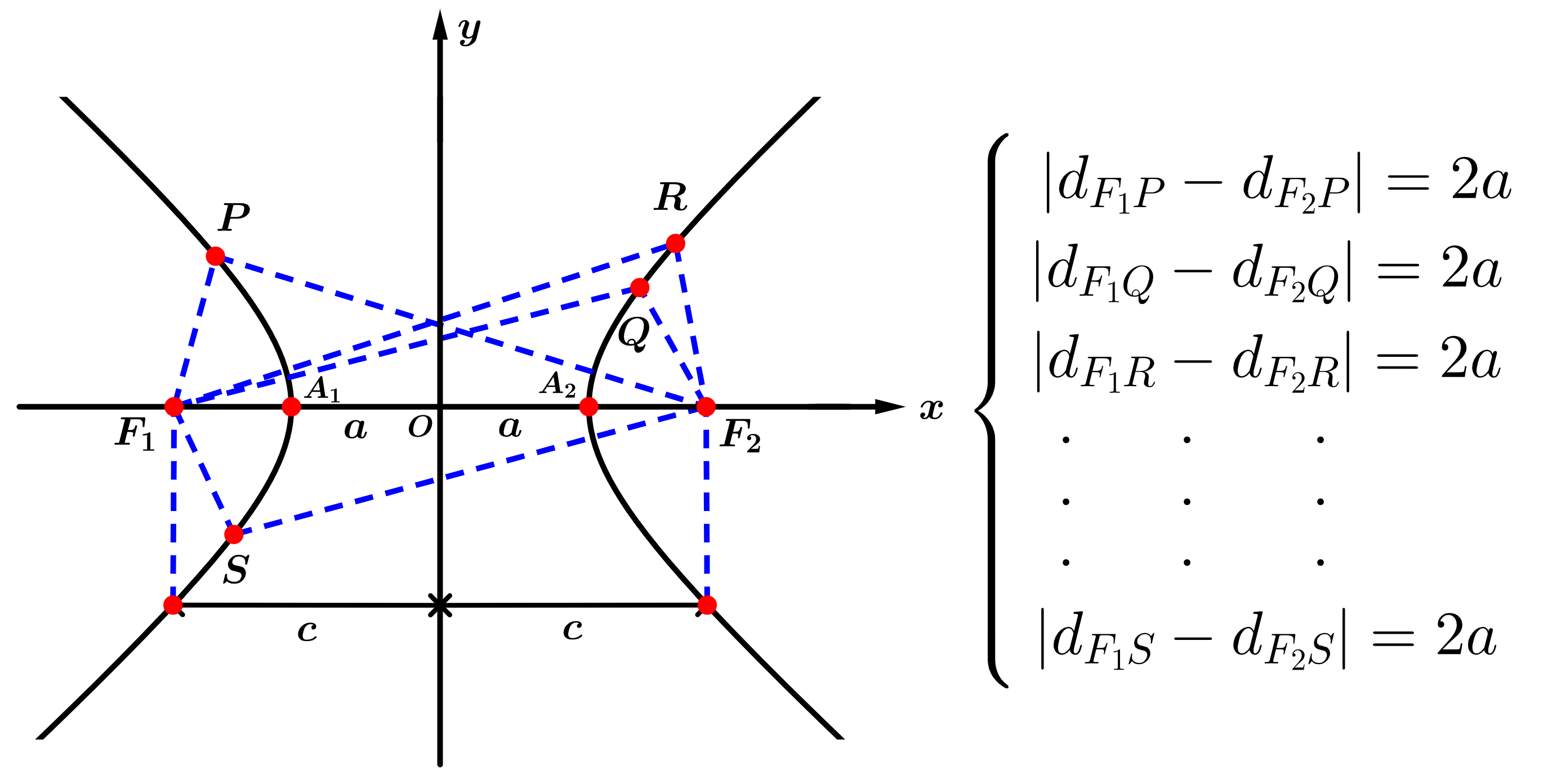
Figura 2.20: Hipérbole. Fonte: Só Matemática, 2023.

Como se pode observar na Figura 2.20 e pela equação (2.8), a hipérbole é uma curva formada por dois ramos, onde se tomarmos um ponto qualquer, este ponto está na hipérbole, se e somente se: \[d(P,F_1) - d(P,F_2) = \pm 2a.\]

Quando o ponto analisado estiver no ramo da direita, a diferença será de \(+2a\), caso esteja no ramo da esquerda será \(-2a\).

Observação. A hipérbole é a cônica definida por um plano que penetra paralelo ao eixo de simetria de dois cones circulares retos e opostos pelos vértices.

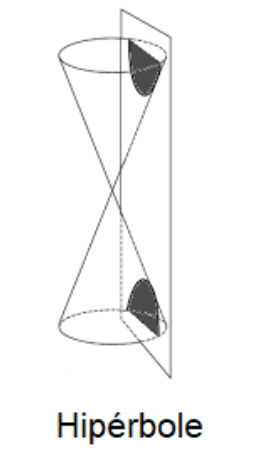
Figura 2.21: Cônica - Hipérbole.

Terminologia

• Os pontos \(F_1\) e \(F_2\) descritos na Figura 2.22 são conhecidos como focos da hipérbole. O segmento \(F_1F_2\) de comprimento \(2c\) é o segmento focal da hipérbole e \(2c\) é a distância focal da hipérbole;
• A reta \(r\) contendo \(F_1\) e \(F_2\) é denominada reta focal da hipérbole;
• A intersecção de \(H\) com \(r\) consiste de dois pontos \(A_1\) e \(A_2\) que são os vértices da hipérbole sobre a reta focal. O segmento \(A_1A_2\) de comprimento \(2a\) é conhecido como eixo transverso da hipérbole;
• O ponto médio \(O \in r\) do segmento \(F_1F_2\) é o centro da hipérbole;
• O segmento \(B_1B_2\) de comprimento \(2b\) (onde \(c^2 = a^2 + b^2\)), cujos extremos \(B_1\) e \(_B2\) estão simetricamente localizados em relação ao centro \(O\) da hipérbole sobre a reta \(s\) perpendicular a \(r\) por \(O\), é denominado eixo conjugado da hipérbole;
• Os números \(a\), \(b\) e \(c\) são conhecidos como parâmetros geométricos da hipérbole;
• As retas \(r-\) e \(r+\) pelo centro \(O\) de inclinação \(\dfrac{-b}{a}\) e \(\dfrac {b}{a}\) respectivamente são as assíntotas da hipérbole;
• Qualquer segmento cujos extremos estão sobre \(H\) é chamado de corda da hipérbole;
• Dá-se o nome de amplitude focal da hipérbole ao comprimento de uma corda que contenha um dos focos da hipérbole e que seja perpendicular à reta focal desta;
• Uma hipérbole é dita equilátera quando os parâmetro geométricos \(a\) e \(b\) dessa hipérbole são iguais.

Os elementos citados podem ser observados na Figura 2.22:

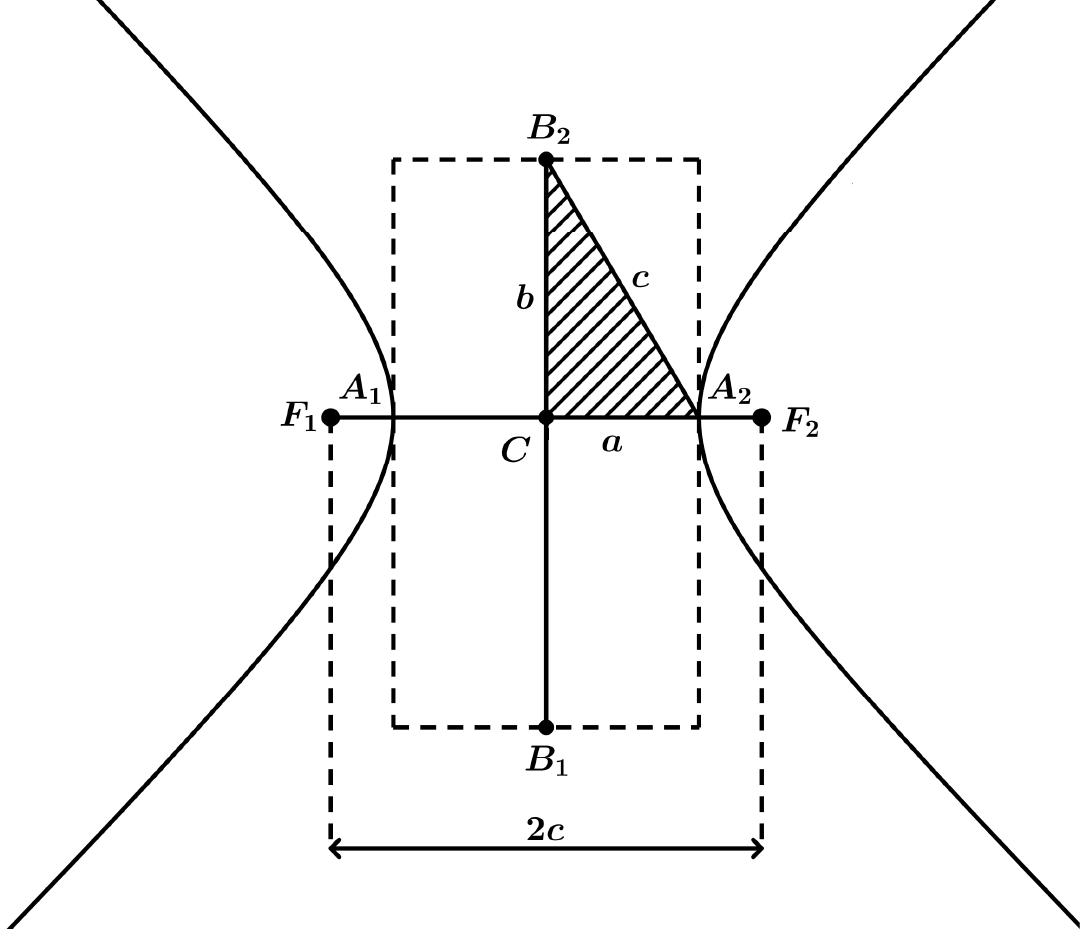
Figura 2.22: Elementos - Hipérbole

Na Figura 2.22 é possível perceber que \(a, b\) e \(c\) são as medidas dos lados do triângulo retângulo \(B_2CA_2\). O valor de \(b\) é então definido através da relação \(c^2 = a^2 + b^2\).

Se considerarmos uma circunferência de raio \(c\) tendo como centro \(C\), e tomarmos um valor para \(a\) e marcarmos os pontos \(A_1\) e \(A_2\) como vértices da hipérbole. Traçando por estes pontos, cordas perpendiculares ao diâmetro \(F_1F_2\), as quatro estremidades destas cordas são os vértices de um retângulo inscrito nesta circunferência. Como vemos na Figura 2.23.

O retângulo contruido tem dimenções \(2a\) e \(2b\) e as retas \(r\) e \(s\), que contêm as diagonais do retângulo, são as chamadas assíntotas da hipérbole.

As assíntotas são as retas das quais a hipérbole se aproxima à medida que os pontos se afastam dos focos. Esta aproximação é contínua, de maneira que a tendência da hipérbole é tangenciar suas assíntotas no infinito.

Na Figura 2.23 também é possível observar o ângulo \(\theta\) , que indica a abertura da hipérbole. Em uma hipérbole também encontramos a excentricidade que, que está relacionada a abertura, e que é dada por: \(e= \dfrac {c}{a}\), onde \(c > a \therefore e > 1\).

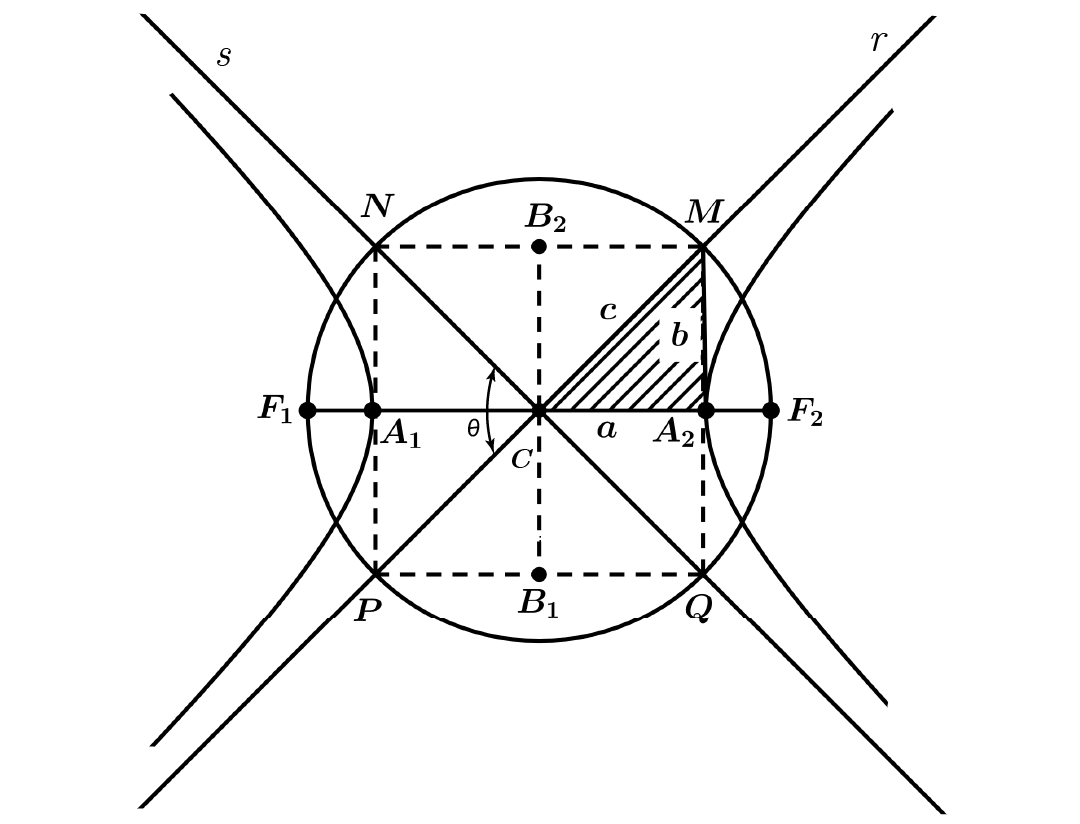
Figura 2.23: Assíntotas

A equação de uma hipérbole pode ser reduzida, para isso vamos tomar \(F_1(-c,0)\) e \(F_2(c,0)\), considerando \(P(x,y)\) como sendo um ponto qualquer sobre a hipérbole, temos então:

\[\begin{align} \lvert d(P,F_1) - d(P,F_2)\rvert &= 2a \\ d(P,F_1) - d(P,F_2) &= 2a \\ \sqrt{(x+c)^2 + (y-0)^2} - \sqrt {(x-c)^2 + (y-0)^2} &= \pm 2a \\ \sqrt{(x+c)^2 + y^2} &= \sqrt {(x-c)^2 + y^2} \pm 2a \\ x^2 + 2cx + c^2 + y^2 &= x^2 - 2cx + c^2 + y^2 \pm 4a \sqrt {(x-c)^2 + y^2} + 4a^2 \\ 4cx - 4a^2 &= 4a \sqrt{(x-c)^2 + y^2} \\ cx - a^2 &= \pm a \sqrt{(x-c)^2 + y^2} \\ c^2x^2 - 2a^2cx + a^4 &= a^2x^2 - 2a^2cx + a^2c^2 + a^2y^2 \\ c^2x^2 - a^2x^2 - a^2y^2 &= a^2c^2 - a^4 \\ (c^2 - a^2)x^2 - a^2y^2 &= a^2 (c^2-a^2) \end{align}\]

Tomando \(c^2 - a^2 = b^2\), e fazendo a substituição, temos: \[b^2x^2 - a^2y^2 = a^2b^2\text{.}\]

Dividindo tudo por \(a^2b^2\), obtemos a equação da hipérbole: \[\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1 .\]

2.3.1 Equação da Hipérbole de Centro na origem do Sistema

2.3.1.1 Eixo real sobre o eixo \(x\)

A Figura 2.24 nos traz uma hipérbole de centro na origem e eixo real sobre o eixo \(x\), tendo como equação: \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\).

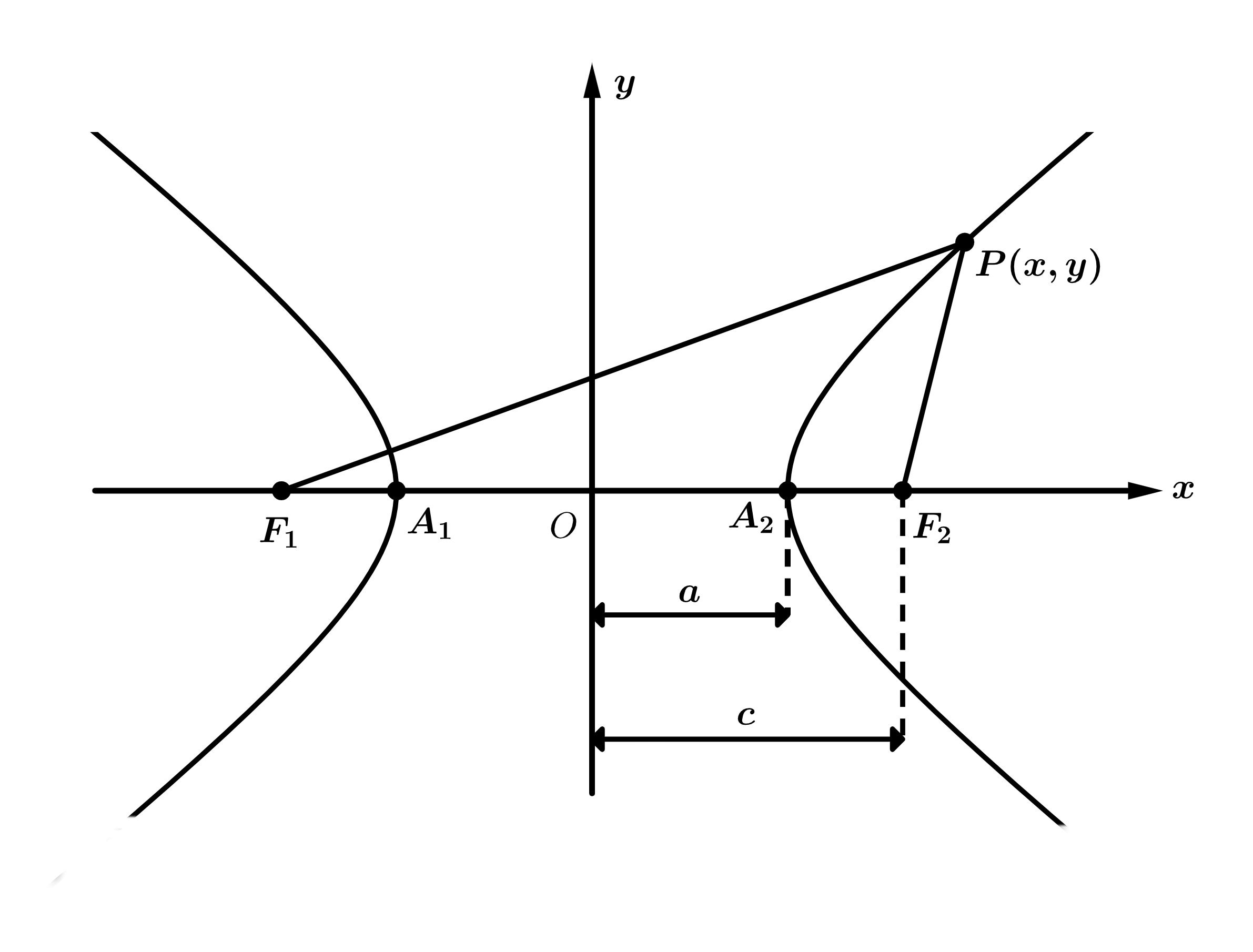
Figura 2.24: Hipérbole de eixo real sobre o eixo \(x\).

2.3.1.2 Eixo real sobre o eixo \(y\)

Já a Figura 2.25 traz uma hipérbole de centro na origem e eixo real sobre o eixo \(y\), tendo como equação: \(\dfrac{y^2}{a^2} - \dfrac{x^2}{b^2} = 1\).

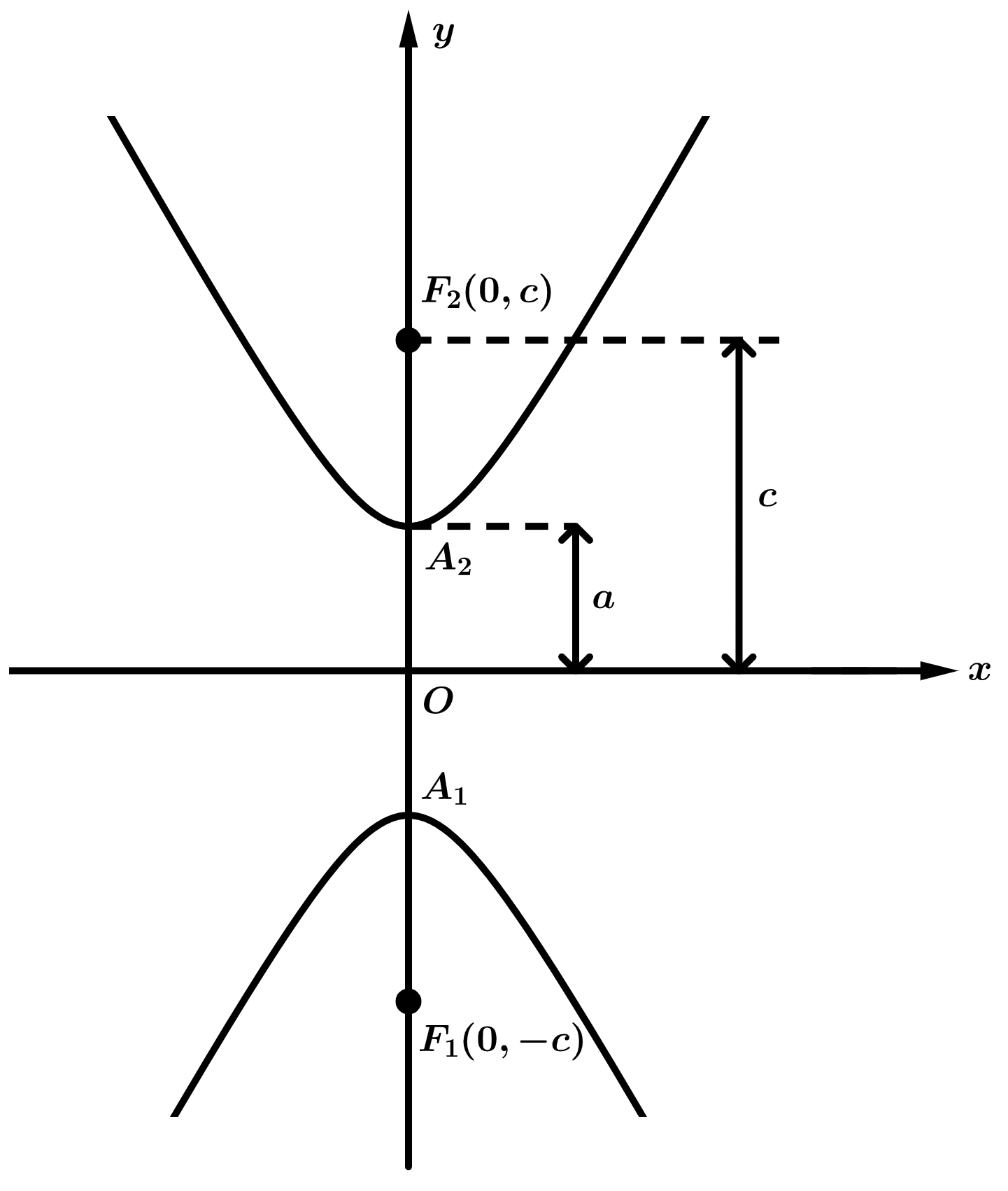
Figura 2.25: Hipérbole de eixo real sobre o eixo \(y\).

Exemplo 2.1 Dada a equação \(9x^2 - 7y^2 - 63 = 0\), determine para a hipérbole o que se pede:

1. A medida dos semieixos.
2. Um esboço gráfico.
3. Os vértices.
4. Os focos.
5. A excentricidade.
6. As equações das assíntotas.

Solução. Tomando \(9x^2 - 7y^2 - 63 = 0\), vamos colocar na forma da equação reduzida da hipérbole: \[\begin{align} 9x^2 - 7y^2 - 63 &= 0 \\ 9x^2 - 7y^2 &= 63 \end{align}\]

Dividindo tudo por \(63\), temos: \[\begin{align} \dfrac{9x^2}{63} - \dfrac{7y^2}{63} &= \dfrac{63}{63} \\ \dfrac{x^2}{7} - \dfrac{y^2}{9} &= 1 \end{align}\]

Que é a equação reduzida da hipérbole cujo eixo real está sobre o eixo \(x\)

Assim:

Solução (a). \[\begin{align} a^2 = 7 \therefore a &= \pm \sqrt {7} \\ b^2 = 9 \therefore b &= \pm 3\end{align}\]

Solução (b). Esboço da hipérbole:

Figura 2.26: Hipérbole de eixo real sobre o eixo \(y\).

Solução (c). Sendo \(a = \pm \sqrt {7}\), temos como vértices da hipérbole: \(A_1(- \sqrt {7}, 0)\) e \(A_2( \sqrt {7}, 0)\).

Solução (d). Para determinar os focos devemos encontrar o valor de \(c\). Sabendo que \(c^2 = a^2 + b^2\):

\[\begin{align} c^2 &= a^2 + b^2 \\ c^2 &= 7 + 9 \\ c^2 &= 16 \\ c &= \pm 4 \end{align}\]

Logo, os focos são: \(F_1(-4,0)\) e \(F_2(4,0)\).

Solução (e). Excentricidade: \[e = \frac {c}{a} = \frac {4}{\sqrt {7}}\]

Solução (f). As assíntotas são as retas que passam pela origem, portanto, suas equações são do tipo: \(y = mx = \dfrac{b}{a}x\), onde \(m\) é a declividade.

Assim:

A assíntota \(r\) tem declividade: \(m_1 = \dfrac{b}{a}\), enquanto que \(s\) tem declividade \(m_2 = - \dfrac{b}{a}\). Logo, as equações das assíntotas são: \[y = \dfrac{3}{\sqrt{7}}x \text{ e } y = -\dfrac{3}{\sqrt{7}}x\]

2.3.2 Aplicações práticas da Hipérbole

As hipérboles aparecem em vários objetos na vida real. Podemos encontrar figuras hiperbólicas na arquitetura, em vários edifícios e estruturas, sendo ela muito comum não só na arquitetura como na engenharia civil. Também encontramos hipérboles na explosão sônica de aviões, na construção de telescópios refletores e até mesmo na forma das torres de resfriamento de usinas nucleares.

Na navegação também há o uso da hipérbole com o chamado LORAN, que é um sistema de localização em navegação (Navegação de Longa Distância) usado pelos navios e aviões de vários países. LORAN consiste num sistema de hiperbólicas que permite ao navegante achar sua posição.Seu funcionamento é considerado simples, pois consiste em estações localizadas em dois pontos fixos da terra, que seriam \(F_1\) e \(F_2\), enviam sinais que são captados pelo navegante em um ponto \(O\). Em \(O\) calcula-se o intervalo de tempo \(\Delta = t_2 - t_1\), onde \(t_1\) e \(t_2\) é o tempo em que O recebe o sinal de \(F_1\) e \(F_2\) respectivamente. A diferença entre os instantes \(t_1\) e \(t_2\) determina \(2a\) obtendo a característica da hipérbole.