BLOQUE 6: Introducción al análisis de series temporales

Clase 1. Características de las series temporales y la sorprendente “regresión espuria”

Los datos de series temporales consisten en una secuencia de \(T\) observaciones (datos, en general, relativos a comportamientos humanos agregados) ordenados cronológicamente (y, habitualmente, equiespaciados).

Una variable, \(y\) se denomina serie temporal añadiéndole un índice “temporal” \(t\): de tal forma que- si escribimos- \(y_t\) estamos hablando de una serie temporal. En general, diremos que \(t=0,1,...,T\), indicando \(t=0\) el momento “inicial” de la serie y \(t=T\) el final, como convención.

Un instrumento importante para analizar series temporales son los gráficos donde, en el eje de abscisas, se representa la variable “tiempo” y en el eje de ordenadas la magnitud que se está considerando. Además, conviene acostumbrarse a hacer una buena inspección gráfica para obtener las ideas más relevantes que compondrán la serie.

Por ejemplo, apoyémonos en ciertos gráficos de series temporales obtenidos del INE, Yahoo finanzas y Google para tener una primera idea de lo que buscamos en las series.

Frecuencia

La frecuencia de una serie indica cada cuánto tiempo se representa la información disponible. En el INE abundan, por ejemplo, las series anuales y trimestrales (por el coste que supone recoger información con mayor frecuencia). Las series bursátiles son diarias y las de consumo eléctrico pueden ser horarias.

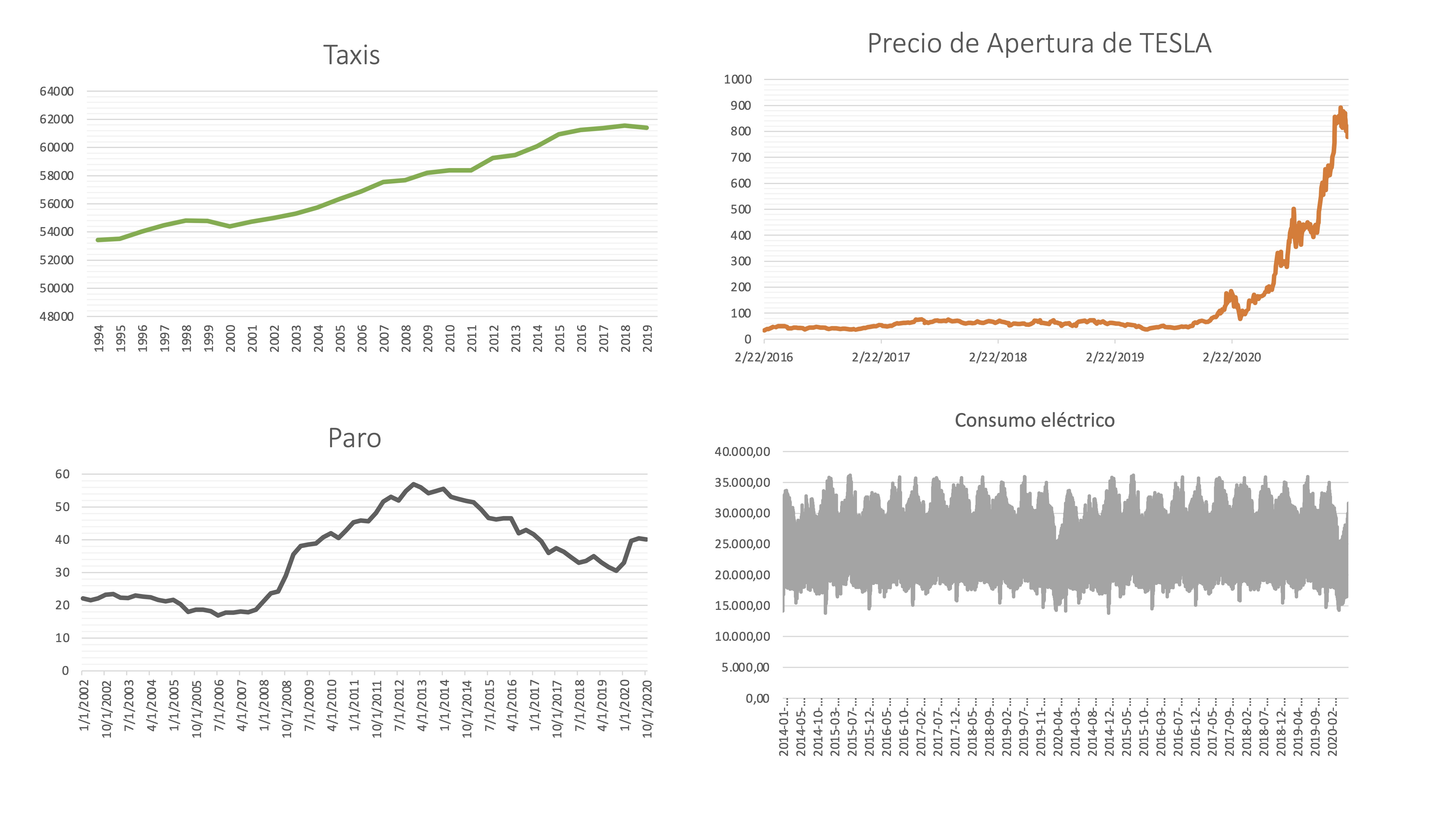
FIG 1: Diferentes series temporales

Taxis, con frecuencia anual, representa el número de taxis en circulación en España.
Precio Apertura TESLA, con frecuencia diaria, representa el precio de la acción de esta empresa.
Paro, con frecuencia trimestral, representa la tasa de paro de individuos menores de 25 años.
Consumo eléctrico, con frecuencia horaria, representa el consumo en MW hora.

Estacionalidad

Es una característica que pueden tener las series recogidas con frecuencia superior al año. Está relacionada con el concepto “estación del año” y tiene que ver con que el comportamiento humano se adapta a las estaciones y, por tanto, se suele modificar. En el ejemplo anterior, la tasa de paro tiene cierto comportamiento estacional (subidas sistemáticas del paro al acabar verano y navidades), y la serie de consumo eléctrico. Sin embargo, la serie del precio de TESLA no parece tener estacionalidad (de hecho, si esto fuera así, sería más predecible el mercado de acciones, ¿no?).

Ejemplo

En esta serie de turistas mensuales se puede ver claramente la pauta estacional

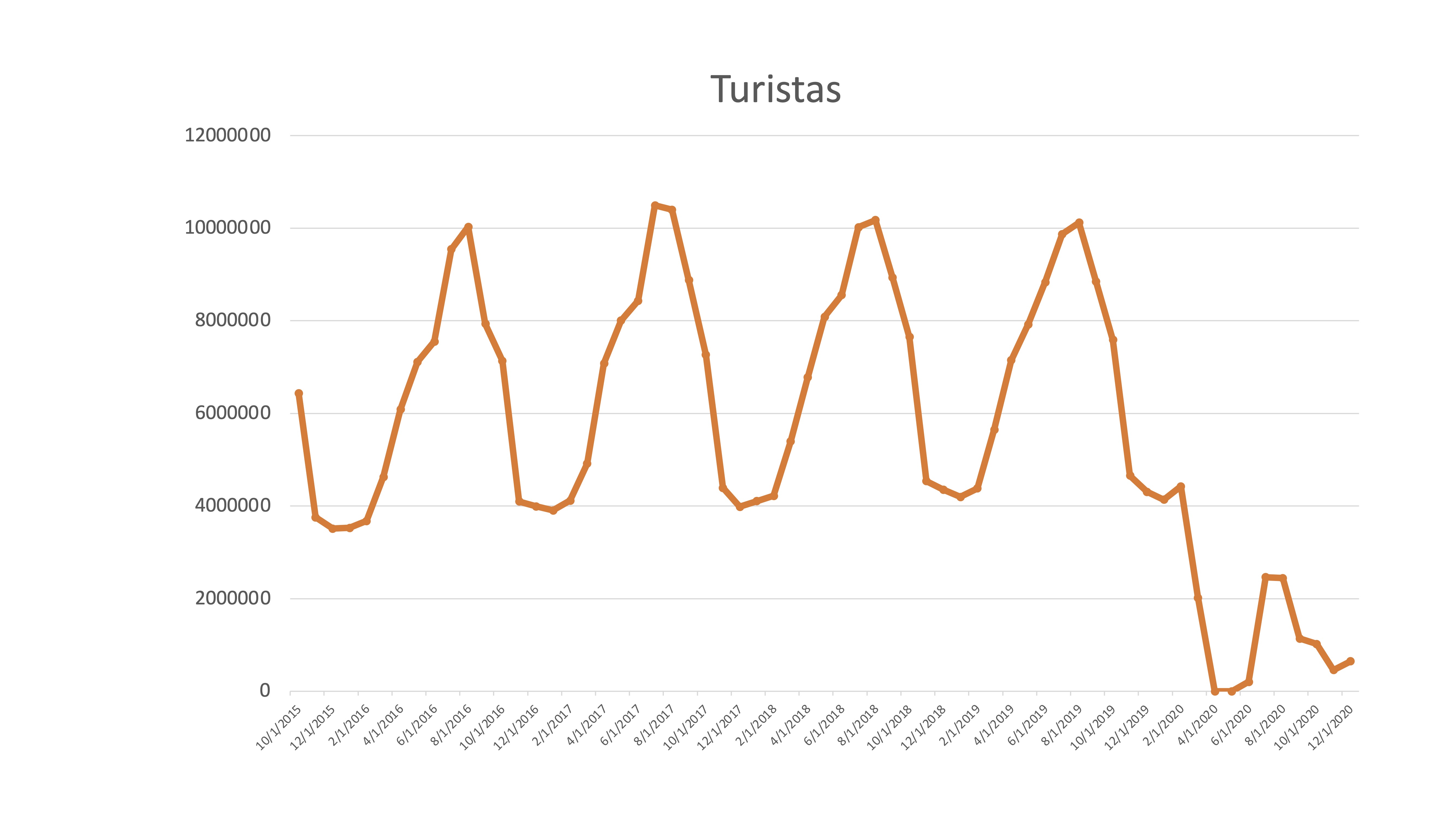
FIG 2: Serie temporal de turistas en España

que, obviamente, se ha modificado con claridad desde el mes de marzo de 2020. Hasta ese momento ¿no era una serie muy previsible? ¿Cómo predeciremos el comportamiento de la serie?

Estacionariedad en media

una serie temporal es estacionaria en media cuando la media es un buen “resumen” de la serie, es decir, es representativa. Una forma de ver si una serie es estacionaria en media, mediante el gráfico, es ver si las observaciones cortan o no, de manera reiterada dicha media.

Ejemplo

Dos series temporales: el número de taxis y su variación. La serie de Taxis, como vemos, tiene una tendencia creciente, por lo que la media no puede ser representativa. Note que, sin embargo, su variación (calculada como \(y_{t}-y_{t-1})\) sí que parece estar razonablemente bien resumida por su media.

Importante Vemos que una transformación estacionaria de la media de una serie consiste en calcular su variación. A esto se le llama también “diferencia” y se suele denotar como \(\Delta y_t=y_{t}-y_{t-1}\)

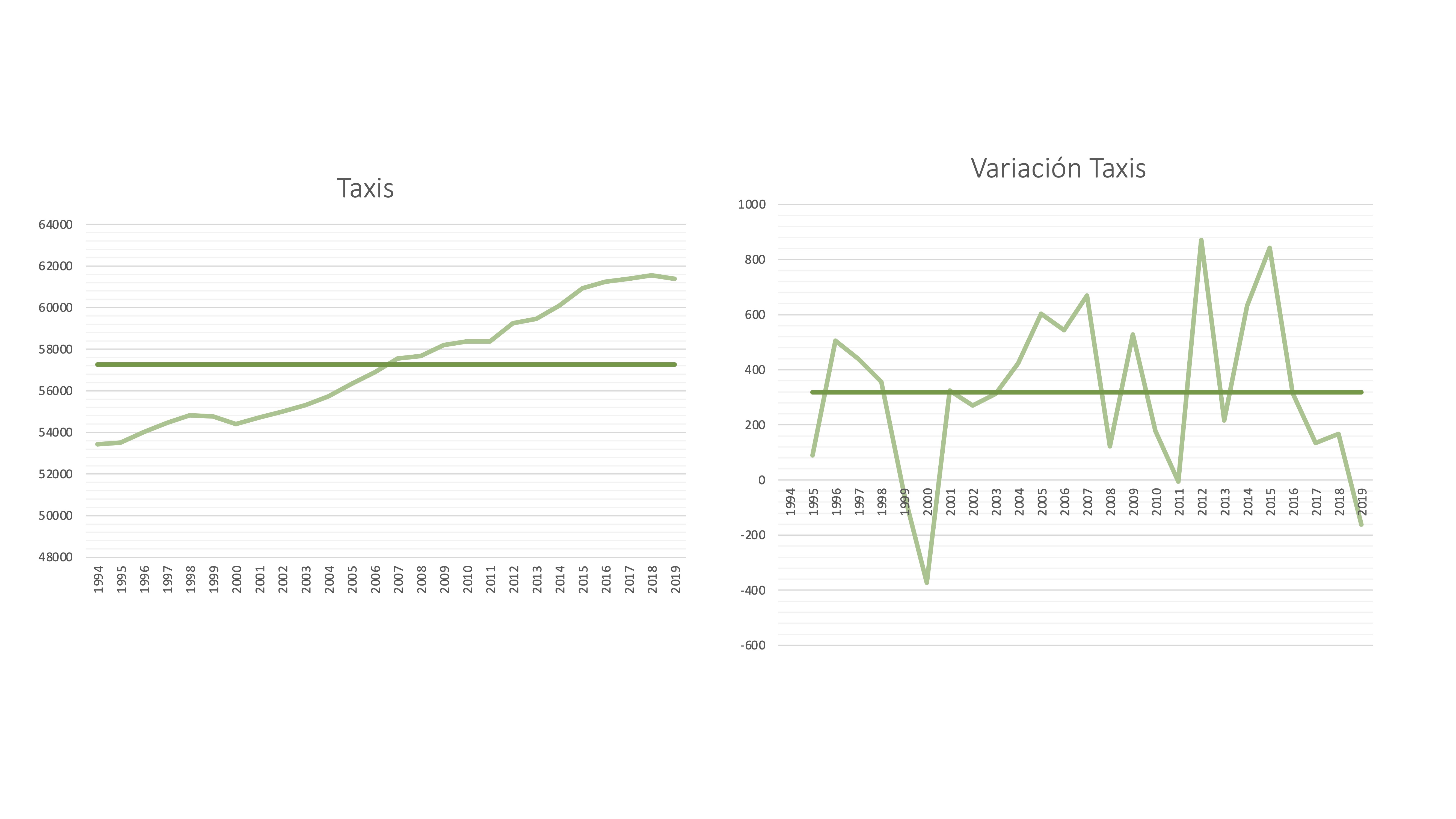
FIG 3: La serie de “taxis” en España

Nota: una serie con estacionalidad no puede ser estacionaria en media: puesto que la media en cada estación es distinta. Piense en la venta de helados ¿tiene sentido decir que la venta media anual de helados anual es de 1000? ¿Si vende 2000 en verano y 0 en invierno? ¿Le sirve para algo esa media?¿Gestionaría bien su almacén?

Estacionariedad en varianza

También nos interesará analizar si la varianza de la serie es razonablemente estable (estacionaria) o no. Para ello, debemos observar si la evolución de la serie está acotada, de manera aproximada, por un rango similar en todo su dominio temporal

Ejemplo

Por ejemplo, la serie de variación porcentual de stocks y de consumo eléctrico parecen tener una variabilidad constante, ya que se podría resumir con una sola “caja”. Sin embargo, la tasa de paro parece que va cambiando su fluctuación según aumentan los valores del nivel de la serie, por lo que esta no parece estacionaria en varianza.

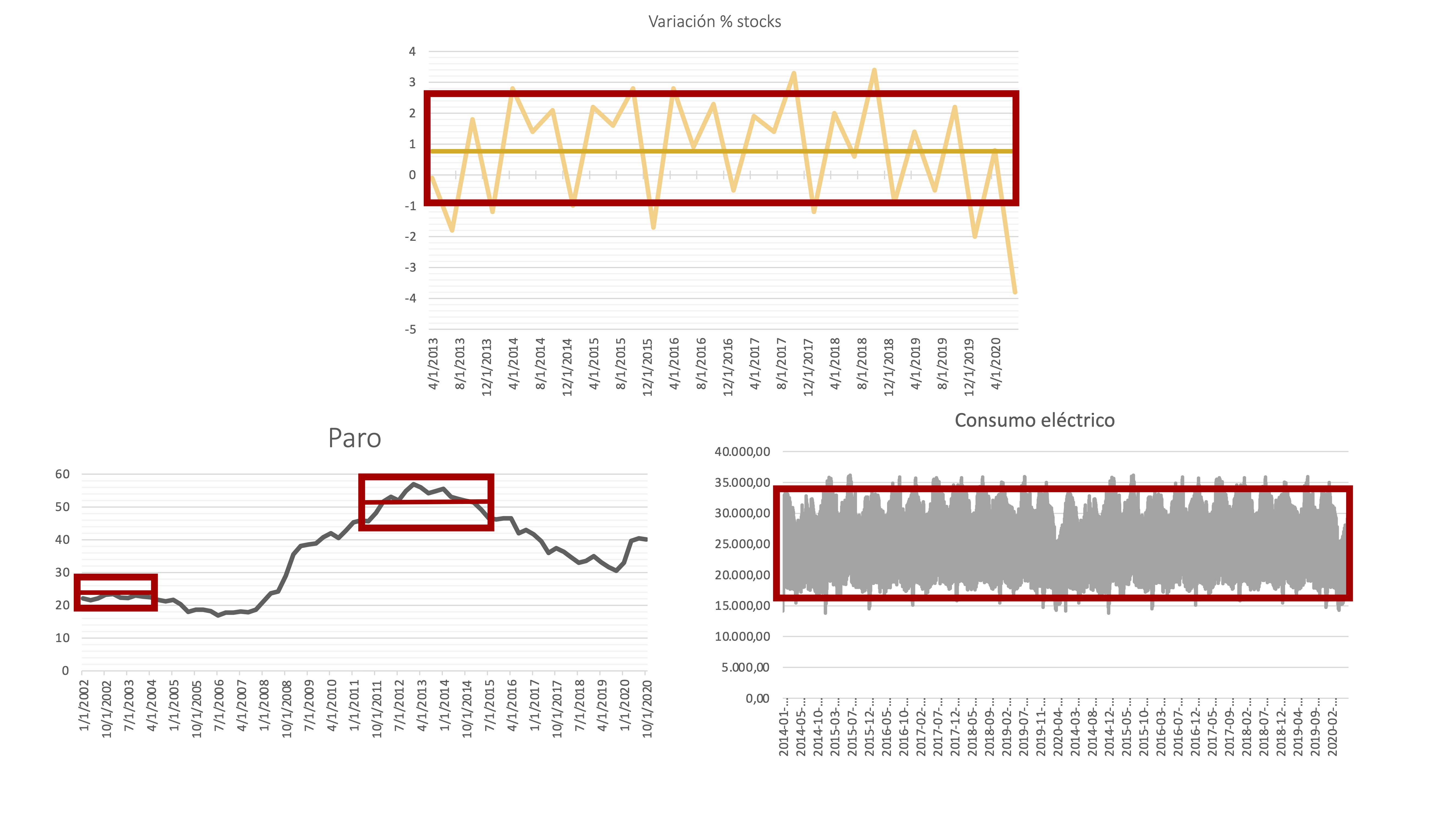
FIG 4: Aálisis temporal de la varianza

Una manera de inducir estacionariedad en varianza en una serie temporal es mediante la aplicación del logaritmo neperiano. Es decir, si la serie \(y_t\) es no estacionaria en varianza, la serie \(\log y_t\) `podría serlo (esto funciona en un alto porcentaje de casos)

Las dos transformaciones: \(\Delta \log y_t\) se denominan “primera diferencia del logaritmo de una serie y buscan estacionariedad en media y varianza

Muestre que la serie de paro, al sufrir esta transformación es estacionaria en media y varianza

¿Cómo se interpreta \(\Delta \log y_t\) ? PAra ello, calcule la tasa de variación de la serie de paro y compare el resultado. ¿Qué obtiene?

Introducción a los Procesos Estocásticos

Los modelos teóricos o poblacionales que usaremos en este capítulo proceden de la teoría de los procesos estocásticos. Un proceso estocástico puede definirse, de forma poco rigurosa, como una secuencia de variables aleatorias ordenadas cronológicamente. Un proceso estocástico gobernado por la variable \(x\) se escribe así \(\left\{ x_{t}\right\} _{t\geq0}\). Como ocurre con cualquier variable aleatoria, podremos calcular sus medias, varianzas, covarianzas, etc… para poder caracterizarlo.

Sin embargo, en este curso pasaremos por encima de todo este armamento teórico. Simplemente, presentaremos dos procesos estocásticos muy famosos y sus características más importantes, las cuales iremos necesitando posteriormente.

En la FIG5, mostramos la idea subyacente del proceso estocástico. Debemos imaginarnos que en cada momento temporal (\(t=\{0,1,2,....\}\)) el proceso \(\left\{ x_{t}\right\} _{t\geq0}\) está conformado por una distribución de probabilidades. Diremos que un proceso es estacionario si está conformado por aquel cuyas distribuciones de probabilidades para la variable aleatoria \(x\) no cambian para ningún \(t\). Lo contrario para un proceso no estacionario, donde las distribuciones de probabilidad pueden tener distintas medias, varianzas, kurtosis, asimetrías, etc…

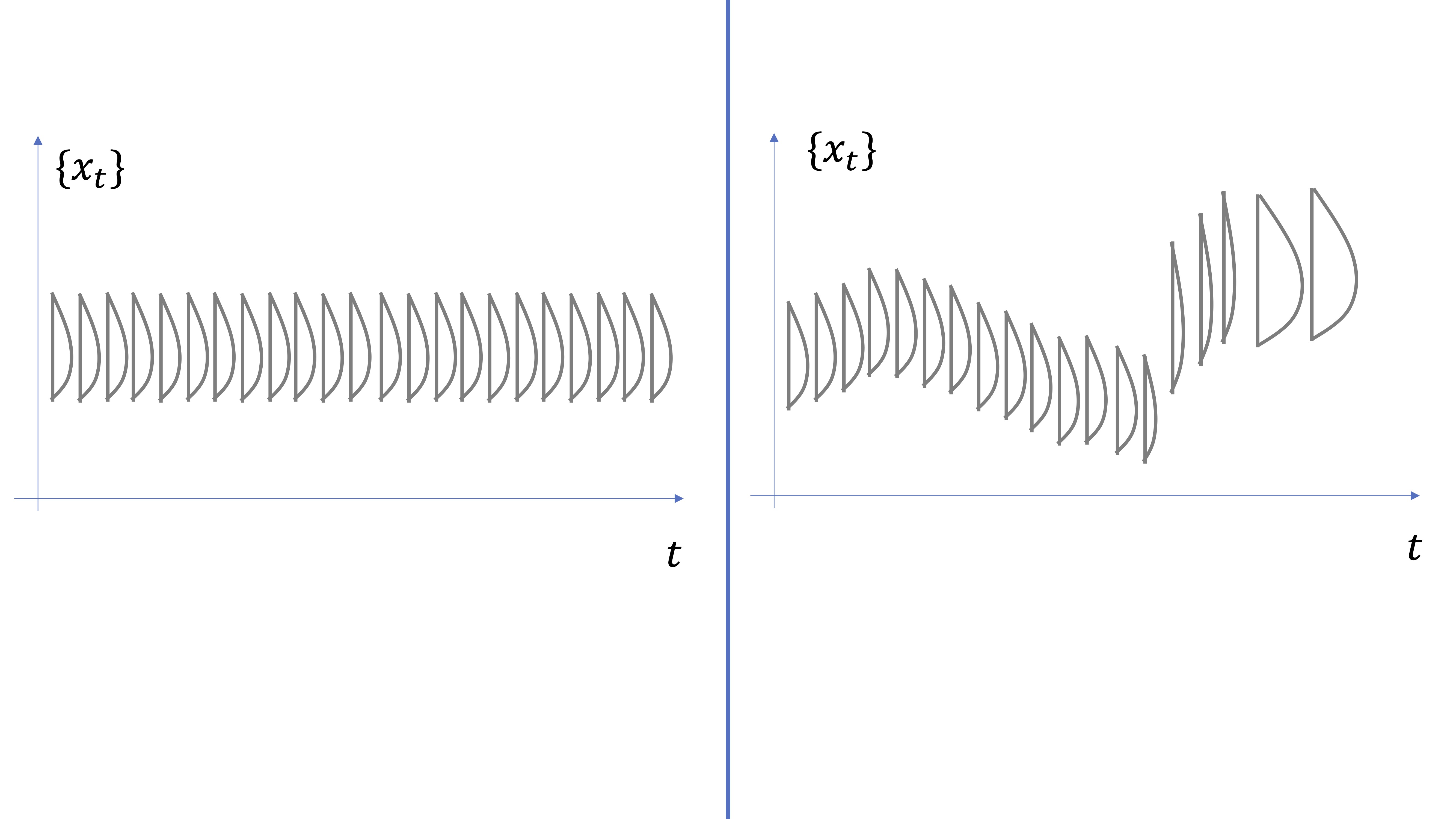
FIG 5: Idea de proceso estocástico

De hecho, podemos considerar una serie temporal (que es lo que observamos en la vida real) como una realización posible de la variable aleatoria: es decir, como si en cada momento \(t\), un ente desconocido hiciera un sorteo y decidiera el valor de la serie temporal (ver FIG6).

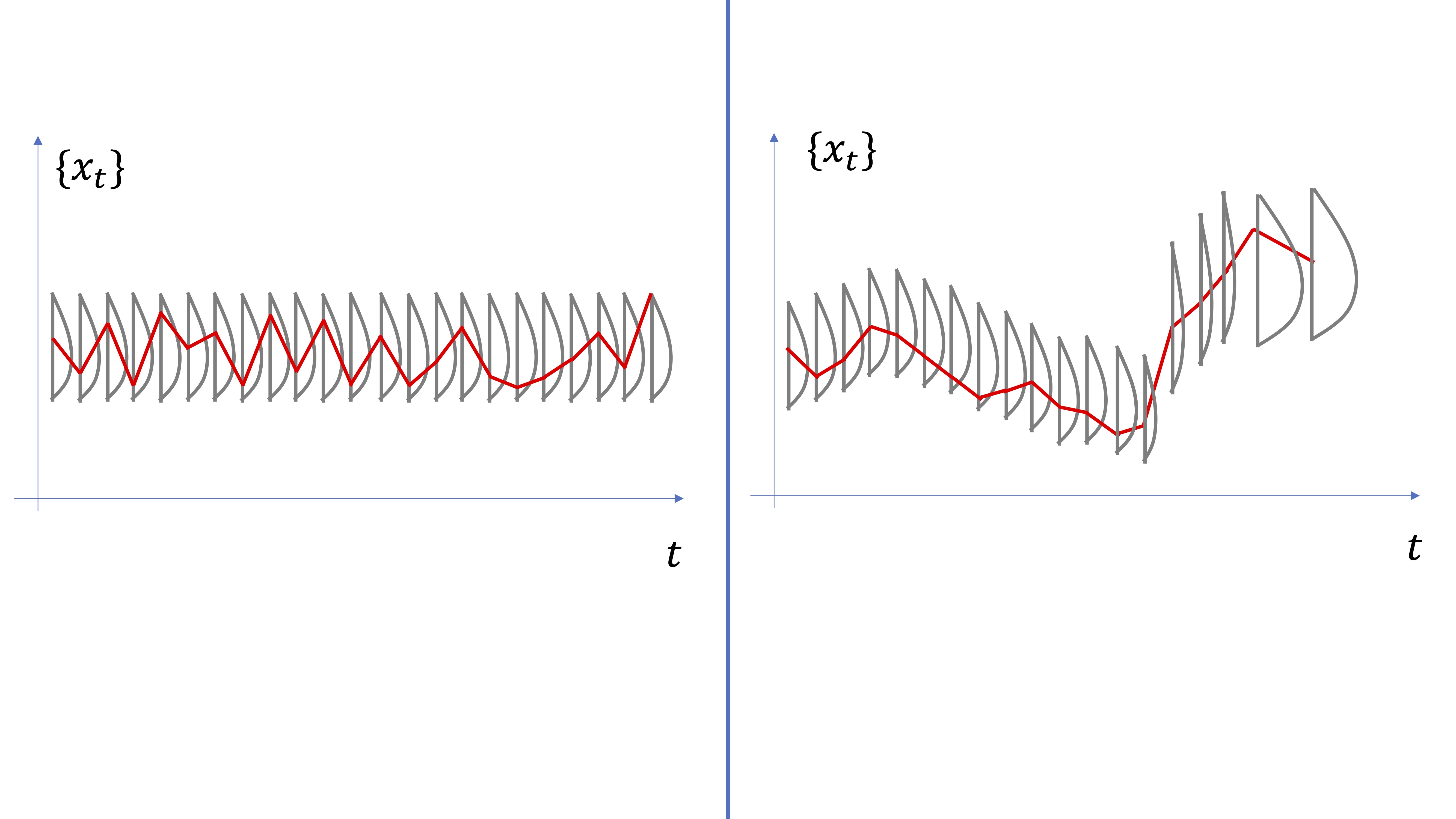
FIG 6: Una serie temporal vista como una “realización aleatoria” del proceso

Entonces, un proceso estacionario necesitará que la distribución conjunta de este permanezca invariante en el tiempo (por ejemplo, que la distribución conjunta de \(x_{t_{1}},x_{t_{2}},x_{t_{3}},...,x_{t_{n}}\) sea la misma que la de \(x_{t_{1}+h},x_{t_{2}+h},x_{t_{3}+h},...,x_{t_{n}+h}\) para cualquier \(h\neq0\). Sin embargo, es muy complicado verificar esto en la práctica (cuando sólo se tiene una serie temporal como testigo de todo el proceso). Es por ello que, en general, definiremos el concepto de estacionariedad en sentido débil, que requerirá:

Media y vairanza constantes

Autocovarianza constante

Dos procesos estocásticos muy célebres

De nuevo, vamos a usar la simulación para entender conceptos relacionados con procesos estocásticos.

Proceso 1: ruido blanco

El concepto “ruido blanco” proviene de la ingeniería y consiste en una secuencia de valores imprevisibles, equivalentes a cuando se va la televisi?n a “negro” y vemos estas secuencias aleatorias de puntos blancos y negros.

FIG 7: La idea de un ruido blanco

Llevándolo a un concepto estadístico, diremos que un ruido blanco es un proceso estocástico definido como \[ x_{t}=a_{t} \]

donde \[ a_{t}\rightarrow i.i.d(\mu,\sigma^{2}) \]

y donde \(i.i.d\) significa “independiente e idénticamente distribuido como”. E indicamos, en este caso, una media y varianza de la distribución (trabajaremos, habitualmente, con distribuciones como la Normal, que queda definida correctamente con estos dos parámetros).

Ejercicio 1 Atendiendo a estas ideas, trate de dibujar cómo sería una serie temporal que se comporte como un ruido blanco.

Ejercicio 2 Simule en R cómo sería un ruido blanco.

Proceso 2: paseo aleatorio

El paseo aleatorio está ampliamente documentado en la literatura estadística.

Lo definiremos como \[ x_{t}=x_{t-1}+a_{t} \]

donde \[ a_{t}\rightarrow i.i.d(\mu,\sigma^{2}) \]

Como puede observar, es un proceso con “inercia” y “persistencia”: el valor en el momento \(t\) depende del valor en el momento \(t-1\) más un ruido blanco.

y, además, podemos analizar sus propiedades teóricas.

Sea el proceso \[ x_{t}=x_{t-1}+a_{t} \]

con \[ a_{t}\rightarrow i.i.d(\mu=0,\sigma^{2}=2) \]

Podemos iterar para tratar de analizar el valor que tomará el proceso pasados \(T\) periodos de tiempo. Supongamos, sin pérdida de generalidad, que \(x_0=0\).

Empezamos para \(t=1\):

\[ x_{1}=x_{0}+a_{1}\Rightarrow x_{1}=a_{1}, \]

entonces, para \(t=2\),

\[ x_{2}=x_{1}+a_{2}\Rightarrow x_{2}=a_{1}+a_{2} \]

y, sucesivamente,

\[ x_{3}=x_{2}+a_{3}\Rightarrow x_{3}=a_{1}+a_{2}+a_{3} \]

de manera general, \[ x_{T}=a_{1}+a_{2}+...+a_{T} \]

Tenemos, por tanto, que la media (o esperanza de este proceso) será: \[ E\left(x_{t}\right)=E(a_{1}+a_{2}+...+a_{t})=0 \] y la varianza:

\[ V\left(x_{t}\right)=V(a_{1}+a_{2}+...+a_{t})=V(a_{1})+V(a_{2})+...+V(a_{t}) \]

donde hemos usado que la varianza de una suma es la suma de las varianzas si las variables son \(i.i.d\) (y las \(a_{t}\) lo son)

\[ V\left(x_{t}\right)=t\sigma^{2}=2t \]

Como ve, es un proceso donde la varianza no está acotada. Irá creciendo con el valor de \(t\).

Ejericio Simule en R el siguiente paseo aleatorio:

\(y_t=2+y_{t-1}+u_{t}\)

donde \(u_t\) es un ruido blanco con media cero y varianza 1 y \(y_0=0\). ¿Qué características observa?

La regresión espuria

Lo primero que deberá hacer es buscar la palabra “espurio” en el diccionario, si no recuerda lo que significa. Ahora, acuda al INE y busque la siguiente información:

Matrimonios nacionales (https://www.ine.es/jaxiT3/Tabla.htm?t=6540&L=0)

Turistas entrados en nuestras fronteras (https://ine.es/jaxiT3/Tabla.htm?t=10821&L=0)

Preguntas:

¿Qué observa en el gráfico? ¿Cuál es la correlación entre ambas series?

Estime la siguiente regresión:

\[ Turistas_{t}=\alpha+\beta Matrimonios_{t}+u_{t} \]

Describa lo que encuentra en dicha regresión:

library(readxl)
install.packages("xts")
library(xts)
install.packages("fpp")
library(fpp)


datos <- read_excel("datos_INE.xlsx")
matrimonios.t=ts(datos[,2],frequency=12,start=c(2015,10))
turistas.t=ts(datos[,3],frequency=12,start=c(2015,10))

mod1<-lm(turistas.t~matrimonios.t)



Call:
lm(formula = turistas.t ~ matrimonios.t)

Residuals:
     Min       1Q   Median       3Q      Max 
-6204903 -1420016   227532  1303045 10500661 

Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)   3421072.6   894792.8   3.823 0.000275 ***
matrimonios.t    3009.6      526.1   5.721 2.18e-07 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3515000 on 73 degrees of freedom
Multiple R-squared:  0.3096,    Adjusted R-squared:  0.3001 
F-statistic: 32.73 on 1 and 73 DF,  p-value: 2.184e-07

Un \(\mathbb{R}^2\) no despreciable

Una desviación típica estimada del coeficiente muy pequeña, comparada con el parámetro estimado y, por tanto, un t-estadistico alto y, por tanto, Un p- valor cercano a cero en el coeficiente

¿podríamos, entonces, mejorar el turismo si fomentamos los matrimonios? ¿Por cada matrimonio en España se reciben 3009 turistas? ¿Son los invitados a la boda?

En realidad, no. Acaba de encontrar una regresión que-pese a lo que dicen todos los indicadores que habitualmente se miran- no parece tener sentido. A esto se denomina: regresión espuria.

Clase 2: La regresión espuria y la cointegración

Lo que pudo observar en la clase anterior fue algo que descubrieron Engle y Granger, premios Nobel, a mediados del siglo pasado. Las series temporales con comportamiento no estacionario (paseo aleatorio) al relacionarse entre ellas suelen:

Mostrar una correlación elevada

En la regresión todo parece “muy significativo”

Pero, a todas luces, no tienen sentido. Se llaman: regresiones espurias donde “espurio” significa falso. El problema es que, al tener un comportamiento tendencial similar, es la tendencia común la que explica esa relación entre ellas. Es decir, el número de turistas y de nacimientos dependen de variables comunes no especificadas: bonanza económica, estación del año, etc…

Una forma de ver que, efectivamente, no hay mucha relación entre ambas, es generar la diferencia de ambas series (para eliminar la tendencia) y estimar una regresión en “primeras diferencias”, esto es:

\[ \Delta Turistas_{t}=\alpha+\beta \Delta Matrimonios_{t}+u_{t} \]

library(readxl)
install.packages("xts")
library(xts)
install.packages("fpp")
library(fpp)


datos <- read_excel("datos_INE.xlsx")
matrimonios.t=ts(datos[,2],frequency=12,start=c(2015,10))
turistas.t=ts(datos[,3],frequency=12,start=c(2015,10))
d_matrimonios<-diff(matrimonios.t)
d_turistas<-diff(turistas.t)

mod2<-lm(d_turistas~d_matrimonios)


lm(formula = d_turistas ~ d_matrimonios)

Residuals:
     Min       1Q   Median       3Q      Max 
-3956740 -1018875   265210  1243441  4308444 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)
(Intercept)   -69500.0   230677.2  -0.301    0.764
d_matrimonios   -200.7      259.5  -0.773    0.442

Residual standard error: 1984000 on 72 degrees of freedom
Multiple R-squared:  0.008238,  Adjusted R-squared:  -0.005537 
F-statistic: 0.598 on 1 and 72 DF,  p-value: 0.4419

Ahora, las conclusiones son bien distintas.

De esto se dieron cuenta Engle y Granger y elaboraron la teoría de la cointegración. Es un tema muy extenso y aquí vamos a resumir de una forma “ligera” para poder trabajar de manera sensata con series temporales sin tener- para ello- que cubrir mucha teoría.

COINTEGRACIÓN

Un conjunto de series temporales (en este caso, dos: \(x_t\), \(y_t\)) cointegran (es decir, tienen una relación estable y verdadera a largo plazo) si

\(x_t\), \(y_t\) son paseos aleatorios (series no estacionarias)

en la regresión:

\[ y_{t}=\alpha+\beta x_{t}+u_{t} \]

los residuos \(\hat u_t\) son un ruido blanco.

Nota que en caso contrario se dirá que NO COINTEGRAN y que, por tanto, la relación es espuria. Por otro lado, no se dice nada de las series que ya son estacionarias. La cointegración se estudia sólo cuando las series con las que trabajamos son no estacionarias

Ahora, la pregunta es ¿cómo ver si los residuos son ruido blanco? Empecemos analizando los residuos de la regresión de la clase anterior.

library(readxl)
install.packages("xts")
library(xts)
install.packages("fpp")
library(fpp)


datos <- read_excel("datos_INE.xlsx")
matrimonios.t=ts(datos[,2],frequency=12,start=c(2015,10))
turistas.t=ts(datos[,3],frequency=12,start=c(2015,10))


mod1<-lm(turistas.t~matrimonios.t)

ts.plot(mod1$residuals)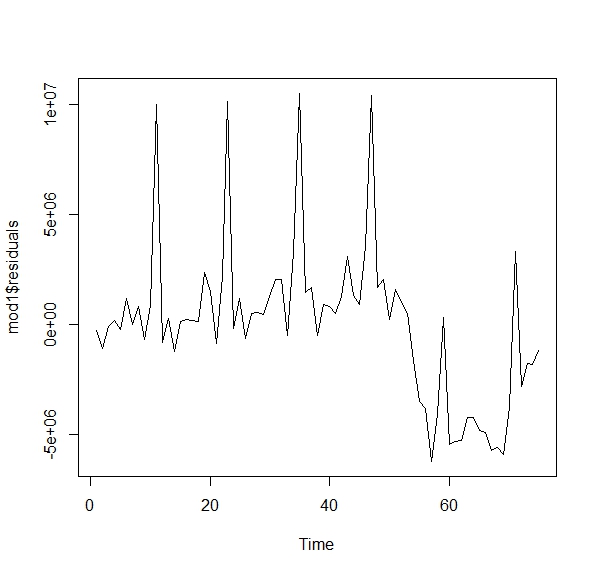

FIG 1: Gráfico de los residuos Como ve, no parecen aleatorios. Si fueran aleatorios, sería difícil entender la pauta que marcan. Una forma de ver esto es con lo que se llama la función de autocorrelación. Esta consiste en analizar la relación que tiene un residuo en tiempo \(t\) con su pasado \(t-1,t-2,...\). Si fuera aleatorio (ruido blanco) no debería existir tal relación

mod1<-lm(turistas.t~matrimonios.t)

acf(mod1$residuals)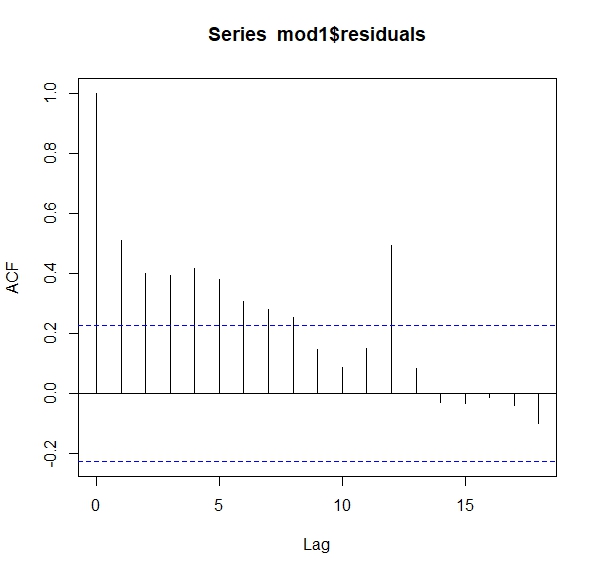

FIG 2: función de autocorrelación de los residuos Ahora tenemos otro modelo, donde queremos predecir la inflación utilizando un índice de incertidumbre económica. Sospechamos que la incertidumbre puede afectar a la inflación y queremos estimar el modelo:

\[ IPC_{t}=\alpha+\beta Incertidumbre_{t}+u_{t} \]

¿qué puede decir?

library(readxl)
install.packages("xts")
library(xts)
install.packages("fpp")
library(fpp)


inflacion<- read_excel("datos_inf.xlsx")
IPC.t=ts(inflacion[,2],frequency=12,start=c(2002,1))
UNC.t=ts(inflacion[,3],frequency=12,start=c(2002,1))


mod1<-lm(IPC.t~UNC.t)

ts.plot(mod1$residuals)

Es fácil ver que las series no son estacionarias en media y que, además, los residuos no son ruido blanco. Las series no cointegran. Sin embargo, en este caso:

Conceptualmente, nos parece de interés ver el impacto de la incertidumbre en la inflación

Puede haber más maneras de relacionar ambas variables, como hemos visto antes

Si no cointegran podemos probar qué tal funciona la relación en primeras diferencias:

d_IPC.t=diff(IPC.t)
d_UNC.t=diff(UNC.t)


mod2<-lm(d_IPC.t~d_UNC.t)

De acuerdo con el p-valor, el índice de incertidumbre no parece ser “estadísticamente” significativo. Sin embargo, deberemos discutir la magnitud del efecto, o la capacidad predictiva de este índice. Por ejemplo, si analiza el rango de la variable \(\Delta UNC_t\), este va de -235.38 (mínimo) a 207.10 (máximo) ¿Qué implica respecto de la predicción de \(\Delta IPC_t\) es decir, la inflación?

Haga sus cuentas y discuta el resultado.

Si las series cointegran, entonces puede utilizar el modelo especificado con las variables en sus niveles originales.

Ejercicio Por ejemplo, descargue los valores de dos acciones de interés (bancarias, de empresas importantes, etc…). ¿Cointegran? Piense en el modelo que implementaría y cómo lo utilizaría para predecir.

COINTEGRACIÓN

Lo que aquí presentamos es algo “muy básico” que le permitirá entender la idea, aunque es un tema muy extenso y lleno de complejidad estadística. Sin embargo, lo visto aquí le permitirá plantearse cualquier respuesta que pueda dar, precipitada, sobre la relación de series temporales con tendencia.

Clase 3: Los modelos con indicadores adelantados: juicio a la capacidad predictiva

Imagine que sigue pensando que este modelo no es desdeñable para predecir la inflación, dado que el impacto que ha medido parece cuantitativamente remarcable.

Este es el modelo:

\[ \Delta IPC_{t}=\alpha+\beta \Delta Incertidumbre_{t}+u_{t} \]

Sin embargo, una vez estimado, si quiere predecuir la inlación del mes siguiente, utilizando el índice de incertidumbre, deberá tener una predicción de la incertidumbre para el mes siguiente. Estamos en las mismas.

Lo normal, de cara a predecir, es tratar de buscar modelos que constituyan “indicadores adelantados”, esto es, su pasado ayude a predecir el futuro de la variable de interés. De esta manera, no necesitará jugar a adivinar lo que valdrán las variables predictoras. Modelos de indicadores adelantados para nuestro ejemplo sería,

\[ \Delta IPC_{t}=\alpha+\beta \Delta Incertidumbre_{t-1}+u_{t} \]

ya que, cuando quiera predecir la inflación en el periodo \(t+1\)

\[ \Delta IPC_{t+1}=\alpha+\beta \Delta Incertidumbre_{t}+u_{t+1} \]

Neceistará conocer el dato real de \(\Delta Incertidumbre\). Por cierto, la prediccion la escribimos como

\[ \mathbb{E} (\Delta IPC_{t+1}|\Delta Incertidumbre_{t})=\alpha+\beta \Delta Incertidumbre_{t} \]

es decir, ¿qué espero de la inflación mañana, en \(t+1\), con la información de la incertidumbre que tengo hoy, en \(t\) ? Como ve, el error tiene esperanza cero (espero, en promedio, no equivocarme, aunque sé que lo haré con cierta probabilidad).

Otras versiones de modelos con indicadores adelantados serán:

\[ \Delta IPC_{t}=\alpha+\beta_1 \Delta Incertidumbre_{t-1}+\beta_2\Delta Incertidumbre_{t-2}+...+\beta_k\Delta Incertidumbre_{t-k}+u_{t} \]

¿Cómo decidir \(k\)? Como nuestro objetivo es predecir lo mejor posible, lo lógico es buscar alguna manera de analizar la habilidad predictiva del modelo para diferentes \(k\). Efectivamente, validación cruzada es una buena manera de ello.

Validación cruzada en series temporales

En series temporales también se puede realizar validación cruzada. La particularidad de estos datos (el orden ha de ser cronológico) hace que no se pueda realizar como con datos de individuos (donde se puede realizar un conjunto de remuestreos aleatorios y seleccionar un amplio número de submuestras con las que entrenar el modelo). En este caso, además, se une el hecho habitual de que las series temporales no son excesivamente amplias.

Lo normal para hacer validación cruzada consiste en elegir una muestra de datos de entrenamiento (desde el principio o desde una observación adecuada para nuestros objetivos), entrenar el conjunto de modelos correspondientes para esa muestra y, posteriormente, realizar predicciones al horizonte correspondiente y validarlas con los datos no utilizados en el entrenamiento.

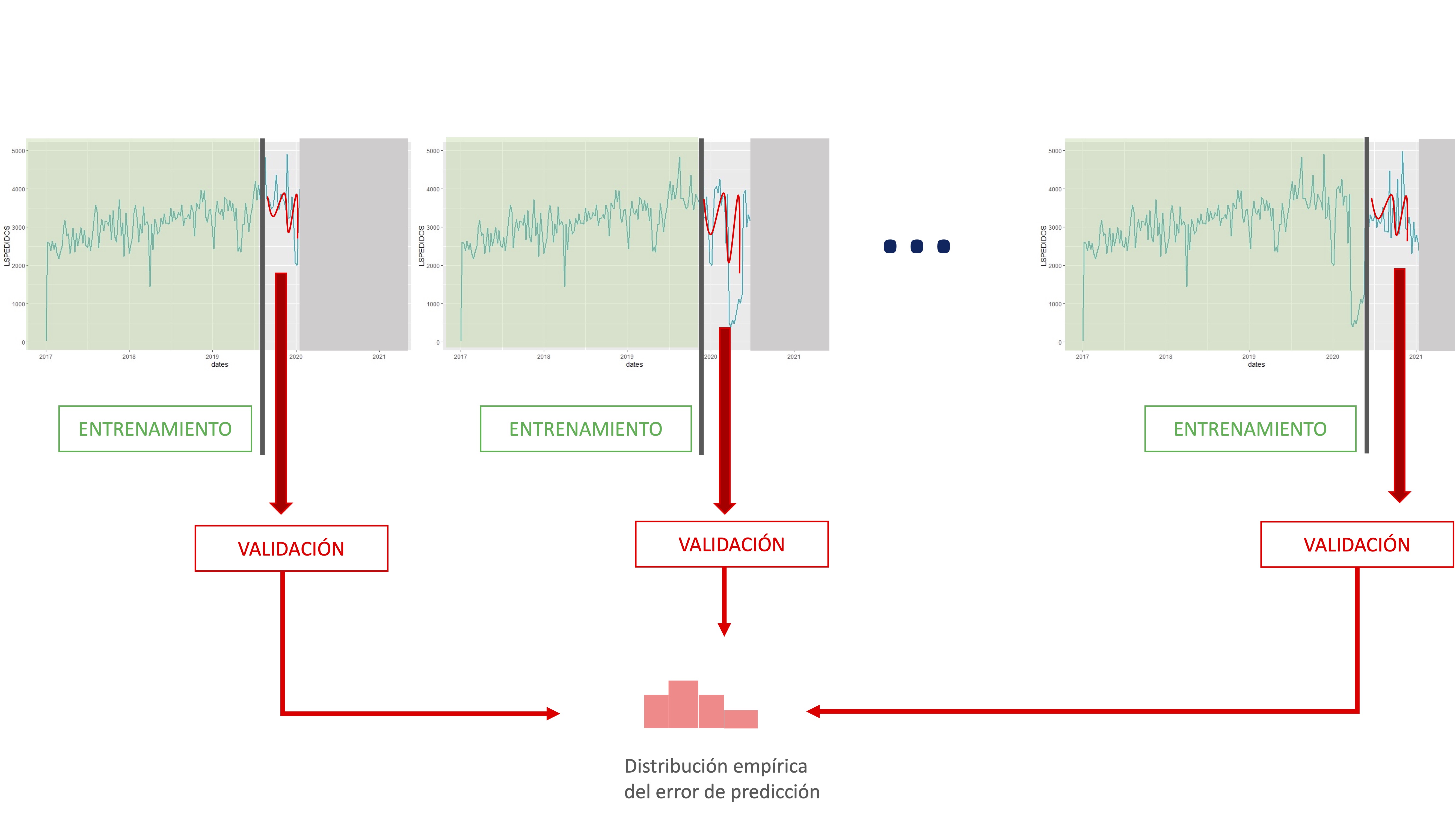
FIG 1:La validación cruzada en series temporales

De esta manera, vamos obteniendo información asociada a la habilidad predictiva de cada modelo mediante el almacenamiento de sus errores de predicción. Presentamos, a continuación, un esquema numérico para la realización de la validación cruzada. El ejemplo lo vamos a realizar con la serie de inflación, tratando de ver qué especificación de “indicador adelantado” es mejor. Para ello, en el modelo

\[ \Delta IPC_{t}=\alpha+\beta_1 \Delta Incertidumbre_{t-1}+\beta_2\Delta Incertidumbre_{t-2}+...+\beta_k\Delta Incertidumbre_{t-k}+u_{t} \]

Entrenaremos cuatro versiones \(k=1\), \(k=2\), \(k=3\) y \(k=4\). Nos parece razonable pensar que, como mucho, la incertidumbre pasada que afecte a la inflación será la de 4 periodos (meses) atrás.

library(readxl)
install.packages("xts")
library(xts)
install.packages("fpp")
library(fpp)
install.packages("dynlm")
library(dynlm)


inflacion<- read_excel("datos_inf.xlsx")
IPC.t=ts(inflacion[,2],frequency=12,start=c(2002,1))
UNC.t=ts(inflacion[,3],frequency=12,start=c(2002,1))

d_IPC.t=diff(IPC.t)
d_UNC.t=diff(UNC.t)


#Elijo cuantos datos quiero tener para empezar
T <- 100
#obtengo el total de datos de la muestra
n<-length(d_IPC.t) 
#genero dos vectores vacíos para almacenar errores
error1<-vector() 
error2<-vector() 
error3<-vector() 
error4<-vector() 
#Creo un bucle que va a ir elaborando predicciones a horizonte 1

for(i in 1:(n-T-1)) {
  #extrae la muestra con la que entrenará
  IPCshort <- d_IPC.t[1:(T+i)] 
  d_UNCshort <- d_UNC.t[1:(T+i)] 
  #extrae el dato real con el que comparar
  IPCnext <- d_IPC.t[(T+i+1)]
  IPCshort = ts(IPCshort, frequency = 12, start=c(2002,02)) 
  d_UNCshort = ts(d_UNCshort, frequency = 12, start=c(2002,02)) 
  #entrena dos modelos: el que identificamos previamente y otro automático que tiene R
  
  
  fit1 <- dynlm(IPCshort~L(d_UNCshort,1))
  fit2 <- dynlm(IPCshort~L(d_UNCshort,1)+L(d_UNCshort,2))
  fit3 <- dynlm(IPCshort~L(d_UNCshort,1)+L(d_UNCshort,2)+L(d_UNCshort,3))
  fit4 <- dynlm(IPCshort~L(d_UNCshort,1)+L(d_UNCshort,2)+L(d_UNCshort,3)+L(d_UNCshort,4))
  
  #obtengo las predicciones (a mano) de cada modelo. 
  
  forecast1<-fit1$coefficients[1]+ fit1$coefficients[2]*tail(d_UNCshort,n=1)
  forecast2<-fit2$coefficients[1]+ fit2$coefficients[2]*tail(d_UNCshort,n=1)+fit2$coefficients[3]*tail(d_UNCshort,n=2)[1]
  forecast3<-fit3$coefficients[1]+ fit3$coefficients[2]*tail(d_UNCshort,n=1)+fit3$coefficients[3]*tail(d_UNCshort,n=2)[1]+fit3$coefficients[4]*tail(d_UNCshort,n=3)[1]
  forecast4<-fit4$coefficients[1]+ fit4$coefficients[2]*tail(d_UNCshort,n=1)+fit4$coefficients[3]*tail(d_UNCshort,n=2)[1]+fit4$coefficients[4]*tail(d_UNCshort,n=3)[1]+fit4$coefficients[5]*tail(d_UNCshort,n=4)[1]
 
  #obtengo los errores de predicción
  
  
  error1[i]<-abs(IPCnext-forecast1)
  error2[i]<-abs(IPCnext-forecast2)
  error3[i]<-abs(IPCnext-forecast3)
  error4[i]<-abs(IPCnext-forecast4)
  
  
  }

¿Con qué modelo quedarse?

En general, no hay un criterio claro que nos permita decantarnos por un único modelo. Puede darse el caso de que los candidatos predigan de forma similar (donde podría ser interesante promediar las predicciones de cada uno de los modelos elegidos) o que haya interesantes diferencias entre ellos. En general, parece sensato buscar alguna forma de combinar los modelos. Una propuesta para combinarlos puede ser desde hacer una media aritmética de las predicciones o, por ejemplo, una media ponderada en función de cuál prediga mejor.

Ejercicio Elija una ponderación con la que quedarse.

¿y la estacionalidad? ¿y la inercia de la propia serie?

Como vimos antes, una serie temporal puede presentar estacionalidad. En este caso, la inflación la presenta. ¿Cómo se puede mejorar el modelo?

Hay muchas maneras de tratar la estacionalidad. Nosotros vamos a utilizar una muy sencilla que consiste en introducir una dummy para cada mes del año (excepto uno, recuerde)

\[ \Delta IPC_{t}=\alpha+\beta_1 \Delta Incertidumbre_{t-1}+\beta_2\Delta Incertidumbre_{t-2}+...+\beta_k\Delta Incertidumbre_{t-k}+ \alpha_1 Ene_t+\alpha_2 Feb_t+...\alpha_{11}Nov_t+ u_{t}, \]

Por otro lado, una serie temporal, en general, tiene un comportamiento suave. Esto quiere decir que no suele exhibir cambios bruscos: el pasado de esta ayuda a explicar parte del presente. Esto se conoce como parte autorregresiva de la serie. Podemos incluir un término autorregresivo de la siguiente manera:

De nuevo, modelar esta parte de la serie tiene cierta complejidad que está fuera del alcance del curso

\[ \Delta IPC_{t}=\alpha+\beta_1 \Delta Incertidumbre_{t-1}+\beta_2\Delta Incertidumbre_{t-2}+...+\beta_k\Delta Incertidumbre_{t-k}+ \phi_1\Delta IPC_{t-1}+ u_{t}, \]

como ve, el propio pasado de la serie ayuda a explicar el presente. Veamos cómo incluir ambas cosas en un modelo:

install.packages("forecast")
library(forecast)
library(readxl)
install.packages("xts")
library(xts)
install.packages("fpp")
library(fpp)
install.packages("dynlm")
library(dynlm)


inflacion<- read_excel("datos_inf.xlsx")
IPC.t=ts(inflacion[,2],frequency=12,start=c(2002,1))
SEAS<-seasonaldummy(IPC.t) #creamos la variable de dummies estacionales (gracias al paquete forecast)
UNC.t=ts(inflacion[,3],frequency=12,start=c(2002,1))

#introducimos diferencias en todas las series con las que vamos a trabajar

d_IPC.t=diff(IPC.t)
d_UNC.t=diff(UNC.t)
d_SEAS=diff(SEAS)

#finalmente, usaremos la función "auto.arima" que especifica la parte dinámica del modelo (la parte autorregresiva). Para ello, creamos previamente un vector de variables predictoras:

Predictors1<-cbind(stats::lag(d_UNC.t,-1),d_SEAS)

#y así se especifica el modelo

fit1 <- auto.arima(d_IPC.t, xreg=Predictors1,
stationary=TRUE)

En este caso, hemos usado una función “auto.arima” que determina el número de retardos de la variable dependiente y permite incluir diferentes especificaciones para la variable predictora.

Ejercicio Adapte el código de validación cruzada para estos nuevos modelos con estacionalidad y retardos. Para hacer la predicción, use la funcíón “predict”.

Compare el error de predicción utilizando “auto.arima” sin ningua variable predictora y añadiéndolas. ¿Considera que mejora la habilidad predictiva de la serie?

Clase 5: elaboración de predicciones probabilísticas

Uno de los intereses que tiene un ejercicio de predicción es ser capaces de otorgar una probabilidad (o verosimilitud) a un escenario. Esto le permitirá entrar en un debate más sano que aquel en el que se proporciona una predicción central sin dar información sobre la incertidumbre que se tiene sobre dicha predicción.

Una manera de poder hacer esto es mediante la técnica del bootstrapping. Usted, a partir de un modelo inicial, podrá generar un conjunto grande de estimaciones alternativas de los parámetros de los modelos sin tener que asumir distribuciones (generalmente rígidas) sobre la distribución de los errores o de los parámetros de los modelos.

Sin embargo, el bootstrapping con series temporales tiene una particularidad: no debe mueestrear (con reemplazamiento) directamente en la serie temporal, puesto que una de las características de máximo interés en una serie temporal es el orden. Es decir, si su serie temporal es esta:

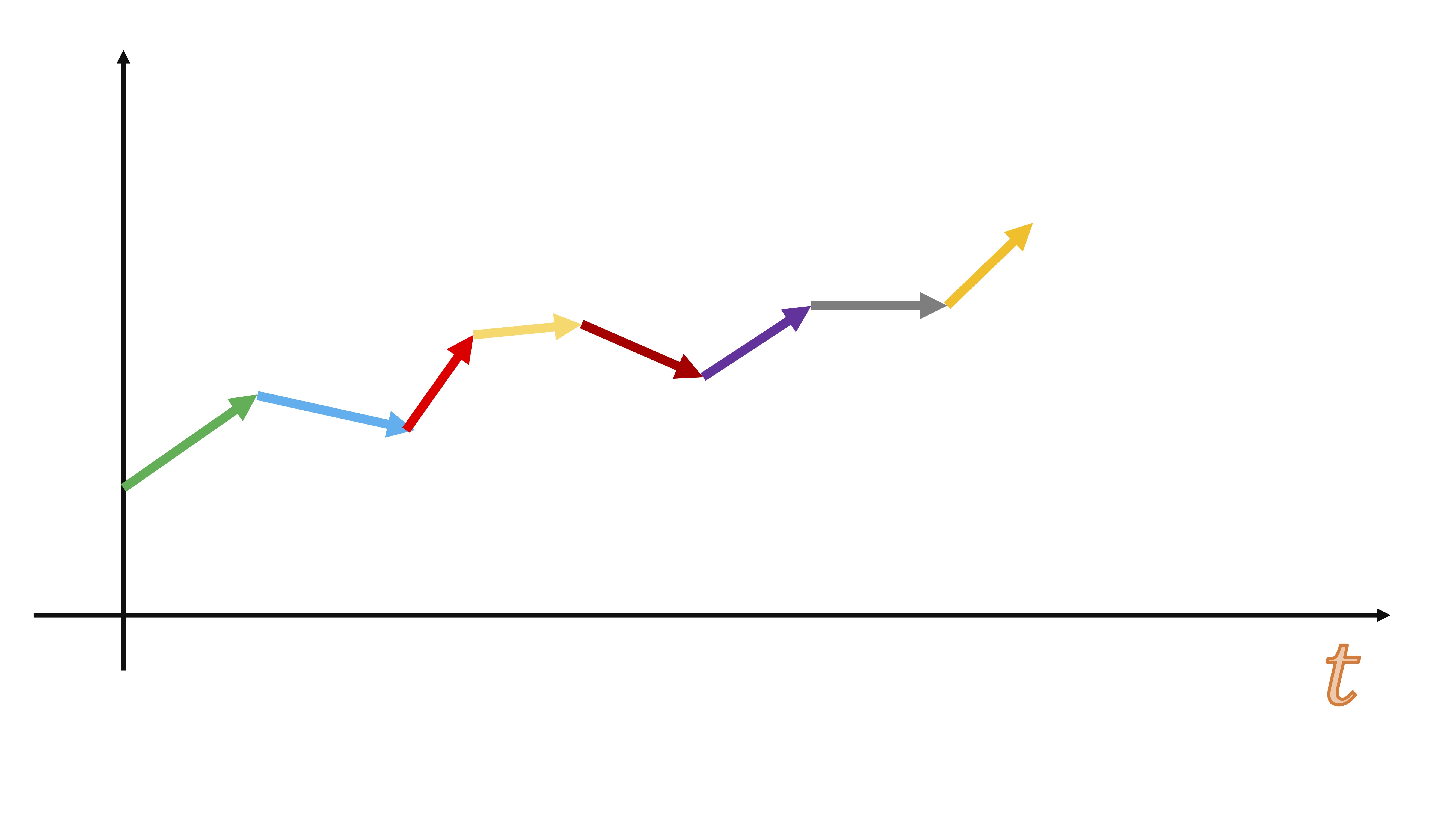
FIG 1:Un ejemplo de una serie temporal

un muestreo con reemplazamiento erróneo sería, por ejemplo, hacer esto:

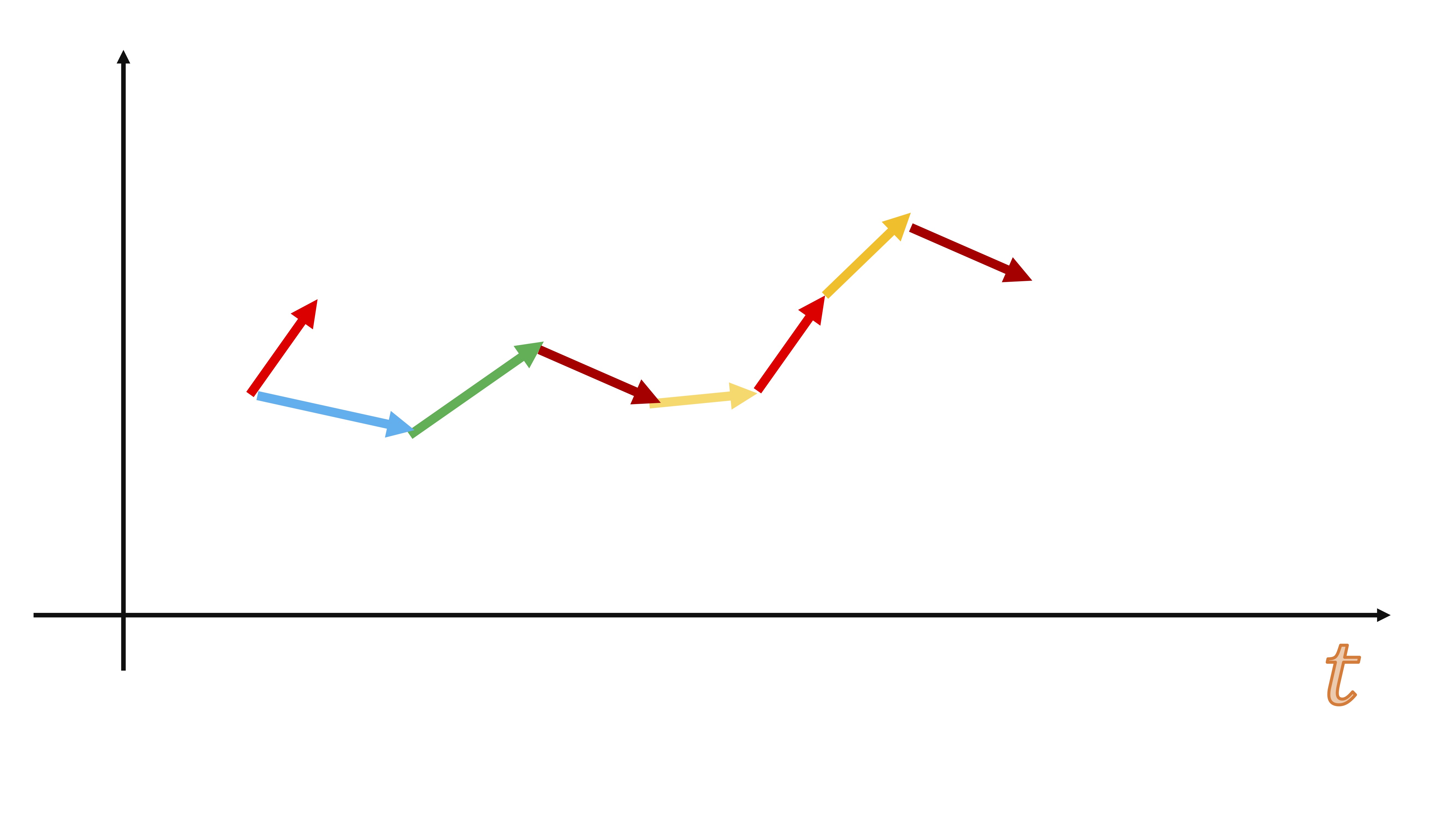
FIG 2:Un ejemplo de un muestreo con reemplazamiento

de repente, el orden de la serie se ha perdido…y podrían pasar cosas desastrosas como esto:

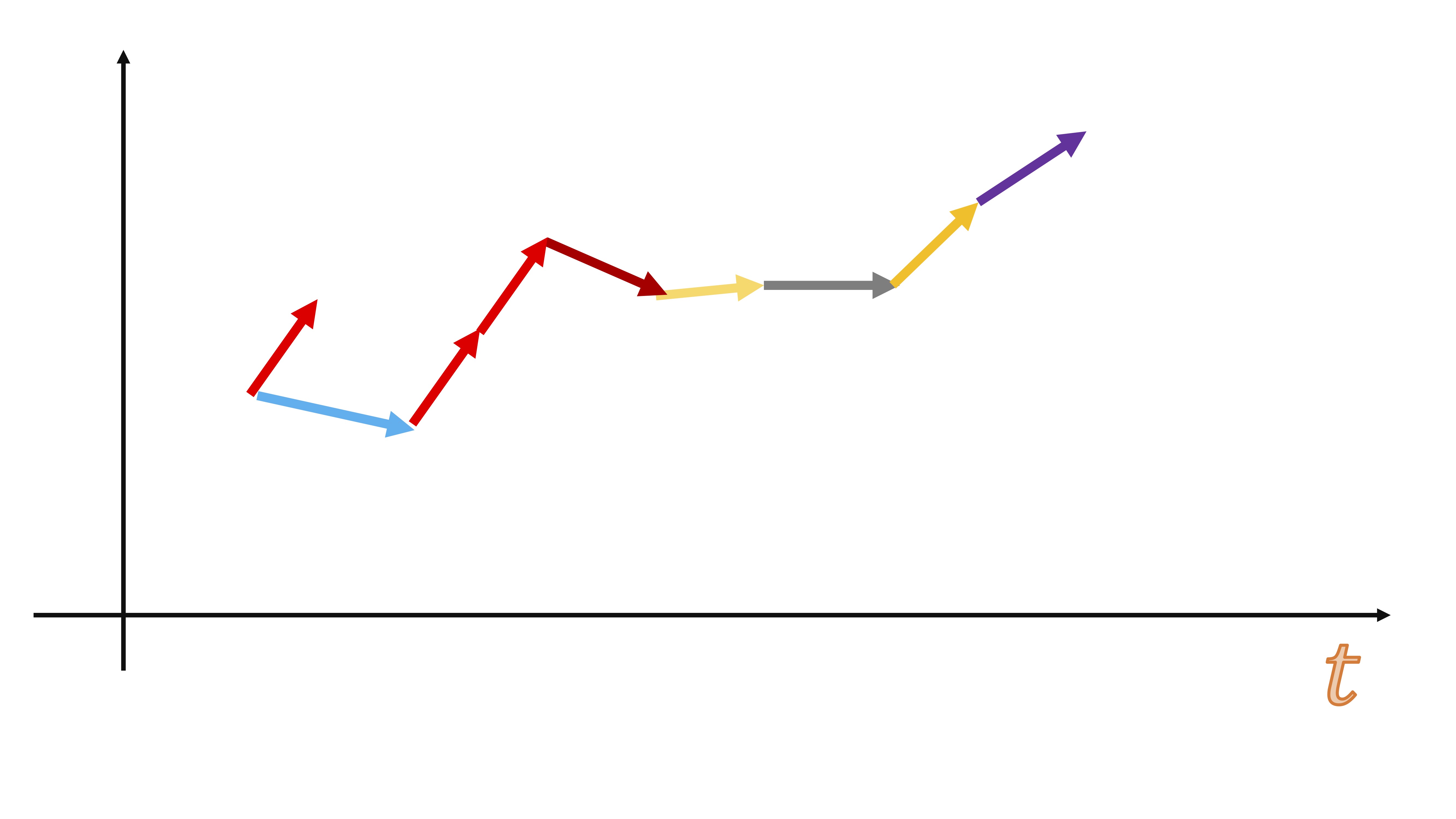
FIG 3:Un ejemplo de un muestreo con reemplazamiento

es decir, sería equivalente a tener datos de paro (inflación, beneficios, ventas, etc…) y juntar mezclarlos aleatoriamente ¿qué podría analizar de eso? nada, puesto que en una serie temporal su tendencia es uno de los componentes más importantes.

La idea del bootstrapping en series temporales es la siguiente:

Usted parte de su modelo de series temporales

FIG 4:Un ejemplo de una serie temporal

Ajuste el modelo que corresponda

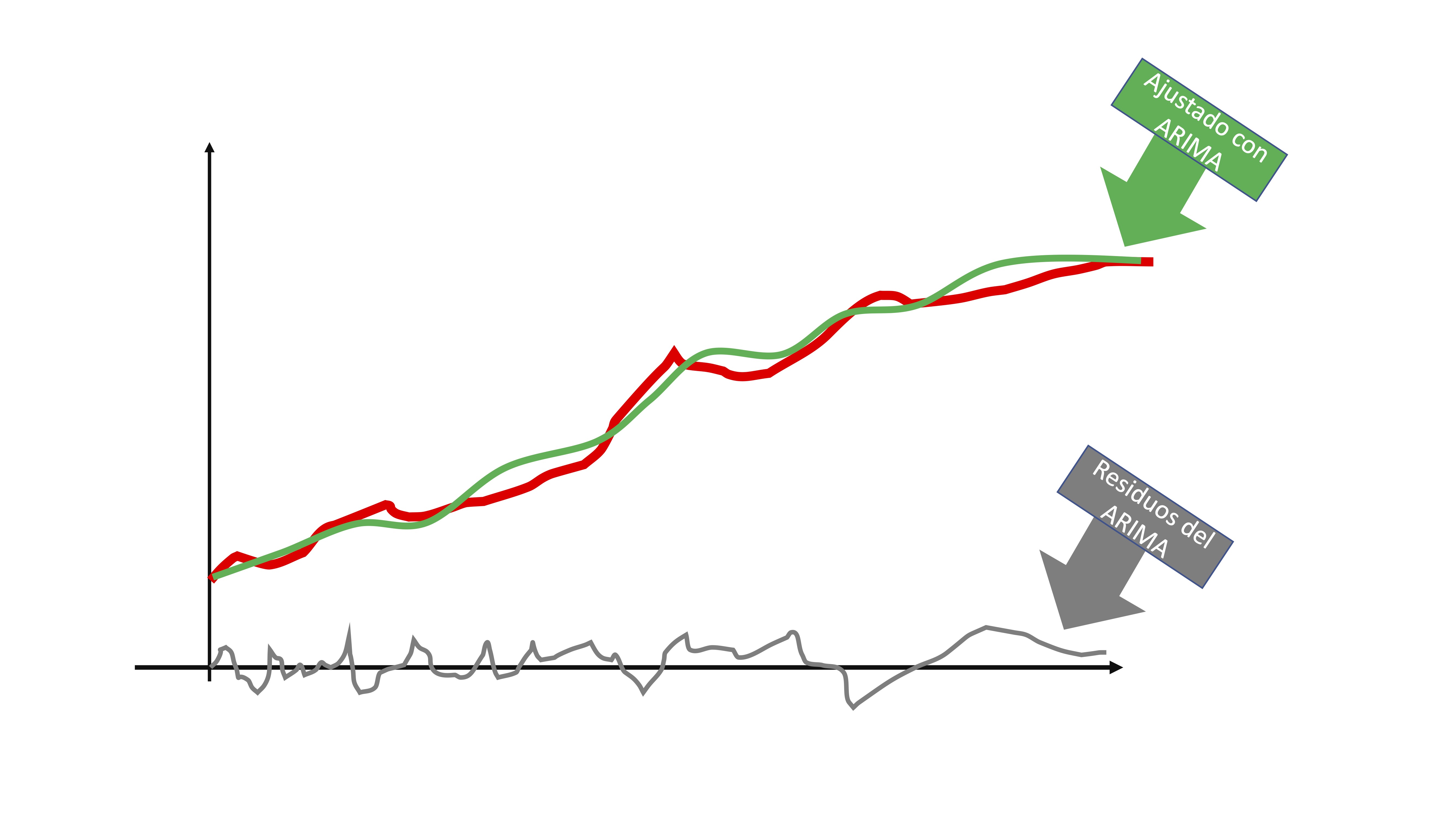
FIG 5:modelo ARIMA ajustado

entonces, obtendrá dos elementos: la línea verde de la FIG5 que sería la serie que es capaz de predecir con su modelo y la línea gris que son los residuos. Puede interpretar los residuos, al ser i.i.d, como una secuencia de shocks o sorpresas que no puede captar el modelo por ser completamente aleatorio.

Remuestree con reemplazamiento esos residuos

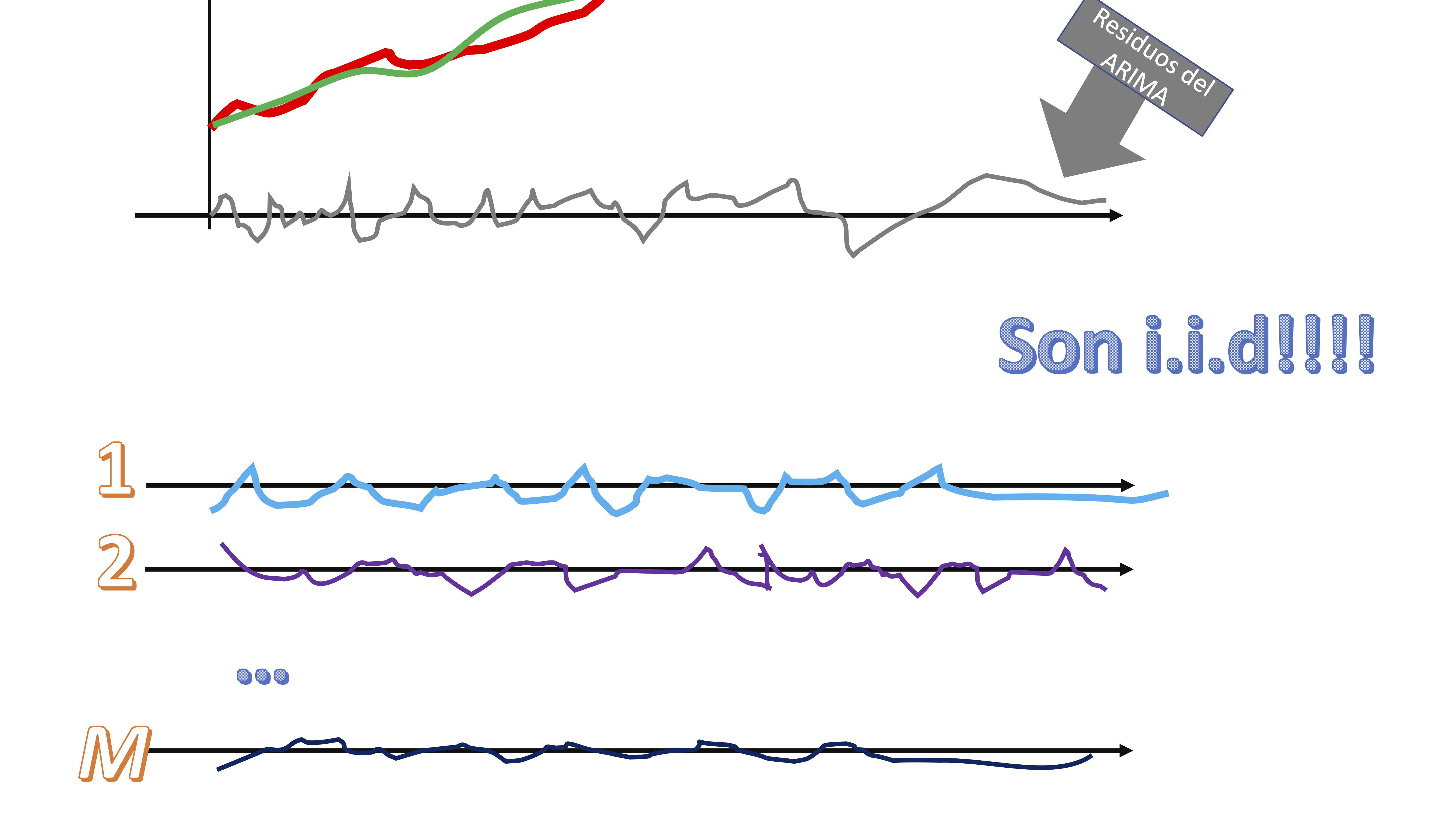
FIG 6:Un ejemplo de un muestreo con reemplazamiento

claro, los residuos, al ser i.i.d, su orden nos da igual. Tendremos, entonces \(M\) secuencias de “shocks” que podrían haber ocurrido a la serie original.

Súmele cada secuencia de shocks a la serie ajustada por el modelo ARIMA y tendrá diferentes versiones de la serie original, afectadas por shocks alternativos

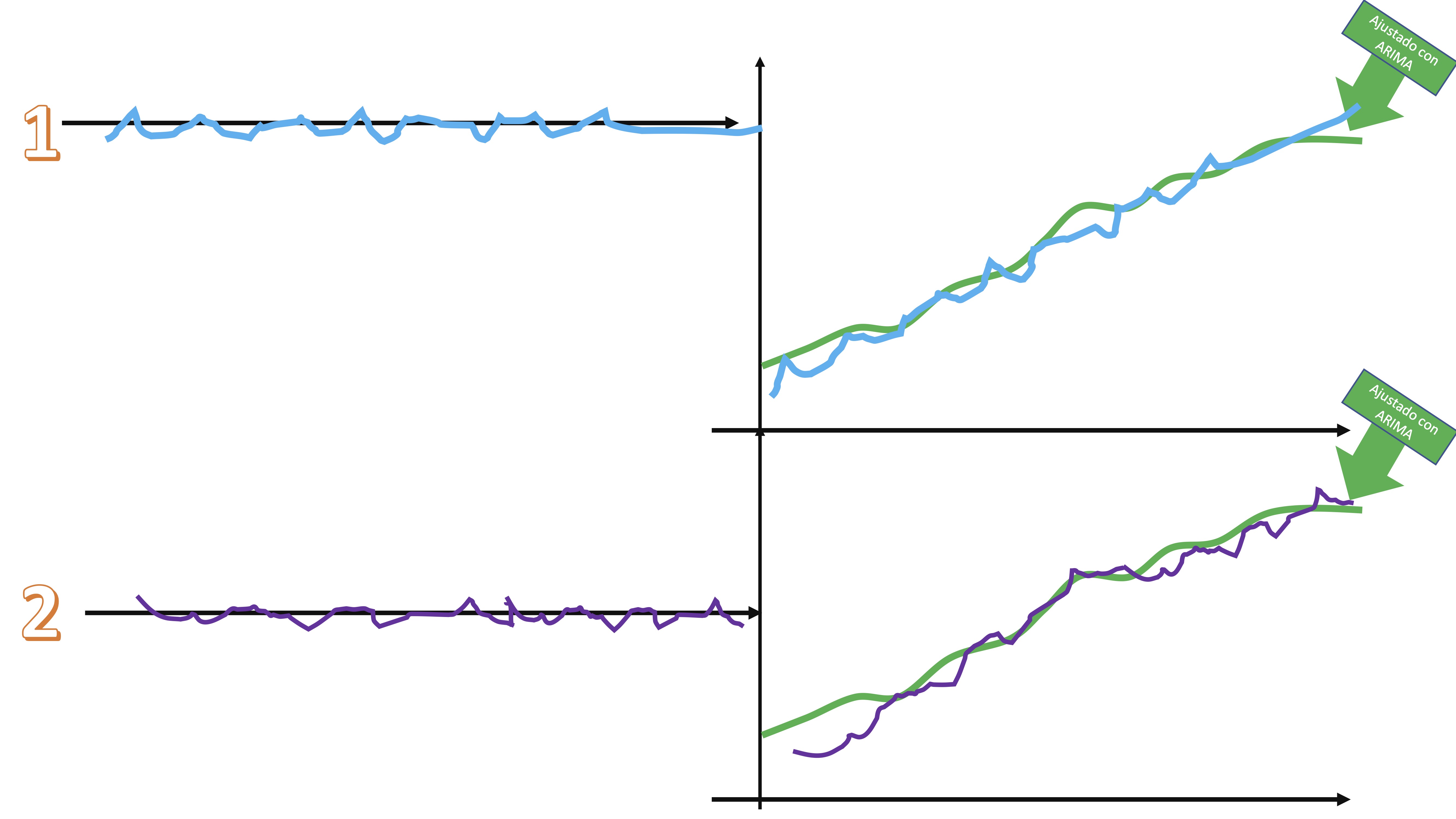
FIG 7:Un ejemplo de dos series nuevas

Las características principales de la serie no se pierden, pero sí son versiones “perturbadas” de la serie original.

Estime los correspondientes \(M\) modelos y obtenga las predicciones. De esta manera, al finalizar, podrá tener distribuciones de la variable aleatoria prevista.

Así puede hacerse en R. Vamos a generar una predicción dos meses adelante (recuerde que la predicción con modelos ARIMA sólo está justificada para horizontes cortoplacistas)

Supongamos que queremos predecir la inflación para el mes siguiente con el primer modelo estimado anteriormente (por simplificación)

library(readxl)
install.packages("xts")
library(xts)
install.packages("fpp")
library(fpp)
install.packages("forecast")
library(forecast)

#cargamos los datos hasta la última observación disponible

inflacion<- read_excel("datos_inf.xlsx")
IPC.t=ts(inflacion[,2],frequency=12,start=c(2002,1))
SEAS<-seasonaldummy(IPC.t)
UNC.t=ts(inflacion[,3],frequency=12,start=c(2002,1))

d_IPC.t=diff(IPC.t)
d_UNC.t=diff(UNC.t)
d_SEAS=diff(SEAS)


Predictors1<-cbind(stats::lag(d_UNC.t,-1),d_SEAS)



# generamos una matriz donde guardaremos los 1000 posibles escenarios para el horizonte temporales que vamos a usar
FORECAST<-matrix(0,1000,1)
#estimamos el modelo de indicadores adelantados

AM1<- auto.arima(d_IPC.t, xreg=Predictors1,stationary=TRUE)
#obtenemos los datos ajustados
fitted<-AM1$fitted
#obtenemos los residuos, que es lo que remuestrearemos
res<-AM1$residuals
n<-length(res)
n_d_IPC.t<-d_IPC.t

for (i in 1:(1000)){
 
  AM1<-auto.arima(n_d_IPC.t, xreg=Predictors1,stationary=TRUE)
  #almacenamos las predicciones para horizonte 1
  
  newreg<-tail(Predictors1,n=1)
  FORECAST[i]<-predict(AM1,newxreg=newreg)$pred
 
  #remuestreamos el error a través de los residuos
  new_error<-sample(res, n+1, replace = TRUE) 
  #importante: para no sesgar los resultados, nos aseguramos que
  #el error tenga media cero
  m_error<-mean(new_error)
  new_error<-new_error-m_error
  #damos estructura de serie temporal al nuevo error
  new_error.t=ts(new_error,frequency=12,start=c(2002,1))
  
  #generaamos la nueva serie temporal
  n_d_IPC.t<-fitted+new_error.t
   
}

hist(FORECAST)

Entonces, tenemos una distribución de posibles valores de la inflación de un mes al siguiente (FIG8)

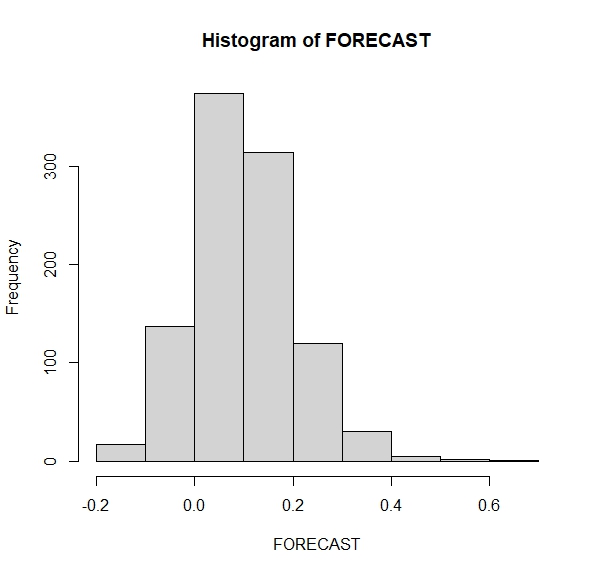FIG 8:Un ejemplo de la predicción de la inflación para el mes siguiente De aquí podemos hacernos preguntas. Por ejemplo,

¿Qué probabilidad hay de que la inflación en el mes siguiente caiga?

¿qué probabilidad hay de que la inflación en el mes siguiente sea mayor que 0.20?

¿qué probabilidad hay de que la inflación en el mes siguiente sea el doble que la de este mes?

Deberemos contar cuántas veces la predicción está en esa zona y dividirlo por el total de simulaciones (1000 en este caso)

Prob1<-sum(FORECAST<=0)/length(FORECAST)

Prob2<-sum(FORECAST>=0.20)/length(FORECAST)

Prob3<-sum(FORECAST>=0.62)/length(FORECAST)

Ahora bien, ¿Cómo interpreta las probabilidades de cada escenario? Este hilo de Twitter de Kiko Llaneras lo explica muy bien: https://twitter.com/kikollan/status/1294926143758508033