BLOQUE 2: TÉCNICAS DE APRENDIZAJE SUPERVISADO

Clase 1. La validación de modelos

Un paso importante en el proceso de análisis de datos es buscar alguna manera imparcial de analizar el desempeño de un modelo. En general, no es sensato utilizar magnitudes que analizan el grado de ajuste de un modelo (\(R^2\), ECM, etc…) ya que cuanto mayor sea el conjunto de variables utilizado en un modelo, mayor será el grado de ajuste (y menor su ECM): es decir, podemos estar cayendo en sobreajustar un modelo: asumiendo error como si fuera señal, que suele decirse. Sin embargo, ello no quiere decir que el modelo sea más útil para realizar una predicción.

Técnica 1: Entrenamiento+Test

Una técnica sencilla para analizar cómo se desenvuelve un modelo es la partición entre entrenamiento y test. Generalmente, se elige una proporción alta para el entrenamiento (en torno al 70%) y el resto se dedica a test:

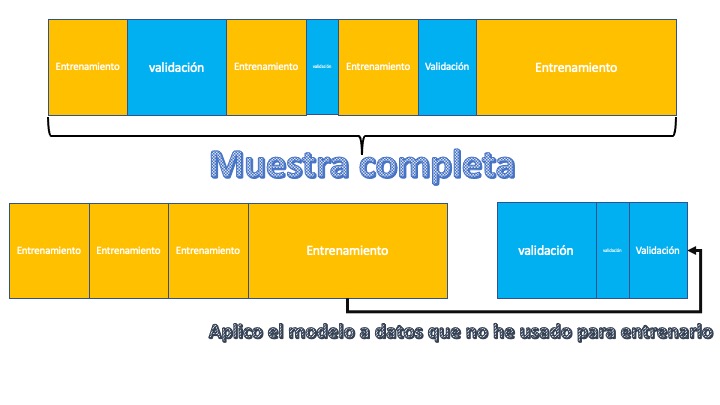
FIG 1: División entre entrenamiento y test.

Esta elección se realiza de manera aleatoria de tal forma que la partición realizada nos permita analizar, de manera adecuada, la población de estudio tanto en el entrenamiento de modelos como en su testado. El modo de trabajo es sencillo:

  1. Elija la muestra de entrenamiento y validación, así como la variable que quiere predecir (\(y_T,y_V\)) y los predictores (los almacenamos en una matriz: \(\bf{X_T,X_v}\))
  2. Utilice la muestra de entrenamiento para estimar los modelos que considere (haciendo, por ejemplo, un análisis descriptivo previo sólo a ese conjunto de datos), de tal forma que tiene, por ejemplo, \(N\) modelos: \(y_T=f_1(\bf{X_T})\),\(y_T=f_2(\bf{X_T})\),…,\(y_T=f_N(\bf{X_T})\), donde \(f_1,f_2,...,f_N\) son los modelos.
  3. con el modelo que ha entrenado, seleccione la muestra de test y se lo aplica. De esta forma tendrá, por ejemplo con el modelo \(j\), \(\hat{y}=f_j(\bf{X_V})\) las predicciones que realiza dicho modelo con los datos de validación de \(\bf{X}\). De esta forma, podrá comparar la predicción del modelo (\(\hat{y}\)) con las observaciones que tiene almacenadas del conjunto de validación (\(y_V\)).
  4. Puede calcular, entonces, alguna medida de error promedio que le interese o, lo que es más interesante, analizar la distribución empírica de los errores de predicción para distintos modelos alternativos.
  • Esta técnica podría utilizarla como un complemento a la inferencia estadística tradicional. Si considera que una variable es significativa (o relevante), entonces mediante este análisis, debería proporcionarle un error predictivo menor, por ejemplo, que otra variable menos relevante.
  • Esta técnica le puede ayudar a elegir modelos (si tiene varios modelos candidatos y quiere quedarse con uno de ellos, puede elegir el que menor error le proporcione en la validación)
  • Sin embargo, esta técnica está muy condicionada por la elección del entrenamiento y la validación.

Técnica 2: Validación Cruzada aleatoria

Una manera de mejorar el último aspecto de la técnica anterior, consistirá en tener más información sobre el error de predicción. Para ello, se puede hacer un muestreo tanto de los datos que se destinarán a entrenamiento como aquellos que se utilizarán para validación. La idea de la validación cruzada es hacer “un montón de veces” la partición entre entrenamiento y validación utilizando para ello extracciones aleatorias (sin reemplazamiento) de las muestras. Visualmente, consiste en el esquema de la FIG2:

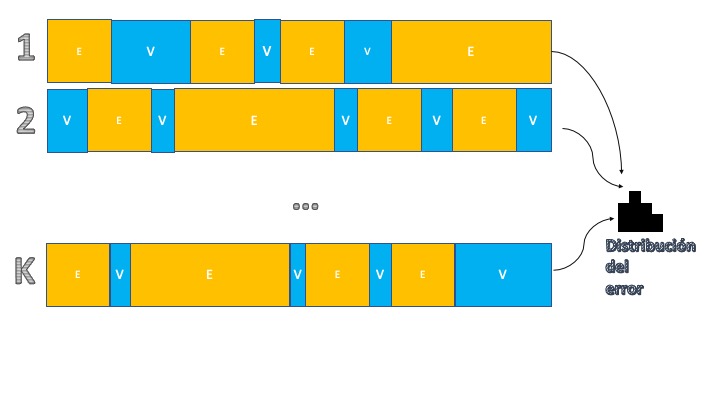
FIG 2: Idea de la validación cruzada aleatoria.

Como se puede ver, consiste en replicar la estructura anterior pero ahora se hará \(K\) veces, particionando la muestra entre entrenamiento y validación. Ello nos permitirá tener \(K\) observaciones de la medida de error que le interese y, por tanto, tener una distribución dicha medida del error de predicción. Esto es ventajoso, pues nos permite comparar entre modelos de una manera más objetiva, puesto que las particiones aleatorias permiten ver cómo funciona el modelo en submuestras distintas. Para entender el algoritmo de validación cruzada, tiene aquí un ejemplo en el que se quiere discutir qué modelo es mejor:

\[ Rating=\beta_0+\beta_1Homer+u \] \[ Rating=\beta_0+\beta_1Homer+\beta_2D+\beta_3 Homer\times D+u \]

Donde \(D\) es la variable dicotómica que modela el cambio brusco en la audiencia de los episodios a partir de 2000. El objetivo sería ver qué modelo de los dos presentados aquí, predice mejor el Rating

#usamos el set de datos que hemos llamado FINAL_SIMPSON

FINAL_SIMPSON$D<-ifelse(FINAL_SIMPSON$id<200,1,0) #generamos una variable Dummy para indicar los primeros 200 episodios


N<-100 #Decido el número de simulaciones que quiero hacer

error1f<-rep(0,N) #Creo un vector para almacenar errores para el modelo 1
error2f<-rep(0,N) #Creo un vector para almacenar errores para el modelo 2

for(i in 1:N){  #Inicio el bucle
  sample <- sample.int(n = nrow(FINAL_SIMPSON),size = floor(.7*nrow(FINAL_SIMPSON)), replace = F) #me da el sorteo de filas aleatorias
  train <- FINAL_SIMPSON[sample, ] #Obtengo la muestra de entrenamiento
  test <- FINAL_SIMPSON[-sample, ] #y la muestra de validación
  
  
  Mtrain1<-lm(imdb_rating~sumH, data=train)# Entreno el modelo 1 con la muestra de train
  Mtrain2<-lm(imdb_rating~sumH*D, data=train) # Entreno el modelo 2 con la muestra de train
   
  
  prediction_1<-predict(Mtrain1, test) #predigo con el modelo 1 y la muestra de validación
  prediction_2<-predict(Mtrain2, test) #predigo con el modelo 2 y la muestra de validación
   
  error1<-test$imdb_rating-prediction_1 #obtenemos el error de predicción 1 para cada elemento de validación
  error2<-test$imdb_rating-prediction_2 #obtenemos el error de predicción 2 para cada elemento de validación
  
  error1f[i]<-mean(error1)
  error2f[i]<-mean(error2)
  
}



E1 <- data.frame( errors = error1f )
E2 <- data.frame( errors = error2f )
CombinedData <- rbind (E1,E2)

ggplot(CombinedData, aes(x=errors)) +
  geom_histogram(data = E1, fill = "red", alpha = 0.2) + 
  geom_histogram(data = E2, fill = "green", alpha = 0.9)

Ejercicio Dibuje histogramas de los errores, así como analice sus descriptivos más básicos. Discuta sobre qué modelo prefiere.

Ejercicio Dibuje histogramas de errores de dos modelos donde nos interesaría combinar las predicciones de ambos modelos para obtener una predicción global menos sesgada.

Consejos de utilización:

  • Si en su pregunta pretende analziar si un factor (o conjunto de factores) son buenos predictores de otro, le recomendamos utilizar la primera técnica (y realizar, además, un análisis previo descriptivo con la muestra de entrenamiento, no con la muestra completa)
  • Si su pregunta consiste en analizar el poder predictivo que tendría un conjunto de modelos preseleccionados, puede usar la segunda técnica para obtener una estimación del error de predicción.

Clase 2. Más sobre validación cruzada

Cómo combinar modelos

Una idea extendida en estadística es que, en general, no hay “un mejor” modelo. Casi siempre funcionará mejor, si su objetivo es predecir, tener un conjunto de posibles modelos para los cuales, la predicción final, será una combinación de ellos. ¿Cómo combinar los modelos? Hay mucha literatura al respecto pero:

  • Puede elegir usted basado en algún criterio de experto. Ojo, porque eso tendrá que argumentarlo bien
  • Puede hacer una media/mediana de la predicción.
  • Puede tratar de estimar pesos en función de algún criterio.

Ejercicio Con los datos de los SIMPSON busque cómo, realizando validación cruzada, combinar modelos a los que se les penalice realizar predicciones que se alejen +/- 0.5 puntos.

FINAL_SIMPSON$D<-ifelse(FINAL_SIMPSON$id<200,1,0) #generamos una variable Dummy para indicar los primeros 200 episodios


N<-100 #Decido el número de simulaciones que quiero hacer

error1f<-rep(0,N) #Creo un vector para almacenar errores para el modelo 1
error2f<-rep(0,N) #Creo un vector para almacenar errores para el modelo 2
w1<-rep(0,N) #Creo un vector para almacenar  pesos del modelo 1
w2<-rep(0,N) #Creo un vector para almacenar  pesos del modelo 2
for(i in 1:N){  #Inicio el bucle
  sample <- sample.int(n = nrow(Resto_SIMPSON),size = floor(.7*nrow(Resto_SIMPSON)), replace = F) #me da el sorteo de filas aleatorias
  train <- Resto_SIMPSON[sample, ] #Obtengo la muestra de entrenamiento
  test <- Resto_SIMPSON[-sample, ] #y la muestra de validación
 
 
  Mtrain1<-lm(imdb_rating~sumH, data=train)# Entreno el modelo 1 con la muestra de train
  Mtrain2<-lm(imdb_rating~sumH*D, data=train) # Entreno el modelo 2 con la muestra de train
 
 
  prediction_1<-predict(Mtrain1, test) #predigo con el modelo 1 y la muestra de validación
  prediction_2<-predict(Mtrain2, test) #predigo con el modelo 2 y la muestra de validación
 
  error1<-test$imdb_rating-prediction_1 #obtenemos el error de predicción 1 para cada elemento de validación
  error2<-test$imdb_rating-prediction_2 #obtenemos el error de predicción 2 para cada elemento de validación
 
  m1_pos<-sum(abs(error1)<0.5) # número de predicciones que no se equivocan en más/menos 0.5
  m2_pos<-sum(abs(error2)<0.5) # número de predicciones que no se equivocan en más/menos 0.5
  w1[i]<-m1_pos/(m1_pos+m2_pos)
  w2[i]<-m2_pos/(m1_pos+m2_pos)
 
}

#obtengo los pesos finales
W1<-mean(w1)
W2<-mean(w2)
W1_f<-W1/(W1+W2)
W2_f<-W2/(W1+W2)

Cómo analizar medidas de error

Con el conjunto de datos: datos_clínicos.csv trata de explorar los mecanismos de validación cruzada. Haz los siguientes ejercicios que te servirán para discutir posibles malas prácticas (o prácticas irreales) de esta técnica.

    1. Utiliza validación cruzada para analizar el impacto de la edad y la diabetes sobre la probabilidad de desarrollar anemia. Diseñe una metodología sensata para poder responder a esa pregunta (desde definir los modelos, el conjunto de entrenamiento y test y la medida de “error” que va a utilizar)
    1. Ahora, piense que ganaría mucho dinero si obtiene el menor error predictivo (lo que hacen en los hackatones). Desarrolle primeramente, una manera de trabajar poco higiénica y que, seguramente proporcione resultados sesgados. Use esa técnica para asegurar que su error va a ser bajo (quizás más bajo que el de sus compañeros). Ahora piense, a la manera de los Hackatones, cómo obtener un resultado más realista del error de predicción utilizando validación cruzada (pista: quizás tenga que partir la muestra en más trozos)

Propuesta de solución

En el caso 1 queremos aprovechar la validación cruzada para analizar qué variable tiene mayor poder predictivo sobre la variable de interés que es desarrollar o no anemia. Es una variable dicotómica (toma valor 1 si el individuo desarrolla anemia y cero en caso contrario). Entonces, utilizaremos la partición “entrenamiento + test”. De esta forma, el 70% de la muestra lo utilizaremos para entrenar los modelos candidatos y el 30% restante para ver cuál de las variables tiene mayor poder predictivo. Vamos a entrenar cuatro modelos logísticos:

  • M1: Muerte es explicada por la “ejection fraction” del individuo
  • M2: Muerte es explicada por la variable “edad”
  • M3: Muerte es explicada por la variable “ejection fraction” y “edad” de forma conjunta
  • M4: Muerte es explicada por edad,ejection fraction y diabetes.
clinicos <- read_delim("clinicos_final.csv", 
                       delim = ";", escape_double = FALSE, trim_ws = TRUE)


N<-100 #Decido el número de simulaciones que quiero hacer

error1f<-rep(0,N) #Creo un vector para almacenar errores para el modelo 1
error2f<-rep(0,N) #Creo un vector para almacenar errores para el modelo 2
error3f<-rep(0,N) #Creo un vector para almacenar errores para el modelo 1
error4f<-rep(0,N) #Creo un vector para almacenar errores para el modelo 1




for(i in 1:N){  #Inicio el bucle
  
  sample <- sample.int(n = nrow(clinicos),size = floor(.7*nrow(clinicos)), replace = F) #me da el sorteo de filas aleatorias
  train <- clinicos[sample, ] #Obtengo la muestra de entrenamiento
  test <-  clinicos[-sample, ] #y la muestra de validación
  Mtrain1<-glm(DEATH_EVENT~ejection_fraction,family=binomial, data=train)# Entreno el modelo 1 con la muestra de train
  Mtrain2<-glm(DEATH_EVENT~age,family=binomial, data=train)# Entreno el modelo 2 con la muestra de train
  Mtrain3<-glm(DEATH_EVENT~ejection_fraction+age,family=binomial, data=train)# Entreno el modelo 2 con la muestra de train
  Mtrain4<-glm(DEATH_EVENT~ejection_fraction+diabetes+age,family=binomial, data=train)# Entreno el modelo 3 con la muestra de train
  
  
  prediction_1<-predict.glm(Mtrain1, test,type="response") #predigo con el modelo 1 y la muestra de validación
  prediction_2<-predict.glm(Mtrain2, test,type="response") #predigo con el modelo 2 y la muestra de validación
  prediction_3<-predict.glm(Mtrain3, test,type="response") #predigo con el modelo 3 y la muestra de validación
  prediction_4<-predict.glm(Mtrain4, test,type="response") #predigo con el modelo 4 y la muestra de validación
  
  death_pred1<-prediction_1>0.5
  death_pred2<-prediction_2>0.5
  death_pred3<-prediction_3>0.5
  death_pred4<-prediction_4>0.5

  error1<-test$DEATH_EVENT-as.numeric(death_pred1) #obtenemos el error de predicción 1 para cada elemento de validación
  error2<-test$DEATH_EVENT-as.numeric(death_pred2)#obtenemos el error de predicción 2 para cada elemento de validación
  error3<-test$DEATH_EVENT-as.numeric(death_pred3) #obtenemos el error de predicción 3 para cada elemento de validación
  error4<-test$DEATH_EVENT-as.numeric(death_pred4) #obtenemos el error de predicción 3 para cada elemento de validación
  
  
  error1f[i]<-(sum(error1==1)/sum(test$DEATH_EVENT))
  error2f[i]<-(sum(error2==1)/sum(test$DEATH_EVENT))
  error3f[i]<-(sum(error3==1)/sum(test$DEATH_EVENT))
  error4f[i]<-(sum(error4==1)/sum(test$DEATH_EVENT))

  
  
}



E1 <- data.frame( errors = error1f )
E2 <- data.frame( errors = error2f )
E3 <- data.frame( errors = error3f )
E4 <- data.frame( errors = error4f )
CombinedData <- data.frame(E1,E2,E3,E4)

boxplot(CombinedData,names=c("E.F","age","EF+age","EF+age+diabetes"))

La medida del error es una decisión sensible que no se puede tomar a la ligera, ya que condicionará muchos de los resultados de su análisis. En este caso observamos, por ejemplo, mean(clinicos$DEATH_EVENT) que el porcentaje de fallecidos (30%) en la muestra es bastante inferior al de no fallecidos. Eso hará que al modelo le “cueste” aprender de qué mecanismos hace que un individuo fallezca, ya que es algo “menos común”. Lo ideal sería tener un 50% de cada caso para poder estudiar en igualdad de condiciones a ambos tipos de individuos.

Es por ello que nuestra medida de error, en este caso, tratará de analizar qué modelo es mejor prediciendo “muerte”, esto es, qué modelo se equivoca menos adelantando el fallecimiento de un individuo que, al final, ocurre.

Como podemos ver en la figura:

  • La variable ejection fraction comete-en mediana-un error algo menor que la variable edad. Aunque ambas muestran, por separado, un desempeño modesto en la predicción de los casos de muerte.
  • Conjuntamente, sin embargo, mejoran la habilidad predictiva del modelo, puesto que, en promedio, se equivocan un 60% del total de muertes que deberían predecir
  • Añadir una variable como la diabetes, sin embargo, no parece contribuir a la predicción una vez añadimos la edad y la variable de “ejection fraction”.
  • Habrá que seguir buscando nuevos modelos para predecir el fallecimiento de los individuos que, quizás, mejoren estos resultados.

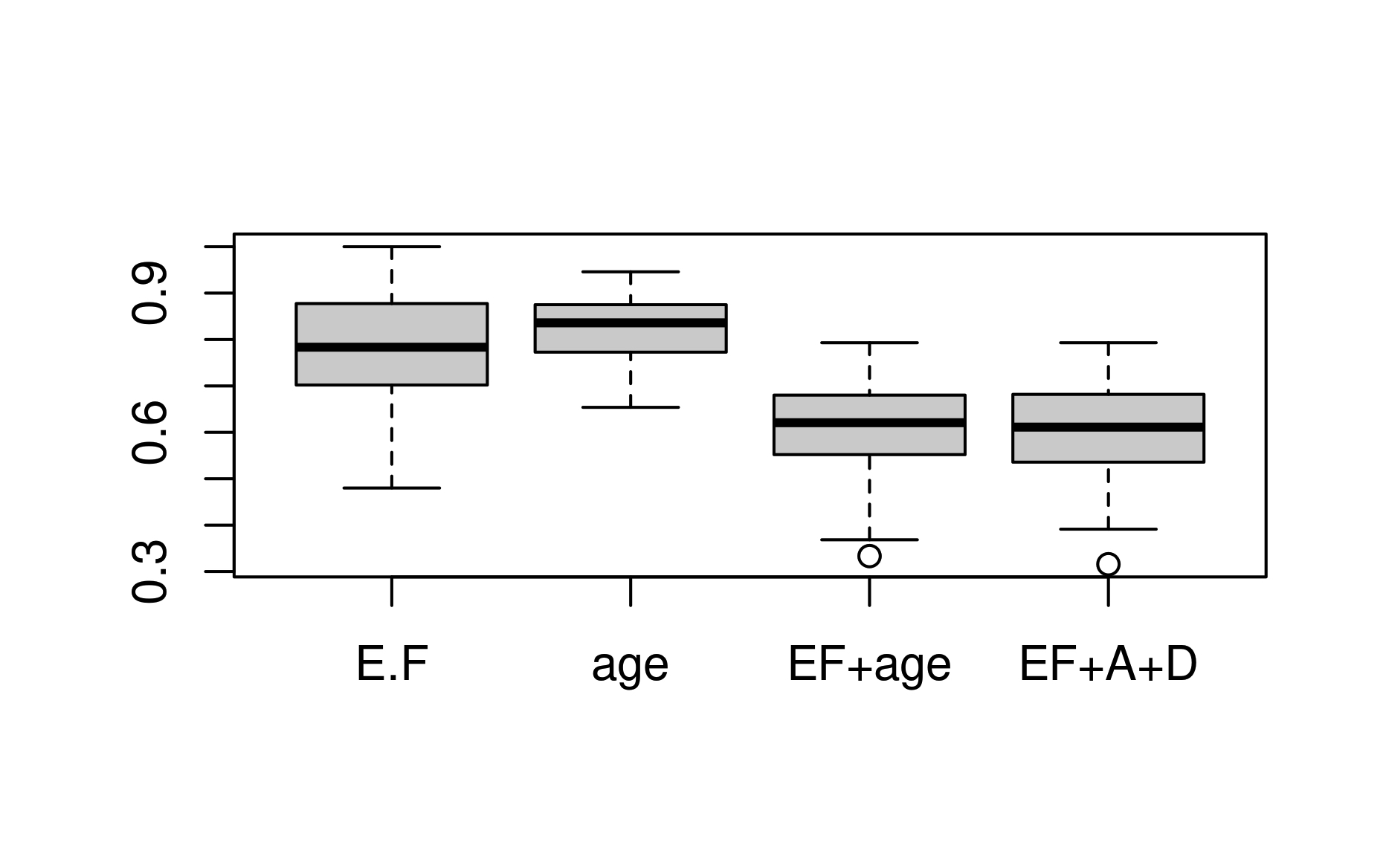
FIG 2 Resultado Validación Cruzada.

Respecto al caso 2, como ya se ha comentado, hay que tener cuidado con el uso indiscriminado de la validación cruzada, puesto que podemos “aprender” modelos que obtengan errores pequeños en base a los modelos que funcionan peor en el proceso de entrenar-validar. Por eso es bueno tener una muestra adicional guardada que no se utilizará para la validación cruzada.

Ejercicio Con los datos de los Simpson, elabore de nuevo un modelo que consista en la combinación de los dos modelos anteriores y que, finalmente, le permita obtener -mediante una muestra de reserva- una medida “real” del error que espera cometer después de combinar los modelos.

FINAL_SIMPSON$D<-ifelse(FINAL_SIMPSON$id<200,1,0) #generamos una variable Dummy para indicar los primeros 200 episodios


N<-100 #Decido el número de simulaciones que quiero hacer

error1f<-rep(0,N) #Creo un vector para almacenar errores para el modelo 1
error2f<-rep(0,N) #Creo un vector para almacenar errores para el modelo 2
w1<-rep(0,N) #Creo un vector para almacenar  pesos del modelo 1
w2<-rep(0,N) #Creo un vector para almacenar  pesos del modelo 2


#test_final# Obtengo una muestra final para dar una medida del error
sample_final <- sample.int(n = nrow(FINAL_SIMPSON),size = floor(.2*nrow(FINAL_SIMPSON)), replace = F) #me da el sorteo de filas aleatorias
muestra_final<- FINAL_SIMPSON[sample_final, ]
Resto_SIMPSON<-FINAL_SIMPSON[-sample_final, ]



for(i in 1:N){  #Inicio el bucle
  sample <- sample.int(n = nrow(Resto_SIMPSON),size = floor(.7*nrow(Resto_SIMPSON)), replace = F) #me da el sorteo de filas aleatorias
  train <- Resto_SIMPSON[sample, ] #Obtengo la muestra de entrenamiento
  test <- Resto_SIMPSON[-sample, ] #y la muestra de validación
 
 
  Mtrain1<-lm(imdb_rating~sumH, data=train)# Entreno el modelo 1 con la muestra de train
  Mtrain2<-lm(imdb_rating~sumH*D, data=train) # Entreno el modelo 2 con la muestra de train
 
 
  prediction_1<-predict(Mtrain1, test) #predigo con el modelo 1 y la muestra de validación
  prediction_2<-predict(Mtrain2, test) #predigo con el modelo 2 y la muestra de validación
 
  error1<-test$imdb_rating-prediction_1 #obtenemos el error de predicción 1 para cada elemento de validación
  error2<-test$imdb_rating-prediction_2 #obtenemos el error de predicción 2 para cada elemento de validación
 
  m1_pos<-sum(abs(error1)<0.5) # número de predicciones que no se equivocan en más/menos 0.5
  m2_pos<-sum(abs(error2)<0.5) # número de predicciones que no se equivocan en más/menos 0.5
  w1[i]<-m1_pos/(m1_pos+m2_pos)
  w2[i]<-m2_pos/(m1_pos+m2_pos)
 
}

#obtengo los pesos finales
W1<-mean(w1)
W2<-mean(w2)
W1_f<-W1/(W1+W2)
W2_f<-W2/(W1+W2)



#Predicción ponderada
Mfinal1<-lm(imdb_rating~sumH, data=Resto_SIMPSON)# Entreno el modelo 1 con la muestra de train
Mfinal2<-lm(imdb_rating~sumH*D, data=Resto_SIMPSON) # Entreno el modelo 2 con la muestra de train

prediction_final1<-predict(Mfinal1, muestra_final) #predigo con el modelo 1 y la muestra de validación
prediction_final2<-predict(Mfinal2, muestra_final) #predigo con el modelo 2 y la muestra de validación



Pred_final<-W1_f*prediction_final1+W2_f*prediction_final2
error_final<-muestra_final$imdb_rating-Pred_final #obtenemos el error de predicción 1 para cada elemento de validación

¿Qué puede decir al respecto, comparando con la validación cruzada de la última clase?

Clase 3. Los árboles de clasificación

Vamos ahora a presentar una técnica que permite predecir, de la misma manera que hemos hecho hasta ahora, una variable objetivo (por ejemplo, la puntuación de los episodios de los Simpson, el tener una enfermedad o no, etc…) utilizando un conjunto de variables explicativas. Vamos a entender, primeramente, la filosofía.

variable objetivo cualitativa: árbol de clasificación

Imagine que tiene una base de datos donde cuenta con dos variables explicativas (\(X_{1},X_{2})\) y pretende explicar la variable \(Y\) que, en este caso, sólo presenta dos posibles valores \(Y=\{S\acute{I},NO\}.\) Piense, por ejemplo, en que \(Y\) se corresponde con la devolución (o no) de un crédito y \(X_{1},X_{2}\) son variables continuas que miden dos características de cada individuo. Entonces, podemos visualizar la información disponible en este gráfico:

FIG 1: Los datos de partida.

Si observa detenidamente, es fácil encontrar cierta manera, usando rectángulos, de clasificar en bloques los síes y los noes:

FIG 2: Los datos de partida con una “regla de clasificación”.

Ahora bien, si quiere representar la regla que le permita saber, de un vistazo, si conceder o no el crédito, puede hacer un diagrama de árbol. Consiste en poner la misma información que tiene en la FIG2 de una manera más sistemática, de tal forma que le sea fácil de seguir:

FIG 3: El árbol que se deduce de la figura 2: fíjese que, a la izquierda van los caminos que cumplen la regla que aparece en cada rama y, por tanto, a la derecha, los caminos que no la cumplen.

Sin embargo, en la vida real los datos, en general, tendrán una estructura caótica, nada obvia en muchos casos y, por lo tanto, deberemos dejar a los ordenadores que construyan estos árboles. Veamos los pasos que seguirá un algoritmo que genera árboles de clasificación.

Los datos, ahora, serán ligeramente diferentes, para que el ejercicio tenga “más gracia”

PASO 1: Elegir un punto de corte

Lo primero que hace su computadora es “rastrear” entre las \(n\) variables explicativas disponibles. Por ejemplo, empieza por \(X_{1}\) , la discretiza (es decir, la convierte en una variable discreta tomando un tamaño predefinido para el corte, por ejemplo \(X_{1}=\{0,0.1,0.2,0.3,....,12\}\) y se va parando en cada uno de esos valores. Entonces, hace unas cuentas que vamos a ir desarrollando. Para que se vea bien la idea, vamos a suponer que, en su trabajo de rastreo, se para en \(X_{1}=3:\)

FIG 4: El algoritmo se detiene en \(X_{1}=3\).

PASO 2: Plantearse cómo de bueno es ese punto de corte

Necesitamos alguna medida que nos permita analizar si el punto de corte debe ser \(X_{1}=3\) o debemos seguir buscando. Una idea, que parece bastante clara, es contabilizar qué tal discrimina, el corte en \(X_{1}=3\), los síes y los noes. La mejor discriminación sería, obviamente, que a la izquierda (es decir, \(X_{1}<3)\) hubiera sólo síes y a la derecha (\(X_{1}>3)\) hubiera sólo noes. Eso no es así (salvo en contadas ocasiones relacionadas con el problema de predicción perfecta del que hablamos en clases pasadas) y, por tanto, debemos asumir que hay cierta heterogeneidad en los grupos. A esa heterogeneidad la llamaremos caos o entropía. Cuanto más caos o entropía haya en un grupo, peor lo estará haciendo el método. Por ejemplo, en el grupo que se forma si \(X_{1}<3\) vemos que, claramente, los síes ganan a los noes. Ese grupo es poco caótico o, dirá, tendrá una entropía baja. Esto quiere decir que, si \(X_{1}<3\), nos podemos apostar el cuello a que la mejor predicción es SÍ ya que, seguramente, no nos equivocaremos. Pero ¿se atrevería a jugarse todo su dinero para predecir qué ocurrirá con el individuo si \(X_{1}>3?\) Seguramente, no. Y eso es, naturalmente, porque el grupo está más desorganizado o caótico. No sabría, entonces, si apostar al SÍ o al NO.

Entran las matemáticas

Es el momento de plantearse cómo cuantificar el grado de caos o, como hemos dicho, entropía presenta cada grupo. Hay varias expresiones pero nosotros vamos a elegir una clásica:

\[ E\left(p_{1},p_{2},...,p_{n}\right)=\sum_{i=1}^{n}-p_{i}\log_{2}(p_{i}) \]

donde \(n\) es el número de posibles valores de la variable dependiente (en nuestro caso, 2) y \(p_{i}\) representa la frecuencia relativa de cada una de las categorías en el grupo (es decir, la probabilidad que tienen de pertenecer al grupo). Por ejemplo, en este caso, en el grupo generado por \(X_{1}<3\), tendremos:

\[ {\color{green}P(S\acute{I})=\frac{10}{12}=\frac{5}{6}},{\color{red}P(NO)=\frac{2}{12}=\frac{1}{6}} \]

de tal forma que la entropía será: \[ E_{1}=-\frac{5}{6}\log_{2}\frac{5}{6}-\frac{1}{6}\log_{2}\frac{1}{6}=0.35 \]

Por otro lado, en el grupo generado por \(X_{1}>3\), tendremos:

\[ {\color{green}P(S\acute{I})=\frac{15}{28}},{\color{red}P(NO)=\frac{13}{28}} \]

de tal forma que la entropía será: \[ E_{2}=-\frac{15}{28}\log_{2}\frac{15}{28}-\frac{13}{28}\log_{2}\frac{13}{28}=0.64 \]

Finalmente, necesitamos una medida global de caos para la participación que ha realizado el algoritmo. Para ello, obtendremos una media ponderada de la entropía \[ E=\frac{12}{40}(0.35)+\frac{28}{40}(0.64)=0.55 \]

PASO 3: decidir sobre el resultado

¿Qué tal es ese 0.55 que hemos obtenido? Pues no lo sabemos. Deberemos compararlo con otro corte. Lo que hará su ordenador es obtener las entropías asociadas a cada corte y quedarse con la que dé un valor menor. Por ejemplo, si corta en \(X_{1}=6,\) como en la figura:

FIG 5: Un nuevo corte en \(X_{1}=6\).

de nuevo, haciendo los números, tendrá, si \(X_{1}<6\)

\[ {\color{green}P(S\acute{I})=\frac{13}{22}},{\color{red}P(NO)=\frac{9}{22}} \]

de tal forma que la entropía será: \[ E_{1}=-\frac{13}{22}\log_{2}\frac{13}{22}-\frac{9}{22}\log_{2}\frac{9}{22}=0.60 \]

Por otro lado, en el grupo generado por \(X_{1}>6\), tendremos:

\[ {\color{green}P(S\acute{I})=\frac{12}{18}=\frac{2}{3}},{\color{red}P(NO)=\frac{6}{18}=\frac{1}{3}} \]

de tal forma que la entropía será: \[ E_{2}=-\frac{2}{3}\log_{2}\frac{2}{3}-\frac{1}{3}\log_{2}\frac{1}{3}=0.55 \]

Finalmente, necesitamos una medida global de caos. Para ello, obtendremos una media ponderada:

\[ E=\frac{22}{40}(0.60)+\frac{18}{40}(0.55)=0.57 \]

que, como ve, es ligeramente peor que el anterior.

Resumiendo:

el ordenador, entonces, lo que hará es tomar nota de las diferentes entropías asociadas a cada una de las particiones en torno a \(X_{1}\). Elegirá, por tanto, el corte que menor entropía produzca. A continuación, hará lo mismo con \(X_{2}\). El árbol entonces, se empezará por la variable cuyo corte genere menor entropía global es decir, entre las entropías para cada corte de \(X_{1}\)y \(X_{2}\) elegirá el corte de la variable que menor entropía tenga. A partir de ese corte, irá eligiendo cortes sucesivos en ambas variables, de manera alternativa.

Con \(N\) variables, sucede lo mismo: del conjunto \(\{X_{1},...,X_{N}\}\) de variables, elegirá aquella que -al hacer una primera partición- devuelva una menor entropía. A partir de ahí, hará lo mismo: realizará cortes en todas las variables e irá quedándose el resultado que menor entropía proporcione en cada iteración. ¿Hasta cuándo? Necesitaremos un criterio de parada. Ese criterio lo veremos en la siguiente clase.

EJERCICIO

Busque una librería de [R] que entrene árboles de clasificación, y trate de- siguiendo la documentación- ser capaz de entrenar un árbol para predecir si un individuo tendrá anemia dado si tiene diabetes y su edad. Trate de interpretar dicho árbol

propuesta de solución Aquí elegimos la librería rpart pero puede elegir cualquier otra de las disponibles.

  install.packages("rpart")
  library(rpart)
  install.packages("rpart.plot")
  library(rpart.plot)
  ANEMIA<-as.factor(clinicos$anaemia) #Hacemos que la variable output sea un factor
  tree.v1 <-rpart(ANEMIA~age+diabetes,data=clinicos, method="class") 
  summary(tree.v1)
  rpart.plot(tree.v1)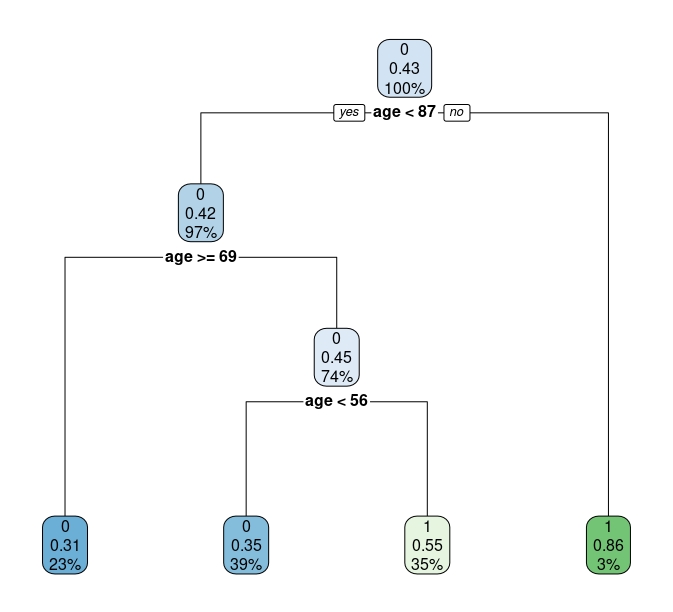

FIG 6: Ejemplo del árbol.

Explicamos lo que significa con detalle:

  • El primer nodo tiene el 100% de la muestra (que tiene un 42% de eventos iguales a 1). Si nos quedáramos en ese nodo y no siguiéramos, deberíamos predecir que una persona, elegida al azar de la población de este estudio, tiene un 43% de probabilidades de tener anemia (que es, justo, el porcentaje de individuos con Anemia en la muestra. Nada nuevo. Debemos avanzar)
  • Si vamos al siguiente nodo, si una persona tiene más de 87 años directamente predecimos que tiene anemia (además, el 3% de la muestra son individuos mayores de 87 años con anemia). En caso contrario, debemos seguir haciendo el camino:
  • como vemos, la probabilidad de tener anemia se concentra entre los individuos entre 56 y 69 años.

Sin embargo, este árbol nos ha servido para entrenarnos parece muy pobre porque sólo utiliza la variable edad para clasificar. En la clase siguiente, verá cómo poder elegir un buen árbol.

Clase 4. Los árboles de clasificación (elección del árbol)

Es el momento de indagar más sobre la construcción de los árboles. En general, diremos que los árboles tienden a sobreajustar la muestra. De hecho, son muy sensibles a la propia muestra, cambiando (bastante) el resultado si se añaden o eliminan observaciones. La razón es sencilla: el procedimiento que hemos contado anteriormente nos puede llevar a hacer árboles que clasifiquen perfectamente la muestra (para ello, sólo se necesita añadir ramas y más ramas). Sin embargo, esto será perjudicial cuando intentemos utilizar el propio árbol para predecir. Es por ello que parece sensato, de nuevo, utilizar validación cruzada para la elección de un árbol óptimo.

Sin embargo, lo normal es que en la propia validación cruzada se decida sobre un conjunto de árboles posibles:

  • basados en subconjuntos de variables distintas
  • basados en diferentes tamaños del propio árbol

Nos enfocamos en la idea segunda. Tenemos que pensar que cada rama que se añade, esta supone un “coste” puesto que hace el árbol más complejo.

Lo normal es que se utilice una medida de coste:

\[ CP(T)=R(T)+\alpha T \] con \(\alpha>0\). \(R(T)\) es una medida de error de clasificación para el árbol con T ramas. Por otro lado, se penaliza el número de ramas (T) mediante un parámetro \(\alpha\). La librería rpart no permite que el usuario proponga un valor, sino que lo estima internamente.

AL acto de elegir el número de ramas que irán en el árbol se le denomina podado o pruning.

Por ejemplo, aquí puede ver el resultado para el árbol de la FIG6

> summary(tree.v1)
Call:
rpart(formula = ANEMIA ~ age + diabetes, data = clinicos, method = "class", 
    control = rpart.control(cp = 0.03))
  n= 240 

          CP nsplit rel error   xerror       xstd
1 0.04854369      0 1.0000000 1.000000 0.07444509
2 0.04368932      1 0.9514563 1.077670 0.07499175
3 0.03000000      3 0.8640777 1.058252 0.07488693

Si se fija en la función que ha generado este árbol, en “control” se puso que CP debía llegar a 0.03, como mucho. Al llegar ahí se para. Se ha fijado 0.03 para que el árbol no fuera muy “grande”. Verá que si no pone nada, el árbol sale más grande (R tiene la orden interna de usar 0.01) como parámetro interno.

De esta forma, usted puede jugar con dichos parámetros de control en la validación cruzada. A continuación le mostramos una posible idea:

  • Como puntos importantes, creamos un vector con diferentes parámetros de control (es decir, valores umbral para podar el árbol)
  • Para ello, tenemos que tener dos bucles: uno para almacenar errores y otro para probar distintos parámetros de control
  • Por otro lado, elegimos una medida de error (en este caso, ele elemento 1,2 de la matriz de confusión-como se ve en la última línea de código- es decir, predecir que el individuo tiene anemia y que, en realidad, no la tenga )
 clinicos <- read_delim("clinicos_final.csv", 
                         delim = ";", escape_double = FALSE, trim_ws = TRUE)
  
  sample <- sample.int(n = nrow(clinicos),size = floor(.20*nrow(clinicos)), replace = F) #me da el sorteo de filas aleatorias
  Muestra_validacion_final<-clinicos[sample,]
  
  clinicos<-clinicos[-sample,] #mi muestra sin los datos que me he guardado para jugar a se Kaggle
  
  
  error<-mat.or.vec(50, 4) #creamos un vector que almacenará 50 errores
  cpv<-c(0.001,0.01,0.05,0.1) #creamos un vector que contiene los diferentes valores del parámetro de control
  for(i in 1:50){     #Iniciamos los subíndices: este es el de la iteración
    for (j in 1:4){    #este es el subíndice del parámetro de control
      random <- sample(1:nrow(clinicos), size = floor(.9*nrow(clinicos))) # Elegimos la muestra de entrenamiento al azar
      train<-clinicos[random,]
      test <-clinicos[-random, ] #por lo que la muestra de test es la contraria
      tree.v1 <-rpart(anaemia~age+diabetes,data=train,control = rpart.control(cp = cpv[j],minsplit=10), method="class") #permitimos que el parámetro de control cp, varíe y minsplit es el número mínimo de observaciones en un nodo
      tree.pred <- predict(tree.v1, newdata = test, type = "class") #predecimos con la muestra «test»
      xt1<-table(tree.pred, test$anaemia) #obtenemos la tabla de confusión...
      error[i,j]<-xt1[1,2]/length(tree.pred) #...y de la tabla seleccionamos la(s) magnitud(es) que nos interesen
    }}

Atendiendo al gráfico, se puede intuir que el modelo 2 (asociado a un cp=0.01) parece ser el que mejor se comporta en este error especificado

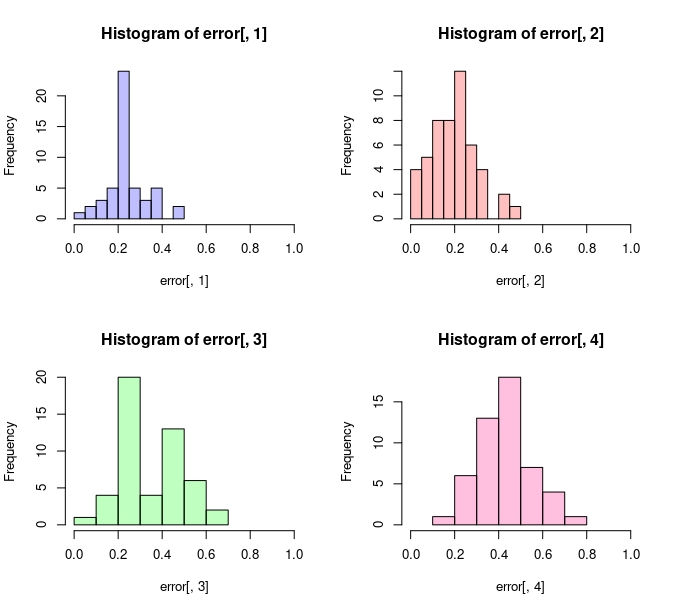
FIG 1: Errores de predicción

Puede generar estos errores usando este script

  p1 <- hist(error[,1])                   
  p2 <- hist(error[,2])
  p3 <- hist(error[,3])
  p4 <- hist(error[,4])

 par(mfrow=c(2,2))  
 plot( p1, col=rgb(0,0,1,1/4), xlim=c(0,1))  
 plot( p2, col=rgb(1,0,0,1/4), xlim=c(0,1)) 
 plot( p3, col=rgb(0,1,0,1/4), xlim=c(0,1)) 
 plot( p4, col=rgb(1,0,1/2,1/4), xlim=c(0,1))

Y, además, puede obtener los descriptivos asociados a cada error

 > summary(error)
       V1                V2                V3                V4            
 Min.   :0.04167   Min.   :0.04167   Min.   :0.08333   Min.   :0.1667    
 1st Qu.:0.20833   1st Qu.:0.12500   1st Qu.:0.20833   1st Qu.:0.3750     
 Median :0.22917   Median :0.18750   Median :0.31250   Median :0.4167   
 Mean   :0.24167   Mean   :0.20333   Mean   :0.34833   Mean   :0.4400  
 3rd Qu.:0.29167   3rd Qu.:0.28125   3rd Qu.:0.50000   3rd Qu.:0.5000   
 Max.   :0.45833   Max.   :0.50000   Max.   :0.62500   Max.   :0.7500

Aunque si quiere prometer un error más fiable, deberá haberse guardado otro porcentaje de muestra (como hemos hecho al principio) y probar el segundo modelo sobre ese porcentaje

tree.vf <-rpart(anaemia~age+diabetes,data=clinicos,control = rpart.control(cp = 0.01,minsplit=10), method="class") #permitimos que el parámetro de control cp, varíe y minsplit es el número mínimo de observaciones en un nodo
 tree.pred <- predict(tree.vf, newdata = Muestra_validacion_final, type = "class") #predecimos con la muestra «test»
 xt1<-table(tree.pred,  Muestra_validacion_final$anaemia) #obtenemos la tabla de confusión...
 error<-xt1[1,2]/length(tree.pred) #...y de la tabla seleccionamos la(s) magnitud(es) que nos interesen

y, pese a que el error mediano no llega al 18% en el modelo 2, en esta muestra nos sale del 25%.

Los árboles de regresión

Por otra parte, si la variable que quiere predecir es continua (o discreta, pero no cualitativa) podrá ajustar un árbol de regresión. La idea de su mecanismo es similar a lo que acaba de ver. Supongamos que tenemos dos variables candidatas (por ejemplo, \(x_1\),\(x_2\)) para explicar una tercera (\(y\)). Podemos visualizar los datos disponibles en la FIG 3

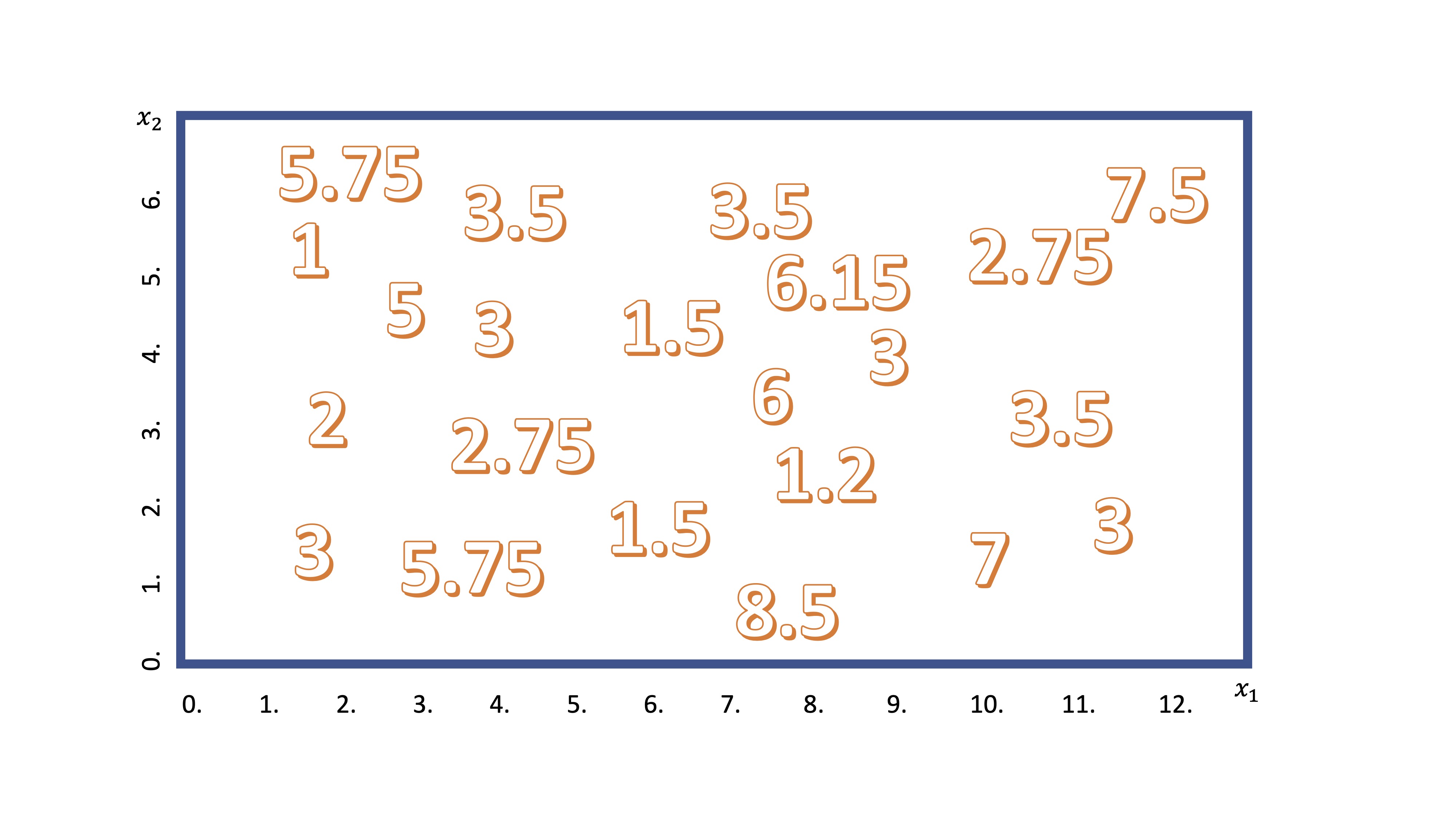
FIG 3: Idea del árbol de regresión

Ahora, como ya sabe, el algoritmo empezará a realizar un corte en una de las variables. De manera secuencial, discretizará la variable \(x_1\), en porciones pequeñas (por ejemplo, \(x_1=[0,0.5,1,1.5,2,....,12])\) y realizará cortes para ver cuál es mejor. Imagine que se para en el corte \(x_1=5\), entonces, tendrá algo así:

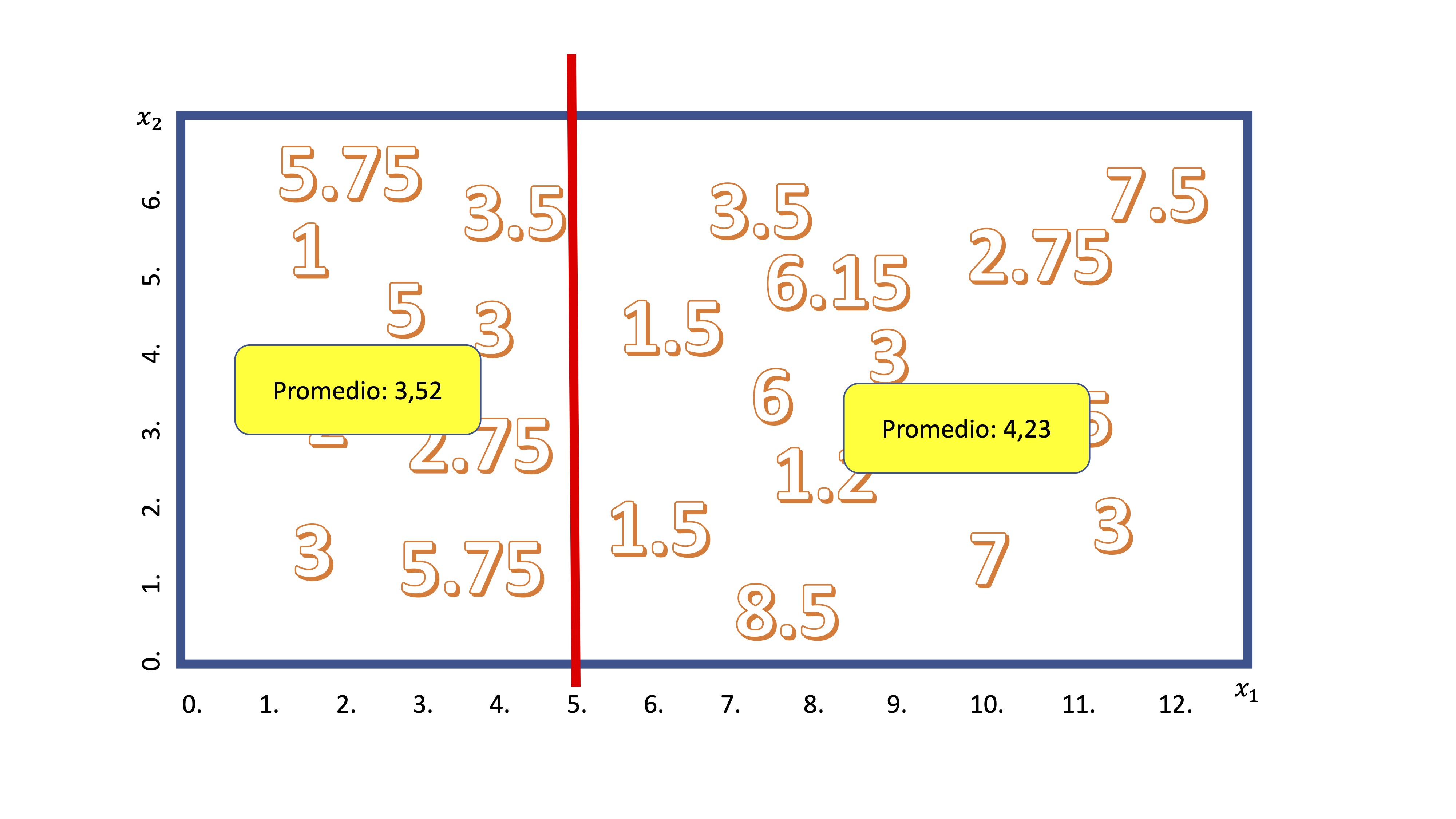FIG 4: Un corte en un árbol de regresión Como ahora el promedio de la variable \(y\) tiene sentido, el algoritmo calcula - para cada grupo- la media condicionada al corte. En este caso, diremos que si \(x_1<5\), entonces el valor esperado para \(y\) es 3.52 y, en caso contrario es 4.23. Ahora debemos preguntarnos si el corte es “bueno”. Para ello, el algoritmo calcula el Error cuadrático Medio. Para el grupo \(x_1<5\) será \(ECM_1=\frac{(5.75-3,52)^2+(3.5-3.52)^2+....+(5.75-3,52)^2}{9}\) y lo mismo para el otro grupo \(ECM_2=\frac{(3.5-4,23)^2+(6.15-4.23)^2+....+(3-4,23)^2}{13}\). La suma de ambos será el error cuadrático de la partición. Buscará aquella partición que minimice esta suma. Luego, alternatá entre todas las variables explicativas y elegirá empezar a cortar el árbol por aquella que minimice dicha suma. De la misma manera, irá alternando entre las variables de acuerdo con algún criterio de parada, de nuevo, relacionado con el parámetro de control (que regula cuántas ramas tendrá el árbol).

El siguiente esquema le permite ajustar un árbol de regresión. Tendrá que poner en “method” la palabra anova que significa “análisis de varianza”. Esto infica a la librería rpart que ha de entrenar un árbol con variable explicada continua.

rating<-SIMPSONS_FINAL$rating_imdb
BART<-SIMPSONS_FINAL$Bart
HOMER<-SIMPSONS_FINAL$Homer

arbol_simpsons<- rpart(formula = rating ~BART+HOMER, method  = "anova", control=list(cp = 0.01, xval = 10))
  rpart.plot(arbol_simpsons)

Obtendrá algo así,

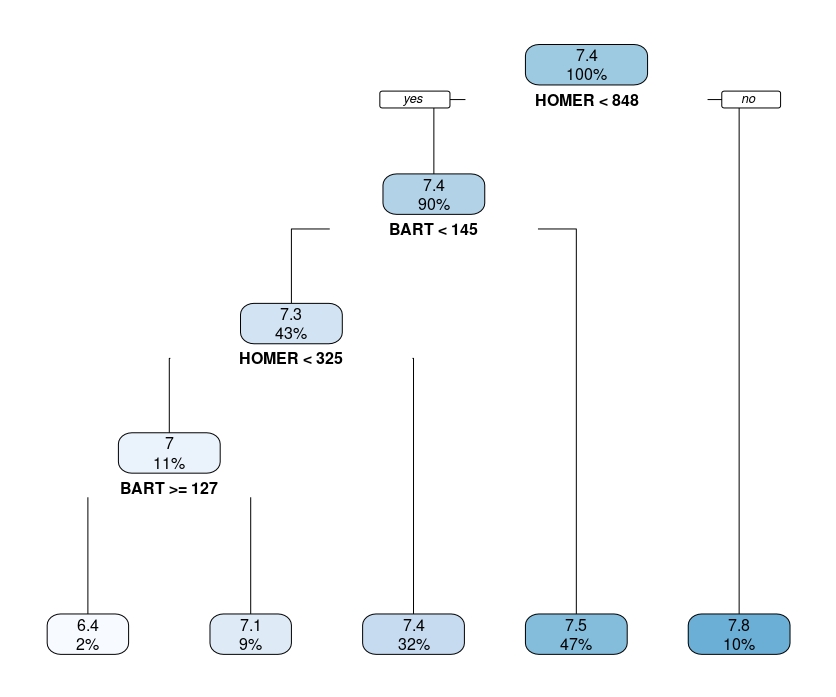
FIG 5: Un árbol de regresión

que, recuerde, deberá interpretar como el promedio condicional. Por ejemplo, el último nodo de la derecha quiere decir que cuando Homer tiene más de 848 líneas de guión los episodios tienen, de media un 7.8. Y eso pasa en el 10% de la muestra.