BLOQUE 1: Introducción a la minería de datos
Estos apuntes están pensados para desarrollar ciertas habilidades del futuro científico de datos. Contrariamente a lo que pensará, no es una profesión concebida únicamente para desarrollar nuevas metodologías de análisis de datos (lo cual no ocurre todos los días), ni en ser capaz de saberse más líneas de código de memoria o hacer scripts de [R] o Python sin despeinarse. Una primera misión del científico de datos consistirá en tener una filosofía de trabajo basada, fundamentalmente, en establecer un conjunto de preguntas de interés y, como consecuencia de ello, tener un conjunto de habilidades analíticas y técnicas para indagar en las posibles respuestas.
Desde ya, el científico de datos tendrá que asumir que:
- las preguntas que realice deberán formularse con la mayor precisión posible
- no siempre la respuesta está clara: esta profesión implica entender la incertidumbre asociada a un resultado que viene dada por los datos disponibles
- las respuestas, muchas veces, son compatibles con diversas hipótesis iniciales
- no hay una única técnica para abordar un proyecto (o una parte de un proyecto), ni consiste en hacer el trabajo tirando de recetas. En estadística, en general, no hay técnicas prohibidas, sino que es más conveniente ser capaz de entender las limitaciones de estas a la hora de aplicarlas a un conjunto de datos.
- sin embargo, esta profesión puede ser todo lo estimulante que uno quiera: los datos siempre son un reto y una buena excusa para pensar, discutir y, por qué no, sentir el placer de entender algo más este mundo.
Clase 1. La realización de preguntas en ciencia (de datos)
IMPORTANTE
Esta clase va asociada a un vídeo. Debe verlo antes de entrar al aula, puesto que se discutirán varios aspectos que en él se mencionan
Vea la introducción del vídeo: minutos 0.00 a 1.50. Reflexione sobre cómo definiría la Ciencia de Datos con la información que tiene hasta ahora. Piense en si discrepa con las opiniones de los entrevistados.
Desde el minuto 2 al 10.50 se trabajan varios aspectos:
- Se plantea una pregunta inicial (¿existe un tamaño de clase óptimo?) que se va mejorando, según aprendemos de los expertos
- Vemos otros casos sobre cómo se accede a preguntas (¿Está en una empresa?¿Tiene una línea de investigación?¿Está interesado en una cuestión que le parece relevante?)
EJERCICIO 1
Trate de elaborar preguntas con interés en ciencia de datos a partir de las siguientes preguntas algo más vagas y generales. Utilice ideas e intuiciones teóricas para ello.
- Los determinantes del precio de la vivienda
- El ingreso en urgencias de pacientes COVID
- El turismo en España
- Número de jóvenes en paro en España
Preguntas concretas: Lo normal es empezar pensando: una pregunta puede ser ¿cómo afecta el gasto en publicidad en mis ventas?. El problema de esa pregunta es que, en general, es demasiado amplia y ya sabemos la respuesta “afecta mucho” (seguramente). Ante una pregunta vaga, una respuesta vaga. Debemos pensar en otras opciones. Si el cliente nos pregunta ¿cómo afecta el gasto en publicidad? Nosotros tenemos el deber de reformularla y, por supuesto, confirmar si son enfoques válidos. Es decir, no debemos tener miedo en repreguntar
Por ejemplo:
- ¿Cuántas semanas dura el impacto de un incremento en el gasto en publicidad sobre las ventas?
- ¿Tiene algún umbral mínimo y máximo el efecto del gasto en publicidad sobre las ventas?
- ¿Se producen efectos cruzados entre un incremento del gasto en publicidad y una estrategia en precio sobre las ventas?
Estas preguntas se diferencian de la primera en que tratan de enfocarse en un aspecto concreto de la posible relación entre el gasto en publicidad y las ventas. Dirigen a la persona a realizar un conjunto de anílisis acotados y, por supuesto, a poder tener más claro en qué tipo de datos y de experimentos deberá concentrarse.
Preguntas cuantificables, medibles: De nuevo, hay que enfocar la pregunta a forzar una respuesta cuantitativa. Los métodos con que se trabaja en este campo pretenden cuantificar efectos e indagar en la incertidumbre asociada a esas mediciones. Por tanto, hay que ir en esa línea.
- ¿Cómo de probable es que la elasticidad precio de mi producto sea mayor que la unidad?
- ¿En qué porcentaje se reducirán las ventas el año que viene con el cierre de dos centros de producción?
- ¿Cómo de rentable es la publicidad en la marca asociada al coste estacional de dicha inversión?
Evitar un clásico: análisis de los determinantes de… es muy común creer que, en general, con estas metodologías uno puede responder con claridad a la pregunta de cuáles son los determinantes de un hecho de interés (las ventas de un producto, el precio de la electricidad, etc…). Lamentablemente, esa pregunta no suele ser interesante porque, en general, se requiere un modelo teórico claro que testar-el cual, especificará de antemano dichos determinantes- y el analista, en todo caso, será quien cuantifique dichos impactos. Sin embargo, esta pregunta suele ser pretenciosa y difícil de abordar, si no imposible, con las técnicas existentes, en general.
¿Qué viene primero: el set de datos o la pregunta? En realidad, eso no es muy importante. Una pregunta puede venir estimulada por un análisis del conjunto de datos disponible y de ideas previas del analista. Lo contrario también es factible: una pregunta dada permitirá hacer acopio de los datos necesarios para tratar de responderla.
EJERCICIO 2
En el curso hay varias bases de datos. Vamos a centrarnos en la de los Simpsons y la de la liga de fútbol. Abra las bases de datos, lea la descripción de las variables y trate de pensar en preguntas concretas que podrían estimular un estudio. Ambos datos son lo suficientemente generales como para no necesitar grandes conocimientos teóricos
Finalmente, vea del minuto 10.50 al final.
EJERCICIO 3
| Piense en esa pregunta corta y concreta que le gustaría analizar. Además, escriba en un párrafo, por qué es importante, cuáles son sus objetivos, qué tipo de datos necesitará, piense qué población va a tratar de analizar y qué espera encontrarse según su conocimiento o intuición. Puede inspirarse en algún artículo-científico o de prensa- que le interese o le haya interesado. |
Puede leer el texto de la intranet obtenido del libro “The art of Data Science”, donde se reflexiona sobre la formulación de preguntas iniciales.
EJERCICIO ENTREGABLE
Deberá entregar en la fecha que se le indique en clase ese párrafo. Aquí le dejamos un ejemplo con el caso del tamaño del aula que se va a trabajar en los vídeos.
Ejemplo: Nos interesa investigar si el efecto del tamaño del aula sobre las notas de los estudiantes puede fluctuar con la clase social del alumno. Esta idea surge de la lectura de un artículo (DENNY, Kevin; OPPEDISANO, Veruska. The surprising effect of larger class sizes: Evidence using two identification strategies. Labour economics, 2013, vol. 23, p. 57-65.) que sugiere que el efecto del tamaño de la clase tiene un efecto positivo sobre los resultados académicos. Utilizan datos de PISA, los cuales suelen presentar mucha heterogeneidad, ya que incluyen tipos distintos de colegios, países, etc… y resumen demasiado, a nuestro juicio, la información muestral. Pretendemos analizar, entonces, si ese efecto que miden puede variar atendiendo a una variable socioeconómica proporcionada por PISA: el estatus social.
Clase 2 Aspectos relevantes en la modelización estadística (I): el análisis descriptivo
IMPORTANTE
Esta clase va asociada a un vídeo. Debe verlo antes de entrar al aula, puesto que se discutirán varios aspectos que en él se mencionan
Vea la introducción del vídeo: minutos 0.00 a 1.50. Reflexione sobre la importancia del análisis descriptivo para tratar de buscar respuestas, cualitativas, a las preguntas que se ha realizado. Piense, además, cómo esta pregunta puede (y debe) ir evolucionando según lee sobre el tema y analiza los datos.
EJERCICIO 1
Queremos explicar una variable \(y\) en función de una variable \(x\) . La variable \(y\) presenta un coeficiente de variación muy elevado, comparado con el de la variable \(x\) ¿Qué podríamos esperar acerca de nuestra capacidad de explicar los cambios en la \(y\) ante cambios en la \(x\)?
Queremos explicar una variable \(y\) en función de una variable \(x\) . La variable \(y\) presenta un alto coeficiente de asimetría comparado con el de la variable \(x\) ¿Qué podríamos esperar acerca de nuestra capacidad de explicar los cambios en la \(y\) ante cambios en la \(x\)?
Vea de los minutos 2.00 al 10.00 del vídeo de esta sesión. En esencia, se discute sobre la necesidad de hacer un buen análisis descriptivo para poder entender nuestra pregunta nosotros mismos, hacerla evolucionar, proponer hipótesis razonables y- muy importante- conseguir que nos entiendan.
Como verá, hacia el minuto 10.00, después de haber estudiado los datos con calma, nuestra pregunta evoluciona: ya no tenemos tan claro que el efecto del tamaño de la clase sea muy importante y, además, podría confundirse con el tamaño de la ciudad.
EJERCICIO 2
Trate de mejorar las respuestas a las preguntas del EJERCICIO 1. Para ello, piense sobre este caso práctico:
Se dispone de una base de datos de precios, gastos en publicidad y ventas de un producto. Se presenta un análisis descriptivo en la tabla adjunta. Comente qué le llama la atención de estos resultados, indicando:
- Anomalías posibles en las variables.
- Características de las variables que pueden afectar al tratar de explicar las ventas con los gastos en publicidad y el precio.
- ¿Qué particularidad tiene la variable ventas que no tienen ni los gastos ni el precio? (compare la media y la mediana)
| Estadístico | Gastos | Precios | Ventas |
|---|---|---|---|
| Mediana | 10 100 | 1.40 | 95 000 |
| Media | 10 000 | 1.37 | 50 000 |
| D. Típica | 700 | 2 | 20 000 |
| Máx | 11 000 | 1.50 | 850 000 |
| Min | 9 500 | -0.75 | 7 560 |
| N | 1000 | 1000 | 1000 |
El siguiente ejercicio está pensado para que desarrolle habilidad para analizar distribuciones. No será la última vez que se “enfrente” a este conjunto de datos, puesto que en las clases siguientes seguiremos utilizándolos.
EJERCICIO 3
Observe los siguientes gráficos y los percentiles asociados. Se corresponden con las distribuciones de la respuesta de un conjunto de individuos a un tratamiento antidepresivo (cuanto mayor sea el valor de “value”, mejor se sienten). Los rojos han recibido el tratamiento, mientras que los verdes han recibido un placebo. Describe el efecto del tratamiento para cada uno de estos posibles gráficos.
| paciente | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | media | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| tratado | 4.02 | 4.69 | 5.22 | 5.61 | 5.97 | 6.35 | 6.82 | 7.34 | 8.00 | 6.00 | ||
| placebo | 3.93 | 4.63 | 5.08 | 5.47 | 5.87 | 6.26 | 6.66 | 7.18 | 7.84 | 5.87 |
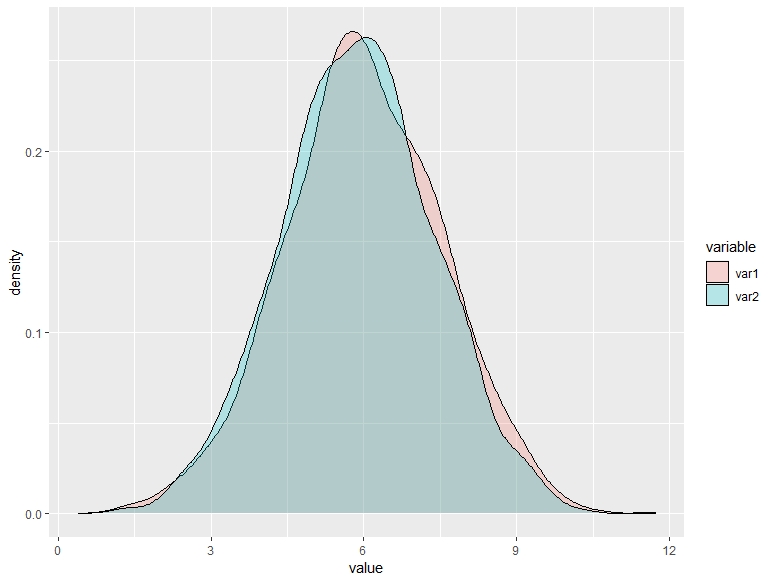
A.
| paciente | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | media | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| tratado | 1.23 | 2.83 | 4.04 | 4.99 | 5.95 | 6.90 | 7.90 | 9.06 | 10.83 | 5.98 | ||
| placebo | 0.81 | 1.59 | 2.42 | 3.29 | 4.41 | 5.69 | 7.30 | 9.39 | 11 | 6.00 |
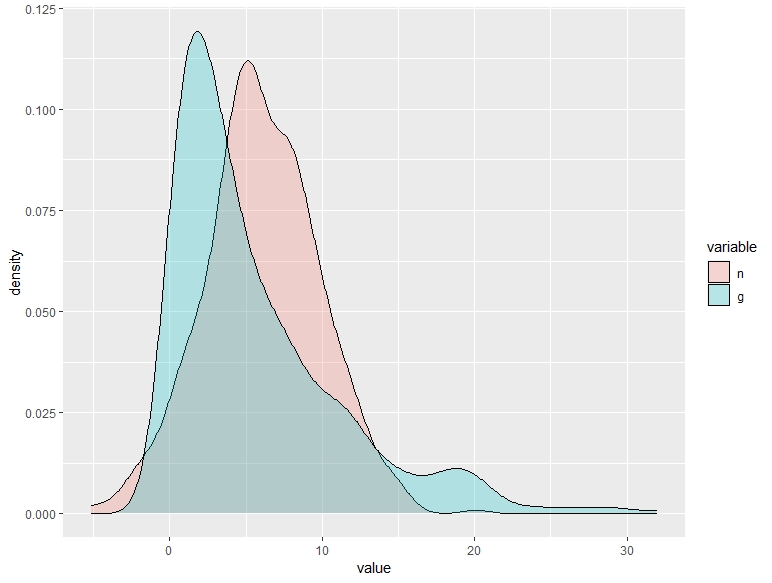
B.
| paciente | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | media | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| tratado | 4.85 | 5.26 | 5.57 | 5.82 | 6.04 | 6.26 | 6.49 | 6.77 | 7.14 | 6.02 | ||
| placebo | 2.95 | 3.33 | 3.61 | 3.87 | 4.12 | 4.33 | 4.57 | 4.86 | 5.25 | 4.10 |
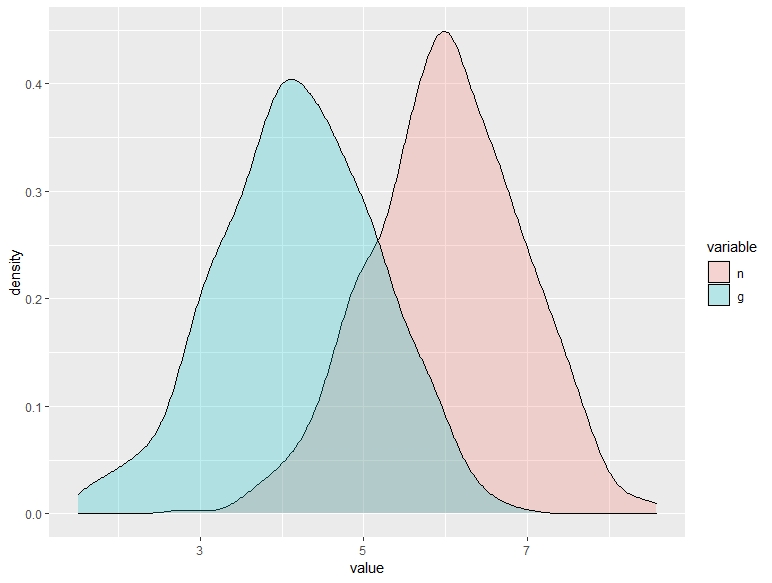
C.
En el vídeo se menciona la paradoja de Yule-Simpson. No es necesario que piense en términos de esa paradoja; es muy común que esto ocurra con las bases de datos con encuestas a individuos: hay mucha heterogeneidad y esta puede afectar a la medición del efecto que está buscando. Para ello, deberá tener en cuenta esto y establecer hipótesis de cuáles pueden ser las fuentes de heterogeneidad. De nuevo, aquí es importante su labor como analista: eso no lo puede pensar una máquina.
- Si le interesa leer más acerca de la paradoja de Simpson-Yule, tiene a su disposición:
- Este hilo de Twitter https://twitter.com/dadosdelaplace/status/1420294893797355526?lang=es
- Esta entrada en un blog https://blogs.elpais.com/alternativas/2017/07/caf%C3%A9-salud-y-la-paradoja-de-simpson.html
- Esta noticia de un periódico: https://elpais.com/ciencia/2021-07-26/infecciones-en-vacunados-de-covid-19-la-utilizacion-sin-contexto-de-datos-estadisticos-conduce-a-conclusiones-falsas.html
EJERCICIO 4
En la base de datos “Paradox”, tiene la relación entre el tamaño del aula y las notas de un conjunto de alumnos para distintos grupos (de estatus socio-económico). Trate de analizar, gráficamente, el impacto del tamaño del aula sobre las calificaciones. Piese sobre lo que ha aprendido.
EJERCICIO ENTREGABLE
Piense sobre lo que ha aprendido hoy para escribir el entregable.
Ejemplo: Pensamos que el estatus social o el tamaño de la ciudad pueden ser una fuente de heterogeneidad muestral importante, puesto que representan a distintas poblaciones estadísticas de estudio. Tras un análisis descriptivo, vemos que podríamos encontrar un efecto relevante del tamaño de la clase si dividimos la muestra entre ciudad grande versus ciudad pequeña y permitimos que el impacto el tamaño sobre el resultado académico esté influido por la clase social. ¿Será mayor la diferencia de pasar a tener 15 alumnos en un aula a tener 30 en una ciudad grande de clase social alta frente a una ciudad pequeña de clase baja?
Finalmente, vea del minuto 10.00 al final. Aquí se remarca lo importante que es dedicar tiempo a analizar los datos, puesto que de este análisis obtendremos las respuestas más importantes a nuestros planteamientos iniciales.
Clase 3 Aspectos relevantes en la modelización estadística (II): la causalidad
IMPORTANTE
Esta clase va asociada a un vídeo. Debe verlo antes de entrar al aula, puesto que se discutirán varios aspectos que en él se mencionan
En general, cuando pretendemos acercarnos a un conjunto de datos con la idea de analizarlos, una vez formulamos la pregunta que tenemos en mente, solemos tener muy claro qué variable queremos predecir y cuáles serán los predictores. De una manera abstracta, tendremos algo así:
\[ (x_{1},x_{2},...,x_{n},u)\mapsto y \]
de tal forma que estamos indicando que un conjutno de inputs \(x_{1},x_{2},...,x_{n}\) y un error aleatorio \(u\) tienen impacto sobre la variable “output” \(y\). Da lo mismo qué función vincule a esas variables, puesto que lo que vamos a contar aquí se puede generalizar a la mayor parte de metodologías que aprenderemos durante el curso.
Vea la introducción, de los minutos 0.00 a 3.00.
EJERCICIO 1
Tenemos una muestra con consumo de vitaminas (suplementos farmacéuticos) y longevidad de individuos. Encontramos una relación creciente entre ambas variables. ¿Estamos en disposición de decir que hay una relación de causa-efecto entre el consumo de vitaminas y la longevidad?
Vea, ahora, de los minutos 3 al 10.34, trabajaremos con las ideas que se nos muestran en los distintos casos que nos cuentan los científicos entrevistados.
EJERCICIO 2
Utilice el set de datos de los Simpson. Retome la pregunta que formuló en la CLASE 1. Utilice gráficos para:
- Analizar sólo el impacto de Homer Simpson sobre la variable que haya decidido y que, desde su punto de vista, mide una relación causal
- Utilizar el hecho de que la audiencia general de las televisiones estadounidenses se desplomó en torno a 2000, por el ascenso de plataformas y canales alternativos.
Asimismo, obtenga estadísticos descriptivos de las variables “us_viewers_in_millions”, “imdb_rating”, “sumH” y juzgue la calidad de la muestra para poder medir los efectos de interés. Explique con claridad las limitaciones.
Ahora, analizamos un ejemplo que guarda similitudes con la idea, presentada en el vídeo, del uso de un modelo para predecir supervivencia a una enfermedad.
EJERCICIO 3
Con la base de datos de ensayos clínicos trate de analizar la probabilidad de muerte por paro cardiaco. Tenga en cuenta que son datos registrados a pacientes ingresados porque satisfacían requisitos previos de riesgo cardiaco:
- Analice el posible efecto de la variable “ejection fraction” sobre la variable “Death Event”. “Ejection fraction” consiste en el porcentaje de sangre que libera el corazón en cada contracción.
- Analice el posible efecto de tener anemia sobre la probabilidad de muerte por ataque cardiaco usando esta información médica “Anemia is common in patients with heart failure, and is a multifactorial and multidimensional problem.There has been increasing appreciation of the significance of anemia in the pathophysiology, treatment, and prognosis of heart failure. Once considered a downstream complication of heart failure, anemia is now emerging as a crucial and potentially modifible factor in the overall treatment strategy for patients with chronic heart failure.”
- Piense, también, sobre este otro factor “Diabetes does not directly cause anemia, but certain complications and conditions associated with diabetes can contribute to it. For example, both diabetes-related kidney disease (nephropathy) and nerve damage (neuropathy) can contribute to the development of anemia. In addition, taking certain oral diabetes drugs can raise the risk of developing anemia. People with diabetes can also have anemia as a result of not eating well or of having a condition that interferes with the absorption of nutrients.”
- Piense sobre las limitaciones de los resultados obtenidos anteriormente. ¿Estamos tratando de medir (i) el efecto causal de un conjunto de características médicas que permitan predecir probabilidad de muerte por infarto a un individuo elegido al azar de la población (ii) un modelo que nos permita discriminar qué pacientes han de ser ingresados en urgencia por riesgo a un ataque al corazón (iii) Un modelo que nos permite analizar probabilidad de supervivencia de pacientes ya ingresados dadas sus características.
Otro ejemplo que se formula en el vídeo tiene que ver con predecir los resultados de un partido.
Los datos de la Liga de Fútbol
Disponemos de datos (football-data.co.uk/spainm.php) de la liga española en la temporada 2019/20. Una pregunta de interés para cualquier analista (para ser usada, por ejemplo, en beneficio personal en apuestas \(\clubsuit\)) tendrá que ver con la capacidad de predecir adecuadamente el resultado de un conjunto de partidos de fútbol. En nuestro caso, pretendemos saber si
Podemos predecir los goles de los equipos (local FTHG y visitante FTAG), utilizando-para ello- el resultado conocido en el primer tiempo del partido
Un primer paso necesario para realizar cualquier análisis
es conocer bien el conjunto de los datos con los que trabajaremos.
Es habitual preguntarse <
El coeficiente de correlación (llamado habitualmente \(\rho\)) mide el grado de relación lineal entre dos variables, donde \(-1\leq\rho\leq1\). Por lo tanto:
- No es cierto que dos variables con correlación baja no están relacionadas (cualquier relación no lineal- por ejemplo, parabólica, logarítmica, etc…- tendrá un coeficiente de correlación bajo)
- No es cierto que dos variables con correlación alta implicará que una tenga un alto poder predictivo sobre la otra (no deberíamos confundir la causalidad con que exista una relación estadística-regularidad empírica- entre variables).
Para ello, indaguemos en la relación entre las variables del fichero de “la liga”.
Una forma inicial para analizar relaciones entre pares de variables (en este caso, los goles frente a las posibles variables predictoras como los tiros a puerta durante el partido) es mediante el análisis gráfico. Por ejemplo, un gráfico de nube de puntos:
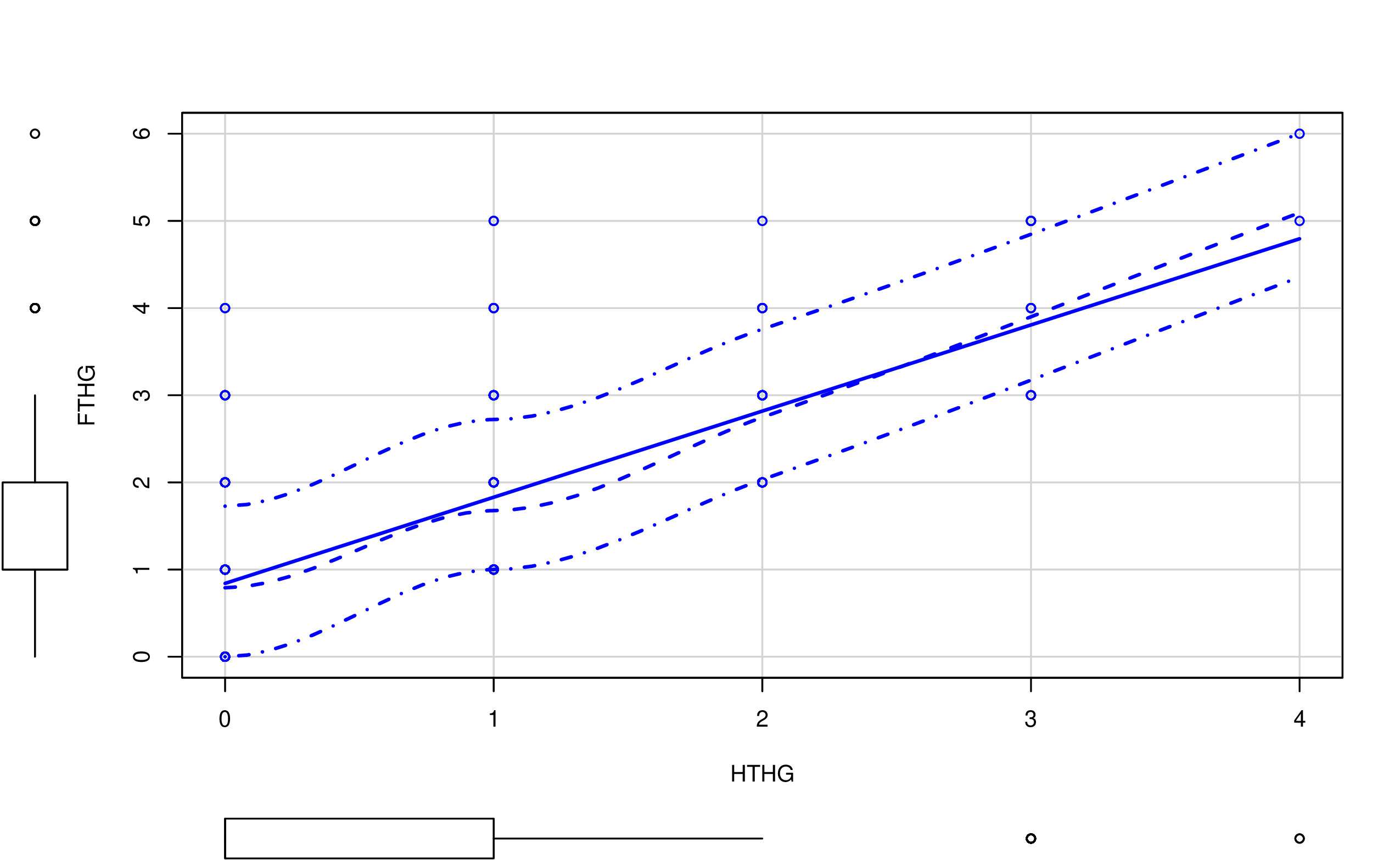
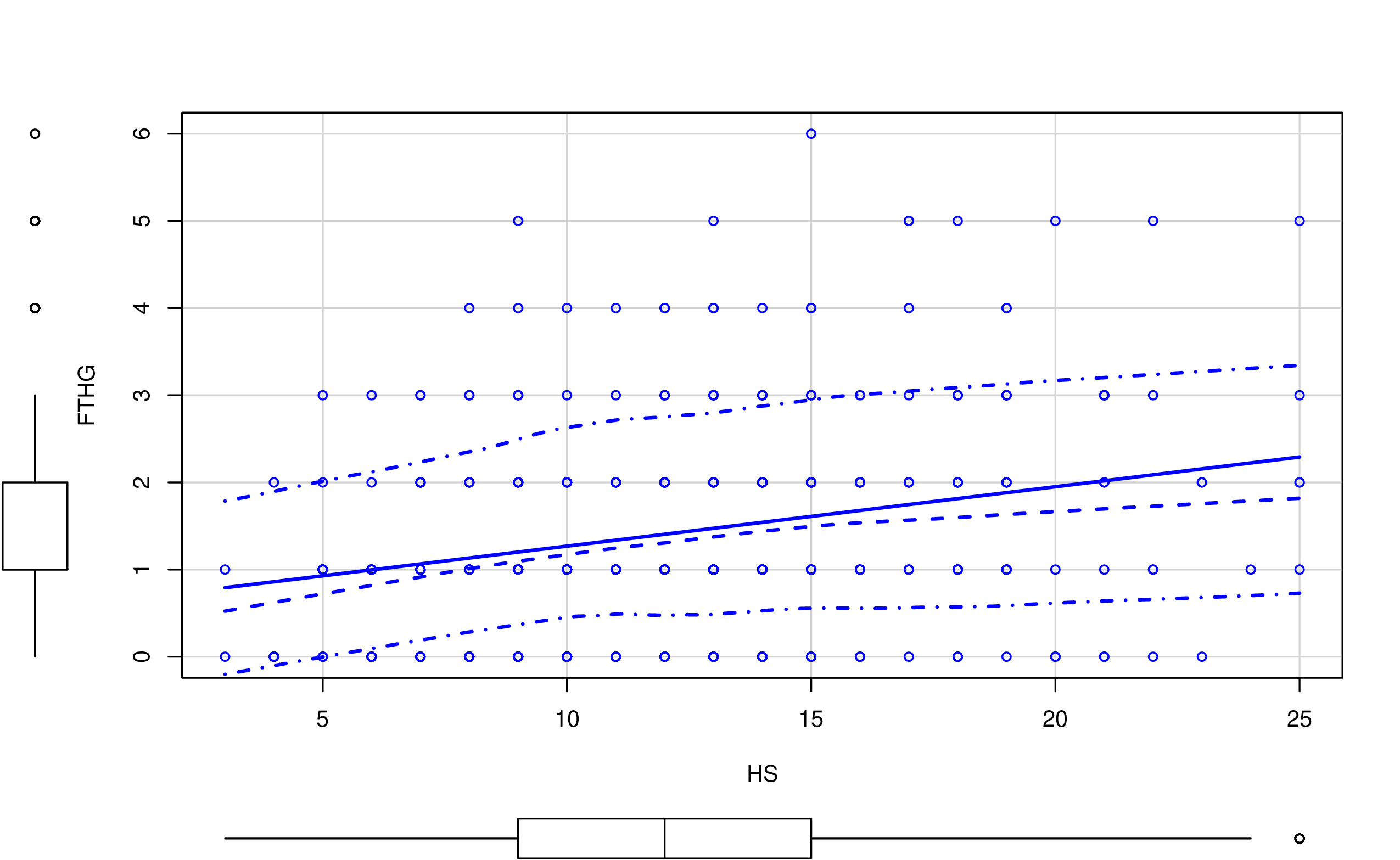
En las FIG1 y FIG2, puedes ver dos tipos de relaciones distintas: por un lado, HTHG y FTHG parecen claramente una relación lineal (y positiva), mientras que HS y FTHG no parecen tener una relación lineal tan clara. De hecho, parece más una relación dónde, para cierto valor de HS, FTHG ya no crece (se satura). Por otro lado, merece la pena destacar:
- Con variables discretas (como puede ser este caso) la nube de puntos está menos justificada. No quiere decir que no se pueda usar (recuerde que en estadística está prohibido prohibir el uso de técnicas)
- Este diagrama de “nube de puntos” añade la distribución univariante de la variable (en forma de diagrama de cajas). Es importante tener también esa información puesto que, antes de entrenar cualquier modelo, uno tiene que conocer perfectamente el tipo de variables que tiene y los valores que cabría encontrarse.
- Por otro lado, tenga cuidado con un gráfico como el de la FIG3. Como ya decimos, podría hacer pasar relaciones importantes (no lineales) entre variables como si estas no existieran.
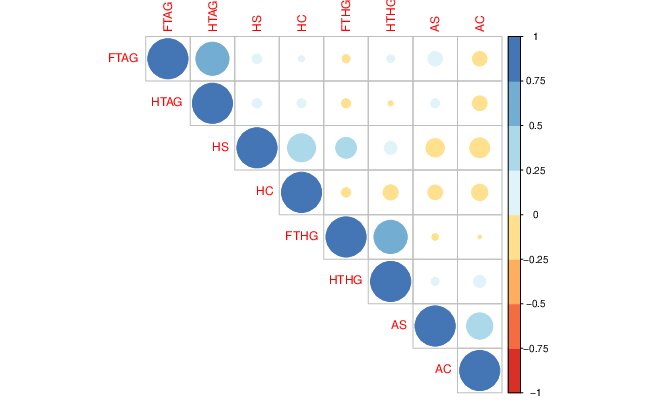
FIG 3. Gráfico de correlaciones.
Este código te permitirá hacer un análisis similar:
LIGA <- read_csv("LaLIGA_FINAL_1920.csv")
install.packages("car")
install.packages("corrplot")
library("car")
library("corrplot")
futbol<-data.frame(LIGA["FTHG"],LIGA["FTAG"],LIGA["HTHG"],LIGA["HTAG"],LIGA["HS"],LIGA["AS"],LIGA["HC"],LIGA["AC"])plot(LIGA["FTHG"],LIGA["HS"])
scatterplot(futbol$HS,futbol$FTHG) # Hace el gráfico de nube de puntos
M<-cor(futbol)
corrplot(M)Sin embargo, podría ser que todo lo que estamos empezando a hacer, a modo de análisis preliminar, no sirva para mucho:
ARGUMENTO 1
Quiere vivir de predecir resultados de fútbol, apostando y, por lo tanto, ganando dinero a expuertas por ello. ¿Usaría estos datos para entrenar un modelo predictivo? Seguro que no tarda un minuto en responder que NO.
No tiene ningún sentido ser capaz de averiguar el resultado de un partido teniendo, como predictores, los resultados a mitad del partido. Las apuestas se cierran antes de que el partido empiece. Además, ¿de verdad necesita un modelo para predecir el resultado de un partido si ya conoces lo que ha ocurrido hasta el descanso?
ARGUMENTO 2
Regularidad empírica versus causalidad: es habitual encontrar variables que tengan una relación lineal (o no lineal) alta, ¿significa eso algo? desafortunadamente, suele indicar que dichas variables ocurren simultaneamente (quizás bajo la influencia de una variable común que afecta a ambas), aunque también podría ser una relación causal.
El riesgo de tratar con “regularidades empíricas” es que, pese a que tengas un modelo con-aparentemente- buenas propiedades, no será muy útil. Piensa, de nuevo, en el caso del fútbol.
La selección de variables es una tarea clave. No consiste en buscar simplemente variables con un aparente grado de relación, sino hay que pensar en la estructura causal. ¿Qué variable(s) ocurre(n) antes en el tiempo? Cuando quiera predecir tendrá la información disponible de las variables predictoras?
De hecho, con el conjunto de variables que tenemos, no podríamos formular ningún modelo predictivo, ya que todas estas conforman datos de estadísticas relativas al encuentro que se suceden, prácticamente, a la vez. En casos como estos, donde hay simultaneidad entre las variables, resulta difícil acceder a buenas variables predictivas. Esto ocurre también en bases de datos de clientes, por ejemplo, donde las variables predictivas suelen ser un subconjunto bastante inferior al conjunto original de variables. Hacer ciencia de datos no consiste en “probar todas” las relaciones aprovechando la capacidad de cálculo del ordenador. Consiste en sentarse antes con las unidades de negocio correspondientes y tratar de entender qué información del cliente se tiene con antelacón para ser capaz de ver cómo predecir sus movimientos.
Un tema muy importante que, quizás, no se le dedica todo el esfuerzo
que se debiera. Seguro que no es la primera vez que se plantea estas
cuestiones. Podemos remontarnos al filósofo David Hume, que decía:
CAUSALITY
we may define a cause to be an object, followed by another, and where all the objects similar to the first are followed by objects similar to the second. Or in other words where, if the first object had not been, the second never had existed. According to Hume, causal events are ontologically reducible to noncausal events, and causal relations are not directly observable, but can be known by means of the experience of constant conjunctions (see A Treatise of Human Nature 1739-40, vol. I, book I, part III, section 2-6, 14, 15)
podemos traducirlo, para entendernos, como sigue:
Si el evento A causa al B (\(A\rightarrow B)\), entonces, A antecede en el tiempo a B y la distribución de probabilidades de B cambia si A entra en acción.
Sin embargo, este tema es bastante peliagudo. En ciencias sociales, donde no se experimenta en laboratorios, no está tan claro qué variables causan a cuáles. Por ejemplo, si quiere analizar el efecto que tiene el ratio alumno/profesor sobre la nota de estos, podría pensar que el ratio causa la nota. Pero ¿Y si los alumnos que sacan buenas notas y, por tanto, pueden elegir van a colegios con menores ratios?
Esto, en general, es un tema complicado. En este curso trataremos de usar la lógica y, siempre que se pueda, hacer asunciones sensatas a este respecto basadas en modelos teóricos previos.
Puede ver el vídeo desde el minuto 10.34 hasta el final. Aquí nos hablan de los premios Nobel de 2021, destinados a quienes pensaron en estos temas y desarrollaron metodologías para tratar de medir relaciones causales en lo que se conoce como “quasi experimentos”. Puede leer esta noticia de prensa donde lo explican muy bien
https://elpais.com/politica/2021/10/14/actualidad/1634222568_419481.html
Clase 4 Aspectos relevantes en la modelización estadística (IV): explorando el modelo de regresión lineal
El objetivo de estas notas es “conceptual”. Apenas si contarán con expresiones matemáticas porque, aquí, relevante es aprender ciertos conceptos relacionados con lo visto en las sesiones anteriores.
Este es un modelo de regresión lineal simple poblacional:
\[ y=\alpha+\beta x+u \]

FIG 1. Idea abstracta del modelo poblacional: los valores de los parámetros y el error sólo los conoce “el Dios de la estadística”.
Tenemos que hacer un ejercicio de “imaginación estadística” para entender el marco conceptual que supone un modelo de regresión como el presentado en la ecuación. De hecho, a esta ecuación, le hemos puesto el nombre “poblacional” por lo siguiente:
- Supone que conoce todos los valores \((y,x)\) de todos los individuos de la población (recuerde que los tamaños de las poblaciones suelen tender a infinito).
- Los parámetros \(\alpha,\beta\) son fijos. ¿Qué significa que sean fijos? Pues que no provienen de una variable aleatoria, sino que son dos valores (dos números)
- Sin embargo, los parámetros \(\alpha,\beta\) son desconocidos. Ese desconocimiento hará que elaboremos un aparato estadístico para tratar de hacer inferencia sobre sus valores.
- La variable \(u\) es el error que se comete, en la población, al relacionar las dos variables \(x\) e \(y\) mediante el modelo lineal. Esta variable no se puede observar en la población (lo errores no van por la calle de paseo) pero, sin embargo, es una variable aleatoria. Esto quiere decir que cada individuo de la población tendrá un error asociado que será una extracción de un posible valor de la distribución de este. En este caso, se asume que esta es normal con media cero y varianza constante:
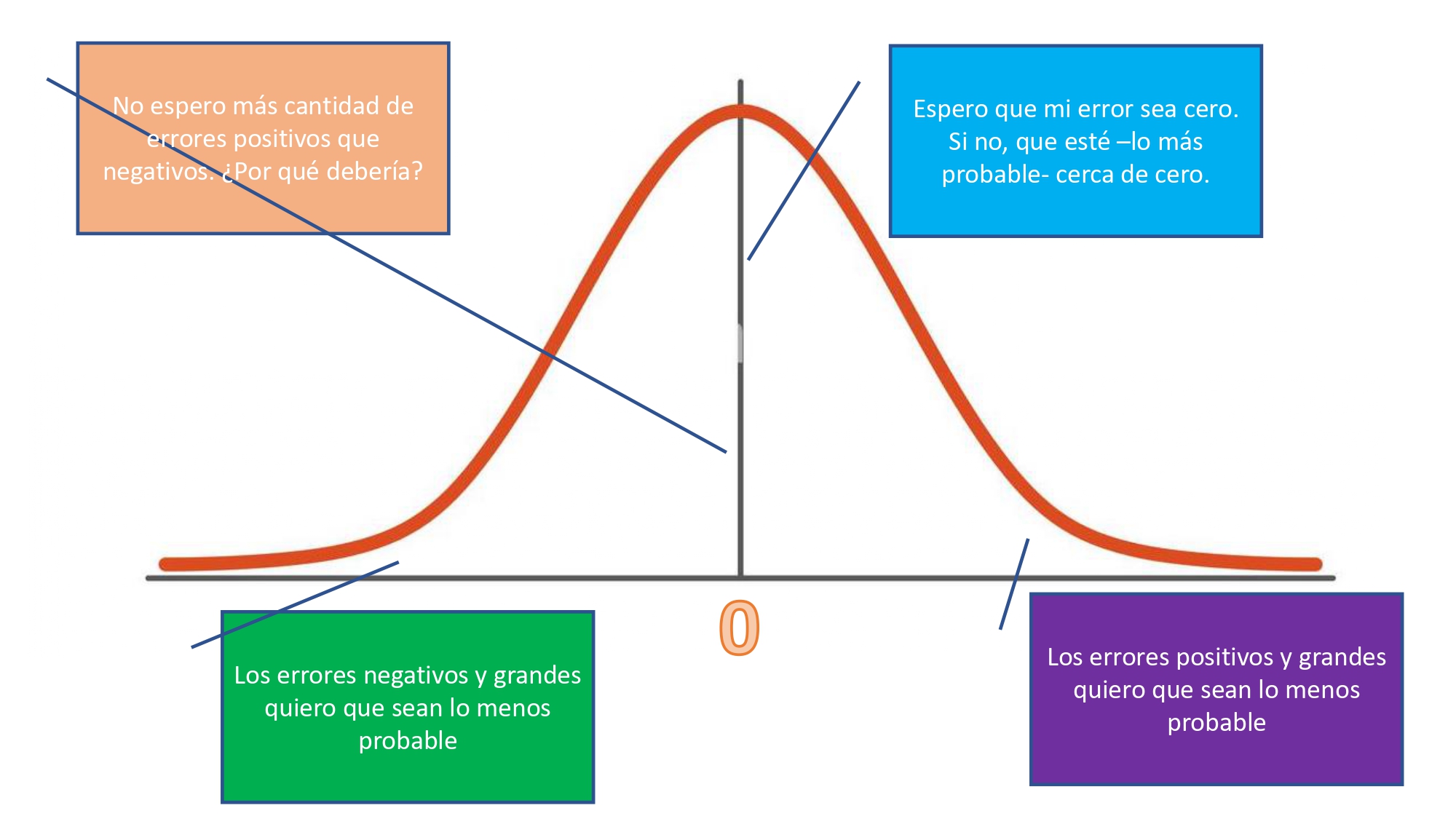
FIG 2. ¿Por qué asumimos que el error se distribuye normal?
es una hipótesis, a la luz de la FIG2, razonable. Decimos que \(E(u)=0\), porque- en promedio- el error esperable es 0. Y, como se explica en la FIG2, la distribución normal parece una propuesta sensata puesto que no cabría pensar en que va a haber un desequilibrio entre errores positivos o negativos (asimetrías): ¿por qué pensar que nos vamos a equivocar más por exceso que por defecto?. Además, la normalidad implica que cuanto más se aleje uno de la media, menos probable es obtener dichos valores inferiores o superiores.
¿Qué hacer ahora para obtener información?
Debemos utilizar la estadística para poder trabajar de forma razonable:
- Estimar los valores de los parámetros con, al menos, una muestra
- Asegurarnos qué propiedades tienen estos estimadores
- Tener la cautela suficiente sobre posibles resultados, su interpretación, y su forma de obtenerlos.
1.Estimación
Para estimar los valores de los parámetros, nos dirigimos a la población, y extraemos una muestra (de tamaño finito, digamos que \(n\)). Como en la FIG3
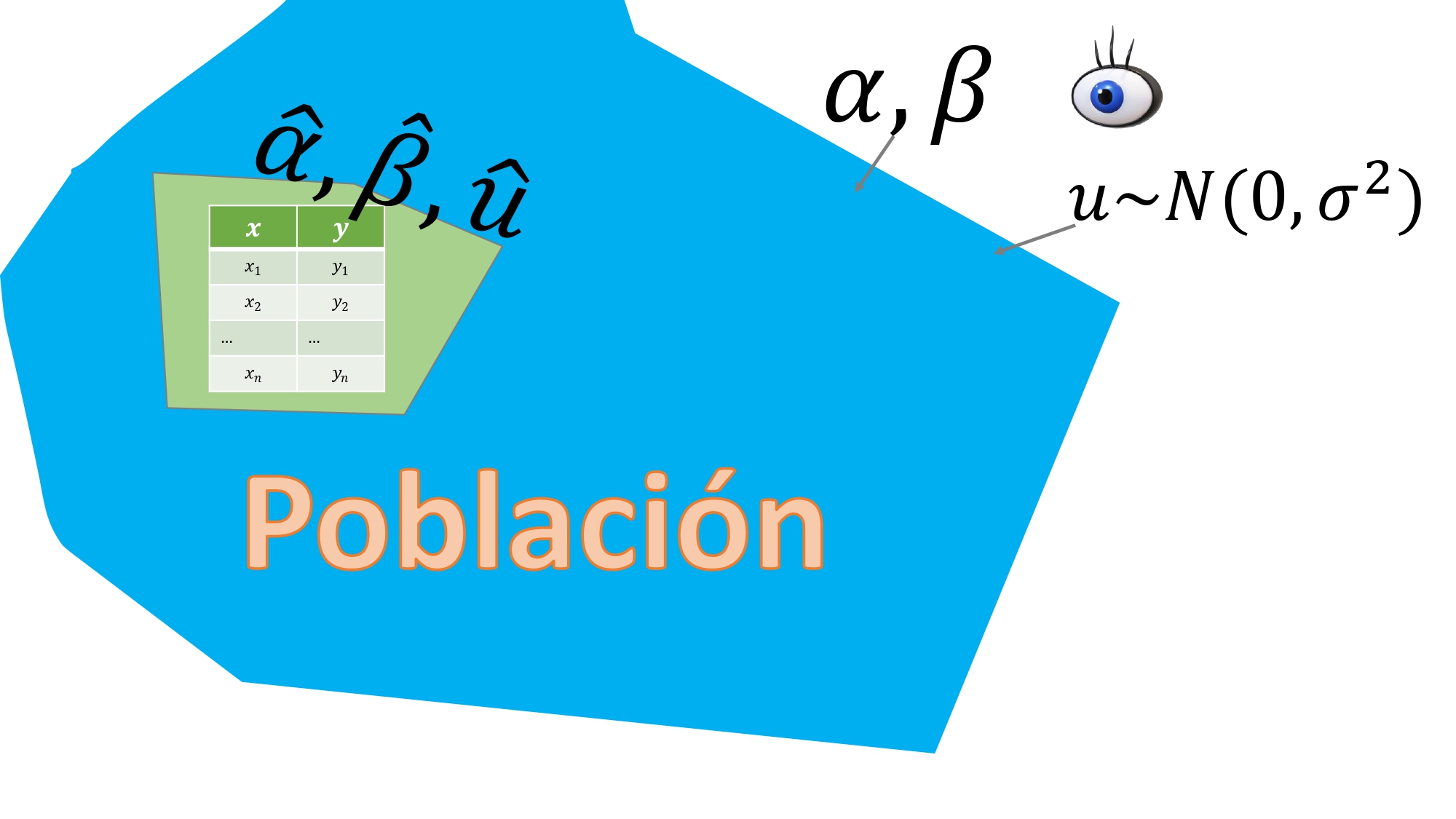
FIG 3. Hacemos un “muestreo” en la población
gracias a esa muestra, podremos obtener la siguiente ecuación:
\[ y_{i}=\hat{\alpha}+\hat{\beta}x_{i}+\hat{u}_{i}\;\;i=1,...,n \]
Ahora, versus el modelo poblacional, observará lo siguiente:
- Dispone de un valor estimado para los parámetros desconocidos \(\alpha\) y de \(\beta\). Por eso, al ser valores “estimados” se les pone el gorrito: \(\hat{\alpha},\hat{\beta}.\)
- Una estimación posible de \(u\): a esto se le llama “residuo” y también va con gorrito \(\hat{u}\), puesto que es el error obtenido con esa muestra.
Sin embargo, esta es “una estimación posible” de otras muchas que podría haber obtenido. ¿Cómo? En la FIG4 se esboza la idea: usted puede acudir a su población y realizar un muestreo aleatorio, de nuevo, bajo las mismas condiciones que hizo el primero y obtendrá otra estimación de parámetros y otros residuos.
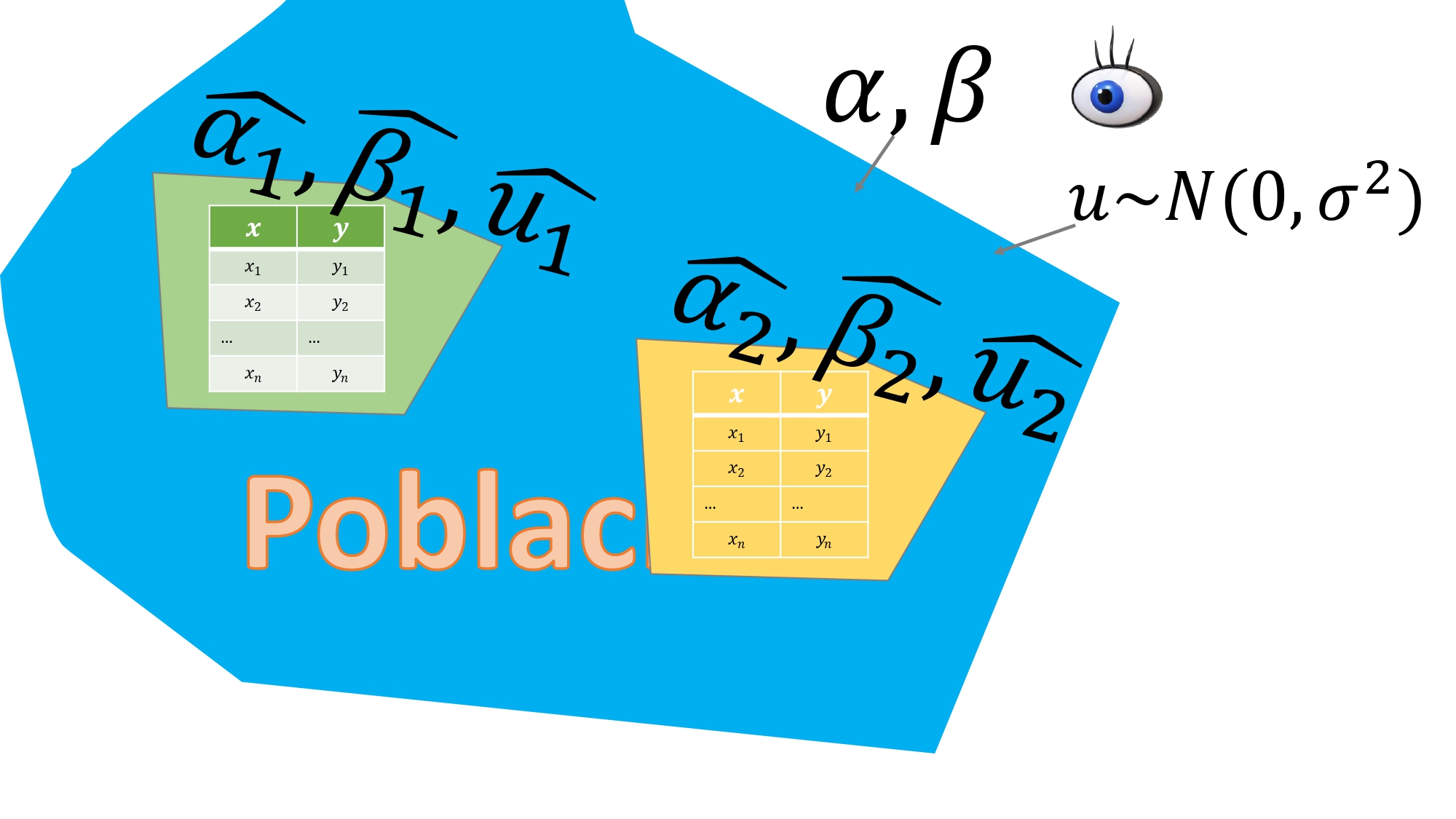
FIG 4. Hacemos dos “muestreos” en la población
De tal forma que si lo hiciera con muchas, muchas muestras, tendría otras tantas estimaciones de los parámetros de interés. Entonces, las estimaciones- al depender de la muestra- diremos que son variables aleatorias. De hecho, se dice que, si el muestreo es aleatorio y la variable \(x\) es exógena ( a continuación desarrollamos mejor esa idea), entonces
PROPIEDAD 1
\[ \hat{\alpha}\sim N\left(\alpha,var(\hat{\alpha})\right) \]
\[ \hat{\beta}\sim N\left(\beta,var(\hat{\beta})\right) \]
Esto quiere decir que “si todo va bien”, los estimadores se distribuirán como una normal cuya esperanza (media) será el verdadero valor desconocido y su varianza, la varianza muestral. ¡ Y eso es una buena noticia! Puesto que ya sabe que su estimación se encontrará dentro de “lo esperado”. Ahora bien ¿qué significa “si todo va bien”? Veamos dos ejemplos antagónicos
Ejemplo 1: estamos en un laboratorio. En este caso, usted puede fijar el valor de \(x\) que desee. Elige bien a los individuos (aleatoriamente, etc…) y observa el valor de la variable \(y\) en cada muestra para cada valor de \(x\). Aquí se dice que:
- \(x\) es determinista o exógena (usted elige los valores para cada individuo)
- \(y\) es aleatoria (depende del individuo)
Si \(x\) es determinista o exógena, entonces la PROPIEDAD 1 se cumple. Esto es equivalente a decir que tenemos estimadores insesgados
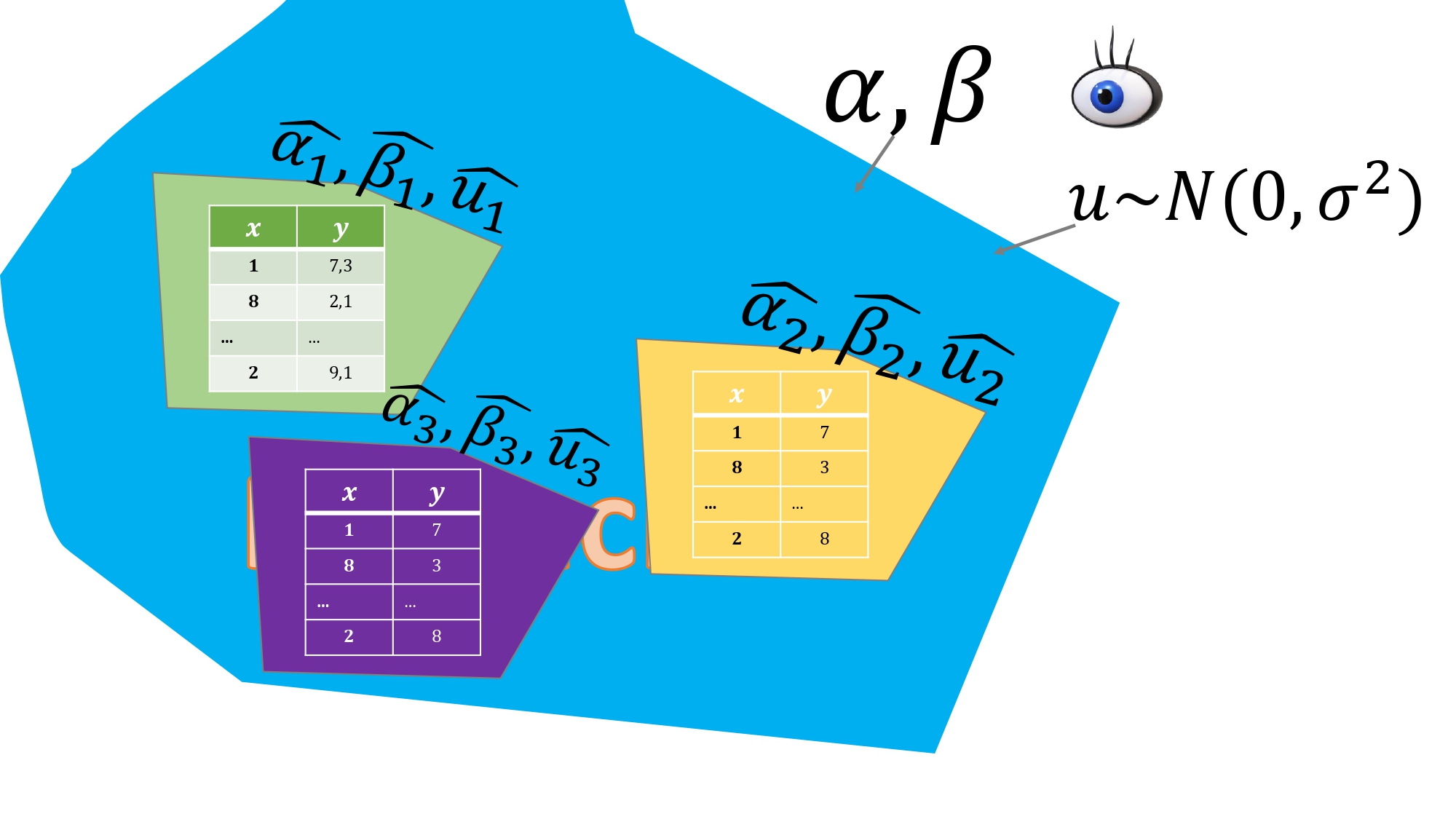
FIG 5. Controlamos el experimento dando los mismos valores a la “x” y viendo cómo responde el individuo midiendo el valor de “y”
IDEA
Esto es de lo que hablan en el vídeo 2 tanto Könrad Kording (U. Pennsylvania) como Yannete Interian (Google) de cuando se pueden hacer experimentos aleatorizados en la población
Ejemplo 2: tomamos datos de encuestas. Imaginemos que podemos hacer tantos muestreos como queramos. Mire aténtamente los datos de la FIG6.
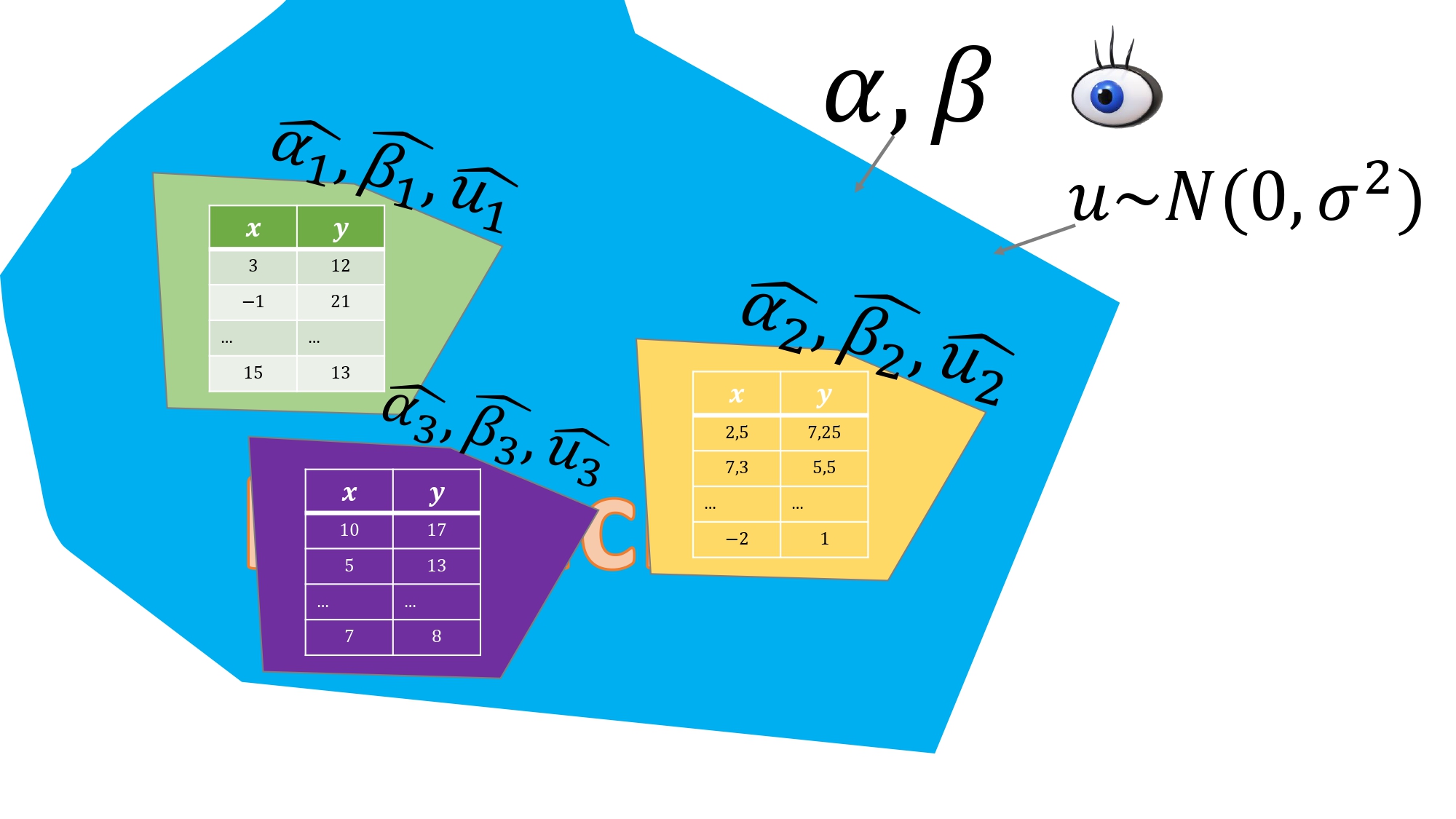 De lejos, se parecen a los del Ejemplo 1. Pero no. Aquí, los individuos
responden a varias cuestiones simultáneamente, esto es, usted no fija el valor de \(x\) y mira cómo se comporta el individuo midiendo su \(y\). Entonces, es normal pensar que
podría haber algún factor difícil de observar que condicione las respuestas a ambas variables (piense en lo que vio en el vídeo 3)
De lejos, se parecen a los del Ejemplo 1. Pero no. Aquí, los individuos
responden a varias cuestiones simultáneamente, esto es, usted no fija el valor de \(x\) y mira cómo se comporta el individuo midiendo su \(y\). Entonces, es normal pensar que
podría haber algún factor difícil de observar que condicione las respuestas a ambas variables (piense en lo que vio en el vídeo 3)
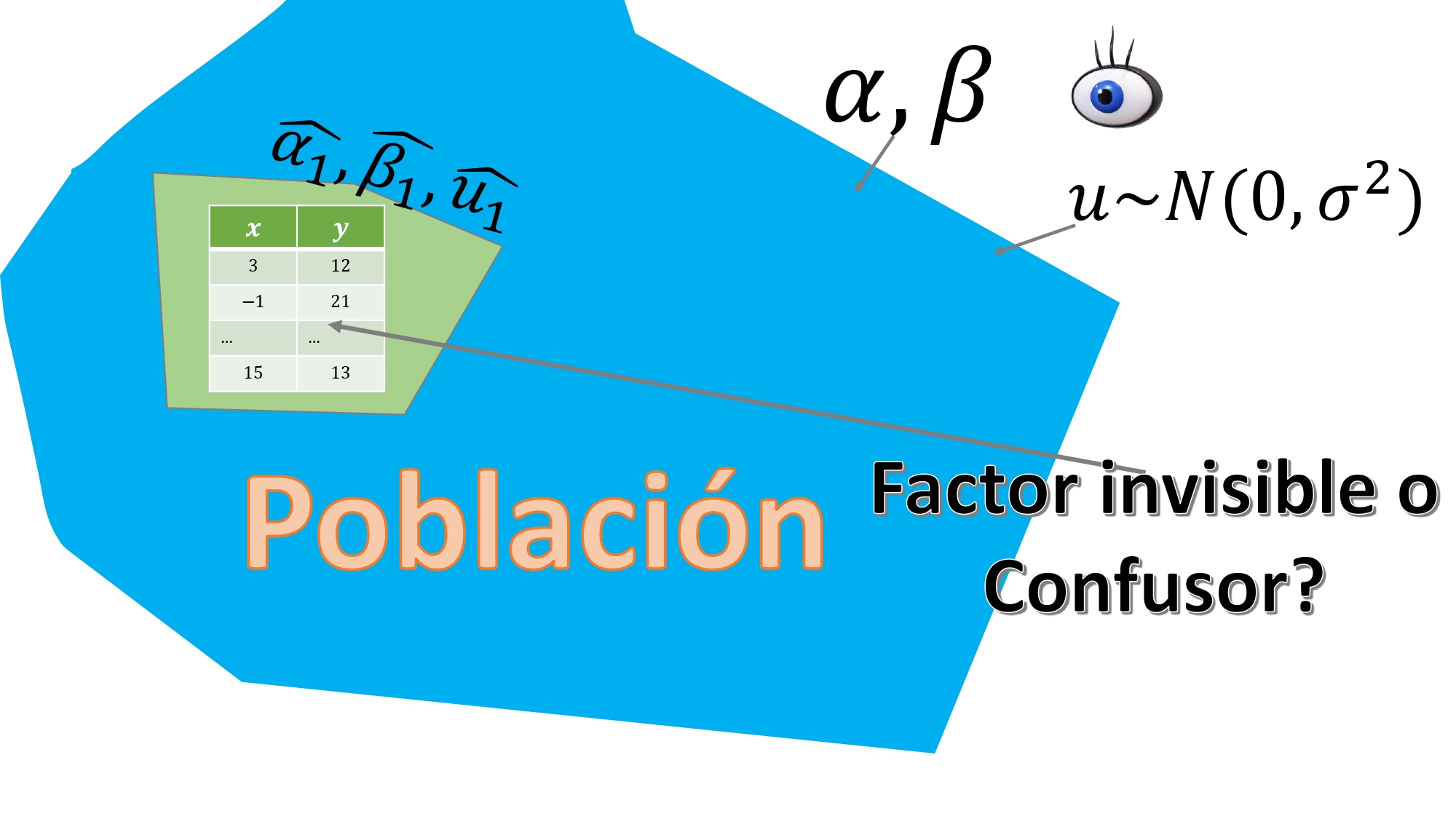
FIG 7. Ahora trabajamos con datos de encuestas
Por ejemplo, en el caso del vídeo 3, la habilidad del individuo podría estar condicionando tanto el valor de la \(x\) (el tamaño del aula) y de la \(y\) (la nota obtenida).
Pero más aún, en este caso, tendremos que asumir que la variable \(x\) también es aleatoria. De hecho, si hiciéramos varias encuestas, en igualdad de condiciones, obtendríamos lo que se ve en la FIG 6: usted no controla ningún factor.
Aquí, entonces, es más difícil que se satisfaga la PROPIEDAD 1, puesto que para que el estimador sea insesgado, no debería haber factores “ocultos” que condicionen las estimaciones. Y este es un tema controvertido:
- En general, sólo dispondremos de una muestra por lo que la PROPIEDAD 1 no debería agobiarnos. En la vida real las muestras son caras y, por tanto, no se pueden hacer-en general-promedios de resultados obtenidos mediante distintos muestreos en igualdad de condiciones.
- Lo primero que deberá pensar, entonces, es en la Ley de los Grandes Números (cuanto mayor sea mi tamaño muestral, más me acercaré al verdadero valor poblacional)
- Pero eso no es cierto en presencia de factores “confusores”.
- Sin embargo, debería tener esto en cuenta para no ser dogmático con su proceso de modelización y realizar análisis más cuidadosos, como los que hemos visto. Use distintas metodologías y compare resultados, puesto que con estos problemas (denominados sesgo e inconsistencia) se convive habitualmente en estadística.
Hay una cita de un conocido estadístico que dice: “todos los modelos están mal, pero algunos sirven para algo”.
EJERCICIO 1
1.¿Qué podría implicar que, a la hora de estimar nuestro modelo de regresión, que la variable \(y\) sea una variable no simétrica?
2.- Si la variable \(y\) toma valores discretos, este modelo es adecuado?
Recuerde, entonces, que si la variable \(y\in\{0,1\}\) podrá entonces estimar un modelo logit-probit. La ecuación de regresión será, entonces,
\[ logit(y_{i})=\frac{1}{1+e^{-\left(\alpha+\beta x_{i}\right)}} \]
EJERCICIO 2
Dibuje la función logit anterior para \(\alpha=0.5\) y \(\beta=1.2\) donde \(x={-5,15}\).
A continuación, realizaremos un conjunto de ejercicios utilizando las bases de datos del curso.
EJERCICIO 3
Tome los datos “Experimentos distribuciones”, que se corresponden con los gráficos del EJERCICIO 2 de la CLASE 2. Tome, por ejemplo, el conjunto **Experimentos_distribuciones_1*. Vamos a estimar, utilizando un modelo de regresión, la diferencia de medias en la muestra. Para ello, deberá construir la variable \(y\), con las observaciones de las dos variables (var1, var2) y, a continuación, una variable dicotómica, \(x\), que tome valor 1 cuando las observaciones se correspondan con alguna de las dos variables. Interprete el coeficiente \(\hat{\beta}\) de dicho modelo.
install.packages("dplyr")
library(dplyr)
library(reshape)
library(readxl)
Experimento1 <- read_excel("Experimentos_distribuciones1.xlsx")
View(Experimento1)
datos1<-data.frame(Experimento1)
y<-melt(datos1)
x<-ifelse(y$variable=="var1",1,0)
summary(lm(y$value~x))
#Ahora mira el resultadoEn próximas clases usaremos de nuevo este resultado
EJERCICIO 4
Utilice los datos de los SIMPSON, para estimar diferentes modelos: \[ Calidad_{i}=\beta_{0}+\beta_{1}Homer_{i}+u_{i} \] \[ Audiencia_{i}=\gamma_{0}+\gamma_{1}Calidad_{i}+\epsilon_{i} \]
A partir de esos modelos generales, diseñe cómo estimar los modelos donde se recoja la heterogeneidad muestral que se observó en la CLASE 3.
En próximas clases usaremos de nuevo este resultado
EJERCICIO 5
Utilice los datos de HEART FAILURE para estimar un modelo de regresión lineal: \[ DEATH_{i}=\beta_{0}+\beta_{1}ejectionfraction_{i}+u_{i} \] y un modelo logit tal que \[ logit(DEATH_{i})=\frac{1}{1+e^{-(\alpha_{0}+\alpha_{1}ejection_{i})}} \] trate de explicar lo que quieren decir los coeficientes estimados y trate de obtener gráficos que predigan la probabilidad de muerte del individuo para valores de “ejection fraction” de 0 a 100. Analice, además, si la elección del rango de valores de “ejection fraction” resulta adecuada dada la muestra disponible.
En próximas clases usaremos de nuevo este resultado
EJERCICIO 6
¿Y si la variable que quiere predecir está compuesta por varias categorías?
- Si son ordinales?
- Si son nominales?
Clase 5 Aspectos relevantes en la modelización estadística (V): el p valor
IMPORTANTE
Esta clase va asociada a un vídeo. Debe verlo antes de entrar al aula, puesto que se discutirán varios aspectos que en él se mencionan
Como ya sabrá, muchos métodos de estimación parmétrica suelen proporcionar, asociado a un conjunto de hipótesis nulas de interés, un p-valor. ¿Recuerda qué es exactamente un p-valor?
Vea la introducción (minutos 0.00 al 2.39) de este vídeo
ahora, piense sobre este ejercicio:
EJERCICIO 1
Utilice los datos de “datos distribuciones tratamiento” para discutir si el tratamiento tiene efecto en la población o no, mediante contrastes de hipótesis.
- Trate de especificar la hipótesis nula y la alternativa (la nula, en general, es que el tratamiento no tiene efecto en la población)
- Use los gráficos de la CLASE 2, así como los resultados de la CLASE 4 para tratar de responder a la pregunta
Quizás sea un buen momento para que continúe viendo el vídeo. Concretamente, de los minutos 2.39 a 9.22 ¿Cómo se puede “manipular” un p-valor?
Antes, trabajemos sobre algunas ideas básicas:
Repaso de la inferencia paramétrica básica
Primero, recuerde del ejercicio 3 de la clase anterior. Del modelo de regresión, usted -haciendo uso de un enfoque particular de los contrastes de hipótesis- podrá decir:
Residuals:
Min 1Q Median 3Q Max
-5.4857 -1.0056 -0.0174 1.0361 5.7139
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.87875 0.02417 243.232 < 2e-16 ***
x 0.12280 0.03418 3.593 0.000329 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.529 on 7998 degrees of freedom
Multiple R-squared: 0.001611, Adjusted R-squared: 0.001486
F-statistic: 12.91 on 1 and 7998 DF, p-value: 0.0003294
- El parámetro asociado a la variable \(x\), que recordemos que es una variable binaria que significa que el individuo ha sido tratado, es significativo
- Eso lo sabe porque en el p-valor asociado tiene este valor y la grafía con tres asteriscos (0.000329 ***)
- Sin embargo, ya habíamos visto que no parece que el tratamiento haya tenido efecto. Mire, para recordarlo, los histogramas de ambas variables (no tratamiento/sí tratamiento) cómo se solapan.
¿Qué puede estar pasando aquí? Para entenderlo, vamos a razonar sobre cómo se llega a dicho p-valor.
El error estándar El error estándar, o desviación típica del estimador, es una medida de la precisión con la que usted estima el efecto. Dado lo que sabemos de regresión, si tiene
\[ \hat{\beta}\sim N\left(\beta,0.034)\right) \]
\[ \hat{\beta}\sim N\left(\beta,280)\right) \]
usted preferirá, claramente, la primera opción, porque la distribución estará más concentrada. Eso es una idea de medir algo con precisión. Veremos, sin embargo, que mucha precisión también puede ser perjudicial (y que, en BIG DATA, es lo normal).
Resulta que esta es la expresión del error estándar (o desviación típica del estimador) para un modelo simple (la del múltiple es similar, pero tiene alguna sutileza)
\(dt\left(\hat{\beta}\right)=\sqrt{\frac{\hat{\sigma}^{2}}{n\times var(x)}}\)
Entonces, ¿qué influye en la precisión?
- Que \(\hat{\sigma}^{2}\) sea pequeña (es decir, la varianza del error del modelo sea lo menor posible)
- Que \(n\) sea grande (como hemos dicho, con muestras grandes, más precisión)
- Que \(var(x)\) sea grande (lo que ya hablamos en la segunda clase: cuando más varíe la variable explicativa, mayor precisión tendremos capturando su efecto sobre la variable dependiente).
El t value
Como veremos, este valor consiste en la división entre el coeficiente estimado y el error estándar ( \(0.12280/0.03418=3.593\)): ahora veremos de dónde sale.
El p-valor
Repasemos, a continuación, de dónde viene:
Recuerde que, en un modelo de regresión, el test de hipótesis general para un sólo parámetro se especifica como \[ H_{0}:\beta=\beta^{*} \]
\[ H_{1}:\beta\neq\beta^{*} \]
(observe que las hipótesis se realizan siempre sobre parámetros poblacionales) se resuelve utilizando este ratio:
\[ T=\frac{\hat{\beta}-\beta^{*}}{dt\left(\hat{\beta}\right)} \]
el cual, si se cumplen las hipótesis básicas del modelo de regresión que vimos en la CLASE 4, entonces se distribuye
\[ \frac{\hat{\beta}-\beta^{*}}{dt\left(\hat{\beta}\right)}\sim t_{\alpha/2,n-2} \]
esto es, como una t de student, donde \(\alpha\) es el nivel de significación del contraste y \(n\) es el tamaño muestral. Si la muestra es grande (más de 100 elementos), entonces podemos aproximar el resultado utilizando la normal (mediante el TCL, que veremos más adelante en el curso). \[ \frac{\hat{\beta}-\beta^{*}}{dt\left(\hat{\beta}\right)}\sim z_{\alpha/2}, \]
donde \(z\) es el valor crítico de la normal (0,1). Por ejemplo, en el caso que nos ocupa, queremos contrastar
\[ H_{0}:\beta=0 \]
\[ H_{1}:\beta\neq0 \]
utilizando la información anterior, \[ T=\frac{0.1228-0}{0.03418}=3.593 \]
que, como ve, es el valor que aparece en la pantalla de R en el lugar de t-value. Este valor lo tiene que comparar con el punto crítico de la distribución (al nivel de significación elegido que, para seguir la tradición, elegiremos 5%) y que, en este caso, resulta ser -1.96,1.96.
FIG1.
y se dice:
“al 5% de significación, rechazamos la nula de que el parámetro es cero en la población’’.
Esto es equivalente a decir: “al 5% de significación, las medias poblacionales son distintas’’.
Que, en el fondo, es lo mismo que decir que “el tratamiento tiene efecto en la población”.
Como ya sabrá, la elección del 5% de significación es arbitraria y uno podría preguntarse a qué niveles de significación rechazaría y a cuáles no, la hipótesis nula. Para eso, se puede utilizar el p-valor. ¿Qué es el p-valor? Habrá visto en el vídeo varias cosas:
- Tiene una definción rigurosa, que no es fácil explicar con palabras llanas: es la probabilidad de encontrar una muestra con las mismas características que la que tengo pero que, asumiendo cierta la hipótesis nula, obtenga un resultado más extremo al que he obtenido. En nuestro caso \[ P\left(\hat{\beta}<-0.1228|\beta=0\right)\cup P\left(\hat{\beta}>0.1228|\beta=0\right) \] dese cuenta de que estamos trabajando con una hipótesis alternativa bilateral, por lo que tenemos que mirar las dos colas de la distribución.
FIG2.
- ¿ Cómo calculo esta probabilidad? Sabemos que \[ \frac{\hat{\beta}-\beta^{*}}{dt\left(\hat{\beta}\right)}\sim z_{\alpha/2} \] e imponemos que \(\beta^{*}=0\), entonces, dada la simetría de la distribución, calculo una de ellas y luego la multiplico por 2: \[ P\left(\frac{\hat{\beta}-0}{dt\left(\hat{\beta}\right)}>\frac{0.1228-0}{0.03418}\right)=P\left(N(0,1)>3.593\right)=0.000165 \] Por lo que el p-valor de este contraste será:
\[ p-valor=2\times0.000165=0.00329 \] puedes verificar que es el mismo resultado que tenemos en la tabla de R.
- Se suele comparar este resultado (el p-valor) con los niveles de significación (generalmente, sin tener muy claro por qué, el 5%) y se decide si se rechaza o no la hipótesis.
EJERCICIO 2
Dado este p-valor, ¿qué concluiría sobre el efecto que tiene el tratamiento en la población?
Ahora bien, tratemos de entender, de nuevo, todo lo que ha aprendido por ahora. Responda a estas preguntas:
- En el caso del primer ejemplo ¿qué vio en los gráficos? Se ve claramente que: las dos distribuciones son prácticamente iguales ¿Es creíble, entonces, decir que el tratamiento tiene un efecto significativo? uhm, no lo parece
- Sin embargo ¿qué concluye con el contraste? Que sí, a cualquier nivel de significación. Se dice, muchas veces que “el efecto es muy significativo”.
Desmontando el p-valor
Como ha visto en el vídeo, la comunidad científica no se siente muy cómoda utilizando el p-valor tan a la ligera. Y usted acaba de verlo en este ejemplo: obtenemos un resultado algo antiintuitivo, dada la evidencia gráfica. ¿Qué está pasando? Para entenderlo, destripemos la definición de p-valor. Asumiendo una muestra grande (da lo mismo si es pequeña, pero de manera cómoda emplearemos la distribución normal en lo que sigue: sustitúyala por la t sin ninguna pérdida de generalidad), tenemos que:
\[ p-valor=P\left(N(0,1)>\frac{\hat{\beta}}{dt(\hat{\beta})}\right) \]
Recuerde, ahora sí, cómo se obtiene \(dt\left(\hat{\beta}\right)=\sqrt{\frac{\hat{\sigma}^{2}}{n\times var(x)}}\), es decir,
\[ p-valor=P\left(N(0,1)>\frac{\hat{\beta}}{\sqrt{\frac{\hat{\sigma}^{2}}{n\times var(x)}}}\right) \]
Como ya sabe, para que el p-valor sea pequeño (y rechazamos la nula), necesitamos que (en valor absoluto) \(\frac{\hat{\beta}}{\sqrt{\frac{\hat{\sigma}^{2}}{n\times var(x)}}}\) sea un número grande. ¿Cómo lo conseguimos?
- Si \(\hat{\beta}\) es “grande”
- \(\sqrt{\frac{\hat{\sigma}^{2}}{n\times var(x)}}\) es “pequeño”.
El primer caso es sencillo: cuanto mayor sea el impacto que recoja \(\hat{\beta}\) a través de la relación de \(x\) con \(y\), más pequeño será el p-valor. Este caso nos interesa, porque nos está diciendo que “el tamaño del efecto’’ es grande: y eso es lo que estamos buscando para rechazar la hipótesis nula.
El segundo caso tiene más derivadas. Para empezar \(dt\left(\hat{\beta}\right)=\sqrt{\frac{\hat{\sigma}^{2}}{n\times var(x)}}\) podemos considerarlo como una medida de la “incertidumbre/imprecisión” con la que somos capaces de estimar el parámetro. Al final, es lo que mide una desviación típica: cuánta incertidumbre tienes. Cuanto más pequeña sea esta, menos incertidumbre tendrá y, por tanto, con mayor precisión medirá el efecto. Sin embargo, el “exceso” de precisión, puede llevarnos a que rechacemos cualquier nula que queramos. Por un lado, si \(\hat{\sigma}^{2}\) es pequeño, entonces \(\sqrt{\frac{\hat{\sigma}^{2}}{n\times var(x)}}\) será pequeña. ¿Qué implica? Simplemente que hay poco “error” en el modelo, esto es, los puntos están poco dispersos en la nube y, por tanto, estamos capturando la relación de manera muy precisa. Si \(n\) es grande, de igual manera, \(\sqrt{\frac{\hat{\sigma}^{2}}{n\times var(x)}}\) será pequeña. Esto es, con muestras grandes todo lo grandes que podamos (y homogéneas) entonces podemos conseguir un p-valor casi tan pequeño como queramos. Si \(var(x)\) es grande, de nuevo \(\sqrt{\frac{\hat{\sigma}^{2}}{n\times var(x)}}\) será pequeño. ¿Se acuerda de la idea “tan extraña” que vio en la CLASE 2? Aquí se ve de nuevo: cuanto más varíe la \(x\), más precisos seremos capturando su efecto sobre la \(y.\) Claro, “al variar mucho la \(x\), aprendemos más de su relación con la \(y"\).
Esto es importante:
IDEA
El uso mecánico del p-valor, como mecanismo “científico” para tomar decisiones estadísticas basadas en modelos, afortunadamente, está generando mucha controversia entre los científicos de datos más relevantes. Las revistas “Nature” y “Science” llevan años publicando artículos de gran impacto llamando la atención sobre este hecho. Vamos a explicar en qué consiste esta crítica en el contexto de un modelo de regresión para, a continuación, discutir sobre ello.
EJERCICIO 4
- Piense qué podría ocasionar baja precisión en la estimación y qué ocurriría con el p-valor en ese caso.
- Observe cómo en el caso del tratamiento A, tiene un problema con el tamaño de la muestra. Elija, de manera aleatoria, una submuestra de menor tamaño (por ejemplo, 100 datos) ¿quó observa? ¿y si elige una muestra de 50 datos? Haga un gráfico con el p-valor asociado a la nula que se ha contrastado durante toda la clase para diferentes tamaños muestrales.
- Haga lo mismo con el tratamiento B. Discuta lo que ha obtenido frente al gráfico que observó en la CLASE 2.
#Puede adptar este script
S <- c(50,75,100,200,500,1000,2000,4000) #selecciona distintos valores muestrales
p_value<-vector()
effect<-vector()
for (i in (1:8)) {
datos_inter<-datos1[sample(nrow(datos1), S[i]),] #selecciona una muestra la azar
y<-melt(datos_inter)
x<-ifelse(y$variable=="var1",1,0)
mod<-summary(lm(y$value~x)) #estima el modelo de nuevo
effect[i]<-mod$coefficient[2,1] #almacena la información
p_value[i]<-mod$coefficients[2,4]
}
plot(S,p_value)
plot(S,effect)Este mecanismo que parece “bastante científico” está siendo muy criticado. Y veremos que con razón.
FIG 2: Sobre el p-valor y los mecanismos de contraste estándar.
FIG 3: Evite mirar a la columna del p-valor y piense más en el conjunto: efecto estimado versus precisión.
FIG 4: Piense en los intervalos de confianza.
FIG 5: En definitiva: evite el exceso de automatización en la toma de decisiones.
De hecho, en 2016, la ASA (American Statistical Association: https://www.amstat.org/) presentó los “seis principios” sobre el p valor y la inferencia estadística:
- Los p valores “pueden” indicar cómo de incompatibles son los datos con un modelo estadístico especificado es decir, podría ser que un p valor grande simplemente esté advirtiendo de que el modelo elegido no es adecuado, esto es, no es compatible con nuestros datos.
- Los p valores no miden la probabilidad de que la hipótesis nula sea cierta o de que los resultados del efecto estimado sean fruto de la aleatoriedad No olvidemos que el p -valor asume que la hipótesis nula es cierta, por lo que no puede calcular la probabilidad de dicha hipótesis.
- Conclusiones científicas o de negocios no deberían estar basadas en un p-valor La expansión, nada sensata, de la regla \(P\leq 0.05\) que dictamina si una variable tiene efecto sobre otra (o es significativa) de manera dicotómica, sin tener en cuenta posibles contextos y resultados de los efectos puede ser pernicioso y contraproducente.
- Inferencia adecuada requiere un análisis pormenorizado y transparente Hay muchas técnicas para hacer “p hacking”. Si sólo se presentan los resultados donde el p-valor apoya una conclusión, se está ocultando el verdadero mecanismo de la toma de decisiones
- Un p valor no mide la importancia del efecto que se está buscando analizar La significatividad estadística no es equivalente a la significatividad científica, humana o económica. p-valores pequeños no implican, necesariamente, efectos relevantes. De hecho, efectos similares pueden tener distintos p valores atendiendo a la precisión con la que estos se estiman.
- Un p valor no proporciona evidencia a favor de una hipótesis sobre un modelo un p valor grande, no implica evidencia a favor de una hipótesis nula. Podría haber multitud más de hipótesis que no se rechazarían.
Aquí tiene la fuente original de este resumen: https://amstat.tandfonline.com/doi/full/10.1080/00031305.2016.1154108#.YUiYN2YzaH0
Puede ver, de manera opcional, este vídeo donde la ASA nos explica su declaración sobre el p-valor
CLASE 6: Aspectos relevantes en la modelización estadística (VI): propuestas ante el p-valor.
IMPORTANTE
Esta clase va asociada a un vídeo. Debe verlo antes de entrar al aula, puesto que se discutirán varios aspectos que en él se mencionan
¿Cómo deberíamos trabajar, entonces?. Aquí vienen algunas propuestas que tratan de ser sencillas y sensatas ante lo complicado que es pronunciarse a la hora de trabajar con datos.
Vea la introducción del vídeo (minutos 0.00 a 1.50) y reflexione sobre la manera de trabajar e interactuar habitual con modelos de regresión.
Para entender lo que viene a continuación, será deseable ver los minutos 1.56 a 7.50 donde se discute lo que vamos a ver aquí con otro ejemplo.
Supongamos que estima un modelo, en este caso, con la base de datos de los Simpson. Por ejemplo, analicemos mediante una regresión la nota en IMBD de los episodios, dada la importancia de Homer Simpson,
library(readxl)
SIMPSON <- read_excel("datos_SIMPSON.xlsx")
View(SIMPSON)
mod1<-lm(imdb_rating~sumH, data=SIMPSON)
#y obtenemos
Call:
lm(formula = imdb_rating ~ sumH, data = SIMPSON)
Residuals:
Min 1Q Median 3Q Max
-2.8421 -0.4976 -0.1332 0.5501 1.8178
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.2330425 0.0650102 111.260 < 2e-16 ***
sumH 0.0003840 0.0001194 3.217 0.00137 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.7236 on 566 degrees of freedom
Multiple R-squared: 0.01795, Adjusted R-squared: 0.01622
F-statistic: 10.35 on 1 and 566 DF, p-value: 0.001371
Residual standard error: 384.5 on 566 degrees of freedom
Multiple R-squared: 0.01788, Adjusted R-squared: 0.01614
F-statistic: 10.3 on 1 and 566 DF, p-value: 0.001403Obtenemos, por tanto, que el coeficiente, de acuerdo con el p-valor, será significativamente distinto de cero al 5%. Sin embargo, recordemos que este resultado, que depende del t-estadístico, se puede obtener de dos maneras:
- Debido a que el coeficiente estimado sea “grande”
- Debido a que se estima con suficiente precisión (error estándar bajo)
Nos interesará, en todo caso, si rechazamos la nula, asegurarnos de que el efecto que supone Homer Simpson sobre la calidad de los episodios sea remarcable.
Del modelo tenemos que por cada línea de guión adicional, Homer contribuye con 0.0003849 puntos adicionales al episodio. Recuerde que, para ver si eso es “mucho o poco” debe analizar si aumentar una línea de guión es “mucho o poco”. Para ello, una manera de hacerlo es obteniendo una desviación típica de la variable que representan las líneas de guión de Homer. De esta forma, está obteniendo una variación promedio de la propia variable:
sd(SIMPSON$sumH)
[1] 254.5754Es decir, las variaciones promedio, entre epiosdios, de Homer son de 255 líneas, aproximadamente. Por tanto, cabe esperar que un cambio “típico” en el personaje, reporte en la nota:
\[ efecto=0.0003840\times 255=0.097 \]
puntos. Lo cual, no representa apenas una décima de nota. No parece que el efecto sea relevante, pese a que ha salido que es “estadísticamente significativo”.
Ejercicio 1
Piense un par de medidas relativas del efecto de Homer, de la misma manera que se hace en el vídeo con el efecto del tamaño del aula sobre la nota.
respuesta Podemos centrarnos, por ejemplo, en la predicción que hace el modelo para distintos casos. Pensemos, primeramente, en la distirbución de Homer. Veamos qué significa un episodio “normal”, un episodio en el que sale “poco” y un episodio en el que sale “mucho”.
ggplot(SIMPSON, aes(x=sumH)) + geom_histogram()+
geom_vline(xintercept = median(SIMPSON$sumH), colour="green", linetype = "longdash")+
geom_vline(xintercept = quantile(SIMPSON$sumH)[2], colour="green", linetype = "longdash")+
geom_vline(xintercept = quantile(SIMPSON$sumH)[4], colour="green", linetype = "longdash")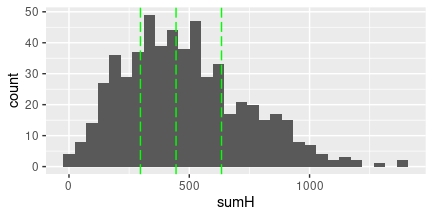
FIG 1: Esta es la distribución de las líneas de guión de Homer con su primer, segundo y tercer cuartiles.
quantile(SIMPSON$sumH)
0% 25% 50% 75% 100%
0 297 445 634 1387 De hecho, podríamos decir que un episodio “normal” de Homer es que tenga 445 líneas de guión, un episodio en el que sale “poco” podría estar en torno a 297 líneas y un episodio en el que sea “protagonista” alcanzará las 634 líneas. Según el modelo, si Homer no sale en un episodio, la nota que predice la calidad del episodio es 7.23 puntos (la constante del modelo). Vamos a predecir la nota para estos tres casos
new <- data.frame(sumH = c(297, 445, 634))
predict(mod1, newdata = new)
1 2 3
7.347076 7.403901 7.476468 Esto es lo que incrementa la calidad nuestro personaje, en promedio. Si no sale, el modelo predice que el episodio obtendrá 7.23 puntos y, en cambio, si sale mucho… ¡7.47 puntos! ¿está dispuesto a creer que 0.24 puntos es mucho? ¿Es eso “muy significativo”? Esto le debería hacer sospechar que, por muy pequeño que sea el p-valor asociado al protagonsita, no parece que el efecto que hemos medido sea de especial relevancia: lo que usted está midiendo es, en realidad, un exceso de precisión debido a la cantidad muestral.
Ahora bien, ¿qué hacer cuando tenemos poca precisión?
Vea del minuto 7.50 al minuto 10.00 donde se habla de la función p-valor.
Piense
Piense cómo haría, utilizando R, para generar una función p-valor. ¿Qué datos necesita de entrada? ¿Cómo tiene que ser la salida?
Por ejemplo, suponga que tiene que analizar el impacto del precio sobre las ventas de un producto. Recuerde que, si ambas variables están en logaritmos, entonces la interpretación del coeficiente es directamente la elasticidad (si incremento un 1% el precio, las ventas caen un 0.97%, en el CASO 1)
CASO 1
\[ ln(ventas)=5.32-0.97ln(precio)+\hat{u} \]
con error estándar asociado al parámetro de interés es \(0.65\)
CASO 2
\[ ln(ventas)=5.32-0.37ln(precio)+\hat{u} \]
con el error estándar asociado al parámetro de interés de \(0.08\),
Si quiere tener la función p-valor, puede ejecutar el siguiente script
alt<-c(-3, -2.75,-2,-1.5, -1, -0.5,0,0.5,1, 1.5)
beta_est<--0.97
desv_beta<-0.65
p_value<-vector()
for (i in 1:length(alt)){
t_test<-(beta_est-alt[i])/desv_beta
p_value[i]<-2*(pnorm(-abs(t_test)))
}
plot(alt,p_value,type = "S")EJERCICIO 3
Asegúrese de que entiende todas las líneas del script.
Entonces, de acuerdo con la FIG 1, tendrá la función p-valor:
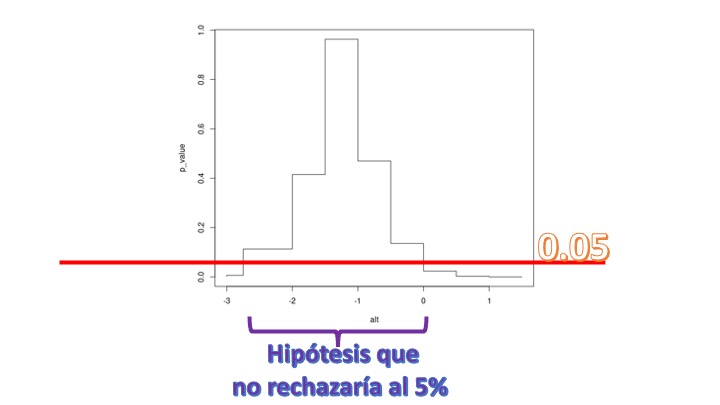 de tal forma que en el eje \(y\), tenemos los distintos p-valores del cada constraste y en el eje \(x\) el valor de las diferentes \(\beta\) para la hipótesis nula. Como vemos, si elegimos el 5% de nivel de significación, no rechazaría muchas hipótesis. No rechazaría que \(\beta=-2.5\), pero tampoco rechazaría que \(\beta=-1\) y ni siquiera que \(\beta=0\). Son hipótesis con un significado económico muy distinto: en el primer caso no rechazo que el bien sea elástico, en el segundo caso con elasticidad unitaria y en el tercero inelástico. Como vemos, aquí realizar un test resulta pernicioso: pese a que intuímos que el impacto del precio sobre el producto tiene importancia, si realizamos un test de significatividad podríamos concluir lo contrario. Y lo que es peor: podríamos concluir cosas muy dispares.
de tal forma que en el eje \(y\), tenemos los distintos p-valores del cada constraste y en el eje \(x\) el valor de las diferentes \(\beta\) para la hipótesis nula. Como vemos, si elegimos el 5% de nivel de significación, no rechazaría muchas hipótesis. No rechazaría que \(\beta=-2.5\), pero tampoco rechazaría que \(\beta=-1\) y ni siquiera que \(\beta=0\). Son hipótesis con un significado económico muy distinto: en el primer caso no rechazo que el bien sea elástico, en el segundo caso con elasticidad unitaria y en el tercero inelástico. Como vemos, aquí realizar un test resulta pernicioso: pese a que intuímos que el impacto del precio sobre el producto tiene importancia, si realizamos un test de significatividad podríamos concluir lo contrario. Y lo que es peor: podríamos concluir cosas muy dispares.
Si realiza lo mismo para el CASO 2, verá que ahora el test es muy rotundo. Rechaza la nula de que \(\beta=0\) pero, en realidad, rechaza un montón más de hipótesis nulas: esto se debe a que la precisión con la que estamos estimando es muy alta (medida por el valor de la desviación típica del estimador). En ese contexto, tampoco nos conviene hacer un test. Rechazaremos casi siempre. Es mucho mejor pensar, como nos propone la ASA, sobre la relevancia o no del efecto. En este caso, como ya dijimos, no parece muy relevante.
Mire del minuto 10.43 al 12.30 y vea una manera de proporcionar información.
EJERCICIO 4
Trate de hacer, con el modelo de los Simpsons, que habrá mejorado en el EJERCICIO 2, algo similar a lo que se plantea en el vídeo. Trate de analizar:
- Cuánto fluctúa la audiencia final del episodio ante diferentes valores de interés del personaje Homer, diferentes valores del resto de protagonistas y teniendo en cuenta la posible heterogeneidad muestral. ¿Cómo podría discutir si el efecto es o no relevante? ¿Cómo de categóricos podemos ser?
- ¿sería fiable analizar qué pasaría si Homer dejara de aparecer? Razone por qué (utilizando argumentos ya aprendidos a lo largo de estas sesiones)
Importante, fin de bloque. Cosas que debe saber:
- Plantear adecuadamente una pregunta de investigación
- Conocer las principales “paradojas” iniciales que uno puede hallar en el estudio aplicado con datos
- Tener una idea clara del conjunto de pasos iniciales que se deben dar en un estudio con datos (y practicarlo)
- Entender que la idea de “analizar” la significatividad de una variable trasciende a la idea de mirar un p-valor y conocer las principales críticas a este uso lanzadas por los científicos
Por otra parte >- Debería tener clara la base de datos con la que va a realizar el proyecto y la pregunta que quiere responder >- Debería haber realizado un análisis similar a los realizados en los ejercicios y en los vídeos.





