Chapter 6 Handout 4: ggplot2, Revisited

Handout 4 covers linear regression, which works no different in the tidyverse (the tidyverse focuses on data processing, not the analysis itself). So, this chapter is dedicated to how linear regression is represented on a ggplot.

You may want to refer back to Handout 2 for a reminder on the basics of ggplot.

6.1 Review of Regression

You know the drill!

library(tidyverse) # loads the tidyverse into your R environment
data <- mtcars # this is a dataset about cars
head(data)

##                    mpg cyl disp  hp drat    wt  qsec vs am gear carb
## Mazda RX4         21.0   6  160 110 3.90 2.620 16.46  0  1    4    4
## Mazda RX4 Wag     21.0   6  160 110 3.90 2.875 17.02  0  1    4    4
## Datsun 710        22.8   4  108  93 3.85 2.320 18.61  1  1    4    1
## Hornet 4 Drive    21.4   6  258 110 3.08 3.215 19.44  1  0    3    1
## Hornet Sportabout 18.7   8  360 175 3.15 3.440 17.02  0  0    3    2
## Valiant           18.1   6  225 105 2.76 3.460 20.22  1  0    3    1

What if we wanted to see the effects of having a higher horsepower (hp) car on the car’s miles-per-gallon (mpg)? We can use a linear regression (with a pipe, because why not?):

# takes the results of lm and applies summary() to it
lm(mpg ~ hp, data = data) %>%
  summary()

## 
## Call:
## lm(formula = mpg ~ hp, data = data)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -5.7121 -2.1122 -0.8854  1.5819  8.2360 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 30.09886    1.63392  18.421  < 2e-16 ***
## hp          -0.06823    0.01012  -6.742 1.79e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.863 on 30 degrees of freedom
## Multiple R-squared:  0.6024, Adjusted R-squared:  0.5892 
## F-statistic: 45.46 on 1 and 30 DF,  p-value: 1.788e-07

6.2 Plotting Univariate Regressions

To plot the above linear regression in base R, we use the following code:

plot(data$hp, data$mpg, xlab = "hp", ylab = "mpg", pch = 19)
abline(lm(data$mpg ~ data$hp))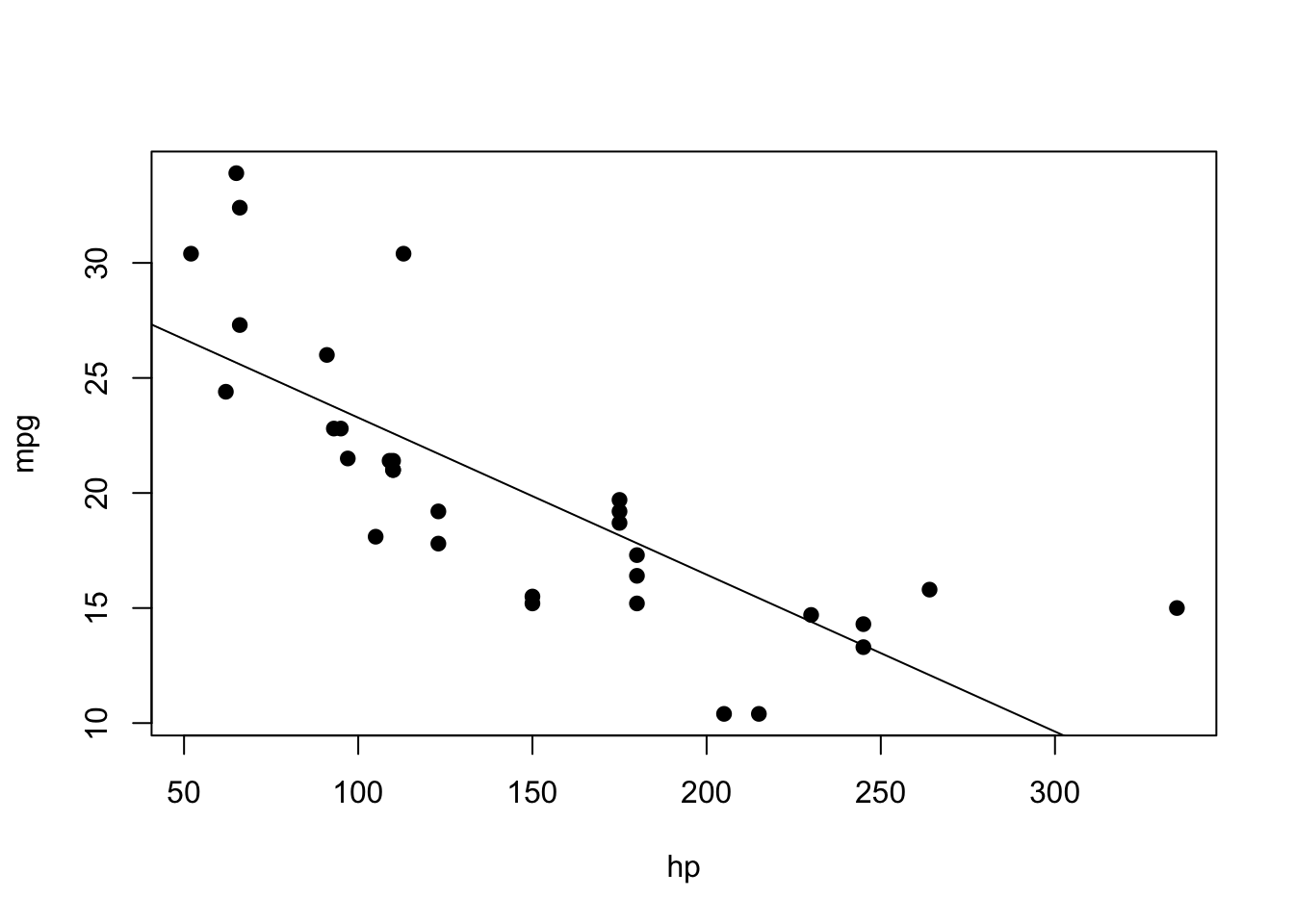

Now, let’s try ggplot, step by step again.

First, create the ggplot object:

ggplot(data)

Specify the x- and y-variables in the aesthetics:

ggplot(data, aes(x = hp, y = mpg))

Next, add in a geom layer to display the points:

ggplot(data, aes(x = hp, y = mpg)) + 
  geom_point()

Then, add in the linear regression geom. This is specified as geom_smooth(method = "lm")

ggplot(data, aes(x = hp, y = mpg)) + 
  geom_point() + 
  geom_smooth(method = "lm")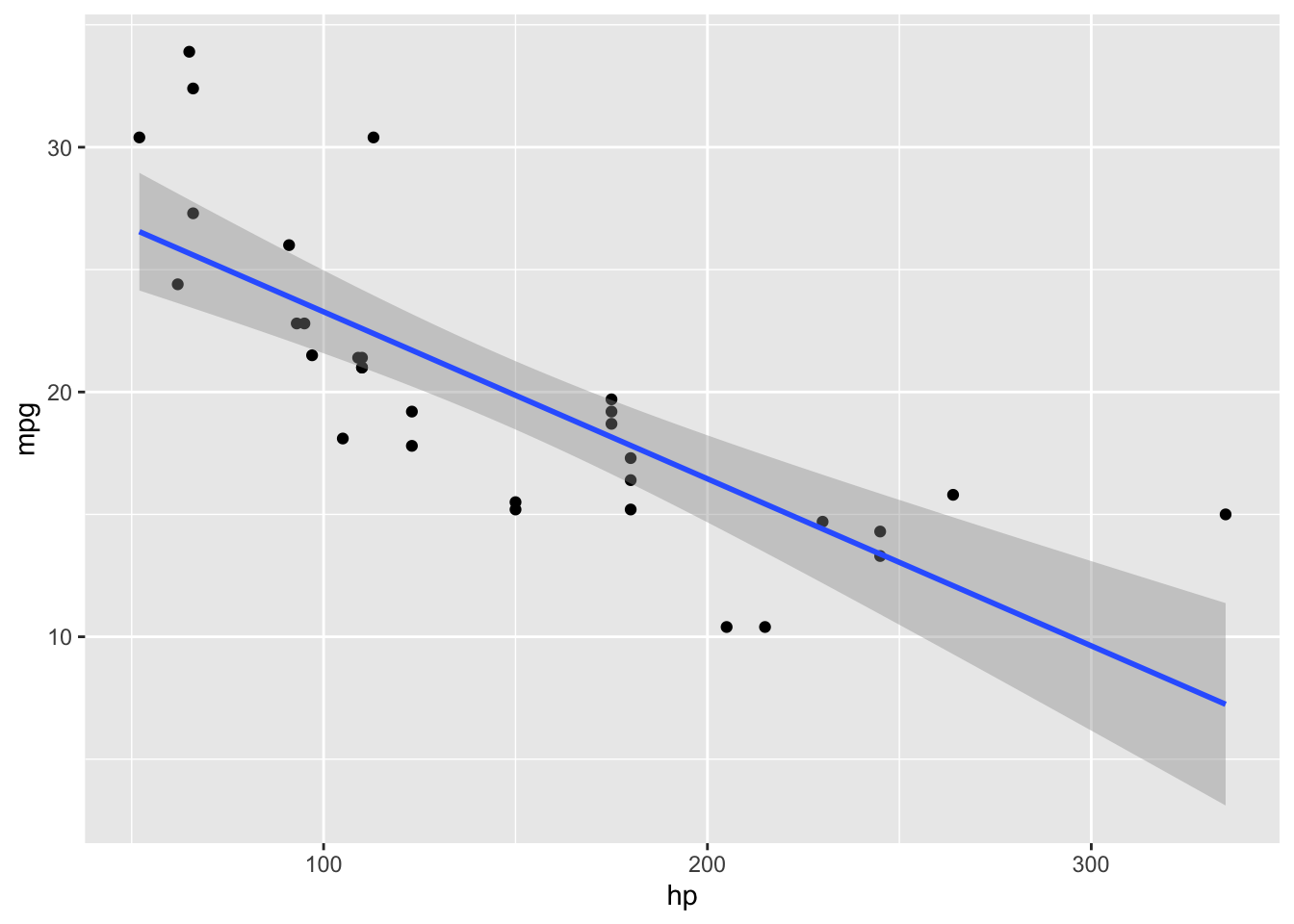

Note that the procedure was largely the same as before: ggplots are very consistent, since the only thing that is really changing is the geom layer. Finally, we can add some added touches to make it prettier. In particular, labs() specifies the labels:

ggplot(data, aes(x = hp, y = mpg)) + 
  geom_point() + 
  geom_smooth(method = "lm") + 
  labs(x = "Horsepower", y = "MPG", title = "Miles per Gallon vs. Horsepower") + 
  theme_minimal()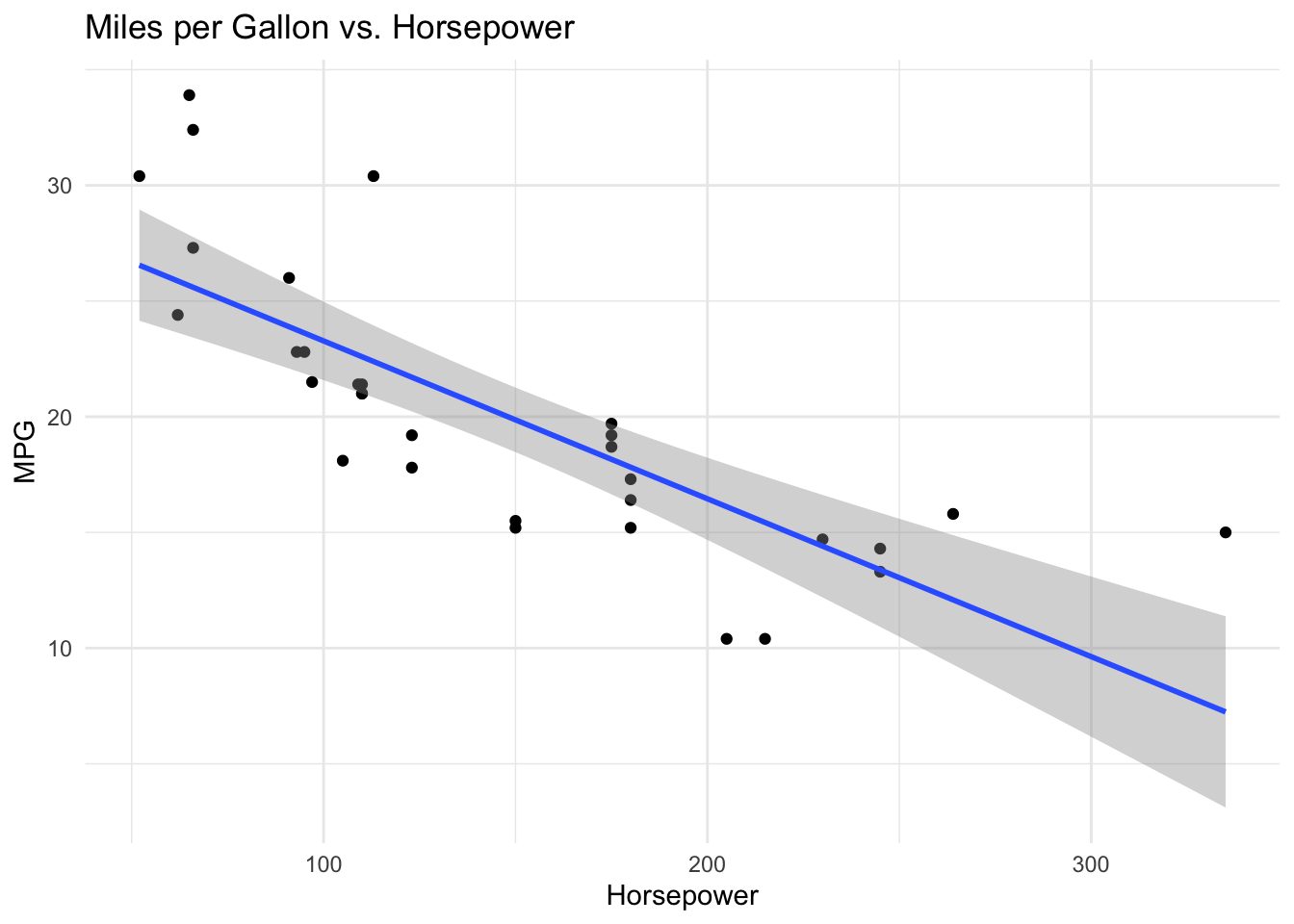

Again, once you understand the basics of ggplot, getting skilled at ggplot involves mainly learning about the various geoms, themes, and customizations out there.