5 Monte Carlo Simulations
5.1 Review
In the theoretical part of the class you learned about statistical properties of estimators. To be precise, let \(\hat{\theta}_n\) be an estimator of a parameter \(\theta\). The estimator is a functions of the sample, say \(\{X_1, X_2, \ldots, X_n\}\). The sample consists of random variable and any function of the sample, including \(\hat{\theta}_n\), is a random variable as well. That is, for different realizations of the data, we get different realizations of the estimator.
These arguments can be confusing because in practice we typically only have one data set and therefore only one realization of the estimator. But we could also think of all the other realizations of the data we could have obtained. For example, consider your starting salary after graduating from Bonn. Let \(\theta\) be the expected starting salary, which is a fixed number that we do not know. After everyone started working and we see your actual starting salaries, we can calculate the sample average as an estimate of the expected value, but this estimate is just one potential realization. If things had turned out slightly different, your starting salaries might have been different and we would have seen a different realization of the estimator.
Since an estimator is a random variable, it has a distribution and (typically) a mean and a variance. You learned that we call an estimator unbiased if \[E\left(\hat{\theta}_n\right) = \theta\] That is, the average value of the estimator over all the hypothetical data sets we could have obtained is equal to \(\theta\). Unbiasedness can hold for any sample size \(n\) and is therefore called a small-sample property. Unbiasedness does not imply that \(\hat{\theta}_n\) is necessarily close to \(\theta\).
You also saw that an estimator can be weakly consistent: \[\hat{\theta}_n \rightarrow_P \theta\] and asymptotically normally distributed \[\sqrt{n}\left(\hat{\theta}_n - \theta \right) \rightarrow_D N(0,v^2) \] as \(n \rightarrow \infty\). These properties only hold in the limit and are called large-sample properties. Knowing the large-sample distribution is particularly useful because it allows us to test hypotheses and obtain confidence intervals. For example, let \(\hat{v}_n\) be a weakly consistent estimator of \(v\). Then \[P\left( \theta \in \left[ \hat{\theta}_n - 1.96\frac{\hat{v}_n}{\sqrt{n}} , \, \hat{\theta}_n + 1.96\frac{\hat{v}_n}{\sqrt{n}} \right] \right) \rightarrow 0.95\] and the interval \[\left[ \hat{\theta}_n - 1.96\frac{\hat{v}_n}{\sqrt{n}} , \, \hat{\theta}_n + 1.96\frac{\hat{v}_n}{\sqrt{n}} \right]\] is a \(95\%\) confidence interval for \(\theta\). That is, looking at all hypothetical data sets, \(\theta\) is in \(95\%\) of the confidence intervals. Notice that in different data sets, we get different intervals, but the parameter \(\theta\) does not change.
The \(95\%\) coverage probability only holds in the limit, but for any fixed sample size \[P\left( \theta \in \left[ \hat{\theta}_n - 1.96\frac{\hat{v}_n}{\sqrt{n}} , \, \hat{\theta}_n + 1.96\frac{\hat{v}_n}{\sqrt{n}} \right] \right) \] could be much smaller than \(95\%\). This actual coverage probability is unknown in applications.
The goal of Monte Carlo simulations is typically to investigate small sample properties of estimators, such as the actual coverage probability of confidence intervals for fixed \(n\). To do so, we can simulate many random samples from an underlying distribution and obtain the realization of the estimator for each sample. We can then use the realizations to approximate the actual small sample distribution of the estimator and check properties, such as coverage probabilities of confidence intervals. Of course, the properties of the estimator depend on which underlying distribution we sample from.
5.2 Simple Simulation Example
As a simple example, let \(\{X_1, X_2, \ldots, X_n\}\) be a random sample from some distribution \(F_X\). Define \(\theta = E(X)\) and let \[\hat{\theta}_n = \bar{X}_n = \frac1n \sum_{i=1}^n X_i\] and \[s_n = \sqrt{\frac{1}{n-1} \sum_{i=1}^n \left(X_i - \bar{X}_n\right)^2} \] Applications of a Law of Large Numbers and a Central Limit Theorem for iid data imply that \[\hat{\theta}_n \rightarrow_P \theta,\] \[s_n \rightarrow_P sd(X),\] and \[\sqrt{n}\left(\hat{\theta}_n - \theta \right) \rightarrow_D N(0,Var(X)) \] The previously discussed confidence interval for \(E(X)\) is \[\left[ \bar{X}_n - 1.96\frac{s_n}{\sqrt{n}} , \, \bar{X}_n + 1.96\frac{s_n}{\sqrt{n}} \right]\]
Exercise: Suppose \(X \sim U[0,2]\) where \(U[0,2]\) denotes the uniform distribution on the interval \([0,2]\). It is easy to show (make sure to verify this!) that \(E(X) = 1\). Now repeat the following two steps at least \(1,000\) times:
- Take a random sample from the distribution of \(X\) with sample size \(n = 20\).
- Calculate the sample average and a \(95\%\) confidence interval for \(E(X)\) using the sample from (1).
You should now have \(1,000\) sample averages and \(1,000\) confidence intervals, which you can use to answer the following questions:
What is average of your \(1,000\) sample averages.
What is the standard deviation of your \(1,000\) sample averages.
How many times is \(E(X)\) in the \(95\%\) confidence interval?
The answers to these questions changes when change the underlying distribution of \(X\) or the sample size.
5.3 Consistency
The estimator \(\hat{\theta}_n\) is weakly consistent if for any \(\varepsilon > 0\) \[P\left( \left|\hat{\theta}_n - \theta \right| > \varepsilon \right) \rightarrow 0\] or \[P\left( \left|\hat{\theta}_n - \theta \right| \leq \varepsilon \right) \rightarrow 1\] That is, as long as \(n\) is large enough, \(\hat{\theta}_n\) is in an arbitrarily small neighborhood around \(\theta\) with arbitrarily large probability.
To illustrate this property, let’s return to the example with sample averages and expectations. Let \(\{X_1, X_2, \ldots, X_n\}\) be a random sample from the Bernoulli distribution with \(p = P(X_i = 1) = 0.7\). Let \(\theta = E(X) = p\) and let \(\hat{\theta}_n\) be the sample average. We start with a sample size of 20 and set the parameters:
n <- 20
p <- 0.7
theta = pWe now want to take \(S\) random samples and obtain \(S\) corresponding sample averages, where \(S\) is ideally a large number. The larger \(S\), the more precise our results will be. It is also useful to set a seed.
set.seed(4519)
S <- 10000
X <- replicate(S,rbinom(n,1,p))
theta_hat <- colMeans(X)Now for some \(\varepsilon > 0\), we can check \(P\left( \left|\hat{\theta}_n - \theta \right| \leq \varepsilon \right)\):
eps <- 0.1
mean(abs(theta_hat - p) <= eps)## [1] 0.647We can also calculate this probability for different values of \(\varepsilon > 0\). I use a loop here for readability, but you can try using matrices on your own. Since I want to repeat the following steps for different sample sizes, it is useful to first define a functions that performs all operations:
calc_probs_consistency <- function(n,S,p,all_eps) {
n_eps = length(all_eps)
X <- replicate(S,rbinom(n,1,p))
theta_hat <- colMeans(X)
probs = rep(0, n_eps)
for (i in 1:n_eps) {
probs[i] = mean(abs(theta_hat - p) <= all_eps[i])
}
return(probs)
}We can now call the function for any \(n\), \(S\), \(p\), and a vector containing different values for \(\varepsilon\). For each of these values, the function then returns a probability.
all_eps = seq(0.01, 0.5, by= 0.01)
probs <- calc_probs_consistency(n = 20, S = 1000, p = 0.7, all_eps = all_eps)Next, we can plot all probabilities:
plot(all_eps,probs,ylim = c(0,1),xlab="epsilon",ylab="Probability", col = 'blue')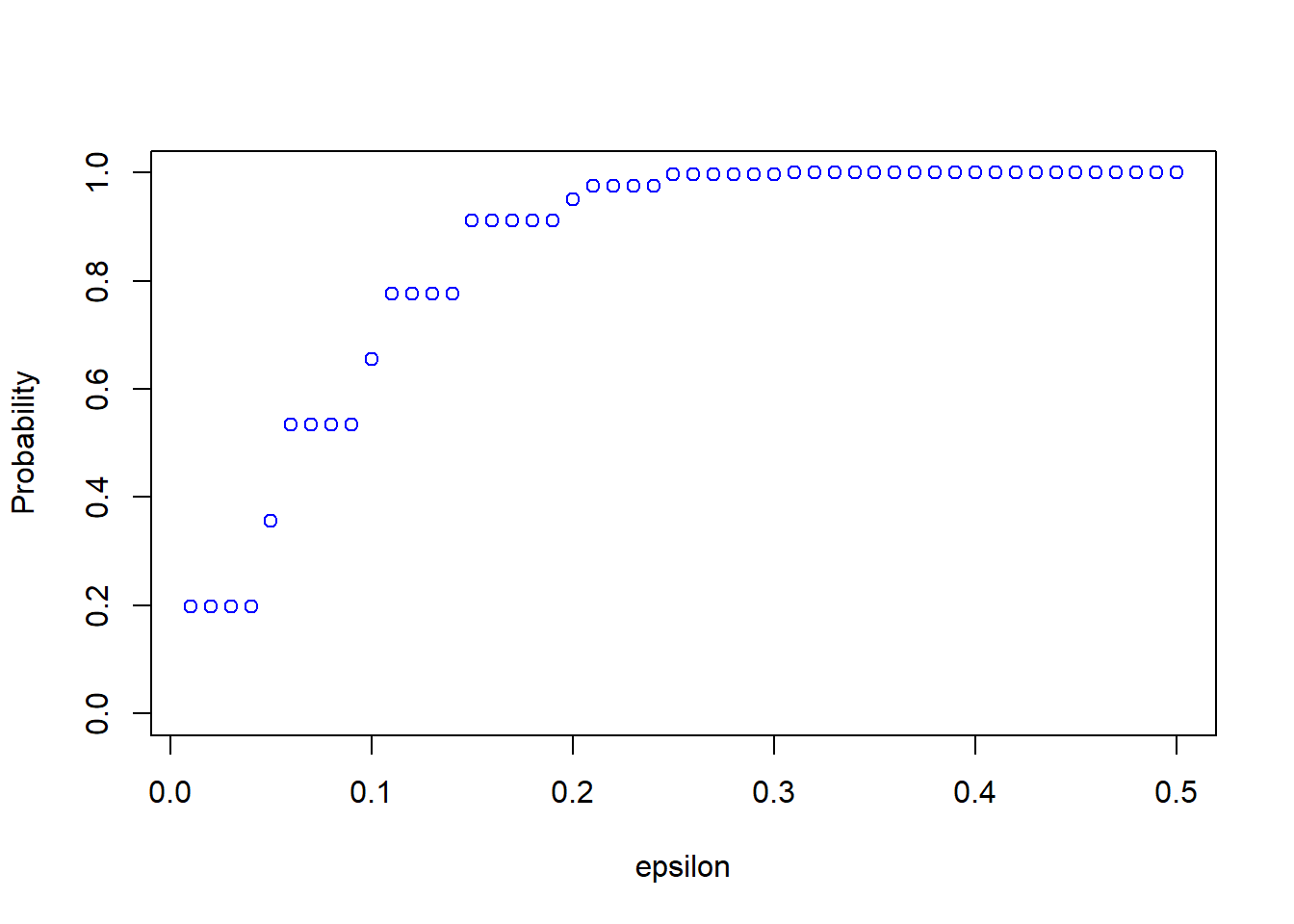
We can see from the plot that \(P\left( \left|\hat{\theta}_n - \theta \right| \leq \varepsilon \right)\) is quite small for small values of \(\varepsilon\). Consistency means that for any \(\varepsilon > 0\), the probability approaches \(1\) as \(n \rightarrow \infty\). We can now easily change the sample size and see how the results change. For example, take \(n=200\):
probs <- calc_probs_consistency(n = 200, S = 10000, p = 0.7, all_eps = seq(0.01, 0.5, by= 0.01))
plot(all_eps,probs,ylim = c(0,1),xlab="epsilon",ylab="Probability", col = 'blue')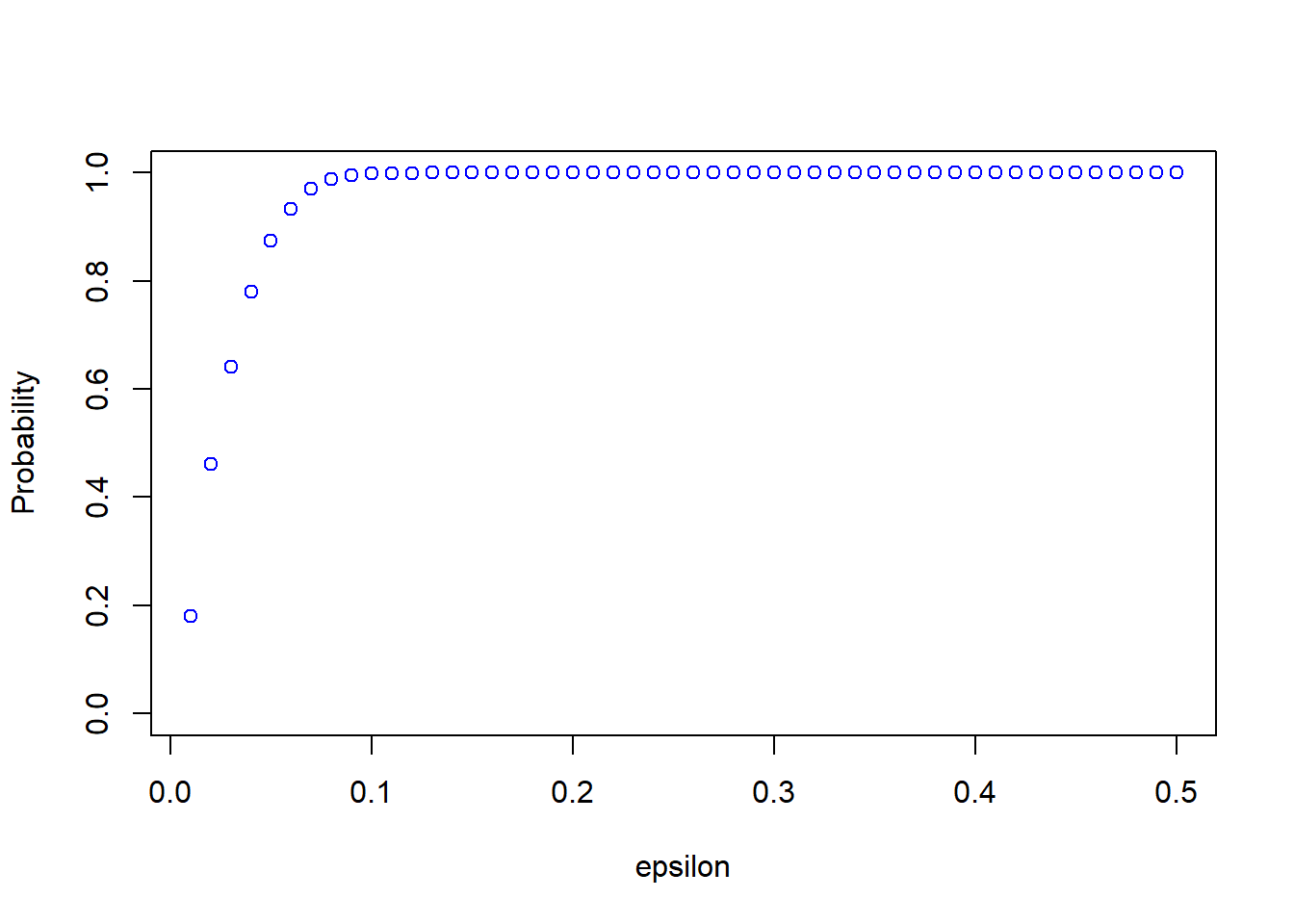
5.4 Asymptotic Normality
We know from the Central Limit Theorem that \[\frac{\sqrt{n}(\bar{X}_n - E(X))}{s_n} \rightarrow_D N(0,1)\] where \(s_n\) is the sample standard deviation. Convergence in distribution means that the distribution of the normalized sample average converges to the distribution function of a standard normal random variable.
Again, we can use the previous simulation setup to illustrate this property. To do so, we calculate \[P\left(\frac{\sqrt{n}(\bar{X}_n - E(X))}{s_n} \leq z\right)\] and compare it to the standard normal cdf evaluated at \(z\). We then plot the results as a function of \(z\). Just as before, we define a function that calculates the probabilities:
calc_probs_asymp_normal <- function(n,S,p,z) {
n_z = length(z)
X <- replicate(S,rbinom(n,1,p))
theta_hat <- colMeans(X)
stds <- apply(X, 2, sd)
probs = rep(0, n_z)
for (i in 1:n_z) {
probs[i] = mean( sqrt(n)*(theta_hat - p)/stds <= z[i])
}
return(probs)
}We can now plot the results for different sample sizes such as
z = seq(-3,3,by=0.01)
probs <- calc_probs_asymp_normal(n = 20, S = 10000, p = 0.7, z = z)
plot(z,probs,ylim = c(0,1),xlab="z",ylab="Probability", col = 'blue')
lines(z, pnorm(z, 0, 1), col = 'red',lwd = 2)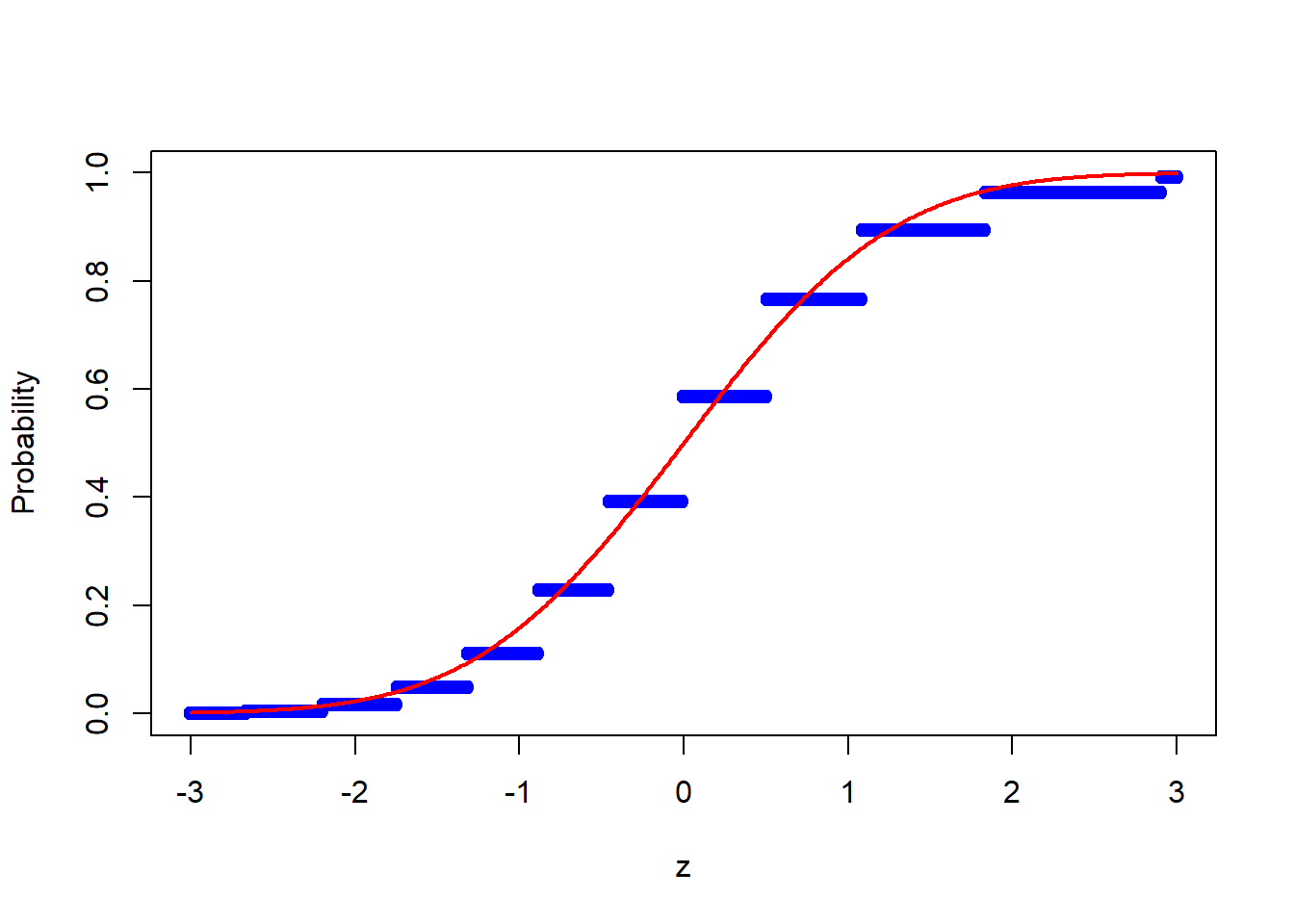
or
probs <- calc_probs_asymp_normal(n = 2000, S = 10000, p = 0.7, z = z)
plot(z,probs,ylim = c(0,1),xlab="z",ylab="Probability", col = 'blue')
lines(z, pnorm(z, 0, 1), col = 'red',lwd = 2)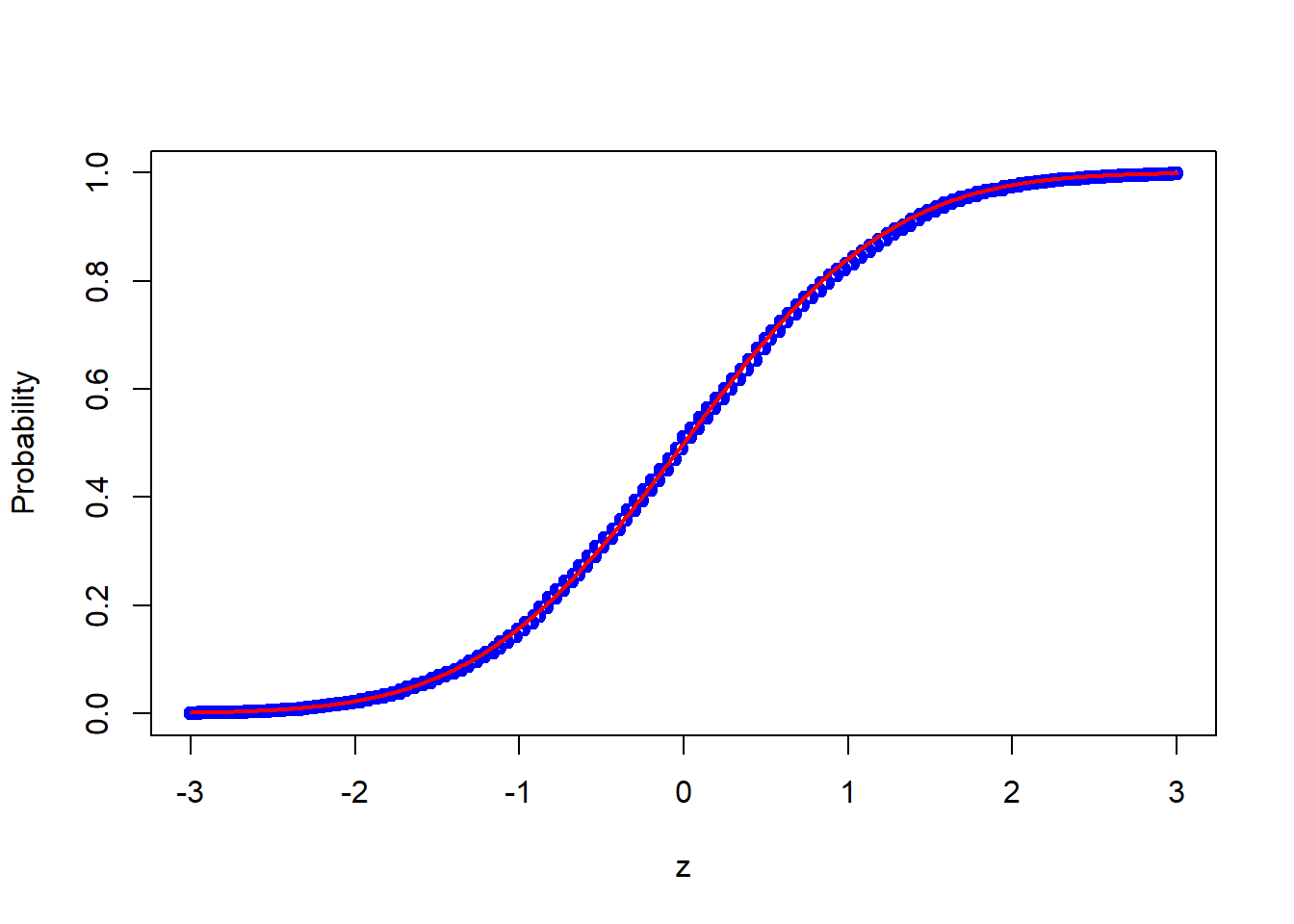
5.5 Testing
Let \(\{X_1, X_2, \dots, X_n\}\) be a random sample and define \(\mu = E(X)\). Suppose we want to test \(H_0: \mu = \mu_0\) where \(\mu_0\) is a fixed number. To do so, define \[t = \frac{\sqrt{n}(\bar{X}_n - \mu_0)}{s_n} \] An immediate consequence of the Central Limit Theorem is that if \(H_0\) is true then \[t = \frac{\sqrt{n}(\bar{X}_n - \mu_0)}{s_n} = \frac{\sqrt{n}(\bar{X}_n - \mu)}{s_n} \rightarrow_D N(0,1) \] and therefore \[P\left(|t| > 1.96 \mid \mu = \mu_0\right) \rightarrow 0.05\] Hence, if we reject when \(|t|>1.96\), we only reject a true null hypothesis with probability approaching 5%.
If the null hypothesis is false, we can write \[t = \frac{\sqrt{n}(\bar{X}_n - \mu_0)}{s_n} = \frac{\sqrt{n}(\bar{X}_n - \mu)}{s_n} + \frac{\sqrt{n}(\mu - \mu_0)}{s_n} \rightarrow_D N(0,1) \] Since in this case \(\sqrt{n}|\mu - \mu_0| \rightarrow \infty\), it follows that \[P\left(|t| > 1.96 \mid \mu \neq \mu_0\right) \rightarrow 1\] That is, we reject a false null hypothesis with probability approaching \(1\). However, for a small sample size, the rejection probability is typically much smaller when \(\mu_0\) is close to \(\mu\).
We now want to calculate the small sample rejection probabilities using Monte Carlo simulations. We could either vary \(\mu_0\) (the value we test) or \(\mu\) (the true mean). We take the latter because we can then plot the power functions you have seen in the theoretical part of the class to illustrate the results.
We work with the Bernoulli distribution again and define a function that calculates certain rejection probabilities.
calc_rej_probs <- function(n,S,mus,mu0,alpha) {
n_mus = length(mus)
probs = rep(0, n_mus)
for (i in 1:n_mus) {
X <- replicate(S,rbinom(n,1,mus[i]))
theta_hat <- colMeans(X)
stds <- apply(X, 2, sd)
probs[i] = mean(abs( sqrt(n)*(theta_hat - mu0)/stds ) > qnorm(1-alpha/2) )
}
return(probs)
}We can now call the function for different values of \(\mu\) and plot the rejection probabilities
mus = seq(0.5,0.9,by=0.01)
probs <- calc_rej_probs(n = 200, S = 10000, mus = mus, mu0 = 0.7, alpha = 0.05)
plot(mus,probs,ylim = c(0,1),xlab="True mean",ylab="Rejection Probability", col = 'blue')
abline(h=0.05, col = 'red',lwd = 2)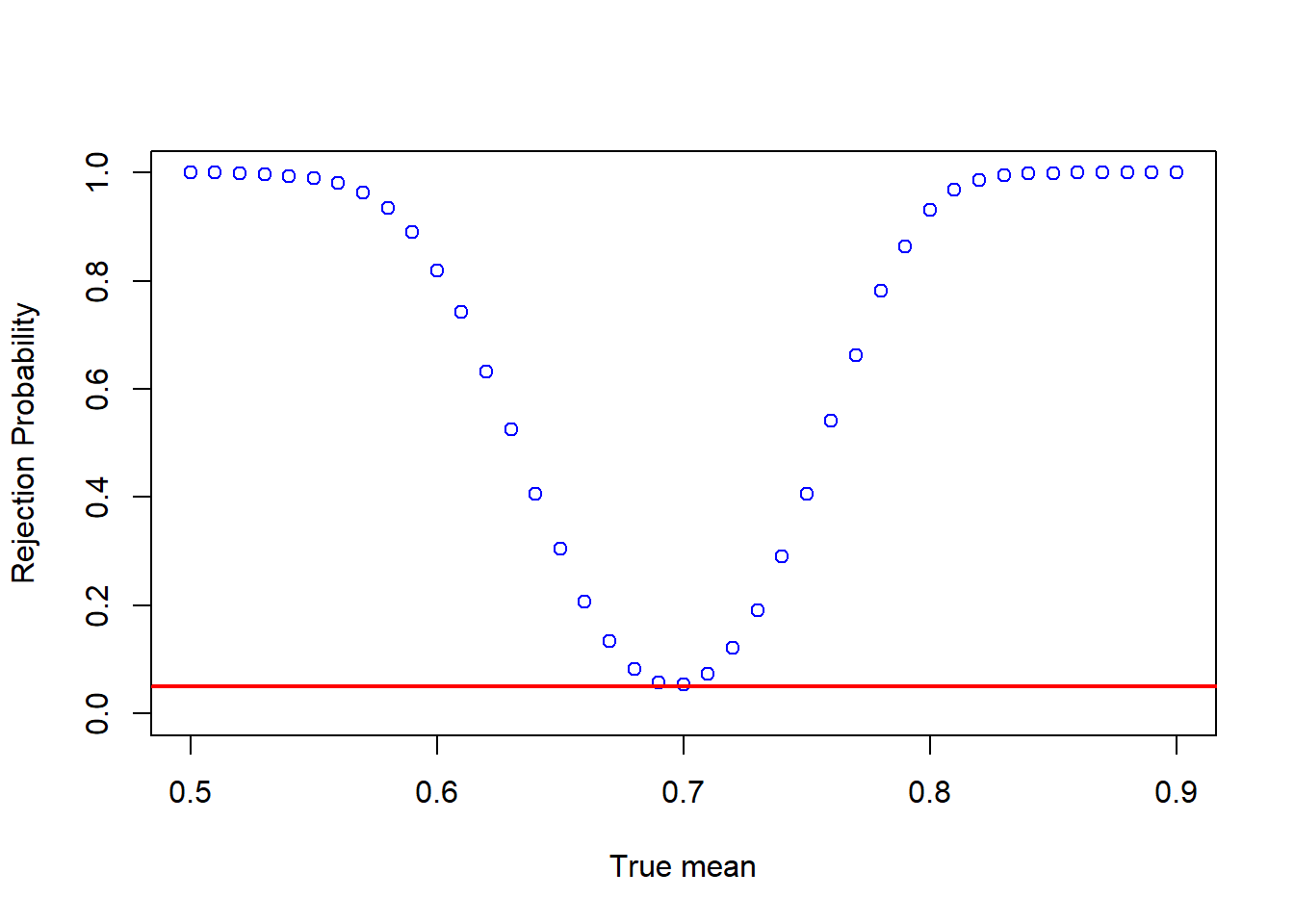
Think about how the figure changes as the sample size increases.
5.6 Regression
In the previous section, we considered a simple parameter (an expected value) and a simple estimator (the sample average). We can analyze analogous issues in other settings, such as the linear regression model. Also in this case, we have parameters (the regression coefficients) and estimators (the OLS estimators). The parameters are random and have certain known small and large sample properties that you discussed in the theoretical part of the class. Many other small sample properties, such as actual coverage rates of confidence intervals are unknown, but can be studies in Monte Carlo simulations.
Here is a task for you to think about on your own. We will discuss the solutions in class.
Exercise: Let \[Y_i = \beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2}+ \varepsilon_i, \qquad i = 1, 2, \ldots, n.\] where \[\begin{pmatrix}X_{i1}\\X_{i2}\\\end{pmatrix} \sim N\left( \begin{pmatrix}2\\-3 \end{pmatrix}, \begin{pmatrix}1& \rho \\ \rho &1 \end{pmatrix} \right)\] and \((\beta_0, \beta_1, \beta_2) = (-1,2,1)\). Let \(\varepsilon_i \sim U[-2,2]\) and assume that \(\varepsilon_i\) is independent of \((X_{i1},X_{i2})\). Assume that the data is a random sample. Let \((\hat{\beta}_0, \hat{\beta}_1, \hat{\beta}_2)\) be the OLS estimator of \((\beta_0, \beta_1, \beta_2)\).
For different values of \(n\) and \(\rho\) use simulations to calculate
- \(E(\hat{\beta}_1)\),
- \(Var(\hat{\beta}_1)\),
- the probability that \(\beta_1\) is in a \(95\%\) confidence interval,
- the expected length of the confidence interval,
- the probability that we reject \(H_0: \beta_1 = 2\) using a two-sided t-test and a \(1\%\) significance level, and
- the probability that we reject \(H_0: \beta_1 = 1.8\) using a two-sided t-test and a \(1\%\) significance level.
Discuss the results.
How do you think the results will change if \(X_{i1}\) and \(\varepsilon_i\) are correlated?