Data Analytics Module
Lecturer: Hans van der Zwan
Lab 04
Topic: asscociation analysis


EXERCISE 4.1

The RDWregr.xlsx file contains data of a number of vehicles.1 Open this file in Excel.

  1. Analyse the relationship between the variables BRAND and COLOR.
  2. Analyse the relationship between PRICE and BRAND.
  3. Analyse the relationship between MASS and BRAND.


EXERCISE 4.2

The RDWregr.xlsx file contains data of a number of vehicles including the mass and the selling price.

  1. Generate a table with the most important statistics concerning the two variables.
  2. Create boxplots.

It may be assumed that there is a relationship between mass and selling price.

  1. Create a scatterplot; examine the outliers; does the graph support the assumption about a relationship between mass and selling price.
  2. The strength of the relationship can be measured with the correlation coefficient r (see below); what’s the value of r (use Excel function correl() )?
  3. The relationship can be described by a mathematical equation; right click on the dots in the graph and choose the option to plot the best fitting line and display the equation on chart.


EXERCISE 4.3

The file 20191126_forsale_berlin.csv contains information about properties for sale in Berlin on November 26, 2019 (source: https://www.immobilienscout24.de). Open the data file in Excel. Inspect the data and perform some datacleaning:

  • remove the observations for which the price is given in a certain range
  • create a couple of numerical variables:
    • the area in square meters
    • the number of rooms
    • the price in euro

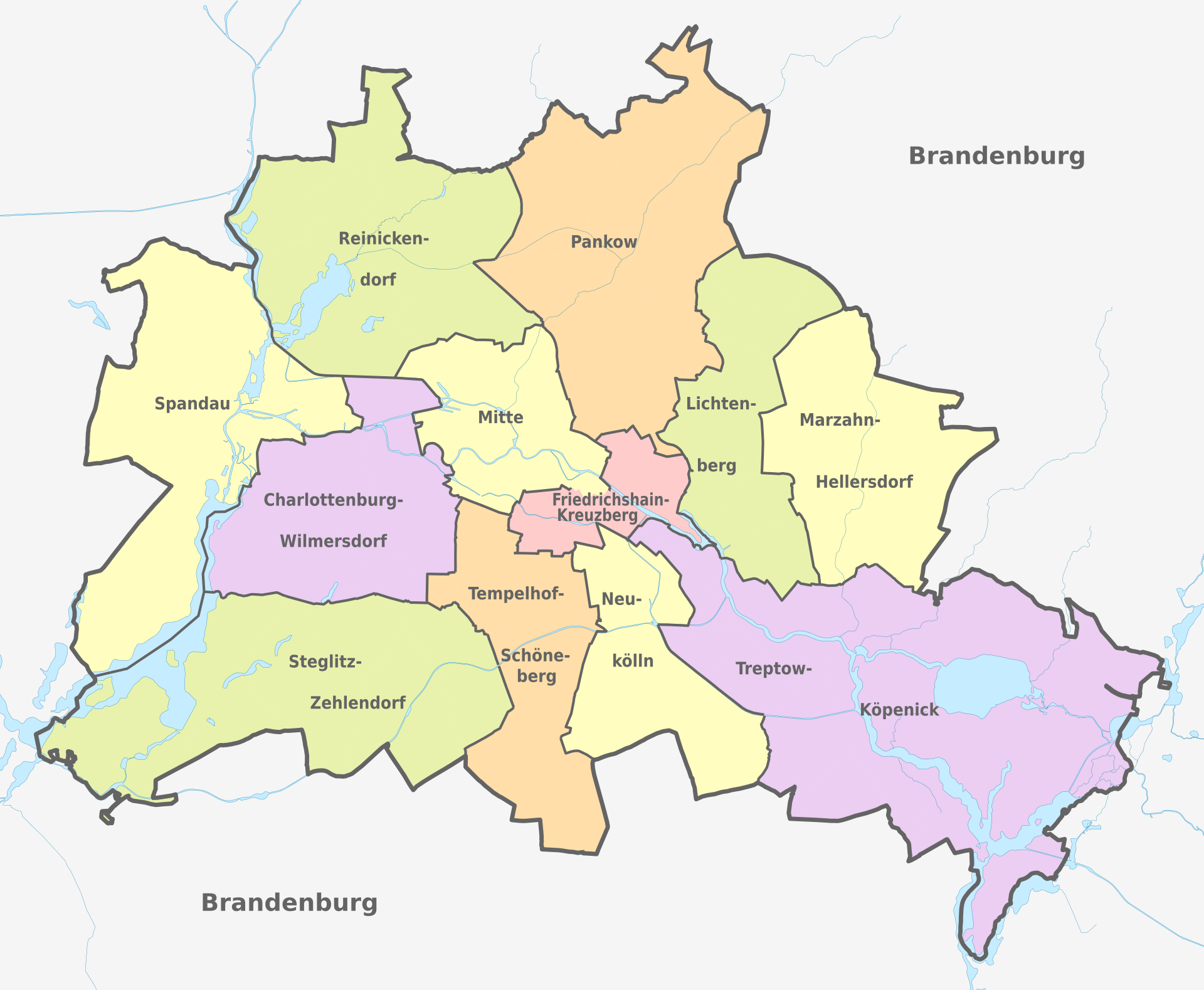
Figure 1. The districts of Berlin. Source: https://en.wikipedia.org/wiki/Boroughs_and_neighborhoods_of_Berlin.

  1. In which area do you expect the highest house prices?
  2. Create a table with summary statistics for the house prices per district.
  3. Create a scatterplot with PRICE as Y-variable and AREA as X-variable.
  4. Generate a regression model with PRICE as response and AREA as explanatory variable.
  5. Assess the regression model.

  1. The data set is not a random sample from all registered cars in the Netherlands; it is a random sample from registered cars from three brands, KIA, BMW and AUDI; because of didactic reasons, KIA PICANTO’s are excluded from the sample.↩