Topic 6 Solutions for Public Goods Problems and Prisoners’ Dilemmas
6.1 Hypotheses
There are four to know about:
Repeated Interactions will Reduce Defection
In the first explanation of this hypothesis, it would be near impossible to analyze the costs and the benefits associated with payoffs if the game were to go on for a long period of time. Because of this, rational calculations (i.e., a kind of strategy rooted in logic) isn’t always applicable.
Alternatively, another explanation is that people don’t want to harm the other party when they think that their relationships are going to be continued (i.e., defecting or going against their partner might cause problems down the road).
Communication enhances trust and cooperation
People show defecting behavior in prisoner’s dilemmas or other games, simply because they do not trust each other, which is again because they do not have chances to talk to each other. Hence, communication among players will help them build trust, which will make it easier to coordinate their behavior and eventually enhance cooperative behavior.
– Yamagishi and Sato (1986)
If we think about the prisoner’s dilemma, we realize that the prisoners (i.e., the players) don’t have a means to communicate with one another. However, if communication is allowed, there is then a question of whether or not a player can trust the other.
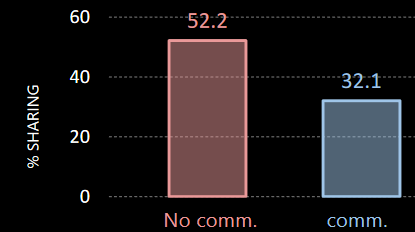
Figure 6.1: Outcome of the Sharing Game
In one of the class activities that we did regarding point sharing, more people shared when there was no communication. This falls in line with what somebody named “Samuelson” said: communication gives people the ability to lie.
Punishments will reduce defections

Figure 6.2: Payoff Matrix for Punishment
If some sort of penalty \(\alpha\) were to be introduced into Axelrod’s two-person prisoner’s dilemma game, the best payoffs will then be \(R > T - \alpha > S > P - \alpha\) as opposed to the typical \(T > R > P > S\) preferred payoff scheme. This was what a researched named Coleman came up with in 1973.
However, one thing to note is that the penalty can be difficult to implement - a higher authority (e.g., the government) isn’t always going to be around to enforce the penalty. Because of this, these kinds of payoff matrices are also known as second-order prisoner’s dilemmas: somebody has to be altrutistic enough to want to dole out punishments for little to no reward.
Peer pressure will lead to less free-riding
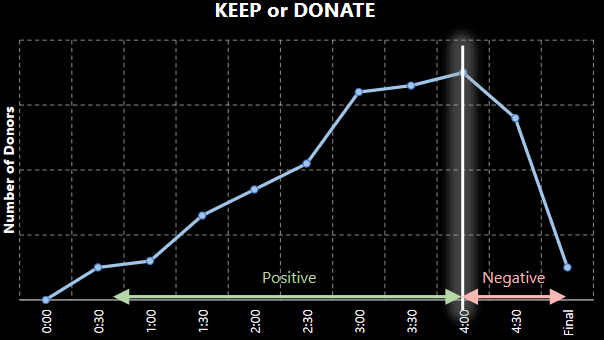
Figure 6.3: Outcomes of the Keeping and Donating Game
The one thing about peer-pressure is that it doesn’t always lead to a good outcome. You can think of peer pressure as a sort of penalty, but different people will have their own ways of dealing with peer pressure (i.e., some people will just march to the beat of their own drums).
6.2 Evolutionary Theory
We need to get some things out of the way first:
- Darwin did not come up with evolution.
- “Survival of the fittest” is not what drives evolution.
- Humans are not descendants of chimpanzees or monkeys.
That said, we study evolutionary theory because we want to see how new patterns in behavior and order come up without an authority. On top of that, evolutionary theory helps us understand human behavior without assuming too much.
6.2.1 Lamarckian versus Darwinian Evolution

Figure 6.4: Differences Between Darwinian and Lamarckian Evolution
There were two scientists: Lamarck and Darwin.
Lamarck would say that if a giraffe has a long neck, its parents must have worked hard for its long neck by stretching their necks. From the context of this course, the giraffe’s parents made a rational decision by choosing to stretch their necks - though, this assumes that the individual in question is able to make their own decisions.
On the other hand, Darwin’s model would suggest that rational thinking is irrelevant. Just group diversity would suffice; the players would behave as programmed by their own genes.
6.2.3 Evolutionary Game Theory
This model assumes a couple of things:
- There are interactions that happen over and over again for an indefinite amount of time over generations.
- There are no rational players; the players in this game don’t make decisions.
- The players display behavioral traits from their parents.
- The reproductive success is the payoff.
- Populations, not individuals, are considered.
6.2.4 Tit for Tat
This strategy was proposed by Rapoport - in each subsequent round of the game, somebody doing tit-for-tat would basically just copy what their other player did in the previous round.
Not only is this strategy not very cognitively intensive (i.e., just a bit of memory would do), but it also results in largely cooperative outcomes. The payoffs can be just as high as the other player’s payoffs.

