Topic 8 Coordination Problems
8.1 Types of Games
8.1.1 Classical Prisoner’s Dilemma
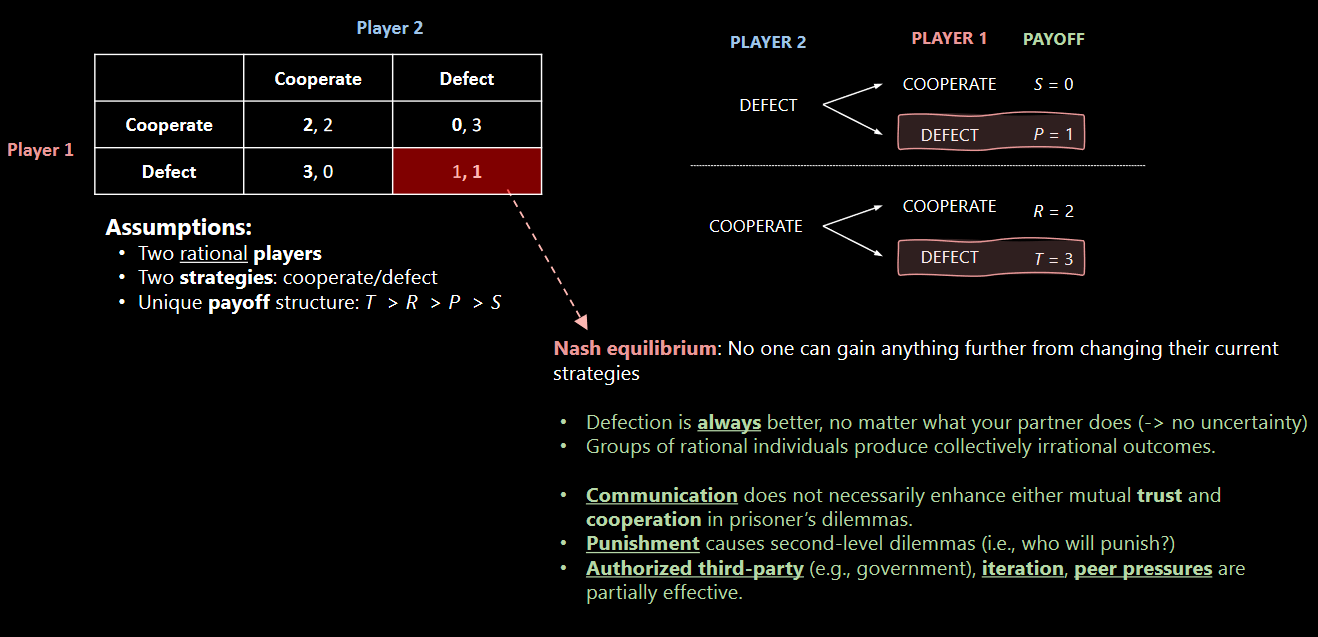
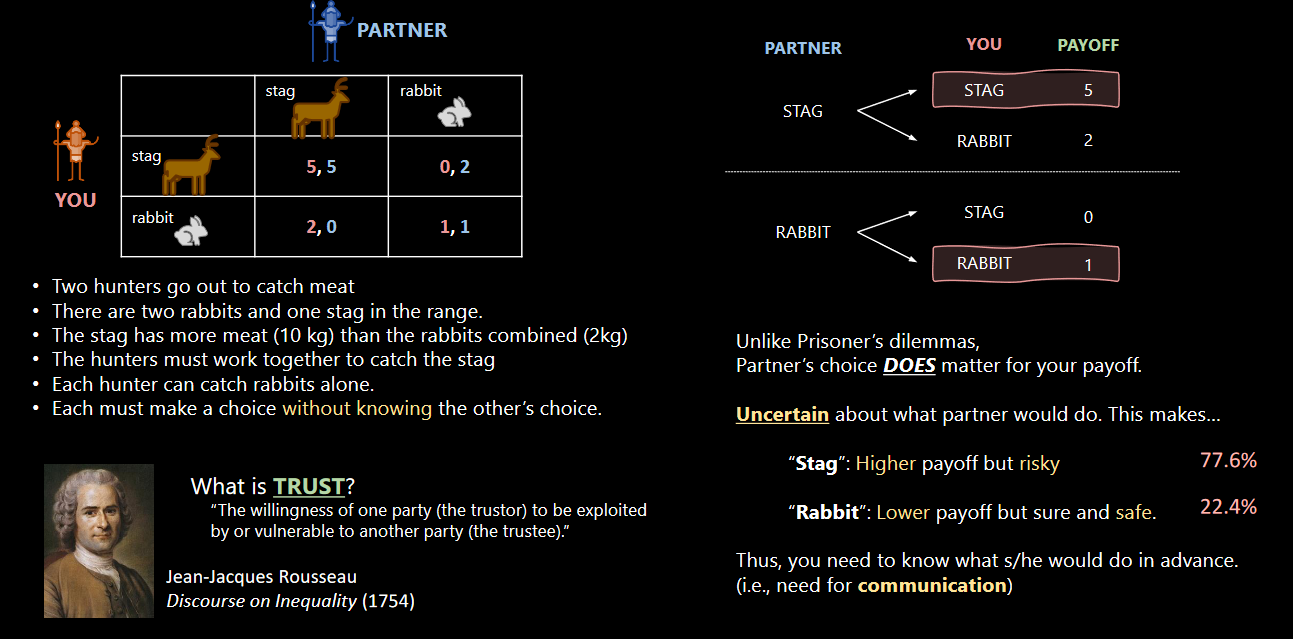
Figure 8.1: A Classic Game
In the normal prisoner’s dilemma game, we assume that there are two rational problems and that there are only two kinds of strategies. The payoff strategies in order of favorability is also \(T > R > P > S\).
Communication doesn’t matter here and the best thing to do would be to always defect no matter what. Punishing players would result in second-order dilemmas, but it’s effective.
8.1.2 Evolutionary
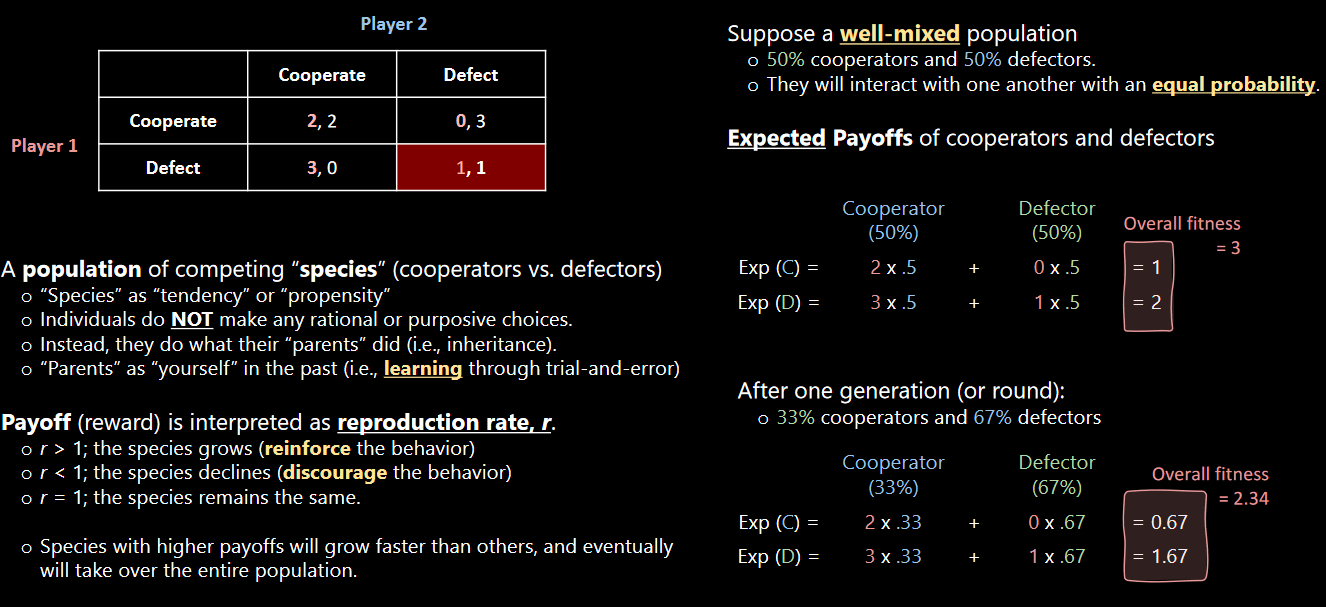
Figure 8.2: An Evolutionary Prisoner’s Dilemma Game
Like the previous weeks’ lecture mentions, the payoff in this game are the reproductive rates \(r\). If \(r > 1\), then the species grows; if \(r = 1\), then the species remains the same and so on.
The players here are populations and do not make choices. Instead, the players’ previous generations did what their parents did.
8.2 Coordination Problems
8.2.1 Network Effects
This just states that the value of a product or a service will increase the more people use it.
8.2.2 Solving Coordination Problems
In such scenarios, people’s payoffs are better if and only if the other is better off and whatnot. So, the only way for individuals to maximize their payoffs is to play well with others.
There are multiple Nash equilibria and because of this, this is a major source of uncertainty.
8.2.2.1 Using Luck
This means that each player has a 50% chance of getting the correct strategy combination. However, this isn’t a great solution as the probability will drop the more people play the game.
8.2.2.2 Rational Calculation
This doesn’t work as all strategies have good outcomes. There is no “good” associated with each of the strategies.
8.2.2.3 Other, Working Solutions
There are a few that prof. Oh lists:
Standardization
This refers to authorities, but this isn’t always possible.
Conventions
This is informal, but only works if there’s a common convention that all players follow. It’s because of this that we cannot say which convention is better than others (i.e., cultural relativism).
Communication
This should work, but only if players share a common language.
One thing to note is that these kinds of problems can also resolve by themselves through evolution. If their decisions wrok, people don’t choose the same strategy and vice versa.