Topic 1 Problem Solving Fundamentals

The term collective problem solving can mean many things. It can mean solving problems as a group (i.e., collectively), or it may also mean solving collective problems (i.e., problems that you’d encounter as a group) instead of individual, personal ones.

1.1 What is Problem Solving?

Problem solving is really just how we choose different solutions for a given problem. This isn’t any different from stuff like decision-making, search processes, and also selection.

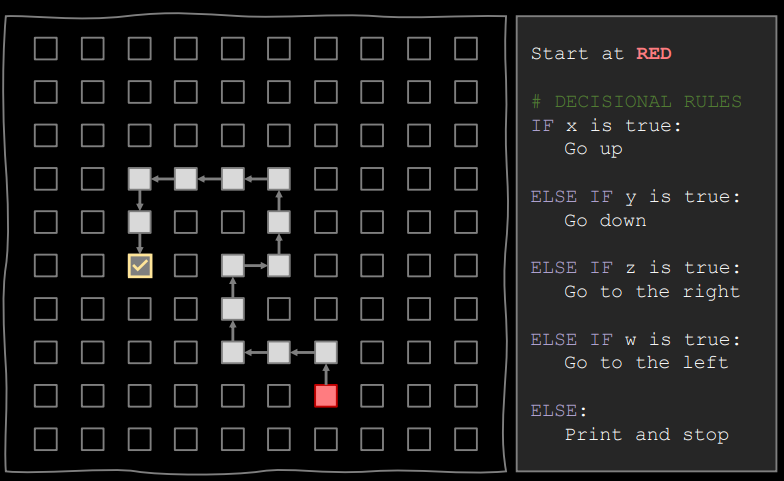
An Example of a Path-Finding Algorithm

Figure 1.1: An Example of a Path-Finding Algorithm

With that said, an algorithm is a series of steps that are followed to achieve something.

A problem can have many different solutions, and this “many different solutions” is known as a solution space in fancy-speak.

However, if a problem has the following characteristics, then the problem will probably be difficult to solve as well:

  1. There are a lot of possible solutions (i.e., the solution space is massive)
  2. What constitutes a “solution” isn’t very clear (i.e., there is no well-defined solution)
  3. Decision rules for arriving at a solution is super complicated.
  4. It takes a super long time to get to a solution
  5. There isn’t much available helpful information.

1.1.1 Sub-Optimal Solutions

The thing about the “perfect solution” to a problem is that it may not always exist either because:

  1. It just doesn’t exist.
  2. Achieving perfection would be way too costly.

So, more often than not, subpar solutions are often good enough, and this is especially true when there’s not enough information to make informed decisions (i.e., like in most real life scenarios).

Example of a Sub-Optimal Solution

Figure 1.2: Example of a Sub-Optimal Solution

For instance, \(\pi\) has all sorts of digits, yet for most people, the value \(3.14\) will be good enough (though the same thing probably cannot be said for rocket scientist and other highly technical professions). This could be considered a “sub-optimal” solution as although nobody will be able to fully list down the digits of \(\pi\), the \(3.14\) approximation will be good enough in most cases.

1.2 Path Dependence

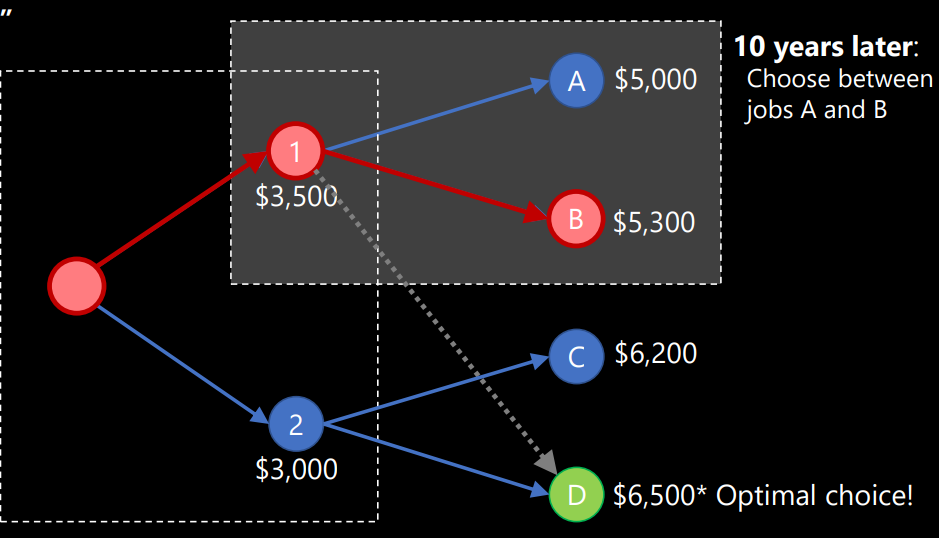
Example of Path Dependence

Figure 1.3: Example of Path Dependence

Path Dependence (or “lock in”) is a phenomenon whereby the choices that you have are a result of the choices that have been made before and / or by others.

1.2.1 Example: QWERTY Keyboards

The QWERTY versus the Dvorak Keyboard

Figure 1.4: The QWERTY versus the Dvorak Keyboard

At some point in the history of mechanical typewriters, it used to be so that the typewriter’s keys would jam if too many keys were pressed at the same time. Because of this, the QWERTY layout was introduced to solve this problem.

But suffice to say that we don’t use typewriters nowadays, yet the keyboard that most laptops use is the QWERTY layout (even though other variants like the “Dvorak” keyboard claim to be more efficient and easier to learn).

This is an example of path dependence because it has been used by so many people for so long (even though the QWERTY keyboard doesn’t really have any benefits nowadays).