1 Introducción

En este apartado se expondrán la teoría y los métodos de la inferencia estadística que servirán como base para los modelos estadísticos. Un problema de inferencia estadística es un problema en el cual se han de analizar datos que han sido generados de acuerdo con una distribución de probabilidad desconocida y en la que se debe realizar algún tipo de inferencia (“conocer su comportamiento”) acerca de tal distribución. En la mayoría de situaciones reales, existe un número infinito de distribuciones posibles distintas que podrían haber generado los datos. En la práctica, dado el tipo de variable aleatoria considerada, se suele asumir un modelo de distribución de probabilidad que es completamente conocida salvo excepto por los valores de los parámetros que la especifican completamente. Utilizamos los datos de la muestra para obtener información sobre dichos parámetros desconocidos y poder asumir de esta forma una distribución de probabilidad completa para todos los datos de la población.

Por ejemplo, se podría saber que la duración de cierto tipo de marcapasos tiene una distribución exponencial con parámetro $\lambda$ pero desconocer el valor exacto de dicho parámetro. Si se puede observar la duración de varios marcapasos de este tipo, entonces, a partir de estos valores observados y de cualquier otra información relevante de la que se pudiera disponer, es posible producir una inferencia acerca de ese valor desconocido $\lambda$. Podría interesar producir la mejor estimación del valor de dicho parámetro o especificar un intervalo en el cual se piensa que pueda estar incluido el verdadero valor de $\lambda$, o decidir si dicho parámetro es menor que un valor específico, ya que en ningún caso es posible obtener el verdadero valor de $\lambda$ ya que sería necesario obtener la información de todos los sujetos de la población y no sólo los de la muestra.

En un problema de inferencia estadística, cualquier característica de la distribución que genera los datos experimentales que tenga un valor desconocido, como $\lambda$ en el ejemplo anterior, se llama parámetro de la distribución. El conjunto $\Omega$ de todos los valores posibles de dicho parámetro se llama espacio parámetrico. Cuando nuestra distribución de probabilidad tiene dos parámetros (por ejemplo la distribución Normal) el espacio paramétrico vendrá dado por todo el conjunto de parejas de valores de $\mu$ y $\sigma^2$.

2 Estimador y estimación

Si tenemos una variable aleatoria $X$ cuya función de distribución viene caracterizada por un parámetro o conjunto de parámetros $\delta$, y una muestra aleatoria de tamaño $n$, $X_1,...,X_n$, a partir de la cual se observan el conjunto de datos muestrales $x_1,...,x_n$ vamos a definir dos conceptos relevantes en todo proceso de inferencia: estimador y estimación.

Un estimador del parámetro $\delta$, basado en las variables aleatorias $X_1,...,X_n$, es una función $\delta(X_1,...,X_n)$ que especifica una valor para $\delta$. Se trata de una función matemática que tiene la misma forma independientemente de la muestra utilizada. Por ejemplo, los estimadores para la media, varianza (y cuasivarainza), y proporción poblacionales vienen dados por: Media muestral

\[\delta_1 (X_1,...,X_n)=\bar{X}=\frac{(X_1+X_2+...+X_n}{n}\]

Varianza muestral

\[\delta_2 (X_1,...,X_n)=S^2=\frac{\sum_{1=1}^n (X_i-\bar{X})}{n}\]

Cuasi-Varianza muestral

\[\delta_3 (X_1,...,X_n)=S_q^2 = \frac{n}{n-1} S^2\]

Para una variable de tipo discreto se aplican las mismas definiciones si consideramos cada $X_i$ como una realización de dicha variable. Para una variable que mide “éxito” o “fracaso” los valores de $X_i$ serán 1 o 0 respectivamente, de forma que la media muestral coincide con la proporción muestral ya que tendríamos la suma de 1 en el numerador dividido por el tamaño de muestra en el denominador.

Una estimación es el valor numérico del estimador para unos datos dados $(x_1,...,x_n)$, es decir, sustituimos en $\delta(X_1,...,X_n)$ por sus valores observados y obtendríamos la estimación del parámetro. De forma habitual se identifica con el “gorro” encima del parámetro indica la estimación de un parámetro:

\[\hat{\mu} = \bar{x}\]

\[\hat{\sigma}^2 = s^2\]

3 Información contenida en la muestra

Antes de comenzar a describir los procesos de inferencia estadística es necesario conocer como podemos relacionar la información contenida en una muestra con la distribución de probabilidad de la variable aleatoria de interés. Para ello una vez fijada la población del estudio y el objetivo principal es necesario:

Establecer la variable de interés, $X$ (y su tipo), en función del objetivo principal.
Establecer una distribución de probabilidad para la variable aleatoria, $f(X|\theta)$, acorde con el tipo de dicha variable y lo más sencilla posible, donde θ representa el parámetro o parámetros que especifican dicha distribución.
Muestra aleatoria de tamaño n de la variable de interés, $X_1,X_2,...,X_n$ de forma que cada observación tiene probabilidad $f(X_1 |\theta)$, $f(X_2 |\theta)$,…,$f(X_n |\theta)$ respectivamente y sus valores observados vienen dados por $x_1,...,x_n$.
Obtener los descriptivos muestrales habituales: media, varianza, desviación típica, o proporción.

Se define entonces la función de verosimilitud L(X|θ) como:

\[L(X|\theta)=\prod_{i=1}^n f(X_i |\theta)\]

La función de verosimilitud contiene toda la información sobre la muestra y la relaciona con el parámetro o parámetros de interés a través de la distribución de probabilidad establecida. Se convierte por tanto en la herramienta más importante, desde el punto de vista de la estadística frecuentista, para los procesos de inferencia estadística que estudiaremos a continuación. Además, se utiliza como base para la caracterización de la distribución en el muestreo de los diferentes estimadores, aproximaciones numéricas del verdadero valor del parámetro o parámetros de la distribución de probabilidad asumida, que se utilizan en los procesos inferenciales.

Para evitar la complejidad matemática que supone trabajar con productos se suele definir el logaritmo de la función de verosimilitud, log-verosimilitud, $LL(X|θ)$ como:

\[LL(X|\theta)=log\left(\prod_{i=1}^n f(X_i |\theta)\right) = \sum_{i=1}^n log(f(X_i |\theta))\]

3.1 Verosimilitud para una población Bernouilli

Consideramos una variable de tipo discreto, $X,$ que sólo puede tomar valores 1 (“éxito”) con probabilidad $\theta$ y valor 0 (fracaso) con probabilidad $1-\theta$. La distribución de probabilidad asociada con esta variable se conoce como distribución Bernouilli (Binomial de tamaño n = 1) y su función de densidad viene dada por:

\[f(X=1|\theta)=\theta; f(X=0|\theta)=1-\theta\]

Si obtenemos una muestra de tamaño $n$, $X_1,X_2,...X_n$, y denotamos por $s$ a la suma de todos los valores $X_i$ iguales a 1 la función de verosimilitud y log-verosimilitud vienen dadas por:

\[L(X|\theta)=f(X_1 |\theta)f(X_2 |\theta)⋯f(X_n |\theta)=\theta^s (1-\theta)^{n-s}\]

\[LL(X|\theta)=s*log(\theta)+(n-s)*log(1-\theta)\]

3.2 Verosimilitud para una población Normal

Consideramos una variable de tipo continuo, $X$, cuya distribución de probabilidad es $N(\mu,\sigma^2)$ de forma que su función de densidad viene dada por:

\[f(X|\mu,\sigma^2)=\sqrt{\frac{1}{2\pi\sigma^2}} exp\left(\frac{(X-\mu)^2}{2\sigma^2}\right)\]

Si obtenemos una muestra de tamaño $n$, $X_1,X_2,...X_n,$ y denotamos por $bar{X}$ a la media muestral y $S^2$ a la varianza muestral, la función de verosimilitud y log-verosimilitud vienen dadas por:

\[L(X|\mu,\sigma^2)=\left(\frac{1}{2\pi\sigma^2}\right)^{n/2} exp\left(\frac{nS^2+n(\mu-\bar{X})^2}{2\sigma^2}\right)\]

\[LL(X|\mu,\sigma^2)=-\frac{n}{2}*log(2\pi\sigma^2)+\left(\frac{nS^2+n(\mu-\bar{X})^2}{2\sigma^2}\right)\]

En este caso la representación gráfica es más compleja ya que debemos hacerlo en un gráfico bidimensional, pero utilizando las expresiones la forma de la verosimilitud, resulta posible descomponerla de la siguiente forma:

\[L(X|\mu,\sigma^2)=\left(\frac{1}{2\pi\sigma^2}\right)^{n/2} exp\left(\frac{nS^2}{2σ^2}\right)exp\left(\frac{n(\mu-\bar{X})^2}{2\sigma^2}\right)\]

donde el radical y la primera exponencial dependen únicamente de las varianzas, mientras que la segunda exponencial depende de las medias dado el valor de la varianza poblacional.

4 Procedimientos de inferencia estadística

Estudiamos en este punto los distintos procedimientos de inferencia que tratamos en esta unidad. Realizamos una pequeña introducción de cada uno de ellos y ejemplificaremos su uso en el análisis de una población.

4.1 Estimación puntual

Es el procedimiento de inferencia estadística más sencillo y consiste en obtener un único valor aproximado del parámetro de interés a partir de un estimador de dicho parámetro y de los datos observados de una muestra. Aunque en las situaciones más sencillas (media, varianza y proporción) tanto el estimador como la estimación son fáciles de obtener, hay que establecer un procedimiento general para obtener dichas estimaciones.

Dicho procedimiento consiste en encontrar el máximo de la función de verosimilitud (o más concretamente de la log-verosimilitud) para el parámetro o parámetros involucrados en dicha función, es decir, el valor o valores que se obtienen al igualar a cero la derivada de la función de log-verosimilitud:

\[\frac{d}{d\theta} LL(X|θ)=0\]

4.1.1 Estiamdor de una proporción

La estimación de proporciones surge de forma natural en poblaciones Bernouilli cuya función de log-verosimilitud viene dada por:

\[LL(X|\theta)=s*log(\theta)+(n-s)*log(1-\theta)\]

Derivando e igualando a cero:

\[\frac{d}{d\theta} LL(X|\theta)=\frac{s}{\theta}- \frac{n-s}{1-\theta}=0\]

Despejando obtenemos:

\[\hat{\theta}=\frac{s}{n}\]

que es el estimador habitual para obtener la proporción muestral.

4.1.2 Estiamdor de la media

Si asumimos que la variable aleatoria es $N(\mu,\sigma^2)$ la función de log verosimilitud viene dada por:

\[LL(X|\mu,\sigma^2)=-\frac{n}{2}*log(2\pi\sigma^2)+\left(\frac{nS^2+n(\mu-\bar{X})^2}{2\sigma^2}\right)\]

Si derivamos respecto de μ e igualamos a cero:

\[\frac{d}{d\mu} LL(X|\mu,\sigma^2)=-\frac{2n(\mu-\bar{X})}{2\sigma^2} = 0\]

Despejando obtenemos el estimador para la media:

\[\hat{\mu}=\bar{X}\]

4.1.3 Estiamdor de la varianza

De forma similar, derivando respecto de σ^2 e igualando a cero la función de log-verosimilitud tenemos que el estimador para la varianza viene dado por:

\[\hat{\sigma}^2=S^2\]

Podemos ver que en las situaciones habituales los estimadores de los parámetros poblacionales coinciden con las funciones que nos permiten obtener las medidas de localización y dispersión muestrales.

El problema con la estimación puntual es que únicamente nos da un valor posible para el parámetro poblacional pero sin ninguna medida del posible error que estamos cometiendo, dado que la estimación obtenida depende de la muestra seleccionada. Dos muestras distintas podrían dar dos estimaciones distintas y por tanto dos valores para el parámetro poblacional. Para introducir una medida del error cometido con la muestra seleccionada se utiliza los procedimiento de inferencia basados en intervalos de confianza, pero antes de pasar con ellos es necesario describir un poco más el comportamiento aleatorio de los estimadores que acabamos de obtener.

4.2 Distribución en el muestreo

Dado que todos los estimadores se construyen a partir de una colección de realizaciones aleatorias $X_1,...X_n$ de la variable aleatoria $X$, resulta que dicho estimador es una nueva variable aleatoria (que toma valores según los datos observados de la muestra) y por tanto su distribución puede ser deducida a partir de las distribuciones de cada una de las $X_i$, utilizando la función de verosimilitud. En algunos casos (variables discretas) será necesario utilizar el Teorema Central del Límite para determinar una forma aproximada de dicha distribución de probabilidad que nos permita realizar los procesos inferenciales sin demasiada complejidad matemática. La distribución de los estimadores se conoce con el nombre de distribución en el muestreo

En los puntos siguiente se muestran las distribuciones en el muestro para los estimadores obtenidos en este apartado. Se eliminan todos los desarrollos matemáticos y simplemente se muestran las distribuciones obtenidas.

4.2.1 Distribución en el muestreo de una media poblacional con varianza poblacional conocida

Tenemos una población de N sujetos sobre la que se desea estudiar una variable aleatoria de tipo continuo ($X$) que sigue una distribución $N(\mu,\sigma^2)$ y cuyo parámetro de interés es la media ($\mu$) pero donde conocemos el valor de $\sigma^2$. Por la aplicación directa del Teorema Central del Límite la distribución en el muestreo de $\bar{X}$ viene dada por:

\[\bar{X} \sim N\left(\mu, \frac{\sigma^2}{n}\right)\]

y por tanto la variable tipificada tiene distribución Normal estándar, es decir:

\[\frac{\bar{X}-\mu}{\sigma/√n}∼N(0,1)\]

4.3 Distribución en el muestreo de una media poblacional con varianza poblacional desconocida

Cuando la varianza es desconocida también se puede obtener la distribución en el muestreo de la media muestral sin más que sustituir la varianza poblacional por un estimador. Tipificando tenemos que:

\[T = \frac{\bar{X} - \mu}{S/√(n-1)} = \frac{\bar{X} - \mu}{S_q/√n}\]

se distribuye según una distribución t de Student con n-1 grados de libertad,

\[T \sim t_{n-1}\]

4.4 Distribución en el muestreo de una varianza poblacional

En la situación poblacional anterior la distribución en el muestreo de la varianza si consideramos la variable aleatoria:

\[\chi^2 = \frac{nS^2}{\sigma^2} = \frac{(n-1)S_q^2}{\sigma^2}\]

que se distribuye según una distribución Chi cuadrado con n-1 grados de libertad,

\[\chi^2 \sim \chi_{n-1}^2\]

La obtención de esta distribución se hace a partir de la forma de la función de verosimilitud para una población Normal con ambos parámetros desconocidos.

4.5 Distribución en el muestreo para una proporción poblacional

Tenemos una población de N sujetos sobre la que se desea estudiar una variable aleatoria de tipo discreto ($X$) cuyo parámetro de interés es la proporción de sujetos ($\theta$) que cumplen con cierta condición. En esta situación si obtenemos una muestra de tamaño $n$ de dicha variable $X_1,...,X_n$ (donde cada uno de ellos toma el valor 1 si cumple con la condición y 0 si no cumple), la proporción de éxito muestral ($\hat{\theta}$) viene dada por:

\[\hat{\theta}=\frac{\sum_{i=1}^n X_i}{n}\]

En esta situación la distribución en el muestreo para $\hat{\theta}$, cuando $n$ es grande ($n \geq 30$), viene dada por:

\[\hat{\theta} \sim N\left(θ,\frac{θ(1-θ)}{n}\right)\]

de forma que la variable aleatoria tipificada $Z$ cumple que:

\[Z=\frac{\hat{\theta}-\theta}{\sqrt{\frac{θ(1-θ)}{n}}} \sim N(0,1)\]

La obtención de estas distribuciones en el muestreo nos permite realizar cálculos de probabilidades sobre dichas cantidades aleatorias, con lo que resulta posible conocer cuál es la probabilidad de que la media muestral supere cierto valor, y por tanto, podamos tener una mayor certeza del verdadero valor del parámetro poblacional.

4.6 Error estándar

Para cuantificar la bondad de la estimación obtenida se define el error estándar (es()) como la desviación típica de la distribución en el muestreo del estimador. De esta forma:

Error estándar de la media en una población Normal con varianza conocida

\[es(\bar{X})=\frac{\sigma}{\sqrt{n}}\]

Error estándar de la media en una población Normal con varianza desconocida

\[es(\bar{X})=\frac{S{\sqrt{n}}\]

Error estándar de una proporción en una población Bernouilli

\[es(\bar{X})=\sqrt{\frac{\hat{θ}(1-\hat{θ})}{n}}\]

5 Estimación por intervalos de confianza

Un intervalo de confianza al nivel $100*(1-\alpha)%$ representa la confianza que tenemos en que el verdadero valor del parámetro de la población se encuentre contenido entre los limites de dicho intervalo, que se construye a partir de la información muestral y la distribución en el muestreo del estimador. Si tenemos un intervalo de confianza al 95%, es decir $\alpha = 0.05$, lo que estamos indicando es que si obtuviéramos 100 muestras y calculáramos los 100 intervalos asociados, solo en 95 de ellos contendrían al verdadero valor del parámetro poblacional. Dado que habitualmente tomamos una única muestra debemos confiar en que el intervalo producido sea uno de los 95 que contiene al verdadero valor del parámetro poblacional. El valor de $\alpha$ se conoce como significatividad.

Supongamos que tenemos una población sobre la deseamos estudiar una variable aleatoria $X$ cuya función de distribución es conocida y viene caracterizada por el parámetro $\theta$, $f(X|\theta)$. Vamos a obtener una muestra de tamaño $n$, $X_1,...,X_n$ y consideramos el estimador $\hat{\theta}$ de $\theta$ del que conocemos su distribución en el muestreo, $f_n$,y podemos especificar su error estándar, $es(\hat{\theta})$. Si fijamos el valor de $\alpha$ el intervalo de confianza para el parámetro poblacional viene dado por la expresión:

\[IC_{1-\alpha} (\theta)=(\hat{\theta}-q_{\alpha/2}*es(\hat{\theta}),\hat{\theta}+q_{1-\alpha/2}*es(\hat{\theta}))\]

donde $q_{\alpha/2}$ y $q_{1-\alpha/2}$ son los cuantiles $\alpha/2$ y $1-\alpha/2$ de la distribución en el muestreo, es decir,

\[P(\hat{\theta} \leq q_{\alpha/2})=\alpha/2\]$

\[P(\hat{\theta} \leq q_{1-\alpha/2})=1-\alpha/2\]

Si la distribución en el muestreo es simétrica $q_{1-\alpha/2}= - q_{\alpha/2}$

Antes de estudiar la forma explicita de los intervalos de confianza para una proporción, una media, y una varianza vamos a ver una herramienta de simulación que nos permite comprobar el funcionamiento de dichos intervalos. El funcionamiento de la aplicación es:

Fijar valor del parámetro poblacional
Fijar el tamaño de la muestra
Establecer el límite de confianza
Establecer el número de muestras de trabajo y simularlas representando los intervalos de confianza obtenidos.
Podemos ver entonces cuantos de esos intervalos contienen al verdadero valor del parámetro.

5.1 Intervalo de confianza para una proporción

El intervalo de confianza al nivel $100*(1-\alpha)%$ para una proporción poblacional viene dado por:

\[IC_{1-\alpha} (\theta)=\left(\hat{\theta}-q_{1-\alpha/2}*\sqrt{\frac{\hat{θ}(1-\hat{θ})}{n}},\hat{\theta}+q_{1-\alpha/2}*\sqrt{\frac{\hat{θ}(1-\hat{θ})}{n}})\right)\] donde $q_{1-\alpha/2}$ es el cuantil $1-\alpha/2$ de una distribución Normal estándar, $\hat{\theta}$ es la proporción muestral y $n$ es el tamaño muestral.

Ejemplo. Como parte de un estudio sobre la salud alimenticia de las jóvenes entre 12 y 15 se midieron los niveles de hierro de 786 chicas y se detecto que 71 de ellas tenían deficiencia de hierro. Veamos como obtener un intervalo de confianza al 95% para la proporción de mujeres entre 12 y 15 años con deficiencia de hierro.

# Para realizar el proceso de estimación utilizamos la función 
# prop.test()
deficiencia <- 71
muestra <- 786
# Estimador puntual
analisis <- prop.test(deficiencia, muestra, conf.level = 0.95)
analisis$estimate

##          p 
## 0.09033079

# Intervalo de confianza
analisis$conf.int

## [1] 0.07166294 0.11310912
## attr(,"conf.level")
## [1] 0.95

La conclusión que podemos extraer es: “Con una confianza del 95% la proporción de mujeres entre 12 y 15 años con deficiencia de hierro se sitúa entre el 7.61% y el 11.3%. La estimación de la proporción de mujeres con deficiencia de hierro se sitúa en el 9.03%”

Veamos gráficamente la representación del intervalo de confianza. Se puede ver la distribución en el muestreo, la estimación obtenida (línea azul), los límites del intervalo de confianza para el parámetro (líneas rojas), y el intervalo de confianza obtenido (zona amarilla).

# Distribución en el muestreo
# Rango de valores (Tomamos solo valores entre 0 y 2 dada la esimacion puntual obtenida)
probabilidades <- seq(0,0.2,0.0001)
# media y desviación tipica de la distribución en el muestreo
media <- analisis$estimate
dtip <-  sqrt(media*(1-media)/muestra)
densidad <- dnorm(probabilidades,media,dtip)

# Función para representar el IC
dnorm_IC <- function(x,m,sd,ic){
  norm_ic <- dnorm(x,m,sd)
  # Valores NA fuera del rango del intervalo de confianza:
  norm_ic[x <= ic[1] | x >= ic[2]] <- NA
  return(norm_ic)
}

# Plot:
df <- data.frame(x = probabilidades, y = densidad)
# Gráfico
base <- ggplot(df,aes(x,y)) + 
  geom_line() + 
  scale_x_continuous(breaks = seq(0, 0.2, 0.02)) + 
  labs(x = "Probabilidad de éxito") + 
  geom_vline(xintercept = c(analisis$conf.int[1], analisis$conf.int[2]), colour = "red") + 
  geom_vline(xintercept = c(analisis$estimate), colour = "blue") + 
  stat_function(fun = dnorm_IC, args = list(m=media, sd = dtip, ic = analisis$conf.int), geom = "area", fill = "yellow", alpha = 0.3)
base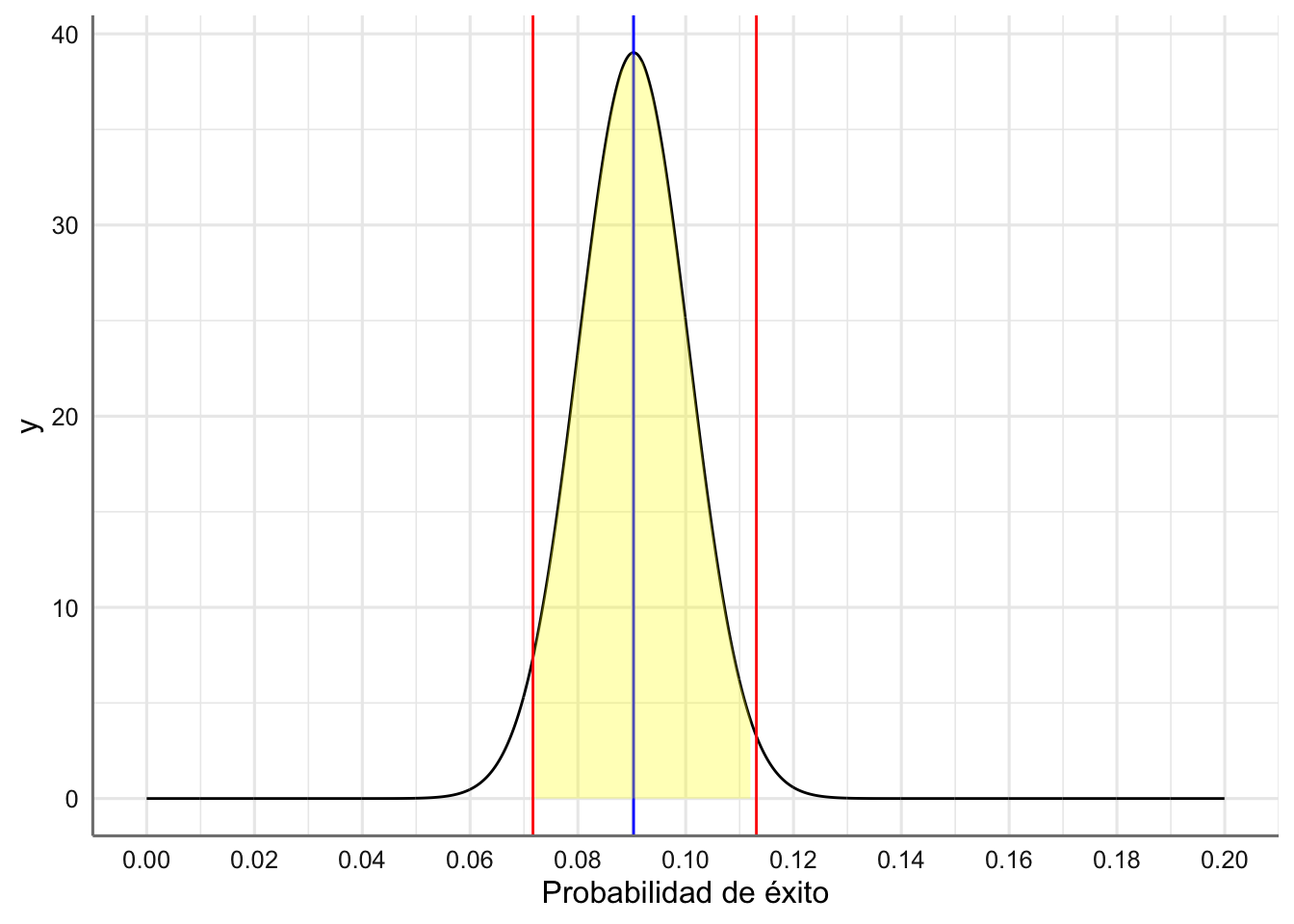

5.2 Intervalo de confianza para la media

El intervalo de confianza al nivel $100*(1 - \alpha)\%$ para la media de una población Normal con varianza desconocida viene dado por:

\[IC_{1-\alpha}(\mu) = \left(\bar{x} - q_{1-\alpha/2}*\frac{s}{\sqrt{n-1}},\bar{x} + q_{1-\alpha/2}*\frac{s}{\sqrt{n-1}}\right)\] donde $q_{1-\alpha/2}$ es el cuantil $1-\alpha/2$ de una distribución $t$ se Student con $n-1$ grados de libertad, $\bar x$ es la media muestral, $s$ es la desviación típica muestral, y $n$ es el tamaño de muestra.

Ejemplo. Human beta-endorphin (HBE) es una endorfina secretada pro la galdula pituitaria bajo condiciones de stres. Un investigador lleva a cabo una investigación para conocer si un programa de ejercico regular puede reducir el nivel de stres. Para ello se toman 10 sujetos y se mide su nivel de HBE (en pg/ml) antes de comenzar el porhgrama y seis meses después de manterner el prohgrama de ejercicio físico. La diferencia (medida antes - medida después) en los niveles de HBE de los diez sujetos vienen dados a continuación: 20, 18, 28, 0, 7, 34, 16, -5, 8, 4. Veamos como obtener un intervalo de confianza al 95% para la reducción media del nivel de HBE después del programa de ejercicio.

# Para realizar el proceso de estimación utilizamos la función t.test()
datos <- c(20, 18, 28, 0, 7, 34, 16, -5, 8, 4)
# Estimador puntual
analisis <- t.test(datos,conf.level = 0.95)
analisis$estimate

## mean of x 
##        13

# Intervalo de confianza
analisis$conf.int

## [1]  4.129062 21.870938
## attr(,"conf.level")
## [1] 0.95

La reducción media del nivel de HBE tras el programa de ejercicio se ha situado en 13 pg/ml. Con una confianza del 95% la reducción media del nivel de HBE se sitúa entre 4.13 pg/ml y 21.87 pg/ml.

5.3 Intervalo de confianza para la varianza

El intervalo de confianza al nivel $100*(1 - \alpha)\%$ para la varianza de una población Normal viene dado por:

\[IC_{1-\alpha}(\sigma^2) = \left(\frac{(n-1)s^2}{q_{1-\alpha/2}}, \frac{(n-1)s^2}{q_{\alpha/2}}\right)\] donde $q_{1-\alpha/2}$ y $q_{\alpha/2}$ son los cuantiles $1-\alpha/2$ y $\alpha/2$ de una distribución $Chi^2$ con $n-1$ grados de libertad, $s^2$ es la varianza muestral, y $n$ es el tamaño de muestra.

Ejemplo. Para los datos del ejemplo anterior obtén un intervalo de confianza al 95% de la varianza poblacional de la reducción de HBE tras el programa de ejercicios.

# Para realizar el proceso de estimación debemos crear una función para la otención del IC
# Función para el IC
var.IC <-function(x, conf.level)
{
  n <- length(x)
  varianza <- var(x)
  alfa <- 1 - conf.level
  l1 <- (n - 1) * varianza / qchisq(1 - alfa / 2,n - 1)
  l2 <- (n - 1) * varianza / qchisq(alfa / 2,n - 1)
  ic <- c(l1,l2)
  return(ic)
}

## Obtención del IC
datos <- c(20, 18, 28, 0, 7, 34, 16, -5, 8, 4)
# Estimador puntual
var(datos)

## [1] 153.7778

# Intervalo de confianza
var.IC(datos,0.95)

## [1]  72.75492 512.51866

La variabilidad de la reducción del nivel de HBE tras el programa de ejercicio se ha situado en 153.78. Con una confianza del 95% la variabilidad de la reducción del nivel de HBE se sitúa entre 72.75 y 512.52.

6 Contraste de hipótesis

Un procedimiento de contraste de hipótesis tiene por objetivo valorar la evidencia proporcionada por los datos a favor de alguna hipótesis planteada sobre el parámetro o parámetros que identifican a la población bajo estudio. En el caso más sencillo, imaginemos que tenemos un parámetro poblacional $\theta$ que puede tomar valores en el conjunto $\Theta$

Ejemplo: Estamos interesados en conocer si la proporción de alumnos que superan la asignatura de Estadística en la convocatoria de junio es mayor o igual al 50%. El parámetro de interés, $\theta$, es entonces la proporción de aprobados en la convocatoria de junio, y el conjunto de posibles valores de dicho parámetro puede tomar valores entre 0 y 100. El contraste de interés viene dado por:

\[\theta \geq 0.5\]

Para resolver cualquier procedimiento de contraste debemos establecer dos subconjuntos disjuntos del espacio paramétrico, $\Theta_0$ y $\Theta_1$ cumpliendo que $\Theta = \Theta_0 \cup \Theta_1$, con los posibles valores del parámetro de interés que denominamos hipótesis:

Hipótesis nula, que se denota por $H_0$, y que generalmente expresa el valor o conjunto de valores del parámetro,$\Theta_0$, que corresponde con la idea que deseamos verificar.
Hipótesis alternativa, que se denota por $H_a$, y que generalmente expresa el valor o conjunto de valores complementarios, $\Theta_1$, a los dados en la hipótesis nula. Formalmente, el problema de contraste de hipótesis se plantea como: \[\left\{\begin{array}{ll} H_0: & \theta \in \Theta_0\\ H_a: & \theta \in \Theta_1\end{array}\right.\]

Estas hipótesis se deben establecer antes de obtener la información muestral ya que deben reflejar conocimiento previo sobre el parámetro poblacional de interés. La muestra recogida aportará las evidencias suficientes para rechazar o no rechazar la hipótesis nula planteada.

En nuestro ejemplo

\[\left\{\begin{array}{ll} H_0: & \theta \geq 0.5\\ H_a: & \theta < 0.5\end{array}\right.\]

6.1 Posibles contrastes

Dada la estructura del procedimiento de contraste se plantean únicamente dos tipos de posibilidades:

Contraste bilateral: El conjunto de posibles valores del parámetro de interés establecidos en la hipótesis nula se concentra en un único valor, $\theta_0$, es decir, \[\left\{\begin{array}{ll} H_0: & \theta = \theta_0\\ H_a: & \text{ no } \theta_0 \end{array}\right.\]
Contraste unilateral: El conjunto de posibles valores del parámetro de interés establecidos en la hipótesis nula se concentra en un conjunto de valores dado por una desigualdad con respecto a $\theta_0$, es decir,

\[\left\{\begin{array}{ll} H_0: & \theta \geq \theta_0\\ H_a: & \text{ no } \theta_0 \end{array}\right.\] \[\left\{\begin{array}{ll} H_0: & \theta \leq \theta_0\\ H_a: & \text{ no } \theta_0 \end{array}\right.\]

6.2 Resolución de contraste

Para establecer evidencias a favor de una hipótesis u otra se debe:

Elegir un nivel de significación, $\alpha$, que refleja el riesgo que tomamos cuando rechazamos la hipótesis nula o probabilidad de rechazar la hipótesis nula cuando es cierta, es decir: \[\alpha = P(\text{ Rechazar } H_0 | H_0 \text{ cierta})\]

Normalmente se eligen valores pequeños, $\alpha=0,1, 0.05, y 0.01$ que resultan los equivalentes del 90%, 95%, y 99% al nivel de confianza en el proceso de estimación.

Ejemplo. Si tomamos una significación del 5%, tendremos una probabilidad de 0.05 de rechazar la hipótesis nula cuando en realidad es cierta.

Establecer estadístico de contraste ($EC$) que nos permita, utilizando la información muestral, estudiar la compatibilidad de dicha información con la hipótesis nula planteada. La forma habitual suele ser:

\[EC = \frac{\theta - \hat{\theta}}{es(\hat{\theta})}\]

donde $\hat{\theta}$ es un estimador puntual del parámetro poblacional y $es(\hat{\theta})$ es una medida del error estándar que cometemos con el estimador utilizado.

Para decidir sobre el contraste planteado utilizaremos el $p-valor$, que representa la probabilidad de que el valor del EC sea superior al valor de dicho estadístico evaluado en los datos muestrales, $EC_{obs}$,atendiendo a la distribución en el muestreo, es decir,

\[p-valor = P(EC \geq EC_{obs})\]

Para tomar una decisión sobre el contraste miramos si el p-valor obtenido y concluimos que:

Si $p-valor < \alpha$, tenemos evidencias estadísticas suficientes para rechazar la hipótesis nula a favor de la hipótesis alternativa.
Si $p-valor > \alpha$, no tenemos evidencias estadísticas suficientes para rechazar la hipótesis nula.

A continuación vemos como ampliar el procedimiento de contraste para una proporción y una media. El proceso de contraste sobre una varianza no suele tener interés práctico ya que resulta más habitual obtener un intervalo de confianza. Como veremos en el tema siguiente, si que resulta relevante el proceso de contraste cuando se involucran dos poblaciones y estamos interesados en comparar la variabilidad de ambas.

6.3 Una proporción

Tenemos una población de tipo Bernouilli que viene especificada a partir de la proporción de sujetos que alcanzan el “éxito”, $\theta$, y una estimación de dicho parámetro dada por $\hat{\theta}$. Anteriormente ya hemos visto que para una muestra de tamaño $n$ el error estándar viene dado por:

\[es(\hat{\theta}) = \sqrt{\frac{\hat{\theta} (1-\hat{\theta}))}{n}}.\]

Tanto para el contraste unilateral como el bilateral el estadístico de contraste viene dado por: \[EC = \frac{\theta - \hat{\theta}}{\sqrt{\frac{\hat{\theta} (1-\hat{\theta}))}{n}}}\] cuya distribución en el muestreo es $N(0,1)$. Dicho estadístico valora lo cerca que queda el estimador respecto del valor poblacional teniendo en cuenta el error cometido en el proceso de estimación.

Ejemplo. Se está estudiando el efecto de los rayos X sobre la viabilidad huevo-larva en Tribolium casteneum. Se plantean tres situaciones: a) la proporción de viabilidad es del 50%, b) la proporción de viabilidad es superior al 60%, c) la proporción de viabilidad es inferior al 55%. Los contrastes asociados con cada situación son: \[\left\{\begin{array}{ll} H_0: & \theta = 0.5\\ H_a: & \theta \neq 0,5 \end{array}\right.\] \[\left\{\begin{array}{ll} H_0: & \theta \geq 0.6\\ H_a: & \theta < 0.6 \end{array}\right.\] \[\left\{\begin{array}{ll} H_0: & \theta \leq 0.55\\ H_a: & \theta > 0.55 \end{array}\right.\]

Para verificar dichios contarstes se irradiaron 1000 huevos de los que resultaron 572 larvas.

Para resolver contrastes en estas situaciones utiliamos la función prop.test()

# Situación 1
n <- 1000
larvas <- 572
# Debemos fijar el valor del contraste, el tipo (two.sided), y el nivel de significación o su análogo como el nivel de confianza
prop.test(larvas, n, p = 0.5, alternative = "two.sided", conf.level = 0.95)

## 
##  1-sample proportions test with continuity correction
## 
## data:  larvas out of n
## X-squared = 20.449, df = 1, p-value = 6.124e-06
## alternative hypothesis: true p is not equal to 0.5
## 95 percent confidence interval:
##  0.5406126 0.6028273
## sample estimates:
##     p 
## 0.572

El p-valor resultante es 6.124e-06 que resulta inferior al nivel de significación prefijado de 0.05. Por lo tanto hay evidencias para rechazar la hipótesis nula y concluir que la proporción de viabilidad una vez irradiamos los huevos con rayos X es distinta del 50%.

# Situación 2
n <- 1000
larvas <- 572
# Debemos fijar el valor del contraste, el tipo (two.sided), y el nivel de significación o su análogo como el nivel de confianza
prop.test(larvas, n, p = 0.6, alternative = "less", conf.level = 0.95)

## 
##  1-sample proportions test with continuity correction
## 
## data:  larvas out of n
## X-squared = 3.151, df = 1, p-value = 0.03794
## alternative hypothesis: true p is less than 0.6
## 95 percent confidence interval:
##  0.0000000 0.5980029
## sample estimates:
##     p 
## 0.572

El p-valor resultante es 0.03794 que resulta inferior al nivel de significación prefijado de 0.05. Por lo tanto hay evidencias para rechazar la hipótesis nula y concluir que la proporción de viabilidad una vez irradiamos los huevos es mayor o igual al 60%.

# Situación 2
n <- 1000
larvas <- 572
# Debemos fijar el valor del contraste, el tipo (two.sided), y el nivel de significación o su análogo como el nivel de confianza
prop.test(larvas, n, p = 0.55, alternative = "greater", conf.level = 0.95)

## 
##  1-sample proportions test with continuity correction
## 
## data:  larvas out of n
## X-squared = 1.8677, df = 1, p-value = 0.08587
## alternative hypothesis: true p is greater than 0.55
## 95 percent confidence interval:
##  0.545601 1.000000
## sample estimates:
##     p 
## 0.572

El p-valor resultante es 0.08587 que resulta superior al nivel de significación prefijado de 0.05. Por lo tanto hay evidencias para no rechazar la hipótesis nula y concluir que la proporción de viabilidad una vez irradiamos los huevos puede ser menor o igual al 55%.

6.4 Una media

Tenemos una población Normal que viene especificada a partir de la media ($\mu$) y varianza ($\sigma^2$). Por el momento estamos interesados en los procedimientos de contraste sobre la media cuando desconocemos el valor de la varianza poblacional. Tomamos los estimadores habituales $\bar X$, $S^2$, y consideramos el error estándar: \[es(\bar X) = \frac{s}{\sqrt{n-1}}.\] Tanto para el contraste unilateral como el bilateral el estadístico de contraste viene dado por: \[EC = \frac{\mu - \bar X}{\frac{s}{\sqrt{n-1}}}\] cuya distribución en el muestreo es una $t$ de Student con n-1 grados de libertad.

Ejemplo. La concentración media de dióxido de carbono en el aire en una cierta zona no es habitualmente mayor que 335 ppmv (partes por millon en volumen). Se sospecha que esta concentración es mayor en la capa de aire más próxima a la superficie. Los investigadores quieren comprobar si la concentración en la superficie es mayor o igual a dicho valor con una significación de 0.05. Se plantea el contraste:

\[\left\{\begin{array}{ll} H_0: & \mu \geq 335\\ H_a: & \mu < 335 \end{array}\right.\] Para tratar de ratificar su hipótesis Se ha analizado el aire en 20 puntos elegidos aleatoriamente a una misma altura cerca del suelo, resultando los siguientes datos: 332, 320, 312, 270, 330, 354, 356, 310, 341, 313, 223, 224, 305, 321, 325, 333, 332, 345, 312, 331.

Para resolver este contraste utilizamos la función t.test()

datos <- c(332, 320, 312, 270, 330, 354, 356, 310, 341, 313, 223, 224, 305, 321, 325, 333, 332, 345, 312, 331)
# Debemos fijar el valor del contraste, el tipo (two.sided), y el nivel de significación o su análogo como el nivel de confianza
t.test(datos, mu = 335, alternative = "less", conf.level = 0.95)

## 
##  One Sample t-test
## 
## data:  datos
## t = -2.5219, df = 19, p-value = 0.01038
## alternative hypothesis: true mean is less than 335
## 95 percent confidence interval:
##      -Inf 328.5403
## sample estimates:
## mean of x 
##    314.45

El p-valor resultante es 0.01038 que resulta inferior al nivel de significación prefijado de 0.05. Por lo tanto hay evidencias para rechazar la hipótesis nula y concluir que la media del nivel de dióxido de carbono en la capa de aire más cercana a la superficie es menor a 335 ppmv.

7 Inferencia para dos poblaciones

En este tema completamos el estudio inferencial visto en el tema anterior. Más concretamente se muestra el análisis inferencial para la comparación de dos proporciones o dos medias. En la situación de la comparación de dos medias veremos también la influencia que tiene el estudio de las varianzas de ambas poblaciones. No se presentan todas las formulaciones y distribuciones asociadas con estos análisis sino que se presenta directamente la forma de resolverlos. se pueden consultar los desarrollos estadísticos en cualquier libro de estadística básica.

7.1 Poblaciones Bernouilli

Sean dos poblaciones sobre las que se desea estudiar una misma característica de interés de tipo discreto (1 = éxito; 0 = fracaso), que identificamos por $X_{P1}$ y $X_{P2}$ respectivamente. El parámetro de interés en cada población es la proporción de éxito, $\theta_1$ y $\theta_2$ respectivamente, pero el interés inferencial principal es la comparación de $\theta_1$ y $\theta_2$, es decir, comprobar si la proporción de éxito en la población 1 es comparable con la proporción de éxito en la población 2. Para realizar dicha comparación se utiliza el parámetro que viene dado por la diferencia de proporciones de éxito: \[\theta_1 - \theta_2\]

Si las proporciones son iguales la diferencia debería estar próximo a cero, mientras que si son distintas la diferencia sería estadísticamente diferente a cero.

7.2 Poblaciones Normales

Sean dos poblaciones normales sobre las que se desea estudiar una misma característica de interés de tipo continuo que identificamos por $X_{P1}$ y $X_{P2}$ respectivamente. Cada población viene caracterizada por su media y varianza, es decir, \[X_{P1} \sim N(\mu_1,\sigma^2_1) \text{ ; } X_{P2} \sim N(\mu_2,\sigma^2_2)\] En este caso el proceso inferencial se centras en todos los parámetros, medias y varianzas, pero habitualmente el objetivo inferencial principal se centra en comprobar si las medias de ambas poblaciones pueden considerarse iguales o diferentes. Por tanto, el parámetro de interés es la diferencia de medias poblacionales: \[\mu_1 - \mu_2\] Como ocurre con las proporciones, se considera que las medias son iguales cuando la diferencia de las medias es estadísticamente cero. Sin embargo, para poder realizar dicho estudio es necesario conocer en primer lugar si las varianzas de ambas poblaciones pueden considerarse iguales o distintas. En función del resultado de dicha comparación se deberá utilizar un proceso inferencial diferente para la comparación de medias. Dado que las varianzas siempre son positivas el parámetro de interés para la comparación de varianzas viene dado por su cociente: \[\frac{\sigma^2_1}{\sigma^2_1}\]

7.3 Inferencia para dos proporciones

Dada una muestra aleatoria en cada una de las poblaciones de interés de tamaños $n_1$ y $n_2$, utilizamos los estimadores habituales de la proporción poblacional dados por las proporciones muestrales $\hat{\theta}_1$ y $\hat{\theta}_2$. Como ya hemos dicho el parámetro objetivo en esta situación es la diferencia de proporciones poblacionales.

Ejemplo: La angina de pecho es una afección cardíaca en la que el paciente sufre ataque períodicos de dolor. En un estudio para analizar la efectividad de una nueva droga para prevenir dichos ataques se han seleccionado dos grupos de sujetos. Al primero de ellos se les dará la nueva droga mientras que al otro se les dará el tratamiento estándar. Los resultados obtenidos después de un periodo de 28 semanas viene dados en la tabla siguiente:

Estado / Tratamiento	Droga nueva	Droga antigua
Sin angina	44	19
Con angina	116	128
Total	160	147

Se está interesado en conocer con una confianza del 90% (significación de 0.1) si la porporción de pacientes mejorados con la nueva droga es diferente con respecto a la droga antigua.

library(tidyverse)
# carga de datos 
muestra <- c(160,147) 
mejoras <- c(44,19) 
# Tabla 
res <- data.frame(mejoras, muestra)
colnames(res) <- c("mejoras","muestra")
res

##   mejoras muestra
## 1      44     160
## 2      19     147

7.4 Estimador puntual

El estimador puntual de la diferencia de proporciones poblacionales se consigue partir de los estimadores puntuales de cada una de las proporciones de éxito muestrales.

Para los datos de nuestro ejemplo, si la población 1 identifica a los usjetos que toman la nueva droga y la pobalción 2 a los que toman la droga antigua, tendríamos: $\widehat{\theta_1 - \theta_2} = \widehat{\theta_1} - \widehat{\theta_2} = \frac{44}{160} - \frac{19}{147} = 0.1457$

Se observa una diferencia en la mejora de los sujetos del 14.57% de los que toman la droga nueva frente a los que toman la droga estándar.

7.5 Estimador por intervalos de confianza

Para obtener el intervalo de confianza para la diferencia de proporciones utilizamos la función prop.test(). Esta función también nos permite realizar el correspondiente contarte pero por le momento solo pediremos los resultados referidos al intervalo de confianza.

analisis <- prop.test(mejoras,muestra,conf.level = 0.90)
# Intervalo de confianza
analisis$conf.int

## [1] 0.0654468 0.2260498
## attr(,"conf.level")
## [1] 0.9

Para los datos de nuestro ejemplo el intervalo de confianza al 90% indica que la diferencia de proporciones de mejora entre los que usan la droga nueva frente a os que usan la droga estándar se sitúa entre el 6.5% y el 22.6%

7.6 Contraste de hipótesis

EL contraste habitual en esta situación viene dado por:

\[\left\{\begin{array}{ll} H_0: & \theta_1 = \theta_2\\ H_a: & \theta_1 \neq \theta_2 \end{array}\right.\] donde estamos interesados en verificar si las proporciones de éxito poblacionales pueden considerarse iguales o distintas.

Para los datos de nuestro ejemplo tenemos:

analisis <- prop.test(mejoras,muestra,conf.level = 0.90)
# Resultados completos
analisis

## 
##  2-sample test for equality of proportions with continuity correction
## 
## data:  mejoras out of muestra
## X-squared = 9.1046, df = 1, p-value = 0.00255
## alternative hypothesis: two.sided
## 90 percent confidence interval:
##  0.0654468 0.2260498
## sample estimates:
##    prop 1    prop 2 
## 0.2750000 0.1292517

Dado que el pvalor obtenido (0.00255) es inferior al nivel de siginificación prefijado (0.1) hay eviedencias estadísticas para rechazar la hipótesis nula, es decir, hay evidendaicas para concluir que las proporciones de mejora con mabsa drogas son distintas. Además el intervalo de confianza ya nos indicaba qye dicha mejoría era a favor de la droga nueva con los valores obtenidos en el aprtado anterior

Podríamos plantearnos contrastes unilaterales pero siempre antes de ver los resultados muestrales. Si estamos tratando de probar un nuevo tratamiento lo más lógico hubiera sido plantear el contraste: \[\left\{\begin{array}{ll} H_0: & \theta_1 = \theta_2\\ H_a: & \theta_1 > \theta_2 \end{array}\right.\]

En nuestro ejemplo:

analisis <- prop.test(mejoras,muestra,alternative = "greater", conf.level = 0.90)
# Resultados completos
analisis

## 
##  2-sample test for equality of proportions with continuity correction
## 
## data:  mejoras out of muestra
## X-squared = 9.1046, df = 1, p-value = 0.001275
## alternative hypothesis: greater
## 90 percent confidence interval:
##  0.08174166 1.00000000
## sample estimates:
##    prop 1    prop 2 
## 0.2750000 0.1292517

La conclusión es que rechazamos que las proporciones de mejora sean iguales frente a que la proporción de de mejora en la población 1 sea mayor al de la población 2.

7.7 Inferencia para dos medias

Los problemas de inferencia asociados con la comparación de dos medias poblacionales para variables Normales presentan diferentes situaciones:

Estudio de dos poblaciones independientes con variabilidades iguales
Estudio de dos poblaciones independientes con variabilidades distintas
Estudio de la evolución de una población (medidas antes - después)

A continuación se detalla como realizar el análisis de cada uno de ellos, pero antes de pasar con ellos debemos estudiar el problema de como comparar las variabilidades en dos poblaciones independientes. Presentamos en primer lugar los diferentes ejemplos de trabajo.

Ejemplo 1. Para realizar un estudio de la concentración de una hormona en una solución vamos a utilizar dos métodos. Disponemos de 10 dosis preparadas en el laboratorio y medimos la concentración de cada una con los dos métodos. Se obtienen los siguientes resultados:

Dosis	1	2	3	4	5	6	7	8	9	10
Método A	10.7	11.2	15.3	14.9	13.9	15	15.6	15.7	14.3	10.8
Método B	11.1	11.4	15	15.1	14.3	15.4	15.4	16	14.3	11.2

Se desea realizar el estudio inferencial con una confianza del 95%

Ejemplo 2. Una compañía contrata 10 tubos con filamentos del tipo A y 12 tubos con filamentos del tipo B. Las duraciones medias observadas se muestran en la siguiente tabla:

Tipo/Duración	1	2	3	4	5	6	7	8	9	10	11	12
A	1614	1094	1293	1643	1466	1270	1340	1380	1081	1497
B	1383	1138	920	1143	1017	961	1627	821	1711	865	1662	1698

Se desea realizar el estudio inferencial con una confianza del 90%

Ejemplo 3. En una unidad del sueño se está probando con un nuevo somnífero. Para comprobar su eficacia se toman 10 individuos al azar. Un día no se les suministra el somnífero y se les anota el número de horas de sueño, al día siguiente se les suministra y se vuelve a comprobar las horas de sueño. Los resultados entes y después del tratamiento han sido los siguientes:

Instante/Sujeto	1	2	3	4	5	6	7	8	9	10
Antes	7.3	8.2	6.3	5.2	6.9	5.8	5.3	7.1	6.9	8.1
Después	8.2	7.9	6.4	5.1	7.1	6.3	5.9	8.2	7.1	7.7

Se desea realizar el estudio inferencial con una confianza del 90%

7.8 Análisis de dos varianzas poblacionales

Supongamos que tenemos dos poblaciones Normales y que deseamos comprobar si la variabilidad en ambas poblaciones pueden considerarse estadísticamente iguales o distintas. Como ya vimos en la introducción este problema se reduce a la comparación de ambas varianzas a través del cociente de ambas. Para resolver este problema utilizamos la función var.test(). El contraste utilizado es:

\[\left\{\begin{array}{ll} H_0: & \frac{\sigma^2_1}{\sigma^2_2} = 1\\ H_a: & \frac{\sigma^2_1}{\sigma^2_2} \neq 1 \end{array}\right.\]

Para los datos del ejemplo 1

# Cargamos los datos
MetodoA <- c(10.7, 11.2, 15.3, 14.9, 13.9, 15, 15.6, 15.7, 14.3, 10.8)
MetodoB <- c(11.1, 11.4, 15, 15.1, 14.3, 15.4, 15.4, 16, 14.3, 11.2)
var.test(MetodoA, MetodoB, conf.level = 0.95)

## 
##  F test to compare two variances
## 
## data:  MetodoA and MetodoB
## F = 1.1229, num df = 9, denom df = 9, p-value = 0.8657
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  0.2789187 4.5208902
## sample estimates:
## ratio of variances 
##           1.122925

Dado que el pvalor resultante es superior a la significatividad prefijada, tenemos evidencias estadísticas para no rechazar la hipótesis nula, y por tanto concluir que ambas varianzas no pueden considerarse distintas.

Para los datos del ejemplo 2

# Cargamos los datos
TipoA <- c(1614,1094,1293,1643,1466,1270,1340,1380,1081,1497)
TipoB <- c(1383,1138,920,1143,1017,961,1627,821,1711,865,1662,1698)
var.test(TipoA, TipoB, conf.level = 0.9)

## 
##  F test to compare two variances
## 
## data:  TipoA and TipoB
## F = 0.3052, num df = 9, denom df = 11, p-value = 0.08543
## alternative hypothesis: true ratio of variances is not equal to 1
## 90 percent confidence interval:
##  0.1053789 0.9468807
## sample estimates:
## ratio of variances 
##          0.3052007

Puesto que el pvalor es inferior a la significatividad prefijada podemos concluir que hya evidencias estad´sitivas apra concluir que las varaibilidades en ambas poblaciones pueden considerarse distintas.

En todos los análisis inferenciales asociados con la comparación de dos medias utilizamos la función t.test(), aunque con difrentes opciones en función de que las varianzas sean iguales o no, o de que las muestras sean independientes o no.*

7.9 Dos medias para poblaciones independientes con varianzas iguales

El contraste de hipótesis para esta situación viene dado por:

\[\left\{\begin{array}{ll} H_0: & \mu_1 = \mu_2\\ H_a: & \mu_1 \neq \mu_2 \end{array}\right.\]

Utilizamos los datos del ejemplo 1, ya que como hemos visto anteriormente las varianzas de ambas pobalciones puden considerarse iguales

# Cargamos los datos
MetodoA <- c(10.7, 11.2, 15.3, 14.9, 13.9, 15, 15.6, 15.7, 14.3, 10.8)
MetodoB <- c(11.1, 11.4, 15, 15.1, 14.3, 15.4, 15.4, 16, 14.3, 11.2)
t.test(MetodoA, MetodoB, alternative = "two.sided", var.equal = TRUE, conf.level = 0.95)

## 
##  Two Sample t-test
## 
## data:  MetodoA and MetodoB
## t = -0.20323, df = 18, p-value = 0.8412
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -2.040763  1.680763
## sample estimates:
## mean of x mean of y 
##     13.74     13.92

Dado que el pavalor es superior a la significatividad prefijada, hay evidencias estadísticas para concluir que las medias de concentración con ambos métodos pueden considerarse iguales

7.10 Dos medias para poblaciones independientes con varianzas distintas

El constaste de hipótesis en esta situación es el mismo que en el punto anterior.

Utilizamos los datos del ejemplo 2, ya que como hemos visto anteriormente las varianzas de ambas pobalciones puden considerarse distintas

# Cargamos los datos
TipoA <- c(1614,1094,1293,1643,1466,1270,1340,1380,1081,1497)
TipoB <- c(1383,1138,920,1143,1017,961,1627,821,1711,865,1662,1698)
t.test(TipoA, TipoB, alternative = "two.sided", var.equal = TRUE, conf.level = 0.9)

## 
##  Two Sample t-test
## 
## data:  TipoA and TipoB
## t = 0.98508, df = 20, p-value = 0.3364
## alternative hypothesis: true difference in means is not equal to 0
## 90 percent confidence interval:
##  -91.82747 336.42747
## sample estimates:
## mean of x mean of y 
##    1367.8    1245.5

Dado que el pvalor es superior a la significatividad prefijada, hay evidencias estadísticas para concluir que las medias de duración de los filamentos en ambos tipos pueden considerarse iguales

7.11 Dos medias para poblaciones emparejadas

Es muy habitual que en ciertas situaciones experimentales nos encontramos que queremos estudiar la evolución (medidas antes -después) de un grupo de sujetos después de ser sometidos a cierta prueba experimental. En esta caso no tenemos dos poblaciones independientes sino sólo una que medimos en dos ocasiones. Por tanto, los procedimientos anteriores tienen que ser modificados para tener en cuenta esta situación. El constaste de hipótesis para esta situación viene dado por:

\[\left\{\begin{array}{ll} H_0: & \mu_{antes} = \mu_{despues}\\ H_a: & \mu_{antes} \neq \mu_{despues} \end{array}\right.\]

De nuevo podemos utilizar la función t.test() con el parámetro paired.

Utilizamos los datos del ejemplo 3, donde tenemos una única muestra se sujetos

# Cargamos los datos
antes <- c(7.3,8.2,6.3,5.2,6.9,5.8,5.3,7.1,6.9,8.1)
despues <- c(8.2,7.9,6.4,5.1,7.1,6.3,5.9,8.2,7.1,7.7)
t.test(antes, despues, alternative = "two.sided", paired = TRUE, var.equal = TRUE, conf.level = 0.9)

## 
##  Paired t-test
## 
## data:  antes and despues
## t = -1.7925, df = 9, p-value = 0.1066
## alternative hypothesis: true difference in means is not equal to 0
## 90 percent confidence interval:
##  -0.566341394  0.006341394
## sample estimates:
## mean of the differences 
##                   -0.28

Dado que el pvalor es superior a la significatividad prefijada, hay evidencias estadísticas para concluir que las horas medias de sueño antes y después de tomar el somnifero no pueden considerarse estadísticamente distintas

8 Tests no paramétricos

Todos los procedimientos de inferencia sobre dos medias se basan en la suposición de que las variables sobre las que estamos trabajando se puede considerar que se distribuyen normalmente. Sin embargo, cuando tenemos tamaños muestrales pequeños o simplemente por el tipo de variable que estamos midiendo, dicha suposición no resulta creible y es necesario comporbarla antes de poder aplicar estos procedimientos. SI la distribución no resulta Normal podemos utilizar los procedimientos denominados no parámetricos para la comparación de dos medias. A continuación presentamso el test de normalidad y los contrastes no paramétricos.

8.1 Normalidad

Este requisito implica que la variable objetivo tiene que distribuirse según una normal para cualquiera de las pobalciones donde se pueda medir. El test utilizado para resolver este problema es el de Shapiro-Wilks. En R utilizamos la función shapiro.test() para concluir estadísticamente sobre este contraste. Siempre utilizamos significatividad de 0.05 en estas situaciones.

Para los datos del ejemplo 1 comprobamos si los datos muestrales en cada población pueden considerarse que se distribuyen según una normal.

# Cargamos los datos
MetodoA <- c(10.7, 11.2, 15.3, 14.9, 13.9, 15, 15.6, 15.7, 14.3, 10.8)
MetodoB <- c(11.1, 11.4, 15, 15.1, 14.3, 15.4, 15.4, 16, 14.3, 11.2)
shapiro.test(MetodoA)

## 
##  Shapiro-Wilk normality test
## 
## data:  MetodoA
## W = 0.8058, p-value = 0.01705

shapiro.test(MetodoB)

## 
##  Shapiro-Wilk normality test
## 
## data:  MetodoB
## W = 0.80577, p-value = 0.01704

En ambos casos las conclusión es que rechazamos que los datos se distribuyan según una normal, ya que el pvalor es inferior a la significatividad prefijada

Para los datos del ejemplo 2:

# Cargamos los datos
TipoA <- c(1614,1094,1293,1643,1466,1270,1340,1380,1081,1497)
TipoB <- c(1383,1138,920,1143,1017,961,1627,821,1711,865,1662,1698)
shapiro.test(TipoA)

## 
##  Shapiro-Wilk normality test
## 
## data:  TipoA
## W = 0.95009, p-value = 0.6696

shapiro.test(TipoB)

## 
##  Shapiro-Wilk normality test
## 
## data:  TipoB
## W = 0.86377, p-value = 0.05451

En ambos casos no podemos rechzar que los datos sean normales, ya que el pvalor es superior a la significatividad.

8.2 Dos medianas en poblaciones independientes

El test no paramétrico no se centra en la comparación de medias sino en la comparación de las medianas. Esto es así porque uno de los incumplimientos más habituales de la normalidad es porque los datos no son simétricos, es decir, la media coincide con la mediana. Para resolver este contraste utilizamos el test de Wilcoxon y su función en R wilcox.test().

Dado que los datos del ejmplo 1 no pueden considerarse normales, utilizamos el test no paramétrico apra concluir si las medianas de ambas poblaciones pueden considerarse iguales o distintas. Fijamos la significatividad en 0.05.

# Cargamos los datos
MetodoA <- c(10.7, 11.2, 15.3, 14.9, 13.9, 15, 15.6, 15.7, 14.3, 10.8)
MetodoB <- c(11.1, 11.4, 15, 15.1, 14.3, 15.4, 15.4, 16, 14.3, 11.2)
wilcox.test(MetodoA,MetodoB)

## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  MetodoA and MetodoB
## W = 44, p-value = 0.6768
## alternative hypothesis: true location shift is not equal to 0

Dado que el pvalor es superior a la significatividad, tenemos evidencias para concluir que no podemos considerar que las medianas de ambas poblaciones sean distintas.

8.3 Dos medianas en poblaciones dependientes

También existe una versión del test de wilcoxon para la comparación en poblaciones dependientes. Este es muy habitual ya que en este tipo de situaciones lo nomral es tener pocos sujetos, y por tanto la hipótesis de normalidad es muy difícil de verificar.

Para los datos del ejmplo 3 tenemos:

# Cargamos los datos
antes <- c(7.3,8.2,6.3,5.2,6.9,5.8,5.3,7.1,6.9,8.1)
despues <- c(8.2,7.9,6.4,5.1,7.1,6.3,5.9,8.2,7.1,7.7)
wilcox.test(antes, despues,paired = TRUE)

## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  antes and despues
## V = 12.5, p-value = 0.1389
## alternative hypothesis: true location shift is not equal to 0

Dado que el pvalor es superior a la significatividad, podemos conluir que la mediana antes y después no pueden considerarse distintas.

9 Ejercicios

Ejercicio 1. Una cadena de supermercados vende pan recién horneado. Los cálculos realizados conforme a la teoría de inventarios indican que para balancear los costos del pan no vendido (por estar duro) y la satisfacción de los clientes, la cadena debería agotar sus existencias de pan el 20% de los días. Se elige una muestra aleatoria de 50 tiendas y se comprobó que 14 de ellas quedaron desabastecidas. Realiza un análisis inferencial con una confianza del 95% para esta situación.

Ejercicio 2. El anterior director (por muchos años) de servicios municipales de la ciudad obtuvo del gobierno federal la subvención solicitada el 50% de las veces que pidió ayuda. Se nombró un nuevo director de servicios municipales de la ciudad quién presento 18 solicitudes de ayuda al gobierno federal durante su primer año. Si 7 de las 18 solicitudes fueron subvencionadas, el concejo municipal quieres saber si hay un cambio en la tasa de resultados positivos bajo la nueva dirección. Realiza un análisis inferencial con una confianza del 95% para esta situación.

Ejercicio 3. El gerente de investigación y desarrollo de una compañía de alimentos comprobó que sólo el 40% de los nuevos productos potenciales que se han sometido a prueba con los clientes son comercializados. Para determinar qué productos han de someterse a prueba por los clientes, el gerente toma 20 nuevos productos potenciales de los cuales 8 fueron comercializados. Realiza un análisis inferencial con una confianza del 90% para esta situación.

Ejercicio 4. Un distribuidor minorista de computadoras está tratando de decidir entre dos métodos para dar servicio a los equipos de los clientes. El primer método enfatiza el mantenimiento preventivo; el segundo una respuesta rápida a los problemas. Se atienden dos muestras de clientes, cada una con uno de esos métodos. Después de seis meses, se encuentra que 171 de los 200 clientes atendidos con el primer método están muy satisfechos con el servicio, comparados con los 153 de los 200 clientes atendidos con el segundo método. Realiza un análisis inferencial con una confianza del 90% para esta situación.

Ejercicio 5. Se realizan pruebas de fiabilidad muy severas con dos muestras de 30 motores eléctricos para impresoras. De los motores del proveedor 1, pasaron la prueba 22; de los motores del proveedor 2, sólo 16 se aprobaron. Realiza un análisis inferencial con una confianza del 95% para esta situación.

Por el momento, en todos los ejercicios que siguen asumiremos que todas las distribuciones son normales. NO hace falta comporbar la hipótesis de normalidad.

Ejercicio 6. El gerente de una organización para la conservación de la salud ha fijado como objetivo que aquellos pacientes que no acudan por alguna emergencia esperen menos de 30 minutos en ser atendidos. En un control por sondeo se recogen los tiempos de espera de 22 pacientes obteniendo los resultados siguientes:

tiempos <- c(28.0,47.9, 38.8, 45.7, 47.3, 34.3, 41.1, 26.9, 26.4, 
             21.8,39.3, 31.5, 37.5, 25.4, 24.1, 30.8, 22.3, 44.5, 
             43.1, 45.8, 42.0, 57.2)