Introducción a la probabilidad
1 Introducción
La probabilidad o el azar juega un papel muy importante en el razonamiento científico. Ejemplos de procesos biológicos donde la probabilidad juega un papel relevante son: i) la segregación de cromosomas en la formación de gametos o la ocurrencia de mutaciones genéticas. En otras ocasiones es el propio diseño experimental el que introduce la aleatoriedad como por ejemplo cuando dividimos un grupo de sujetos en función del tratamiento al que se van a ver sometidos.
Las conclusiones del análisis estadístico de datos se expresan en muchas ocasiones en términos de probabilidad, ya que implícitamente se está introduciendo la aleatoriedad debida a la muestra de sujetos con el que estamos trabajando, y que generalmente no coincide con toda la población bajo estudio.
En las unidades anteriores hemos visto que el estudio estadístico se centra en la información recogida sobre alguna variable relacionada directamente con el objetivo u objetivos del diseño experimental planteado. Un hecho cierto es que debido a la aleatoriedad e los sujetos resulta imposible saber con certeza el valor de dicha variable para un sujeto en particular. Se introduce de esta forma el concepto de variable aleatoria que hace referencia a todas aquellas en las que intrínsecamente se reconoce variabilidad en la respuesta de los sujetos.
En este punto introducimos algo de notación que nos resultará de utilidad de aquí en adelante. Las variables aleatorias siempre se denotan en mayúsculas, \(Y\), mientras que los valores observados para un conjunto de sujetos en esa variable (muestra) se denotan por minúsculas e indicando la posición que el sujeto ocupa en el banco de datos \(y_1,y_2,...,y_n\).
Por razones obvias se definen entonces las variables aleatorias discretas y las variables aleatorias continuas. Una variable discreta es aquella que sólo puede tomar un número finito o contable de posibles resultados, de forma que es posible conocer de antemano cuales son los posibles resultados que se pueden observar. Una variable continua es aquella que puede tomar infinitos valores numéricos, y por tanto es imposible identificar cada uno de los posibles valores de la variable, aunque si es posible conocer el rango de posibles resultados que se pueden observar. De forma natural se puede establecer una equivalencia entre la definición de variables categóricas y numéricas introducidas en unidades anteriores con las variables discretas y continuas.
Se puede describir de forma completa una variable aleatoria sin más que especificar la probabilidad asociada a cada uno de sus posibles valores. Esta especificación se conoce con el nombre de distribución de probabilidad. Sin embargo, la forma en que se puede especificar dicha distribución de probabilidad depende del tipo de variable aleatoria con la que estemos trabajando. En el caso de variables discretas basta con determinar la probabilidad de cada uno de los posibles resultados observables de la variable, pero no ocurre así en las variables continuas donde es imposible conocer todos sus posibles valores.
Imaginemos la situación donde tenemos dos dados iguales y deseamos estudiar el comportamiento de la variable aleatoria \(X\) definida como la suma obtenida al lanzar los dos dados. Nos encontramos ante una variable discreta con posibles resultados ${2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. Para establecer la distribución de probabilidad es necesario calcular: \[P(X = x), x = 2,3,...,12\]
Dichas probabilidades se pueden obtener de forma sencilla contando todas la combinaciones de los dos dados que podemos obtener (casos favorables) y los que corresponden con el valor asociado (casos posibles) para cada uno de los resultados, obteniéndose la distribución de probabilidad:
| x | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| \(P(X = x)\) | \(\frac{1}{36}\) | \(\frac{2}{36}\) | \(\frac{3}{36}\) | \(\frac{4}{36}\) | \(\frac{5}{36}\) | \(\frac{6}{36}\) | \(\frac{5}{36}\) | \(\frac{4}{36}\) | \(\frac{3}{36}\) | \(\frac{2}{36}\) | \(\frac{1}{36}\) |
A partir de la especificación de esta distribución resulta posible obtener cualquier probabilidad que involucre los valores de la variable.
- ¿Cuál es la probabilidad de que la suma sea mayor que 10?
\[P(X > 10) = P(X = 11) + P(X = 12) = 3 / 36 = 1/12 \]
- ¿Cuál es la probabilidad de que la suma a lo sumo de 4?
\[P(X \leq 4) = P(X = 2) + P(X = 3) + P(X = 4) = 6 / 36 = 1/6 \]
- ¿Cuál es la probabilidad de que la suma tome valores entre 7 y 9 (ambos incluidos)?
\[P(7 \leq X \leq 9) = P(X = 7) + P(X = 8) + P(X = 9) = 15 / 36 \]
2 Función de densidad
La función de densidad, \(f\), es una representación matemática y lo más compacta posible de la distribución de probabilidad asociada con una variable aleatoria.
En el caso de variables discretas dicha función de densidad viene dada por: \[f(x) = P(X = x)\]
En el ejemplo visto en la introducción la función de densidad asociada con la suma de la puntuación obtenida al lanzar dos dados viene dada por:
\[f(x) = \frac{1}{36} min(x-1,13-x), \text{ con } x = 2,3,...,12\]
La función de densidad para variables de tipo continuo no se puede especificar directamente, ya que como vimos en el tema anterior no es posible obtener la probabilidad de cada de los infinitos posibles resultados que puede tomar la variable. En el punto siguiente veremos como es posible obtenerla a partir de lo que definiremos con función de distribución.
Las propiedades principales de la función densidad son:
- La función de densidad siempre es mayor o igual a cero para cualquier valor de la variable
- La suma de las densidades de todos los valores de la variable es igual a uno.
Las funciones de densidad se pueden representar gráficamente para dar una idea general del reparto de probabilidades para el Rango de valores de la variable. En realidad si seleccionamos dos valores del rango de valores de la variable, el área bajo la curva de densidad entre esos dos puntos corresponde con la probabilidad de dicho intervalo. Como en la práctica resulta complicado poder realizar estos cálculos se recurre a la función de distribución.
3 Función de distribución
La funicón de distribución, \(F\), asociada con una variable aleatoria \(X\) se define como:
\[F(x) = P(X \leq x)\] Esta función se puede especificar tanto para variables aleatorias discretas como continuas, y sus propiedades son:
- \(F(-\infty) = 0\)
- \(F(+\infty) = 0\)
- Si \(a \leq b\) entonces \(F(a) \leq F(b)\)
A partir de la última propiedad resulta posible obtener la probabilidad de cualquier rango de valores dado que: \[P(a \leq X \leq b) = P(X \leq b) - P(X \leq a) = F(b) - F(a)\]
Para variables aleatorias de tipo continuo se define la función de densidad asociada como la derivada de la función de distribución:
\[f(x) = \frac{d}{dx} F(x).\]
En algunos casos (distribuciones de variables notables) ya se dispone de una expresión para la función de densidad y no hace falta hacer ningún cálculo matemático para obtenerla. Para representar la función de distribución se usa un gráfico de lineas que muestra la probabilidad acumulada para cada valor de la variable aleatoria considerada.
4 Distribuciones-Modelos
En la Unidad anterior se ha visto que el objetivo principal de muchos análisis estadísticos es estudiar el comportamiento de los sujetos de una población, a partir de la información recogida en una muestra de sujetos seleccionados de dicha población. Sin embargo, cuando hablamos de una población lo hacemos teniendo en mente las variables que se han medido sobre ellos. Imaginemos que estamos interesados en conocer la nota media de acceso de todos los estudiantes de primero de grado en la Universidad Miguel Hernández de Elche (UMH). En este caso es evidente que la población objetivo son todos los estudiantes de primero de grado que han accedido a la UMH, aunque esa población contiene información sobre muchas otras variables (sexo, edad, localidad de residencia,…).Por lo tanto, todas las poblaciones se considerarán poblaciones de valores de alguna variable especificada. Si la población es infinita, nunca podremos obtener todos sus valores, e incluso si la población es finita, generalmente no queremos medir todos sus valores. En cualquier caso, deseamos obtener información sobre características particulares de la población a partir de un número restringido de valores de muestra. Por ejemplo, en el estudio de la nota de acceso podríamos querer utilizar la media de la nota media de todos los estudiantes como referencia de la población, aunque podríamos utilizar otros como el percentil 80, etc…
Para proceder de esta forma, necesitamos formular un modelo adecuado para los valores \(x\) que componen la población, relacionar las características de interés con los aspectos apropiados del modelo y luego usar los datos de la muestra para proporcionar estimaciones de estos aspectos.La característica esencial de tales valores \(x\) en su imprevisibilidad, y lo mejor que podemos hacer es especificar la probabilidad de obtener un valor dado o un valor en un rango dado. Por lo tanto, las distribuciones de probabilidad proporcionan los modelos más apropiados para las poblaciones variables de respuesta. Más específicamente, la función de densidad de probabilidad \(f(x)\) o la función de distribución de probabilidad \(F(x)\) proporcionan la información necesaria, por lo que constituye el modelo de población para la variable aleatoria \(X\). Por supuesto, dado que nunca conocemos esta distribución con una certeza total, debemos suponer una forma funcional específica (modelo matemático) para \(f(x)\) y \(F(x)\). Esta forma funcional usualmente involucra uno o más parámetros que pueden ser variados, y leso que se espera es que habrá algunos valores específicos de estos parámetros para los cuales la distribución resultante se ajusta adecuadamente a nuestros datos observados. Tal modelo se llama modelo paramétrico para \(X\). En el tema siguiente se presentarán los modelos paramétricos más frecuentes para una variable aleatoria \(X\).
Por el momento, supongamos que hemos especificado alguna función adecuada \(f(x)\) como la densidad de probabilidad de nuestra población. ¿Qué valores resumen de esta densidad se relacionan con las características de la población que generalmente son de interés? Para responder a esta situación, centrémonos en las variables discretas e interpretemos la probabilidad como una frecuencia relativa. Si la variable aleatoria \(X\) tiene valores posibles \(x_1, x_2, x_3, ... ,x_n\) y si \(p_i = P(X = x_i)\), entonces podemos pensar en \(p_i\) como la frecuencia relativa con la que el valor \(x_i\) ocurre en toda la población.
Definimos el valor esperado de \(X\) por la ecuación:
\[E(X) = \sum_{i=1}^n x_i p_i\]
Utilizando la interpretación de frecuencia relativa de \(p_i\) dada anteriormente, \(E(X)\) puede interpretarse como el promedio de los valores \(X\) en toda la población, por lo que es la media poblacional. Este es claramente uno de los principales valores de resumen para la población. A menudo se denota \(\mu\) y como mide el “centro” de la población también se lo conoce como el parámetro de localización de la población.
De forma similar se define la varianza de la población, \(\sigma2\), como:
\[\sigma^2 = V(X) = E\{(X-\mu)^2\} = \sum_{i=1}^n (x_i - \mu)^2 p_i\]
La desviación típica poblacional, \(\sigma\), se obtiene a partir de la raíz cuadrada de la varianza poblacional:
\[\sigma = DT(X) = \sqrt{V(X)}\]
Siguiendo con el ejemplo de la variable aleatoria que representa la suma del lanzamiento de dos dados ¿Cuál es el valor esperado de la suma de ambos lanzamientos? ¿Cuál es la desviación típica? En este caso ¿la distribución es aproximada o la distribución poblacional?
En el caso de variables aleatorias continuas, donde denotamos por \(R\) el rango de todos los valores posibles, se define la media, varianza y desviación típica poblacional como
\[\mu = E(X) = \int_R x f(x) dx\]
\[\sigma^2 = V(X) = \int_R (x - \mu)^2 f(x) dx\]
\[\sigma = DT(X) = \sqrt{V(X)}\]
Para las variables de tipo continuo más habituales la esperanza, varianza y desviación típica poblacionales se aproximan de forma precisa (si la muestra de trabajo es adecuada) por la media, varianza y desviación típica muestral.
5 Aproximaciones
Como se ha explicado en el punto anterior se debe utilizar la información muestral para aproximar la función de densidad de una variable aleatoria. En este punto estudiamos como obtener dichas aproximaciones (distribuciones empíricas) desde un punto de vista gráfico, aunque en la unidad siguiente se plantearan los métodos numéricos necesarias para obtener dicha aproximación. Si la muestra es representativa de la población, tanto la función de densidad como de distribución empíricas que obtendremos se deben parecer a las de toda la población, con lo que sería posible conocer la probabilidad de cualquier valor o rango de valores en la población. Para ejemplificar utilizaremos el banco de datos storm que venimos usando en los temas anteriores.
En primer lugar cargamos los datos de trabajo
library(tidyverse)
library(forcats)
library(nasaweather)
storm <- nasaweather::storms # Guardamos los datos en un nuevo objeto5.1 Caso 1
En primer lugar vamos a trabajar con la variable discreta tipo de tormenta. Reordenamos el factor para mantener la relevancia de cada tipo de tormenta y obtenemos la tabla de frecuencias relativas y acumuladas de cada nivel de respuesta para aproximar tanto la función de densidad como la función de distribución:
# Generamos nuevo factor ordenado
type_levels <- c("Tropical Depression", "Extratropical", "Tropical Storm", "Hurricane")
storm$type2 <- factor(storm$type,levels = type_levels)
# Calculamos las frecuencias relativas
tabla_tipo <- storm %>%
group_by(type2) %>%
summarise(n=n())
mutate(tabla_tipo,frel=n/sum(n),facum=cumsum(frel))## # A tibble: 4 x 4
## type2 n frel facum
## <fct> <int> <dbl> <dbl>
## 1 Tropical Depression 513 0.187 0.187
## 2 Extratropical 412 0.150 0.337
## 3 Tropical Storm 926 0.337 0.674
## 4 Hurricane 896 0.326 1Esta tabla nos proporciona la probabilidad de que ocurra cada uno de los eventos considerados o lo que hemos definido como función de densidad de la variable tipo de tormenta.
Para representar la función de densidad hacemos uso de la función ..prop.. que nos proporciona los porcentajes asociados a cada nivel del factor.
ggplot(storm, aes(type2)) +
geom_bar(aes(y = ..prop.. , group = 1), width = 0.5) +
xlab("Tipo de Tormenta") + ylab("Frecuencia relativa")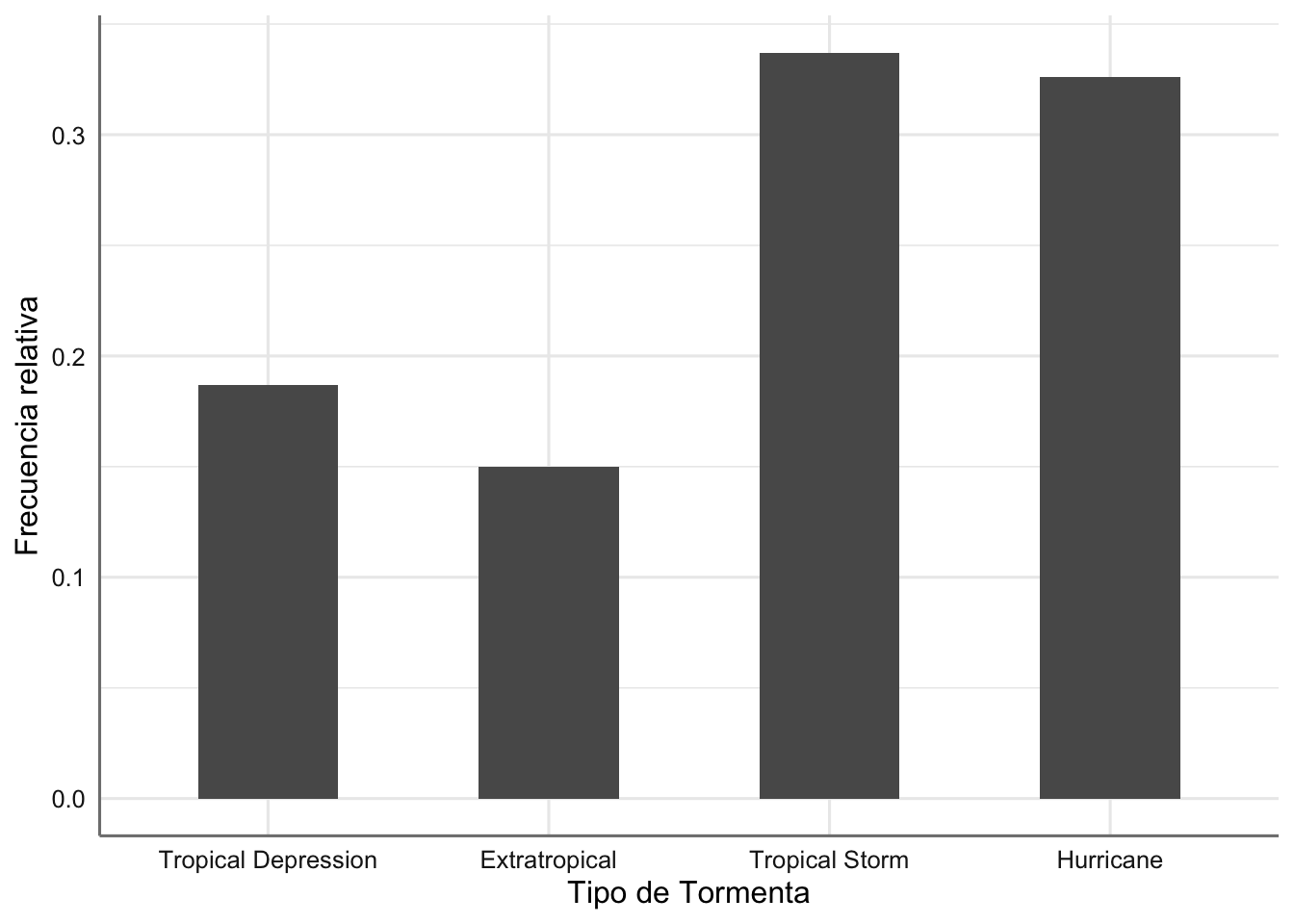
Para representar la función de distribución hacemos uso de la función cumsum que nos permite las suma acumulados e los porcentajes que obtenemos con ..prop...
ggplot(storm, aes(type2)) +
geom_bar(aes(y = cumsum(..prop..) , group = 1), width = 0.5) +
xlab("Hasta este nivel") + ylab("Frecuencia acumulada")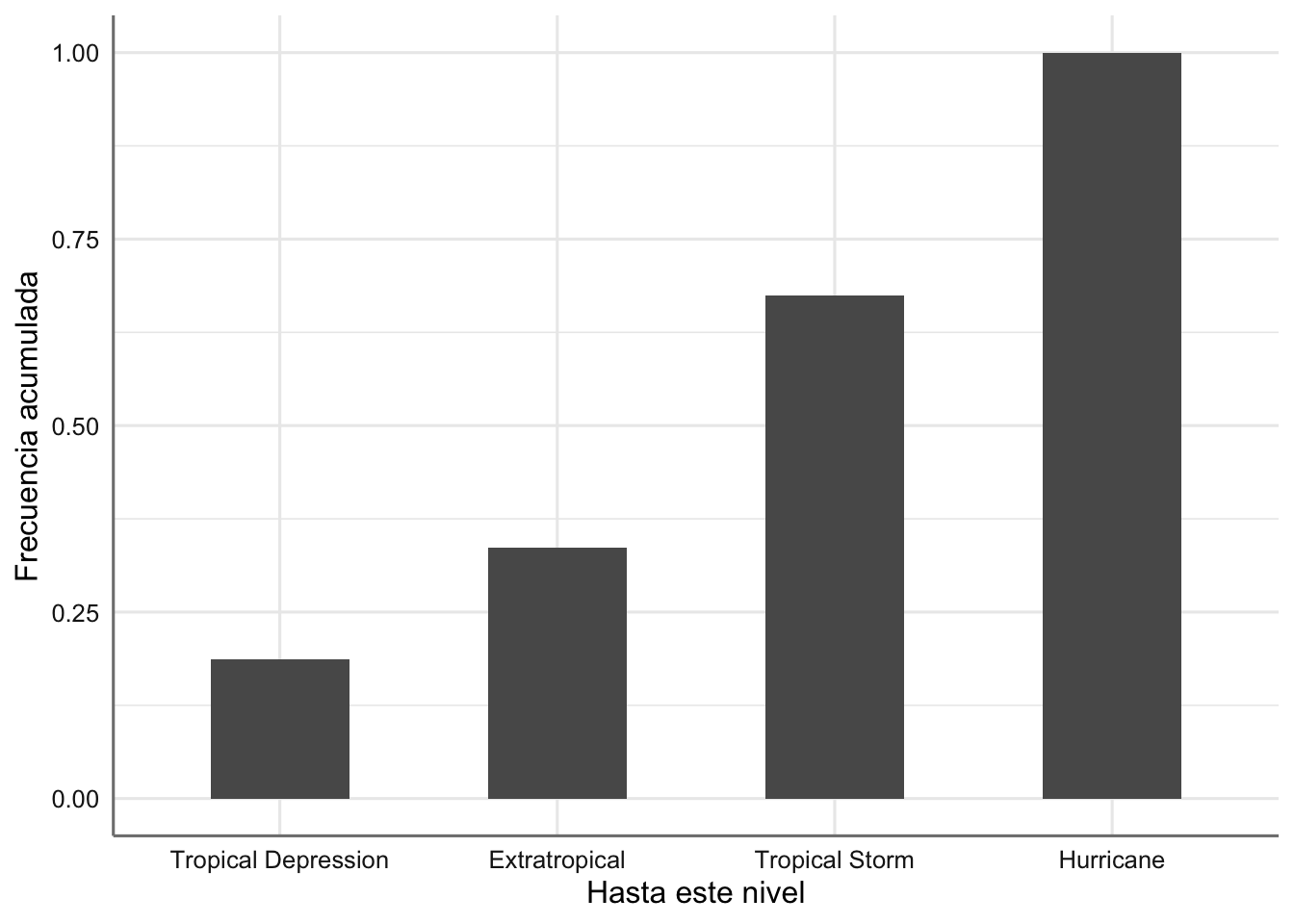
5.2 Caso 2
Se selecciona ahora la variable presión atmosférica. De nuevo estamos interesados en obtener una aproximación de la función de densidad y de distribución. Dado Que estamos con una variable continua no podemos calcular la probabilidad en un punto sino en un intervalo. La mejor forma de representar dicha información es con el histograma.
En primer lugar representamos la función de densidad. Se utiliza tanto el histograma de frecuencias relativas como la aproximación de la densidad con la función geom_density.
ggplot(storm, aes(x = pressure)) +
geom_histogram(aes(y = ..density..), binwidth = 7) +
geom_density(color="red")+
xlab("Presión Atmosférica (mbar)") + ylab("Densidad")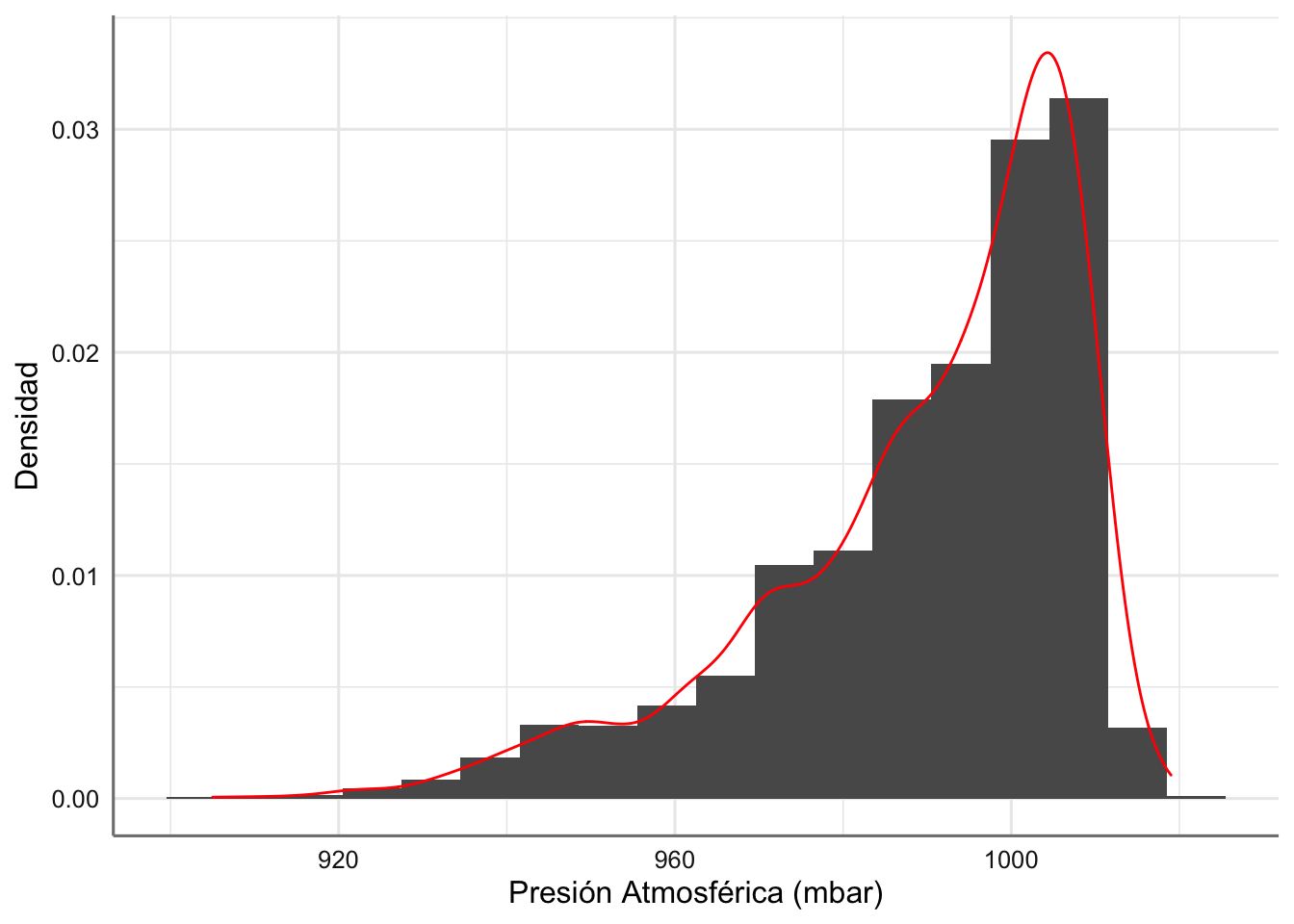
Para obtener la función de distribución se hace uso de la función stat_ecdf que permite obtener la función de distribución empírica para una variable de tipo numérico.
ggplot(storm, aes(x = pressure)) +
stat_ecdf(geom = "step", pad = FALSE) +
scale_y_continuous(breaks = seq(0,1,0.1)) +
xlab("Presión Atmosférica (mbar)") + ylab("Frecuencia acumulada")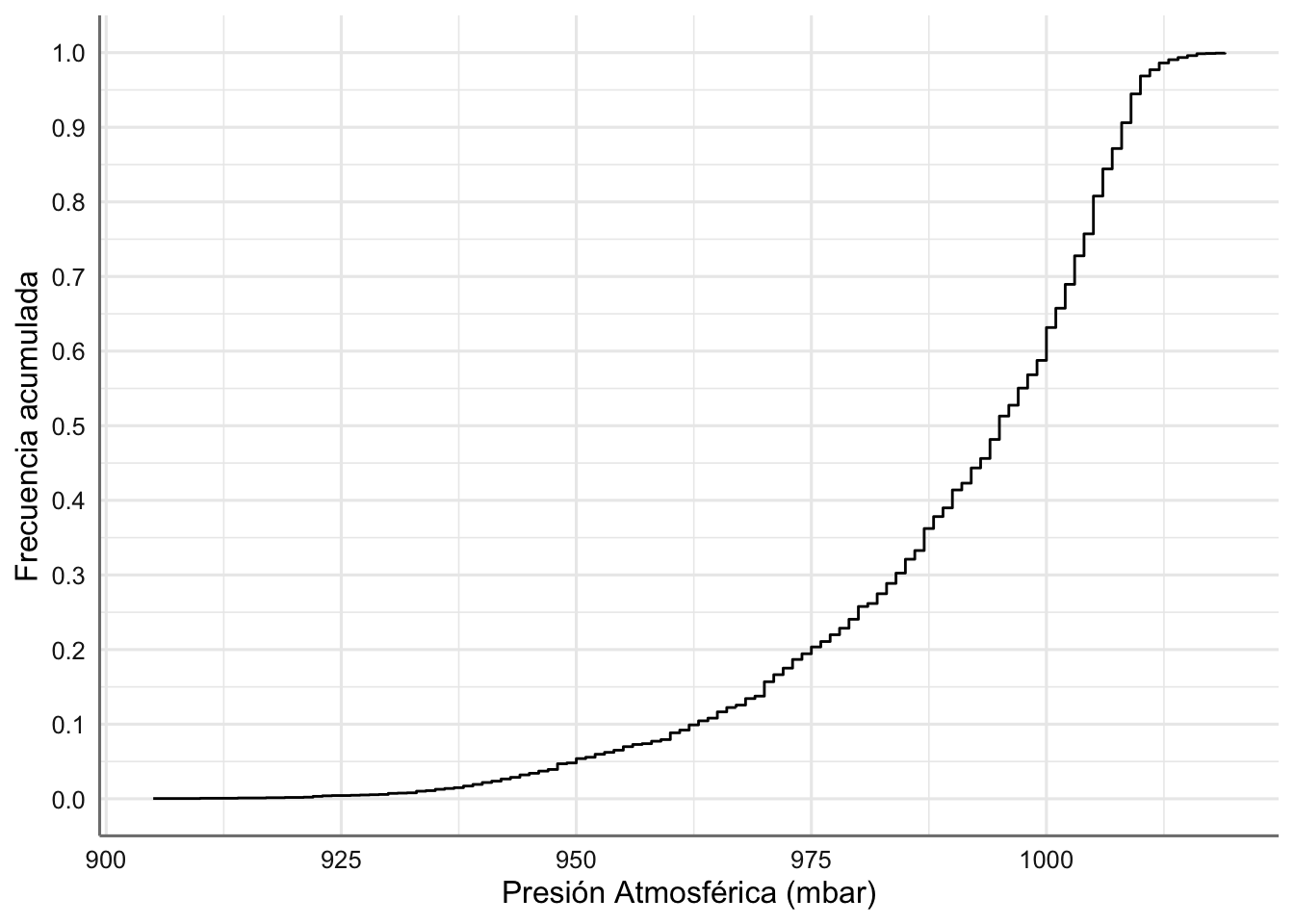
Podemos que ver que la probabilidad de observar una presión atmosférica menor o igual a 1000 milibares se sitúa en torno a 0.6. De forma similar, la probabilidad de observar un viento entre 950 y 975 milibares es aproximadamente \(0.20 - 0.05 = 0.15\), con lo que a partir de esta función resulta posible cualquier probabilidad.
5.3 Caso 3
Comparamos ahora el comportamiento de la variable presión atmosférica con respecto al tipo de tormenta. En primer lugar obtenemos las funciones de densidad de la variable presión atmosférica para cada tipo de tormenta.
ggplot(storm, aes(x = pressure, color = type2)) +
geom_density()+
xlab("Presión Atmosférica (mbar)") + ylab("Densidad")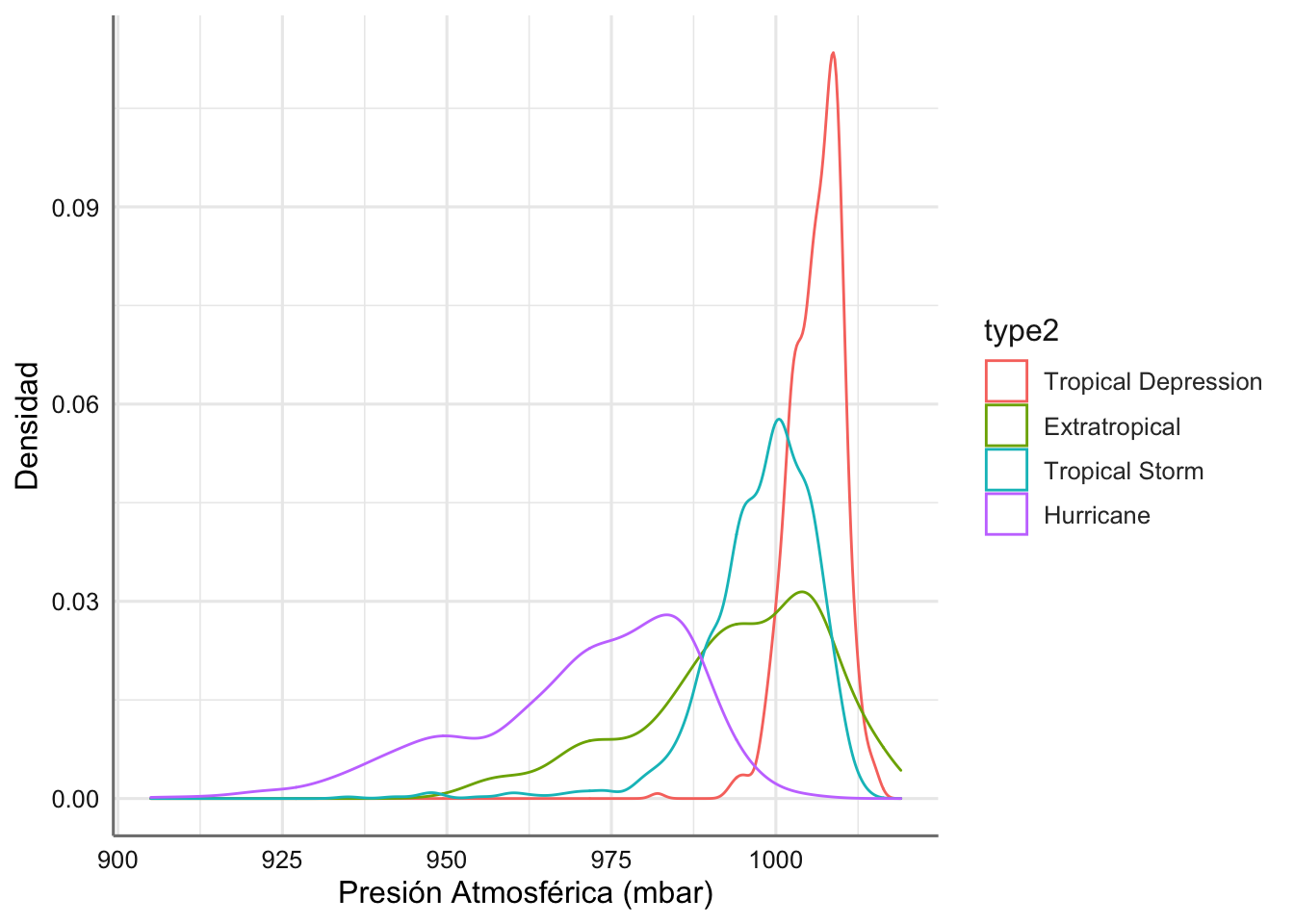
Se puede apreciar que los rangos de valores con mayores probabilidades varían en función del tipo de tormenta, lo que implica que las poblaciones definidas por ese factor tienen comportamientos diferentes.
A continuación se obtienen las funciones de distribución asociadas
ggplot(storm, aes(x = pressure, color = type2)) +
stat_ecdf(geom = "step", pad = FALSE) +
scale_y_continuous(breaks = seq(0,1,0.1)) +
xlab("Presión Atmosférica (mbar)") + ylab("Frecuencia acumulada")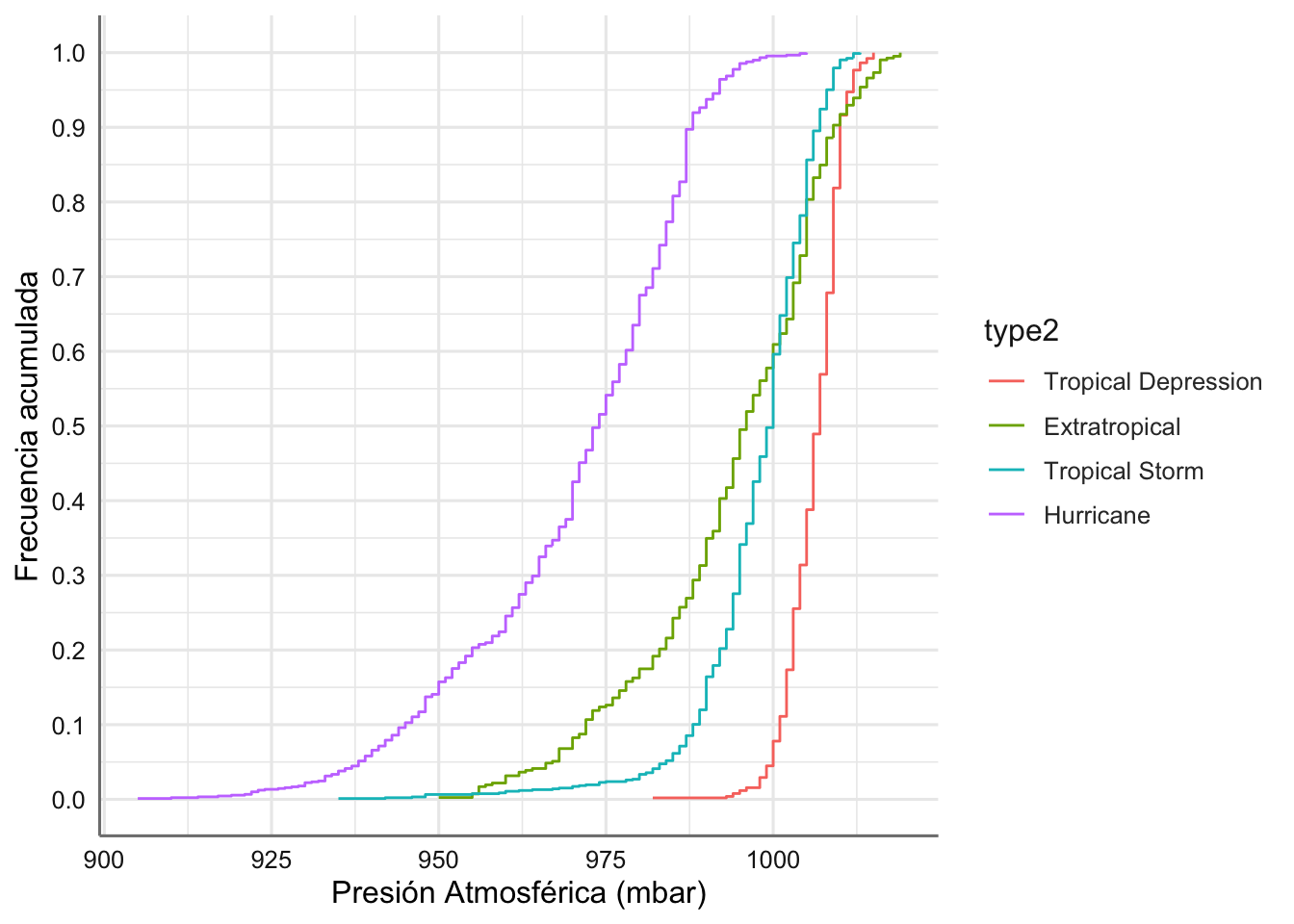
Podemos ver en este caso que las probabilidades de observar presiones atmosféricas por debajo de 1000 milibares son: 1 (Tropical Depression); 0.6 (Extratropical y Tropical Storm); y 0.05 (Hurricane). En este caso resulta posible calcular cualquier probabilidad pero además podemos establecer comparaciones en función del tipo de tormenta. Esta forma de proceder sienta las bases de los procedimientos que se presentan en la unidad siguiente.
6 Distribuciones Notables
Sería muy complicado y farragoso si para cada experimento aleatorio ligeramente diferente de otro ya realizado, tuviéramos que determinar las distribuciones de probabilidad desde cero. Afortunadamente, podemos hacer uso de las similitudes que existen entre ciertos tipos o familias de experimentos y ciertas distribuciones de probabilidad, conocidas con le nombre de distribuciones notables, que nos permiten el desarrollo de las funciones de distribución que representen las características generales del experimento.
Por ejemplo, muchos experimentos comparten el elemento común de que sus resultados se pueden clasificar en uno de dos eventos: una moneda puede salir cara o cruz; un niño puede ser hombre o mujer; una persona puede morir o no morir; una persona puede ser empleada o desempleada. Estos resultados a menudo se etiquetan como “éxito” o “fracaso”, teniendo en cuenta que aquí no hay connotación de “bondad”; por ejemplo, al observar los nacimientos, el estadístico podría calificar el nacimiento de un niño como un “éxito” y la el nacimiento de una niña como un “fracaso”, pero los padres no necesariamente verían las cosas de esa manera. Esta situación experimental se conoce como experimento Bernouilli, asignando probabilidad \(\theta\) al suceso calificado como éxito y probabilidad \(1-\theta\) al suceso calificado como de fracaso. Dichas probabilidades son diferentes para cada situación y se pueden aproximar mediante la obtención de datos experimentales. La distribución de probabilidad que surge en este experimento se conoce como distribución Bernouilli y es la primera distribución de probabilidad notable conocida.
En los puntos siguientes se presentan las otras tres distribuciones notables más habituales: Binomial, Poisson y Normal. Las dos primeras se usan en situaciones experimentales donde la variable aleatoria que se relaciona con el objetivo del experimento aleatorio es de tipo categórico, mientras que la última se utiliza para variables aleatorias de tipo continuo.
6.1 Binomial
A menudo nos interesa el resultado de los ensayos independientes y repetidos de Bernoulli, es decir, el número de éxitos en ensayos repetidos. En esta situación se considera:
- sucesos independientes: el resultado de un ensayo no afecta el resultado de otro ensayo.
- repeticiones: las condiciones son las mismas para cada prueba, es decir, la probabilidad de éxito y fracaso permanecen constantes a través de los diferentes ensayos realizados.
Una distribución binomial nos da las probabilidades asociadas con los ensayos independientes y repetidos de Bernoulli. En una distribución binomial, las probabilidades de interés son las de observar un cierto número de éxitos, \(r\), en \(n\) ensayos independientes, cada uno de los cuales tiene solo dos resultados posibles y la misma probabilidad, \(\theta\), de éxito. Por ejemplo, usando una distribución binomial, podemos determinar la probabilidad de obtener 4 caras en 10 lanzamientos de una misma moneda.
La distribución de probabilidad para este experimento queda completamente determinado si conocemos \(n\) (número de repeticiones realizadas) y \(\theta\) (probabilidad de éxito). Si \(X\) denota la variable aleatoria asociada con este experimento, la función de densidad de probabilidad se define como: \[P(X = x) = {n \choose x} \theta^x (1-\theta)^{n-x}\] donde \({n \choose x}\) representa el número combinatorio de \(n\) sobre \(x\), y \(x\) el número de éxitos observados. Dicha distribución se denota habitualmente: \[ X \sim Bi(n, \theta)\]
Esta distribución se puede evaluar para cualquier valor entre 0 y el número de repeticiones del experimento \(n\). En R la función dbinom permite obtener cualquier probabilidad de la distribución binomial una vez fijamos el valor que deseamos evaluar (\(x\)), el número de repeticiones (\(n\)), y la probabilidad de éxito asociada (\(\theta\)). Por ejemplo, podemos obtener la función de densidad de probabilidad asociada a un experimento binomial con 5 repeticiones y probabilidad de éxito 0.2 (\(X \sim Bi(5,0.2)\)) de la siguiente forma:
library(tidyverse)
# Establecemos los posibles resultados del experimneto (número de éxitos posibles)
exito <- 0:5
# Obtenemos ahora la función de densidad
fden <- dbinom(exito,5,0.2)
# Tabla
res <- as.data.frame(cbind(exito,fden))
colnames(res) <- c("Exito","Probabilidad")
res## Exito Probabilidad
## 1 0 0.32768
## 2 1 0.40960
## 3 2 0.20480
## 4 3 0.05120
## 5 4 0.00640
## 6 5 0.00032# Representamos gráficamente
ggplot(res,aes(Exito,Probabilidad)) +
geom_bar(stat = "identity", width = 0.05) +
labs(xlab = "Número de éxitos",ylab = "Probabilidad",title = "Binomial(5, 0.2)")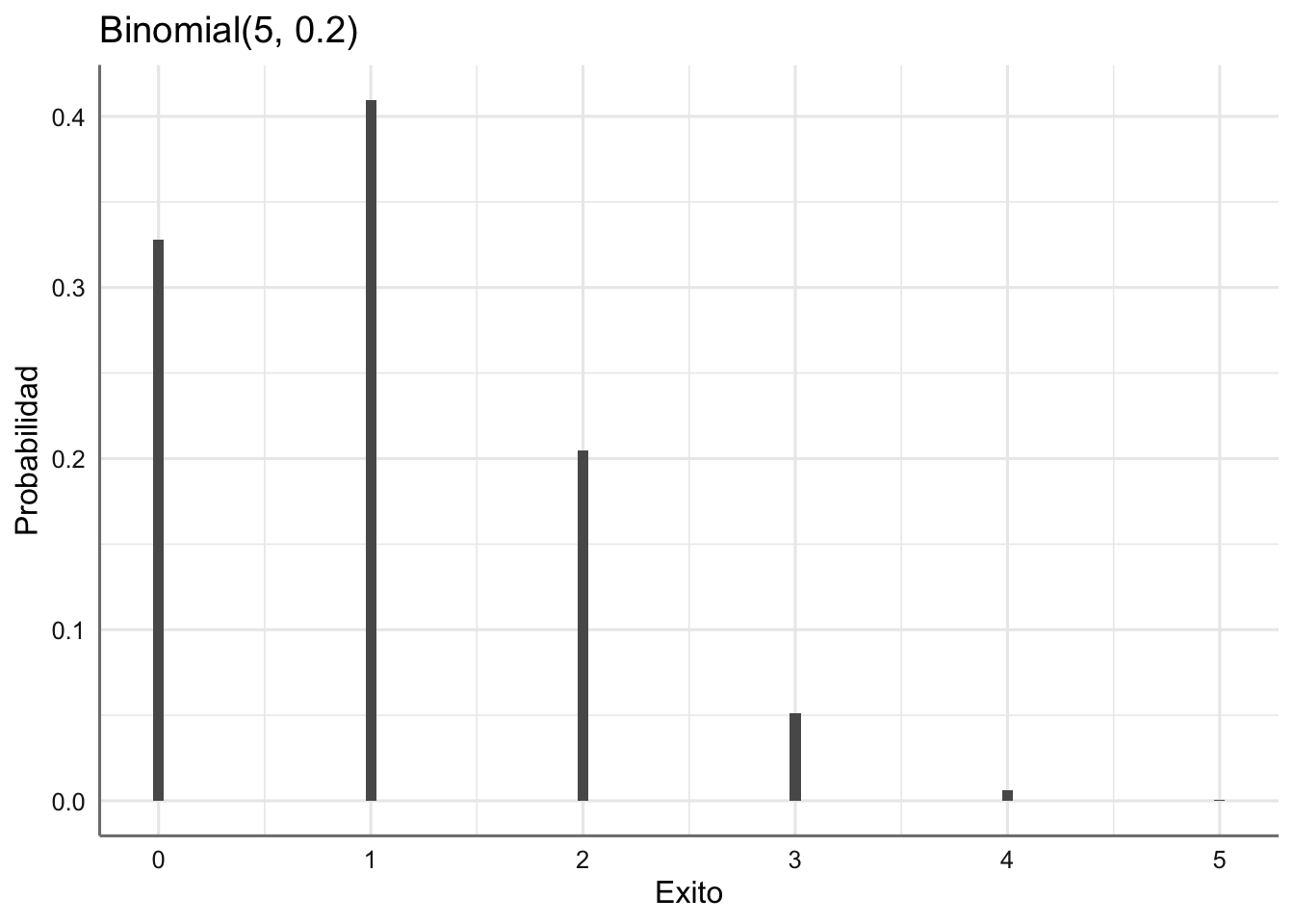
A la vista de los resultados podemos concluir que el la situación más probable es que observemos un éxito en las cinco repeticiones con una probabilidad de 0.41.
Una vez establecida la función de densidad de probabilidad resulta posible obtener el valor esperado del número de éxitos, así como conocer su variabilidad haciendo uso de las definiciones expuestas en el tema anterior. En concreto, para una variable que sigue una distribución de probabilidad Binomial (\(X \sim Bi(n,\theta)\)) tenemos que: \[E(X) = n \theta\] \[V(X) = n \theta (1-\theta)\] \[DT(X) = \sqrt{n \theta (1-\theta)}\]
En nuestro ejemplo tendríamos que el número esperado de éxitos se situaría en \(5 * 0.2 = 1\) y la variabilidad (en términos de la desviación típica) en \(\sqrt{5 * 0.2 * 0.8} = 0.89\), lo que implica que los valores más probables se sitúan entre 1 y 3 éxitos (\(1 \pm 1\)).
6.1.1 Cálculos de probabilidad
A continuación se presentan diferentes situaciones prácticas para ilustrar el cálculo de probabilidades con la distribución Binomial.
En la situación experimental anterior, \(X \sim Bi(5,0.2)\) ¿Cuál es la probabilidad de observar 3 éxitos?
## [1] 0.0512La función pbinom permite la evaluación de la función de distribución de probabilidad en las situaciones de cálculo en que es necesaria. Los parámetros de la función son los mismos que los de la función dbinom.
En la situación experimental anterior (\(n=5\) y \(\theta = 0.2\)) ¿Cuál es la probabilidad de observar como mucho dos éxitos? En otras palabras: \[P(X \leq 2)\] que es el valor de la función de distribución Binomial para \(X = 2\).
## [1] 0.94208En la situación experimental anterior (\(n=5\) y \(\theta = 0.2\)) ¿Cuál es la probabilidad de observar al menos tres éxitos? En otras palabras: \[P(X \geq 3) = 1 - P(X \leq 2)\]
## [1] 0.05792En la situación experimental anterior (\(n=5\) y \(\theta = 0.2\)) ¿Cuál es la probabilidad de observar entre dos y cuatro éxitos (ambos incluido)? En otras palabras: \[P(2 \leq X \leq 4) = P(X \leq 4) - P(X \leq 2)\]
## [1] 0.0576En este enlace se pueden representar y calcular tanto la función de densidad como la función de distribución para diferentes situaciones experimentales relacionadas con la distribución Binomial.
6.1.2 Ejemplos
Utilizando la aplicación anterior o calculando directamente con las funciones de R contesta a las siguientes situaciones:
- En una población de sujetos se conoce que el 39% de ellos sufre algún tipo de mutación genética. Si se obtiene una muestra de 20 sujetos ¿cuál es la probabilidad de observar tres sujetos con esa mutación genética?
- En una población de moscas de la fruta se conoce que el 30% son de color negro y el 70% son de color gris. Si se extrae una muestra de 15 moscas ¿cuál es la probabilidad de observar al menos cuatro moscas de color negro? ¿y de color gris?
- Una cierta droga causa daños en el hígado en el 1% de los pacientes. Se van a realizar estudios completos sobre 50 pacientes que están tomando dicha droga para detectar daños en el hígado. ¿Cuál es la probabilidad de que ninguno de lo pacientes muestre daños en el hígado? ¿Cuál es la probabilidad de que al menos uno de los pacientes muestre daños en el hígado?
- Los estudios realizados concluyen que el 10% de las adolescentes de EEUU tienen deficiencia de hierro. Se obtiene una muestra de 14 adolescentes y se desea conocer ¿cuál es la probabilidad de que al menos el 50% de ellas tengan una deficiencia de hierro?
6.1.3 Ajuste de la distribución Binomial
En este apartado vemos como obtener la distribución Binomial asociada a una muestra de datos correspondientes a un estudio experimental. El ajuste de dicha distribución nos permitirá obtener la probabilidad asociada a cualquier situación experimental de la población bajo estudio.
Ejemplo 1. Los estudiantes de una clase de botánica van a realizar un experimneto para conocer el grado de germinación de un tipo de planta. Para ello cada estudiante planta en un semillero cinco semillas de dicha planta y contabiliza cuantas de ellas han germinado al cabo de una semana. Los datos obtenidos para el conjunto de todos los estudiantes (280 en total) se muestran en la tabla siguiente:
| Semillas germinadas | Semillas no germinadas | Número de estudiantes |
|---|---|---|
| 0 | 5 | 17 |
| 1 | 4 | 53 |
| 2 | 3 | 94 |
| 3 | 2 | 79 |
| 4 | 1 | 33 |
| 5 | 0 | 4 |
El estudio desea conocer cual es la probabilidad de germinación y el número esperado de germinaciones en base a dicha información experimental.
# En primer lugar cargamos los datos
germinadas <- 0:5
estudiantes <- c(17,53,94,79,33,4)
design <- data.frame(Germinadas = germinadas, Frecuencia = estudiantes)
# Para calcular la probabilidad de germinacion utilizamos la definición de probabilidad
# Casos favorables: semillas germinadas por frecuencia de estudiantes
favorables <- sum(germinadas*estudiantes)
# Casos posibles: 5 semillas por cada estudiante
posibles <- 5*280
# Probabilidad de germinación
probabilidad <- round(favorables/posibles,4)
# Número esperado de semillas germinadas
esperanza <- posibles*probabilidad
c(probabilidad,esperanza)## [1] 0.45 630.00La probabilidad de germinación es de 0.45 y el número esperado de semillas germinadas es de 630 sobre las 1400 plantadas por los estudiantes.
Podemos obtener ahora la función de densidad de probabilidad asociada con un experimento donde deseamos sembrar 20 semillas de dicha planta.
# Establecemos los posibles resultados del experimneto (número de éxitos posibles)
exito <- 0:20
# Obtenemos ahora la función de densidad
fden <- round(dbinom(exito,20,0.45),6)
# Tabla
res <- as.data.frame(cbind(exito,fden))
colnames(res) <- c("Exito","Probabilidad")
res## Exito Probabilidad
## 1 0 0.000006
## 2 1 0.000105
## 3 2 0.000816
## 4 3 0.004006
## 5 4 0.013930
## 6 5 0.036471
## 7 6 0.074600
## 8 7 0.122072
## 9 8 0.162300
## 10 9 0.177055
## 11 10 0.159349
## 12 11 0.118524
## 13 12 0.072731
## 14 13 0.036620
## 15 14 0.014981
## 16 15 0.004903
## 17 16 0.001254
## 18 17 0.000241
## 19 18 0.000033
## 20 19 0.000003
## 21 20 0.000000# Representamos gráficamente
ggplot(res,aes(Exito,Probabilidad)) +
geom_bar(stat = "identity", width = 0.05) +
labs(xlab = "Número de éxitos",ylab = "Probabilidad",title = "Binomial(20, 0.45)")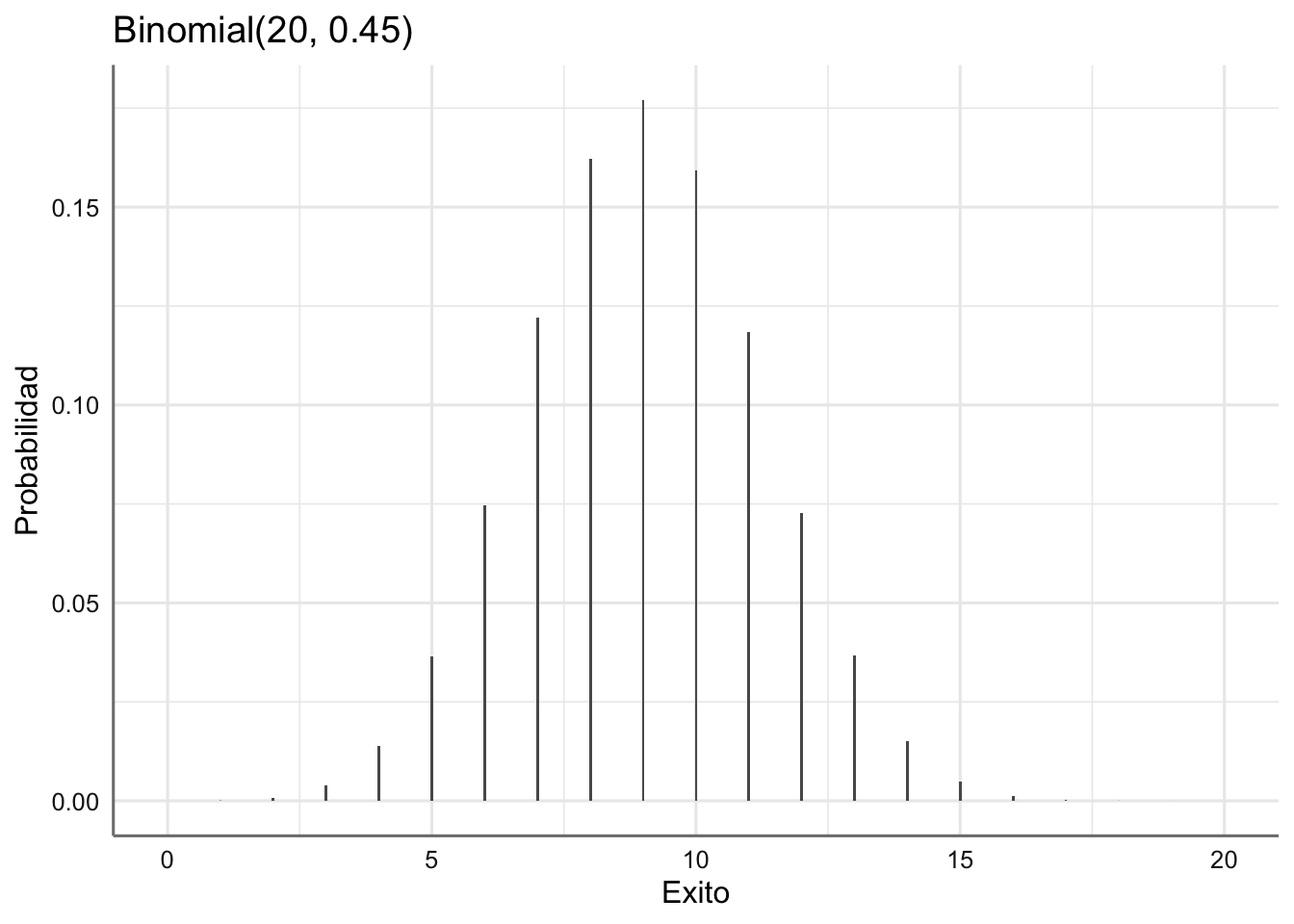
Los valores más probables son los correspondientes a los valores de germinación entre 7 y 11.
Ejemplo 2. Una empresa que se dedica a la elaboración de alimentos funcionales desea estudiar la línea de producción de sus nuevos embutidos con quinoa. Para ellos toma muestras de cinco productos durante 559 días y valora si el producto cumple con los estándares de calidad necesarios para su venta. Lo datos obtenidos se muestran en la tabla siguiente:
| Cumplen con los estándares | Número de días | |
|---|---|---|
| 0 | 16 | |
| 1 | 27 | |
| 2 | 80 | |
| 3 | 152 | |
| 4 | 180 | |
| 5 | 104 |
El estudio desea conocer cual es la probabilidad de cumplir con el estádar y el número esperado de productos que cumplen con el estándar en base a dicha información experimental.
# En primer lugar cargamos los datos
grado <- 0:5
dias <- c(16,27,80,152,180,104)
design <- data.frame(Grado = grado, Dlias = dias)
# Casos favorables:
favorables <- sum(grado*dias)
# Casos posibles:
posibles <- 5*559
# Probabilidad de germinación
probabilidad <- round(favorables/posibles,4)
# Número esperado de semillas germinadas
esperanza <- posibles*probabilidad
c(probabilidad,esperanza)## [1] 0.6737 1882.9915La probabilidad de cumplir con el estándar es de 0.6737 y el número esperado de productos que cumplene es de 1883 sobre las 2795 que han sido probados.
Podemos obtener ahora la función de densidad de probabilidad asociada con un experimento donde deseamos saber que ocurriría con 25 nuevos embutidos.
# Establecemos los posibles resultados del experimneto (número de éxitos posibles)
exito <- 0:25
# Obtenemos ahora la función de densidad
fden <- round(dbinom(exito,25,0.6737),6)
# Tabla
res <- as.data.frame(cbind(exito,fden))
colnames(res) <- c("Exito","Probabilidad")
res## Exito Probabilidad
## 1 0 0.000000
## 2 1 0.000000
## 3 2 0.000000
## 4 3 0.000000
## 5 4 0.000000
## 6 5 0.000001
## 7 6 0.000010
## 8 7 0.000053
## 9 8 0.000247
## 10 9 0.000965
## 11 10 0.003186
## 12 11 0.008971
## 13 12 0.021610
## 14 13 0.044617
## 15 14 0.078959
## 16 15 0.119551
## 17 16 0.154270
## 18 17 0.168626
## 19 18 0.154736
## 20 19 0.117702
## 21 20 0.072905
## 22 21 0.035839
## 23 22 0.013454
## 24 23 0.003623
## 25 24 0.000623
## 26 25 0.000051# Representamos gráficamente
ggplot(res,aes(Exito,Probabilidad)) +
geom_bar(stat = "identity", width = 0.05) +
labs(xlab = "Número de éxitos",ylab = "Probabilidad",title = "Binomial(25, 0.6737)")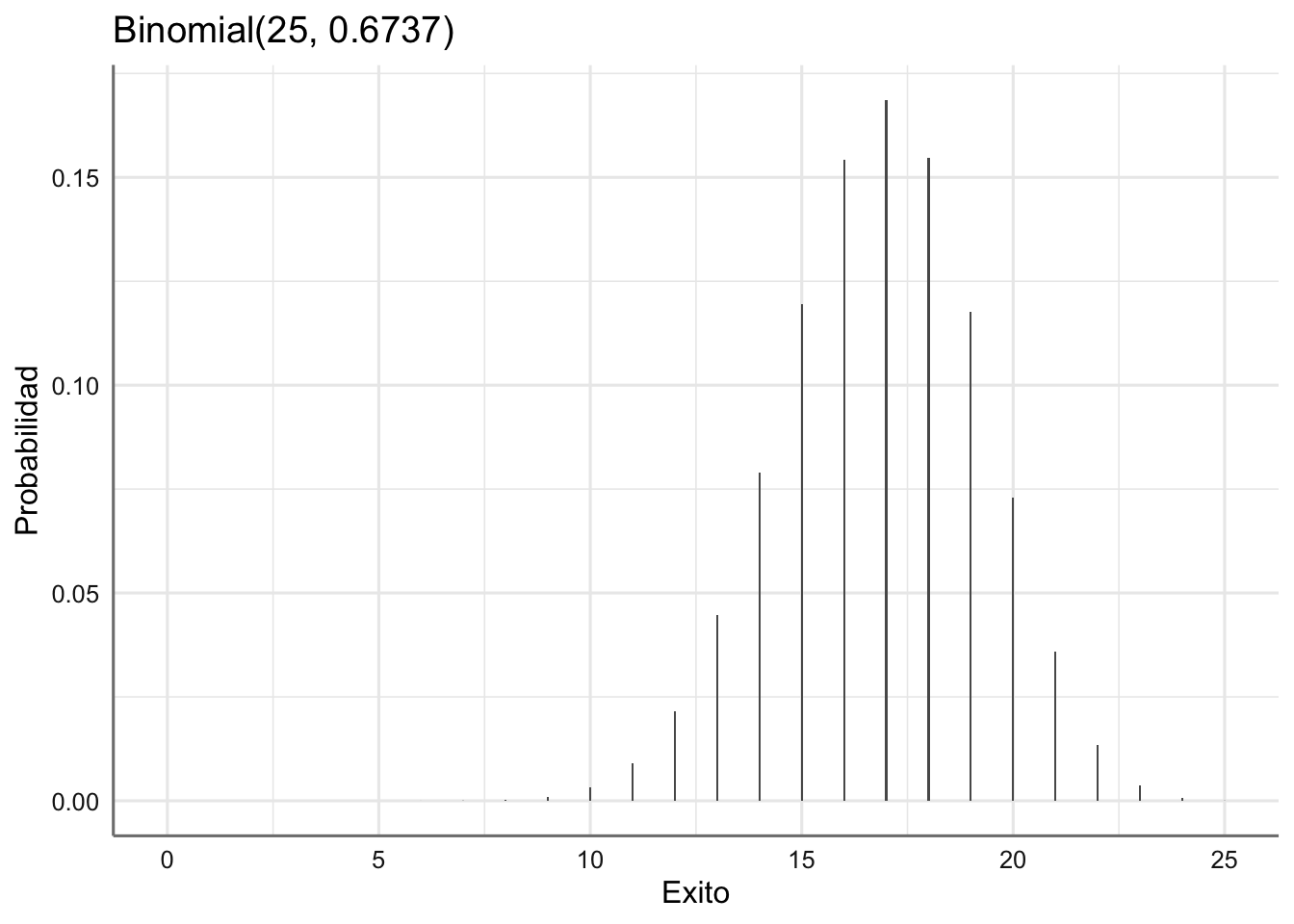
Los valores más probables son los correspondientes a los valores comprendidos entre 15 y 20, es decir, que esperamos que de los nuevos 25 que vamos a producir entre 15 y 20 cumplan con el estándar de calidad.
6.2 Poisson
La distribución de Poisson se emplea como un modelo para variables aleatorias de tipo discreto cuando se quieren obtener las probabilidades de ocurrencia de un evento que se distribuye al azar en el espacio o el tiempo. Algunos ejemplos de esta distribución son:
- Ejemplo 1: En el estudio de cierto organismo acuático, se toman un gran número de muestras de un lago y se cuentan el número de organismos que aparecen en cada muestra. El interés principal radica en conocer cuál es la probabilidad de encontrar algún organismo en una muestra próxima si la media observada en el conjunto de nuestras es de 2 organismos.
- Ejemplo 2: En un estudio sobre la efectividad de un insecticida sobre cierto tipo de insecto, se fumiga una gran región. Posteriormente se crea una cuadrícula sobre el terreno, se selecciona de forma aleatoria un conjunto de ellas, y se cuenta el número de insectos vivos dentro de cada una. Estamos interesados en conocer cuál es la probabilidad de que no encontremos ningún insecto vivo en una cuadrícula próxima si se sabe que que la media de insectos vivos en las cuadriculas analizadas es de 0.5.
- Un grupo de investigadores observó la ocurrencia de hemangioma capilar retiniano (RCH) en pacientes con la enfermedad de von Hippel-Lindau (VHL). RCH es un tumor vascular benigno de la retina. Usando una revisión retrospectiva de series de casos consecutivos, los investigadores encontraron que el número de medio de tumores RCH por ojo para pacientes con VHL era de 4. Están interesados en conocer cuál es la probabilidad de que se detecten más de cuatro tumores por ojo.
Como se puede ver en los ejemplos la distribución de Poisson es muy habitual en los campos de la biología y la medicina. En una distribución de Poisson, las probabilidades de interés son las de observar un número de eventos, \(x\), en un tiempo o espacio determinado. La distribución de probabilidad para este experimento queda completamente determinada si conocemos el número de eventos y \(\lambda\) la tasa o media del número de eventos que ocurren por unidad de tiempo o espacio. Si \(X\) denota la variable aleatoria asociada con este experimento, la función de densidad de probabilidad se define como: \[P(X = x) = \frac{e^{-\lambda} \lambda^x}{x!}\] Dicha distribución se denota habitualmente: \[ X \sim Po(\lambda)\]. Esta distribución se puede evaluar para cualquier valor entre 0 y el número de máximo de ocurrencias que pueden ocurrir. Dado que este valor no se conoce de antemano se debe prefijar un valor máximo que asegure que la probabilidad de ese valor sea cero.
En R la función dpois permite obtener cualquier probabilidad de la distribución de Poisson una vez fijamos el valor que deseamos evaluar (\(x\)), y la tasa o media del número de eventos (\(\lambda\)). Por ejemplo, podemos obtener la función de densidad de probabilidad asociada a un experimento de Poisson con media de ocurrencias de 5:
# Establecemos los posibles resultados del experimneto (número de ocurrencias)
eventos <- 0:20
# Media del número de eventos
media <- 5
# Obtenemos ahora la función de densidad
fden <- dpois(eventos,media)
# Tabla
res <- as.data.frame(cbind(eventos,fden))
colnames(res) <- c("Eventos","Probabilidad")
res## Eventos Probabilidad
## 1 0 6.737947e-03
## 2 1 3.368973e-02
## 3 2 8.422434e-02
## 4 3 1.403739e-01
## 5 4 1.754674e-01
## 6 5 1.754674e-01
## 7 6 1.462228e-01
## 8 7 1.044449e-01
## 9 8 6.527804e-02
## 10 9 3.626558e-02
## 11 10 1.813279e-02
## 12 11 8.242177e-03
## 13 12 3.434240e-03
## 14 13 1.320862e-03
## 15 14 4.717363e-04
## 16 15 1.572454e-04
## 17 16 4.913920e-05
## 18 17 1.445271e-05
## 19 18 4.014640e-06
## 20 19 1.056484e-06
## 21 20 2.641211e-07# Representamos gráficamente
ggplot(res,aes(Eventos,Probabilidad)) +
geom_bar(stat = "identity", width = 0.05) +
labs(xlab = "Número de eventos",ylab = "Probabilidad",title = "Poisson(5)")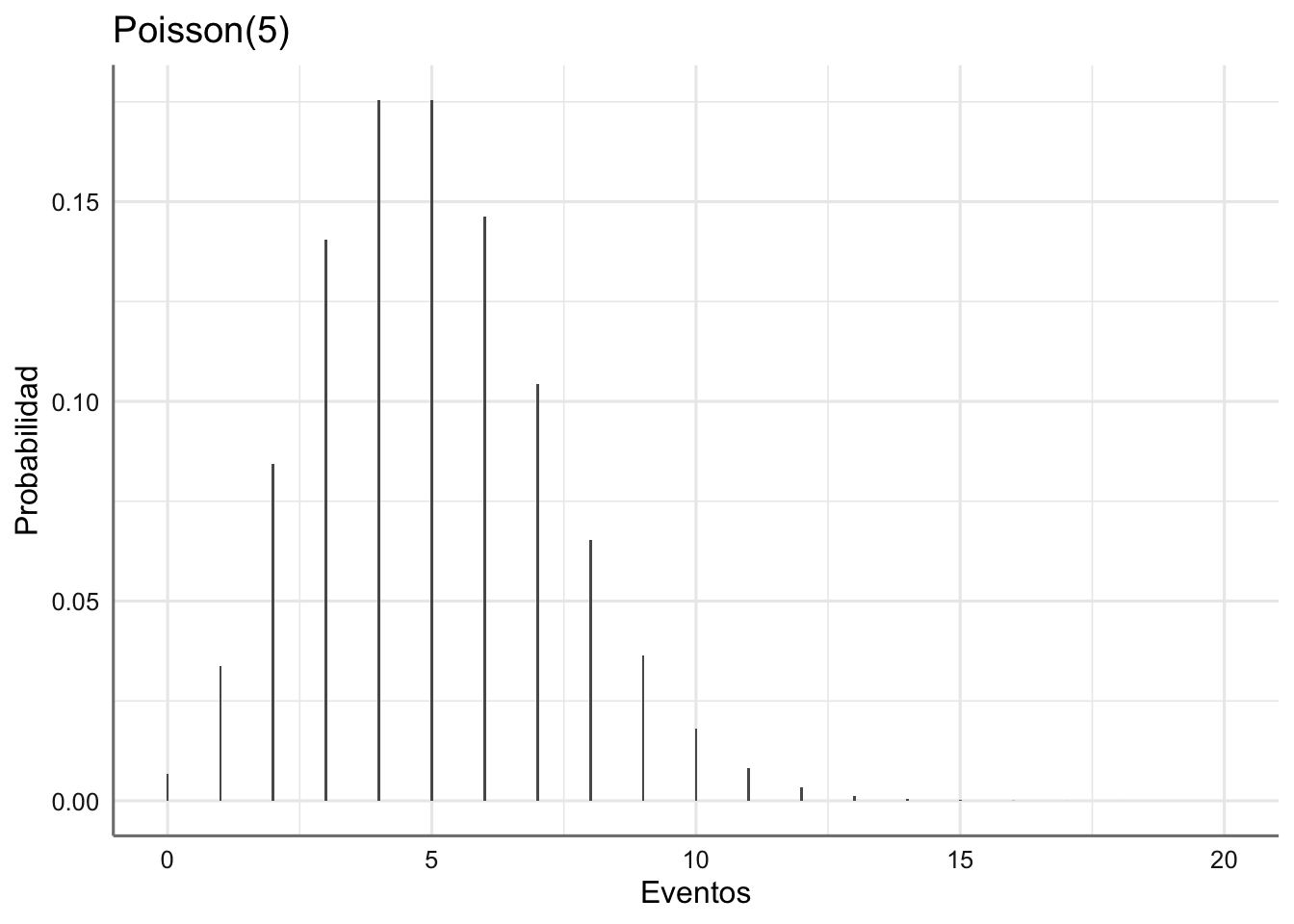 Como se puede ver en el gráfico los valores más probables se concentran alrededor de la tasa media de ocurrencia del evento.
Como se puede ver en el gráfico los valores más probables se concentran alrededor de la tasa media de ocurrencia del evento.
Una vez establecida la función de densidad de probabilidad resulta posible obtener el valor esperado del número de eventos ocurridos, así como conocer su variabilidad haciendo uso de las definiciones expuestas en el tema anterior. En concreto, para una variable que sigue una distribución de probabilidad Poisson (\(X \sim Po(\lambda)\)) tenemos que: \[E(X) = \lambda\] \[V(X) = \lambda\] \[DT(X) = \sqrt{\lambda}\]
En nuestro ejemplo tendríamos que el número esperado de eventos se situaría en \(5\) y la variabilidad (en términos de la desviación típica) en \(\sqrt{5} = 2.24\), lo que implica que los valores más probables se sitúan entre 3 y 7 eventos (\(5 \pm 2\)).
6.2.1 Cálculos de probabilidad
A continuación se calculan las probabilidades de interés para cada uno de los ejemplos anteriores.
- Ejemplo 1. Estamos interesados en calcular la \(P(X >= 1) = 1 - P(X = 0)\) para una variable Poisson con media 2.
## [1] 0.8646647- Ejemplo 2. Estamos interesados en calcular la \(P(X = 0)\) para una variable Poisson con media 0.5.
## [1] 0.6065307- Ejemplo 3. Estamos interesados en calcular la \(P(X > 4) = 1 - P(X <= 4)\) para una variable Poisson con media 4. En este caso usamos la función
ppoisque nos permite calcular la función de distribución asociada.
## [1] 0.37116316.2.2 Otras situaciones
Exploramos ahora situaciones donde necesitamos reajustar la tasa de eventos para el calculo de probabilidades. Un laboratorio es capaz de realizar 20 análisis de cierto tipo en un hora. ¿Cuál es la probabilidad de realizar entre 30 y 36 análisis en las próximas dos horas?¿y la probabilidad de realizar más de 36?
En este caso conocemos la tasa media por hora pero al preguntarnos por una unidad de tiempo mayor es necesario adaptar dicha tasa.
# Tasa por hora
tasa <- 20
# Unidad de tiempo
horas <- 2
# Tasa en el intervalo de tiempo solicitado
media <- tasa*horas
media## [1] 40## [1] 0.2346519## [1] 0.75758586.2.3 Ajuste de la distribución Poisson
En este apartado vemos como obtener la distribución de Poisson asociada a una muestra de datos correspondientes a un estudio experimental. El ajuste de dicha distribución nos permitirá obtener la probabilidad asociada a cualquier situación experimental de la población bajo estudio.
Ejemplo 1. Se ha contabilizado el número de reacciones químicas (en realidad cambios de temperatura) que se producen en un compuesto durante un período de cinco horas. Las mediciones se han realizado todos los días durante 20 semanas. Las mediciones obtenidas aparecen en la tabla siguiente:
| Reacciones químicas | Número de días | |
|---|---|---|
| 0 | 12 | |
| 1 | 10 | |
| 2 | 19 | |
| 3 | 17 | |
| 4 | 10 | |
| 5 | 8 | |
| 6 | 7 | |
| 7 | 5 | |
| 8 | 5 | |
| 9 | 3 | |
| 10 | 3 | |
| 11 | 1 |
Ajustamos la distribución de Poisson correspondiente y calculamos cuál es la probabilidad de que ocurran más de 9 reacciones químicas
# En primer lugar cargamos los datos
reacciones <- 0:11
frecuencia <- c(12,10,19,17,10,8,7,5,5,3,3,1)
design <- data.frame(reacciones, frecuencia)
# Para calcular la tasa debemos calcular la media ponderada del número de eventos
# Mediciones totales
total <- sum(frecuencia)
# Media ponderada
media <- sum(reacciones*frecuencia)/total
# Número esperado de reacciones
media## [1] 3.64La media de reacciones químicas se sitúa en 3.64. Calculamos ahora la probabilidad de interés
## [1] 0.012455Ejemplo 2. La probabilidad de que un individuo sufra una reacción al inyectarle un suero es 0.001. Determinar la probabilidad de que de un total de 2000 personas más de dos individuos sufran una reacción. Para poder ajustar la distribución de Poisson es necesario ajustar la tasa media de eventos que en este caso viene dada por el producto del número de repeticiones por la probabilidad de sufir una reacción
## [1] 0.5939942Hay una probabilidad de 0.59 de observar dos reacciones entre los 2000 sujetos. Este problema también se podría haber resuelto a partir de la distribución Binomial pero cuando el tamaño de la muestra multiplicado por la probabildiad de exíto (\(n\theta\)) es muy pequeña en comparación con dicho tamaño (2000),se considera la denominda aproximación de la Binomial por la Poisson que es lo que hemos hecho en este caso. Esto implica que en los caso de uso de la Binomial habrá que comprobar esta propiedad en primer lugar para conocer si el cálculo de probabilidad lo debemos hacer con la distribución de Poisson obtenida de esta forma.
6.3 Normal
Hasta ahora todas las distribuciones consideradas eran de tipo de discreto. En este punto tratamos la distribución de probabilidad de tipo continuo y más concreta mente la más famosa y utilizada de todas ellas: la distribución de probabilidad Normal. Una variable de tipo continuo es aquella que puede tomar cualquier valor dentro de un rango de valores, es decir, existe un infinito número de valores posibles para la variable aleatoria. Para representar gráficamente una distribución de una variable aleatoria continua se debe construir un subconjunto de clases o intervalos consecutivos para el rango de valores de la variable considerada y considerar el histograma resultante. Cuando consideramos un número muy grande de clases o intervalos podríamos obtener la curva suavizada que representa la función de densidad de probabilidad de la variable aleatoria. A continuación se muestra la representación gráfica de una variable continua cuando consideramos 5, 10, 20, 50 0 75 clases, así como la función de densidad teórica correspondiente. Como se observa cuanto mayor es el número de intervalos considerados más se parece el histograma a la función de densidad de probabilidad.
set.seed(1492)
df <- data.frame(x = rnorm(5000))
x <- df$x
# 5 clases
base <- ggplot(df, aes(x)) + geom_histogram(aes(x,..density..),bins = 5) + stat_function(fun = dnorm, colour = "red")
base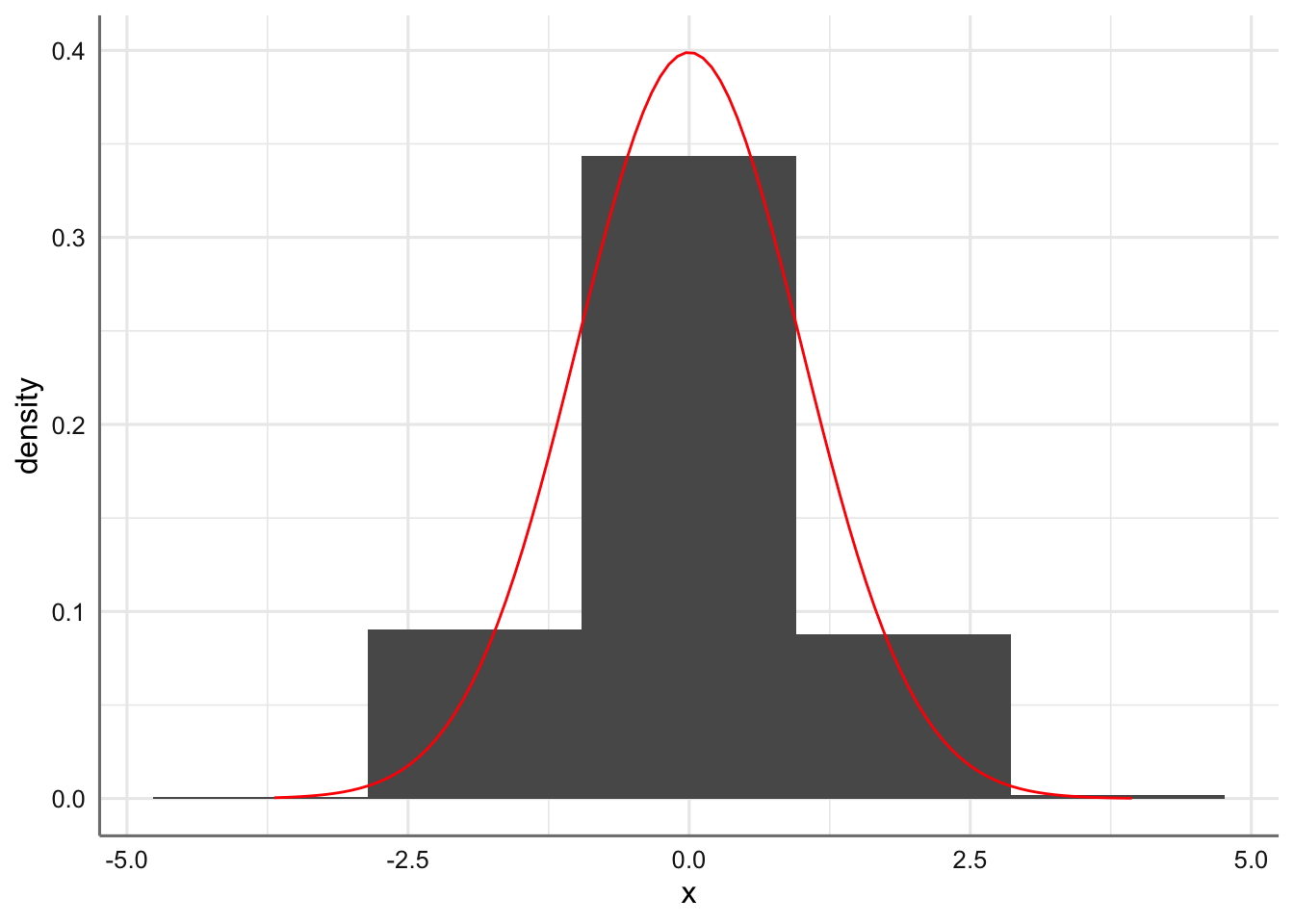
# 10 clases
base <- ggplot(df, aes(x)) + geom_histogram(aes(x,..density..),bins = 10) + stat_function(fun = dnorm, colour = "red")
base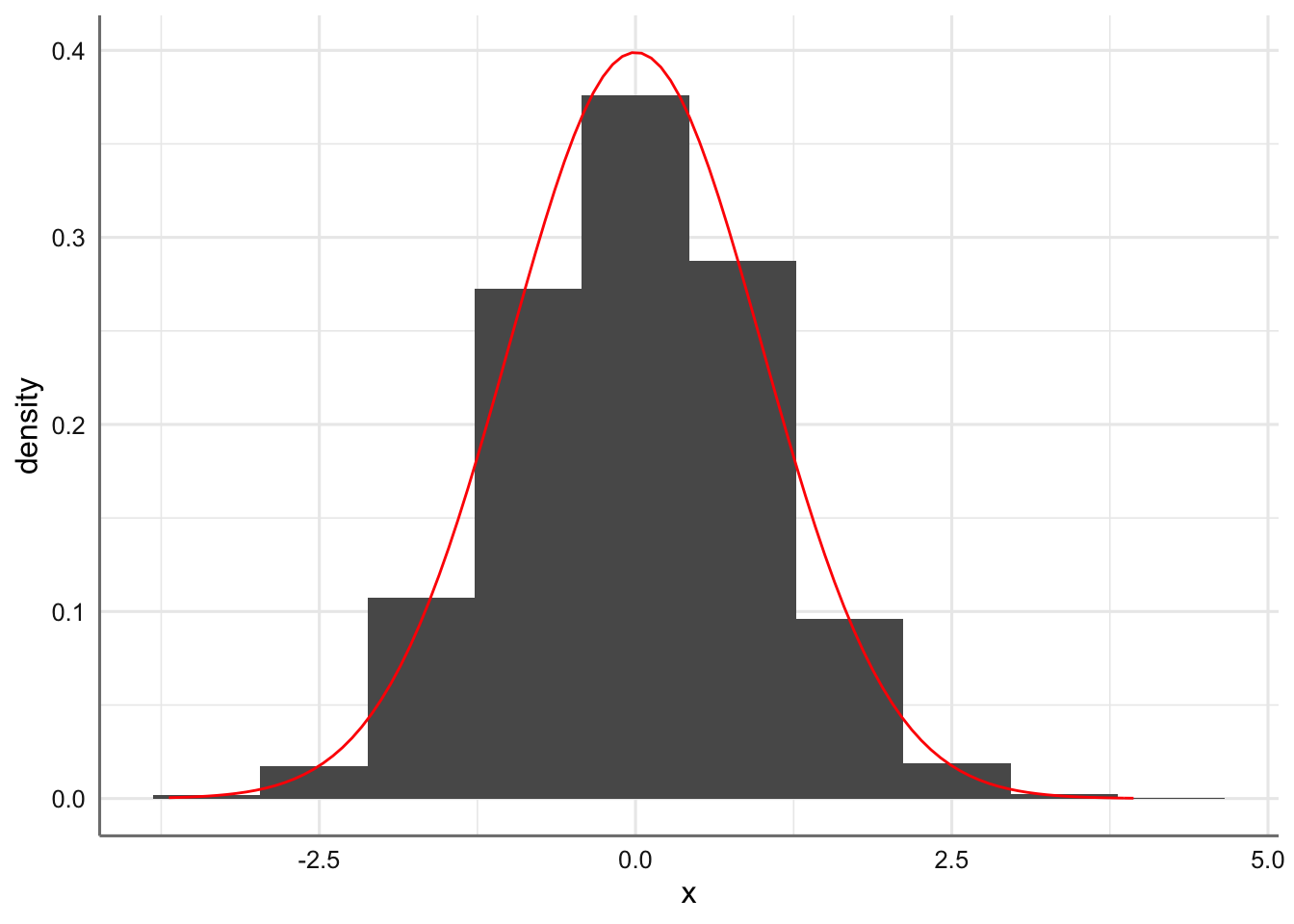
# 20 clases
base <- ggplot(df, aes(x)) + geom_histogram(aes(x,..density..),bins = 20) + stat_function(fun = dnorm, colour = "red")
base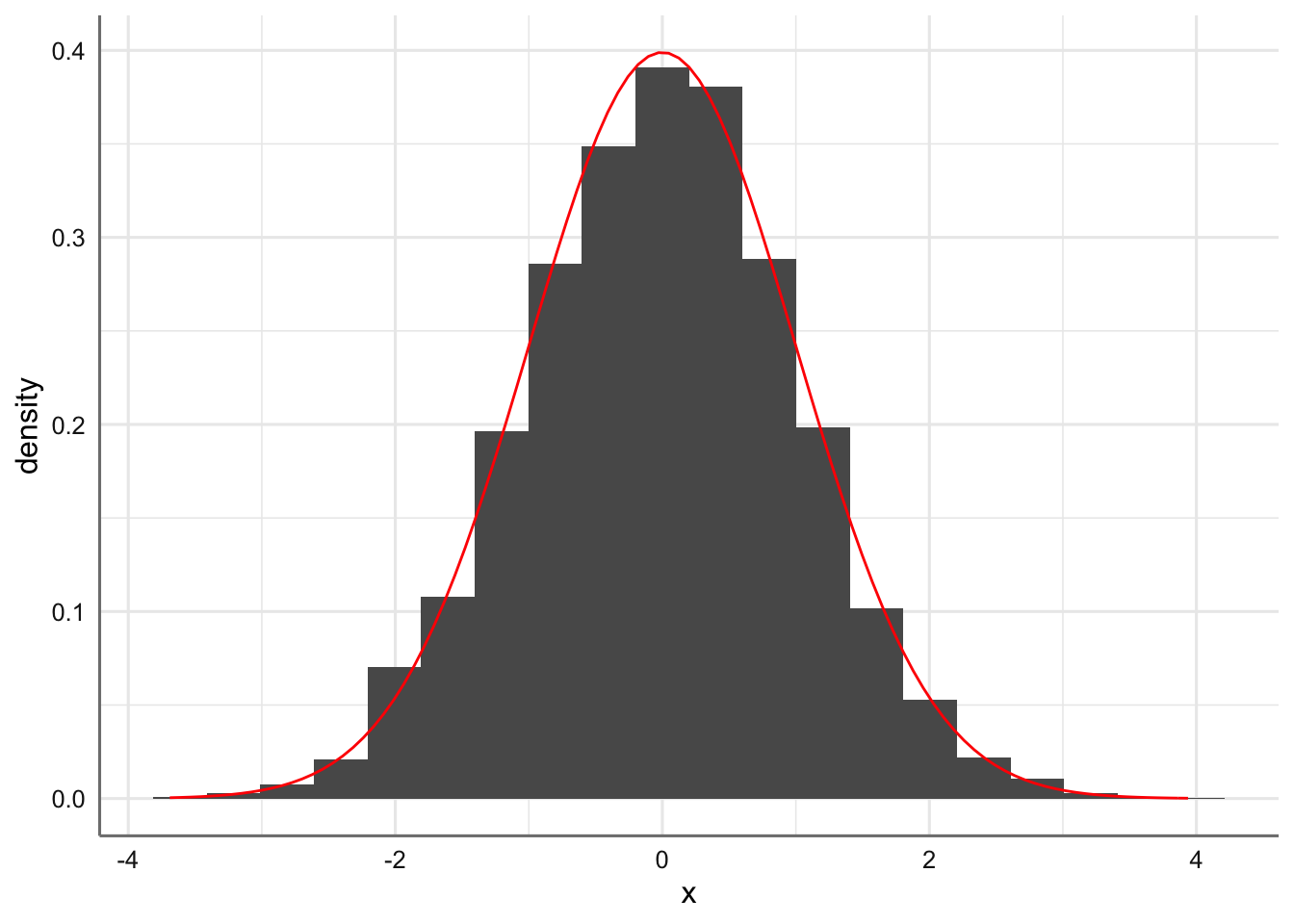
# 50 clases
base <- ggplot(df, aes(x)) + geom_histogram(aes(x,..density..),bins = 50) + stat_function(fun = dnorm, colour = "red")
base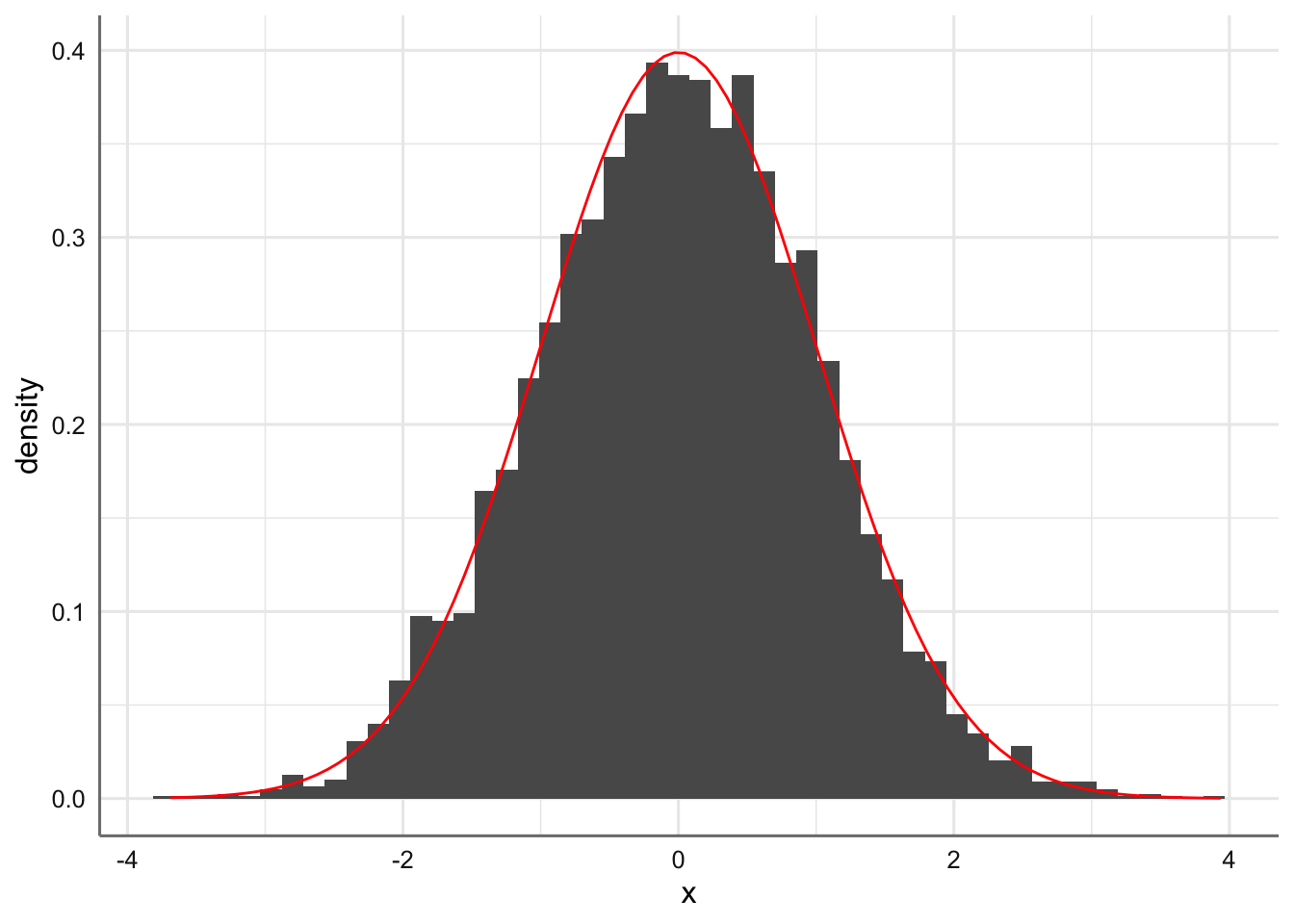
# 75 clases
base <- ggplot(df, aes(x)) + geom_histogram(aes(x,..density..),bins = 75) + stat_function(fun = dnorm, colour = "red")
base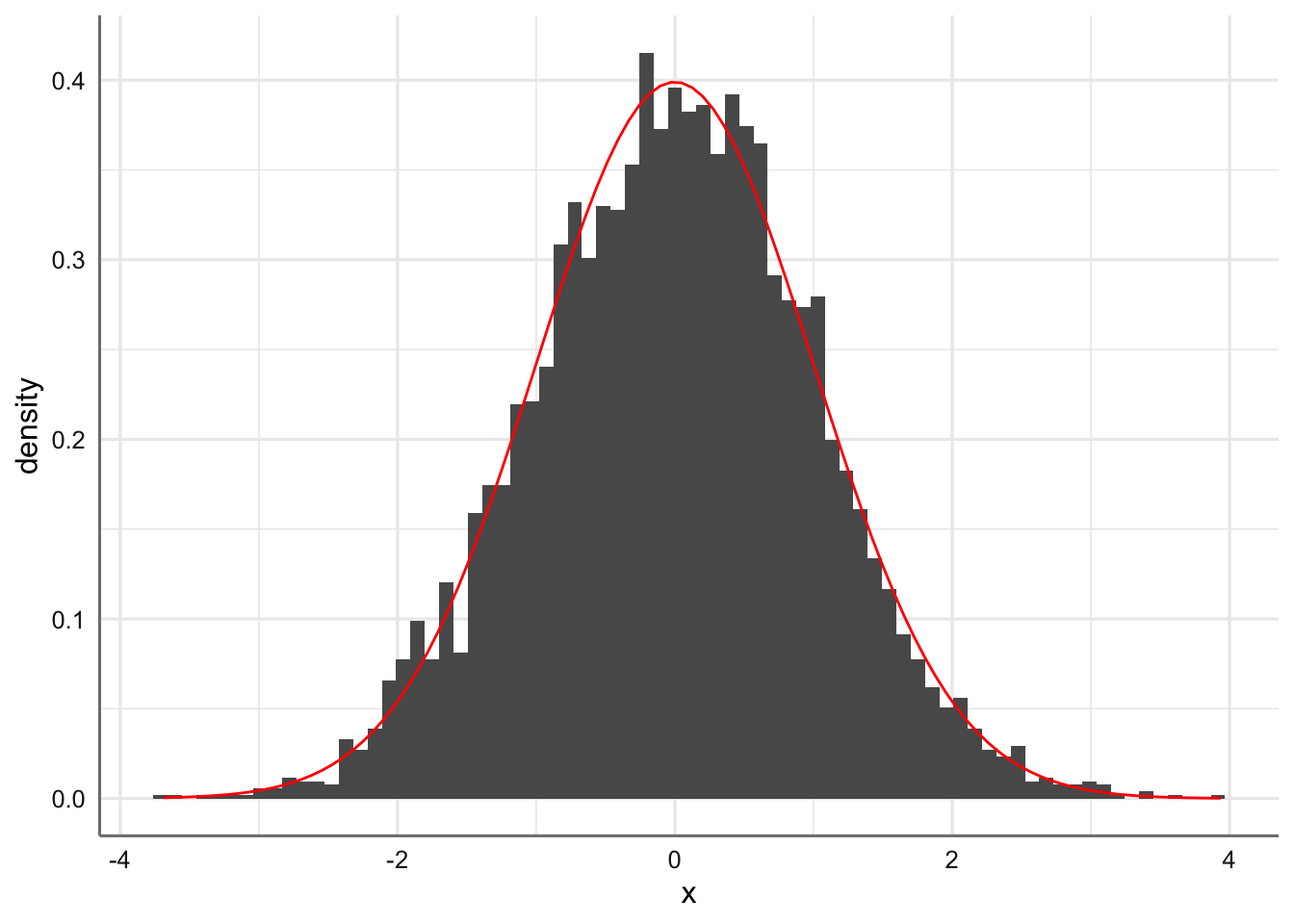
Esta aproximación gráfica nos permite extraer varias conclusiones muy relevantes para el cálculo de probabilidades en variables aleatorias de tipo continuo: 1. Dado que la probabilidad total para el rango de valores de la variable debe ser uno esto implica que el área bajo la curva de densidad obtenida debe ser igual a uno, ya que representa la función de densidad de probabilidad de todos ellos. 2. La función de densidad de probabilidad en un único valor es siempre cero ya que el área de un punto del eje x es cero 3. Solo podemos calcular probabilidades para una rango de valores de la variable, que coincide exactamete con el area bajo la curva que queda englobada entre los dos valores del eje x correspondientes a la variable de interés.
Para el ejemplo anterior ¿cuál es la probabilidad entre los valores de x comprendidos entre -1 y 1?
set.seed(1492)
df <- data.frame(x = rnorm(5000))
x <- df$x
base <- ggplot(df, aes(x)) + geom_histogram(aes(x,..density..),bins = 75) + stat_function(fun = dnorm, colour = "red")
base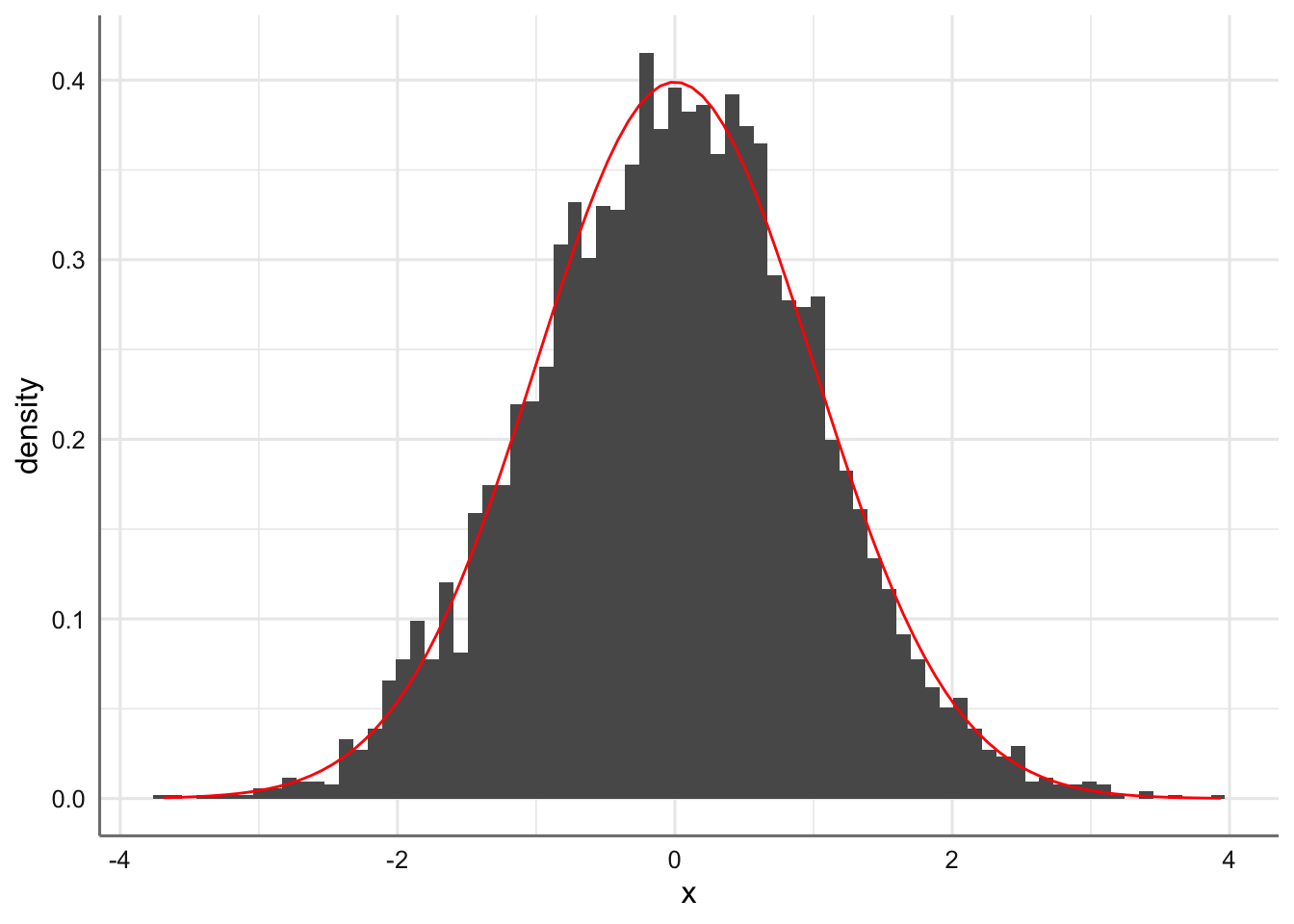
# Shading from x = -1 to x = 1 (within one std deviation):
dnorm_one_sd <- function(x){
norm_one_sd <- dnorm(x)
# Have NA values outside interval x in [-1, 1]:
norm_one_sd[x <= -1 | x >= 1] <- NA
return(norm_one_sd)
}
# Plot:
base + stat_function(fun = dnorm) +
stat_function(fun = dnorm_one_sd, geom = "area", fill = "yellow", alpha = 0.3)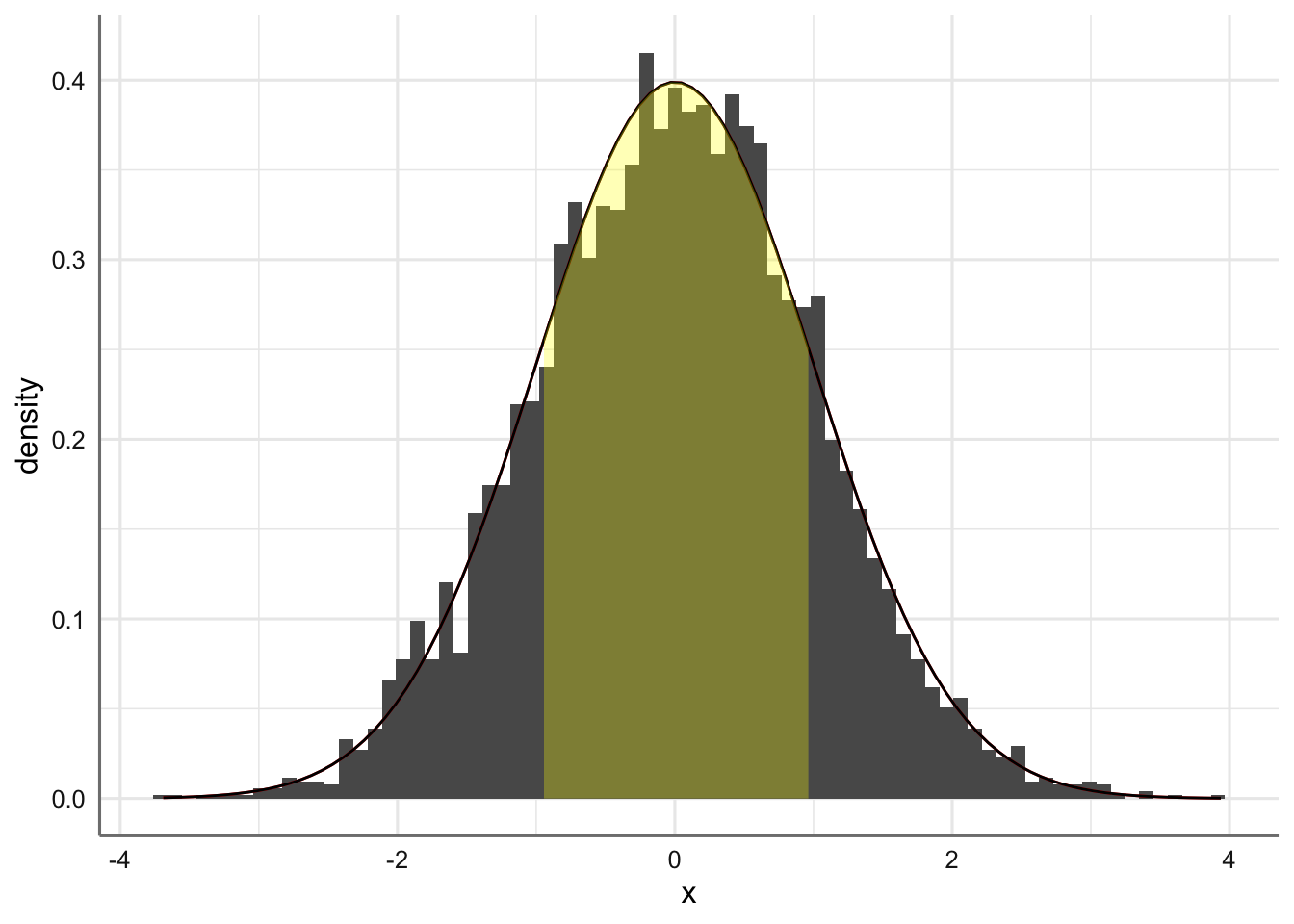
Por tanto, el histograma se trata de una aproximación a la probabilidad real, lo que resulta de una gran relevancia ya que si asumimos una distribución teórica para el conjunto de datos experimentales sera posible evaluar cualquier probabilidad asociada con ella.
La función de densidad de probabilidad para una variable aleatoria \(X\) que sigue una distribución Normal con parámetros \(\mu\) y \(\sigma\), denotada por \(N(\mu, \sigma^2)\) viene dada por: \[f(x) = \frac{1}{2\pi\sigma^2} exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right)\] Los dos parámetros de la distribución son \(\mu\) que representa la medida de localización y \(\sigma\) la medida de dispersión. Habitualmente los conocemos por sus nombres más habituales como son la media y la desviación típica. En concreto, para una variable que sigue una distribución de probabilidad Normal (\(X \sim N(\mu, \sigma^2)\)) tenemos que: \[E(X) = \mu\] \[V(X) = \sigma^2\] \[DT(X) = \sigma\]
A continuación se representan diferentes funciones de densidad para diferentes valores de los parámetros:
- Distribuciones con media cero pero con desviaciones típicas 1 y 2 respectivamente. El efecto del aumento de la dispersión provoca que la función de densidad se convierta en más plana y asigne probabilidad a rangos de valores más extremos.
normal2 <- function(x){dnorm(x, mean = 0, sd = 3)}
grafico <- ggplot(data.frame(x = c(-10, 10)), aes(x)) + stat_function(fun = dnorm)
grafico <- grafico + stat_function(fun = normal2,colour = "red")
grafico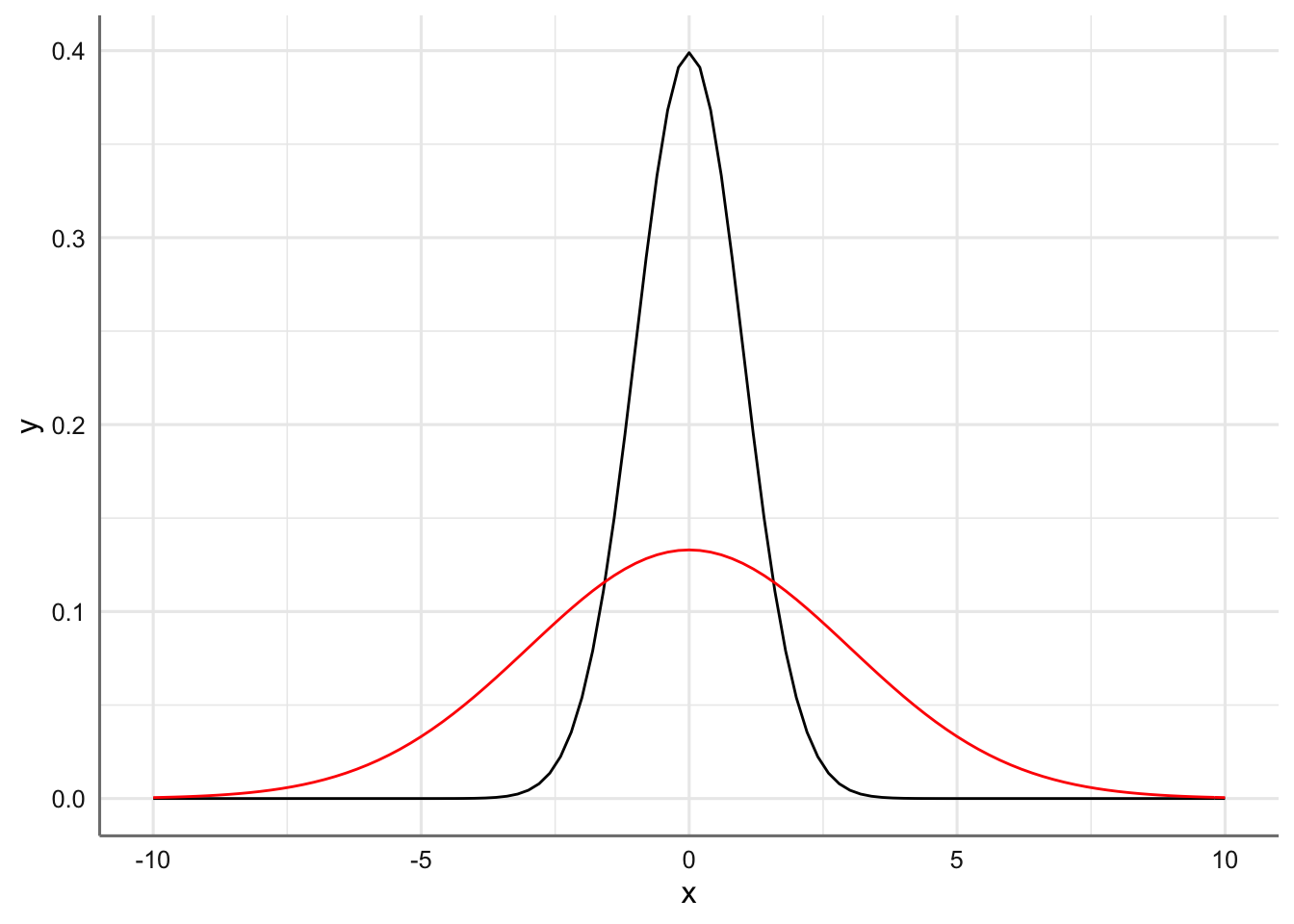
- Distribuciones con medias 0 y 3 pero con desviación típica 1. El efecto de la localización provoca un desplazamiento de la función de densidad para centrarse en el valor de la media.
normal2 <- function(x){dnorm(x, mean = 3, sd = 1)}
grafico <- ggplot(data.frame(x = c(-10, 10)), aes(x)) + stat_function(fun = dnorm)
grafico <- grafico + stat_function(fun = normal2,colour = "red")
grafico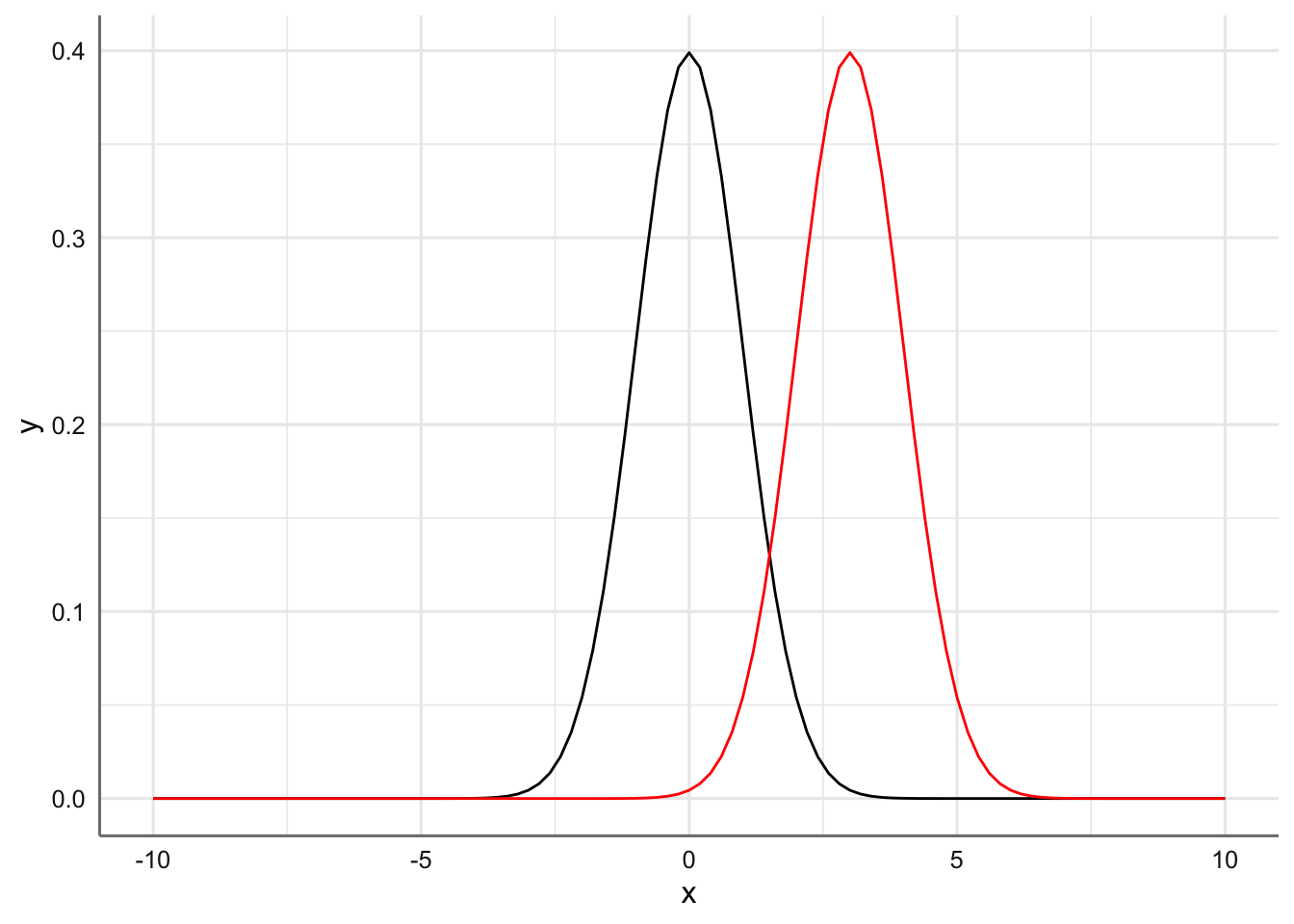
6.3.1 Características de la distribución Normal
A continuación se presentan algunas de las características más importantes de la distribución Normal:
- Es una distribución simétrica alrededor de la media, \(\mu\).
- La media, la mediana y la moda son iguales.
- La distribución Normal queda completamente especificada a partir de los valores de \(\mu\) y \(\sigma\). Los diferentes valores de la media y la desviación típica desplazan hacia un lado o el otro, o consiguen una distribución más puntiaguda (desviaciones típicas más pequeñas) o más achatada (desviaciones típicas más grandes).
- El intervalo definido por \(\mu - 5 * \sigma, \mu + 5 * \sigma\) tiene probabilidad 1, es decir, la probabilidad de los extremos inferior y superior del rango de valores se puede considerar despreciable.
- Dada una variable aleatoria Normal con media \(\mu\) y desviación típica \(\sigma\) y tenemos un escalar \(a\) tenemos que:
\[ X \sim N(\mu, \sigma^2) \Longrightarrow aX \sim N(a\mu, a^2\sigma^2)\] * Dada dos variables aleatorias Normales, \(X e Y\), con medias y desviaciones típicas respectivas: \(\mu_1\), \(\sigma_1\) y \(\mu_2\), \(\sigma_2\) y dos escalares \(a\) y \(b\) tenemos que
\[ X \sim N(\mu_1, \sigma^2_1), Y \sim N(\mu_2, \sigma^2_2) \Longrightarrow aX + bY\sim N(a\mu_1+b\mu_2, a^2\sigma^2_1+b^2\sigma^2_2)\]
Esta última propiedad se puede generalizar para el caso de \(m\) variables aleatorias en lugar de 2.
6.3.2 Teorema Central de Límite
Si las variables aleatorias \(X_1,...X_n\) son una muestra aleatoria de una distribución con media \(\mu\) y desviación típica \(\sigma\) entonces las variables aleatorias suma (\(T = X_1+...+X_n\)) y media (\(M = (X_1+...+X_n)/n\)) tienen distribuciones: \[ T \sim N\left(n\mu,n\sigma^2\right)\] \[ M \sim N\left(\mu,\frac{\sigma^2}{n}\right)\] Ejemplo. Supóngase que las personas que asisten a una fiesta sriven bebidas de una botella que contiene 63 onzas de un cierto líquido. Su el tamaño esperado de cada bebida es de 2 onzas con una deviación típica de 0.5 onzas. ¿Cuál es la probabilidad de que la botella no está vacia después de haber servido 36 bebidas?
6.3.3 Cálculos de probabilidad
Ejemplo. Imaginemos que los valores de colesterol de una cierta población pueden asimilarse a una distribución Normal con media de 200 mg/100 ml y desviación típica de 20 mg/100 ml. Si se selecciona a un individuo de la población y se analiza su nivel de colesterol: i) ¿Cuál es la probabilidad de que el nivel de colesterol se sitúe entre 180 y 200 mg/100 ml?, ii) ¿Cuál es la probabilidad de que el nivel de colesterol sea inferior a 150 mg/100 ml?, iii) ¿Cuál es la probabildiad de que el nivel de colesterol sea superior a 225 mg/100 ml?, iv) ¿Cuál es la probabilidad de que el nivel de colesteril se sitúe entre 190 y 210 mg/100 ml?
Para realizar los calculos de probabilidad utilizamos la función pnorm() que nos permite obtener la función de disttribución normal
# ¿Cuál es la probabilidad de que el nivel de colesterol se sitúe entre 180 y 200 mg/100 ml?
pnorm(200, mean = 200, sd = 20) - pnorm(100, mean = 200, sd = 20)## [1] 0.4999997# ¿Cuál es la probabilidad de que el nivel de colesterol sea inferior a 150 mg/100 ml?
pnorm(150, mean = 200, sd = 20)## [1] 0.006209665# ¿Cuál es la probabildiad de que el nivel de colesterol sea superior a 225 mg/100 ml?
1 - pnorm(225, mean = 200, sd = 20)## [1] 0.1056498# ¿Cuál es la probabilidad de que el nivel de colesterol se sitúe entre 180 y 200 mg/100 ml?¿Cuál es la probabilidad de que el nivel de colesteril se sitúe entre 190 y 210 mg/100 ml?
pnorm(210, mean = 200, sd = 20) - pnorm(190, mean = 200, sd = 20)## [1] 0.38292496.3.4 Tipificación
Dada una variable aleatoria \(X\) con distribución de probabilidad \(N(\mu,\sigma^2)\) la variable aleatoria \(Z\) definida como \[Z=\frac{X-\mu}{\sigma}\] tiene una distribución de probabilidad \(N(0,1)\) (denominada Normal estándar), es decir, \[Z \sim N(0,1)\]
La tipificación toma la distribución de una variable aleatoria y la transforma en otra sin más que restar por la media y dividir por la desviación típica. Esta distribución tipificada se utiliza habitualmente para el cálculo de probabilidades y para representar variables que no dependen de la media ni la desviación típica. En este caso \(E(Z) = 0\) y \(V(Z) = 1\).
En este enlace se pueden realizar los cálculos de probabilidad (así como su representación gráfica) asociados con la normal estándar.
Para los datos del ejemplo anterior, los valores tipificados en cada situación vienen dados por:
# ¿Cuál es la probabilidad de que el nivel de colesterol se sitúe entre 180 y 200 mg/100 ml?
(200 - 200) / 20## [1] 0## [1] -5# ¿Cuál es la probabilidad de que el nivel de colesterol sea inferior a 150 mg/100 ml?
(150 - 200) / 20## [1] -2.5# ¿Cuál es la probabildiad de que el nivel de colesterol sea superior a 225 mg/100 ml?
(225 - 200) / 20## [1] 1.25# ¿Cuál es la probabilidad de que el nivel de colesterol se sitúe entre 180 y 200 mg/100 ml?¿Cuál es la probabilidad de que el nivel de colesteril se sitúe entre 190 y 210 mg/100 ml?
(210 - 200) / 20## [1] 0.5## [1] -0.5Utilizando el enlace anterior comprueba que las probabildiades obtenidas son las mismas que las obtenidas anteriormente.
6.4 Variables aleatorias a partir de la distribución Normal
A partir de la distribución de probabilidad Normal se pueden obtener otras distribuciones de probabilidad que resultan de gran utilidad para los procesos de generalización de resultados de un diseño experimental a una población que veremos en la unidad siguiente.
6.4.1 Distribución Chi-cuadrado
Sean n variables aleatorias \(X_1,...,X_n\) independientes entre sí cuya distribución de probabilidad es idéntica para todas ellas e igual a una Normal estándar (\(N(0,1)\)). Si definimos la variable aleatoria suma como: \[X = X_1 + ... + X_n,\] entonces decimos que \(X\) se distribuye según una distribución Chi-cuadrado con \(n\) grados de libertad y la denotamos por \[X \sim \chi^2_n.\]
6.4.2 T se Student
Si tenemos dos variables aleatorias independientes \(Y\) y \(Z\) con distribuciones de probabilidad \[Z \sim N(0,1); Y \sim \chi^2_n,\] y consideramos la variable aleatoria \(X\) dada por: \[X = \frac{Z}{\sqrt{Y/n}},\] entonces decimos que dicha variable sigue una distribución \(t\) de Student con \(n\) grados de libertad, y se denota por \[X \sim t_n.\]
6.4.3 F de Snedecor
Si tenemos dos variables aleatorias independientes \(Y\) y \(Z\) con distribuciones de probabilidad \[Z \sim \chi^2_n; Y \sim \chi^2_m,\] y consideramos la variable aleatoria \(X\) dada por: \[X = \frac{Z/n}{Y/m},\] entonces decimos que dicha variable sigue una distribución \(F\) de Snedecor con \(n\) y \(m\) grados de libertad, y se denota por \[X \sim F_{n,m}.\]
6.5 Otras dostribuciones de probabilidad de interés
En este punto se presentan otras distribuciones de probabilidad que aunque resultan muy habituales en la práctica no son el objetivo de este temario. Se muestran como ejemplos de otros tipos de distribuciones.
6.5.1 Distribución Geométrica
La distribución de probabilidad Geométrica es de tipo discreto y se utiliza para modelizar situaciones experimentales donde se está interesado en saber cuantos fracasos han ocurrido hasta que aparece un éxito. Un ejemplo habitual es contar el número de piezas sin defectos hasta que encontramos una con defecto. Si \(\theta\) denota la probabilidad de éxito, la función de densidad de probabilidad de una variable aleatoria \(X\) de tipo geométrica, \(X \sim Ge(\theta)\) viene dada por: \[f(x) = (1 - \theta)^k \theta, k=1,2,3,...\] donde \(k\) representa el número de fracasos, es decir, que la función de densidad representa la probabilidad de encontrar \(k\) fracasos hasta el primer éxito. Una vez especifica la probabilidad de éxito \(\theta\) tenemos que: \[E(X) = \frac{1}{\theta}\] \[V(X) = \frac{1-\theta}{\theta^2}\] \[DT(X) = \sqrt{\frac{1-\theta}{\theta^2}}\] Para los cálculos de probabilidad debemos usar las funciones dgeom() y pgeom().
6.5.2 Distribución Exponencial
La distribución exponencial es el equivalente continuo de la distribución geométrica discreta. Esta distribución describe procesos en los que nos interesa saber el tiempo hasta que ocurre determinado evento, sabiendo que, el tiempo que pueda ocurrir desde cualquier instante dado t, hasta que ello ocurra en un instante tf, no depende del tiempo transcurrido anteriormente en el que no ha pasado nada.
Ejemplos de este tipo de distribuciones son:
- El tiempo que tarda una partícula radiactiva en desintegrarse. El conocimiento de la ley que sigue este evento se utiliza en Ciencia para, por ejemplo, la datación de fósiles o cualquier materia orgánica mediante la técnica del carbono 14, C14;
- El tiempo que puede transcurrir en un servicio de urgencias, para la llegada de un paciente;
- En un proceso de Poisson donde se repite sucesivamente un experimento a intervalos de tiempo iguales, el tiempo que transcurre entre la ocurrencia de dos sucesos consecutivos sigue un modelo probabilístico exponencial. Por ejemplo, el tiempo que transcurre entre que sufrimos dos veces una herida importante.
La distribución exponencial viene completamente especificada, a través del parámetro \(\lambda >0\) que mide el número medio de veces que ocurre el evento de interés, mediante la función de densidad: \[f(x) =\lambda e^{-\lambda t}, t \geq 0\] Si \(X \sim Exp(\lambda)\) entonces tenemos que: \[E(X) = \frac{1}{\lambda}\] \[V(X) = \frac{1}{\lambda^2}\] \[DT(X) = \frac{1}{\lambda}\] Para los cálculos de probabilidad debemos usar las funciones dexp() y pexp().
7 Funciones para el cálculo de probabilidades
Funciones para el cálculo de probabilidades onjunta, marginales, teorema de Bayes y teorema de la probabilidad total:
# Cálculo de probabilidades
calculo.probabilidades <- function(npmarg,etimarg,probmarg,npcond,etimarg2,probcond)
# Suceso A
# npmarg = número de probabildiades marginales
# etimarg = etiquetas para las probabilidades marginales
# probmarg = probabilidades marginales
# Suceso B dado A
# npcond = número de probabildiades condicionadas por cada valor de A
# etimarg2 = etiquetas para las probabilidades marginales por cada valor de A
# probcond = probabilidades marginales ordenadas para lemento de A
{
# Probabilidad marginal P(A)
pmarginal <- matrix(rep(probmarg,npcond),nrow = npmarg)
# Probabilidad condicionada P(B|A)
pcondicional <- matrix(probcond, nrow = npmarg, byrow=T)
# Probabilidad conjunta P(A,B)
pconjunta <- pmarginal*pcondicional
rownames(pconjunta) <- etimarg
colnames(pconjunta) <- etimarg2
# Probabilidad Total
ptotal <- apply(pconjunta,2,sum)
# Teorema de Bayes
res <-matrix(rep(ptotal,npmarg),nrow = npmarg, byrow =T)
pbayes <- pconjunta / res
# Resultado
return(list(Conjunta = round(pconjunta,4), Total = round(ptotal,4), Bayes = round(pbayes,4)))
}Función para probabilidad de screening
Screening <- function(positivos,negativos,etitest,etienfermedad,incidencia)
# positivos = resultados positivos del test empezando por los que padecen la enfermedad
# negativos = resultados negativos del test empezando por los que padecen la enfermedad
# etitest = etiquetas del test diagnóstico
# etienfermedad = etiquetas de enfermos y sanos
# incidencia = incidencia de la enfermedad en la población
{
# Tabla de resultados
tabla <- matrix(c(positivos,negativos), ncol = 2, byrow = T)
rownames(tabla) <- etitest
colnames(tabla) <- etienfermedad
# Calculo de totales
total.test <- apply(tabla,1,sum)
total.enfermedad <- apply(tabla,2,sum)
total <- sum(total.test)
# Probabilidades marginales
marginal.enfermos <- tabla[,1]/total.enfermedad[1]
marginal.sanos <- tabla[,2]/total.enfermedad[2]
# Resultados
Sensibilidad <- marginal.enfermos[1]
Especificidad <- marginal.sanos[2]
Predictivo.positivo <- (Sensibilidad*incidencia)/(Sensibilidad*incidencia + (1-Especificidad)*(1-incidencia))
Predictivo.negativo <- (Especificidad*(1-incidencia))/(Especificidad*(1-incidencia) + (1-Sensibilidad)*incidencia)
return(round(data.frame(Sensibilidad,Especificidad,Predictivo.positivo,Predictivo.negativo),4))
}7.1 Ejemplos de uso
Calculo de probabilidades
## $Conjunta
## Rendimiento 1 Rendimiento 2 Rendimiento 3
## Proyecto A 0.10 0.3 0.10
## Proyecto B 0.15 0.2 0.15
##
## $Total
## Rendimiento 1 Rendimiento 2 Rendimiento 3
## 0.25 0.50 0.25
##
## $Bayes
## Rendimiento 1 Rendimiento 2 Rendimiento 3
## Proyecto A 0.4 0.6 0.4
## Proyecto B 0.6 0.4 0.6Screening
## Sensibilidad Especificidad Predictivo.positivo Predictivo.negativo
## + 0.9689 0.99 0.9251 0.9968 Ejercicios
Colección de ejercicios
8.1 Probabilidad básica
Ejercicio 1. Se hacen dos inversiones de 10000 € en dos proyectos. Se supone que el proyecto A va a producir un rendimiento neto de 800, 1000 y 1200 euros con probabilidades respectivas de 0.2, 0.6, 0.2. Se supone que el proyecto B va a producir una ganancia neta de 800, 1000, y 1200 euros con probabilidades respectivas 0.3, 0.4, 0.3. Si asumimos que lo que se gana con un proyecto es independiente de lo que se gana con el proyecto.
- ¿Cuál es la probabilidad de que la ganancia total sea de 2000 euros exactamente?
- ¿Cuál es la probabilidad de que la ganancia total sea igual o superior a 2000 euros?
- ¿Cuál es la probabilidad de que la ganancia sea inferior a 2000 euros?
Ejercicio 2. Un fabricante de galletas presenta muchos productos nuevos cada año, de los cuales cerca del 60% fracasan, 30% tienen un éxito moderado y un 10% tienen un gran éxito. Para mejorar sus posibilidades, el fabricante somete a una prueba sus nuevos productos ante un grupo de clientes, que actúa como jurado calificador. De los fracasos, 50% se califican como malos, 30% como regulares y 20% como buenos. Para los que tuvieron un éxito moderado, la calificación es mala para un 20%, regular para un 40% y buena para otro 40%. Para los que tuvieron gran éxito, los porcentajes son: malos 10%, regulares 30% y buenos 60%.
- ¿Cuál es la probabilidad conjunta de que un producto sea nuevo y reciba una mala calificación?
- Si un nuevo producto tienen una buena calificación, ¿cuál es la probabilidad de que fracase?
- ¿Cuál es la probabilidad de que un producto tenga éxito dado que éste obtuvo una mala calificación?
Ejercicio 3. El 1% de los préstamos que hace cierta empresa financiera no son saldados (es decir, la cantidad prestada no le es devuelta en su totalidad). La compañía efectúa un estudio rutinario de las posibilidades crediticias de los solicitantes. Encuentra que el 30% de los préstamos no saldados se hicieron a clientes de alto riesgo, el 40% a clientes de riesgo moderado y el restante 30% a clientes de bajo riesgo. De los préstamos que fueron saldados, el 10% se hicieron a clientes de alto riesgo, el 40% a clientes de riesgo moderado y el 50% a clientes de bajo riesgo.
- ¿Cuál es la probabilidad de que un préstamo de alto riesgo no sea saldado?
- ¿Cuál es la probabilidad de que una deuda no saldada, dado que el riesgo es moderado?
Ejercicio 4. Una empresa manufacturera tiene tres operarios para una máquina que produce cierto tipo de componentes. El operario A tiene una tasa de defectos del 5%; el operario B, del 3%, y el operario C, del 2%. Los tres operarios producen el mismo número de componentes. Si un componente elegido al zar resulta defectuoso ¿cuál es la probabilidad de que el componente haya sido producido por A, B, o C?
Ejercicio 5. Un departamento de compras encuentra que el 75% de sus pedidos especiales se reciben a tiempo. De los pedidos que se reciben a tiempo, el 80% cumple totalmente las especificaciones; de los pedidos que llegan con retraso, el 60% cumple con las especificaciones.
- ¿Cuál es la probabilidad de que un pedido llegue a tiempo y cumpla con las especificaciones?
- ¿Cuál es la probabilidad de que un pedido cumpla con las especificaciones?
- Si se han recibido cuatro pedidos ¿cuál es la probabilidad de que los cuatro pedidos cumplan con las especificaciones?
Estudio de caso. Los problemas de inventario tratan de dar respuesta a las necesidades de almacenamiento de las empresas para satisfacer la demanda de los consumidores. En concreto, en este caso se plantea el problema de un distribuidor del mercado central especializado en la venta de fresas. Dicho comerciante compra cajas al precio de 20€, y las vende por 50€, y se plantea dos problemas relacionados directamente con lo que denominamos “inventario”:
- Si los clientes solicitan más cajas de las disponibles el comerciante pierde 30€ por cada caja de menos disponible.
- Si el comerciante almacena más cajas de las solicitadas por los clientes, el producto se debe tirar y pierde 20€ por cada caja que no vende.
Para tratar de determinar el número de cajas que debe comprar y almacenar recoge información sobre la demanda realizada por los clientes en la campaña anterior cuyos datos vienen dados en la tabla siguiente:
| Cajas vendidas | Número de días | |
|---|---|---|
| 10 | 15 | |
| 11 | 20 | |
| 12 | 40 | |
| 13 | 25 |
La empresa te proporciona en la tabla siguiente las ganancias esperadas diarias (en euros) asociadas con el número de cajas vendidas y las cajas que debería almacenar:
| Demanda | Almacenar 10 cajas | Almacenar 11 cajas |
|---|---|---|
| 10 | 300 | 280 |
| 11 | 300 | 330 |
| 12 | 300 | 330 |
| 13 | 300 | 330 |
En base a esta información se debe obtener la ganancia esperada para cada acción de inventario, y determinar aquella que proporcione mayores beneficios, es decir, las mayores ganancias diarias. ¿Qué recomendación se debería hacer al distribuidor?
Por otro lado, los asesores convencen al distribuidor de que para tener mayor certeza de sus ganancias debería realizar un estudio marginal, que se basa en el hecho de que cuando se compra una unidad adicional de un artículo (en este caso una caja) pueden ocurrir dos cosas: la unidad se vende o no se vende. De esta forma:
- ¿Cuál es la probabilidad de que la demanda sea al menos de 11 cajas?
- ¿y de al menos 12? ¿y al menos 13?
- ¿Cuál resulta la ganancia y pérdida marginal esperada por la venta o no de una caja más con cada una de las probabilidades anteriores?
- ¿Qué opción recomiendas al distribuidor?
8.2 Tests diagnósticos
Ejercicio 1. Se quiere estudiar la capacidad predictiva de un nuevo síntoma a la hora de detectar cierta enfermedad. Se toma una muestra aleatoria de 775 sujeto enfermos de los cuales 744 muestran el síntoma. Por otro lado se toma una muestra de 1380 sujetos sin la enfermedad de los cuales 21 muestran el síntoma.
- En este contexto ¿qué podemos entender como un falso positivo? ¿y un falso negativo?
- Obtén la sensibilidad y especifidad del síntoma
- Si la incidencia de la enfermedad es del 0.1% ¿cuál es el valor predictivo positivo?¿cuál es el valor predictivo negativo?
Ejercicio 2. En la siguiente tabla se muestran los resultados de un estudio para evaluar la utilidad de una tira reactiva para el diagnóstico de infección urinaria.
| Tira reactiva | Con infección | Sin infección |
|---|---|---|
| Positiva | 60 | 80 |
| Negativa | 10 | 200 |
¿Cuál es la sensibilidad y especificidad del test? ¿Podríamos representar el valor predictivo positivo en función de la incidencia de la enfermedad?¿Como lo harías?
Ejercicio 3. El jefe de enfermería del Hospital ha decidido evaluar la validez de la determinación de la palidez palmar para diferenciar los niños y niñas que tienen baja concentración de hemoglobina de aquellos que tienen una concentración de hemoglobina normal. De esta manera, podrá ampliar la detección del problema que actualmente está reducida por falta de capacidad del laboratorio para procesar las muestras de sangre de los centros de salud. Para esto capacitará a personal de enfermería de los Centros de Salud en la identificación de la palidez palmar y les pedirá que clasifiquen a los niños y niñas atendidos para consulta de control durante una semana en dos grupos: CON PALIDEZ PALMAR y SIN PALIDEZ PALMAR. Otra enfermera realizará una toma de muestra de sangre capilar para realizar un hematocrito, la que será enviada al laboratorio del Hospital donde se determinará la concentración de hemoglobina de cada niño o niña. Luego de una semana de trabajo, la jefa de enfermería obtuvo 124 informes de niños y niñas en los que el personal de enfermería evaluó la palidez palmar. Entre estos encontró que 28 fueron clasificados como CON PALIDEZ PALMAR mientras que el resto fue clasificado como SIN PALIDEZ PALMAR. Luego verificó los resultados obtenidos para cada niño o niña según los informes de laboratorio. Encontró que entre los 28 niños o niñas CON PALIDEZ PALMAR 18 tenían una concentración de hemoglobina baja mientras que el resto tenía concentración normal de hemoglobina. A su vez, encontró que, entre los niños y niñas SIN PALIDEZ PALMAR, 14 tenían concentración de hemoglobina baja, mientras que el resto tenía concentración normal de hemoglobina. Obtén la sensibilidad, especificidad y valores predictivos para esta situación.
Ejercicio 4. Se ha decidido incorporar una nueva técnica de diagnóstico de infección por Streptococo en pacientes con sospecha de faringitis con el fin de disminuir la indicación empírica de antibióticos en el consultorio ambulatorio del Hospital. Previo a incorporar esta nueva técnica se ha decidido evaluar su validez comparándola con el cultivo de fauces como prueba patrón. Para ello se estudiaron 320 personas que consultaron durante una semana por dolor de garganta y a todas ellas se les realizó la nueva técnica de diagnóstico rápido y se envió una muestra de fauces para el cultivo. La nueva técnica de diagnóstico rápido identificó a 212 personas como positivas para Streptococco. Luego de estudiarse las muestras en el laboratorio, se encontró que hubo 128 casos con aislamiento de Streptococco por cultivo, 84 de los cuales habían sido identificados por la nueva técnica rápida como positivos. Obtén la sensibilidad, especificidad y valores predictivos para esta situación.
8.3 Binomial
Ejercicio 1. Se conoce que la probabilidad de que el vapor se condense en un tubo de aluminio de cubierta delgada a 10 atm de presión es de 0.40. Si se prueban 12 tubos de ese tipo y bajo esas condiciones, determina la probabilidad de que: a) el vapor se condense en 4 de los tubos, b) en más de 2 tubos se condense el vapor, c) el vapor se condense en exactamente 5 tubos.
Ejercicio 2. La probabilidad de que el nivel de ruido de un amplificador de banda ancha exceda de 2 dB (decibelios) es de 0.15, si se prueban 10 amplificadores de banda ancha, determina la probabilidad de que; a) en solo 5 de los amplificadores el nivel de ruido exceda los 2 dB, b) por lo menos en 2 de los amplificadores, el ruido exceda de 2 dB, c) encuentra el número esperado de amplificadores que se exceden de un nivel de ruido de 2 dB y su desviación estándar.
Ejercicio 3. En un experimento se comprobó que la aplicación de un tratamiento químico aumentaba la resistencia a la corrosión de un material en un 80 % de los casos. Si se tratan ocho piezas, determina: (i) probabilidad de que el tratamiento sea efectivo para más de cinco piezas, (ii) probabilidad de que el tratamiento sea efectivo para al menos tres piezas, (iii) número de piezas para las que espera que el tratamiento sea efectivo.
Ejercicio 4. Se dispone de un cristal que tiene dos tipos de impurezas que absorben radiación de la misma longitud de onda. Una de ellas emite un electrón tras la absorción de un fotón, mientras que la segunda no emite electrones. Las impurezas están en igual concentración y distribuidas homogéneamente en el cristal. Sin embargo, la sección eficaz de absorción, que es una medida de la probabilidad de absorber un fotón, es 90 veces mayor para la impureza que emite electrones que el de la impureza que no los emite. Suponiendo que sobre el cristal inciden 200 fotones y que este es lo suficientemente grande para absorber todos, calcula la probabilidad de que al menos se emitan tres electrones.
Ejercicio 5. Un contrato estipula la compra de componentes en lotes grandes que deben contener un máximo de 10% de piezas con algún defecto. Para comprobar la calidad se toman 11 unidades y se acepta el lote si hay como máximo 2 piezas defectuosas. ¿Es un buen procedimiento de control?
Ejercicio 6. Las piezas de un proceso de fabricación pueden ser aceptables o defectuosas. Cuando el proceso está bajo control, el porcentaje de piezas defectuosas fabricadas es 3%. De la producción de cada hora se toma una muestra de 200 piezas al azar.
Ejercicio 7. El ingeniero de calidad decide que si el número de defectuosas en la muestra es 8 o más, se detenga el proceso y se analice si está bajo control.
- ¿Cuál es la probabilidad de parar el proceso de manera injustificada?
- Calcular la probabilidad de parar el proceso, cuando está fabricando con un porcentaje de defectuosas del 5%.
- Calcular la probabilidad de no detener el proceso si está fabricando un 6% de piezas defectuosas.
- Repetir el cálculo del apartado 3 para p (porcentaje de defectuosas) entre 1% y 10%. Dibujar las probabilidades en función de p.
Ejercicio 8. El 0.1$ de una población son alérgicos a una cierta vacuna. Se inyecta esta vacuna a 1200 personas. Calcular la probabilidad de que tengan una reacción alérgica:
- Exactamente dos personas
- Más de dos personas
8.4 Poisson
Ejercicio 1. En la inspección de una hojalata producida por un proceso electrolítico continuo, se identifican 0.2 imperfecciones en promedio por minuto. Determina las probabilidades de identificar a) una imperfección en 3 minutos, b) al menos dos imperfecciones en 5 minutos, c) un máximo de una imperfección en 15 minutos.
Ejercicio 2. Consideremos que el número de trozos de chocolate en una determinada galleta sigue una distribución de Poisson. Queremos que la probabilidad de que una galleta seleccionada al azar tenga por lo menos tres trozos de chocolate sea mayor que 0.8. Encontrar el valor entero más pequeño de la media de la distribución que asegura esta probabilidad.
Ejercicio 3. Un fabricante de maquinaria pesada tiene instalados en el campo 3840 generadores de gran tamaño con garantía. Sí la probabilidad de que cualquiera de ellos falle durante el año dado es de 1/1200 determine la probabilidad de que a) 4 generadores fallen durante el año en cuestión, b) que más 1 de un generador falle durante el año en cuestión.
Ejercicio 4. En un proceso de manufactura, en el cual se producen piezas de vidrio, ocurren defectos o burbujas, ocasionando que la pieza sea indeseable para la venta. Se sabe que en promedio 1 de cada 1000 piezas tiene una o más burbujas. ¿Cuál es la probabilidad de que en una muestra aleatoria de 8000 piezas, menos de 3 de ellas tengan burbujas?
Ejercicio 5. Un fabricante cultiva virus (para la fabricación de una vacuna) que guarda en un medio líquido. Se supone que los virus se distribuyen al azar y, por tanto, el número de virus por \(cm^3\) cada una, se han obtenido los datos siguientes:
| n virus | 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|---|
| frecuencia | 45 | 24 | 7 | 1 | 1 |
¿Cuál es la distribución teórica asumida? En base a la información obtenida ¿cuál es el parámetro de interés? ¿Cuál es la función de densidad de probabilidad? ¿Cuanto se parecen las frecuencias experimentales con las teóricas obtenidas a partir de la distribución de probabilidad?
Ejercicio 6. Se sabe que el número de microorganismos por gramo de una cierta muestra de suelo diluida en agua destilada se distribuye según una variable aleatoria de media 0.08. Si una preparación con un gramo de esta disolución se vuelve turbia, este gramo contiene al menos un microorganismo. Hallar la probabilidad de que una preparación que se ha vuelto turbia contenga:
- Un solo microorganismo
- Menos de tres microorganismos
- Más de dos microorganismos
Ejercicio 7. En un monte, el número de plantas de romero por círculo de un metro de radio, se distribuye según una variable aleatoria. Se eligen 1o plantas al azar y se mide la distancia a la planta que tiene más próxima. Las distancias observadas fueron (medidas en metros): 0.7, 1.7, 1.2, 0.4, 0.2, 0.5, 0.7, 0.8, 1.5, y 2.1. A partir de estos datos estima los parámetros de interés de la distribución y calcula cuantas plantas es de esperar que habrá en una zona del monte de unos 12500 \(m^2\) de superficie.
8.5 Exponencial
Ejercicio 1. Una fuente radiactiva emite partículas según un proceso de Poisson de media 10 partículas por minuto. Se desea calcular:
- Tiempo medio entre partículas
- Calcula la función de densidad del tiempo en segundos entre dos partículas y dibújala
- Probabilidad de que aparezca la primera partícula antes de 4 segundos
- Probabilidad de un minuto sin partículas.
Ejercicio 2. En un experimento de laboratorio se utilizan 10 gramos de \(\,_{84}^{210}\!Po\). Sabiendo que la duración media de un átomo de esta materia es de 140 días, ¿cuantos idas transcurrirán hasta que haya desaparecido el \(90\%\) de este material?
Ejercicio 3. Se ha comprobado que el tiempo de vida de cierto tipo de marcapasos sigue una distribución exponencial con media de 16 años. ¿Cuál es la probabilidad de que a una persona a la que se le ha implantado este marcapasos se le deba reimplantar otro antes de 20 años? Si el marcapasos lleva funcionando correctamente 5 años en un paciente, ¿cuál es la probabilidad de que haya que cambiarlo antes de \(25\%\) años?
Ejercicio 4. En una tienda departamental el tiempo promedio de espera para ser atendido en cajas al pagar la mercancía es de 7 minutos. Determine la probabilidad de que: a) Un cliente espere menos de 4 minutos. b) Un cliente espere más de 9 minutos.
Ejercicio 5. La vida media de un dispositivo es de 7 años. ¿Cuál es la probabilidad de que un dispositivo de este tipo falle después del 7°-año de uso?
Ejercicio 6. Los administradores de cierta industria han notado que su producto tiene un tiempo de duración que puede considerarse una variable aleatoria con distribución exponencial con una vida media de 5 años. a)¿cuál es la probabilidad de que al elegir un artículo de dicha producción dure más de 10 años? b)¿si el tiempo de garantía asignado por los administradores es de 1 año, qué porcentaje de sus productos tendrá que reparar la industria durante el periodo de garantía?
Ejercicio 7. Un motor eléctrico tiene una vida media de 6 años. Si la vida útil de este tipo de motor puede considerarse como una variable aleatoria distribuida en forma exponencial. ¿Cuál debe ser el tiempo de garantía que debe tener el motor si se desea que a lo más el 15 % de los motores fallen antes de que expire su garantía?.
8.6 Geométrica
Ejercicio 1. Un matrimonio quiere tener una hija, y por ello deciden tener hijos hasta el nacimiento de una hija. Calcular el número esperado de hijos (entre varones y hembras) que tendrá el matrimonio. Calcular la probabilidad de que la pareja acabe teniendo tres hijos o más.
Ejercicio 2. Se estima que el 70 % de una población de consumidores prefiere una marca en particular de pasta de dientes A ¿cuál es la probabilidad que al entrevistar a un grupo de consumidores.
- sea necesario entrevistar exactamente 4 personas para encontrar el primer consumidor que prefiere la marca A?
- se tenga que entrevistar como mínimo a 6 personas para encontrar el primer consumidor que prefiere la marca A?
Ejercicio 3. La probabilidad de que una muestra de aire contenga una molécula rara es de 0.01 si se supone que las muestras son independientes con respecto a la presencia de la molécula rara.¿Cuál es la probabilidad de que sea necesario analizar exactamente 125 muestras antes de detectar una molécula rara?
Ejercicio 4. Sea una máquina despachadora de refrescos que arroja un poco más de 20 ml por vaso derramándose el líquido en un 5% de los vasos despachados. Podemos definir la variable aleatoria X: “cantidad de vasos despachados hasta obtener el primero que se derramará” Considere que la forma de despachar el líquido por la máquina es independiente de vaso en vaso.
- Calcula la probabilidad de que el primer vaso que se derrame se encuentre después del 15vo. vaso despachado.
- ¿Qué vaso despachado se espera sea el primero en el que se derrame el líquido?.
8.7 Normal
Ejercicio 1. Cierto tipo de batería de almacenamiento dura,en promedio, 3.0 años, con una desviación típica de 0.5 años. Suponga que la duración de las baterías se distribuye normalmente, encuentre la probabilidad de que una batería dure menos de 2.3 años.
Ejercicio 2. Una empresa eléctrica fabrica focos que tienen una duración media de 800 horas y una desviación típica de 40 horas. Si la duración de los focos sigue una distribución normal, encuentre la probabilidad de que un foco se funda en el intervalo de 778 a 834 horas.
Ejercicio 3. En un proceso industrial el diámetro de un cojinete es una parte importante de un componente. El comprador establece que las especificaciones en el diámetro sean 3.0 ± 0.1 cm. Se sabe que en el proceso el diámetro de un cojinete tiene una distribución normal con media 3.0 cm y una desviación típica de 0.005 cm. En promedio, ¿cuántos cojinetes se descartarán?.
Ejercicio 4. El 6.3% de las observaciones de una magnitud que sigue una distribución normal tiene un valor superior a 3.287, mientras que el 51.2 % tiene valores mayores que 2.897. Calcule la media y la varianza de la distribución.
Ejercicio 5. Considere un experimento de medida del pH de una disolución acuosa caracterizado por \(\mu_{pH}\)= 5.50 y \(\sigma^2_{pH}\) = 0.06. Determine el intervalo de valores en el que espera encontrar el 95% de las medias muestrales de los experimentos que combinen el resultado de 25 determinaciones del pH de la disolución indicada.
Ejercicio 6. La longitud X de ciertos tornillos es una variable aleatoria con distribución normal de media 30 mm y desviación típica 0.2 mm. Se aceptan como válidos aquellos que cumplen \(29.5 \leq X \leq 30.4\). Obtén:
- Proporción de tornillos no aceptables por cortos.
- Proporción de tornillos no aceptables por largos.
- Proporción de tornillos válidos.
Ejercicio 7. Un país está habitado por dos grupos étnicos: A (alpinos) y N (nórdicos), que se encuentran en las proporciones 0.75 y 0.25. Se sabe que la talla de los individuos adultos varones sigue una distribución aleatoria con media 170 cm y desviación típica de 7 cm para los del grupo A, y media de 176 cm y desviación típica de 7 cm para el grupo N. Se considera que un individuo varón es “alto” si su talla es superior a 180 cm. Se pide:
- Hallar la proporción de individuos altos en A y B.
- Se elige un individuo al azar y resulta ser alto. Calcula la probabilidad de que sea nórdico.
- Se eligen 6 individuos al azar. Calcular la probabilidad de que 2 de elloss sean alpinos.
Ejercicio 8. La longitud L (en micras) de ciertas larvas parásitas de moluscos, sigue la distribución Normal, pero de media y desviación típica distinats, según la larva se encuentre en estadio 1 o en estadio 2 de su crecimiento. La media y la desviación típica son: 219 y 20 para el estadio 1, y 241 y 14 para el estadio 2. Para identificar el estadio en que se encuentra la larva, se adopta el criterio siguiente: Si \(L \leq 230\) pertenece al estadio 1, en otro caso pertenece al estadio 2. Resolver las siguientes cuestiones:
- Calcular la probabilidad de la presencia del suceso \(L \leq 230\) para larvas del estadio 1. Idem. para larvas en el esatdio 2.
- Desde que nace una larva hasta que llega al estadio 3 de su desarrollo (que es fácilmente identificable), trasncurren 12 horas, permaneciendo 8 horas en el estadio 1 y 4 horas en el estadio 2. La observación de una larva cualquiera se hace en un instante que puede considerarse elegido al azar durante estas 12 horas (se desconoce cuando ha nacido la larva). Entonces, si se ha observado que una larva mide L = 225 y, por lo tanto, se considera que pertenece al estadio 1, calcular la probabilidad de equivocarnos al tomar esta decisión.
Ejercicio 9. Se ha tomado una muestra de 45 piezas de un proceso que fabrica un promedio de 25% de piezas fuera de especificación. ¿Cuál es la probabilidad de que en la muestra haya exactamente 13 elementos defectuosos? ¿Cuál es la probabilidad de que la muestra contenga 13 o más piezas defectuosas?
Ejercicio 10. El abastecimiento de energía eléctrica de una comarca depende de tres centrales: una nuclear, una téermica de carbón y una hidráulica con potencias instaladas de 500 MW, 300 MW y 200 MW, respectivamente. Desde el punto de vista de fiabilidad, cada central sólo puede estar en uno de estos dos estados: disponible (con toda su potencia) o averiada (con potencia cero). En un díıa, la probabilidad de avería de la central nuclear es 0.10, de la térmica es 0.12 y de la hidráulica 0.05. Las averíaıas son independientes y supondremos como hipóotesis simplificadora que a lo largo de un díıa la central no cambia de estado.
- Para un día, calcular la función de distribución de la variable aleatoria Y = Potencia disponible en la comarca.
- Un pais tiene 30 centrales de cada uno de los tipos del apartado 1. Calcular la probabilidad de que en un día la potencia disponible en el pais sea menor que 24000 MW. (Utilizar la aproximación normal).
- La potencia máxima diaria demandada en el pais es una variable aleatoria con distribución normal de media 23000 MW y desviación típica 1000 MW. ¿Cuál es la probabilidad de que en un día la demanda sea superior a la potencia disponible?
Ejercicio 11. En el proceso de fabricación de unas piezas intervienen dos máquinas: la máquina A produce un taladro cilíndrico y la máquina B secciona las piezas con un grosor determinado. Ambos procesos son independientes. El diámetro del taladro producido por A (en mm.) se distribuye según una N(23,0.5). El grosor producido por B (en mm.) se distribuyes según una N(11.5,0.4).
- Calcula qué porcentaje de piezas tienen una taladro comprendido entre 20.5 y 24 mm.
- Encuentra el porcentaje de piezas que tienen un grosor entre 10.5 y 12.7 mm.
- Suponiendo que sólo son válidas las piezas cuyas medidas son las dadas en los apartados anteriores, calcula qué porcentaje de piezas aceptables se consiguen.
Ejercicio 12. Supongamos que el diámetro de las aceitunas rellenas de anchoa varía entre 15 y 17 mm. Debido a al sequía del último año, la producción de aceituna verde se ha distribuido según una normal de media 15.5 mm. y desviación típica 1.2 mm. ¿Qué porcentaje de aceitunas podría ser aprovechado para rellenar de anchoa?
Ejercicio 13. La duración media de un lavavajillas es de 15 años y su desviación típica 0.5. Sabiendo que la vida útil del lavavajillas se distribuye normalmente, hallar la probabilidad de que al adquirir un lavavajillas, este dure más de 15 años.
Ejercicio 14. Una normativa europea obliga a que en los envases de yogur no debe haber menos de 120 gr. La máquina dosificadora de una empresa láctea hace los envases de yogur según una distribución normal de desviación típica de 2 gr. y media 122 gr.
- ¿Qué tanto por ciento de los envases de yogur de esa empresa cumplirá la normativa?
- ¿Cuál deberá ser la media de la distribución normal con la cual la máquina dosificadora debe hacer los envases para que el 98% de la producción de yogures de la empresa cumpla la normativa?. (La desviación típica sigue siendo de 2 gr.).
Ejercicio 15. Una barra recta se forma conectando tres secciones A,B y C, cada una fabricada con una máquina distinta. La longitud de la sección A, en pulgadas, tiene una distribución normal con media 20 y varianza 0.04. La longitud de la sección B tiene una distribución normal con media 14 y varianza 0.01. La longitud de la sección C tiene una distribución normal con media 26 y varianza 0.04. Las tres secciones e unen de forma que se superponen 2 pulgadas en cada conexión. Si la barra se utiliza en la construcción del ala de un avión y su longitud debe estar entre 55.7 y 56.3 pulgadas ¿cuál es la probabilidad de que la barra sea utilizada?
Ejercicio 16. Los diámetros de los pernos de una caja siguen una distribución normal con una media de 2 centímetros y una desviación típica de 0.03 centímetros. Además tenemos unas tuercas de otra caja que siguen una distribución normal con media 2.02 centímetros y desviación típica de 0.04 centímetros. Un perno y una tuerca ajustarán si el diámetro del agujero de la tuerca es mayor que el diámetro del perno y la diferencia entre estos diámetros no es mayor de 0.05 centímetros. Si seleccionamos ala azar un perno y una tuerca ¿cuál es la probabilidad de que ajusten?
Ejercicio 17. En un experimento de laboratorio se mide el tiempo de una reacción química. Se ha repetido el experimento 98 veces y se obtiene que la media de los 98 experimentos es de 5 segundos con una desviación de 0,05 segundos. ¿Cuál es la probabilidad de que la media poblacional m difiera de la media muestral en menos de 0,01 segundos?
Javier Morales, email: j.morales@.umh.es.
Mª Asunción Martínez, email: am.mayoral@umh.es.