Capítulo 6 Modelos de supervivencia con variable cambiantes en el tiempo
6.1 Tiempo hasta evento
En el análisis e superviviencia la variable respuesta es el tiempo hasta el evento de interés.
Normalente los datos se obtienen de un estudio de cohorte con seguimiento ya sea prospectivo o retrospectivo. Transcurrido el periodo de seguimiento o “follow-up time” algunos de los individuos de la muestra pueden no haber tenido el evento, ya sea porque ha finalizado el seguimiento o porque se han perdido o han tenido un evento diferente del de interés que ha interrumpido su seguimiento. Luego decimos que estos individuos están censurados.
Es muy importante registrar el tiempo que ha pasado des del inicio hasta el evento para los no censurados y también el momento que se ha perdido el seguimiento para los censurados.
Así hay que definir bien el momento de inicio y el momento final para cada participante del estudio. Y también es importante que el mecanimso usado para obtener la información del seguimiento sea el mismo para todos.
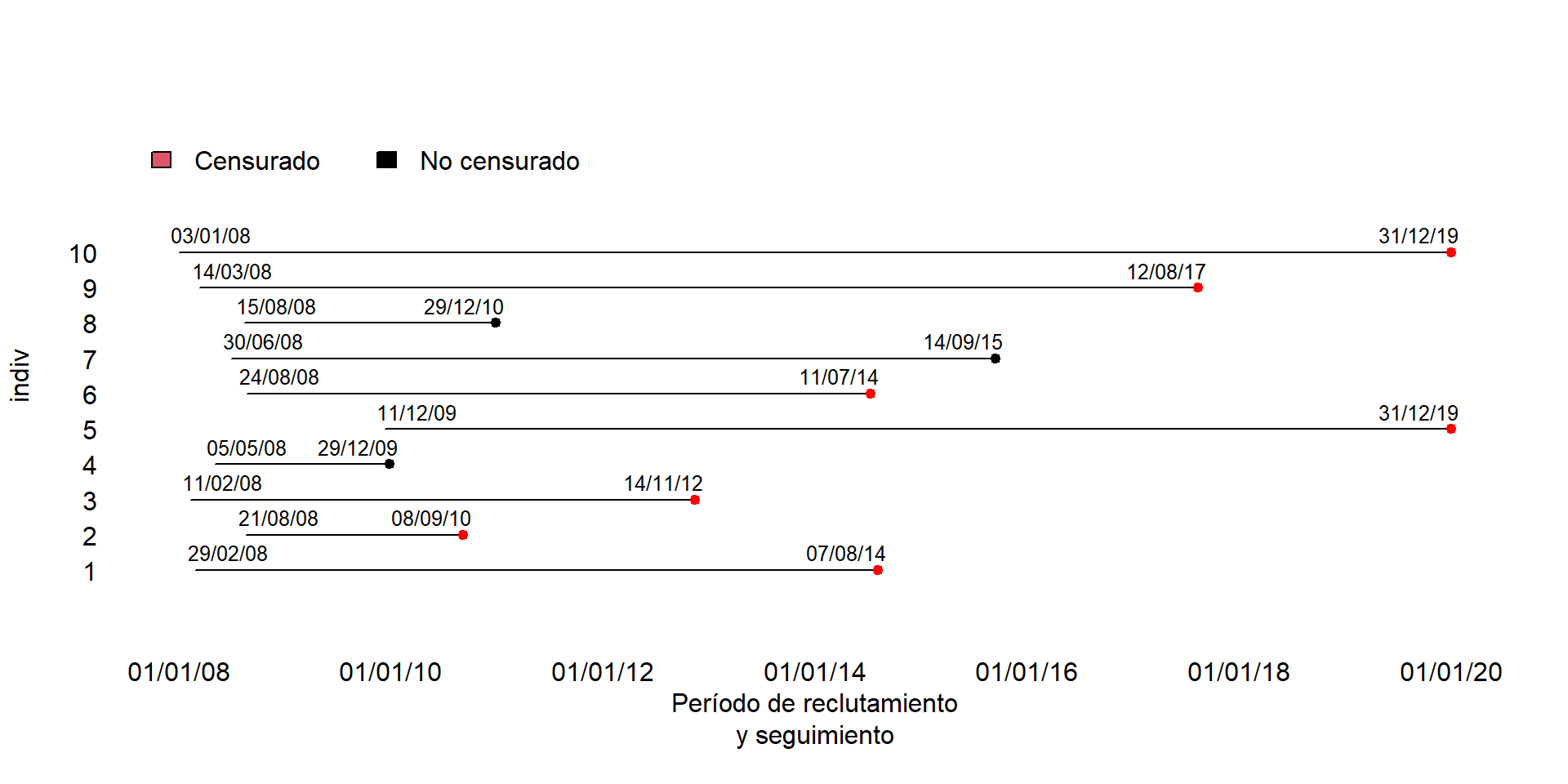
Pasamos a “tiempo cero”:

6.1.1 Ejemplos
Pacientes diagnosticados de cancer de próstata. Seguimiento hasta recidiva o muerte. El inicio sería la fecha del diagnóstico y la fecha final sería la fechad e recidiva o muerte (para los no censurados) y la fecha de final de seguimiento para los censurados.
Estudio de una cohorte prospectiva a 10 años para estudiar el riesgo de infarto agudo de miocardio incidente. La fecha de inicio sería la fecha de inclusión en el estudio, y la fecha final sería la fecha de ingreso por infarto o muerte por infarto (para los no censurados), y la fecha de final de seguimiento o fecha de muerte por otra causa (para los censurados).
6.1.2 Otros tipos de censura
La censura que se ha descrito es concretamente censura por la derecha. Esto quiere decir que cuando un dato está censurado significa que és superior al tiempo observado.
Existen otros tipo de censura que no estudiaremos:
Censura por la izquierda: el tiempo es menor que el observado.
Censura por intervalo: el tiempo se encuentra entre dos fechas o momentos determinados.
Truncamiento por la izquierda: en realidad no es una censura, sino que es un retraso en el inicio del seguimiento. O sea, que el individuo lleva un tiempo en riesgo pero que ha entrado más tarde en el estudio.
6.2 Kaplan-Meier
El método de Kaplan-Meier se usa para estimar la supervivencia o su complementario, la probabilidad de que el evento ocurra antes del tiempo \(t\).
Si no hubieran eventos censurados antes del tiempo \(t\), la probabilidad de que ocurra el evento en este periodo es simplemente \(d_t/n\) donde \(d_t\) es el númerod e eventos antes de \(t\) y \(n\) el número de individuos de la cohorte. Pero qué pasa cuando un individuo está censurado antes de \(t\)? Lo contamos en el denominador o no? Ambas opciones dan resultados sesgados.
Kaplan-Meier propone un método para estimar el riesgo en cada momento \(t\) (o su supervivencia) que da resultados no sesgados.
Ejemplo
Datos predimed del package compareGroups. Se trata de una cohorte con tres grupos de intervención y con un seguimiento de unos 7 años. El evento de interés es el cardiovascular.
group sex age smoke bmi
Control :2042 Male :2679 Min. :49 Never :3892 Min. :19.6
MedDiet + Nuts:2100 Female:3645 1st Qu.:62 Current: 858 1st Qu.:27.2
MedDiet + VOO :2182 Median :67 Former :1574 Median :29.8
Mean :67 Mean :30.0
3rd Qu.:72 3rd Qu.:32.5
Max. :87 Max. :51.9
waist wth htn diab hyperchol famhist
Min. : 50 Min. :0.301 No :1089 No :3322 No :1746 No :4895
1st Qu.: 93 1st Qu.:0.584 Yes:5235 Yes:3002 Yes:4578 Yes:1429
Median :100 Median :0.626
Mean :100 Mean :0.628
3rd Qu.:107 3rd Qu.:0.669
Max. :177 Max. :1.000
hormo p14 toevent event
No :5564 Min. : 0.00 Min. :0.016 No :6072
Yes : 97 1st Qu.: 7.00 1st Qu.:2.858 Yes: 252
NA's: 663 Median : 9.00 Median :4.789
Mean : 8.68 Mean :4.355
3rd Qu.:10.00 3rd Qu.:5.791
Max. :14.00 Max. :6.998 Para crear una variable censurada por la derecha se usa la función Surv del package survival:
library(survival)
# evento (censurado marcado con un '+')
with(predimed, Surv(toevent, event=='Yes'))[1:10] [1] 5.37440 6.09719+ 5.94661+ 2.90760 4.76112+ 3.14853 0.71458+ 4.90075+
[9] 0.04381 0.88159+Call: survfit(formula = Surv(toevent, event == "Yes") ~ 1, data = predimed)
time n.risk n.event survival std.err lower 95% CI upper 95% CI
1 6196 45 0.993 0.00106 0.991 0.995
2 5602 39 0.986 0.00147 0.984 0.989
3 4524 48 0.977 0.00196 0.973 0.981
4 3723 44 0.967 0.00250 0.962 0.972
5 2803 38 0.956 0.00301 0.950 0.962
6 1116 23 0.945 0.00380 0.938 0.953plot(survfit(Surv(toevent, event=='Yes')~1, predimed), ylim=c(0.8,1),
xlab="Tiempo de seguimiento (años)", ylab="Supervivencia")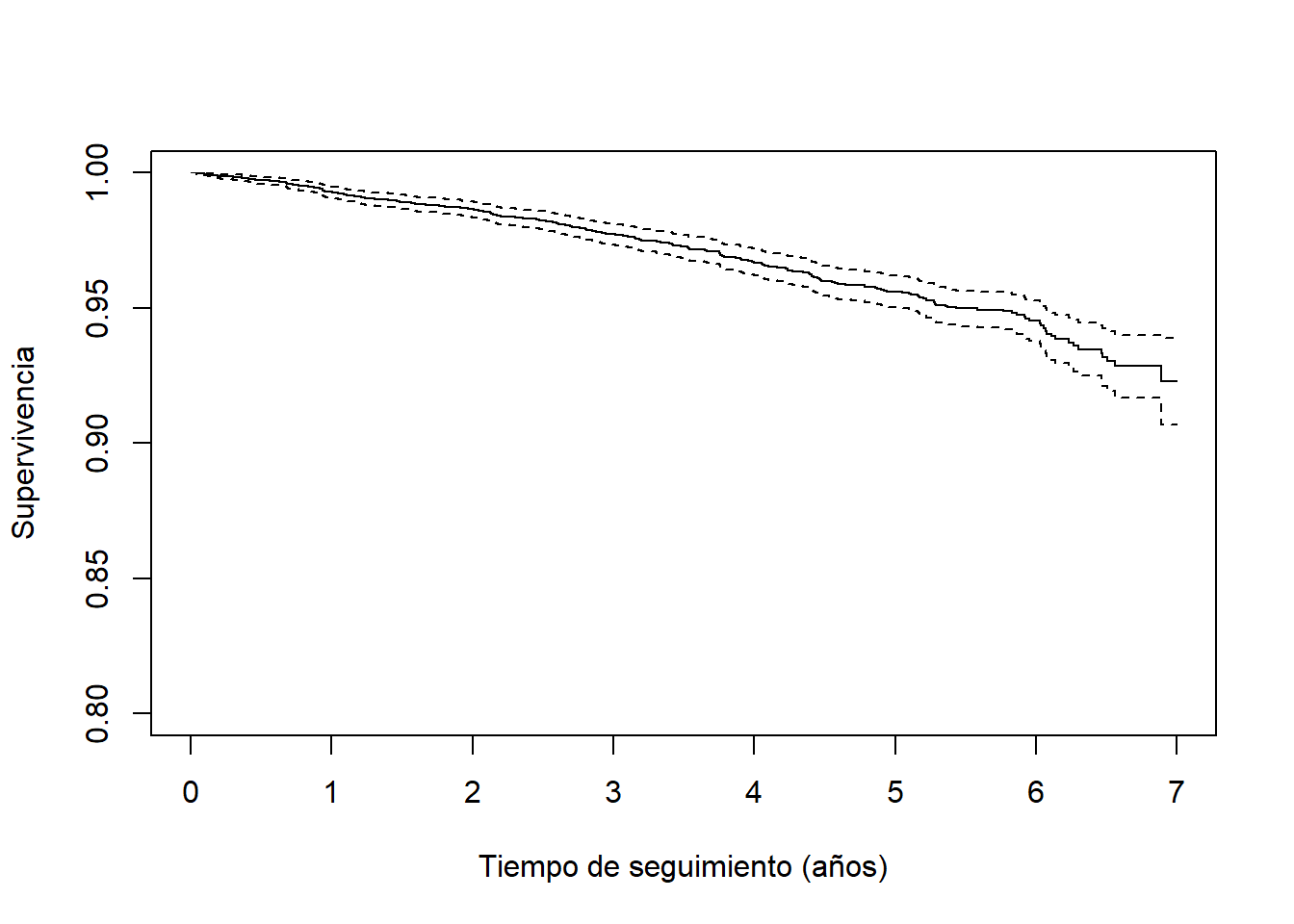
Por grupos de intervención:
plot(survfit(Surv(toevent, event=='Yes')~group, predimed), ylim=c(0.8,1),
xlab="Tiempo de seguimiento (años)", ylab="Supervivencia", col=1:3)
legend("bottomleft", levels(predimed$group), lty=1, col=1:3, bty="n")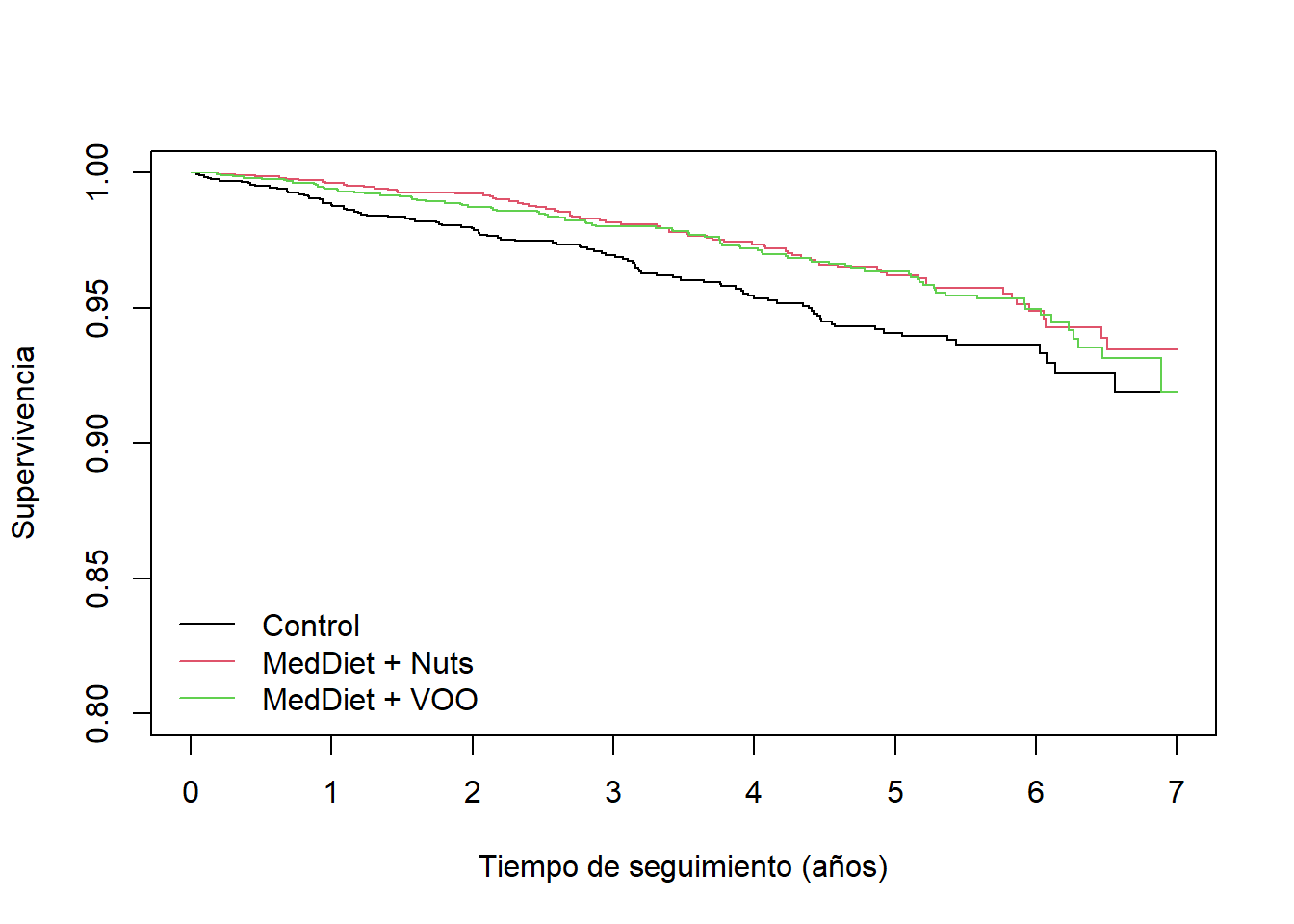
Test log-rank para comparar la supervivencia entre grupos:
Call:
survdiff(formula = Surv(toevent, event == "Yes") ~ group, data = predimed)
N Observed Expected (O-E)^2/E (O-E)^2/V
group=Control 2042 97 75.4 6.194 8.85
group=MedDiet + Nuts 2100 70 82.7 1.946 2.90
group=MedDiet + VOO 2182 85 93.9 0.848 1.35
Chisq= 9 on 2 degrees of freedom, p= 0.01 6.3 Medidas
- Supervivencia: probabilidad de estar libre de evento en el momento \(t\) (se supone que el evento ocurre después)
\[S(t) = \text{Pr}(T>t)\]
- Riesgo: probabilidad de evento antes de tiempo \(t\). Es el complementario de la funciónd e supervivencia
\[\text{Pr}(T\leq t) = 1-S(t)\]
- Hazard: o riesgo instantànea. Es la probabilidad que ocurra el evento en un intervalo infinitamente pequeño dado que no lo ha tenido hasta el momento \(t\)
\[\lambda(t) = \lim_{\delta \rightarrow 0} \frac{\text{Pr}\left(T \in (t, t+\delta) \right)}{S(t)} \]
- Hazard acumulado: es la suma o integral del riesgo instantáneo hasta el momento \(t\)
\[\Lambda(t) = \int_{0}^{t} \lambda(s) ds\] Existe la siguiente relación entre el hazard acumulado y la función de supervivencia
\[S(t) = \text{exp} \left(-\Lambda(t)\right)\] o bien
\[\Lambda(t) = -\text{ln}\left(S(t)\right)\]
6.4 Modelo de regresión de Cox
Los modelos de regresión de Cox sirven para evaluar el efecto de variables sobre el tiempo hasta el evento, o para crear un moelo de predicción.
Los modelos de cox asumen riesgos proporcionales, esto es, se separa el riesgo (“Hazard”) de paceder un evento antes del momento \(t\) como un producto del
\(\Lambda_0(t)\): riesgo basal, cuando todas las variables independientes \(x\) valen cero) y
\(\sum_{k=1} \beta_k x_{ik}\): combinación lineal de las variables independientes (predictor lineal).
\[\Lambda(t|\vec{x}_i) = \Lambda_0(t)\cdot \text{exp}\left(\sum_{k=1} \beta_k x_{ik}\right)\]
donde los coeficientes \(\beta_k\) son los log-Hazard Ratios.
Cox propone un método para estimar los coeficientes \(\beta_k\) sin suponer ninguna distribución sobre la variable respuesta \(T\) (tiempo hasta evento). Por esto se llama método semiparamétrico y se basa en estimar la “partial-likelihood”. Existen otros métodos que suponen una distribución de la \(T\), y por lo tanto parametrizan la incidencia basal \(\Lambda_0(t)\). Por ejemplo,la regresión de Weibull que supone una distribución Weibull sobre \(T\). Una de las ventaja que tienen los métodos no paramétricos es que permiten estimar la media o la mediana de \(T\) aunque más de la mitad de los individuos de la muestra estén censurados (o sea, que no se llegue al 50% de eventos en el seguimiento). La desventaja es que suponen una distribución sobre \(T\) que puede no ser correcta y que conllevaría a resultados sesgados. Estos métodos no los tocaremos en el curso.
Ejemplo
Para ajustar un modelo de Cox en R se usa la función coxph del paquete survival.
Hay diferentes aspectos a validar del modelo de Cox. Entre ellos la proporcionalidad de los efectos. Quiere decir que se supone que las \(\beta_k\) no dependen del tiempo (por ejemplo, el efecto del sexo es el mismo tanto a 1 años como a 5 años). Ésto se puede comprovar mediante la siguiente función:
chisq df p
age 0.33102 1 0.565
sex 0.17845 1 0.673
p14 0.00189 1 0.965
group 5.75156 2 0.056
GLOBAL 6.35652 5 0.273Aparece un p-valor para cada variable y uno global. En este caso parece que se cumple la proporcionalidad para todas las variables. No obstante, si no se cumpliera la proporcionalidad de una variable categórica, por ejemplo el sexo, ésta se puede poner como strata (se asume una curva de indidencia basal \(\Lambda_0(t)\) para cada sexo).
Call:
coxph(formula = Surv(toevent, event == "Yes") ~ age + strata(sex) +
p14 + group, data = predimed)
n= 6324, number of events= 252
coef exp(coef) se(coef) z Pr(>|z|)
age 0.0679 1.0703 0.0101 6.72 1.8e-11 ***
p14 -0.1222 0.8850 0.0305 -4.01 6.0e-05 ***
groupMedDiet + Nuts -0.3950 0.6737 0.1577 -2.50 0.012 *
groupMedDiet + VOO -0.3146 0.7301 0.1489 -2.11 0.035 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
exp(coef) exp(-coef) lower .95 upper .95
age 1.070 0.934 1.049 1.092
p14 0.885 1.130 0.834 0.939
groupMedDiet + Nuts 0.674 1.484 0.495 0.918
groupMedDiet + VOO 0.730 1.370 0.545 0.978
Concordance= 0.652 (se = 0.018 )
Likelihood ratio test= 71.8 on 4 df, p=1e-14
Wald test = 73 on 4 df, p=5e-15
Score (logrank) test = 73.9 on 4 df, p=3e-15En este gráfico se obtiene una curba de supervivencia para cada sexo y ajustando por las demás covariables (nota que el efecto de las demás covariables se suponen el mismo para ambdos sexos).
plot(survfit(modelo2), ylim=c(0.8,1), lty=1:2)
legend("bottomleft", levels(predimed$sex), lty=1:2, bty="n")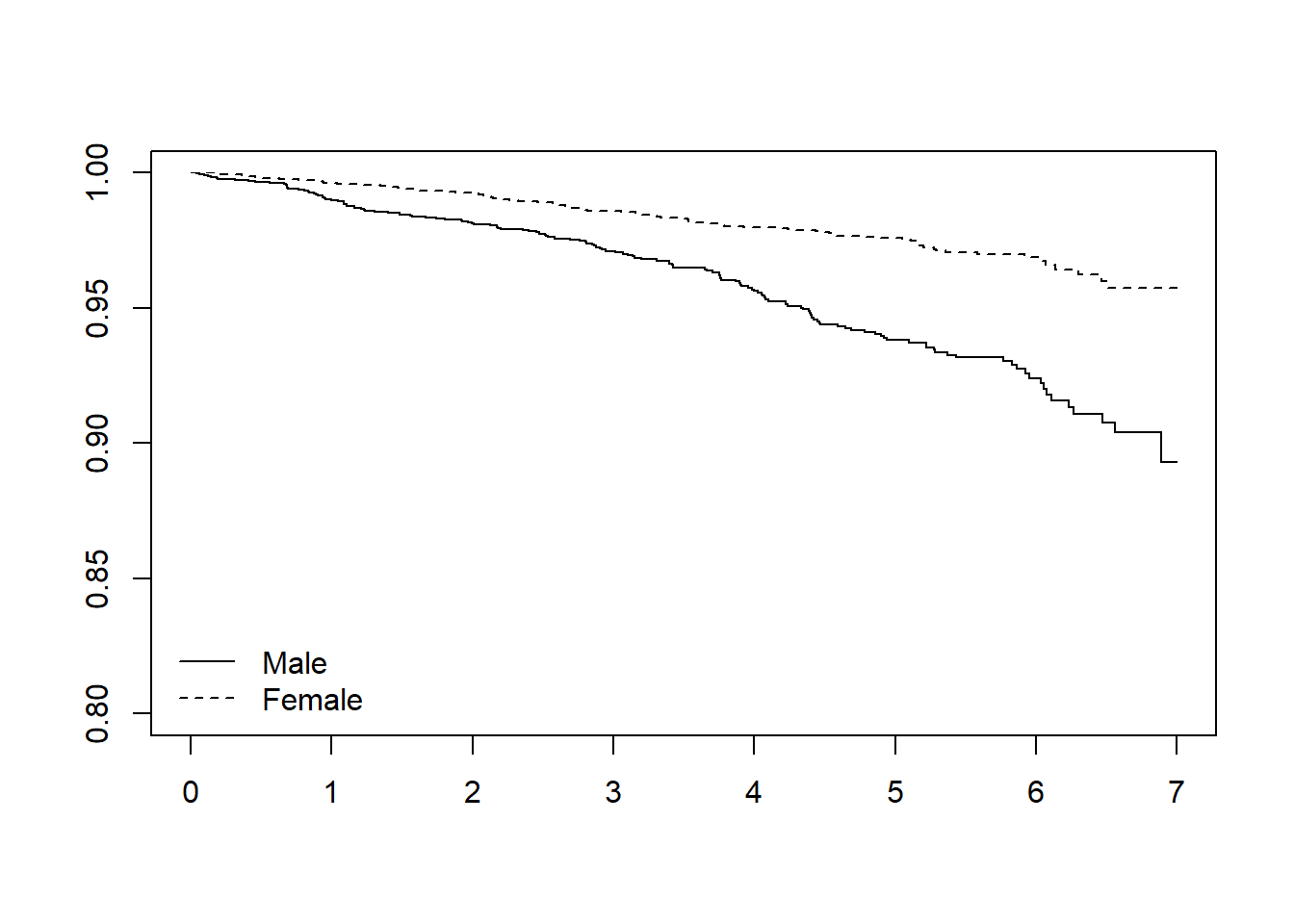
También se puede evaluar la capacidad de predicción y la calibración, que no veremos en el curso.
6.4.1 Efectos tiempo-dependientes
El efecto tiempo-dependiente (no confundir con variables tiempo-dependientes) se da cuando el efecto de una variable \(\beta_k\) no es constante a lo largo del tiempo. En este caso, como se ha comentado en la anterior subsección, si se trata de una variable categórica se puede poner en el modelo como strata. Si se trata de una variable continua, se puede incorporar la interacción de la variable \(x_k\) con el tiempo.
Otra estrategia que se usa habitualmente es dividir el tiempo de seguimiento en dos o tres tramos (a corto y a largo plazo), y realizar análisis por separado.
De la anterior ecuación sobre la incidencia acumulada, se suponía que los efectos eran fijos y no dependían del tiempo. Pero si dependieran del tiempo en general se debería reescribir como:
\[\Lambda(t|\vec{x}_i) = \Lambda_0(t)\cdot \text{exp}\left(\sum_{k=1} \color{blue}{\beta_k(t)} x_{ik}\right)\] donde \(\beta_k(t)\) representa una función del tiempo.
Este tipo de modelos con efectos tiempo dependientes no los veremos.
6.4.2 Variables tiempo-dependientes
Los modelos con variables tiempo-dependientes se tienen cuando en el seguimiento de los individuos de la muestra se han ido actualizando los valores de todas o algunas de las variables indepndientes (\(x_k\)). Así pues, en cada momento \(t\) el riesgo acumulado se tiene que estimar teniendo en cuenta el valor que toma cada \(x_k\) en el momento \(t\)
\[\Lambda(t|\vec{x}_i = \Lambda_0(t)\cdot \text{exp}\left(\sum_{k=1} \beta_k \color{blue}{x_{itk}}\right)\] donde \(x_{itk}\) representa el valor de la variable \(x_k\) del individuo \(i\) en el momento \(t\)
6.4.3 Estructura de los datos
Para ajustar estos modelos, el reto principal (y único), es estructurar bien la base de datos. Así, para cada individuo tendremos tantas filas como actualizaciones tengamos de cada variable \(x_k\). Además hay que anotar el momento de estos cambios. Además habrá una fila final donde se indicará el tiempo de evento o censura.
Veámoslo con un ejemplo: base de datos aids del package joineR
obstime indica cuándo se han tomado las medidas de CD4. Mientras que la variable time y death indica el tiempo observado y si el individuo se ha muerto o sigue vivo al finalizar el seguimiento. En este caso el evento de interés es la muerte y los individuos vivos serán los censurados.
La variable tiempo-dependiente es la variable CD4.
Sin embargo, para ajustar un modelo con variables tiempo-dependientes se ha de reestructurar esta base de datos.
- Creamos una base de datos con una fila por individuo y con los tiempos de muerte
temp <- subset(aids, select=c(id, time, death, drug, gender, prevOI))
x <- rep(1,nrow(temp))
base <- aggregate(x, temp, sum)
base <- tmerge(base, base, id=id, endpt = event(time, death))
head(base) id time death drug gender prevOI x tstart tstop endpt
1 351 12.27 0 ddC female noAIDS 4 0 12.27 0
2 336 12.57 0 ddC female noAIDS 3 0 12.57 0
3 377 13.50 0 ddC female noAIDS 4 0 13.50 0
4 343 14.43 0 ddC female noAIDS 3 0 14.43 0
5 42 17.37 0 ddC female noAIDS 1 0 17.37 0
6 30 18.87 0 ddC female noAIDS 2 0 18.87 0- Luego hacemos uso de la función
tmergepara crear la base de datos en el formato deseado. Las variables tiempo dependientes se especifican mediante la funcióntdcen que se indica también la variable que recoge cuando se han tomado sus medidas.
6.4.4 Ajuste del modelo
Así tenemos un intervalos con los tiempo tstart y tstop que se usará como tiempos (de entrada y de salida). Finalmente se usará la función coxph con estos dos tiempos:
Call:
coxph(formula = Surv(tstart, tstop, endpt) ~ CD4 + drug + gender,
data = aids2)
n= 1405, number of events= 188
coef exp(coef) se(coef) z Pr(>|z|)
CD4 -0.1944 0.8233 0.0243 -7.99 1.4e-15 ***
drugddI 0.3170 1.3730 0.1467 2.16 0.031 *
gendermale -0.3258 0.7220 0.2425 -1.34 0.179
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
exp(coef) exp(-coef) lower .95 upper .95
CD4 0.823 1.215 0.785 0.864
drugddI 1.373 0.728 1.030 1.830
gendermale 0.722 1.385 0.449 1.161
Concordance= 0.697 (se = 0.018 )
Likelihood ratio test= 96.3 on 3 df, p=<2e-16
Wald test = 67.6 on 3 df, p=1e-14
Score (logrank) test = 75.2 on 3 df, p=3e-16Fíjate que tanto las variables tiempo-dependientes (en este caso CD4) como las no-tiempo-dependientes (drug y gender) se ponen de la misma manera y de forma habitual en la fórmula.
La interpretación de los resultados es exactamente la misma que para un modelo de Cox sin variables tiempo-dependientes.
Comparación con el modelo sin variables tiempo-dependientes
Estos resultados los podríamos comparar si sólo se tuviera en cuenta la primera medida de CD4:
aids1obs <- subset(aids, obstime==0)
modelo1obs <- coxph(Surv(time, death) ~ CD4 + drug + gender, aids1obs)
summary(modelo1obs)Call:
coxph(formula = Surv(time, death) ~ CD4 + drug + gender, data = aids1obs)
n= 467, number of events= 188
coef exp(coef) se(coef) z Pr(>|z|)
CD4 -0.1830 0.8328 0.0222 -8.23 <2e-16 ***
drugddI 0.2669 1.3060 0.1465 1.82 0.068 .
gendermale -0.2024 0.8168 0.2422 -0.84 0.403
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
exp(coef) exp(-coef) lower .95 upper .95
CD4 0.833 1.201 0.797 0.87
drugddI 1.306 0.766 0.980 1.74
gendermale 0.817 1.224 0.508 1.31
Concordance= 0.703 (se = 0.019 )
Likelihood ratio test= 92.5 on 3 df, p=<2e-16
Wald test = 70.8 on 3 df, p=3e-15
Score (logrank) test = 78.2 on 3 df, p=<2e-16Validación del modelo
La validación del modelo con variables tiempo-dependientes se hace de la misma manera que para el modelo de Cox “clásico”. Por ejemplo, también se puede aplicar la función coxz.ph. Sin embargo, la discriminación y la calibración que necesitan del cálculo del riesgo predicho a tiempo \(t_0\) no és fácil de calcular: ¿cómo se tiene en cuenta que el valor de \(x_k\) cambia y que ello conlleva a un cambio del riesgo \(\Lambda\).
chisq df p
CD4 0.2875 1 0.59
drug 0.0034 1 0.95
gender 1.6437 1 0.20
GLOBAL 1.9692 3 0.58Términos no lineales: “splines”
También, como en los modelo de Cox “clásicos” se pueden introducir términos polinómicos o de splines (psplines) para las \(x_k\) cuantitativas.
modelo.splines <- coxph(Surv(tstart, tstop, endpt) ~ pspline(CD4) + drug + gender, data=aids2)
coef(summary(modelo.splines)) coef se(coef) se2 Chisq DF p
pspline(CD4), linear -0.1900 0.02554 0.02527 55.359 1.000 1.004e-13
pspline(CD4), nonlin NA NA NA 5.670 3.093 1.367e-01
drugddI 0.3164 0.14684 0.14682 4.644 1.000 3.117e-02
gendermale -0.3282 0.24253 0.24249 1.831 1.000 1.760e-01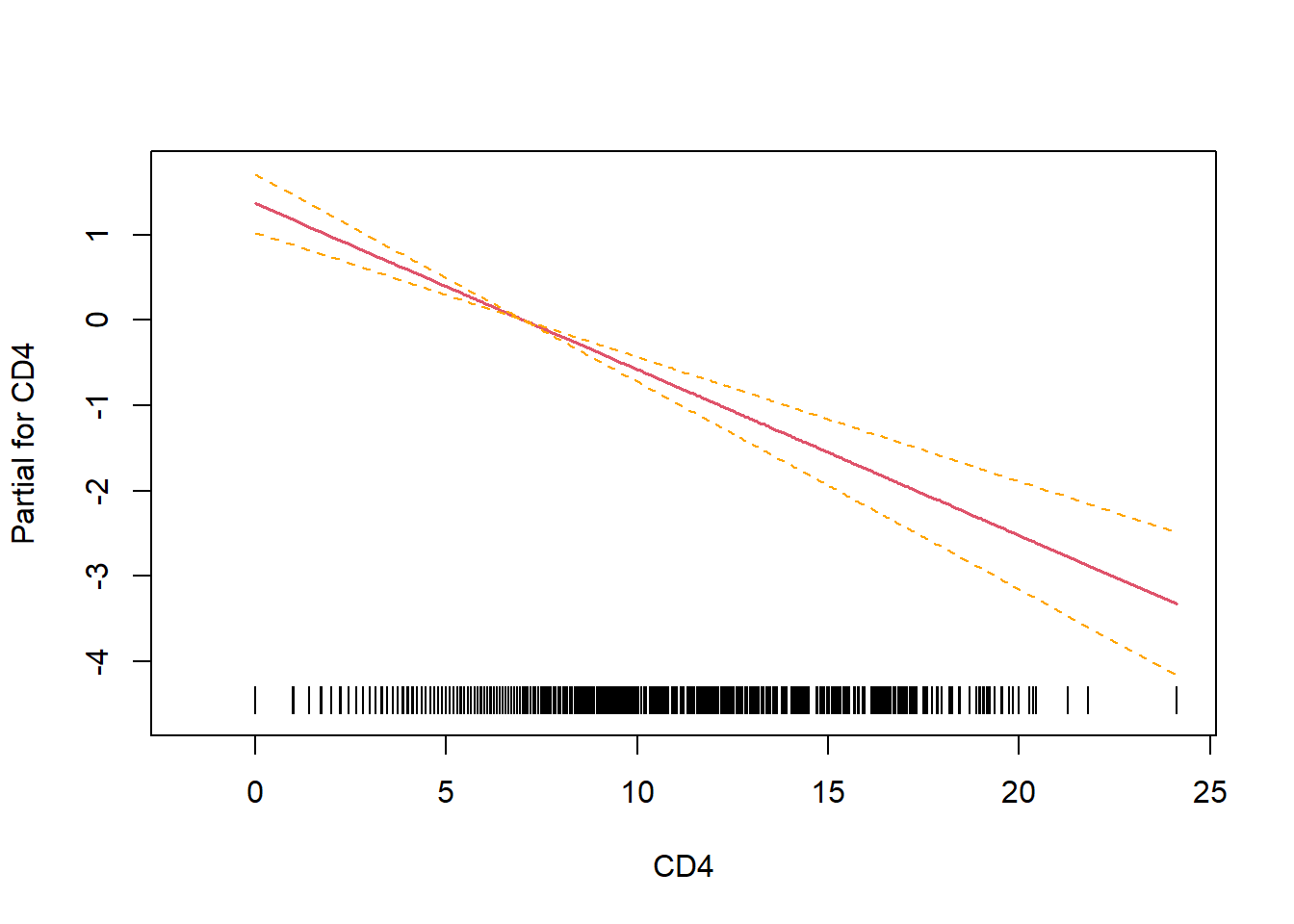
Se comprueba como el efecto de CD4 es lineal (no hay términos cuadráticos, ni cúbicos, ni puntos de inflexión, …).
6.5 Otros
- “Joint Models”
Un paso más allá y ligado con el tema de variables tiempo-dependientes se encuentran los “Join Models”. Estos modelos tienen en cuenta las variables tiempo-dependientes para modelizar el tiempo hasta evento con posible censura por la derecha. Estos modelos surgen cuando hay valores faltantes en algunas medidas de las variables \(x_k\). Para solventarlo, modelizan una regresión de supervivencia de Cox, y en lugar de condicionar por los valores observados de \(x_k\), se condiciona por los valores ajustados de ellos según modelos de datos longitudinales. Así se fusiona los modelos de medidas repetidas con los modelos de Cox.
El package joineR permite ajustar este tipo de modelos. Además también tiene incorporadas funciones y opciones para tener encuenta eventos competitivos.
- Modelos de riesgos competitivos “Competing risk”
Tienen en cuenta no sólo un único evento sinó varios posibles eventos que pueden ocurrir y que estén relacionados con él. Por ejemplo, muerte por causa coronaria, muerte por ictus, muerte por cancer, etc.
Se puede usar el package cmprsk. Este package no permite variables cambiantes en el tiempo.
- Modelos de transición
Se basan en cadenas de Markov. Permiten ajustar modelos de supervivencia con variables cambiantes en el tiempo, así como eventos recurrentes o de cambios de estado (p.ej, sano, recaída, recuperación, muerte).
En R existe el package msm para