Chapter 16 Appendix 2. Mapping climate space
author: Kearney, M. R.
16.1 Introduction
This module integrates what you’ve learnt in the previous modules to make and map calculations of the climatic limits on the distribution of the Desert Iguana. Specifically, you will apply calculations of climate space from module 9 to the microclimate grids that you worked with in module 15. You will see what the actual climate space available in Australia and North America looks like and then compute where that climate space maps to in physical space in North America.
16.2 Initial setup
First you should set up a folder on your computer to work in, and put the materials for this prac into it. There should be this file and a csv file of the distribution of the Desert Iguana ‘dipso_dist.csv’. You’ll also need to add the ‘climate_space_pars.csv’ file you used in module 9, and the microclimate data you unzipped from module 15 (from the files ‘microclim_aust.zip’ and ‘microclim_NAm.zip’).
Next, as in the previous pracs, open R-Studio and open a new script in which to paste and comment/modify the commands from this document as you go. And, as before, set the working directory to be the folder you created for the prac.
16.3 Getting the climate space available in Australia
In module 9 you recreated Figure 12 of Porter and Gates (1969) which shows the bounding combinations of radiation (solar plus infra-red) and air temperature available on earth. Recall that this was an approximation that assumed, unrealistically, that the ground temperature was equal to air temperature when computing the clear night sky bounding curve. It also attempted to capture the fact that sun angles are typically lower in the places with very low air temperatures (except for high tropical mountains), but only very roughly by assuming the zenith angle declined linearly with latitude.
Now that we have the microclim data, however, we can make a much better estimate of the bounding radiation and air temperature combinations available on earth at different times of year and at different times of day. We will do this first for Australia.
In module 9, we developed the equation Qbound. It computes the direct and diffuse radiation received by cylindrical organisms lying on the ground by a rough estimation of direct and diffuse solar radiation given the zenith angle, some parameters about the transmissivity of the atmosphere and the position of the earth in its orbit around the sun. We have this from the microclim dataset in the form of the solar radiation grids, so we can now just use them directly. These solar radiation estimates are of course already adjusted for the zenith angle and, what’s more, for variations in atmospheric transmissivity due to elevation and spatial effects (including variation in aerosols and ozone).
Our Qbound function also estimated the infra-red radiation coming down from the sky from the Swinbank formula (an empirical model) given an air temperature measured at weather station height. We can now compute this from the ‘sky temperature’ layers of the microclim data set, which inherently include the effects of cloud cover. We can also compute the infra-red radiation from the ground using the microclim substrate surface temperature estimate, rather than simply assuming ground temperature equals air temperature.
So, in summary, for our calculations of climate space boundaries from microclim we need to get the solar radiation, air temperature (we’ll choose 1cm, but we could use 120cm depending on the height of the animal of interest), substrate temperature and sky temperature. We need the latter two in the 0% shade scenario since we are interested in the extremes (what line on the climate space graph would the 100% shade scenario give us?).
We have these for January and July, which will give us the seasonal extremes. Let’s first load these layers into memory, pinching code from the previous module.
library(raster)
# put your path here for microclim data folder for Australia
path<- 'microclim_Aust/'
# read the January solar radiation file into memory
solar_jan_Aust<-brick(paste0(path,"solar_radiation_Wm2/SOLR_1.nc"))
# read the July solar radiation file into memory
solar_jul_Aust<-brick(paste0(path,"solar_radiation_Wm2/SOLR_7.nc"))
# read the January 1cm air temperature in 0% shade file into memory
Tair_jan_Aust<-brick(paste0(path,"air_temperature_degC_1cm/soil/0_shade/TA1cm_soil_0_1.nc"))
# read the July 1cm air temperature in 0% shade file into memory
Tair_jul_Aust<-brick(paste0(path,"air_temperature_degC_1cm/soil/0_shade/TA1cm_soil_0_7.nc"))
# read the January sky temperature in 0% shade file into memory
Tsky_jan_Aust<-brick(paste0(path,"sky_temperature_degC/0_shade/TSKY_0_1.nc"))
# read the January sky air temperature in 0% shade file into memory
Tsky_jul_Aust<-brick(paste0(path,"sky_temperature_degC/0_shade/TSKY_0_7.nc"))
# read the January surface temperature in 0% shade file into memory
D0cm_jan_Aust<-brick(paste0(path,"substrate_temperature_degC/soil/0_shade/D0cm_soil_0_1.nc"))
# read the July surface temperature in 0% shade file into memory
D0cm_jul_Aust<-brick(paste0(path,"substrate_temperature_degC/soil/0_shade/D0cm_soil_0_7.nc")) Now, let’s modify the Qbound function to make it work with the grids, giving it the name Qbound_micro. Have a close look at how this differs from Qbound. Note that since we now have total solar radiation (direct plus diffuse) as an input, we need to repartition it into direct and diffuse using the parameter ‘pctdiff’ (with the value used in the original calculations for microclim, which was 15%). Air temperature is no longer an input - why? What has replaced it? Note also that we also have only one output, ‘Q_rad’, because we are making these calculations for each hour of the day so it could be for day or night.
# Computes climate space following the equations of Porter and Gates (1969),
# using the microclim layers as input
# inputs
# hg, A grid of estimated solar radiation (direct and diffuse, i.e. 'global') flux
# on horizontal ground, W/m2
# Tsub, A grid of values (for each air temperature), of substrate temperatures, degrees C
# alpha_s, Solar absorptivity of object, decimal percent
# alpha_g, Solar absorptivity of the ground, decimal percent
# pctdiff, Proportion diffuse solar radiation, decimal percent
# outputs
# Q_rad, radiation load, W/m2
Qbound_micro <-
function(hg = hg, Tsub = Tsub, Tsky = Tsky, alpha_s = 0.8, alpha_g = 0.8, pctdiff = 0.15) {
sigma <- 5.670373e-8 # W/m2/k4 Stephan-Boltzman constant
Q_ground <- (1 * sigma * (Tsub + 273.15) ^ 4) # ground radiation
Q_sky <- (1 * sigma * (Tsky + 273.15) ^ 4) # sky thermal radiation
hd <- hg * (1 - pctdiff) # direct solar on horizontal ground
hS <- hg * pctdiff # diffuse (scattered) solar on horizontal ground
r <- 1 - alpha_g # ground solar reflectance
Q_rad <- (alpha_s * hS * (2 / pi) + alpha_s * hd + alpha_s * r * hg
+ Q_sky + Q_ground) / 2 # eq. 13 of Porter and Gates 1969
}Let’s now apply our function to the January data, with both our cylindrical animal and the ground having a solar absorptivity of 80%.
# getting bounding radiation conditions across Australia for January
hg = solar_jan_Aust # define the solar radiation input
Tsub = D0cm_jan_Aust # define the ground temperature input
Tsky = Tsky_jan_Aust # define the sky temperature input
alpha_s = 0.8 # animal solar absorptivity
alpha_g = 0.8 # ground solar absorptivity
# compute the total radiation load
Q_rad_jan_Aust <- Qbound_micro(hg = hg, Tsub = Tsub, Tsky = Tsky, alpha_s = alpha_s, alpha_g = alpha_g)Now the variable ‘Q_rad’ has, for each hour of the day in January, an estimate of the total radiation load that would be present on a cylindrical animal in the open with 80% solar absorptivity. The next code chunk plots this for 4am and 12pm, together with the associated 1cm air temperatures.
par(mfrow = c(2,2)) # set to plot 2 rows of 2 panels
plot(Q_rad_jan_Aust[[5]], main = "radiation (W/m2), 4am January")
plot(Q_rad_jan_Aust[[13]], main = "radiation (W/m2), 12pm January")
plot(Tair_jan_Aust[[5]], main = "1cm air temperature (C), 4am January")
plot(Tair_jan_Aust[[13]], main = "1cm air temperature (C), 12pm January")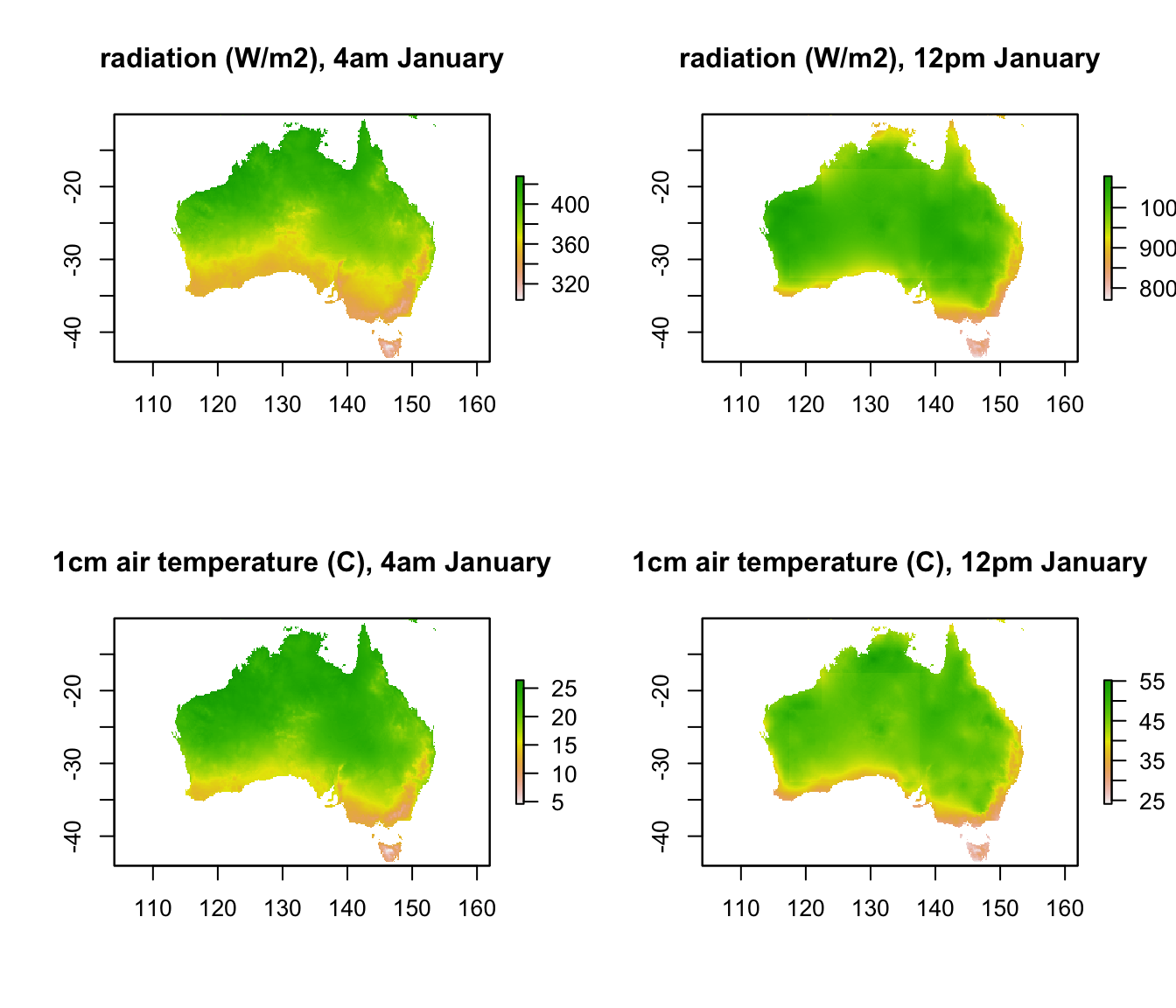
It should be clear that by projecting this data from geographic space to environmental space, i.e. to a graph of radiation vs. air temperature, we will be able to see the full range of climate space present within Australia at these times. The next code chuck creates such a graph for these two times, extracting the data from raster format into a table of values using the ‘raster’ package function values and the cbind function.
par(mfrow = c(1,1)) # revert to 1 panel
i = 5 # layer number to plot (layer 5 is 4am, because layer 1 is midnight)
# extract the radiation and air temperatures from the rasters and bind them together into a table
RadTair <- cbind(values(Q_rad_jan_Aust[[i]]),values(Tair_jan_Aust[[i]]))
plot(RadTair[,1],RadTair[,2],ylim = c(-40,60), xlim = c(0,1300), pch=16, col = 'blue',
xlab = 'radiation, W/m2', ylab = 'air temperature, deg C',
main = "available climate space, January")
i = 13 # layer number to plot (layer 5 is 4am, because layer 1 is midnight)
RadTair=cbind(values(Q_rad_jan_Aust[[i]]),values(Tair_jan_Aust[[i]]))
points(RadTair[,1],RadTair[,2],ylim = c(-40,60), xlim = c(0,1300), pch=16, col = 'red',
xlab = 'radiation, W/m2', ylab = 'air temperature, deg C',
main = "available climate space, January")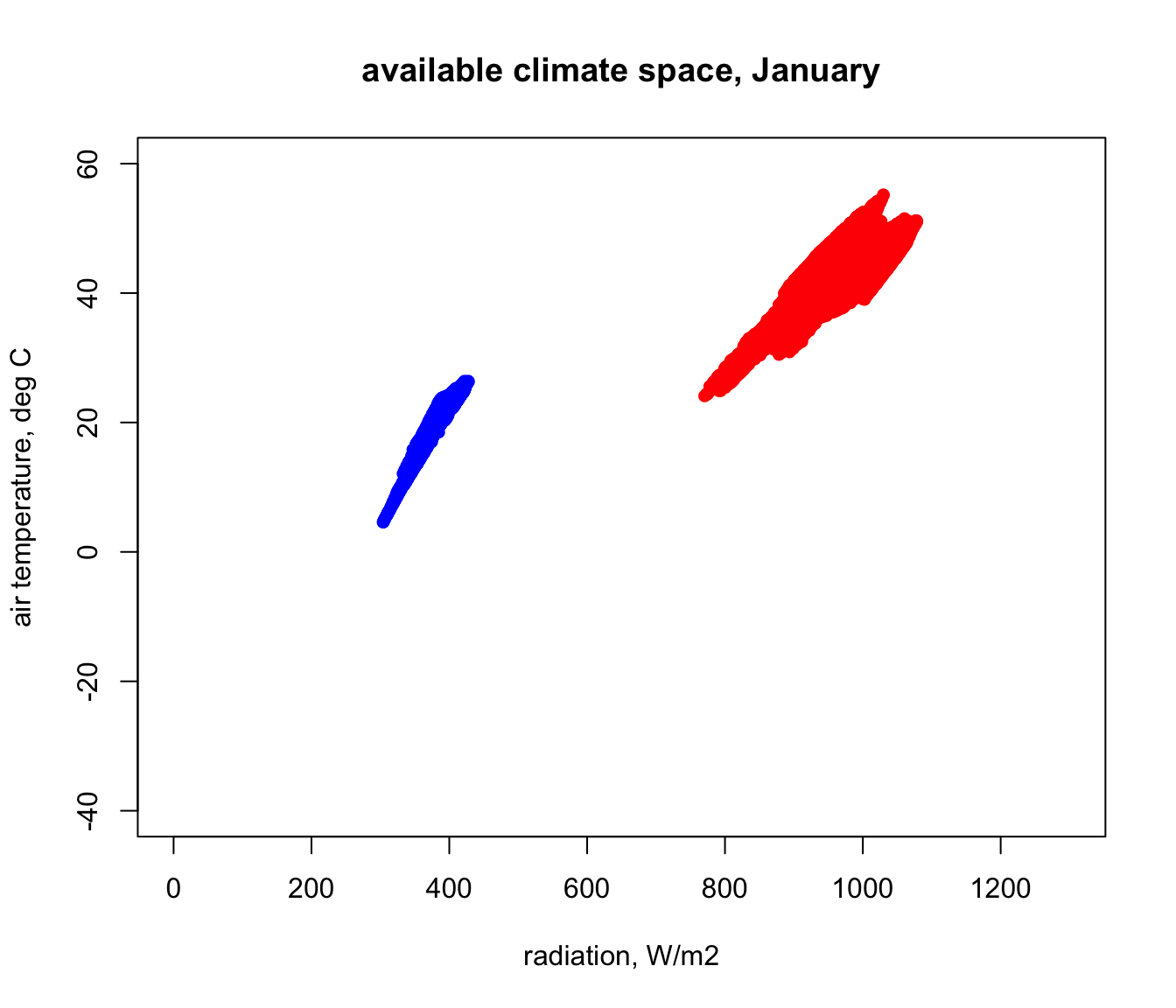
Next we will modify this code to create a loop to go through each hour, adding points to the map, for both January and July. Note that, although loops are a basic aspect of programming, they are slow in R and there are often alternatives to using them (e.g. https://www.datacamp.com/community/tutorials/tutorial-on-loops-in-r#gs.B6zaV0g).
# first, get the conditions for July
# getting bounding radiation conditions across Australia for July
hg = solar_jul_Aust # define the solar radiation input
Tsub = D0cm_jul_Aust # define the ground temperature input
Tsky = Tsky_jul_Aust # define the sky temperature input
# compute the total radiation load
Q_rad_jul_Aust <- Qbound_micro(hg = hg, Tsub = Tsub, Tsky = Tsky,
alpha_s = alpha_s, alpha_g = alpha_g)
# now loop through each hour and plot the results for each month
for(i in 1:24) { # start of the loop, from i = 1 to 24
# first do January, in red
# extract the radiation and air temperatures from the rasters and bind them together into a table
RadTair <- cbind(values(Q_rad_jan_Aust[[i]]),values(Tair_jan_Aust[[i]]))
if(i == 1){ # check if it is the first step, and make the first plot
plot(RadTair[,1],RadTair[,2],ylim = c(-40,60), xlim = c(0,1300), pch = 16, col = 'red',
xlab = 'radiation, W/m2', ylab = 'air temperature, deg C', main = "available climate space")
}else{
# it's not the first step, so use 'points' to add data to the plot
points(RadTair[,1],RadTair[,2], col = 'red', pch = 16)
} # end of the check for first plot
# next do July, in blue
# extract the radiation and air temperatures from the rasters and bind them together into a table
RadTair <- cbind(values(Q_rad_jul_Aust[[i]]),values(Tair_jul_Aust[[i]]))
# add the July values to the graph
points(RadTair[,1],RadTair[,2], col = 'blue', pch = 16)
} # end of the loop through each hour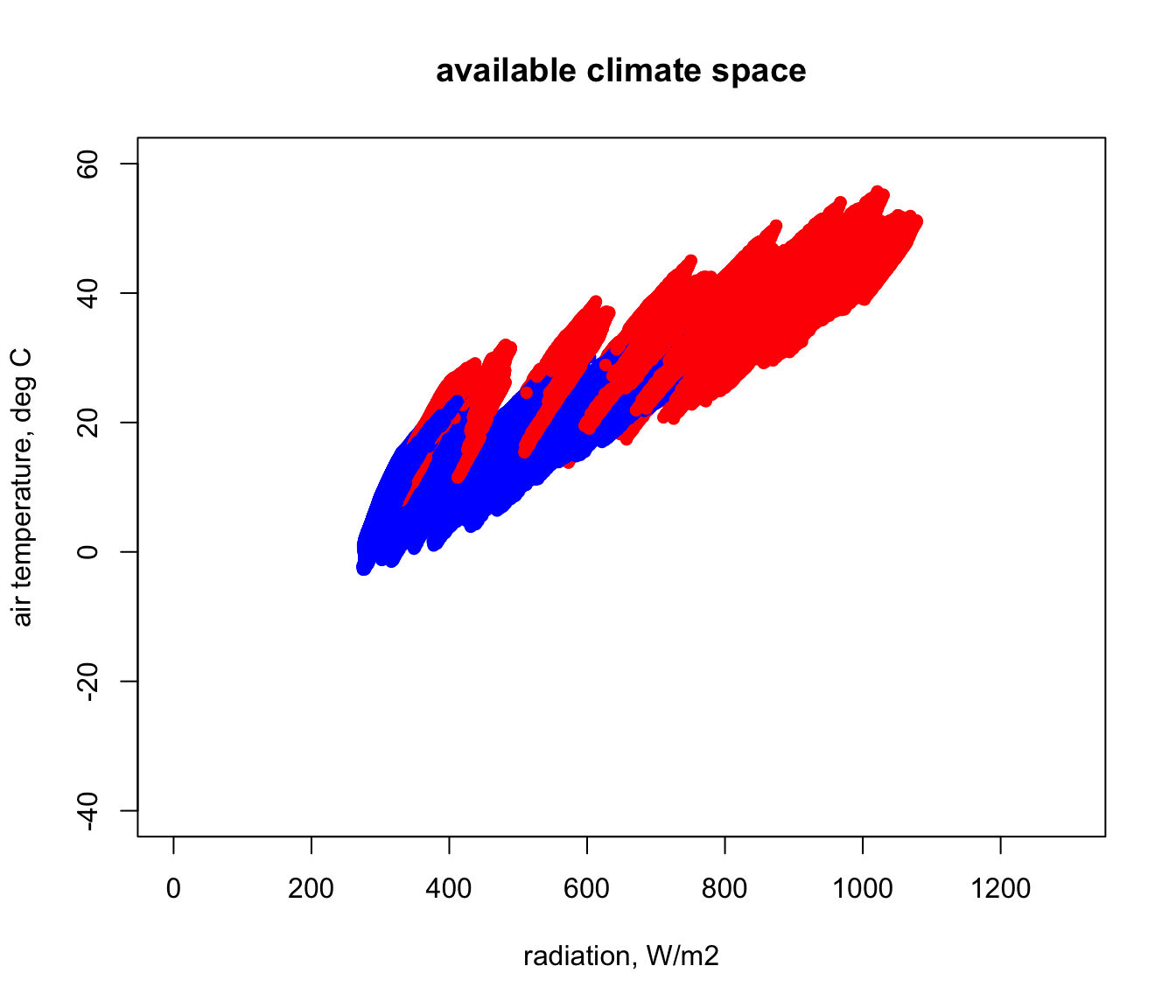
In the next figure you can see how this compares with the Figure 12 of Porter and Gates (1969). This was done by simply re-running that code and using points for the first plot to ensure that it got added onto the one we just made. How would you explain the discrepancies with our estimate for Australia using microclim?
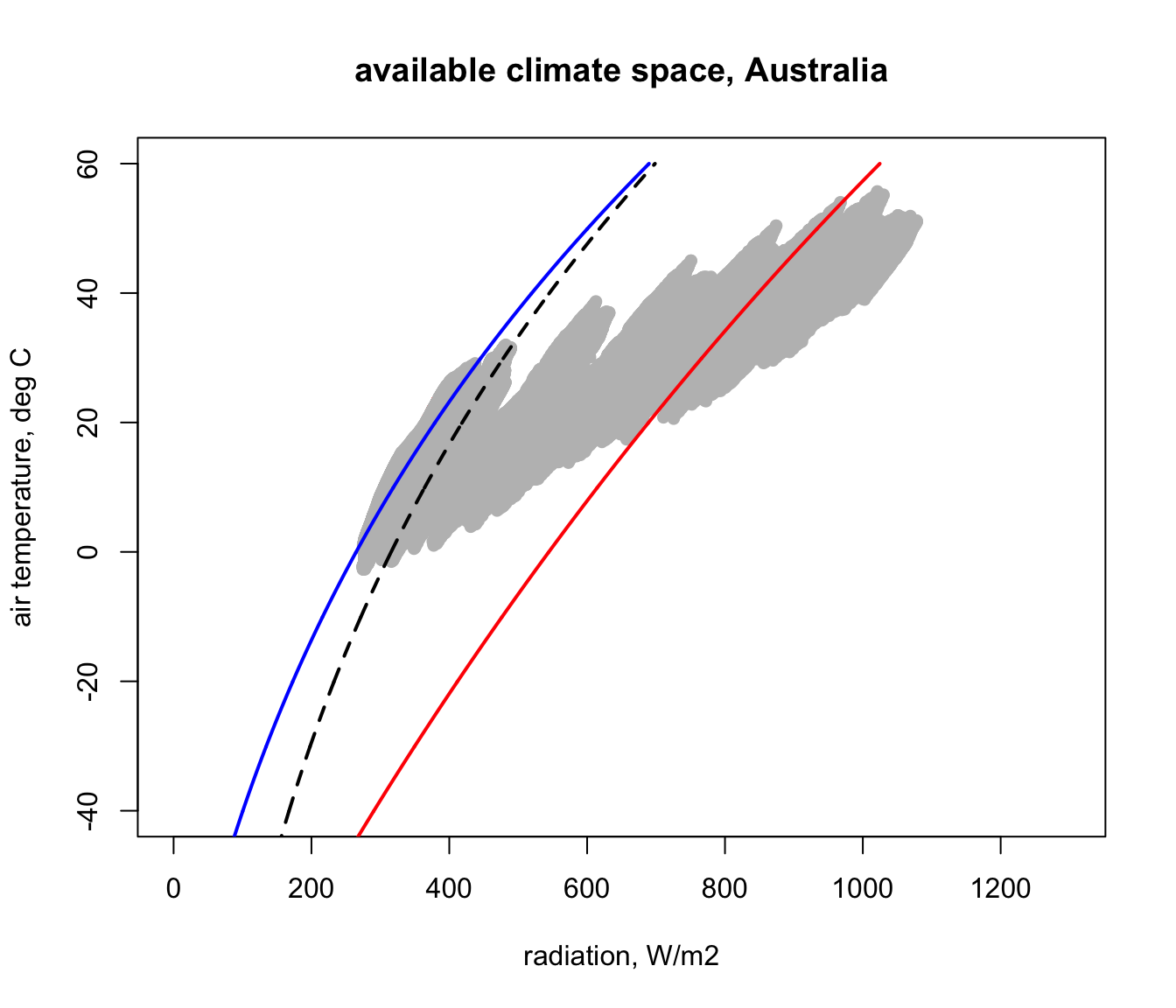
It should be an easy task to recalculate all of this for North America. Have a try, appending ‘_NAm’ to all the variables that previously had ‘_Aust’, and see if you can produce the following figure. Note how much colder it gets in North America compared with Australia.
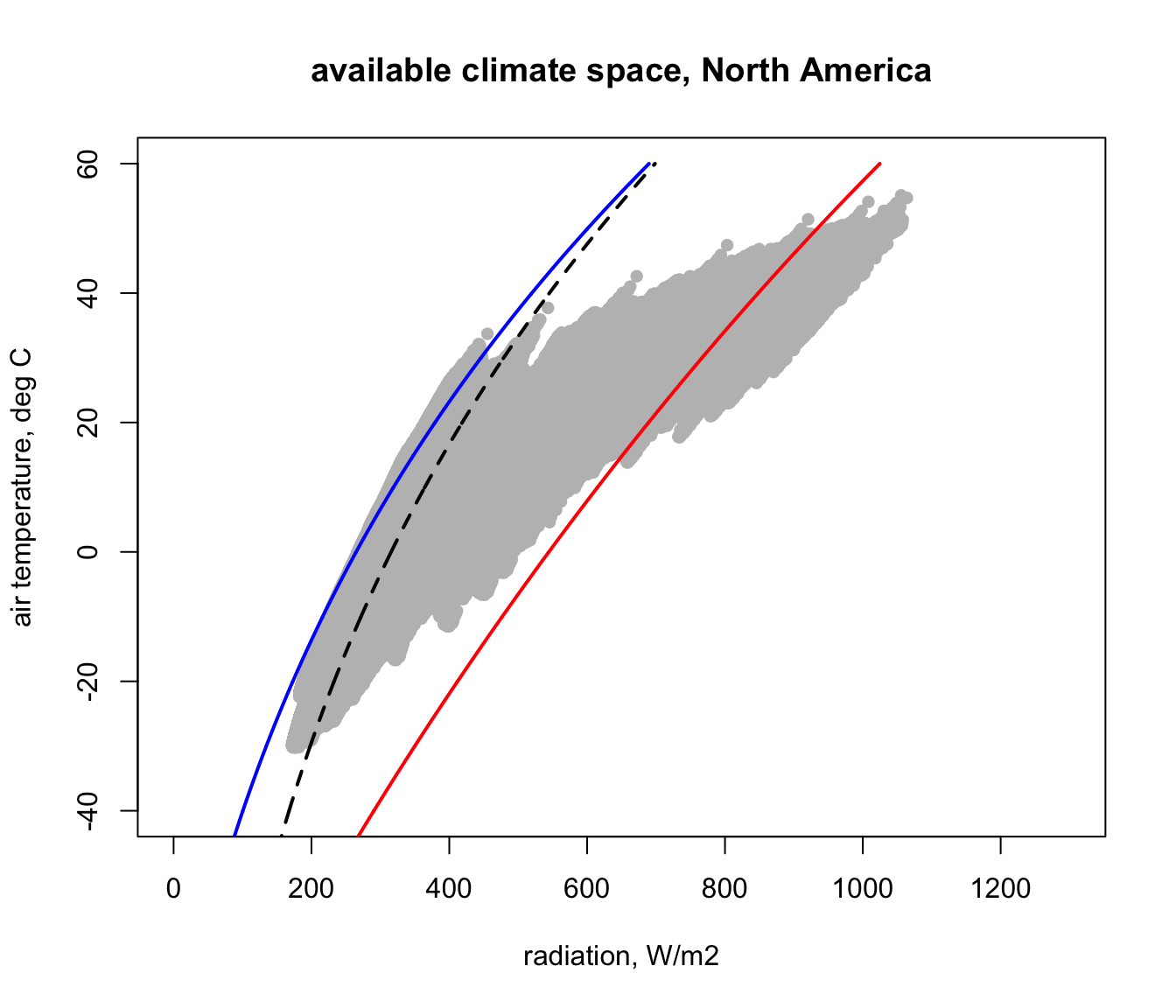
16.4 Mapping the climate space of the Desert Iguana in North America
In module @ref(climate space) we computed the climate space of the Desert Iguana in terms of its survivable limits of 3-45 degrees C. Here are those limits for a wind speed of 0.1 m/s mapped onto our North America climate space diagram. This was done simply by using the code we developed in module @ref(climate space).
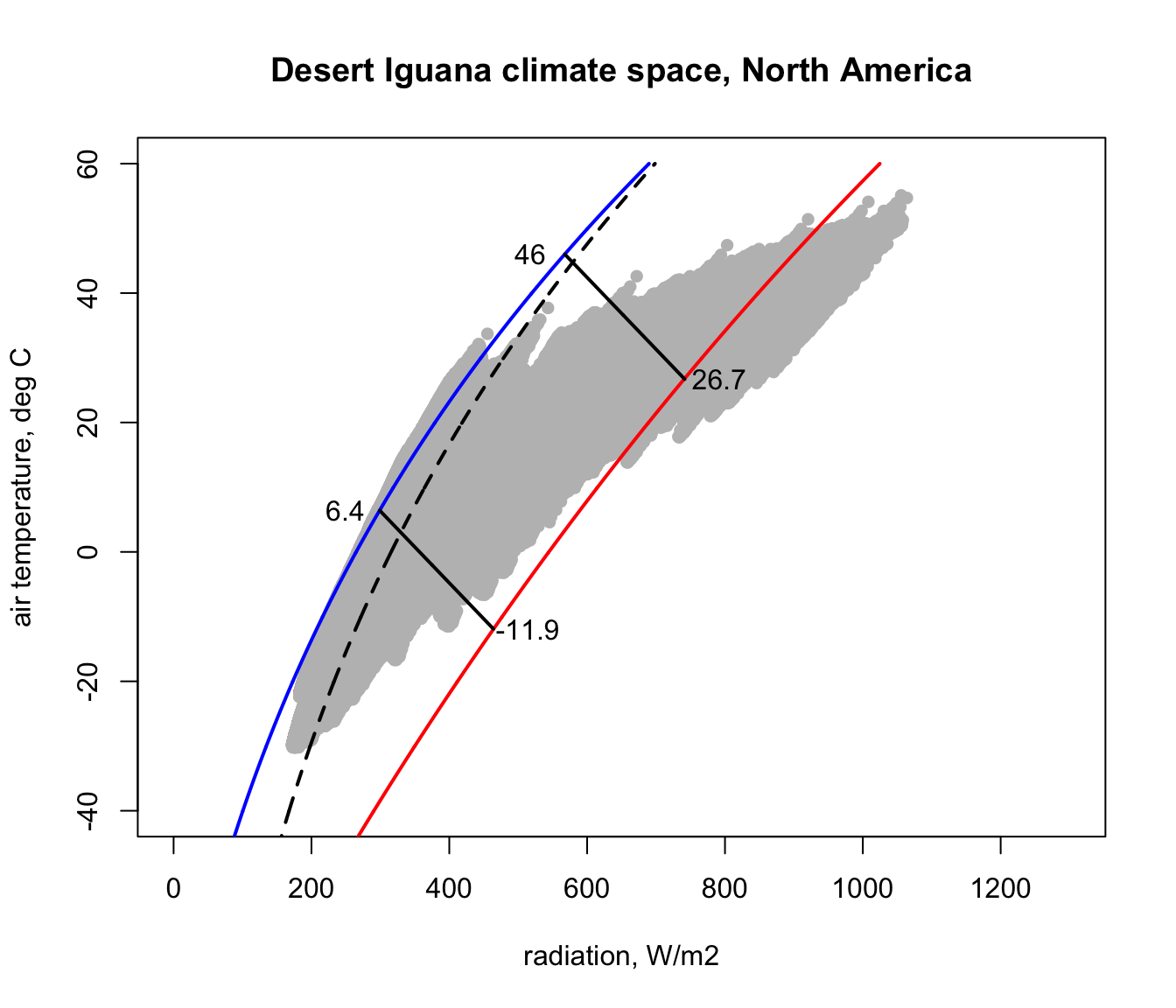
You can see that there are places within North America that are too hot and too cold for this lizard - i.e. that are outside the fundamental or ‘thermodynamic’ niche of this species with respect to temperature. We now want to see where those situations are in space and time.
To do this we can use the heat budget equation we developed in module @ref(climate space), which gives us the radiation load for a given air temperature and wind speed that would result in a particular temperature. In module @ref(climate space) we gave that equation a vector of air temperatures and a single wind speed, so we could work out those lines on the climate space diagram. But now we can give the equation grids of air temperature and wind speed and get, for each pixel, the radiation load needed to balance the heat budget at our chosen body temperature. Let’s try that now.
First, we need to define our heat budget equation as in module @ref(climate space) - remember we had one for ectotherms and one for endotherms? We need the ectotherm one of course, which has been copied and pasted here from module @ref(climate space).
# function to compute absorbed radiation required given a specific core temperature, air temperature,
# and wind speed
# organism inputs
# D, organism diameter, m
# T_b, body temperature at which calculation is to be made, deg C
# M, metabolic rate, W/m2
# E_ex, evaporative heat loss through respiration, W/m2
# E_sw, evaporative heat loss through sweating, W/m2
# K_b, thermal conductance of the skin, W/m2/C
# epsilon, emissivity of the skin, -
# environmental inputs
# Tair, A value, or vector of values, or grid of air temperatures, degrees C
# V, A value, or vector of values, or grid of wind speeds, m/s
# output
# Q_abs, predicted radiation absorbed, W/m2
Qabs_ecto <-
function(D, T_b, M, E_ex, E_sw, K_b, epsilon, T_air, V) {
sigma <- 5.670373e-8 # W/m2/k4 Stephan-Boltzman constant
T_r <- T_b - (M - E_ex - E_sw) / K_b
h_c <- 3.49 * (V^(1/2) / D^(1/2))
Q_abs <- epsilon * sigma * (T_r + 273.15)^4 + h_c * (T_r - T_air) - M + E_ex + E_sw
return(Q_abs)
}Next, we need the environmental variables for North America, including the wind speed.
# put your path here for microclim data folder for Australia
path<- 'microclim_NAm/'
# read the January wind speed file for North America into memory
wind_jan_NAm<-brick(paste0(path,"wind_speed_ms_1cm/V1cm_1.nc"))
# read the July wind speed file for North America into memory
wind_jul_NAm<-brick(paste0(path,"wind_speed_ms_1cm/V1cm_7.nc"))
# read the January solar radiation file into memory
solar_jan_NAm<-brick(paste0(path,"solar_radiation_Wm2/SOLR_1.nc"))
# read the July solar radiation file into memory
solar_jul_NAm<-brick(paste0(path,"solar_radiation_Wm2/SOLR_7.nc"))
# read the January 1cm air temperature in 0% shade file into memory
Tair_jan_NAm<-brick(paste0(path,"air_temperature_degC_1cm/soil/0_shade/TA1cm_soil_0_1.nc"))
# read the July 1cm air temperature in 0% shade file into memory
Tair_jul_NAm<-brick(paste0(path,"air_temperature_degC_1cm/soil/0_shade/TA1cm_soil_0_7.nc"))
# read the January sky temperature in 0% shade file into memory
Tsky_jan_NAm<-brick(paste0(path,"sky_temperature_degC/0_shade/TSKY_0_1.nc"))
# read the January sky air temperature in 0% shade file into memory
Tsky_jul_NAm<-brick(paste0(path,"sky_temperature_degC/0_shade/TSKY_0_7.nc"))
# read the January surface temperature in 0% shade file into memory
D0cm_jan_NAm<-brick(paste0(path,"substrate_temperature_degC/soil/0_shade/D0cm_soil_0_1.nc"))
# read the July surface temperature in 0% shade file into memory
D0cm_jul_NAm<-brick(paste0(path,"substrate_temperature_degC/soil/0_shade/D0cm_soil_0_7.nc")) We have the environmental variables; now we need the organism’s parameters. As in module @ref(climate space), we read in the climate space parameters ‘csv’ file, subset it for the Desert Iguana data, and convert to SI units where necessary.
climate_space_pars <- as.data.frame(read.csv("data/climate_space_pars.csv"))
pars <- subset(climate_space_pars, Name=="Desert Iguana")
# convert heat flows from cal/min/cm2 to J/s/m2 = W/m2
pars[,4:6] <- pars[,4:6] * (4.185 / 60 * 10000)
# convert thermal conductivities from cal/(min cm C) to J/(s m C) = W/(m C)
pars[,14:15] <- pars[,14:15] * (4.185 / 60 * 100)
pars[,c(7:8,11,16)] <- pars[,c(7:8,11,16)] / 100 # convert cm to m16.5 Mapping the cold limits of the Desert Iguana
First, let’s work out the radiation required for the Desert Iguana to be 3 degrees C, the low body temperature threshold for survival. This is row one in our dataset.
a_max <- pars$abs_max[1] # get the maximum solar absorptivity value, choosing row 1
D <- pars$D[1] # diameter, m
T_b_lower <- pars$T_b[1] # body temperature, deg C
M <- pars$M[1] # metabolic rate, W/m2
E_ex <- pars$E_ex[1] # evaporative heat loss from respiration, W/m2
E_sw <- pars$E_sw[1] # evaporative heat loss from sweating, W/m2
k_b <- pars$k_b[1] # thermal conductivity of the skin, W/(m C)
K_b <- k_b/pars$d_b[1] # thermal conductance of the skin, W/(m2 C)
epsilon <- 1 # emissivityNow, let’s define our input arguments for wind speed and air temperature as the microclim grids for North America in January - the coldest month in this part of the world.
V <- wind_jan_NAm # wind speed, m/s
T_air<-Tair_jan_NAm # air temperature range to consider, degrees CFinally, we can run the Qabs_ecto function.
# compute the total radiation load for each air temperature and wind speed combination that would
# give a Tb of 3 degrees, the lower survivable limit
Q_abs_lower <- Qabs_ecto(D = D, T_b = T_b_lower, M = M, E_ex = E_ex, E_sw = E_sw, K_b = K_b, epsilon = epsilon, T_air = T_air, V = V)Now we have the amount of radiation needed at each air temperature and wind speed combination available across North America through each hour of the day such that a Desert Iguana in the open would be 3 degrees C. Let’s plot that for 4am and 12pm.
par(mfrow = c(1,1)) # set to plot 1 row of 2 panels
plot(Q_abs_lower[[5]], main = "radiation required (W/m2), 4am January", zlim = c(-1000, 1300))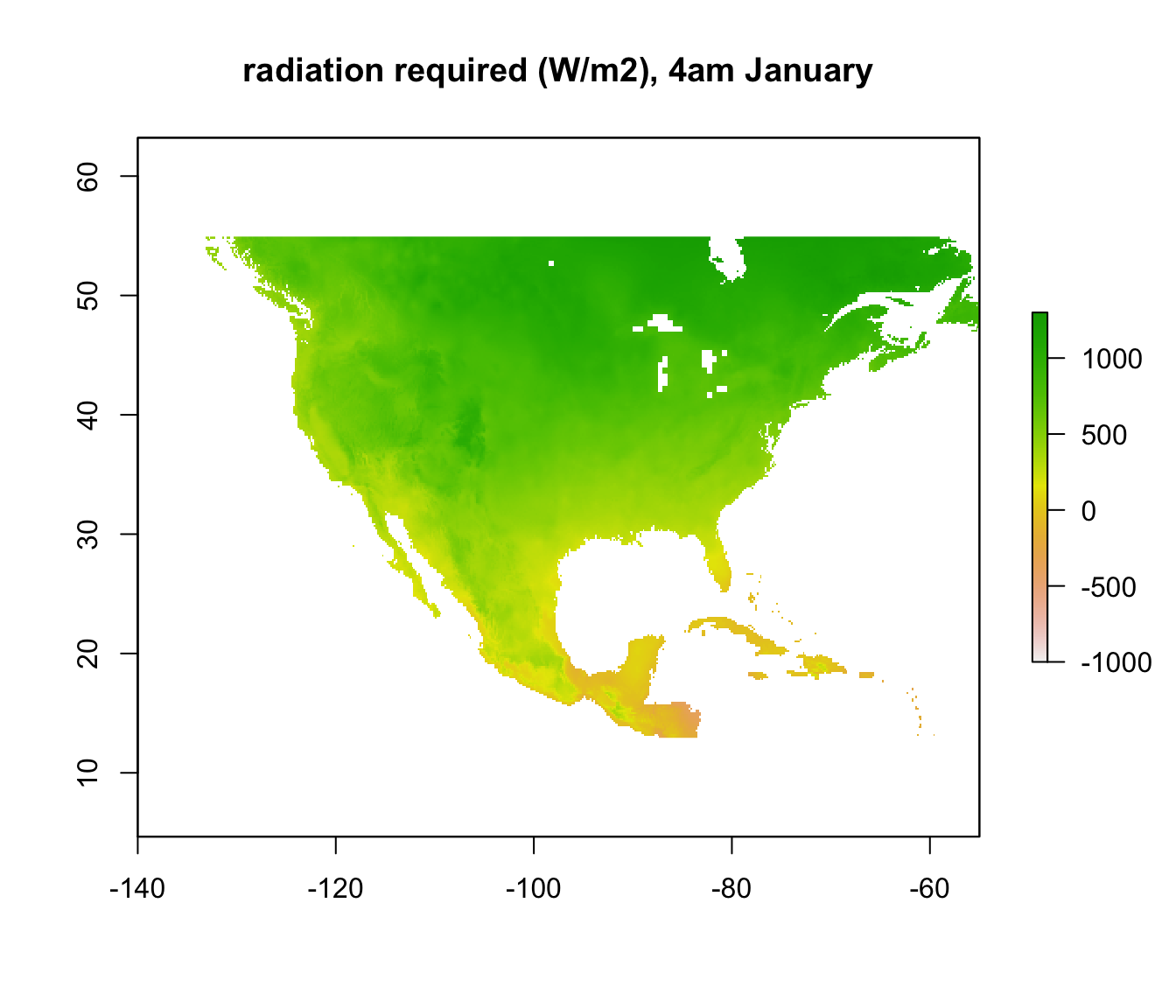
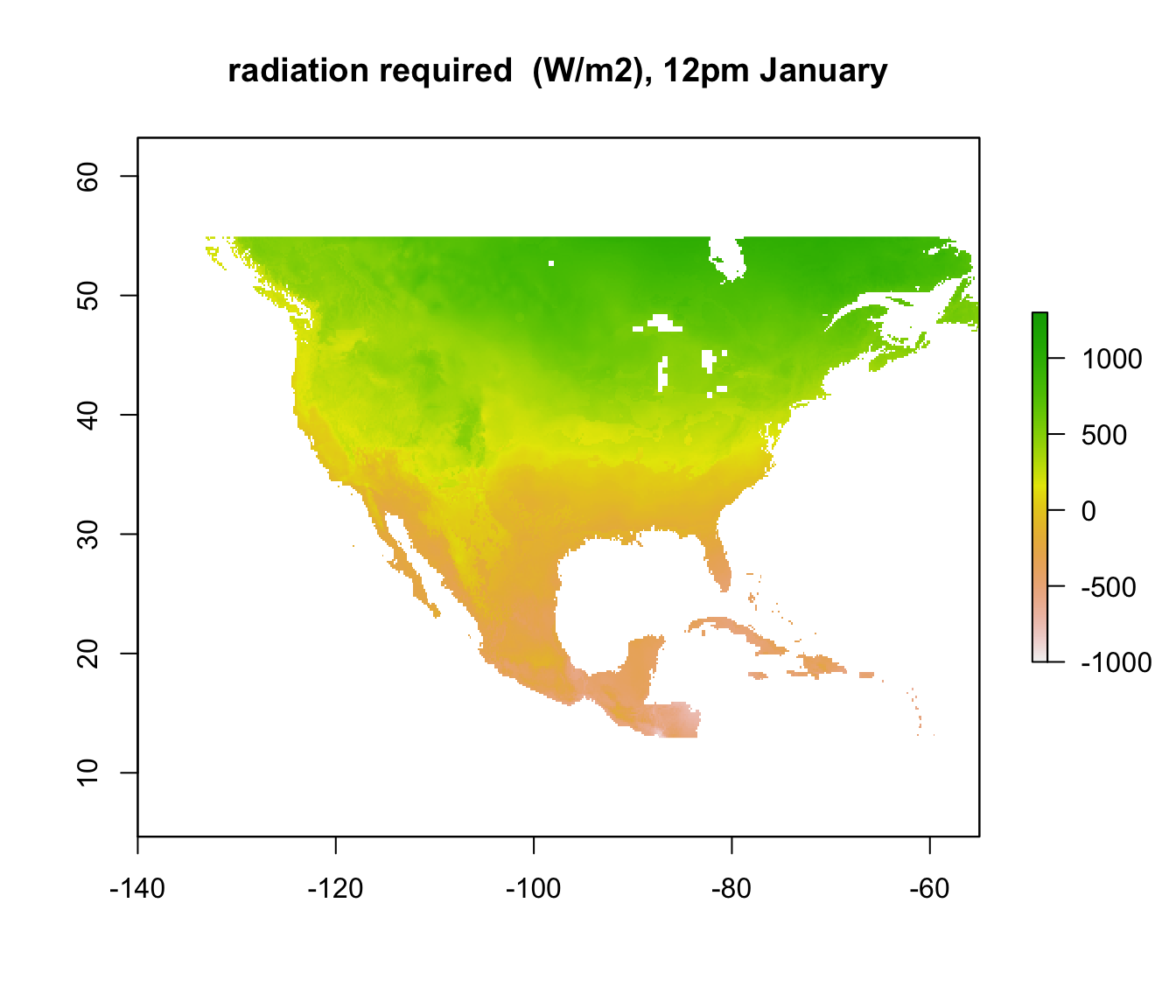
Note that some areas are negative! You can’t have negative radiation - in such places, it would clearly be physically impossible to be colder than 3 degrees C due to the particular combination of wind speed and air temperature at that time and location. The air temperature is simply too high, no matter what the ground or sky temperature is. Those places are thus within the climate space of the Desert Iguana in terms of cold tolerance.
In other places, however, where the required radiation is positive, there still may not be enough radiation available to be 3 degrees C. We want to know where those places are. We have already calculated the available radiation at each place and time - the ‘Q_rad_Jan_NAm’ and ‘Q_rad_Jan_NAm’ grids which should still be in R’s memory. Let’s replot the ones for January at 4am and 12pm again for comparison.
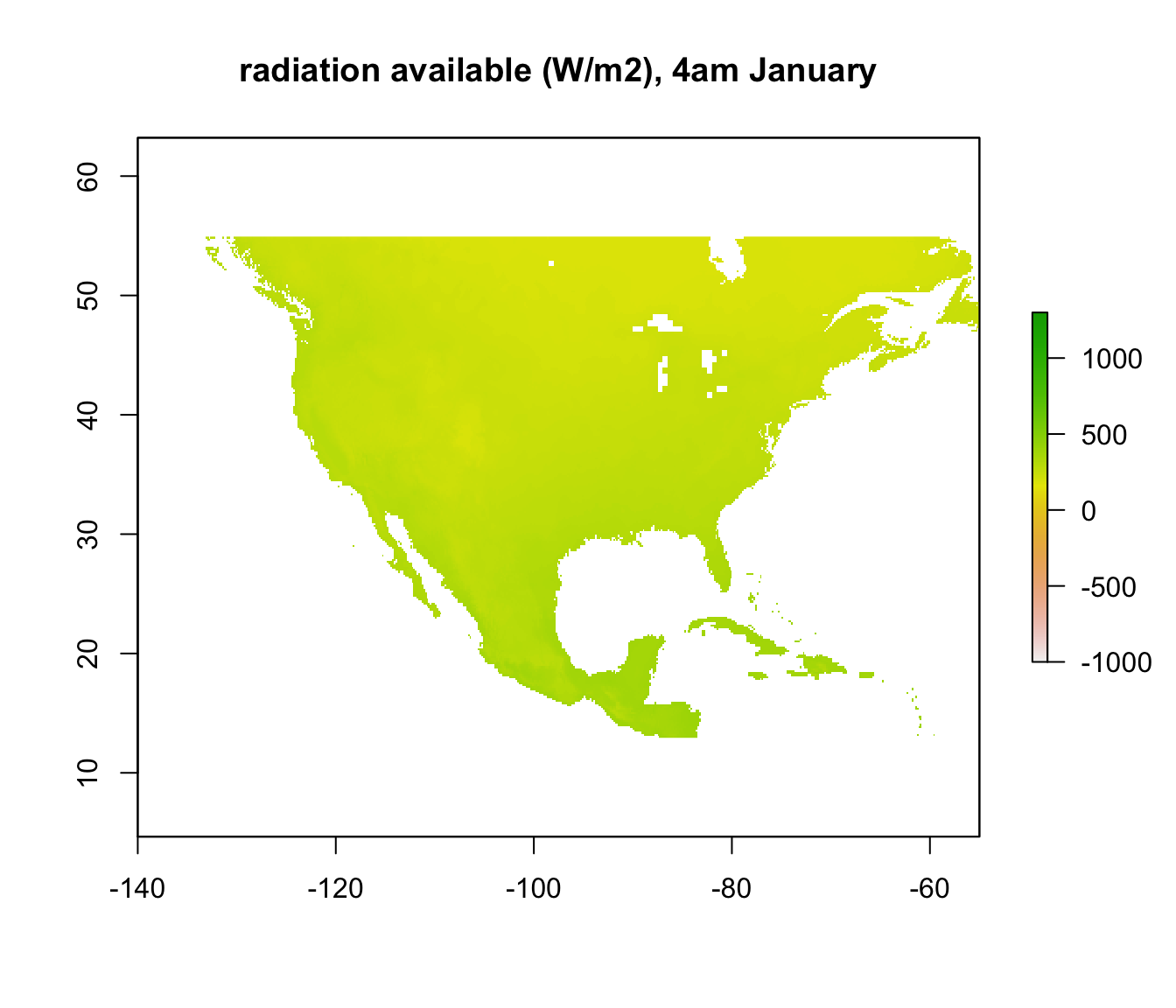
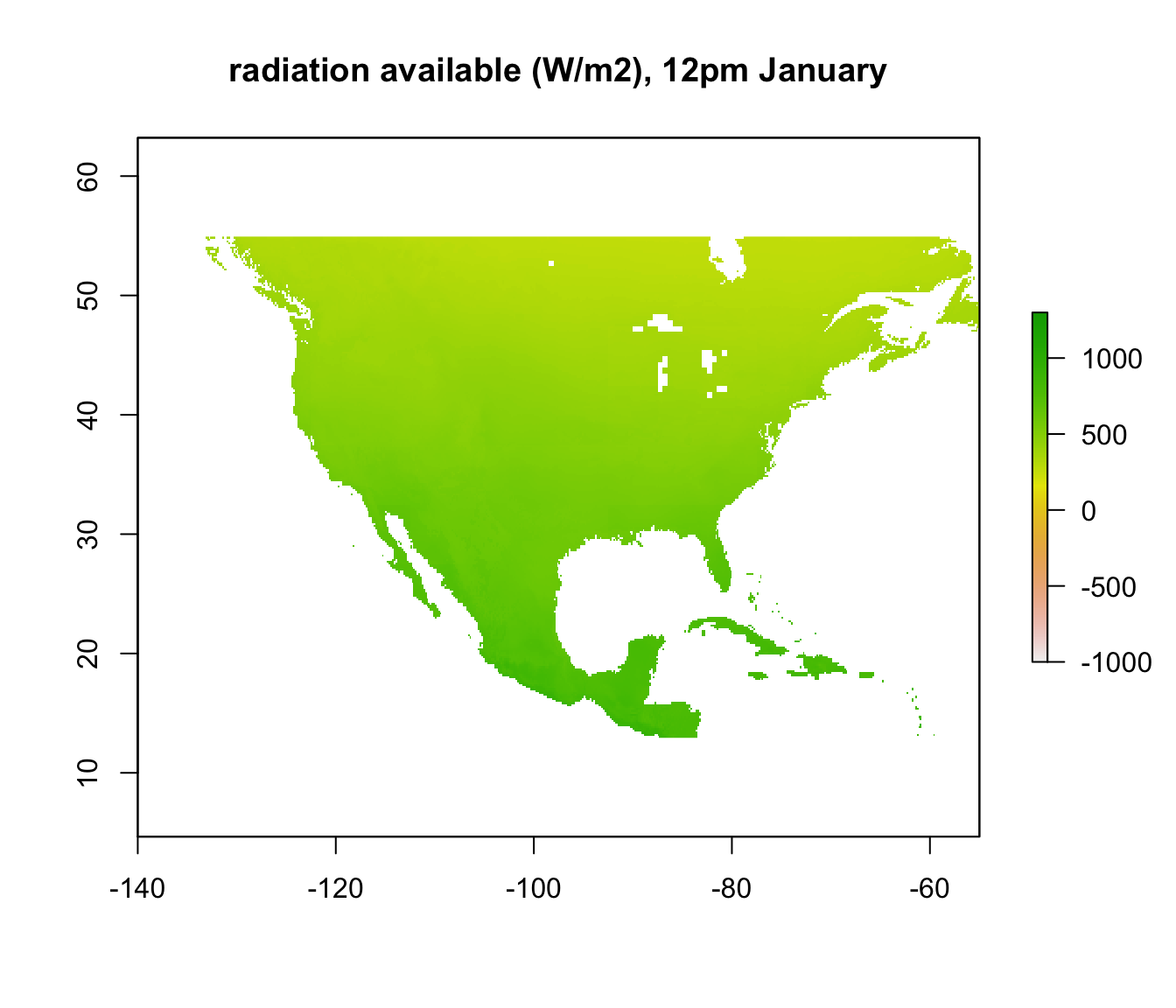
If we subtract the required radiation values from the available radiation values, all the places we get a positive result will be the places that are too cold to be 3 degrees C or warmer. The next code chunk makes this calculation and plots it, making the upper z-limit zero so only areas where the lizard would be 3 degrees C or warmer are coloured.
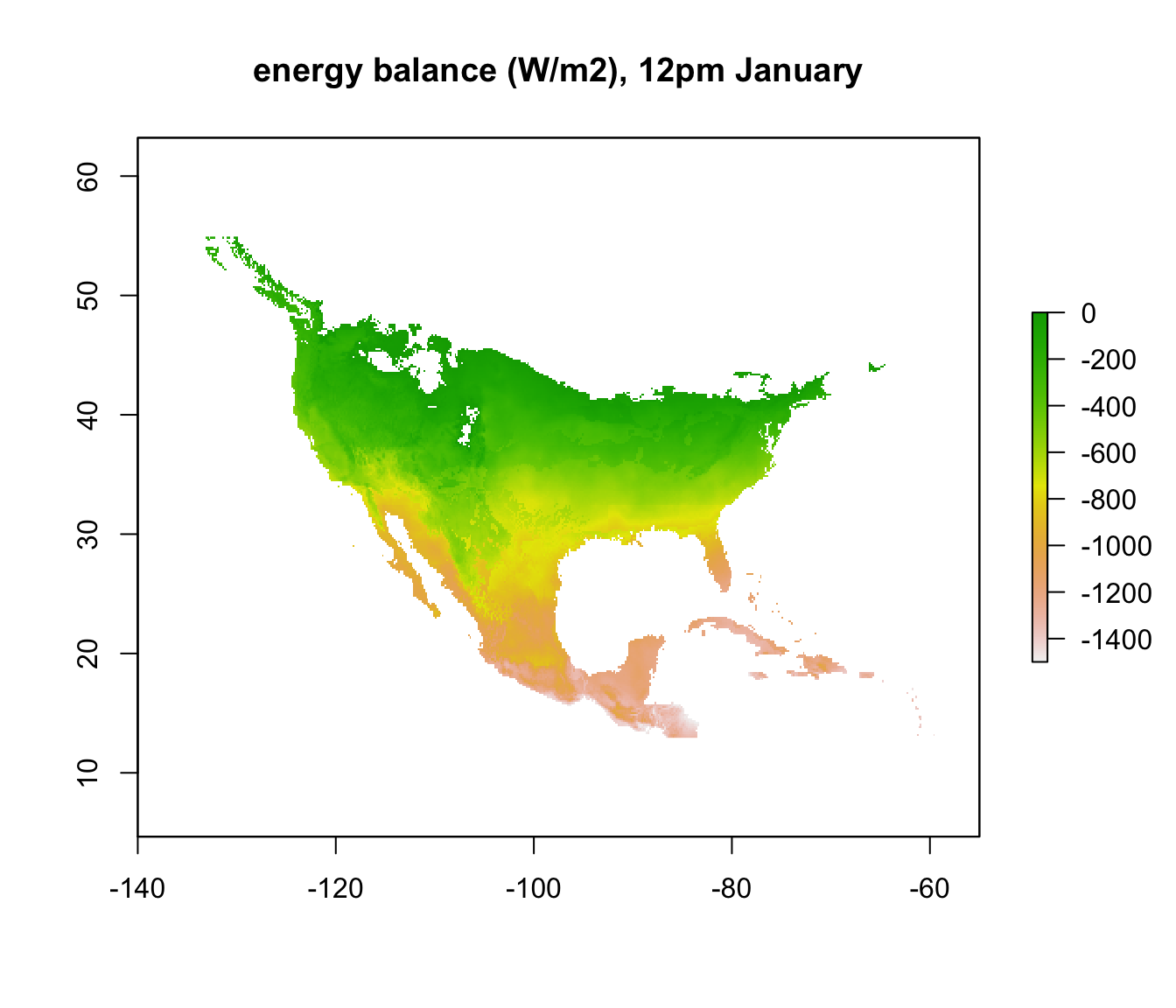
enbal_cold <- Q_abs_lower - Q_rad_jan_NAm # subtract required from available radiation for 3 degrees Tb
plot(enbal_cold[[5]], main = "energy balance (W/m2), 4am January", zlim = c(-1500,0))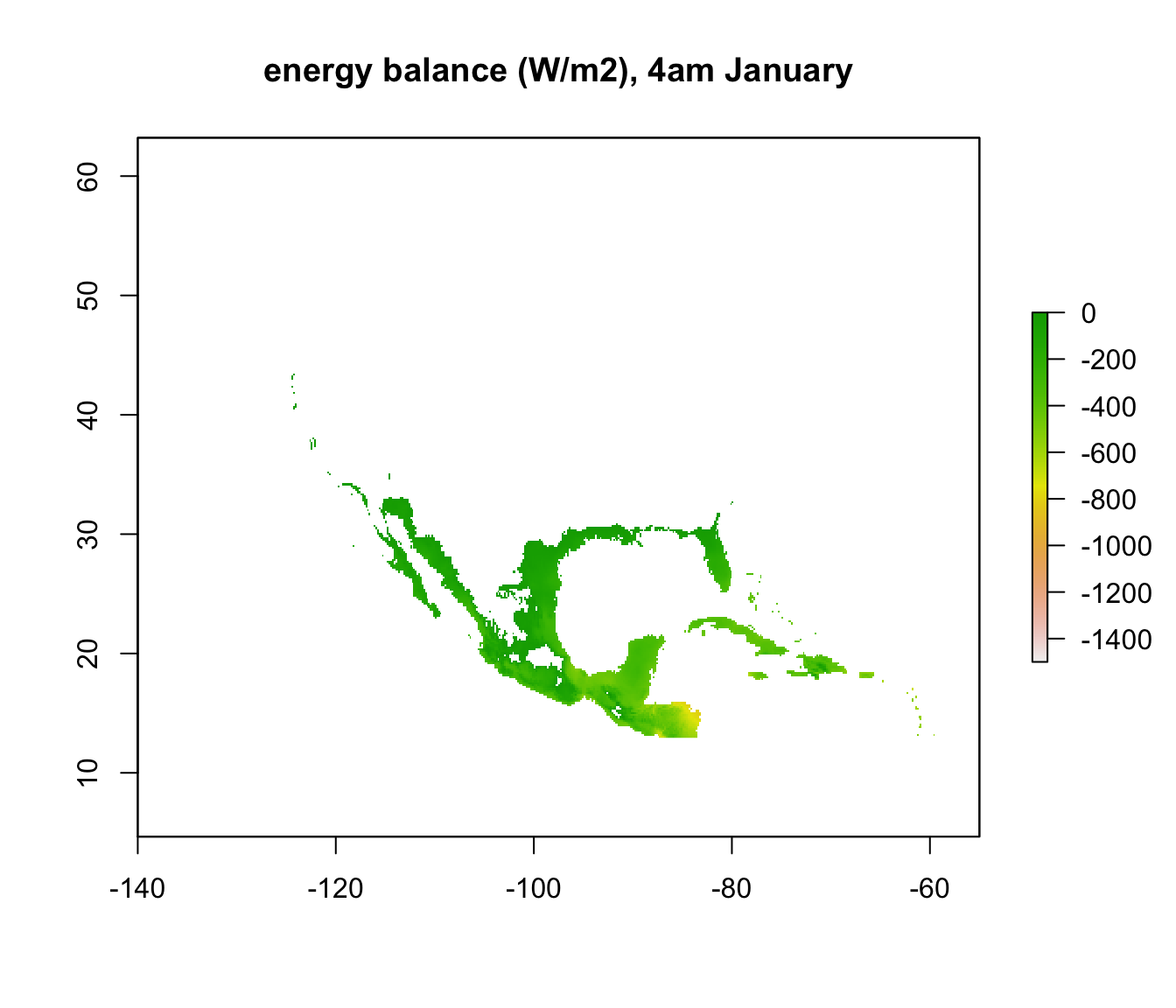
To make things a bit clearer, you can add outline map of the world using the following code.
library(maps)
map('world', add = TRUE)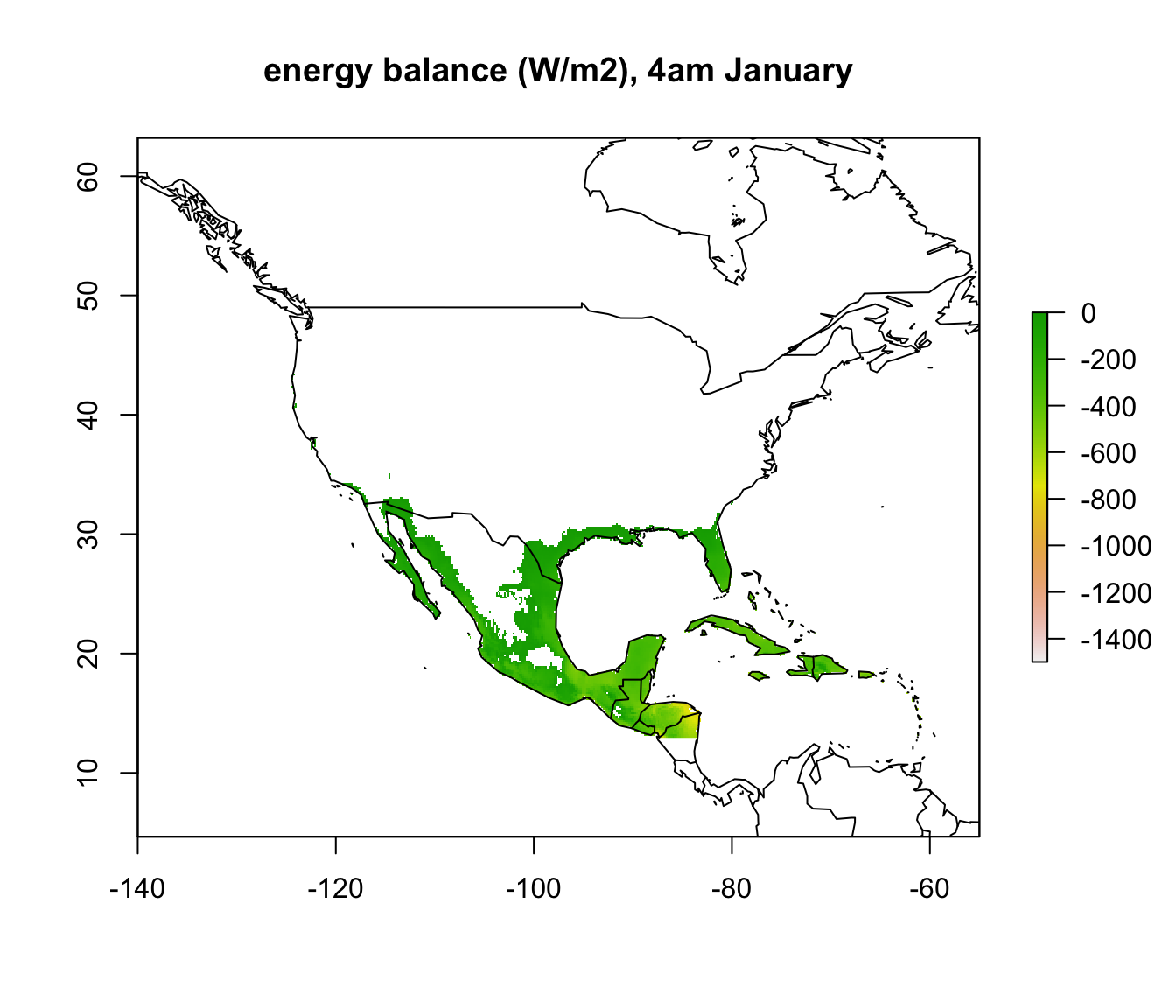
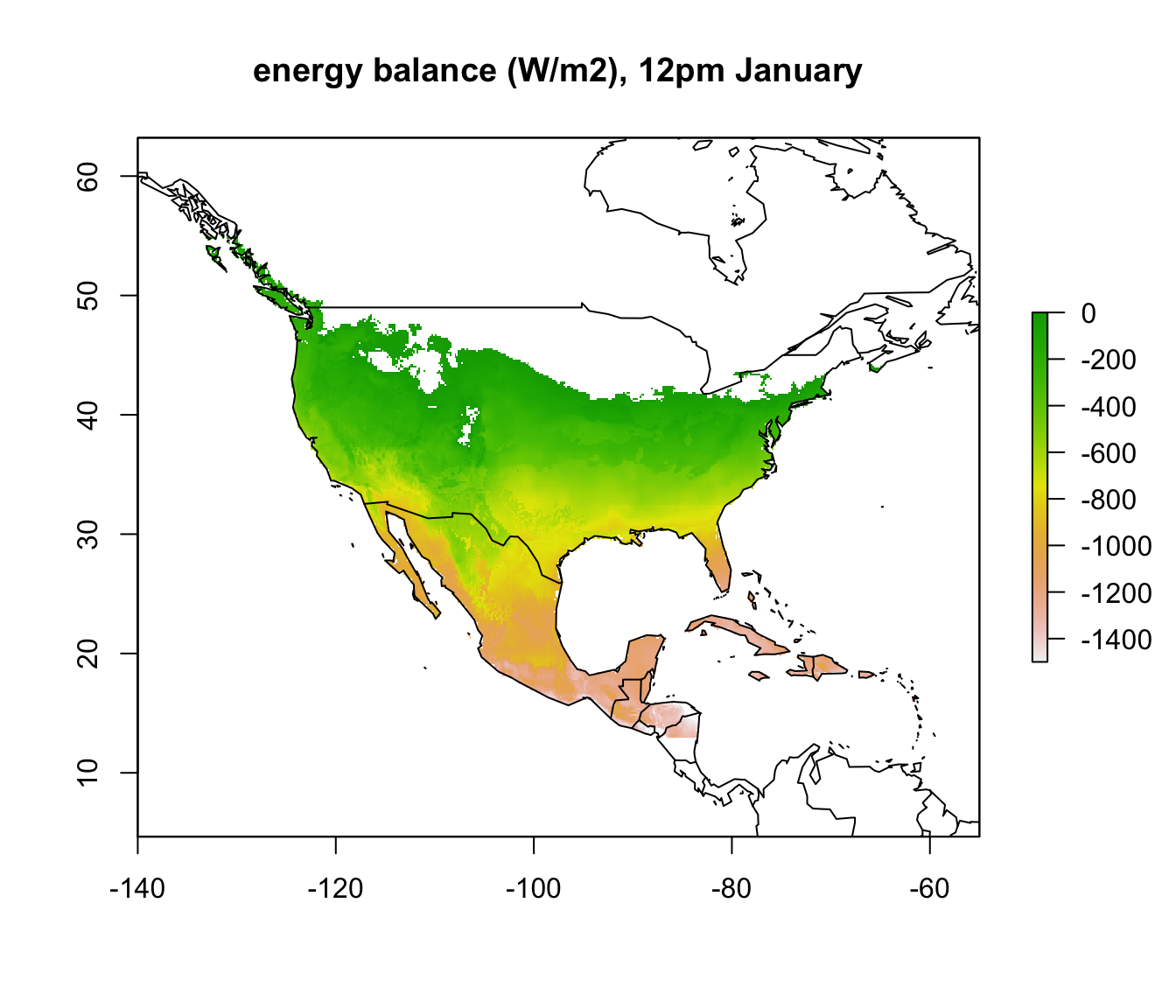
In parts of Mexico and Central America you can see that it is warm enough for a Desert Iguana to be sitting out in the open at 4am in January and be warmer than 3 degrees, and the area where this is the case is much greater at midday. Let’s now plot the actual distribution of the Desert Iguana onto these maps. You’ve been supplied with this data in the file ‘dipso_dist.csv’ which was obtained using the gbif function of the ‘dismo’ package, specifically the code:
library(dismo)
dipso_dist <- gbif("Dipsosaurus", "dorsalis", geo = T)
write.csv(dipso_dist, file = "dipso_dist.csv")You can read it in with dipso_dist<-read.csv("dipso_dist.csv") and add the points to each map with the following code inserted after each plot:
points(dipso_dist$lon, dipso_dist$lat, col = "black", cex = 0.5)
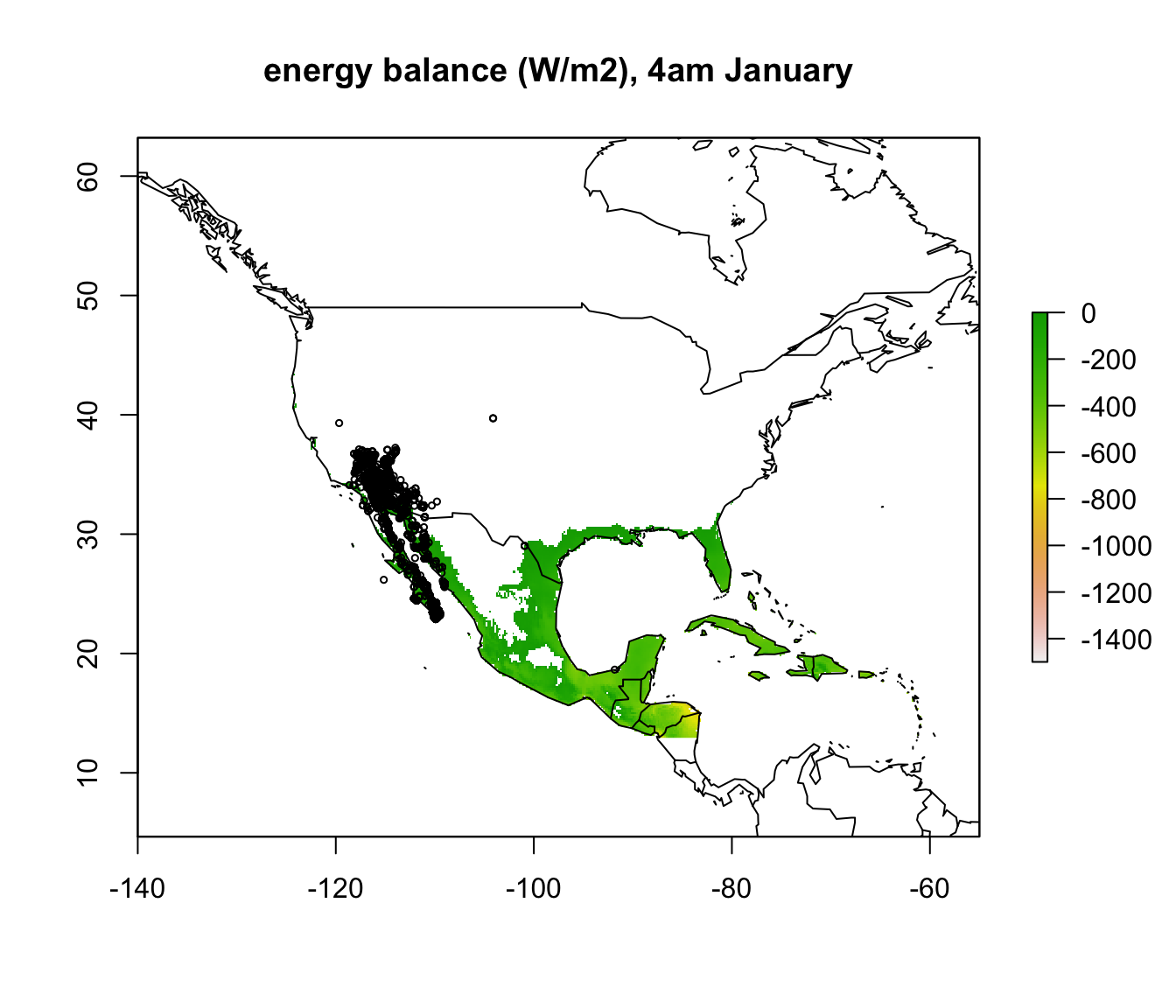
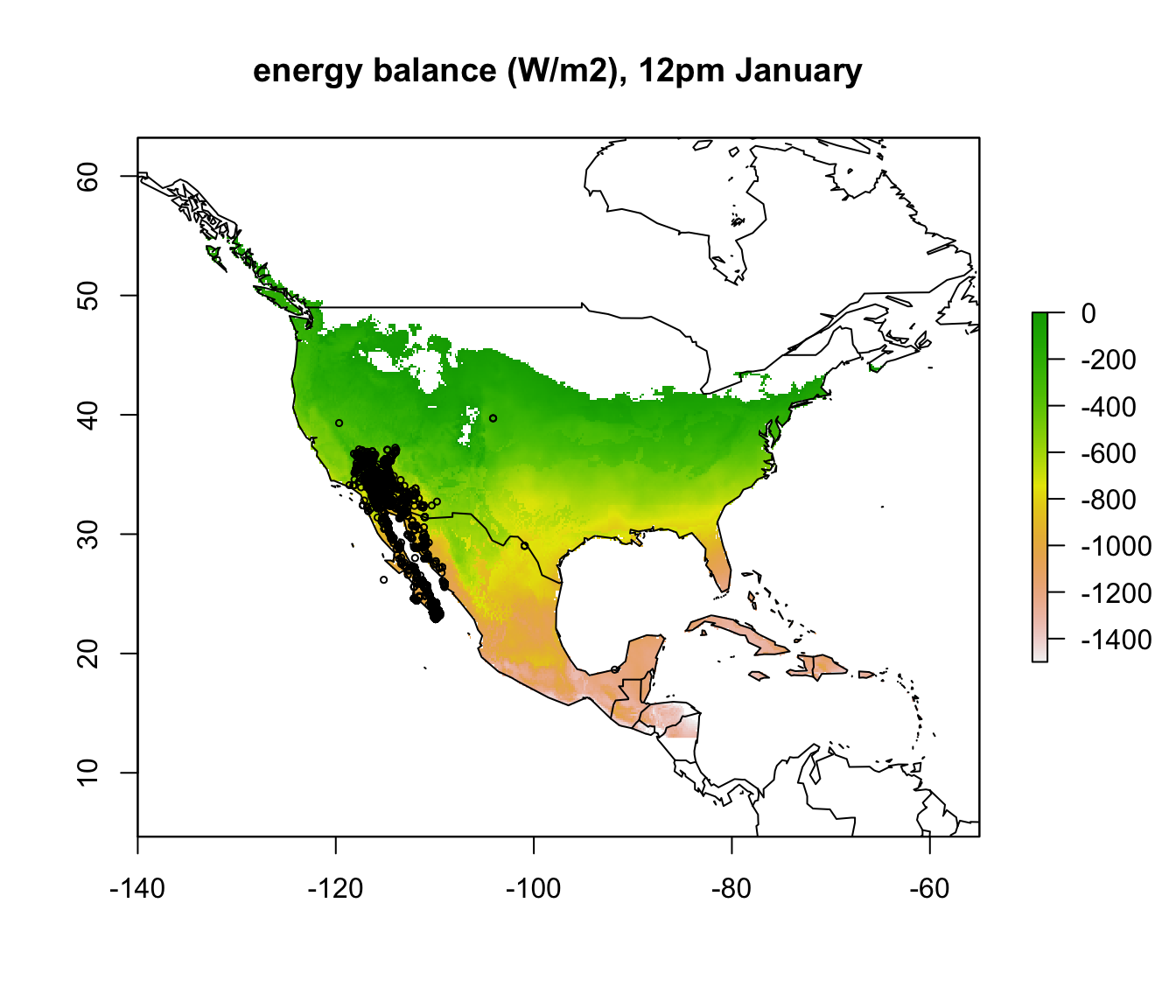
What would you conclude about cold as a limiting factor on the distribution of the Desert Iguana at this point?
16.6 Mapping the heat limit of the Desert Iguana
Now we will repeat the procedure and map the heat limits for the Desert Iguana, but this time in the hottest month, July. Note that we will use the minimum absorptivity observed for the Desert Iguana of 0.6 rather than 0.8 that we used for the cold limit.
# choose the high temperature (45 degrees C) parameters
a_min <- pars$abs_min[5] # get the minimum solar absorptivity value, choosing row 5
D <- pars$D[5] # diameter, m
T_b_upper <- pars$T_b[5] # body temperature, deg C
M <- pars$M[5] # metabolic rate, W/m2
E_ex <- pars$E_ex[5] # evaporative heat loss from respiration, W/m2
E_sw <- pars$E_sw[5] # evaporative heat loss from sweating, W/m2
k_b <- pars$k_b[5] # thermal conductivity of the skin, W/(m C)
K_b <- k_b/pars$d_b[5] # thermal conductance of the skin, W/(m2 C)
# choose the July wind speed and air temperature
V <- wind_jul_NAm # wind speed, m/s
T_air<-Tair_jul_NAm # air temperature range to consider, degrees C
# compute the total radiation load for each air temperature and wind speed combination that would
# give a Tb of 45 degrees, the upper survivable limit
Q_abs_upper <- Qabs_ecto(D = D, T_b = T_b_upper, M = M, E_ex = E_ex, E_sw = E_sw, K_b = K_b, epsilon = epsilon, T_air = T_air, V = V)
# subtract available radiation from required for 45C degrees Tb
enbal_hot <- Q_rad_jul_NAm - Q_abs_upper Now we can plot the results for the heat energy budget at the upper thermal limit. Now, where the ‘enbal_hot’ layer is positive, it means the radiation load on the lizard at that site in the open would exceed that which would result in a body temperature of 45 at the particular wind speed and air temperature at that location.
# plot the results
plot(enbal_hot[[5]], main = "energy balance (W/m2), 4am January", zlim = c(-1500,0))
map('world', add = TRUE)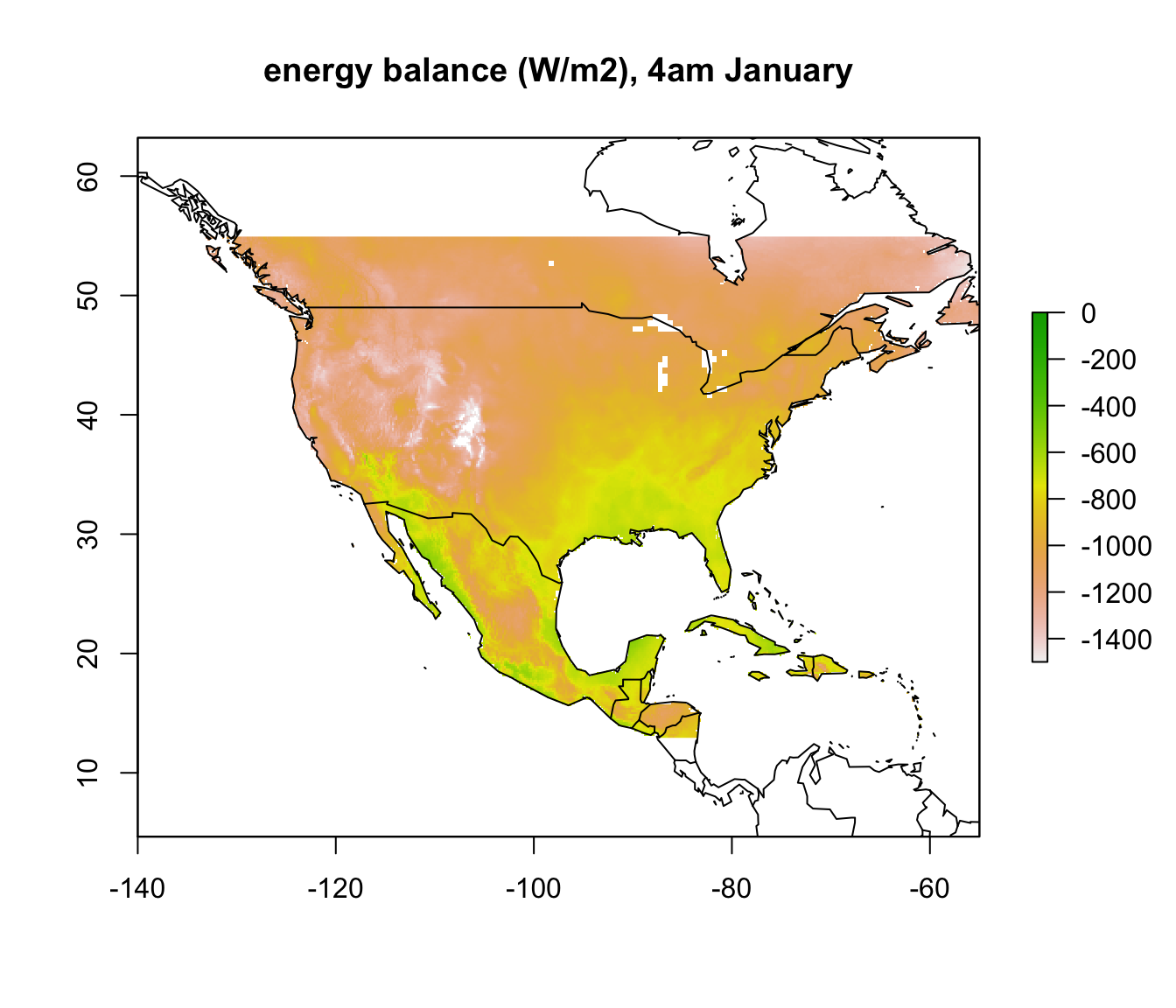
plot(enbal_hot[[13]], main = "energy balance (W/m2), 12pm January", zlim = c(-1500,0))
map('world', add = TRUE)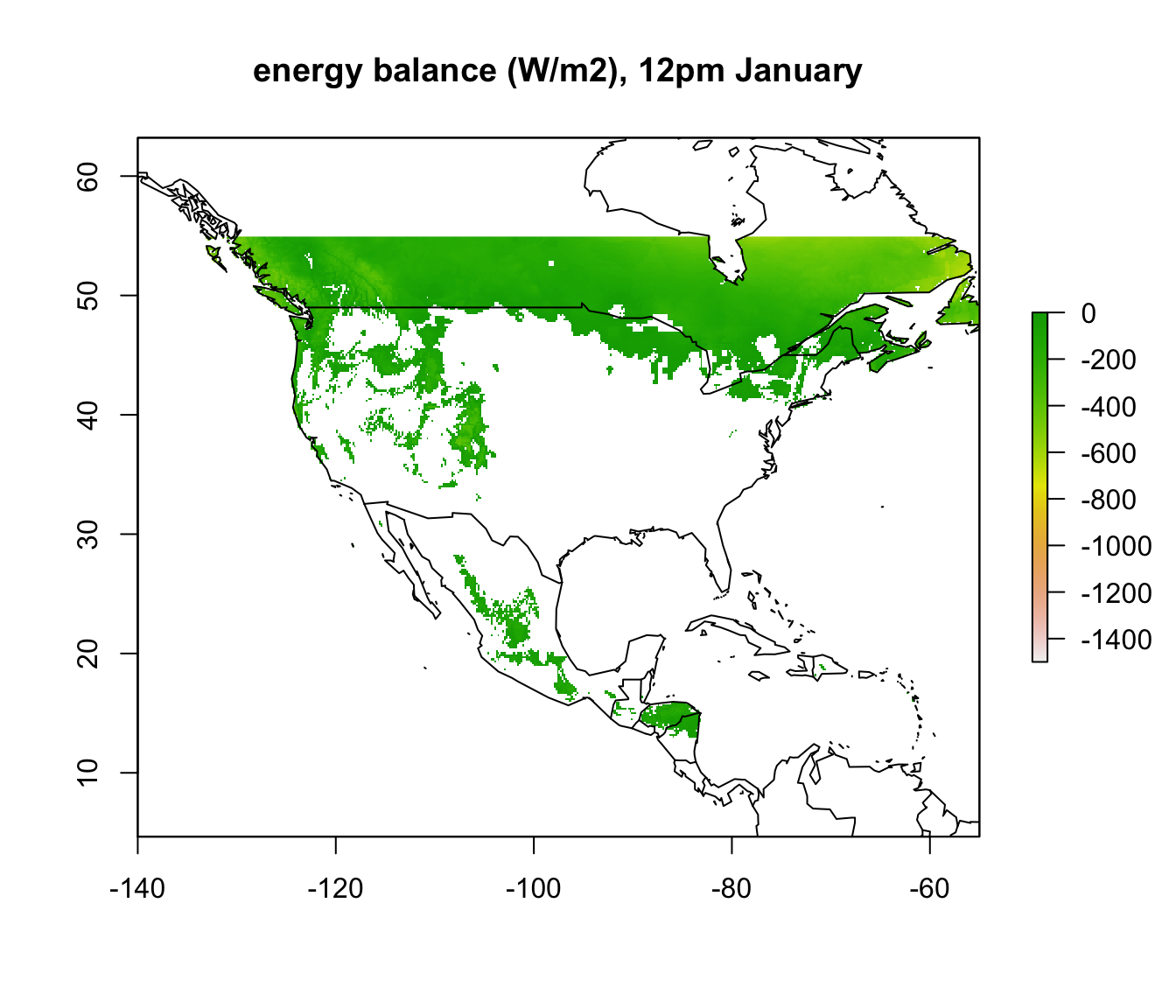
To summarise our calculations so far, let’s make our results binary with values of 1 for pixels that are inside the climate space limits and 0 for pixels that are outside. We’ll use the ifelse native R function together with the ‘raster’ function values which together allow you to conditionally replace values in a raster. We will then make a final result brick called ‘enbal’ where we multiply the two sets of rasters together so you can see at what times and places they would be both above their lower thermal limit and below their upper thermal limit, considering both January and July.
enbal_hot_binary <- enbal_hot
# replace values greater than zero, i.e. where there is too much radiation available to match
# the level needed to produce a 45 degree C body temperature for each wind speed and air
# temperature combination across North America, otherwise give value 1
values(enbal_hot_binary) <- ifelse(values(enbal_hot) > 0, 0, 1)
enbal_cold_binary <- enbal_cold
# replace values greater than zero, i.e. where there isn't enough radiation available to match
# the level needed to produce a 3 degree C body temperature for each wind speed and air
# temperature combination across North America, otherwise give value 1
values(enbal_cold_binary) <- ifelse(values(enbal_cold) > 0, 0, 1)
enbal = enbal_hot_binary * enbal_cold_binaryIf you install the ‘animate’ package in R, you can check out the results as an animation. You’ll have to click the stop button on the console window to stop the animation when you’re finished admiring your work.
library(animation)
times <- paste0(seq(0,23),":00 hrs") # sequence of labels of hours of the day
animate(enbal, main = times)Now we’ll sum the final raster brick to get the total number of hours the Desert Iguana would spend inside its climate space in open habitat and then add the distribution points to this map.
sumembal=sum(enbal) # sum the total number of hours within climate space at at each site
# first plot without the distribution records, so you can see the results clearly
plot(sumembal, main = "Total hours spent within climate space")
map('world', add = TRUE)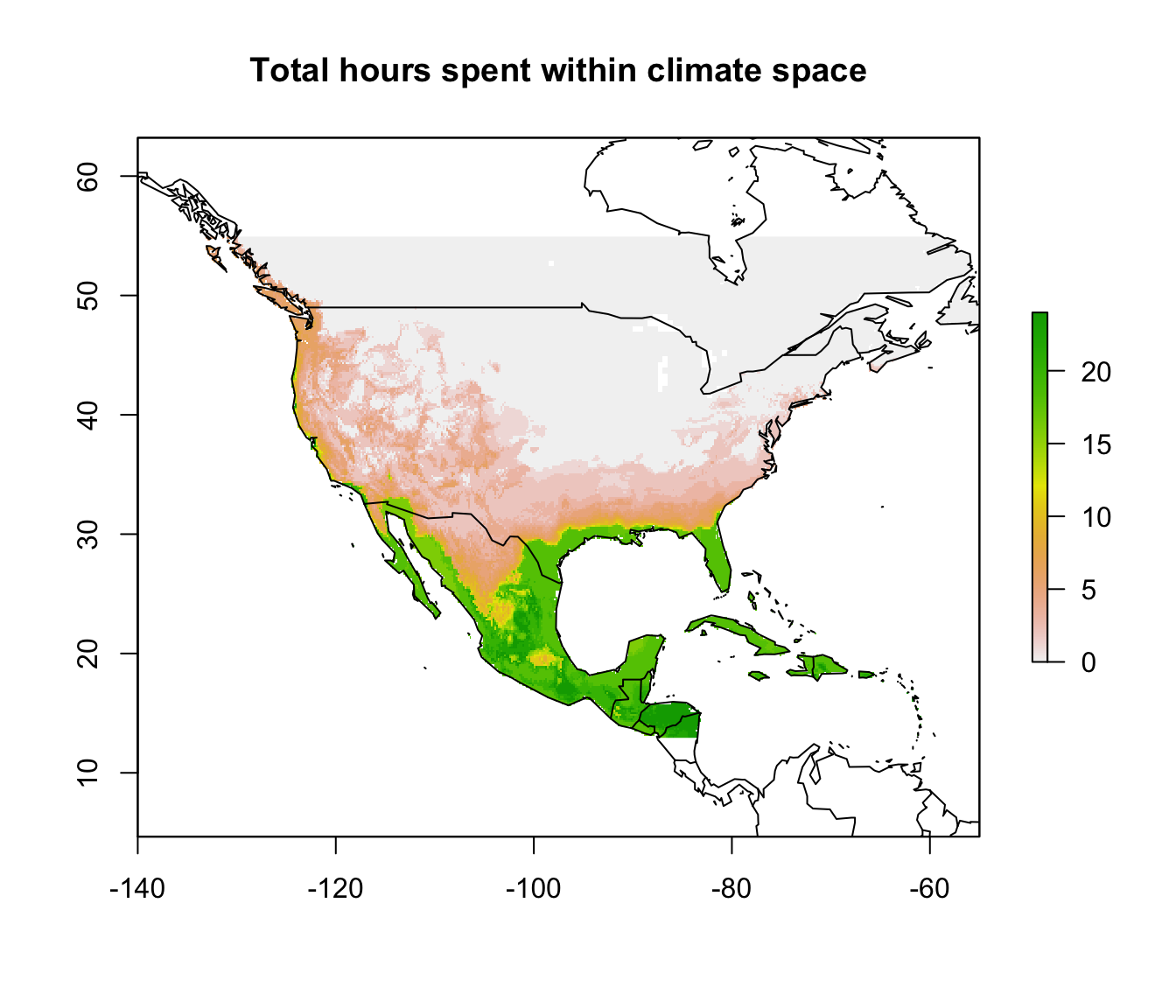
# now plot again with the distribution records
plot(sumembal, main = "Total hours spent within climate space")
points(dipso_dist$lon, dipso_dist$lat, col = "black", cex = 0.5)
map('world', add = TRUE)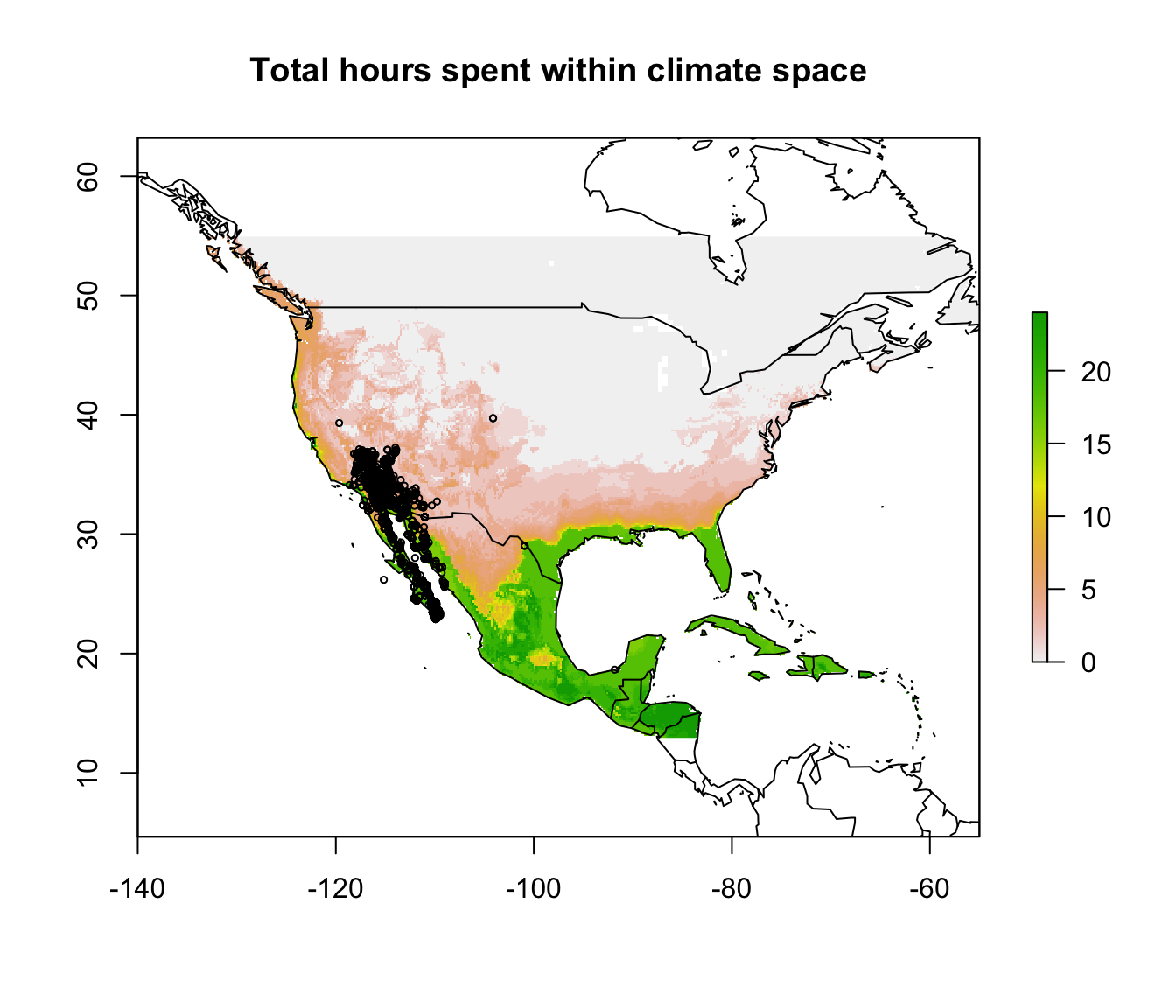
What can you say from this analysis about the distribution limits of this lizard? Have you identified any areas as definitely outside the fundamental or ‘thermodynamic’ niche of this species?
16.7 LITERATURE CITED
Porter, W. P., and D. M. Gates. 1969. Thermodynamic equilibria of animals with environment. Ecological Monographs 39:227-244.