Chapter 1 Boden, Pflanze, Atmosphäre
Die Notitzen sind eine Kenntnisse-Sammelung aus Kurs Boden, Pflanze, Atmosphäre (Goldberg 2021a).
1.1 Interdisziplinäre Bedeutung des Aufgabengebietes
BPA-System spielt Schlüsselrolle bei Energie- und Stoffaustauschen über Landoberflächen in Klimaszstemen aller Skalen.
1.1.1 Hintergrund
Pflanze ist eine Schnittstelle zwischen Boden und Atmospäre. Das Wachstum der Pflanze abhängigt von H2O-, CO2-, N- Flüssen.
Eigenschaften der Pflanze (BPA-System): unter allen natürlichen Oberflächentypen ist es
- (raumlich) heterogensten
- zeitlich variabelsten
- stärksten anthropogen beeinflusst (System mit großen, kurzfristigen Eingriffsmöglichkeiten des Menschen)
Unsicherheitn:
- Unsicherheitn bei der Quantifizierung der Energie- und Stofftransporte in allen Skalenebenen, z.B. Globaler Kohlenstoffhaushalt
- Unsicherheit der C-Quelle / Senke: Emissionen durch Landnutzungsünderungenö; Senke der Oberfläche; Netto-FLuss über Land.
1.1.2 Forschungen
IGBP (International Geosphere-Biosphere Programme)
DFG-Ammer Methoden zur Kopplung hydrologischer und biologischer Prozesse auf der Landschaftsebene
Bild aus Skript(Goldberg 2021a)
1.2 Skalenbetrachtung und raum-zeitliche Abhängigkeit des Systems BPA
1.2.1 Raum-Zeit-Skala
- Skale der Landoberfläche bestimmt Skale der Wechselwirkung mit der Atmosphäre
- Generell ergolgt bestimmter Raum-Zeit-Bezug im System BPA durch dominierende Prozesse
- Jedoch: Prozesse innerhalb des Systems haben, abhängig von betrachteter Komponente, unterschiedlichen Raum-Zeit-Bezug
- Intensität und Wahrnehmbarkeit der Wechselwirkung wird bestimmt vom Grad der Kopplung LOF-Atmosphäre, die von der Komplexität der LOF abhängt (z.B. Wald-starke Wechselwirkung, Kurzgras-schwache Wechselwirkung)
Raumliche und zeitliche Skalen sind eigentlich anhängig, die Skalen werden in der Regel in Makro, Meso, Local und Micro geteilt.
Nach Smagorinski, 1974; aus Skript(Goldberg 2021a)
Bedeutung eines Prozesses und des
entsprechenden Werkzeugs zur Prozessbeschreibung hängt ab von der
betrachteten Skale!(Goldberg 2021a)
1.2.2 Raum-zeitliche Wechselwirkung von Klima und Landschaft
- Benachbarte Kleiklimate beeinflussen sich wechselseitig
- Die Intensität der Wechselwirkung hängt von Größe und Komplexität der Landnutzungsstrukturen ab
- Die Charakteristik der Wechselwirkungen wird gesteuert über den Energie- und Stoffaustauschen zwischen Landschaft und Atmosphäre
1.2.3 Globale und regionale Wechselwirkungen und Rückkopplungen
- Rückkopplung zwischen Energie- und Stoffaustausch und den “Antriebskräften” des Austauches (Gradienten, Randbediengungen)
- Charakter der Wechselwirkung abhängig vom Raum-Zeit-Maßtab der beteiligten Komponenten: linear: gleicher Maßstab; nicht-linear: unterschiedlicher Maßtab
Bild aus Skript(Goldberg 2021a)
- ScaLN < 0.1\(\times\)zAGS: Dominanz vertikaler Wechselwirkung
- ScaLN > 10\(\times\)zAGS und geringe therm. Unterschiede: Dominanz vertikaler, Beginn horiz. Wechselwirkung
- ScaLN > 10\(\times\)zAGS und große therm. Unterschiede:Dominanz horizontaler Wechselwirkung
Bild aus Skript(Goldberg 2021a)
Schema der Wechselwirkungs- und Rückkopplungsprozesse infolge Landdegradation
1.3 CO2-Düngeeffekt
Anstieg der regional differenzierten Karbonisationsrate in den wichtigsten Nahrungsmittelpflanzen bei einer Erhöhung der atmosphärischen CO2-Konzentation um 100 ppm.
“Ergünunug” der Erde durch CO2-Düngung \(\rightarrow\) Zunahme der Biomasse (LAI)
Kompensation des anthropogenen, CO2-Anstieges in der Zukunft durch mehr C-Aufnahme der Pflanzen:
Antsieg der Respiration
Sättigungseffekt (Anpassung der Pflanzen an CO2-Anstieg, Nachteil für C4-Pflanzen)
Limitiertes Nähstoffangebot im Boden
Änderung Wasserhaushalt (Limitierung durch Trockenheit)
1.4 Systemkomponenten
Space free atmosphere
entralnment layer | 0.1zf
mixed layer
surface layer | 0.1zf
merge layer | 3hv
vegetation | hv
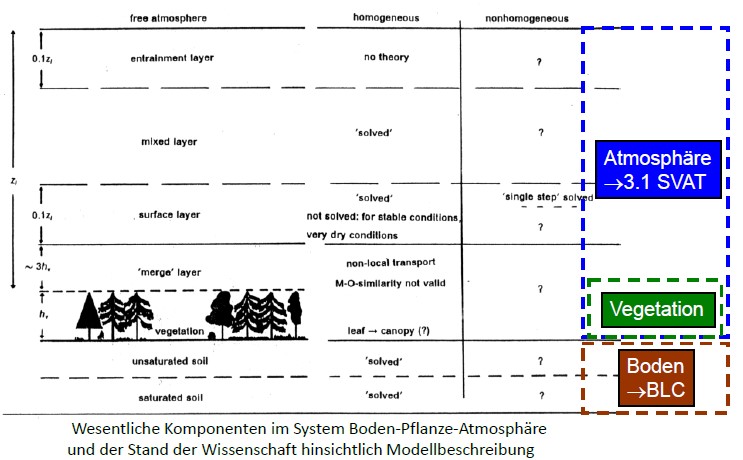
1.5 Energie- und Stoffflüsse
Unterschied zur unbewachsenen Oberfläche:
primäre Energieumsatzfläche (meist) nicht mehr am Erdboden, sondern im Bereich der maximalen Konzentration an Biomasse der Vegetation
sekundäre Umsatzfläche an der Erdoberfläche
Partitionierung der Flüsse zwischen den Umsatzflächen erfolgt i. allg. über die Verwendung von (linearen) Gewichtsfunktionen
Bild aus Skript(Goldberg 2021a)
Bestimmung von Gebietsmitteln in einer fraktionierten Landschaft \(\rightarrow\) Kombination der flächengewichteten Anteil der Energie un Stoffflüsse
\[ F=f_vF_1+(1-f_v)F_2 \]
\(F\): Energie- oder Stoddluss, \(F_1\): primäre, \(F_2\): sekundäre Umsatzfläche, \(f_v\): Vegetationsanteil des Landschaftsausschnitts
1.6 Raum-Zeit_Verhalten der Systemgröße
1.6.1 Strukturparameter der Vegetation:
- Kronenschlussgrad: Anteil des durch Vegetation überdeckten Himmelsbereich
Bild aus Skript(Goldberg 2021a)
- Bestandeshöhe: mottlere Wuchshöhe der Vegetation (hv)
- Blattflächendichete (leaf area density, plant area density)
\[ LAD=\frac{Gesamtoberfläche\,der\,Blätt\,(Vegetationselemente)}{Einheitsvolumen} \bigg[\frac{m^2}{m^3}\bigg] \]
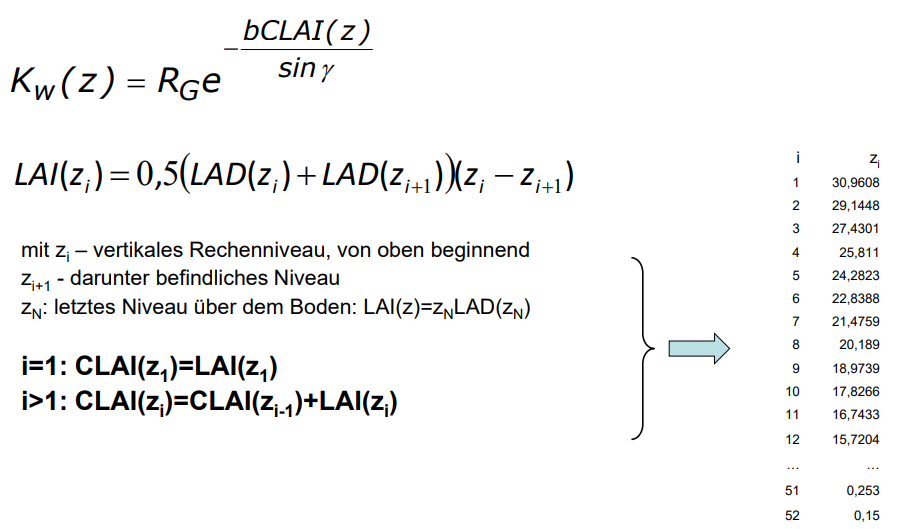
- (kumalativer) Blattflächenindex ((cumulative) leaf area index, plant area index)
\[ LAI=\frac{Gesamtoberfläche\,der\,Blätt\,(Vegetationselemente)}{Grundfläche^*} \bigg[\frac{m^2}{m^2}\bigg] \]
\[ LAI=\int_0^{h_v}LAD(z'){\rm d}z' \]
\[ CLAI=\frac{Gesamtoberfläche\,der\,Blätt\,einer\,Teilschicht}{Grundfläche^*} \bigg[\frac{m^2}{m^2}\bigg] \]
\[ CLAI(z)=\int_z^{h_v}LAD(z'){\rm d}z' \]
- Albedo
- Formwiderstand (form drag)
\[ c_d=\frac{\tau_0}{\rho \int_0^{h_v} u(z)^2 LAD(z){\rm d}z} \]
\(\tau_0\): Schubspannung am Oberrand der Vegetation, \(u(z)\): horizontale WIndgeschwindigkeit
Bild aus Skript(Goldberg 2021a)
1.6.2 Merkmale des Klimas von Vegetationsräumen
1.6.2.1 Strahlung
- Kurzwellige Absorption
Beersches Gesetz:
\[ K_{w,0}=R_G\,e^{-\frac{b\,LAI}{{\rm sin}\gamma}} \]
\(K_{w,0}\): kurzwellige Einstrahlung am Erdboden im Bestand, \(R_G\): Globalstrahlung über dem Bestand, \(b\): Extinktionskoeffizient (b=0.5) für zufällige Blattverteilung, \(LAI\): Blattflächenindex, \(\gamma\): Sonnenwinkel.
bzw.
\[ K_{w}(z)=R_G\,e^{-\frac{b\,CLAI(z)}{{\rm sin}\gamma}} \]
zeitliche Dynamik
Großenverteilung
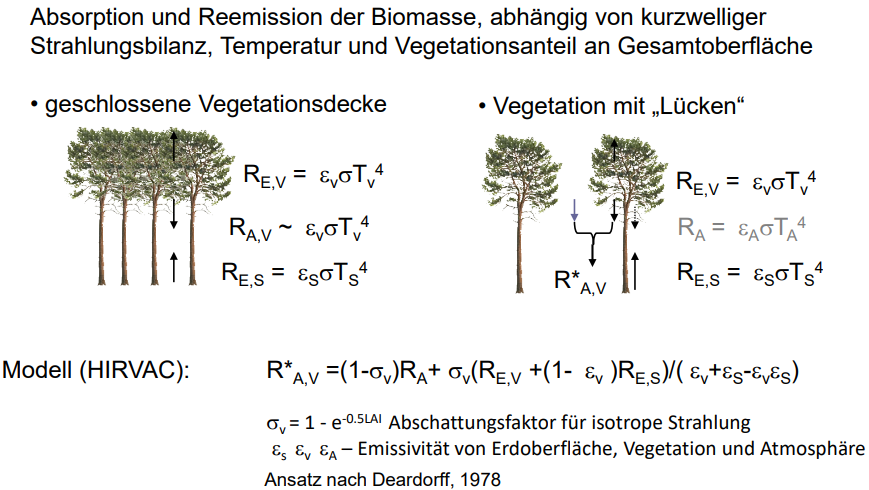
- langwellige Strahlung
Absorption und Reemission der biomasse, abhängig von kurzwelliger Strahlungsbilanz, Temperatur und Vegetaionsanteil an Gesamtoberfläche.
Hirvac:
\[ R_{A,V}^*=(1-\sigma_V)R_A+\frac{\sigma_V(R_{E,V}+(1-\epsilon_V)R_{E,V})}{\epsilon_V+\epsilon_S-\epsilon_V \epsilon_S} \]
\(\sigma_V=1-e^{0.5LAI}\) Abschttungsfaktor für isotrope Strahlung, \(\epsilon_S\), \(\epsilon_V\), \(\epsilon_A\): Emissivität von Erdoberfläche, Vegetation und Atmosphäre.
- Strahlungbilanz
Kombination des Vegetationseinflusses auf kurzwellige und langwellige Bilanz, dominiert von kurzwelliger Absorption
häufig Anwendung des Beerschen Extinktionsansatzes für die strahlungsbilanz
Ansatz nach Impens und Lemeur, 1969:
am Erdboden:
\[ R_{N,0}=R_{N,h}\,e^{-0.622\,LAI+0.055\,LAI^2} \]
im Niveau z
\[ R_{N}(z)=R_{N,h}\,e^{-0.622\,CLAI(z)+0.055\,CLAI(z)^2} \]
über der Vegetation:
\[ R_{N,h}=-R_{E,V}+R_A+(1-a_V)R_G \]
1.6.2.2 Temperatur
Temperaturregime im Vegetationsraum ist eng gekoppelt mit Strahlungsregime:
Absorption am Tage \(\rightarrow\) Temperaturmaximum im Kronenraum
nächtliche Differenzen gring
1.6.2.3 Feuchte
Feuchteregime des Vegetationsraumes abhängig von Unterlage (Evaporation) und Aktivität der Biomasse (Transpiration)
1.6.2.4 Wind
Windregime des Vegetationsraumes abhängig von der Vegetationsverteilung
Exponentialansatz:
\[ v_h(z)=v_H\,e^{a(z/H-1)} \]
\(a\): Extinktionskoeffizient, \(v_h(z)\): Windgeschwindigkeit in der Höhe z, \(v_H\): Windgeschwindigkeit in Bestandeshöhe.
für \(z H\):
\[ v_h(z)=\frac{v_*}{K}{\rm ln}\frac{z-d}{z_0}\qquad d=\frac{2}{3}H\qquad z_0=0.1H \]
\[ v_i=v_j(\frac{z_i}{z_j})^c\qquad v_j=v_i(\frac{z_j}{z_i})^c \]
??was ist i und j
Rauigkeitsparameter (Exponent) im Potenzwindgesetz (aus Häckel, Meteorologie, 1993)
1.6.2.5 Turbulente Wärmeströme
\[ H=-\rho c_PK_H\frac{{\rm d}\Theta}{{\rm d}z} \]
\[ LE=-\rho LK_E\frac{{\rm d}q}{{\rm d}z} \]
1.7 Übung
1.7.1 Strahlungbilanz
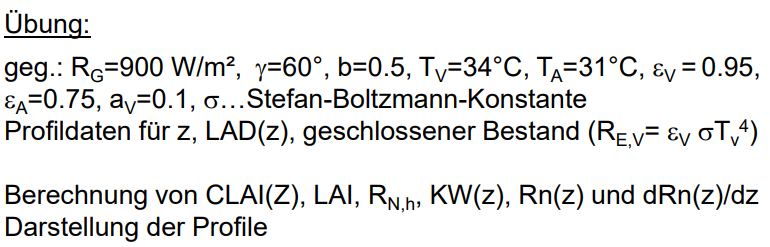
LAD1 <- read.table("F:\\OneDrive\\Kurse\\Boden_Pflanze_Atmos\\LAD1.dat", skip = 1)
LAD2 <- read.table("F:\\OneDrive\\Kurse\\Boden_Pflanze_Atmos\\LAD2.dat", skip = 1)
R_G = 900 # W/m2
gamma_ = 60 # deg
b_ = 0.5
T_V = 34 # Cel
T_A = 31 # Cel
epsilon_V = 0.95
epsilon_A = 0.75
a_V = 0.1
LAI_LAD <- function(LAD_, z_){
LAD_i1 <- c(LAD_[-1], 0)
z_i1 <- c(z_[-1], 0)
LAI_ <- 0.5 * (LAD_ + LAD_i1) * (z_ - z_i1)
return(LAI_)
}
dx_dz <- function(x_, z_){
x_i1 <- c(x_[-1], 0)
z_i1 <- c(z_[-1], 0)
dx_dz <- (x_i1 - x_) / (z_i1 - z_)
return(dx_dz)
}
CLAI_LAI <- function(LAI_) cumsum(LAI_)
R_epsilon_T <- function(epsilon_, T_Cel){
R_ <- 5.67e-8 * (T_Cel + 273.15)^4 * epsilon_ ##sigma_ [J/m2K4s] [W/m2K4]
return(R_)
}
RN_CLAI_RNh <- function(R_Nh, CLAI_){
R_N <- R_Nh * exp(-0.622 * CLAI_ + 0.055 * CLAI_ * CLAI_)
}
KW_RG_CLAI <- function(R_G, CLAI_, b_, gamma_){
K_W <- R_G * exp(-b_ * CLAI_ / sin(gamma_))
}
LAI1 <- LAI_LAD(LAD1[,2], LAD1[,1])
LAI2 <- LAI_LAD(LAD2[,2], LAD2[,1])
CLAI1 <- CLAI_LAI(LAI1)
CLAI2 <- CLAI_LAI(LAI2)
R_A <- R_epsilon_T(epsilon_A, T_A)
R_EV <- R_epsilon_T(epsilon_V, T_V)
R_Nh <- -R_EV + R_A + (1 - a_V) * R_G
R_N1 <- RN_CLAI_RNh(R_Nh, CLAI1)
K_W1 <- KW_RG_CLAI(R_G, CLAI1, b_, gamma_)
dCLAI_dz1 <- dx_dz(CLAI1, LAD1[,1])
dRN_dz1 <- R_N1 * (-0.622 + 0.11 * CLAI1) * dCLAI_dz1