3 Markov Chain Monte Carlo
3.0.1 What does Monte Carlo mean?
Monte Carlo sampling is a stochastic method used to generate independent samples (realizations) from a known probability distribution.
3.0.2 Why would we use Monte Carlo?
- Approximate a probability distribution
- Approximate the moments of distributions
- Approximate moments of functions of random variables (derived quantities)
3.0.3 Monte Carlo in action
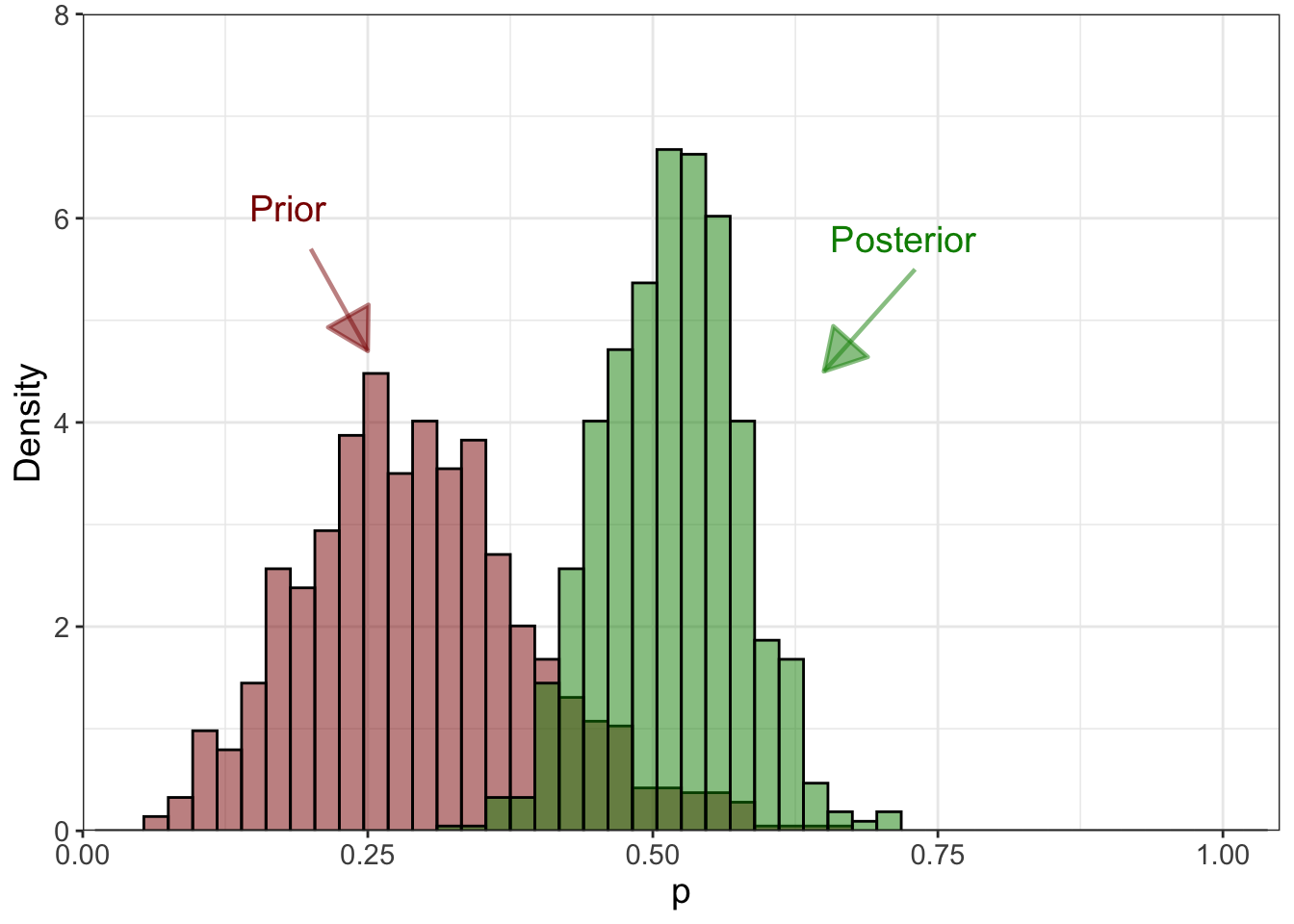
We have a field planted with corn that might be affected by a disease. We want to infer the probability of finding a diseased plant.
- Response y: diseased (1) or health (0)
- We sample 50 plants; 30 diseased
- y = 30
- Assume that:
- the location of the plants is independent of each other
- the probability of a plant being diseased is constant
- Then we say \(y \sim binomial(n=50,p)\)
- We don’t know what p is
- Give p a distribution, called prior
- We know, before taking the samples, \(E[p]=0.3\), and \(\sigma=0.1\)
- Likelihood: \[y \sim binomial(n=50, p),\]
- Prior: \[p \sim beta(\alpha=6,\beta=14)\]
- Posterior: \[[p|y] \propto binomial \boldsymbol{\cdot} beta\]
- Posterior is: \[[p|y] \sim beta \left(y + \alpha,~ n - y + \beta \right)\]
- Conjugate distributions: beta-binomial model.
3.0.4 Why do we need MCMC in Bayesian inference and not only Monte Carlo?
Sophisticated models.
The MCMC algorithms are used in Bayesian inference to find the marginal posterior distributions of the model parameters while avoiding formal integration.
3.0.5 What does Markov Chain Monte Carlo mean?
The MCMC is also a stochastic sampling method like MC, but it is Markov because now we obtain dependent samples instead of independent ones.
3.0.6 MCMC-based sampling techniques
A general form of MCMC is called Metropolis-Hasting.
-> Proposal distribution
Random walk sampler
Hamiltonian Monte Carlo
Gibbs sampler
MCMC: Rejection sampling (accept-reject sampling) and Gibbs sampling
3.0.7 Commonly used and open Bayesian software programs
JAGS: can run cross-platform and can run from R via rjags
Stan: Bayesian inference engine using Hamiltonian Monte Carlo. It can be run from R, Python, Julia, MATLAB and Stata
NIMBLE: includes sequential Monte Carlo as well as MCMC. R package using JAGS-model language to develop a model