2 Linear regression

2.1 Introduction to linear models

  • What is a model?

  • What is a linear model?

    • Most widely used model in science, engineering, and statistics.

    • Scalar form: \(y_i=\beta_{0}+\beta_{1}x_{i}+\varepsilon_i\)

    • Which part of the model is the mathematical model.

    • Which part of the model makes the linear model a “statistical” model.

    • Visual

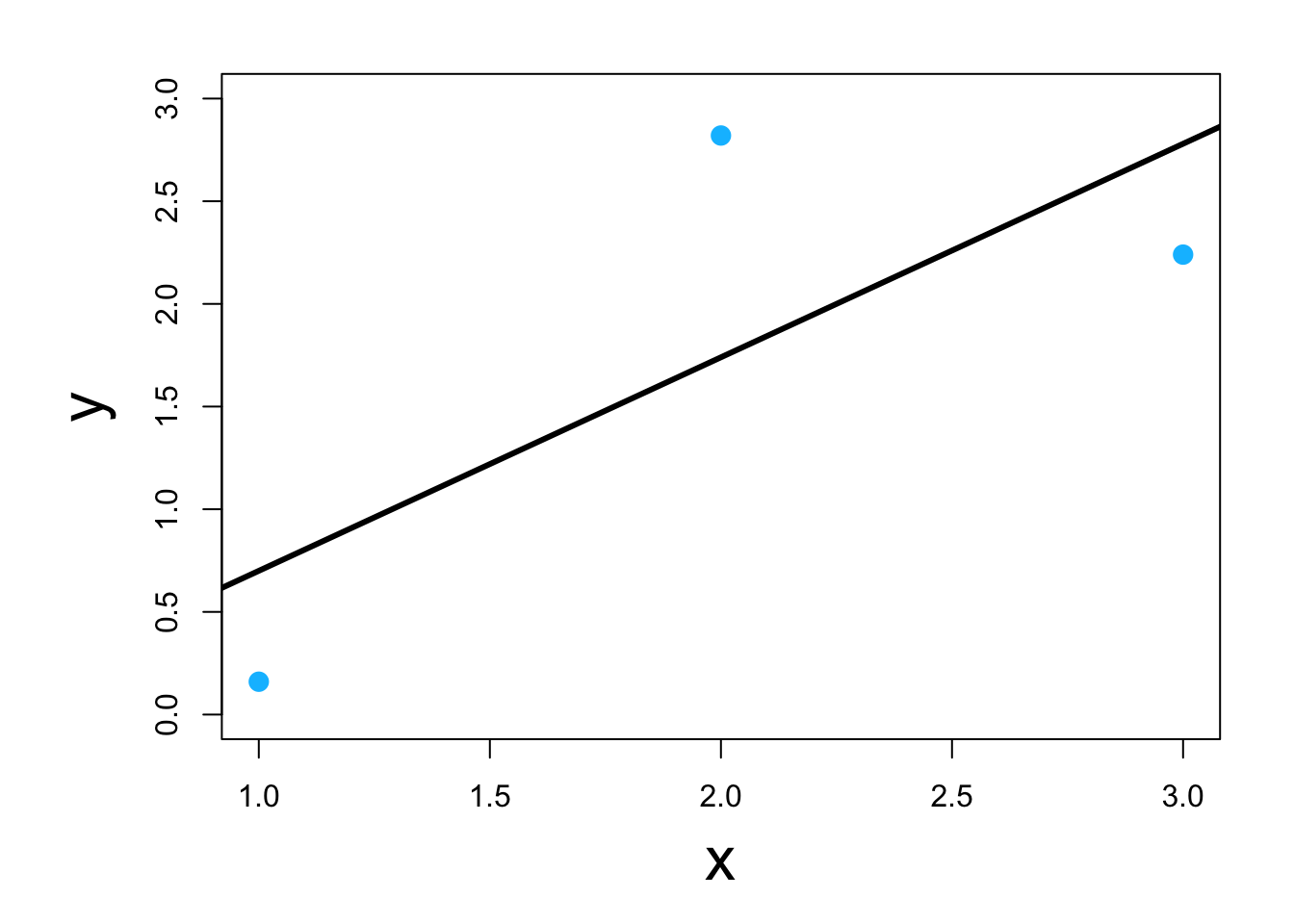
2.2 Estimation and inference

  • Three options to estimate \(\beta_0\) and \(\beta_1\)
    • Minimize a loss function
    • Maximize a likelihood function
    • Find the posterior distribution
    • Each option requires different assumptions

2.3 Loss function approach

  • Define a measure of discrepancy between the data and the mathematical model
    • Find the values of \(\beta_0\) and \(\beta_1\) that makes \(\beta_{0}+\beta_{1}x_i\) “closest” to \(y_i\)
    • Visual
  • Real data example 
    # Preliminary steps
url <- "https://www.dropbox.com/scl/fi/nr1deg9v53wyclgsjkddm/Fig3_data.csv?rlkey=iqrmjmwhtv1xha2kviq0fjrln&dl=1"
df.all <- read.csv(url)
df.fp <- df.all[which(df.all$Scenario=="Scenario A"),]

# Plot data for field pea
plot(df.fp$Ndfa,df.fp$PartNbalance,
 xlab="Ndfa (%)",ylab="Partial N balance (kg/ha)",
 xlim=c(0,110),ylim=c(-100,200),main="Field pea")
abline(a=0,b=0,col="gold",lwd=3)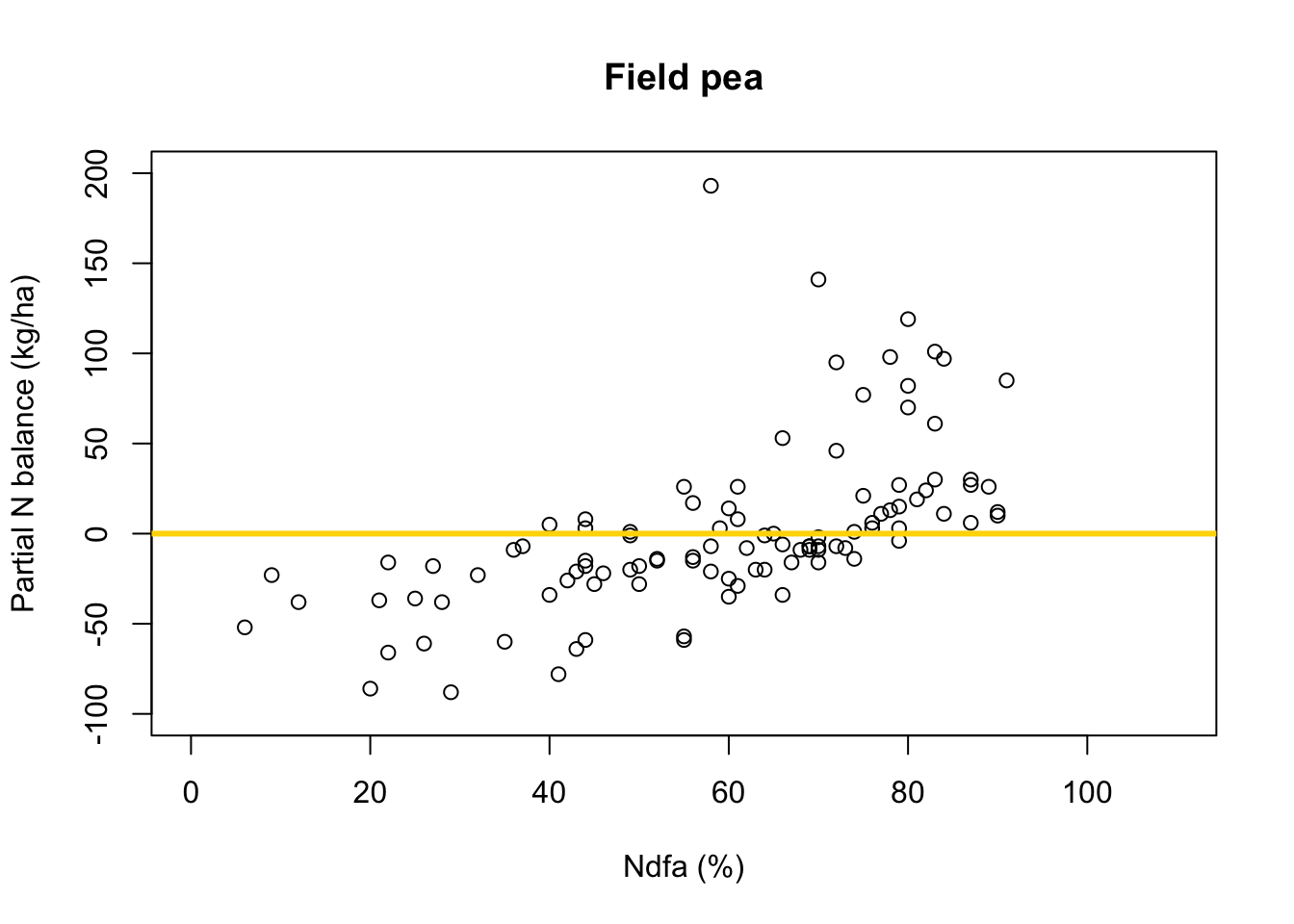
    • Fit linear model to data using least squares
    # Fit simple linear regression model using least squares
m1 <- lm(PartNbalance ~ Ndfa,data=df.fp)
    • What value of Ndfa is needed to achieve a neutral N balance?
    beta0.hat <- as.numeric(coef(m1)[1])
beta1.hat <- as.numeric(coef(m1)[2])
theta.hat <- -beta0.hat/beta1.hat
theta.hat
    ## [1] 58.26843
    • Visual representation of \(\theta\)
    # Plot data, line of best fit and theta 
plot(df.fp$Ndfa,df.fp$PartNbalance,
 xlab="Ndfa (%)",ylab="Partial N balance (kg/ha)",
 xlim=c(0,110),ylim=c(-100,200),main="Field pea")
abline(a=0,b=0,col="gold",lwd=3)
abline(m1,col="red",lwd=3)
abline(v=58,lwd=3,lty=2,col="green")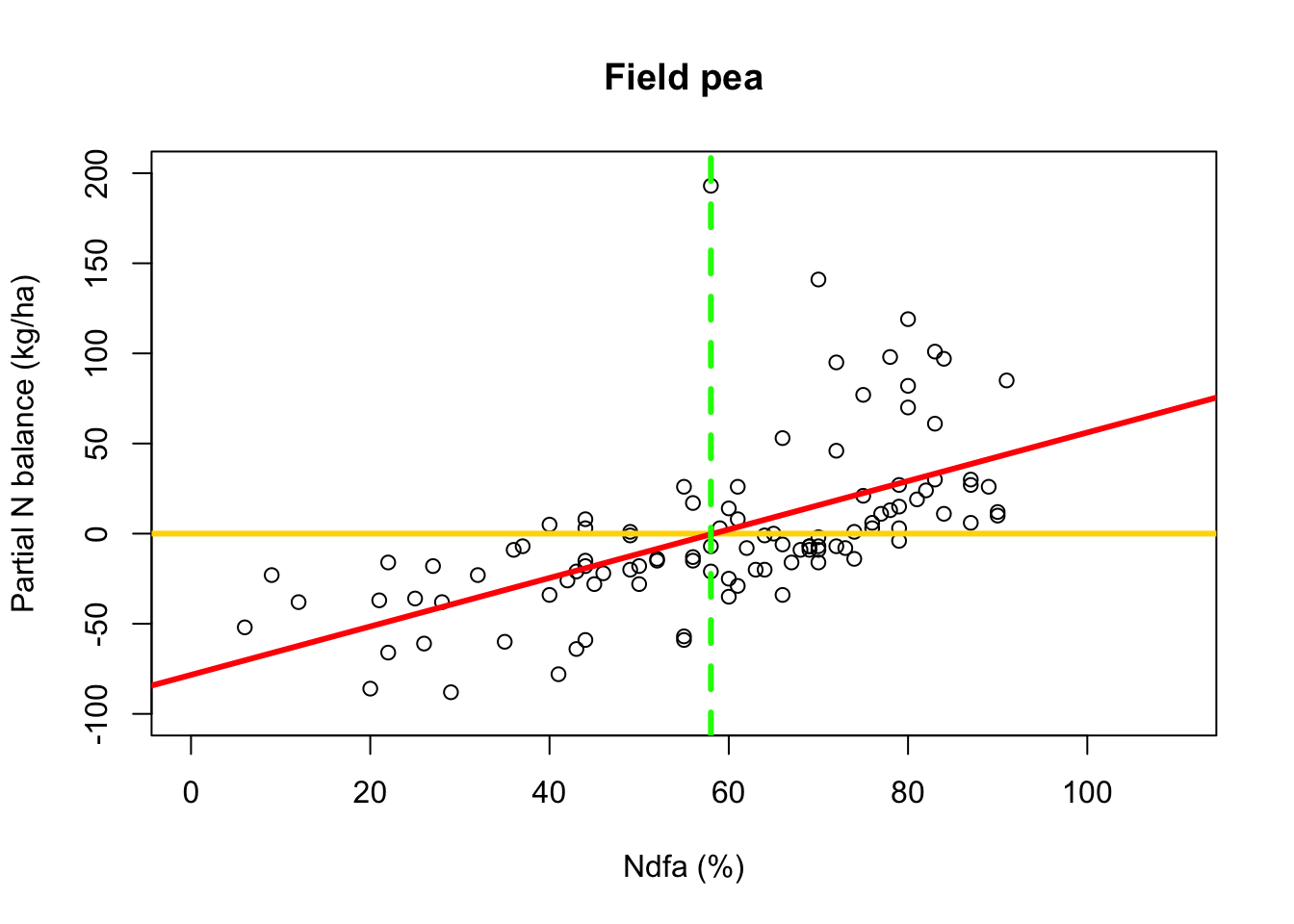

2.4 Likelihood-based approach

  • Assume that \(y_i=\beta_{0}+\beta_{1}x_{i}+\varepsilon_i\) and \(\varepsilon_i\sim \text{N}(0,\sigma^2)\)
  • Maximum likelihood estimation for the linear model
    • Visual
  • We added assumptions to our model, so what else do we get?
    • Full likelihood-based statistical inference (e.g, p-values, confidence intervals, prediction intervals, etc)
  • Real data example
    • Fit linear model to data using using maximum likelihood estimation
    library(nlme)
# Fit simple linear regression model using maximum likelihood estimation
m2 <- gls(PartNbalance ~ Ndfa,data=df.fp,method="ML")
    • What value of Ndfa is needed to achieve a neutral N balance?
    # Use maximum likelihood estimate (MLE) to obtain estimate of theta
beta0.hat <- as.numeric(coef(m2)[1])
beta1.hat <- as.numeric(coef(m2)[2])
theta.hat <- -beta0.hat/beta1.hat
theta.hat
    ## [1] 58.26843
    # Use delta method to obtain approximate approximate standard errors and
# then construct Wald-type confidence intervals
library(msm)
theta.se <- deltamethod(~-x1/x2, mean=coef(m2), cov=vcov(m2))

theta.ci <- c(theta.hat-1.96*theta.se,theta.hat+1.96*theta.se)
theta.ci
    ## [1] 52.88317 63.65370
    • Visual representation of \(\theta\)
    # Plot data, line of best fit and theta 
plot(df.fp$Ndfa,df.fp$PartNbalance,
 xlab="Ndfa (%)",ylab="Partial N balance (kg/ha)",
 xlim=c(0,110),ylim=c(-100,200),main="Field pea")
abline(a=0,b=0,col="gold",lwd=3)
abline(m1,col="red",lwd=3)
abline(v=58.3,lwd=3,lty=2,col="green") 
abline(v=52.9,lwd=1,lty=2,col="green") 
abline(v=63.7,lwd=1,lty=2,col="green")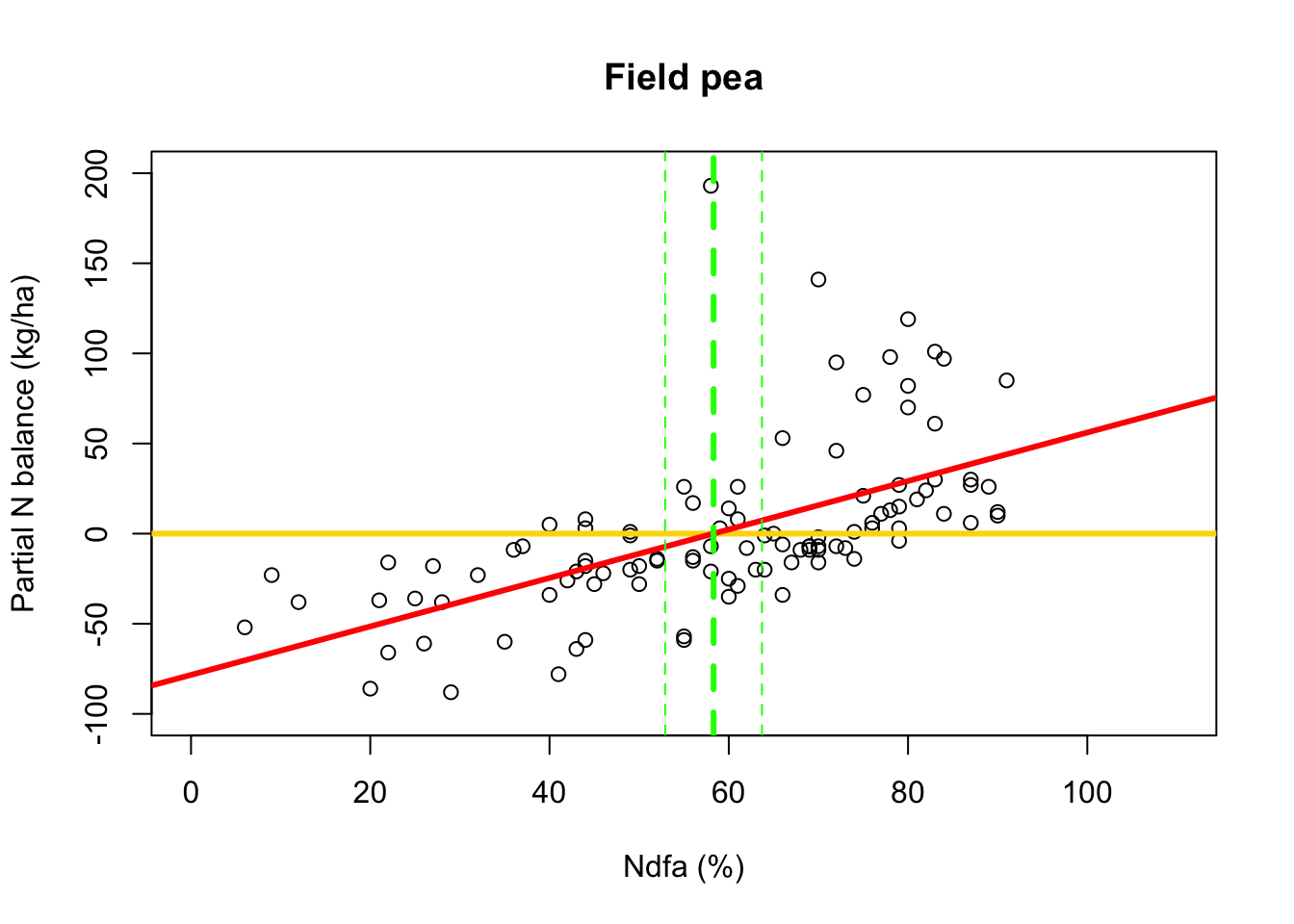

2.5 Bayesian approach

  • Assume that \(y_i=\beta_{0}+\beta_{1}x_{i}+\varepsilon_i\) with \(\varepsilon_i\sim \text{N}(0,\sigma^2)\), \(\beta_{0}\sim \text{N}(0,10^6)\) and \(\beta_{1}\sim \text{N}(0,10^6)\)

  • Statistical inference

    • Using Bayes rule (Bayes 1763) we can obtain the joint posterior distribution \[[\beta_0,\beta_1,\sigma_{\varepsilon}^{2}|\mathbf{y}]=\frac{[\mathbf{y}|\beta_0,\beta_1,\sigma_{\varepsilon}^{2}][\beta_0][\beta_1][\sigma_{\varepsilon}^{2}]}{\int\int\int [\mathbf{y}|\beta_0,\beta_1,\sigma_{\varepsilon}^{2}][\beta_0][\beta_1][\sigma_{\varepsilon}^{2}]d\beta_0d\beta_1,d\sigma_{\varepsilon}^{2}}\]
      • Statistical inference about a paramters is obtained from the marginal posterior distributions \[[\beta_0|\mathbf{y}]=\int[\beta_0,\beta_1,\sigma_{\varepsilon}^{2}|\mathbf{y}]d\beta_1d\sigma_{\varepsilon}^{2}\] \[[\beta_1|\mathbf{y}]=\int[\beta_0,\beta_1,\sigma_{\varepsilon}^{2}|\mathbf{y}]d\beta_0d\sigma_{\varepsilon}^{2}\] \[[\sigma_{\varepsilon}^{2}|\mathbf{y}]=\int[\beta_0,\beta_1,\sigma_{\varepsilon}^{2}|\mathbf{y}]d\beta_0d\beta_1\]
      • Derived quantities can be obtained by transformations of the joint posterior

  • Computations

    norm.reg.mcmc <- function(y,X,beta.mn,beta.var,s2.mn,s2.sd,n.mcmc){

  #
  #  Code Box 11.1
  #

  ###
  ### Subroutines 
  ###

  library(mvtnorm)

  invgammastrt <- function(igmn,igvar){
q <- 2+(igmn^2)/igvar
r <- 1/(igmn*(q-1))
list(r=r,q=q)
  }

  invgammamnvr <- function(r,q){  #  This fcn is not necessary
mn <- 1/(r*(q-1))
vr <- 1/((r^2)*((q-1)^2)*(q-2))
list(mn=mn,vr=vr)
  }

  ###
  ### Hyperpriors
  ###

  n=dim(X)[1]
  p=dim(X)[2]
  r=invgammastrt(s2.mn,s2.sd^2)$r
  q=invgammastrt(s2.mn,s2.sd^2)$q
  Sig.beta.inv=diag(p)/beta.var

  beta.save=matrix(0,p,n.mcmc)
  s2.save=rep(0,n.mcmc)
  Dbar.save=rep(0,n.mcmc)
  y.pred.mn=rep(0,n)

  ###
  ### Starting Values
  ###

  beta=solve(t(X)%*%X)%*%t(X)%*%y

  ###
  ### MCMC Loop
  ###

  for(k in 1:n.mcmc){


###
### Sample s2
###

tmp.r=(1/r+.5*t(y-X%*%beta)%*%(y-X%*%beta))^(-1)
tmp.q=n/2+q

s2=1/rgamma(1,tmp.q,,tmp.r) 

###
### Sample beta
###

tmp.var=solve(t(X)%*%X/s2 + Sig.beta.inv)
tmp.mn=tmp.var%*%(t(X)%*%y/s2 + Sig.beta.inv%*%beta.mn)

beta=as.vector(rmvnorm(1,tmp.mn,tmp.var,method="chol"))

###
### Save Samples
###

beta.save[,k]=beta
s2.save[k]=s2

  }

  ###
  ###  Write Output
  ###

  list(beta.save=beta.save,s2.save=s2.save,y=y,X=X,n.mcmc=n.mcmc,n=n,r=r,q=q,p=p)

}

  • Model fitting

    • MCMC
    samples <- norm.reg.mcmc(y = df.fp$PartNbalance,X = model.matrix(~ Ndfa,data=df.fp),
                      beta.mn = c(0,0),beta.var=c(10^6,10^6),
                      s2.mn = 10, s2.sd = 10^6,
                      n.mcmc = 5000)

burn.in <- 1000
# Look a histograms of posterior distributions
par(mfrow=c(2,1),mar=c(5,6,1,1))
hist(samples$beta.save[1,-c(1:1000)],xlab=expression(beta[0]*"|"*bold(y)),ylab=expression("["*beta[0]*"|"*bold(y)*"]"),freq=FALSE,col="grey",main="",breaks=30)
hist(samples$beta.save[2,-c(1:1000)],xlab=expression(beta[1]*"|"*bold(y)),ylab=expression("["*beta[1]*"|"*bold(y)*"]"),freq=FALSE,col="grey",main="",breaks=30)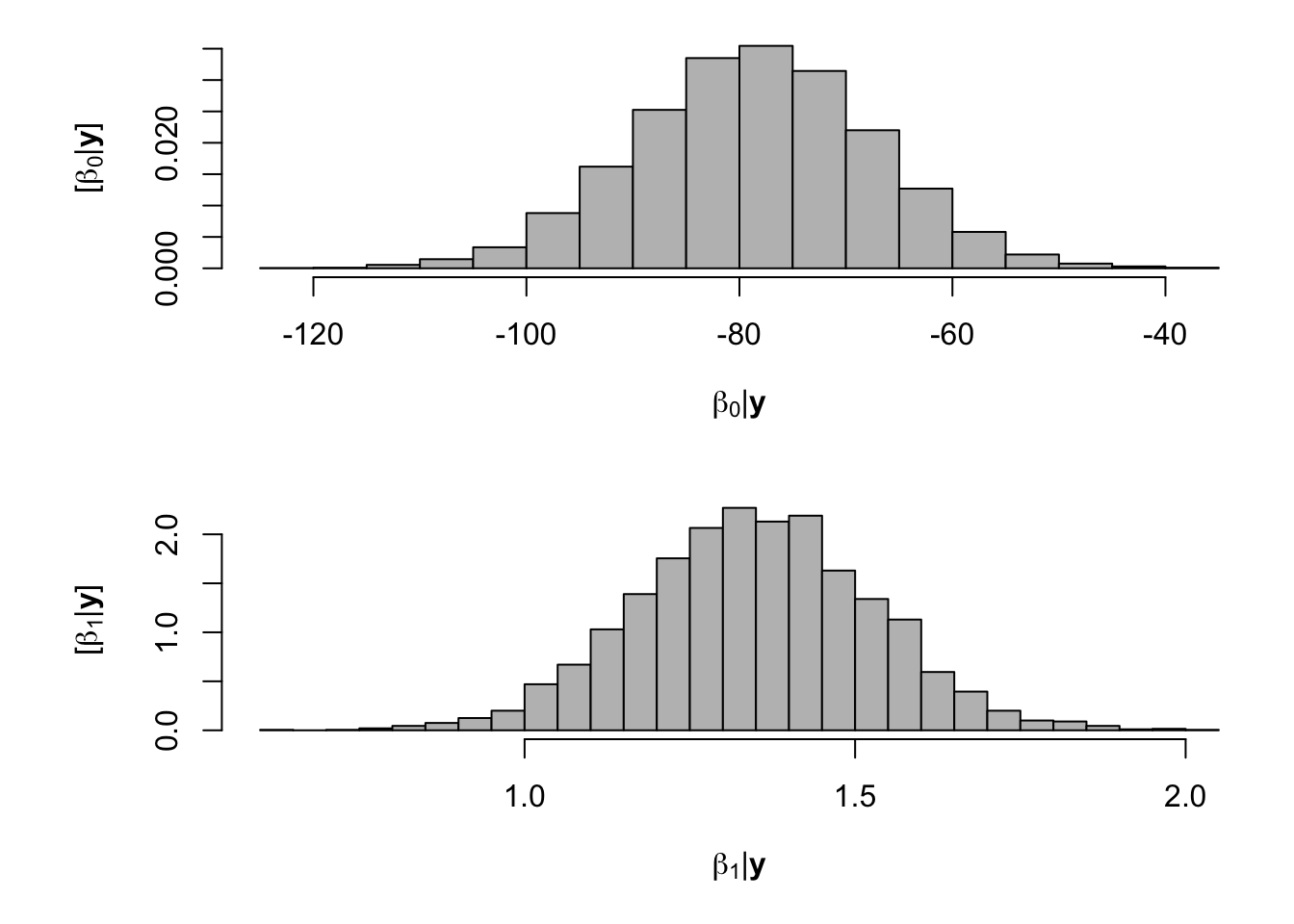

  • What value of Ndfa is needed to achieve a neutral N balance?

    hist(-samples$beta.save[1,-c(1:1000)]/samples$beta.save[2,-c(1:1000)],xlab=expression(theta*"|"*bold(y)),ylab=expression("["*theta*"|"*bold(y)*"]"),freq=FALSE,col="grey",main="",breaks=30)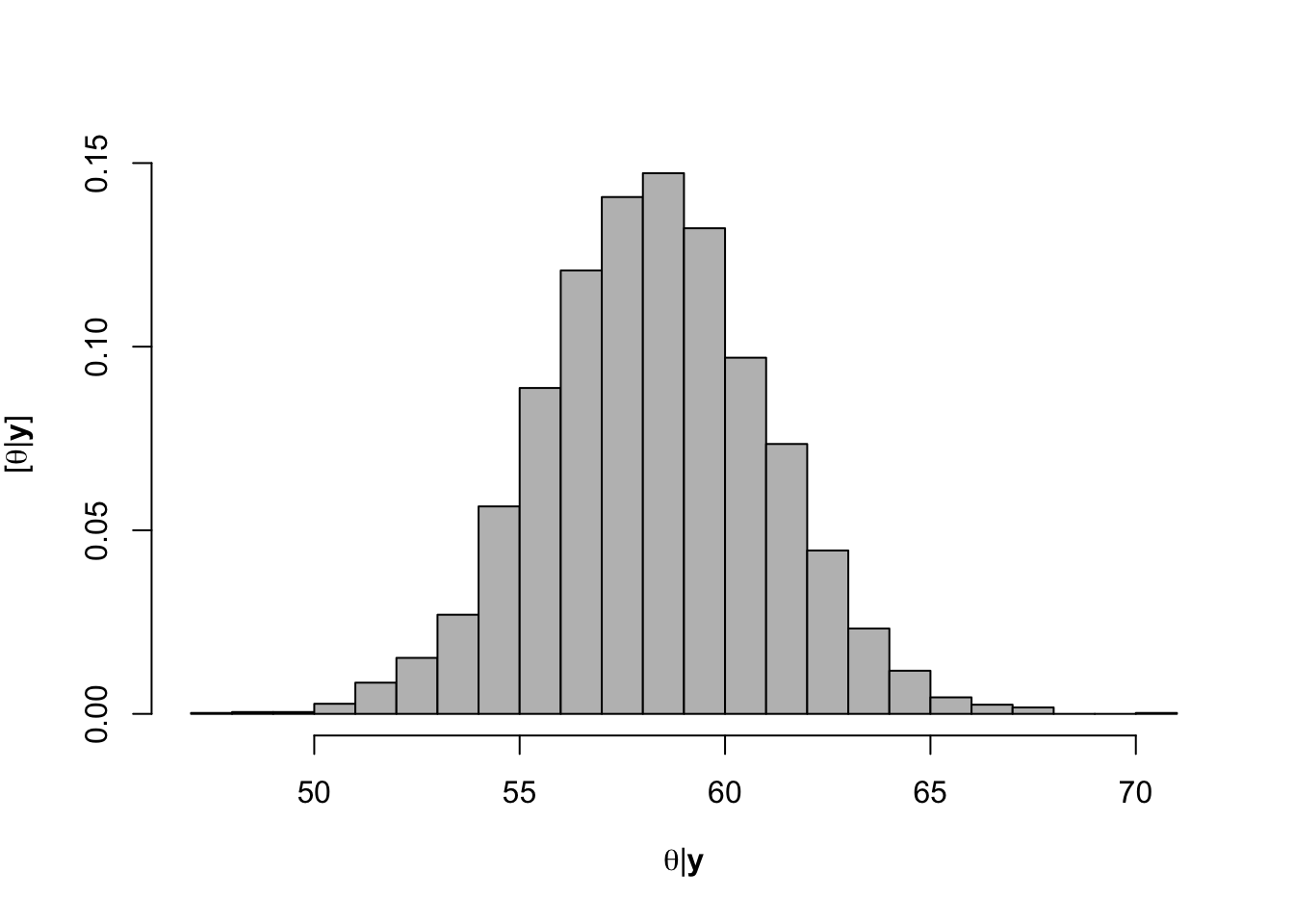

    # Expected value (mean) of theta        
mean(-samples$beta.save[1,]/samples$beta.save[2,])
    ## [1] 58.25853
    # 95% credible intervals for theta
quantile(-samples$beta.save[1,]/samples$beta.save[2,],prob=c(0.025,0.975))
    ##     2.5%    97.5% 
## 52.74394 63.73624
    • Visual representation of posterior distribuiton of theta \(\theta\)
    # Plot data and theta 
plot(df.fp$Ndfa,df.fp$PartNbalance,
 xlab="Ndfa (%)",ylab="Partial N balance (kg/ha)",
 xlim=c(0,110),ylim=c(-100,200),main="Field pea")
abline(a=0,b=0,col="gold",lwd=3)
abline(v=58.3,lwd=3,lty=2,col="green") 
abline(v=52.7,lwd=1,lty=2,col="green") 
abline(v=63.7,lwd=1,lty=2,col="green") 
rug(-samples$beta.save[1,]/samples$beta.save[2,],col=gray(0.5,0.03))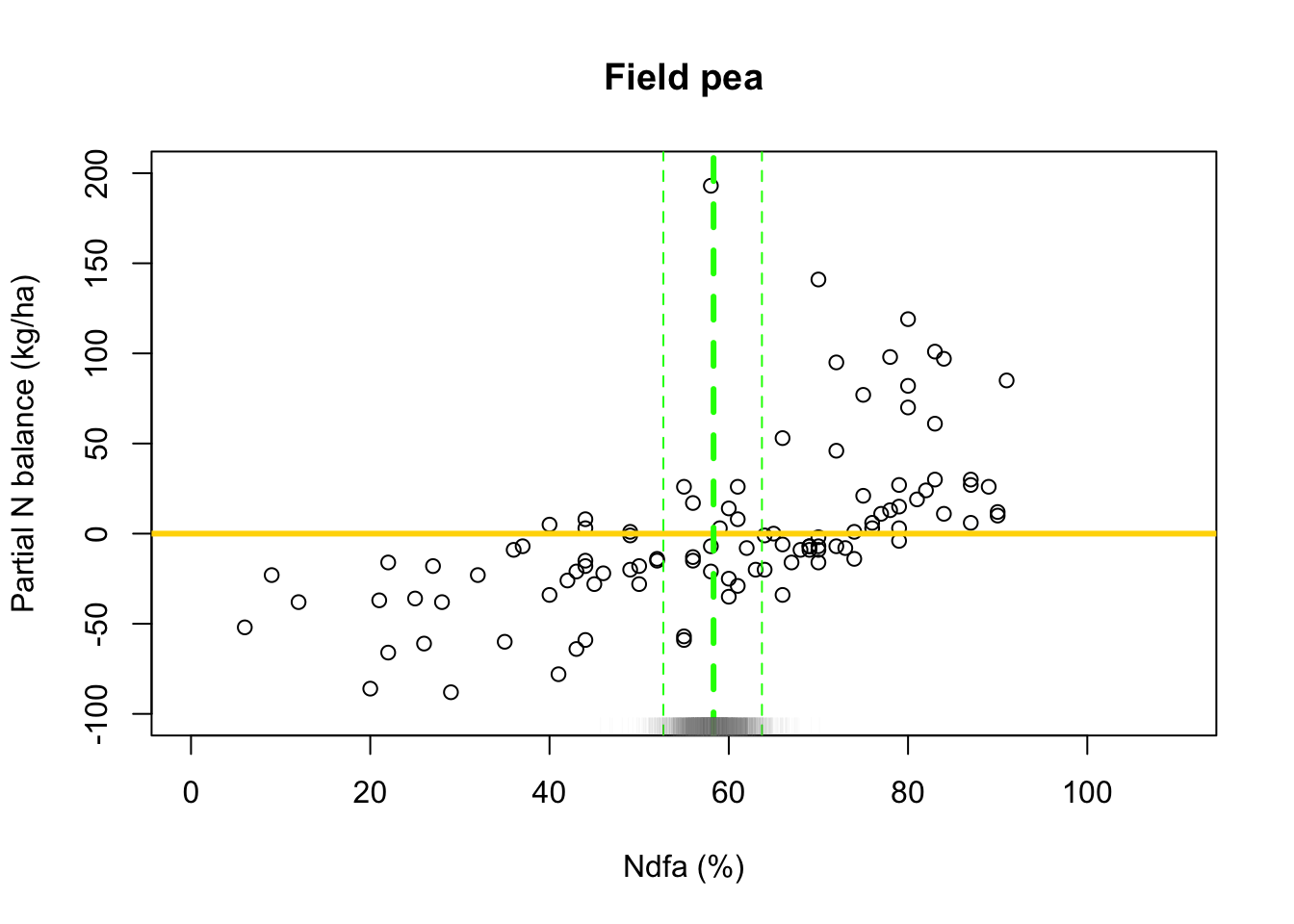

2.6 Exercise

  • What value of Ndfa is needed to achieve a neutral N balance?

    df.wl <- df.all[which(df.all$Scenario=="Scenario B"),]
plot(df.wl$Ndfa,df.wl$PartNbalance,
 xlab="Ndfa (%)",ylab="Partial N balance (kg/ha)",
 xlim=c(0,110),ylim=c(-100,200),main="White lupin")
abline(a=0,b=0,col="gold",lwd=3)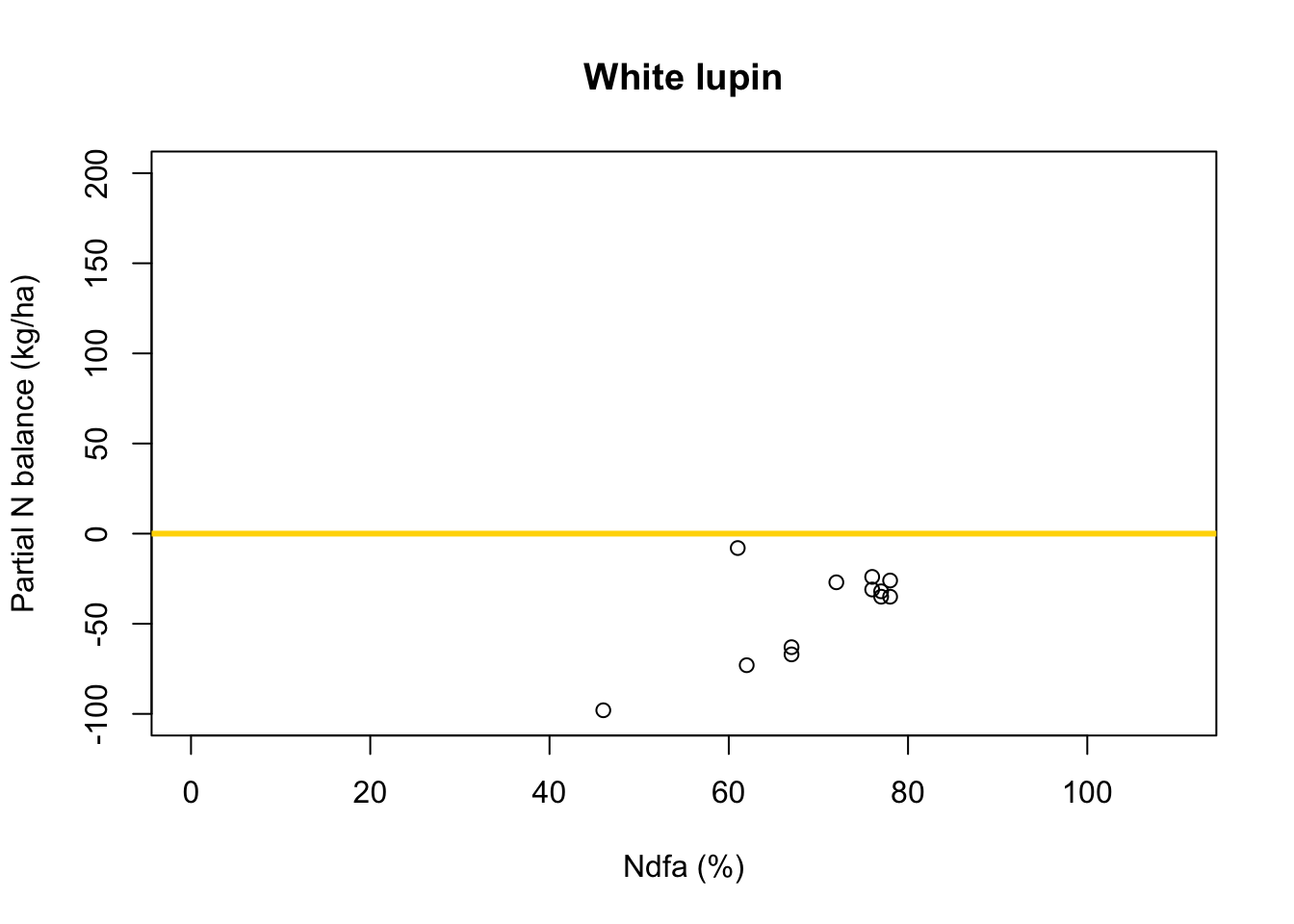

  • Using least squares

    m1 <- lm(PartNbalance ~ Ndfa,data=df.wl)
    • What value of Ndfa is needed to achieve a neutral N balance?
    beta0.hat <- as.numeric(coef(m1)[1])
beta1.hat <- as.numeric(coef(m1)[2])
theta.hat <- -beta0.hat/beta1.hat
theta.hat
    ## [1] 93.09456
    • Visual representation of \(\theta\)
    # Plot data, line of best fit and theta 
plot(df.wl$Ndfa,df.wl$PartNbalance,
 xlab="Ndfa (%)",ylab="Partial N balance (kg/ha)",
 xlim=c(0,110),ylim=c(-100,200),main="White lupin")
abline(a=0,b=0,col="gold",lwd=3)
abline(m1,col="red",lwd=3)
abline(v=93.1,lwd=3,lty=2,col="green")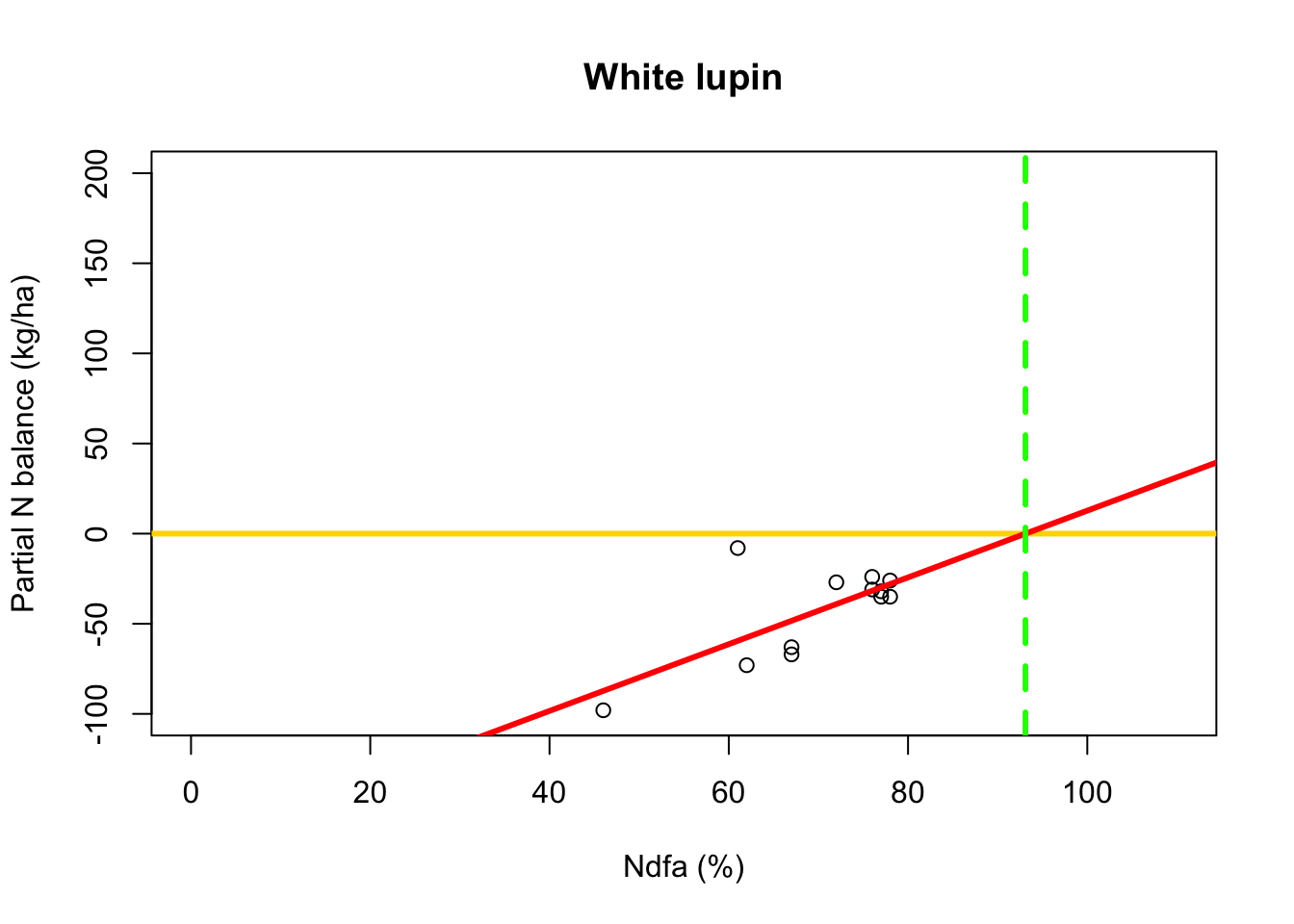

  • Using likelihood-based inference

    • Fit linear model to data using using maximum likelihood estimation
    library(nlme)
# Fit simple linear regression model using maximum likelihood estimation
m2 <- gls(PartNbalance ~ Ndfa,data=df.wl,method="ML")
    • What value of Ndfa is needed to achieve a neutral N balance?
    # Use maximum likelihood estimate (MLE) to obtain estimate of theta
beta0.hat <- as.numeric(coef(m2)[1])
beta1.hat <- as.numeric(coef(m2)[2])
theta.hat <- -beta0.hat/beta1.hat
theta.hat
    ## [1] 93.09456
    # Use delta method to obtain approximate approximate standard errors and
# then construct Wald-type confidence intervals
library(msm)
theta.se <- deltamethod(~-x1/x2, mean=coef(m2), cov=vcov(m2))

theta.ci <- c(theta.hat-1.96*theta.se,theta.hat+1.96*theta.se)
theta.ci
    ## [1]  76.91135 109.27778
    • Visual representation of \(\theta\)
    # Plot data, line of best fit and theta 
plot(df.wl$Ndfa,df.wl$PartNbalance,
 xlab="Ndfa (%)",ylab="Partial N balance (kg/ha)",
 xlim=c(0,110),ylim=c(-100,200),main="White lupin")
abline(a=0,b=0,col="gold",lwd=3)
abline(m1,col="red",lwd=3)
abline(v=93.1,lwd=3,lty=2,col="green") 
abline(v=76.9,lwd=1,lty=2,col="green") 
abline(v=109.2,lwd=1,lty=2,col="green")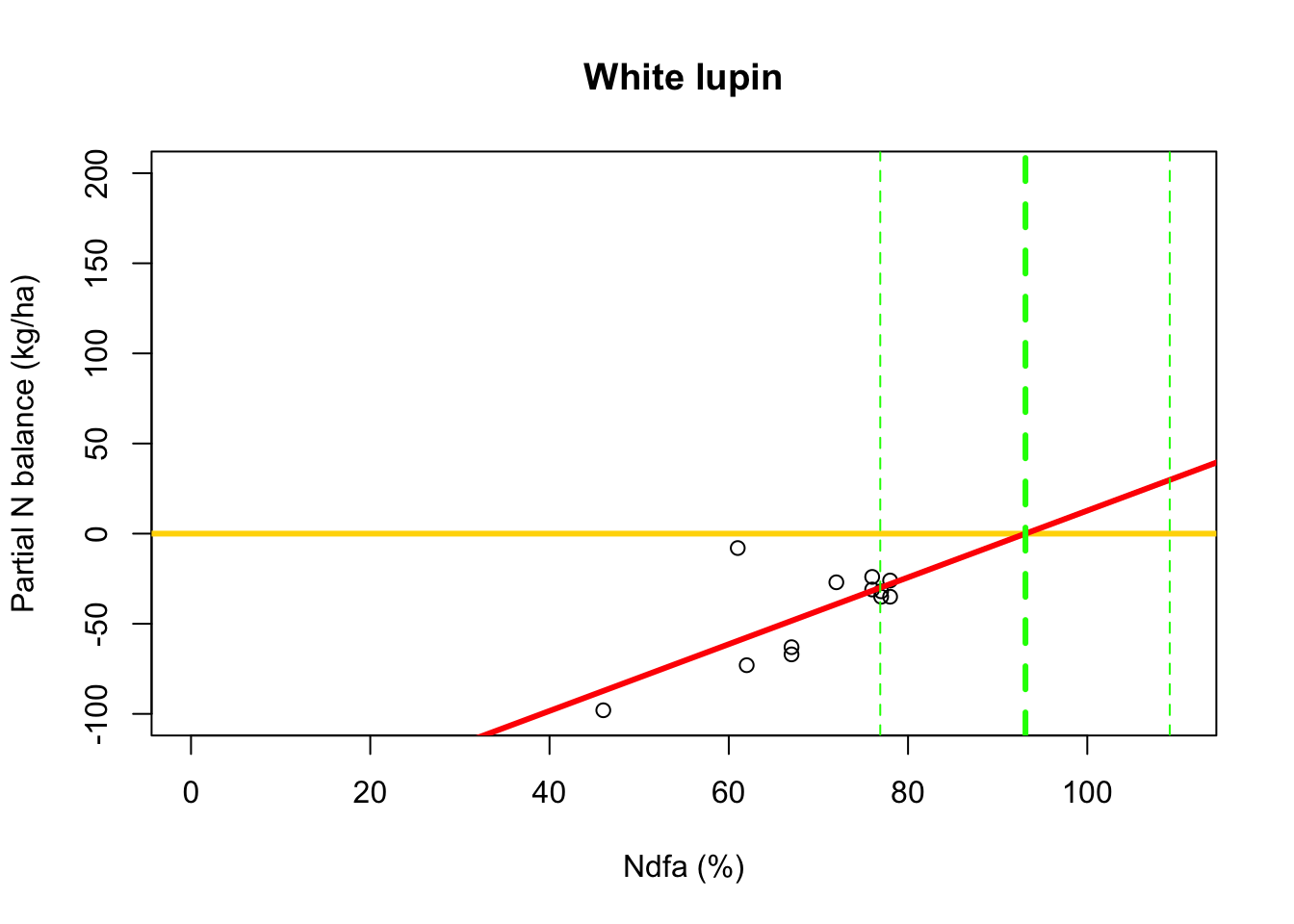

  • Using Bayesian inference

    • Assume that \(y_i=\beta_{0}+\beta_{1}x_{i}+\varepsilon_i\) with \(\varepsilon_i\sim \text{N}(0,\sigma^2)\), \(\beta_{0}\sim \text{N}(0,10^6)\) and \(\beta_{1}\sim \text{N}(2.5,0.1)\)
    • Model fitting
    samples <- norm.reg.mcmc(y = df.wl$PartNbalance,X = model.matrix(~ Ndfa,data=df.wl),
                      beta.mn = c(0,2.5),beta.var=c(10^6,0.1),
                      s2.mn = 10, s2.sd = 10^6,
                      n.mcmc = 5000)

burn.in <- 1000
# Look a histograms of posterior distributions
par(mfrow=c(2,1),mar=c(5,6,1,1))
hist(samples$beta.save[1,-c(1:1000)],xlab=expression(beta[0]*"|"*bold(y)),ylab=expression("["*beta[0]*"|"*bold(y)*"]"),freq=FALSE,col="grey",main="",breaks=30)
hist(samples$beta.save[2,-c(1:1000)],xlab=expression(beta[1]*"|"*bold(y)),ylab=expression("["*beta[1]*"|"*bold(y)*"]"),freq=FALSE,col="grey",main="",breaks=30)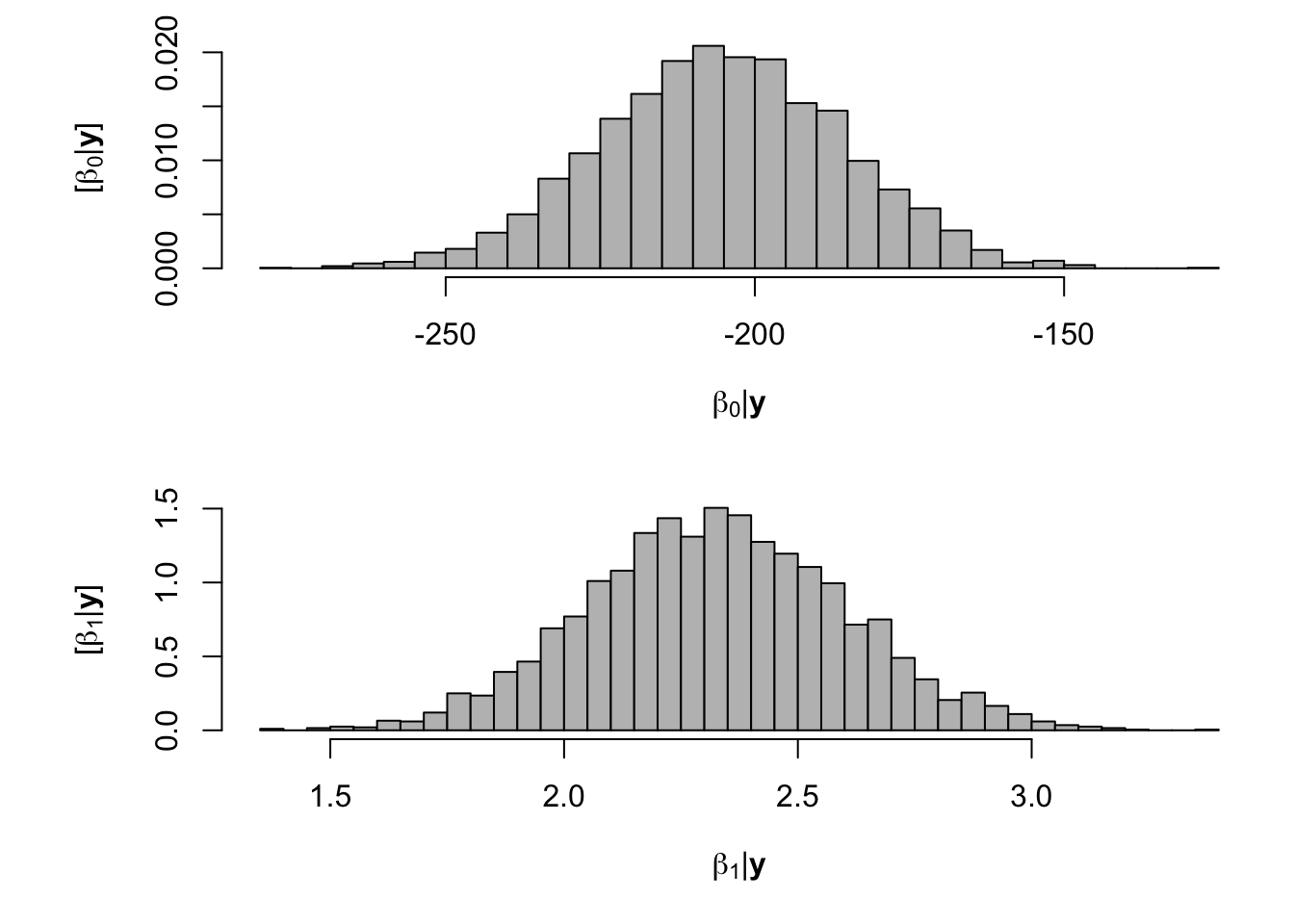

    • What value of Ndfa is needed to achieve a neutral N balance?
    hist(-samples$beta.save[1,-c(1:1000)]/samples$beta.save[2,-c(1:1000)],xlab=expression(theta*"|"*bold(y)),ylab=expression("["*theta*"|"*bold(y)*"]"),freq=FALSE,col="grey",main="",breaks=30)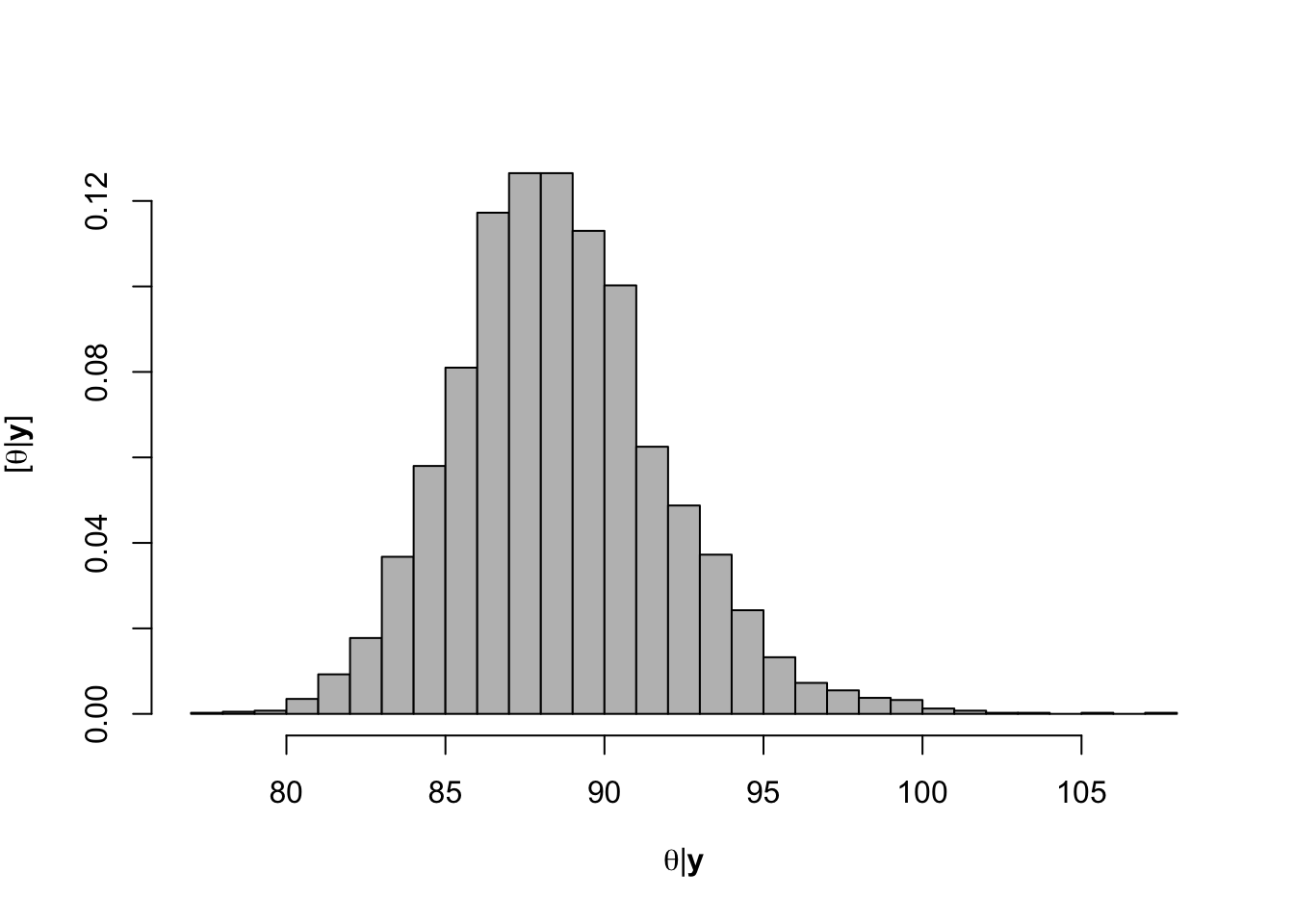

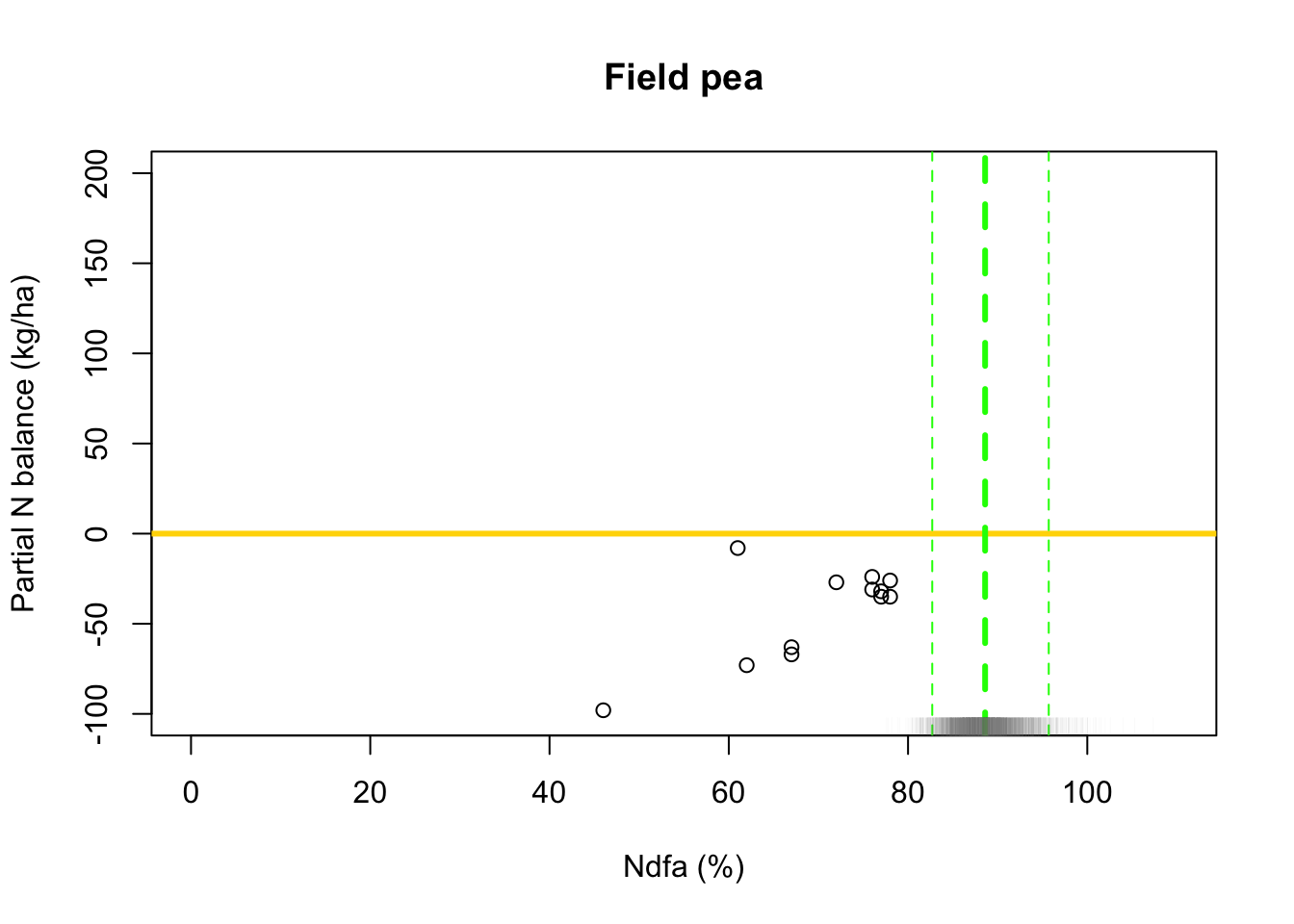
    # Expected value (mean) of theta        
mean(-samples$beta.save[1,]/samples$beta.save[2,])
    ## [1] 88.59593
    # 95% credible intervals for theta
quantile(-samples$beta.save[1,]/samples$beta.save[2,],prob=c(0.025,0.975))
    ##     2.5%    97.5% 
## 82.68149 95.74078
    # Plot data and theta 
plot(df.wl$Ndfa,df.wl$PartNbalance,
 xlab="Ndfa (%)",ylab="Partial N balance (kg/ha)",
 xlim=c(0,110),ylim=c(-100,200),main="Field pea")
abline(a=0,b=0,col="gold",lwd=3)
abline(v=88.6,lwd=3,lty=2,col="green") 
abline(v=82.7,lwd=1,lty=2,col="green") 
abline(v=95.7,lwd=1,lty=2,col="green") 
rug(-samples$beta.save[1,]/samples$beta.save[2,],col=gray(0.5,0.03))