4 Практична частина. Інфографіка
4.1 Трохи про графіку в R
4.2 Звідки несе гидоту?
Обчислення усереднених концентрацій забруднюючих речовин в повітрі в залежності від напрямків вітру - доволі простий але дуже цікавий метод. Іще цікавішим він стає коли ми не просто обчислюємо якісь числові показники, а й візуалізуємо винайдені нами залежності. Ми можемо наглядно показати — звідки вітер приносить найбільші концентрації пилу або формальдегіду. Також ми можемо збагатити наші кінцеві діаграми додатковими елементами. Наприклад — показати кількість випадків (вимірювань), які пов’язані з конкретними напрямками вітру.
У главі 3 ми підготували декілька таблиць із даними. Нас цікавлять таблиці, у яких поєднано дані моніторингу забруднення повітря та метеорологічні показники. Нам треба дослідити — чи впливає напрямок вітру на усереднені показники забруднення повітря. Здоровий глузд підказує — що такий вплив однозначно є! Ми використаємо таблицю air_pollution.join, яку отримали в процесі підготовки даних.
Давайте подивимось — чи залежать медіанні та середні значення концентрацій формальдегіду від напрямків вітру.
#Завантажуємо пакет dplyr:
library(dplyr)
#Запускаємо таблицю air_pollution.join в тунель
tbl_df(air_pollution.join) %>%
#Вибираємо потрібні нам поля напрямків вітру та концентрацій формальдегіду:
select(DD.meteo.from, CH2O) %>%
#Групуємо дані за напрямками вітру:
group_by(DD.meteo.from) %>%
#Обчислюємо медіани та середні арифметичні для кожної групи:
summarize(CH2O.mean = mean(CH2O, na.rm = TRUE),
CH2O.median = median(CH2O, na.rm = TRUE))## Warning: Factor `DD.meteo.from` contains implicit NA, consider using
## `forcats::fct_explicit_na`## # A tibble: 19 x 3
## DD.meteo.from CH2O.mean CH2O.median
## <ord> <dbl> <dbl>
## 1 N 0.0116 0.008
## 2 NNE 0.0116 0.009
## 3 NE 0.0110 0.008
## 4 ENE 0.00939 0.0075
## 5 E 0.00841 0.007
## 6 ESE 0.00758 0.007
## 7 SE 0.00752 0.005
## 8 SSE 0.00931 0.0075
## 9 S 0.00817 0.007
## 10 SSW 0.00891 0.007
## 11 SW 0.00954 0.0065
## 12 WSW 0.00714 0.005
## 13 W 0.00588 0.005
## 14 WNW 0.00678 0.006
## 15 NW 0.00692 0.005
## 16 NNW 0.00634 0.005
## 17 VRB 0.0125 0.009
## 18 CALM 0.00651 0.005
## 19 <NA> 0.00839 0.005Ми бачимо, що різниця в показниках є. Але що ми зробили неправильно? — Ми згрупували дані тільки по напрямкам вітру. У той же час у нас дані аж з 5-ти постів моніторингу і ці пости розташовані в різних частинах міста. Нам треба згрупувати дані не тільки по напрямках вітра, але й по окремих постах моніторингу.
#Запускаємо таблицю air_pollution.join в тунель
tbl_df(air_pollution.join) %>%
#Вибираємо потрібні нам поля назв постів моніторингу,
#напрямків вітру та концентрацій формальдегіду:
select(name, DD.meteo.from, CH2O) %>%
#Групуємо дані за назвами постів моніторингу та напрямками вітру:
group_by(name, DD.meteo.from) %>%
#Обчислюємо медіани та середні арифметичні для кожної групи:
summarize(CH2O.mean = mean(CH2O, na.rm = TRUE),
CH2O.median = median(CH2O, na.rm = TRUE))## Warning: Factor `DD.meteo.from` contains implicit NA, consider using
## `forcats::fct_explicit_na`## # A tibble: 95 x 4
## # Groups: name [5]
## name DD.meteo.from CH2O.mean CH2O.median
## <fct> <ord> <dbl> <dbl>
## 1 ПСЗ-1 N 0.0104 0.0065
## 2 ПСЗ-1 NNE 0.00930 0.009
## 3 ПСЗ-1 NE 0.0118 0.008
## 4 ПСЗ-1 ENE 0.00759 0.006
## 5 ПСЗ-1 E 0.009 0.0085
## 6 ПСЗ-1 ESE 0.00692 0.0055
## 7 ПСЗ-1 SE 0.0067 0.004
## 8 ПСЗ-1 SSE 0.00842 0.0105
## 9 ПСЗ-1 S 0.00744 0.006
## 10 ПСЗ-1 SSW 0.00721 0.007
## # … with 85 more rowsНезручно користуватись такими великими таблицями? Навіть якщо ми переставимо групування місцями (спочатку напрямки вітру, а потім назви постів моніторингу) — все-одно таблиця буде дуже незручною для швидкого ознайомлення з даними. Щоб наочно відобразити закономірності ми використаємо візуалізацію. Оскільки нам треба відобразити залежність числових (концентрації формальдегіду) та категоріальних (напрямки вітру) величин — ми використаємо так звані «Діаграми Тьюкі». Цей різновид графіків відомий також під назвами «Ящики з вусами» та «Боксплоти». Остання назва — англомовна назва цих діаграм у більшості засобів візуалізації даних.
Нам треба побудувати діаграму Тьюкі на якій будуть відображатись варіації концентрацій формальдегіду в залежності від напрямків вітру. Також нам не слід забувати те, що таблиця містить дані одразу з 5-ти постів моніторингу повітря. При візуалізації нам треба відокремити всі пості. Для побудови діаграм ми використаємо функцію geom_boxplot пакету ggplot2.
#Завантажуємо пакет ggplot2:
library(ggplot2)
#Запускаємо таблицю air_pollution.join в тунель
tbl_df(air_pollution.join) %>%
#Вибираємо потрібні нам поля назв постів моніторингу,
#напрямків вітру та концентрацій формальдегіду:
select(name, DD.meteo.from, CH2O) %>%
#Вибираємо тільки не порожні значення напрямків вітру:
filter(! is.na(DD.meteo.from)) %>%
#Будуємо діаграму
ggplot(aes(y = CH2O, x = DD.meteo.from, fill = name)) +
geom_boxplot() +
stat_summary(fun.y = median, geom = "line", aes(group = 2),
colour = "red", size = 1) +
#Розбиваємо діаграму на частини для окремих постів моніторингу:
facet_grid(.~name)## Warning: Removed 1693 rows containing non-finite values (stat_boxplot).## Warning: Removed 1693 rows containing non-finite values (stat_summary).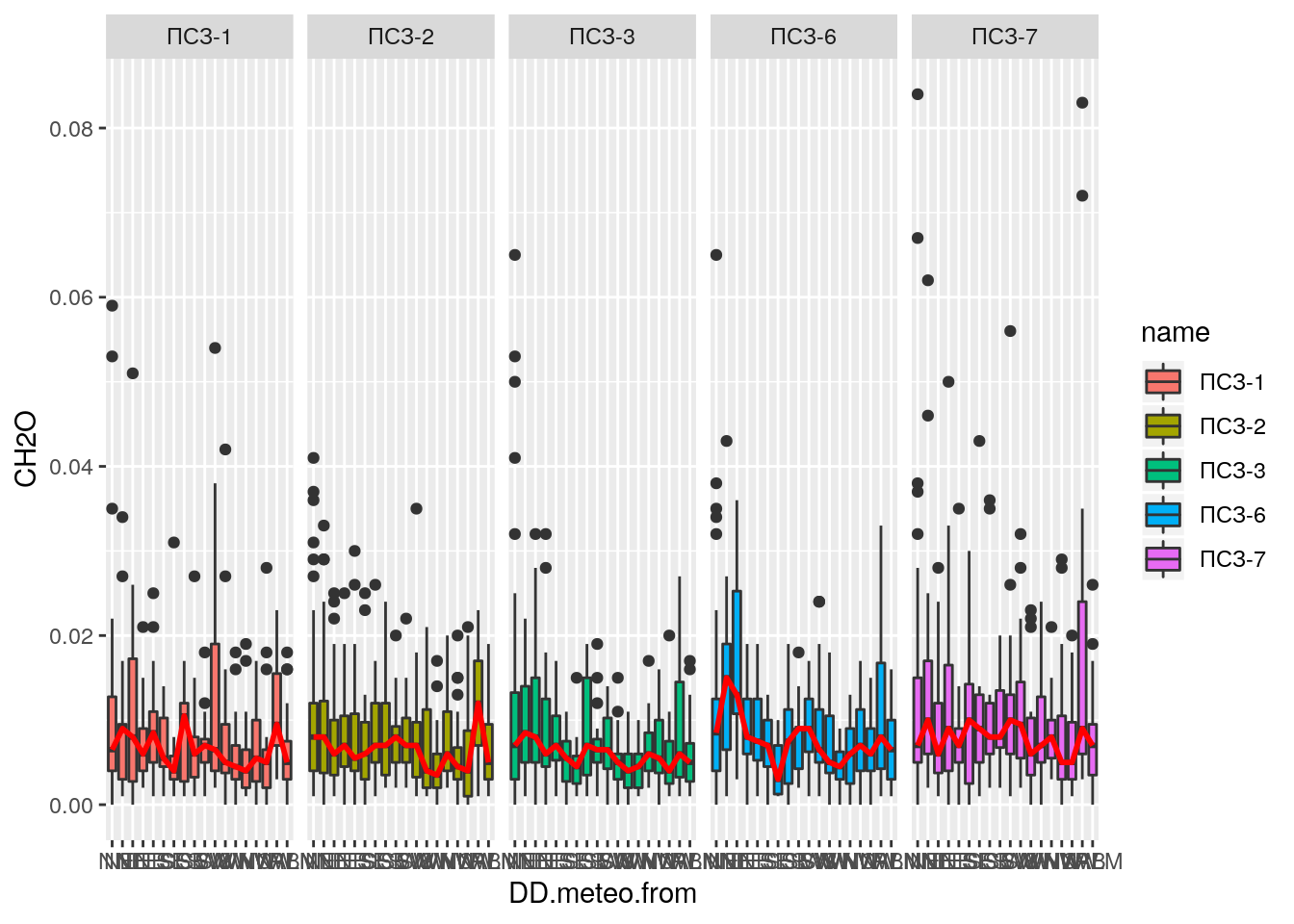
Як ми можемо побачити — деякі значення концентрацій формальдегіду занадто високі. Ці значення закривають собою основний масив даних. Давайте перебудуємо діаграму, видаливши при цьому значення концентрацій формальдегіду більше 0,04 мг/м³. І заразом позбавимось від легенди, яка займає багато місця на діаграмі. Легенда не потрібна, оскільки в заголовку каждої частини графіку відображено назву посту моніторингу.
#Запускаємо таблицю air_pollution.join в тунель
tbl_df(air_pollution.join) %>%
#Вибираємо потрібні нам поля назв постів моніторингу,
#напрямків вітру та концентрацій формальдегіду:
select(name, DD.meteo.from, CH2O) %>%
#Вибираємо тільки не порожні значення напрямків вітру:
filter(! is.na(DD.meteo.from), CH2O <= 0.04) %>%
#Будуємо діаграму
ggplot(aes(y = CH2O, x = DD.meteo.from, fill = name)) +
geom_boxplot() +
stat_summary(fun.y = median, geom = "line", aes(group = 2),
colour = "red", size = 1) +
#Розбиваємо діаграму на частини для окремих постів моніторингу:
facet_grid(.~name) +
guides(fill = FALSE)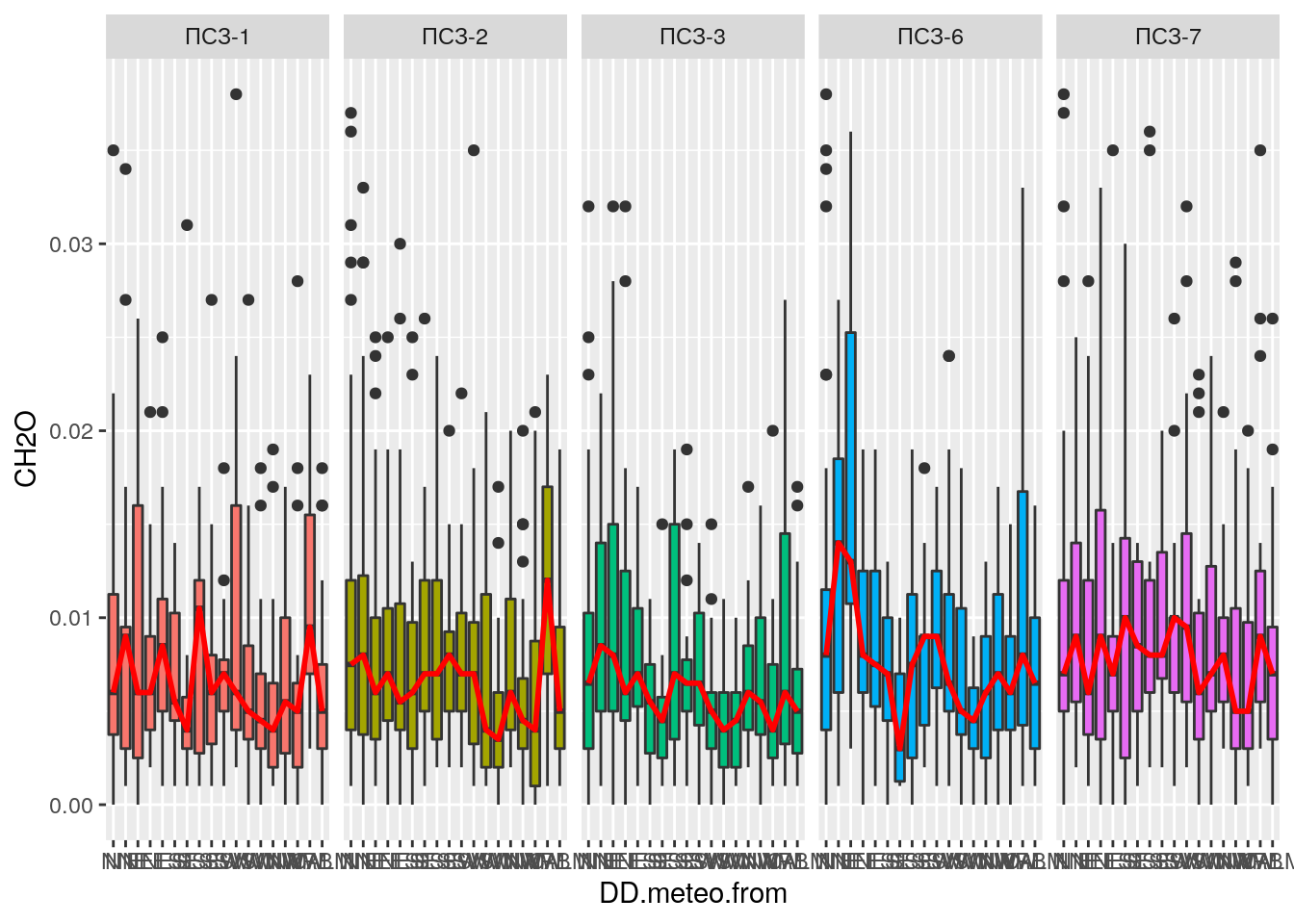
4.3 Кореляція гидоти
Кореляційний аналіз є одним з базових елементів будь-якого дослідження у природничих науках. Хоча не завжди доцільно його використовувати. Але, тим не менш, обчислення кореляційних зв’язків дозволяє швидко оцінити взаємозалежність показників уникаючи при цьому складних теоретичних припущень.
У цьому розділі я не буду зупинятись на питаннях вибору того чи іншого коефіцієнту кореляції. Зауважу лише те, що стандартним набором, реалізованим у найбільш розповсюджених пакетах R є три коефіцієнти кореляції: r-Пірсона, тау-Кендала та ро-Спірмена. Причому обчислення цих коефіцієнтів реалізовано в одних і тих самих функціях. Також при обчисленні кореляцій можна обирати декілька дуже важливих додаткових параметрів. Наприклад, функція cor базового пакету stats в якості параметру method дозволяє вибирати коефіцієнт кореляції, а в якості параметру use — тип співставлення даних при обчисленні кореляції. Що за «співставлення»? Це як буде поводитись функція cor зустрічаючи порожнє значення (NA). За умовчанням вона буде намагатись взяти в обчислення всі значення масиву. Якщо там буде хоча-б одне порожнє — результатом також буде порожнє значення. Ми можемо вказати функції — викинути всі рядки, які містять хоча-б одне порожнє значення у будь-якому стовпці. Але це може призвести до того, що один стовпець який містить дуже багато порожніх значень примусить функцію cor видалити багато даних з інших стовпців. Можемо поступити іще розумніше — наказати функції попарно обчислювати кореляцію і видаляти порожні значення лише для конкретної пари стовпців. Наприклад стовпець NO містить 100 адекватних значень; стовпець CO — 90 адекватних та 10 порожніх; стовпець SO2 — 50 адекватних та 50 порожніх. Якщо видалити всі порожні значення, то кореляції між цими трьома показниками буде пораховано лише на базі 50 значень. Якщо ж застосувати попарне видалення порожніх значень, то кореляційні коефіцієнти буде обчислено: між NO та CO — на основі 90 значень, між NO та SO2 — на основі 50 значень, між CO та SO2 — також на основі 50 значень. Таким чином ми вберегли стовпці NO та CO від примусового видалення адекватних та співставних значень.
Давайте обчислемо коефіцієнти кореляції тау-Кендала між усіма числовими полями таблиці air_pollution (це поля від 4 до 12). При цьому ми спочатку виберемо обчислення тільки на основі повного співпадіння всіх показників, а потім — на основі попарного співпадіння:
#Обчислюємо кореляцію тау-Кендала для числових даних таблиці air_pollution.
#Обираємо повне співпадіння показників
cor(air_pollution[, 4:12], use = "complete.obs", method = "kendal")## [1] "Error in cor(air_pollution[, 4:12], use = \"complete.obs\", method = \"kendal\") : no complete element pairs"#Обчислюємо кореляцію тау-Кендала для числових даних таблиці air_pollution.
#Обираємо попарне співпадіння показників
cor(air_pollution[, 4:12], use = "pairwise.complete.obs", method = "kendal")## TSP SO2 CO NO2 NO H2S
## TSP 1.0000000 0.2494186 0.1430857 0.1062223 NA 0.2048163
## SO2 0.2494186 1.0000000 0.1987689 0.1243857 0.1276164 0.2227603
## CO 0.1430857 0.1987689 1.0000000 0.2053470 0.1934061 0.2044601
## NO2 0.1062223 0.1243857 0.2053470 1.0000000 0.7228344 0.2202797
## NO NA 0.1276164 0.1934061 0.7228344 1.0000000 0.1295874
## H2S 0.2048163 0.2227603 0.2044601 0.2202797 0.1295874 1.0000000
## C6H6O 0.1621353 0.1456188 0.1772134 0.1875490 0.1204818 0.5691236
## NH3 0.2119104 0.2475331 0.2505082 0.2072914 0.1563242 0.4631916
## CH2O 0.1935991 0.1347579 0.1742752 0.1781922 0.1305676 0.2598744
## C6H6O NH3 CH2O
## TSP 0.1621353 0.2119104 0.1935991
## SO2 0.1456188 0.2475331 0.1347579
## CO 0.1772134 0.2505082 0.1742752
## NO2 0.1875490 0.2072914 0.1781922
## NO 0.1204818 0.1563242 0.1305676
## H2S 0.5691236 0.4631916 0.2598744
## C6H6O 1.0000000 0.4194216 0.2061131
## NH3 0.4194216 1.0000000 0.2144520
## CH2O 0.2061131 0.2144520 1.0000000Чому в першому варіанті ми отримали відповідь про помилку? Все дуже просто! Справа у тому, що концентрації пилу (TSP) вимірюються на трьох постах: «ПСЗ-2», «ПСЗ-6» та «ПСЗ-7». Натомість концентрації оксиду азоту (NO) вимірюються тільки на пості «ПСЗ-1». Між пилом та оксидом азоту в нашій таблиці немає жодного співпадіння. Тому в першому варіанті функція cor була вимушена видалити всі рядки таблиці, оскільки ніде немає повного співпадіння. А от у другому варіанті обчислення ми бачемо, що кореляція між пилом та оксидом азоту дорівнює NA, тобто порожньому значенню.
Тепер для чистоти експерименту просто видалемо стовпець TSP при обчисленні кореляції і наново спробуємо перший варіант обчислення.
#Обчислюємо кореляцію тау-Кендала для числових даних таблиці air_pollution.
#Не беремо стовпець TSP та обираємо тільки повне співпадіння показників
cor(air_pollution[, 5:12], use = "complete.obs", method = "kendal")## SO2 CO NO2 NO H2S C6H6O
## SO2 1.0000000 0.1847546 0.1617559 0.1698569 0.1342335 0.0264545
## CO 0.1847546 1.0000000 0.2033586 0.1934061 0.1632965 0.1422831
## NO2 0.1617559 0.2033586 1.0000000 0.6813172 0.1433044 0.1524980
## NO 0.1698569 0.1934061 0.6813172 1.0000000 0.1250176 0.1199974
## H2S 0.1342335 0.1632965 0.1433044 0.1250176 1.0000000 0.4466558
## C6H6O 0.0264545 0.1422831 0.1524980 0.1199974 0.4466558 1.0000000
## NH3 0.1774394 0.2472527 0.1086010 0.1512097 0.3104415 0.2071411
## CH2O 0.1155147 0.1825950 0.1731634 0.1305676 0.2343193 0.1499930
## NH3 CH2O
## SO2 0.1774394 0.1155147
## CO 0.2472527 0.1825950
## NO2 0.1086010 0.1731634
## NO 0.1512097 0.1305676
## H2S 0.3104415 0.2343193
## C6H6O 0.2071411 0.1499930
## NH3 1.0000000 0.1934329
## CH2O 0.1934329 1.0000000Зверніть увагу — як зміняться коефіцієнти кореляції у порівнянні з попереднім варіантом. Наприклад, кореляція фенолу (C6H6O) з сірководнем (H2S) в попередньому варіанті обчислень становила 0.5691236, а тепер становить 0.4466558. Авжеж — коефіцієнти кореляції між показниками в цих двох варіантах обчислюються за різною кількістю даних. Не забувайте про це! І пам’ятайте про те, що мова R — це програмний продукт в якому реалізовано величезну кількість алгоритмів. Головне — не загубитись.
Проте не слід забувати, що окрім сили кореляційного зв’язку в кореляційному аналізі науковці радять використовувати ще два показника. Перший це показник статистичної значущості зв’язку. Другий — це поправка на множинні порівняння.
Показник значущості кореляційного зв’язку показує нам — наскільки достовірним (зі статистичної точки зору) є обчислений нами коефіцієнт кореляції. Інколи трапляється так, що сила кореляції висока, але достовірність — низька. Тобто ми випадково отримали високий кореляційний зв’язок між показниками, хоча насправді вони можуть взагалі не корелювати. Саме для перевірки цього і використовують показник значущості кореляційного зв’язку.
Поправка на множинні порівняння застосовується тоді, коли ми аналізуємо зв’язок одразу декількох змінних. При багатократному порівнянні «всіх з усіма» знижується статистична значущість обчислених кореляційних зв’язків. Наші дані екологічного моніторингу містять декілька змінних (хімічних речовин). До цих даних бажано застосовувати поправку на множинні порівняння. Існує декілька алгоритмів обчислення цієї поправки. У функції p.adjust базового пакету stats реалізовано низку алгоритмів обчислення цієї поправки: Бонферонні, Хольма, Хохберга, Хоммеля, Беньяміні-Хохберга, Беньяміні-Йекутілі. В подальших обчисленнях ми будемо використовувати поправку Беньяміні-Йекутілі. При цьому ми не будемо використовувати функцію p.adjust напряму, а скористаємось можливостями пакету psych, який дозволяє швидко обчислювати кореляційні матриці та проводити суміжні обчислення. Власне результат роботи функції corr.test пакету psych ми використаємо для графічного відображення отриманих результатів кореляційного аналізу.
Завантажуємо пакет psych:
##
## Attaching package: 'psych'## The following objects are masked from 'package:ggplot2':
##
## %+%, alphaТепер давайте обчислемо коефіцієнти кореляції між хімічними речовинами в таблиці air_pollution. При цьому ми одразу застосуємо поправку на множинні порівняння. Також будуть окремо збережені ще декілька таблиць з додатковою інформацією про результати обчислення. Зокрема — таблиця з інформацією про кількість співпадінь для кожної пари хімічних речовин. Для визначення кореляції ми обчислемо коефіцієнт кореляції тау-Кендала. Результати обчислення збережемо в об’єкт air.corr.
#Обчислюємо кореляцію тау-Кендала для числових даних таблиці air_pollution,
#застосовуємо поправку Беньяміні-Йекутілі, зберігаємо результат в air.corr:
corr.test(air_pollution[, 4:12], method = "kendall",
adjust = "BY", use = "pairwise") -> air.corr## Warning in sqrt(n - 2): NaNs produced## Warning in corr.test(air_pollution[, 4:12], method = "kendall", adjust
## = "BY", : Number of subjects must be greater than 3 to find confidence
## intervals.## Warning in sqrt(n[lower.tri(n)] - 3): NaNs producedПід час виконання обчислення ми отримали декілька повідомлень про те, що в результаті обчислень створено значення NaN (Not a Number). Це пов’язано з тим, що у нас немає парних вимірювань між пилом (TSP) та оксидом азоту (NO). На перехресті цих двух речовин в наших обчисленнях ми отримали значення NA. Також виникли проблеми з обчисленням довірчих інтервалів для цієї пари забруднюючих речовин.
Об’єкт air.corr, в який ми зберегли результати обчислень, має формат «Список» (List). Він складається аж з 9-ти окремих підоб’єктів — таблиць та простих записів. Щоб викликати конкретний підоб’єкт об’єкту «Список» ми повинні зазначити його номер у подвійних квадратних дужках: air.corr[[1]].
Давайте більш детально розглянемо результати нашого обчислення. Переглянемо деякі цікаві для нас підоб’єкти отриманого об’єкту air.corr. Для цього будемо викликати ці підоб’єкти по черзі та обговорювати їхній зміст.
## TSP SO2 CO NO2 NO H2S
## TSP 1.0000000 0.2494186 0.1430857 0.1062223 NA 0.2048163
## SO2 0.2494186 1.0000000 0.1987689 0.1243857 0.1276164 0.2227603
## CO 0.1430857 0.1987689 1.0000000 0.2053470 0.1934061 0.2044601
## NO2 0.1062223 0.1243857 0.2053470 1.0000000 0.7228344 0.2202797
## NO NA 0.1276164 0.1934061 0.7228344 1.0000000 0.1295874
## H2S 0.2048163 0.2227603 0.2044601 0.2202797 0.1295874 1.0000000
## C6H6O 0.1621353 0.1456188 0.1772134 0.1875490 0.1204818 0.5691236
## NH3 0.2119104 0.2475331 0.2505082 0.2072914 0.1563242 0.4631916
## CH2O 0.1935991 0.1347579 0.1742752 0.1781922 0.1305676 0.2598744
## C6H6O NH3 CH2O
## TSP 0.1621353 0.2119104 0.1935991
## SO2 0.1456188 0.2475331 0.1347579
## CO 0.1772134 0.2505082 0.1742752
## NO2 0.1875490 0.2072914 0.1781922
## NO 0.1204818 0.1563242 0.1305676
## H2S 0.5691236 0.4631916 0.2598744
## C6H6O 1.0000000 0.4194216 0.2061131
## NH3 0.4194216 1.0000000 0.2144520
## CH2O 0.2061131 0.2144520 1.0000000Перший підоб’єкт являє собою таблицю з обчисленими коефіцієнтами кореляції. Можемо побачити, що на перехресті пилу (TSP) та оксиду азоту (NO) містяться значення NA.
## TSP SO2 CO NO2 NO H2S C6H6O NH3 CH2O
## TSP 950 950 950 950 0 949 950 950 950
## SO2 950 2360 1900 2360 535 2359 2360 2360 1901
## CO 950 1900 1900 1900 382 1899 1900 1900 1900
## NO2 950 2360 1900 2360 535 2359 2360 2360 1901
## NO 0 535 382 535 535 535 535 535 382
## H2S 949 2359 1899 2359 535 3608 3608 3608 1900
## C6H6O 950 2360 1900 2360 535 3608 3609 3609 1901
## NH3 950 2360 1900 2360 535 3608 3609 3609 1901
## CH2O 950 1901 1900 1901 382 1900 1901 1901 1901Другий підоб’єкт містить таблицю, в якій зазначено кількість парних спостережень. Тобто коефіцієнт кореляції між пилом (TSP) та дікосидом сірки (SO2) було обчислено на основі 950 спостережень. А коефіцієнт кореляції між діоксидом сірки (SO2) та діоксидом азоту (NO2) обчислено на основі 2360 спостережень.
## TSP SO2 CO NO2 NO
## TSP 0.000000e+00 4.948769e-14 4.948578e-05 4.878000e-03 NA
## SO2 6.137486e-15 0.000000e+00 2.008013e-17 8.079989e-09 1.366388e-02
## CO 9.546832e-06 2.213642e-18 0.000000e+00 1.602146e-18 7.135063e-04
## NO2 1.041896e-03 1.336112e-09 1.545435e-19 0.000000e+00 4.866965e-86
## NO NA 3.106768e-03 1.425662e-04 1.341341e-87 0.000000e+00
## H2S 1.904421e-10 6.534594e-28 2.273140e-19 2.579333e-27 2.673100e-03
## C6H6O 5.059471e-07 1.174724e-12 7.187916e-15 4.005343e-20 5.264198e-03
## NH3 4.167657e-11 2.774919e-34 1.410799e-28 2.549232e-24 2.837839e-04
## CH2O 1.784763e-09 3.666748e-09 2.008363e-14 5.001629e-15 1.063400e-02
## H2S C6H6O NH3 CH2O
## TSP 1.201750e-09 2.719697e-06 2.749467e-10 1.036143e-08
## SO2 1.185517e-26 8.118869e-12 8.054888e-33 2.046854e-08
## CO 2.199450e-18 5.490711e-14 2.925138e-27 1.457443e-13
## NO2 4.159528e-26 4.844374e-19 3.699888e-23 4.270136e-14
## NO 1.212396e-02 2.247152e-02 1.372921e-03 4.409689e-02
## H2S 0.000000e+00 1.090129e-306 1.660403e-189 2.569810e-29
## C6H6O 7.511017e-309 0.000000e+00 4.372902e-152 1.230595e-18
## NH3 2.288044e-191 9.038821e-154 0.000000e+00 4.292485e-20
## CH2O 1.062363e-30 1.102248e-19 3.253286e-21 0.000000e+00У четвертому підоб’єкті містятся рівні значущості обчислених коефіцієнтів кореляції. Оскільки при обчисленні ми використали поправку на множинні порівняння, то в цьому підоб’єкті внесено одразу два типи рівнів значущості: із поправкою та без поправки. Рівні значущості з поправкою на множинні порівняння внесені вище основної діагоналі таблиці. Рівні значущості без поправки — нижче основної діагоналі. На рівні 0,05 всі наші обчислені коефіцієнти кореляції є значущими. Зверніть увагу — при застосуванні поправки значущість коефіцієнту кореляції між формальдегідом (CH2O) та оксидом азоту (NO) дорівнює 0.04 (4.409689e-02), а без введення поправки — 0.01 (1.0634e-02).
Іще цікаву інформацію містить восьмий підоб’єкт. Він являє собою таблицю із довірчими інтервалами коефіцієнтів кореляції. Також цей підоб’єкт містить обчислений рівень значущості коефіцієнтів кореляції (без поправки на множинні порівняння).
## [1] TRUEБільш детально з результатами роботи функції corr.test ви можете ознайомитись в документації до пакету psych (Revelle 2016).
Але великі таблиці придатні для великих звітів! Ми можемо піти далі — візуалізувати матрицю кореляцій. При цьому ми можемо додати до візуалізації додаткові дані, наприклад — обчислені рівні значущості. Мова R має дуже широкі можливості для візуалізації отриманих результатів! Ми використаємо пакет ggcorrplot, який є надбудовою до пакету ggplot2 і призначений для візуалізації результатів кореляційного аналізу. За допомогою цього пакету ми в зручній формі візуалізуємо коефіцієнти кореляції та зробимо якісне графічне оформлення.
Функція ggcorrplot для візуалізації кореляційних матриць використовує синтаксис пакету ggplot2. При цьому ми повинні точно вказати — де міститься інформація про коефіцієнти кореляції та рівні значущості. Давайте розглянемо скрипт, який будує та графічно оформлює візуалізацію кореляційного аналізу.
#Викликаємо функцію ggcorrplot,
#вказуємо що інформація про коефіцієнти кореляції міститься в air.corr[[1]],
#а інформація про рівні значущості - в air.corr[[4]]
ggcorrplot(air.corr[[1]], lab = TRUE, p.mat = air.corr[[4]],
#задаємо параметри графічного відображення
#sig.level = 0.01 - будуть захреслені коефіцієнти з рівнями значущості більше 0.01
#method = "square" - графік у вигляді квадратів
#зберігаємо нашу візуалізацію в об’єкт air.ggcorr1
lab_col = "black", lab_size = 4, sig.level = 0.01,
pch.col = "red4", pch.cex = 10, method = "square") -> air.ggcor1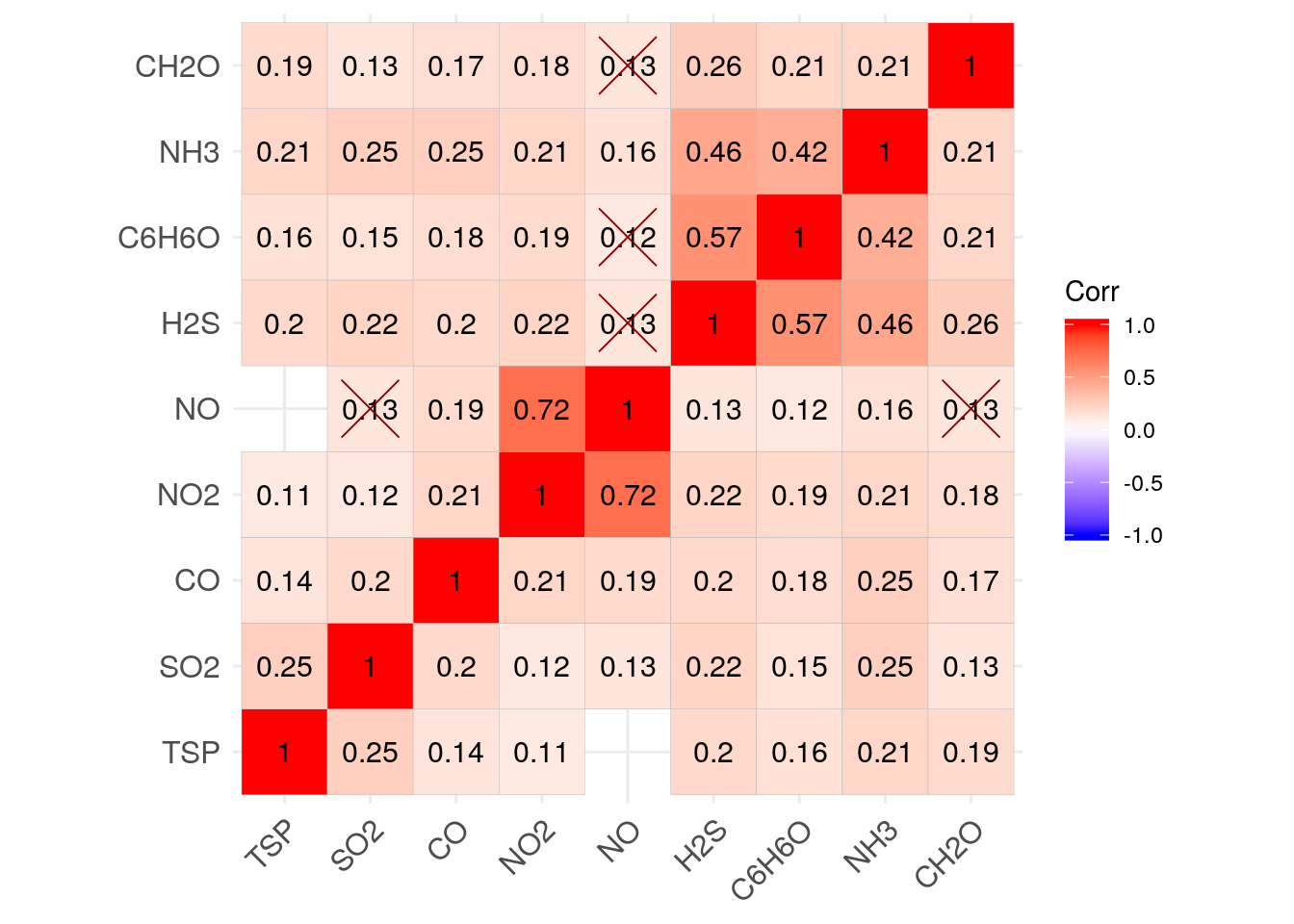
Квадрати в комірках нашої діаграми заповнюють весь вільний простір. Сила кореляційного зв’язку відображується цифрами всередині та кольором квадратів. Для більшої наочності ми можемо обрати не квадрати, а кола. У цьому випадку, окрім кольору та цифр, сила кореляційного зв’язку буде відображена розміром кіл.
ggcorrplot(air.corr[[1]], lab = TRUE, p.mat = air.corr[[4]],
lab_col = "black", lab_size = 4, sig.level = 0.01,
pch.col = "red4", pch.cex = 10, method = "circle")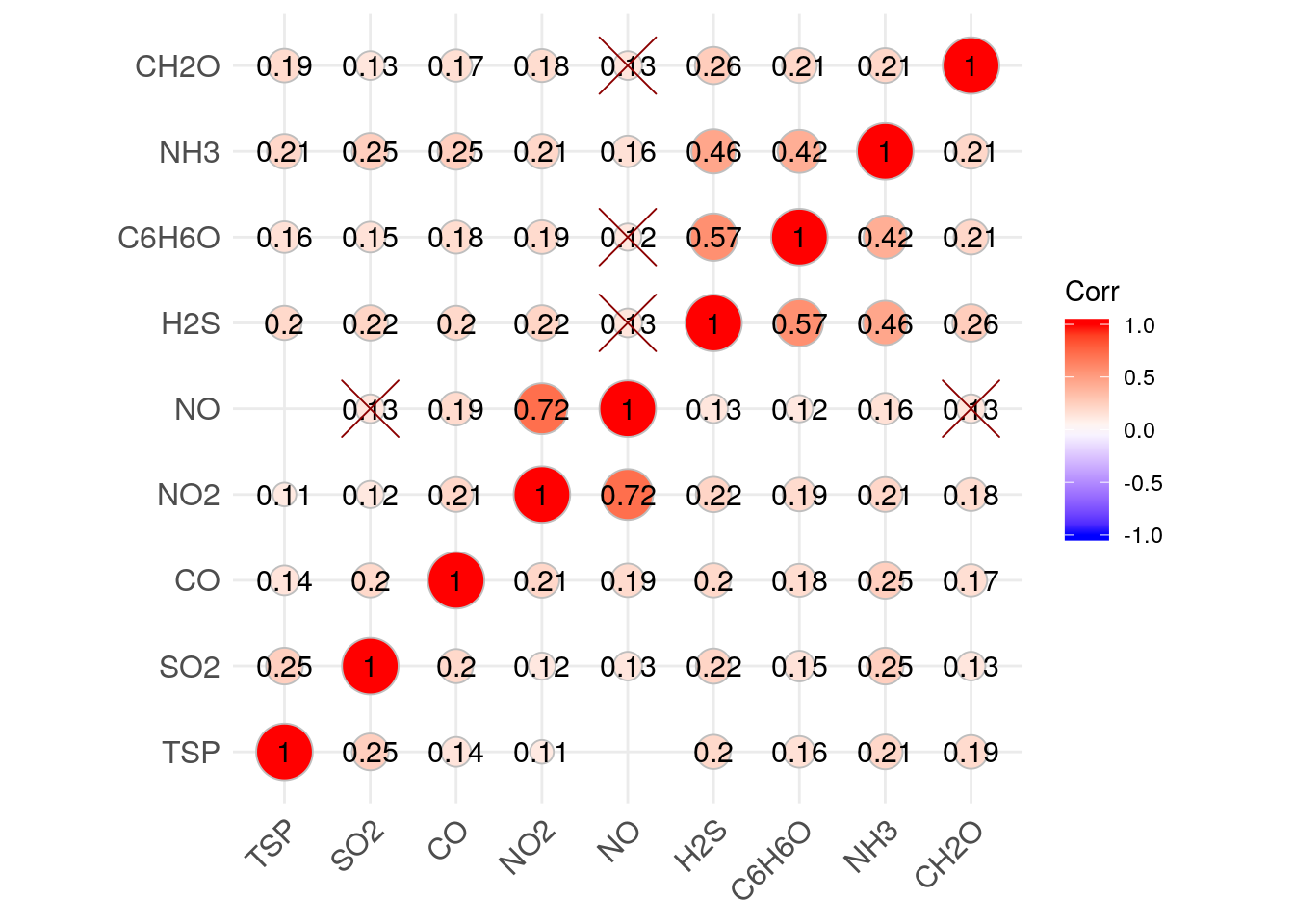
Виглядає наочно і зрозуміло! Ми пам’ятаємо, що обчислений рівень значущості для кореляції між формальдегідом (CH2O) та оксидом азоту (NO) становить 0.01 (1.0634e-02) без введення поправки та 0.04 (4.409689e-02) із поправкою на множинні порівняння. Для візуалізації ми вибрали граничний рівень значущості 0.01 і в обох випадках кореляція між цими двома речовинами зображена недійсною. А от кореляція між фенолом (C6H6O) та оксидом азоту (NO) при введенні поправки на множинні порівняння є недійсною, а без поправки — дійсною. Те саме стосується пар SO2-NO та H2S-NO.
Проте не слід забувати про можливості пакету ggplot2 для оформлення графічних матеріалів. Давайте доповнимо нашу візуалізацію air.ggcor1 шрифтами, кольорами та підписами! Нагадаю вам, що в синтаксисі пакету ggplot2 додавання додаткових функцій при побудові графіків здійснюється за допомогою знаку «плюс»: +.
#Викликаємо збережену візуалізацію air.ggcor1
air.ggcor1 +
#додаємо до візуалізації градієнтну кольорову шкалу
#для шкали додаємо заголовок та граничні кольори
scale_fill_gradientn(name = "Сила кореляційного зв’язку (тау-Кендала)",
limits = c(-1, 1), colors = c("royalblue3", "seashell2", "red3")) +
#додаємо заголовок діаграми та графічне оформлення
labs(title = "Кореляція забруднюючих речовин в повітрі") +
theme(plot.title = element_text(hjust = 0.5),
text = element_text(family = "FreeSans",
face = "italic", size = 12, colour = "firebrick4", lineheight = 0.9),
legend.position = "bottom",
legend.text = element_text(family = "FreeSans",
face = "italic", size = 12, colour = "firebrick4", lineheight = 0.8, angle = 0),
axis.text.x = element_text(colour = "gray15", face="bold",
size= 12, angle = 90, vjust = 0.5, hjust = 1.0),
axis.text.y = element_text(colour = "gray15", face="bold",
size= 12, angle = 0, vjust = 0.5, hjust = 1.0),
axis.ticks = element_line(colour = "orange", size = 0.2),
plot.background = element_rect(fill = "gray95"),
panel.grid.major = element_line(colour = "orange", size = 0.2),
panel.grid.minor = element_line(colour = "gray90"),
panel.background = element_rect(fill="gray95")) ->
#зберігаємо все в об’єкт air.ggcor2
air.ggcor2Тепер нам залишилось зберегти отриману візуалізацію у зовнішній графічний файл. Ми збережемо її у файл формату PNG.
#Створюємо порожній графічний файл
png("air.ggcor2.png", width = 180,
height = 200, units = "mm", res = 150)
#викликаємо всередині файлу візуалізацію air.ggcor2
air.ggcor2
#записуємо графічний файл у файлову систему
dev.off()Кінцева візуалізація результатів кореляційного аналізу буде виглядати отак:
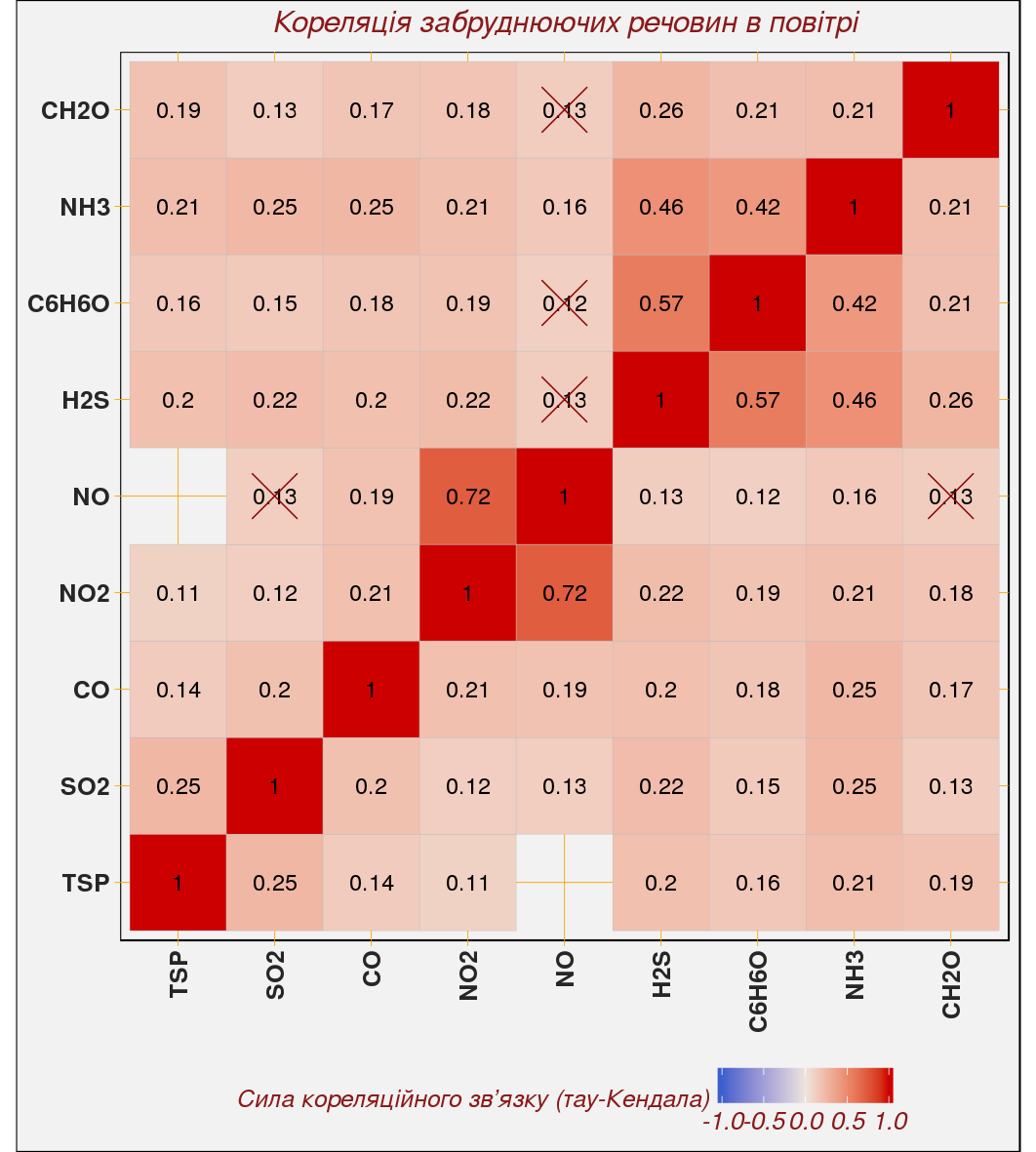
Figure 4.1: Кінцевий вигляд візуалізації кореляційного аналізу
Що ми маємо в результаті? - Готові скрипти, які дозволяють виконати нам весь цикл роботи — від первинних обчислень до кінцевої візуалізації!
В отриманих нами результатах ми бачимо, що сильну кореляцію (0.72) мають оксид азоту (NO) та діоксид азоту (NO2). Це цілком логічно. Також у нас виділяється три речовини, які пов’язані між собою середньою за силою кореляцією: аміак (NH3), фенол (C6H6O) та сірководень (H2S). На нашу думку — кореляція між цими трьома забруднюючими речовинами є доказом того, що вони мають спільне або близько розташоване джерело. При цьому викиди цих трьох речовин відбуваються синхронно. Цим джерелом може бути коксохімічне виробництво, яке розташоване в Південному промисловому вузлі Кривого Рогу.
У розділі 4.2 ми розглядали методи аналізу, які дозволяють швидко визначити напрям з якого приносить забруднення в місця наших спостережень. А зараз давайте дослідимо — з якими метеорологічними показниками корелюють концентрації забруднюючих речовин. Для цього ми використаємо таблицю air_pollution.join, яку отримали в розділі 3.5.1.
#Обчислюємо кореляцію тау-Кендала для числових даних таблиці air_pollution.join,
#застосовуємо поправку Беньяміні-Йекутілі, зберігаємо результат в air.corr:
corr.test(air_pollution.join[, c(2:10, 13:17)], method = "kendall",
adjust = "BY", use = "pairwise") -> air.corr.join## Warning in sqrt(n - 2): NaNs produced## Warning in corr.test(air_pollution.join[, c(2:10, 13:17)], method =
## "kendall", : Number of subjects must be greater than 3 to find confidence
## intervals.## Warning in sqrt(n[lower.tri(n)] - 3): NaNs producedggcorrplot(air.corr.join[[1]], lab = TRUE, p.mat = air.corr.join[[4]],
lab_col = "black", lab_size = 2.5, sig.level = 0.01,
pch.col = "red4", pch.cex = 10, method = "square")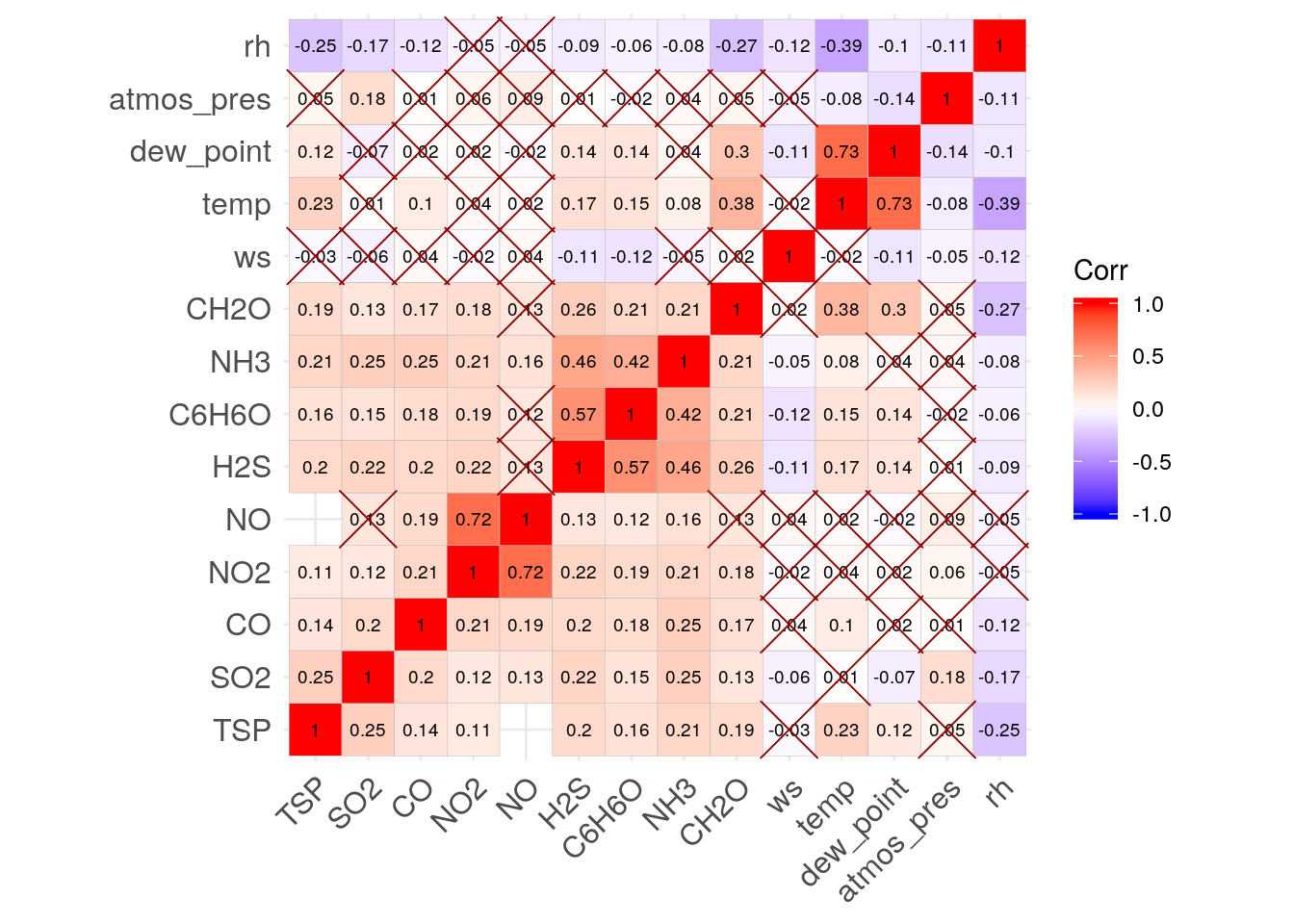
Як бачимо на кореляційній діаграмі — середню позитивну кореляцію (0,38) мають формальдегід (CH2O) та температура повітря (temp). Це цілком логічно, оскільки формальдегід може утворюватись в повітрі при високій температурі та інтенсивній сонячній радіації — у теплі безхмарні дні. З іншого боку — це доволі низька кореляція. Це може свідчити про те, що окрім «атмосферного» формальдегіду в повітрі Кривого Рогу присутній також первинний формальдегід, який викидається в повітря в «готовому» вигляді.
4.4 Чи залежить гидота від гидоти
4.5 Гидотний календар
Календарні діаграми дозволяють зручно візуалізувати дані із прив’язкою до календарних дат: днів-місяців-років. Основна сила цих діаграм у тому, що вони дозволяють візуалізувати масив щоденних даних одразу за декілька років у дуже наглядній формі.
Для побудови календарних діаграм ми не будемо використовувати статистичний аналіз. Основними операціями при побудові подібної графіки є перебудова та компіляція таблиць даних.
Щоб побудувати календарну діаграму нам треба провести деякі підготовчі маніпуляції. Зокрема — нам треба із поля «дата-час» витягнути інформацію про рік, назву місяця року, номер тижня в місяці та назву дня тижня. Так-так! Саме «назву місяця року» та «назву дня тижня». Мова програмування R володіє дуже потужними засобами для роботи з даними типу «дата» та «дата-час». Ми можемо оперувати повними назвами («січень»), скороченими назвами («січ»), або взагалі номерами («1»). Головна умова для подібних перетворень — записи «дата-час», з яких ми намагаємось витягнути назви днів-місяців — повинні в нашому робочому середовищі мати клас «дата» або «дата-час», а не звичайного тексту. У таблицях, які ми використовуємо в цій книзі, ми всюди конвертуємо поля дати та часу в єдине поле «дата-час» формату POSIXct. Також не слід забувати про різні часові пояси. Всім відомо, що коли в Японії ранок понеділка, в Європі ще ніч неділі. Подивитись, які варіанти перетворення доступні можна за допомогою довідки до функції strptime:
Основним ускладнюючим моментом при побудові календарних діаграм є те, що в наших даних можуть бути відсутніми деякі дні. Наприклад, в даних спостережень Гідрометеоцентру України відсутні вимірювання по неділях та державних святах (таблиця air_pollution). У даних моніторингу повітря від ПАТ «АрселорМіттал Кривий Ріг» також трапляються пропуски, які охоплюють період більше однієї доби (таблиці Landau2a, Ordzh52 та Podlepy41). Але ж для побудови нормального календаря нам треба відобразити ВСІ дні, включно з вихідними та державними святами! Тобто при побудові календарної діаграми нам треба примусово вставити в нашу таблицю пропущені дні та надати порожні значення (NA) концентраціям досліджуваних хімічних речовин. Одним з найпростіших варіантів вирішення цієї проблеми є створення окремого часового вектору без пропусков та приєднання до нього наших даних. Оскільки для побудови календарної діаграми ми будемо використовувати усереднені за день значення — нам простіше спочатку усереднити значення концентрацій, а потім приєднати їх до новоствореного часового вектору.
А тепер давайте візьмемся за роботу! Ми побудуємо календарну діаграму концентрацій пилу на одному з постів ПАТ «АрселорМіттал Кривий Ріг» (таблиця Podlepy41) та календарну діаграму кратності перевищень середньодобових концентрацій формальдегіду на постах Гідрометеоцентру України (таблиця air_pollution). При цьому концентрації формальдегіду обчислемо як середнє значення з усіх п’яти постів. У першу чергу з’ясуємо ситуацію з пилом, а потім — візьмемось за формальдегід.
#Завантажуємо пакет dplyr:
library(dplyr)
#Запускаємо таблицю Podlepy41 в тунель
tbl_df(Podlepy41) %>%
#Вибираємо потрібні нам поля дати-часу та концентрацій пилу:
select(date.time, TSP) %>%
#Перетворюємо поле date.time із формату factor у формат POSIXct:
mutate(tmp.date_time = as.POSIXct(as.character(date.time),
format = "%d/%m/%Y %H:%M:%S", tz = "Europe/Kiev")) %>%
#Отримуємо значення дати з поля tmp.date_time
#і зберігаємо проміжний результат в таблицю Podlepy41.date:
mutate(tmp.date = as.Date(format(tmp.date_time, "%Y%m%d"), "%Y%m%d")) -> Podlepy41.dateЩоб пересвідчитись у тому, що ми отримали те що нам потрібно — давайте переглянемо таблицю з проміжними результатами Podlepy41.date:
## # A tibble: 47,686 x 4
## date.time TSP tmp.date_time tmp.date
## <fct> <dbl> <dttm> <date>
## 1 01/01/2015 00:00:00 0.229 2015-01-01 00:00:00 2015-01-01
## 2 01/01/2015 00:00:00 NA 2015-01-01 00:00:00 2015-01-01
## 3 01/01/2015 00:10:00 NA 2015-01-01 00:10:00 2015-01-01
## 4 01/01/2015 00:11:00 NA 2015-01-01 00:11:00 2015-01-01
## 5 01/01/2015 00:20:00 0.217 2015-01-01 00:20:00 2015-01-01
## 6 01/01/2015 00:20:00 NA 2015-01-01 00:20:00 2015-01-01
## 7 01/01/2015 00:30:00 NA 2015-01-01 00:30:00 2015-01-01
## 8 01/01/2015 00:31:00 NA 2015-01-01 00:31:00 2015-01-01
## 9 01/01/2015 00:40:00 0.233 2015-01-01 00:40:00 2015-01-01
## 10 01/01/2015 00:40:00 NA 2015-01-01 00:40:00 2015-01-01
## # … with 47,676 more rowsІз таблиці Podlepy41.date нам потрібні тільки два поля: TSP та tmp.date. Нам треба усереднити значення концентрацій пилу (TSP) для кожного дня:
#Запускаємо таблицю Podlepy41.date в тунель:
tbl_df(Podlepy41.date) %>%
#Групуємо таблицю по значенням поля tmp.date:
group_by(tmp.date) %>%
#Обчислюємо середнє арифметичне значення концентрацій пилу,
#округляємо результати до другого знаку після коми
#та записуємо кінцевий результат в таблицю Podlepy41.mean:
summarise(TSP.mean = round(mean(TSP, na.rm = TRUE), 2)) -> Podlepy41.meanДалі нам треба створити вектор, в якому будуть всі дні без пропусків. Але перед цим нам треба дізнатись початкову та кінцеву дату нашого вектору. Щоб дізнатись ці дати ми просто використаємо функцію summary до поля tmp.date отриманої вище таблиці Podlepy41.mean:
## Min. 1st Qu. Median Mean 3rd Qu.
## "2015-01-01" "2015-03-21" "2015-06-12" "2015-05-29" "2015-08-02"
## Max.
## "2015-09-22"Як бачимо — початкова дата становить 1 січня 2015 року, кінцева — 22 вересня 2015 року. Тепер в цих самих інтервалах створимо потрібний нам вектор часу:
#Створюємо вектор часу date.vector1 від 1.01.2015 до 22.09.2015:
date.vector1 <- seq(from = as.Date("2015-01-01"), to = as.Date("2015-09-22"), by = "days")От тепер можна порівняти довжину вектору часу date.vector1 із довжиною таблиці Podlepy41.mean:
## [1] 205## [1] 265Ми бачемо, що в порівнянні з вектором часу date.vector1 в таблиці Podlepy41.mean не вистачає аж 60 днів!
Нарешті ми можемо об’єднати два наших об’єкти. Для цього ми використаємо вже знайому нам функцію left_join з пакету dplyr. Але, оскільки, функція left_join не працює з об’єктами класу Date, нам треба перетворити їх на клас character.
#Створюємо таблицю данних (data.frame):
date.vector1.table <- data.frame(tmp.date = date.vector1)
#Перетворюємо поле all.date таблиці date.vector1.table на клас character:
date.vector1.table$tmp.date <- as.character(date.vector1.table$tmp.date)
#Створюємо поле tmp.date2 таблиці Podlepy41.mean як клас character:
Podlepy41.mean$tmp.date2 <- as.character(Podlepy41.mean$tmp.date)
#Приєднуємо таблицю з даними моніторингу повітря
#до таблиці з усіма датами:
Podlepy41.mean.join <- dplyr::left_join(date.vector1.table, Podlepy41.mean, by = c("tmp.date" = "tmp.date2"))І, нарешті, ми можемо приступити до візуалізації! Давайте побудуємо календарну діаграму на основі таблиці Podlepy41.mean.join. Уважно слідкуйте за послідовністю команд! Нам треба здійснити декілька перетворень наших даних, оскільки календарна діаграма насправді являє собою набір окремих діаграм всередині однієї кінцевої діаграми. І розбиття на ці суб-діаграми здійснюється на основі результатів цих перетворень.
Завантажуємо пакет ggplot2:
Щоб одразу оформити градієнтну заливку в залежності від середньодобових концентрацій пилу — одразу переглянемо і запам’ятаємо мінімальне та максимальне значення середньодобових концентрацій пилу:
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 0.02000 0.04000 0.07000 0.07868 0.10000 0.30000 60Тепер будуємо та оформлюємо календарну діаграму:
#Запускаємо таблицю Podlepy41.mean.join в тунель:
tbl_df(Podlepy41.mean.join) %>%
#Перетворюємо поле tmp.date на клас Data:
mutate(tmp.date = as.Date(tmp.date)) %>%
#Отримуємо значення номеру року з поля tmp.date:
mutate(year = as.numeric(format(tmp.date, "%Y")),
#Отримуємо значення назви місяця з поля tmp.date
#і створюємо впорядковані категорії (для правильної послідовності на діаграмі):
month.order = factor(format(tmp.date, "%B"), levels = c("січень", "лютий", "березень", "квітень", "травень", "червень", "липень", "серпень", "вересень", "жовтень", "листопад", "грудень")),
#Отримуємо значення назви дня з поля tmp.date
#і створюємо впорядковані категорії (для правильної послідовності на діаграмі):
weekday.order = factor(format(tmp.date, "%a"),
levels = rev(c("пн", "вт", "ср", "чт", "пт", "сб", "нд"))),
#Отримуємо значення номеру дня місяця з поля tmp.date:
day.month = as.integer(format(tmp.date, "%d")),
#Отримуємо значення короткої назви місяця та номеру року з поля tmp.date:
year.month = format(tmp.date, "%h %Y"),
#Отримуємо значення номеру тижня в році з поля tmp.date:
week = as.numeric(format(tmp.date, "%W"))) %>%
#Групуємо масив даних за значенням поля year.month:
group_by(year.month) %>%
#Створюємо поле зі значеннями номерів тижнів у місяцях:
mutate(monthweek = 1 + week - min(week)) %>%
#Починаємо побудову календарної діаграми:
ggplot(aes(monthweek, weekday.order, fill = TSP.mean)) +
geom_tile(colour = "gray15") +
#Задаємо розбивку графіків на субграфіки за полями year та month.order:
facet_grid(year ~ month.order) +
#Задаємо налаштування градієнтної заливки:
scale_fill_gradient2(name = "Середньодобова концентрація пилу (мг/м³): ",
limits = c(0.0, 0.31), low = "royalblue3", mid = "gold2",
high = "orangered3", midpoint = 0.15) +
#Налаштовуємо підписи на вісі X
scale_x_continuous(breaks=seq(1, 6, 1)) +#(у місяці може бути до 6 тижнів)
#Додаємо на діаграму числові підписи значень концентрацій пилу:
geom_text(aes(label = TSP.mean), vjust = 0.5, family = "FreeSans", size = 2.0, colour = "firebrick4") +
#Налаштовуємо візуальне оформлення діаграми:
labs(y = "день тижня\n", x = "\nтиждень місяця",
title = "Середньодобові концентрації пилу\nза даними посту «Подлєпи-41»") +
theme(plot.title = element_text(hjust = 0.5),
text = element_text(family = "FreeSans",
face = "italic", size = 14, colour = "firebrick4", lineheight = 0.9),
legend.position = "bottom",
legend.text = element_text(family = "FreeSans",
face = "italic", size = 14, colour = "firebrick4", lineheight = 0.8, angle = 0),
axis.text.x = element_text(colour = "gray15", face="bold",
size= 12, angle = 0, vjust = 0.5, hjust = 0.5),
axis.text.y = element_text(colour = "gray15", face="bold",
size= 12, angle = 0, vjust = 0.5, hjust = 1),
axis.ticks = element_line(colour = "orange", size = 0.2),
plot.background = element_rect(fill = "gray95"),
panel.grid.major = element_line(colour = "orange", size = 0.2),
panel.grid.minor = element_line(colour = "gray90"),
panel.background = element_rect(fill="gray95")) ->
#Зберігаємо календарну діаграму в об’єкт calendar.TSP:
calendar.TSPЩоб переглянути отриману календарну діаграму безпосередньо в робочому середовищі R, нам достатньо просто викликати цей об’єкт. Але виглядати він буде не дуже презентабельно: літери дрібні, підписи не читаються… Ми вже стикались у попередніх розділах із тим, що «всередині» R графіка пакету ggplot2 та його похідних виглядає не дуже красиво через інтерактивність графічного середовища. Тому після перегляду в робочому середовищі ми експортуємо нашу календарну діаграму в зовнішній PNG-файл.
## Warning: Removed 60 rows containing missing values (geom_text).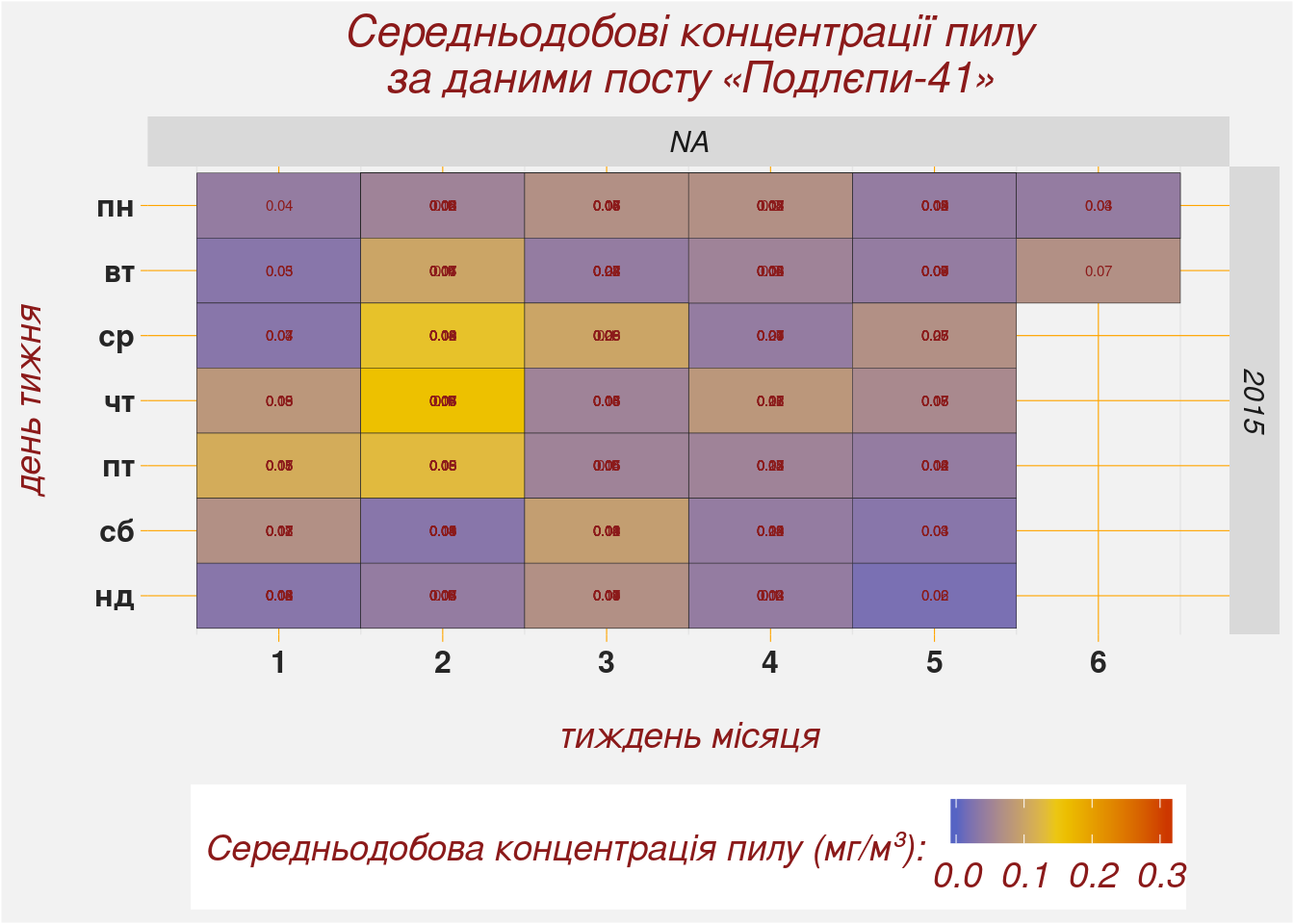
#Створюємо порожній графічний файл
png("calendar_TSP.png", width = 297,
height = 210, units = "mm", res = 150)
#викликаємо всередині файлу візуалізацію calendar.TSP:
calendar.TSP
#записуємо графічний файл у файлову систему
dev.off()Кінцева версія календарної діаграми середньодобових концентрацій пилу буде виглядати отак:
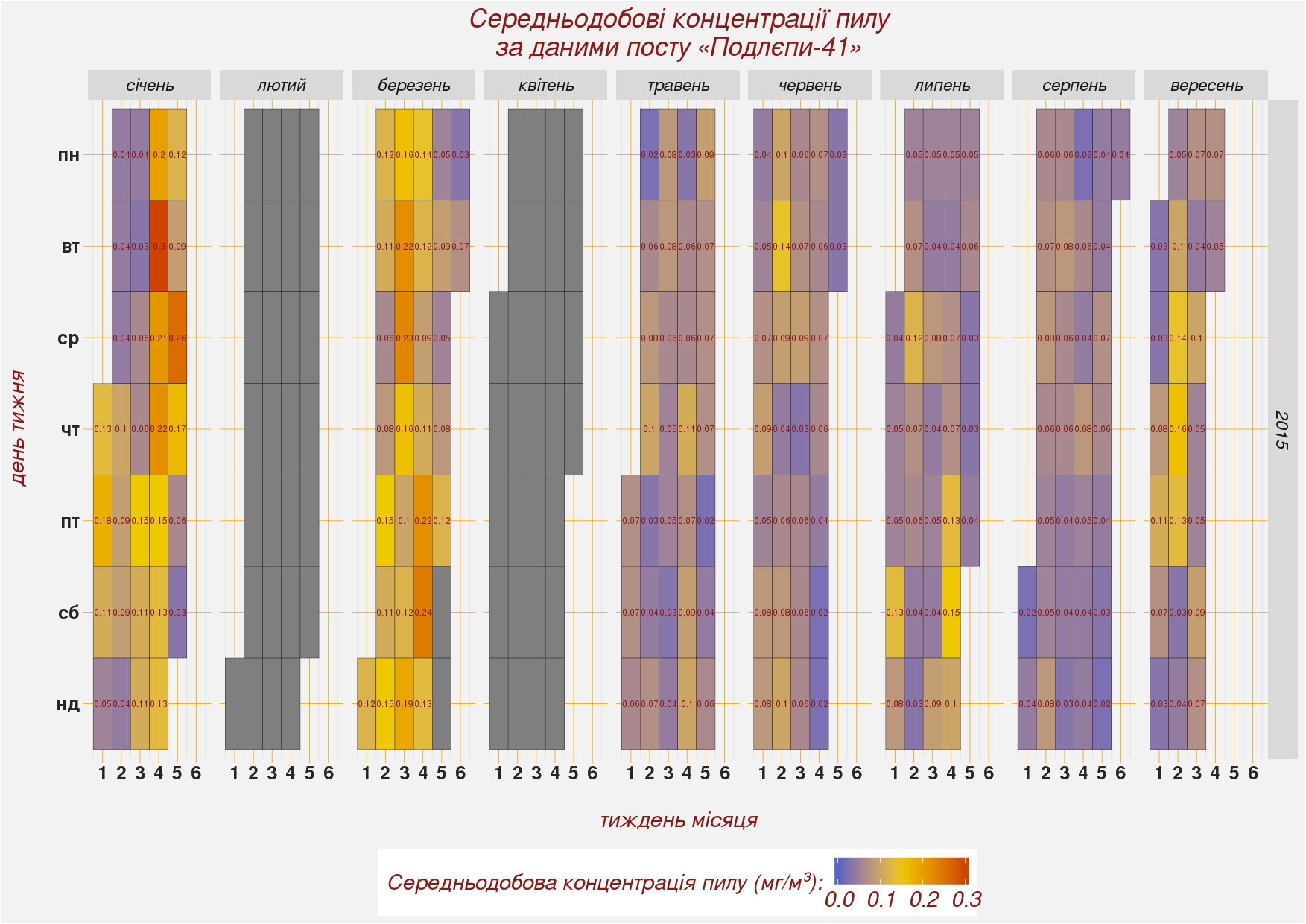
Figure 4.2: Кінцевий вигляд календарної діаграми концентрацій пилу
Коли ми будували цю діаграму, то командою facet_grid(year ~ month.order) задали розділення її на окремі субграфіки. Уздовж горизонталі діаграму поділено на місяці, уздовж вертикалі — на роки. Але наші дані охоплюють лише неповний рік. Якби масив даних охоплював два-три роки, то застосований нами скрипт автоматично розділив-би і місяці і роки. До того-ж наші дані мають два значних пробіли: у лютому та в квітні. Дні, за які відсутні значення показано сірим кольором.
Цифри всередині діаграми виглядають дуже дрібними. Щоб нормально відобразити числові значення — бажано щоб вони містили 1-2 цифри. Ми використали аж три цифри. Щоб нормально вмістити довгі числа треба або збільшувати лінійні розміри вихідного файлу, або зменшувати розмір символів.
Давайте повторимо нашу методику для побудови календарної діаграми концентрацій формальдегіду. При цьому для зручності відображення ми не будемо використовувати абсолютні концентрації формальдегіду в повітрі, а обчислемо для кожного дня кратність перевищення граничної допустимої концентрації. Для роботи ми використаємо первинну таблицю air_pollution, а не її похідні. Нам треба повторити всю послідовність дій: вибрати два потрібні нам поля (дата та концентрації формальдегіду), усереднити дані для кожної доби, створити вектор часу без пропущених днів та об’єднати дані про концентрації формальдегіду з вектором часу.
#Запускаємо таблицю air_pollution в тунель
tbl_df(air_pollution) %>%
#Вибираємо потрібні нам поля дати та концентрацій формальдегіду:
select(date.proba, CH2O) %>%
#Групуємо таблицю по значенням поля tmp.proba:
group_by(date.proba) %>%
#Обчислюємо середнє арифметичне значення концентрацій формальдегіду,
#округляємо результати до четвертого знаку після коми
#та записуємо кінцевий результат в таблицю air.pollution.mean:
summarise(CH2O.mean = round(mean(CH2O, na.rm = TRUE), 4)) -> air.pollution.meanТепер дивимось мінімальне та максимальне значення дати в таблиці air.pollution.mean:
## Min. 1st Qu. Median Mean 3rd Qu.
## "2016-01-02" "2016-02-29" "2016-05-01" "2016-05-01" "2016-07-01"
## Max.
## "2016-08-30"Ми бачемо, що початкова дата наших вимірювань — 2 січня 2016 року, а кінцева дата — 30 серпня 2016 року. Тепер нам треба створити часовий вектор. Але ми створимо його починаючи не з 2, а з 1 січня. І закінчення вектору буде не 30, а 31 серпня. Хіба можна з календаря викидувати дні?
#Створюємо вектор часу date.vector2 від 1.01.2016 до 31.08.2016:
date.vector2 <- seq(from = as.Date("2016-01-01"), to = as.Date("2016-08-31"), by = "days")Порівнюємо довжину вектору часу date.vector2 із довжиною таблиці air.pollution.mean:
## [1] 192## [1] 244Ми бачемо, що в порівнянні з вектором часу date.vector2 в таблиці air.pollution.mean не вистачає 52 дні.
Нам залишилось об’єднати ці два об’єкти:
#Створюємо таблицю данних (data.frame):
date.vector2.table <- data.frame(tmp.date = date.vector2)
#Перетворюємо поле all.date таблиці date.vector2.table на клас character:
date.vector2.table$tmp.date <- as.character(date.vector2.table$tmp.date)
#Перетворюємо поле date.proba таблиці air.pollution.mean на клас character:
air.pollution.mean$date.proba <- as.character(air.pollution.mean$date.proba)
#Приєднуємо таблицю з даними моніторингу повітря
#до таблиці з усіма датами, вказуємо при цьому ключові поля:
air.pollution.mean.join <- dplyr::left_join(date.vector2.table, air.pollution.mean, by = c("tmp.date" = "date.proba"))Якби ми хотіли візуалізувати абсолютні значення концентрацій формальдегіду, то поле CH2O.mean таблиці air.pollution.mean.join можна було б одразу брати для візуалізації. Але ми хочемо візуалізувати у скільки разів було перевищено санітарні норми. Для цього ми під час візуалізації обчислемо там кратність перевищення середньодобової граничної концентрації формальдегіду. Українськими санітарними нормами для повітря населених місць встановлено граничну концентрацію 0,003 мг/м³.
І приступаємо до візуалізації отриманого результату! Скажу наперед, що кратність перевищення санітарних норм становила від 0,5 до 10,6 разів. Ці цифри ми використаємо для інтервалу градієнтної заливки.
#Запускаємо таблицю air.pollution.mean.join в тунель:
tbl_df(air.pollution.mean.join) %>%
#Обчислюємо кратність перевищення граничних концентрацій:
mutate(CH2O.over = round(CH2O.mean/0.003, 1)) %>%
#Перетворюємо поле tmp.date на клас Data:
mutate(tmp.date = as.Date(tmp.date)) %>%
#Отримуємо значення номеру року з поля tmp.date:
mutate(year = as.numeric(format(tmp.date, "%Y")),
#Отримуємо значення назви місяця з поля tmp.date
#і створюємо впорядковані категорії (для правильної послідовності на діаграмі):
month.order = factor(format(tmp.date, "%B"), levels = c("січень", "лютий", "березень", "квітень", "травень", "червень", "липень", "серпень", "вересень", "жовтень", "листопад", "грудень")),
#Отримуємо значення назви дня з поля tmp.date
#і створюємо впорядковані категорії (для правильної послідовності на діаграмі):
weekday.order = factor(format(tmp.date, "%a"),
levels = rev(c("пн", "вт", "ср", "чт", "пт", "сб", "нд"))),
#Отримуємо значення номеру дня місяця з поля tmp.date:
day.month = as.integer(format(tmp.date, "%d")),
#Отримуємо значення короткої назви місяця та номеру року з поля tmp.date:
year.month = format(tmp.date, "%h %Y"),
#Отримуємо значення номеру тижня в році з поля tmp.date:
week = as.numeric(format(tmp.date, "%W"))) %>%
#Групуємо масив даних за значенням поля year.month:
group_by(year.month) %>%
#Створюємо поле зі значеннями номерів тижнів у місяцях:
mutate(monthweek = 1 + week - min(week)) %>%
#Починаємо побудову календарної діаграми:
ggplot(aes(monthweek, weekday.order, fill = CH2O.over)) +
geom_tile(colour = "gray15") +
#Задаємо розбивку графіків на субграфіки за полями year та month.order:
facet_grid(year ~ month.order) +
#Задаємо налаштування градієнтної заливки:
scale_fill_gradient(name = "Кратність перевищення (рази): ",
limits = c(0.0, 11), low = "gold", high = "red3") +
#Налаштовуємо підписи на вісі X
scale_x_continuous(breaks=seq(1, 6, 1)) +#(у місяці може бути до 6 тижнів)
#Додаємо на діаграму числові підписи значень концентрацій пилу:
geom_text(aes(label = CH2O.over), vjust = 0.5, family = "FreeSans", size = 3.0, colour = "firebrick4") +
#Налаштовуємо візуальне оформлення діаграми:
labs(y = "день тижня\n", x = "\nтиждень місяця",
title = "Кратність перевищення санітарних норм формальдегіду") +
theme(plot.title = element_text(hjust = 0.5),
text = element_text(family = "FreeSans",
face = "italic", size = 14, colour = "firebrick4", lineheight = 0.9),
legend.position = "bottom",
legend.text = element_text(family = "FreeSans",
#розвертаємо підписи під легендою на 270 градусів (angle = 270)
face = "italic", size = 14, colour = "firebrick4", lineheight = 0.8, angle = 270),
axis.text.x = element_text(colour = "gray15", face="bold",
size= 12, angle = 0, vjust = 0.5, hjust = 0.5),
axis.text.y = element_text(colour = "gray15", face="bold",
size= 12, angle = 0, vjust = 0.5, hjust = 1),
axis.ticks = element_line(colour = "orange", size = 0.2),
plot.background = element_rect(fill = "gray95"),
panel.grid.major = element_line(colour = "orange", size = 0.2),
panel.grid.minor = element_line(colour = "gray90"),
panel.background = element_rect(fill="gray95")) ->
#Зберігаємо календарну діаграму в об’єкт calendar.CH2O:
calendar.CH2OВсе, що нам залишилось - це експортувати побудовану календарну діаграму в зовнішній графічний файл.
#Створюємо порожній графічний файл
png("calendar_CH2O.png", width = 297,
height = 210, units = "mm", res = 150)
#викликаємо всередині файлу візуалізацію calendar.CH2O:
calendar.CH2O
#записуємо графічний файл у файлову систему
dev.off()Кінцева версія календарної діаграми середньодобових концентрацій формальдегіду буде виглядати отак:
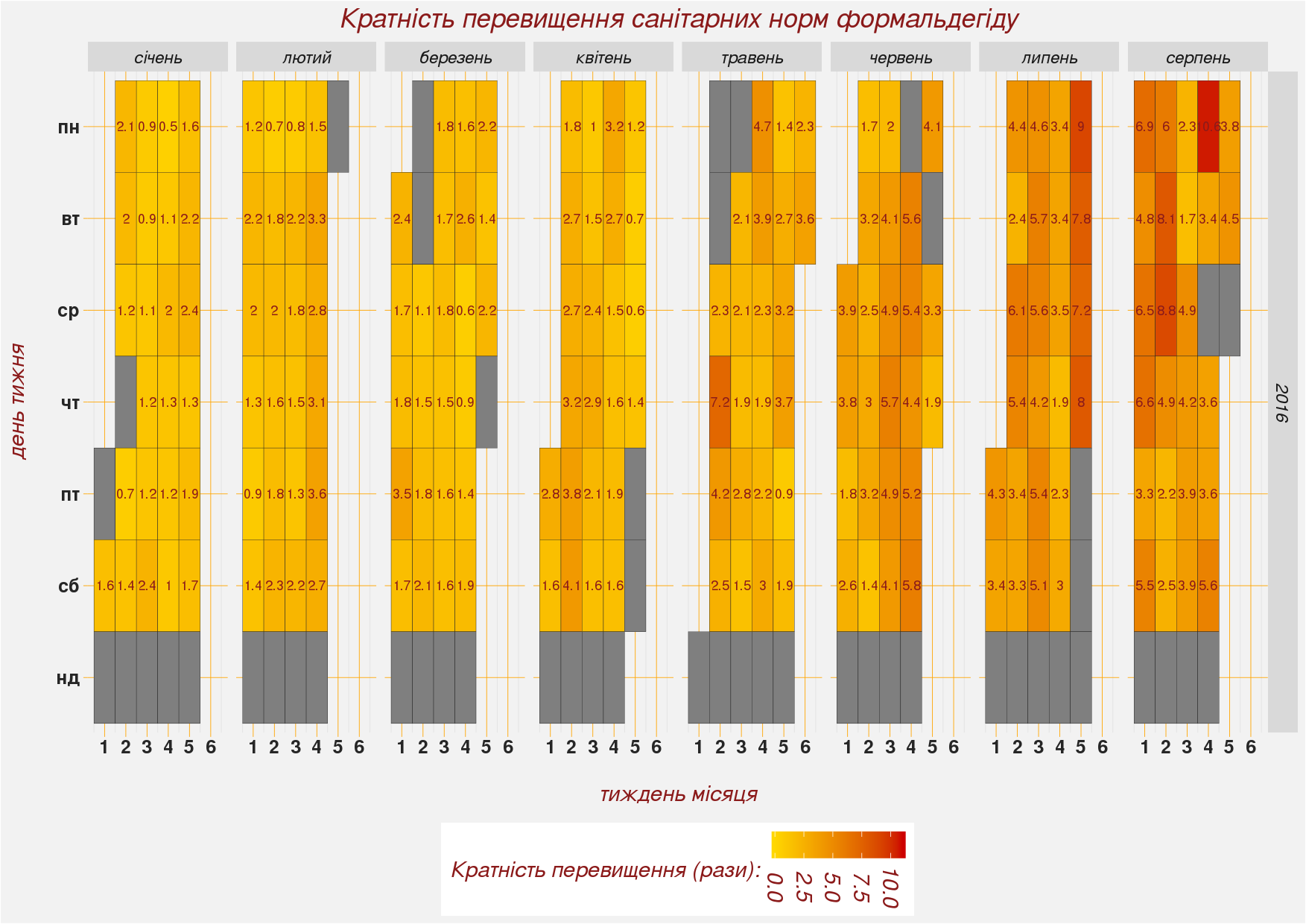
Figure 4.3: Кінцевий вигляд календарної діаграми кратності перевищень концентрацій формальдегіду
4.6 Трикутні діаграми
Трикутна діаграма (Ternary plot) є доволі цікавим методом візуалізації. На цій діаграмі відображується співвідношення трьох будь-яких компонентів. При цьому сума компонентів приймається рівною 100%. Цей метод візуального аналізу широко застосовується у мінералогії, петрографії, матеріаловеденні та інших науках, які розглядають співвідношення компонентів у сумішах. Такі діаграми дозволяють зробити щось на кшалт кластеризації або компонентного аналізу даних — на отриманих трикутниках візуально можна виділити сукупчення точок, які зв’язані схожими умовами. Побудова трикутних діаграм реалізована у декількох пакетах R. Ми використаємо пакет ggtern (Hamilton 2017), який є надбудовою до пакету ggplot2 (Wickham 2009).
Єдиний великий недолік цього методу візуалізації — ми повинні регулювати значення досліджуваних нами змінних таким чином, щоб вони були приблизно рівноцінними. Наприклад, ми хочемо дослідити співвідношення між концентраціями в повітрі монооксиду вуглецю, діоксиду азоту та формальдегіду. При цьому абсолютні значення концентрацій монооксиду вуглецю коливаються в межах 0 - 10. У той час як концентрації формальдегіду коливаються в межах 0 - 0.084, а діоксиду азоту — в межах 0 - 0.31. Якщо ми перерахуємо загальний склад цієї трикомпонентної суміші на 100%, то монооксид вуглецю захопить собі найбільшу частку із цих 100%. Відповідно — варіативність інших двох компонентів буде невиразною. Щоб уникнути цього можна привести значення всіх трьох компонентів до діапазонів 0-1, або просто поділити значення концентрацій монооксиду вуглецю на 100. Ми оберемо останній варіант, просто поділивши значення монооксиду вуглецю. Ясна річ, що подібних проблем не виникає якщо компоненти суміши мають приблизно однакові границі концентрацій.
Тепер давайте перейдемо до діла! Для побудови трикутної діаграми використаємо таблицю air_pollution.join, яку ми отримали на попередніх етапах обробки наших даних. Із цієї таблиці нам треба тільки значення концентрацій монооксиду вуглецю (CO), діоксиду азоту (NO2) та формальдегіду (CH2O). Ми не просто покажемо координати точок в трикомпонентній системі «\(CO - NO_2 - CH_2O\)», а й позначемо кольоровою гамою значення концентрацій формальдегіду для кожної окремої точки. Також ми додамо візуальне оформлення діаграми та розглянемо деякі можливості її оптимізації.
Але для початку не забудемо завантажити пакет ggtern! Не забувайте, що різні пакети можуть використовувати однакові назви функцій і пакет, який було завантажено останнім — перекриє собою однакові за назвою функції попередніх пакетів. Пакет ggtern перекриває функції пакетів psych та ggplot2. Для уникнення плутанини не треба тримати в робочому середовищі безліч завантажених пакетів!
Побудуємо трикутну діаграму зі стандартним оформленням.
## Registered S3 methods overwritten by 'ggtern':
## method from
## +.gg ggplot2
## grid.draw.ggplot ggplot2
## plot.ggplot ggplot2
## print.ggplot ggplot2## --
## Remember to cite, run citation(package = 'ggtern') for further info.
## --##
## Attaching package: 'ggtern'## The following object is masked from 'package:psych':
##
## %+%## The following objects are masked from 'package:ggplot2':
##
## %+%, aes, annotate, calc_element, ggplot, ggplot_build,
## ggplot_gtable, ggplotGrob, ggsave, layer_data, theme,
## theme_bw, theme_classic, theme_dark, theme_gray, theme_light,
## theme_linedraw, theme_minimal, theme_void #запускаємо таблицю air_pollution.join в тунель:
tbl_df(air_pollution.join) %>%
#вибираємо потрібні нам поля таблиці:
select(CO, NO2, CH2O) %>%
#ділимо концентрації монооксиду вуглецю на 100:
mutate(CO = CO/100) %>%
ggplot(aes(x = CO, y = NO2,
z = CH2O, color = CH2O)) +
geom_point(size= 2.5, alpha = 0.75) +
#вказуємо, що нам потрібна трикутна система координат:
coord_tern() +
labs(x = "CO", y = "NO2", z = "CH2O",
title = "Співвідношення концентрацій в системі «CO - NO2 - CH2O»")## Warning: Removed 1709 rows containing missing values (geom_point).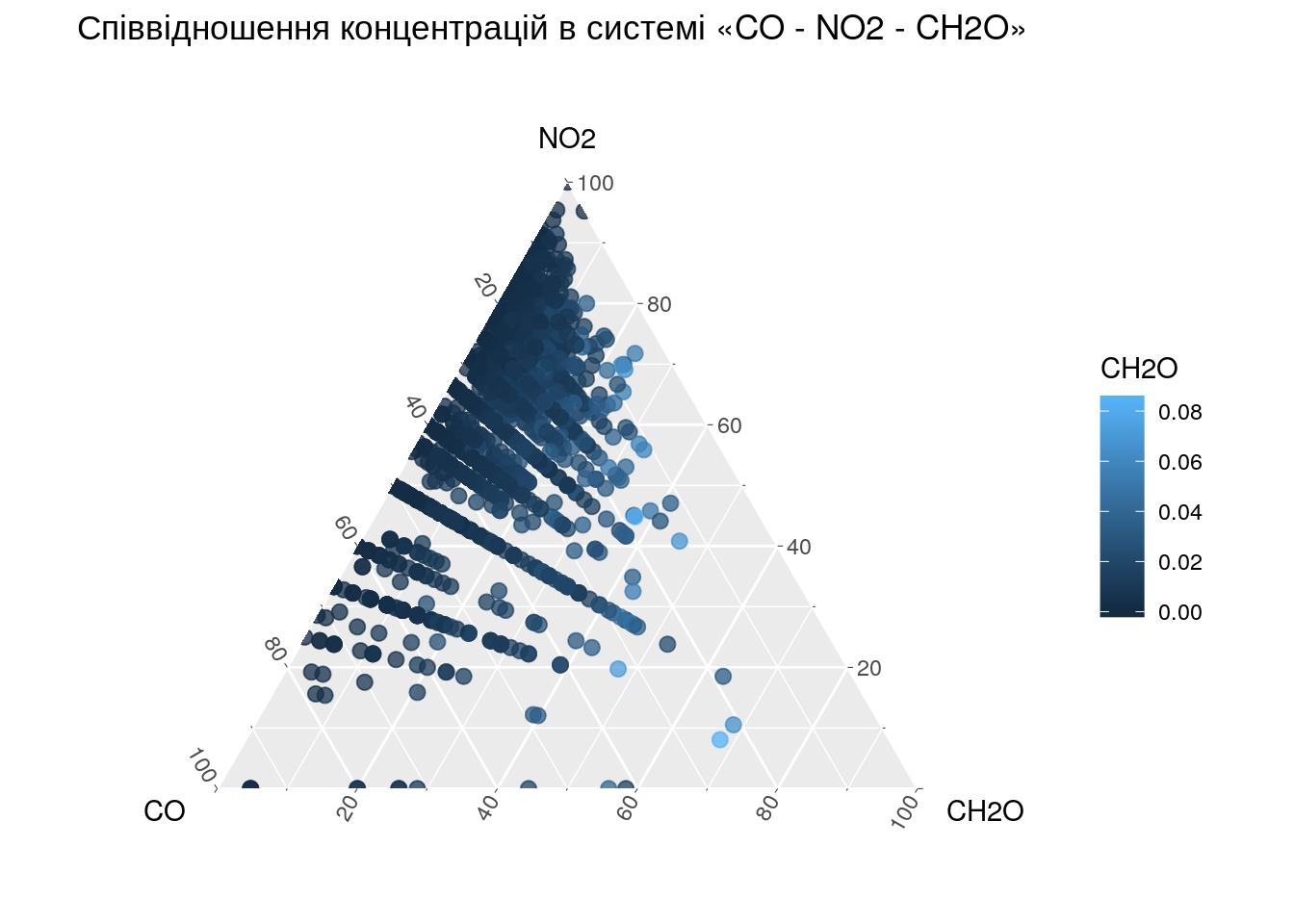
В процесі побудови діаграми R повідомляє нам, що функцією geom_point було усунуто 1709 рядків, які мали порожні значення.
Тепер ми можемо доповнити нашу діаграму візуальними елементами. Ми змінимо кольорову заливку точок діаграми та додамо до неї легенду. Також ми додамо стрілки, які будуть вказувати напрям осей нашої діаграми. А ще ми використаємо можливості розмітки \(\LaTeX\) щоб красиво відобразити формули хімічних речовин. Для змінення кольорової заливки використаємо функцію scale_color_gradient2. Щоб додати стрілки потрібно додати функцію theme_showarrows. А для того, щоб використати розмітку \(\LaTeX\) треба додати функцію theme_latex. Для налаштування підписів стрілок діаграми використовуються параметри xarrow, yarrow та zarrow. Для загального оформлення ми використаємо налаштування оформлення, які використовуємо для всієї графіки в цій книзі.
#запускаємо таблицю air_pollution.join в тунель:
tbl_df(air_pollution.join) %>%
#вибираємо потрібні нам поля таблиці:
select(CO, NO2, CH2O) %>%
#ділимо концентрації монооксиду вуглецю на 100:
mutate(CO = CO/100) %>%
ggplot(aes(x = CO, y = NO2,
z = CH2O, color = CH2O)) +
geom_point(size= 2.5, alpha = 0.75) +
#вказуємо, що нам потрібна трикутна система координат:
coord_tern() +
#змінюємо кольорову заливку та підпис легенди:
scale_color_gradient2(name = "Концентрація формальдегіду, мг/м³: ",
limits = c(0.0, 0.09), low = "royalblue3", mid = "yellow",
high = "orangered3", midpoint = 0.025, na.value = "gray75") +
#додаємо стрілки осей на діаграму
theme_showarrows() +
#підключаємо розпізнавання розмітки LaTeX:
theme_latex() +
#налаштовуємо підписи до стрілок осей параметрами xarrow, yarrow, zarrow:
labs(x = "CO/100", y = "NO2", z = "CH2O",
xarrow = "CO/100, %",
yarrow = "NO_2, %",
zarrow = "CH_2O, %",
title = "Співвідношення концентрацій в системі «CO - NO_2 - CH_2O»") +
#налаштовуємо загальний вигляд діаграми:
theme(plot.title = element_text(hjust = 0.5),
text = element_text(family = "FreeSans",
face = "plain", size = 12, colour = "firebrick4", lineheight = 0.9),
legend.position = "bottom",
legend.box = "vertical",
legend.key.width = unit(1.25, "cm"),
legend.text = element_text(family = "FreeSans",
face = "plain", size = 12, colour = "firebrick4",
lineheight = 0.8, angle = 0),
legend.background = element_rect(fill="white",
size=0.25, linetype="solid", colour ="gray15"),
strip.text.x = element_text(size = 12, face = "bold"),
axis.text.x = element_text(colour = "gray15", face="bold",
size= 12, angle = 0, vjust = 0.0, hjust = 0.5),
axis.text.y = element_text(colour = "gray15", face="bold",
size= 12, angle = 0, vjust = 0.5, hjust = 1),
axis.ticks = element_line(colour = "orange", size = 0.2),
plot.background = element_rect(fill = "gray95"),
panel.grid.major = element_line(colour = "orange", size = 0.2),
panel.grid.minor = element_line(colour = "gray90"),
panel.background = element_rect(fill="gray95")) +
guides(fill = guide_legend(reverse = TRUE))## Warning: Removed 1709 rows containing missing values (geom_point).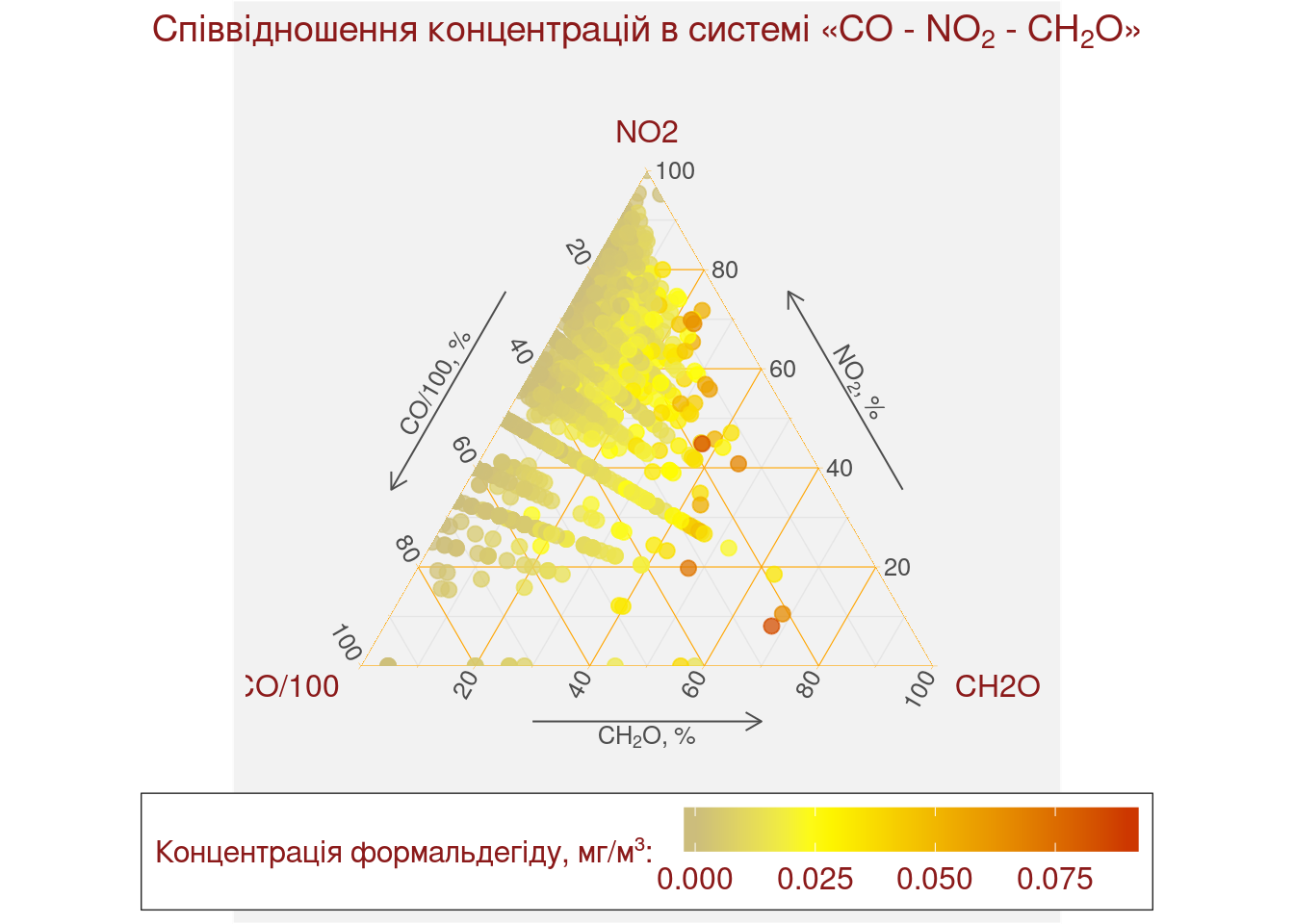
4.7 Хто як моніторить (різниця в даних)
4.8 Експорт проміжних таблиць
Посилання
Hamilton, Nicholas. 2017. Ggtern: An Extension to ’Ggplot2’, for the Creation of Ternary Diagrams. https://CRAN.R-project.org/package=ggtern.
Revelle, William. 2016. Psych: Procedures for Psychological, Psychometric, and Personality Research. Evanston, Illinois: Northwestern University. https://CRAN.R-project.org/package=psych.
Wickham, Hadley. 2009. Ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag New York. http://ggplot2.org.