Capítulo 2 MAUC-Absorción oral
Última actualización: 2023-11-08
En este capítulo se recopilan ejercicios para el modelo de un compartimento con administración oral.
2.1 Ecuaciones del modelo
Ecuación (2.1): Ecuación integrada general con tiempo de latencia
\[\begin{equation} C=C^0 \cdot e ^{-K_{el}\cdot t}- A^0 \cdot e ^{-K_{a}\cdot t} \tag{2.1} \end{equation}\]
Donde:
- \(C\) Es la concentración plasmática al tiempo \(t\)
- \(C^0\) Es la ordenada del origen de las fases de absorción y eliminación en un modelo de un compartimiento con administración extravasal
- \(K_{el}\) Es la constante de eliminación
- \(A^0\) Es la ordena del origen de la fase de abosorción
- \(K_a\) es la constante de absorción
Ecuación (2.2): Ecuación integrada sin tiempo de latencia
\[\begin{equation} Cp= \frac{F \cdot D \cdot K_a}{V_d \cdot (K_a-K_{el})} \cdot [e ^{-K_{el}\cdot t}- e ^{-K_{a}\cdot t}] \tag{2.2} \end{equation}\]
Donde:
- \(F\) es la biodisponibilidad del fármacos (fracción del fármaco absorbida)
La ecuación (2.2) puede ser interpretada como: Ecuación (2.3): Ecuación integrada general sin tiempo de latencia
\[\begin{equation} C= \frac{FD}{V_d}\cdot \frac{K_a}{(K_a-K_{el})} \big(e ^{-K_{el}\cdot t}- e ^{-K_{a}\cdot t}\big) \tag{2.3} \end{equation}\]
Ecuación (2.4): Volumen de distribución
\[\begin{equation} V_d= \frac{F\cdot D}{C^0}\cdot \frac{K_a}{(K_a-K_{el})} \tag{2.4} \end{equation}\]
Ecuación (2.5): Aclaramiento
\[\begin{equation} Cl=V_d \cdot K_{el} \tag{2.5} \end{equation}\]
Ecuación (2.6): Tiempo de latencia
\[\begin{equation} tl=\frac{ln\frac{A^0}{C^0}}{K_a-K_{el}} \tag{2.6} \end{equation}\]
Ecuación (2.7): tmax sin tiempo de latencia
\[\begin{equation} tmax= \frac{ln\big(\frac{K_a}{K_{el}}\big)}{(K_a-K_{el})} \tag{2.7} \end{equation}\]
Ecuación (2.8): tmax con tiempo de latencia
\[\begin{equation} tmax=\frac{ln\bigg( \frac{K_a}{K_{el}} \cdot \frac{A^0}{C^0}\bigg)}{K_a-K_{el}} \tag{2.8} \end{equation}\]
Ecuación (2.9): Concentración plasmática máxima con tiempo de latencia
\[\begin{equation} Cpmax=C^0 \cdot e ^{-K_{el}\cdot tmax}- A^0 \cdot e^{-K_a\cdot tmax} \tag{2.9} \end{equation}\]
Ecuación (2.10): Concentración plasmática máxima sin tiempo de latencia
\[\begin{equation} Cpmax=\frac{F \cdot D}{V_d}\big(e^{-K_{el}\cdot tmax}\big) \tag{2.10} \end{equation}\]
Ecuación (2.11): Área bajo la curva de tiempo cero a tiempo t \[\begin{equation} ABC^t_0=\frac{C^0}{K_{el}}\cdot\big(1-e^{-K_{el}\cdot t}\big)- \frac{A^0}{K_a}\cdot\big(1-e^{-K_{a}\cdot t}\big) \tag{2.11} \end{equation}\]
Ecuación (2.12): Área bajo la curva de tiempo cero a infinito \[\begin{equation} ABC^\infty_0=\frac{C^0}{K_{el}}-\frac{A^0}{K_a} \tag{2.12} \end{equation}\]
Ecuación (2.13): Biodisponibilidad en magnitud \[\begin{equation} F=\frac{(ABC^\infty_0)_{oral}}{(ABC^\infty_0)_{ref}}\cdot \frac{D_{ref}}{D_{oral}} \cdot \frac{Cl_{oral}}{Cl_{ref}} \tag{2.13} \end{equation}\]
Ecuación (2.14): Concentración plasmática máxima sin tiempo de latencia, formula no abreviada \[\begin{equation} Cmax=\frac{K_a\cdot F \cdot D}{V_d(K_a-K_{el})}\cdot \bigg(e^{-K_{el} \cdot tmax}- e^{-K_a \cdot tmax} \bigg) \tag{2.14} \end{equation}\]
2.2 Problemas
Ejemplo 2.1 En el estudio de biodisponibilidad de unos comprimios de 500 mg de principio activo, se obtienen los datos de concentraciones plasmáticas que se detallan en la siguiente tabla:
| Tiempo (h) | Conc µg/mL |
|---|---|
| 0.25 | 10.2 |
| 0.5 | 29.38 |
| 1 | 49.03 |
| 2 | 53.46 |
| 4 | 34.07 |
| 8 | 10.48 |
| 16 | 0.95 |
| 24 | 0.09 |
A partir de los datos anteriores y sabiendo que la biodisponibilidad de los comprimidos es del 85% y la dosis fue de 500mg. Determine:
- tmax
- Cpmax
- Vd
- \(t_{1/2}\)
- ABC
Ejercicio tomado de: Biofarmacia y farmacocinética Ejercios y problemas resueltos. Antonio Aguilar Ros, María Consuelo Montejo Rubio, Manuel Caamaño Somoza, Félix Ramón Martín Martín. 2da Edición. España. 2014
Ejercicio 2.1 A un paciente se le administra un comprimido de 250 mg de un fármaco y se obtienen las siguiente concentraciones plasmáticas. La biodisponibilidad es de 100% .
| t (h) | Cp (µg/mL) |
|---|---|
| 0.25 | 1.56 |
| 0.5 | 2.66 |
| 1 | 3.91 |
| 1.5 | 4.41 |
| 2 | 4.51 |
| 3 | 4.2 |
| 4 | 3.68 |
| 5 | 3.17 |
| 6 | 2.71 |
| 7 | 2.31 |
Calcule:
- cmax
- tmax
- ABC de cero al infinito
- concentración plasmática a las 0.75 h
Ejercicio 2.2 Dosis 500mg y biodisponibilidad de 100%. Calcule los mismos parámetros que el problema 2.1. analice que pasa con los parámetros si se dobla la dosis y que si la F es del 65%.
| t (h) | Cp (µg/mL) |
|---|---|
| 0.5 | 5.36 |
| 1 | 9.95 |
| 2 | 17.18 |
| 4 | 25.78 |
| 6 | 29.78 |
| 12 | 26.63 |
| 18 | 19.4 |
| 24 | 13.26 |
| 36 | 5.38 |
| 48 | 2.56 |
| 72 | 0.49 |
Ejercicio 2.3 Los fármacos A y B se ajustan a un MAUC-extravasal y siguen una cinética de primer orden. Con una dosis de 500mg y F de 1. Calcule tmax y cmax para cada uno. Asuma un tiempo de latencia de 0 h
| Fármaco | \(K_a \ h^{-1}\) | \(K_{el} \ h^{-1}\) | \(V_d\) (mL) |
|---|---|---|---|
| A | 1 | 0.2 | 10000 |
| B | 0.2 | 1 | 20000 |
Ejercicio tomado de: Applied Biopharmaceutics and Pharmacokinetics. Shargel Leon., Andrew B.C. 8a. Ed. Editorial Appleton & Plange. Noewalk, USA. 2022.
Ejercicio 2.4 En un estudio de biodisponibilidad se ensayan dos formas farmaceúticas, una solución para administración intravenosa de 300 mg y un comprimido de 500 mg. Después del análisis de los resultados obtenidos para la vía parenteral, se llega a la conclusión de que estos se ajustan a un modelo monocompatimental cuya ecuación es:
\[ C=16.67 \cdot e^{-0.9 \cdot t} \]
Los datos obtenidos en la administración oral han sido los siguientes:
| Tiempo (h) | Conc µg/mL |
|---|---|
| .5 | 1.653 |
| 1 | 7.484 |
| 2 | 11.668 |
| 3 | 11.462 |
| 4 | 9.892 |
| 6 | 6.465 |
| 8 | 3.998 |
| 12 | 1.481 |
| 24 | 0.074 |
- Dertermine Ka y tiempo de latencia
- Compare las constantes de velocidad obtenidas por las distintas vías
- Determine si existe fenómeno de flip-flop
Ejercicio tomado de: Biofarmacia y farmacocinética Ejercios y problemas resueltos. Antonio Aguilar Ros, María Consuelo Montejo Rubio, Manuel Caamaño Somoza, Félix Ramón Martín Martín. 2da Edición. España. 2014
Ejercicio 2.5 Se administró en un grupo de sujetos una tableta masticable de 50 mg de un fármaco experimental. Los promedios de las concentraciones plasmáticas del grupo de 20 sujetos se muestran en la siguiente tabla:
| Tiempo (h) | Cp (ug/mL) |
|---|---|
| 0.5 | ND |
| 1 | 0.03468 |
| 2 | 0.09896 |
| 3 | 0.1034 |
| 4 | 0.08812 |
| 5 | 0.02748 |
| 16 | 0.0176 |
| 24 | 0.00012 |
- Calacular los parámetros del sistema, asumiendo un modelo abierto de un compartimento con una cinética de primer orden
Se sabe que además, que la administración de 30 mg de este mismo fármaco por vía IV dio los siguientes resultados:
\[ ABC^\infty_0=23.688 \mu \cdot h/mL \]
\[ K_{el \ ref}=0.347 h^{-1} \]
- Calcula la biodisponibilidad absoluta
Ejercicio 2.6 En el estudio de una formulación sólida con 500 mg de un ansiolítico se obtuvieron los siguientes datos:
| Tiempo (h) | Conc. (ug/mL) |
|---|---|
| 0.5 | ND |
| 1 | 0.867 |
| 2 | 2.474 |
| 3 | 2.585 |
| 4 | 2.203 |
| 8 | 0.687 |
| 16 | 0.044 |
| 24 | 0.003 |
La administración de una dosis de 300 mg de este mismo fármaco por vía IV dio los siguientes resultados
\(ABC^\infty _0= 59.22 \ \mu g \cdot h/mL\)
- Con los datos anteriores calcular los parámetros del sistema para la formulación sólida
- Biodisponibilidad absoluta en magnitud de la formulación sólida
Ejercicio 2.7 Después de la administración de un comprimido de 500 mg con recubrimiento entérico de un ansiolítico a un grupo de voluntarios sanos con un peso promedio de 70 kg, se obtuvieron las siguientes concentraciones plasmáticas:
| Tiempo (h) | Conc. (ug/mL) |
|---|---|
| 0.5 | ND |
| 1.5 | ND |
| 2 | 4.04 |
| 2.5 | 8.43 |
| 3 | 10.79 |
| 4 | 12.02 |
| 8 | 6.19 |
| 12 | 2.37 |
| 24 | 0.12 |
- Grafique en papel semilogarítmico
- Identifique la ecuación del sistema
- Identifique el tiempo de latencia de forma gráfica
- Estime el tiempo de latencia con la formula
Adaptado de: Biofarmacia y farmacocinética Ejercios y problemas resueltos. Antonio Aguilar Ros, María Consuelo Montejo Rubio, Manuel Caamaño Somoza, Félix Ramón Martín Martín. 1era Edición. España. 2008
Ejercicio 2.8 Se han obtenido los siguientes datos farmacocinéticos tras la administración de un comprimido sublingual con 100 mg de fármaco:
- \(F=0.94\)
- \(Cmax= 3.06 \mu g/mL\)
- \(tmax=1.95 h\)
- \(t_{latencia}= 0.06 h\)
- \(V_d= 19.07 L\)
- \(t_{1/2} Eliminación= 2.77 h\)
- \(t_{1/2} absorción= 0.714 h\)
A partir de los datos anteriores:
- Calcular la ecuación que permite calcular la concentración plasmática.
- Calcular la cantidad de fármaco en el lugar de absorción a las 2 horas de la administración.
- Calcular la cantidad de fármaco eliminado en ese mismo tiempo
- Calcular la concentración plasmática a la 4 horas de la administración
- ¿Cuánto tiempo deberá de transcurrir desde el comienzo del proceso de absorción para dicho proceso verifique en un 87.5%? Es decir, que el 87.5% del fármaco se absorba.
Ejercicio 2.9 Después de la administración una dosis oral de 100 mg de un fármaco antihistamínico a un grupo de voluntarios se obtuvieron los siguientes datos plasmáticos promedios:
| t (horas) | Cp (ug/mL) |
|---|---|
| 1 | 1.88 |
| 2 | 2.06 |
| 3 | 2.27 |
| 5 | 2.65 |
| 7 | 2.87 |
| 9 | 2.46 |
| 12 | 2.08 |
| 18 | 1.33 |
| 24 | 0.813 |
| 36 | 0.297 |
| 48 | 0.107 |
- Grafique los datos en papel semilogarítmico
- ¿Cuál es el tiempo medio de eliminación del fármaco en este grupo de voluntarios?
- ¿Cuál es la velocidad de absorción del fármaco?
- Indentifique si hay tiempo de latencia
- Estime el resto de los parámetros del modelo
- Indique la ecuación del modelo
Ejercicio adaptado de:https://www.u-cursos.cl/faciqyf/2010/2/FBQI4201/2/material_docente/bajar?id_material=566335
Ejercicio 2.10 Al administrar una dosis de 500 mg de un fármaco por vía oral se encuentra que la ecuación que describe la concentración plasmática en función del tiempo es:
\[ Cp=28.5\big(e^{-0.123\cdot t}-e^{-0.438\cdot t}\big) \]
Determine:
- Si hay tiempo de latencia
- \(tmax\)
- \(Cpmax\)
- \(t_{1/2}\)
- \(V_d\)
Ejercicio adaptado de:https://www.u-cursos.cl/faciqyf/2010/2/FBQI4201/2/material_docente/bajar?id_material=566335
Ejercicio 2.11 A un paciente se le administra un comprimido de 250 mg de un fármaco y se determina la concentración sanguínea a diversos tiempos posteriores a la administración obteniéndose los siguientes resultados:
| t (horas) | Cpl (ug/mL) |
|---|---|
| 0.25 | 1.56 |
| 0.5 | 2.66 |
| 1 | 3.91 |
| 1.5 | 4.41 |
| 2 | 4.51 |
| 3 | 4.20 |
| 4 | 3.68 |
| 5 | 3.17 |
| 6 | 2.71 |
| 7 | 2.31 |
Estimar:
- Si existe tiempo de latencia
- Todos los paramétros del sistema
- El volumen de distribución suponiendo una biodisponibilidad del 100
- Si se duplica la dosis que sucede con los parámetros del sistema
Ejercicio adaptado de:https://www.u-cursos.cl/faciqyf/2010/2/FBQI4201/2/material_docente/bajar?id_material=566335
Ejercicio 2.12 Al administrar un comprimido de un fármaco X, los niveles plasmáticos son los señalados siguiente tabla:
| Tiempo (horas) | Cpl (ug/mL) |
|---|---|
| 0.5 | 5.2 |
| 1.0 | 20.0 |
| 1.5 | 23.0 |
| 2.0 | 25.1 |
| 3.0 | 16.8 |
| 4.0 | 11.4 |
| 5.0 | 7.6 |
| 6.0 | 5.2 |
| 7.0 | 3.5 |
Calcule:
- Tiempo de vida media
- Ka
- Kel
- Tiempo de latencia
- El Volúmen de distribución
- Si se duplica el volumen de distribución con respecto a la estimación anterior, que sucede con los parámetros del sistema
Gráfique:
- Los valores de Cp vs T
- Los valoles de Cp vs T en papel semilogarítimco
- Las regresiones de eliminación y de absorción
La dosis de este fármaco fueron 500 mg
Ejercicio 2.13 La administración IV de un bolo de 100mg generó los siguientes resultados:
| Tiempo (horas) | Cpl (ug/mL) |
|---|---|
| 0.25 | 3.75 |
| 0.5 | 2.8 |
| 1.0 | 1.75 |
| 1.5 | 1.1 |
| 2 | 0.55 |
La administración de la misma dosis oral en forma de comprimido generó los siguientes resultados:
| Tiempo (horas) | Cpl (ug/mL) |
|---|---|
| 0.5 | 0.57 |
| 1.0 | 0.88 |
| 1.5 | 1.03 |
| 2.0 | 1.07 |
| 2.5 | 1.04 |
| 3.0 | 0.98 |
| 4.0 | 0.82 |
| 6.0 | 0.50 |
| 8.0 | 0.29 |
| 12.0 | 0.09 |
- Calcule los parámetros del sistema para el bolo
- Calcule los parámetros del sistema para comprimido
- Compare las constantes y describe sus observaciones
- ¿Hay fenómeno de flip-flop?
- Estime la Biodisponibilidad absoluta
- ¿Si en la formulación oral se invierten las constantes absorción y eliminación que sucede con los parámetros del sistema?
Ejercicio 2.14 Se recolectaron muestras de plasma de un paciente después de una dosis oral de 10 mg de una nueva solución de benzodiazepina de la siguiente manera:
| tiempo (h) | Concentración (ng/mL) |
|---|---|
| 0.25 | 2.85 |
| 0.50 | 5.43 |
| 0.75 | 7.75 |
| 1.00 | 9.84 |
| 2.00 | 16.20 |
| 4.00 | 22.15 |
| 6.00 | 23.01 |
| 10.00 | 19.09 |
| 14.00 | 13.90 |
| 20.00 | 7.97 |
De los datos dados:
Determine la constante de eliminación del fármaco.
Determine la constante de absorción por el método de los residuales
Determine la ecuación que describe la concentración de fármaco en plasma de la nueva benzodiazepina.
Suponiendo que el fármacose absorbe en un 80%, encuentre:
- la vida media de eliminación, \(t_{1/2}\);
- el tmax,
- el volumen de distribución del paciente.
Ejercicio 2.15 Se administró una dosis oral única (100 mg) de un antibiótico a un paciente masculino adulto (43 años, 72 kg). Según la literatura, la farmacocinética de este fármaco se ajusta a un modelo abierto de un compartimento. La ecuación que mejor se ajusta a la farmacocinética del fármaco es:
\[ Cp=45\cdot \big(e^{-0.17\cdot t}-e^{-1.5\cdot t}\big) \]
A partir de la ecuación anterior, calcule:
- \(tmax\)
- \(Cpmax\)
- \(t_{1/2}\)
- ¿Hay tiempo de latencia?
Suponga que Cp está en \(\mu g/mL\) y las constantes de velocidad de primer orden están en \(h^{-1}\)
Ejercicio 2.16 La biodisponibilidad del clorhidrato de fenilpropanolamina se estudió en 24 sujetos varones adultos. Los siguientes datos representan las concentraciones medias de clorhidrato de fenilpropanolamina en sangre (ng/mL) después de la administración oral de una dosis única de 25 mg de solución de clorhidrato de fenilpropanolamina:
| Tiempo (h) | Cocentración (ng/mL) | Tiempo (h) | Cocentración (ng/mL) |
|---|---|---|---|
| 0 | 0 | 3 | 62.98 |
| 0.25 | 51.33 | 4 | 52.32 |
| 0.5 | 74.05 | 6 | 36.08 |
| 0.75 | 82.91 | 8 | 24.88 |
| 1.0 | 85.11 | 12 | 11.83 |
| 1.5 | 81.76 | 18 | 3.88 |
| 2 | 75.51 | 24 | 1.27 |
A partir de los datos anteriores, obtenga:
- la constante de velocidad de absorción, \(K_a\), y la constante de velocidad de eliminación, \(K_{el}\), por el método de los residuos.
- ¿Es razonable suponer que \(K_a\) > \(K_{el}\) para un fármaco en solución? ¿Cómo determinaría inequívocamente qué constante de velocidad representa la constante de eliminación \(K_{el}\)?
- A partir de sus valores, calcule el \(tmax\). ¿Cómo se relaciona su valor con el \(tmax\) observado obtenido de los sujetos en los datos tabulados?
Ejercicio 2.17 Se administraron 500 mg de un fármaco por vía oral a un grupo de 40 individuos sanos de un peso promedio de 70 kg. Las concentranciones séricas promedio se encuentran en la siguiente tabla:
| Tiempo (h) | Cp (ug/mL) |
|---|---|
| 1 | 10.72 |
| 2 | 19.9 |
| 4 | 34.36 |
| 8 | 51.56 |
| 16 | 59.56 |
| 24 | 53.26 |
| 36 | 38.8 |
| 48 | 26.52 |
| 72 | 11.76 |
| 96 | 5.12 |
| 144 | 0.98 |
Se sabe que la biospinibilidad del fármaco es del 100%.
- Estime los parámetros del modelo
- ¿Se trata de un fármaco de liberación prolongada? Justifique su respuesta
Ejercicio 2.18 Después de la adminsitración oral de un fármaco a un grupo de voluntarios sanos, la ecuación representativa del tránsito de este fármaco en el organimo es la siguiente:
\[ C=57.5\cdot e^{-0.312 \cdot t} - 69.2 \cdot e^{-1.05 \cdot t} \]
- Determine los parámetros del sistema. El fármaco tiene una biodisponibilidad del 85%. Suponga que Cp está en \(\mu g/mL\) y las constantes de velocidad de primer orden están en \(h^{-1}\) y que la dosis fue de 500 mg.
2.3 Resolución ejemplos
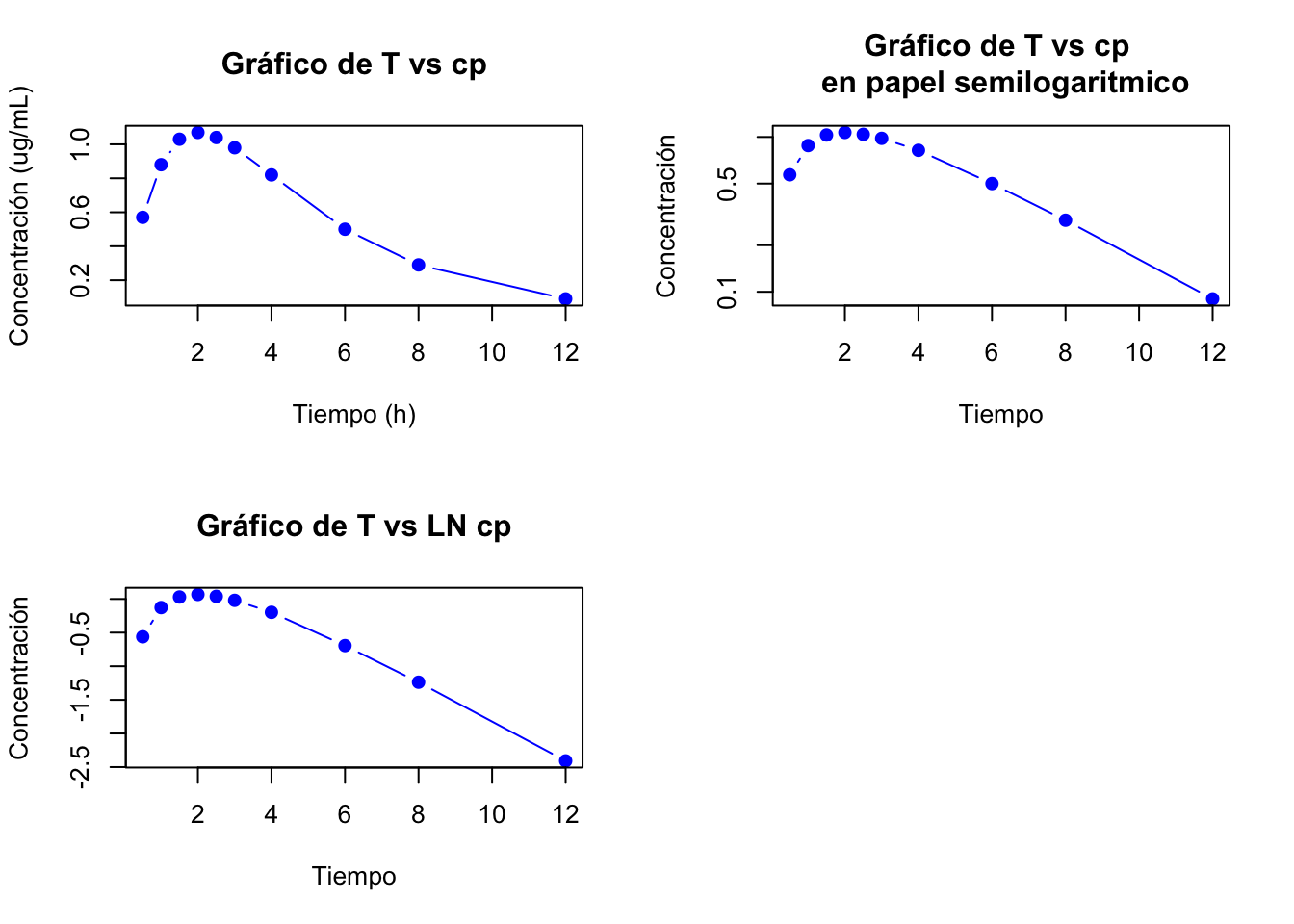
2.3.1 Resolucoión ejemplo 2.1
- Graficar los datos de Cp vs T
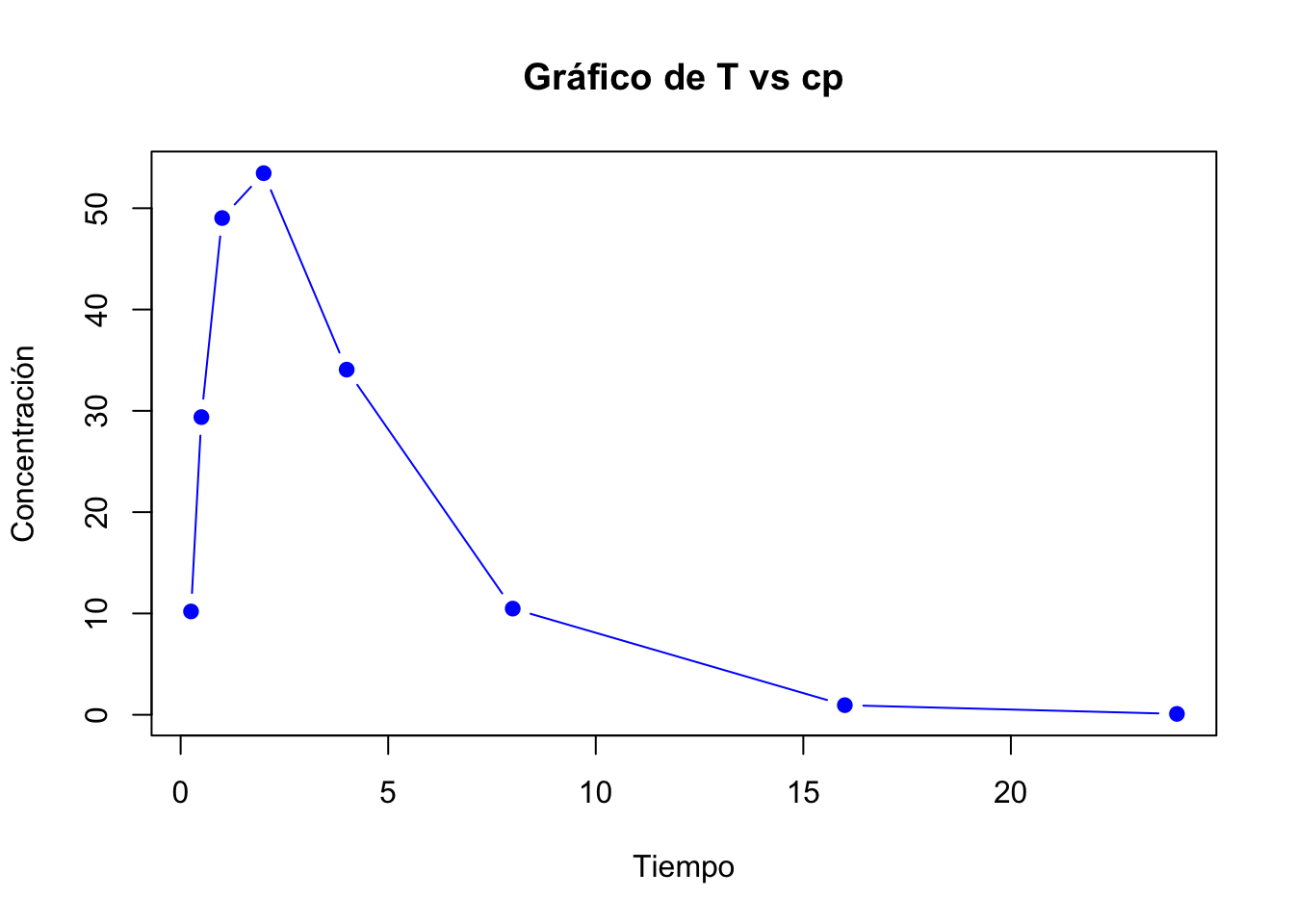
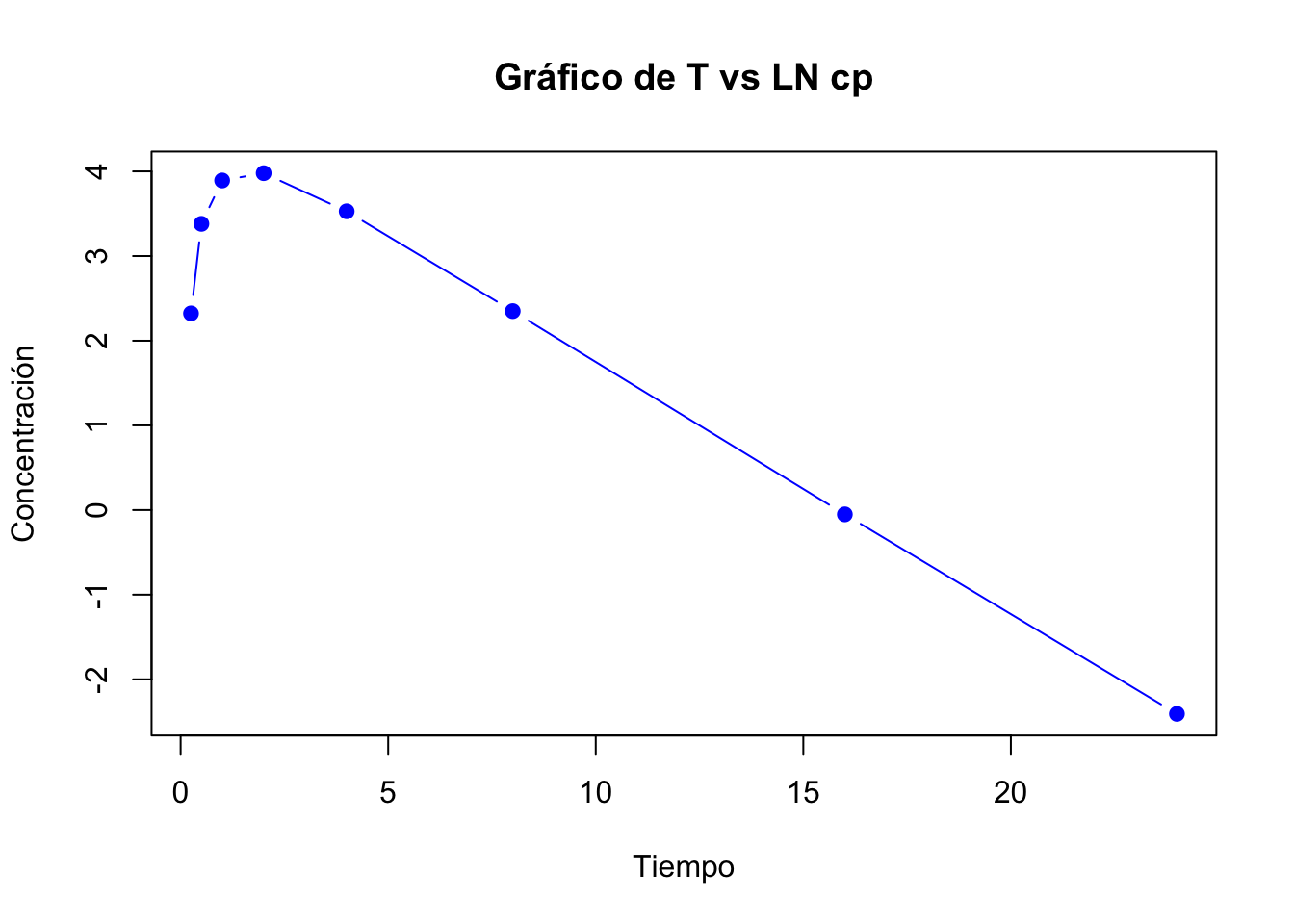
- Graficar los datos de Cp vs T en papel semilogarítmico
Si no puede graficar los datos en papel semilogarítmico, puede gráfica el LN de Cp vs T. En este caso se graficó utilizando el LN
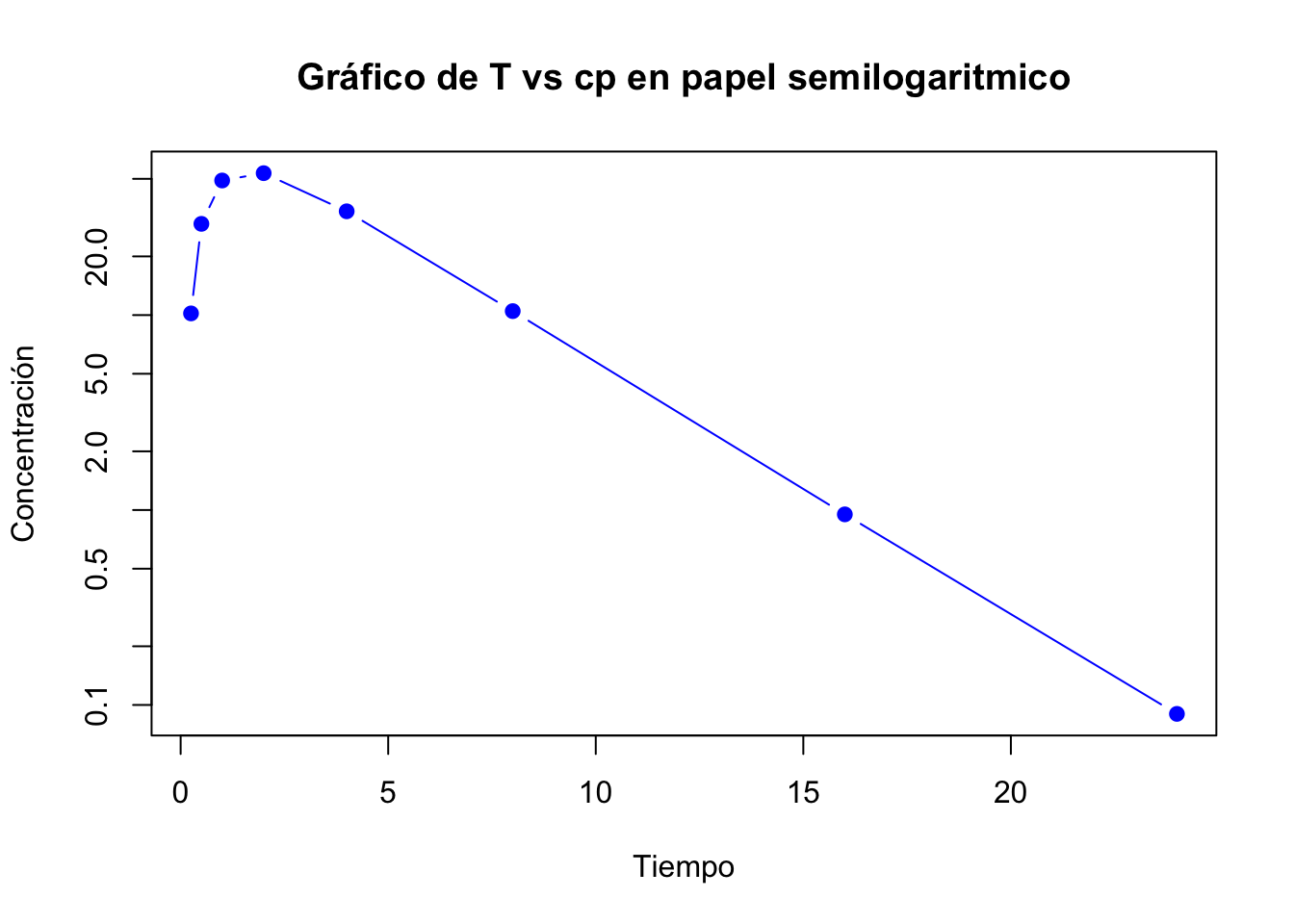
La siguiente es el ejemplo de como debería de quedar al gráfica en el papel semilogaritmico
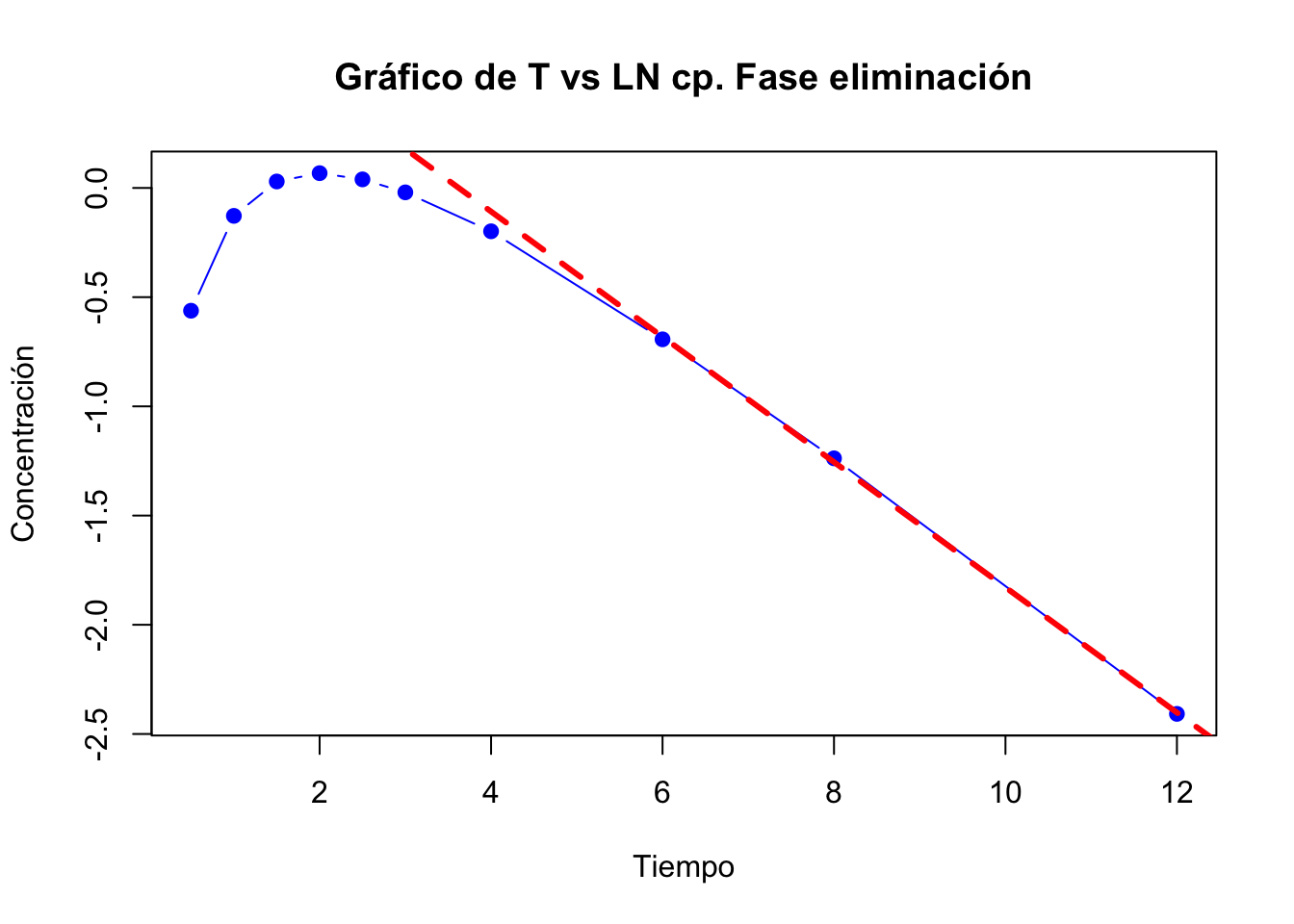
- Identificar la fase de eliminación
Para identificar la fase de eliminación, puede tirar una línea recta que conecte la mayoria de los puntos de la fase de eliminación, comenzando del último punto al más cercano a la concentración plasmática máxima. Los puntos que toquen esta línea serán considerados en la fase de eliminación y realizaremos una regresión con ellos.
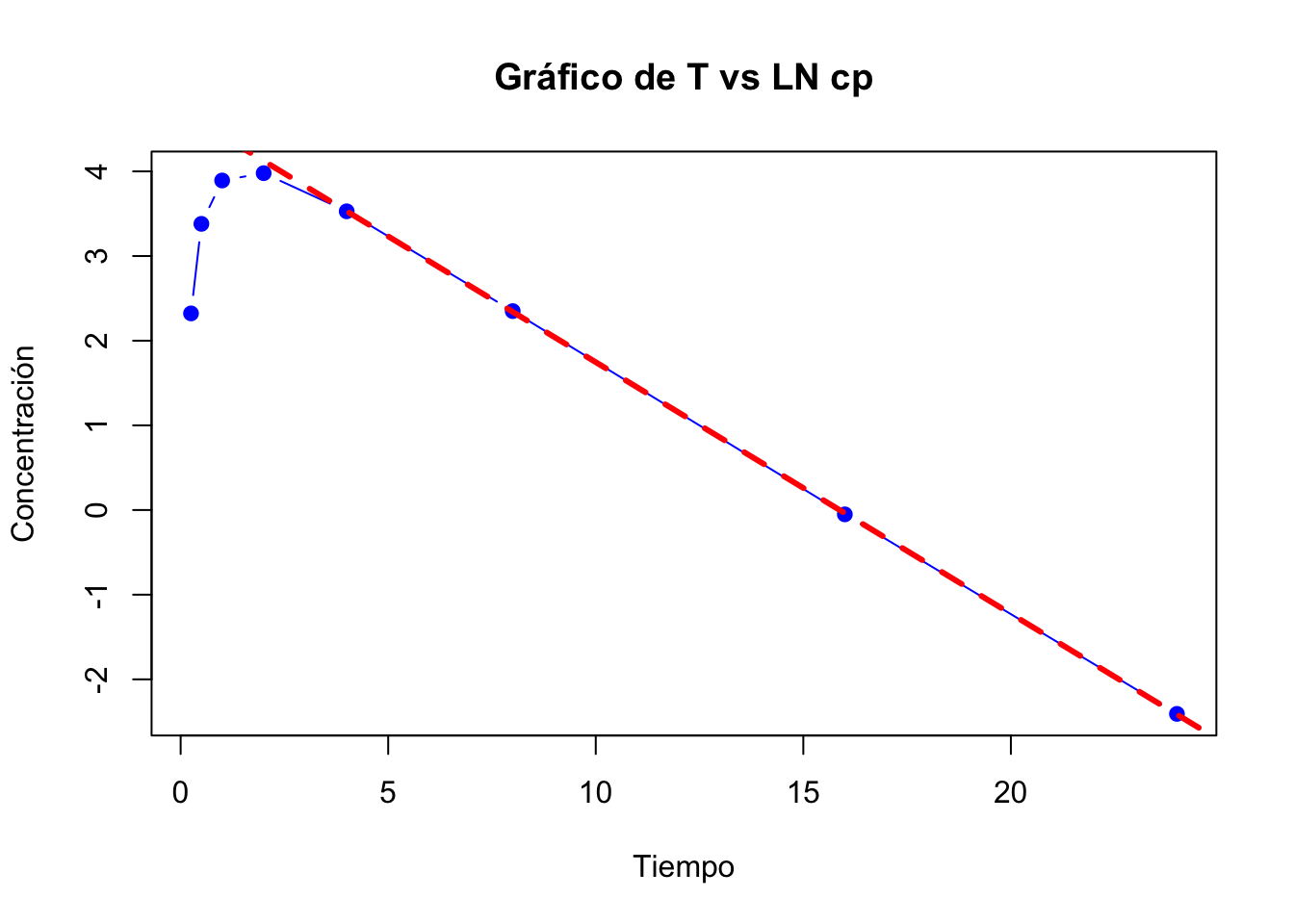
La línea punteada roja muestra la fase de eliminación, podemos notar que solo toca los últimos 4 puntos. Con estos 4 puntos se deberá realizar una regresión como se muestra enseguida.
- Regresión de la fase de eliminación
Con los tiempos seleccionados para la fase de eliminación, se construye una regresión. Puede realizarla de dos maneras, la primera es utilizar una regresión exponencial con los datos crudos de Cp y T. La segunda opción es utilizar una regresión lineal con los LN de Cp vs t. Si utiliza esta segunda opción, deberá calcular en antilogaritmo del intercepto, para obtener el valor de \(C^0\) real. En cualquiera de las opciones, el valor de la pendiente será igual a \(K_{el}\). Independientemente del tipo de regresión, no es necesario calcular antilogaritmo ni realizar ninguna modificación a nuestro valor de la pendientes.
Los parámetros de la regresión son:
##
## Call:
## lm(formula = log(Conc_kel) ~ Tiempo_kel, data = Datos)
##
## Residuals:
## 5 6 7 8
## -0.001242 0.008697 -0.014289 0.006834
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.7185471 0.0125887 374.8 7.12e-06 ***
## Tiempo_kel -0.2972219 0.0008337 -356.5 7.87e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.01281 on 2 degrees of freedom
## (4 observations deleted due to missingness)
## Multiple R-squared: 1, Adjusted R-squared: 1
## F-statistic: 1.271e+05 on 1 and 2 DF, p-value: 7.868e-06Note como la regresión fue obtenida con los valrores de LN, por lo tanto el valor real para el intercepto (\(C^0\)) es: 112.0054011, resultado obtenido despues de estimar el antilogaritmo del valor original
- Valores extrapolados
Con los parámetros de la regresión de eliminación, realice una extrapolación para cada uno de los valores de \(t\) que no fueron seleccionados en la fase de eliminación, es decir, solo para los primero 4 datos.
En un calculadora puede utilizar el función de \(\hat{y}\) de lo contrario emplee la siguiente formula:
\[ Cp=C^0 \cdot e^{-K_{el} \cdot t} \] Para el tiempo de \(0.25 \ h\) el cálculo sería:
\[ Cp=112.0 \mu g/L \cdot e^{0.29 h^{-1} \cdot 0.25h}= 103.98 \mu g/L \]
Los datos extrapolados se muestran en la siguiente tabla:
| Tiempo (h) | Conc \(\mu g/L\) | Extrapolados mu g/L |
|---|---|---|
| 0.25 | 10.20 | 103.98 |
| 0.50 | 29.38 | 96.54 |
| 1.00 | 49.03 | 83.21 |
| 2.00 | 53.46 | 61.81 |
| 4.00 | 34.07 | Fase eliminación |
| 8.00 | 10.48 | Fase eliminación |
| 16.00 | 0.95 | Fase eliminación |
| 24.00 | 0.09 | Fase eliminación |
- Residuales
Dado que los valores extrapolados, son unicamente válidos si no existiera un proceso de absorción, debemos de obtener la diferencia del valor extrapalado y la concentración plasmática. Para ello restamos el valor extrapolado de la concentración plásmatica. Estos valores de residuales son servirán para estimar la regresión de nuestra fase de absorción. La siguiente tabla muestra los valores de residuales:
| Tiempo (h) | Conc \(\mu g/L\) | Extrapolados \(\mu g/L\) | Residuales \(\mu g/L\) |
|---|---|---|---|
| 0.25 | 10.20 | 103.98 | 93.78 |
| 0.50 | 29.38 | 96.54 | 67.16 |
| 1.00 | 49.03 | 83.21 | 34.18 |
| 2.00 | 53.46 | 61.81 | 8.35 |
| 4.00 | 34.07 | Fase eliminación | Fase eliminación |
| 8.00 | 10.48 | Fase eliminación | Fase eliminación |
| 16.00 | 0.95 | Fase eliminación | Fase eliminación |
| 24.00 | 0.09 | Fase eliminación | Fase eliminación |
- Regresión para la fase de absorción
Utilizando los valores de los residuales y los valores de tiempo de los primero cuatro datos (datos que no fueron seleccionados en la fase de eliminación) se realiza una regresión exponencial o una regresión lineal con los valores de LN de los residuales vs tiempo. Comience del primer dato al último. Los valores de la regresión utilizando LN son:
##
## Call:
## lm(formula = log(Conc_abs) ~ Tiempo_abs, data = Datos)
##
## Residuals:
## 1 2 3 4
## -0.011030 0.001096 0.017658 -0.007724
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.89798 0.01352 362.4 7.61e-06 ***
## Tiempo_abs -1.38400 0.01173 -118.0 7.18e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.01572 on 2 degrees of freedom
## Multiple R-squared: 0.9999, Adjusted R-squared: 0.9998
## F-statistic: 1.393e+04 on 1 and 2 DF, p-value: 7.18e-05El valor real del intercepto (\(A^0\)) es: 134.0188543 mientras que el valor de la pendiente corresponde a \(K_a\)
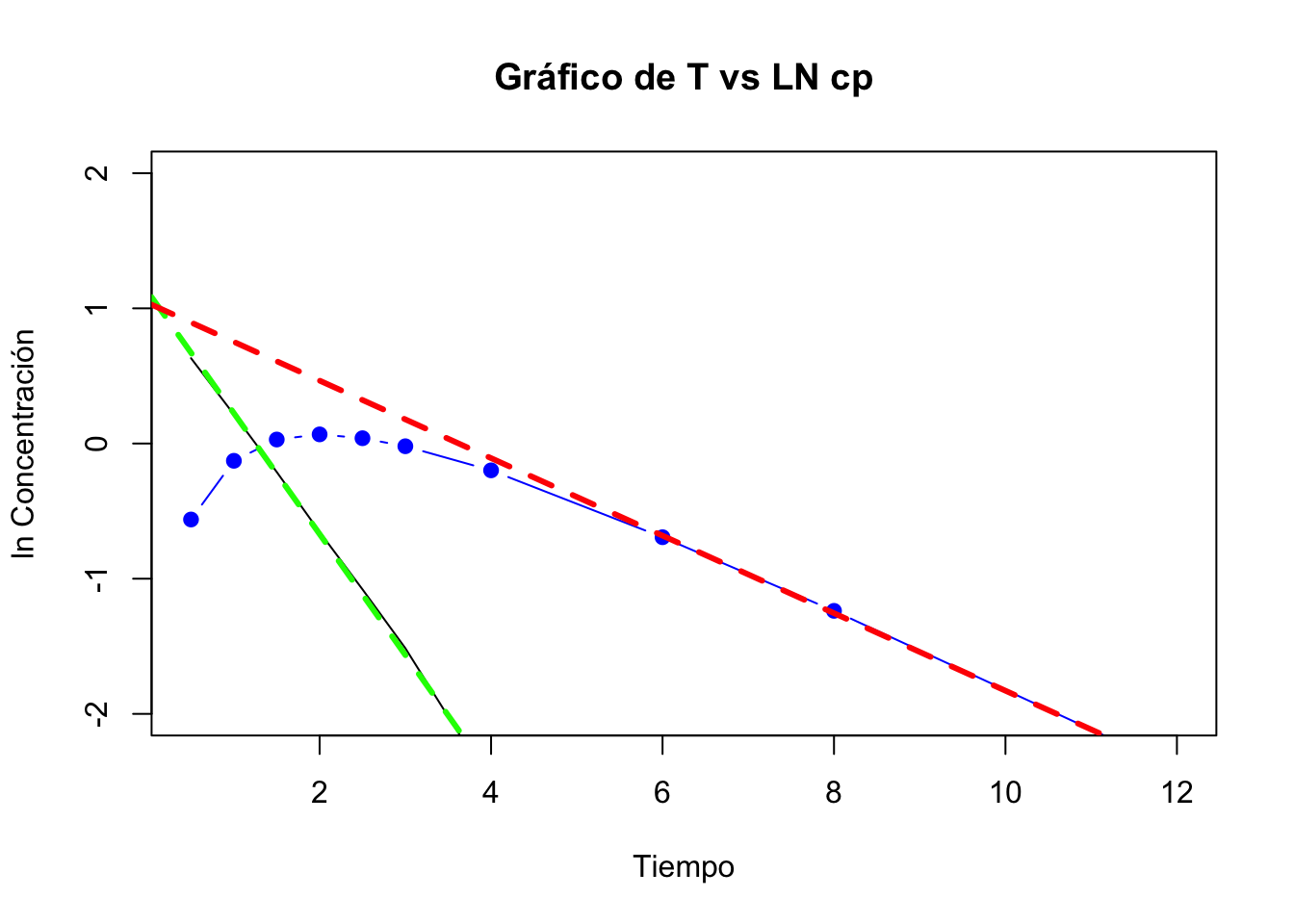
- Graficar los datos de la regresión de la fase de absorción
Se grafican los datos de la regresión de la fase de absorción, junto con la regresión de la fase de elimnación y los valores de Cp vs t para obtener la siguiente gráfica:
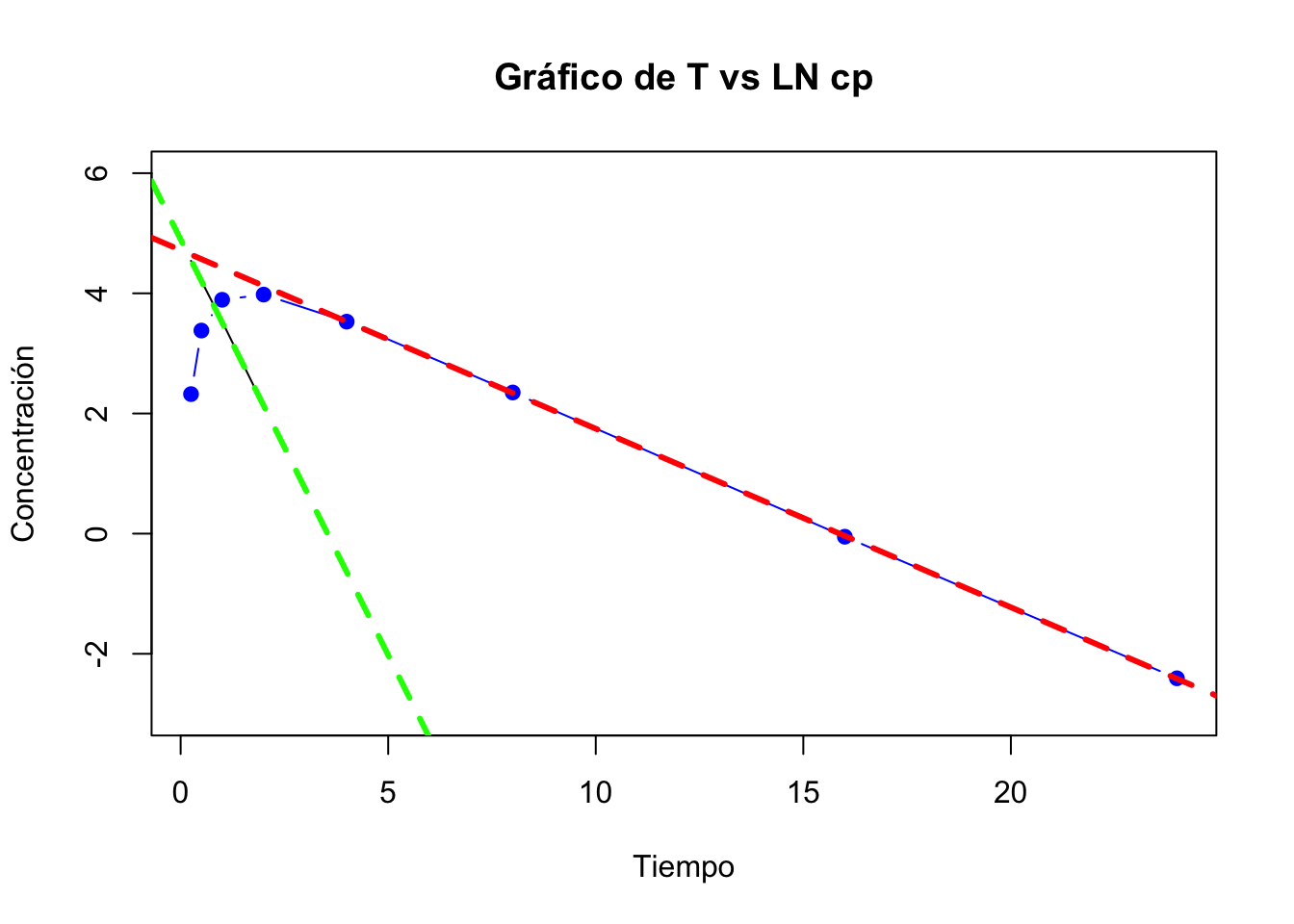
La linea verde representa la fase de absorción y la roja la fase de eliminación. Note como las líneas no se juntan en el eje de las \(y\), por lo que se puede suponer que hay tiempo de latencia.
- Sustituir las formulas para obtener los parámetros del modelo
Los valores de \(C^0\), \(K_{el}\), \(A^0\) y \(K_a\) para los problemas son: 112.01, 0.3, 134.02 y 1.38 respectivamente.
Los resultados de la estimación de los parámetros son:
Parámetros Resultados
1 C0 112.01
2 Kel 0.30
3 A0 134.02
4 Ka 1.38
5 Vd 4.85
6 tl 0.17
7 Cl 1.45
8 tmax 1.58
9 Cpmax 54.58
10 Tiempo vida media 2.31
11 ABC cero infinito 276.252.4 Resolución ejercicios
2.4.1 Resolución ejemplo 2.1
- Graficar los datos de Cp vs T
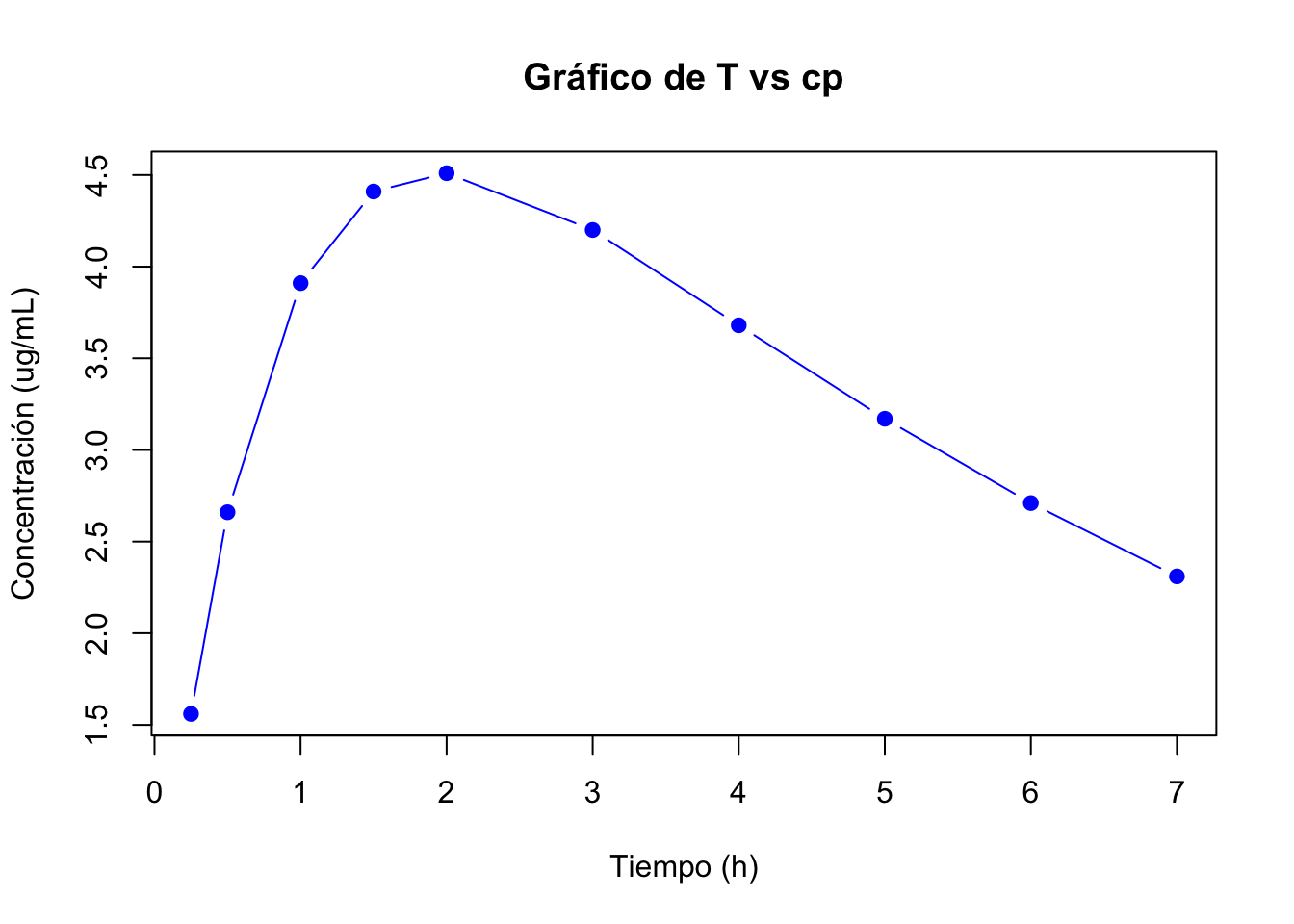
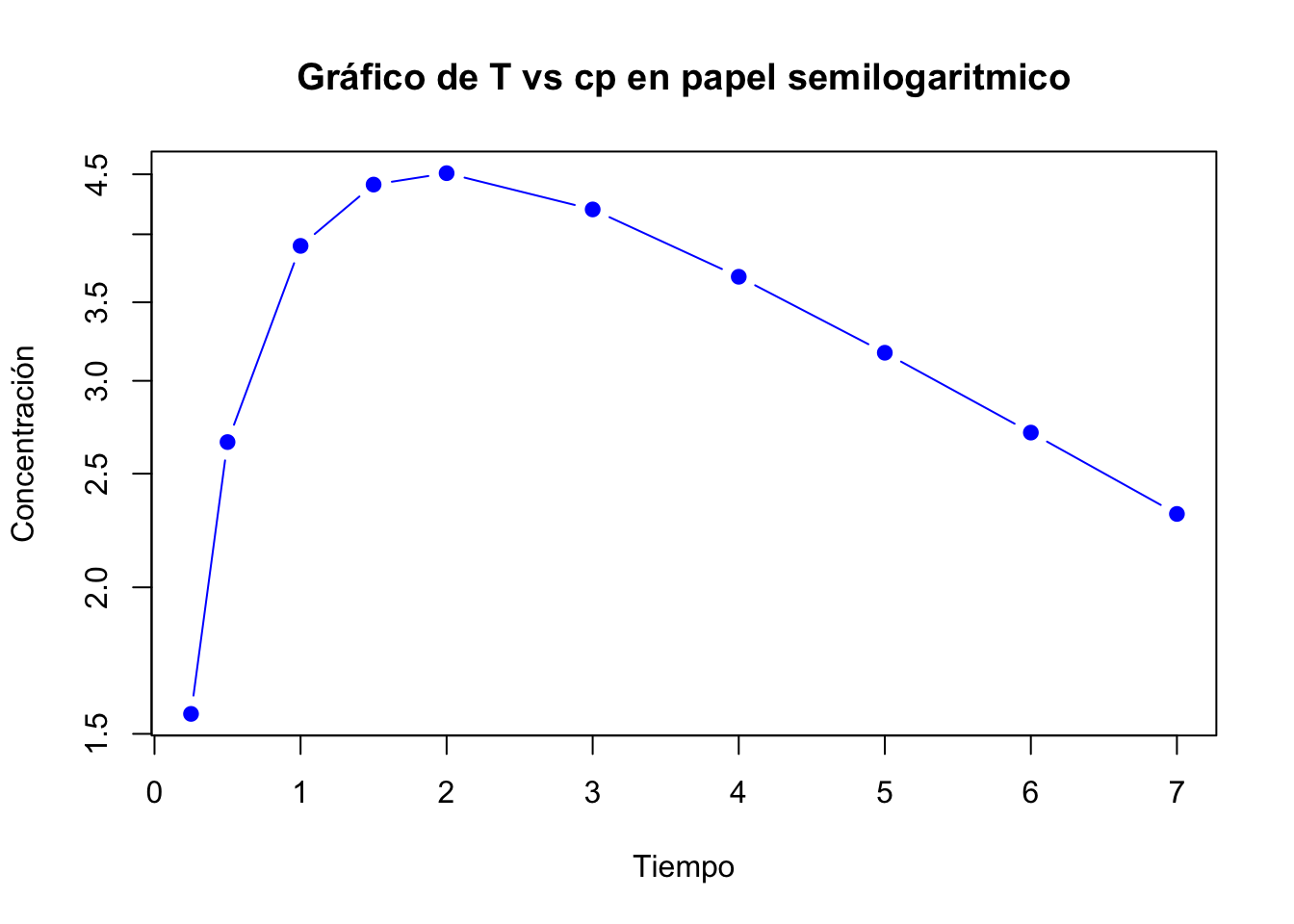
- Graficar los datos de \(Cp\) vs \(t\).en papel semilogarítmico o graficar el \(ln\) de \(Cp\) vs \(t\).
La siguiente gráfica muestra los datos de \(Cp\) vs \(t\) en papel semilogarítmico:
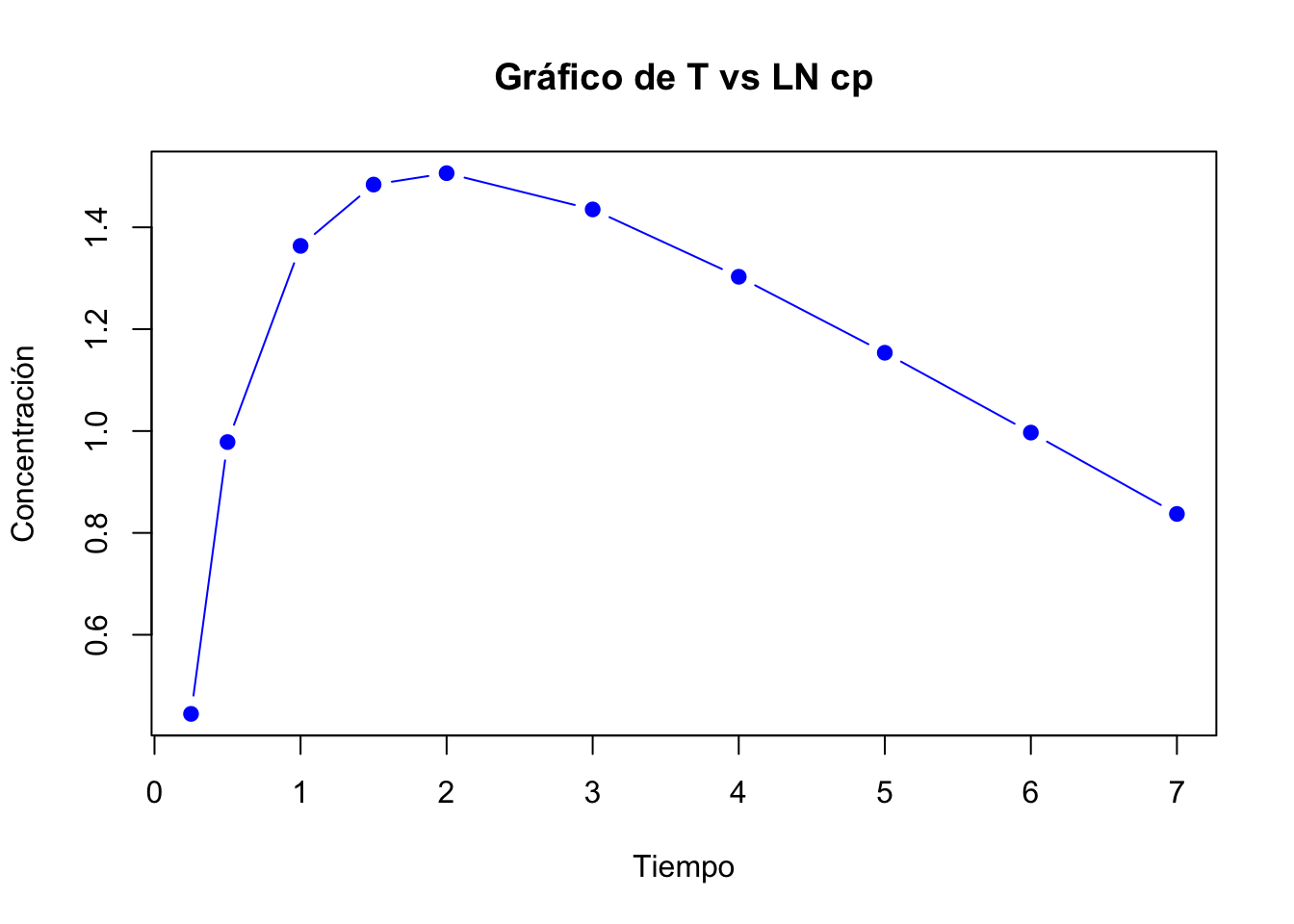
La siguiente gráfica muestra los valores del \(ln\) de \(Cp\) vs \(t\):
- Identificar la fase de eliminación
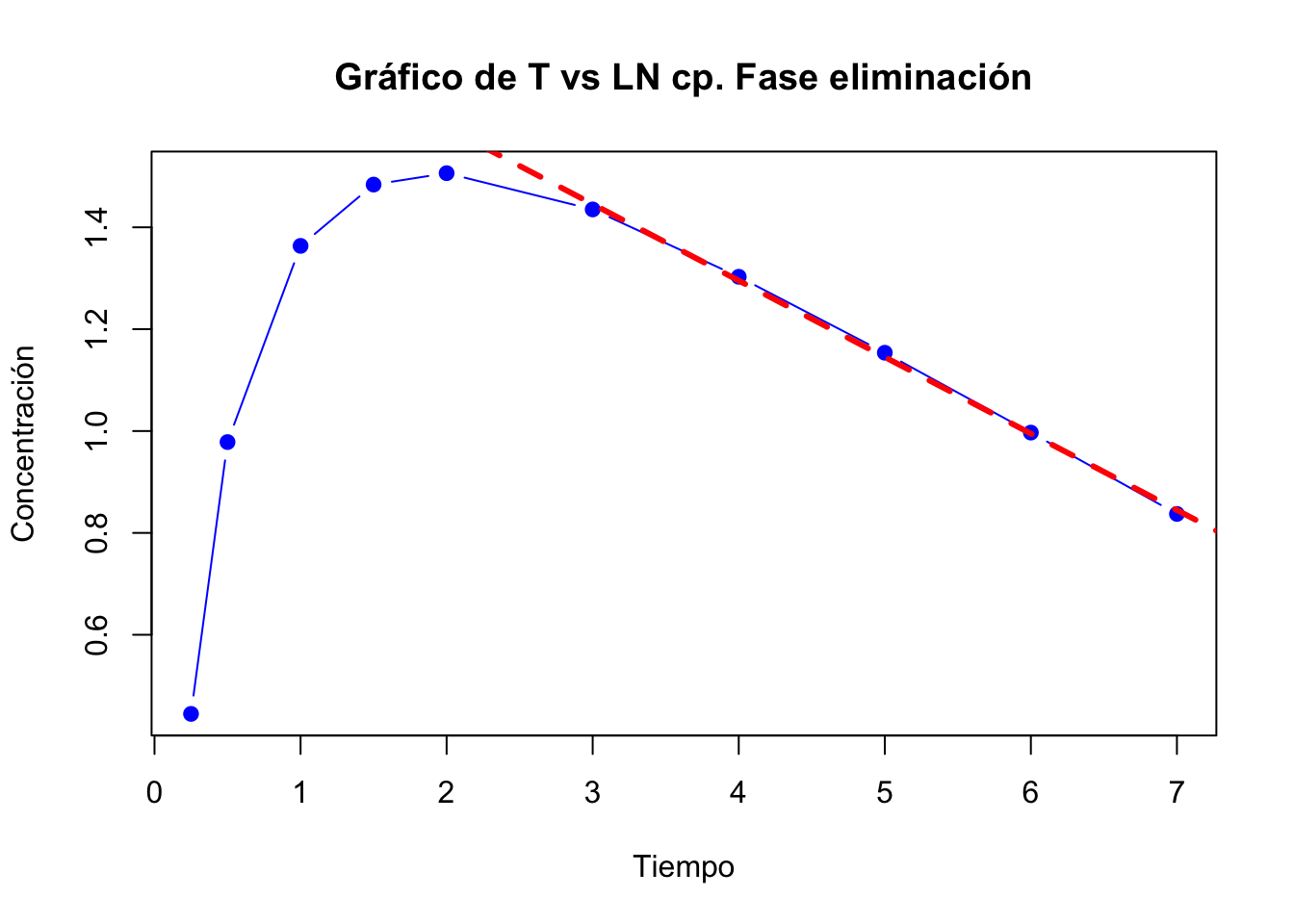
- Regresión de la fase de eliminación
Los parámetros de la regresión son:
##
## Call:
## lm(formula = log(Conc_kel) ~ Tiempo_kel, data = Datos)
##
## Residuals:
## 6 7 8 9 10
## -0.010428 0.007564 0.008547 0.001927 -0.007610
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.896004 0.016449 115.27 1.44e-06 ***
## Tiempo_kel -0.150164 0.003166 -47.44 2.06e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.01001 on 3 degrees of freedom
## (5 observations deleted due to missingness)
## Multiple R-squared: 0.9987, Adjusted R-squared: 0.9982
## F-statistic: 2250 on 1 and 3 DF, p-value: 2.063e-05Note como la regresión fue obtenida con los valores de LN, por lo tanto el valor real para el intercepto (\(C^0\)) es: 6.6592313, resultado obtenido después de estimar el anti logaritmo del valor original
- Valores extrapolados
Los datos extrapolados se muestran en la siguiente tabla:
## Tiempo Conc Extrapolados
## 1 0.25 1.56 6.41
## 2 0.50 2.66 6.18
## 3 1.00 3.91 5.73
## 4 1.50 4.41 5.32
## 5 2.00 4.51 4.93- Residuales
La siguiente tabla muestra los valores de residuales:
## Tiempo Conc Extrapolados Residuales
## 1 0.25 1.56 6.41 4.85
## 2 0.50 2.66 6.18 3.52
## 3 1.00 3.91 5.73 1.82
## 4 1.50 4.41 5.32 0.91
## 5 2.00 4.51 4.93 0.42- Regresión para la fase de absorción
Los valores de la regresión utilizando LN son:
##
## Call:
## lm(formula = log(Conc_abs) ~ Tiempo_abs, data = Datos)
##
## Residuals:
## 1 2 3 4 5
## -0.028829 -0.001561 0.034386 0.036811 -0.040807
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.95559 0.03519 55.57 1.28e-05 ***
## Tiempo_abs -1.39114 0.02862 -48.61 1.92e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.04097 on 3 degrees of freedom
## Multiple R-squared: 0.9987, Adjusted R-squared: 0.9983
## F-statistic: 2363 on 1 and 3 DF, p-value: 1.917e-05El valor real del intercepto (\(A^0\)) es: 7.0681121 mientras que el valor de la pendiente corresponde a \(K_a\)
- Graficar los datos de la regresión de la fase de absorción
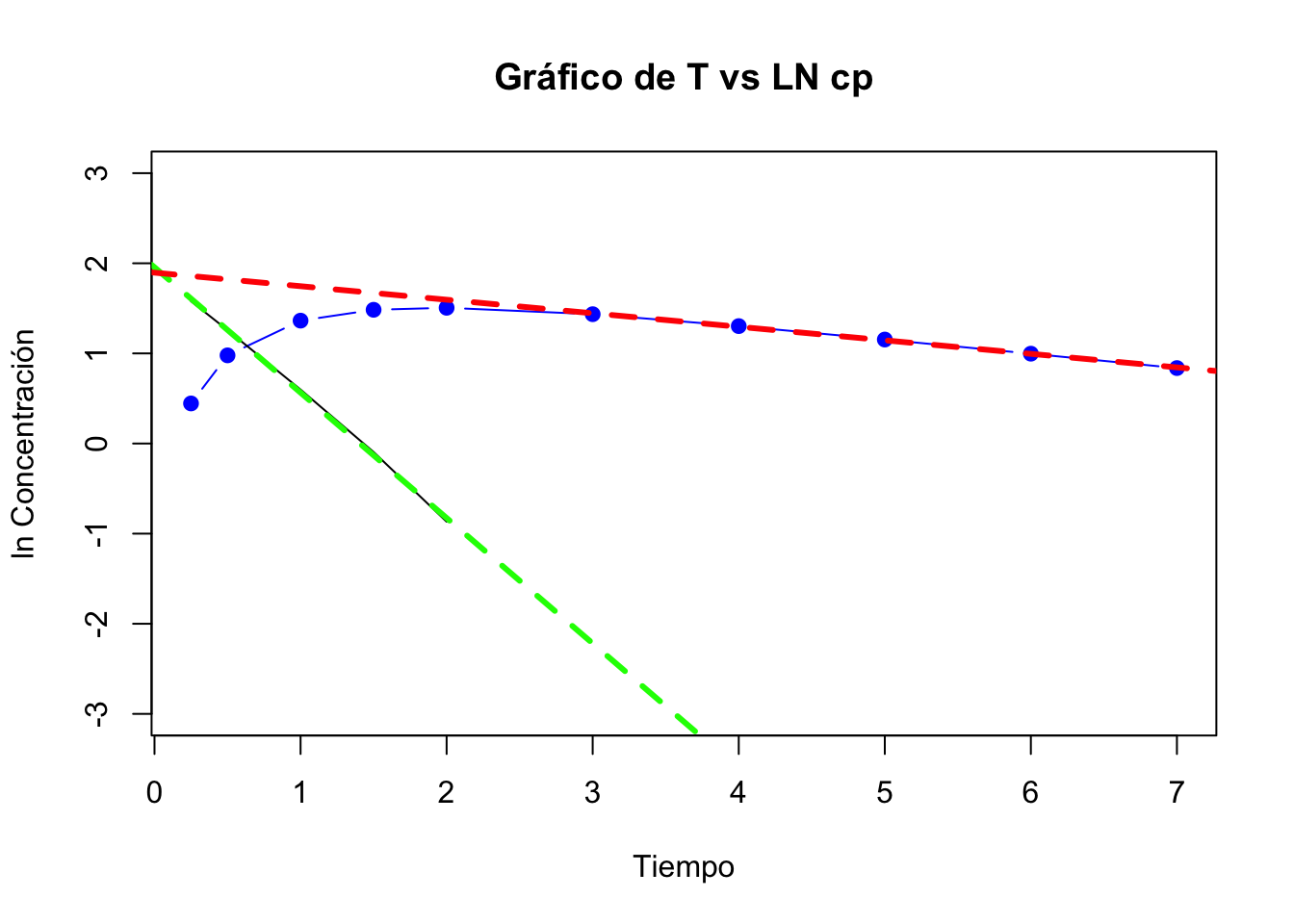
No hay periodo de latencia
- Sustituir las formulas para obtener los parámetros del modelo
Los valores de \(C^0\), \(K_{el}\), \(A^0\) y \(K_a\) para los problemas son: 6.66, 0.15, 7.07 y 1.39 respectivamente.
Los resultados de la estimación de los parámetros son:
Parámetros Resultados Unidades
1 C0 6.66 ug/mL
2 Kel 0.15 h-1
3 A0 7.07 ug/mL
4 Ka 1.39 h-1
5 Vd 42.08 Litros
6 tl 0.05 Horas
7 Cl 6.32 Volumen/Tiempo
8 tmax 1.84 Horas
9 Cpmax 4.51 ug/mL
10 Tiempo vida media 4.62 Horas
11 ABC cero infinito 39.27 ug*h/mL2.4.2 Resolución ejercicio 2.2
- Graficar los datos de Cp vs T
- Graficar los datos de \(Cp\) vs \(t\).en papel semilogarítmico o graficar el \(ln\) de \(Cp\) vs \(t\).
La siguiente gráfica muestra los datos de \(Cp\) vs \(t\) en papel semilogarítmico:
La siguiente gráfica muestra los valores del \(ln\) de \(Cp\) vs \(t\):
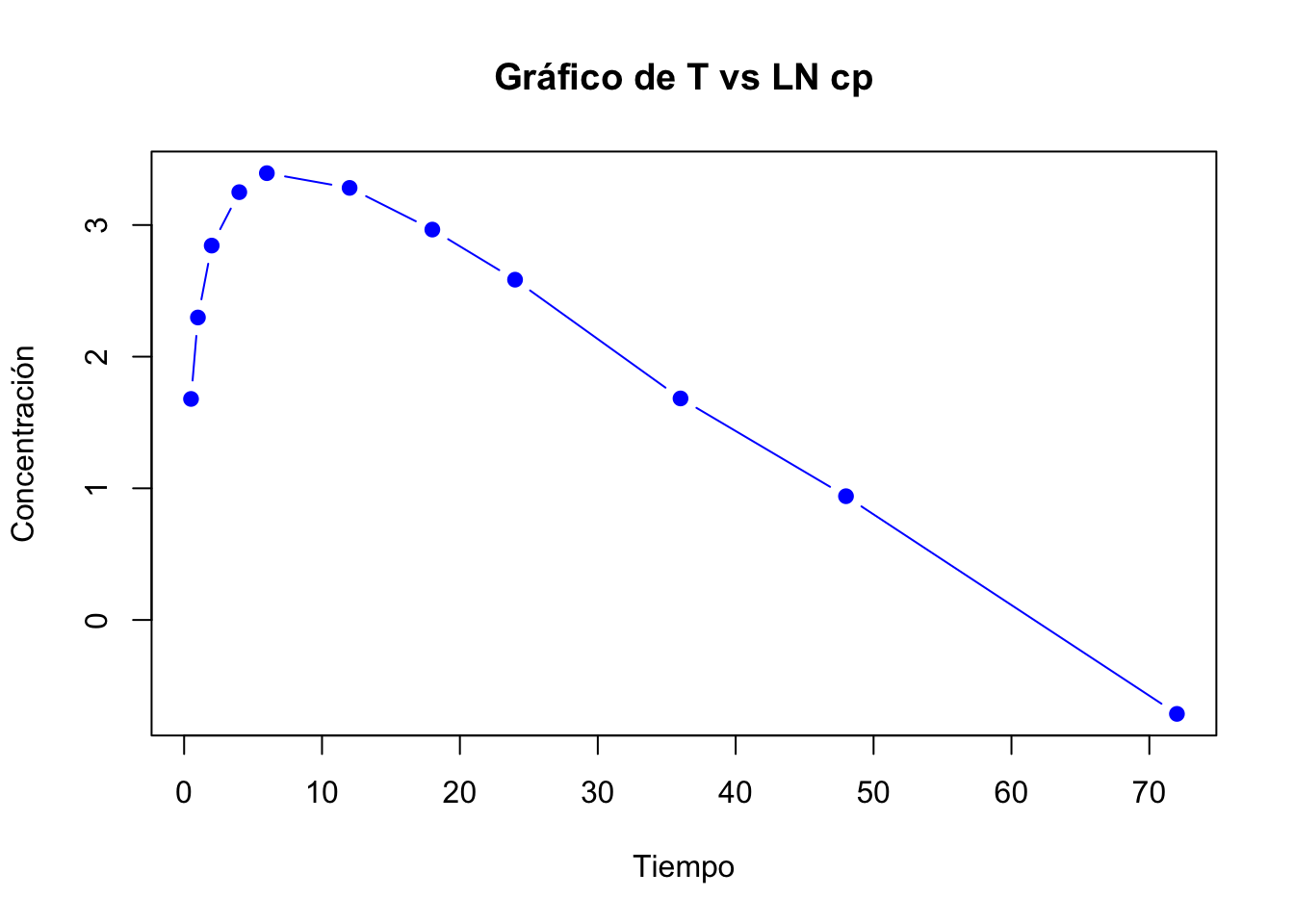
- Identificar la fase de eliminación
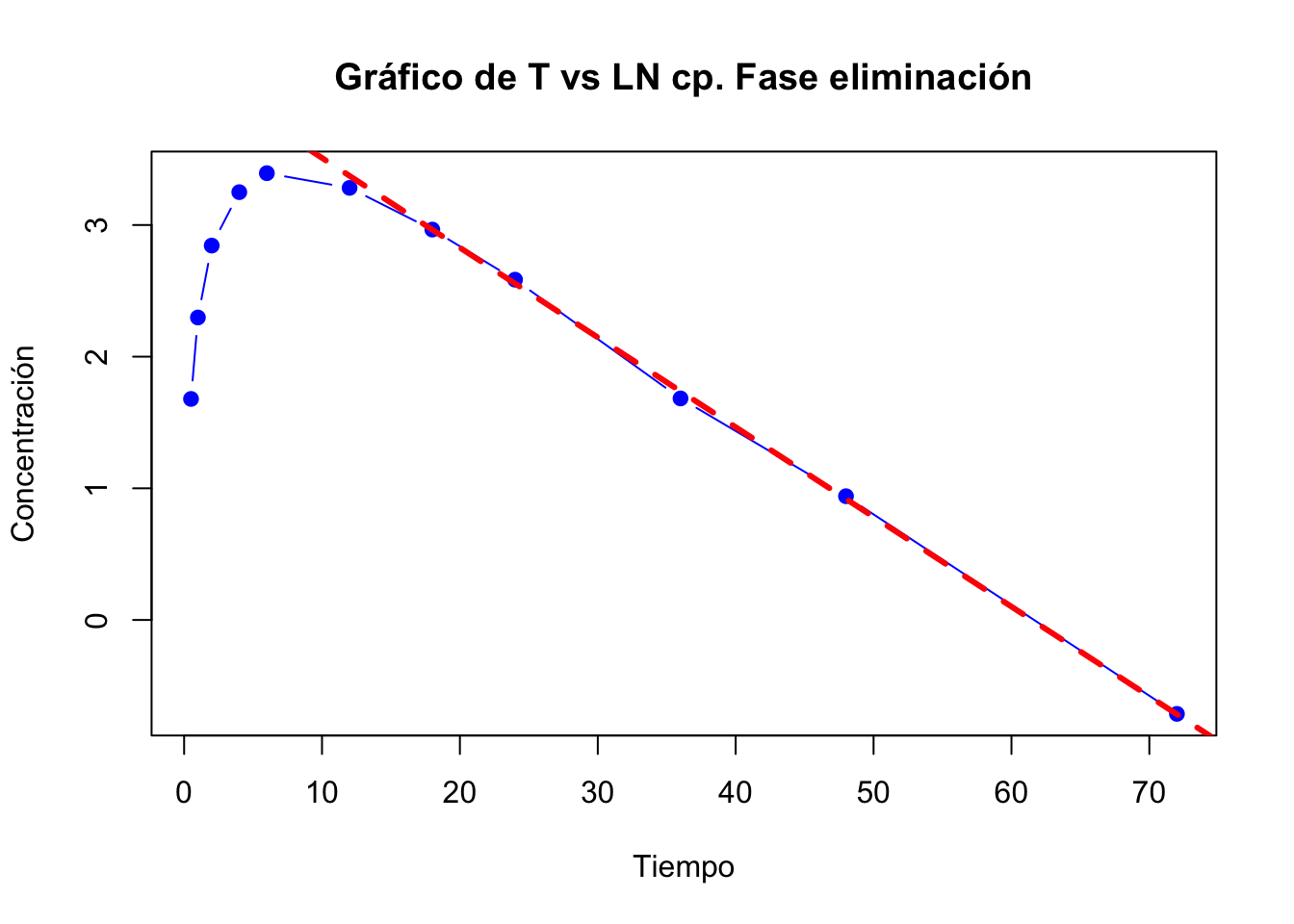
- Regresión de la fase de eliminación
Los parámetros de la regresión son:
##
## Call:
## lm(formula = log(Conc_kel) ~ Tiempo_kel, data = Datos)
##
## Residuals:
## 7 8 9 10 11
## 0.0009827 0.0294661 -0.0545885 0.0207394 0.0034003
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.1913039 0.0387672 108.11 1.74e-06 ***
## Tiempo_kel -0.0681674 0.0008809 -77.39 4.76e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.03782 on 3 degrees of freedom
## (6 observations deleted due to missingness)
## Multiple R-squared: 0.9995, Adjusted R-squared: 0.9993
## F-statistic: 5988 on 1 and 3 DF, p-value: 4.756e-06Note como la regresión fue obtenida con los valores de LN, por lo tanto el valor real para el intercepto (\(C^0\)) es: 66.108932, resultado obtenido después de estimar el anti logaritmo del valor original
- Valores extrapolados
Los datos extrapolados se muestran en la siguiente tabla:
## Tiempo Conc Extrapolados
## 1 0.5 5.36 63.89
## 2 1.0 9.95 61.75
## 3 2.0 17.18 57.68
## 4 4.0 25.78 50.33
## 5 6.0 29.78 43.92
## 6 12.0 26.63 29.17- Residuales
La siguiente tabla muestra los valores de residuales:
## Tiempo Conc Extrapolados Residuales
## 1 0.5 5.36 63.89 58.53
## 2 1.0 9.95 61.75 51.80
## 3 2.0 17.18 57.68 40.50
## 4 4.0 25.78 50.33 24.55
## 5 6.0 29.78 43.92 14.14
## 6 12.0 26.63 29.17 2.54- Regresión para la fase de absorción
Los valores de la regresión utilizando LN son:
##
## Call:
## lm(formula = log(Conc_abs) ~ Tiempo_abs, data = Datos)
##
## Residuals:
## 1 2 3 4 5 6
## -0.037684 -0.023317 0.003627 0.049101 0.043461 -0.035189
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.243739 0.026048 162.92 8.51e-09 ***
## Tiempo_abs -0.273032 0.004498 -60.71 4.41e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.04334 on 4 degrees of freedom
## Multiple R-squared: 0.9989, Adjusted R-squared: 0.9986
## F-statistic: 3685 on 1 and 4 DF, p-value: 4.41e-07El valor real del intercepto (\(A^0\)) es: 69.6678725 mientras que el valor de la pendiente corresponde a \(K_a\)
- Graficar los datos de la regresión de la fase de absorción
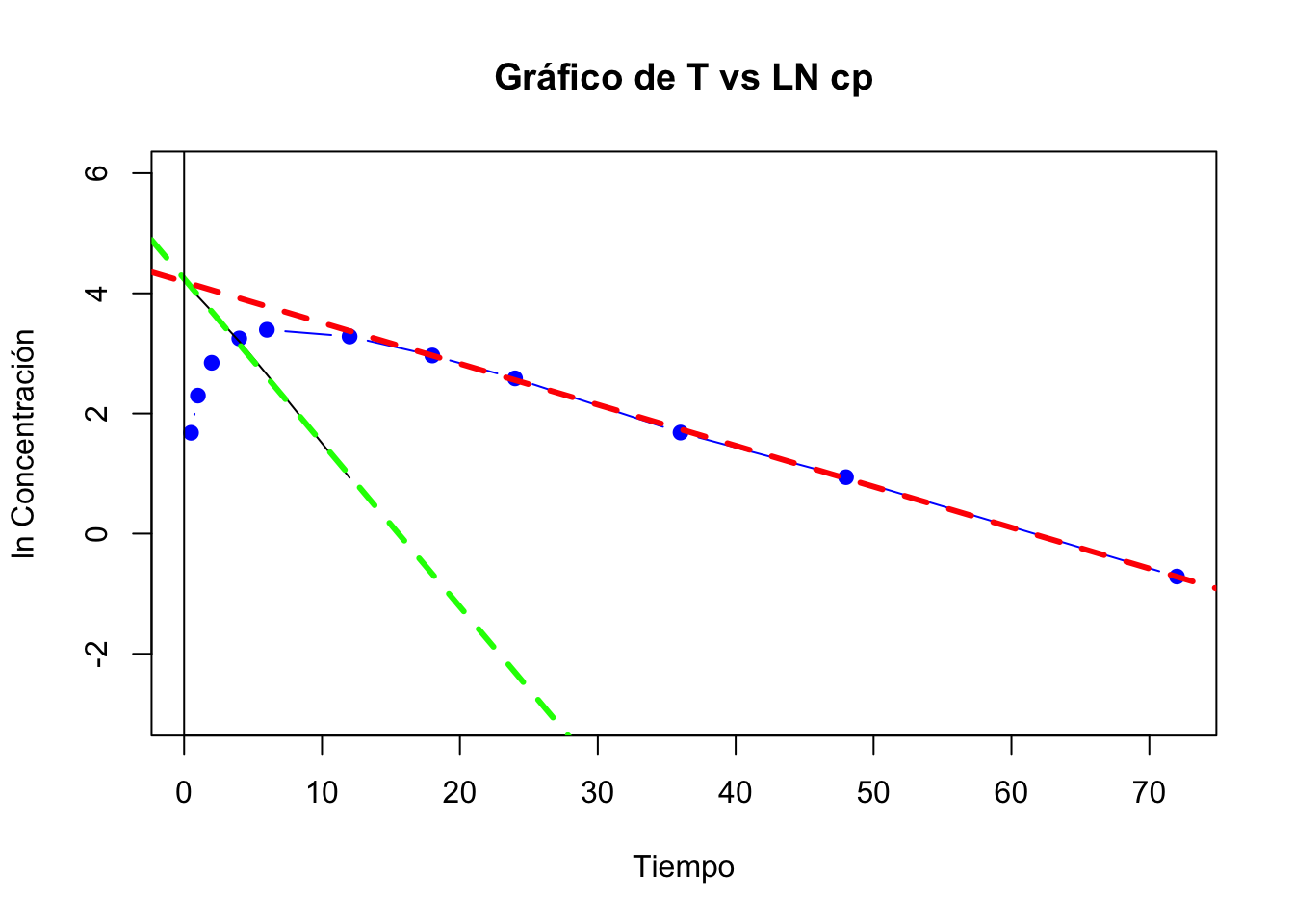
No hay periodo de latencia
- Sustituir las formulas para obtener los parámetros del modelo
Los valores de \(C^0\), \(K_{el}\), \(A^0\) y \(K_a\) para los problemas son: 66.11, 0.07, 69.67 y 0.27 respectivamente.
Los resultados de la estimación de los parámetros son:
Parámetros Resultados Unidades
1 C0 66.11 ug/mL
2 Kel 0.07 h-1
3 A0 69.67 ug/mL
4 Ka 0.27 h-1
5 Vd 10.08 Litros
6 tl 0.26 Horas
7 Cl 0.69 Volumen/Tiempo
8 tmax 6.77 Horas
9 Cpmax 31.26 ug/mL
10 Tiempo vida media 10.17 Horas
11 ABC cero infinito 714.64 ug*h/mLPara la \(Cp\) a las 0.75 se utiliza la ecuación (2.2). Ecuación integrada general sin tiempo de latencia
\[\begin{equation} C= \frac{FD}{V_d}\cdot \frac{K_a}{(K_a-K_{el})} \big(e ^{-K_{el}\cdot t}- e ^{-K_{a}\cdot t}\big) \tag{2.3} \end{equation}\]
Sustituyendo:
\[ Cp 0.75h= \frac{1 \cdot 500 mg \cdot 0.27 h^{-1} }{10.08 L \cdot (0.27 h^{-1}- 0.07h^{-1})}\cdot \big(e ^{-0.07h^{-1}\cdot 0.75 h}- e ^{-0.27h^{-1}\cdot 0.75 h}\big)=8.85 \]
2.4.3 Resolución ejercicio 2.3
Para obtener el \(tmax\) utilizamos la ecuación (2.7).
Para el fármaco A
\[ tmax= \frac{ln\frac{1.0}{0.2}}{1.0-0.2}= 2.01 h ^{-1} \] Para el fármaco B
\[ tmax= \frac{ln\frac{0.2}{1.0}}{0.2-1.0}= 2.01 h ^{-1} \] Dado que la \(K_a\) y la \(K_{el}\) son muy diferente se utiliza la ecuación (2.14)
Para el fármaco A
\[ Cpmax= \frac{1 \cdot 500 mg \cdot 1 h ^{-1}}{10L(1 h ^{-1}-0.2h ^{-1})}\cdot \bigg(e^{-0.2 h ^{-1} \cdot 2.01h}- e^{-1h ^{-1} \cdot 2.01 h} \bigg)=33.4 \mu g /mL \]
Para el fármaco B
\[ Cpmax= \frac{1 \cdot 500 mg \cdot 0.2 h ^{-1}}{20L(1 h ^{-1}-1.0h ^{-1})}\cdot \bigg(e^{-1.0 h ^{-1} \cdot 2.01h}- e^{-0.2h ^{-1} \cdot 2.01 h} \bigg)=3.34 \mu g /mL \]
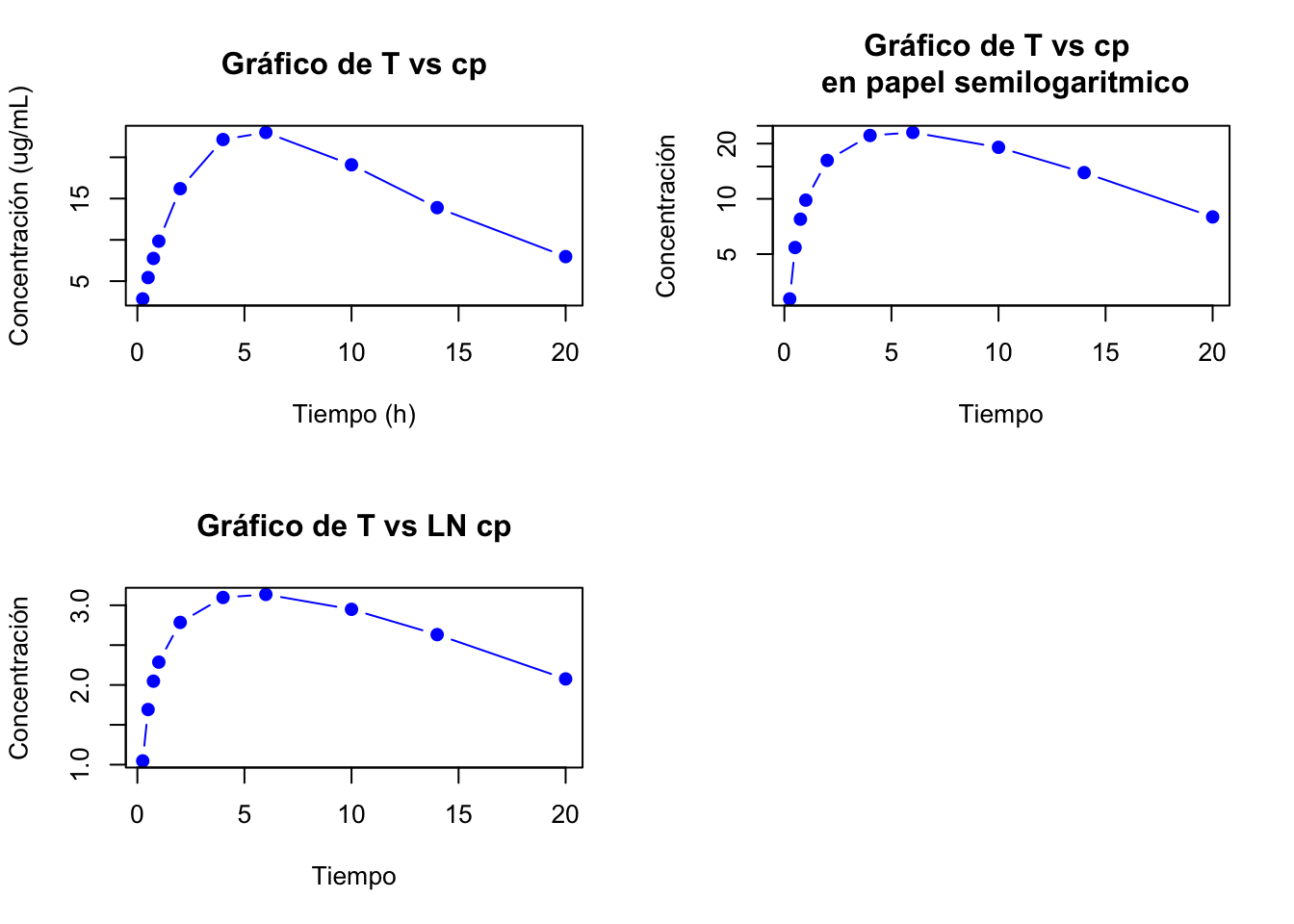
2.4.4 Resolución ejercicio 2.4
Del problema podemos obtener: la \(K_{el}=0.9\) y la dosis de 300 mg para la vía de administración parenteral. Ahora solo debemos de estimar los valores para el comprimido
Las gráficas de los datos son:
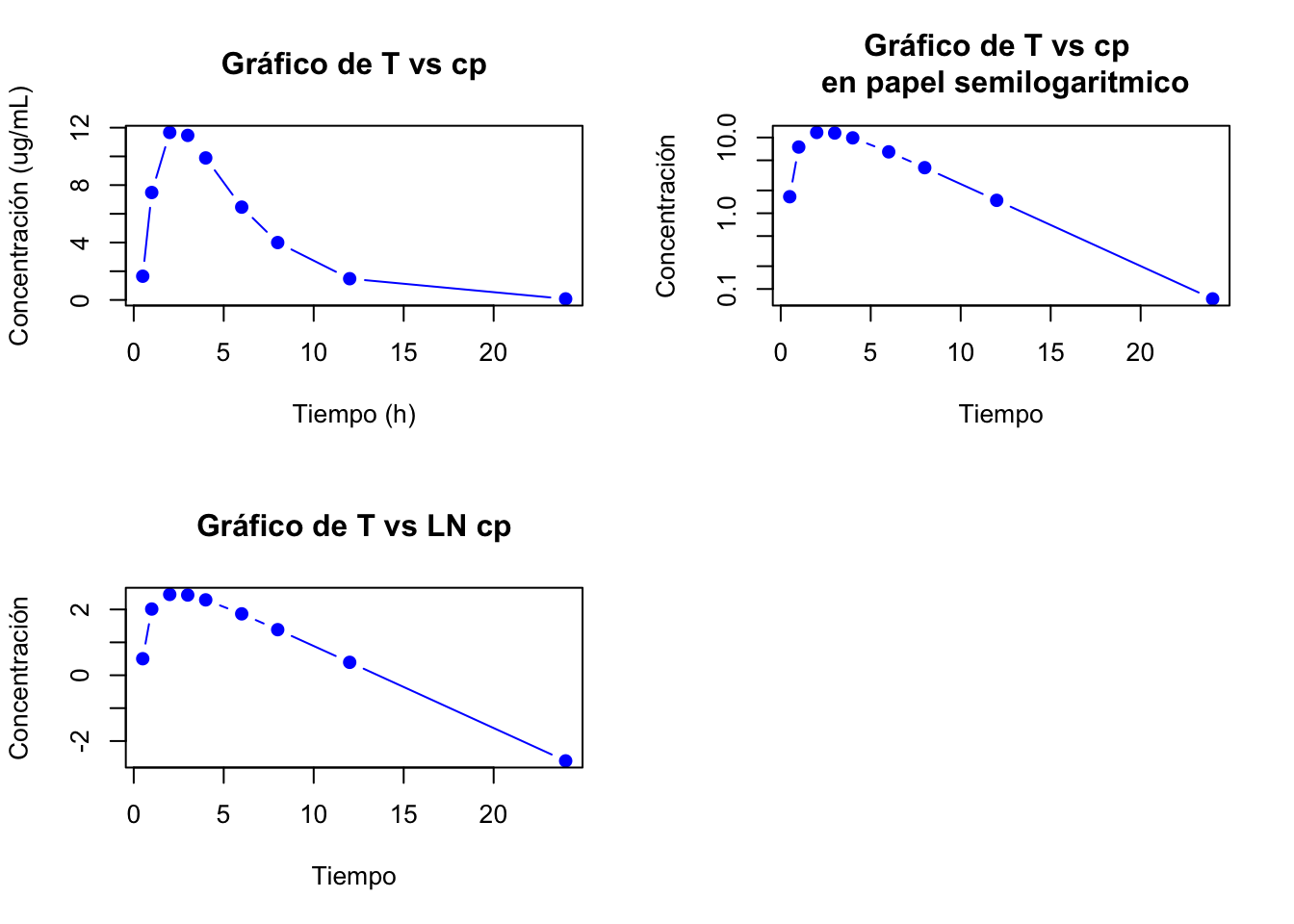
Gráfica de la fase de eliminación
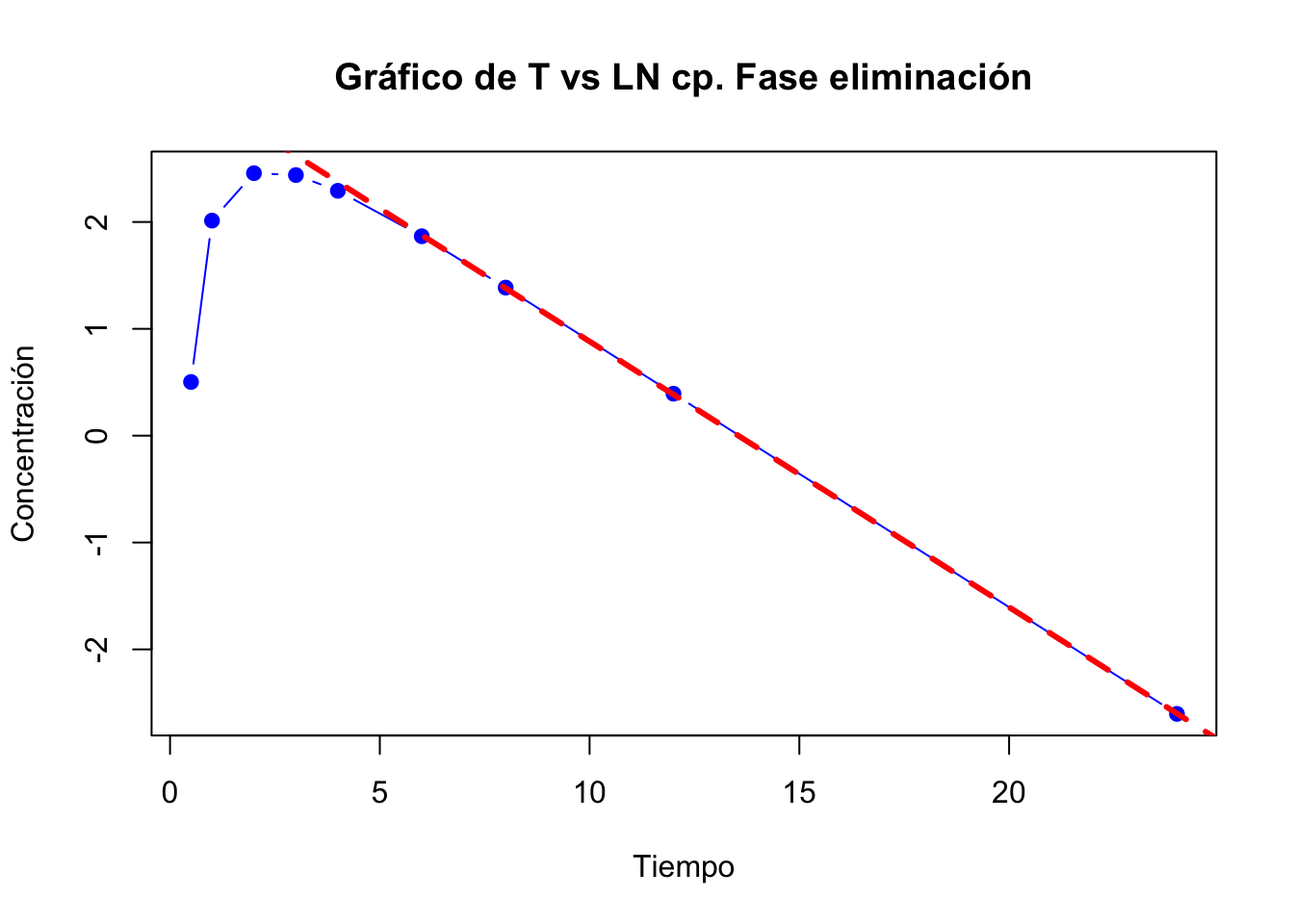
Se tomaron los últimos 4 puntos para la fase de eliminación.
Los valores extrapolados y los residuales se muestran en la siguiente tabla:
## Tiempo Conc Extrapolados Residuales
## 1 0.5 1.653 25.67 24.02
## 2 1.0 7.484 22.67 15.19
## 3 2.0 11.668 17.68 6.01
## 4 3.0 11.462 13.78 2.32
## 5 4.0 9.892 10.75 0.86Gráfica de absorción y fase de eliminación
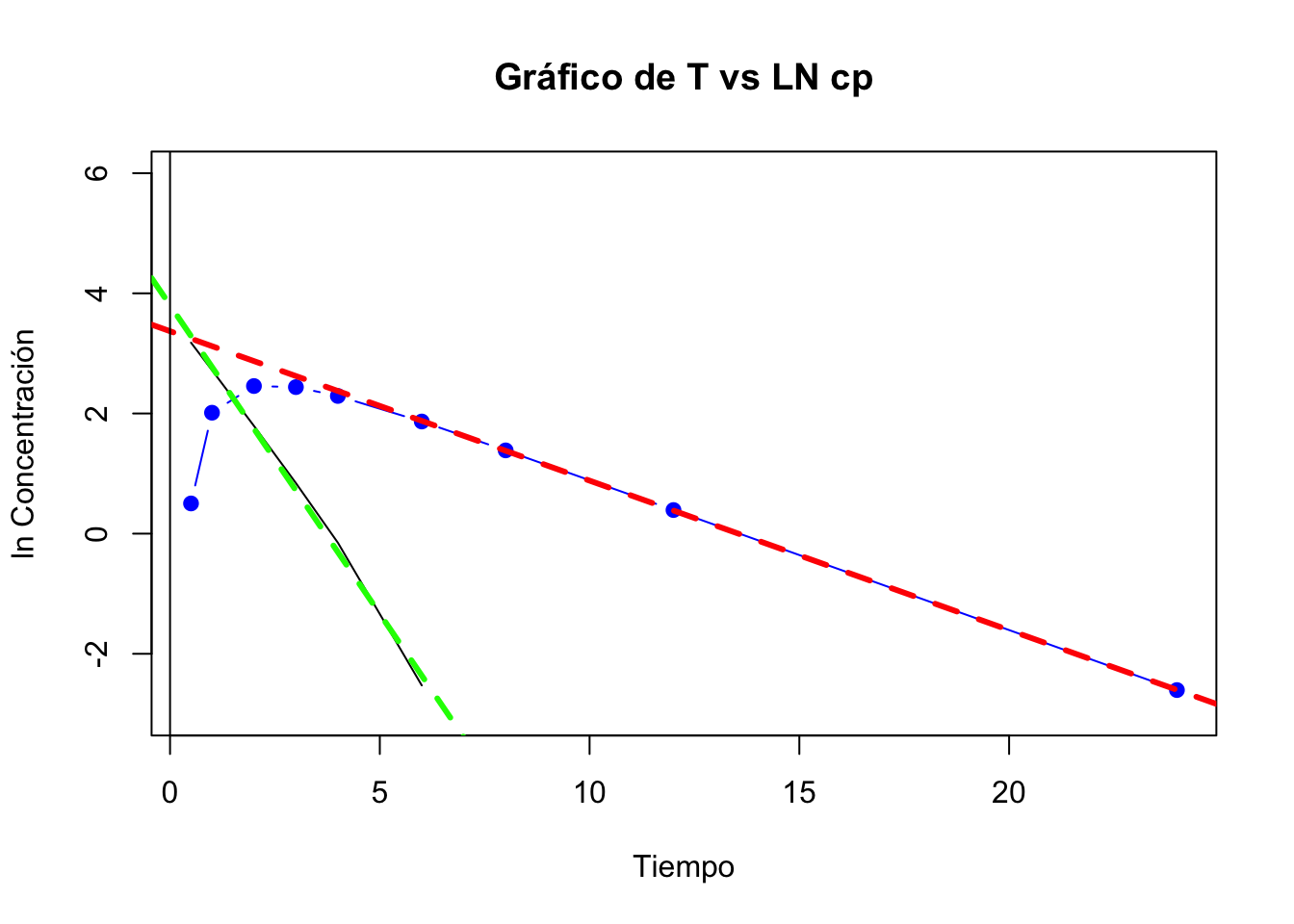
Hay tiempo de latencia, los resultados de la estimación de los parámetros con una biodisponibilidad de 1 son :
## Parámetros Resultados Unidades
## 1 C0 29.07 ug/mL
## 2 Kel 0.25 h-1
## 3 A0 44.77 ug/mL
## 4 Ka 1.03 h-1
## 5 Vd 22.70 Litros
## 6 tl 0.55 Horas
## 7 Cl 5.65 Volumen/Tiempo
## 8 tmax 2.38 Horas
## 9 Cpmax 12.20 ug/mL
## 10 Tiempo vida media 2.79 Horas
## 11 ABC cero infinito 73.29 ug*h/mLDado que los parámetros fueron estimados utilizando una biodisponiilidad de 1, algunos parámetros no son correctos.
Hay fenómeno de flip-flop, ya que las constantes de \(K_a\) y la \(K_{el}\) de la administración intravenosa están intercambiados.
| Constante | IV | Oral |
|---|---|---|
| \(K_a\) | – | 1.03 |
| \(k_{el}\) | 0.9 | 0.25 |
2.4.5 Resolución ejercicio 2.5
No se puede resolver los datos de las concentraciones plasmáticos no permiten la visualización del modelo ni se ajustan a un cinética de primer órden
2.4.6 Resolución ejercicio 2.6
El dato del primer tiempo (0.5 h) no se toma en cuenta para los cálculos de los residuales.
Las gráficas de estos datos son:
Gráfica de la fase de eliminación:
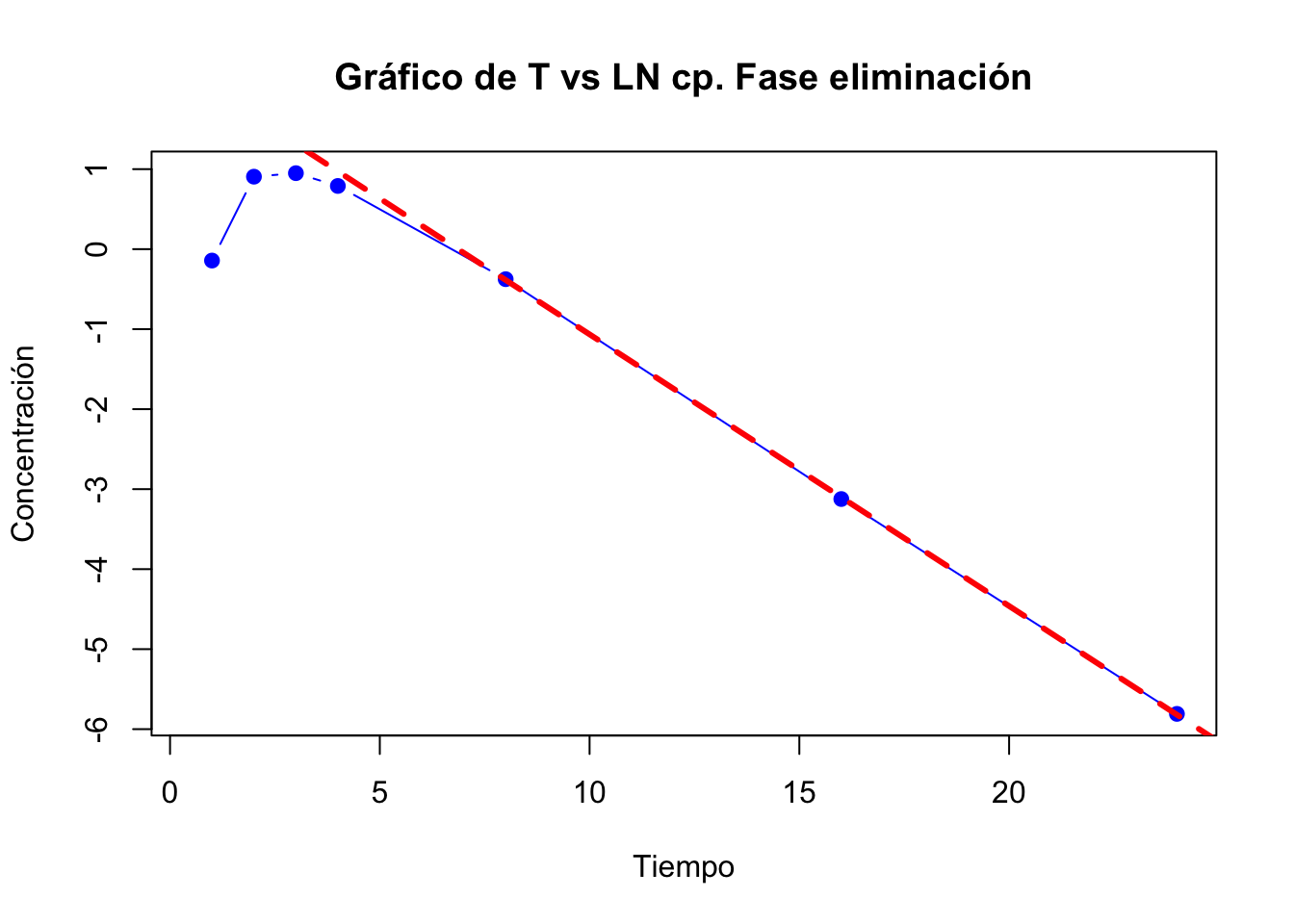
Se tomaron en cuenta los últimos 3 datos para la fase de eliminación.
Los valores extrapolados y los residuales se muestran en la siguiente tabla:
## Tiempo Conc Extrapolados Residuales
## 1 0.5 NA 8.68 NA
## 2 1.0 0.867 7.33 6.46
## 3 2.0 2.474 5.22 2.75
## 4 3.0 2.585 3.71 1.12
## 5 4.0 2.203 2.64 0.44Gráfica de absorción y fase de eliminación
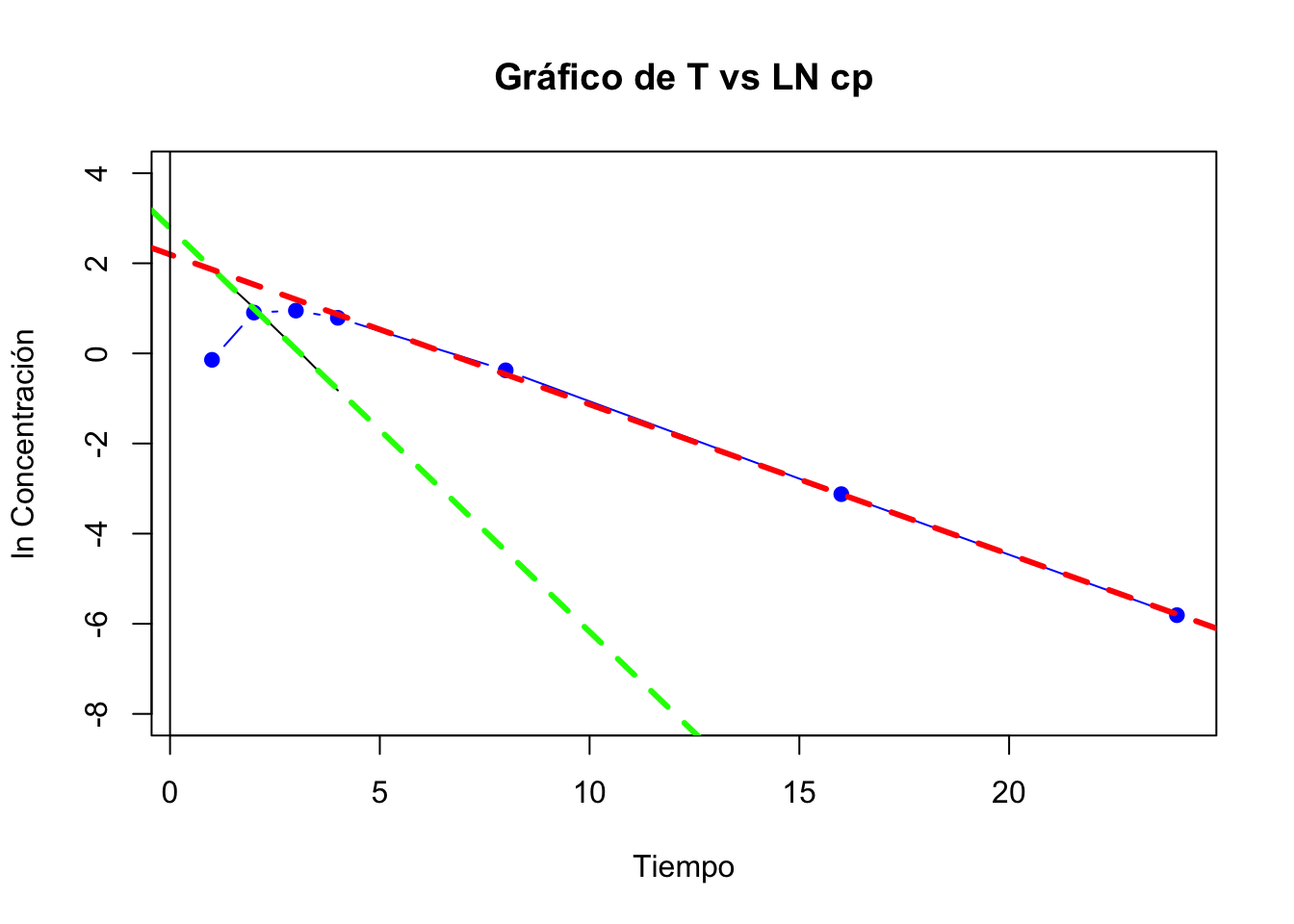
Hay tiempo de latencia, los resultados de la estimación de los parámetros con una biodisponibilidad de 1 son :
## Parámetros Resultados Unidades
## 1 C0 10.29 ug/mL
## 2 Kel 0.34 h-1
## 3 A0 16.15 ug/mL
## 4 Ka 0.90 h-1
## 5 Vd 78.27 Litros
## 6 tl 0.81 Horas
## 7 Cl 26.58 Volumen/Tiempo
## 8 tmax 2.55 Horas
## 9 Cpmax 2.68 ug/mL
## 10 Tiempo vida media 2.04 Horas
## 11 ABC cero infinito 12.27 ug*h/mLLos parámetros que dependen directamente de la biodisponibilidad no se encuentran estimados de forma correcta ya que asumimos una biodisponibilidad de 1, sin embargo la estimación del área bajo la curva que se base en la ecuación (2.1) está correctamente estimada.
Dado que se trata de un mismo fármaco y que tanto la administración IV como la oral se basan en un modelo de con cinética de primer orden, la ecuación (2.13) se puede simplificar como:
\[\begin{equation} F=\frac{(ABC^\infty_0)_{oral}}{(ABC^\infty_0)_{ref}}\cdot \frac{D_{ref}}{D_{oral}} \end{equation}\]
Sustituyendo los valores en la ecuación anterior obtenemos:
\[\begin{equation} F=\frac{12.27 \mu g \cdot h/mL}{59.22\mu g \cdot h/mL}\cdot \frac{300 mg}{500 mg} =0.12 \end{equation}\]
2.4.7 Resolución ejercicio 2.7
Los dos primeros datos no se toma en cuenta para los cálculos de los residuales.
Las gráficas de estos datos son:
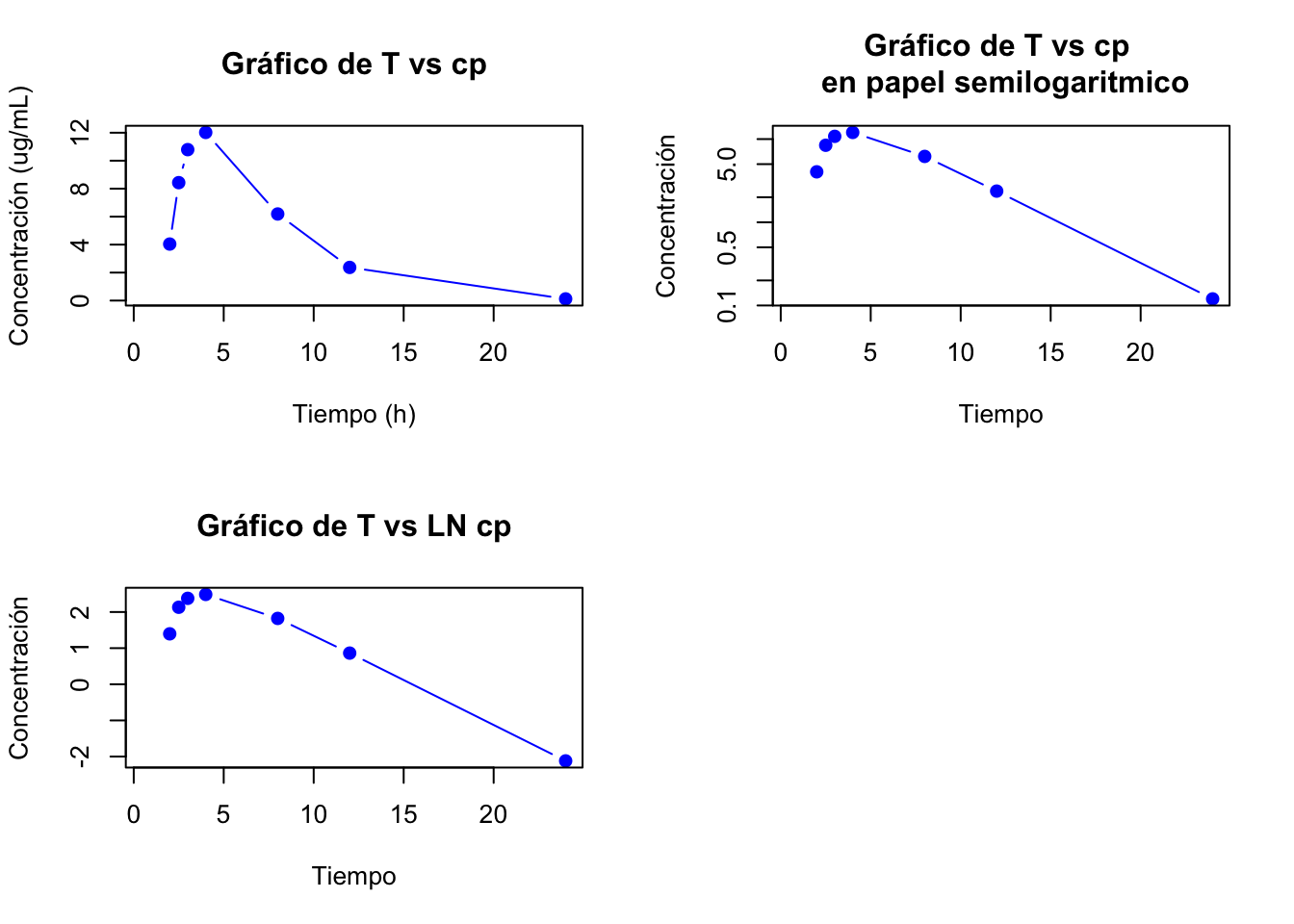
Gráfica de la fase de eliminación:
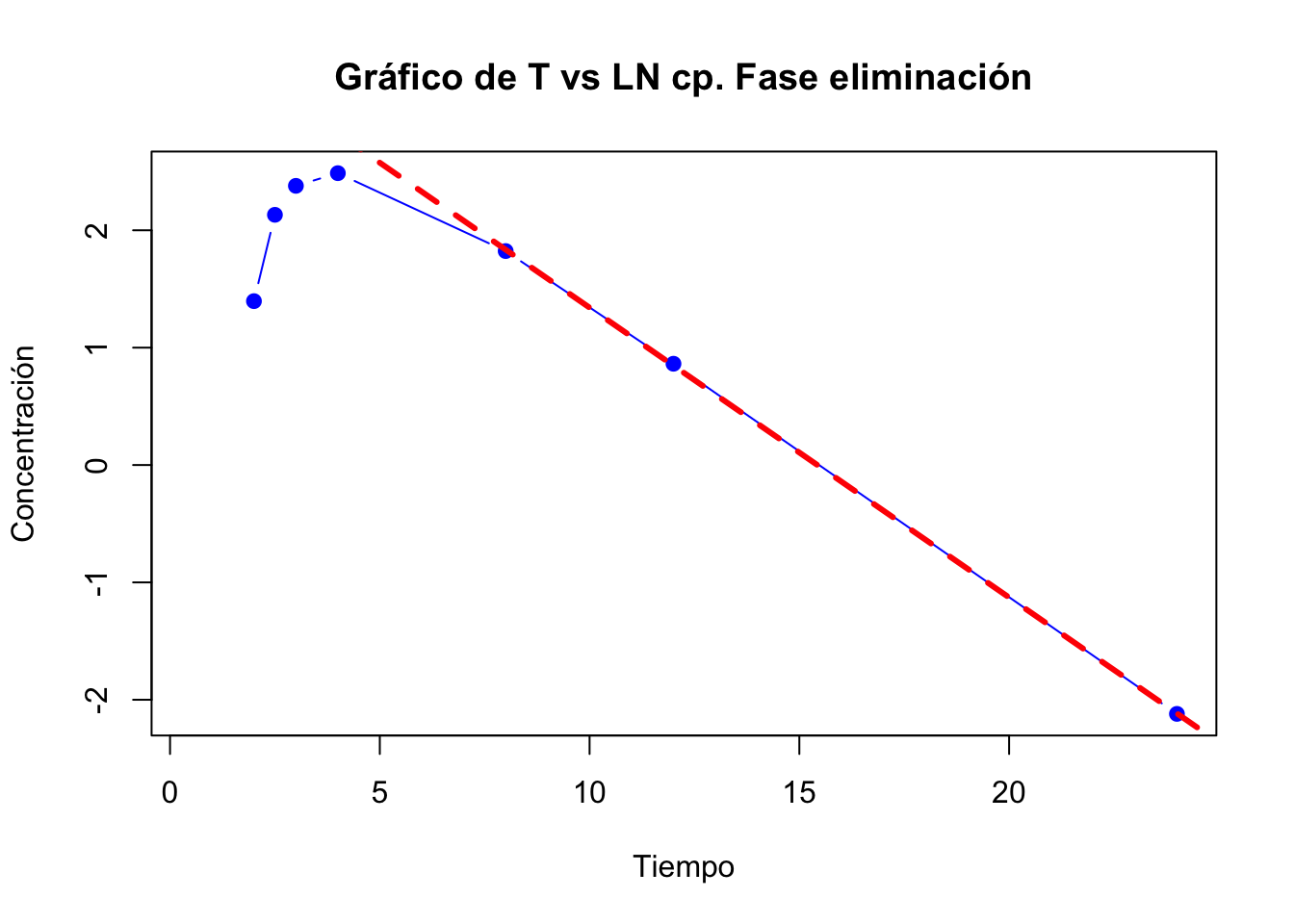
Se tomaron en cuenta los últimos 3 datos para la fase de eliminación.
Los valores extrapolados y los residuales se muestran en la siguiente tabla:
## Tiempo Conc Extrapolados Residuales
## 1 0.5 NA 39.92 NA
## 2 1.5 NA 31.19 NA
## 3 2.0 4.04 27.56 23.52
## 4 2.5 8.43 24.36 15.93
## 5 3.0 10.79 21.53 10.74
## 6 4.0 12.02 16.82 4.80Gráfica de absorción y fase de eliminación
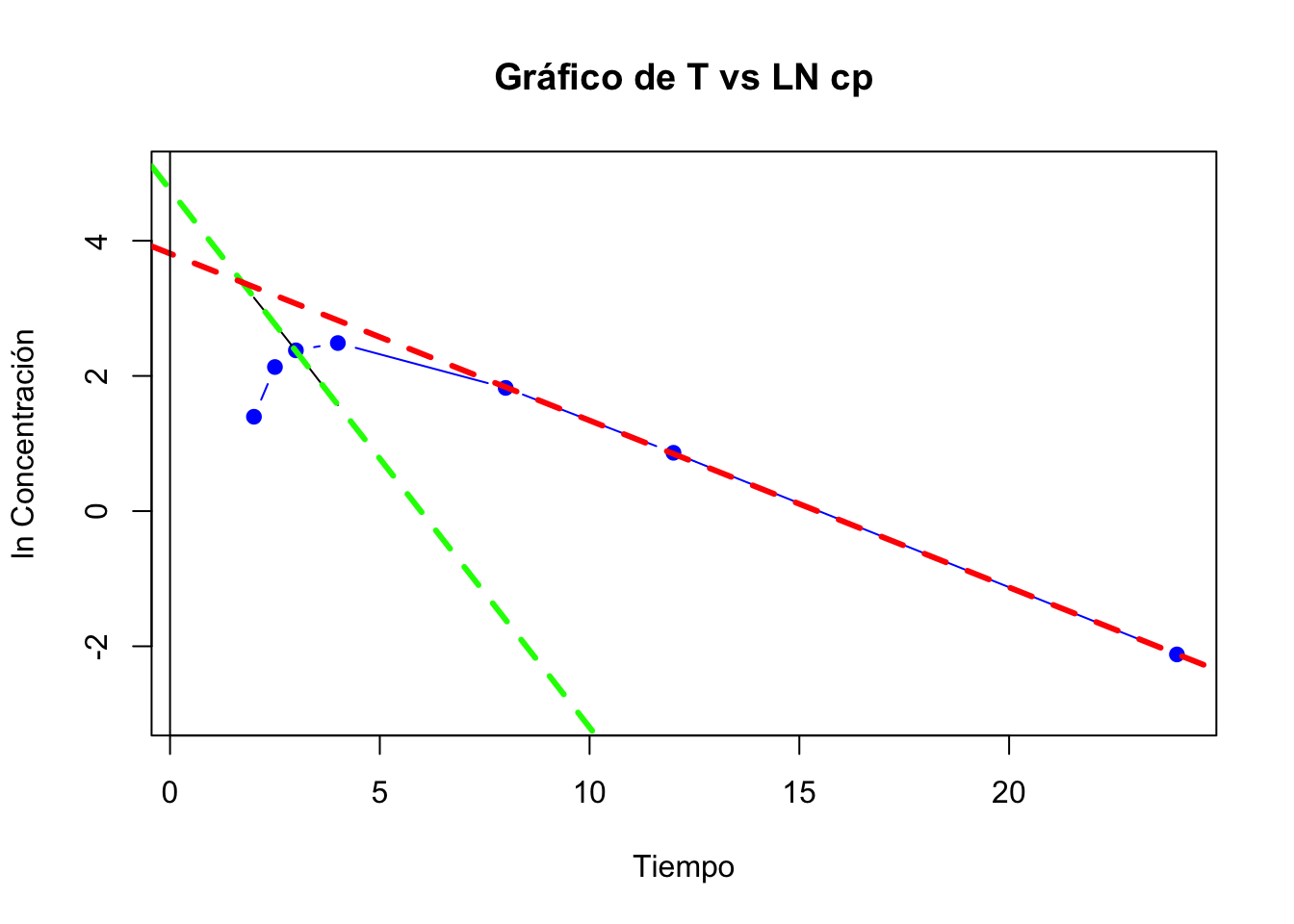
Hay tiempo de latencia, los resultados de la estimación de los parámetros con una biodisponibilidad de 1 son :
## Parámetros Resultados Unidades
## 1 C0 45.17 ug/mL
## 2 Kel 0.25 h-1
## 3 A0 116.01 ug/mL
## 4 Ka 0.80 h-1
## 5 Vd 16.05 Litros
## 6 tl 1.72 Horas
## 7 Cl 3.96 Volumen/Tiempo
## 8 tmax 3.85 Horas
## 9 Cpmax 12.03 ug/mL
## 10 Tiempo vida media 2.81 Horas
## 11 ABC cero infinito 37.04 ug*h/mLPara la identificación del tiempo de latencia en la gráfica solo es necesario tirar una linea donde las dos regresiones se juntan. En la siguiente gráfica la linea rosa representa el tiempo de latencia.
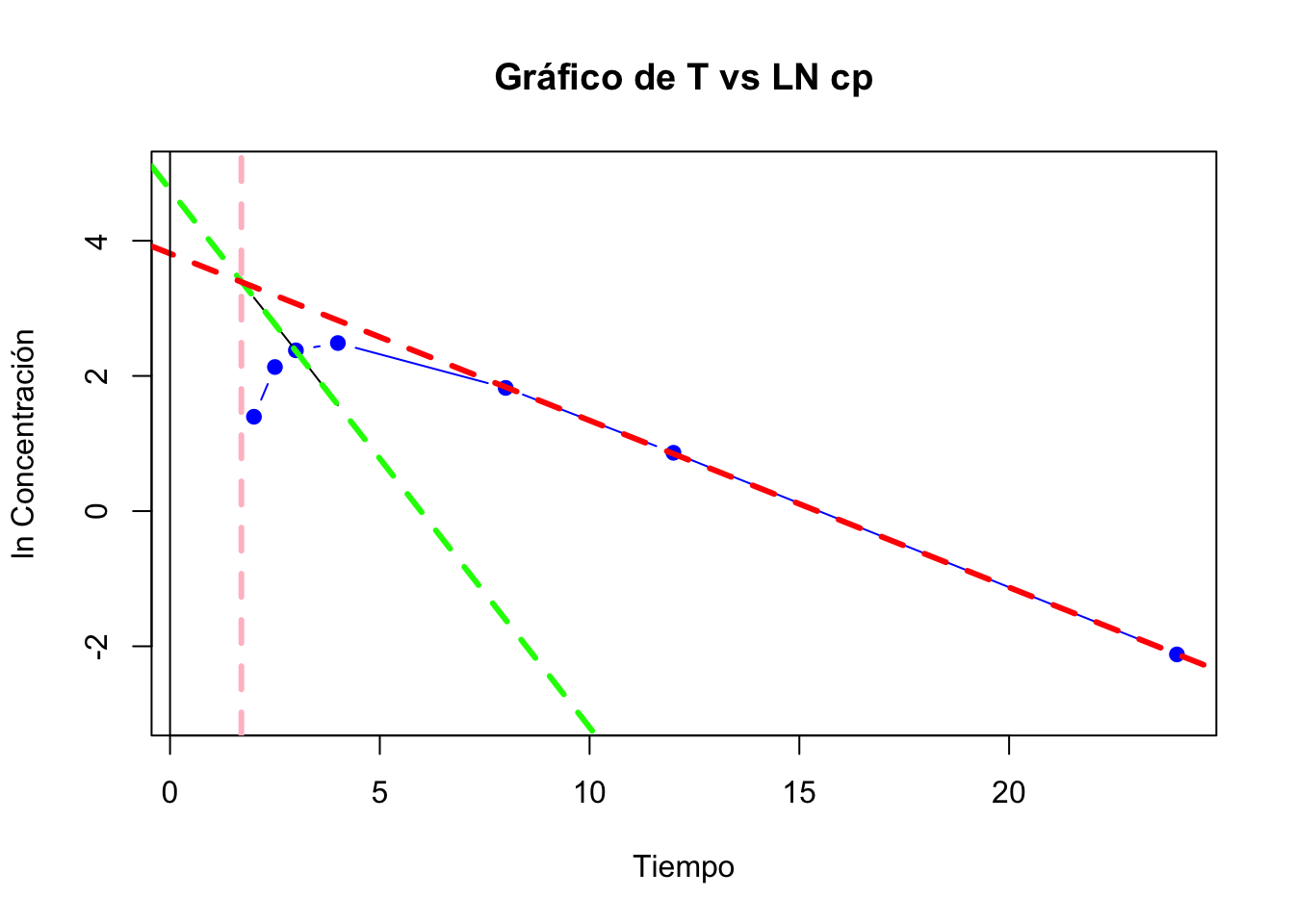
Para la ecuación del sistema solo debemos de sustituir los valores de las constantes y los interceptos en la ecuación (2.1). La ecuación del sistema es:
\[ Cp=45.17 \cdot e^{-0.25 \cdot t}-116.01\cdot e^{-0.80 \cdot t} \] ### Resolución ejercicio 2.8
No se puede resolver. Si hay tiempo de latencia es necesario conocer los interceptos
2.4.8 Resolución ejercicio 2.9
Las gráficas de estos datos son:
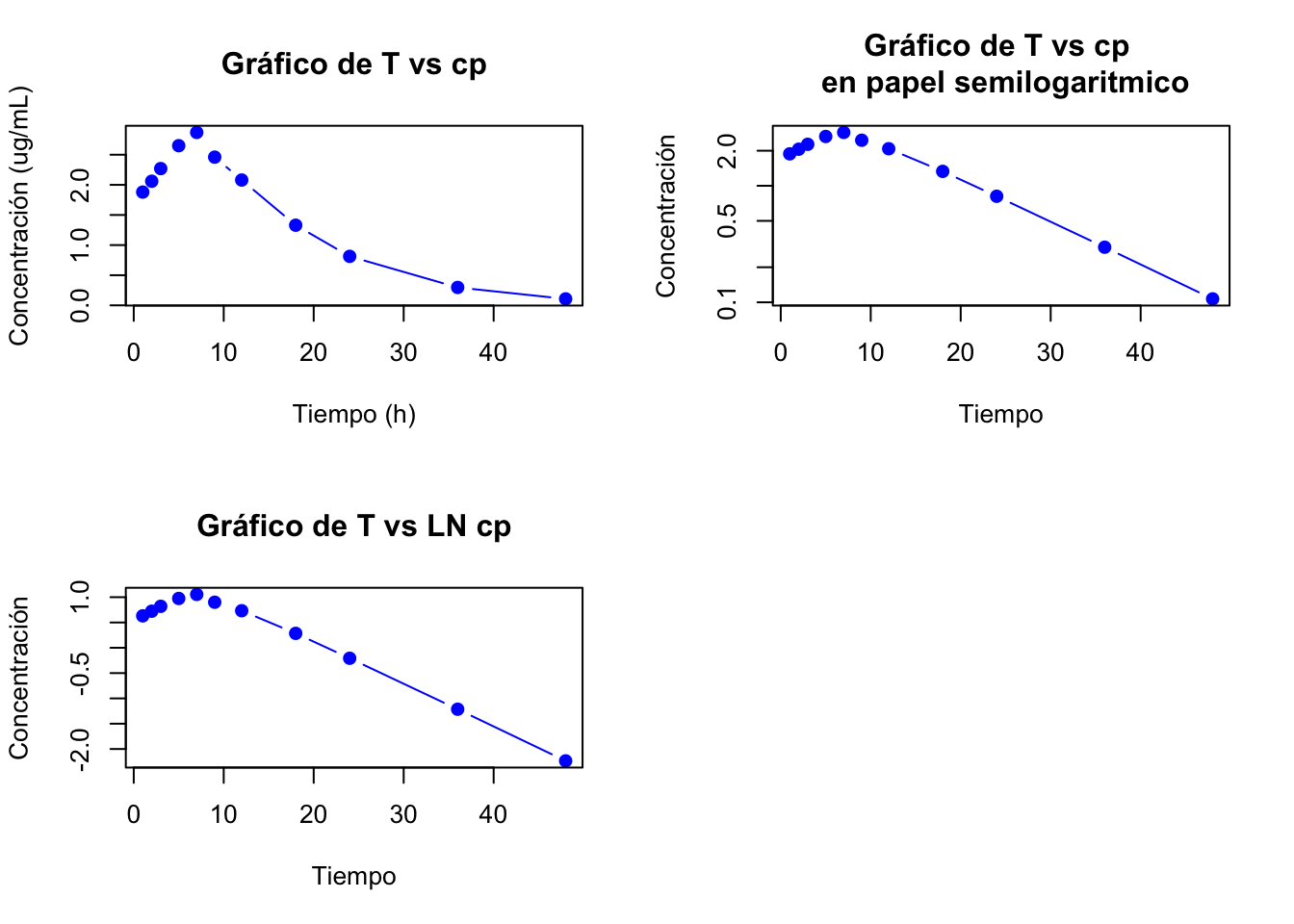
Gráfica de la fase de eliminación:
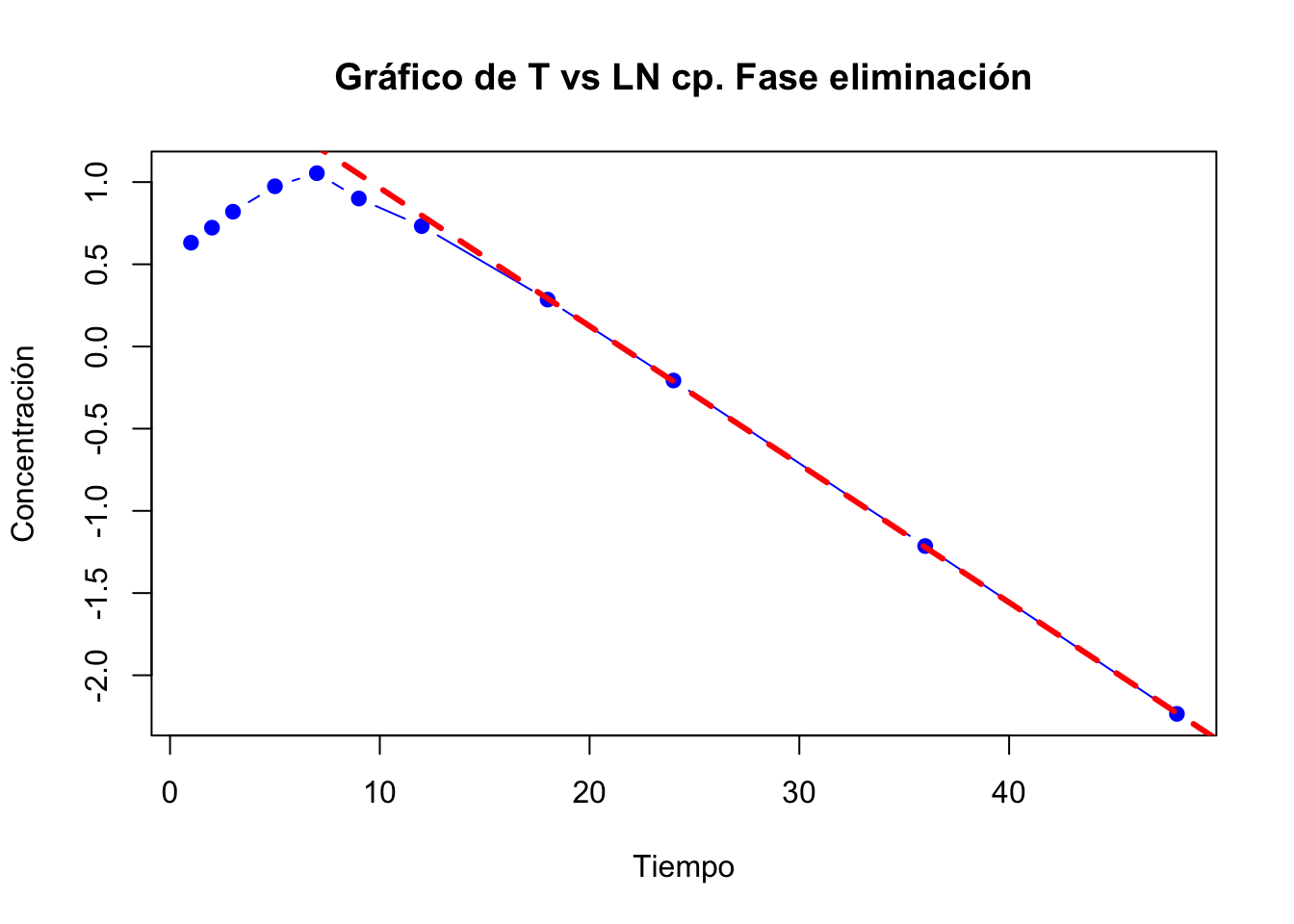
Se tomaron en cuenta los últimos 3 datos para la fase de eliminación.
Los valores extrapolados y los residuales se muestran en la siguiente tabla:
## Tiempo Conc Extrapolados Residuales
## 1 1 1.88 5.59 3.71
## 2 2 2.06 5.14 3.08
## 3 3 2.27 4.73 2.46
## 4 5 2.65 3.99 1.34
## 5 7 2.87 3.38 0.51
## 6 9 2.46 2.85 0.39Gráfica de absorción y fase de eliminación
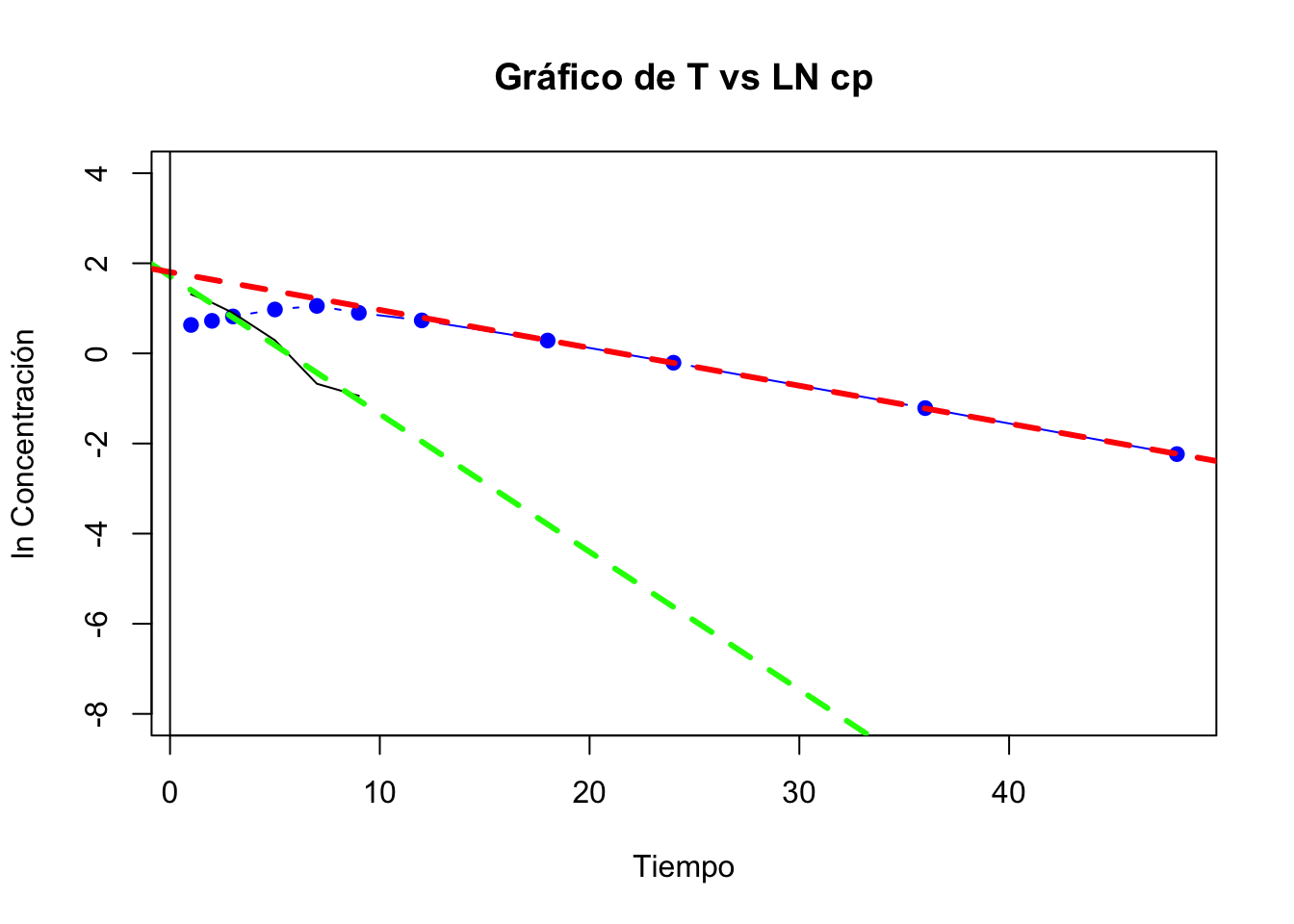
No hay tiempo de latencia
## Parámetros Resultados Unidades
## 1 C0 6.08 ug/mL
## 2 Kel 0.08 h-1
## 3 A0 5.54 ug/mL
## 4 Ka 0.31 h-1
## 5 Vd 22.68 Litros
## 6 tl -0.42 Horas
## 7 Cl 1.91 Volumen/Tiempo
## 8 tmax 5.82 Horas
## 9 Cpmax 2.70 ug/mL
## 10 Tiempo vida media 8.25 Horas
## 11 ABC cero infinito 54.23 ug*h/mLNote como los parámetros casí no se modifican si se estiman con tiempo de latencia
## Parámetros Resultados Unidades
## 1 C0 6.08 ug/mL
## 2 Kel 0.08 h-1
## 3 A0 5.54 ug/mL
## 4 Ka 0.31 h-1
## 5 Vd 22.68 Litros
## 6 tl -0.42 Horas
## 7 Cl 1.91 Volumen/Tiempo
## 8 tmax 5.40 Horas
## 9 Cpmax 2.80 ug/mL
## 10 Tiempo vida media 8.25 Horas
## 11 ABC cero infinito 54.23 ug*h/mLPara el tiempo de vida media la constante de eliminación:
\[ t_{1/2}=\frac{ln2}{0.08 h^{-1}}=8.66 h \]
La velocidad de absorción es igual a \(K_a\), por lo tanto la velocidad de absorición es \(0.31h^{-1}\)
La ecuación del modelo es:
\[ Cp=6.08 \cdot e^{-0.08 \cdot t}-5.54\cdot e^{-0.31 \cdot t} \]
2.4.9 Resolución ejercicio 2.10
De la ecuación dada en el problema, podemos asumir que \(A^0\) y \(C^0\) son iguales por lo tanto despejando las ecuaciones del modelo obtenemos:
- Si hay tiempo de latencia: No hay tiempo de latencia, \(A^0\) y \(C^0\) son iguales.
- \(tmax: 4h\)
- \(Cpmax: 12.5 \mu g /mL\)
- \(t_{1/2}=5.6 h\)
- \(V_d=24.4 L\)
2.4.10 Resolución ejercicio 2.11
Las gráficas de estos datos son:
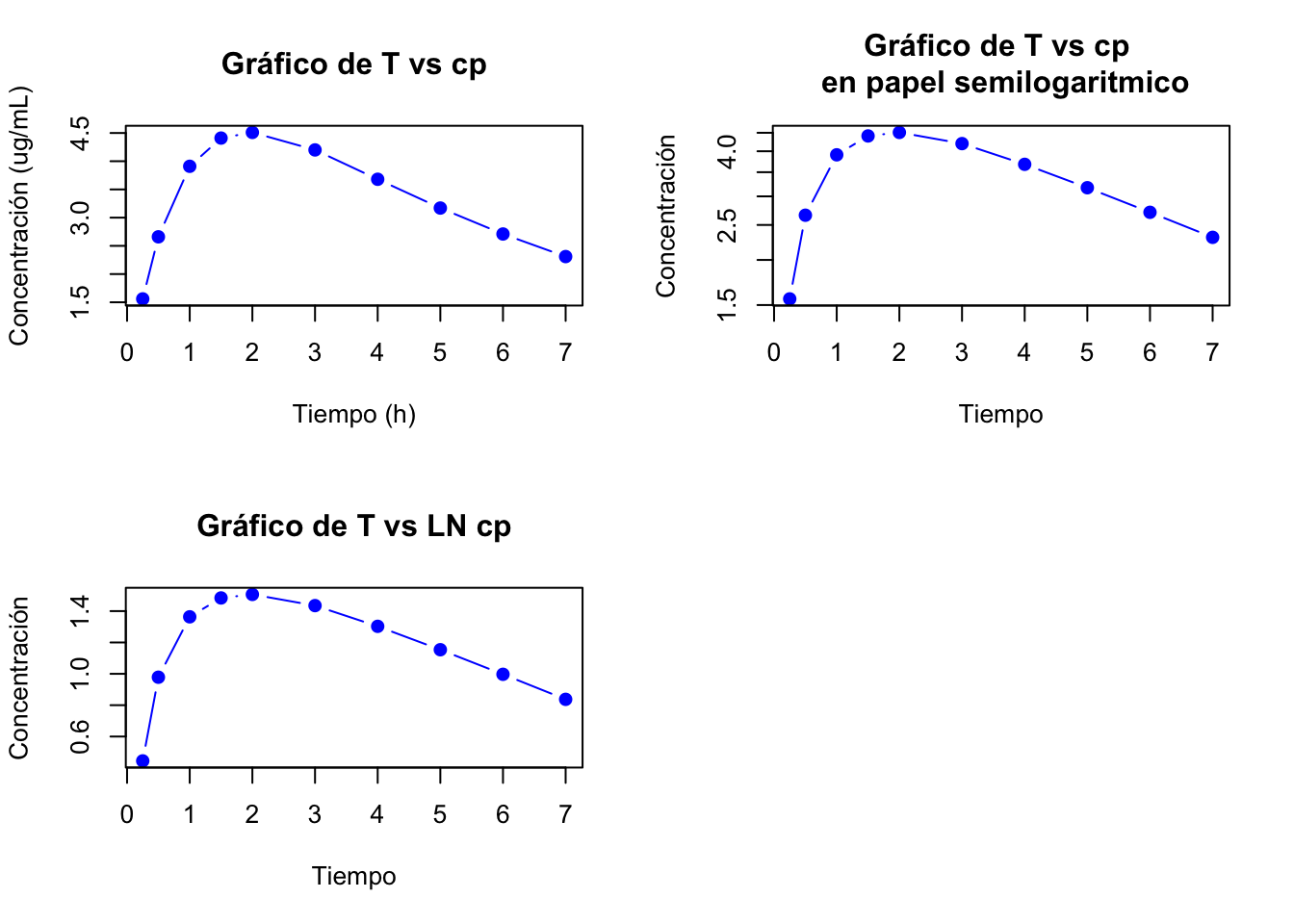
Gráfica de la fase de eliminación:
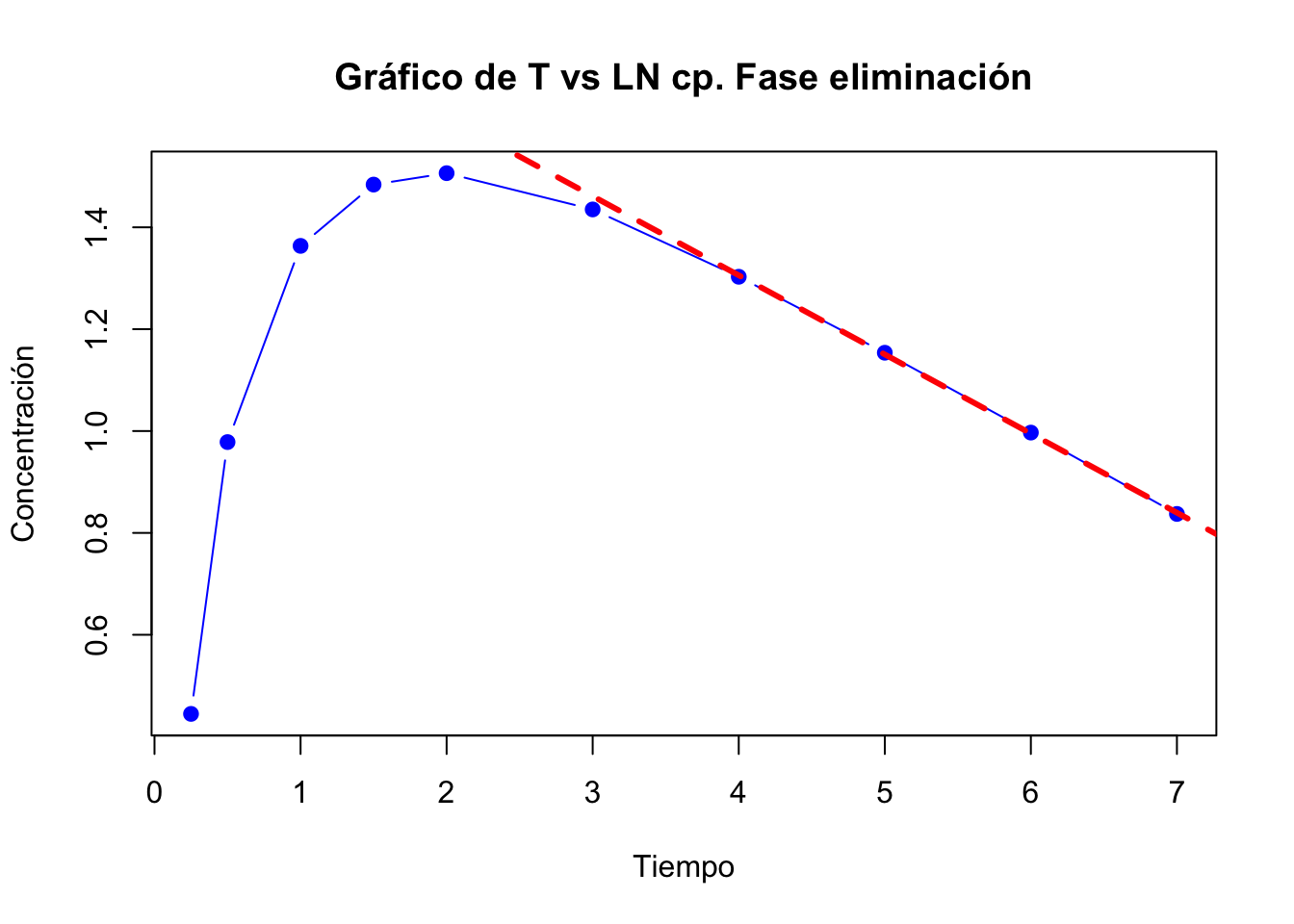
Se tomaron en cuenta los últimos 4 datos para la fase de eliminación.
Los valores extrapolados y los residuales se muestran en la siguiente tabla:
## Tiempo Conc Extrapolados Residuales
## 1 0.25 1.56 6.61 5.05
## 2 0.50 2.66 6.36 3.70
## 3 1.00 3.91 5.88 1.97
## 4 1.50 4.41 5.44 1.03
## 5 2.00 4.51 5.04 0.53
## 6 3.00 4.20 4.31 0.11Gráfica de absorción y fase de eliminación
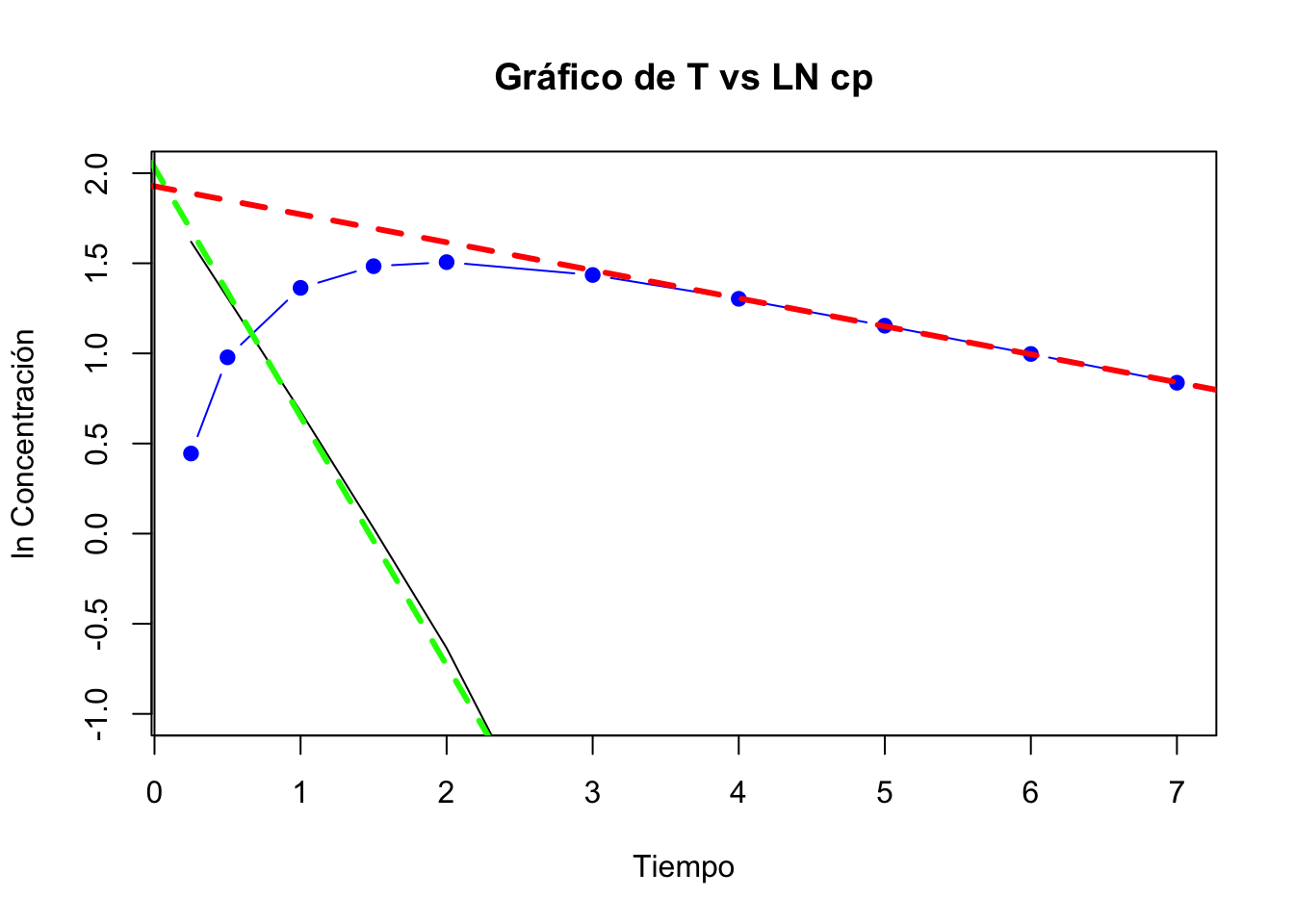
Hay tiempo de latencia
Hay tiempo de latencia, los resultados de la estimación de los parámetros con una biodisponibilidad de 1 son:
## Parámetros Resultados Unidades
## 1 C0 6.87 ug/mL
## 2 Kel 0.16 h-1
## 3 A0 7.61 ug/mL
## 4 Ka 1.38 h-1
## 5 Vd 41.00 Litros
## 6 tl 0.08 Horas
## 7 Cl 6.37 Volumen/Tiempo
## 8 tmax 1.87 Horas
## 9 Cpmax 4.56 ug/mL
## 10 Tiempo vida media 4.46 Horas
## 11 ABC cero infinito 38.71 ug*h/mLAl duplicar la dosis, los parámetros del sistema cambian de la siguiente manera:
## Parámetros Resultados Unidades
## 1 C0 6.87 ug/mL
## 2 Kel 0.16 h-1
## 3 A0 7.61 ug/mL
## 4 Ka 1.38 h-1
## 5 Vd 82.01 Litros
## 6 tl 0.08 Horas
## 7 Cl 12.74 Volumen/Tiempo
## 8 tmax 1.87 Horas
## 9 Cpmax 4.56 ug/mL
## 10 Tiempo vida media 4.46 Horas
## 11 ABC cero infinito 38.71 ug*h/mLSe modifican el volumen de distribución y el aclaramiento.
2.4.11 Resolución ejercicio 2.12
Las gráficas de estos datos son:
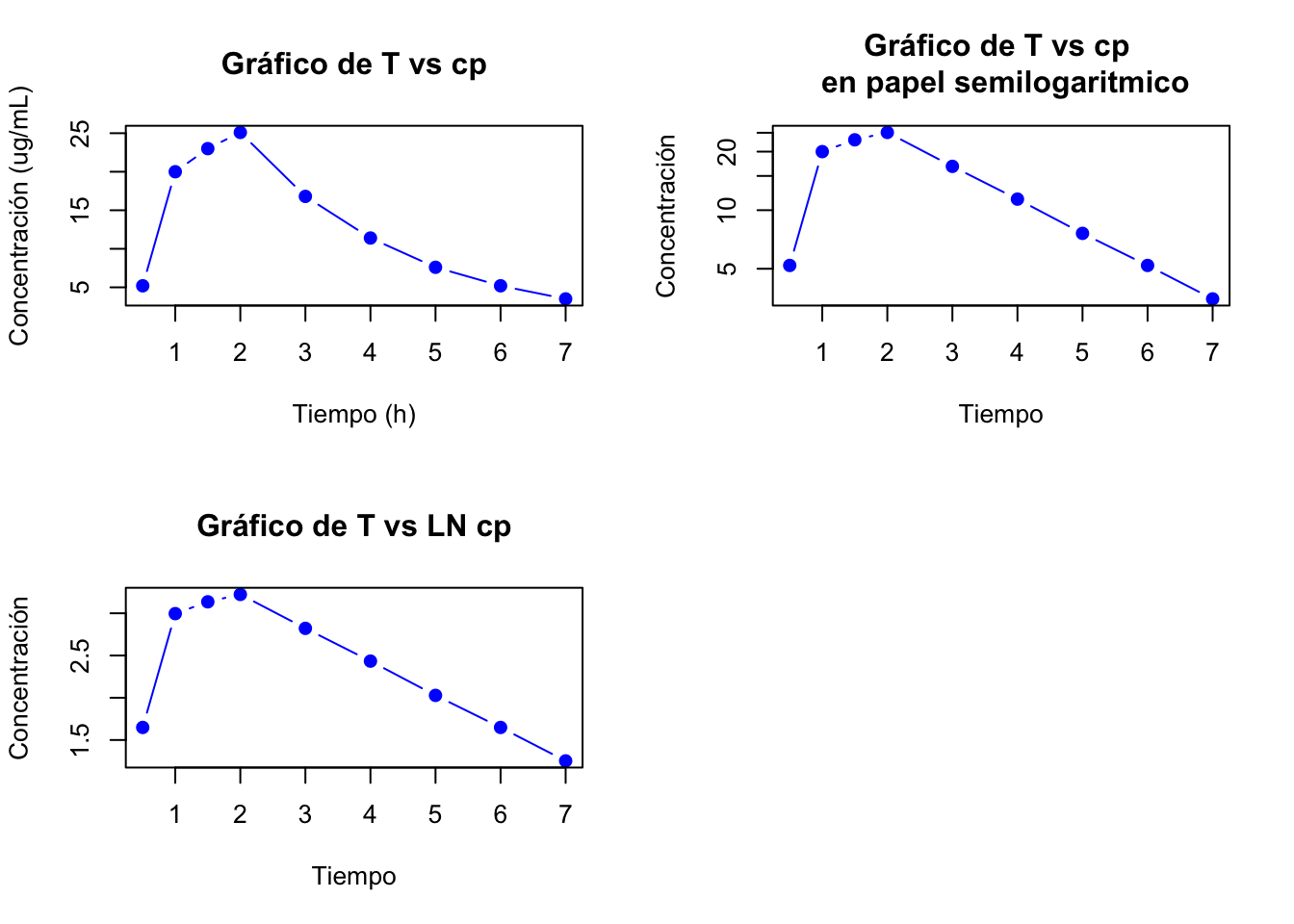
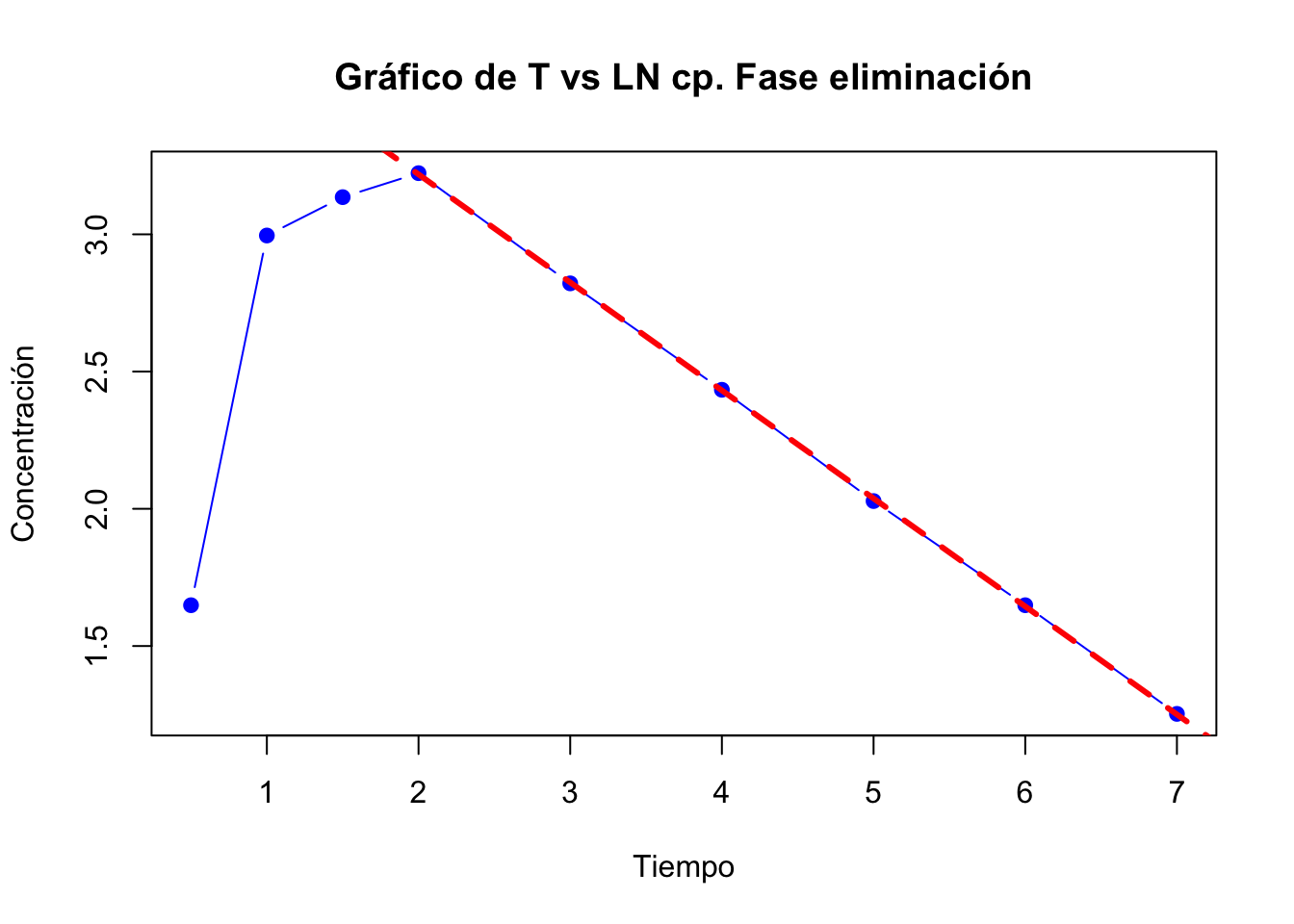
Se tomaron en cuenta los últimos 6 datos para la fase de eliminación, si toma menos valores a partir del 4 tiempo los valores de los residuales se hacen negativos.
Los valores extrapolados y los residuales se muestran en la siguiente tabla:
## Tiempo Conc Extrapolados Residuales
## 1 0.5 5.2 45.09 39.89
## 2 1.0 20.0 37.04 17.04
## 3 1.5 23.0 30.42 7.42Gráfica de absorción y fase de eliminación
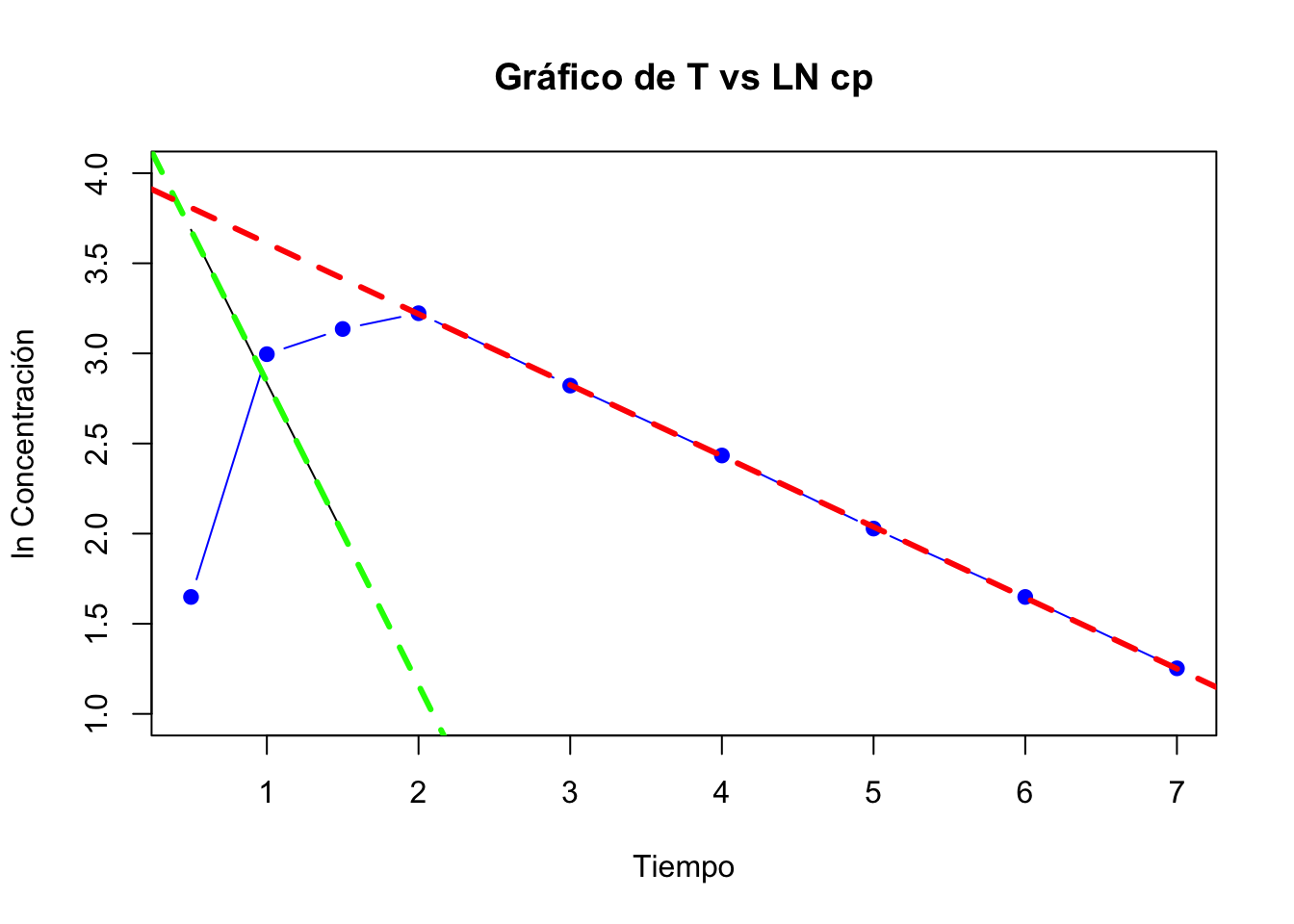
Si hay tiempo de latencia, corto pero si lo hay:
## Parámetros Resultados Unidades
## 1 Kel 0.39 h-1
## 2 Ka 1.68 h-1
## 3 tl 0.40 Horas
## 4 Cl 4.68 Cantidad/TiempoCon los datos de aclaramiento y \(K_{el}\) podemos estimar el \(V_d\), el resto de la formulas requieren de una dosis, la cual no está descrita en el problema.
\[ Cl= V_d \cdot K_{el} \longrightarrow V_d=\frac{Cl}{K_{el}}= \frac{4.68 L/h}{0.39 h^{-1}}= 12 L \]
De los parámetros anterior solamente se modifica el \(Cl\).
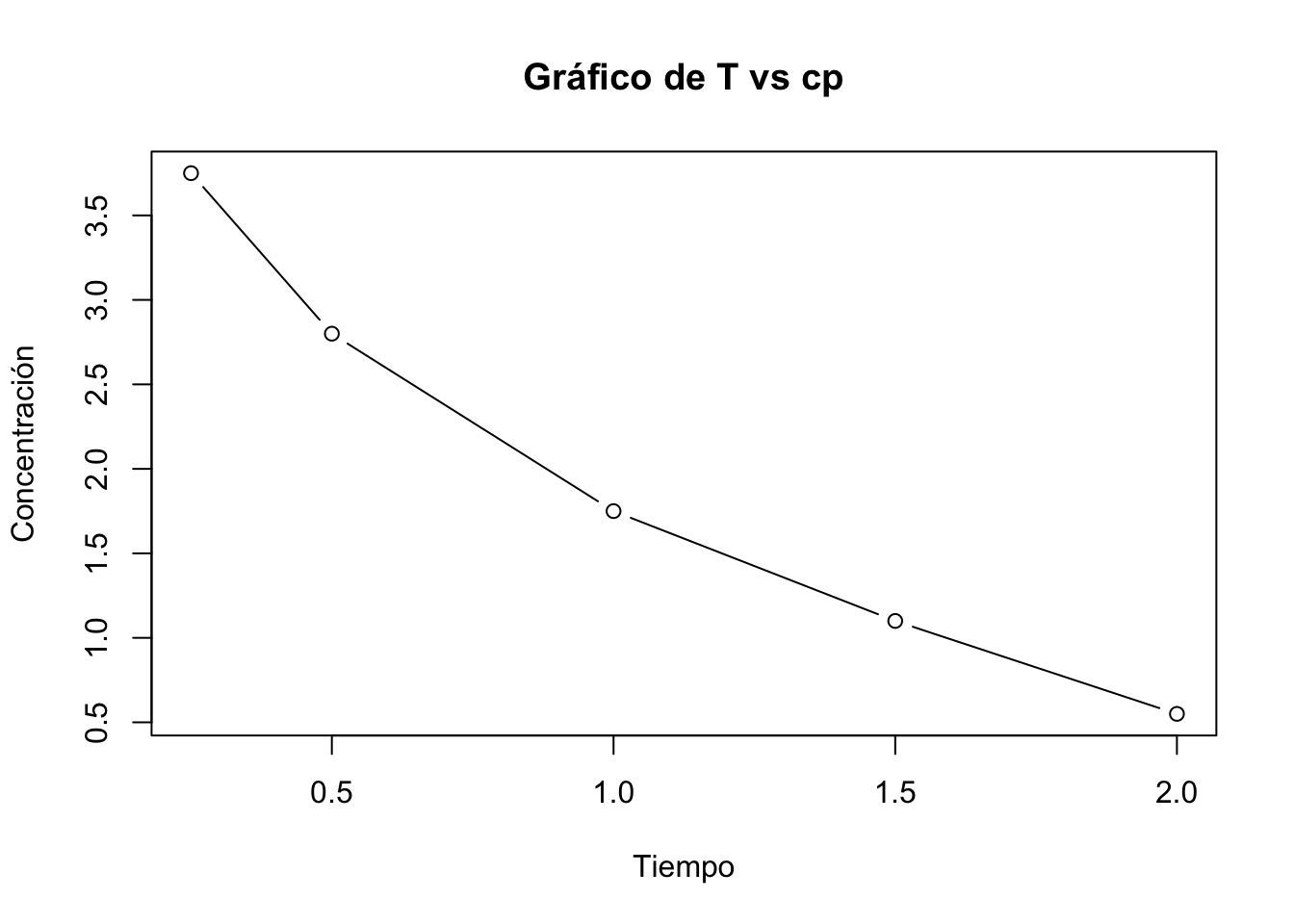
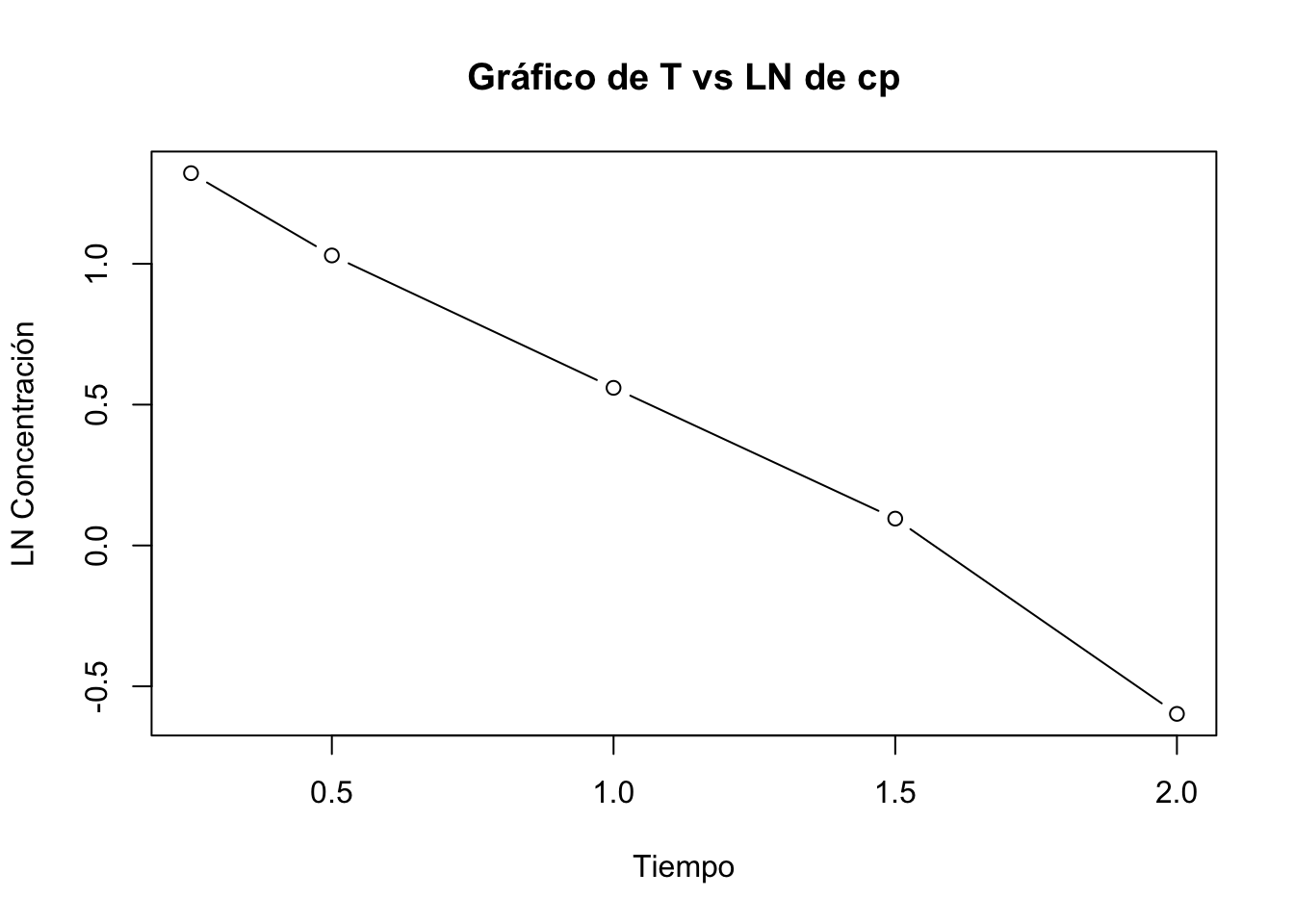
2.4.12 Resolución ejercicio 2.13
Los parámetros del sistema por administracion IV son:
## [1] "Regresión"
##
## Call:
## lm(formula = log(Conc) ~ Tiempo)
##
## Residuals:
## 1 2 3 4 5
## -0.009393 -0.036075 0.024832 0.091436 -0.070801
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.59660 0.06150 25.96 0.000125 ***
## Tiempo -1.06182 0.05001 -21.23 0.000229 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.0716 on 3 degrees of freedom
## Multiple R-squared: 0.9934, Adjusted R-squared: 0.9912
## F-statistic: 450.9 on 1 and 3 DF, p-value: 0.0002285
##
## [1] "Kel"
## [1] 1.062
## [1] "Cp0"
## [1] 4.94
## [1] "Tiempo de vida media"
## [1] 0.65
## [1] "Volumen de distribución"
## [1] 20.24
## [1] "Aclaramiento"
## [1] 21.49
## [1] "Area bajo la curva de 0 a infinito"
## [1] 4.65Los parámetros para el modelos absorción oral son:
Las gráficas de estos datos son:
Gráfica de la fase de eliminación:
Se tomaron en cuenta los últimos 3 datos para la fase de eliminación.
Los valores extrapolados y los residuales se muestran en la siguiente tabla:
## Tiempo Conc Extrapolados Residuales
## 1 0.5 0.57 2.45 1.88
## 2 1.0 0.88 2.12 1.24
## 3 1.5 1.03 1.84 0.81
## 4 2.0 1.07 1.59 0.52
## 5 2.5 1.04 1.38 0.34
## 6 3.0 0.98 1.20 0.22
## 7 4.0 0.82 0.90 0.08Gráfica de absorción y fase de eliminación
No hay tiempo de latencia y si lo hay, es muy corto. Se estiman los parámetros del modelo con y sin tiempo de latencia.
Parámetros con tiempo de latencia y biosdisponibilidad de 1.
## Parámetros Resultados Unidades
## 1 C0 2.83 ug/mL
## 2 Kel 0.29 h-1
## 3 A0 3.06 ug/mL
## 4 Ka 0.89 h-1
## 5 Vd 52.08 Litros
## 6 tl 0.13 Horas
## 7 Cl 14.93 Volumen/Tiempo
## 8 tmax 2.00 Horas
## 9 Cpmax 1.08 ug/mL
## 10 Tiempo vida media 2.42 Horas
## 11 ABC cero infinito 6.43 ug*h/mLParámetros sin tiempo de latencia y biosdisponibilidad de 1.
## Parámetros Resultados Unidades
## 1 C0 2.83 ug/mL
## 2 Kel 0.29 h-1
## 3 A0 3.06 ug/mL
## 4 Ka 0.89 h-1
## 5 Vd 52.08 Litros
## 6 tl 0.13 Horas
## 7 Cl 14.93 Volumen/Tiempo
## 8 tmax 1.87 Horas
## 9 Cpmax 1.12 ug/mL
## 10 Tiempo vida media 2.42 Horas
## 11 ABC cero infinito 6.43 ug*h/mLSi hay fenómeno de flip-flop.
Para la biosdiponibilidad absoluta se utiliza la ecuación (2.13)
\[ F=\frac{6.43 \mu g\cdot h/mL}{4.65\mu g\cdot h/mL}\cdot \frac{100 mg}{100 mg}\cdot \frac{14.93 L/h}{21.49 L/h}=0.96 \] Tome en cuenta que la estimación del \(Cl\) para la administración oral, se basó en un valor de \(F=1\). Lo ideal sería tener otros datos para poder estimar el valor de la biodisponibilidad absoluta.
Si se invierten los valores de las constantes para formulación oral, los valores de \(V_d\) y \(Cl\) serán negativos.
2.4.13 Resolución ejercicio 2.14
Las gráficas de los datos son:
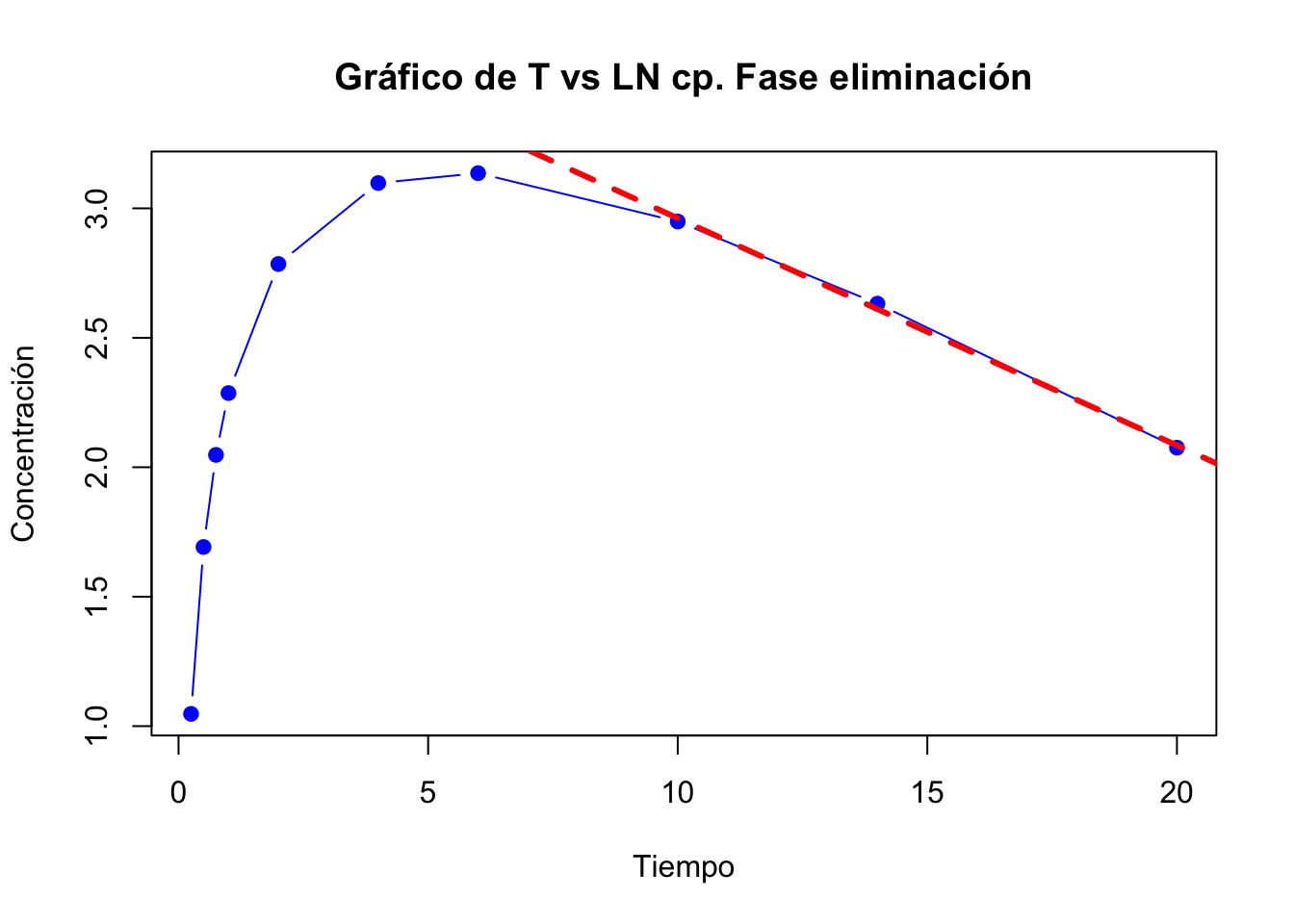
Se tomaron en cuenta los últimos 3 datos para la fase de eliminación.
Los valores extrapolados y los residuales se muestran en la siguiente tabla:
## Tiempo Conc Extrapolados Residuales
## 1 0.25 2.85 45.50 42.65
## 2 0.50 5.43 44.51 39.08
## 3 0.75 7.75 43.54 35.79
## 4 1.00 9.84 42.60 32.76
## 5 2.00 16.20 39.02 22.82
## 6 4.00 22.15 32.74 10.59
## 7 6.00 23.01 27.47 4.46Gráfica de absorción y fase de eliminación
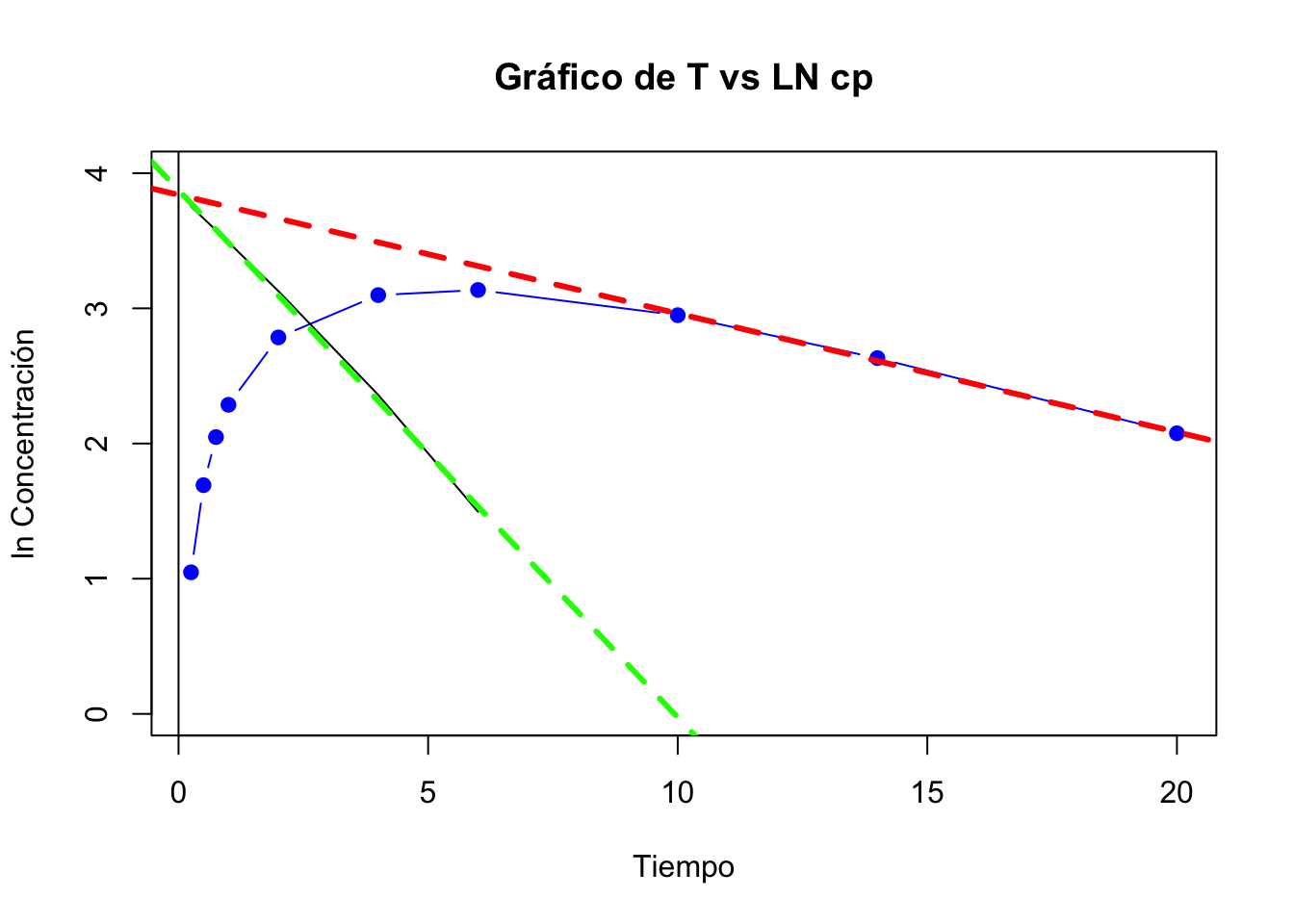
Si hay tiempo de latencia. Los parámetros del modelo son:
## Parámetros Resultados Unidades
## 1 C0 46.50 ng/mL
## 2 Kel 0.09 h-1
## 3 A0 48.18 ng/mL
## 4 Ka 0.39 h-1
## 5 Vd 0.22 Litros
## 6 tl 0.12 Horas
## 7 Cl 0.02 Volumen/Tiempo
## 8 tmax 5.05 Horas
## 9 Cpmax 23.13 ng/mL
## 10 Tiempo vida media 7.90 Horas
## 11 ABC cero infinito 406.33 ug*h/mLEl correcto cálculo del \(V_d\) es:
\[ C^0=\frac{46.50 ng}{mL}\cdot \frac{1000 ml}{1 L}\cdot \frac{1 mg}{1000000 ng}=0.0465 mg/L \] Con este dato y sustituyendo la ecuación (2.4)
\[ V_d=\frac{0.85\cdot 10 mg}{0.0465mg/L}\cdot \frac{0.39}{0.39-0.09}=223.65 L \]
2.4.14 Resolución ejercicio 2.15
Con los datos del problema se puede utilizar la ecuación (2.7) para el \(tmax\)
\[ tmax=\frac{ln\frac{1.5}{0.17}}{1.5-0.17}= 1.64 h \]
Conocido el \(tmax\) se puede utilizar la ecuación del problema. Toma en cuenta que esta ecuación es la versión simplificada de la ecuación (2.1)
\[ Cpmax= 45 \cdot (e^{-0.17 \cdot 1.64}-e^{-1.5 \cdot 1.64})=30.2 \mu g/mL \] Para el tiempo de \(t_{1/2}\)
\[ t_{1/2}=\frac{0.693}{0.17}=4.08 h \]
No hay tiempo de latencia \(C^0\) y \(A^0\) son iguales
2.4.15 Resolución ejercicio 2.16
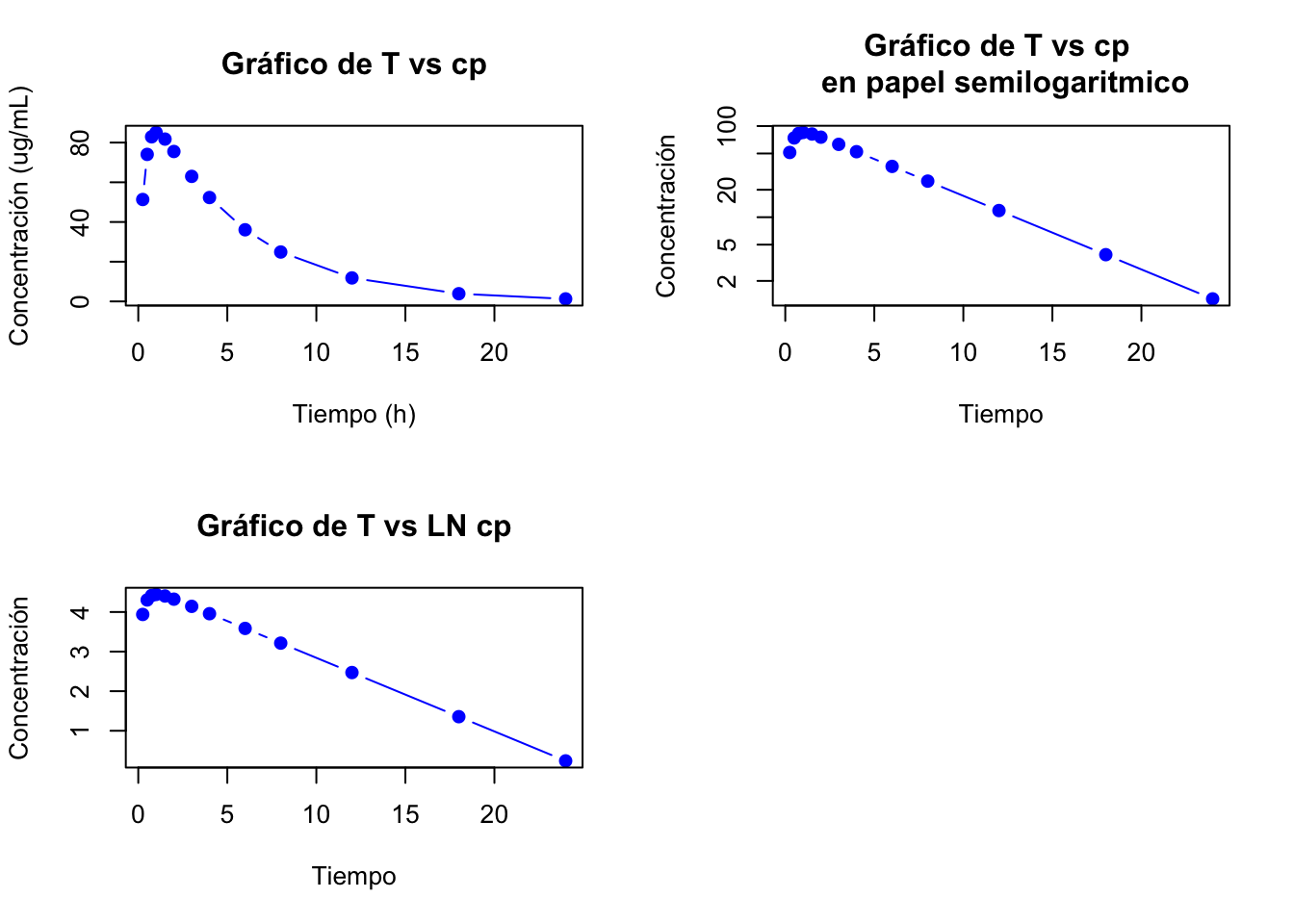Gráfica de la fase de eliminación:
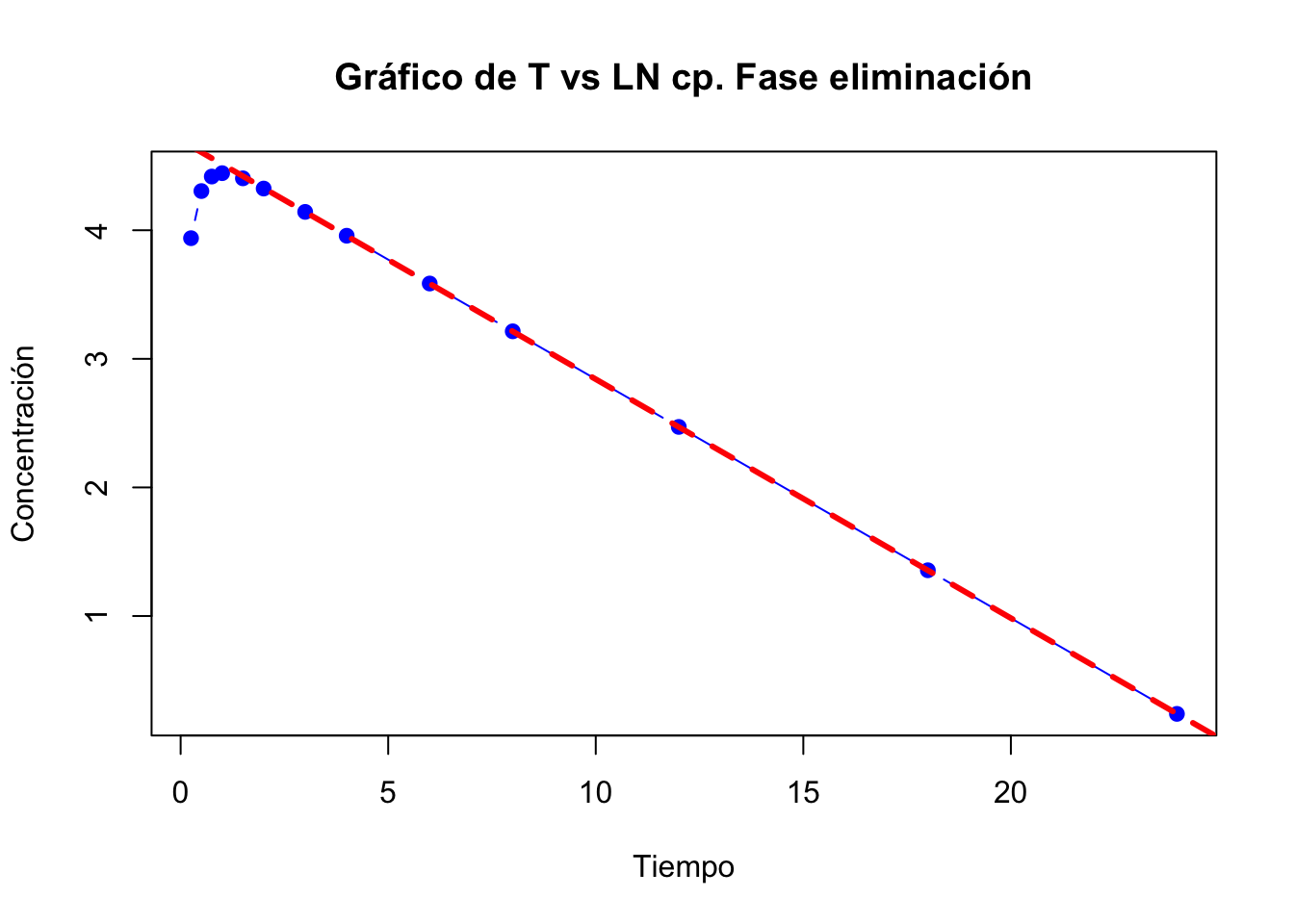
Se tomaron en cuenta los últimos 8 datos para la fase de eliminación.
Los valores extrapolados y los residuales se muestran en la siguiente tabla:
## Tiempo Conc Extrapolados Residuales
## 1 0.25 51.33 104.91 53.58
## 2 0.50 74.05 100.15 26.10
## 3 0.75 82.91 95.60 12.69
## 4 1.00 85.11 91.26 6.15
## 5 1.50 81.76 83.16 1.40Gráfica de absorción y fase de eliminación
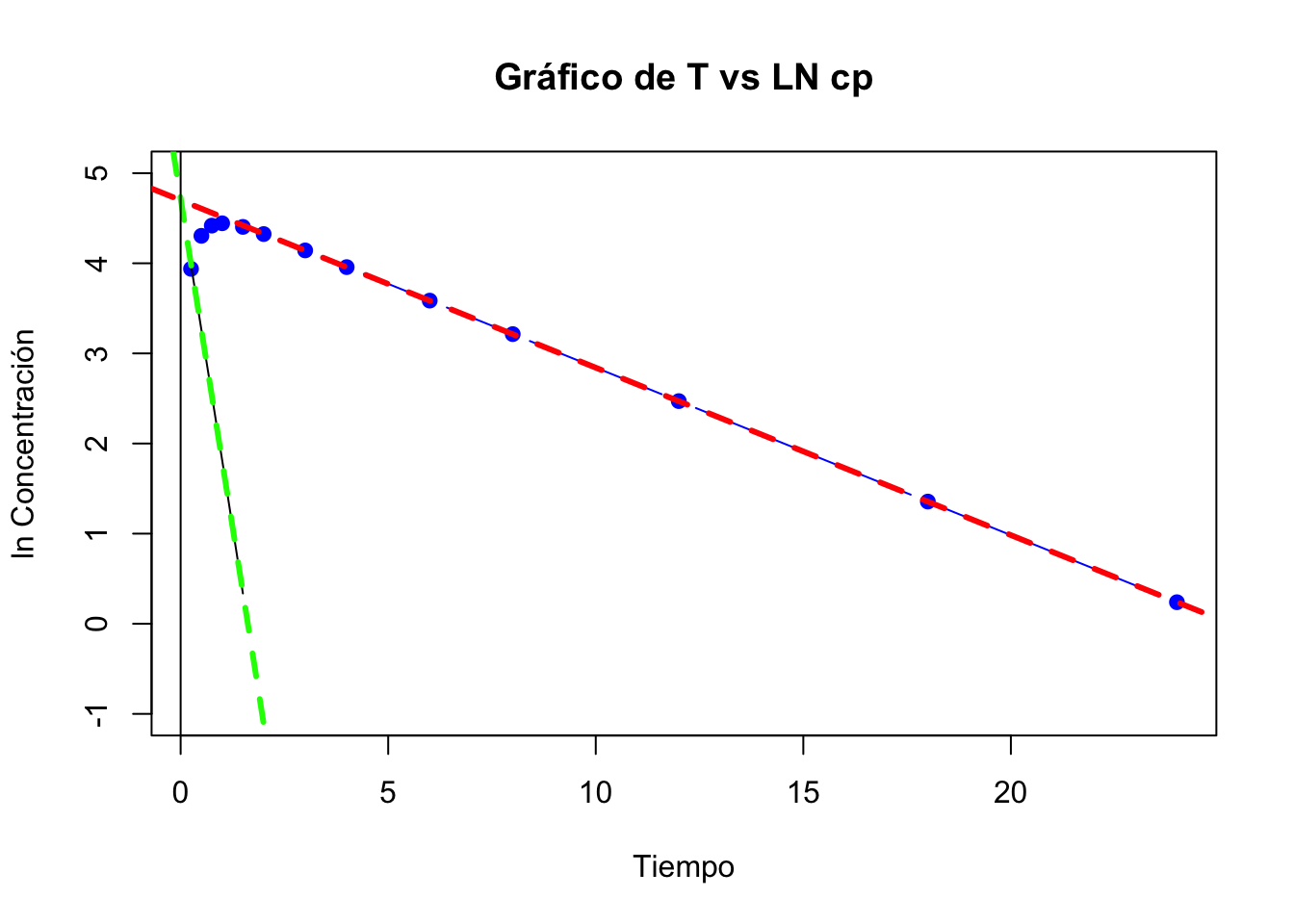No hay tiempo de latencia
## Parámetros Resultados Unidades
## 1 C0 109.89 ng/mL
## 2 Kel 0.19 h-1
## 3 A0 112.10 ng/mL
## 4 Ka 2.92 h-1
## 5 Vd 0.24 Litros
## 6 tl 0.01 Horas
## 7 Cl 0.04 Volumen/Tiempo
## 8 tmax 1.02 Horas
## 9 Cpmax 85.19 ng/mL
## 10 Tiempo vida media 3.73 Horas
## 11 ABC cero infinito 553.02 ug*h/mL- \(K_a=2.92\)
- \(K_{el}=0.19\)
- Si tiene sentido que que \(K_a > K_{el}\), en la mayoría de las formas orales, \(K_a > K_{el}\) con excepción de las formas de liberación controlada.
- Mediante IV
- \(tmax=1.02 h\)
2.4.16 Resolución ejercicio 2.17
Las gráficas de los datos son:
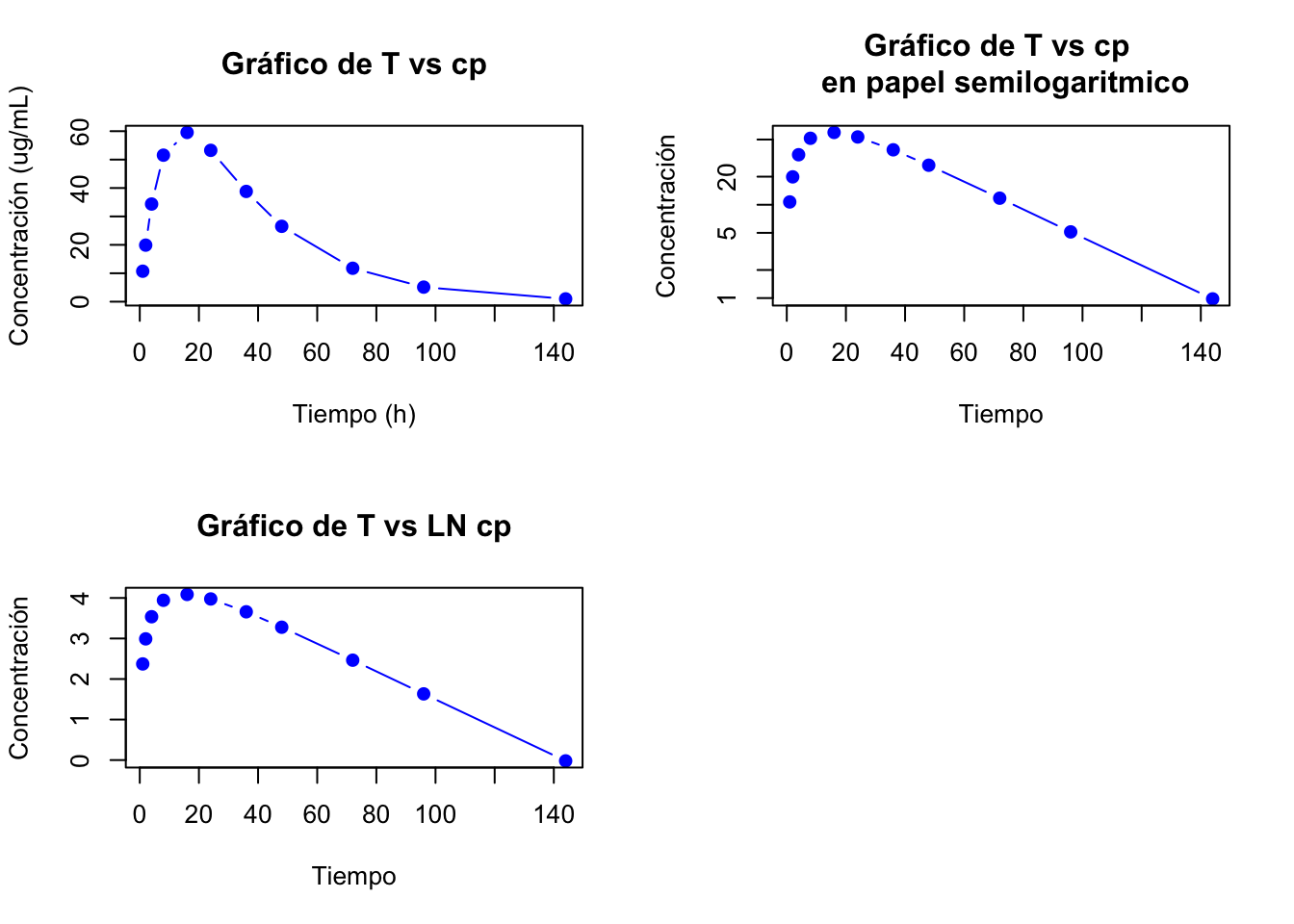
Gráfica de la fase de eliminación:
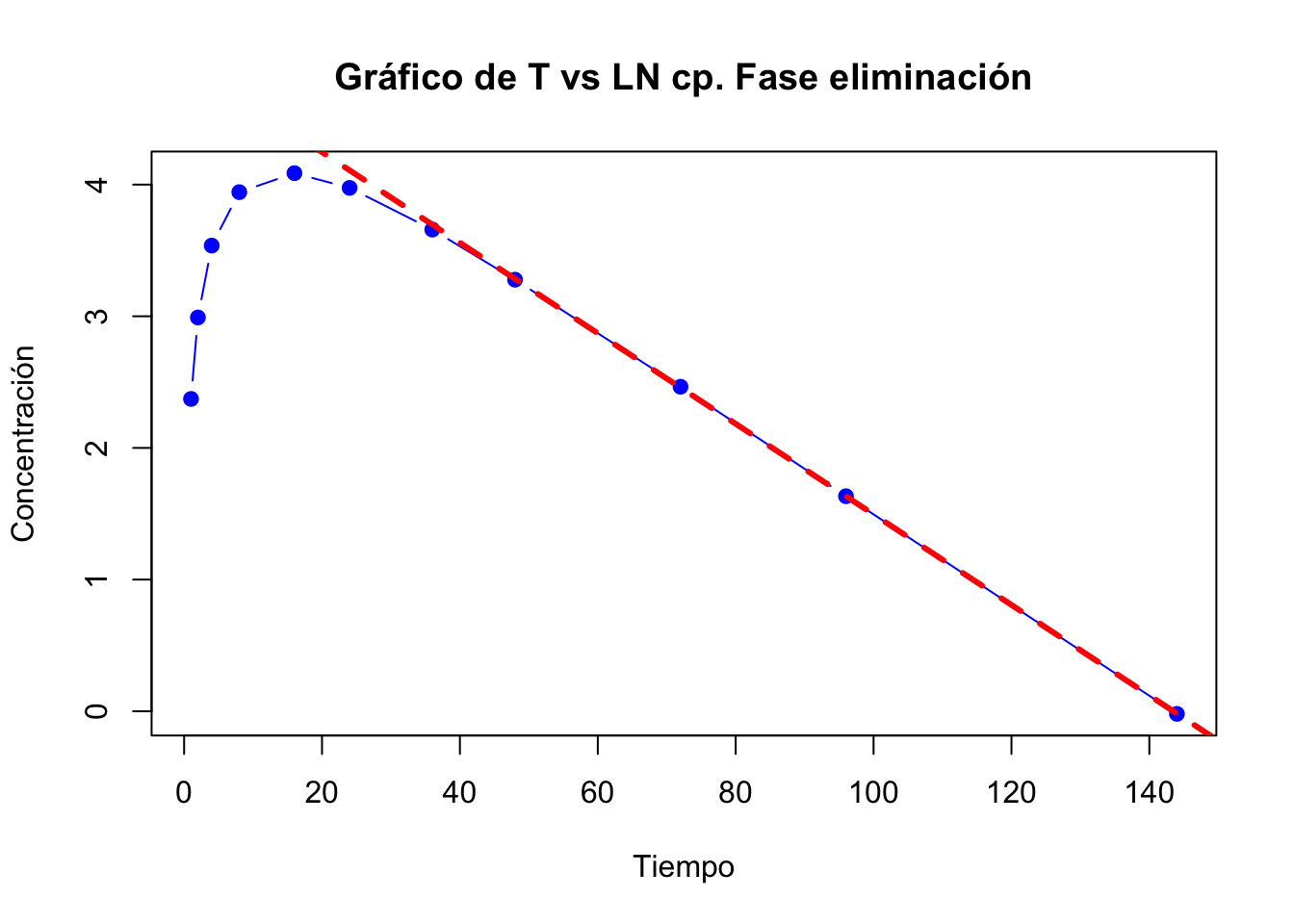
Se tomaron en cuenta los últimos 4 datos para la fase de eliminación.
Los valores extrapolados y los residuales se muestran en la siguiente tabla:
## Tiempo Conc Extrapolados Residuales
## 1 1 10.72 134.24 123.52
## 2 2 19.90 129.70 109.80
## 3 4 34.36 121.08 86.72
## 4 8 51.56 105.52 53.96
## 5 16 59.56 80.14 20.58
## 6 24 53.26 60.87 7.61
## 7 36 38.80 40.29 1.49Gráfica de absorción y fase de eliminación
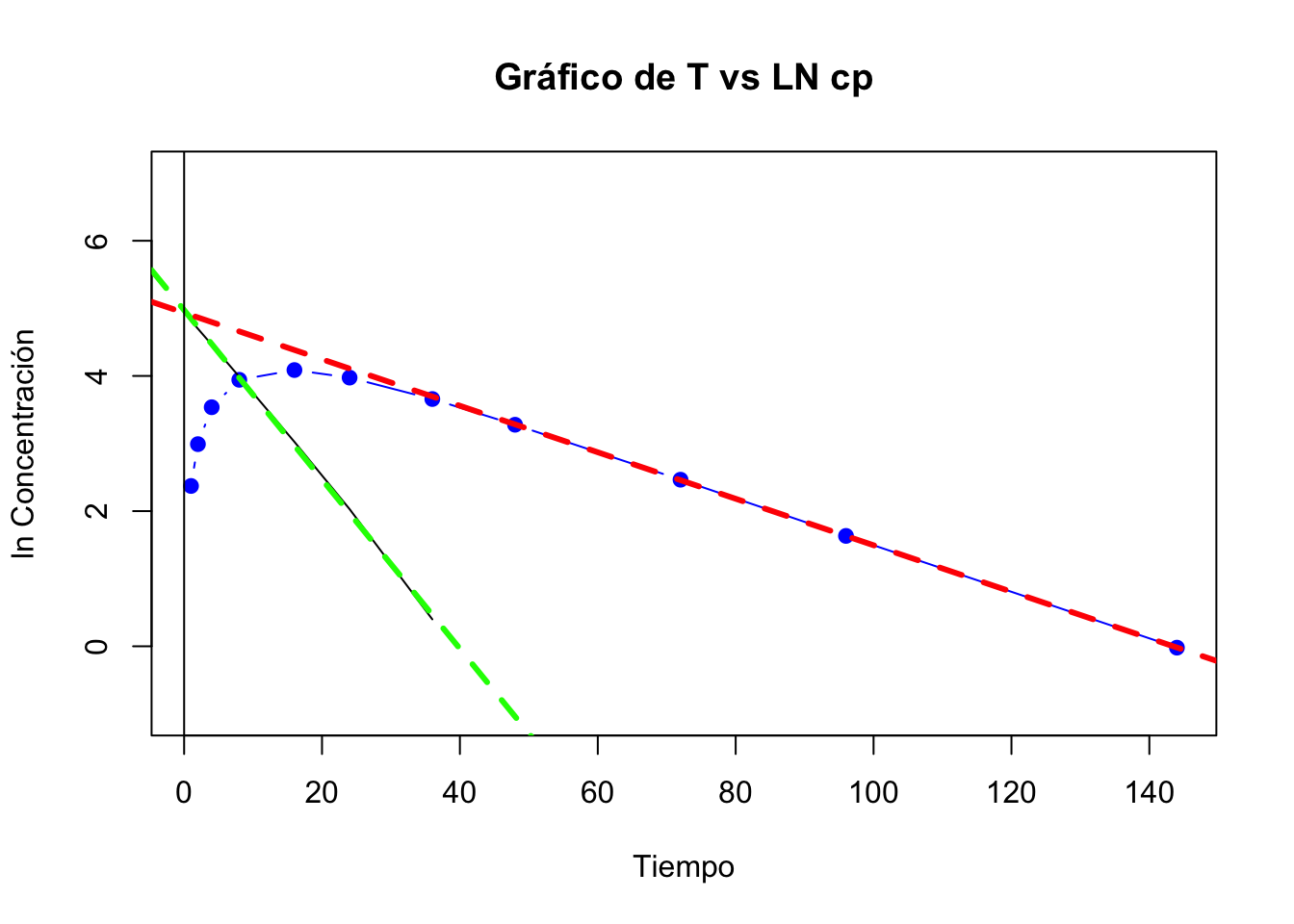
Hay tiempo de latencia, los parámetros del modelo son:
## Parámetros Resultados Unidades
## 1 C0 138.94 ug/mL
## 2 Kel 0.03 h-1
## 3 A0 144.59 ug/mL
## 4 Ka 0.13 h-1
## 5 Vd 4.96 Litros
## 6 tl 0.44 Horas
## 7 Cl 0.17 Volumen/Tiempo
## 8 tmax 14.66 Horas
## 9 Cpmax 60.87 ug/mL
## 10 Tiempo vida media 20.16 Horas
## 11 ABC cero infinito 2885.75 ug*h/mL- No es una forma de liberación prolongada, \(K_{el}\) es menor que \(K_a\)
2.4.17 Resolución ejercicio 2.18
## Parámetros Resultados Unidades
## 1 C0 57.50 ug/mL
## 2 Kel 0.31 h-1
## 3 A0 69.20 ug/mL
## 4 Ka 1.05 h-1
## 5 Vd 10.52 Litros
## 6 tl 0.25 Horas
## 7 Cl 3.28 Volumen/Tiempo
## 8 tmax 1.90 Horas
## 9 Cpmax 22.37 ug/mL
## 10 Tiempo vida media 2.22 Horas
## 11 ABC cero infinito 118.39 ug*h/mL