Capítulo 1 MUAC-IV

Última actualización: 2023-11-08

En este capítulo se recopilan ejercicios para el modelo de un compartimento para administración intravenosa en forma de bolo.

1.1 Ecuaciones del modelo

Ecuación (1.1): Ecuación integrada del modelo

\[\begin{equation} Q= Q_0 \bullet e^{-K_{el} \bullet t} \tag{1.1} \end{equation}\]

Donde:

$Q_0$: Es la cantidad de fármaco inicial
$K_{el}$: Es la constante de eliminación

Ecuación (1.2): Ecuación integrada del modelo

\[\begin{equation} Cp= Cp0 \bullet e^{-K_{el} \bullet t} \tag{1.2} \end{equation}\]

Donde: - $Cp$: Es la concentración plasmática al tiempo $t$ - $Cp_0$: Es la concentración plasmática al tiempo 0 - $K_{el}$: Es la constante de eliminación - $t$: Es el tiempo

Ecuación (1.3): Ecuación integrada del modelo con logaritmos

\[\begin{equation} In (Cp)= In (Cp0)-K{el} \bullet t \tag{1.3} \end{equation}\]

Ecuación (1.4): Ecuación integrada del modelo tomando en cuenta todos las premisas del modelo

\[\begin{equation} Cp= \frac{D}{V_d} \bullet e^{-K_{el} \bullet t} \tag{1.4} \end{equation}\]

Donde:

$Cp$: Es la concentración plasmática al tiempo $t$
$Cp_0$: Es la concentración plasmática al tiempo 0
$K_{el}$: Es la constante de eliminación
$t$: Es el tiempo
$D$: Es la dosis
$V_d$: Es el volumen de distribución

Ecuación (1.5): Volumen de distribución

\[\begin{equation} V_d= \frac{D}{C_o} \tag{1.5} \end{equation}\]

Donde:

$V_d$ es el volumen de distribución
$D$ es la dosis
$C_o$ Es la concentración inicial.

Ecuación (1.6): Tiempo de vida media

\[\begin{equation} t_{1/2}= \frac{ln2}{K_{el}} \tag{1.6} \end{equation}\]

Donde:

$t_{1/2}$ es el tiempo de vida media
$ln2$ Es el logaritmo natural de 2
$K_{el}$: Es la constante de eliminación.

Ecuación (1.7): Aclaramiento

\[\begin{equation} Cl=V_d \bullet K_{el} \tag{1.7} \end{equation}\]

Donde:

$Cl$ es el aclaramiento
$V_d$ Es el volumen de distribución
$K_{el}$: Es la constante de eliminación.

Ecuación (1.8): Área bajo la curva de tiempo 0 a $\infty$

\[\begin{equation} ABC^\infty _0= \frac{C_0}{K_{el}} \tag{1.8} \end{equation}\]

Donde:

$ABC^\infty _0$: Es el área bajo la curva del tiempo 0 a infinito
$C_0$: Es la concentración inicial
$K_{el}$: Es la constante de eliminación

Ecuación (1.9): Área bajo la curva de 0 a $\infty$ tomando en cuenta el aclaramiento

\[\begin{equation} ABC^\infty _0 \bullet Cl = D \tag{1.9} \end{equation}\]

Donde:

$ABC^\infty _0$: Es el área bajo la curva del tiempo 0 a infinito
$Cl$: Es el aclaramiento
$D$: Es la dosis

Ecuación (1.10): Área bajo la curva del tiempo $t$ a $\infty$

\[\begin{equation} ABC^\infty _t= \frac{C_t}{K_{el}} \tag{1.10} \end{equation}\]

Donde:

$C_t$ es la concentración al tiempo $t$
$K_{el}$ es la constante de eliminación

Ecuación (1.11): Área bajo la curva del tiempo 0 al tiempo $t$

\[\begin{equation} ABC^t _0= \frac{Cp_0}{K_{el}}\bullet (1-e^{-K_{el}} \bullet t) \tag{1.11} \end{equation}\]

Donde:

$ABC^t _0=$: Es área bajo la curva de tiempo 0 a tiempo $t$
$Cp_0$ es la concentración al tiempo 0
$K_{el}$ es la constante de eliminación

1.2 Problemas

Ejercicio 1.1 En grupo de voluntarios se administró un fármaco por vía intravenosa en forma de bolo a una dosis de 150 mg. Después de 4 y 6 horas los promedios de las concentraciones plasmáticas fueron: 0.96 mg/L y 0.48 mg/L respectivamente. Además, se sabe que el aclaramiento renal en este grupo de sujetos es de 0.17 L cada minuto. Asumiendo un modelo monocompartimental y una cinética de primer orden. Calcule:

tiempo de vida media
Área bajo la curva de cero a infinito
Volumen de distribución
Concentración inicial
Constante de eliminación
Concentración plasmática a la 8 h

Ejercicio 1.2 Para un fármaco que presenta una $t_{1/2}$ de 4 h y un $V_d$ de 25 L (en un individuo de 70 Kg), calcular la dosis requerida para que al ser administrado un bolo por vía intravenosa se alcance una concentración de 2.4 mg/L a las 6 h después de su administración

Ejercicio tomado de: https://www.u-cursos.cl/faciqyf/2010/2/FBQI4201/2/material_docente/bajar?id_material=566335

Ejercicio 1.3 La siguiente tabla contiene los datos de un grupo de pacientes a los que les fue administrado 75 mg de un fármaco experimental en forma de bolo

Tiempo (h)	Conc. (mg/mL)
1.2	3.15
3	1.8
6	0.87
7.5	0.48
10.5	0.195
15	0.0615

Determine:

$t_{1/2}$
$K_{el}$
$V_d$
$ABC^\infty _0$
Se sabe que el fármaco deja de tener efecto cuando la concentración baja un 85% de la concentración incial. ¿A que tiempo se presentará la perdida de efecto?
Si se administra el doble de la dosis ¿Qué es loq ue ocurre con los parámetros del modelo?

Ejercicio 1.4 Después de la administración de 250 mg de un fármaco, este presenta la siguiente ecuación para sus niveles plasmáticos en función del tiempo:

\[ Cp=15.0 \cdot e^{-0.250 \cdot t} \]

Donde las concentraciones están expresadas en $\mu g/L$

Graficar en papel e identificar $Cp0$, determinar pendiente forma gráfica
Obtener $V_d$, $Cl$ y tiempo de vida media
Calcular la cantidad de fármaco que queda después de 5 horas
Calcular el % de fármaco que se eliminó después de 5 h
Si se administra una dosis de 1000mg que pasaría con el aclaramiento, , volumen de distribución, semivida y ABC. Asuma un comportamiento lineal del modelo

Para la determinación de la pendiente de forma gráfica utilice:

\[ Pendiente = \frac{y2-y1}{x2-x1} \]

Ejercicio 1.5

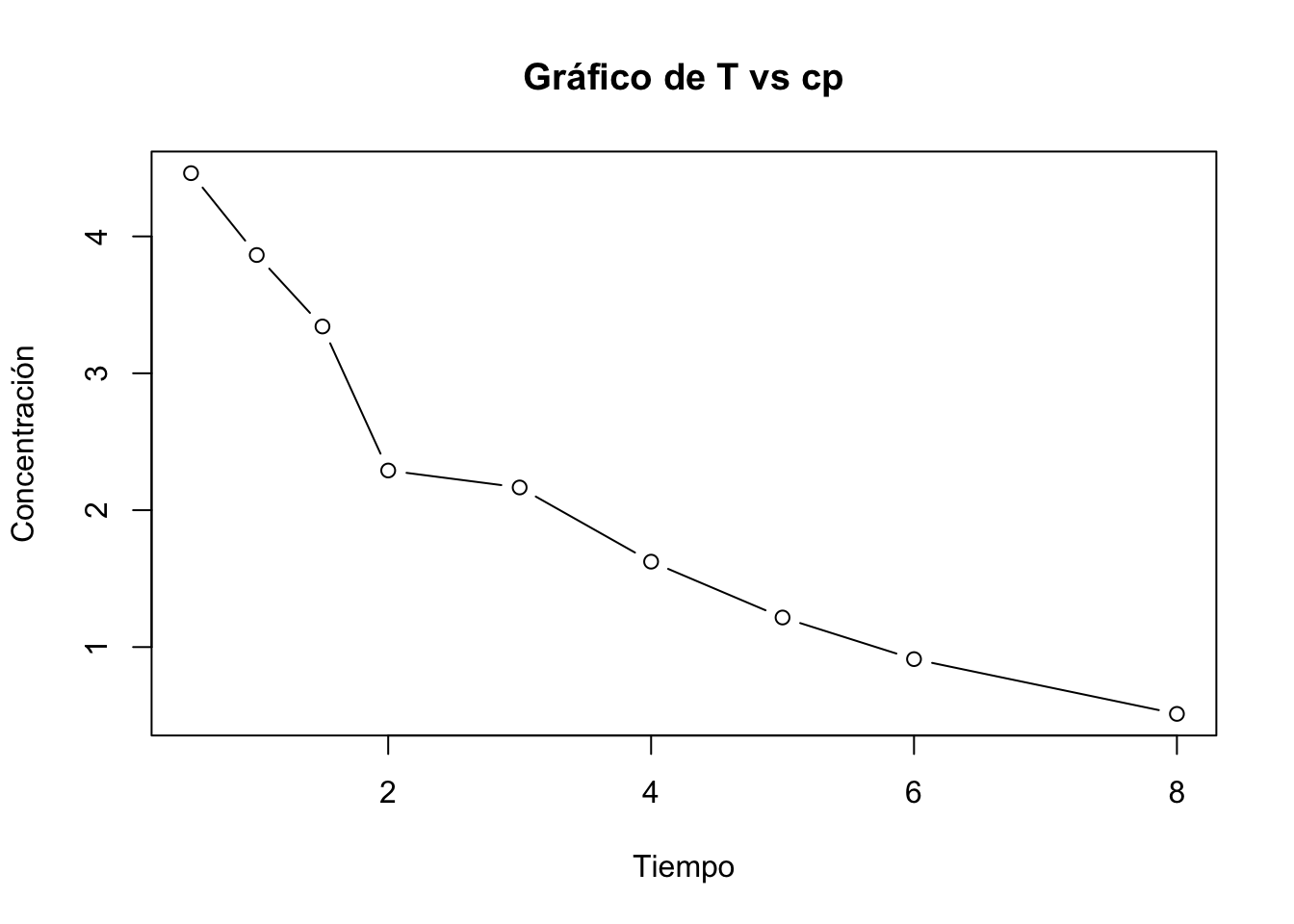
A un grupo de individuos sanos se les administra una dosis intravenosa de 500 mg de ceftriaxona, obteniéndose los siguientes niveles plasmáticos:

Tiempo (h)	Conc. ($mu g/mL$)
0.5	4.462
1	3.864
1.5	3.342
2	2.29
3	2.166
4	1.624
5	1.216
6	0.912
8	0.512

la constante de velocidad de eliminación
la vida media de eliminación,
el volumen aparente de distribución,
la depuración total (aclaramiento)
Área bajo la curva desde cero hasta tiempo infinito,
ABC desde la 4h hasta infinito.
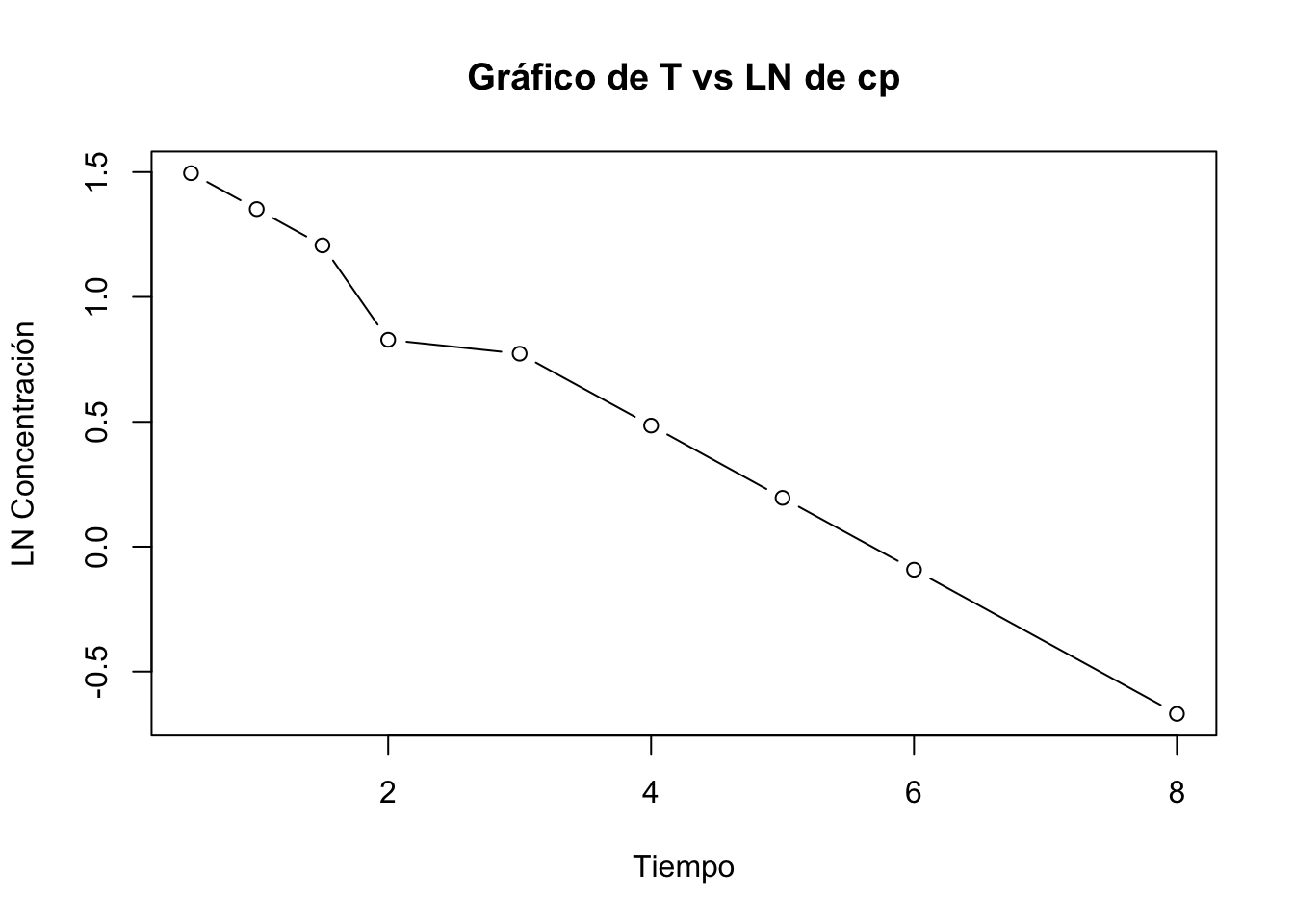
Grafique en papel semi-logarítmico e identifique visualmente la Cp0 y kel.
¿A que tiempo se habrá consumido el 90% del fármaco?

Ejercicio 1.6 Se inyecta por vía intravenosa 500 mg de un fármaco cuya vida media biológica es de 7 horas y cuyo comportamiento farmacocinético puede describirse de acuerdo con un modelo monocompartimental. a. Calcular la cantidad de fármaco presente en el organismo 18 horas después de la inyección.

Ejercicio tomado de: https://www.u-cursos.cl/faciqyf/2010/2/FBQI4201/2/material_docente/bajar?id_material=566335

Ejercicio 1.7 A un voluntario de 70 kg de peso se le administro un antibiótico en forma de bolo. Después de 5 horas la concentración plasmática fue de 0.3 µg/mL y las 2 horas la concentración fue de 1.2 µg/mL. Asumiendo una cinética de primer orden. Determine el tiempo de vida media

Ejercicio 1.8

La aminofilina presenta una variabilidad interindividual alta, de forma tal que la t1/2 que aparece en la literatura sólo puede servir como referencia. A un paciente se le inyecta por vía i.v. rápida una dosis de aminofilina que genera inmediatamente después de la dosis una Cp de teofilina de 20 ug/mL. Al cabo de 6 horas la Cp es de 5 ug/mL. Calcule la vida media de teofilina en este paciente.

Ejercicio tomado de: https://www.u-cursos.cl/faciqyf/2010/2/FBQI4201/2/material_docente/bajar?id_material=566335

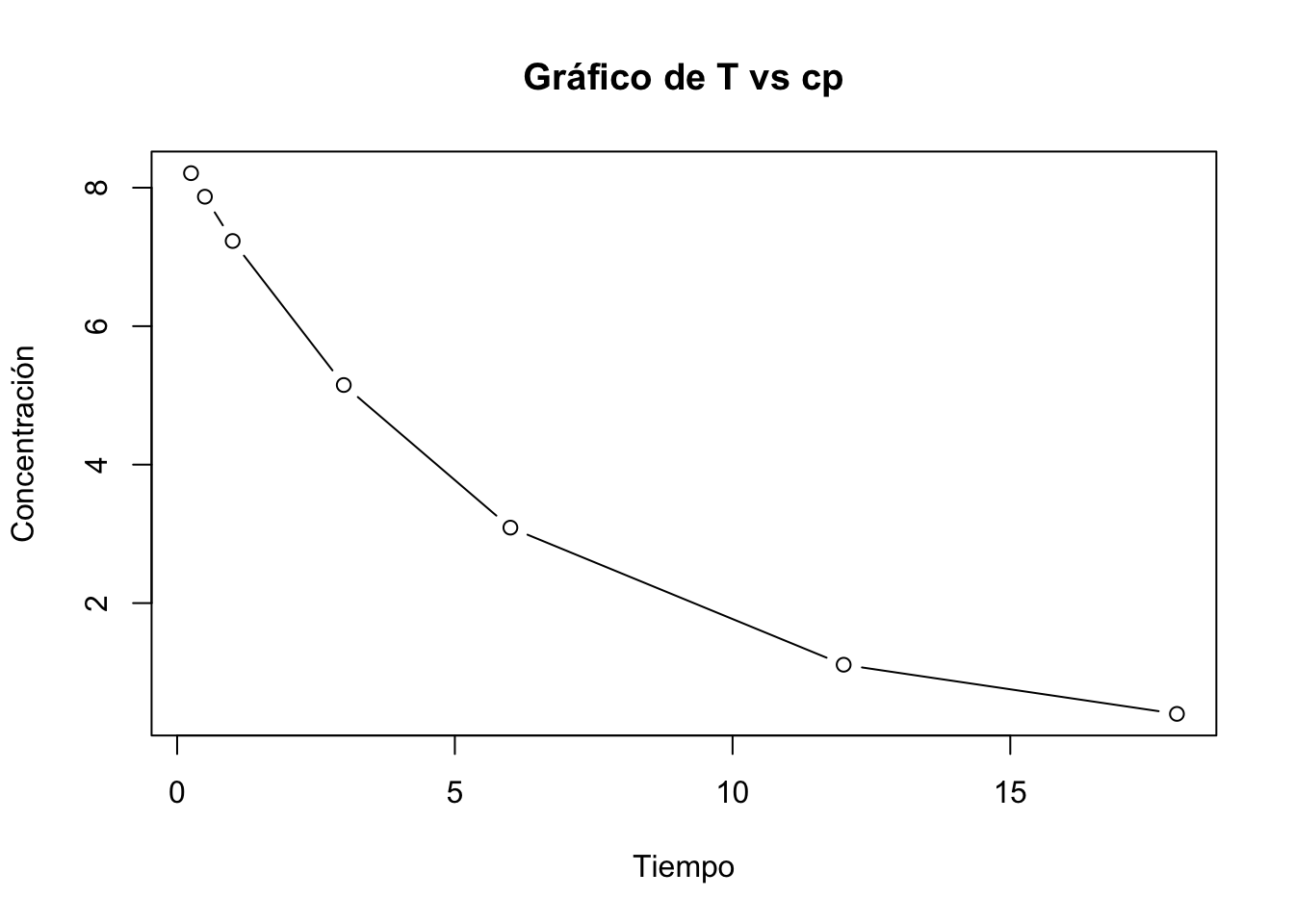
Ejercicio 1.9 A una mujer de 50 kg se le administró una sola dosis de 6mg/kg de un antimicrobiano. Se realizaron tomas sanguíneas a diferentes tiempos. Obteniendo los siguientes resultados:

h	µg/mL
0.25	8.21
0.5	7.87
1	7.23
3	5.15
6	3.09
12	1.11
18	0.4

Determine el Volumen de distribución, la constante de eliminación, el tiempo de vida media
Se sabe que el fármaco pierde su efectividad cuando las concentraciones plasmáticas disminuyen a menos de 2 µg/mL. ¿Cuál es la duración del efecto del fármaco?
¿Cuánto tiempo tiene que pasar para poder eliminar el 99.9% del fármaco?
Si se duplica la dosis describa que pasaría con la duración del efecto

Ejercicio 1.10 Un nuevo fármaco fue administrado en una sola dosis de 4 mg/kg a 5 adultos con edades de 23 a 38 años con un promedio de peso de 75kg. La farmacocinética del fármaco se ajusta a un modelo lineal de un compartimento. La ecuación del modelo es la siguiente:

\[ Cp= 78 \cdot e^{-0.46 \cdot t} \]

Asumiendo que las unidades de Cp son µg/mL y la variable dependiente en h. Calcule lo siguiente:

Tiempo de vida media
Volumen de distribución
Cp a las 4 h
Predecir qué sitios podría ocupar este medicamento y explicar por qué hizo esta predicción
Si la ventana terapéutica se pierde a concentraciones menores de 2 µg/mL ¿A qué tiempo es necesario administrar la siguiente dosis de fármaco?

1.3 Resolución de problemas

1.3.1 Resolución del problema 1.1

Del problema podemos obtener:

$Cl=0.17 \ L$
$C_{4h}=0.96$
$C_{6h}=0.43$

Como la concentración media de la segunda muestra es exactamente la mitad que en la primera extracción, podemos considerar que la $t_{1/2}$ es de 2 h.

Para hacer más fácil su manipulación, podemos cambiar las unidades del $Cl$ a $L/h$

\[ Cl= \frac{270 \ mL}{min} \cdot \frac{60 \ min}{1 \ h} \cdot \frac{1 \ L }{1000 \ mL}=16.2 \ L/h \]

Para estimar el $ABC^\infty _0$ y dado que conocemos la dosis y el aclaramiento podemos emplear la siguiente formula y despejar para obtener el $ABC^\infty _0$

\[ ABC^\infty _0 \cdot Cl= D \longrightarrow ABC^\infty _0 = \frac{D}{Cl}= \frac{105 \ mg}{10.2 \ L/h}= 14.71 \frac {mg \cdot h}{L} \]

Por lo tanto, conociendo los datos de $t_{1/2}$ podemos estimar la $K_{el}$:

\[ t_{1/2}=\frac{ln2}{K_{el}} \longrightarrow \ K_{el}= \frac{ln2}{t_{1/2}}= \frac{0.693}{2\ h}=0.347 \ h^{-1} \]

Conociendo los valores de $K_{el}$: y de $Cl$ podemos estimar el $V_d$ con la siguiente formula

\[ Cl= V_d \cdot K_{el} \longrightarrow V_d= \frac{Cl}{K_{el}}= \frac{0.17 \ L/min}{0.35 \ h ^{-1}}= \frac{10.2 \ L/h}{0.35 \ ^{h-1}}=29.14 \ L \]

Para estimar la concentración plasmática inicial podemos emplear y despejar la siguiente formula:

\[ V_d= \frac{D}{Cp0} \longrightarrow Cp0=\frac{D}{V_d}=\frac{150 \ mg }{29.14 \ L}=5.14 \ mg/L \]

Para estimar la concentración plásmatica a las 8 h podemos utilizar la ecuación del modelo y despejar para un $t$ de 8 h

\[ Cp8h=Cp0 \cdot e^{-k_{el} \cdot 8 \ h} = 5.14 \ mg/L \cdot e ^{-0.35 \ h ^{-1} \cdot 8 \ h} = 0.31 \ mg/L \]

1.3.2 Resolución del problema 1.2

Del problema podemos obtener:

$t_{1/2}= 4 \ h$
$V_d=25 \ L$
$Cp \ 6h = 2.4 \ mg/L$

Podemos estimar el $K_{el}$ mediante:

\[ K_{el}=\frac{0.693}{4 \ h} = 0.17 \ h ^{-1} \] Ahora podemos estimar $Cp0$ con la ecuación del modelo

\[2.4 \ mg/L = Cp0 \cdot e^{-0.17 \ h ^{-1} \cdot 6 \ h }\] Despejando $Cp$:

\[ Cp0= \frac{2.4 \ mg/L}{e^{-0.17 \ h ^{-1} \cdot 6 \ h}}= 6.65 \ mg/L \]

Ahora ya podemos obtener la dosis mediante:

\[ V_d= \frac{D}{Cp0} \longrightarrow D= V_d \cdot Cp0= 169.70 \ mg \]

1.3.3 Resolución del problema 1.3

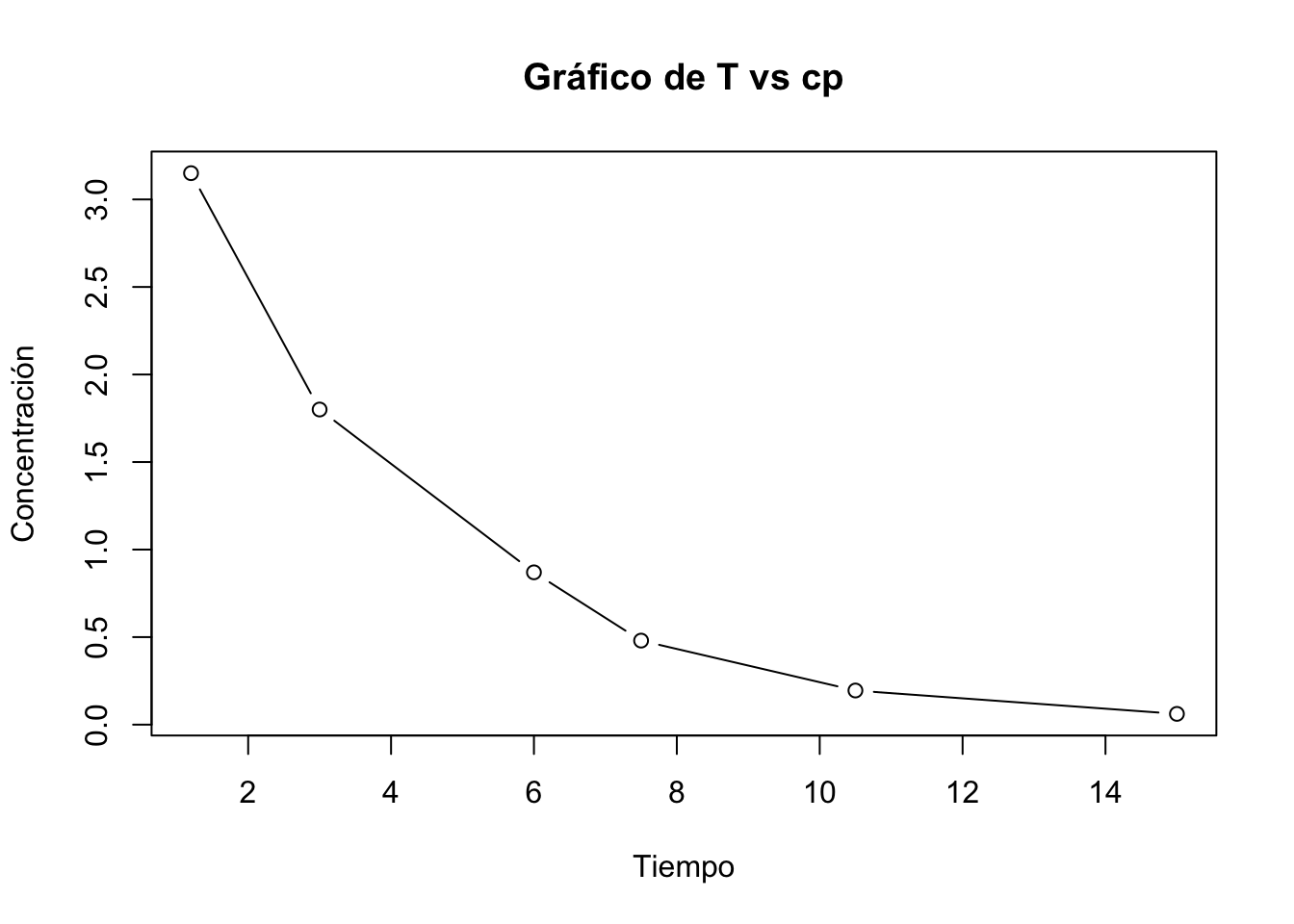
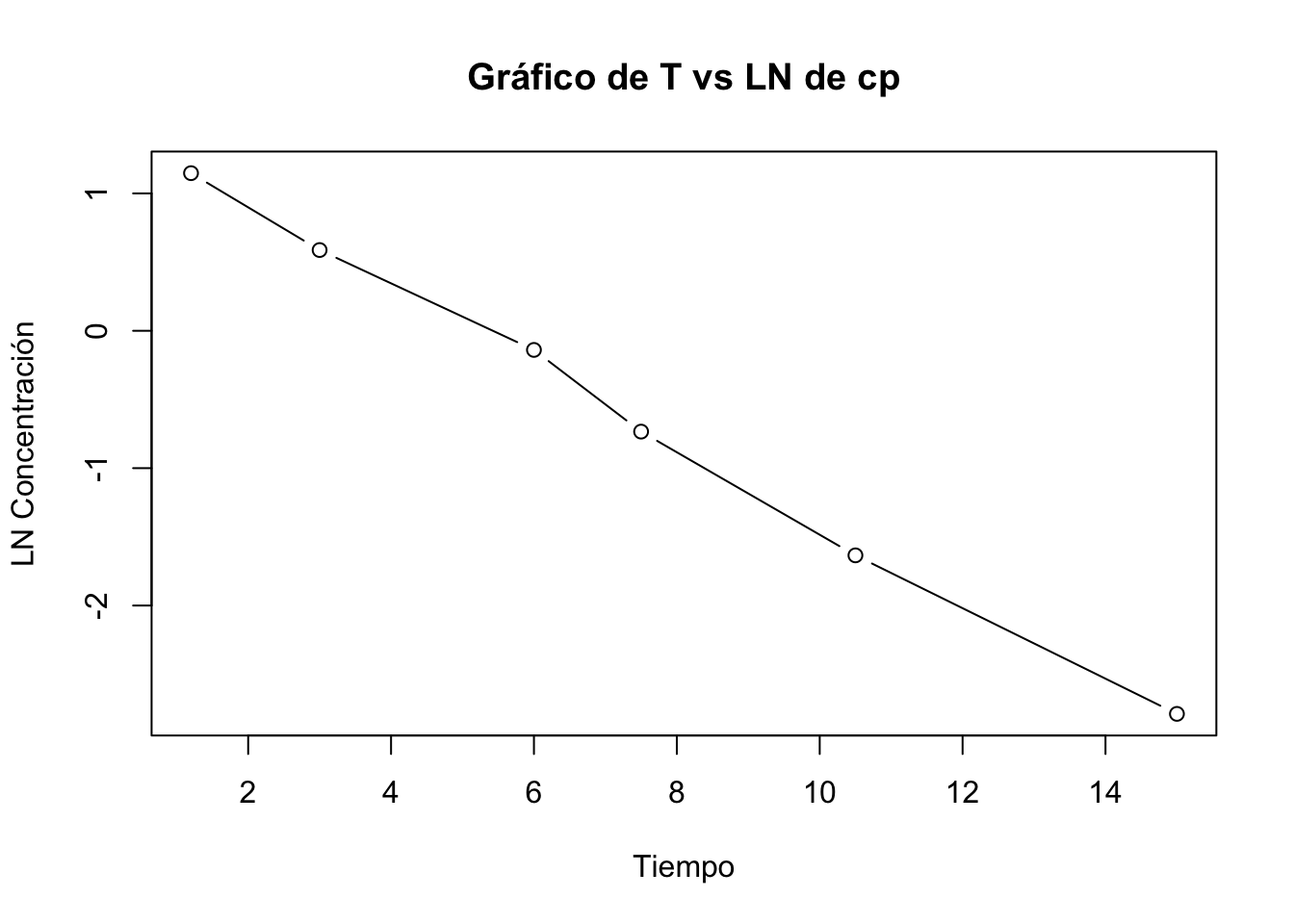
[1] "Regresión"

Call:
lm(formula = log(Conc) ~ Tiempo)

Residuals:
       1        2        3        4        5        6 
 0.01272 -0.02842  0.10867 -0.05397 -0.09062  0.05162 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.480337   0.061809   23.95 1.80e-05 ***
Tiempo      -0.288045   0.007235  -39.81 2.38e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.0815 on 4 degrees of freedom
Multiple R-squared:  0.9975,    Adjusted R-squared:  0.9969 
F-statistic:  1585 on 1 and 4 DF,  p-value: 2.378e-06

[1] "Kel (h^-1)"
[1] 0.288
[1] "Cp0 (mismas unidades concentración)"
[1] 4.39
[1] "Tiempo de vida media (h)"
[1] 2.41
[1] "Volumen de distribución (L)"
[1] 17.08
[1] "Aclaramiento (L/h)"
[1] 4.92
[1] "Area bajo la curva de 0 a infinito"
[1] 15.24

El 15% de la concentración a tiempo 0.6585

La ecuación del modelo podemos despejar para obtener el $t$

\[ Cp=Cp0 \cdot e^{-K_{el} \cdot t} \] Aplicando logaritmos

\[ lnCp=lnCp0-K_{el} \cdot t \] La ecuación anterior también puede ser interpretada como:

\[ lnCp=-K_{el} \cdot t + lnCp0 \]

Despejando con respecto a $t$

\[ t= \frac{ln\frac{Cp}{Cp0}}{-K_{el}} \] Sustituyendo:

\[ t= \frac{ln\frac{0.65 \ mg/L}{4.39 \ mg/L}}{-0.28 h^{-1}}= 6.8 \ h \]

El resultado anterior también puede ser obtenido por interpolación gráfica o de la regresión.

Si se aumenta el doble de la dosis, el modelo se modifca:

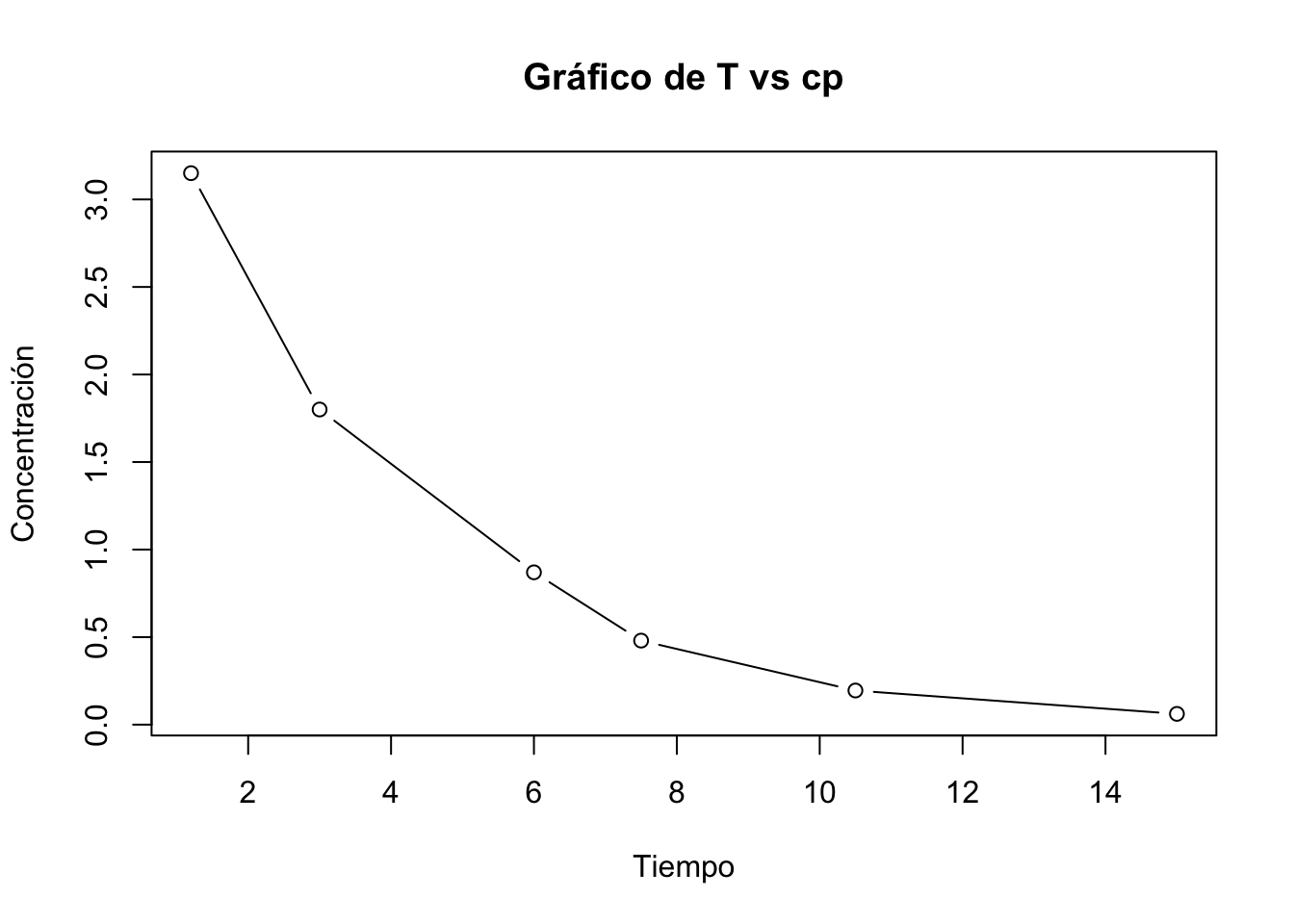
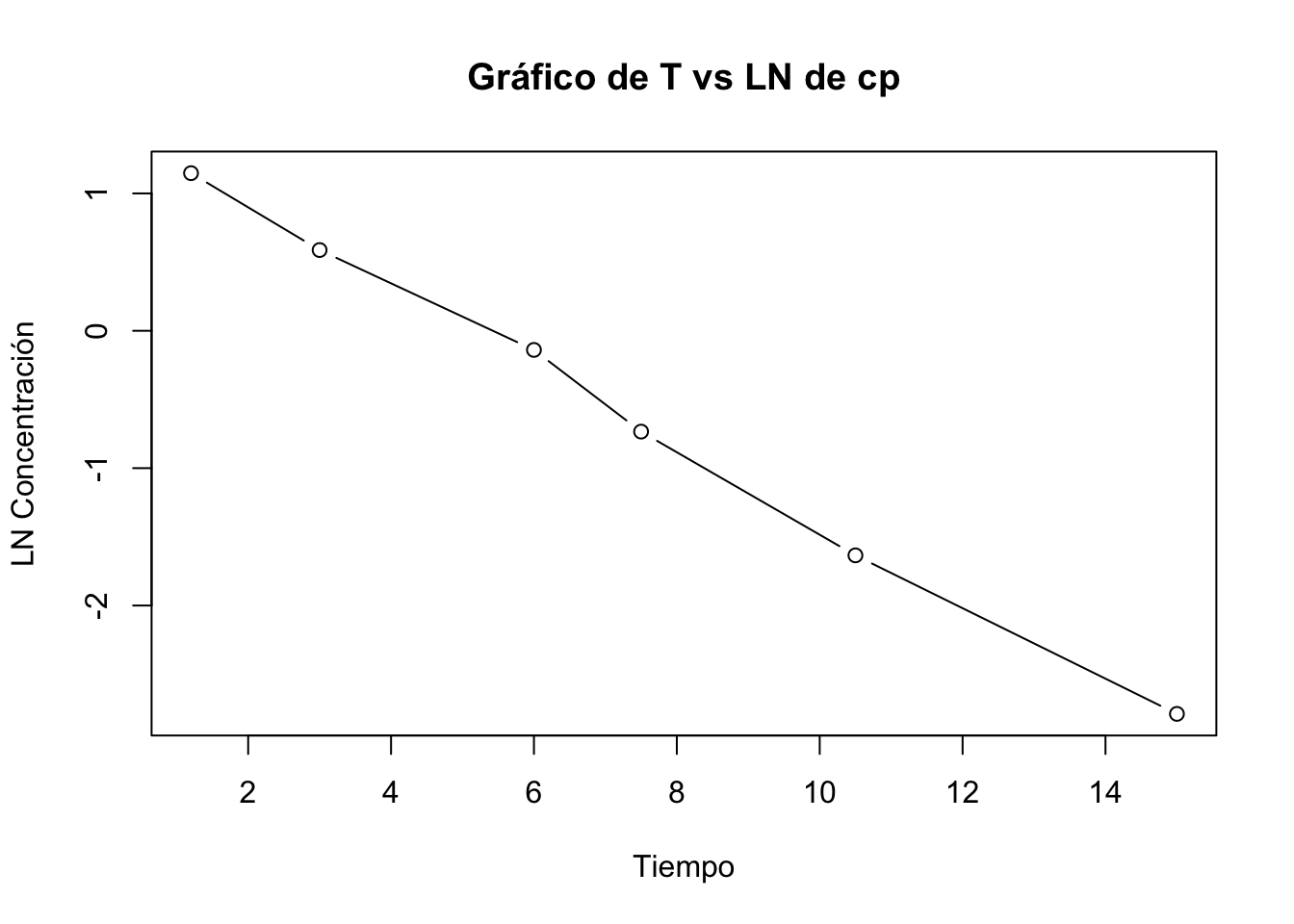
[1] "Regresión"

Call:
lm(formula = log(Conc) ~ Tiempo)

Residuals:
       1        2        3        4        5        6 
 0.01272 -0.02842  0.10867 -0.05397 -0.09062  0.05162 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.480337   0.061809   23.95 1.80e-05 ***
Tiempo      -0.288045   0.007235  -39.81 2.38e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.0815 on 4 degrees of freedom
Multiple R-squared:  0.9975,    Adjusted R-squared:  0.9969 
F-statistic:  1585 on 1 and 4 DF,  p-value: 2.378e-06

[1] "Kel (h^-1)"
[1] 0.288
[1] "Cp0 (mismas unidades concentración)"
[1] 4.39
[1] "Tiempo de vida media (h)"
[1] 2.41
[1] "Volumen de distribución (L)"
[1] 34.17
[1] "Aclaramiento (L/h)"
[1] 9.84
[1] "Area bajo la curva de 0 a infinito"
[1] 15.24

1.3.4 Resolución del problema 1.4

Dado que no se especifican las unidades de $Cp$ asumiremos que son $\mu g/ L$ Del problema podemos obtener: - $Cp0=15 \ \mu g /L$ - $K_{el}= 0.250 \ h ^{-1}$

Sustituyendo las ecuaciones obtenemos:

[1] "Kel (h^-1)"
[1] 0.25
[1] "Cp0 mismas unidades que la conentración"
[1] 15
[1] "Tiempo de vida media (h)"
[1] 2.77
[1] "Volumen de distribución (L)"
[1] 16.67
[1] "Aclaramiento (L/h)"
[1] 4.17
[1] "Area bajo la curva de 0 a infinito"
[1] 60

Para calcular la concentración a la 5 h simplemente sustituimos en la ecuación del modelo:

\[ Cp5h= 15.0 \mu g/L \cdot e ^{-0.250 h ^{-1} \cdot 6 h}= 3.35 \mu g/L \] Por lo tanto la cantidad de fármaco que se eliminó hasta las 5h es:

\[ 15-3.35=11.65 \mu g/L \] Por lo que el porcentaje es:

\[ \frac{11.65 \mu g/L}{15.0 \mu g /L}\cdot100=77.67 \% \] Si se aumenta la dosis a 1000 mg los parametros del modelo cambian:

[1] "Kel (h^-1)"
[1] 0.25
[1] "Cp0 mismas unidades que la conentración"
[1] 15
[1] "Tiempo de vida media (h)"
[1] 2.77
[1] "Volumen de distribución (L)"
[1] 66.67
[1] "Aclaramiento (L/h)"
[1] 16.67
[1] "Area bajo la curva de 0 a infinito"
[1] 60

1.3.5 Resolución del problema 1.5

[1] "Regresión"

Call:
lm(formula = log(Conc) ~ Tiempo)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.198197  0.009297  0.022224  0.038800  0.045788 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.59083    0.04779   33.29 5.72e-09 ***
Tiempo      -0.28204    0.01142  -24.69 4.56e-08 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.08136 on 7 degrees of freedom
Multiple R-squared:  0.9886,    Adjusted R-squared:  0.987 
F-statistic: 609.5 on 1 and 7 DF,  p-value: 4.56e-08

[1] "Kel (h^-1)"
[1] 0.282
[1] "Cp0 (mismas unidades concentración)"
[1] 4.91
[1] "Tiempo de vida media (h)"
[1] 2.46
[1] "Volumen de distribución (L)"
[1] 101.83
[1] "Aclaramiento (L/h)"
[1] 28.72
[1] "Area bajo la curva de 0 a infinito"
[1] 17.41

El $ABC^\infty_4$ se obtiene con la formula:

\[ ABC^\infty _t= \frac{Cp_t}{K_{el}} \]

Por lo que primero, necesitamos estimar la $Cp$ a las 4 h:

\[ Cp4h= 4.91 \mu g/mL \cdot e^{-0.282 h ^{-1} \cdot 4 h}= 1.59 \mu g/mL \]

Sustituyendo:

\[ ABC^\infty _t= \frac{1.59 \mu g/mL}{0.282 h^{-1}}= 5.64 \mu g \cdot h/mL \]

Para el 90% de la dosis:

El 10% de la concentración a tiempo 0.491

La ecuación del modelo podemos despejar para obtener el $t$

\[ Cp=Cp0 \cdot e^{-K_{el} \cdot t} \] Aplicando logaritmos

\[ lnCp=lnCp0-K_{el} \cdot t \] La ecuación anterior también puede ser interpretada como:

\[ lnCp=-K_{el} \cdot t + lnCp0 \]

Despejando con respecto a $t$

\[ t= \frac{ln\frac{Cp}{Cp0}}{-K_{el}} \] Sustituyendo:

\[ t= \frac{ln\frac{0.49 \ mg/L}{4.91 \ mg/L}}{-0.282 h^{-1}}= 8.17 \ h \]

1.3.6 Resolución del problema 1.6

Del problema podemos obtener:

$D= 500 \ mg$
$t_{1/2}= 7 \ h$ Para conocer la $Cp \ 18 \ h$ es necesario conocer antes la $K_{el}$

\[ t_{1/2}=\frac{ln2}{K_{el}} \longrightarrow K_{el}= \frac{0.693 \ h ^{-1}}{7 \ h}=0.10 \ h \] La ecuación del modelo se puede expresar como

\[ Q= Q_0 \cdot e ^{- 0.10 \ h ^{-1} \cdot t} \] Donde:

$Q$ es la cantidad de fármaco en el organismo al tiempo $t$
$Q_0$ es la cantidad de fármaco en el organismo inicial

Por lo tanto la cantidad de fármaco a las 18 h

\[ Q= 500 \ mg \cdot e ^{- 0.10 \ h ^{-1} \cdot 18 \ h}= 84.11 \ mg \]

1.3.7 Resolución del problema 1.7

Del problema obtenemos:

$Cp \ 2h= 1.2 \ \mu g/mL$
$Cp \ 5h= 0.3 \ \mu g/mL$

En 3 h la concentración disminuyó hasta un 1/4 de por lo tanto el $t_{1/2}$ es de 1.5 h

1.3.8 Resolución del problema 1.8

Del problema obtenemos:

$Cp0= 20 \ \mu g/mL$
$Cp \ 6h= 5 \ \mu g/mL$

En 6 h la concentración disminuyó hasta un 1/4 de por lo tanto el $t_{1/2}$ es de 3 h

1.3.9 Resolución del problema 1.9

Se calcula la dosis:

\[ D= \frac{6 \ mg}{kg}\cdot 50 \ kg= 300 \ mg \]

Los parámetros del modelo son:

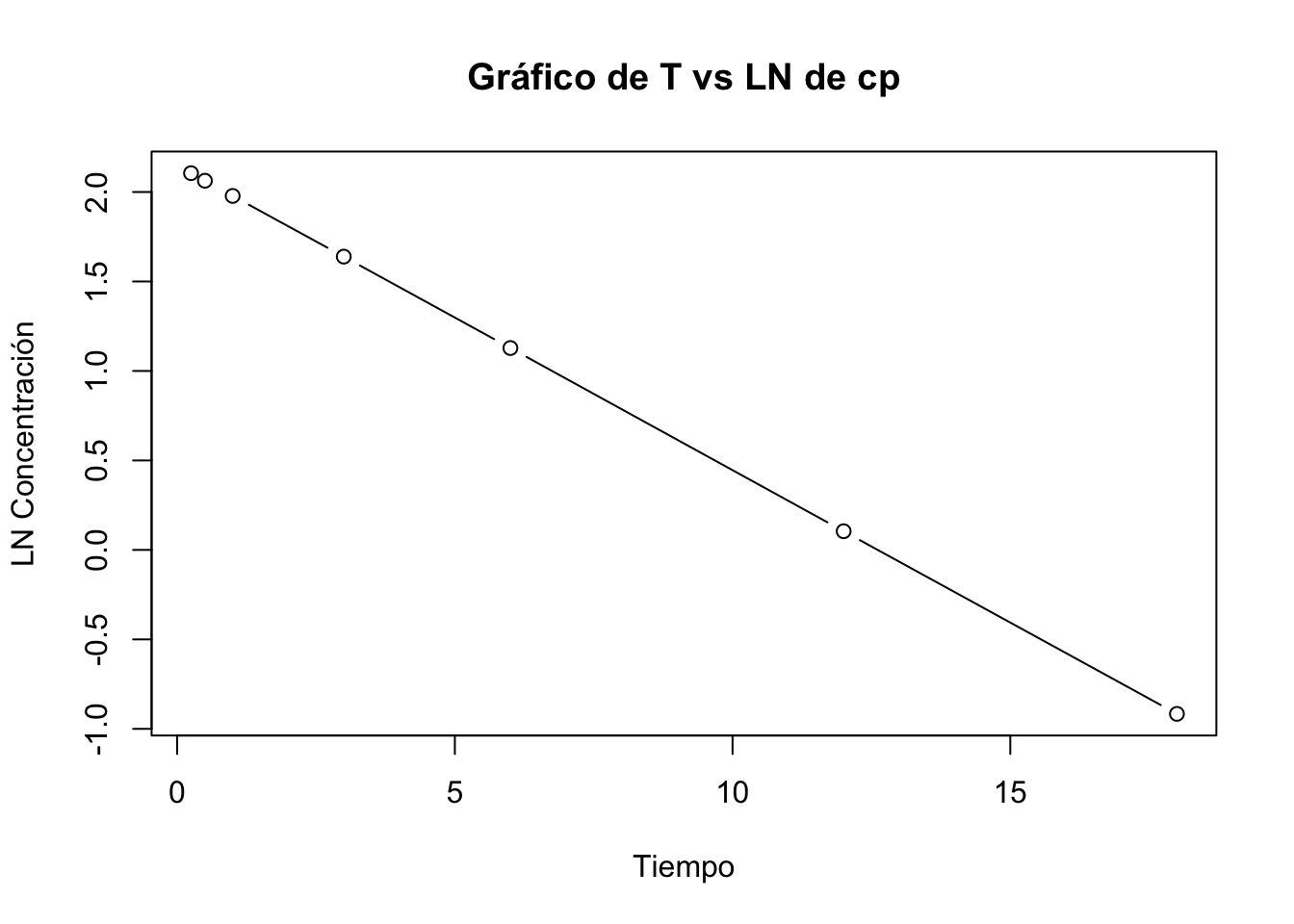
[1] "Regresión"

Call:
lm(formula = log(Conc) ~ Tiempo)

Residuals:
         1          2          3          4          5          6          7 
-7.741e-04 -4.984e-04 -1.764e-04  1.145e-03  1.166e-03 -9.523e-04  8.961e-05 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.149e+00  4.866e-04    4415   <2e-16 ***
Tiempo      -1.703e-01  5.677e-05   -2999   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.0009451 on 5 degrees of freedom
Multiple R-squared:      1, Adjusted R-squared:      1 
F-statistic: 8.996e+06 on 1 and 5 DF,  p-value: < 2.2e-16

[1] "Kel"
[1] 0.17
[1] "Cp0"
[1] 8.57
[1] "Tiempo de vida media"
[1] 4.08
[1] "Volumen de distribución"
[1] 35.01
[1] "Aclaramiento"
[1] 5.95
[1] "Area bajo la curva de 0 a infinito"
[1] 50.41

Para obtener el tiempo al cual se tiene una concentración de $2 \ \mu g/L$ se utiliza la siguiente ecuación:

\[ t= \frac{ln\frac{Cp}{Cp0}}{-K_{el}} \] Sustituyendo:

\[ t= \frac{ln\frac{2 \ \mu g/L}{8.57 \ \mu g/L}}{-0.17 \ h^{-1}}= 8.56 \ h \]

Para que se elimine el 99.9% del fármaco deben de pasar 10 $t_{1/2}$ por lo tanto deben de pasar 40.8 h.

1.3.10 Resolución del problema 1.10

Se estima la dosis:

\[ D= \frac{4 \ mg}{kg}\cdot75 \ kg= 300 \ mg \] Se estiman los parámetroos

\[ t_{1/2}= \frac{0.693}{0.46 \ h^{-1}}= 1.5 \ h \]

\[ V_d= \frac{300 \ mg}{78 \ mg/L}=3.84 \ L \] Según el volumen de distribución el fármaco se mantendría principalmente en circulación

Para el tiempo de la siguiente dosis:

\[ t= \frac{ln\frac{2 \ \mu g/L}{78 \ \mu g/L}}{-0.46 \ h^{-1}}= 7.96 \ h \]

1.3.11 Ejmplo 1.3. Resolución

Dado que se trata de la administración IV se puede suponer una biosdisponibilidad ($F$) de 1. Por lo tanto podemos utilizar la ecuación:

\[ ABC^\infty _0 \bullet Cl= D; \ ABC^\infty _0= \frac{D}{Cl}= \frac{300 \ mg}{16.2 \ L/h}= 18.52 \ mg \cdot h/L = 18.52 \ \mu g \cdot h/mL \]

1.3.12 Ejmplo 1.3. Resolución

Para estimar la $Cp0$ podemos utilizar:

\[ ABC^\infty _0= \frac{Cp0}{K_{el}}; \ Cp0= ABC^\infty _0 \bullet K_{el}= (18.52 \ \mu g \cdot h/mL) \cdot (0.347 \ h^{-1} )= 8.85 \mu g /mL \]