24 时间序列分析
部分笔记摘录自Datacamp,仅供学习交流。
24.1 时间序列的创建
24.1.1 原始数据
这里使用的数据是尼罗河年流量(Nile),使用它需要调用datasets包. >Measurements of the annual flow of the river Nile at Aswan (formerly Assuan), 1871–1970, in 10^8 m^3, “with apparent changepoint near 1898” (Cobb(1978), Table 1, p.249).
str(Nile)
## Time-Series [1:100] from 1871 to 1970: 1120 1160 963 1210 1160 1160 813 1230 1370 1140 ...
print(Nile)
## Time Series:
## Start = 1871
## End = 1970
## Frequency = 1
## [1] 1120 1160 963 1210 1160 1160 813 1230 1370 1140 995 935 1110 994 1020
## [16] 960 1180 799 958 1140 1100 1210 1150 1250 1260 1220 1030 1100 774 840
## [31] 874 694 940 833 701 916 692 1020 1050 969 831 726 456 824 702
## [46] 1120 1100 832 764 821 768 845 864 862 698 845 744 796 1040 759
## [61] 781 865 845 944 984 897 822 1010 771 676 649 846 812 742 801
## [76] 1040 860 874 848 890 744 749 838 1050 918 986 797 923 975 815
## [91] 1020 906 901 1170 912 746 919 718 714 740
length(Nile)
## [1] 100
head(Nile, 10)
## [1] 1120 1160 963 1210 1160 1160 813 1230 1370 1140
tail(Nile, 12)
## [1] 975 815 1020 906 901 1170 912 746 919 718 714 740利用函数将图像画出来.
plot(Nile, xlab = "Year", ylab = "River Volume (1e9 m^{3})",
main = "Annual River Nile Volume at Aswan, 1871-1970",
type ="b")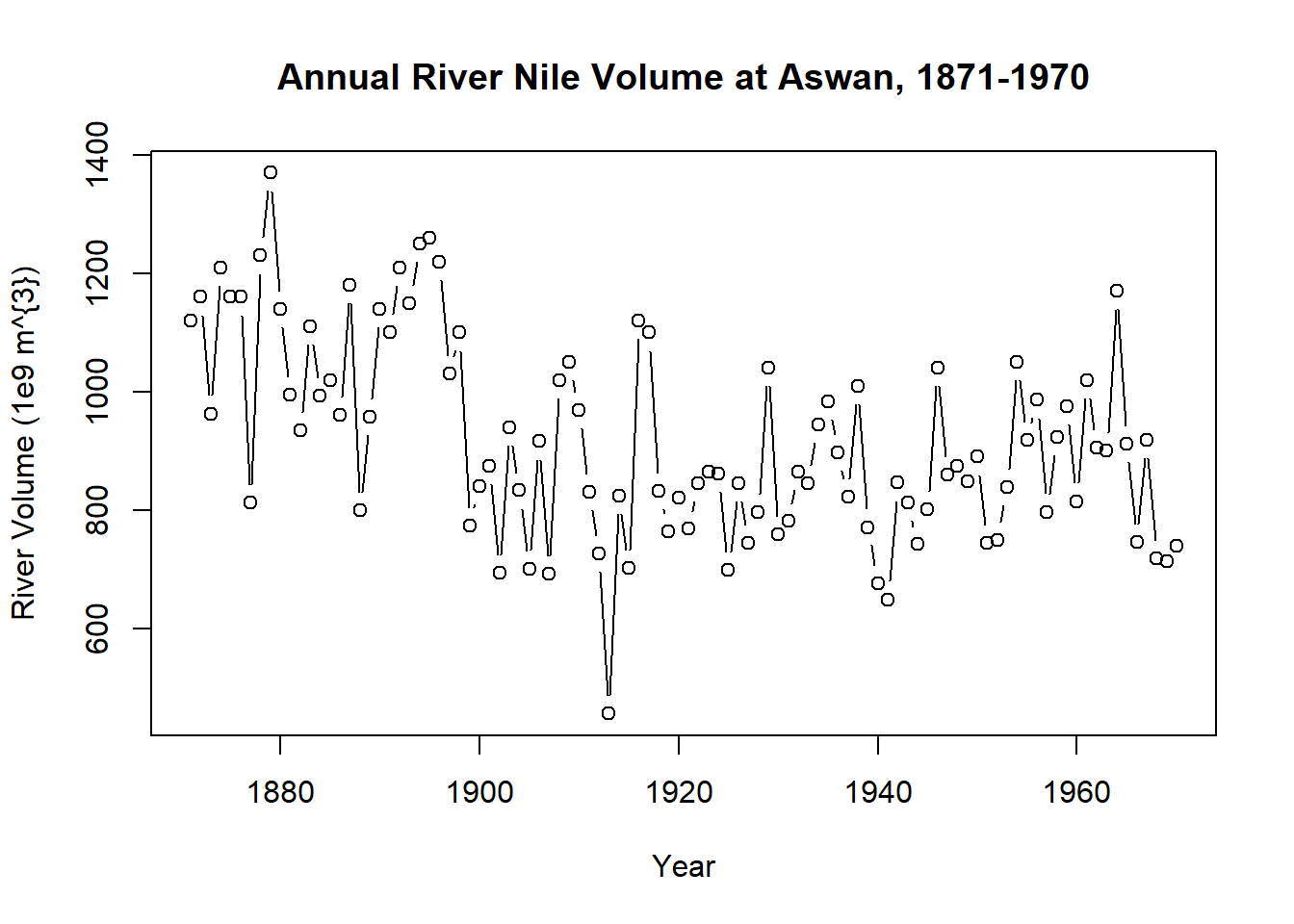
24.1.2 创建时间序列
可以是上一章的xts包创建,或者是自带的函数ts()来创建,我们创建一个白噪声的时间序列.
data <- rnorm(50)
time_series <- ts(data, start = 1990, frequency = 2)
is.ts(time_series)
## [1] TRUE
head(time_series)
## [1] -0.3655271 -1.6449620 0.3807332 -0.9165058 -2.2086408 0.4001792
plot(time_series)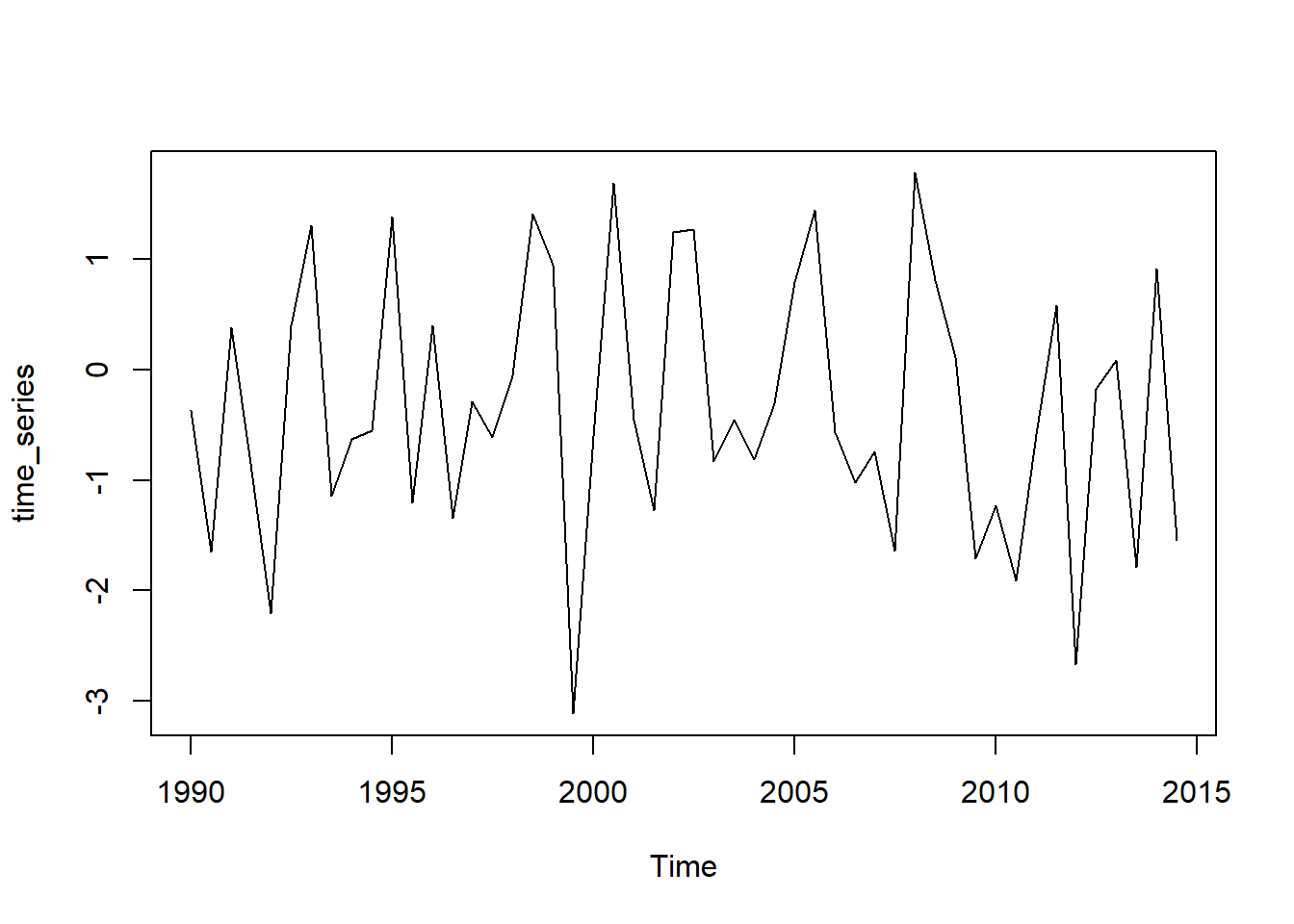
参数
frequency表示时间序列的采样频率,默认值1表示每个单位时间间隔内有一个样本。例如,当数据每天采样,自然时间段为一周时,可以使用7的频率值;当数据每月采样,自然时间段为一年时,可以使用12。4和12的值在(例如)打印方法中被假定为分别意味着季度和月度系列。
start(time_series)
## [1] 1990 1
end(time_series)
## [1] 2014 2
frequency(time_series)
## [1] 224.1.3 多个时间序列
如果遇到一个时间点记录两个或多个时间数据的,即它的形式是矩阵的,如果要画图可以这样,本次创建的时间序列对象是利用xts包.
# 创建数据, 50 * 2的矩阵
x <- matrix(rnorm(100), ncol = 2, nrow = 50)
idx <- as.Date("2023-03-01")+0:49
# 加上列名
colnames(x) <- c("A1", "A2")
# 创建时间序列
obj_xts <- xts(x, order.by = idx)
# 画图
ts.plot(obj_xts, col = 1:2)
# 加标签
legend("topleft", colnames(obj_xts), lty = 1, col = 1:2, bty = "n")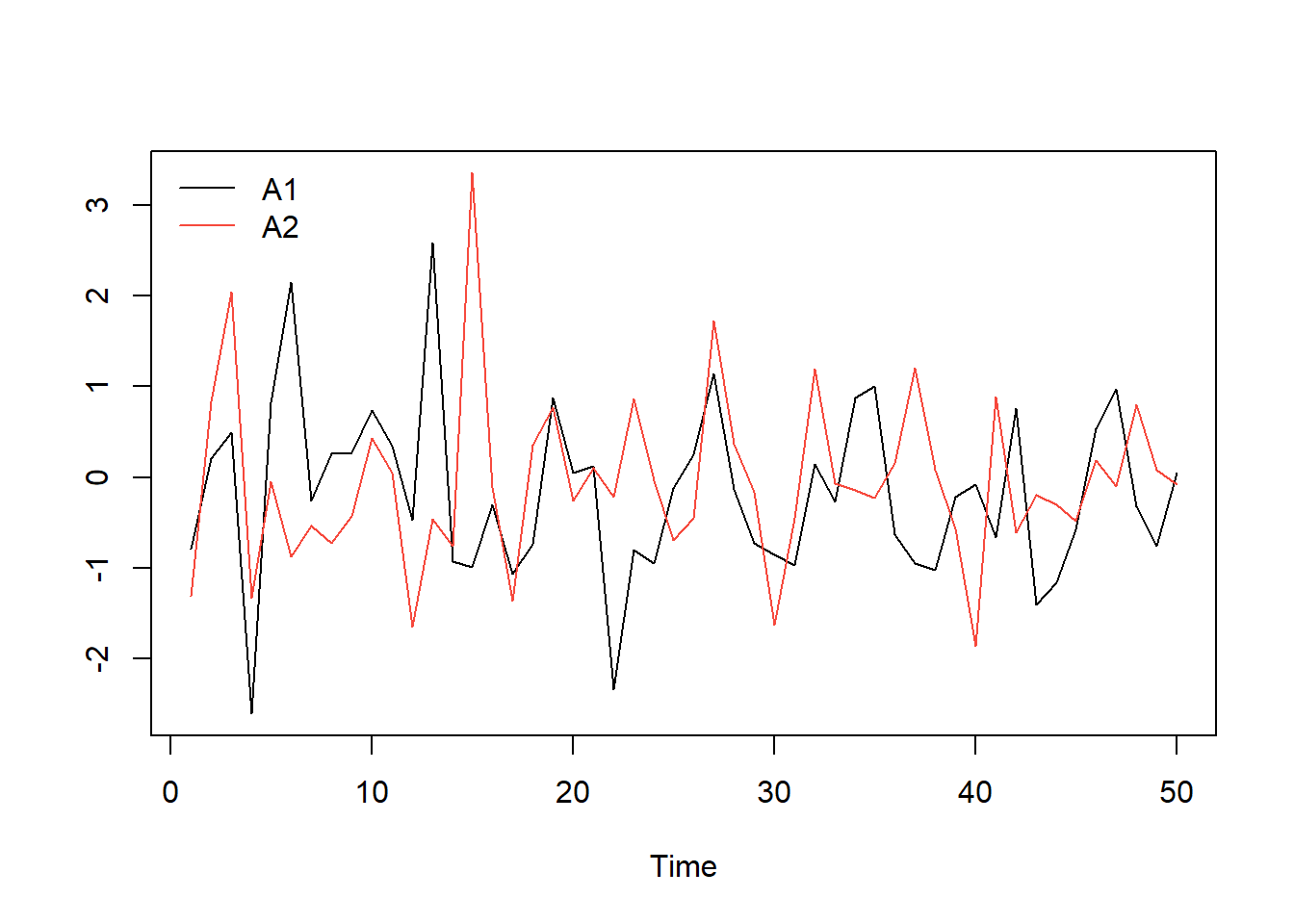
24.1.4 回归率
通常情况下,时间序列的生成方式是: \[ X_{t} = (1+p_{t})X_{t-1} \] 通常情况下,\(p_{t}\)被称为时间序列的回报率或增长率,这个过程往往是稳定的。
For reasons that are outside the scope of this course, it can be shown that the growth rate \(p_{t}\) can be approximated by
\[ Y_{t} = \log{X_{t}} -\log{X_{t-1}} \approx p_{t} \]
我们创建一个新的时间序列(AirPassengers)
par(mfrow = c(2, 1))
plot(AirPassengers)
plot(diff(log(AirPassengers)))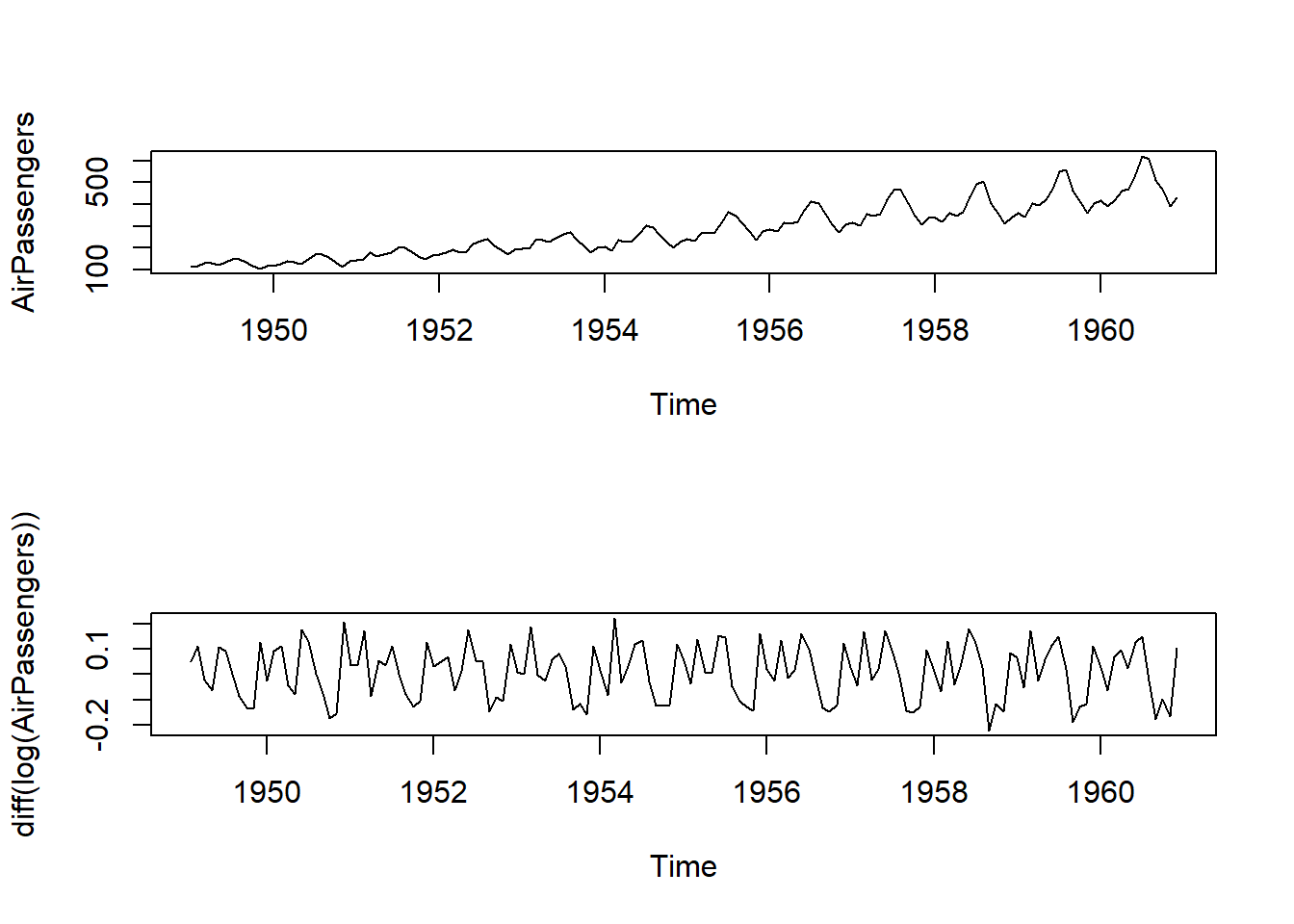
24.2 时间序列预处理
24.2.1 平稳性定义
为什么要研究时间序列的平稳性?
平稳性有两种定义:严平稳和宽平稳.
严平稳(Strictly Stationary)是一种条件比较苛刻的定义,它认为只有序列当所有的统计性质都不会随着时间的推移而发生变化时,该序列才能被认为平稳,其定义如下.
设 \(\left \{ Y_{t} \right \}\)为一时间序列,对任意正整数\(m\),任取 \(t_{1},t_{2},\cdots ,t_{m}\in T\), 对任意整数 \(\tau\),有 \[ F_{t_{1}, t_{2}, \cdots, t_{m}}\left(x_{1}, x_{2}, \cdots, x_{m}\right)=F_{t_{1}+\tau, t_{2}+\tau, \cdots, t_{m}+\tau}\left(x_{1}, x_{2}, \cdots, x_{m}\right) \] 则称时间序列\(\left \{ Y_{t} \right \}\)为 严平稳时间序列
严平稳定义有一定的局限性,它条件太强了:
- 实践中获取随机序列的联合分布非常困难;
- 即使知道随机序列的联合分布,计算和应用也非常不方便.
宽平稳(Weak Stationary)使用随机序列的特征统计量来定义,它认为随机序列的统计性质主要由低阶矩决定,因此又被称为二阶平稳,其定义如下.
如果\(\left \{ Y_{t} \right \}\)满足如下三个条件:
- 任取\(t\in T\), 有 \(EY^{2}_{t}<\infty\) (方差存在)
- 任取\(t\in T\), 有 \(EY_{t}=\mu\), (\(\mu\)为常数)
- 任取\(t, s, k \in T\),且 \(k+s-t \in T\), 有 \(\gamma(t, s)=\gamma(k, k+s-t)\) (时间差相同的自协方差相等)
则称\(\left \{ Y_{t} \right \}\)为宽平稳时间序列.宽平稳也称为弱平稳或二阶平稳.
\[ \text{严平稳} \nLeftrightarrow \text{宽平稳} \]
- 严平稳 \(\nRightarrow\)宽平稳,部分分布函数不存在一,二阶矩, 无法验证二阶平稳,比如柯西分布.
- 宽平稳 \(\nRightarrow\)严平稳,分布函数可能随时间变化, 对应一二阶矩相同分布函数可能不同.
- 只有当随机序列服从多元正态分布时,严平稳和宽平稳可以互推.
24.2.2 白噪声(WN)
白噪声也就是纯随机序列,它的定义如下. 如果\(\left \{ Y_{t} \right \}\)满足如下两条性质:
- 任取 \(t\in T\),有 \(EY_{t}=\mu\);
- 任取\(t, s\in T\),有
\[ \gamma(t, s)=\left\{\begin{array}{ll} \sigma^{2}, & t=s \\ 0, & t \neq s \end{array}\right. \] 称该序列为纯随机序列,也称为白噪声(WhiteNoise)序列,简记为\(Y_{t}\sim WN(\mu, \sigma ^{2})\).
arima.sim()函数可以用来模拟各种时间序列模型的数据。文档
white_noise <- arima.sim(model = list(order = c(0, 0, 0)), n = 100, mean = 100, sd = 10)
ts.plot(white_noise)
ARIMA(p, d, q)模型有三个部分,p是自回归阶数(AR),d是积分(或差分)阶数,q是移动平均阶数(MA)。ARIMA(0, 0, 0)模型,即所有这些部分都是零,只是WN模型。
对于一个给定的时间序列y,我们可以使用arima(..., order = c(0, 0, 0))函数来拟合白噪声(WN)模型。回顾一下,WN模型是一个ARIMA(0,0,0)模型。文档
arima(white_noise, order = c(0, 0, 0))
##
## Call:
## arima(x = white_noise, order = c(0, 0, 0))
##
## Coefficients:
## intercept
## 99.1472
## s.e. 1.0411
##
## sigma^2 estimated as 108.4: log likelihood = -376.18, aic = 756.36
mean(white_noise)
## [1] 99.14725
var(white_noise)
## [1] 109.488624.2.3 随机游走(RW)
对于 \(\left \{ Y_{t} \right \}\), 如果.
\[ Y_{t}=Y_{t-1} +\epsilon_{t} \] 其中 \(\epsilon_{t}\)是白噪声.则称\(\left \{ Y_{t} \right \}\)是随机游走.
随机游走的一阶差分就是白噪声,一般均值为0,所以我们只需要知道方差即可.
# 同行画两张图
layout(matrix(c(1, 2), ncol = 2))
# ‘sd=’可指定差分后白噪声的标准差,默认为1,
# mean即为差分后白噪声的均值(即漂移项)默认为0
random_walk <- arima.sim(model = list(order = c(0, 1, 0)), n = 100)
# random_walk <- cumsum(white_noise) 也可以生成随机游走
ts.plot(random_walk)
# 计算一阶差分
random_walk_diff <- diff(random_walk)
ts.plot(random_walk_diff)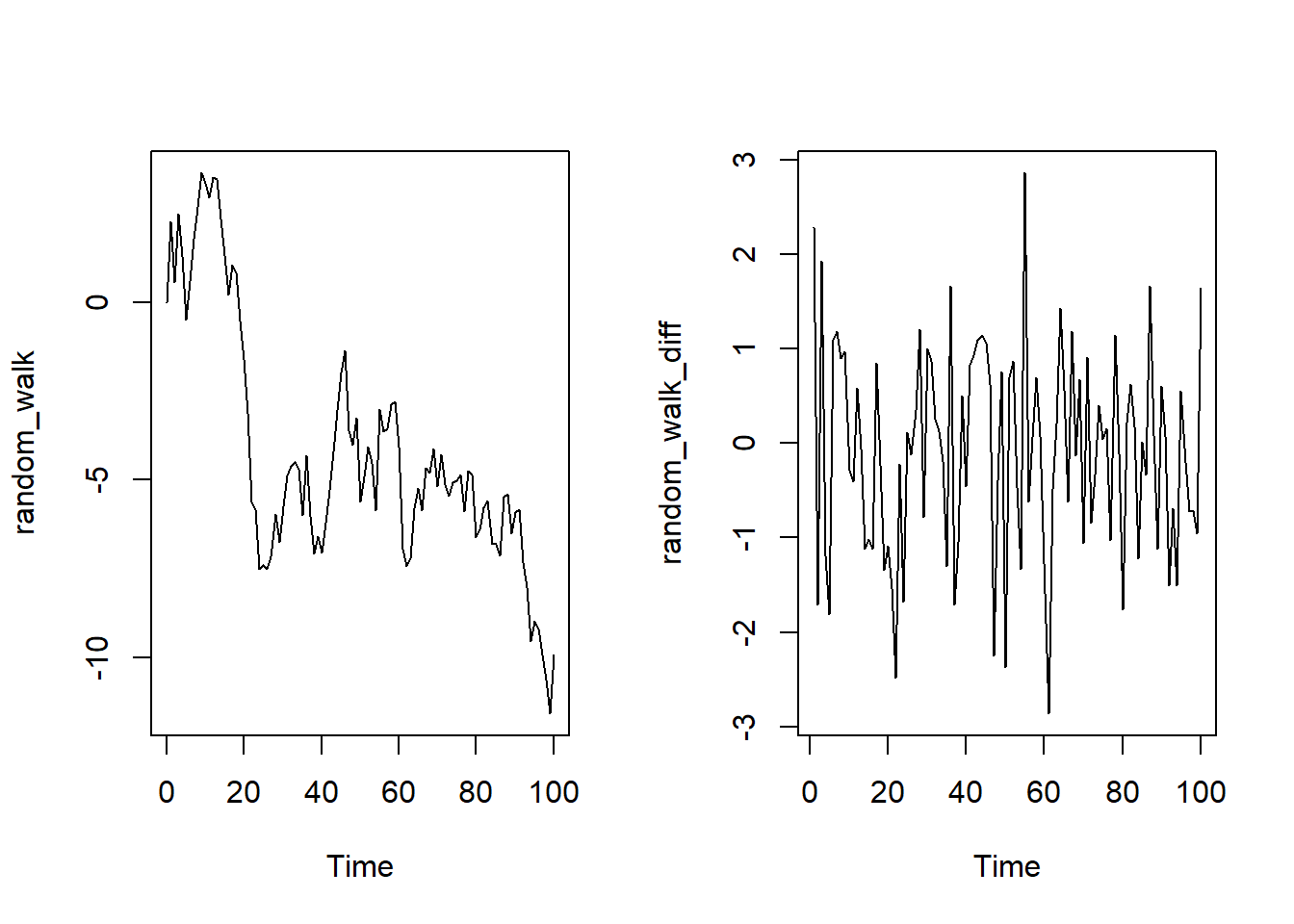
如果带常数,那么称为带漂移的(drift)随机游走,即
\[ Y_{t}=c+Y_{t-1} +\epsilon_{t} \]
- 两个参数:常数 \(c\), 白噪声方差\(\sigma_{\epsilon}^{2}\)
- 差分为: \[ diff(Y) = Y_{t}-Y_{t-1} = c+\epsilon_{t} \]
# 同行画两张图
layout(matrix(c(1, 2), ncol = 2))
# 漂移常数设为1
rw_drift <- arima.sim(model = list(order = c(0, 1, 0)), n = 100, mean = 1)
ts.plot(rw_drift)
# 计算一阶差分
rw_drift_diff <- diff(rw_drift)
ts.plot(rw_drift_diff)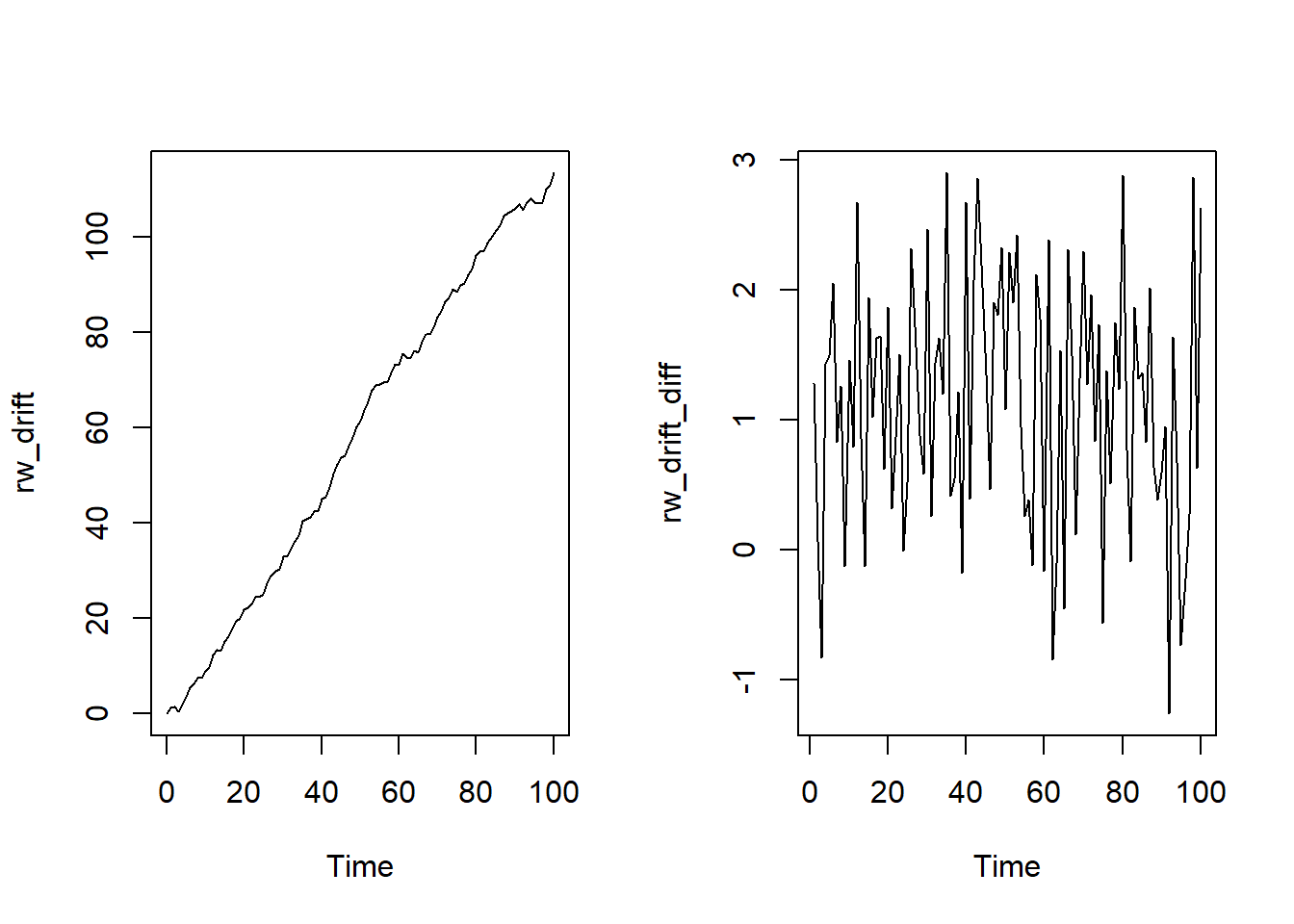
由于有漂移项,差分后的图像在1附近摆动.
估计随机游走模型,我们还是使用arima()函数,对于一个给定的时间序列y,我们可以先对数据进行差分,然后用arima()对差分后的数据进行白噪声(WN)模型的拟合.
# 同行画两张图
layout(matrix(c(1, 2), ncol = 2))
# 计算随机游走(不带漂移)的一阶差分
rw_diff <- diff(random_walk)
ts.plot(rw_diff, main = "一阶差分")
# 将WN模型拟合到差分数据上。
model_wn <-arima(x = rw_diff, order = c(0, 0, 0))
# 估计的时间趋势(截距)的值
int_wn <- model_wn$coef
ts.plot(random_walk, main = "随机游走")
abline(0, int_wn, col = "blue")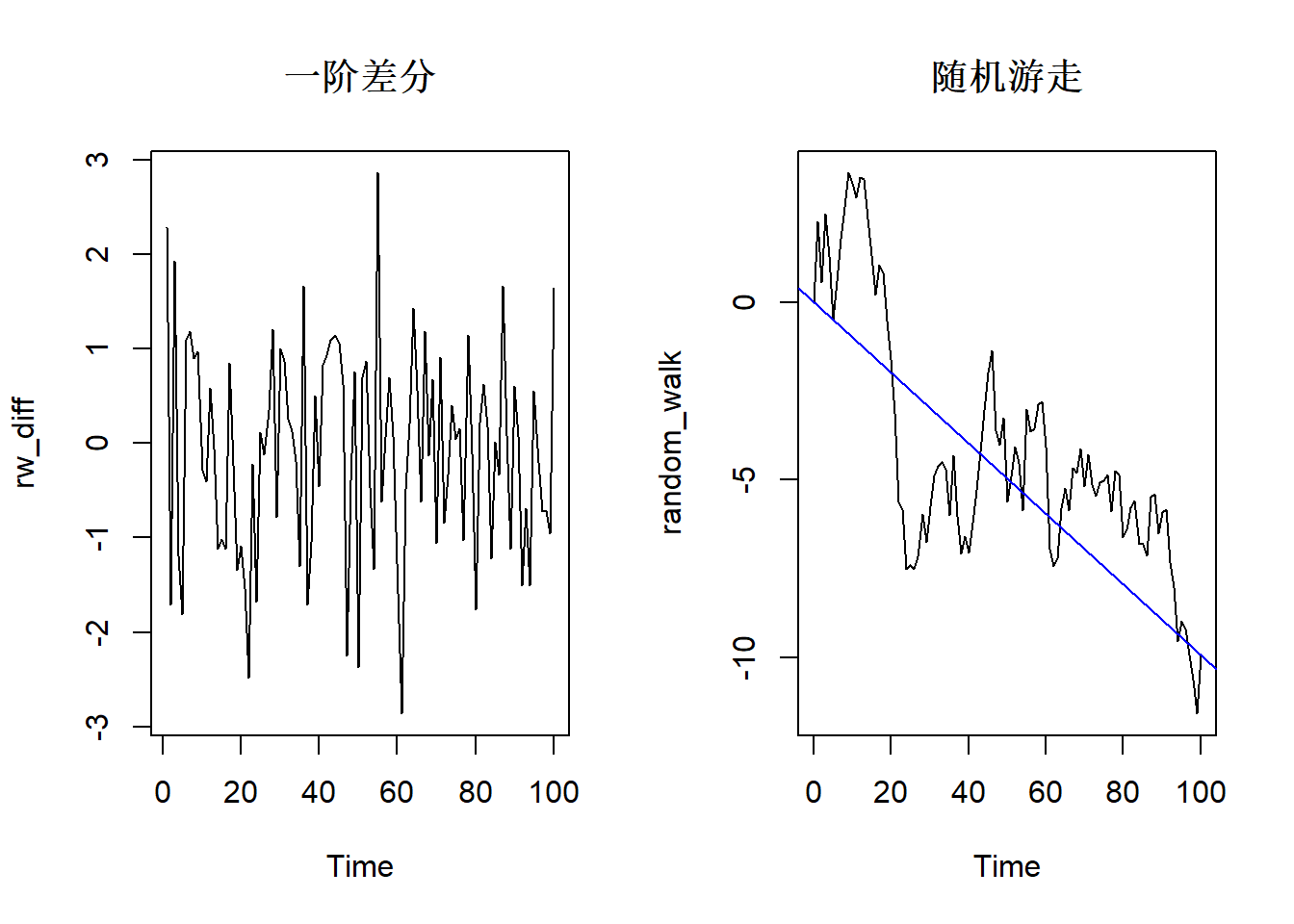
我们可以观察白噪声,随机游走的图,来主观判断是否是平稳的时间序列
# 生成白噪声数据
white_noise <- arima.sim(model = list(order = c(0,0,0)), n= 100)
# 白噪声连加是随机游走
random_walk <- cumsum(white_noise)
# 生成带漂移的白噪声
wn_drift <- arima.sim(model = list(order = c(0,0,0)), mean=0.4, n= 100)
# 生成带漂移的随机游走
rw_drift <- cumsum(wn_drift)
# 绘制所有时间序列
plot.ts(cbind(white_noise, random_walk, wn_drift, rw_drift), main = "合并")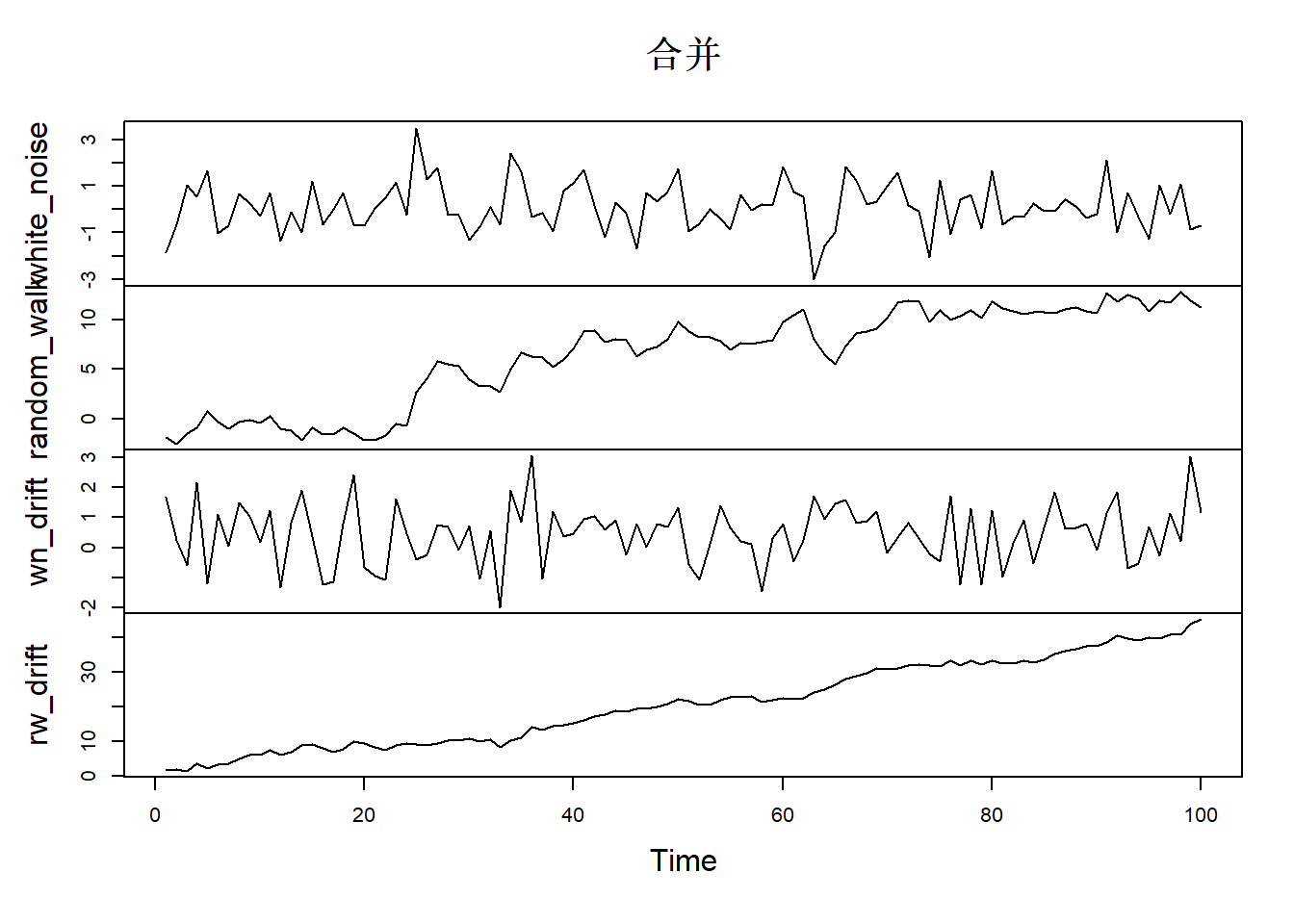
24.2.4 自相关系数
函数acf()计算(并默认绘制)自变量或自相关函数的估计值。每个ACF图包括一对蓝色的水平虚线,代表以零为中心的滞后95%置信区间。这些线用于确定某个滞后期的单个自相关估计值与零的空值(即在该滞后期没有自相关)的统计意义。
layout(matrix(c(1, 2), ncol = 2))
acf(random_walk, main = "随机游走自相关图")
acf(rw_drift, main = "随机游走(带漂移)的自相关图")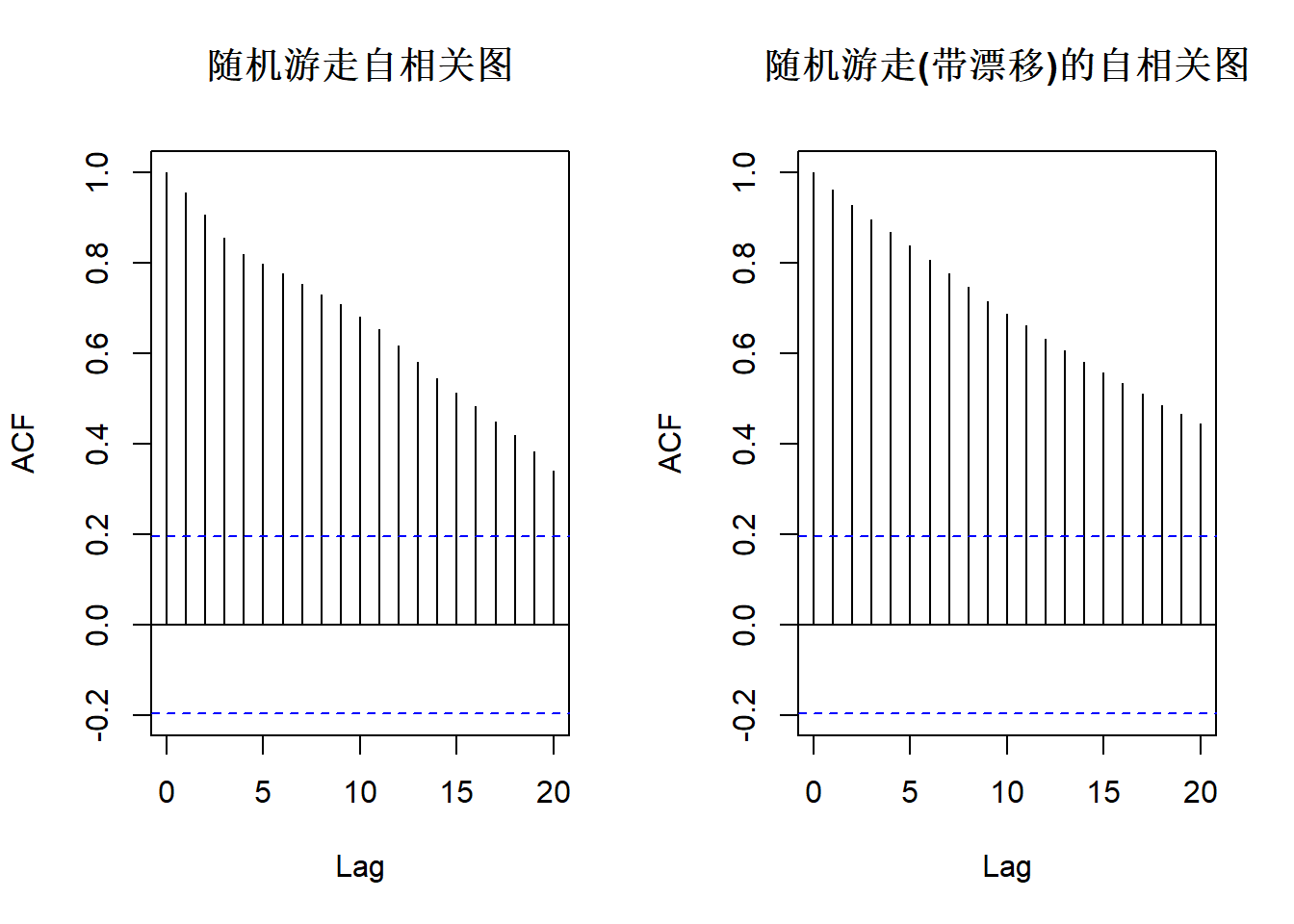
24.2.5 Wold分解定理
1938年, H.Wold在他的博士论文”A Study in the Analysis of Stationary Time Series”中提出了著名的平稳序列分解定理。这个定理是平稳时间序列分析的理论基石。
Wold分解定理(Wold’s decomposition theorem), 对于任意一个离散平稳的时间序列\(\left \{ Y_{t} \right \}\), 它都可以分解为两个不相关的平稳序列之和,其中一个为确定性的(deterministic),另一个为随机性的(stochastic),不妨记作:
\[ Y_{t} = V_{t} + \xi_{t} \] 其中, \(V_{t}\)为确定性的平稳序列,\(\xi_{t}\)为随机性平稳序列.
确定性序列\(\left \{ V_{t} \right \}\)的真实生成机制可以是任意方式。换言之,\(\left \{ V_{t} \right \}\)的真实波动可以是时间的任意函数(前提是保证序列的平稳性).
Wold证明不管\(\left \{ V_{t} \right \}\)的生成机制是怎样的,它都可以等价表达为历史序列值的线性函数 \[ V_{t} = \sum_{i=1}^{\infty}\phi _{i}y_{t-i} \] 所以,Wold分解定理中确定性序列\(\left \{ V_{t} \right \}\)的性质是:序列的当期波动可以由其历史序列值解读的部分.
随机序列\(\left \{ \xi_{t} \right \}\)代表了不能由序列的历史信息解读的随机波动部分.Wold证明这部分信息可以等价表达为 \[ \xi_{t} = \sum_{i=1}^{\infty}\theta _{i}\varepsilon_{t-i} \] 其中\(\varepsilon_{t}\)称为新息过程(innovation process),是每个时期加入的新的随机信息.它们互相独立,不可预测,通常假定\(\varepsilon_{t} \sim N(0, \sigma_{\varepsilon}^{2}), \forall t \ge 0\), 且有\(\theta_{0}=1,\sum_{i=1}^{\infty}\theta _{i}^{2}<\infty\).
所以,Wold分解定理中随机性序列的性质是:序列的当期波动不可以由其历史序列值解读的部分.
24.3 ARMA(p, q)模型
24.3.1 AR(p)模型
24.3.1.1 AR(p)定义
具有如下结构的模型称为\(p\)阶自回归模型,简记为\(AR(p)\)
\[ \left\{\begin{array}{l} y_{t}=\alpha_{0}+\alpha_{1} y_{t-1}+\alpha_{2} y_{t-2}+\cdots+\alpha_{p} y_{p}+\varepsilon_{t} \\ \alpha_{p} \neq 0 \\ E\left(\varepsilon_{t}\right)=0, \operatorname{Var}\left(\varepsilon_{t}\right)=\sigma_{\varepsilon}^{2}, E\left(\varepsilon_{t} \varepsilon_{s}\right)=0, \forall t \neq s \\ E\left(y_{s} \varepsilon_{t}\right)=0, \forall s<t \end{array}\right. \] 特别地,当\(\alpha_{0}=0\)时,称为中心化\(AR(p)\)模型. 若\(\alpha_{0} \ne 0\),令\(\mu=\frac{\alpha_{0}}{1-\alpha_{1}-\alpha_{2}-\cdots-\alpha_{p}}, y_{t}^{\prime}=y_{t}-\mu\),称\(\left \{ y_{t}^{\prime} \right \}\)为\(\left \{ y_{t} \right \}\)的中心化序列.
一般遇到的是1或2阶ar模型,其性质不列在这里了.详细见Wiki.
我们生成几个一阶的AR模型,它的形式是如下的:
\[ Y_{t}-\mu = \phi(Y_{t-1}-\mu)+\epsilon_{t} \]
arima.sim()函数也可以用来模拟AR模型的数据,方法是将模型参数设置为list(ar = phi),其中phi是区间(-1,1)的斜率参数。我们还需要指定一个序列长度n。
x <- arima.sim(model = list(ar = 0.5), n = 100)
y <- arima.sim(model = list(ar = 0.9), n = 100)
# AR 2 模型
z <- arima.sim(model = list(order = c(2, 0, 0), ar = c(1.5, -0.75)), n = 100)
plot.ts(cbind(x, y, z), main = "AR(1)")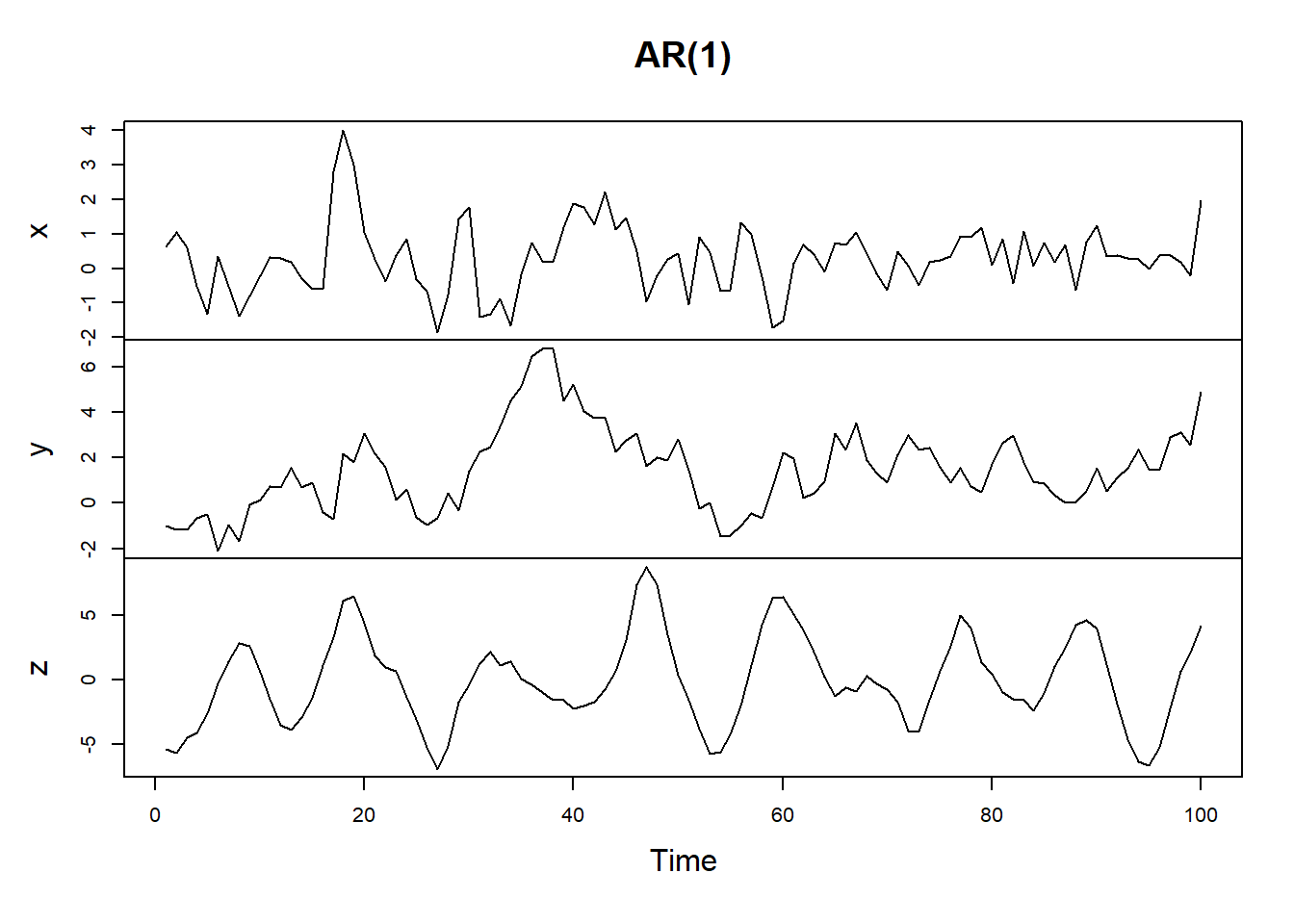
它们的自相关图为
par(mfrow=c(3,1))
acf(x)
acf(y)
acf(z)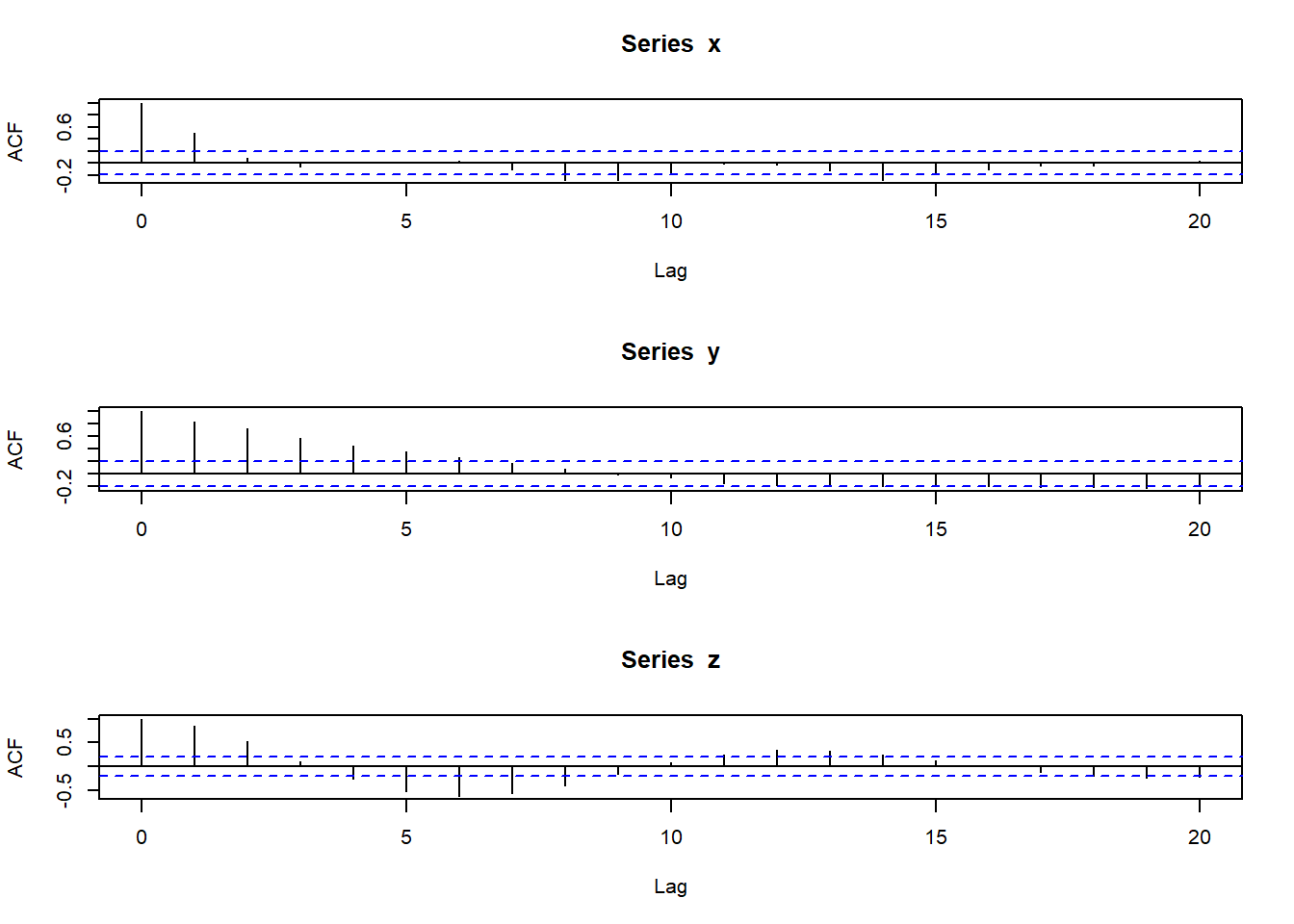
24.3.2 MA(q)模型
24.3.2.1 MA(q)定义
具有如下结构的模型称为\(q\)阶自回归模型,简记为\(MA(q)\): \[ \left\{\begin{array}{l} y_{t}=\theta_{0}+\varepsilon_{t}-\theta_{1} \varepsilon_{t-1}-\theta_{2} \varepsilon_{t-2}-\cdots-\theta_{q} \varepsilon_{t-q} \\ \theta_{q} \neq 0 \\ E\left(\varepsilon_{t}\right)=0, \operatorname{Var}\left(\varepsilon_{t}\right)=\sigma_{\varepsilon}^{2}, E\left(\varepsilon_{t} \varepsilon_{s}\right)=0, \forall t \neq s \end{array}\right. \] 特别地,当 \(\theta_{0}=0\)时,称为中心化\(MA(q)\)模型.如果引入延迟算子,中心化\(MA(q)\)模型又可以简记为 \[ y_{t}=\Theta (B)\varepsilon _{t} \] 其中,\(\Theta (B)\)称为\(q\)阶移动平均系数多项式 \[ \Theta (B)=1-\theta _{1}B-\theta _{2}B^{2}-\cdots -\theta _{q}B^{q} \]
一般来说,我们使用一阶或二阶的MA模型
一阶MA模型形式如下 \[ Y_{t} = \mu +\epsilon_{t} + \theta \epsilon_{t-1} \]
arima.sim()生成指定的数据.
x <- arima.sim(model = list(ma = 0.5), n = 100)
y <- arima.sim(model = list(ma = 0.9), n = 100)
z <- arima.sim(model = list(order = c(0, 0, 1), ma = .9), n = 100)
plot.ts(cbind(x, y, z), main = "MA(1)")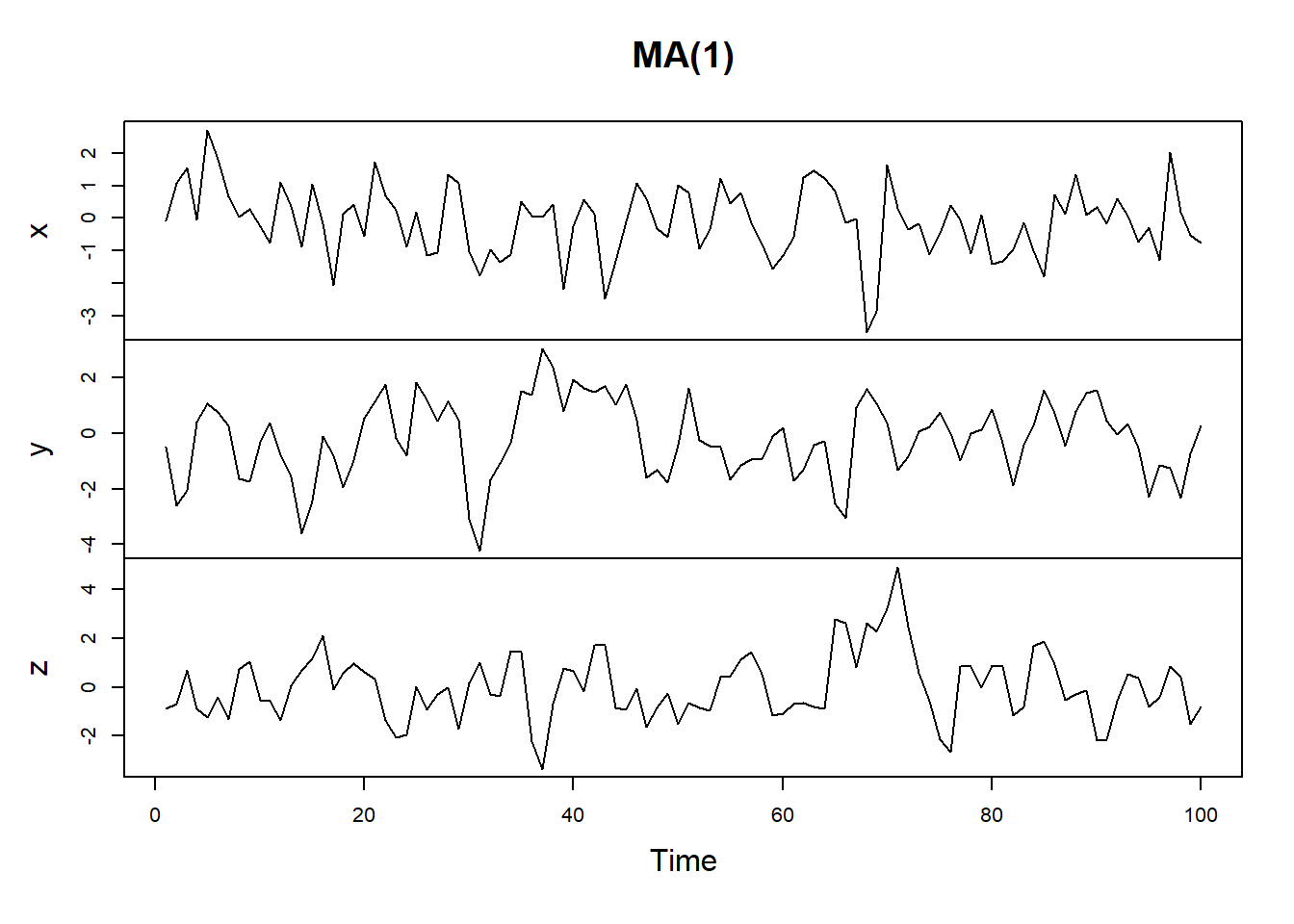
其自相关图为
par(mfrow=c(3,1))
acf(x)
acf(y)
acf(z)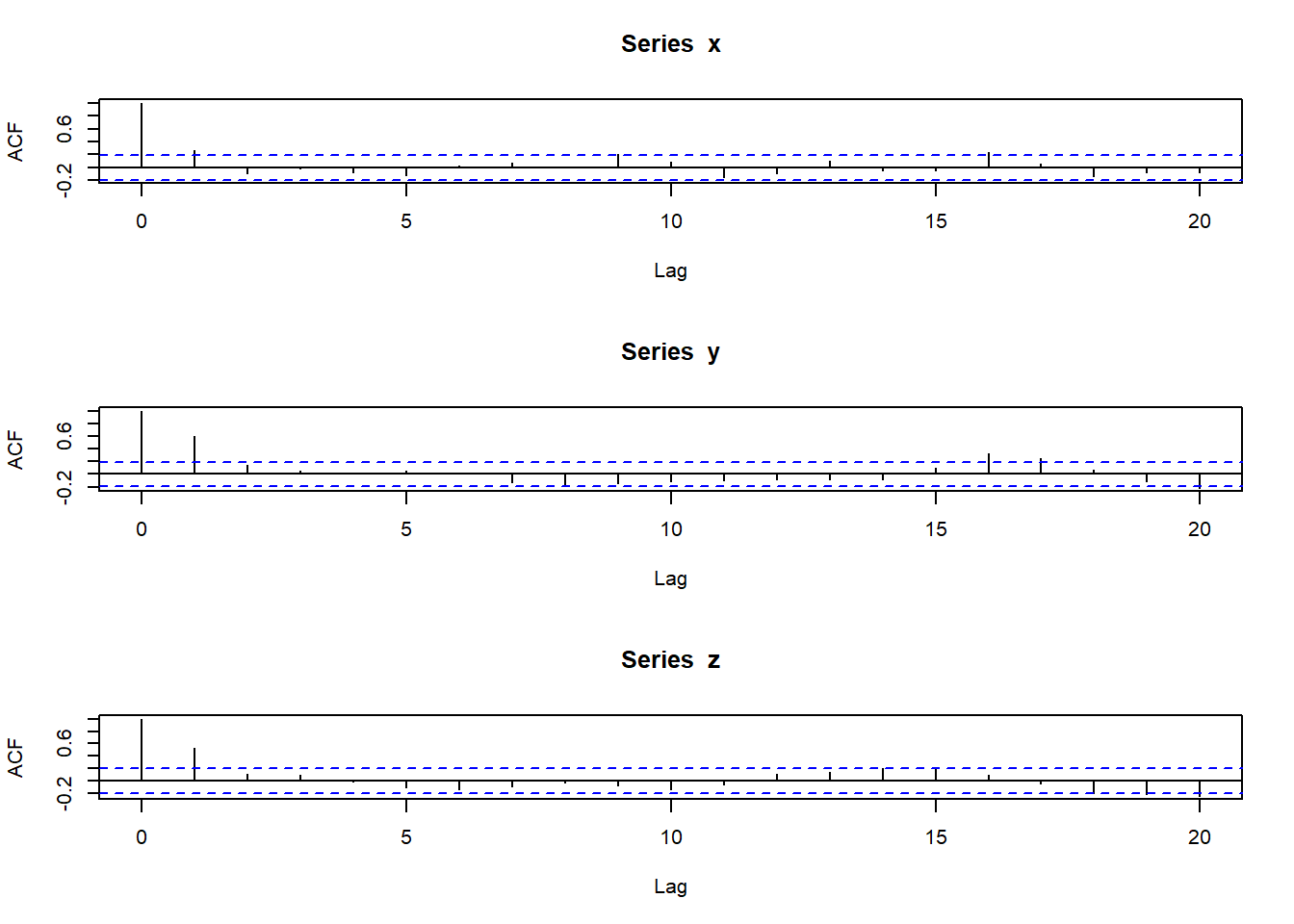
24.3.3 ARMA(p, q)模型
具有如下结构的模型称为自回归移动平均模型,简记为\(ARMA(p,q)\)
\[ \left\{\begin{array}{l} y_{t}=\alpha_{0}+\alpha_{1} y_{t-1}+\alpha_{2} y_{t-2}+\cdots+\alpha_{p} y_{p} \\ \quad+\varepsilon_{t}-\theta_{1} \varepsilon_{t-1}-\theta_{2} \varepsilon_{t-2}-\cdots-\theta_{q} \varepsilon_{t-q} \\ \alpha_{p} \neq 0, \theta_{q} \neq 0 \\ E\left(\varepsilon_{t}\right)=0, \operatorname{Var}\left(\varepsilon_{t}\right)=\sigma_{\varepsilon}^{2}, E\left(\varepsilon_{t} \varepsilon_{s}\right)=0, \forall t \neq s \\ E\left(y_{s} \varepsilon_{t}\right)=0, \forall s<t \end{array}\right. \]
特别地,当\(\alpha_{0}=0\)时,称为中心化的\(ARMA(p,q)\)模型.引入滞后算子, \(ARMA(p,q)\)模型简记为: \[ \Phi(B) y_{t}=\Theta(B) \varepsilon_{t} \]
其中\(\Phi(B)=1-\alpha_{1} B-\alpha_{2} B^{2}-\cdots-\alpha_{p} B^{p}\), \(\Theta(B)=1-\theta_{1} B-\theta_{2} B^{2}-\cdots-\theta_{q} B^{q}\)
24.3.4 AR模型估计
我们先介绍使用astsa包的sarima()函数来估计,然后在介绍R自带的函数
astsa软件包中的sarima()来轻松地对数据进行拟合模型。
# 生成100个AR(1)模型
x <- arima.sim(model = list(order = c(1, 0, 0), ar = .9), n = 100)
plot(x)
acf2(x)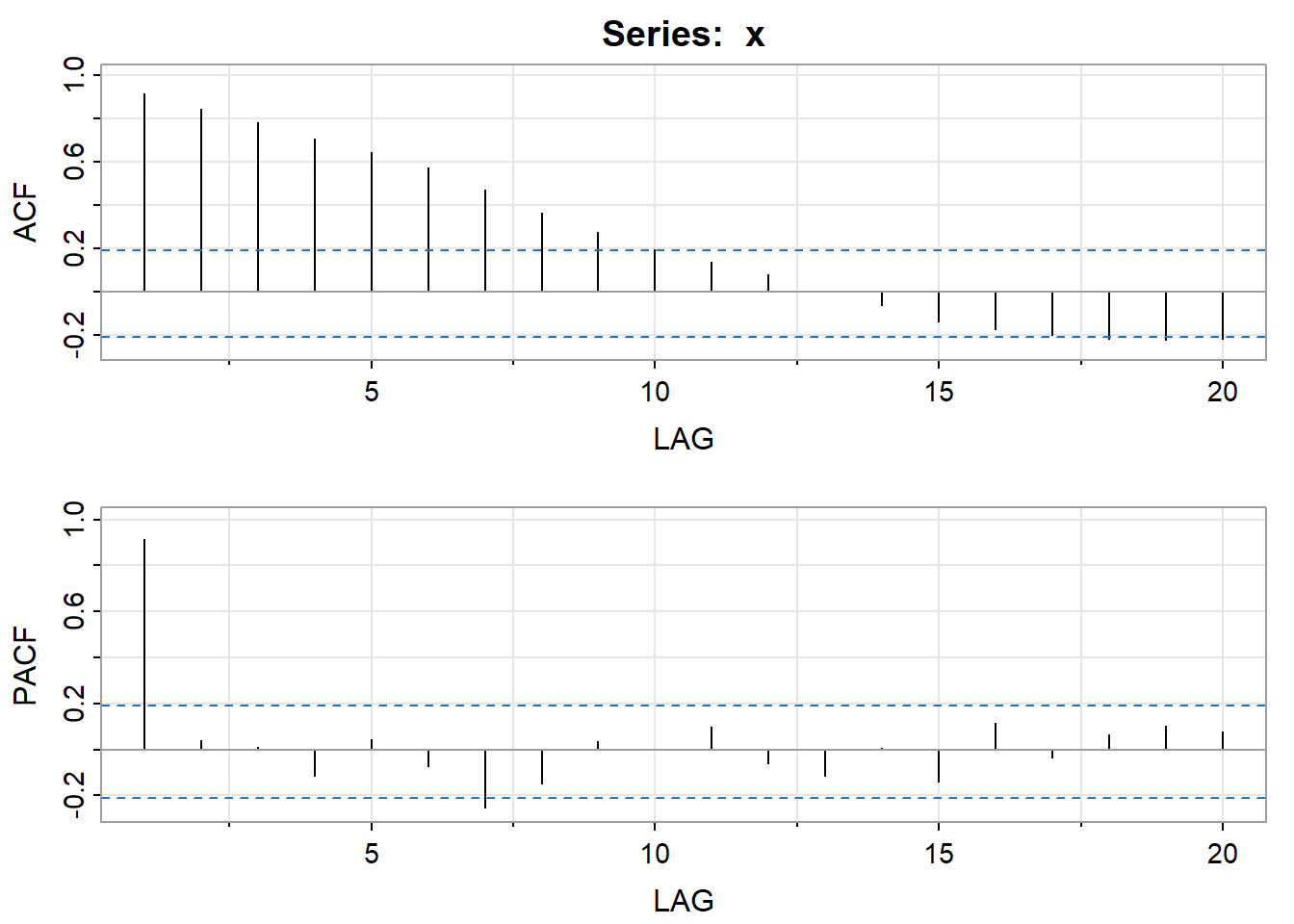
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
## ACF 0.92 0.85 0.78 0.70 0.64 0.57 0.47 0.36 0.28 0.19 0.14 0.08 0.00
## PACF 0.92 0.04 0.01 -0.12 0.04 -0.07 -0.25 -0.15 0.04 0.00 0.10 -0.06 -0.12
## [,14] [,15] [,16] [,17] [,18] [,19] [,20]
## ACF -0.06 -0.14 -0.17 -0.20 -0.22 -0.22 -0.22
## PACF 0.01 -0.14 0.12 -0.04 0.07 0.10 0.08
# 假设不知道,模拟成AR(1)模型,查看估计的参数
sarima(x, 1, 0, 0)$ttable
## initial value 0.861736
## iter 2 value -0.059364
## iter 3 value -0.059372
## iter 4 value -0.059385
## iter 5 value -0.059505
## iter 6 value -0.059505
## iter 7 value -0.059505
## iter 7 value -0.059505
## iter 7 value -0.059505
## final value -0.059505
## converged
## initial value -0.053852
## iter 2 value -0.053920
## iter 3 value -0.054175
## iter 4 value -0.054200
## iter 5 value -0.054233
## iter 6 value -0.054272
## iter 7 value -0.054274
## iter 8 value -0.054280
## iter 9 value -0.054280
## iter 10 value -0.054281
## iter 10 value -0.054281
## iter 10 value -0.054281
## final value -0.054281
## converged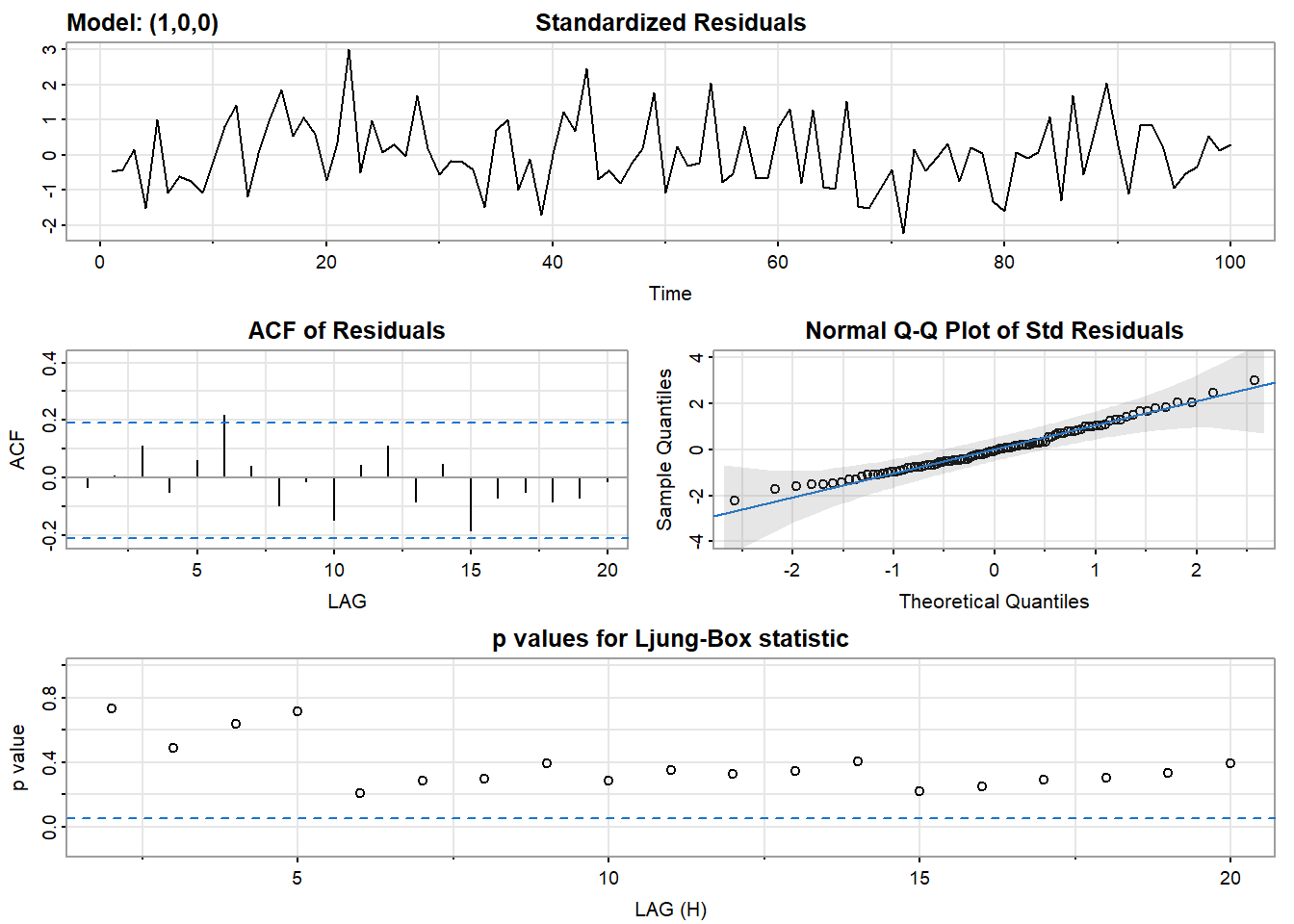
## Estimate SE t.value p.value
## ar1 0.9102 0.0380 23.9411 0.0000
## xmean -0.8155 0.9533 -0.8554 0.3944对于一阶AR模型,我们要估计两个参数,然后给出之后的预测. \[ \hat{Y_{t}} = \hat{\mu} +\hat{\phi}(Y_{t-1}-\hat{\mu}) \] 残差就是今天的实际值减去估计值,即 \[ \hat{\epsilon_{t}} = Y_{t}- \hat{Y_{t}} \]
我们用已经创建好的数据进行,估计
# AR1 创建
idx <- 1:190
x <- arima.sim(model = list(ar = 0.5), n = 200)
# 参数估计
x_fit <- arima(x[idx], order = c(1, 0, 0))
x_fit
##
## Call:
## arima(x = x[idx], order = c(1, 0, 0))
##
## Coefficients:
## ar1 intercept
## 0.4049 -0.2430
## s.e. 0.0661 0.1333
##
## sigma^2 estimated as 1.205: log likelihood = -287.39, aic = 580.79
# 预测
predict_x <- predict(x_fit)
## 一步估计
predict_x$pred[1]
## [1] -0.3686003
## 10步估计
predict(x_fit, n.ahead = 10)
## $pred
## Time Series:
## Start = 191
## End = 200
## Frequency = 1
## [1] -0.3686003 -0.2938432 -0.2635761 -0.2513218 -0.2463603 -0.2443515
## [7] -0.2435382 -0.2432089 -0.2430756 -0.2430217
##
## $se
## Time Series:
## Start = 191
## End = 200
## Frequency = 1
## [1] 1.097673 1.184227 1.197819 1.200032 1.200394 1.200454 1.200463 1.200465
## [9] 1.200465 1.200465如果从图上看的话,其实差别比较大的.
## 绘图准备
x_forecast <- predict(x_fit, n.ahead = 10)$pred
x_forecast_se <- predict(x_fit, n.ahead = 10)$se # 标准差
# 画图
ts.plot(x)
points(x_forecast, type = "l", col = 2) # 预测值
## 两倍标准差范围
points(x_forecast - 2*x_forecast_se, type = "l", col = 2, lty = 2)
points(x_forecast + 2*x_forecast_se, type = "l", col = 2, lty = 2)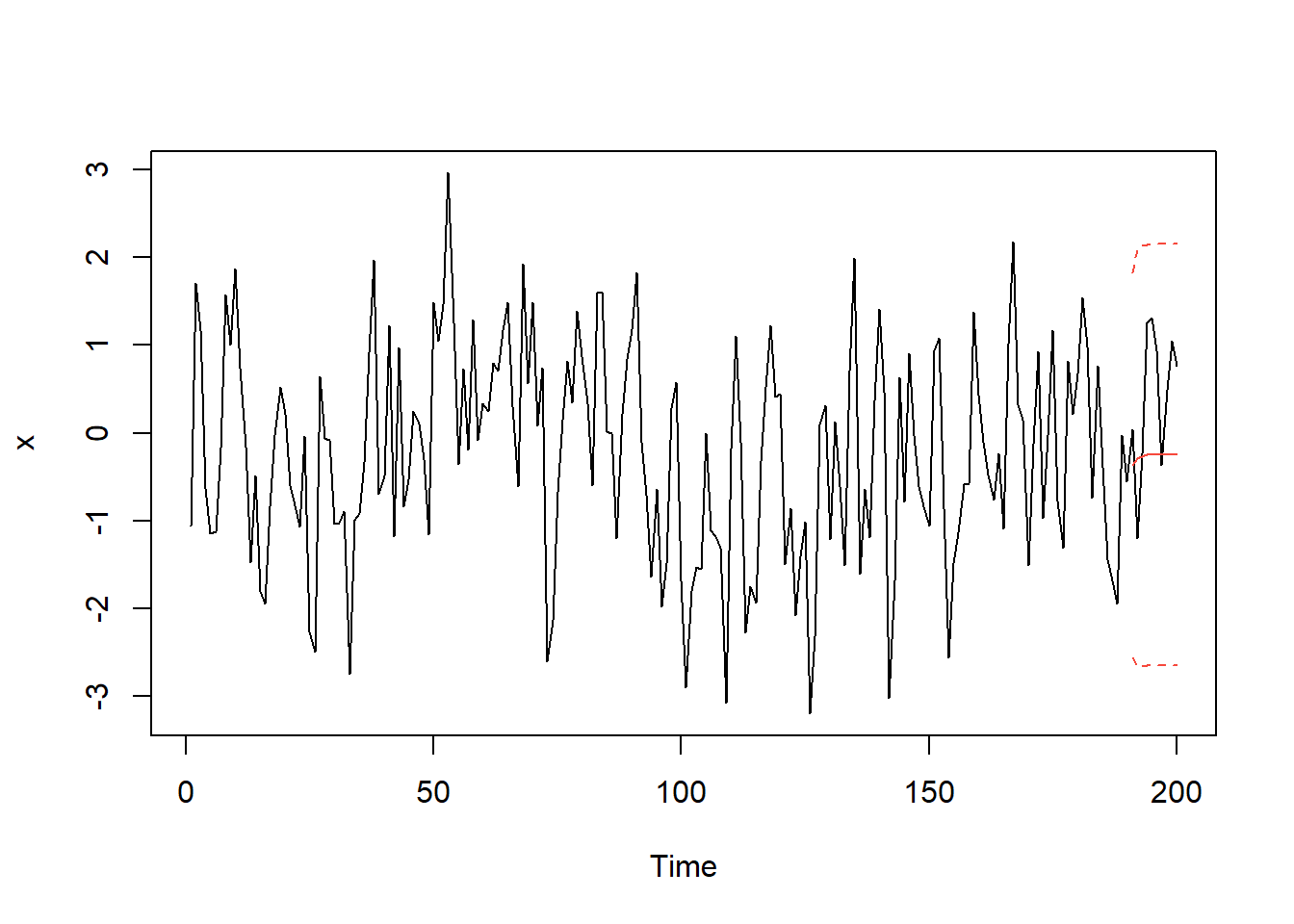
24.3.5 MA模型估计
\[ \hat{Y_{t}} = \hat{ \mu} + \hat{\theta} \hat{\epsilon_{t-1}} \]
残差 \[ \hat{\epsilon_{t}} = Y_{t}- \hat{Y_{t}} \]
我们也先介绍使用
sarima()去拟合参数
x <- arima.sim(model = list(order = c(0, 0, 1), ma = -.8), n = 100)
plot(x)
acf2(x)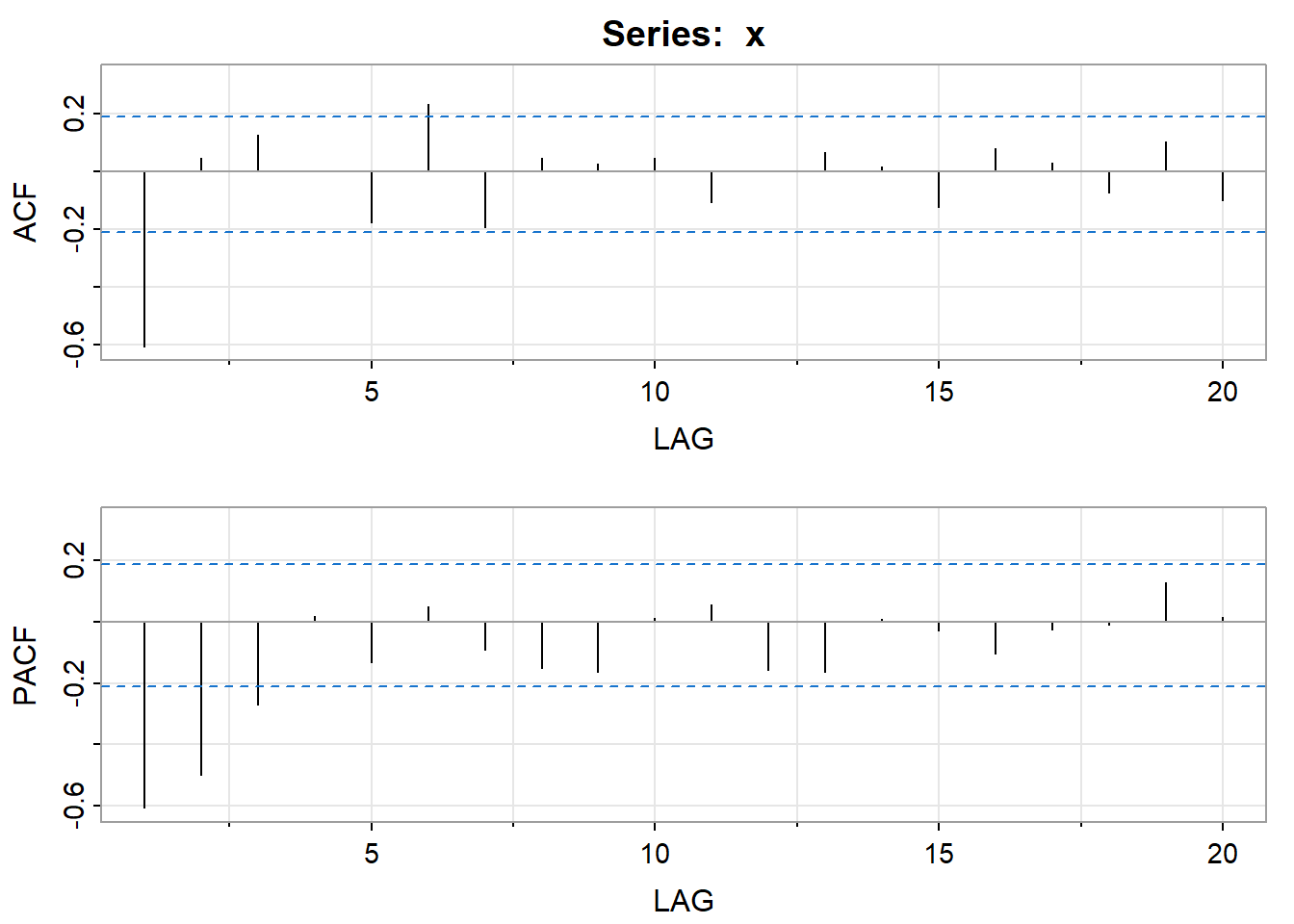
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
## ACF -0.6 0.05 0.13 0.00 -0.18 0.23 -0.19 0.05 0.03 0.05 -0.11 0.01 0.07
## PACF -0.6 -0.50 -0.27 0.02 -0.13 0.05 -0.09 -0.15 -0.16 0.01 0.06 -0.16 -0.16
## [,14] [,15] [,16] [,17] [,18] [,19] [,20]
## ACF 0.02 -0.12 0.08 0.03 -0.07 0.10 -0.10
## PACF 0.01 -0.03 -0.10 -0.02 -0.01 0.13 0.02
sarima(x, 0, 0, 1)$ttable
## initial value 0.419105
## iter 2 value 0.117207
## iter 3 value 0.060312
## iter 4 value 0.057150
## iter 5 value 0.046629
## iter 6 value 0.042245
## iter 7 value 0.042159
## iter 8 value 0.037629
## iter 9 value 0.037576
## iter 10 value 0.028464
## iter 11 value 0.028329
## iter 12 value 0.024758
## iter 13 value 0.024698
## iter 14 value 0.020518
## iter 15 value 0.020491
## iter 16 value 0.018167
## iter 17 value 0.016939
## iter 18 value 0.014733
## iter 19 value 0.011732
## iter 20 value 0.011029
## iter 21 value 0.006264
## iter 22 value 0.005497
## iter 22 value 0.005497
## iter 23 value 0.005139
## iter 24 value 0.005083
## iter 25 value 0.005074
## iter 26 value 0.005074
## iter 26 value 0.005074
## iter 26 value 0.005074
## final value 0.005074
## converged
## initial value 0.062262
## iter 2 value 0.052885
## iter 3 value 0.050157
## iter 4 value 0.048903
## iter 5 value 0.048277
## iter 6 value 0.048024
## iter 7 value 0.047894
## iter 8 value 0.047831
## iter 9 value 0.047805
## iter 10 value 0.047805
## iter 10 value 0.047805
## iter 10 value 0.047805
## final value 0.047805
## converged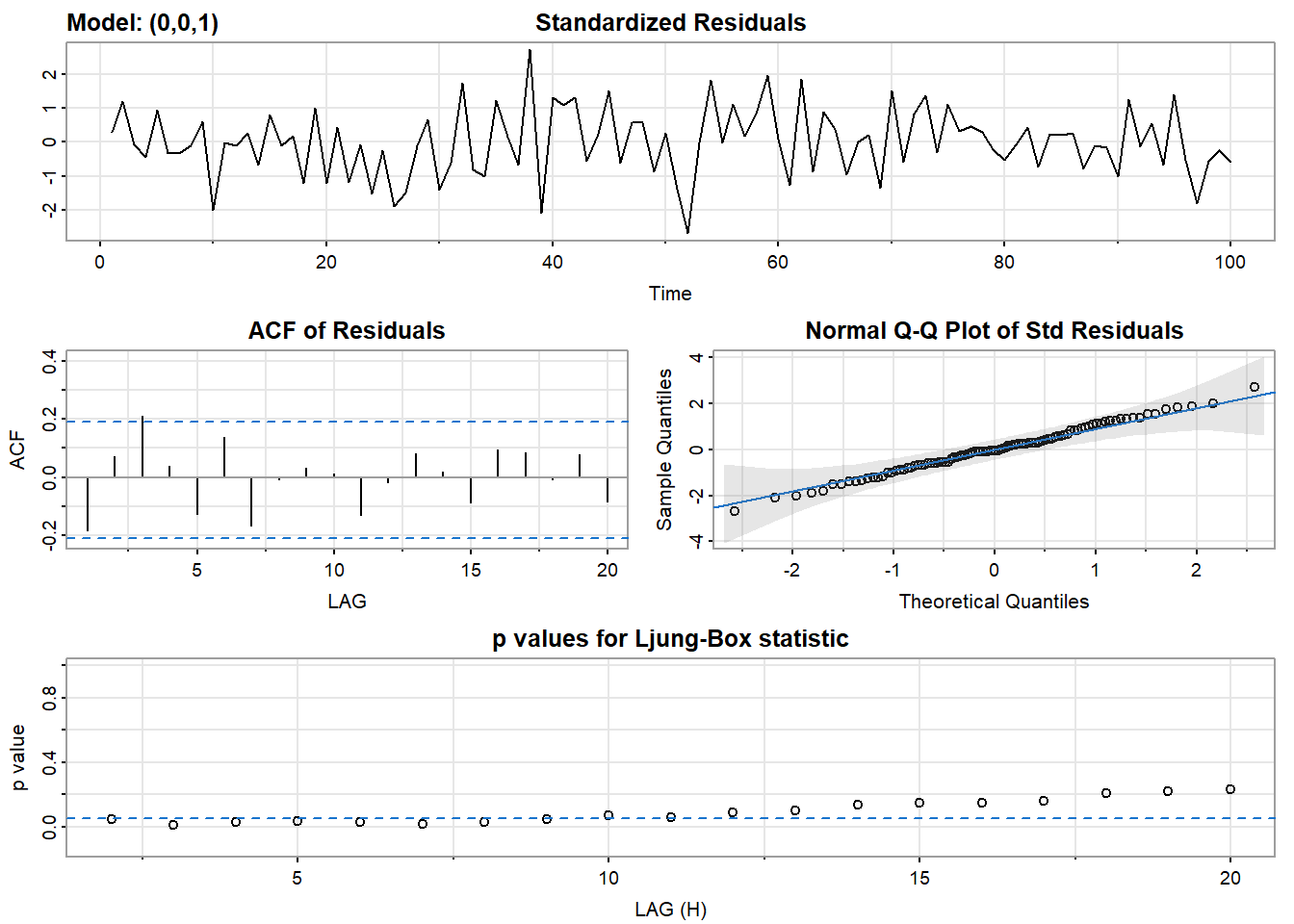
## Estimate SE t.value p.value
## ma1 -0.8977 0.0550 -16.3179 0.0000
## xmean -0.0108 0.0121 -0.8924 0.3744同时,对于ARMA模型的拟合也是一样的.模拟一个\(ARMA(2,1)\)模型,它的数学形式即
\[ Y_t = Y_{t-1}-0.9Y_{t-2}+\epsilon _t+0.8\epsilon _{t-1} \] 使用R语言进行生成和拟合.
x <- arima.sim(model = list(order = c(2, 0, 1), ar = c(1, -.9), ma = .8), n = 250)
plot(x)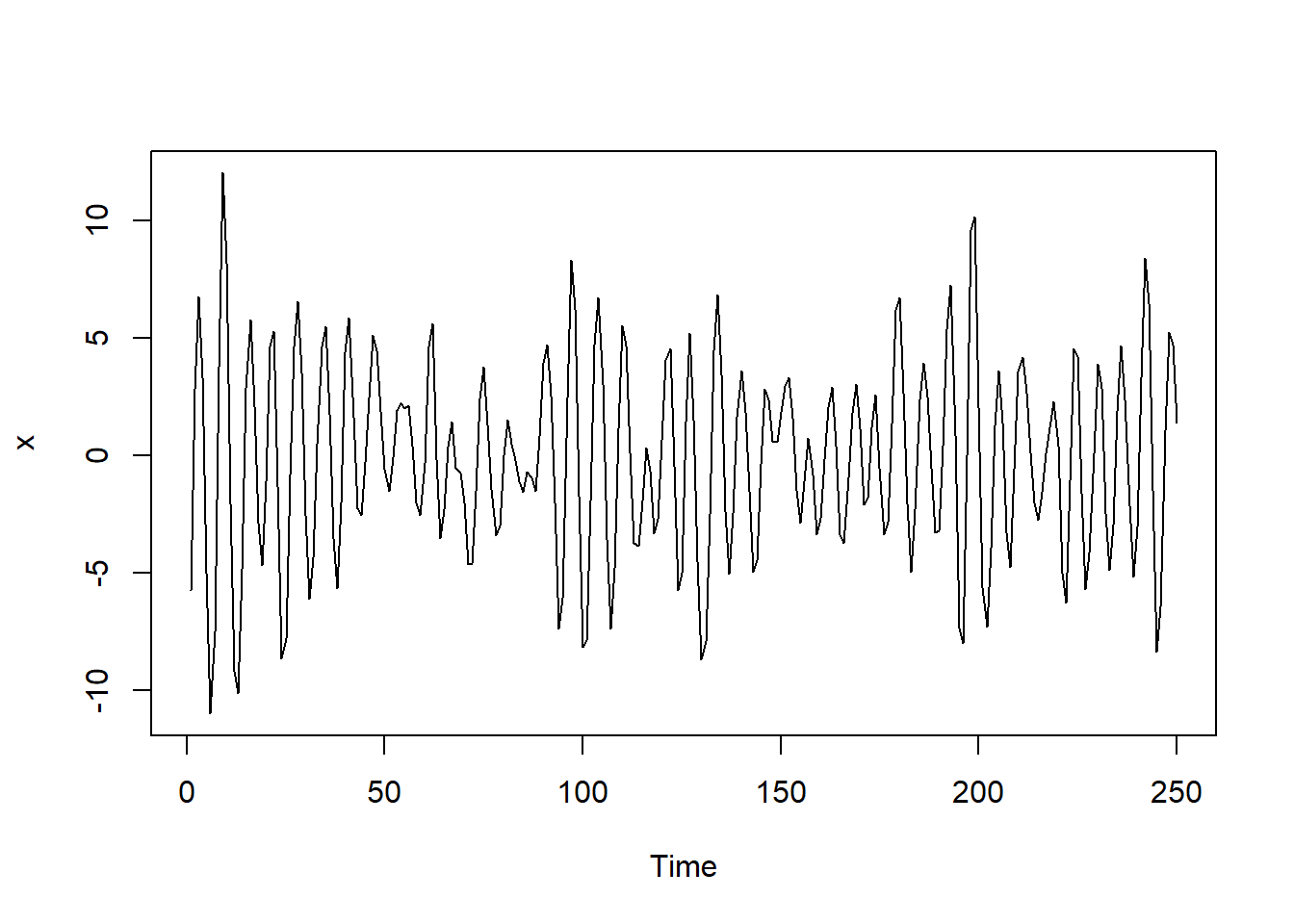
acf2(x)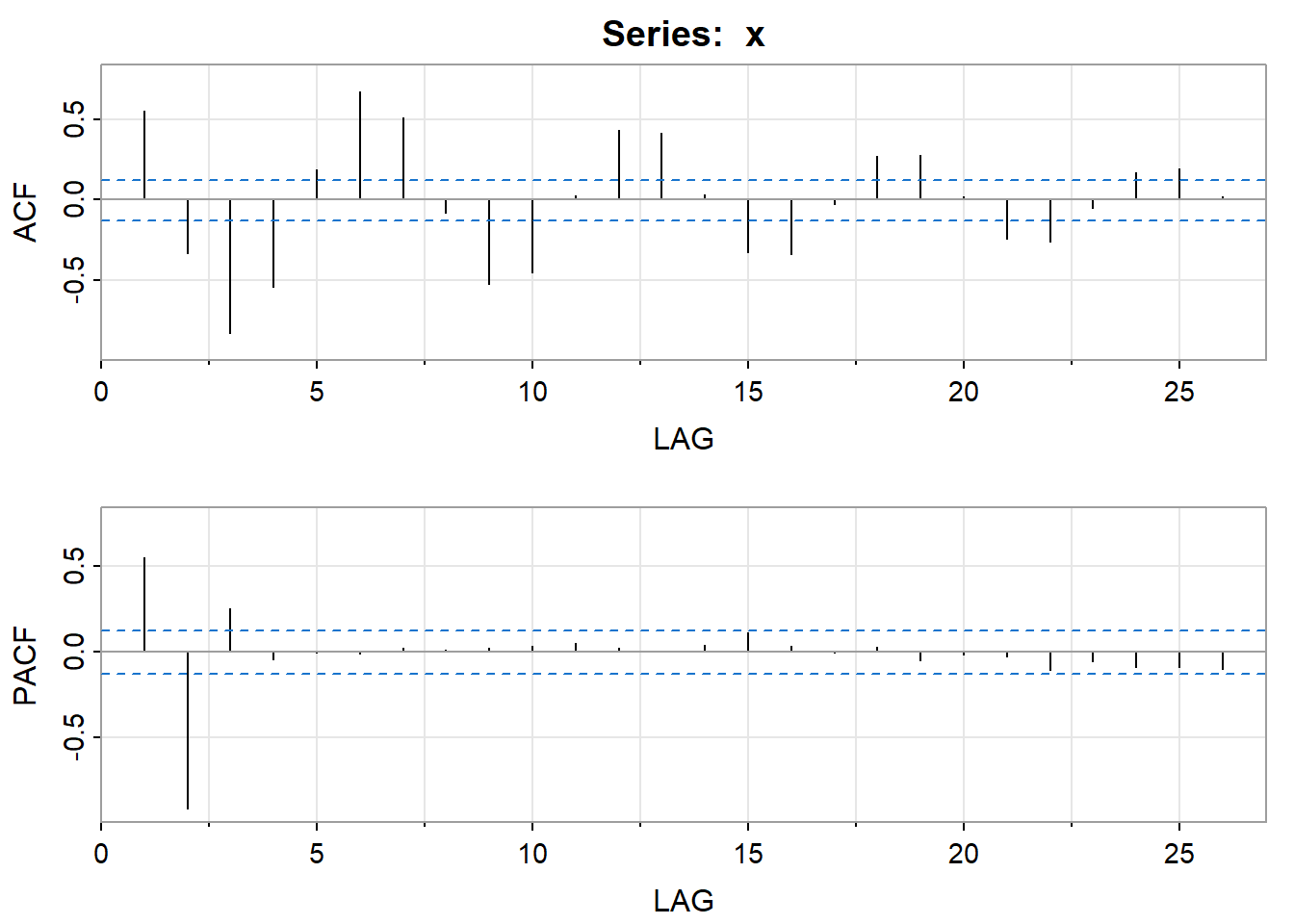
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
## ACF 0.55 -0.33 -0.83 -0.54 0.19 0.67 0.51 -0.08 -0.52 -0.45 0.02 0.43
## PACF 0.55 -0.92 0.25 -0.05 -0.01 -0.01 0.02 0.01 0.03 0.04 0.05 0.02
## [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24]
## ACF 0.42 0.03 -0.33 -0.34 -0.03 0.27 0.28 0.02 -0.24 -0.26 -0.05 0.17
## PACF 0.00 0.04 0.11 0.04 0.00 0.03 -0.05 -0.02 -0.03 -0.10 -0.06 -0.09
## [,25] [,26]
## ACF 0.19 0.02
## PACF -0.09 -0.10
sarima(x, 2, 0, 1)$ttable
## initial value 1.413318
## iter 2 value 0.600735
## iter 3 value 0.355761
## iter 4 value 0.021613
## iter 5 value 0.001253
## iter 6 value -0.008309
## iter 7 value -0.048450
## iter 8 value -0.050213
## iter 9 value -0.050646
## iter 10 value -0.050784
## iter 11 value -0.050855
## iter 12 value -0.050859
## iter 13 value -0.050860
## iter 14 value -0.050861
## iter 15 value -0.050861
## iter 16 value -0.050861
## iter 17 value -0.050861
## iter 17 value -0.050861
## iter 17 value -0.050861
## final value -0.050861
## converged
## initial value -0.031386
## iter 2 value -0.031673
## iter 3 value -0.031843
## iter 4 value -0.032379
## iter 5 value -0.032462
## iter 6 value -0.032476
## iter 7 value -0.032477
## iter 8 value -0.032477
## iter 8 value -0.032477
## iter 8 value -0.032477
## final value -0.032477
## converged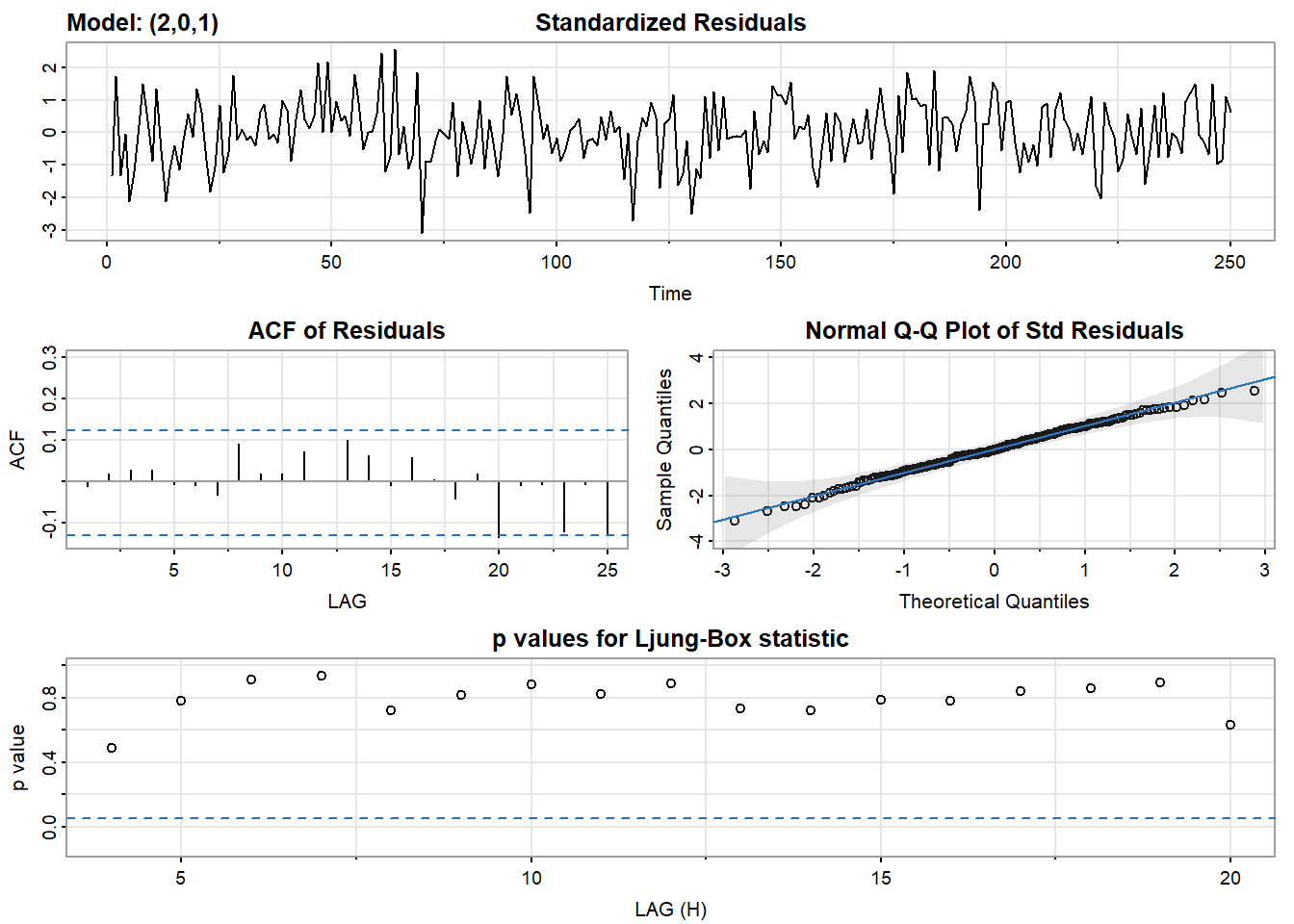
## Estimate SE t.value p.value
## ar1 1.0244 0.0274 37.3684 0.0000
## ar2 -0.9086 0.0266 -34.1324 0.0000
## ma1 0.7846 0.0384 20.4398 0.0000
## xmean -0.1567 0.1222 -1.2826 0.2008参数估计和\(AR\)一样,
arima(x, order = c(0, 0, 1))
##
## Call:
## arima(x = x, order = c(0, 0, 1))
##
## Coefficients:
## ma1 intercept
## 0.9810 -0.1373
## s.e. 0.0149 0.3014
##
## sigma^2 estimated as 5.809: log likelihood = -576.3, aic = 1158.59##模型选择与预测
之前我们使用了
sarima()函数去拟合已经知道的模型,对于未知模型的时间序列数据,我们首先要定模型,然后进行评估.
24.3.6 ARMA模型相关性特征
对于时间序列定模型,可以通过自相关和偏自相关图以及按照以下的”规则”进行模型的识别:
| 模型 | 自相关系数 | 偏自相关系数 |
|---|---|---|
| AR(p) | 拖尾 | p阶截尾 |
| MA(q) | q阶截尾 | 拖尾 |
| ARMA(p, q) | 拖尾 | 拖尾 |
astsa包的
acf2函数可以同时帮助绘制自相关图和偏自相关图
acf2(AirPassengers)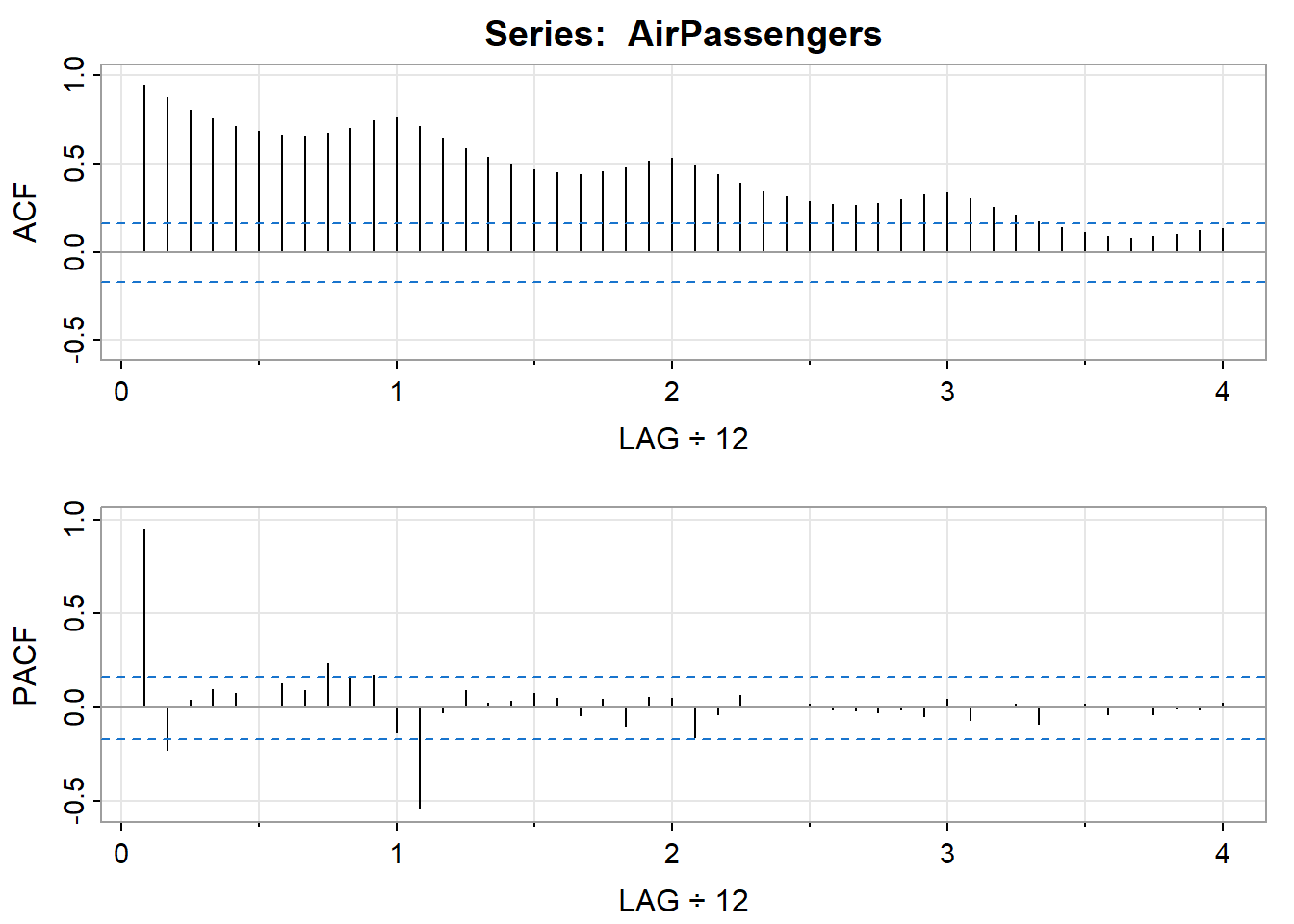
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
## ACF 0.95 0.88 0.81 0.75 0.71 0.68 0.66 0.66 0.67 0.70 0.74 0.76 0.71
## PACF 0.95 -0.23 0.04 0.09 0.07 0.01 0.13 0.09 0.23 0.17 0.17 -0.14 -0.54
## [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25]
## ACF 0.65 0.59 0.54 0.50 0.47 0.45 0.44 0.46 0.48 0.52 0.53 0.49
## PACF -0.03 0.09 0.02 0.03 0.07 0.05 -0.05 0.05 -0.10 0.05 0.05 -0.16
## [,26] [,27] [,28] [,29] [,30] [,31] [,32] [,33] [,34] [,35] [,36] [,37]
## ACF 0.44 0.39 0.35 0.31 0.29 0.27 0.26 0.28 0.30 0.33 0.34 0.30
## PACF -0.04 0.07 0.01 0.01 0.02 -0.01 -0.02 -0.03 -0.01 -0.05 0.05 -0.07
## [,38] [,39] [,40] [,41] [,42] [,43] [,44] [,45] [,46] [,47] [,48]
## ACF 0.25 0.21 0.17 0.14 0.11 0.09 0.08 0.09 0.10 0.12 0.13
## PACF 0.00 0.02 -0.09 0.00 0.02 -0.04 0.00 -0.04 -0.01 -0.01 0.0224.3.7 AIC与BIC评价
为了确定模型的拟合度,你可以测量每个模型的Akaike信息准则(AIC)和Bayesian信息准则(BIC)。主要的想法是这些指标会惩罚具有更多估计参数的模型,以避免过度拟合,较小的值是首选。在所有因素相同的情况下,一个模型如果产生的AIC或BIC比另一个模型低,则被认为是更适合的。
相关函数文档
24.3.8 残差分析
需要清楚原假设
残差分析的基本目标与之前的模型的相同。也就是说,我们要确保残差是白高斯噪声。如果不是,那么我们就没有找到最好的模型。sarima()提供了一个四张图片。
- 标准化残差图应该被检查出模式。从这个图中很难判断噪声是否是白噪声,但很容易判断它是否不是白噪声,例如,残差中是否有明显的模式。
- 残差的ACF可以用来评估白度(whiteness)。95%的ACF值应该在蓝色虚线之间。
- Q-Q图可以评估正态性。如果残差是正常的,那么这些点将与线对齐。两端往往有极端值。只要没有严重偏离直线的情况,那么正态假设就是合理的。
- 最后,有一个Q统计量来测试残差的白度。只要大多数点都在蓝色虚线之上,那么你就可以安全地假定噪声是白色的。然而,如果许多点都在线下,那么残差中仍有一些相关性,你应该尝试拟合另一个模型或添加一个参数。
24.3.9 模型选择
使用的数据是astsa自带的
varve,它的介绍:马萨诸塞州一个地方的沉积物有634年,从近12000年前开始。
我们首先画出时间序列:
ts.plot(varve)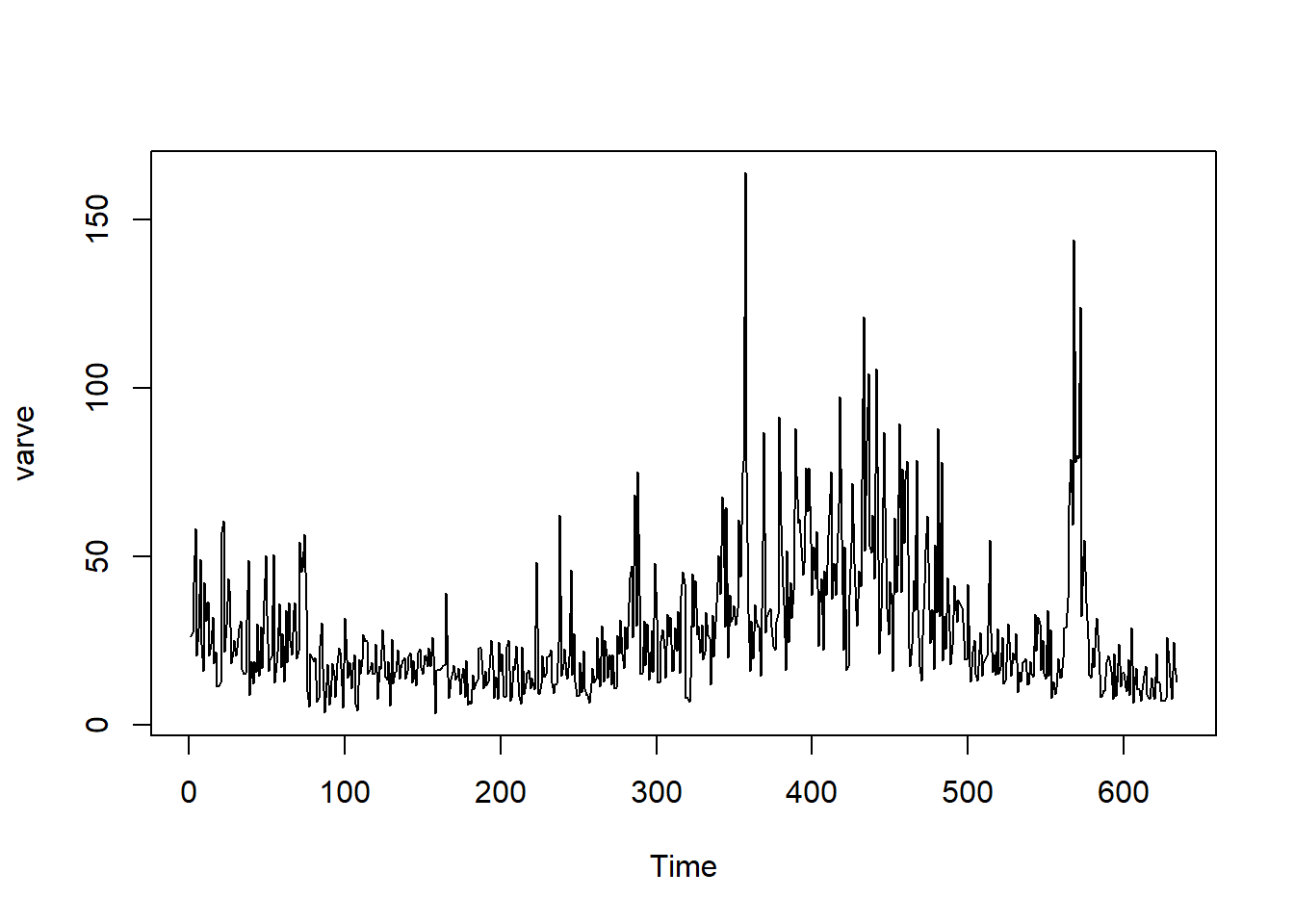
然后选择几个模型,看看AIC和BIC,以及残差图:
# log变换和一阶差分
dl_varve <- diff(log(varve))
# 使用MA(1)
sarima(dl_varve, 0,0,1)## initial value -0.551780
## iter 2 value -0.671633
## iter 3 value -0.706234
## iter 4 value -0.707586
## iter 5 value -0.718543
## iter 6 value -0.719692
## iter 7 value -0.721967
## iter 8 value -0.722970
## iter 9 value -0.723231
## iter 10 value -0.723247
## iter 11 value -0.723248
## iter 12 value -0.723248
## iter 12 value -0.723248
## iter 12 value -0.723248
## final value -0.723248
## converged
## initial value -0.722762
## iter 2 value -0.722764
## iter 3 value -0.722764
## iter 4 value -0.722765
## iter 4 value -0.722765
## iter 4 value -0.722765
## final value -0.722765
## converged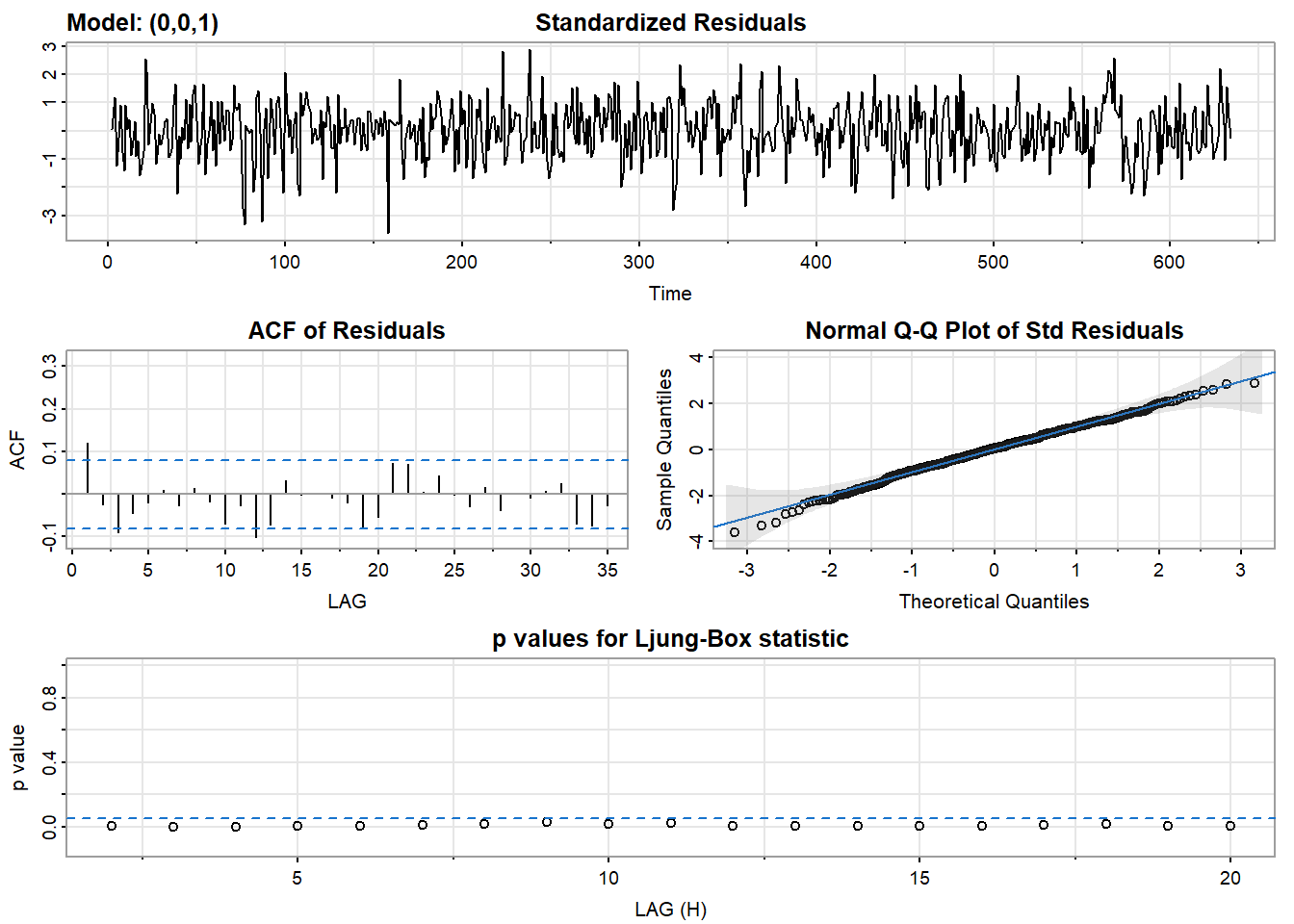
## $fit
##
## Call:
## arima(x = xdata, order = c(p, d, q), seasonal = list(order = c(P, D, Q), period = S),
## xreg = xmean, include.mean = FALSE, transform.pars = trans, fixed = fixed,
## optim.control = list(trace = trc, REPORT = 1, reltol = tol))
##
## Coefficients:
## ma1 xmean
## -0.7710 -0.0013
## s.e. 0.0341 0.0044
##
## sigma^2 estimated as 0.2353: log likelihood = -440.68, aic = 887.36
##
## $degrees_of_freedom
## [1] 631
##
## $ttable
## Estimate SE t.value p.value
## ma1 -0.7710 0.0341 -22.6002 0.0000
## xmean -0.0013 0.0044 -0.2818 0.7782
##
## $AIC
## [1] 1.401826
##
## $AICc
## [1] 1.401856
##
## $BIC
## [1] 1.422918# 使用MA(2)
sarima(dl_varve, 0, 0, 2)## initial value -0.551780
## iter 2 value -0.679736
## iter 3 value -0.728605
## iter 4 value -0.734640
## iter 5 value -0.735449
## iter 6 value -0.735979
## iter 7 value -0.736015
## iter 8 value -0.736059
## iter 9 value -0.736060
## iter 10 value -0.736060
## iter 11 value -0.736061
## iter 12 value -0.736061
## iter 12 value -0.736061
## iter 12 value -0.736061
## final value -0.736061
## converged
## initial value -0.735372
## iter 2 value -0.735378
## iter 3 value -0.735379
## iter 4 value -0.735379
## iter 4 value -0.735379
## iter 4 value -0.735379
## final value -0.735379
## converged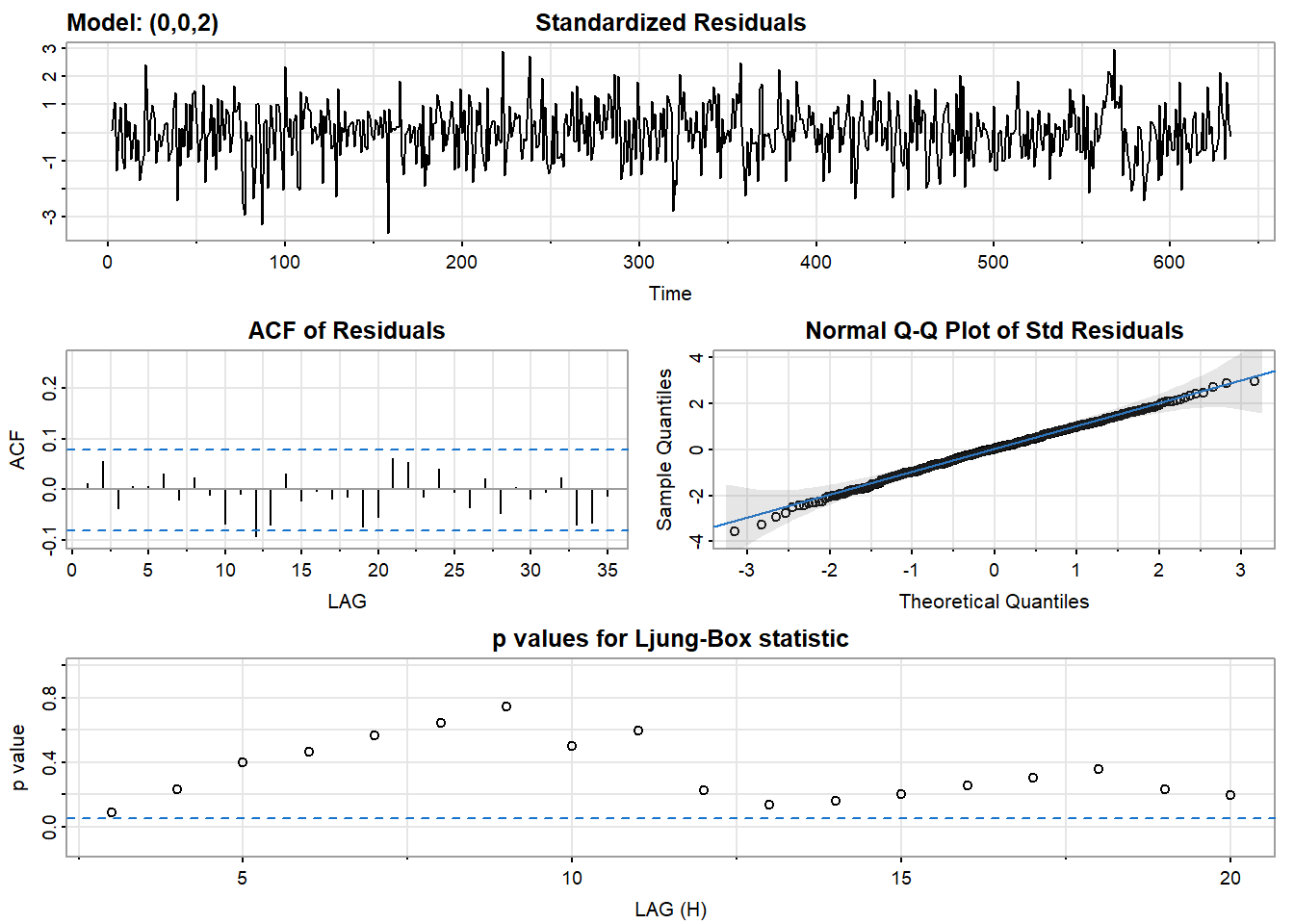
## $fit
##
## Call:
## arima(x = xdata, order = c(p, d, q), seasonal = list(order = c(P, D, Q), period = S),
## xreg = xmean, include.mean = FALSE, transform.pars = trans, fixed = fixed,
## optim.control = list(trace = trc, REPORT = 1, reltol = tol))
##
## Coefficients:
## ma1 ma2 xmean
## -0.6710 -0.1595 -0.0013
## s.e. 0.0375 0.0392 0.0033
##
## sigma^2 estimated as 0.2294: log likelihood = -432.69, aic = 873.39
##
## $degrees_of_freedom
## [1] 630
##
## $ttable
## Estimate SE t.value p.value
## ma1 -0.6710 0.0375 -17.9057 0.0000
## ma2 -0.1595 0.0392 -4.0667 0.0001
## xmean -0.0013 0.0033 -0.4007 0.6888
##
## $AIC
## [1] 1.379757
##
## $AICc
## [1] 1.379817
##
## $BIC
## [1] 1.40788# 使用ARMA(1,1),有提升吗?
sarima(dl_varve, 1, 0, 1)## initial value -0.550994
## iter 2 value -0.648962
## iter 3 value -0.676965
## iter 4 value -0.699167
## iter 5 value -0.724554
## iter 6 value -0.726719
## iter 7 value -0.729066
## iter 8 value -0.731976
## iter 9 value -0.734235
## iter 10 value -0.735969
## iter 11 value -0.736410
## iter 12 value -0.737045
## iter 13 value -0.737600
## iter 14 value -0.737641
## iter 15 value -0.737643
## iter 16 value -0.737643
## iter 17 value -0.737643
## iter 18 value -0.737643
## iter 18 value -0.737643
## iter 18 value -0.737643
## final value -0.737643
## converged
## initial value -0.737522
## iter 2 value -0.737527
## iter 3 value -0.737528
## iter 4 value -0.737529
## iter 5 value -0.737530
## iter 5 value -0.737530
## iter 5 value -0.737530
## final value -0.737530
## converged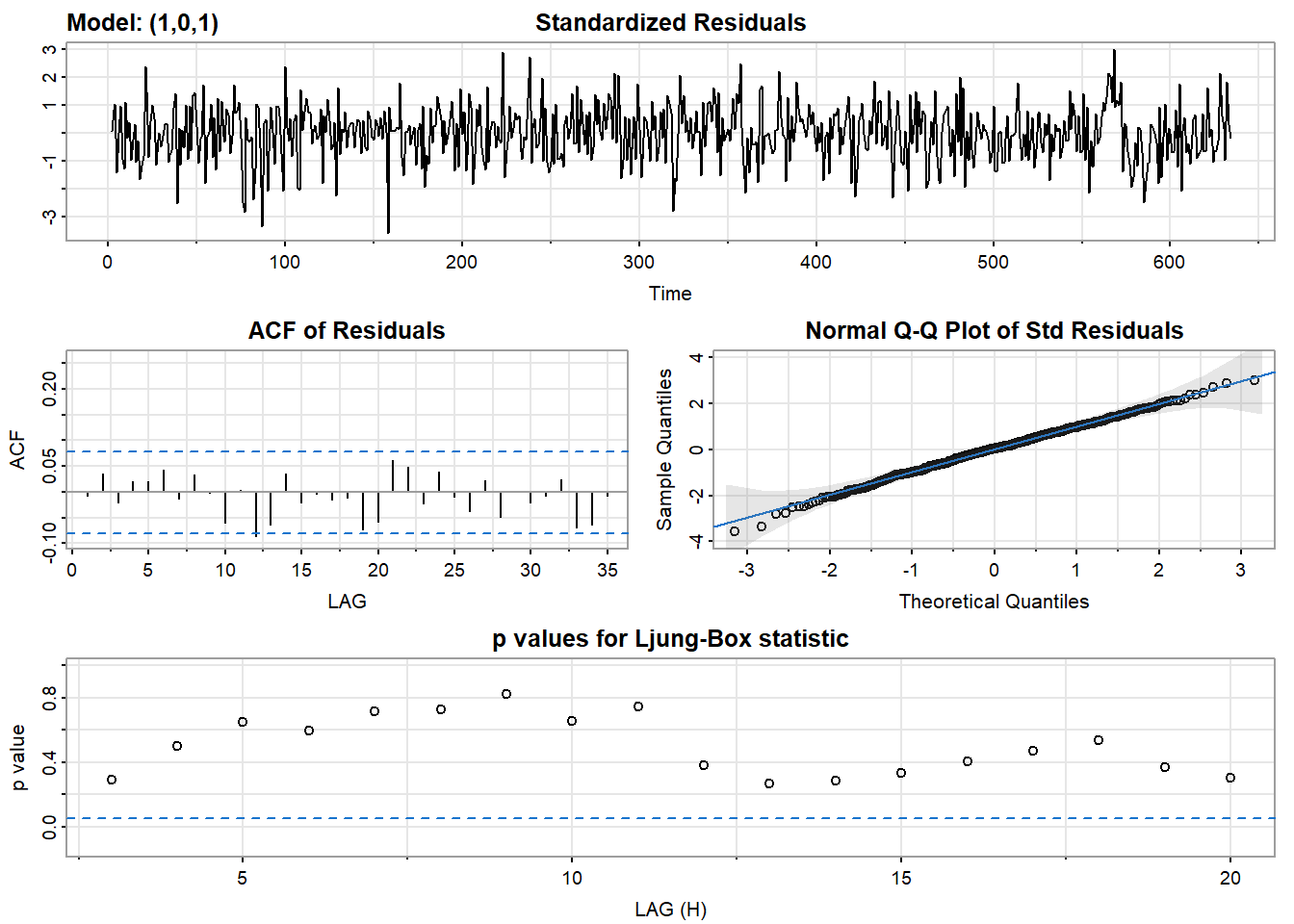
## $fit
##
## Call:
## arima(x = xdata, order = c(p, d, q), seasonal = list(order = c(P, D, Q), period = S),
## xreg = xmean, include.mean = FALSE, transform.pars = trans, fixed = fixed,
## optim.control = list(trace = trc, REPORT = 1, reltol = tol))
##
## Coefficients:
## ar1 ma1 xmean
## 0.2341 -0.8871 -0.0013
## s.e. 0.0518 0.0292 0.0028
##
## sigma^2 estimated as 0.2284: log likelihood = -431.33, aic = 870.66
##
## $degrees_of_freedom
## [1] 630
##
## $ttable
## Estimate SE t.value p.value
## ar1 0.2341 0.0518 4.5184 0.0000
## ma1 -0.8871 0.0292 -30.4107 0.0000
## xmean -0.0013 0.0028 -0.4618 0.6444
##
## $AIC
## [1] 1.375456
##
## $AICc
## [1] 1.375517
##
## $BIC
## [1] 1.403579结论:用MA(1)拟合的残差不是白噪声,ARMA(1,1)模型拟合的残差更像是白噪声.
24.3.10 integrated ARMA
如果一个时间序列(d阶)差分后是\(ARMA(p,q)\),那么这个时间序列被称作\(ARMA(p,d,q)\) 例如: \[ Y_t = 0.9Y_{t-1}+\epsilon _{t} \] 其中\(Y_t =\bigtriangledown X_{t} = X_{t}-X_{t-1}\),在这个情况下, \(\left \{ X_{t} \right \}\)是\(ARIMA(1,1,0)\)模型,因为它一阶差分后是一阶的AR模型.我们用软件生成对应模型的数据,并分析其自相关图:
x <- arima.sim(model = list(order = c(1, 1, 0), ar = .9), n = 200)
# 原始序列
plot(x)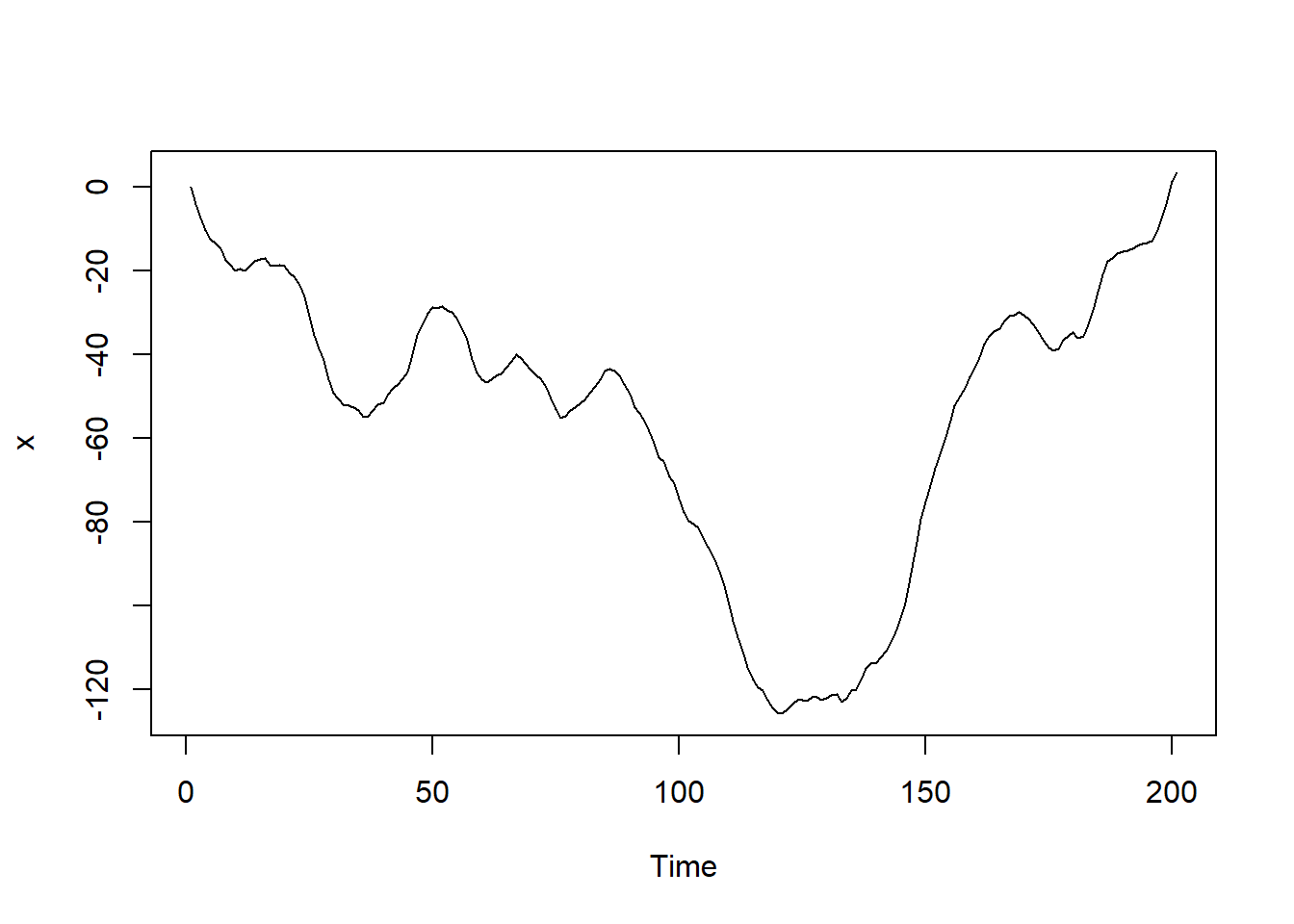
# 查看自相关图和偏自相关图
acf2(x)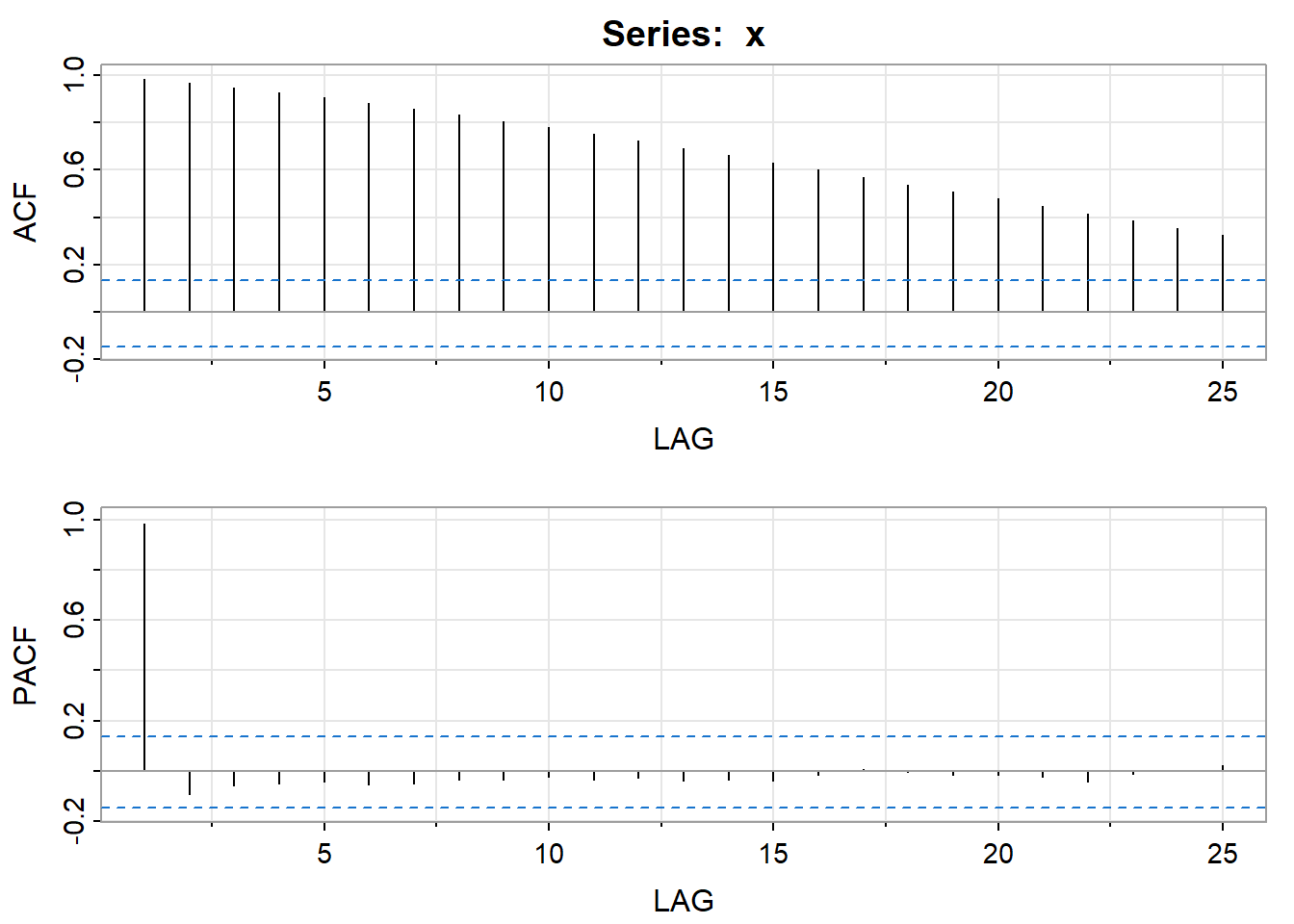
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
## ACF 0.98 0.97 0.95 0.93 0.91 0.88 0.86 0.83 0.81 0.78 0.75 0.72
## PACF 0.98 -0.09 -0.06 -0.05 -0.04 -0.05 -0.05 -0.03 -0.04 -0.02 -0.04 -0.03
## [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24]
## ACF 0.69 0.66 0.63 0.60 0.57 0.54 0.51 0.48 0.45 0.42 0.39 0.36
## PACF -0.04 -0.04 -0.04 -0.02 0.01 0.00 -0.02 -0.01 -0.02 -0.04 -0.01 0.00
## [,25]
## ACF 0.33
## PACF 0.02# 一阶差分后的序列
plot(diff(x))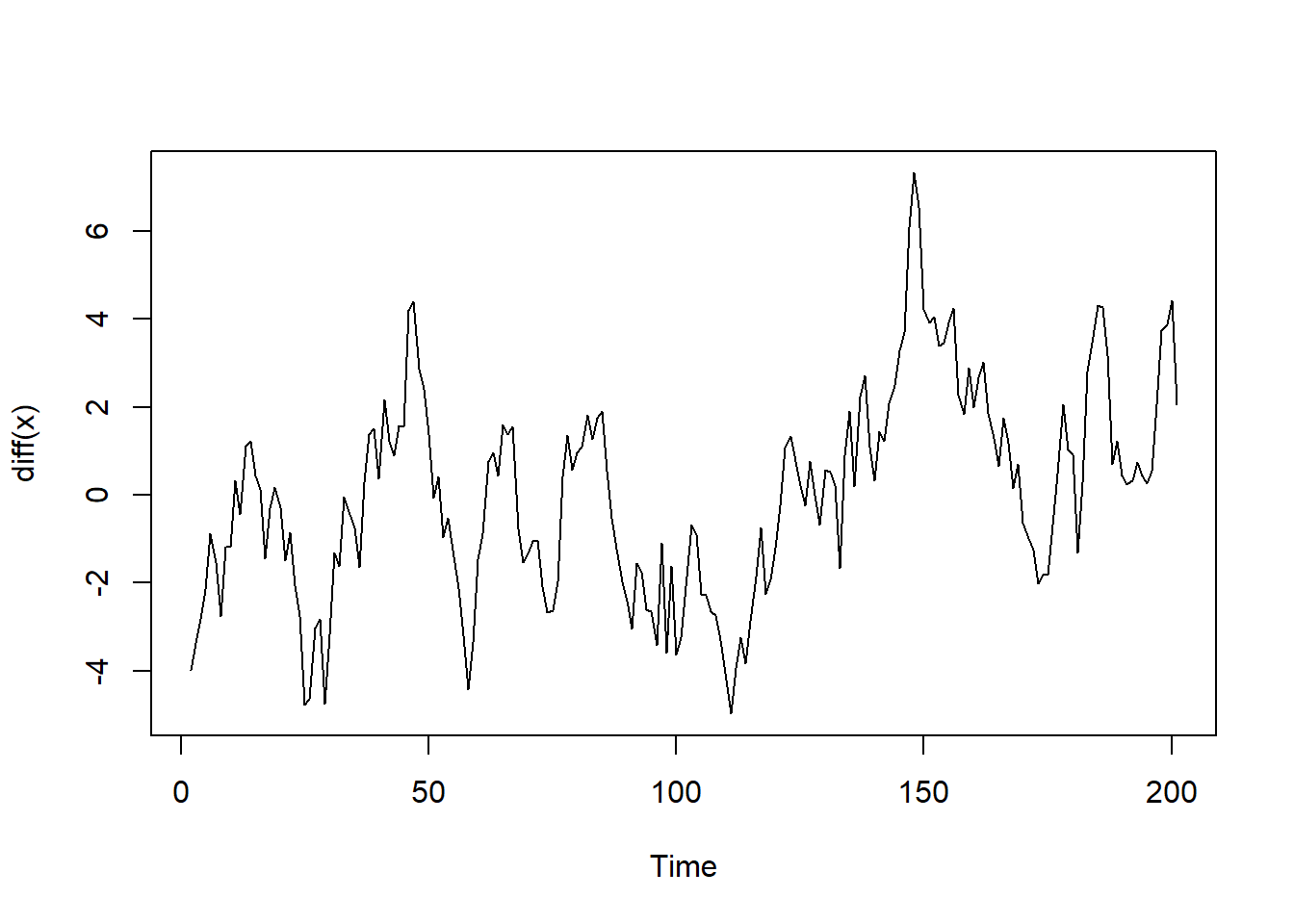
# 一阶差分后的自相关图和偏自相关图
acf2(diff(x))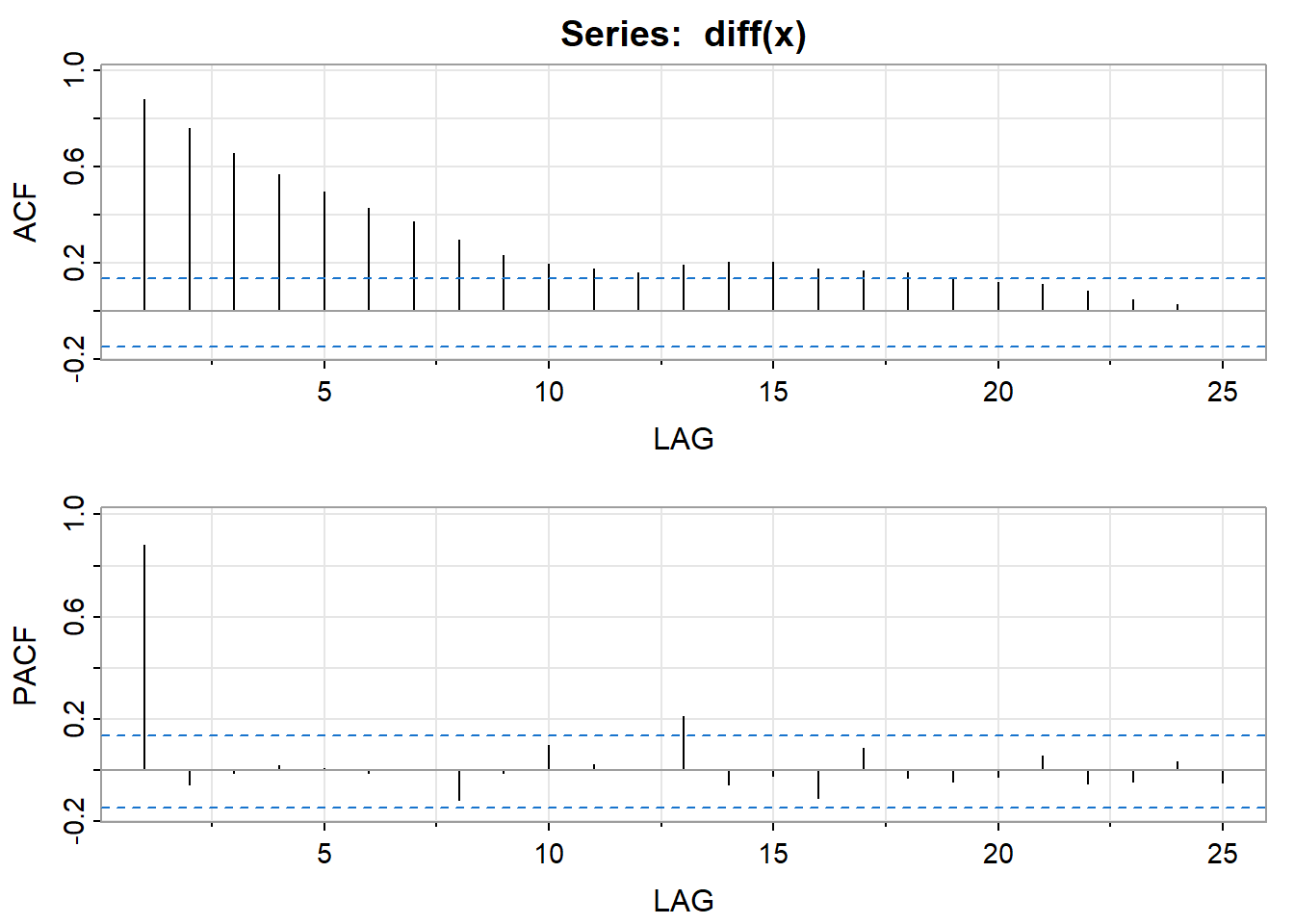
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
## ACF 0.88 0.76 0.66 0.57 0.50 0.43 0.37 0.30 0.23 0.2 0.18 0.16 0.19
## PACF 0.88 -0.06 -0.01 0.02 0.01 -0.01 0.00 -0.11 -0.01 0.1 0.02 0.00 0.21
## [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25]
## ACF 0.21 0.21 0.18 0.17 0.16 0.14 0.12 0.11 0.09 0.05 0.03 0.00
## PACF -0.06 -0.02 -0.11 0.09 -0.03 -0.04 -0.03 0.06 -0.05 -0.04 0.03 -0.05利用astsa包提供的globtemp(the annual global temperature deviations to 2015)数据来分析:
# 查看原始序列
plot(globtemp)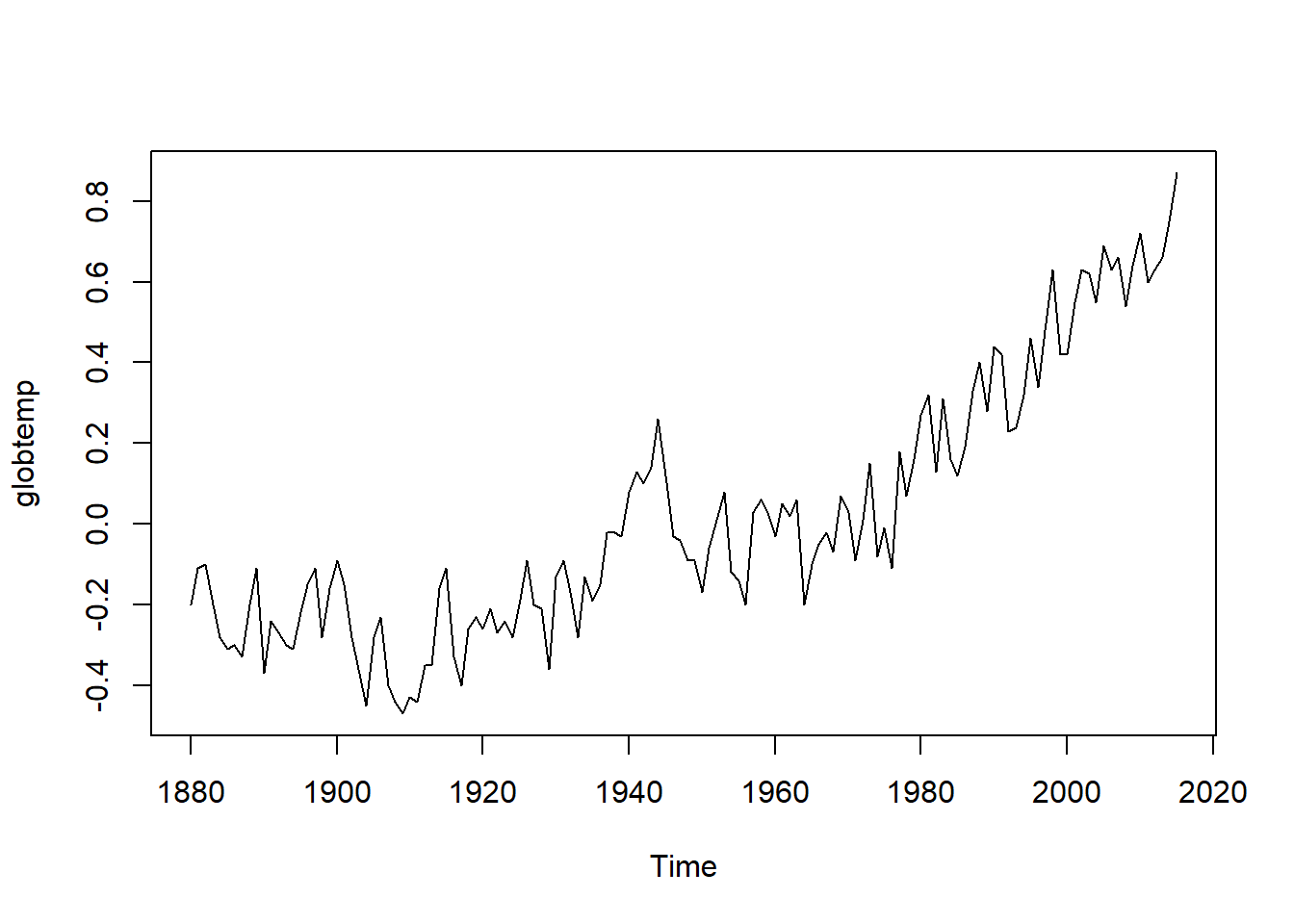
acf2(diff(globtemp))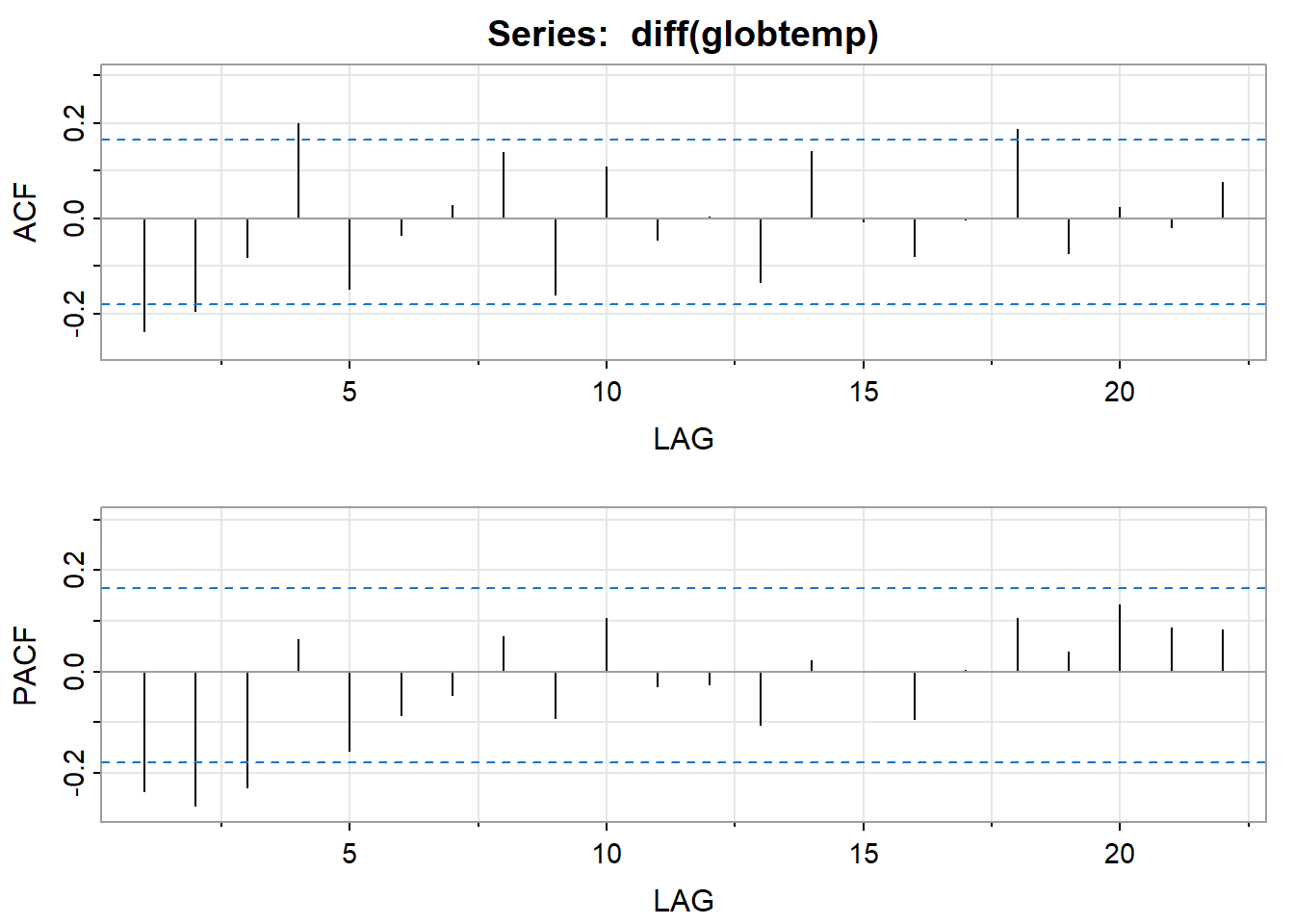
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
## ACF -0.24 -0.19 -0.08 0.20 -0.15 -0.03 0.03 0.14 -0.16 0.11 -0.05 0.00
## PACF -0.24 -0.26 -0.23 0.06 -0.16 -0.09 -0.05 0.07 -0.09 0.11 -0.03 -0.02
## [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22]
## ACF -0.13 0.14 -0.01 -0.08 0 0.19 -0.07 0.02 -0.02 0.08
## PACF -0.10 0.02 0.00 -0.09 0 0.11 0.04 0.13 0.09 0.08# 使用ARIMA(1,1,1)拟合
sarima(globtemp, 1,1,1)## initial value -2.218917
## iter 2 value -2.253118
## iter 3 value -2.263750
## iter 4 value -2.272144
## iter 5 value -2.282786
## iter 6 value -2.296777
## iter 7 value -2.297062
## iter 8 value -2.297253
## iter 9 value -2.297389
## iter 10 value -2.297405
## iter 11 value -2.297413
## iter 12 value -2.297413
## iter 13 value -2.297414
## iter 13 value -2.297414
## iter 13 value -2.297414
## final value -2.297414
## converged
## initial value -2.305504
## iter 2 value -2.305800
## iter 3 value -2.305821
## iter 4 value -2.306655
## iter 5 value -2.306875
## iter 6 value -2.306950
## iter 7 value -2.306955
## iter 8 value -2.306955
## iter 8 value -2.306955
## final value -2.306955
## converged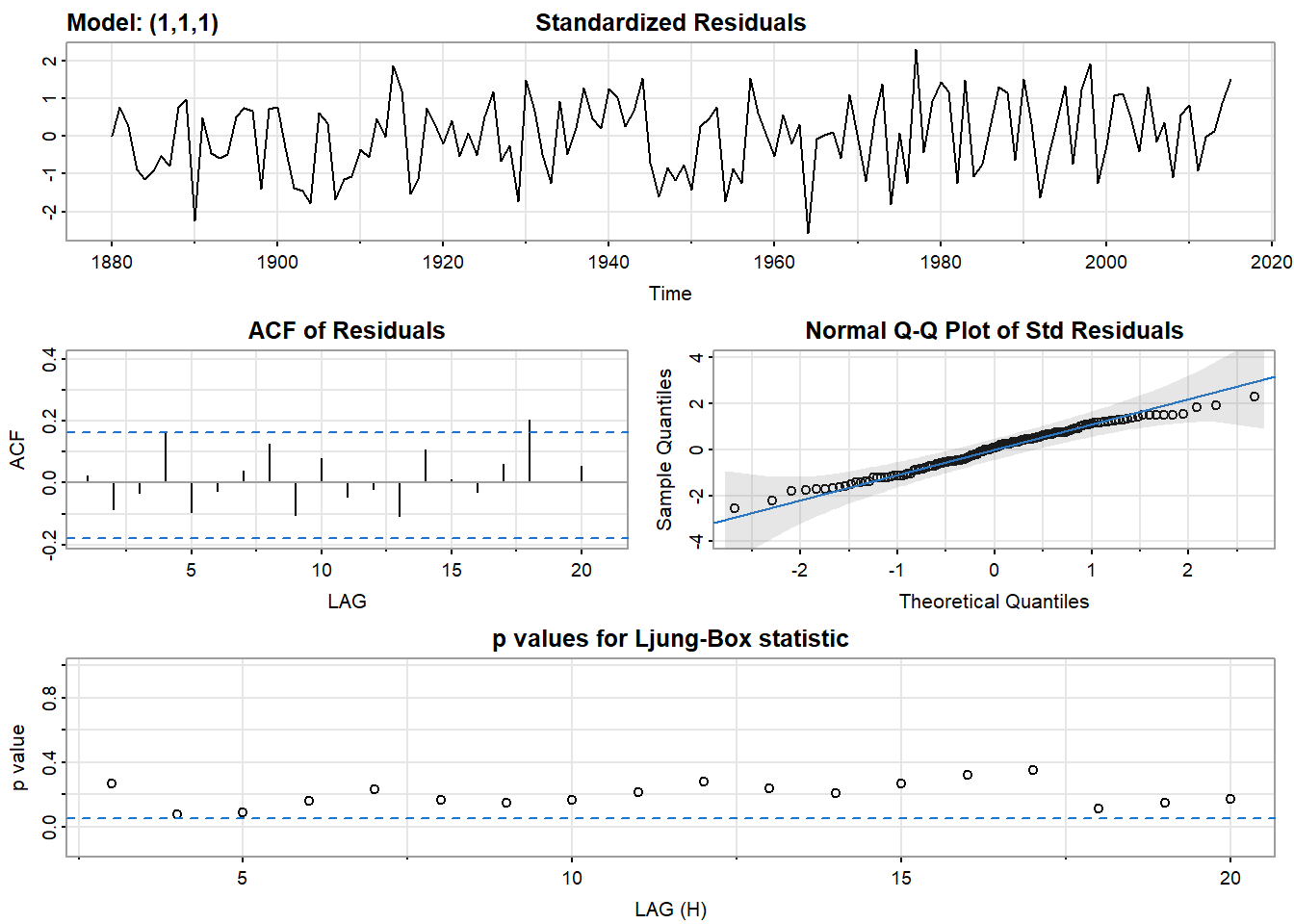
## $fit
##
## Call:
## arima(x = xdata, order = c(p, d, q), seasonal = list(order = c(P, D, Q), period = S),
## xreg = constant, transform.pars = trans, fixed = fixed, optim.control = list(trace = trc,
## REPORT = 1, reltol = tol))
##
## Coefficients:
## ar1 ma1 constant
## 0.3549 -0.7663 0.0072
## s.e. 0.1314 0.0874 0.0032
##
## sigma^2 estimated as 0.009885: log likelihood = 119.88, aic = -231.76
##
## $degrees_of_freedom
## [1] 132
##
## $ttable
## Estimate SE t.value p.value
## ar1 0.3549 0.1314 2.7008 0.0078
## ma1 -0.7663 0.0874 -8.7701 0.0000
## constant 0.0072 0.0032 2.2738 0.0246
##
## $AIC
## [1] -1.716773
##
## $AICc
## [1] -1.715416
##
## $BIC
## [1] -1.630691# 使用ARIMA(0,1,2)拟合,哪个更好?
sarima(globtemp, 0, 1, 2)## initial value -2.220513
## iter 2 value -2.294887
## iter 3 value -2.307682
## iter 4 value -2.309170
## iter 5 value -2.310360
## iter 6 value -2.311251
## iter 7 value -2.311636
## iter 8 value -2.311648
## iter 9 value -2.311649
## iter 9 value -2.311649
## iter 9 value -2.311649
## final value -2.311649
## converged
## initial value -2.310187
## iter 2 value -2.310197
## iter 3 value -2.310199
## iter 4 value -2.310201
## iter 5 value -2.310202
## iter 5 value -2.310202
## iter 5 value -2.310202
## final value -2.310202
## converged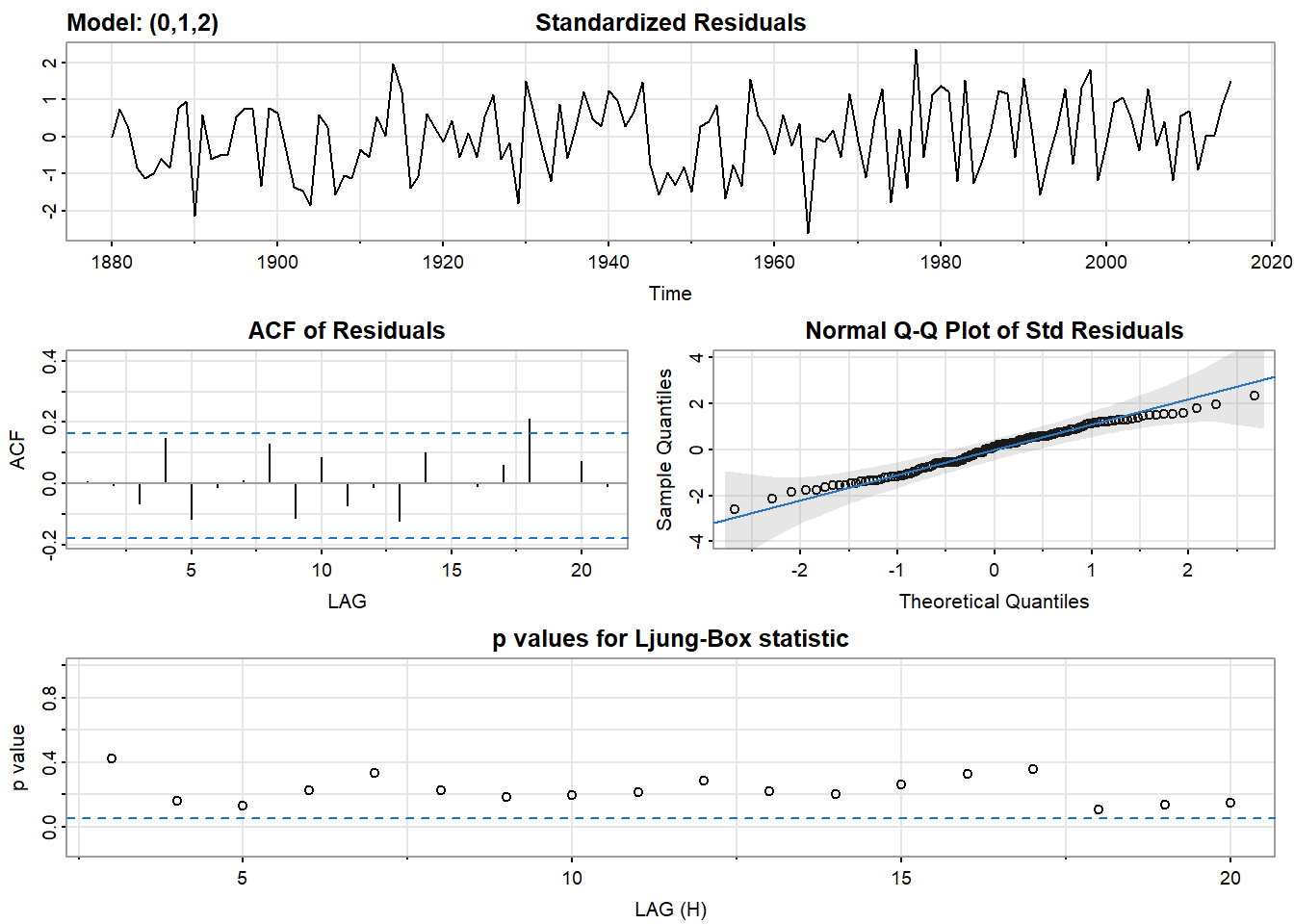
## $fit
##
## Call:
## arima(x = xdata, order = c(p, d, q), seasonal = list(order = c(P, D, Q), period = S),
## xreg = constant, transform.pars = trans, fixed = fixed, optim.control = list(trace = trc,
## REPORT = 1, reltol = tol))
##
## Coefficients:
## ma1 ma2 constant
## -0.3984 -0.2173 0.0072
## s.e. 0.0808 0.0768 0.0033
##
## sigma^2 estimated as 0.00982: log likelihood = 120.32, aic = -232.64
##
## $degrees_of_freedom
## [1] 132
##
## $ttable
## Estimate SE t.value p.value
## ma1 -0.3984 0.0808 -4.9313 0.0000
## ma2 -0.2173 0.0768 -2.8303 0.0054
## constant 0.0072 0.0033 2.1463 0.0337
##
## $AIC
## [1] -1.723268
##
## $AICc
## [1] -1.721911
##
## $BIC
## [1] -1.63718524.3.11 预测
简略的介绍
我们使用astsa包里面的sarima.for()来进行预测,文档.我们使用的数据也是astsa包的oil(原油,WTI现货价格FOB(单位:美元/桶),2000年至2010年中期的每周数据。)
预测有个问题就是,我们只取前面一大部分,想让最后一小部分实际值与我们的预测的进行对照,但是时间序列本身有时间做限制,取子集很困难,我们可以利用window()函数来做到这一点.
# 前面大部分实际数据
oilt <- window(oil, end = 2006)
oilf <- window(oil, end = 2007)
sarima.for(oilt, n.ahead = 52, 1, 1, 1)
## $pred
## Time Series:
## Start = c(2006, 2)
## End = c(2007, 1)
## Frequency = 52
## [1] 60.71882 60.43909 60.74214 60.75455 60.91190 60.99696 61.11808 61.22122
## [9] 61.33332 61.44095 61.55081 61.65956 61.76887 61.87790 61.98706 62.09616
## [17] 62.20529 62.31441 62.42353 62.53265 62.64177 62.75089 62.86001 62.96913
## [25] 63.07825 63.18737 63.29649 63.40561 63.51473 63.62385 63.73297 63.84209
## [33] 63.95121 64.06033 64.16945 64.27857 64.38769 64.49681 64.60593 64.71505
## [41] 64.82417 64.93329 65.04241 65.15153 65.26065 65.36977 65.47889 65.58801
## [49] 65.69713 65.80625 65.91537 66.02449
##
## $se
## Time Series:
## Start = c(2006, 2)
## End = c(2007, 1)
## Frequency = 52
## [1] 1.430557 2.270997 2.776644 3.245575 3.636008 3.996918 4.323903
## [8] 4.629671 4.915600 5.186193 5.443159 5.688620 5.923876 6.150160
## [15] 6.368398 6.579407 6.783853 6.982317 7.175292 7.363212 7.546454
## [22] 7.725351 7.900198 8.071258 8.238767 8.402937 8.563961 8.722013
## [29] 8.877251 9.029820 9.179855 9.327476 9.472797 9.615922 9.756948
## [36] 9.895965 10.033055 10.168297 10.301764 10.433524 10.563640 10.692173
## [43] 10.819180 10.944712 11.068821 11.191554 11.312955 11.433067 11.551931
## [50] 11.669584 11.786062 11.901401
lines(oilf)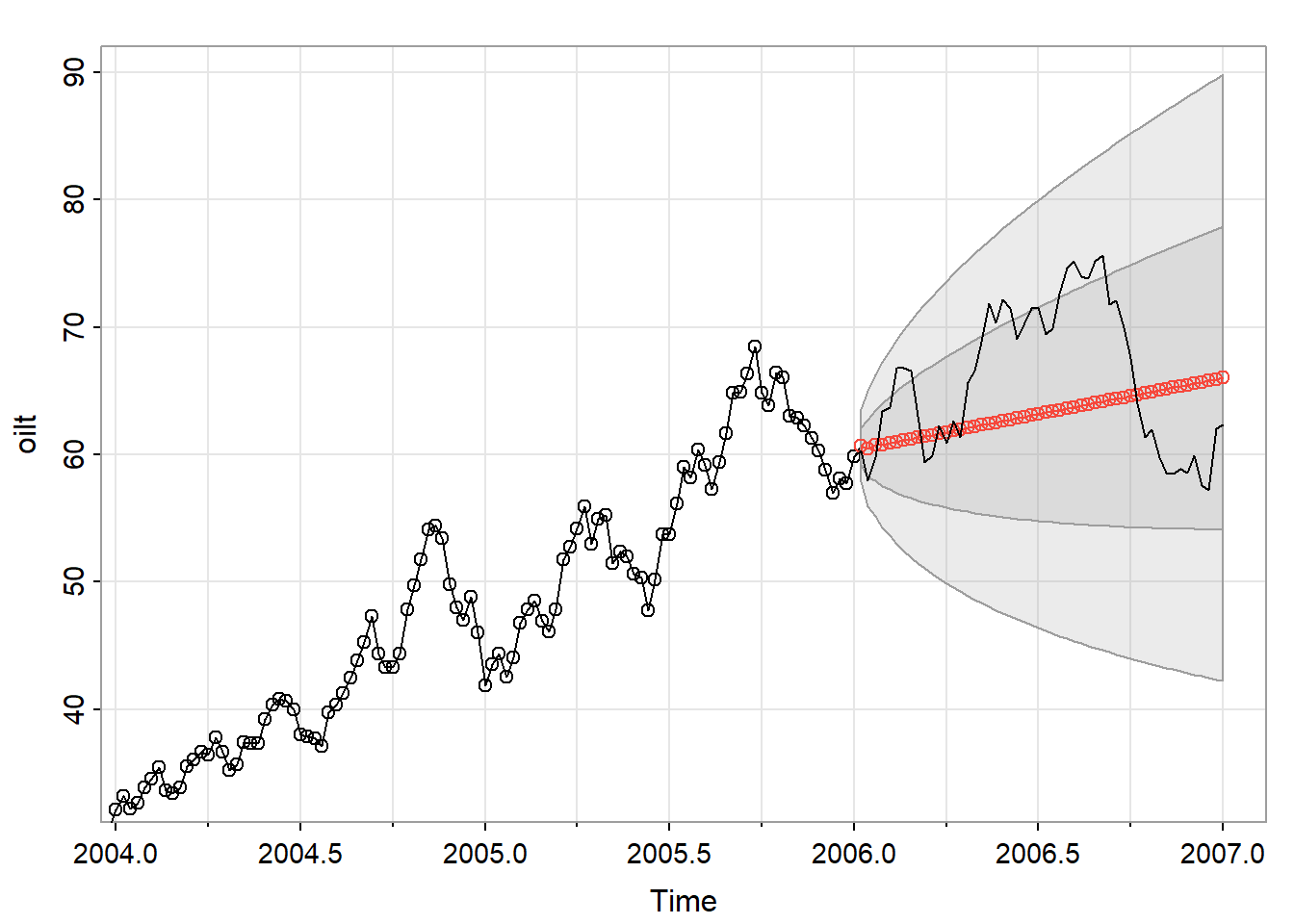
24.4 季节性模型
\[ \begin{matrix} \operatorname{ARIMA} & \underbrace{(p, d, q)}_{\uparrow} & \underbrace{(P, D, Q)_{s}}_{\uparrow} \\ & \left(\begin{array}{l} \text { Non-seasonal part } \\ \text { of the model } \end{array}\right) & \left(\begin{array}{l} \text { Seasonal part } \\ \text { of the model } \end{array}\right) \end{matrix} \]
24.4.1 季节性ARMA模型特征
| 模型 | 自相关系数 | 偏自相关系数 |
|---|---|---|
| SAR(p)s | 拖尾 | ps阶截尾 |
| SMA(q)s | qs阶截尾 | 拖尾 |
| SARMA(p, q)s | 拖尾 | 拖尾 |
一阶的季节性(频率为12)的AR模型,可以表示成如下形式
\[ \left(1-\phi B^{12}\right) y_{t}=\epsilon _{t} \]
或者 \[ y_{t}=\phi y_{t-12}+\epsilon _{t} \]
我们可以生成下面的数据 > 例子来自P146 Time Series Analysis and Its Applications With R by Robert H.Shumway and David S.Stoffer
set.seed(666)
# 参数设置和时间序列创建
phi <- c(rep(0,11),.9)
sAR <- arima.sim(list(order=c(12,0,0), ar=phi), n=37)
sAR <- ts(sAR, freq=12)
# 图形设置,不熟悉
layout(matrix(c(1,1,2, 1,1,3), nc=2))
par(mar=c(3,3,2,1), mgp=c(1.6,.6,0))
# 时间序列图
plot(sAR, axes=FALSE, main='seasonal AR(1)', xlab="year", type='c')
Months <- c("J","F","M","A","M","J","J","A","S","O","N","D")
points(sAR, pch=Months, cex=1.25, font=4, col=1:4)
axis(1, 1:4); abline(v=1:4, lty=2, col=gray(.7))
axis(2); box()
# 自相关与偏自相关图
ACF <- ARMAacf(ar=phi, ma=0, 100)
PACF <- ARMAacf(ar=phi, ma=0, 100, pacf=TRUE)
plot(ACF,type="h", xlab="LAG", ylim=c(-.1,1)); abline(h=0)
plot(PACF, type="h", xlab="LAG", ylim=c(-.1,1)); abline(h=0)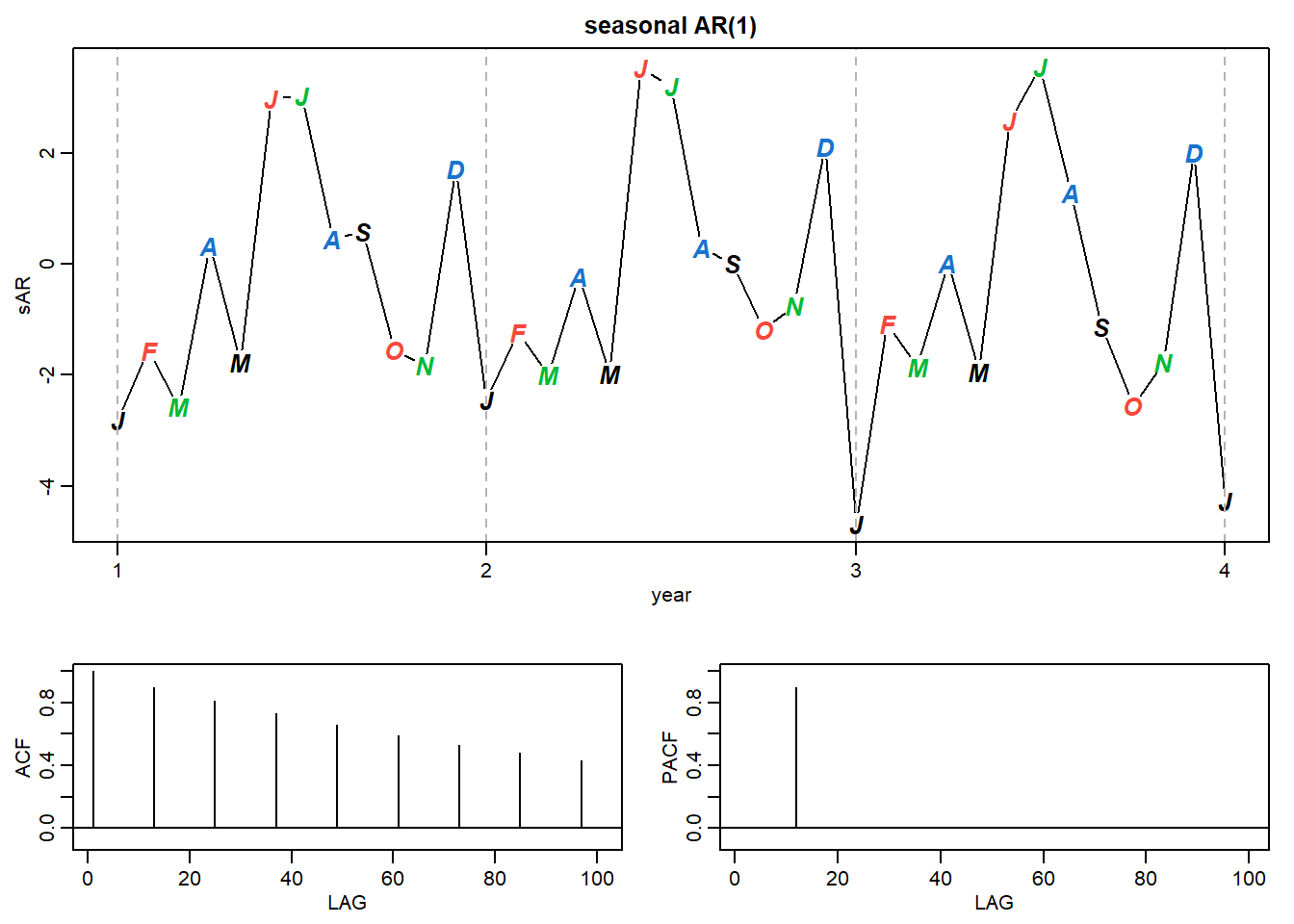
24.4.3 混合季节性模型
数据集unemp(monthly US unemployment)
plot(unemp)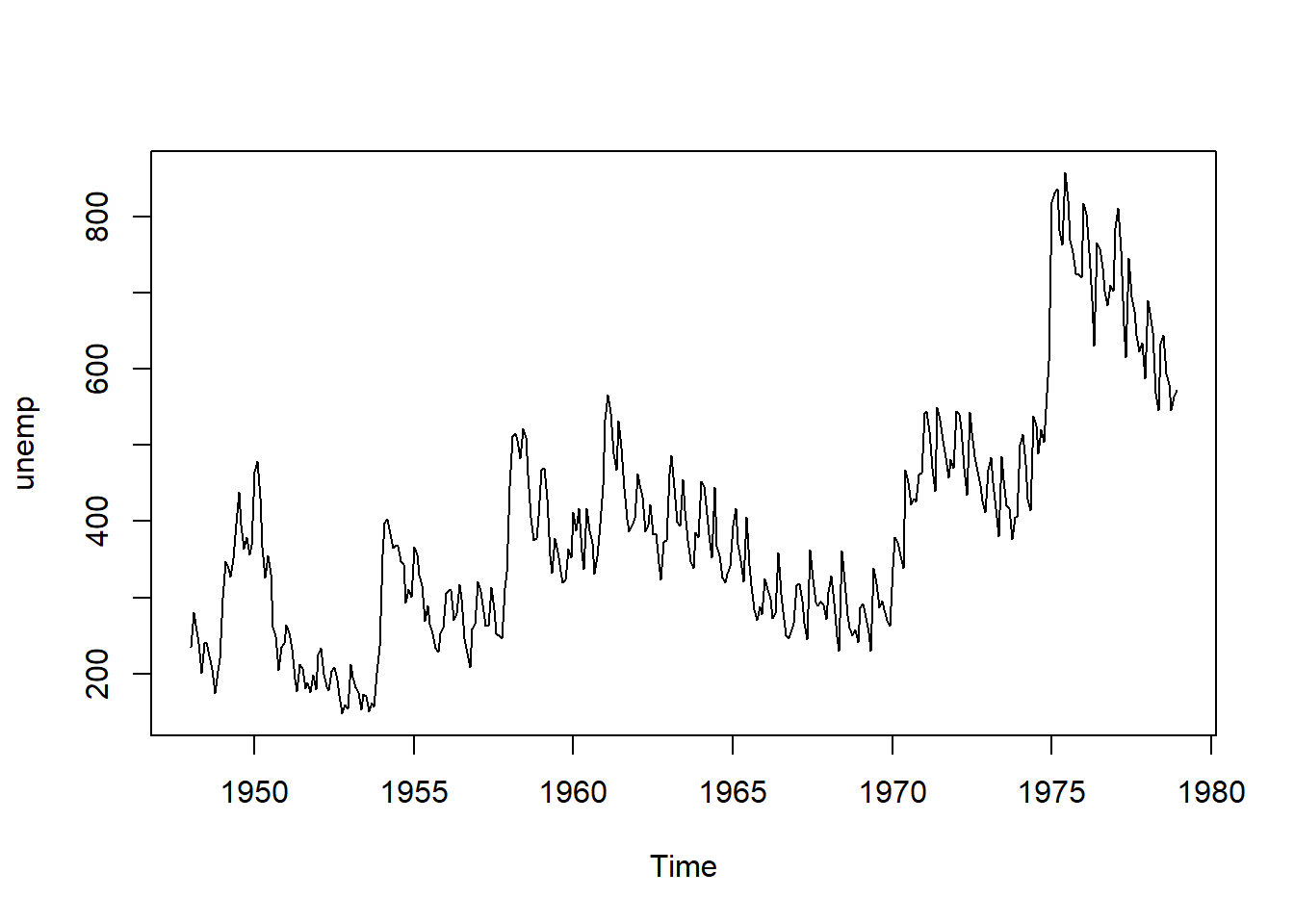
dd_unemp <- diff(diff(unemp), lag = 12)
acf2(dd_unemp, max.lag = 60)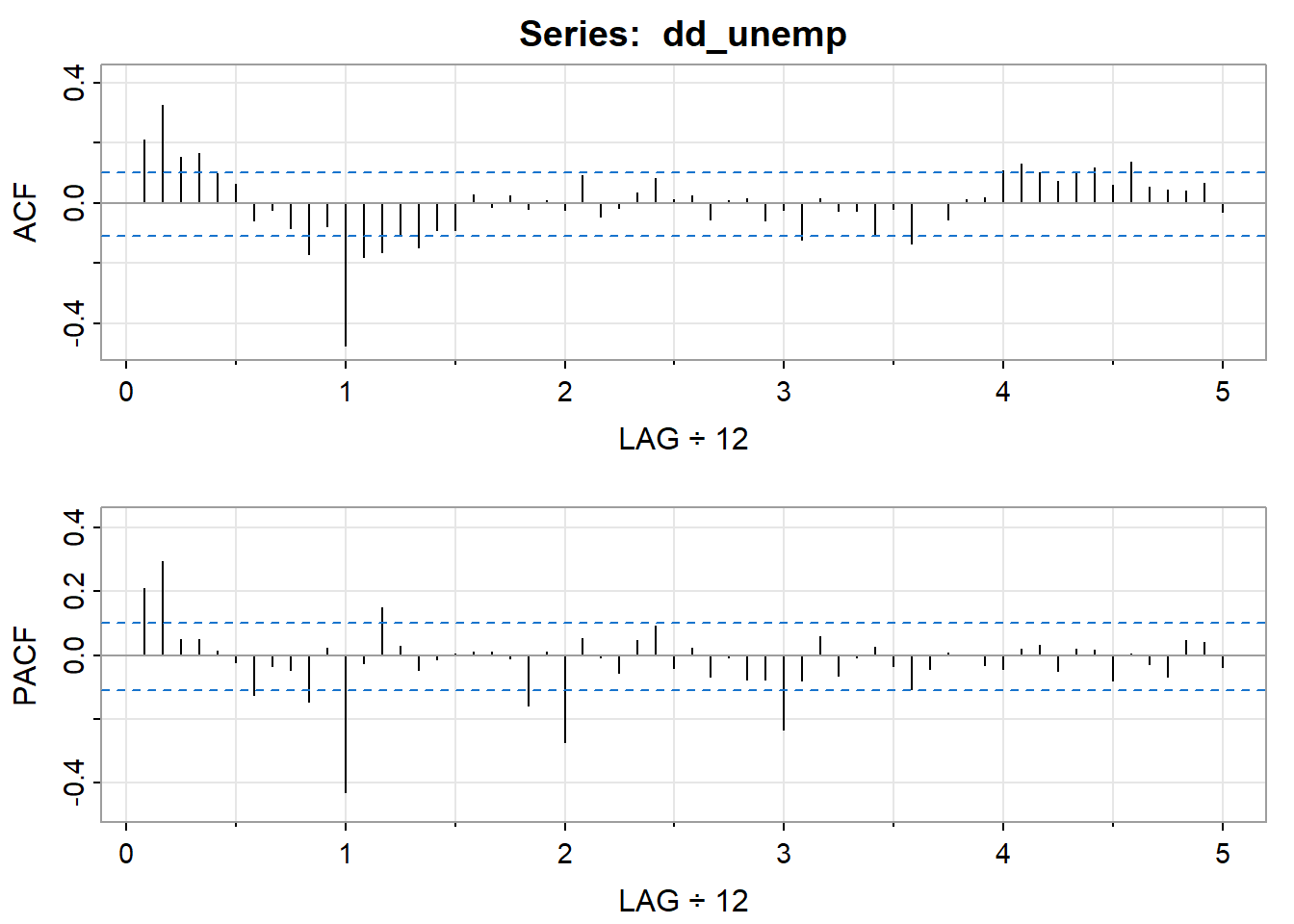
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
## ACF 0.21 0.33 0.15 0.17 0.10 0.06 -0.06 -0.02 -0.09 -0.17 -0.08 -0.48 -0.18
## PACF 0.21 0.29 0.05 0.05 0.01 -0.02 -0.12 -0.03 -0.05 -0.15 0.02 -0.43 -0.02
## [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25]
## ACF -0.16 -0.11 -0.15 -0.09 -0.09 0.03 -0.01 0.02 -0.02 0.01 -0.02 0.09
## PACF 0.15 0.03 -0.04 -0.01 0.00 0.01 0.01 -0.01 -0.16 0.01 -0.27 0.05
## [,26] [,27] [,28] [,29] [,30] [,31] [,32] [,33] [,34] [,35] [,36] [,37]
## ACF -0.05 -0.01 0.03 0.08 0.01 0.03 -0.05 0.01 0.02 -0.06 -0.02 -0.12
## PACF -0.01 -0.05 0.05 0.09 -0.04 0.02 -0.07 -0.01 -0.08 -0.08 -0.23 -0.08
## [,38] [,39] [,40] [,41] [,42] [,43] [,44] [,45] [,46] [,47] [,48] [,49]
## ACF 0.01 -0.03 -0.03 -0.10 -0.02 -0.13 0.00 -0.06 0.01 0.02 0.11 0.13
## PACF 0.06 -0.07 -0.01 0.03 -0.03 -0.11 -0.04 0.01 0.00 -0.03 -0.04 0.02
## [,50] [,51] [,52] [,53] [,54] [,55] [,56] [,57] [,58] [,59] [,60]
## ACF 0.10 0.07 0.10 0.12 0.06 0.14 0.05 0.04 0.04 0.07 -0.03
## PACF 0.03 -0.05 0.02 0.02 -0.08 0.00 -0.03 -0.07 0.05 0.04 -0.04
# 挑选合适的模型
sarima(unemp, p = 2, d = 1, q = 0, P = 0, D = 1, Q = 1, S = 12)
## initial value 3.340809
## iter 2 value 3.105512
## iter 3 value 3.086631
## iter 4 value 3.079778
## iter 5 value 3.069447
## iter 6 value 3.067659
## iter 7 value 3.067426
## iter 8 value 3.067418
## iter 8 value 3.067418
## final value 3.067418
## converged
## initial value 3.065481
## iter 2 value 3.065478
## iter 3 value 3.065477
## iter 3 value 3.065477
## iter 3 value 3.065477
## final value 3.065477
## converged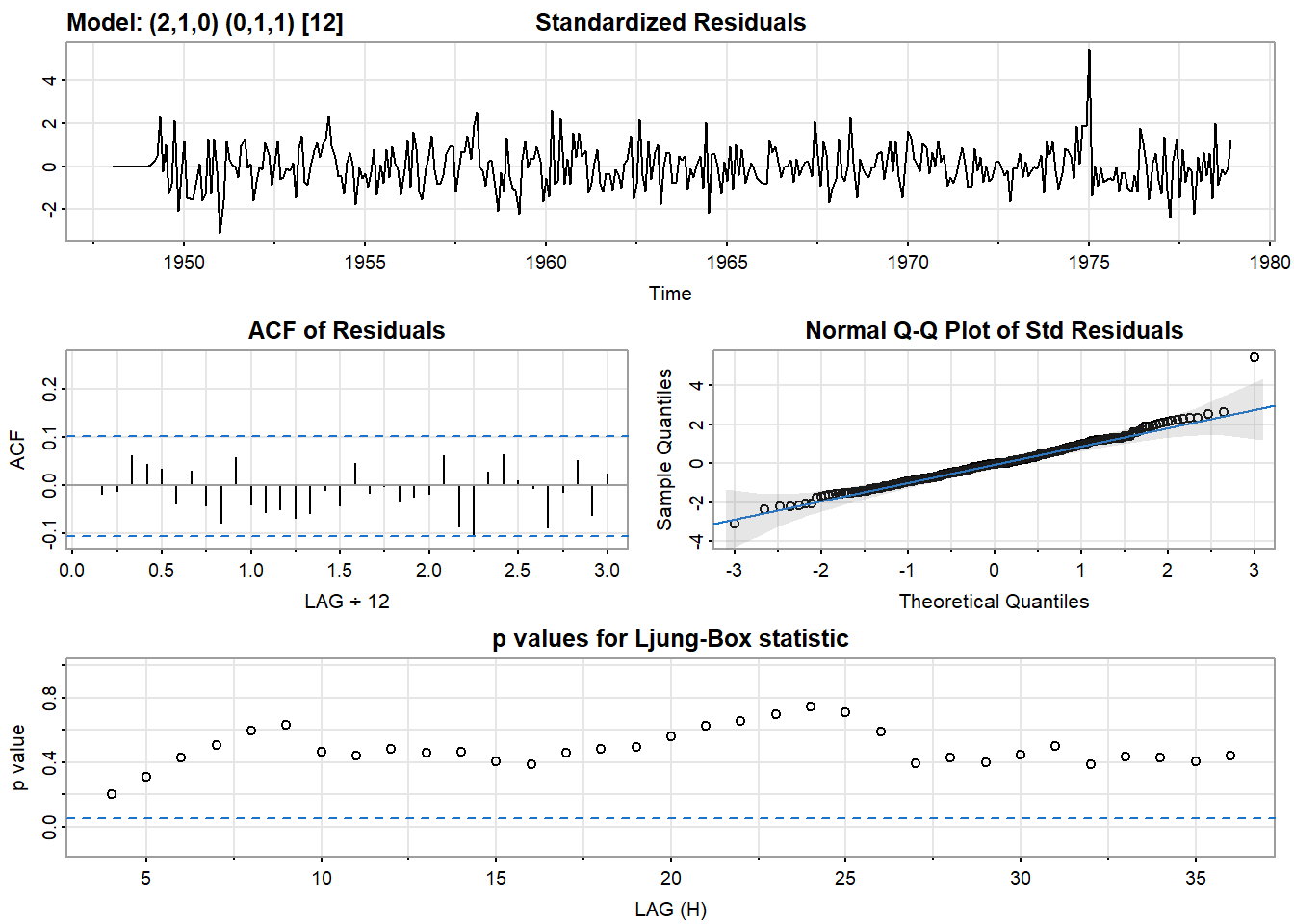
## $fit
##
## Call:
## arima(x = xdata, order = c(p, d, q), seasonal = list(order = c(P, D, Q), period = S),
## include.mean = !no.constant, transform.pars = trans, fixed = fixed, optim.control = list(trace = trc,
## REPORT = 1, reltol = tol))
##
## Coefficients:
## ar1 ar2 sma1
## 0.1351 0.2464 -0.6953
## s.e. 0.0513 0.0515 0.0381
##
## sigma^2 estimated as 449.6: log likelihood = -1609.91, aic = 3227.81
##
## $degrees_of_freedom
## [1] 356
##
## $ttable
## Estimate SE t.value p.value
## ar1 0.1351 0.0513 2.6326 0.0088
## ar2 0.2464 0.0515 4.7795 0.0000
## sma1 -0.6953 0.0381 -18.2362 0.0000
##
## $AIC
## [1] 8.991114
##
## $AICc
## [1] 8.991303
##
## $BIC
## [1] 9.034383季节性预测与之前是一样的
sarima.for(unemp, n.ahead = 36, p = 2, d = 1, q = 0, P = 0, D = 1, Q = 1, S = 12)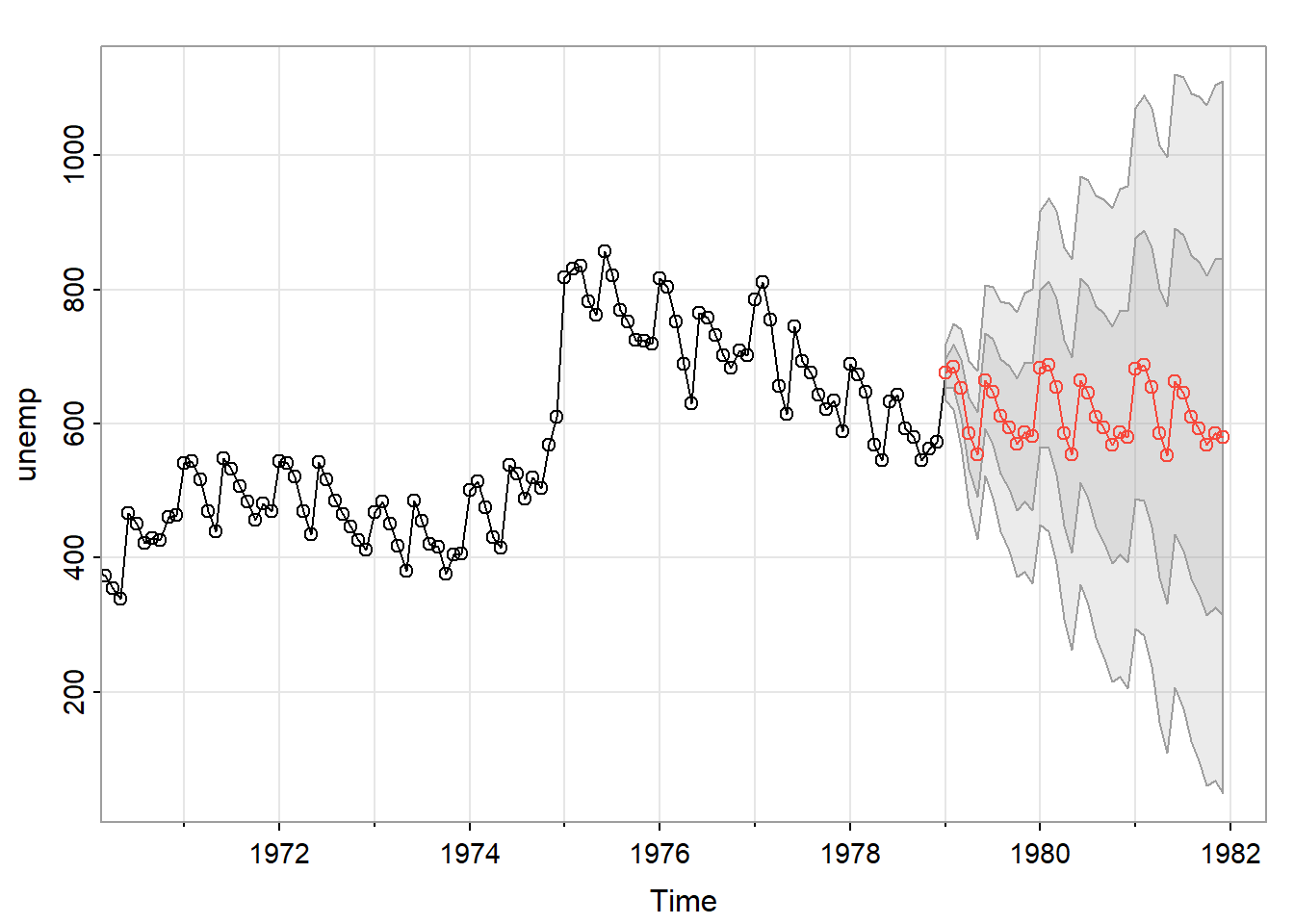
## $pred
## Jan Feb Mar Apr May Jun Jul Aug
## 1979 676.4664 685.1172 653.2388 585.6939 553.8813 664.4072 647.0657 611.0828
## 1980 683.3045 687.7649 654.8658 586.1507 553.9285 664.1108 646.6220 610.5345
## 1981 682.6406 687.0977 654.1968 585.4806 553.2579 663.4398 645.9508 609.8632
## Sep Oct Nov Dec
## 1979 594.6414 569.3997 587.5801 581.1833
## 1980 594.0427 568.7684 586.9320 580.5249
## 1981 593.3713 568.0970 586.2606 579.8535
##
## $se
## Jan Feb Mar Apr May Jun Jul
## 1979 21.20465 32.07710 43.70167 53.66329 62.85364 71.12881 78.73590
## 1980 116.99599 124.17344 131.51281 138.60466 145.49706 152.12863 158.52302
## 1981 194.25167 201.10648 208.17066 215.11503 221.96039 228.64285 235.16874
## Aug Sep Oct Nov Dec
## 1979 85.75096 92.28663 98.41329 104.19488 109.67935
## 1980 164.68623 170.63839 176.39520 181.97333 187.38718
## 1981 241.53258 247.74268 253.80549 259.72970 265.52323