21 Network analysis prediction

网络分析的目的是利用已知节点的特点预测一个未知网络节点属于哪一类。

21.1 具有标签的网络

具有标签的网络(labeled networks)很常见，我们可以从带标签的节点之间的关系去判断没有标签的节点。这里所说的标签其实是节点的属性（attr），标签通常只有两个对立的分类，比如：“喜欢使用R”和“不喜欢使用R”。

该数据是一个客户的社会网络，edgeList数据框的每一行代表网络中的一条边。这个网络中的边是不定向的，权重为1。

# 查看数据
head(edgeList)
##   from   to
## 1    1  393
## 2    1 2573
## 3    1 4430
## 4    2  101
## 5    2  578
## 6    2  691

# 构造igraph对象
network <- graph_from_data_frame(edgeList, directed = FALSE)

# 查看对象
network
## IGRAPH 0ab9427 UN-- 4964 12491 -- 
## + attr: name (v/c)
## + edges from 0ab9427 (vertex names):
##  [1] 1 --393  1 --2573 1 --4430 2 --101  2 --578  2 --691  2 --800  2 --1358
##  [9] 2 --1771 2 --4952 3 --543  3 --551  3 --2051 3 --4835 5 --1322 5 --1611
## [17] 6 --957  6 --1080 6 --1560 6 --4061 6 --4714 7 --25   7 --2029 7 --2061
## [25] 7 --3083 7 --3695 7 --4196 8 --323  8 --476  8 --3338 8 --3387 8 --3950
## [33] 8 --4314 9 --2770 9 --3738 9 --3887 9 --4745 10--1583 10--2641 10--3129
## [41] 10--3722 10--4087 11--2864 11--4061 11--4689 12--217  12--292  12--1360
## [49] 12--1553 12--2463 13--56   13--2939 13--4033 14--874  14--938  14--2407
## [57] 14--2572 14--2764 14--2942 14--3998 14--3999 14--4023 15--2158 15--2536
## + ... omitted several edges

21.1.1 节点添加标签

上面那个关系网是没有节点属性的，下面将使用customers的数据框，其客户ID与网络中的客户ID相同。每个客户都有一个是否流失（churn）的标签，分别用1或0表示。我们可以将这个标签添加到网络中。

head(customers)
##        id churn
## 1       1     0
## 393   393     0
## 2573 2573     0
## 4430 4430     0
## 2       2     0
## 101   101     0

# 流失客户和未流失客户的数量
table(customers$churn)
## 
##    0    1 
## 4190  774

# 添加节点属性(存疑)
V(network)$churn <- customers$churn

21.1.2 不同的标签设置颜色

我们对网络添加好标签之后，自然想到查看流失的客户与非流失的客户在网络是怎么分布的，所以我们绘制图的时候需要针对不同的标签设置不同的颜色。

# 再添加一个节点：颜色
V(network)$color <- V(network)$churn

# 用颜色替换0和1
V(network)$color <- gsub("1", "red", V(network)$color) 
V(network)$color <- gsub("0", "white", V(network)$color)

# 绘图
plot(network, vertex.label = NA, edge.label = NA,
    edge.color = "black", vertex.size = 2)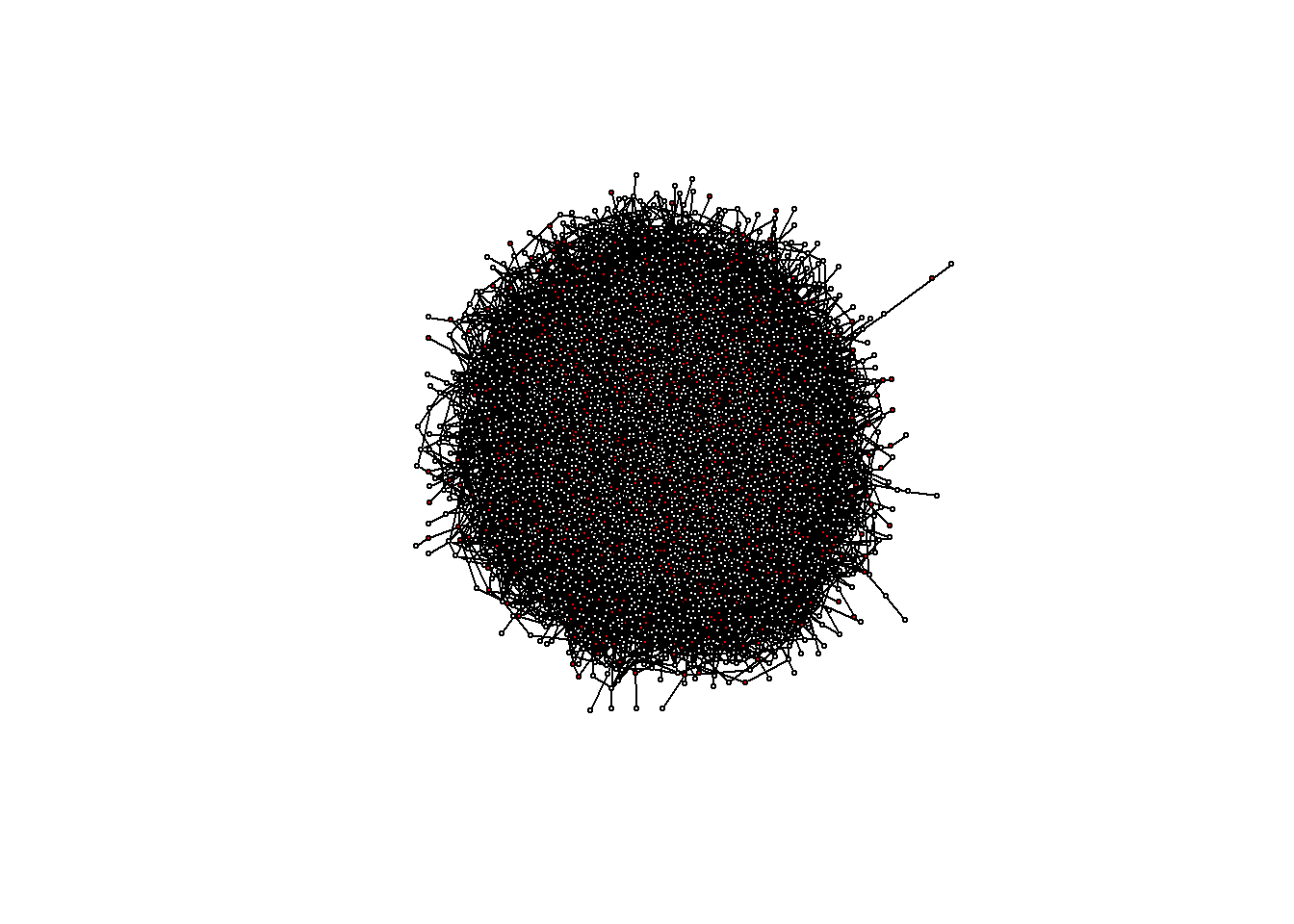

21.1.3 取出特定标签

如果节点很多，节点之间关系也很多，绘制出来的图就很难看到有用的信息。所以需要对流失的客户单独拿出来，看关系图，则需要对这个网络取子集。因为有标签，所以这个操作很容易。

# 创建只有流失客户的网络
churnerNetwork <- induced_subgraph(network, 
                    v = V(network)[which(V(network)$churn == 1)])
                    
# 绘图
plot(churnerNetwork, vertex.label = NA, vertex.size = 2)

21.1.4 领近关系分类

最简单的想法是如果一个节点的邻居(neighbor)的流失多，那么这个节点很有可能流失。所以利用这个想法来找出哪些未流失节点可能流失.下面是我自己想出来的办法，非常笨拙，下一节介绍了更简单的方法

  • from列固定为一个点，to列看作它的邻居
  • 创建一个新的数据框，交换from和to，使得能计算每一个节点的邻居（这一点需要验证数据里面是否已经有交换的节点）
  • 两个数据集合并
  • 内连接1，按照from的ID链接到churn列,得到每个点邻居是否流失
  • 内连接2，按照to的ID链接到churn列,得到每个点是否流失，这一步是因为我们只关心未流失的客户是否会变为流失状态，不关心已经流失节点与它的邻居的情况
  • 计算每个未流失节点的流失邻居数量和未流失邻居数量
  • 计算每个未流失节点的流失概率
inv_edgeList <- data.frame("from" = edgeList$to, "to" = edgeList$from)
fin_edgeList <- rbind.data.frame(edgeList, inv_edgeList)

# 是否已经存在交换的节点
sum(duplicated(fin_edgeList))
## [1] 0

d_churn <- fin_edgeList %>%
  inner_join(customers, by = c("to" = "id")) %>%
  inner_join(customers, by = c("from" = "id"), suffix=c("_neig", "_self")) %>%
  filter(churn_self == 0) %>%
  group_by(from) %>%
  summarise(churn_sum = sum(churn_neig == 1))

d_not_churn <- fin_edgeList %>%
  inner_join(customers, by = c("to" = "id")) %>%
  inner_join(customers, by = c("from" = "id"), suffix=c("_neig", "_self")) %>%
  filter(churn_self == 0) %>%
  group_by(from) %>%
  summarise(not_churn_sum = sum(churn_neig == 0))


d_churn_prob <- d_churn %>% inner_join(d_not_churn, by = "from") %>%
  mutate(churn_prob = churn_sum/(not_churn_sum+ churn_sum)) %>%
  arrange(desc(churn_prob))

head(d_churn_prob)
## # A tibble: 6 × 4
##   from  churn_sum not_churn_sum churn_prob
##   <fct>     <int>         <int>      <dbl>
## 1 100           1             0          1
## 2 106           1             0          1
## 3 1110          2             0          1
## 4 1375          1             0          1
## 5 2580          2             0          1
## 6 391           1             0          1

d_churn_prob %>% filter(churn_sum >= 3) %>% head()
## # A tibble: 6 × 4
##   from  churn_sum not_churn_sum churn_prob
##   <fct>     <int>         <int>      <dbl>
## 1 3995          3             0       1   
## 2 2506          4             1       0.8 
## 3 2572          4             1       0.8 
## 4 1016          3             1       0.75
## 5 1446          3             1       0.75
## 6 21            3             1       0.75

21.1.5 集体推理分类

集体推理（Collective inference）是一种在相互连接的数据中同时标注节点以减少分类误差的程序。

假设你不知道一个未知节点的邻居节点的标签，而是知道每个邻居节点的流失概率，你可以通过找到相邻节点的流失概率的平均值来更新节点的流失概率。

21.2 同性偏好的指标

Birds of a feather flock together

Homophily on Wiki.

21.2.1 边的连接性

网络连接性(network connectance )，我们用p表示。它只是实际边数与网络完全连通时的边数之比。

\[ p = \dfrac{edges}{\binom{nodes}{2} } =\dfrac{2\cdot edges}{nodes\cdot (nodes-1)} \]

要计算客户网络的连接性，我们先匹配from和to用户的流失标签，然后相加，结果分为三种

  • 0：两点均为未流失
  • 1：其中一点为流失
  • 2：两点均为流失

实际编写代码中，我们使用到了一个match()函数，match(x，y)返回x在y中的位置的向量.具体使用方法.

# 添加一列 FromLabel
edgeList$FromLabel <- customers[match(edgeList$from, customers$id), 2]
 
# 添加一列 edgeList$ToLabel
edgeList$ToLabel <- customers[match(edgeList$to, customers$id), 2]
 
# 添加一列 edgeList$edgeType
edgeList$edgeType <- as.numeric(edgeList$FromLabel) + as.numeric(edgeList$ToLabel)
 
# Count the number of each type of edge
table(edgeList$edgeType)
## 
##    0    1    2 
## 8842 2996  653

我们计算三种边的数量

# 计算都是流失的边的数量
ChurnEdges <- sum(edgeList$edgeType == 2)
 
# 计算都是未流失的边的数量
NonChurnEdges <- sum(edgeList$edgeType == 0)
 
# 计算是混合的边的数量
MixedEdges <- sum(edgeList$edgeType == 1)
 
# 全部加起来
edges <- ChurnEdges + NonChurnEdges + MixedEdges

edges
## [1] 12491

接下来我们就可以计算客户图的连接性了

# 计算都是流失的点的数量
ChurnNodes <- sum(customers$churn == 1)
 
# 计算都是未流失的点的数量
NonChurnNodes <- sum(customers$churn == 0)
 
# 计算是混合的点的数量
nodes <- ChurnNodes + NonChurnNodes
 
# 计算连通率
connectance <- 2 * edges/ nodes / (nodes - 1)

connectance
## [1] 0.001014031

21.2.2 二重性(Dyadicity)

有多种方法可以评估网络是否是同性的，并测量节点之间的关系依赖性。例如，您可以计算相同和交叉标签边缘的比率，以了解它们的分布情况。一种更先进的方法是衡量网络的二重性和异质性。事实上，当网络中有两个标签时，需要这两个独立的参数来捕捉网络结构和节点财产之间的详细相互作用。在这节课中，我们关注二重性(Dyadicity)。

二重性衡量具有相同标签的节点之间的连接性。因此，我们需要用这个公式的组合学来计算相同标签边的预期数量。下面的\(n_{l}\)表示我们关注的标签节点的数量。

\[ \binom{n_{l}}{2} \cdot p = \dfrac{n_{l}(n_{l}-1)}{2} \cdot p \] 有了这个标签边的期望值，计算Dyadicity等于实际这个标签数量除以期望标签的数量

\[ D = \dfrac{\text{相同标签边的实际数量}}{\text{相同标签边的期望数量}} \] 计算的结果会有三种

  • \(D>1\) ：表示这个网络是Dyadicity的，表明相同标签之间具有比较高的连接性
  • \(D\approx 1\)：表示这个网络与随机的网络没有区别
  • \(D<1\)：表示这个网络是反Dyadicity的，表明相同标签之间具有比较低的连接性

我们利用上面已经分好的数据，进行分析：流失的客户之间是否有更高的连接性

# 计算预期的流失节点的边
ExpectedDyadChurn <- ChurnNodes * (ChurnNodes - 1) * connectance / 2
 
# 计算二重性
DyadChurn <- ChurnEdges / ExpectedDyadChurn
 
DyadChurn
## [1] 2.152641


# 计算未流失的客户的二重性
ExpectedNotChurn <- NonChurnNodes *(NonChurnNodes-1)*connectance /2

DyadNotChurn <- NonChurnEdges/ExpectedNotChurn

DyadNotChurn
## [1] 0.9935849

可以看到流失的客户之间有更强的二重性

21.2.3 异质性(Heterophilicity)

Heterophily, or love of the different, is the tendency of individuals to collect in diverse groups

与上面二重性正好相反，异质性（Heterophilicty）衡量的是具有相反标签的节点之间的连接性，因此具有不同标签的节点之间有多少互动。关于异质性的解释

首先需要计算交叉标签边的期望数量，假设我们有两种标签，一种是 \(n_{a}\)，另一种是 \(n_{b}\)。 所以期望交叉标签边的数量为（这个公式由课程提供，是否具有意义不知道）

\[ n_{a}n_{b}\cdot p \]

所以异质性为

\[ H = \dfrac{交叉标签边的实际数量}{交叉标签边的期望数量} \] 同样，异质性有三个结果

  • \(H>1\) ：表示这个网络是异质性的，表明不同标签之间具有比较高的连接性
  • \(H\approx 1\)：表示这个网络与随机的网络没有区别
  • \(H<1\)：表示这个网络是反异质性的，表明不同标签之间具有比较低的连接性

对于客户流失网络，我们利用之前计算好的数据计算这个网络的异质性

# 计算不同标签边的期望数量
ExpectedHet <- NonChurnNodes* ChurnNodes*connectance
 
# 计算异质性
Het <- MixedEdges / ExpectedHet
 
Het
## [1] 0.9110363

21.2.4 结论

网络是同性(Homophily 这个词也有同构的意思)的,需要 \(D>1\)和 \(H<1\).

21.3 网络的特征

21.3.1 更换数据

试图构造原本数据，但太消耗时间，故放弃 从现在开始就需要预测了，所以我们更换了客户的数据，客户网络有未来状态这一列了，同时我们对这个数据进行处理，选取其中一部分

g1 <- as_data_frame(g1, what = "vertices")
str(g1)
## 'data.frame':    4964 obs. of  4 variables:
##  $ name        : chr  "1" "393" "2573" "4430" ...
##  $ networkChurn: chr  "No" "No" "No" "No" ...
##  $ futureChurn : chr  "No" "No" "No" "No" ...
##  $ color       : chr  "white" "white" "white" "white" ...

g2 <- g1 %>% 
  filter(futureChurn != "Future") %>%
  mutate(Future = ifelse(futureChurn == "No", 0, 1),
         churn = ifelse(networkChurn == "No", 0, 1))%>%
  select(name, churn, Future, color) %>% sample_n(size = 956)

21.3.2 邻接矩阵

邻接矩阵(adjacency matrix)是网络的另外一种表示方式，它主要用于计算，我们可以使用 igraph包里面的这个函数。

  • as_adjaceny_matrix() : 获取图的一阶邻接矩阵

二阶的邻接矩阵可以通过一阶邻接矩阵相乘得到，如果二阶邻接矩阵 \((i,j)\)元为1，它表示 \(i\)和\(j\)之间的距离为2.我们用客户网络得到一阶邻接矩阵和二阶邻接矩阵，因为我们规定了每个节点不能自指，所以得到的二阶邻接矩阵需要将对角线全部变为0.

# 获取邻接矩阵
AdjacencyMatrix <- as_adjacency_matrix(network)

# 矩阵乘两次
SecondOrderMatrix_adj <- AdjacencyMatrix %*% AdjacencyMatrix

# 调整这个矩阵
SecondOrderMatrix <- ((SecondOrderMatrix_adj) > 0) + 0
diag(SecondOrderMatrix) <- 0

# 查看二阶邻接矩阵
SecondOrderMatrix[1:10, 1:10]
## 10 x 10 sparse Matrix of class "dgCMatrix"
##    [[ suppressing 10 column names '1', '2', '3' ... ]]
##                       
## 1  0 . . . . . . . . .
## 2  . 0 . . . . . . . .
## 3  . . 0 . . . . . . .
## 5  . . . 0 . . . . . .
## 6  . . . . 0 . . . . 1
## 7  . . . . . 0 . . . .
## 8  . . . . . . 0 . . .
## 9  . . . . . . . 0 . .
## 10 . . . . . . . . 0 .
## 11 . . . . 1 . . . . 0

邻接矩阵一个很重要的作用是得到每个节点指定标签的邻居数量，比如，客户流失的标签为1，如果我们想得到每个节点的客户的流失客户邻居的数量，就可以用邻接矩阵乘这个标签的向量。我们通过一个简单的例子.

# 创建一个图并设置标签，注意标签向量
g <- make_empty_graph(n = 5, directed = FALSE) %>%
    add_edges(c(1,2, 2,3, 3,4, 4,5, 5,3, 1,4)) %>%
    set_vertex_attr("churn", value = c(1,0,1,0,0))

# 设置颜色
V(g)$color <- V(g)$churn
V(g)$color <- gsub("1", "red", V(g)$churn)
V(g)$color <- gsub("0", "white", V(g)$churn)

plot(g)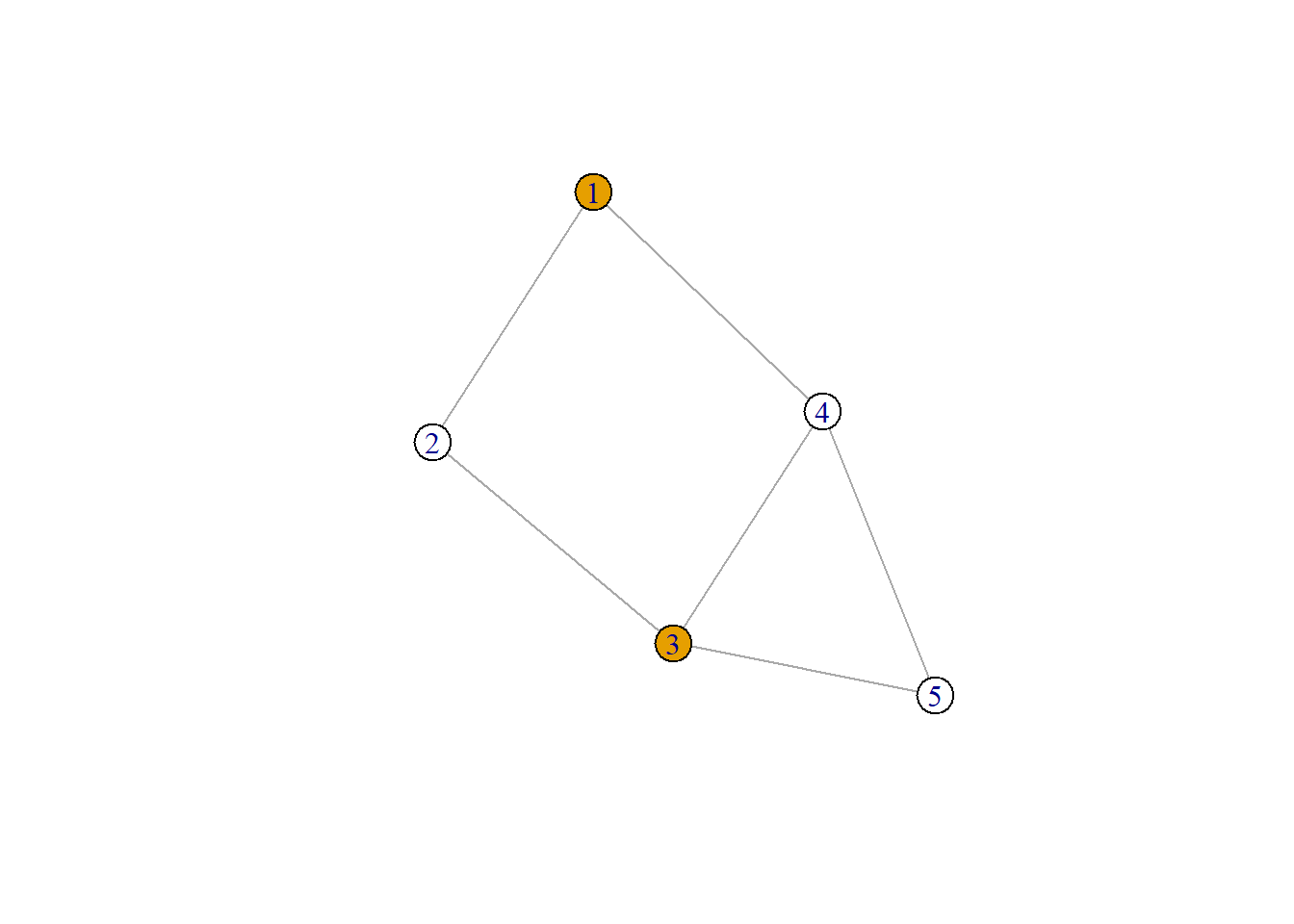

然后我们从图上可以看到1，2，3，4，5分别有0，2，0，2，1个流失客户邻居，我们用邻接矩阵来算算

# 从图上数出来
churn_neig <- c(0, 2, 0, 2, 1)

# 得到邻接矩阵
adm_g <- as_adjacency_matrix(g)

# 得到每个节点流失的邻居数量
churn_comp <- adm_g %*% V(g)$churn  # 矩阵乘法

churn_comp
## 5 x 1 Matrix of class "dgeMatrix"
##      [,1]
## [1,]    0
## [2,]    2
## [3,]    0
## [4,]    2
## [5,]    1

简单的图我们可以直接数出来，如果复杂的图就像我们一直用的客户流失图，包含了4000多个节点，这时候就需要使用邻接矩阵计算了。

21.3.3 基于链接的特征

对于每个节点客户是否流失的可能，我们现在可以简单的用邻接矩阵的方法算出来。你也可以用相同的方法计算由两步邻居流失情况确定的该节点流失概率，用到二阶邻接矩阵

# 计算每个节点流失客户邻居的数量
V(network)$ChurnNeighbors <- as.vector(AdjacencyMatrix %*% V(network)$churn)

# 计算每个节点未流失客户邻居的数量
V(network)$NonChurnNeighbors <- as.vector(AdjacencyMatrix %*% (1 - V(network)$churn))

# 计算流失概率
V(network)$RelationalNeighbor <- as.vector(V(network)$ChurnNeighbors / 
    (V(network)$ChurnNeighbors + V(network)$NonChurnNeighbors))


# 计算每个节点两步邻居的流失数量
V(network)$ChurnNeighbors2 <- as.vector(SecondOrderMatrix %*% V(network)$churn)

# 计算每个节点两步邻居的未流失数量
V(network)$NonChurnNeighbors2 <- as.vector(SecondOrderMatrix %*% (1 - V(network)$churn))

# 计算该点的流失概率
V(network)$RelationalNeighbor2 <- as.vector(V(network)$ChurnNeighbors2 / 
    (V(network)$ChurnNeighbors2 + V(network)$NonChurnNeighbors2))

21.3.4 节点的特征提取

对于更好的预测节点标签，我们还要计算一些特征：

# degree
degree <- degree(network)
V(network)$degree <- degree(network, normalized=TRUE)

# 节点两步度数
degree2 <- neighborhood.size(network, 2)

# 标准化
V(network)$degree2 <- degree2 / (length(V(network)) - 1)

# 计算三角形数量
V(network)$triangles <- count_triangles(network)


# betweenness
V(network)$betweenness <- betweenness(network, normalized=TRUE)

# closeness
V(network)$closeness <- closeness(network, normalized=TRUE)

# eigenCentrality
V(network)$eigenCentrality <- eigen_centrality(network, scale = TRUE)$vector

# 计算每个点的超越性
V(network)$transitivity <- transitivity(network, type='local', isolates='zero')

# 计算整个图的超越性
transitivity(network)
## [1] 0.001053943

21.3.5 使用邻接矩阵计算特征的平均值

相邻节点的特征的值会对这个节点行为产生影响，我们使用邻接矩阵去计算这个节点的邻居对这个节点的影响的总和的平均值（存疑）

# 提取相邻节点的平均度数
V(network)$averageDegree <- 
    as.vector(AdjacencyMatrix %*% V(network)$degree) / degree

# 提取相邻节点的平均三角形数量
V(network)$averageTriangles <- 
    as.vector(AdjacencyMatrix %*% V(network)$triangles) / degree

# 提取相邻节点的平均超越性    
V(network)$averageTransitivity<-
    as.vector(AdjacencyMatrix %*% V(network)$transitivity) / degree

# 提取相邻节点的平均间性  
V(network)$averageBetweenness <- 
    as.vector(AdjacencyMatrix  %*% V(network)$betweenness) / degree

21.4 PageRank算法

Page Rank 是一种衡量节点重要性的一种算法，Wikipedia上面详细介绍了PageRank，这里不在介绍，只是简单列出计算方法。

\[ P R\left(p_{i}\right)=\frac{1-d}{N}+d \sum_{p_{j} \in M\left(p_{i}\right)} \frac{P R\left(p_{j}\right)}{L\left(p_{j}\right)} \] 其中 \(p_1, p_2, ..., p_N\)是需要考虑的页面（节点），\(M(p_i)\)是链接到 \(p_{i}\)的页面的集合，\(L(p_j)\)的外向链接数量, \(N\)是页面的总数. 在任何一步，该人继续点击链接的概率都是\(d\)。转而跳转到任意一个随机页面的概率是\(1-d\)。

对于图网络,我们使用page.rank()函数计算每个节点的重要程度,官方文档.上面所说的 \(d\)可以在函数的参数damping（意为阻尼系数）中设置

下面的好像在函数中无法使用了,详情查看版本更新

使用PageRank算法计算一次迭代(iteration),需要设置参数. 多次迭代之后, >各点PageRank的值会收敛(这个由条件,在随机过程中,但是没学好)

pr <- page_rank(network)$vector

21.4.1 个性化排名

如果事先知道某个节点更重要,可以设置节点,使其有更高的权重.参数personalized表示是否应使用个性化的PageRank算法。当为”true”时，重启向量对网络中的流失者为1（因为我们将流失者标签设为1了），对非流失者为0。默认值为FALSE，即不个性化。

PageRank和个性化的PageRank算法之间的区别，可以创建一个函数boxplots，用两个独立的boxplots来显示churners和non-churners的分数分布。该函数有两个参数。

boxplots <- function(damping=0.85, personalized=FALSE){
  if(personalized){
    V(network)$pp<-page.rank(network,damping=damping,personalized = V(network)$churn)$vector
  }
  else{
    V(network)$pp<-page.rank(network,damping=damping)$vector
  }
  boxplot(V(network)$pp~V(network)$churn)#
}

下面可以看看不同阻尼系数和个性化设置会有什么区别

# 标准PageRank分数的分布情况
boxplots(damping = 0.85)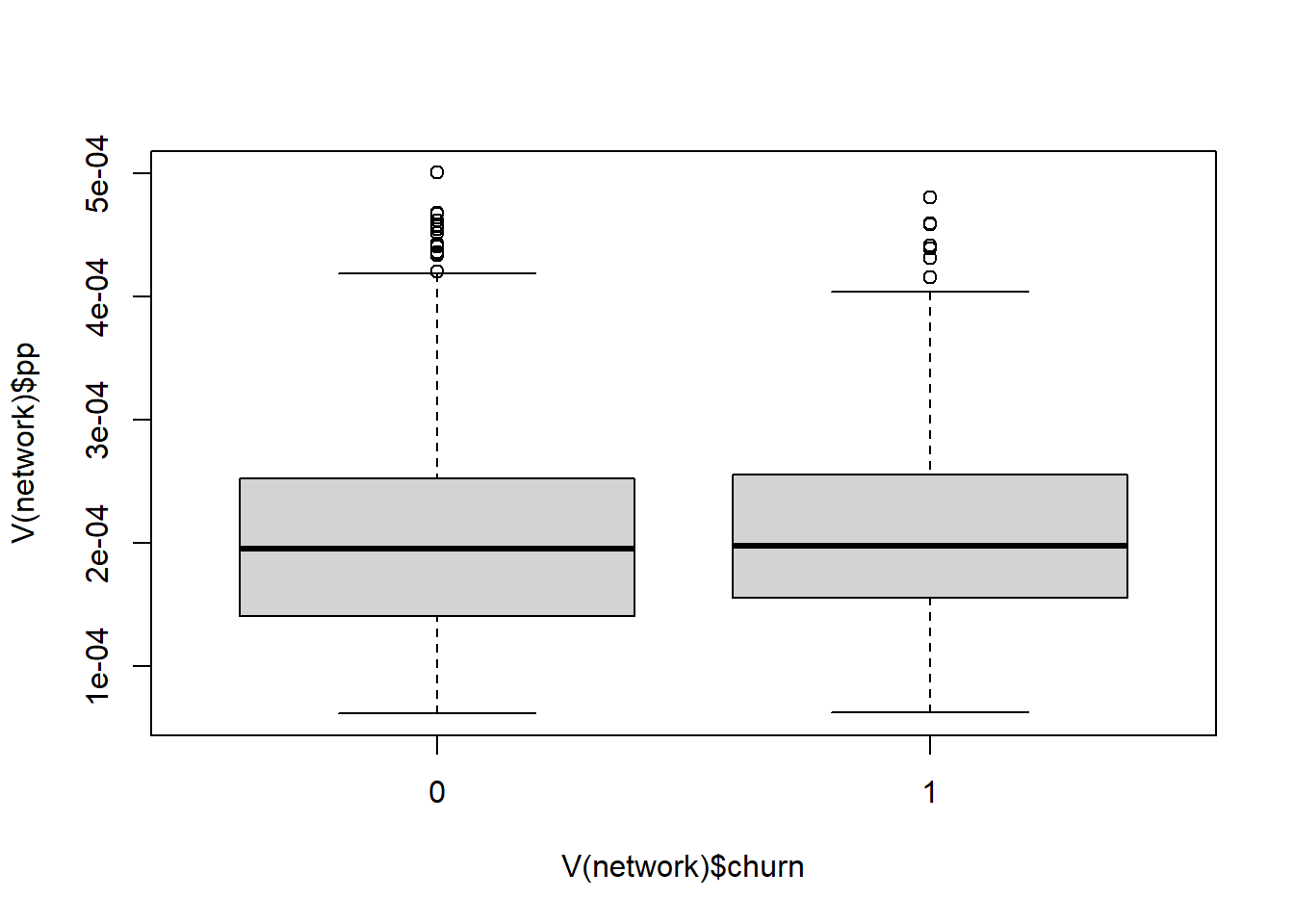


# 个性化的PageRank分数的分布情况
boxplots(damping = 0.85, personalized = TRUE)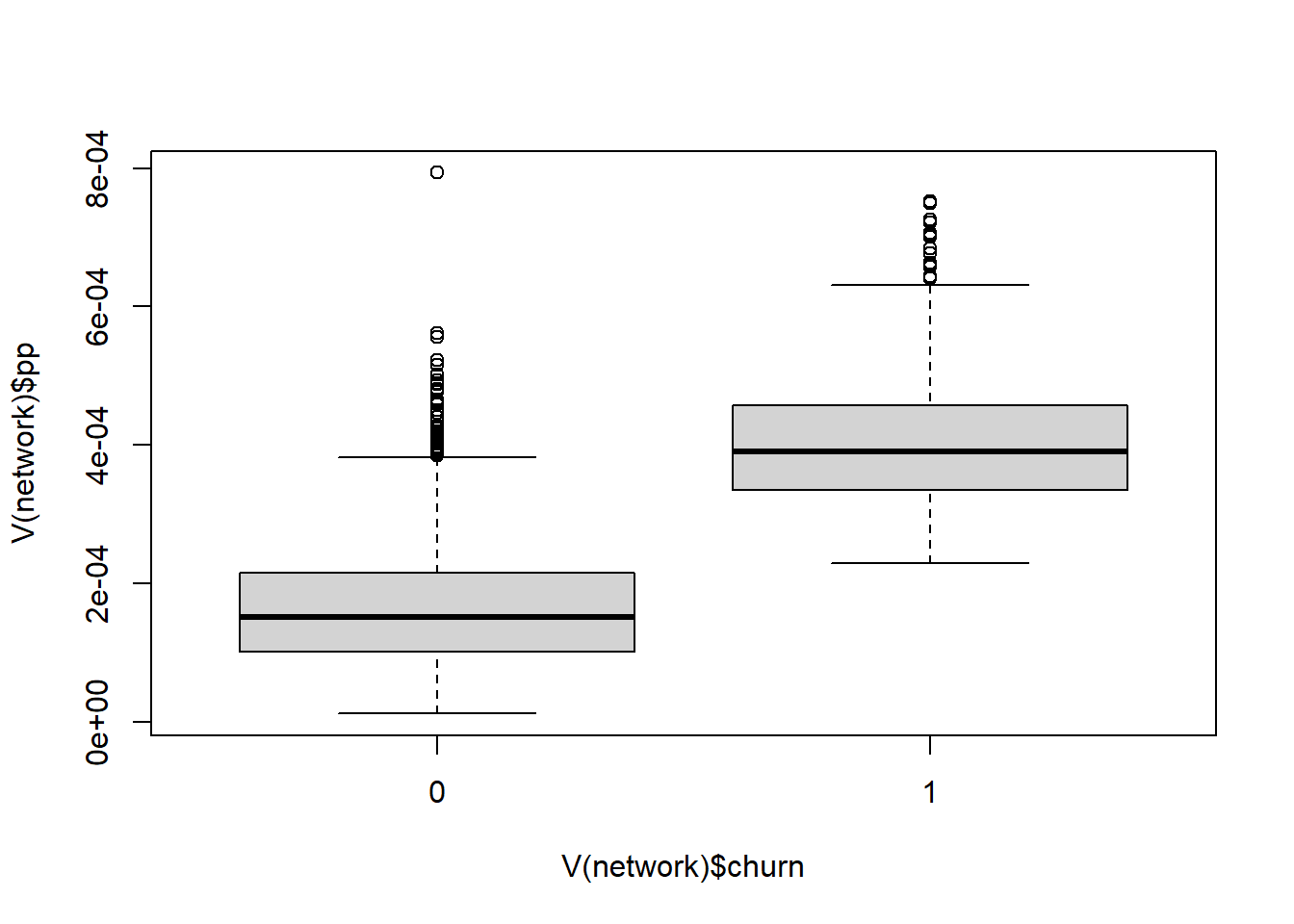


# 阻尼系数为0.2的标准PageRank的分布情况
boxplots(damping = 0.2)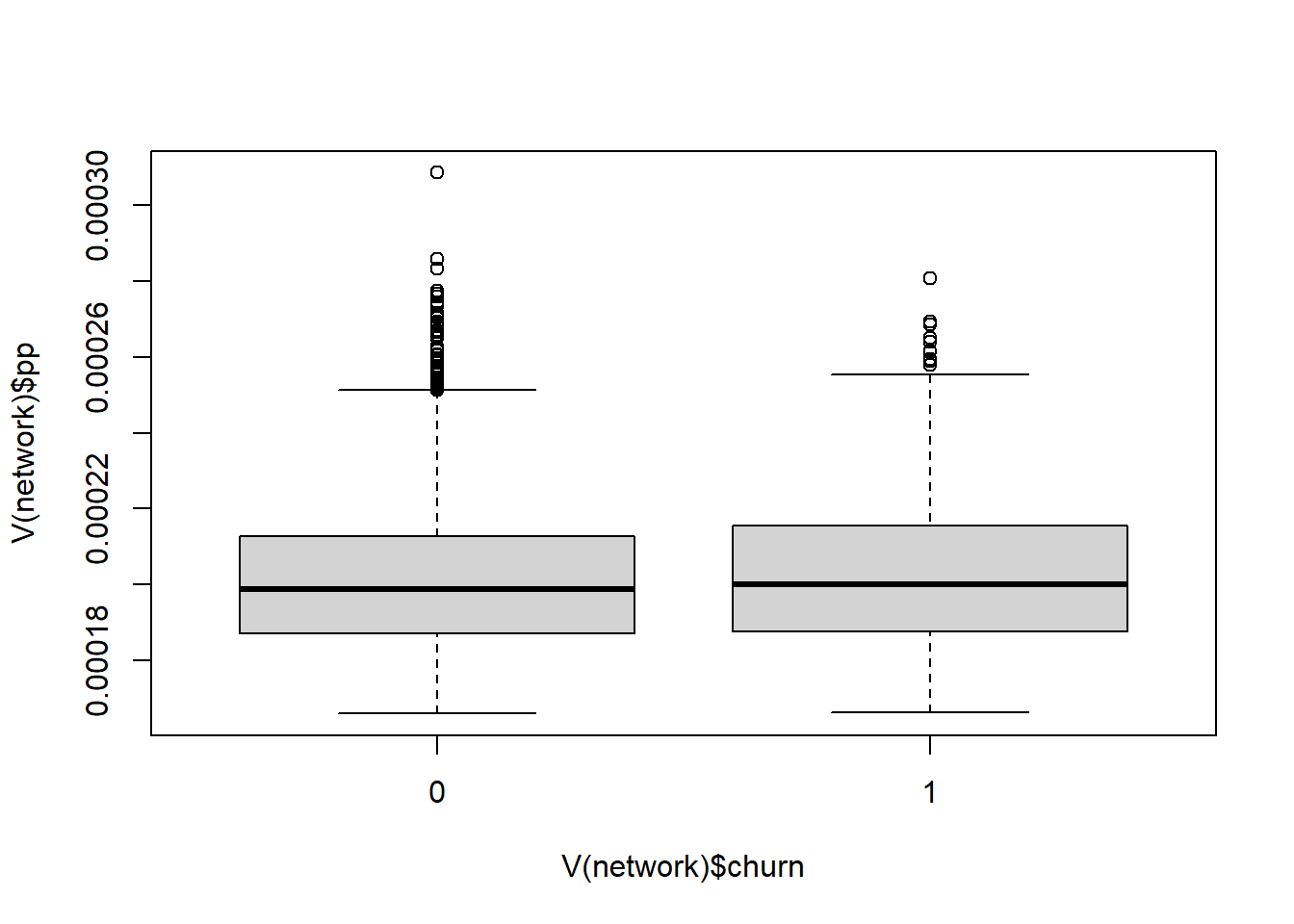


# 阻尼系数为0.99的个性化的PageRank分数
boxplots(damping = 0.99, personalized = TRUE)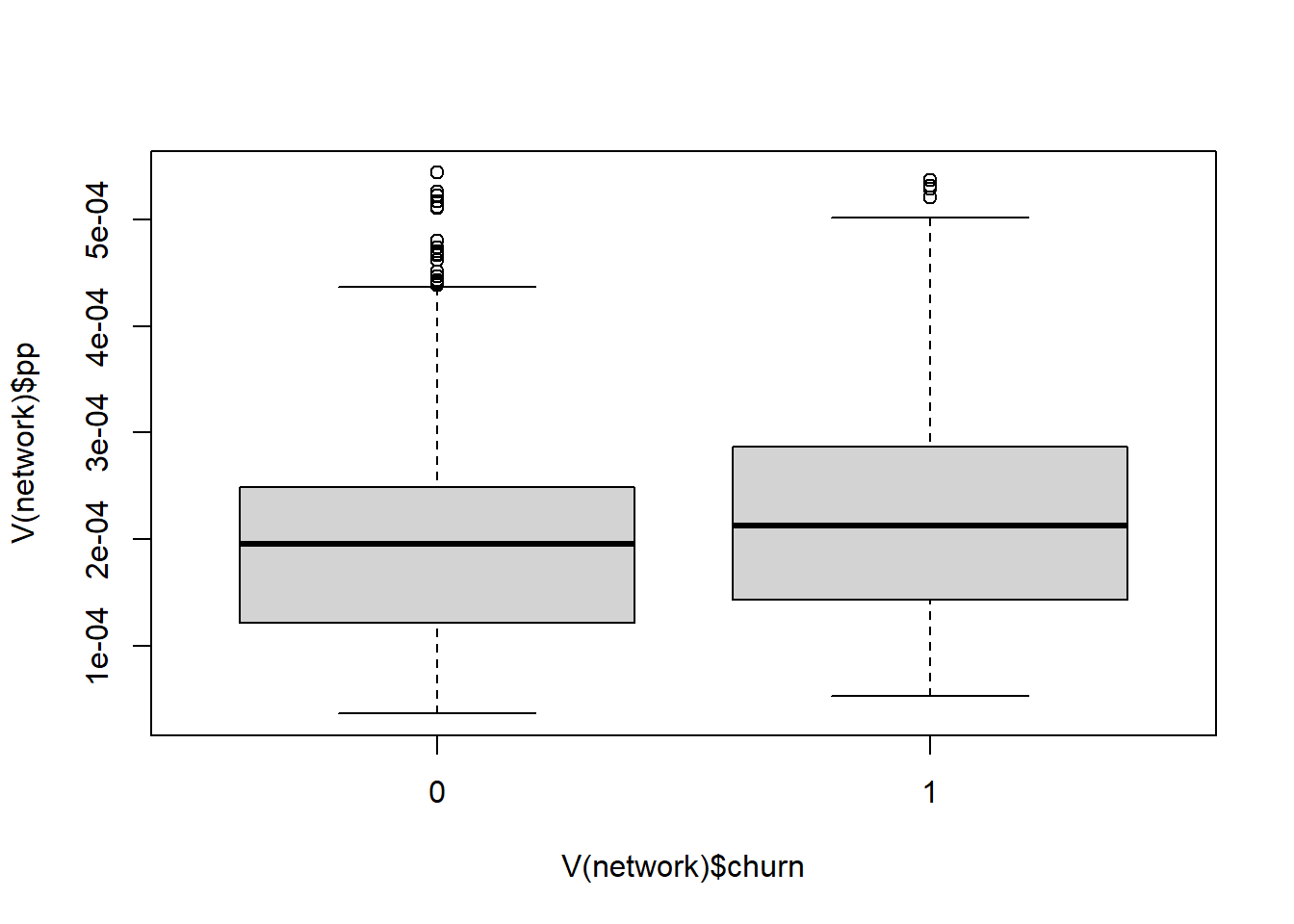

21.4.2 提取不同系数的排名

这里的系数是damping的不同

V(network)$pr_0.85 <- page.rank(network)$vector

V(network)$pr_0.20 <- page.rank(network, damping= 0.2)$vector

V(network)$perspr_0.85 <- page.rank(network, personalized =  V(network)$Churn)$vector

V(network)$perspr_0.99 <- page.rank(network, damping = 0.99, personalized =  V(network)$Churn)$vector

21.5 提取特征信息

21.5.1 转换为数据框

我们为节点添加了很多信息，现在可以使用这些信息进行预测了，首先需要提取这些信息并存储在数据框内。

# 提取信息
studentnetworkdata_full <- as_data_frame(network, what = "vertices")
studentnetworkdata_full$Future <- 0 # 为预测做准备
str(studentnetworkdata_full)
## 'data.frame':    4964 obs. of  25 variables:
##  $ name               : chr  "1" "2" "3" "5" ...
##  $ churn              : num  0 0 0 0 0 0 0 0 0 0 ...
##  $ color              : chr  "white" "white" "white" "white" ...
##  $ ChurnNeighbors     : num  0 2 2 0 1 0 0 0 0 2 ...
##  $ NonChurnNeighbors  : num  3 5 2 2 4 6 6 4 5 1 ...
##  $ RelationalNeighbor : num  0 0.286 0.5 0 0.2 ...
##  $ ChurnNeighbors2    : num  3 3 2 2 1 2 4 0 8 1 ...
##  $ NonChurnNeighbors2 : num  9 27 13 7 25 25 27 21 19 11 ...
##  $ RelationalNeighbor2: num  0.25 0.1 0.1333 0.2222 0.0385 ...
##  $ degree             : num  0.000604 0.00141 0.000806 0.000403 0.001007 ...
##  $ degree2            : num  0.00322 0.00766 0.00403 0.00242 0.00645 ...
##  $ triangles          : num  0 0 0 0 0 0 0 0 0 0 ...
##  $ betweenness        : num  1.93e-04 1.27e-03 3.78e-04 7.03e-05 8.67e-04 ...
##  $ closeness          : num  0.17 0.189 0.178 0.165 0.183 ...
##  $ eigenCentrality    : num  0.0729 0.2212 0.1135 0.0494 0.1748 ...
##  $ transitivity       : num  0 0 0 0 0 0 0 0 0 0 ...
##  $ averageDegree      : num  0.001007 0.001065 0.000957 0.001108 0.001249 ...
##  $ averageTriangles   : num  0 0 0 0 0.2 0 0 0 0 0 ...
##  $ averageTransitivity: num  0 0 0 0 0.00556 ...
##  $ averageBetweenness : num  0.000794 0.000943 0.00075 0.000811 0.001236 ...
##  $ pr_0.85            : num  0.00014 0.000271 0.000173 0.000102 0.00021 ...
##  $ pr_0.20            : num  0.00019 0.000221 0.000201 0.000177 0.000208 ...
##  $ perspr_0.85        : num  0.00014 0.000271 0.000173 0.000102 0.00021 ...
##  $ perspr_0.99        : num  1.22e-04 2.80e-04 1.61e-04 8.17e-05 2.01e-04 ...
##  $ Future             : num  0 0 0 0 0 0 0 0 0 0 ...

# 将已经流失的客户过滤
studentnetworkdata_filtered <- studentnetworkdata_full[-which(studentnetworkdata_full$churn == 1), ]

# 删除没有用的列
studentnetworkdata <- studentnetworkdata_filtered[, -c(1, 2, 3)]

# 观察那一列有Na值
apply(studentnetworkdata,2, function(x){sum(is.na(x))})
##      ChurnNeighbors   NonChurnNeighbors  RelationalNeighbor     ChurnNeighbors2 
##                   0                   0                   0                   0 
##  NonChurnNeighbors2 RelationalNeighbor2              degree             degree2 
##                   0                   0                   0                   0 
##           triangles         betweenness           closeness     eigenCentrality 
##                   0                   0                   0                   0 
##        transitivity       averageDegree    averageTriangles averageTransitivity 
##                   0                   0                   0                   0 
##  averageBetweenness             pr_0.85             pr_0.20         perspr_0.85 
##                   0                   0                   0                   0 
##         perspr_0.99              Future 
##                   0                   0

可以将NA值替换成0，使用which(is.na(x))找到NA值索引

21.5.2 相关系数

我们有很多特征，我们希望查看特征之间是否相关，所以使用 cor()函数查看各个特征之间相关系数，利用corrplot包来绘图(这个包的简介查看这里)

#  
no_future <- studentnetworkdata[,-length(colnames(studentnetworkdata))]

# 
M <- cor(no_future)

# 
corrplot(M, method = "circle")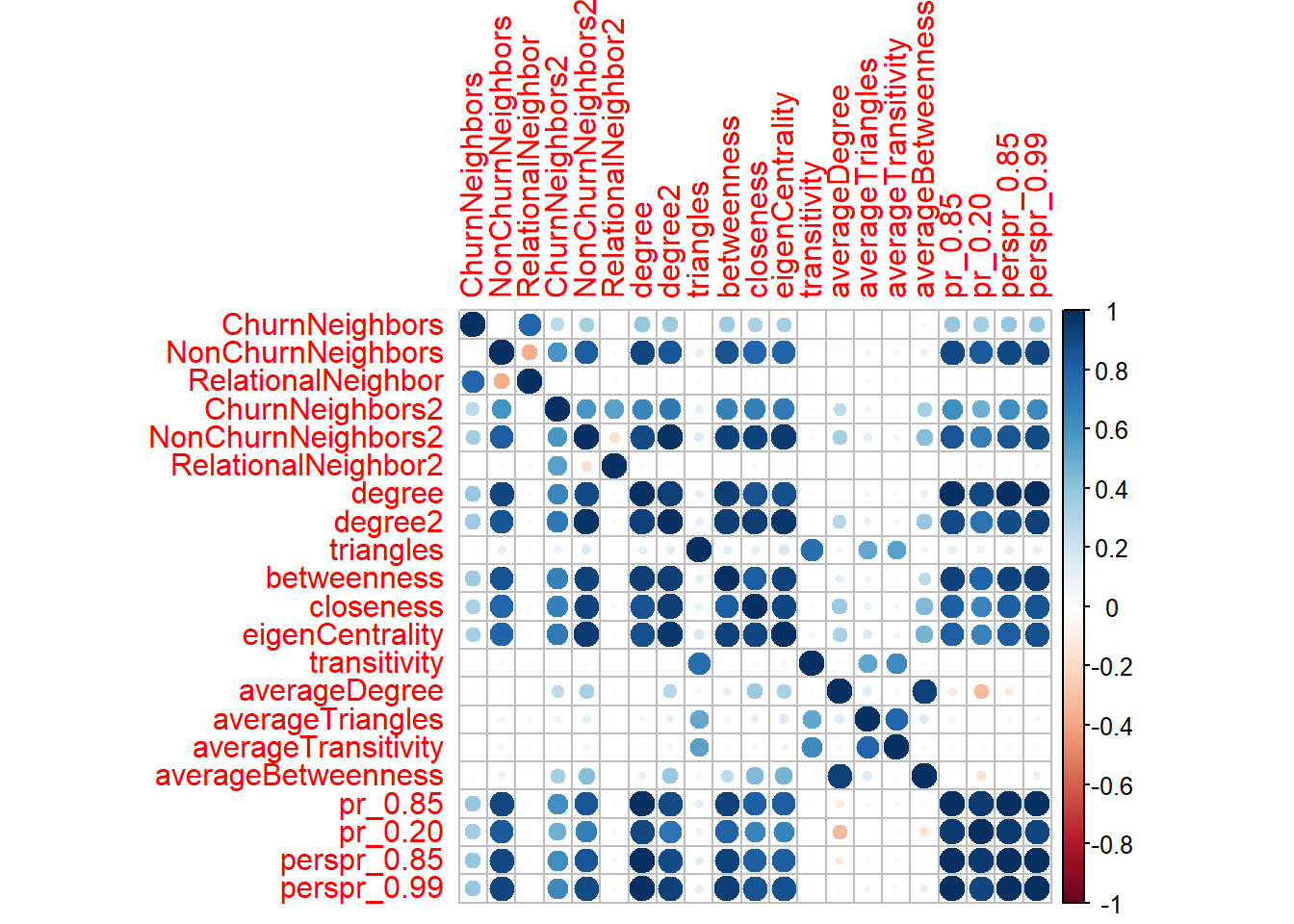

我们需要检查数据集中的相关变量。在应用二元分类器之前，去除它们中一部分是很重要的，特别是在逻辑回归的情况下。当两个或多个变量高度相关时，你应该删除所有的变量，除了一个。

在相关图中，蓝色代表正相关，红色代表负相关。颜色越深表示相关度越高。我们需要从数据集中删除高度相关的变量。

toRemove <- c("NonChurnNeighbors", "NonChurnNeighbors2", "pr_0.85", "perspr_0.99")

studentnetworkdata_no_corrs <- studentnetworkdata[, -match(toRemove, colnames(studentnetworkdata))]

21.6 预测模型

21.6.1 划分数据集

拆成训练集合和测试集合

set.seed(7)

index_train <- sample(1:nrow(studentnetworkdata), 2 / 3 * nrow(studentnetworkdata))

training_set <- studentnetworkdata[index_train,]

test_set <- studentnetworkdata[-index_train,]

21.6.2 创建模型

对于二元分类，首先用逻辑回归

我写到这里发现给的数据不一样，没有提供原数据，如果要构造原数据，会花费较大时间，所以不再继续下去了

firstModel <- glm(Future ~ degree + degree2 + triangles + betweenness + closeness + transitivity, family = "binomial", data = training_set)