Chapter 3 Statistiques descriptives bivariées

La statistique descriptive bivariée étudie les relations entre deux variables pour un même ensemble de données. Cette approche permet d’identifier et d’analyser les corrélations, en explorant comment les variations d’une variable peuvent influencer ou se refléter dans les variations de l’autre. Elle utilise des méthodes telles que le calcul du coefficient de corrélation pour mesurer l’intensité et la direction de la relation, les tableaux croisés pour visualiser les distributions conjointes, et les représentations graphiques comme les nuages de points pour observer visuellement les associations entre variables.

Dans la suite, on suppose que l’on dispose de \(n\) couple de données \(\left\{(x_i, y_i)\right\}_{i=1}^n\), où \((x_i, y_i)\) sont les données d’un couple de variables \((X,Y)\) obervées sur l’individu \(i\).

3.1 Analyse de Deux Variables Quantitatives

  • \((x_i,y_i)\in\mathbb{R}^2\).

3.1.1 Nuage de dpoints ou diagrammes de dispersion

  • Chaque individu \(i\) est représenté par le point de coordonnées \((x_i, y_i)\) dans le plan muni d’un repère;
  • But: Identifier visuellement les tendances, les regroupements et les valeurs aberrantes;

Example 3.1 (Taille vs poids) On a mesuré le poids et la taille de \(n=10\) personnes. Les données sont les suivantes.

require(dplyr)
require(ggplot2)
poidsTaille = data.frame(
    poids = c(58,  59,  61,  64,  66,  69,  72,  74,  77,  79),
    taille = c(158, 160, 162, 165, 167, 170, 172, 175, 177, 180)
  ) 

kableExtra::kable(poidsTaille)
poids taille
58 158
59 160
61 162
64 165
66 167
69 170
72 172
74 175
77 177
79 180 
poidsTaille %>% 
  ggplot(mapping = aes(x = poids, y = taille)) +
    geom_point(pch=20, color="steelblue", size=3)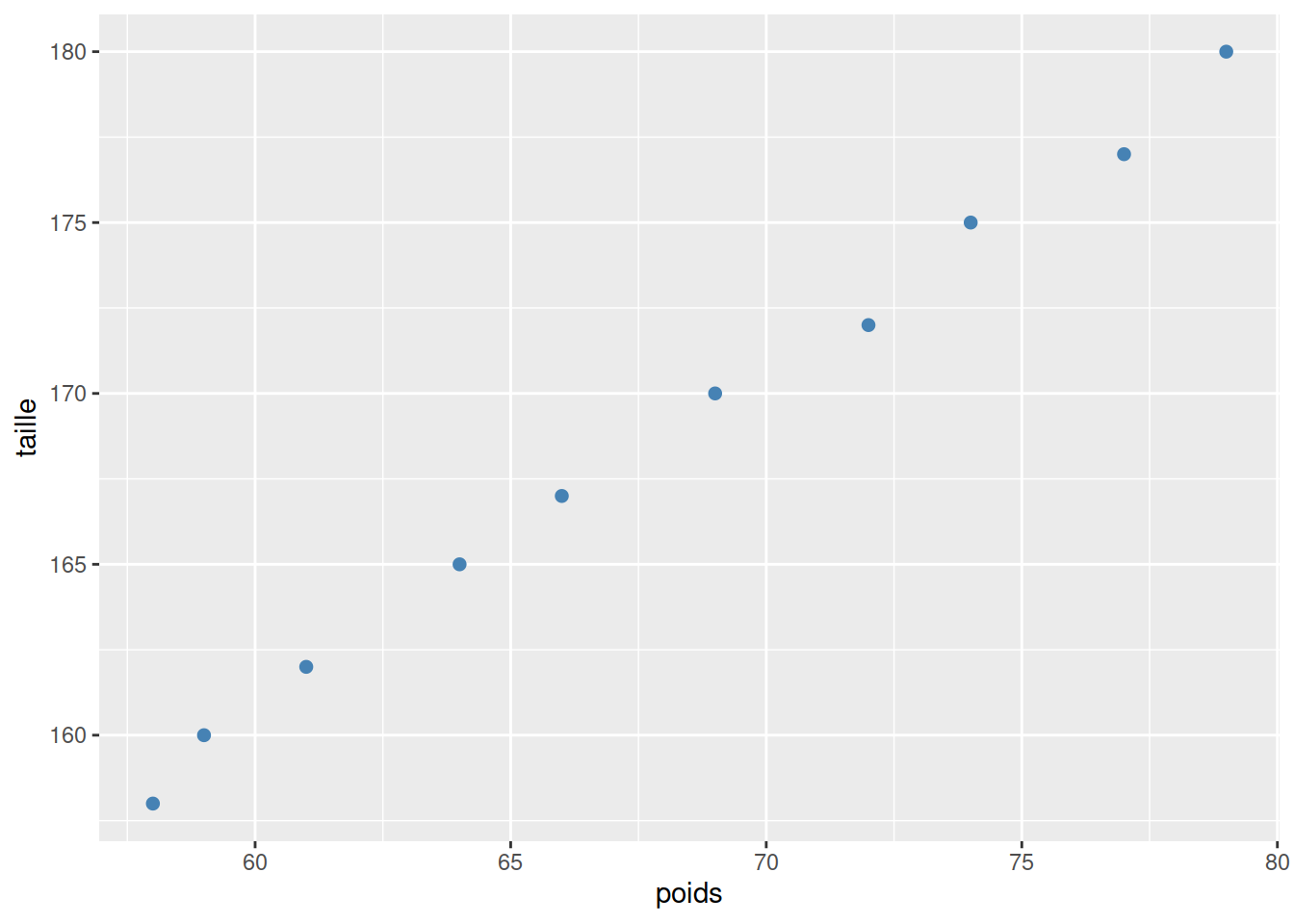

Commentaire: Le figure précédente suggère une relation linéaire croissante entre les deux variables.

3.1.2 Coefficient de corrélation de Pearson - Cavariance

Definition 3.1 (Coefficient de corrélation de Pearson) Le coefficient de corrélation est une mesure de la force de la relation linéaire entre deux variables. \[ r_{X, Y}=\dfrac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}} \]

Propriétés et interprétation:

  • \(r_{X,Y}\in\left[-1,1\right]\)
  • \(r_{X,Y}>0\): Les deux variables varient dans le même sens
  • \(r_{X,Y}<0\): Les deux variables varient en sens contraires
  • \(r_{X,Y}\approx 0\): Pas de lien linéaire entre les deux variables
  • Lien linéaire d’autant fort que \(|r_{X,Y}|\) est proche de \(1\); Le lineaire linéaire est parfait, c’est-à-dire \(y_i=a+bx_i,\ \forall i\), si et seulement si \(|r_{X,Y}|=1\)
  • Lien linéaire d’autant faible que \(|r_{X,Y}|\) est proche de \(0\)

Definition 3.2 (Covariance) La covariance entre \(X\) et \(Y\) est la quantité \[ S_{X,Y}=\dfrac{1}{n}\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)\overset{exo}{=}\dfrac{1}{n}\sum_{i=1}^nx_iy_i-\bar{x}\bar{y} \]

Remarque: \[ r_{X,Y}=\dfrac{S_{X,Y}}{\sqrt{S_X^2}\sqrt{S_Y^2}} \]

3.1.3 Régression linéaire

3.1.3.1 Modèle

On suppose qu’il existe \(\left(a, b\right)\in\mathbb{R}^2\) tels que \[ y_i"\approx" a+bx_i,\ \forall i, \textrm{ où l'approximation est au sens des moindres carrés.} \]

L’approximation \("\approx"\) est au sens de minimiser \[ J(a, b)=\sum_{i=1}^n\left(y_i-a-bx_i\right)^2. \]

3.1.3.2 Droite des moindres carrés

La droite des moindres carrés a pour équation \(y=\widehat{a}+\widehat{b}x\) où \[ J\left(\widehat{a},\widehat{b}\right)=\min_{(a, b)\in\mathbb{R}^2} J(a, b) \]

Proposition 3.1 (Droite des moindres carrés) Si \(S_X^2>0\), alors il existe une solution et une seule de \[ \min_{(a,b)\in\mathbb{R}^2}J(a,b), \]

donnée par \[ \left\{ \begin{array}{l} \widehat{b}=\dfrac{S_{X,Y}}{S_X^2}\\ \widehat{a}=\bar{y}-\widehat{b}\bar{x} \end{array} \right. \]

Proof (Exercice). En exercice.

Remarque: Le point moyen \((bar{x}, \bar{y})\) appartient à la droite des moindres carrés.

3.1.3.3 Prédiction ou valeur ajustée - Résidu

Definition 3.3 (Prédiction ou valeur ajustée)

  • La prédiction de la valeur de la variable à expliquer \(Y\) pour une valeur \(x\) de la variable explicative \(X\) est donnée par: \[ \widehat{y}=\widehat{a}+\widehat{b}x. \]

  • La quantité \(y-\widehat{y}\) est le résidu associé.

Definition 3.4 (Résidu) Saient \(y\) une valeur observée de la variable à expliquer, et \(\widehat{y}\) la valeur prédite par le modèle. Le résidu associé est \[ \widehat{\epsilon}=y-\widehat{y}. \]

Propriétés

  • \(\sum_{i=1}^n\widehat{y}_i=\sum_{i=1}y_i\)

  • \(\sum_{i=1}^n\widehat{\epsilon}_i=0\)

Definition 3.5 (Variance résiduelle) La variance résiduelle est la variance des résidus \(\widehat{\epsilon}_i\): \[ S_{\widehat{\epsilon}}^2=\dfrac{1}{n}\sum_{i=1}^n\widehat{\epsilon}_i^2=\dfrac{1}{n}SCR \]

3.1.3.4 Sommes des carrés - Coefficient de détermination

Definition 3.6 (Sommes des carrés)

  • Somme des carrés des résidus: \(SCR=\sum_{i=1}^n\left(y_i-\widehat{y}_i\right)^2\);

  • Somme des carrés expliqués: \(SCE=\sum_{i=1}^n\left(\widehat{y}_i-\bar{y}\right)^2\);

  • Somme total des carrés: \(SCT=\sum_{i=1}^n\left(y_i-\bar{y}\right)^2\)

Definition 3.7 (Coeff. de détermination) Le coefficient de détermination est une mesure de la qualité d’ajustement de la droite de régression aux données: \[ R^2=\dfrac{SCE}{SCT}=1-\dfrac{SCR}{SCT}. \]

Proposition 3.2

  • \(SCT=SCR+SCE\)

  • \(R^2=r_{X,Y}^2\in[0,1]\)

  • \(S_{\widehat{\epsilon}_i}^2=S_y^2\left(1-r_{X,Y}^2\right)\)

Proof (Exercice). Montrer la proposition précédente.

Interprétation de \(R^2\):

  • 0 signifie que le modèle ne prévoit pas la variable dépendante mieux que la moyenne de cette variable.

  • 1 indique une relation linéaire parfaite entre les deux variables en question: \(y_i=\widehat{y}_i=\widehat{a}+\widehat{b}x_i\) pour tout \(i\).

  • Proximité à 1 : Plus \(R^2\) est proche de 1, plus la qualité de l’ajustement du modèle est bonne. Cela signifie que le modèle explique une grande part de la variance de la variable dépendante (à expliquer) \(Y\).

  • Proximité à \(0\): Un \(R^2\) proche de \(0\) suggère que le modèle linéaire n’est pas approprié pour ajuster les données.

  • Limitations :

    • \(R^2\) ne fournit pas d’informations sur la causalité.

3.2 Analyse de Deux Variables Qualitatives

On suppose maintenant que les variables \(X\) et \(Y\) sont qualitatives. Les ensembles de modalités des deux variables sont notés comme suit:

  • \(X\left(\Omega\right)=\left\{a_1,\cdots,a_k,\cdots, a_K\right\}\)
  • \(Y\left(\Omega\right)=\left\{b_1,\cdots, b_k,\cdots, b_L\right\}\)

3.2.1 Tableaux de contingence

\(X|Y\) \(b_1\) \(\cdots\) \(b_l\) \(\cdots\) \(b_L\) Total
\(a_1\) \(n_{1,1}\) \(\cdots\) \(n_{1,l}\) \(\cdots\) \(n_{1,L}\) \(n_{1,+}\)
\(\vdots\)
\(a_k\) \(n_{k,1}\) \(n_{k,l}\) \(n_{k,L}\) \(n_{k,+}\)
\(\vdots\)
\(a_K\) \(n_{K,1}\) \(n_{K,l}\) \(n_{K,L}\) \(n_{K,+}\)
Total \(n_{+,1}\) \(\cdots\) \(n_{+,l}\) \(\cdots\) \(n_{+,L}\) \(n\)
  • \(n_{k,l}=\sum_{i=1}^n1_{[x_i=a_k]\times 1_{[y_i=b_l]}}\): effectif du couple \((a_k, b_l)\);
  • \(n_{k,+}=\sum_{i=1}^Ln_{k,l}\): effectif marginal de la modalité \(a_k\) de \(X\);
  • \(n_{+,l}=\sum_{k=1}^Kn_{k,l}\): effectif marginal de la modalité \(b_l\) de \(Y\).
  • \(n=\sum_{k=1}^K\sum_{l=1}^Ln_{k,l}=\sum_{k=1}^Kn_{k,+}=\sum_{l=1}^Ln_{+,l}\): effectif total.

3.2.2 Indépendance: Chi-carré d’indépendance - V de Cramèr

Le V de Cramèr, construit à partit du Chi-carré d’indépendance, sert à évaluer l’indépendance entre les deux variables en question. Le Chi-carré est une mesure de la divergence entre les effectifs observés \(n_{k,l}\) et ceux \(\widehat{n}_{k,l}\) attendus sous l’hypothèse d’indépendance.

Proposition 3.3 (Effectifs attendus sous l'indépendance) \[ \widehat{n}_{k,l}=\dfrac{n_{k,+}\times n_{+,l}}{n}. \]

Definition 3.8 (Chi-carré) Le Chi-carré d’indépendance est donné par: \[ \mathbb{X}^2=\sum_{k=1}^K\sum_{l=1}^L\dfrac{\left(n_{k,l}-\widehat{n}_{k,l}\right)^2}{\widehat{n}_{k,l}}. \]

Definition 3.9 (V e Cramèr) Le V de Cramèr est donné par: \[ V=\sqrt{\dfrac{\mathbb{X}^2}{n\times\min\left\{K-1, L-1\right\}}}\in[0, 1] \]

Interprétation:

  • Les deux variables sont d’autant indépendantes que V est proche de \(0\)
  • Elles sont d’autant liées que V est proche de \(1\).

Dans la pratique:

  • \(0\leq V\leq 0.2\): Indépendance
  • \(2<V\leq 0.6\): Liaison modérée
  • \(V>0.6\): Liaison forte.

Example 3.2 (V de Cramèr) Voici un tableau de contingence croisant les modalités de deux variables \(X\) et \(Y\).

\(X|Y\) \(b_1\) \(b_2\) \(b_3\) Total
\(a_1\) 10 15 25 50
\(a_2\) 20 10 20 50
\(a_3\) 30 25 45 100
Total 60 50 90 200
  • Calculer et interpréter le V de Cramèr.

3.3 Analyse d’une Variable Quantitative et d’une Variable Qualitative

Dans cette section, nous supposons que \(Y\) est quantitative et \(X\) qualitative. Notons \(X\left(\Omega\right)=\left\{a_1,\cdots,a_k,\cdots,a_K\right\}\) l’ensemble des modalités de \(X\).

Note:

  • La variable \(X\) partitionne le \(n\)-échantillon en \(K\) groupes, chacun associé à une modalité;
  • Notons \(k\) le groupe associé à \(a_k\), et \(n_k\) son effectif;
  • Notons \(y_{i,k}\) l’observation de la variable \(Y\) sur l’individu \(i\) du groupe \(k\);
  • Effectif total: \(n=\sum_{k=1}^Kn_k\).

3.3.1 Résumé de chaque groupe \(k\)

  • Moyenne: \(\bar{y}_{\cdot,k}=\dfrac{1}{n_k}\sum_{i=1}^{n_k}y_{i,k}\)
  • Variance: \(S_{Y,k}^2=\dfrac{1}{n_k}\sum_{i=1}^{n_k}\left(y_{i,k}-\bar{y}_{\cdot,k}\right)^2\)

Remarque:

  • Moyenne globale: \(\bar{y}=\dfrac{1}{n}\sum_{k=1}^Kn_k\bar{y}_{Y,k}\)

3.3.2 Sommes des carrés

  • Sommes des carrés intra-groupe: \(WSS=\sum_{k=1}^KS_{Y,k}^2\)
  • Sommes des carrés inter-groupe: \(BSS=\sum_{k=1}^Kn_k\left(\bar{y}_{\cdot, k}-\bar{y}\right)^2\)
  • Sommes des carrés totale: \(TSS=\sum_{k=1}^K\sum_{i=1}^{n_k}\left(y_{i,k}-\bar{y}\right)^2\).

Proposition 3.4 \[ TSS=WSS+BSS. \]

Proof. Montrer la proposition précédente en exercice.

Notes

  • \(WSS\) et \(BSS\) varient en sens inverses;

  • L’effet de la variable \(X\) sur la variable \(Y\) est d’autant grand que \(\dfrac{WSS}{TSS}\) est proche de \(0\), ou de façon équivalent \(\dfrac{BSS}{TSS}\) est proche de \(1\).

3.3.3 Diagrammes en bâtons et boîtes à moustaches pour les sous-groupes

Example 3.3 Considérer les données mpg de R.

mpg %>% 
  ggplot() +
  geom_boxplot(aes(x=factor(cyl), y=cty))

3.4 Conclusion

Synthèse des méthodes d’analyse bivariée à venir.

3.5 Exercices

3.5.1 Exercice

  1. Quel coefficient mesure la force et la direction de la relation linéaire entre deux variables quantitatives ?
    • A. Coefficient de détermination \(R^2\)
    • B. Variance
    • C. Coefficient de corrélation de Pearson
  2. Quelle méthode est utilisée pour estimer les paramètres d’une droite de régression ?
    • A. La méthode des moindres carrés
    • B. La méthode de maximisation de la vraisemblance
    • C. La méthode de distribution normale
  3. Qu’indique un coefficient de corrélation de Pearson de -1 ?
    • A. Aucune corrélation
    • B. Corrélation positive parfaite
    • C. Corrélation négative parfaite
  4. Lequel des éléments suivants n’est pas une condition requise pour la régression linéaire simple ?
    • A. Homoscédasticité
    • B. Indépendance des résidus
    • C. Distribution multinomiale des variables
  5. Que représente l’erreur standard de la pente dans une régression linéaire simple ?
    • A. La variance de la pente
    • B. L’écart-type des estimations de la pente
    • C. La moyenne des résidus
  6. Quelle est la principale utilité du coefficient de détermination \(R^2\) dans une régression linéaire ?
    • A. Mesurer l’erreur absolue
    • B. Indiquer la proportion de la variance expliquée par le modèle
    • C. Calculer la pente de la droite de régression
  7. Dans quel cas utiliseriez-vous une analyse de régression linéaire ?
    • A. Pour classer les données en différentes catégories
    • B. Pour prédire la valeur d’une variable quantitative à partir d’une autre
    • C. Pour trouver le mode d’un ensemble de données
  8. Qu’est-ce qu’un résidu dans le contexte de la régression linéaire ?
    • A. La différence entre la valeur observée et la valeur prédite
    • B. La pente de la droite de régression
    • C. Le coefficient de corrélation de Pearson
  9. Quel graphique est le plus utilisé pour visualiser la relation entre deux variables quantitatives ?
    • A. Histogramme
    • B. Diagramme en barres
    • C. Diagramme de dispersion
  10. Qu’indique une pente positive dans l’équation de régression linéaire \(Y = a + bX\) ?
    • A. Que \(Y\) diminue lorsque \(X\) augmente
    • B. Que \(Y\) augmente lorsque \(X\) augmente
    • C. Que \(X\) et \(Y\) sont indépendants

3.5.2 Exercice

  1. Quel tableau résume les effectifs ou les fréquences de combinaison entre les modalités de deux variables qualitatives ?
    • A. Tableau de corrélation
    • B. Tableau de contingence
    • C. Tableau de distribution
  2. Quel coefficient mesure l’association entre deux variables qualitatives ?
    • A. Coefficient de corrélation de Pearson
    • B. Coefficient de détermination \(R^2\)
    • C. Coefficient de Cramér
  3. Quelle méthode est utilisée pour tester l’indépendance de deux variables qualitatives ?
    • A. Analyse de variance (ANOVA)
    • B. Test du chi-carré
    • C. Régression linéaire
  4. Dans un tableau de contingence, que représente la valeur totale en bas à droite du tableau ?
    • A. La somme des carrés
    • B. Le total général des observations
    • C. La moyenne des effectifs
  5. Qu’est-ce qu’une heatmap dans le contexte de l’analyse de deux variables qualitatives ?
    • A. Une carte géographique
    • B. Une représentation graphique de la matrice de corrélation
    • C. Une visualisation des fréquences dans un tableau de contingence
  6. Lequel des suivants n’est pas un avantage du test du chi-carré ?
    • A. Il ne requiert pas que les données suivent une distribution normale
    • B. Il peut être utilisé pour des échantillons de petite taille
    • C. Il fournit une mesure directe de la force de l’association
  7. Quelle affirmation est vraie concernant le coefficient de Cramér ?
    • A. Il varie entre -1 et 1
    • B. Il varie entre 0 et 1
    • C. Il peut prendre n’importe quelle valeur réelle
  8. Quand utilise-t-on une analyse des correspondances ?
    • A. Pour comparer les moyennes de deux groupes
    • B. Pour visualiser la relation entre deux variables qualitatives
    • C. Pour calculer la variance expliquée par une régression
  9. Quelle est la principale limitation du tableau de contingence ?
    • A. Il ne peut être utilisé que pour des variables quantitatives
    • B. Il peut devenir difficile à interpréter avec un grand nombre de modalités
    • C. Il nécessite des données continues
  10. Quel est le principal objectif de l’utilisation de heatmaps dans l’analyse de données qualitatives ?
    • A. Prédire les valeurs d’une variable
    • B. Classifier automatiquement les données
    • C. Visualiser les patterns de fréquences ou d’associations

3.5.3 Exercice

  1. Quelle technique est souvent utilisée pour comparer les moyennes d’une variable quantitative entre les différents groupes d’une variable qualitative ?
    • A. Régression linéaire
    • B. Analyse de variance (ANOVA)
    • C. Coefficient de corrélation de Pearson
  2. Quel type de graphique est idéal pour visualiser la distribution d’une variable quantitative au sein des catégories d’une variable qualitative ?
    • A. Histogramme
    • B. Diagramme en barres
    • C. Boîte à moustaches
  3. Quelle mesure permet d’évaluer l’effet de la taille de l’effet dans une analyse de variance (ANOVA) ?
    • A. Le \(p\)-value
    • B. Le coefficient de détermination \(R^2\)
    • C. L’eta carré (\(\eta^2\))
  4. Dans l’analyse de variance, que signifie rejeter l’hypothèse nulle ?
    • A. Il n’y a pas de différence significative entre les groupes
    • B. Au moins un groupe diffère significativement des autres
    • C. Tous les groupes sont identiques
  5. Quel est l’avantage principal de l’utilisation des boîtes à moustaches pour analyser les données d’une variable quantitative selon les catégories d’une variable qualitative ?
    • A. Elles permettent de calculer la moyenne de chaque groupe
    • B. Elles fournissent un résumé visuel de la distribution, incluant les médianes, quartiles, et valeurs aberrantes
    • C. Elles montrent la corrélation entre les variables
  6. Quelle affirmation est correcte concernant l’interaction entre une variable quantitative et une variable qualitative dans une analyse bivariée ?
    • A. L’interaction n’est pas importante et peut être ignorée
    • B. L’interaction indique la corrélation entre les deux variables
    • C. L’interaction peut révéler comment la relation entre la variable quantitative et la réponse varie selon les catégories de la variable qualitative
  7. Qu’est-ce qu’une analyse de covariance (ANCOVA) ?
    • A. Une technique pour analyser une variable catégorielle unique
    • B. Une extension de l’ANOVA qui inclut une ou plusieurs variables quantitatives comme covariables
    • C. Une méthode pour calculer la variance totale
  8. Quelle hypothèse n’est pas nécessaire pour réaliser une analyse de variance (ANOVA) correctement ?
    • A. Normalité des résidus
    • B. Homogénéité des variances
    • C. Les variables qualitatives doivent être indépendantes
  9. Comment appelle-t-on la technique permettant de visualiser la moyenne d’une variable quantitative pour différentes catégories d’une variable qualitative ?
    • A. Diagramme de dispersion
    • B. Diagramme de corrélation
    • C. Diagramme à barres d’erreur
  10. Quelle est la conclusion appropriée si l’analyse de variance (ANOVA) montre un résultat significatif ?
    • A. Il n’y a aucune différence entre les moyennes des groupes
    • B. Les moyennes de tous les groupes sont égales
    • C. Il existe une différence significative entre les moyennes de au moins deux groupes

3.5.4 Exercice

La consommation de crèmes glacées par individus a été mesurée pendant 30 périodes. L’objectif est déterminé si la consommation dépend de la température. Les données sont dans le tableau 3.15. On sait en outre que

\[ \sum_{i=1}^{n} y_i = 10783, \quad \sum_{i=1}^{n} x_i = 1473, \]

\[ \sum_{i=1}^{n} y_i^2 = 4001293, \quad \sum_{i=1}^{n} x_i^2 = 80145, \]

\[ \sum_{i=1}^{n} x_i y_i = 553747, \]

  1. Donnez les moyennes marginales, les variances marginales et la covariance entre les deux variables.
  2. Donnez la droite de régression, avec comme variable dépendante la consommation de glaces et comme variable explicative la température.
  3. Donnez la valeur ajustée et le résidu pour la première observation du tableau 3.15.

3.5.5 Exercice

Neuf étudiants émettent un avis pédagogique vis-à-vis d’un professeur selon une échelle d’appréciation de 1 à 20. On relève par ailleurs la note obtenue par ces étudiants l’année précédente auprès du professeur.

Étudiants
y = Avis 5 7 16 6 12 14 10 9 8
x = Résultat 8 11 10 13 9 17 7 15 16
  1. Représentez graphiquement les deux variables.
  2. Déterminez le coefficient de corrélation entre les variables X et Y. Ensuite, donnez une interprétation de ce coefficient.
  3. Déterminez la droite de régression Y en fonction de X.
  4. Établissez, sur base du modèle, l’avis pour un étudiant ayant obtenu 12/20.
  5. Calculez la variance résiduelle et le coefficient de détermination.

3.5.6 Exercice

Considérons un échantillon de 10 fonctionnaires (ayant entre 40 et 50 ans) d’un ministère. Soit X le nombre d’années de service et Y le nombre de jours d’absence pour raison de maladie (au cours de l’année précédente) déterminé pour chaque personne appartenant à cet échantillon.

xi 2 14 16 8 13 20 24 7 5 11
yi 3 13 17 12 10 8 20 7 2 8
  1. Représentez le nuage de points.
  2. Calculez le coefficient de corrélation entre X et Y.
  3. Déterminez l’équation de la droite de régression de Y en fonction de X.
  4. Déterminez la qualité de cet ajustement.
  5. Établissez, sur base de ce modèle, le nombre de jours d’absence pour un fonctionnaire ayant 22 ans de service.