Chapter 2 Statistique descriptive univariée
Introduction
2.1 Séries qualitatives
Une série statistique \(x_{1:n}\) est dite qualitative ou catégorielle lorsque la variable soujacente \(X\) est qualitative (nominale ou ordinale). Ses données sont des caractéristiques qui ne peuvent être quantitifées.
Definition 2.2 (Modalité) On appelle modalité toute valeur possible d’une variable.
Definition 2.3 (Série qualitative nominale) Une série statistique qualitative est dite nominale lorsqu’il n’y a pas d’ordre sur ses modalités.
Definition 2.4 (Série qualitative ordinale) Une série statistique qualitative est dite ordinale lorsqu’il y a un ordre sur ses modalités.
2.1.1 Tableau statistique - Mode
Soit \(\left\{m_1,\cdots,m_k,\cdots,m_K\right\}\) l’ensemble des modalités de la série qualitative \(x_{1:n}\);
Soit \(n_k=\sum_{i=1}^n1_{[x_i=m_k]}\), l’effectif de la modalité \(m_k\);
On a: \(n=\sum_{k=1}^Kn_k\)
Fréquence de la modalité \(m_k\): \(f_k=\dfrac{n_k}{n}\);
Definition 2.5 (Mode) Le Mode est toute modalité au plus grand effectif (ou à la plus grande fréquence).
Tableau statistique
| Modalités | \(m_1\) | \(\cdots\) | \(m_k\) | \(\cdots\) | \(m_K\) | Total |
|---|---|---|---|---|---|---|
| Effectifs | \(n_1\) | \(\cdots\) | \(n_k\) | \(\cdots\) | \(n_K\) | \(n\) |
| Fréquences | \(f_1\) | \(\cdots\) | \(f_k\) | \(\cdots\) | \(f_K\) | \(1\) |
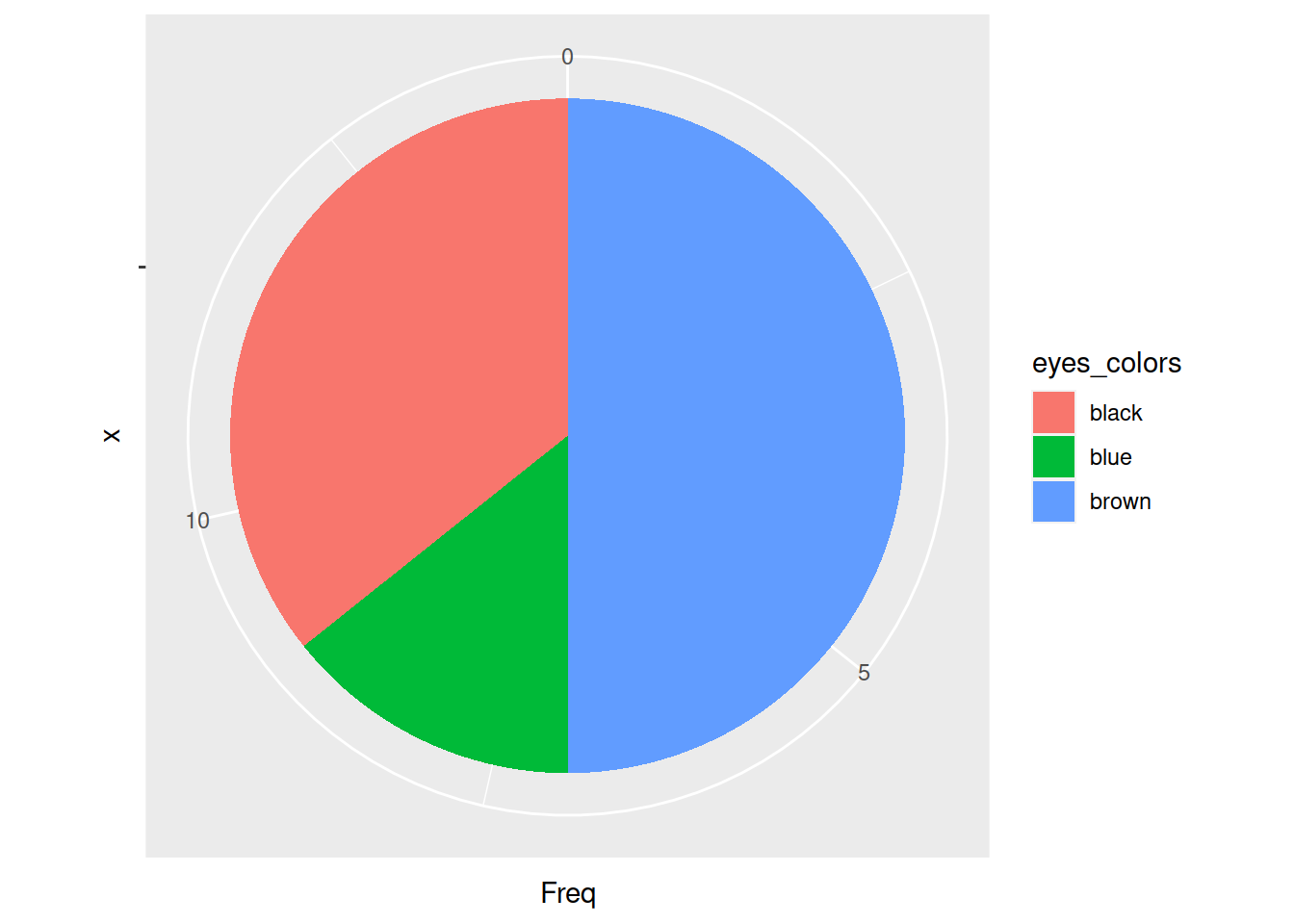
Example 2.1 (Couleur des yeux)
eyes_colors = sample(c(rep("black", 5), rep("blue", 2), rep("brown", 7)), replace = FALSE)
cat(eyes_colors, "\n")## brown brown black blue brown black black brown blue brown black brown black brown## eyes_colors
## black blue brown
## 5 2 7Cas d’une série qualitative ordinale
- Effectifs cumulés: $N_k=\sum_{h=1}^kn_h$
- Fréquences cumulées: $F_k=\sum_{h=1}^kf_h$| Modalités | \(m_1\) | \(\cdots\) | \(m_k\) | \(\cdots\) | \(m_K\) | Total |
|---|---|---|---|---|---|---|
| Effectifs | \(n_1\) | \(\cdots\) | \(n_k\) | \(\cdots\) | \(n_K\) | \(n\) |
| Eff. cum. | \(N_1=n_1\) | \(\cdots\) | \(N_k=\sum_{h=1}^kn_h\) | \(\cdots\) | \(n\) | - |
| Fréquences | \(f_1\) | \(\cdots\) | \(f_k\) | \(\cdots\) | \(f_K\) | \(1\) |
| Fréq. Cum. | \(F_1=f_1\) | \(\cdots\) | \(F_k=\sum_{h=1}^kf_h\) | \(\cdots\) | \(1\) | - |
2.1.2 Graphiques
2.1.2.1 Diagrammes à barres
- Chaque modalité \(m_k\) est représentée par une barre verticale dont la hauteur \(h_k\) est proportionnelle à son effectif (ou de façon equivalente à sa fréquence):
\[ h_k=c^{te}\times f_k \]
Pour \(c^{te}=1\), on a \(h_k=f_k\);
Pour \(c^{te}=n\), on a \(h_k=n\times f_k=n_k\).
2.1.2.2 Diagrammes en secteurs (ou circulaire, ou en camenberts)
- Chaque modalité \(m_k\) est représentée par un angle dont la mesure est proportionnelle à son effectif (ou fréquence):
\[ \alpha_k = 360\times f_k. \]
Example 2.2 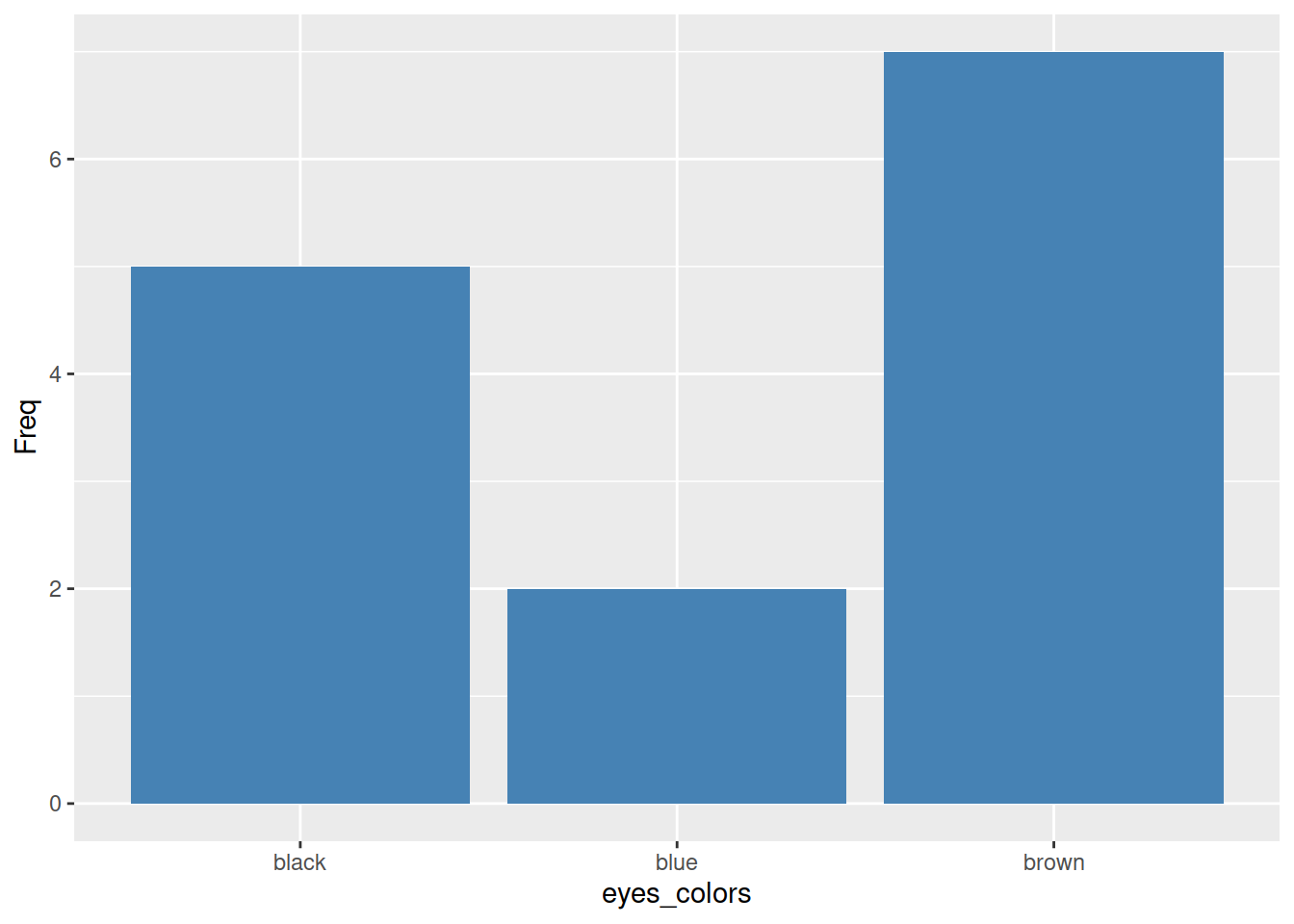
Example 2.3 (Niveaux de satisfaction)
## peu satisfait pas satisfait modérément satisfait modérément satisfait très satisfait modérément satisfait peu satisfait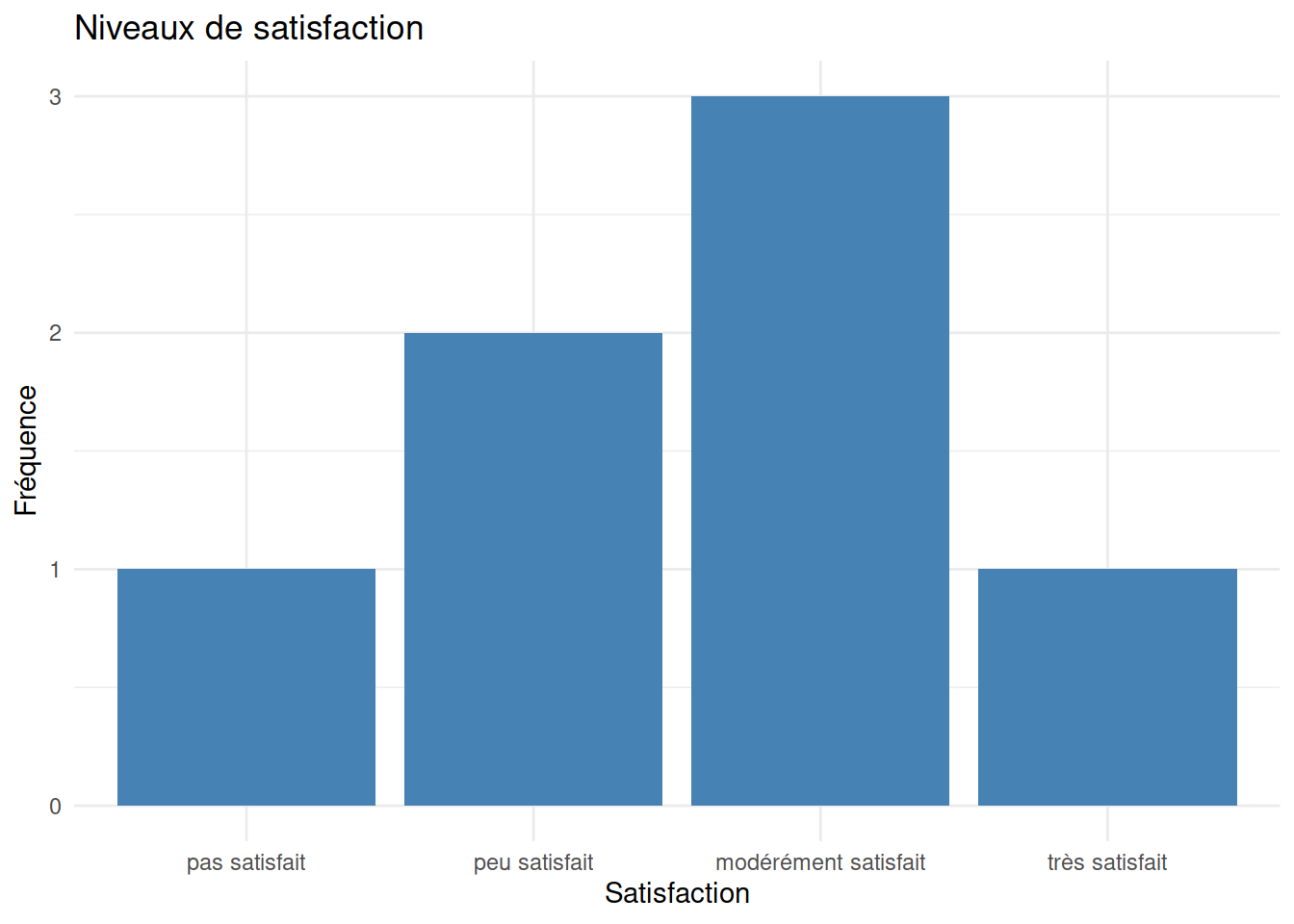
2.2 Séries quantitatives
On considère une série quantitative \(x_{1:n}=\left(x_1,\cdots,x_i,\cdots,x_n\right)\in\mathbb{R}^n\).
Definition 2.6 La série est dite:
Discrète lorsqu’elle ne peut prendre que les valeurs isolées dans \(\mathbb{R}\);
Continue lorsqu’elle peut prendre toute valeur d’un intervalle ouvert non vide de \(\mathbb{R}\).
2.2.1 Paramètres
2.2.1.1 Paramètres de tendance centrale (ou de position)
Definition 2.7 (Mode) On appelle mode toute modalité au plus grand effectif.
Definition 2.8 (Moyenne arithmétique) \[ \bar{x} = \dfrac{1}{n} \sum_{i=1}^{n} x_i \]
Definition 2.9 (Moyenne pondérée) Des fois, chaque données \(x_i\) est accompagnée d’un poids \(\omega_i>0\) vérifiant \(\sum_{i=1}^n\omega_i=1\). La moyenne des données pondérées \(\left(x_i, \omega_i\right)\) est: \[ \bar{x} = \sum_{i=1}^{n} \omega_ix_i \]
Remarques: La moyenne arithméique correspond à la moyenne pondérée avec les poids \(\omega_i=\dfrac{1}{n}\).
Definition 2.10 (Moyenne géométrique) \[ g = \left( \prod_{i=1}^{n} x_i \right)^{\frac{1}{n}} \]
Remarque: Si tous les \(x_i>0\), \[ \ln g = \dfrac{1}{n}\sum_{i=1}^n\ln x_i \]
Definition 2.11 (Moyenne harmonique) La moyenne harmonique est l’inverse de la moyenne des inverses: \[ h = \frac{n}{\sum_{i=1}^{n} \dfrac{1}{x_i}}=\dfrac{1}{\dfrac{1}{n}\sum_{i=1}^n\dfrac{1}{x_i}} \]
Definition 2.12 (Médiane) On appelle médiane toute valeur \(q_{0.5}\) telle que:
\(\dfrac{1}{n}\sum_{i=1}^n1_{[x_i\leq q_{0.5}]}\geq 0.5\) et
\(\dfrac{1}{n}\sum_{i=1}^n1_{[x_i\geq q_{0.5}]}\geq 0.5\).
Dans la pratique
Ranger les données dans l’ordre croissant \(\min\left\{x_1,\cdots,x_n\right\}=x_{(1)}\leq x_{(2)}\leq \cdots, x_{(i)}\leq\cdots,x_{(n)}=\max\left\{x_1,\cdots,x_n\right\}\)
Si \(n\) est impair, prendre \(q_{0.5}=x_{\left(\dfrac{n+1}{2}\right)}\)
Si \(n\) est pair, prendre \(q_{0.5}=\dfrac{1}{2}\left(x_{\left(\dfrac{n}{2}\right)}+x_{\left(\dfrac{n}{2}+1\right)}\right)\)
Definition 2.13 (Quantiles) Soit \(\alpha\in[0, 1]\).
On appelle quantile d’ordre \(\alpha\) de la série \(x_{1:n}\) tout réel \(q_{\alpha}\) vérifiant:
\(\dfrac{1}{n}\sum_{i=1}^n1_{[x_i\leq q_{\alpha}]}\geq \alpha\) et
\(\dfrac{1}{n}\sum_{i=1}^n1_{[x_i\geq q_{\alpha}]}\geq 1-\alpha\).
Remarques:
- La médiane est le quantile d’ordre \(0.5\).
Definition 2.14 (Les quartiles) Les quartiles sont \(q_{\frac{1}{4}}\), \(q_{\frac{1}{2}}\) et \(q_{\frac{3}{4}}\).
2.2.1.2 Paramètres de dispersion
Ces paramètres fournissent une compréhension approfondie de la dispersion des données d’une série quantitative, chacun mettant en lumière différents aspects de la variabilité des données.
Definition 2.15 (Étendu) L’étendue mesure la dispersion totale des données en calculant la différence entre la valeur maximale et minimale:
\[E= x_{(n)} - x_{(1)}\]
:::{.definition name=” distance interquartile”} La distance interquartile (IQ) mesure l’étendue de la moitié centrale des données, réduisant l’impact des valeurs extrêmes ou des outliers:
\[IQ = q_{\frac{3}{4}} - q_{\frac{1}{4}}\] :::
Definition 2.16 (Variance) La variance mesure la dispersion des données autour de leur moyenne. Elle est basée sur les carrés des écarts à la moyenne pour éviter que les différences positives et négatives se compensent:
\[S^2_x = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2\]
Proposition 2.1 (Exercice) \[S^2_x = \frac{1}{n} \sum_{i=1}^{n} x^2_i - \bar{x}^2\]
Definition 2.17 (Écart-type) L’écart-type est la racine carrée de la variance, fournissant une mesure de dispersion dans les mêmes unités que les données originales:
\[S_x = \sqrt{S^2_x}\]
Definition 2.18 (Écart moyen absolu) L’écart moyen absolu est la moyenne des valeurs absolues des écarts à la moyenne, offrant une autre mesure de dispersion: \[\text{eMoyAbs} = \frac{1}{n} \sum_{i=1}^{n} |x_i - \bar{x}|\]
Definition 2.19 (Écart médian absolu) L’écart médian absolu se concentre sur la médiane, calculant la moyenne des valeurs absolues des écarts à la médiane: \[\text{eMedAbs} = \frac{1}{n} \sum_{i=1}^{n} |x_i - q_{\frac{1}{2}}|\]
2.2.1.3 Moments
Definition 2.20 (Moments) Le moment d’ordre \(k\) est le réel \[ \mu_k=\dfrac{1}{n}\sum_{i=1}^nx_i^k \]
Definition 2.21 (Moments centrés) Le moment centré d’ordre \(k\): \[ m_k=\dfrac{1}{n}\sum_{i=1}^n\left(x_i-\bar{x}\right)^k \]
Remark.
- \(\bar{x}=\mu_1\)
- \(S_x^2 = m_2\)
2.2.1.4 Paramètres de Forme
Definition 2.22 (Coefficient d'applatissement (Skewness)) Mesure de l’asymétrie de la distribution autour de sa moyenne. \[g_1 = \frac{m_3}{S^3_x}\]
Definition 2.23 (Coefficient d'asymétrie de Yule) C’es une mesure d’asymétrie basée sur les positions des trois quartiles, normalisé par la distance interquartile: \[A_Y = \frac{q_{\frac{3}{4}} + q_{\frac{1}{4}} - 2q_{\frac{1}{2}}}{q_{\frac{3}{4}} - q_{\frac{1}{4}}}\]
Definition 2.24 (Coefficient d'asymétrie de Pearson) C’est une mesure de l’asymétrie basée sur une comparaison de la moyenne et du mode, standardisé par l’écart-type: \[A_P = \frac{\bar{x} - x_M}{S_x}\] où \(\bar{x}\) est la moyenne, \(x_M\) est le mode, et \(s_x\) est l’écart-type.
2.2.1.5 Paramètre d’aplatissement (Kurtosis)
Definition 2.25 (Kurtosis) C’est une mesure du degré d’aplatissement de la distribution par rapport à une distribution normale: \[\beta_2 = \dfrac{m_4}{S^4_x}\] - Formule de Fisher: \[g_2 = \beta_2 - 3 = \dfrac{m_4}{S^4_x} - 3\] où \(m_4\) est le moment centré d’ordre quatre et \(s_x\) est l’écart-type au carré.
2.2.2 Série quantitative regroupée par intervalles (ou classes)
Les données de séries quantitatives continues sont souvent regroupées en intervalles ou classes pour synthétiser l’information et faciliter son analyse. Cette section décrit la méthode de regroupement et sa représentation à travers des tableaux et des histogrammes, en utilisant des exemples concrets et des instructions pour réaliser ces tâches avec R.
2.2.2.1 Principe de Regroupement - Tableau statistique
- La plage des valeurs de la variable en question est partitionnée en un certain nombre \(K\) d’intervalles;
- Définir le nombre \(K\) d’e classes’intervalles;
- Remplacer chaque observation par l’intervalle qui la contient;
- Établir le tableaux des effectifs des données transformées qui sont alors qualitatives ordinales.
| Classes | Amplitudes | Centres | Effectifs | Freq. | Freq. cum |
|---|---|---|---|---|---|
| \(I_1=[b_0,b_1[\) | \(a_1\) | \(c_1\) | \(n_1\) | \(f_1\) | \(F_1\) |
| \(\cdots\) | \(\cdots\) | \(\cdots\) | \(\cdots\) | \(\cdots\) | \(\cdots\) |
| \(I_k=[b_{k-1},b_k[\) | \(a_k\) | \(c_k\) | \(n_k\) | \(f_k\) | \(F_k\) |
| \(\cdots\) | \(\cdots\) | \(\cdots\) | \(\cdots\) | \(\cdots\) | \(\cdots\) |
| \(I_K=[b_{k-1},b_K]\) | \(c_K\) | \(c_K\) | \(n_K\) | \(f_K\) | \(F_K\) |
avec:
- \(n_k=\sum_{i=1}^n1_{I_k}(x_i)\)
- \(f_k=\dfrac{n_k}{n}\)
- \(F_k=\sum_{h=1}^kf_h\)
- Centre de l’intervalle \(k\): \(c_k=\dfrac{b_{k-1}+b_k}{2}\)
- Amplitude: \(a_k=b_k-b_{k-1}\)
2.2.3 Représentation Graphique : L’Histogramme
L’histogramme est un outil graphique qui représente la distribution des données regroupées en classes. Chaque classe est représentée par un rectangle, dont la base est l’intervalle de classe et la surface est proportionnelle à l’effectif (ou la fréquence) de la classe.
- Histogramme de fréquence: La surface d’une classe est proportionnelle à sa fréquence
\[ \dfrac{a_k\times h_k}{f_k}=1\rightarrow h_k=\dfrac{f_k}{a_k} \]
- Histogramme des effectifs: La surface d’une classe est proportionnelle à son effectif
\[ \dfrac{a_k\times h_k}{n_k}=1\rightarrow h_k=\dfrac{n_k}{a_k} \]
Example 2.4 (Scores à un examen) On considère les scores obtenus par un groupe d’étudiants lors d’un examen:
require(ggplot2)
scores_exam <- c(55, 70, 68, 82, 90, 74, 61, 77, 85, 93, 69, 70, 75, 88, 92, 56, 65, 74, 58, 80)
ggplot(mapping = aes(x=scores_exam, )) +
geom_histogram(color = "coral", fill = "steelblue", breaks = c(50, 60, 70, 85, 100), closed = "left", )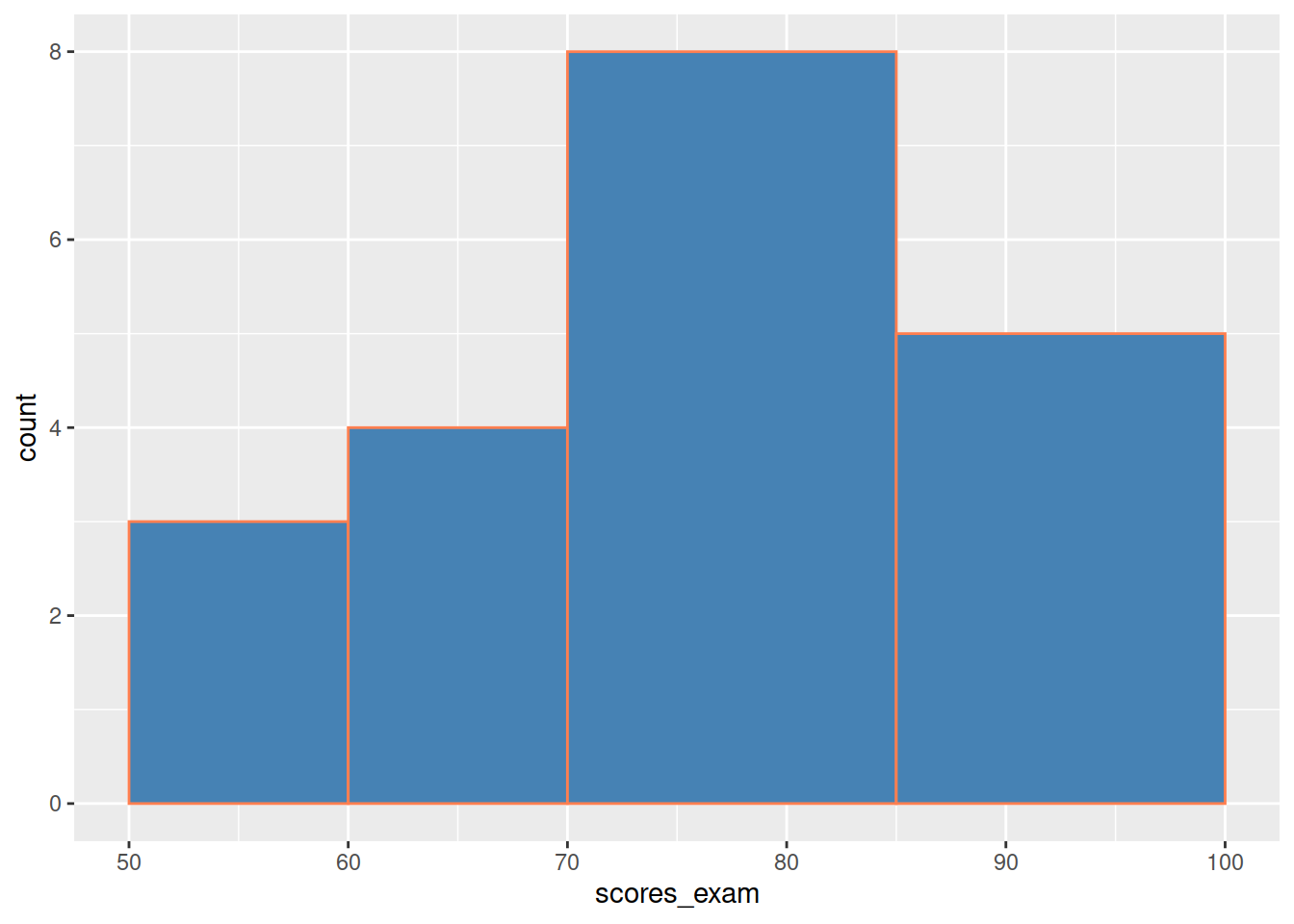
2.2.4 Fonction de répartition
2.2.4.1 Cas d’un échantillon \(x_{1:n}\)
Definition 2.26 (Fonction de répartition) La fonction de répartition, notée \(F_{x_{1:n}}\), est un outil essentiel en statistique descriptive pour analyser la distribution d’un échantillon \(x_1, \ldots, x_n\). Elle indique pour tout réel \(x\), la proportion d’observations de l’échantillon qui sont inférieures ou égales à \(x\). Cette fonction est définie pour tout réel \(x\) par :
\[ F_{x_{1:n}}(x) = \frac{\text{Nombre d'observations} \leq x}{n} = \dfrac{1}{n}\sum_{i=1}^n1_{[x_i\leq x]}. \]
Proposition 2.2 (Fonction de répartition)
- Criossante : Si \(x \leq y\), alors \(F_{x_{1:n}}(x) \leq F_{x_{1:n}}(y)\).
- Limites : \(\lim_{x \to -\infty} F_{x_{1:n}}(x) = 0\) et \(\lim_{x \to +\infty} F_{x_{1:n}}(x) = 1\).
- Droite continue : La \(F_{x_{1:n}}\) est continue à droite pour tout point \(x\).
Example 2.5 (Fonction de répartition) Considérons un échantillon de valeurs \(x_1, \ldots, x_n\) et calculons sa fonction de répartition. Voici comment cette fonction peut être estimée et représentée en R pour un échantillon hypothétique :
# Échantillon hypothétique
x <- c(2, 3, 5, 6, 7, 8, 9, 10, 11, 12)
# Calcul de la fonction de répartition
Fx <- ecdf(x)
# Représentation graphique de la fonction de répartition
plot(Fx, xlab="x", ylab="F(x)")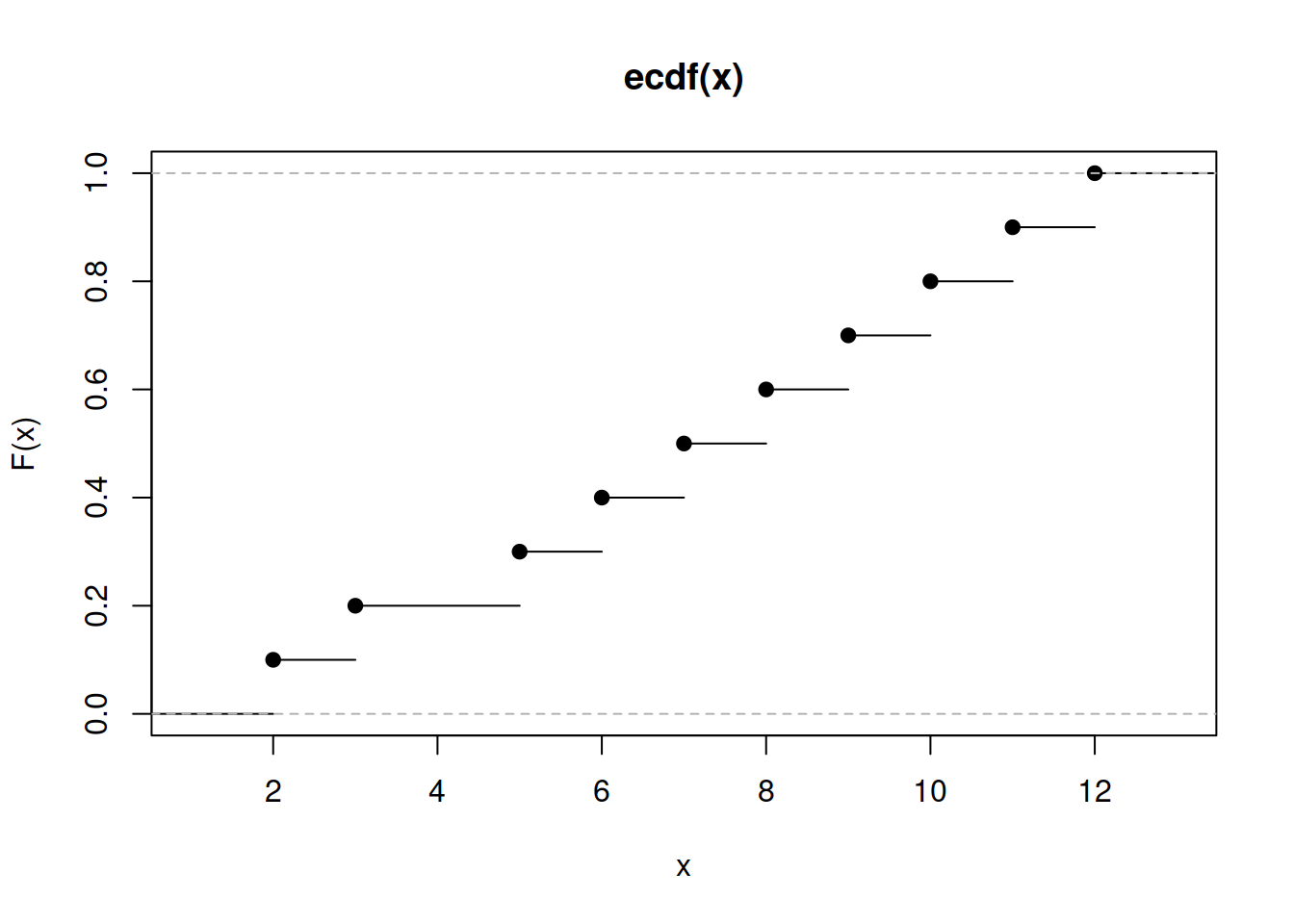
2.2.4.2 Cas de données regroupées par intervalles
Considérons le regroupement en intervalles selon les bornes \(b_0<b_1<\cdots<b_K\), que nous notons \(b_{0:K}\). Pour \(\left(b_{k-1}; b_k\right)\) l’intervalle, notons:
\(n_k\), son effectif;
\(f_k=\dfrac{n_k}{n}\), sa fréquence;
\(F_k = \sum_{h=1}^kf_h\), sa fréquence cumulée, avec \(F_0=0\).
Definition 2.27 (Fdr de données regroupées) Alors la fonction de répartition vérifie:
- \(F_{b_{0:K}}(x)=0\) si \(x\leq b_0\);
- \(F_{b_{0:K}}(x)=1\) si \(x\geq b_K\);
- Pour tout \(x\in\left(b_{k-1}; b_k\right)\), le point \(\left(x, F_{b_{0:K}}(x)\right)\) appartient à la droite passant par \(\left(b_{k-1}, F_{k-1}\right)\) et \(\left(b_k, F_k\right)\).
Example 2.6 Définir et tracer la fonction de répartition associée aux données sur les scores à un examen données dans un exemple précédent.
2.2.5 Autres graphiques
2.2.5.1 Diagramme en bâtons
Le diagramme en bâtons est un outil graphique couramment utilisé pour représenter des données statistiques discrètes (quantitatves discrètes ou catégorielles). Chaque bâton dans le diagramme représente une modalité, avec la hauteur du bâton proportionnelle à l’effectif ou à la fréquence de la modalité représentée.
Caractéristiques Principales
- Simplicité : Facile à lire et à interpréter, idéal pour comparer des fréquences ou des effectifs entre différentes catégories.
- Adaptabilité : Peut être utilisé pour des données qualitatives ou quantitatives discrètes.
- Clarté Visuelle : Permet une visualisation immédiate des tendances et des disparités entre les catégories.
Example 2.7 Prenons un exemple où nous avons le nombre d’enfants par famille dans une petite enquête :
- Nombre d’Enfants : 0, 1, 2, 3, 4, 5, 6
- Effectifs : 18, 32, 66, 41, 32, 9, 2
Pour représenter ces données sous forme de diagramme en bâtons en R, on peut utiliser le code suivant:
# Données
nombre_enfants <- c(0, 1, 2, 3, 4, 5, 6)
effectifs <- c(18, 32, 66, 41, 32, 9, 2)
# Création du diagramme en bâtons
barplot(effectifs, names.arg = nombre_enfants, col = 'skyblue',
xlab = "Nombre d'Enfants", ylab = "Effectifs",
main = "Nombre d'Enfants par Famille")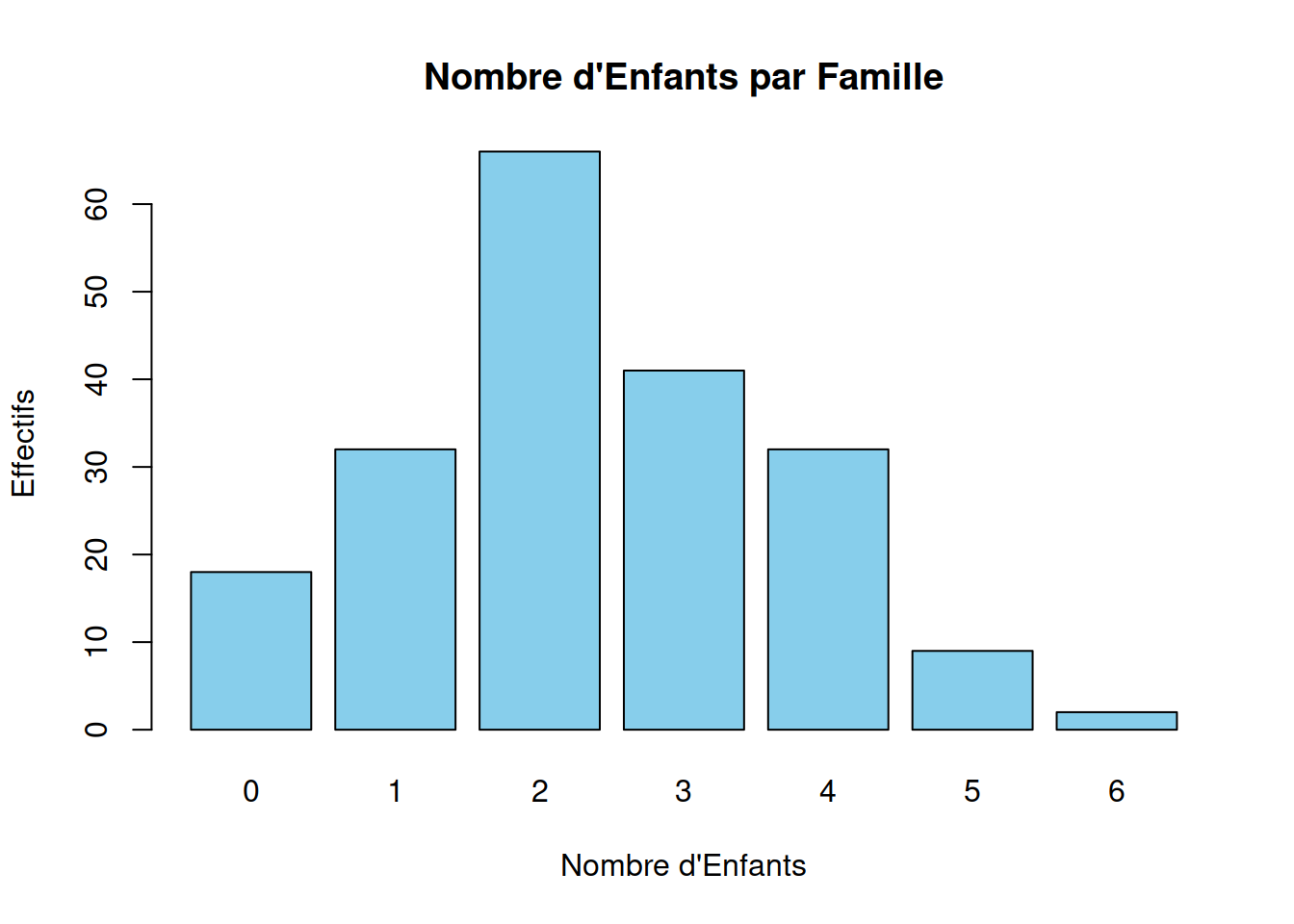
2.2.5.2 Boîte à moustaches (Boxplot)
La boîte à moustaches, également connue sous le nom de diagramme en boîte ou boxplot, est un outil graphique essentiel en statistique descriptive pour résumer la distribution d’une variable quantitative. Ce diagramme fournit une représentation visuelle compacte de la dispersion des données, de leur tendance centrale, et des valeurs aberrantes.
Composition
Le diagramme en boîte est constitué des éléments suivants :
- Rectangle (Boîte) : S’étend du premier quartile \(q_{\frac{1}{4}}\) au troisième quartile \(q_{\frac{3}{4}}\), englobant ainsi la moitié médiane des données. La longueur de la boîte représente l’écart interquartile \(IQR = q_{\frac{3}{4}} - q_{\frac{1}{4}}\), qui mesure la dispersion des données.
- Médiane : Une ligne à l’intérieur de la boîte marque la médiane \(q_{\frac{1}{2}}\), divisant ainsi l’ensemble des données en deux parties égales.
- Moustaches : S’étendent de la boîte jusqu’aux valeurs minimales et maximales, à l’intérieur de l’intervalle \(\left[q_{\frac{1}{4}} - 1.5 * IQR, q_{\frac{3}{4}} + 1.5 * IQR\right]\). Ces lignes indiquent la plage des données régulières.
- Valeurs Extrêmes : Les données qui se trouvent en dehors de l’intervalle des moustaches sont considérées comme des valeurs aberrantes et sont souvent marquées par des points.
Calcul des Bornes
Pour dessiner le diagramme, il est nécessaire de calculer les bornes inférieure et supérieure :
- Borne Inférieure \(b_{−}\) : \(q_{\frac{1}{4}} - 1.5 * IQR\)
- Borne Supérieure \(b_{+}\) : \(q_{\frac{3}{4}} + 1.5 * IQR\)
où \(IQR\) est la distance interquartile.
Example 2.8 Supposons que nous disposons d’un ensemble de données représentant les tailles d’un groupe d’individus. Voici comment créer une boîte à moustaches pour ces données en R :
# Données d'exemple
tailles <- c(160, 165, 170, 175, 180, 185, 190, 195, 200, 205, 210, 215)
# Création du boxplot
boxplot(tailles, main="Boîte à Moustaches des Tailles", ylab="Taille (cm)")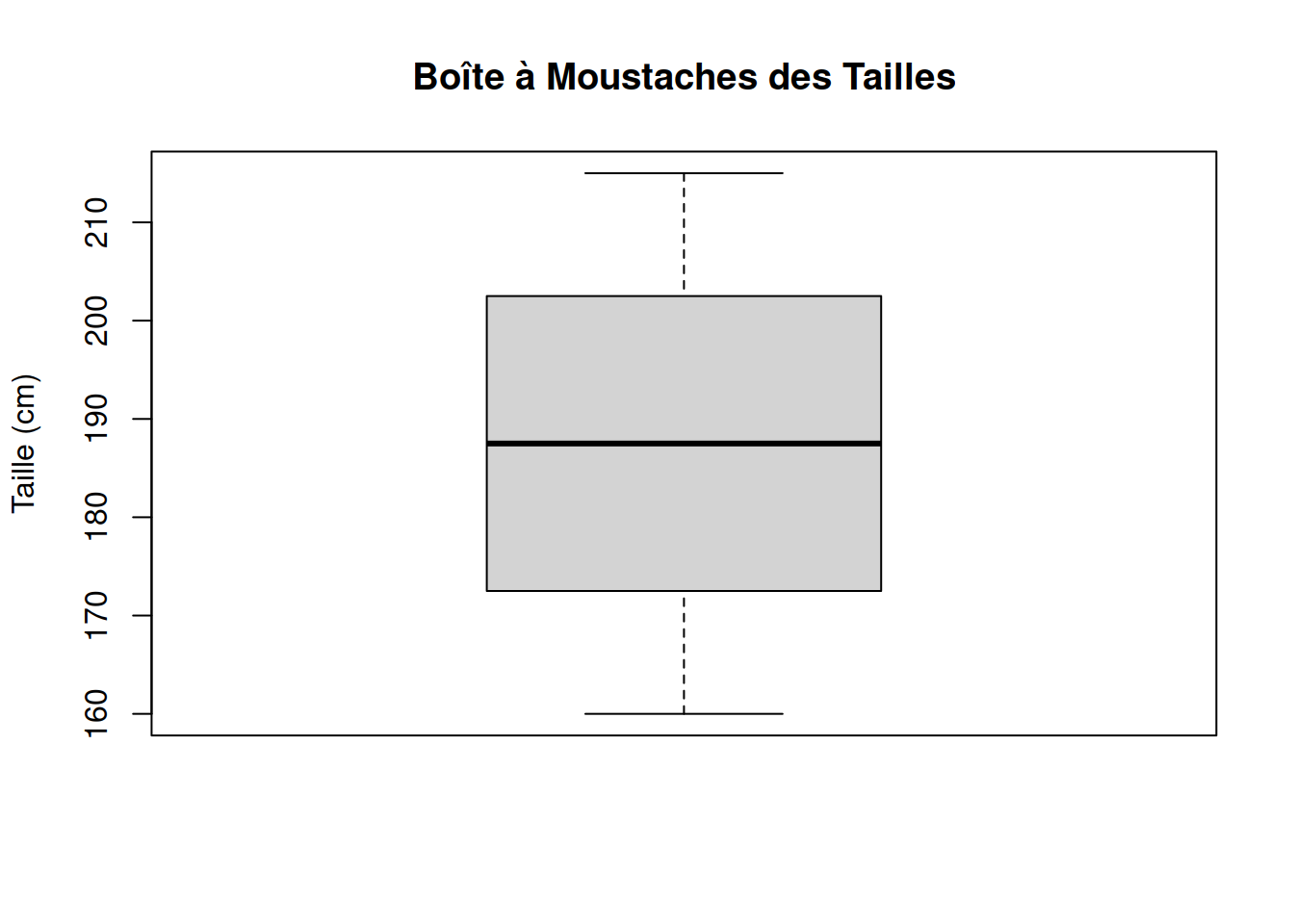
2.3 Exercices
2.3.1 QCM Statistique Descriptive
- Quel paramètre de position représente la valeur la plus fréquente dans un ensemble de données ?
- A) La moyenne
- B) La médiane
- C) Le mode
- D) L’étendue
- Comment calcule-t-on la variance d’une série de données ?
- A) Somme des écarts à la moyenne
- B) Moyenne des carrés des écarts à la moyenne
- C) Racine carrée des écarts à la moyenne
- D) Somme des écarts à la médiane
- Que mesure l’écart-type d’une distribution ?
- A) La dispersion par rapport à la moyenne
- B) La symétrie de la distribution
- C) L’aplatissement de la distribution
- D) La distance entre le premier et le troisième quartile
- Qu’est-ce que l’étendue d’une série de données ?
- A) La différence entre la valeur maximale et minimale
- B) La moyenne des valeurs
- C) Le total des valeurs divisé par leur nombre
- D) La valeur centrale des données
- La médiane d’un ensemble de données est définie comme :
- A) La moyenne des données
- B) La valeur qui sépare la moitié supérieure de la moitié inférieure des données
- C) La valeur la plus fréquente
- D) La somme de toutes les valeurs divisée par leur nombre
- Quel est le but de la normalisation des données ?
- A) Réduire l’asymétrie de la distribution
- B) Augmenter l’aplatissement de la distribution
- C) Rendre les données comparables en les ramenant à une échelle commune
- D) Diminuer la variance des données
- Qu’est-ce que le coefficient d’asymétrie de Fisher mesure ?
- A) L’aplatissement de la distribution
- B) La dispersion des données
- C) La symétrie de la distribution
- D) La moyenne des données
- Lequel des suivants est une mesure de dispersion ?
- A) La moyenne
- B) La médiane
- C) L’écart-type
- D) Le mode
- Quelle est la différence principale entre la variance et l’écart-type ?
- A) L’écart-type est la racine carrée de la variance
- B) La variance est toujours plus grande que l’écart-type
- C) La variance mesure la dispersion, tandis que l’écart-type mesure la centralité
- D) Aucune différence, ils mesurent la même chose
- Quel paramètre mesure le degré d’aplatissement d’une distribution ?
- A) L’étendue
- B) Le coefficient d’asymétrie
- C) Le kurtosis
- D) La variance
- Quelle est la distance interquartile indique ?
- A) La distance entre la valeur la plus haute et la plus basse
- B) La moyenne des données
- C) L’étendue de la moitié centrale des données
- D) La dispersion des données autour de la médiane
- Quel coefficient indique si une distribution est symétrique ?
- A) Le coefficient de variation
- B) Le coefficient d’asymétrie
- C) Le coefficient de corrélation
- D) Le coefficient d’aplatissement
- Pourquoi utilise-t-on le logarithme des données dans l’analyse statistique ?
- A) Pour augmenter l’asymétrie de la distribution
- B) Pour réduire l’impact des valeurs extrêmes
- C) Pour transformer les données en une échelle logarithmique
- D) Pour calculer la moyenne géométrique
- Quel est l’effet d’une distribution leptokurtique sur le kurtosis ?
- A) Le kurtosis est approximativement 0
- B) Le kurtosis est supérieur à 0
- C) Le kurtosis est inférieur à 0
- D) Le kurtosis est exactement 3
- Quelle est l’importance de connaître la distribution des données en statistique ?
- A) Pour choisir les tests statistiques appropriés
- B) Pour déterminer le nombre d’observations nécessaires
- C) Uniquement pour les analyses graphiques
- D) Aucune, les méthodes non paramétriques ne nécessit
- Quelle méthode permet de comparer la dispersion de deux séries de données différentes ?
- A) La moyenne arithmétique
- B) Le coefficient de variation
- C) L’écart-type
- D) La variance
- Qu’est-ce qu’une distribution bimodale ?
- A) Une distribution avec deux moyennes différentes
- B) Une distribution avec deux variances différentes
- C) Une distribution avec deux modes
- D) Une distribution avec un mode unique
- Quel est le but principal de l’analyse des données quantitatives ?
- A) Décrire et résumer les données
- B) Prédire des valeurs futures
- C) Confirmer des hypothèses préétablies
- D) Créer des graphiques complexes
- Comment la médiane est-elle affectée par les valeurs extrêmes ?
- A) La médiane augmente avec les valeurs extrêmes
- B) La médiane diminue avec les valeurs extrêmes
- C) La médiane n’est pas affectée par les valeurs extrêmes
- D) La médiane est toujours égale à la moyenne
- Quelle mesure de tendance centrale est la plus affectée par les valeurs extrêmes ?
- A) La moyenne
- B) La médiane
- C) Le mode
- D) L’étendue
2.3.2 Exercice
Pour chacune des variables suivantes, préciser si elle est qualitative, quantitative discrète ou quantitative continue,
- Revenu annuel.
- Citoyenneté.
- Distance.
- Taille.
2.3.3 Exercice
Vrai ou Faux : 1. Une “variable” est tout caractère étudié. 2. La statistique descriptive recueille les données. 3. Elle résume les données via des tableaux, graphiques et indicateurs. 4. Une variable quantitative mesure une qualité. 5. Elle peut prendre des valeurs dans N. 6. La variance donne une idée de la valeur moyenne étudiée. 7. L’écart-type s’exprime dans l’unité de la variable étudiée. 8. Le mode est la modalité la moins fréquente. 9. La moyenne arithmétique d’une variable qualitative est la modalité la plus fréquente.
2.3.4 Exercice
Pour les sujets d’étude qui suivent, spécifier : l’unité statistique, la variable statistique et son type,
- Étude du temps de validité des lampes électriques.
- Étude de l’absentéisme des ouvriers, en jours, dans une usine.
- Répartition des étudiants d’une promotion selon la mention obtenue sur le diplôme du Bac.
- On cherche à modéliser^1 le nombre de collisions impliquant deux voitures sur un ensemble de 100 intersections routières choisies au hasard dans une ville. Les données sont collectées sur une période d’un an et le nombre d’accidents pour chaque intersection est ainsi mesuré.
2.3.5 Exercice
Quelles formes de présentation de données correspondent ces propriétés ?
- Il donne une bonne idée des données, mais on lui préfère en général les graphiques.
- Il n’est pas nécessaire de lire des nombres. D’un simple coup d’œil, on a une vision d’ensemble des données.
2.3.6 Exercice
On pèse les 50 élèves d’une classe et nous obtenons les résultats résumés dans le tableau suivant :
| 43 | 43 | 43 | 47 | 48 |
| 48 | 48 | 48 | 49 | 49 |
| 49 | 50 | 50 | 51 | 51 |
| 52 | 53 | 53 | 53 | 54 |
| 54 | 56 | 56 | 56 | 57 |
| 59 | 59 | 59 | 62 | 62 |
| 63 | 63 | 65 | 65 | 67 |
| 67 | 68 | 70 | 70 | 70 |
| 72 | 72 | 73 | 77 | 77 |
| 81 | 83 | 86 | 92 | 93 |
- De quel type est la variable poids ?
- Construisez le tableau statistique en adoptant les classes suivantes :
\[40;45\] \[45;50\] \[50;55\] \[55;60\] \[60;65\] \[65;70\] \[70;80\] \[80;100\] - Construisez l’histogramme des effectifs ainsi que la fonction de répartition.
2.3.7 Exercice
Chez un fabricant de tubes de plastiques, on a prélevé un échantillon de 100 tubes dont on a mesuré le diamètre en décimètre.
| 1.94 | 2.20 | 2.33 | 2.39 | 2.45 | 2.50 | 2.54 | 2.61 | 2.66 | 2.85 |
| 1.96 | 2.21 | 2.33 | 2.40 | 2.46 | 2.51 | 2.54 | 2.62 | 2.68 | 2.87 |
| 2.07 | 2.26 | 2.34 | 2.40 | 2.47 | 2.52 | 2.55 | 2.62 | 2.68 | 2.90 |
| 2.09 | 2.26 | 2.34 | 2.40 | 2.47 | 2.52 | 2.55 | 2.62 | 2.68 | 2.91 |
| 2.09 | 2.28 | 2.35 | 2.40 | 2.48 | 2.52 | 2.56 | 2.62 | 2.71 | 2.94 |
| 2.12 | 2.29 | 2.36 | 2.41 | 2.49 | 2.52 | 2.56 | 2.63 | 2.73 | 2.95 |
| 2.13 | 2.30 | 2.37 | 2.42 | 2.49 | 2.53 | 2.57 | 2.63 | 2.75 | 2.99 |
| 2.14 | 2.31 | 2.38 | 2.42 | 2.49 | 2.53 | 2.57 | 2.65 | 2.76 | 2.99 |
| 2.19 | 2.31 | 2.38 | 2.42 | 2.49 | 2.53 | 2.59 | 2.66 | 2.77 | 3.09 |
| 2.19 | 2.31 | 2.38 | 2.42 | 2.50 | 2.54 | 2.59 | 2.66 | 2.78 | 3.12 |
- Identifier la population, les individus, le caractère et son type.
- En utilisant la méthode de Yule puis de Sturge, établir le tableau statistique (Faites débuter la première classe par la valeur 1.94).
- Tracer l’histogramme de cette variable statistique.
- Déterminer par le calcul la valeur du diamètre au-dessous de laquelle se trouvent 50% des tubes de plastique. Que représente cette valeur.
- Déterminer par le calcul le pourcentage de tubes ayant un diamètre inférieur à 2.58.
2.3.8 Exercice
- Identifier la variable statistique et son type.
- Effectif des personnes de groupe sanguin AB.
- Représentations possibles de cette série.
2.3.9 Exercice
- Diagrammes en bâtons des effectifs et cumulés.
- Déterminer mode, moyenne, étendue, variance, écart-type.
2.3.10 Exercice
- Table des fréquences et diagramme en bâtons.
- Calcul de la moyenne et écart-type.
- Médiane, quartiles, box-plot.
- Étude de la symétrie.
2.3.11 Exercice
Le gérant d’un magasin vendant des articles de consommation courante a relevé pour un article particulier qui semble connaître une très forte popularité, le nombre d’articles vendus par jour. Son relevé a porté sur les ventes des mois de Mars et Avril, ce qui correspond à \(52\) jours de vente. Le relevé des observations se présente comme suit :
\[\begin{eqnarray*} & 7 & 13 & 8 & 10 & 9 & 12 & 10 & 8 & 9 & 10 & 6 & 14 & 7 & 15 & 9 & 11 & 12 & 11 & 12 & 5 & 14 & 11 & 8 & 10 & 14 & 12 & 8\\ & 5 & 7 & 13 & 12 & 16 & 11 & 9 & 11 & 11 & 12 & 12 & 15 & 14 & 5 & 14 & 9 & 9 & 14 & 13 & 11 & 10 & 11 & 12 & 9 & 15 \\ \end{eqnarray*}\]
Analyser le nombre d’articles vendus par jour sur \(52\) jours.